Preliminary Results on Tropospheric ZTD Estimation by Smartphone
Abstract
1. Introduction
2. Materials and Methods
2.1. ZTD Estimation from GNSS
2.2. Case Study: Materials, Methods and Processing
2.2.1. Case Study 1
2.2.2. Case Study 2
3. Results
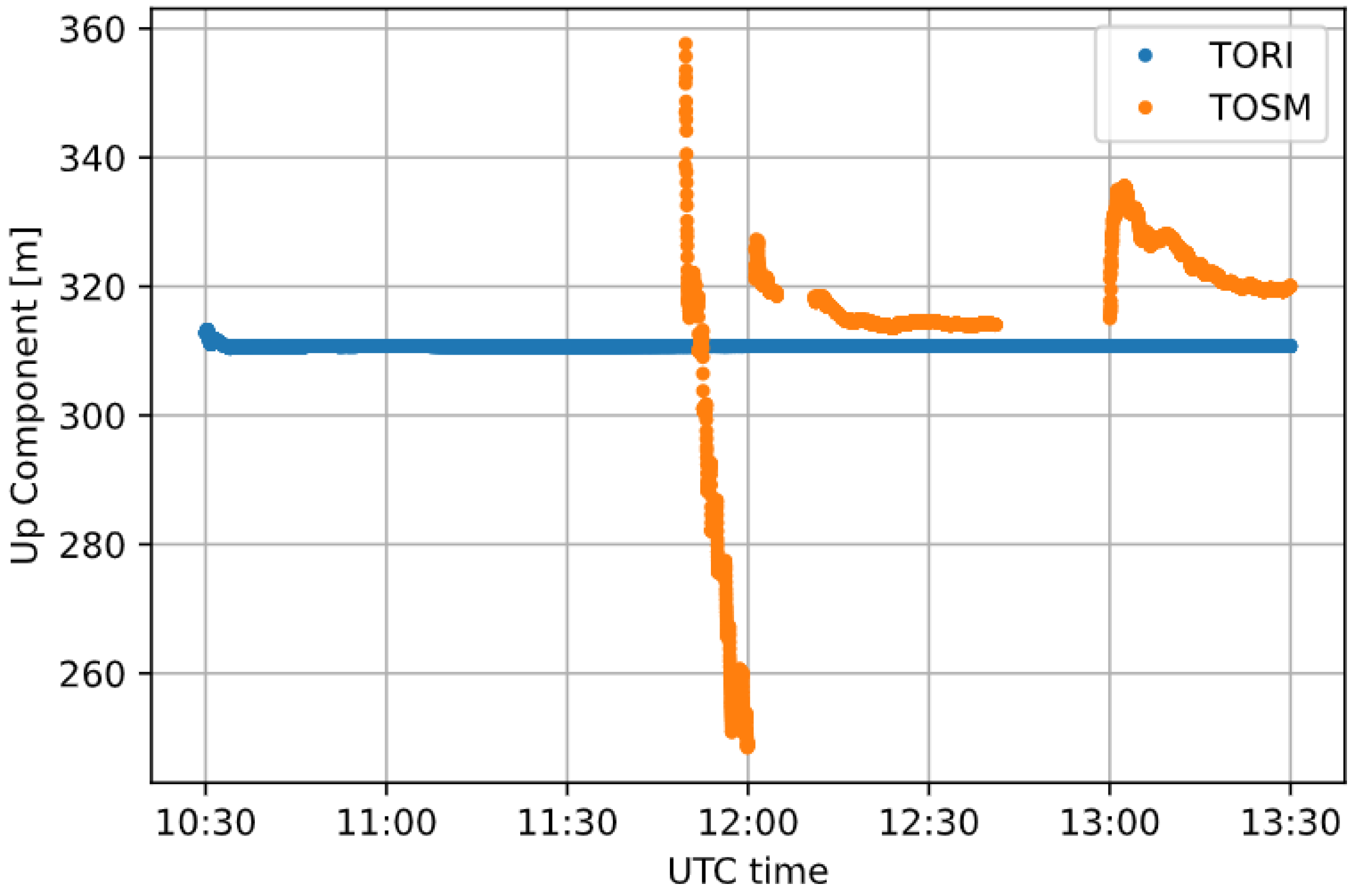
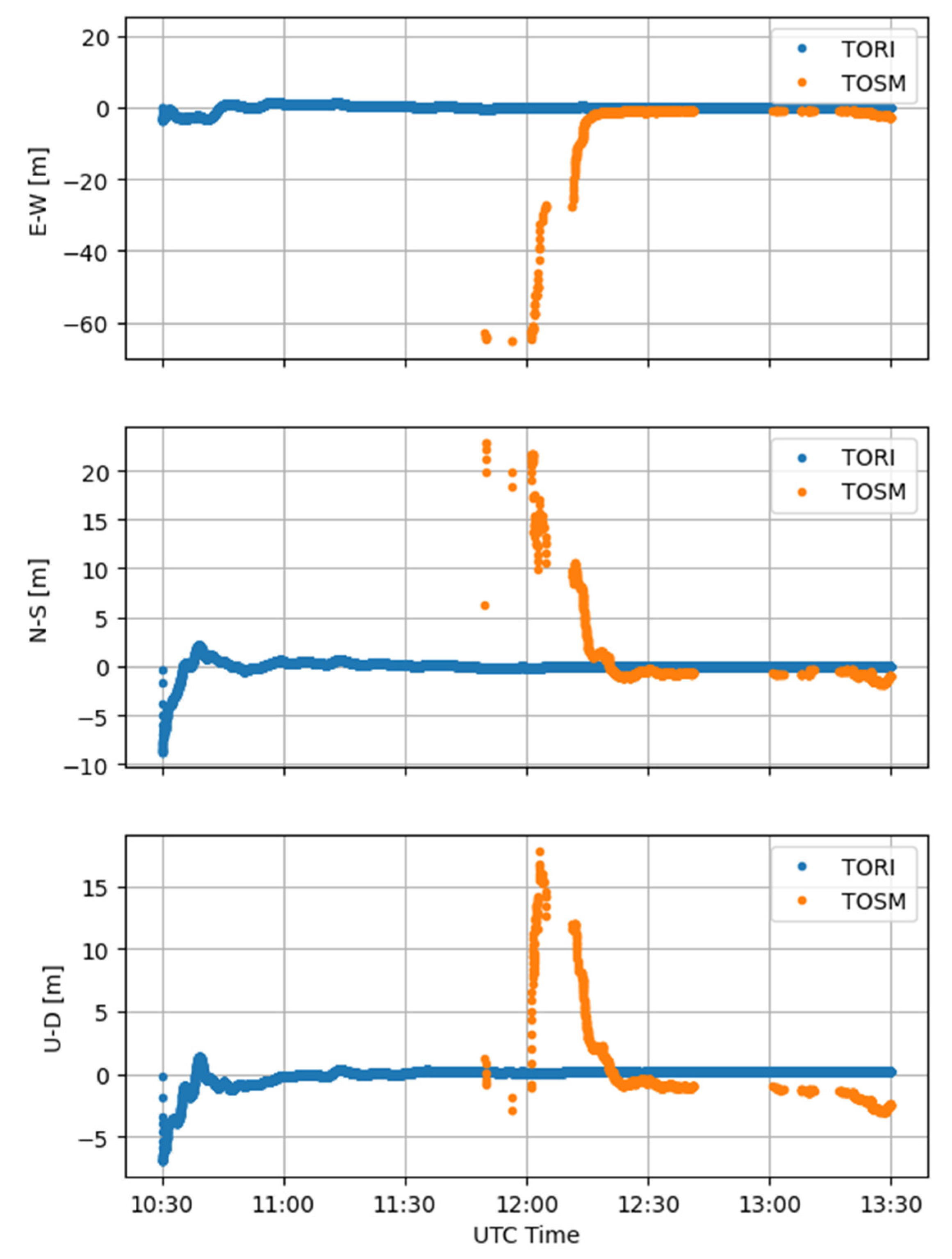
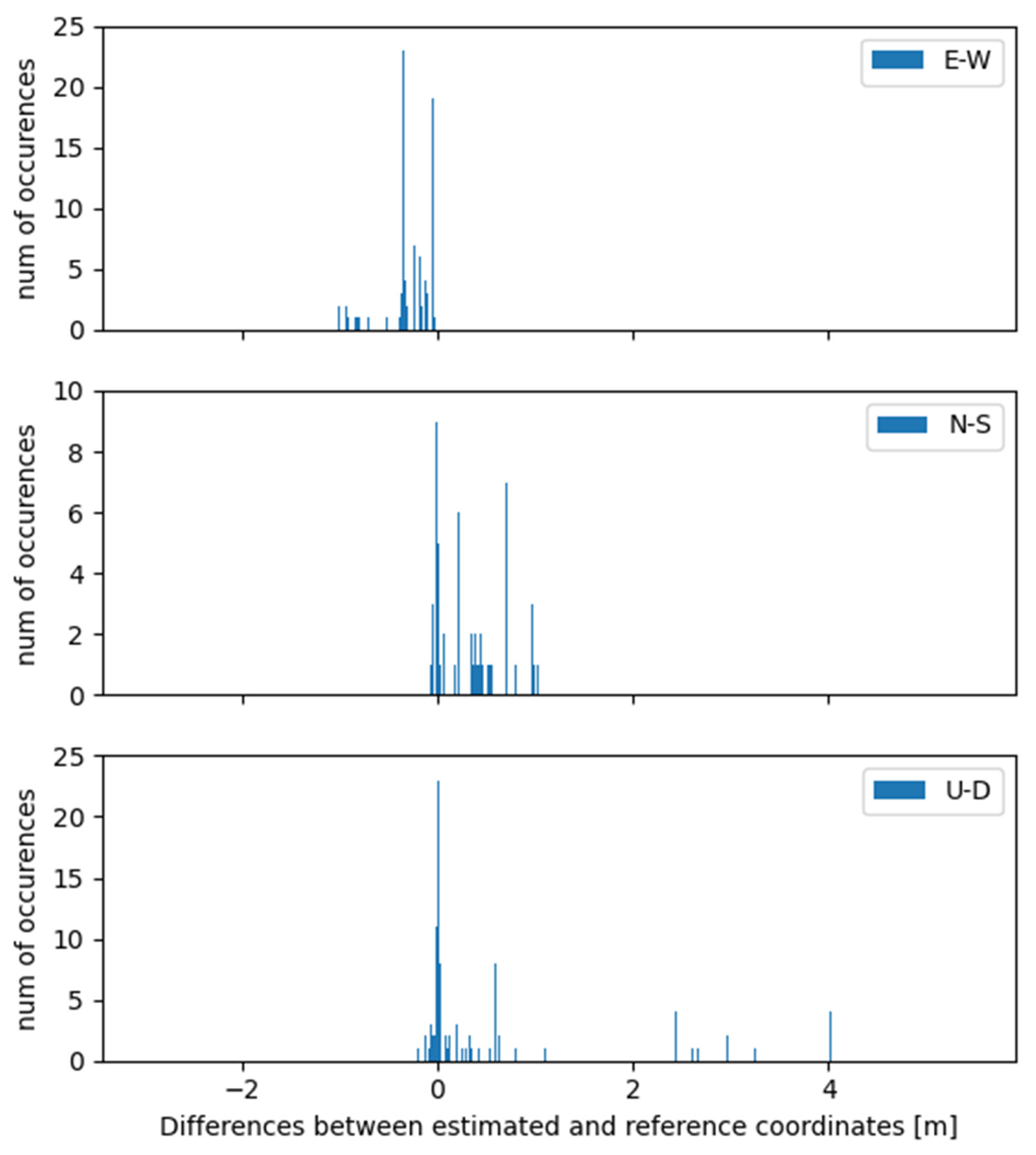
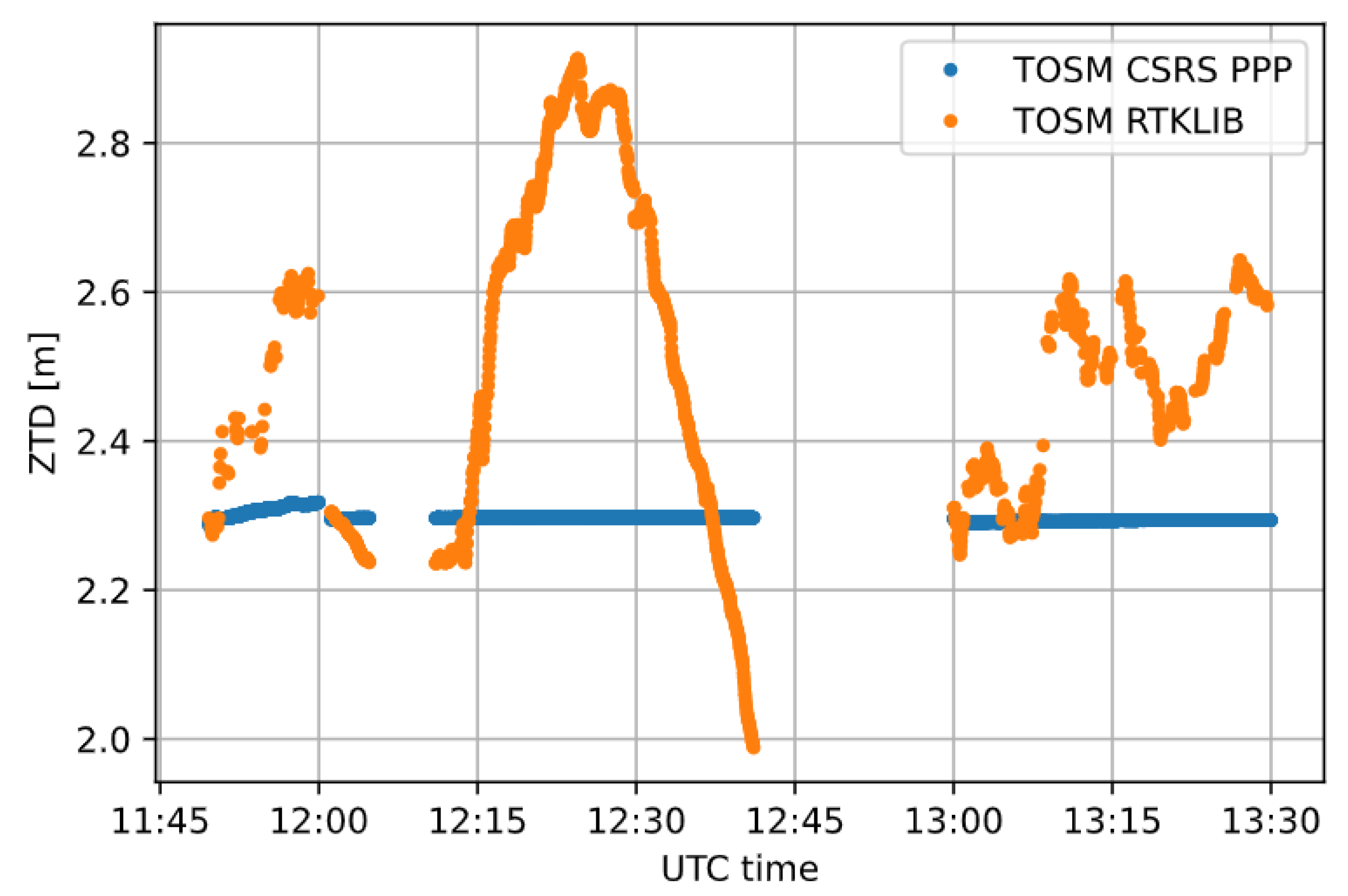
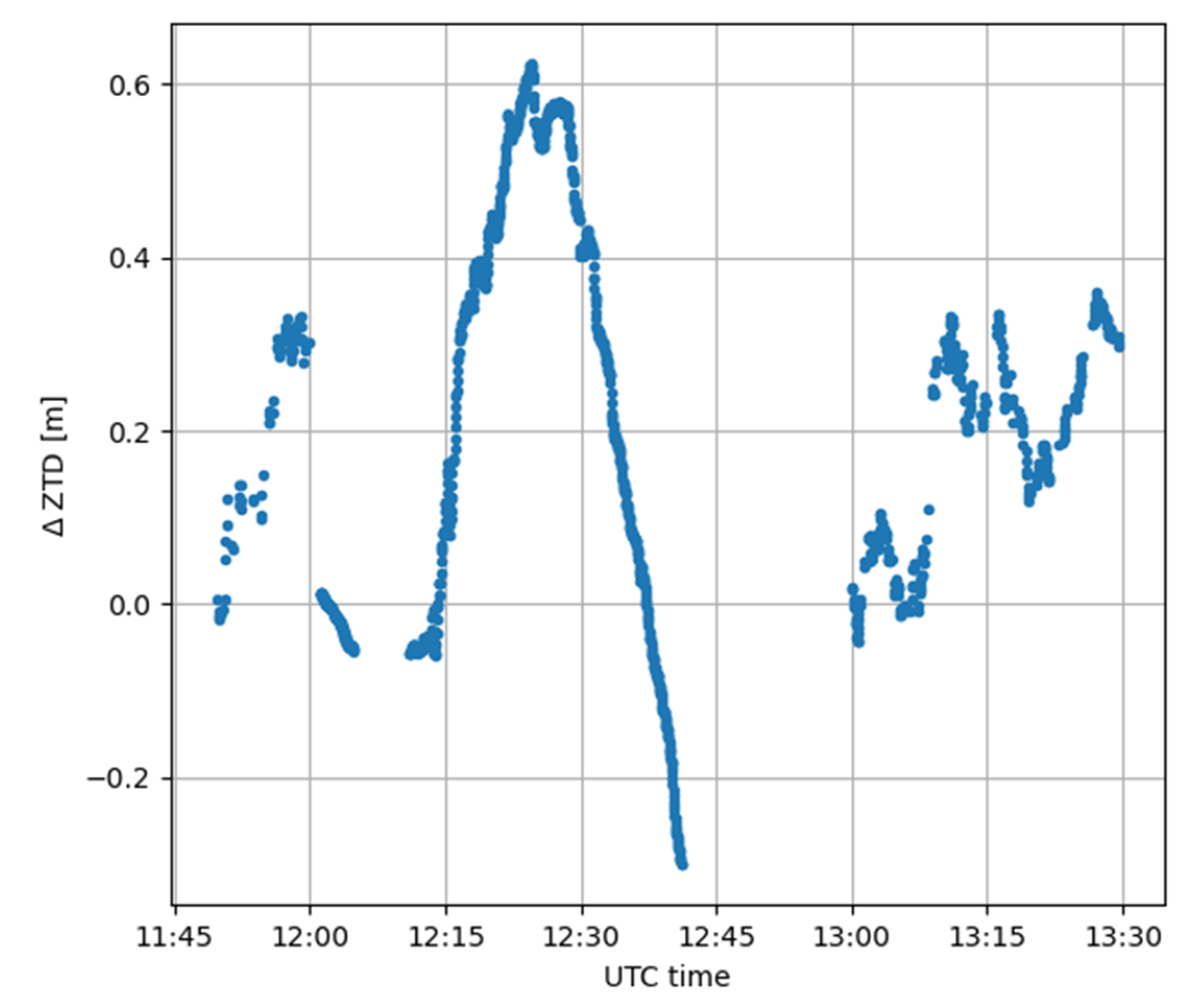
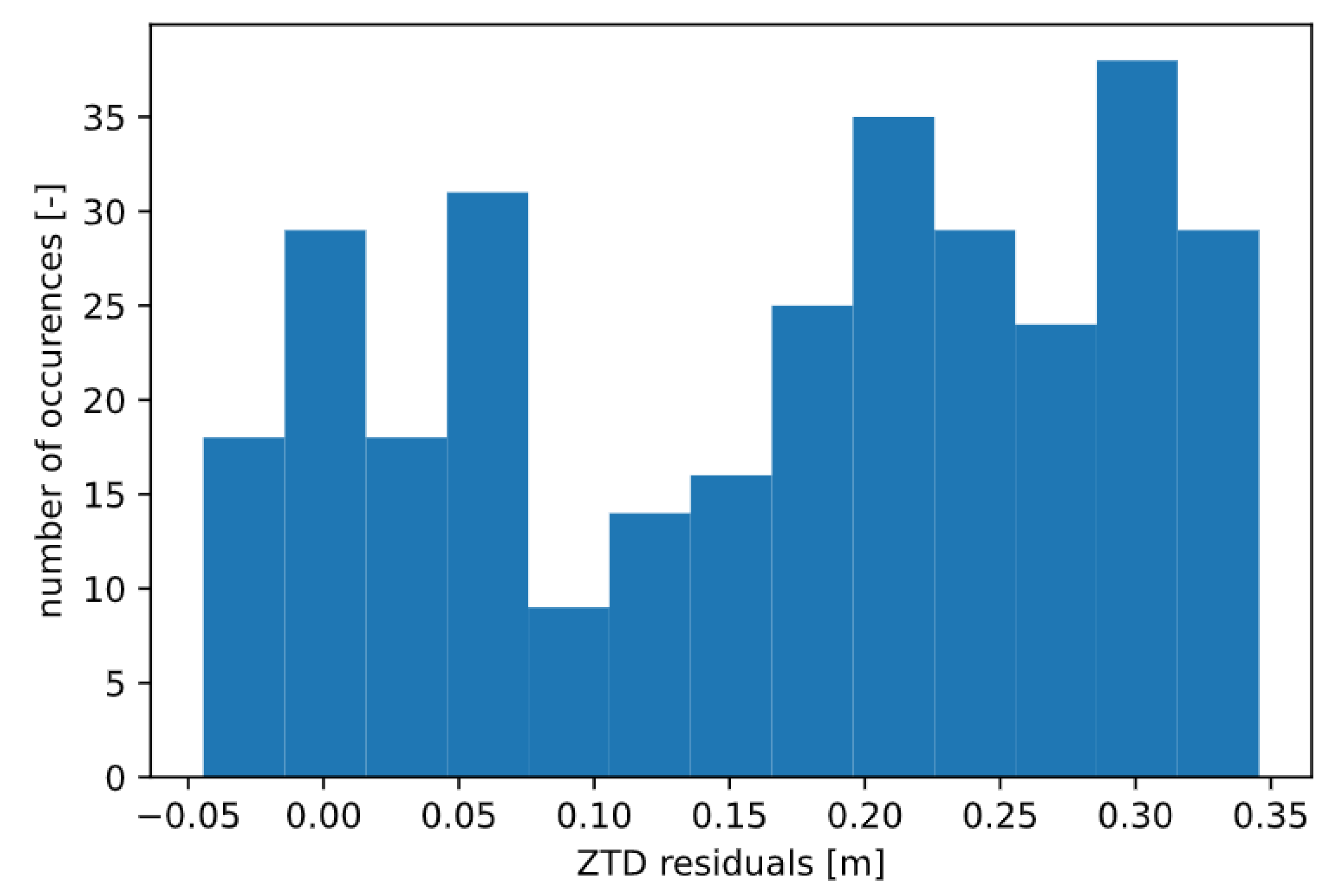
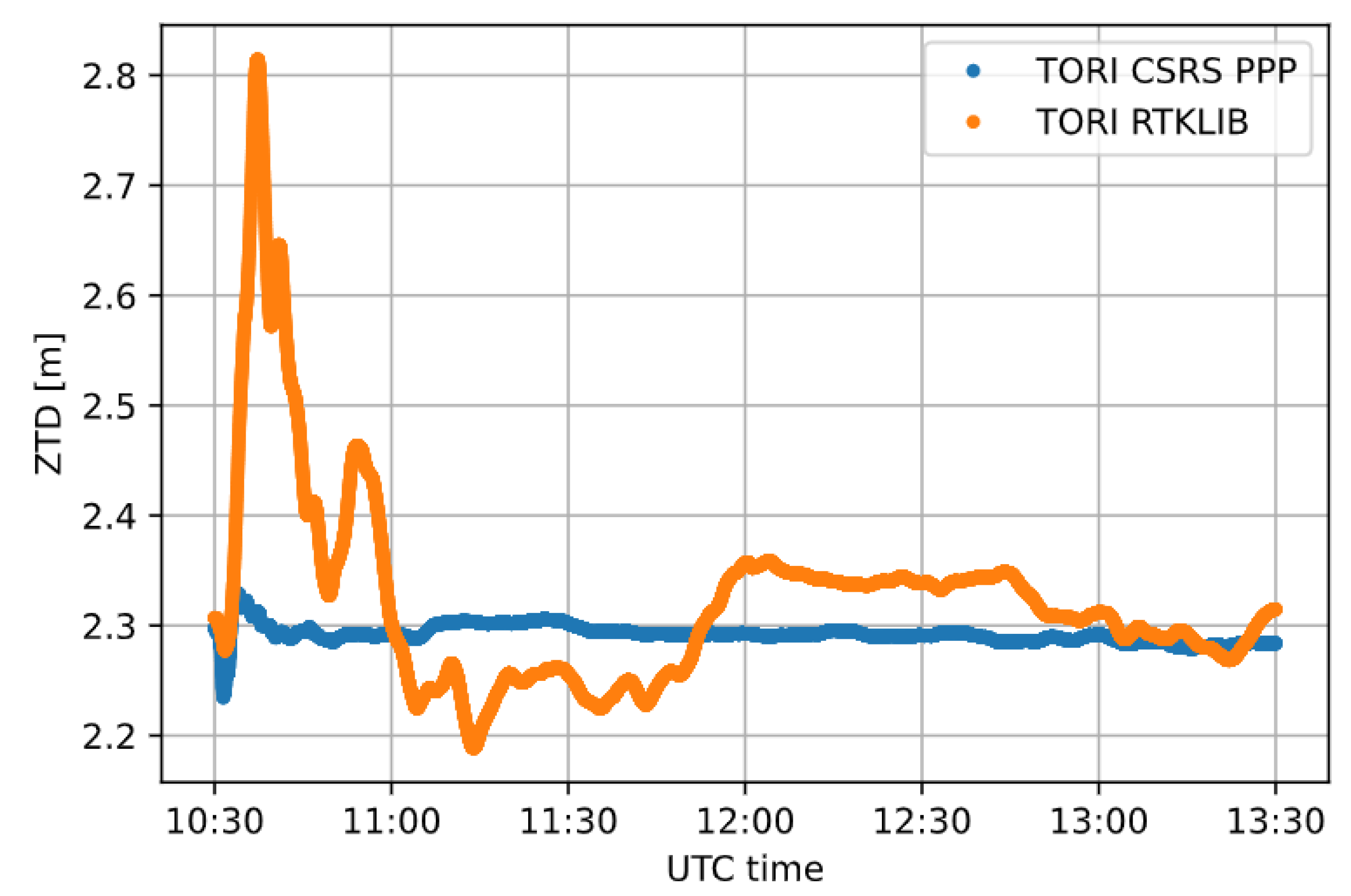
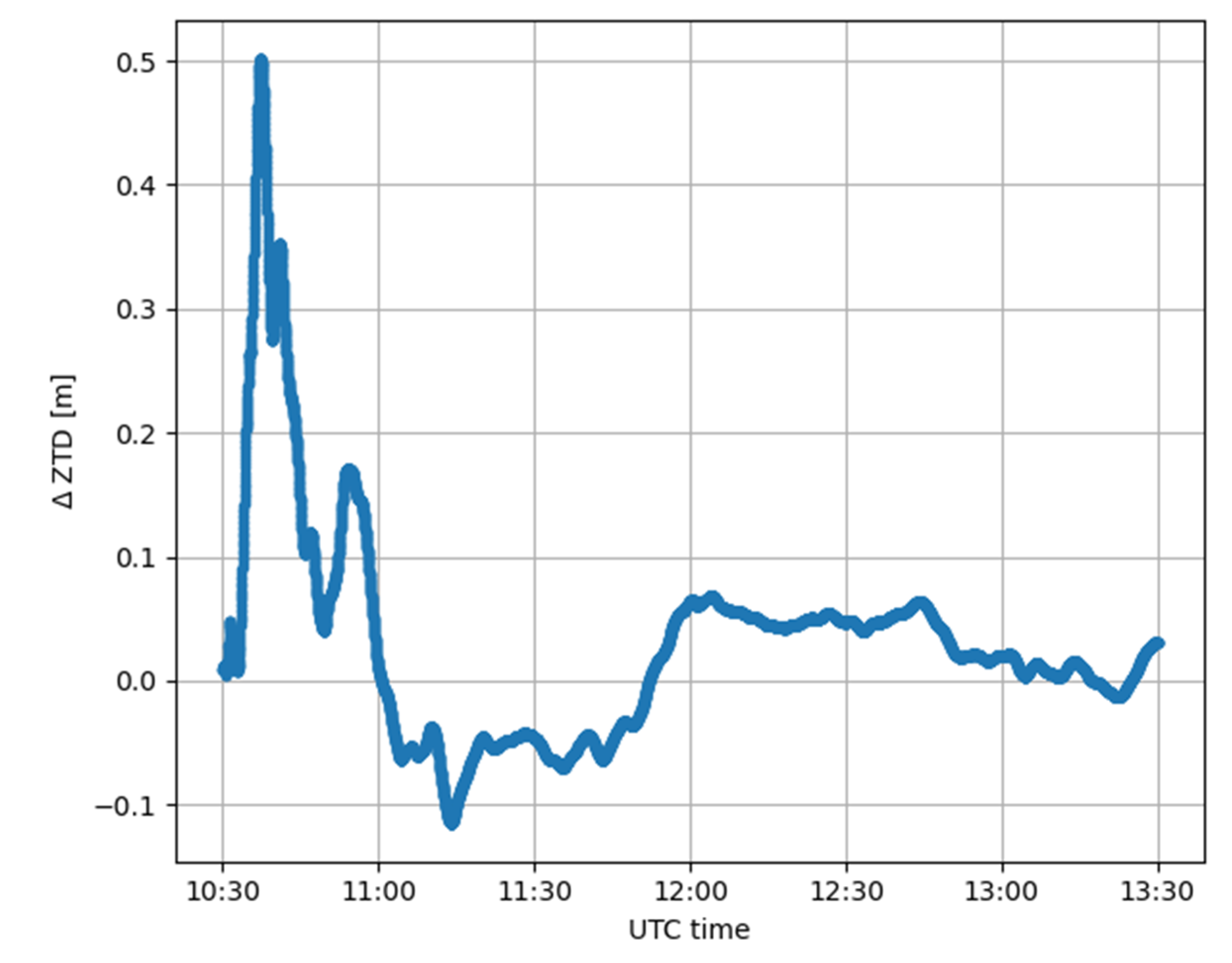
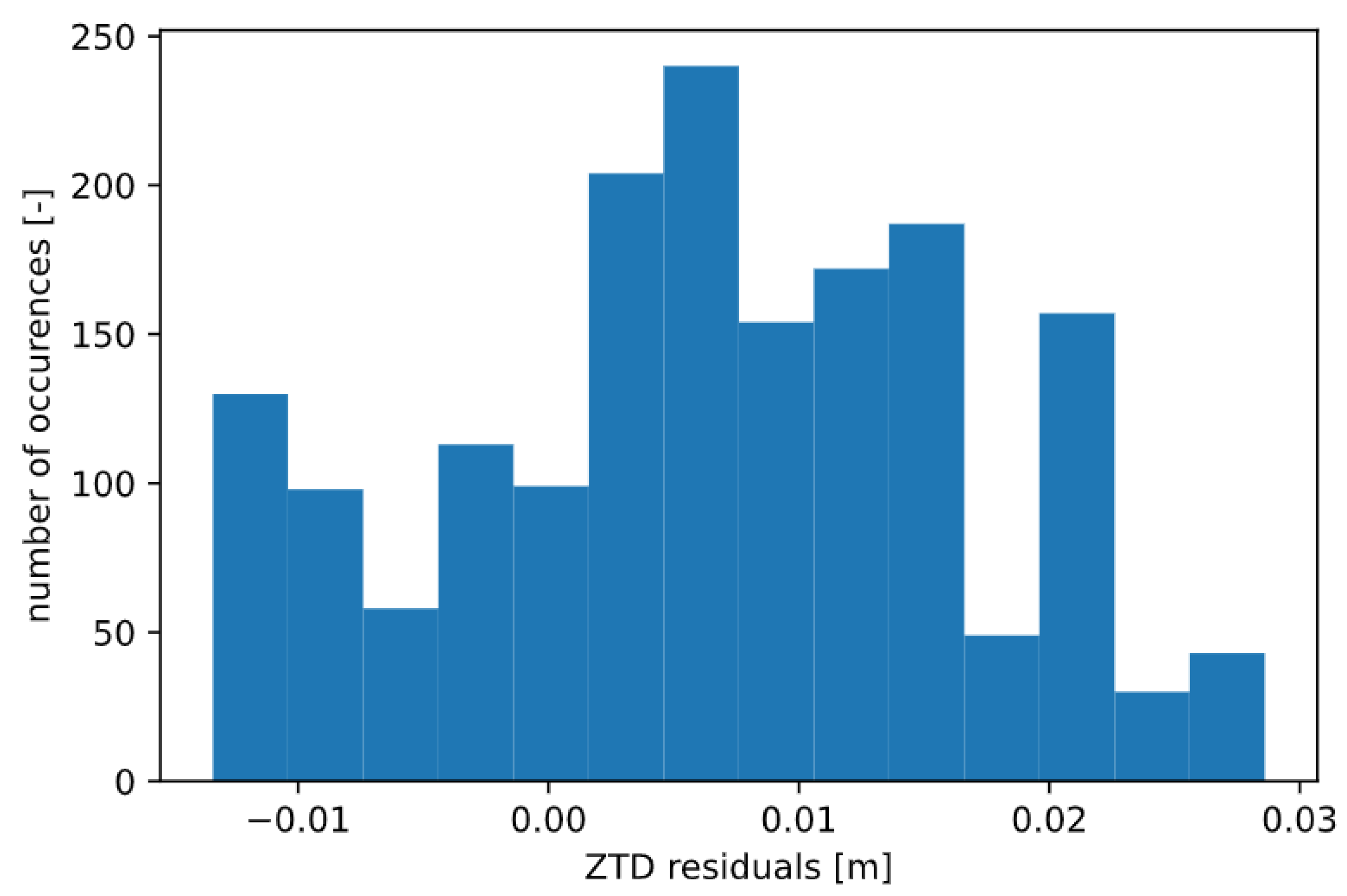
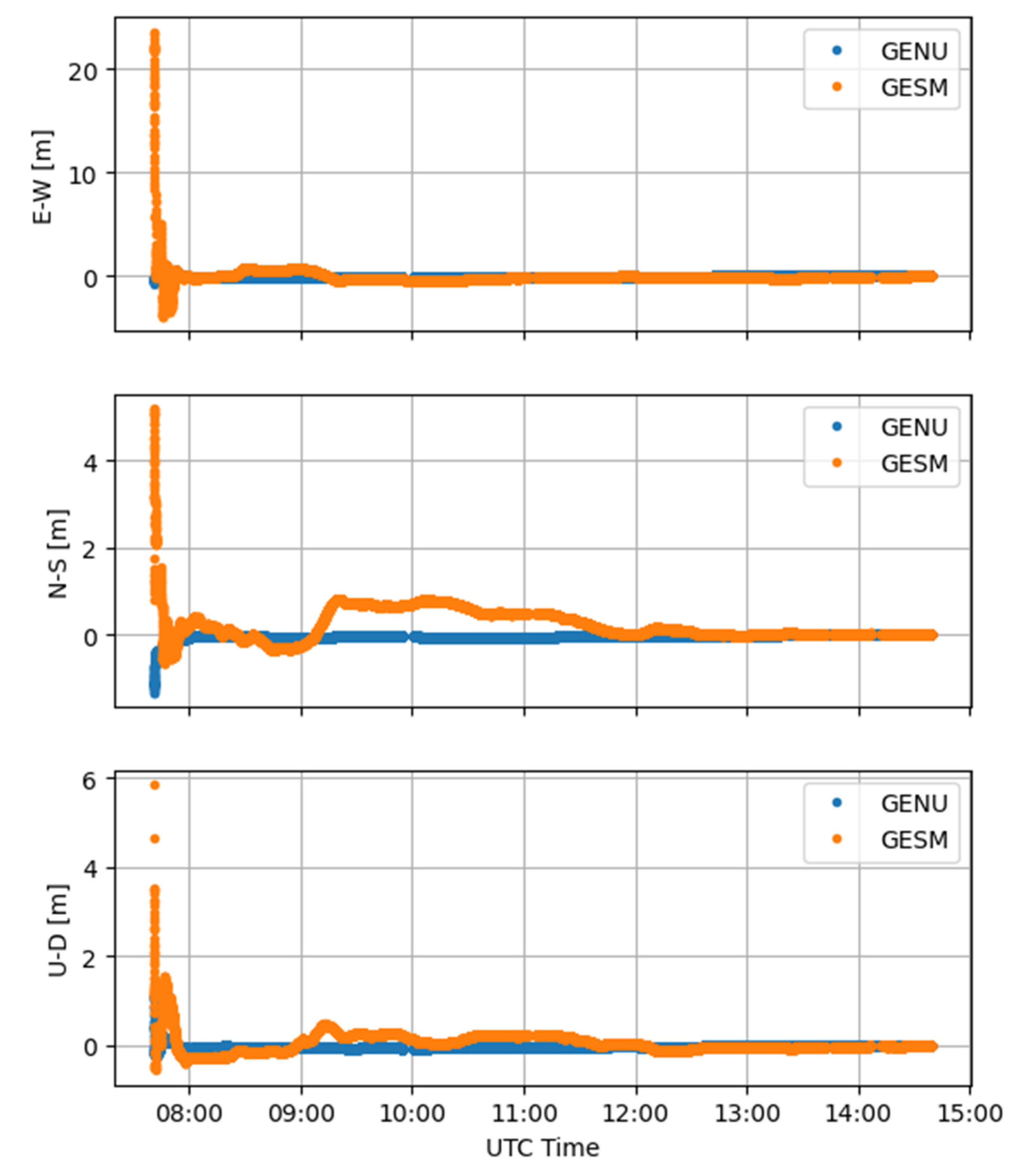
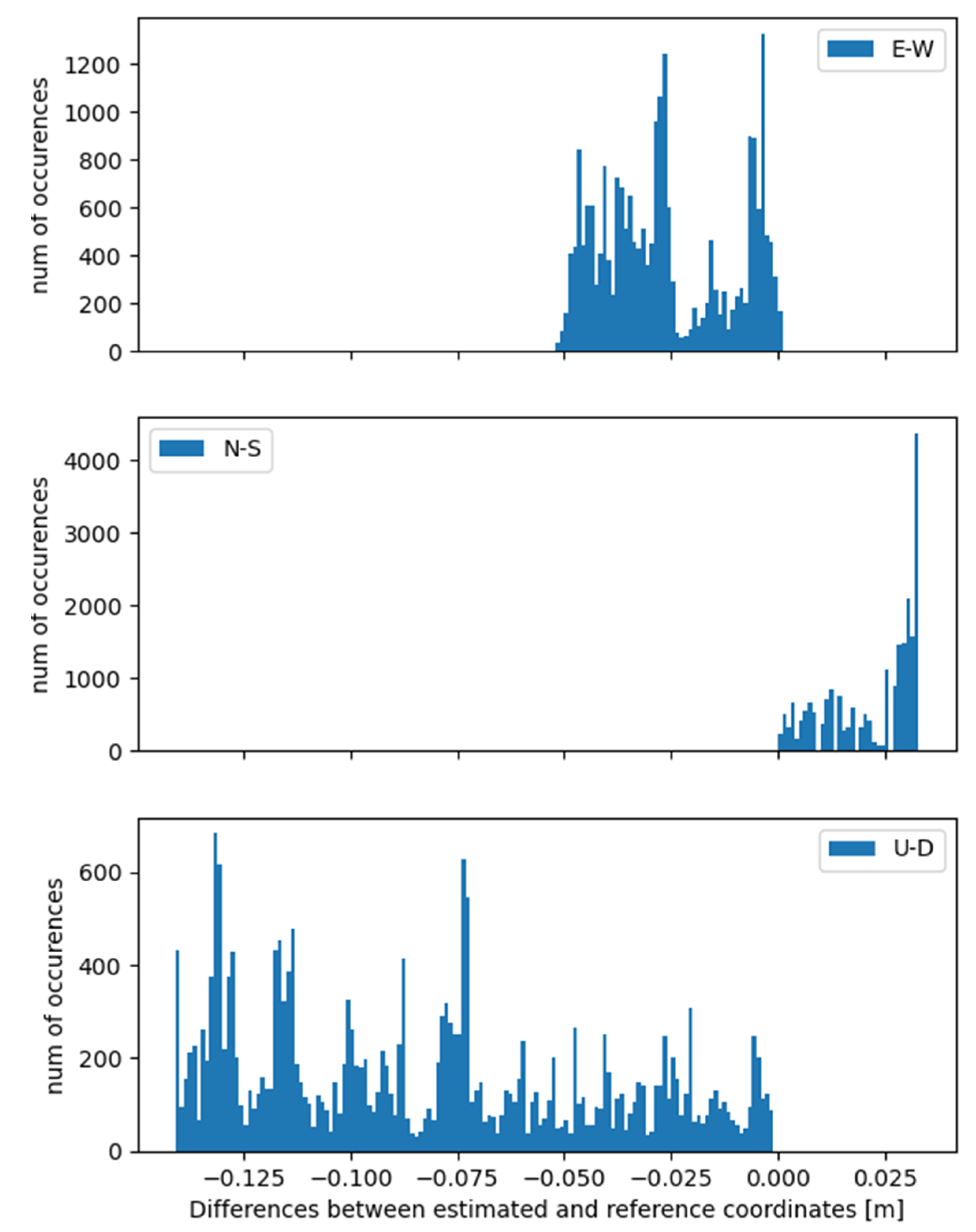
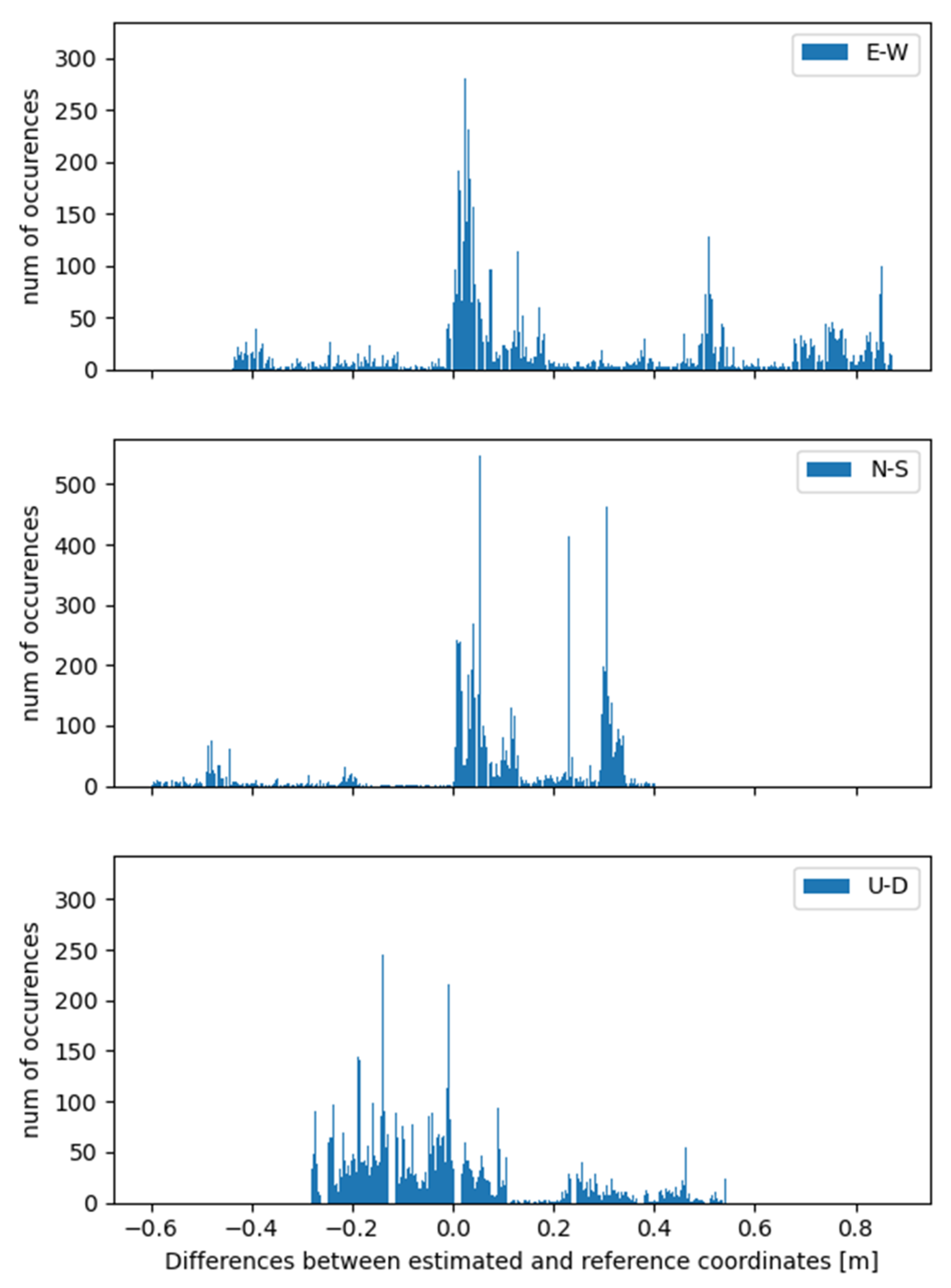
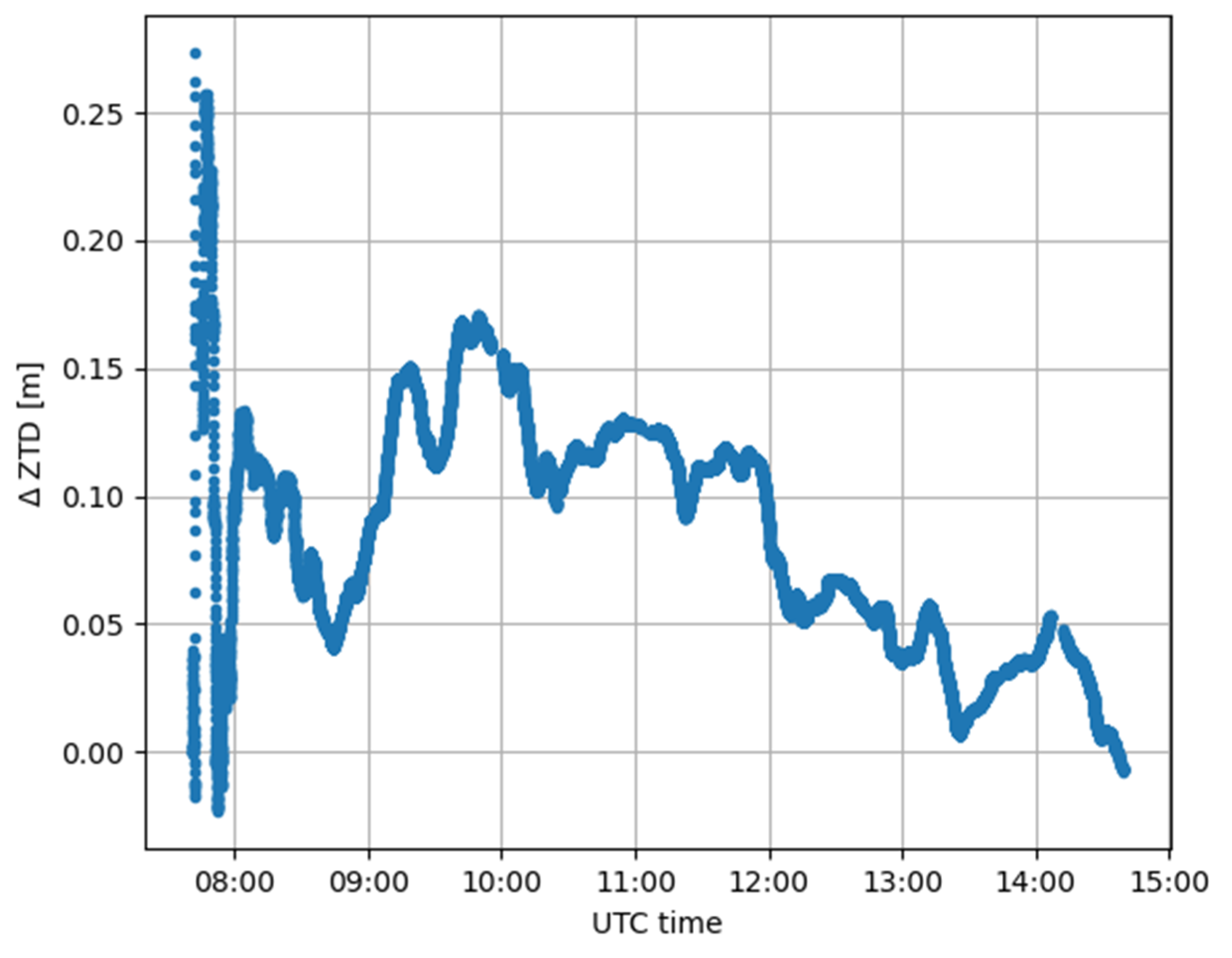
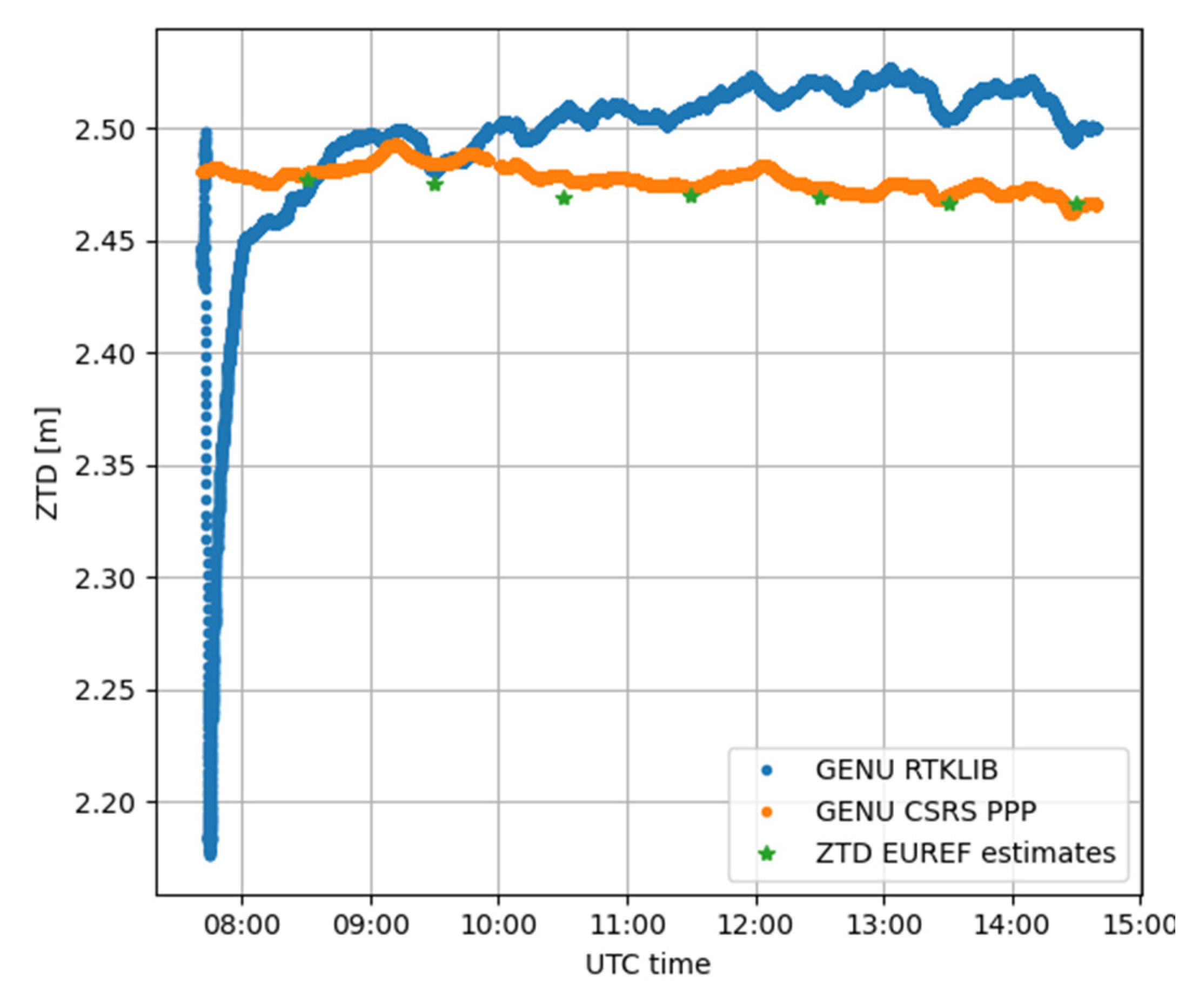
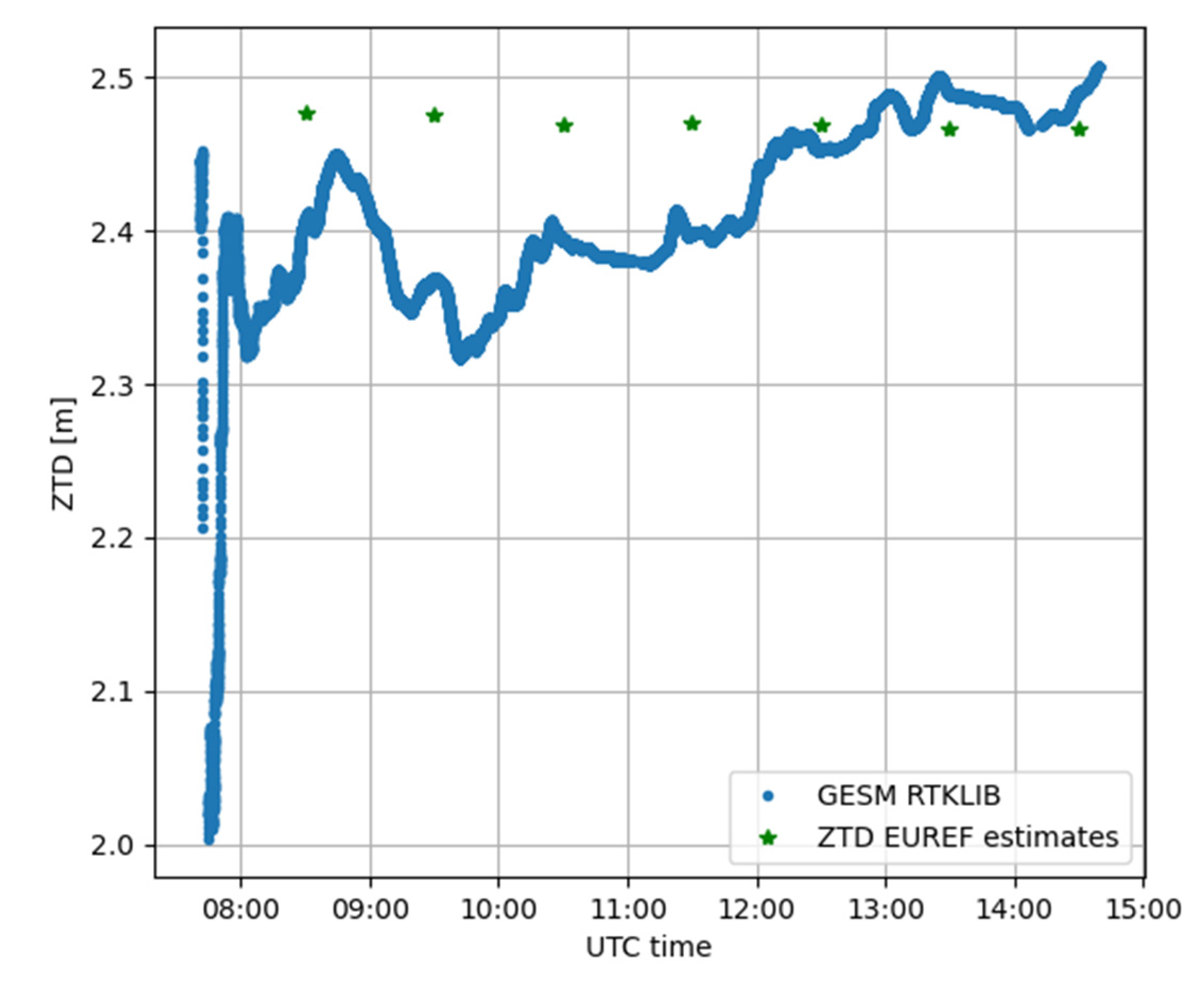
3.1. Case Study 1
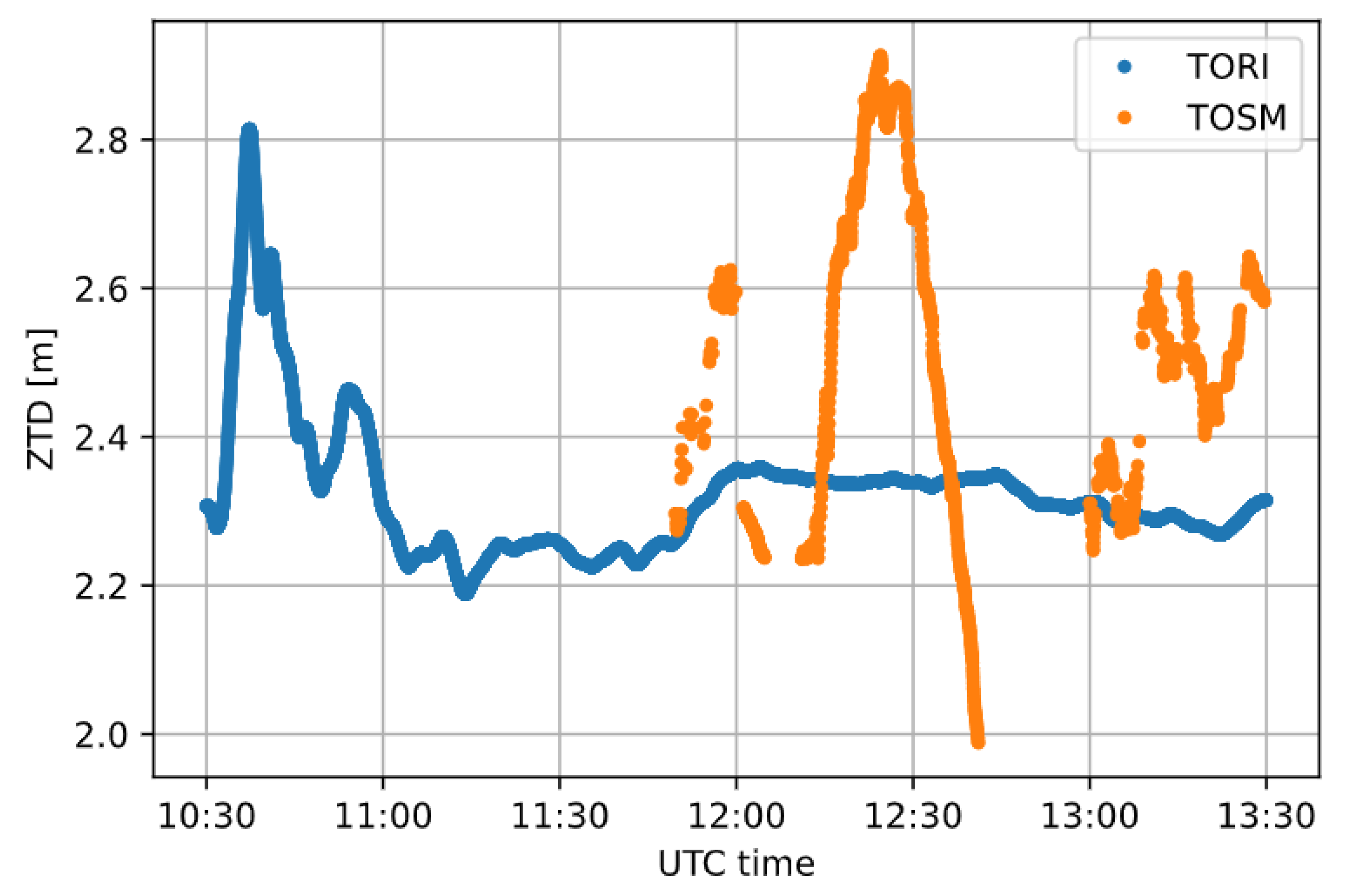
3.2. Case Study 2
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, X.; Montillet, J.P.; Fernandes, R.; Bos, M.; Yu, K.; Hua, X.; Jiang, W. Review of current GPS methodologies for producing accurate time series and their error sources. J. Geodyn. 2017, 106, 12–29. [Google Scholar] [CrossRef]
- Bock, Y.; Melgar, D. Physical applications of GPS geodesy: A review. Rep. Prog. Phys. 2016, 79, 106801. [Google Scholar] [CrossRef]
- Angrisano, A.; Dardanelli, G.; Innac, A.; Pisciotta, A.; Pipitone, C.; Gaglione, S. Performance Assessment of PPP Surveys with Open Source Software Using the GNSS GPS–GLONASS–Galileo Constellations. Appl. Sci. 2020, 10, 5420. [Google Scholar] [CrossRef]
- Mendez Astudillo, J.; Lau, L.; Tang, Y.-T.; Moore, T. Analysing the Zenith Tropospheric Delay Estimates in On-line Precise Point Positioning (PPP) Services and PPP Software Packages. Sensors 2018, 18, 580. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Wang, M.; Wang, N. Precision agriculture—A worldwide overview. Comput. Electron. Agric. 2002, 36, 113–132. [Google Scholar] [CrossRef]
- Moore, T.; Hill, C.; Norris, A.; Hide, C.; Park, D.; Ward, N. The Potential Impact of GNSS/INS Integration on Maritime Navigation. J. Navig. 2008, 61, 221–237. [Google Scholar] [CrossRef]
- Tsuda, T.; Sato, K.; Realini, E.; Oigawa, M.; Iwaki, Y.; Shoji, Y.; Seko, H. A real-time monitoring system of Precipitable Water Vapor (PWV) using a dense GNSS receiver network. J. Disaster Res. 2013, 8, 155–156. [Google Scholar]
- Sguerso, D.; Labbouz, L.; Walpersdorf, A. 14 years of GPS tropospheric delays in the French-Italian border region: A data base for meteorological and climatological analyses. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-5/W3, 7–14. [Google Scholar] [CrossRef]
- Sguerso, D.; Labbouz, L.; Walpersdorf, A. 14 years of GPS tropospheric delays in the French–Italian border region: Comparisons and first application in a case study. Appl. Geomat. 2016, 8, 13–25. [Google Scholar] [CrossRef]
- Ferrando, I.; Federici, B.; Sguerso, D. 2D PWV monitoring of a wide and orographically complex area with a low dense GNSS network. Earth Planets Space 2018, 70, 54. [Google Scholar] [CrossRef]
- Benvenuto, L.; Ferrando, I.; Federici, B.; Sguerso, D. The GNSS for meteorology (G4M) procedure and its application to four significant weather events. In IX Hotine-Marussi Symposium on Mathematical Geodesy. International Association of Geodesy Symposia International; Novák, P., Crespi, M., Sneeuw, N., Sansò, F., Eds.; Springer: Cham, Switzerland, 2020; Volume 151. [Google Scholar] [CrossRef]
- Dabove, P.; Manzino, A.M. GPS & GLONASS mass-market receivers: Positioning performances and peculiarities. Sensors 2014, 14, 22159–22179. [Google Scholar] [CrossRef]
- Cina, A.; Dabove, P.; Manzino, A.M.; Piras, M. Augmented Positioning with CORSs Network Services Using GNSS Mass-market Receivers. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 5-8 May 2014; pp. 359–366. [Google Scholar] [CrossRef]
- Cina, A.; Piras, M. Performance of low-cost GNSS receiver for landslides monitoring: Test and results. Geomat. Nat. Hazards Risk 2015, 6, 497–514. [Google Scholar] [CrossRef]
- Lachapelle, G.; Gratton, P.; Horrelt, J.; Lemieux, E.; Broumandan, A. Evaluation of a low cost hand held unit with GNSS raw data capability and comparison with an Android smartphone. Sensors 2018, 18, 4185. [Google Scholar] [CrossRef] [PubMed]
- Odolinski, R.; Teunissen, P.J.G. An assessment of smartphone and low-cost multi-GNSS single-frequency RTK positioning for low, medium and high ionospheric disturbance periods. J. Geod. 2018, 93, 701–722. [Google Scholar] [CrossRef]
- Paziewski, J. Recent advances and perspectives for positioning and applications with smartphone GNSS observations. Meas. Sci. Technol. 2020, 31, 091001. [Google Scholar] [CrossRef]
- Humphreys, T.E.; Murrian, M.; van Diggelen, F.; Podshivalov, S.; Pesyna, K.M. On the feasibility of cm-accurate positioning via a smartphone’s antenna and GNSS chip. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016; pp. 232–242. [Google Scholar] [CrossRef]
- Pesyna Jr, K.M.; Heath Jr, R.W.; Humphreys, T.E. Centimeter positioning with a smartphone-quality GNSS antenna. In Proceedings of the 27th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2014), Tampa, FL, USA, 8–12 September 2014; pp. 1568–1577. [Google Scholar]
- Zhang, X.; Tao, X.; Zhu, F.; Shi, X.; Wang, F. Quality assessment of GNSS observations from an Android N smartphone and positioning performance analysis using time-differenced filtering approach. GPS Solut. 2018, 22, 70. [Google Scholar] [CrossRef]
- Masiero, A.; Guarnieri, A.; Pirotti, F.; Vettore, A. A particle filter for smartphone-based indoor pedestrian navigation. Micromachines 2014, 5, 1012–1033. [Google Scholar] [CrossRef]
- Wang, L.; Groves, P.D.; Ziebart, M.K. Smartphone shadow matching for better cross-street GNSS positioning in urban environments. J. Navig. 2015, 68, 411–433. [Google Scholar] [CrossRef]
- Wang, L.; Li, Z.; Zhao, J.; Zhou, K.; Wang, Z.; Yuan, H. Smart device-supported BDS/GNSS real-time kinematic positioning for sub-meter-level accuracy in urban location-based services. Sensors 2016, 16, 2201. [Google Scholar] [CrossRef]
- Wang, L.; Li, Z.; Yuan, H.; Zhao, J.; Zhou, K.; Yuan, C. Influence of the time-delay of correction for BDS and GPS combined real-time differential positioning. Electron. Lett. 2016, 52, 1063–1065. [Google Scholar] [CrossRef]
- Adjrad, M.; Groves, P.D. Intelligent urban positioning: Integration of shadow matching with 3D-mapping-aided GNSS ranging. J. Navig. 2017, 71, 1–20. [Google Scholar] [CrossRef]
- Al-Azizi, J.I.; Shafri, H.Z.M. Performance evaluation of pedestrian locations based on contemporary smartphones. Int. J. Navig. Obs. 2017, 2017, 1–10. [Google Scholar] [CrossRef]
- Fissore, F.; Masiero, A.; Piragnolo, M.; Pirotti, F.; Guarnieri, A.; Vettore, A. Towards surveying with a smartphone. In New Advanced GNSS and 3D Spatial Techniques. Lecture Notes in Geoinformation and Cartography; Cefalo, R., Zieliński, J., Barbarella, M., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Realini, E.; Caldera, S.; Pertusini, L.; Sampietro, D. Precise GNSS positioning using smart devices. Sensors 2017, 17, 2434. [Google Scholar] [CrossRef] [PubMed]
- Dabove, P.; Di Pietra, V. Single-baseline RTK positioning using dual-frequency GNSS receivers inside smartphones. Sensors 2019, 19, 4302. [Google Scholar] [CrossRef] [PubMed]
- Dabove, P.; Di Pietra, V. Towards high accuracy GNSS real-time positioning with smartphones. Adv. Space Res. 2019, 63, 94–102. [Google Scholar] [CrossRef]
- Aggrey, J.; Bisnath, S.; Naciri, N.; Shinghal, G.; Yang, S. Multi-GNSS precise point positioning with next-generation smartphone measurements. J. Spat. Sci. 2020, 65, 79–98. [Google Scholar] [CrossRef]
- Hadas, T.; Hobiger, T.; Hordyniec, P. Considering different recent advancements in GNSS on real-time zenith troposphere estimates. GPS Solut. 2020, 24, 1–14. [Google Scholar] [CrossRef]
- Zhou, F.; Cao, X.; Ge, Y.; Li, W. Assessment of the positioning performance and tropospheric delay retrieval with precise point positioning using products from different analysis centers. GPS Solut. 2020, 24, 12. [Google Scholar] [CrossRef]
- CSRS-PPP. Available online: https://webapp.geod.nrcan.gc.ca/geod/tools-outils/ppp.php (accessed on 1 October 2021).
- RTKLIB 2.4.3. Available online: https://github.com/tomojitakasu/RTKLIB_bin/tree/rtklib_2.4.3 (accessed on 1 October 2021).
- Teunissen, P.; Montenbruck, O. (Eds.) Springer Handbook of Global Navigation Satellite Systems; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Marzocchi, R.; Leotta, M.; Federici, B.; Delzanno, G. The NARVALO project: Real time collision avoidance system in a GIS environment based on precise GNSS positioning. Geoing. Ambient. E Min. 2017, 151, 33–38. [Google Scholar]
- Bevis, M.; Businger, S.; Herring, T.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res.: Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Solheim, F.S.; Vivekanandan, J.; Ware, R.H.; Rocken, C. Propagation delays induced in GPS signals by dry air, water vapor, hydrometeors, and other particulates. J. Geophys. Res. 1999, 104, 9663–9670. [Google Scholar] [CrossRef]
- Rocken, C.; Van Hove, T.; Ware, R. Near real-time GPS sensing of atmospheric water vapor. Geophys. Res. Lett. 1997, 24, 3221–3224. [Google Scholar] [CrossRef]
- Seko, H.; Shoji, Y.; Fujibe, F. Evolution and air flow structure of a Kanto thunderstorm on July 21 1999 (the Nerima Heavy Rainfall Event). J. Meteorol. Soc. Jpn. 2007, 85, 455–477. [Google Scholar] [CrossRef][Green Version]
- Inoue, H.Y.; Inoue, T. Characteristics of the water-vapor field over the Kanto district associated with summer thunderstorm activities. Sci. Online Lett. Atmos. 2007, 3, 101–104. [Google Scholar] [CrossRef][Green Version]
- Chen, B.; Dai, W.; Liu, Z.; Wu, L.; Kuang, C.; Ao, M. Constructing a precipitable water vapor map from regional GNSS network observations without collocated meteorological data for weather forecasting. Atmos. Meas. Tech. 2018, 11, 5153–5166. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Li, W.; Zhang, B. A Real-Time Precipitable Water Vapor Monitoring System Using the National GNSS Network of China: Method and Preliminary Results. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1587–1598. [Google Scholar] [CrossRef]
- Zhang, C.; Kuo, Y.; Dai, L.; Chu, Y.; Braun, J.; Zhang, J.; Li, Q.; Chen, M. The design and application of network of ground-based GPS water vapor monitoring stations to improve precipitation prediction in the Greater Beijing metropolitan area. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 517–522. [Google Scholar]
- Oigawa, M.; Realini, E.; Tsuda, T. Study of Water Vapor Variations Associated with Meso-γ Scale Convection: Comparison between GNSS and Non-Hydrostatic Model Data. SOLA 2015, 11, 27–30. [Google Scholar] [CrossRef]
- Barindelli, S.; Realini, E.; Venuti, G.; Fermi, A.; Gatti, A. Detection of water vapor time variations associated with heavy rain in northern Italy by geodetic and low-cost GNSS receivers. Earth Planets Space 2018, 70, 28. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, B.; Li, W.; Yuan, Y.; Li, M. Simultaneous retrieval of precipitable water vapor (PWV) and vertical total electron content (VTEC) by low-cost multi-GNSS single-frequency receivers. Earth Space Sci. 2019, 6, 1694–1709. [Google Scholar] [CrossRef]
- IGS Products. Available online: https://www.igs.org/products/ (accessed on 1 October 2021).
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—Achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- MGEX Products. Available online: https://igs.org/mgex/data-products/#products (accessed on 20 October 2021).
- Bruyninx, C.; Legrand, J.; Fabian, A.; Pottiaux, E. GNSS metadata and data validation in the EUREF Permanent Network. GPS Solut. 2019, 23, 1–14. [Google Scholar] [CrossRef]
- EUREF Permanent GNSS Network Tropospheric Delays. Available online: http://www.epncb.oma.be/_productsservices/troposphere/ (accessed on 4 November 2021).






| RINEX format | RINEX 3 |
| Cut-off angle | 7.5° |
| Ephemeris | Final (MGEX) |
| Clocks | Final (MGEX) |
| Ionosphere | Iono-free |
| OTL | Based on Chalmers grid solution |
| Ambiguity resolution | PPP-AR |
| Average (m) | Standard Deviation (m) | Root Mean Square (m) | ||
|---|---|---|---|---|
| TORI | E-W | 0.16 | 0.29 | 0.33 |
| N-S | −0.10 | 0.20 | 0.22 | |
| U-D | −0.04 | 0.14 | 0.14 | |
| TOSM | E-W | −0.45 | 0.56 | 0.72 |
| N-S | 0.30 | 0.34 | 0.45 | |
| U-D | 0.85 | 1.36 | 1.60 |
| Receiver | Mean (m) | Standard Deviation (m) |
|---|---|---|
| TOSM | 0.170 | 0.114 |
| TORI | 0.007 | 0.011 |
| Average (m) | Standard Deviation (m) | Root Mean Square (m) | ||
|---|---|---|---|---|
| GENU | E-W | −0.03 | 0.02 | 0.03 |
| N-S | 0.02 | 0.01 | 0.02 | |
| U-D | −0.08 | 0.04 | 0.09 | |
| GESM | E-W | 0.23 | 0.35 | 0.42 |
| N-S | 0.07 | 0.23 | 0.24 | |
| U-D | 0.02 | 0.18 | 0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benvenuto, L.; Dabove, P.; Ferrando, I.; Sguerso, D. Preliminary Results on Tropospheric ZTD Estimation by Smartphone. Remote Sens. 2021, 13, 4567. https://doi.org/10.3390/rs13224567
Benvenuto L, Dabove P, Ferrando I, Sguerso D. Preliminary Results on Tropospheric ZTD Estimation by Smartphone. Remote Sensing. 2021; 13(22):4567. https://doi.org/10.3390/rs13224567
Chicago/Turabian StyleBenvenuto, Lorenzo, Paolo Dabove, Ilaria Ferrando, and Domenico Sguerso. 2021. "Preliminary Results on Tropospheric ZTD Estimation by Smartphone" Remote Sensing 13, no. 22: 4567. https://doi.org/10.3390/rs13224567
APA StyleBenvenuto, L., Dabove, P., Ferrando, I., & Sguerso, D. (2021). Preliminary Results on Tropospheric ZTD Estimation by Smartphone. Remote Sensing, 13(22), 4567. https://doi.org/10.3390/rs13224567








