1. Introduction
The partitioning of large-size images, in order to exploit their rich information content for the construction of reliable decision-making systems, is of growing interest in many application fields. Indeed, hyperspectral images are today among the most widely used data thanks to their large spectral range (several hundred spectral bands covering the visible and infrared domains) and their fine spatial resolution (a few tens of centimeters). Due to this richness of information, which allows for better discrimination of objects, interest in hyperspectral images has increased during the last years in many application fields. These fields include geology [
1], medicine [
2,
3,
4,
5,
6,
7], industrial production [
8,
9], safety [
10], and the environment [
11,
12,
13,
14,
15,
16,
17,
18,
19,
20]. In this latter field, hyperspectral imagery has been of great interest and several applications have been treated. These applications include the inventory of vegetation species [
11,
12], the early detection of vegetation diseases [
13,
14] and invasive species [
15,
16], the identification of marine algae [
17,
18], and the human and animal impacts on the environment [
19,
20], etc. Thus, to efficiently meet the needs of all these areas, any partitioning method of hyperspectral images must be conducted while respecting the physical nature of the information provided by these images. A plethora of published methods do not respect the precise information given by these images, where the ground truth (GT) data used is simplified [
21,
22] and the classification of existing methods is sometimes ambiguous and not consistent. For example, in [
23], the authors propose a method using learning samples by defining it as semi-supervised. Other authors introduce in [
24], the number of classes in the partitioning process and qualify their method as unsupervised. In general, it is wrong to consider all algorithms as unsupervised because the introduction of the number of classes by the user to run an algorithm is a supervised operation [
25].
In order to remove all these confusions, we classify according to criteria related to the nature of the knowledge introduced by the users this plethora of methods into three main categories instead of two, as often proposed in the literature (supervised and unsupervised). The confusion is due to the fact that methods that require a priori knowledge of the number of classes are in the same category as those that estimate the number of classes. Thus, we subdivided the category of unsupervised methods into two categories (semi-supervised and unsupervised methods) [
26]. It is important to recall that the methods of each category can be hierarchical or non-hierarchical and parametric or non-parametric. Consequently, the three main categories of classification or partitioning methods opted here are supervised, semi-supervised, and unsupervised, which we will specify after the definition of “partitioning”.
Definition 1.“Data partitioning” is a method of data analysis that consists of dividing a set of data described by quantitative features into different homogeneous “sub-sets” or classes, according to a similarity criterion in the sense that the data in each sub-set share common characteristics. The obtained classes form a partition.
Data partitioning can be performed with or without learning. In the latter case, all classes are located and the unidentified classes as in the case of several domains (environment, medicine, security, biology, etc.) can be analyzed and listed to add them as new known classes for possible learning or not.
We specify that in this article we use the term “partitioning” because it is both more practical and more appropriate to describe the developed data analysis method. In addition, it is more convenient to avoid using a long term, such as “classification of image pixels,” and a false term, such as “image classification,” which is another problem.
Partitioning an image or data consists in creating a partition formally defined as follows:
Let be a set of objects , where each object is charaterized by B quantitative features.
The process of dividing into classes, , consists in creating a partition, , according to one or more objective optimization criteria with: .
This partition, , will therefore highlight the different classes in the dataset, .
The quality of a partition will depend on the degree of homogeneity of the classes formed and consequently on their number. Thus, in order to obtain a correct partitioning result, three requirements must be verified simultaneously:
Completeness: all objects in the dataset must be associated with a class.
Separability: the classes must be sufficiently differentiable so that an object can only be associated with one class.
Relevance: the association of an object to a class must be carried out according to an objective optimization criterion.
The different partitioning methods can be grouped into three categories [
26] which we define as follows:
-
Supervised methods require training samples to accomplish the partitioning task. Methods such as the Maximum Likelihood [
27] and Support Vector Machines [
28] are the most common methods used in this category.
We note that the information required by the methods of this category is not always available for many applications, and even if it exists, it is not always reliable [
21,
22].
-
Semi-supervised methods, considered unsupervised in the literature, require the number of classes and threshold values or other empirical parameters from the operator.
K-means [
29] is a basic semi-supervised algorithm that classifies each object according to their similarity/dissimilarity, requiring the number of classes to be fixed by the user. Furthermore, it is sensitive to the random initialization of class centers, which makes it unstable [
30,
31,
32]. Several extensions of
K-means have been developed [
33,
34,
35,
36] but are still affected by the initial choice of class centers.
The Fuzzy C-Means (FCM) [
37,
38,
39,
40] derived from the
K-means algorithm is another semi-supervised algorithm. This algorithm is also sensitive to the initial class centers and the choice of the fuzzification parameter.
In practice, the knowledge of the number of classes required by supervised and semi-supervised methods is imprecise and not often accessible, in particular for hyperspectral aerial images with large landscape areas. As stated in [
21,
22,
32], prior knowledge of the number of classes is a subjective process in nature, which precludes an absolute judgment as to the relevance of all data analysis. Consequently, these methods do not allow for the discovery of novel relevant classes. In this case, the knowledge of the number of classes in semi-supervised and supervised methods can be considered as a constraint and does not often reflect reality.
In order to partition objects or form learning classes, unsupervised partitioning methods present many advantages with respect to supervised and semi-supervised methods, as defined below.
-
Unsupervised methods do not require the number of classes, associated learning samples, or any other prior knowledge. The number of classes is objectively estimated following a given optimization criterion or several optimization criteria. This category is called exploratory data analysis by Xu and Wunsch [
32]. It is more adapted to explore data analysis or to learn a novel object and discover a novel phenomenon. Indeed, the identification of the nature of each class is defined after the partitioning process and not before. This category leads to a fine and complete analysis of the observed data and does not limit the analysis to known classes. For these reasons, it meets a real need generated by some application domains, such as Earth observation, where the areas to be analyzed are very large or difficult to access. It provides accurate, objective, and consistent solutions that translate real information content of images independently of the GT data or learning samples which can be biased or simplified [
21,
22].
The definition of unsupervised methods given above ensures that no subjective knowledge is introduced by the user.
Several unsupervised methods have been proposed for data partitioning. In [
41], an unsupervised version of the
K-means algorithm, named Modified Linde–Buzo–Gray (MLBG) is proposed. This method improves the different stages of the Linde–Buzo–Gray (LBG) algorithm and is able to automatically determine the number of classes; however, it requires a long computing time. In [
26], an optimized version of the baseline FCM algorithm (FCMO) was presented in order to make it stable and deterministic. Stability is achieved by initializing the class centers through an adaptive incremental procedure. In addition, an unsupervised evaluation criterion, based on the within- and between-class disparities, is introduced to estimate the optimal number of classes. This method can be used in unsupervised or semi-supervised mode.
One of the most elaborate unsupervised partitioning methods is Affinity Propagation (AP) [
42]. This method has six advantages: (i) no a priori knowledge is required, especially the non-introduction of training samples, to give the user the possibility to detect and locate the known classes and new classes called “discovery classes”; (ii) stability of the results thanks to its deterministic character; (iii) possibility to objectively select the samples of the classes in a learning system in order to be able to detect them afterward; (iv) applicable to several domains without learning constraints; (v) it can be used in unsupervised or semi-supervised mode, and; and (vi) it is insensitive to initialization. Due to these advantages, it is widely used in several application areas, such as environmental monitoring and safety [
43,
44,
45,
46,
47], multimedia data management, and pattern recognition [
48,
49,
50,
51,
52,
53,
54,
55,
56,
57].
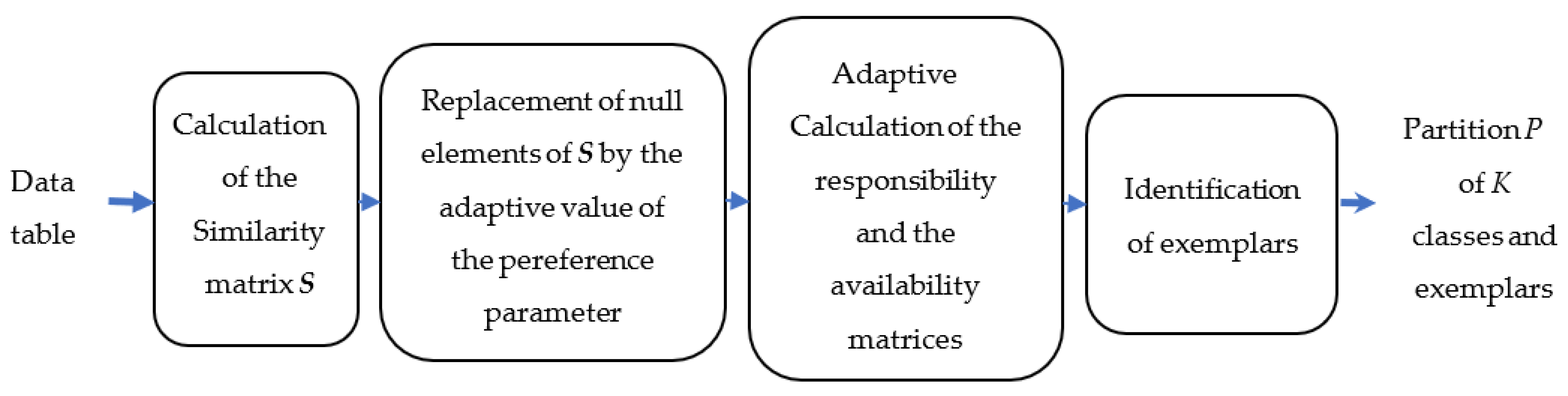
The main drawback of the standard AP method is that it is not applicable to partitioning large-size hyperspectral images. Indeed, the memory space required for each of the four main matrices has a quadratic relationship with the number of pixels to be partitioned. In [
25], Chehdi et al. suggested a reduction in the number of pixels to allow the application of AP to partition large-size images. To reduce this number, the hyperspectral image is divided into blocks and the reduction step is applied independently within each block. Then, the AP method is applied only on exemplars of the duplicated pixels and non-duplicated pixels. However, in its current version, AP does not take into account the presence of identical objects after the reduction step in the calculation of the criteria used. Other drawbacks of the standard AP method are: (i) some parameters are not computed adaptively; and (ii) the criterion of identification of class exemplars may create not perfectly homogeneous classes, as demonstrated in
Section 3.1.2.
To extend the AP method to large-size data, such as hyperspectral aerial images, and to optimize it by adaptively calculating the criteria and parameters used, we propose here a new version without any prior knowledge introduced by the user. We recall that a relevant partitioning method, whatever its nature (supervised, semi-supervised, or unsupervised), must provide results to the end-user, taking into account the physical characteristics provided by measuring instruments [
21,
22].
The main contributions of this work are: (1) modification and optimization of several steps of the standard AP algorithm; (2) introduction of a new approach to partition large size images and proposal of a fusion procedure of the classes obtained in the blocks with stable results regardless of the chosen block size; and (3) generation of hierarchical partitioning. For AP optimization, the improvements are the estimation of the preference parameter value for each object; taking into account the presence of identical objects in the calculation of similarity, responsibility, and availability criteria; updating procedure of estimating the values of the responsibility and the availability criteria; and finally, modification of the decisional criterion used to estimate the number of classes and identify their exemplars. The proposed hierarchical method allows the user to obtain several partitions while indicating the most optimal one. These partitioning results are very important and necessary in several application fields to perform a fine analysis and interpretation of the formed classes.
The remainder of the paper is organized as follows:
Section 2 provides an overview of the standard AP algorithm and related studies.
Section 3 describes the proposed method, named “Unsupervised Partitioning by Optimized Affinity Propagation” (UP-OAP) and its hierarchical version, named “Hierarchical Unsupervised Partitioning approach by OAP” (HUP-OAP).
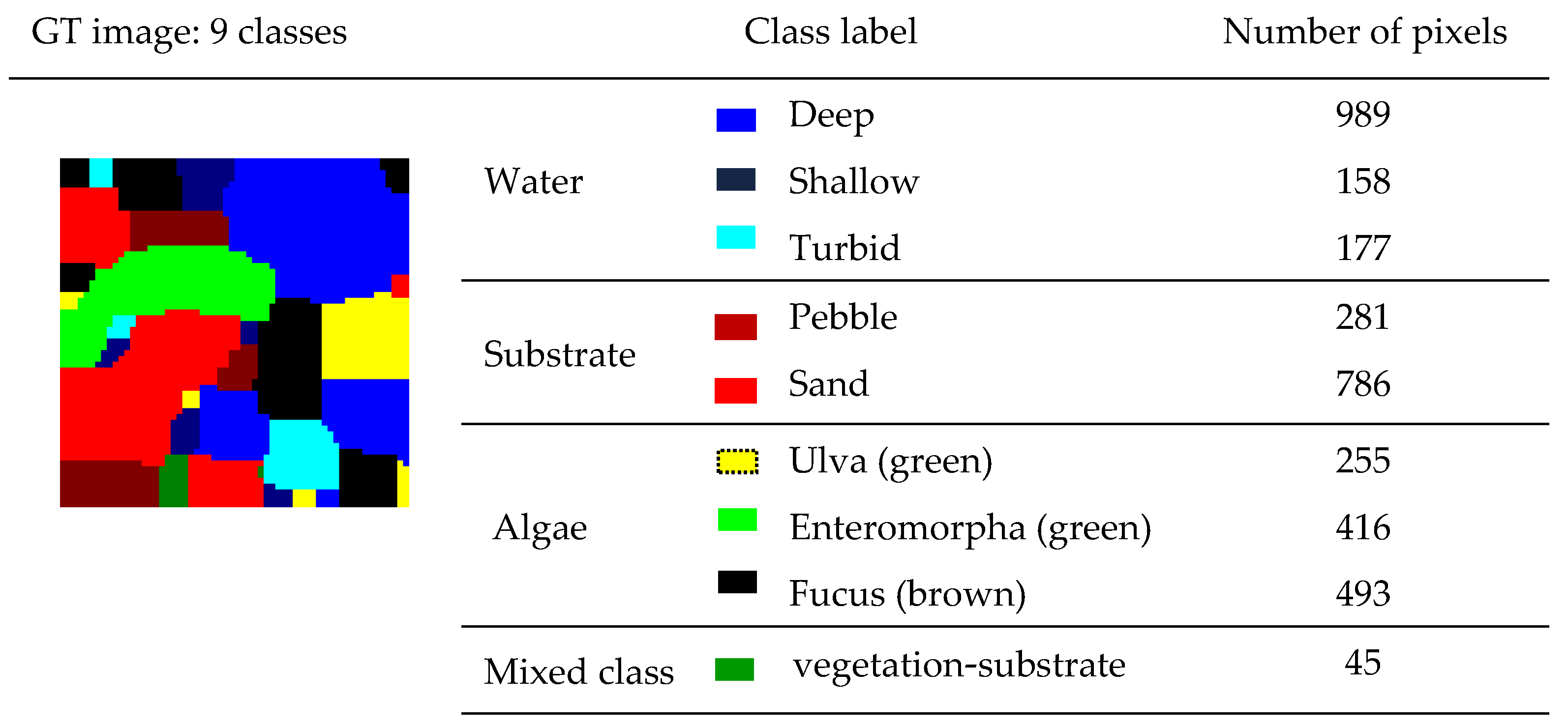
Section 4 presents the assessment results of the proposed method on a synthetic hyperspectral image constructed from a real aerial image acquired by our platform. It is also evaluated on a real aerial large-size hyperspectral image. The target application of these images is the identification of marine algae species. To assess the efficiency of the proposed unsupervised method, each image is provided with validated GT data. Finally,
Section 5 concludes this paper and provides some perspectives.