Abstract
Satellite altimetry over the oceans shows that the rate of sea-level rise is far from uniform, with reported regional rates up to two to three times the global mean rate of rise of ~3.3 mm/year during the altimeter era. The mechanisms causing the regional variations in sea-level trends are dominated by ocean temperature and salinity changes, and other processes such as ocean mass redistribution as well as solid Earth’s deformations and gravitational changes in response to past and ongoing mass redistributions caused by land ice melt and terrestrial water storage changes (respectively known as Glacial Isostatic Adjustment (GIA) and sea-level fingerprints). Here, we attempt to detect the spatial trend patterns of the fingerprints associated with present-day land ice melt and terrestrial water mass changes, using satellite altimetry-based sea-level grids corrected for the steric component. Although the signal-to-noise ratio is still very low, a statistically significant correlation between altimetry-based sea-level and modelled fingerprints is detected in some ocean regions. We also examine spatial trend patterns in observed GRACE ocean mass corrected for atmospheric and oceanic loading and find that some oceanic regions are dominated by the fingerprints of present-day water mass redistribution.
1. Introduction
In recent years, a number of studies have investigated the closure of the sea-level budget at global and regional scales over the altimetry era [1,2,3,4,5]. This is generally carried out by comparing the altimetry-based sea-level change with the sum of contributions using observations (e.g., Gravity Recovery and Climate Experiment (GRACE) satellite gravimetry data for estimating mass changes, and Argo-based ocean temperature and salinity data) or model outputs (e.g., for estimating glacier mass balance). Assessing the closure/non-closure of the sea-level budget has many implications, such as detecting acceleration [2] or an abrupt change in one or several components, for process understanding [5], cross calibrating the different observing systems used to quantify sea-level and its components, detecting possible systematic errors [6,7], placing upper bounds on poorly determined or missing contributions (e.g., from the deep ocean not sampled by Argo [8]), and finally for validating climate models used to simulate future changes. In terms of global average, the sea-level budget is found to be closed up to around 2016 within the observation uncertainties (e.g., [1,2,3,4,5]), although beyond 2016, the global mean budget appears no longer closed [6,7]. A few recent studies have also addressed the closure of basin-scale sea-level budget using either altimetry or tide gauge sea-level data (e.g., [9,10,11,12,13]). The closure of the regional budget is only observed in some regions but not everywhere. For example, using altimetry, GRACE and Argo data over 2005–2015, the authors of [13] came to the conclusion that the regional budget cannot be closed in the Indian-south Pacific region. The global mean sea-level rise is now well explained by global mean ocean thermal expansion plus water mass addition from ice sheet and glacier mass loss. At regional scale, sea-level trends depart from the global mean as a result of regional changes in steric sea-level (regional changes in ocean temperature and salinity), ocean circulation-related mass redistribution, and regional sea-level patterns associated with the Glacial Isostatic Adjustment (GIA) as well as present-day land ice melt and terrestrial water storage change. The latter are known as sea-level fingerprints (or barystatic-GRD fingerprints) and represent sea-level changes induced by changes in Earth gravity, Earth rotation and elastic solid Earth deformation [14]. While at regional scale, sea-level trends are still dominated by steric changes [15,16,17], theoretical studies predict that with accelerated land ice melt, barystatic-GRD fingerprints will become detectable (e.g., [18,19,20]).
In this study, we do not attempt to close the regional sea-level budget, but rather use altimetry-based sea-level corrected for steric effects over the Argo era to try to detect the barystatic-GRD fingerprints due to present-day water mass redistributions. Our study period covers January 2005 to December 2015. We focus on regional patterns and only consider departures from the global averages. Thus, we remove the global mean rises and accelerations of observed sea-level and thermal expansion. When using the GRACE space gravimetry data over the oceans for comparison purposes, we also remove the global mean ocean mass term (with the latter being called barystatic sea-level, [14]), as well as the contribution of atmospheric and oceanic loading. Our study complements recently published articles (e.g., [21,22]) that detect the fingerprints by looking at either ocean basin scale averages or coastal regions.
Section 2 briefly describes the barystatic-GRD fingerprints. The description of the data sources employed in the present study is provided in Section 3. The results of the comparison between the steric-corrected altimetry-based sea-level and barystatic-GRD fingerprints are presented in Section 4.1, while Section 4.2 is dedicated to the relationship between GRACE-observed ocean mass changes corrected for atmospheric and oceanic loading and the barystatic-GRD fingerprints. A short discussion and an overview of our findings are provided in Section 5. Finally, the conclusions are presented in Section 6.
2. Modelled Barystatic-GRD Fingerprints
The response of the solid Earth to water mass redistribution between continents and oceans may become a key contribution of regional sea-level changes [16,23,24]. Ongoing water exchange causes changes in regional sea-level patterns, known as barystatic-GRD fingerprints, hereinafter called relative sea-level fingerprints. This water can come from melting ice sheets and glaciers, or from the hydrological cycle over the continents [25]. The relative sea-level is defined as the height of the ocean water column bounded by the solid Earth surface and the sea surface [19]. Accordingly, the relative sea-level fingerprints are a consequence of the changing gravitational attraction between ice and water bodies on land and the resulting mass change of the oceans, plus the associated deformations of the solid Earth due to the changing load [23]. As an ice sheet loses mass, the crust underneath and in the surrounding area uplifts. Due to the ice loss, the gravitational attraction of the ice sheet on the water also decreases, causing a corresponding decrease in the nearby sea surface height. The two effects cause the relative sea-level to fall in areas near the melting ice mass, while in the far-field, the relative sea-level rises in order to conserve mass [25]. The area of sea-level drop around a melting ice sheet can extend up to 2000 km from the margin of the ice sheet [18]. The sea-level decreases at a rate of about more than an order of magnitude greater than the globally averaged rise, while in the far-field of the melting ice sheet, the sea-level rate of rise is about 10 to 30% higher than the global average [25], mainly dominated by the rotational feedback.
Using as input ice mass change over ice sheets and glaciers, and terrestrial water changes observed by GRACE over 2002–2016, Ref. [19] computed the fingerprints for the relative sea-level, solving the following equation:
where ΔS, ΔN and ΔU are the relative sea-level change, absolute sea-level change and vertical land motion, respectively. (θ), (ϕ) and (Δt) are colatitude, longitude and time period of interest. Tide gauges measure relative sea-level changes (ΔS), satellite altimetry measures absolute sea-level changes (i.e., ΔS + ΔU; i.e., relative sea-level change plus vertical land motion). If geoid height data were used, then the quantity to be considered would be:
where g is Earth’s mean gravitational acceleration (~9.8 m s−2), ΔΦ is the net perturbation in Earth’s surface potential, and ΔC is a spatial invariant that explains the discrepancy between absolute sea level and geoid height [18,26].
In the first part of this study, we focus on absolute sea-level fingerprints as we attempt to detect them in the steric-corrected altimetry-based sea-level. For that purpose, we compare the latter observations with modelled absolute sea-level fingerprints computed by [19]. In the second part of the study, our goal is to detect the fingerprints in the GRACE-based ocean mass change data. Based on [27]’s statement that GRACE observations show ocean mass changes and hence relative sea-level changes (i.e., change in the ocean water column height), we compare GRACE ocean mass change with [19]’s modelled relative sea-level fingerprints.
Ref. [19] included the barystatic term (global mean ocean mass) in the relative sea-level fingerprints (ΔS), in order that the net change water mass from land to be uniformly distributed over the oceans. As our goal is to compare the absolute sea-level fingerprints (relative sea-level plus vertical land motion fingerprints) with the steric-corrected altimetry-based sea-level, we subtracted the barystatic contribution (i.e., global mean ocean mass change) from the modelled relative sea-level fingerprints.
Figure 1 shows the [19]’s modelled absolute sea-level fingerprints (top panel) and relative sea-level fingerprints (bottom panel) over the period January 2005 to December 2015. Ref. [19] used as input for land ice and terrestrial water mass changes GRACE data from the Center for Space Research (CSR) Release-06 (RL06) Level-2 solutions computed in the centre-of-mass reference frame with the rotational feedback included. The fingerprints are publicly available at [28]. The modelled fingerprints based on the Jet Propulsion Laboratory (JPL) RL06 solutions are shown in Figure S1 of the Supplementary Material (SM). Figure S2 of the SM present the differences between the CSR and JPL solutions for both the absolute and relative sea-level fingerprints. The differences fluctuate between ±0.1 mm/yr with positive values in the South Atlantic Ocean and North Pacific Ocean, and negative values in the North Atlantic Ocean and Southwest Pacific Ocean. The difference patterns indicate an overall good agreement.
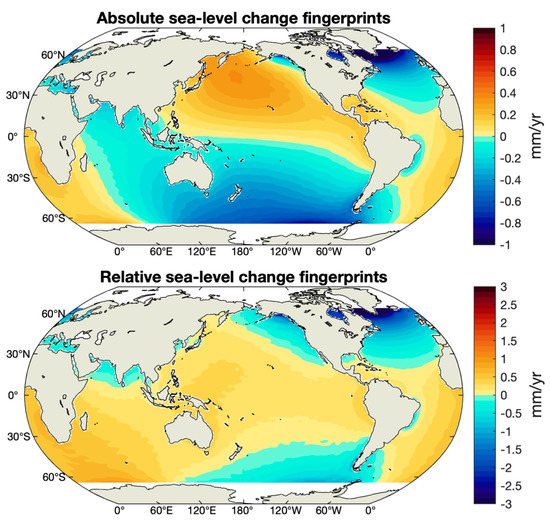
Figure 1.
Linear spatial trends for absolute (top panel) and relative (bottom panel) sea-level fingerprints computed by [19] using GRACE CSR solutions for estimating land ice and terrestrial water mass changes, for the time interval from January 2005 to December 2015. Redrawn from [19].
Both the absolute (top panel of Figure 1) and relative (bottom panel of Figure 1) sea-level fingerprints show negative trends in the proximity of large ice mass losses, e.g., in the vicinity of the Greenland ice sheet and in the Amundsen Sea sector of West Antarctica. Positive trends are observed in the far-field, e.g., in the North Pacific Ocean and South Atlantic Ocean. Ref. [19] provides the 1σ uncertainties of the fingerprint products, that are presented in Figure S3 of the SM. These range between 0.03 and 0.3 mm/yr.
3. Data
3.1. Altimetry-Based Sea-Level Data
We use gridded sea-level time series provided by the Copernicus Climate Change Service (C3S). The C3S data are freely available at https://climate.copernicus.eu/ESOTC/2019/sea-level (accessed on 10 March 2021). The C3S products (used in the present analysis) are monthly sea-level anomalies with 0.25° × 0.25° grid resolution, computed with respect to the 1993–2012 reference period, with a latitude coverage of ±82° [29]. For the period 2005–2015, the C3S sea-level anomalies are based on data from the reference altimetry missions, Jason-1 and Jason-2, complemented by data from Envisat, and SARAL-AltiKa. We corrected the gridded altimetry-based sea-level data are for the GIA effect using the ICE6G-D model from [30]. The corresponding map is presented in Figure S4 of the SM.
3.2. Steric Sea-Level Data
We use an ensemble mean of 1° × 1° gridded steric data (0–2000 m depth range for integration of temperature and salinity effects) at monthly intervals, from four different solutions: NOAA (National Oceanic and Atmospheric Administration) data set [31]; EN4 data set from the Met Office Hadley Center [32]; Scripps Institution of Oceanography (SIO) monthly data [33]; and JAMSTEC (Japan Agency for Marine-Earth Science and Technology) MILA GPV (Mixed Layer data set of Argo, Grid Point Value) product data set [34]. The NOAA, SIO and JAMSTEC data sets are based on temperature and salinity measurements from Argo floats only [35]. The EN4 data set is based on Argo float measurements along with mechanical (MBT) and expandable (XBT) bathythermographs data with the correction from [36].
3.3. GRACE Ocean Mass Data
We consider GRACE RL06 monthly mass concentration (mascon) solutions provided by CSR and JPL, covering the period from January 2005 to December 2015 [37,38,39]. As we are interested in detecting the fingerprints in ocean mass, the GRACE solutions were corrected for atmospheric and oceanic loading. We use the GAD product which represents the monthly mean ocean bottom pressure caused by non-tidal dynamic oceanic and atmospheric mass variations. In this study, we only considered the mascon solutions in order to minimize the leakage problem that affects the spherical harmonics solutions. The leakage problem is due to the coarse spatial resolution of GRACE, in which continental signal may leak into the coastal areas (and to a minor extent vice versa). The leakage problem is already addressed for the JPL mascon solutions by the Coastal Resolution Improvement (CRI) filter [39]. Regarding the CSR mascon solution, the application of a 200 km buffer zone (as in [6]) is sufficient to cope with the leakage issue. The leakage effect between land and ocean remains a challenge to GRACE applications. Some remaining leakage signal will affect the capability of GRACE to accurately quantify the sea-level fingerprint in coastal regions near major mass losses, e.g., North Atlantic near Greenland and the southern oceans near the Amundsen Sea Embayment in West Antarctica. However, in the present study, we focus on the open ocean.
Both the CSR and JPL data centres provide GRACE mascon solutions already corrected for GIA using the ICE6G-D model from [30].
3.4. Data Processing
For all data sets, we select the period from January 2005 to December 2015, over which the [19] fingerprints and the steric sea-level data sets are both available. All data sets were spatially interpolated into 1° × 1° resolution grids, with a latitude coverage ranging between ±65°. For the altimetry-based, steric and ocean mass data, we removed the annual and semi-annual signals, through a least-squares fit of 12- and 6-month periods. In addition, the global mean (area-weighted mean computed over ±65° of latitudes) linear trend was removed from all three data sets. Based on the assumption that the global mean sea-level (GMSL) is accelerating [40,41], we also removed a global mean quadratic trend from the altimetry-based sea-level. However, the results remain unchanged.
4. Results
To detect the fingerprints in steric-corrected altimetry-based sea-level and in GRACE-based ocean mass corrected for atmospheric and oceanic loading, we compared them with the modelled absolute and relative sea-level fingerprints from [19], respectively.
4.1. Comparison between Steric-Corrected Altimetry and Absolute Sea-Level Fingerprints
The altimetry-based sea-level linear trend map from C3S is shown in the top panel of Figure 2. The middle panel shows the linear trend map of the ensemble mean of steric sea-level data sets (NOAA, EN4, SIO and JAMTEC). Both trend maps present similar patterns (note that global mean linear trends have been removed).
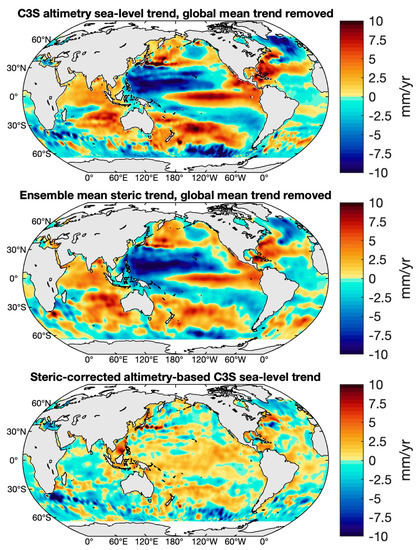
Figure 2.
Regional linear trend maps for the C3S altimetry sea-level (top panel), the ensemble mean steric sea-level (middle panel) and the steric-corrected altimetry-based sea-level (bottom panel) over January 2005–December 2015. The global mean linear trend has been removed in both the altimetry and steric data sets. The altimetry sea-level has been filtered with a 500 km Gaussian filter to minimize very short wavelength signal.
The steric-corrected altimetry-based sea-level, i.e., the difference between the altimetry-based sea-level and the ensemble mean steric sea-level is displayed in the bottom panel of Figure 2. The linear trend map of the steric-corrected altimetry-based sea shows some remarkable regional patterns, for example, the major western boundary currents and the negative trend encircling southern Greenland and extending down to about 50° N.
Since the Greenland ice sheet is an area of intense ice mass loss, we investigate whether the altimetry-based sea-level is able to detect the corresponding sea-level fingerprints. First, we depict in Figure 3 and Figure 4 the regional linear trend uncertainties at 90% confidence level (1.65σ) of the altimetry-based sea-level and steric data sets. The altimetry-based sea-level trend uncertainty is computed through a generalized least squares method using the local sea-level trends variance-covariance matrix presented in [42] and available at https://doi.org/10.17882/74862 ([43], accessed on 17 June 2021). The standard uncertainty of the steric sea-level is estimated as the maximum differences between the trends of the different data sets (NOAA, EN4, SIO and JAMTEC), i.e., the difference between the maximal and minimal linear trends. This product simply represents the dispersion among the limited number of data sets; thus, the amplitude of the steric uncertainty map is likely to be overestimated.
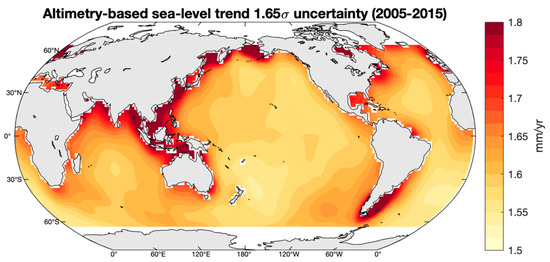
Figure 3.
Uncertainty at 90% confidence level (i.e., 1.65σ) map for the altimetry-based sea-level trend [43] for the time interval January 2005–December 2015.
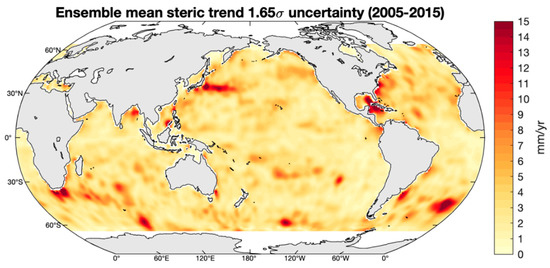
Figure 4.
Uncertainty at 90% confidence level (i.e., 1.65σ) map for the ensemble mean (NOAA, EN4, SIO and JAMTEC) steric sea-level trend for the time interval January 2005–December 2015, based on the maximum differences between the different data sets.
Overall, at a large scale, the spatial trend patterns displayed in the steric-corrected altimetry trend map do not resemble those of the uncertainty maps. The Pearson spatial correlation (see definition below) between the steric-corrected altimetry-based sea-level and the steric uncertainty is presented in the SM (Figure S5), displaying statistically significant correlations smaller than 0.6 in the equatorial Pacific Ocean. Thus, we cannot exclude that the steric-corrected altimetry map is partially contaminated by errors in the data.
In next step, we compared the steric-corrected altimetry time series with the time series of the absolute sea-level fingerprints [19]. Figure 5 shows the map of the statistically significant Pearson correlation coefficients between the two time series. The Pearson’s correlation coefficient is a product-moment correlation coefficient which measures the linear dependence between two random variables. It is computed by the ratio of the covariance of the two variables and the product of their standard deviations (std, defined as the square-root of the variance of the considered variable), thus essentially a normalized measurement of the covariance:
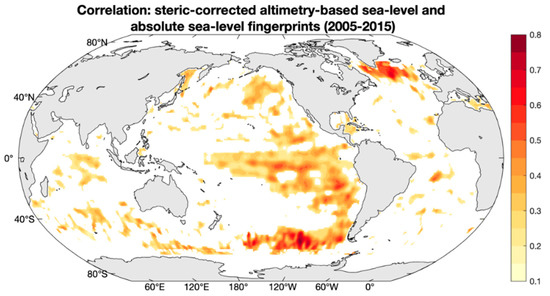
Figure 5.
Pearson’s correlation map between steric-corrected altimetry and modelled absolute sea-level fingerprints time series for January 2005–December 2015. The map only shows positive correlations that are statistically significant at 95% confidence level.
The values of the correlation coefficients can range from −1 to 1, with −1 representing a direct, negative correlation; 0 representing no correlation; and 1 representing a direct, positive correlation. We use the corrcoef function provided by MATLAB to calculate the Pearson’s correlation coefficient. Additionally, this function also returns the p-values for testing the null hypothesis that there is no relationship between the observed phenomena. p-values range from 0 to 1, where values close to 0 correspond to a significant correlation and a low probability of observing the null hypothesis. When the p-value is smaller than the significance level (0.05 at 95% confidence level), the corresponding correlation is considered significant.
Figure 5 shows that in southern Greenland, the correlation is up to 0.7 with a 95% confidence level. There are some other regions where a positive correlation is also found, e.g., in the eastern tropical and south Pacific Ocean.
We also used the concept of explained variance E (e.g., [44]) to compare the spatial fluctuations of the two time series (see Figure 6). The fraction of the variance of the steric-corrected altimetry-based sea-level explained by the fingerprints is defined by Equation (4):
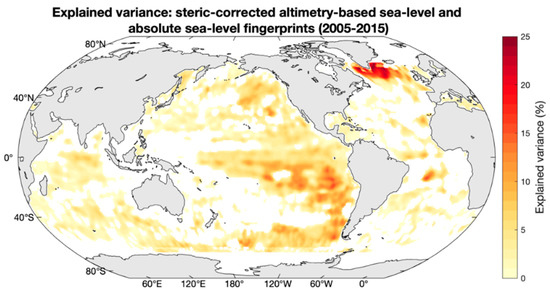
Figure 6.
Explained variance map between steric-corrected altimetry and modelled absolute sea-level fingerprints time series for January 2005–December 2015.
The explained variance can range from −∝ to 1. However, the values shown in Figure 6 range between 0 and 25%, just to focus on the regions that show similar spatial fluctuations in both amplitude and phase. An explained variance of about 25% is observed in the south-eastern Greenland region, the same region where we found the negative trend in the steric-corrected altimetry-based sea-level and where the correlation between this variable and the fingerprints is up to 0.7, as previously mentioned. Accordingly, we conclude that among other contributions, the absolute sea-level fingerprints account for about 25% to the observed altimetry-based sea-level drop in the region nearby the Greenland ice sheet.
As in [21], we also compared the steric-corrected altimetry-based sea-level and absolute sea-level fingerprints at basin scale. For that purpose, we computed the regional averages for 6 ocean basins: North Pacific (65° N–30° N), Tropical Pacific (30° N–30° S), South Pacific (30° S–50° S), North Atlantic (65° N–0°), South Atlantic (0°–65° S) and Indian ocean (up to 50° S). Figure S6 of the SM displayed the contours of the six ocean basins. The regional averages of the two variables (steric-corrected altimetry and absolute sea-level fingerprints) along with the associated Pearson’s correlation coefficient for each ocean basin are shown in Figure 7.
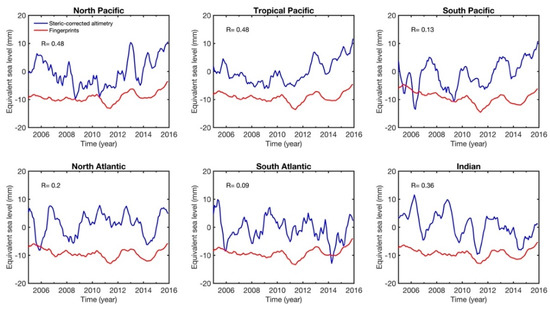
Figure 7.
Regionally averaged time series of steric-corrected altimetry-based sea-level (in blue) and absolute sea-level fingerprints (in red) for 6 ocean basins: North Pacific (65° N–30° N), Tropical Pacific (30° N–30° S), South Pacific (30° S–50° S), North Atlantic (65° N–0°), South Atlantic (0°–65° S) and Indian ocean (up to 50° S); for January 2005–December 2015. A 6 month smoothing was applied to the basin averages. The R number represents the Pearson correlation between both variables in the corresponding ocean basin.
The curves in Figure 7 display important interannual variability and show significant correlations between steric-corrected altimetry and fingerprints. The Lomb–Scargle periodograms of each time series shown in Figure 7 are presented in Figure 8a,b. The Lomb–Scargle periodogram is a method that allows efficient computation of a Fourier-like power spectrum estimator for detecting and characterizing periodic signals in unevenly sampled data. We use the plomb function provided by MATLAB to calculate the power spectral density estimate of the quadratically detrended time series of interest. We consider 12 samples per year and represent the logarithm of the period in years. We also estimate the probability of detection of the estimated characteristic period, which measures the peak significance level. We set the threshold at the 95% confidence level. The detection probability shows the probability that a peak in the spectrum is not due to random fluctuations. The regionally averaged absolute sea-level fingerprints all show a significant peak at ~3 yr, possibly related to the ENSO (El Niño-Southern Oscillation) signal in land hydrology and land ice melt. A ~3 yr peak is also seen in regionally averaged steric-corrected altimetry, although with higher magnitudes than in the fingerprints. As in the altimetry and steric data, only a global mean trend and seasonal cycle were removed, the interannual variability of the mass component of the altimetry-based sea-level is still present in the residuals.
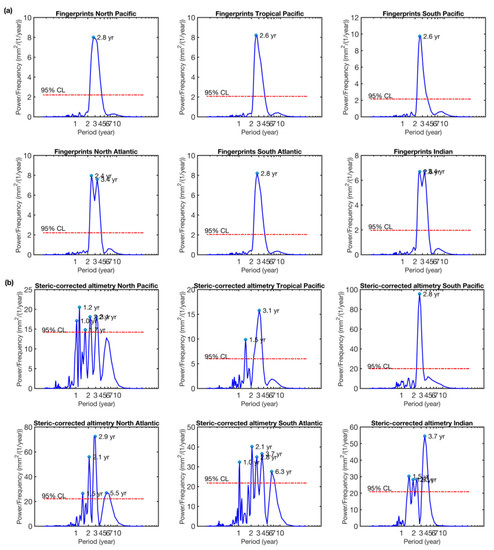
Figure 8.
Periodograms of the regionally averaged absolute sea-level fingerprints (a) and steric-corrected altimetry-based sea-level (b), quadratically detrended time series, for January 2005–December 2015 and with a 6-month smoothing applied to the basin averages. The x-axes are in logarithmic scale. The horizontal red line represents the 95% confidence level (noted CL) of the peaks.
The high and statistically significant (95% confidence level) correlations seen in the North Pacific and Tropical Pacific Ocean basins (Figure 7) suggest a possible detectability of the interannual signal of the far-field fingerprints in the steric-corrected altimetry-based sea-level.
4.2. Comparison between GRACE Data Corrected for Atmospheric and Oceanic Loading and Modelled Relative Sea-Level Fingerprints
Figure 9 shows the regional trends of GRACE ocean mass change (corrected for atmospheric and oceanic loading) from the CSR mascon solutions with the global mean removed (similar results from the JPL solutions are shown in Figure S7 of the SM). The map shows negative trends around Greenland, a dipole pattern in the Atlantic Ocean with positive trends in the southern part and negative trends in the northern part. It also shows positive trends in the Tropical Pacific and south Indian Ocean. In addition, we can also observe the impacts of the 2004 Sumatra and 2011 Japan earthquakes.
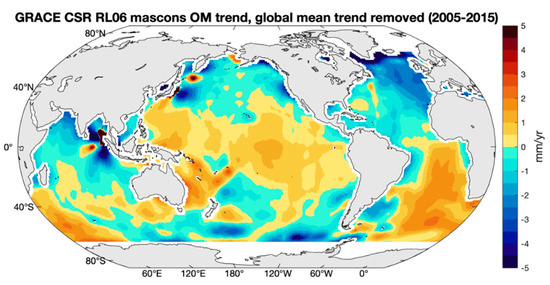
Figure 9.
Regional linear trend map of GRACE ocean mass (OM) from the CSR solution for the time interval January 2005–December 2015. The global mean linear trend has been removed. A 200 km buffer zone has been applied along the coasts.
In Figure S8 of the SM, we present the 1σ uncertainties provided by the JPL mascon solutions. The uncertainties are below 0.1 mm/yr over most of the ocean basins except for some specific locations, such as the earthquake regions.
It is worth noting that some of the spatial trend patterns shown in Figure 9 are also observed in the relative sea-level fingerprints (Figure 1, bottom panel): in particular, the negative trends encircling the Greenland ice sheet and the positive trends over the Southeast Atlantic Ocean. Figure 10 and Figure 11 show the spatial Pearson correlation and spatial explained variance computed between the GRACE mascon solution and the relative sea-level fingerprints time series. Significant correlations are seen in most ocean areas. We conclude that the signature of the relative sea-level fingerprints is partly visible in the GRACE data corrected for atmospheric and oceanic loading, as well as for GIA.
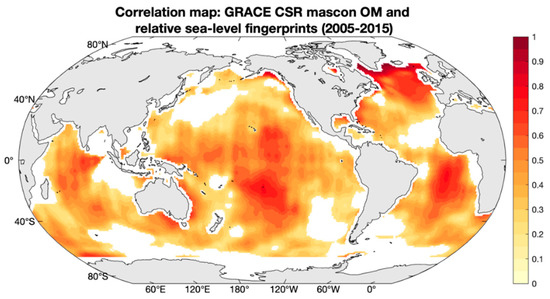
Figure 10.
Pearson’s correlation map between GRACE ocean mass (OM) and relative sea-level fingerprints time series for January 2005–December 2015. The map only shows positive correlations that are statistically significant at 95% confidence level.
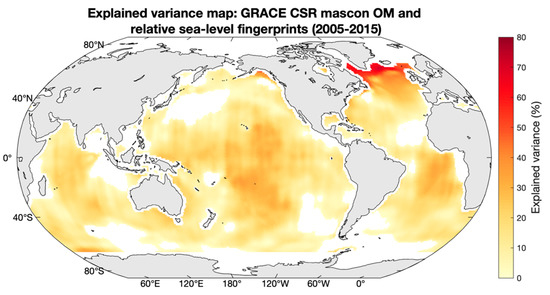
Figure 11.
Explained variance map between GRACE ocean mass (OM) and relative sea-level fingerprints time series for January 2005–December 2015.
It is worth recalling that the modelled relative sea-level fingerprints used GRACE data over land only (ice sheets, glaciers and river basins) to estimate the water mass redistribution, while here we use GRACE over the oceans to detect the corresponding fingerprints. There is thus no circular reasoning in this approach. In effect, even though the sea-level fingerprint calculation uses some information from GRACE on land, it is based on a sea-level equation that considers self-gravitational attraction and loading deformation. This allows us to infer that the spatial trend patterns observed in GRACE data over the oceans likely represent the regional fingerprint signal due to the present-day land ice melt plus terrestrial water mass changes. We suggest that this signal should be removed from GRACE when interpreting GRACE data over the oceans in terms of barotropic contribution of steric-induced circulation changes.
5. Discussion
This study presents an attempt to detect the spatial trend patterns of sea-level change due to the present-day land ice melt and terrestrial water storage change, i.e., the so-called barystatic-GRD fingerprints, in the altimetry-based sea-level data corrected for steric effects, as well as in GRACE data over the oceanic domain. The signal-to-noise ratio in altimetry residuals is still low and only in a few limited regions (e.g., around southern Greenland) the fingerprints seem detectable. We report a statistically significant correlation of 0.7 in regions south to Greenland, with an explained variance of ~25% between the steric-corrected altimetry and the modelled fingerprints. Overall, the correlation is poor globally. One cannot exclude that the fingerprint trend patterns are still hidden in the residual noise due to errors in small-scale, high-energetic signals in the altimetry and steric data. In effect, as discussed in the literature (e.g., [45]), several sources of errors affect the Argo-based steric data sets; for example, measurement errors, uneven sampling of the oceanic domain by Argo floats, processing methodologies for filling the data gaps and gridding, choice of the climatology, etc. It would not be surprising that the steric-corrected altimetry residuals are significantly contaminated by steric sea level uncertainties. This definitely needs further investigation.
Ref. [19] had corrected their fingerprints for the GIA effect using the model presented by [46], displayed in the top panel of Figure S9 of SM, whereas the altimetry sea-level and the GRACE ocean mass have been corrected using the ICE6G-D model from [30]. The two GIA models are shown in middle panel of Figure S9 of the SM. The GIA difference between ICE6G-D [30] and [46] is fairly small, within ±0.1 mm/yr in most regions (and up to 0.2 mm/yr in limited regions). The steric-corrected altimetry-based sea-level rates (with mean rate removed) are up to ~±10 mm/yr (see Figure 2), and the GRACE mascon ocean mass rates (with global mean removed) ranges within ~±5 mm/yr (see Figure 9). Thus, the slight difference between the two GIA models, i.e., [30] and [46], will not affect our comparisons and conclusions.
Dividing the ocean domain into six ocean basins and regionally averaging the steric-corrected altimetry-based sea-level and absolute sea-level fingerprints gives us a different perspective on the detection of fingerprints by the altimetry data. The correlations between the two variables show that only in the North Pacific and Tropical Pacific Ocean (from 30° S up to 65° N), i.e., the so-called far-field, the steric-corrected altimetry seems able to detect the fingerprints. However, in these regions, the reported correlation most likely results from interannual variability seen in regionally averaged time series. This interannual correlation may not represent a direct cause–effect link, but rather the consequence of an ENSO-related forcing in altimetry-based sea-level on the one hand and in the land hydrology and land ice melt-related fingerprints on the other hand.
We have performed an EOF (Empirical Orthogonal Function) decomposition of the steric-corrected altimetry data. The spatial patterns and principal components are shown in Figure 12 and Figure 13. Mode 1 represents the steric-corrected altimetry trend. The following modes (2 to 4) display the interannual/decadal signal that remains in the steric-corrected altimetry data, a consequence of not correcting for interannual variability of water mass. Figure 13 also shows the four first principal components of the EOF decomposition of the absolute sea-level fingerprints (red curves) (spatial patterns of the EOF decomposition of the absolute sea-level fingerprints are presented in Figure S10 of the SM). The principal components of modes 1 and 2 show correlations of ~96% and 60%, respectively. Modes 2 exhibit strong interannual variability. We conclude that the interannual variability present in the residuals clearly have a mass origin since it is correlated with the interannual variability of the fingerprints.
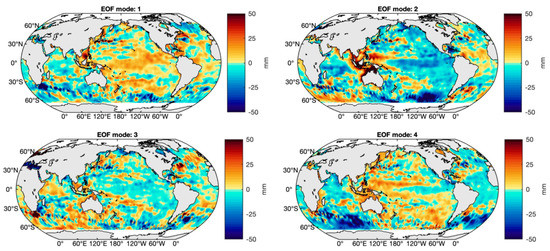
Figure 12.
Modes 1, 2, 3 and 4 of the EOF decomposition of the steric-corrected altimetry-based C3S sea-level data for January 2005–December 2015.
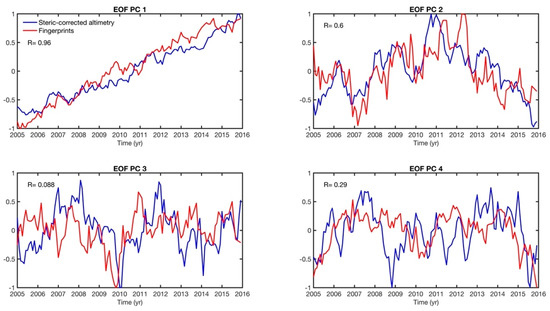
Figure 13.
Principal components (PC) 1, 2, 3 and 4 of the EOF decomposition of steric-corrected altimetry-based sea-level (in blue) and absolute sea-level fingerprints (in red) for January 2005–December 2015. The R number represents the Pearson correlation between both variables in the corresponding principal component.
Another result of this study suggests that GRACE data (corrected for atmospheric and oceanic loading, and GIA) distinctly show the same trend signature as the relative sea-level fingerprints around Greenland, central Pacific and south Atlantic. This suggests that the relative sea-level fingerprint signal needs to be removed before interpreting the GRACE data over the oceans in terms of the barotropic contribution of steric-induced circulation changes.
6. Conclusions
In this paper, we compared the modelled absolute and relative sea-level fingerprints with steric-corrected altimetry-based sea-level data and with GRACE-based ocean mass data (corrected for GIA and atmospheric and oceanic loading), respectively. The goal was to detect the effects of the present-day land ice melt and terrestrial water mass change in the satellite data. We conclude that about 25% of the variability observed in the steric-corrected altimetry-based sea-level in the vicinity of the Greenland ice sheet may be explained by the absolute sea-level fingerprints. On the other hand, the relative sea-level fingerprints explain more than 70% of the variability observed in the GRACE-based ocean mass for the same region.
The principal components of the EOF decomposition of the steric-corrected altimetry and fingerprint variables show a good correlation. Thus, we state that the interannual variability present in the steric-corrected altimetry data has a dominant mass origin (as expected), as it is correlated with the interannual variability present in the fingerprints.
Finally, we compare the steric-corrected altimetry data with the fingerprints at six ocean basins. The results indicate the detectability of the interannual component of the far-field fingerprints in the steric-corrected altimetry-based sea-level.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/rs13224667/s1, Figure S1: Absolute and relative sea-level fingerprints from the GRACE JPL solution; Figure S2: Differences between GRACE CSR and JPL solutions for absolute and relative sea-level change fingerprints; Figure S3: Uncertainties in absolute and relative sea-level change fingerprints; Figure S4: ICE6G-D GIA trend map for absolute sea level; Figure S5: Correlation map between steric-corrected altimetry-based sea-level and steric 1.65σ uncertainty; Figure S6: Contours of ocean basins; Figure S7: Trend map of the JPL GRACE mascon solution; Figure S8: Trend uncertainty of the JPL GRACE mascon solution; Figure S9: GIA trend maps of Caron et al. (2018) and Peltier et al. (2018); Figure S10: Spatial trend patterns of the EOF decomposition of the absolute sea-level fingerprints.
Author Contributions
Conceptualization, A.C. and L.M.; methodology, A.C., L.M. and J.C.; software, L.M.; validation, L.M. and A.B.; formal analysis, A.C., L.M., A.B. and J.C.; writing—original draft preparation, L.M.; writing—revision and editing, L.M., A.C., A.B. and J.C. All authors have read and agreed to the published version of the manuscript.
Funding
L.M. is supported by a post-doctoral fellowship from the International Space Science Institute (ISSI). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (GRACEFUL Synergy Grant agreement No 855677) for A.B. JC was supported by the NASA GRACE and GRACE Follow-On Projects (under contract #NNL14AA00C and JPL subcontract #1478584), and NASA ESI and GRACE Follow-On Science Team Programs (NNX17AG96G and 80NSSC20K0820).
Data Availability Statement
The NOAA Argo data are available from https://www.ncei.noaa.gov/access/global-ocean-heat-content/. The SIO Argo data are available from http://sio-argo.ucsd.edu/RG_Climatology.html. The JAMSTEC MOAA GPV are available from http://www.jamstec.go.jp/ARGO/argo_web/argo/?page_id=83&lang=en. The EN4 Argo data are available from http://hadobs.metoffice.com/en4/download.html. GRACE data are available via https://podaac.jpl.nasa.gov/dataset/TELLUS_GRAC-GRFO_MASCON_CRI_GRID_RL06_V2 and http://www2.csr.utexas.edu/grace/RL06_mascons.html (accessed on 11 June 2021). GAD data were downloaded from http://www2.csr.utexas.edu/grace/RL06_mascons.html, accessed on 11 June 2021. Adhikari et al. (2019) fingerprints are publicly available at https://doi.org/10.7910/DVN/8UC8IR. The GIA corrections were downloaded from: https://podaac-tools.jpl.nasa.gov/drive/files/allData/tellus/L3/gia/1-deg and https://www.atmosp.physics.utoronto.ca/~peltier/data.php (accessed on 11 November 2021).
Acknowledgments
We thank Surendra Adhikari and Erik Ivins for their thorough explanations about the use of the sea-level fingerprint solutions, in particular when using altimetry and GRACE data. The Argo data were collected and made freely available by the international Argo Program and the national programs that contribute to it (https://argo.ucsd.edu, https://www.ocean-ops.org, accessed on 18 November 2021). The Argo Program is part of the Global Ocean Observing System. We thank the four anonymous reviewers for their comments that helped us to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chambers, D.P.; Cazenave, A.; Champollion, N.; Dieng, H.; LloveL, W.; Forsberg, R.; Von Schuckmann, K.; Wada, Y. Evaluation of the Global Mean Sea Level Budget between 1993 and 2014. Surv. Geophys. 2017, 38, 309–327. [Google Scholar] [CrossRef]
- Dieng, H.B.; Cazenave, A.; Meyssignac, B.; Ablain, M. New estimate of the current rate of sea level rise from a sea level budget approach. Geophys. Res. Lett. 2017, 44, 3744–3751. [Google Scholar] [CrossRef]
- WCRP Global Sea Level Budget Group: Global sea-level budget 1993-present. Earth Syst. Sci. Data 2018, 10, 1551–1590. [CrossRef] [Green Version]
- Chen, J.; Tapley, B.; Save, H.; Tamisiea, M.E.; Bettadpur, S.; Ries, J. Quantification of ocean mass change using gravity recovery and climate experiment, satellite altimeter, and Argo floats observations. J. Geophys. Res. Solid Earth 2018, 123, 10212–10225. [Google Scholar] [CrossRef]
- Horwath, M.; Gutknecht, B.D.; Cazenave, A.; Palanisamy, H.K.; Marti, F.; Marzeion, B.; Paul, F.; Le Bris, R.; Hogg, A.E.; Otosaka, I.; et al. Global sea-level budget and ocean-mass budget, with focus on advanced data products and uncertainty characterization. Earth Syst. Sci. Data Discuss. 2021. [Google Scholar] [CrossRef]
- Chen, J.; Tapley, B.; Wilson, C.; Cazenave, A.; Seo, K.-W.; Kim, J.-S. Global ocean mass change from GRACE and GRACE follow-on and altimeter and Argo measurements. Geophys. Res. Lett. 2020, 47, e2020GL090656. [Google Scholar] [CrossRef]
- Barnoud, A.; Pfeffer, J.; Guérou, A.; Frery, M.-L.; Siméon, M.; Cazenave, A.; Chen, J.; Llovel, W.; Thierry, V.; Legeais, J.; et al. Contributions of altimetry and Argo to non-closure of the global mean sea level budget since 2016. Geophys. Res. Lett. 2021, 48, e2021GL092824. [Google Scholar] [CrossRef]
- Llovel, W.; Willis, J.; Landerer, F.; Fukumori, I. Deep-ocean contribution to sea level and energy budget not detectable over the past decade. Nat. Clim. Chang. 2014, 4, 1031–1035. [Google Scholar] [CrossRef]
- Rietbroek, R.; Brunnabend, S.-E.; Kusche, J.; Schröter, J.; Dahle, C. Revisiting the contemporary sea-level budget on global and regional scales. Proc. Natl. Acad. Sci. USA 2016, 113, 1504–1509. [Google Scholar] [CrossRef] [Green Version]
- Frederikse, T.; Riva, R.; Kleinherenbrink, M.; Wada, Y.; van den Broeke, M.; Marzeion, B. Closing the sea level budget on a regional scale: Trends and variability on the Northwestern European continental shelf. Geophys. Res. Lett. 2016, 43, 10864–10872. [Google Scholar] [CrossRef] [Green Version]
- Frederikse, T.; Jevrejeva, S.; Riva, R.E.M.; Dangendorf, S. A Consistent Sea-Level Reconstruction and Its Budget on Basin and Global Scales over 1958–2014. J. Clim. 2018, 31, 1267–1280. Available online: https://journals.ametsoc.org/view/journals/clim/31/3/jcli-d-17-0502.1.xml (accessed on 1 July 2021). [CrossRef]
- Kleinherenbrink, M.; Riva, R.; Sun, Y. Sub-basin-scale sea level budgets from satellite altimetry, Argo floats and satellite gravimetry: A case study in the North Atlantic Ocean. Ocean Sci. 2016, 12, 1179–1203. [Google Scholar] [CrossRef]
- Royston, S.; Vishwakarma, B.D.; Westaway, R.M.; Rougier, J.; Sha, Z.; Bamber, J.L. Can we resolve the basin-scale sea level trend budget from GRACE ocean mass? J. Geophys. Res. Ocean. 2020, 125, e2019JC015535. [Google Scholar] [CrossRef] [Green Version]
- Gregory, J.M.; Griffies, S.M.; Hughes, C.W.; Lowe, J.A.; Church, J.A.; Fukimori, I.; Gomez, N.; Kopp, R.E.; Landerer, F.; Le Cozannet, G.; et al. Concepts and Terminology for Sea Level: Mean, Variability and Change, Both Local and Global. Surv. Geophys. 2019, 40, 1251–1289. [Google Scholar] [CrossRef] [Green Version]
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D.; et al. Sea level change. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 1137–1216. Available online: http://www.climatechange2013.org/images/report/WG1AR5_Chapter13_FINAL.pdf (accessed on 1 July 2021).
- Stammer, D.; Cazenave, A.; Ponte, R.M.; Tamisiea, M.E. Causes for contemporary regional sea level changes. Ann. Rev. Mar. Sci. 2013, 5, 21–46. [Google Scholar] [CrossRef] [Green Version]
- Cazenave, A.; Palanisamy, H.; Ablain, M. Contemporary sea level changes from satellite altimetry: What have we learned? What are the new challenges? Adv. Space Res. 2018, 62, 1639–1653. [Google Scholar] [CrossRef]
- Tamisiea, M. Ongoing glacial isostatic contributions to observations of sea level change. Geophys. J. Int. 2011, 186, 1036–1044. [Google Scholar] [CrossRef]
- Adhikari, S.; Ivins, E.R.; Frederikse, T.; Landerer, F.W.; Caron, L. Sea-level fingerprints emergent from GRACE mission data. Earth Syst. Sci. Data 2019, 11, 629–646. [Google Scholar] [CrossRef] [Green Version]
- Vishwakarma, B.D.; Royston, S.; Riva, R.E.M.; Westaway, R.M.; Bamber, J.L. Sea level budgets should account for ocean bottom deformation. Geophys. Res. Lett. 2020, 47, e2019GL086492. [Google Scholar] [CrossRef] [Green Version]
- Hsu, C.-W.; Velicogna, I. Detection of sea level fingerprints derived from GRACE gravity data. Geophys. Res. Lett. 2017, 44, 8953–8961. [Google Scholar] [CrossRef]
- Jeon, T.; Seo, K.-W.; Kim, B.-H.; Kim, J.-S.; Chen, J.; Wilson, C.R. Sea level fingerprints and regional sea level change. Earth Planet. Sci. Lett. 2021, 567, 116985. [Google Scholar] [CrossRef]
- Mitrovica, J.; Tamisiea, M.; Davis, J.; Milne, G.A. Recent mass balance of polar ice sheets inferred from patterns of global sea-level change. Nature 2001, 409, 1026–1029. [Google Scholar] [CrossRef] [PubMed]
- Milne, G.; Gehrels, W.; Hughes, C.; Tamisiea, M.E. Identifying the causes of sea-level change. Nat. Geosci. 2009, 2, 471–478. [Google Scholar] [CrossRef] [Green Version]
- Tamisiea, M.E.; Mitrovica, J.X. The moving boundaries of sea level change: Understanding the origins of geographic variability. Oceanography 2011, 24, 24–39. [Google Scholar] [CrossRef]
- Spada, G. Glacial isostatic adjustement and contemporary sea level rise: An overview. Surv. Geophys. 2017, 38, 153–185. [Google Scholar] [CrossRef]
- Frederikse, T.; Riva, R.E.M.; King, M.A. Ocean bottom deformation due to present-day mass redistribution and its impact on sea level observations. Geophys. Res. Lett. 2017, 44, 12306–12314. [Google Scholar] [CrossRef] [Green Version]
- Adhikari, S.; Ivins, E.R.; Frederikse, T.; Landerer, F.W.; Caron, L. Changes in relative sea level, geoid height, and bedrock displacement derived from the Release-06 GRACE Level-2 monthly Stokes coefficients. Harv. Dataverse 2019, V3. [Google Scholar] [CrossRef]
- Legeais, J.-F.; Ablain, M.; Zawadzki, L.; Zuo, H.; Johannessen, J.A.; Scharffenberg, M.G.; Fenoglio-Marc, L.; Fernandes, M.J.; Andersen, O.B.; Rudenko, S.; et al. An improved and homogeneous altimeter sea level record from the ESA Climate Change Initiative. Earth Syst. Sci. Data 2018, 10, 281–301. [Google Scholar] [CrossRef] [Green Version]
- Peltier, R.; Argus, D.F.; Drummond, R. Comment on “An assessment of the ICE-6G_C (VM5a) glacial isostatic adjustment model” by Purcell et al. J. Geophys. Res. Solid Earth 2018, 123, 2019–2028. [Google Scholar] [CrossRef]
- Garcia, H.E.; Boyer, T.P.; Baranova, O.K.; Locarnini, R.A.; Mishonov, A.V.; Grodsky, A.; Paver, C.R.; Weathers, K.W.; Smolyar, I.V.; Reagan, J.R.; et al. World Ocean Atlas 2018: Product Documentation. NOAA. Technical Editor: A. Mishonov. Available online: https://data.nodc.noaa.gov/woa/WOA18/DOC/woa18documentation.pdf (accessed on 1 July 2021).
- Good, S.A.; Martin, M.J.; Rayner, N.A. EN4: Quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates. J. Geophys. Res. Ocean. 2013, 118, 6704–6716. [Google Scholar] [CrossRef]
- Roemmich, D.; Gilson, J. The 2004–2008 mean and annual cycle of temperature, salinity and steric height in the global ocean from the Argo program. Prog. Oceanogr. 2009, 82, 81–100. [Google Scholar] [CrossRef]
- Hosoda, S.; Ohira, T.; Nakamura, T. A monthly mean dataset of global oceanic temperature and salinity derived from Argo float observations. JAMSTEC Rep. Res. Dev. 2018, 8, 47–59. [Google Scholar] [CrossRef] [Green Version]
- Argo. Argo float data and metadata from Global Data Assembly Center (Argo GDAC). Seanoe 2000. [CrossRef]
- Gouretski, V.; Reseghetti, F. On depth and temperature biases in bathythermograph data: Development of a new correction scheme based on analysis of a global ocean database. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2010, 57, 812–833. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Save, H. CSR GRACE and GRACE-FO RL06 Mascon Solutions v02. 2020. Available online: http://www2.csr.utexas.edu/grace/RL06_mascons.html (accessed on 11 June 2021). [CrossRef]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Moreira, L.; Cazenave, A.; Palanisamy, H. Influence of interannual variability in estimating the rate and acceleration of present-day global mean sea level. Glob. Planet. Chang. 2021, 199, 103450. [Google Scholar] [CrossRef]
- Hamlington, B.D.; Frederikse, T.; Nerem, R.S.; Fasullo, J.T.; Adhikari, S. Investigating the acceleration of regional sea level rise during the satellite altimeter era. Geophys. Res. Lett. 2020, 47, e2019GL086528. [Google Scholar] [CrossRef]
- Prandi, P.; Meyssignac, B.; Ablain, M.; Spada, G.; Ribes, A.; Benveniste, J. Local sea level trends, accelerations and uncertainties over 1993–2019. Sci. Data 2021, 8, 1. [Google Scholar] [CrossRef]
- Prandi, P.; Meyssignac, B.; Ablain, M.; Spada, G.; Ribes, A. Error variance-covariance, trends, accelerations and uncertainties of regional mean sea level estimated from satellite altimetry. Seanoe 2020. [Google Scholar] [CrossRef]
- Fukumori, I.; Wang, O.; Llovel, W.; Fenty, I.; Forget, G. A near-uniform fluctuation of ocean bottom pressure and sea level across the deep ocean basins of the Arctic Ocean and the Nordic Seas. Prog. Oceanogr. 2015, 134, 152–172. [Google Scholar] [CrossRef]
- MacIntosh, C.R.; Merchant, C.J.; von Schuckmann, K. Uncertainties in Steric Sea Level Change Estimation During the Satellite Altimeter Era: Concepts and Practices. Surv. Geophys. 2017, 38, 59–87. [Google Scholar] [CrossRef] [PubMed]
- Caron, L.; Ivins, E.R.; Larour, E.; Adhikari, S.; Nilsson, J.; Blewitt, G. GIA model statistics for GRACE hydrology, cryosphere, and ocean science. Geophys. Res. Lett. 2018, 45, 2203–2212. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).