1. Introduction
In the social sciences, there is an increasing trend to use fine-grained data to capture political and economic mechanisms. Measured at high levels of resolution such as individuals or households, they allow for a precise analysis of local conditions and the social processes that people are embedded in [
1]. The availability of fine-grained data is usually very good for developed countries, where researchers can rely on extensive surveys or administrative data. For many countries of the Global South, however, the availability of disaggregated data is usually limited. Oftentimes, these countries are unlikely to be covered by surveys, and administrative data shared for research purposes is sparse or does not exist.
For this reason, social science scholars have increasingly turned to alternative sources of data, such as remote sensing. One prominent example in this strand of research is the use of nighttime lights (NTL) data collected by satellites. First attempts have used NTL emissions at aggregated, lower levels of resolution. For example, earlier work has shown that nighttime light emissions can track economic performance and human development at the level of large geographic units, for example countries or states [
2,
3,
4,
5]. However, more recent work has tried to increase the resolution of these tests. For example, Weidmann and Schutte [
6] show that nighttime light emissions correlate well with ground truth measurements of household wealth, as recorded in surveys. This means that satellite-based NTL data can be used also at high levels of resolution, for example for the estimation of wealth, human development or regional inequality between provinces and sub-national administrative units [
7,
8,
9,
10,
11].
In this paper, we build on this work and attempt to use NTL data for the estimation of local inequality. In recent years, and in particular following the influential work by Piketty [
12], inequality has attracted a lot of interest from the research community. Using aggregated country- or group-levels measures of economic inequality, this research has shown for example that inequality can be an important driver of social conflict and political instability [
13]. Again, research in this vein has relied on NTL data, but only at aggregated levels to measure inequality between [
14,
15,
16] or within social groups [
17]. However, recent research has also shown that people do not perceive aggregated/systemic levels of inequality. Rather, it is the local context that matters for explaining individuals’ behavior. In particular, there is a number of studies showing that local inequality, i.e., inequality with an individual’s immediate spatial context, affects citizen’s political preferences in behavior [
18,
19,
20,
21,
22,
23,
24].
To find out how this local context matters in the Global South, we need fine-grained estimates of local inequality. This is what we present in this article. Our study, however, is not the first to study local inequality with NTL data. Existing work, however, has not used night light emissions to measure local inequality directly; rather, these studies first approximate economic performance or wealth from night lights for small geographic units, and then calculate inequality between them [
9,
25,
26]. Our approach, in contrast, operates directly on the NTL data in combination with a population raster, and is therefore able to produce local inequality estimates for arbitrary locations on the globe and at a high levels of resolution.
2. Data and Methods
In this paper, we present an approach to computing satellite-based estimates of local inequality, which we validate with local inequality estimates derived from large-scale survey data. In the following, we first describe the nighttime light data we use for our indicator, before turning to the survey data used for validation.
Our satellite-based estimates of local inequality rely on the VIIRS nighttime light data [
27] (V2). We use the annual composites, where non-stationary light sources and other erroneous influences have been removed by a combination of the different images available for a given year. This methodology is described in Elvidge et al. [
27]. The VIIRS nighttime lights is one of the most recent freely available data products of remote-sensed nighttime light emissions, and it is available for the years 2012–2021. Compared to earlier products such as the frequently-used DMSP-OLS nighttime light data [
28], it has a number of advantages. Most importantly, VIIRS nighttime light rasters have a higher resolution of 15 arc-seconds, which corresponds to about 500m at the equator. Furthermore, VIIRS reduce the problem of top-coding: in the DMSP-OLS NTL data, high emissions are all coded at the maximum value of 63, which eliminates a lot of variation at the upper end of the spectrum. Therefore, with VIIRS data, we can exploit considerably more variation within well-lit areas. Not surprisingly, existing research has concluded that VIIRS-derived data should be preferred for work that uses nighttime lights to study socio-economic processes [
29,
30].
For our approach, we rely on earlier work by Weidmann and Schutte [
6], which has analyzed nighttime light emissions as a proxy for economic wealth at high levels of resolution. This work has shown that on average, more intensely illuminated areas are also the richer ones. However, since variation in illumination to a large extent driven by settlement patterns, more populated areas emit more light at night. In our analysis, we take this into account by using a second spatial data source that maps the global population at a high resolution: the WorldPop dataset, available from
https://www.worldpop.org/ (accessed on 30 July 2021) [
31]. We use the population counts raster from WorldPop, which provides annual population estimates at the level of cells with a resolution of 30 arc-seconds. These counts are computed in a “top-down” fashion, by disaggregating official population statistics for administrative divisions using spatial covariates as described in Lloyd et al. [
32].
For combining the VIIRS NTL data and WorldPop, we aggregate the former to a resolution of 30 arc seconds. Dividing the nighttime light emissions value by the population living in the same cell, we obtain per capita values of nighttime light emissions at the level of the raster cells. This allows us to compute inequality estimates for any given point on the globe: Given a set of longitude/latitude coordinates, we retrieve all cells within a buffer of a certain radius, and simply compute an inequality index—the Gini coefficient—across all of them. For this computation, we need the per capita nighttime light emissions as well as the population counts of each grid cell. In line with results by Weidmann and Schutte [
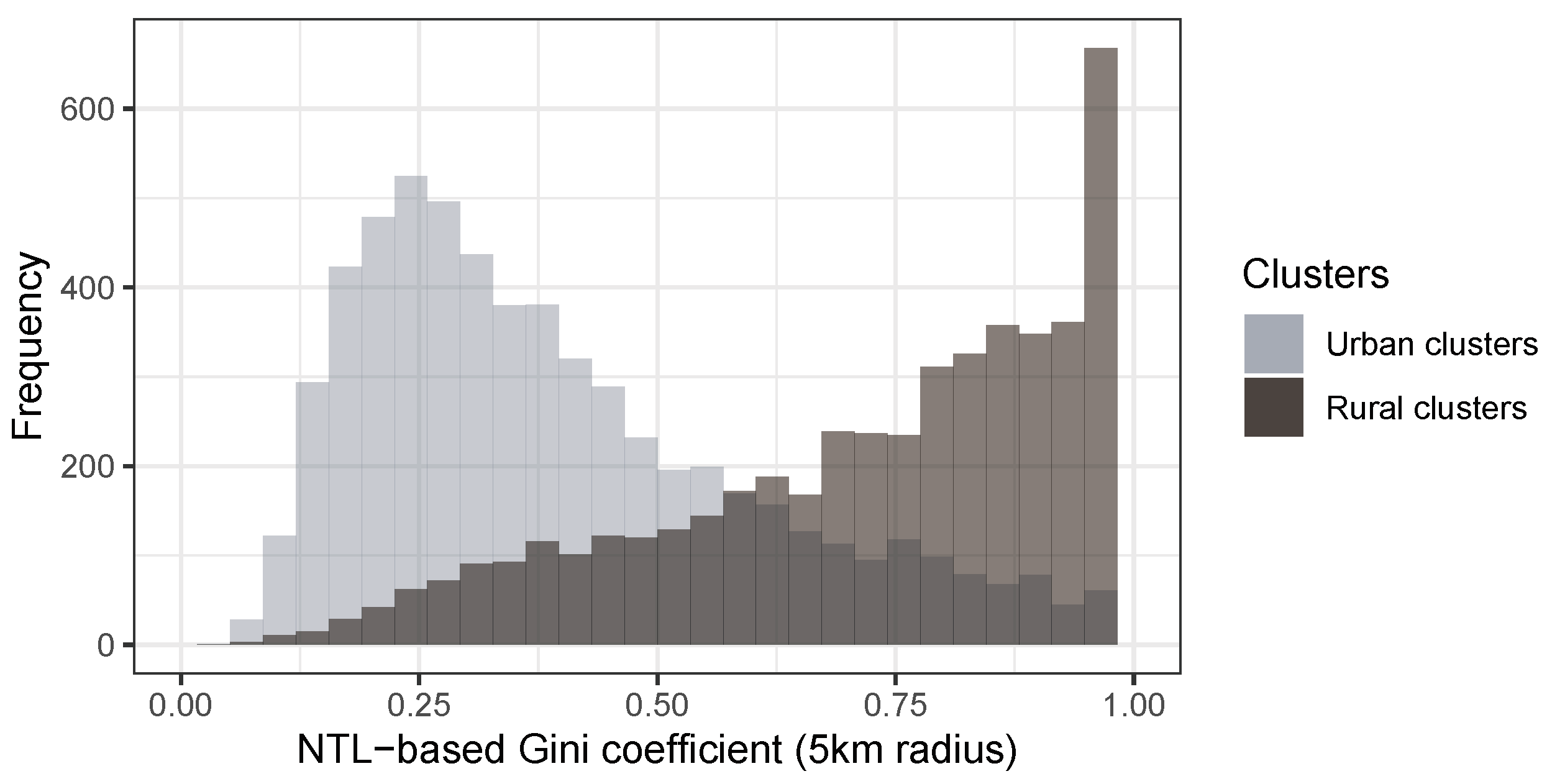
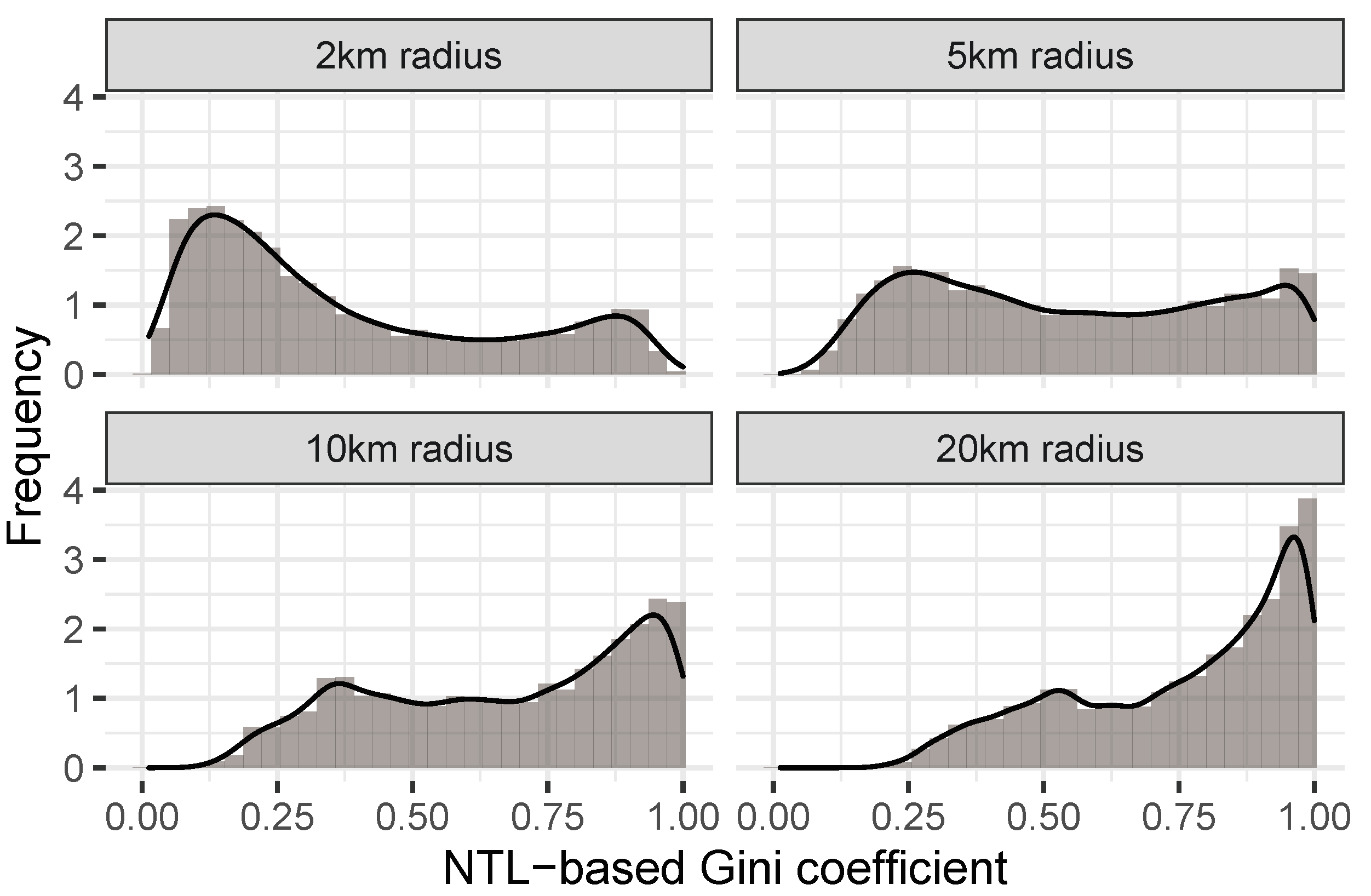
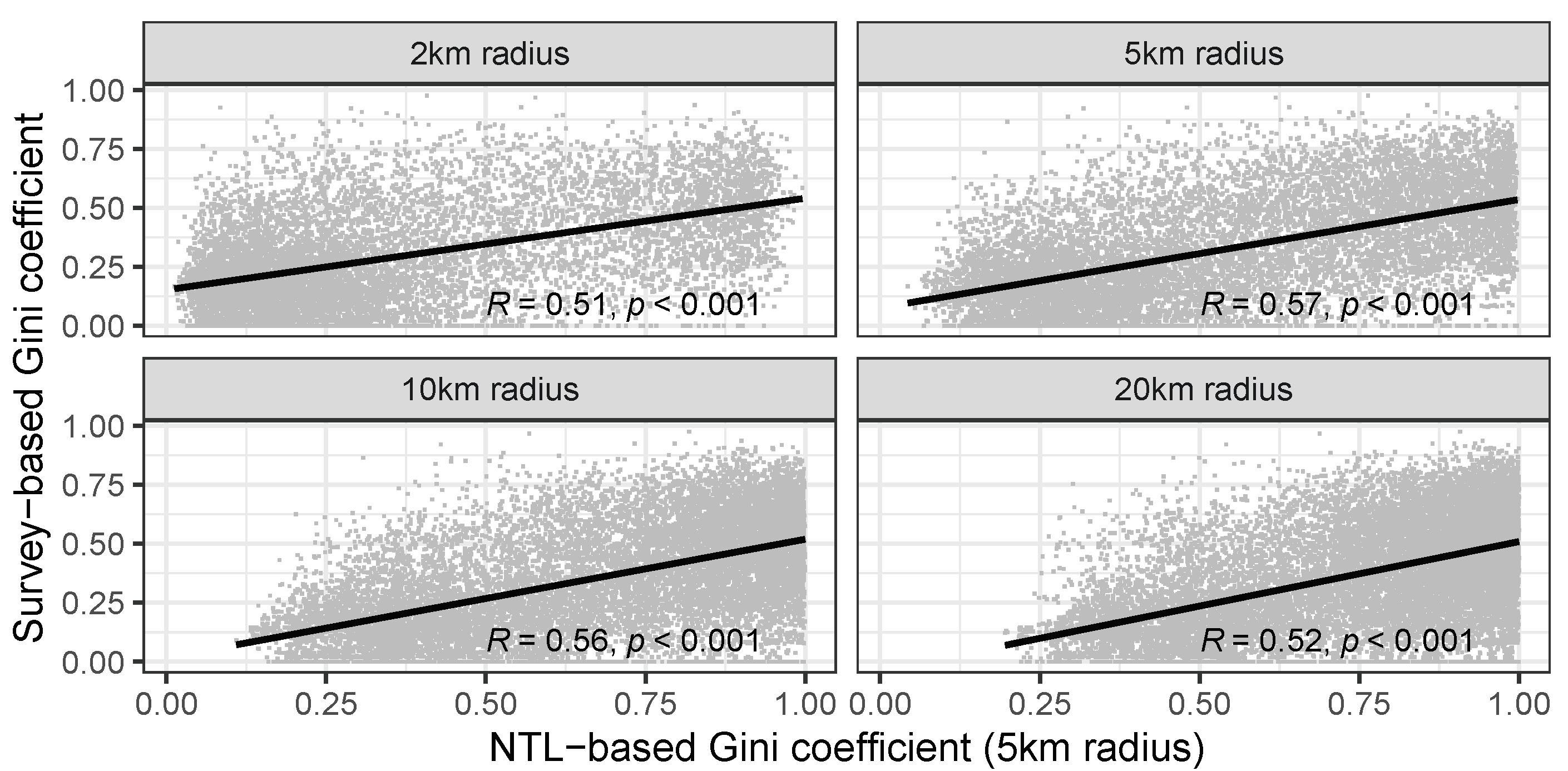
6], we log-transform the nighttime light value before computing the inequality estimates. In our analysis below, we vary the buffer size from 2 km to 20 km, to find out what produces the most accurate estimates of local inequality.
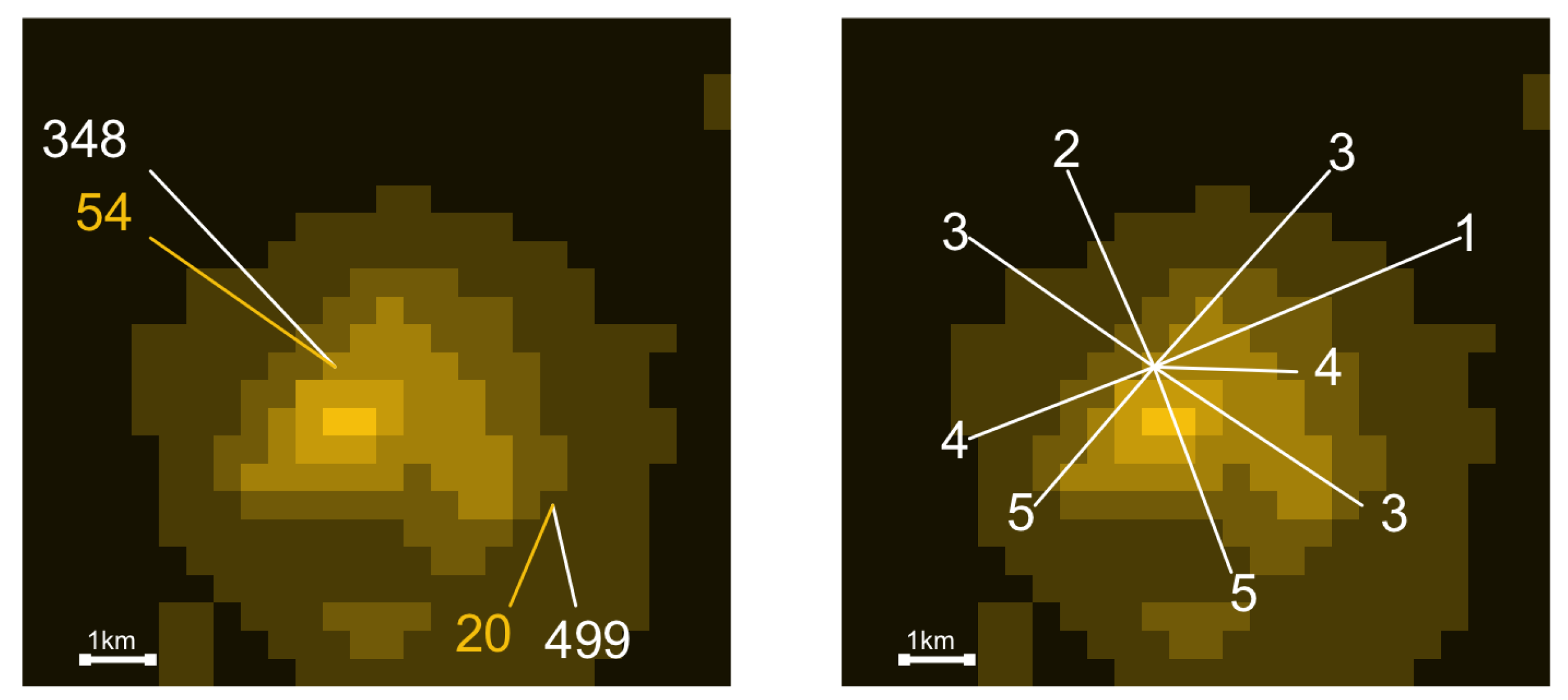
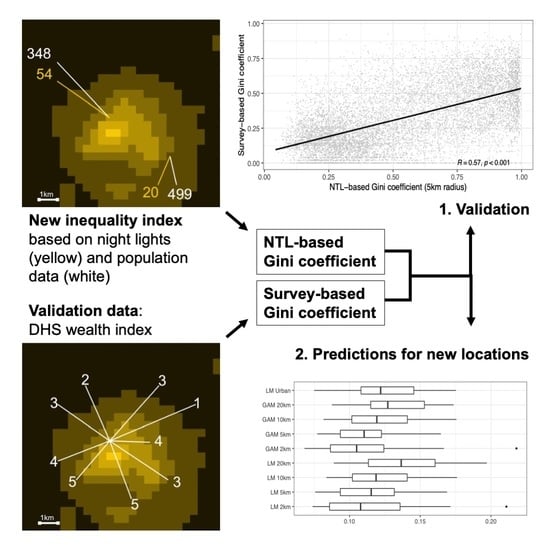
Figure 1 (left panel) illustrates the data we use for this procedure. In principle, it is possible with this approach to compute local inequality estimates for any point on the globe. For our validation exercise below, we do this for the spatial locations where the survey was conducted, which allows us to compare survey-based inequality estimates to those calculated from the nighttime lights.
For our validation exercise, we require alternative estimates of local inequality. For countries where detailed official income or wealth statistics are available, these estimates can easily be computed (as for example in [
33]). However, for many countries in particular in the Global South, these data cannot be used for research purposes, or are simply not collected regularly. This is why we rely on large cross-national survey data from the Demographic and Health Surveys (DHS) project (see
https://dhsprogram.com, accessed on 30 July 2021). The DHS is a regular survey on living conditions and health-related data that is conducted across many countries. It uses the same survey instrument in all countries, which contains questions at the individual level but also the household level. Most importantly, the DHS also include an assessment of the household’s wealth by means of a wealth index. The wealth index is created from different questions answered by the enumerator (not the respondents) about the household’s assets. These answers are collapsed to the most important underlying dimension using factor analysis, and the factor scores are used to assign each household to its corresponding quintile in the distribution of scores in the country [
34]. The household’s quintile (1–5) is the wealth index for this household.
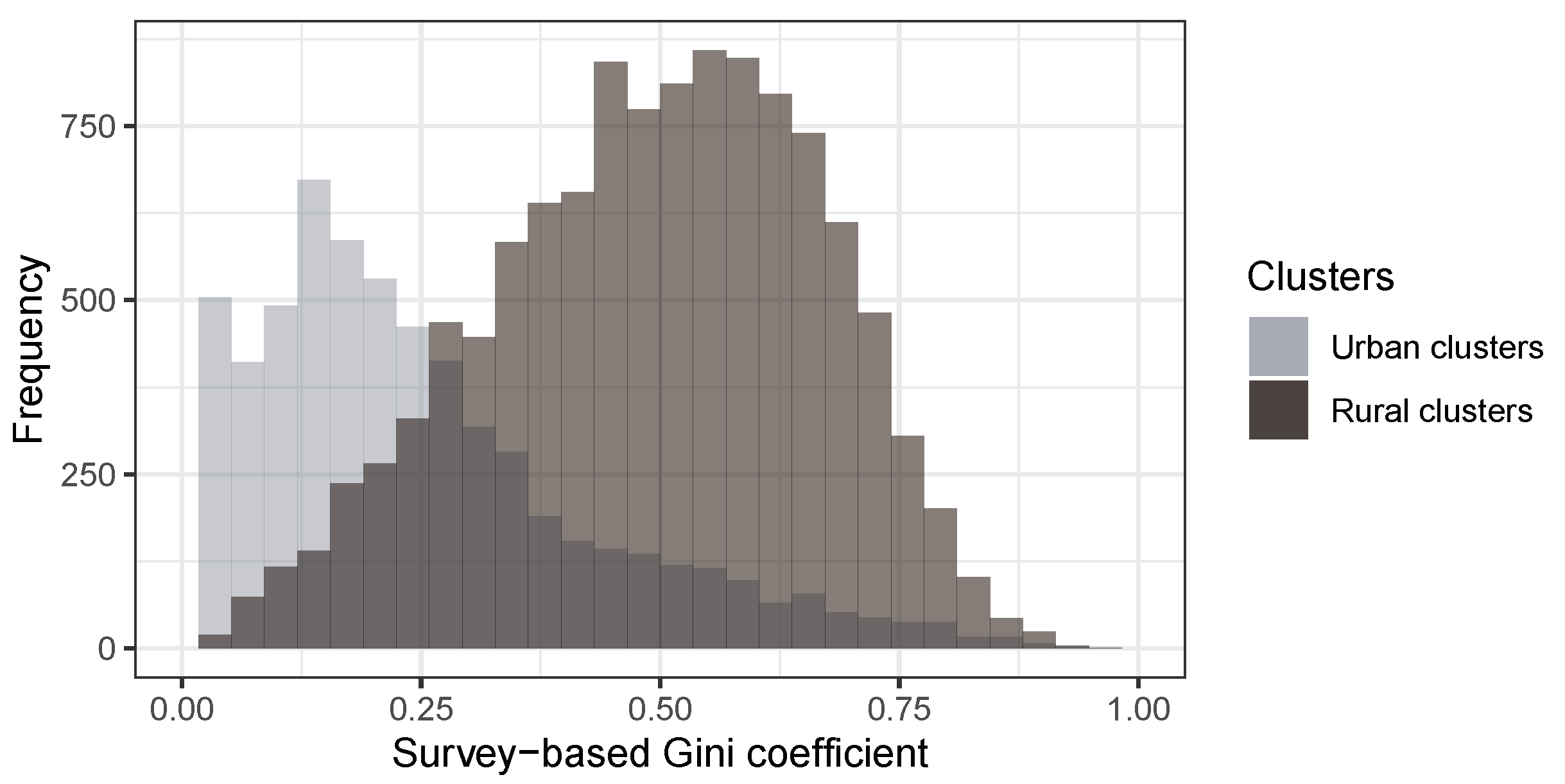
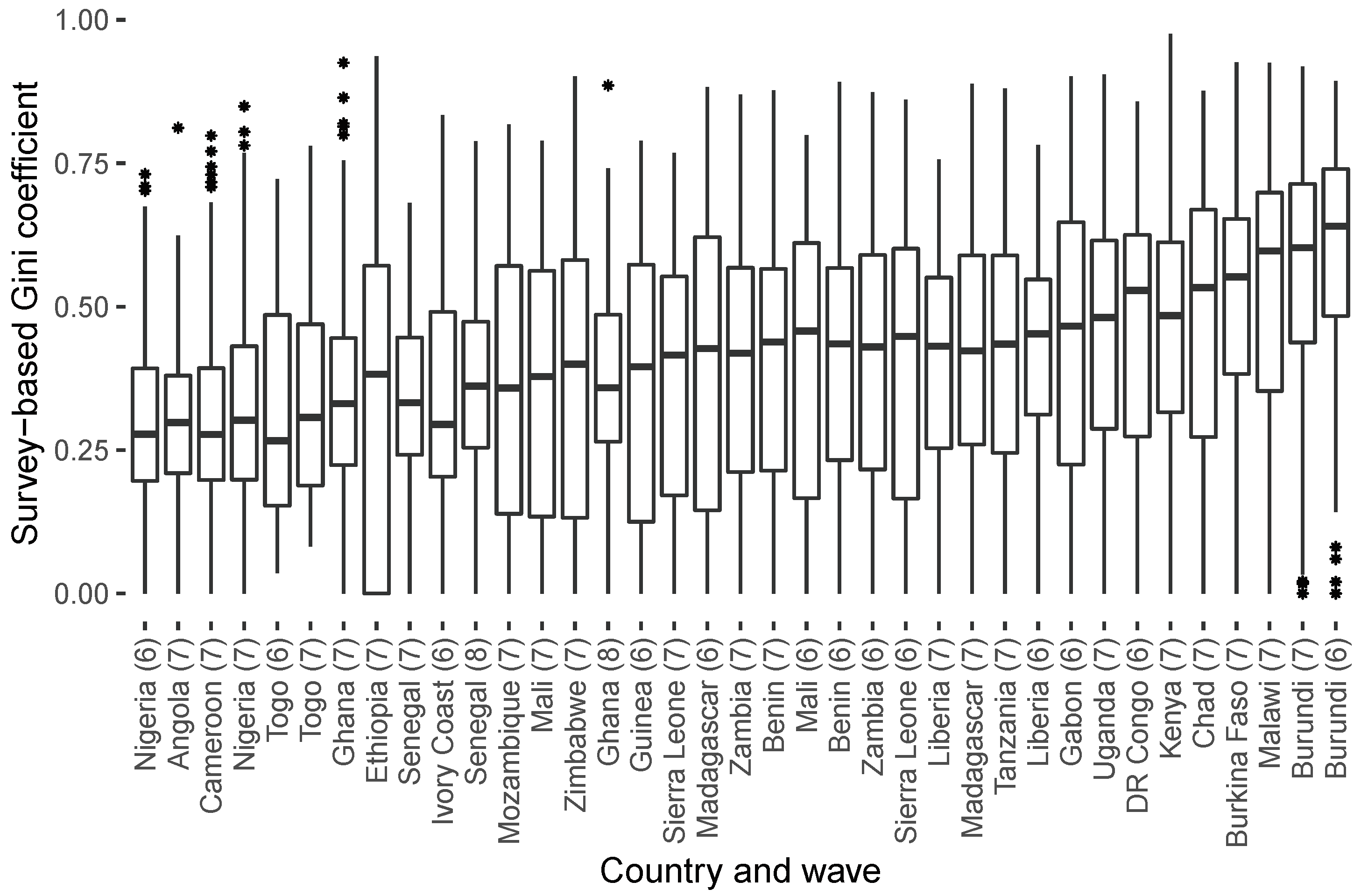
Figure 1 (right panel) gives an example of the DHS data we use for the validation. The entire sample covers 26 countries from DHS survey waves 6, 7 and 8, with data collected in the years 2012–2019.
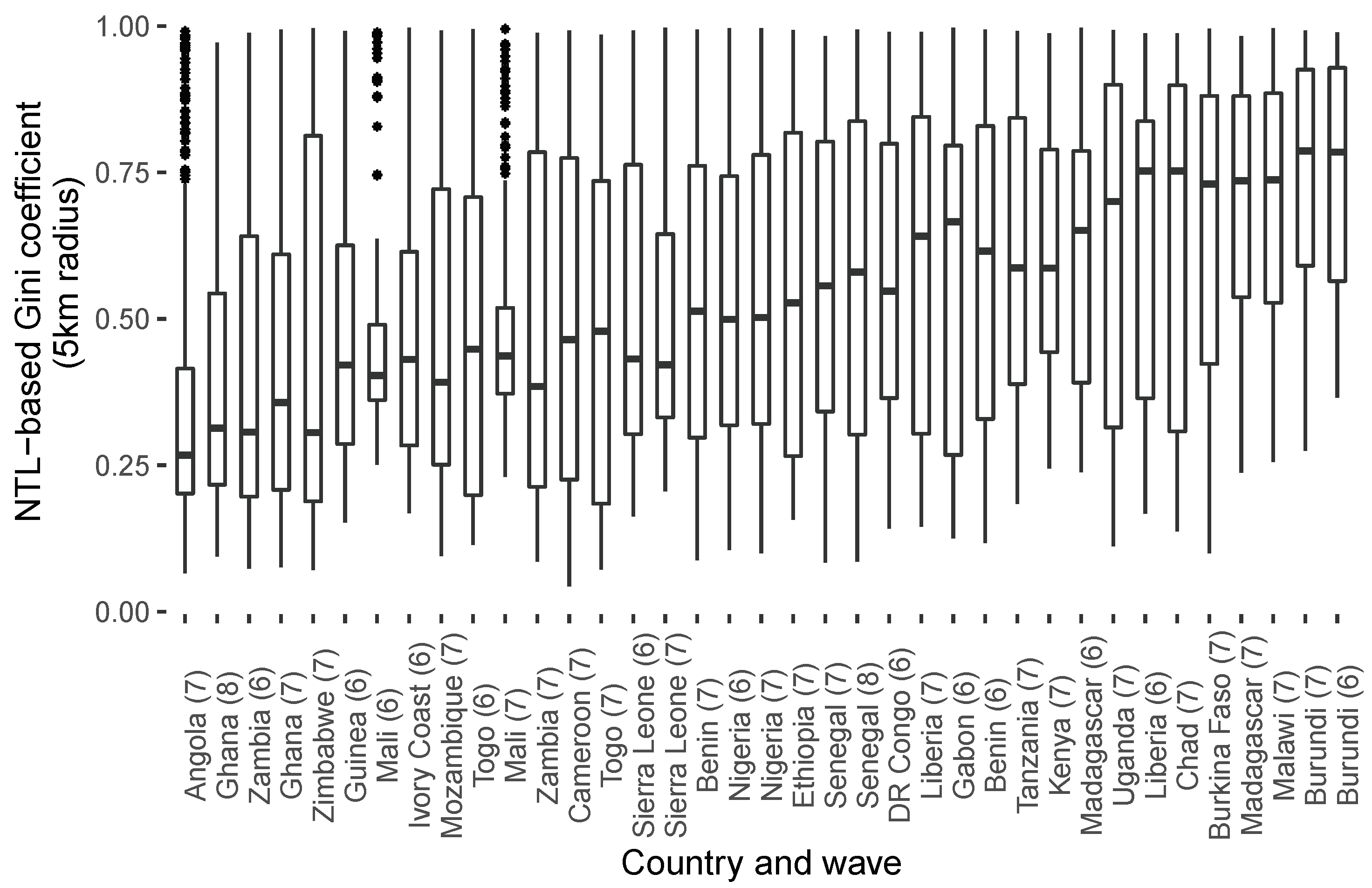
Appendix A lists all the countries and survey waves included in the sample.
To link the survey results to our spatial index of local inequality, we also require geographic information about the location of households in the survey. These coordinates are not provided at the level of households, but at the level of survey
clusters or primary sampling units (PSUs). In the DHS, a cluster is a group of about 25–30 households in close proximity to each other, which were selected according to the DHS’s sampling scheme [
35]. The DHS categorize clusters into urban and rural ones. For each cluster, the DHS provide a point (longitude/latitude) location, which, however, is randomly distorted to preserve anonymity in the data. More precisely, an urban cluster’s location is randomly shifted within a radius of 2 km, while a rural location is assigned a random location with a radius of 5 km of its original location (10 km for a randomly chosen 1% of all rural clusters in a given country and survey wave). Therefore, the spatial reference for the survey cluster is approximate, and we construct the spatial buffers for the computation of our local inequality index such that it contains the original cluster location (with the exception of the randomly chosen 1% of the rural cluster with a spatial error of up to 10 km, which introduces measurement error in our analysis that we cannot prevent).
For our survey-based measure of local inequality, we compute the Gini inequality coefficient over the wealth index values of all households in a cluster. Since the input values have a limited range of 1–5, the upper bound of the Gini coefficients is less than 1 (the usual upper bound of the Gini index). To normalize the resulting coefficient values, we divide them by 0.382. The derivation for this value is presented in
Appendix B.
4. Discussion
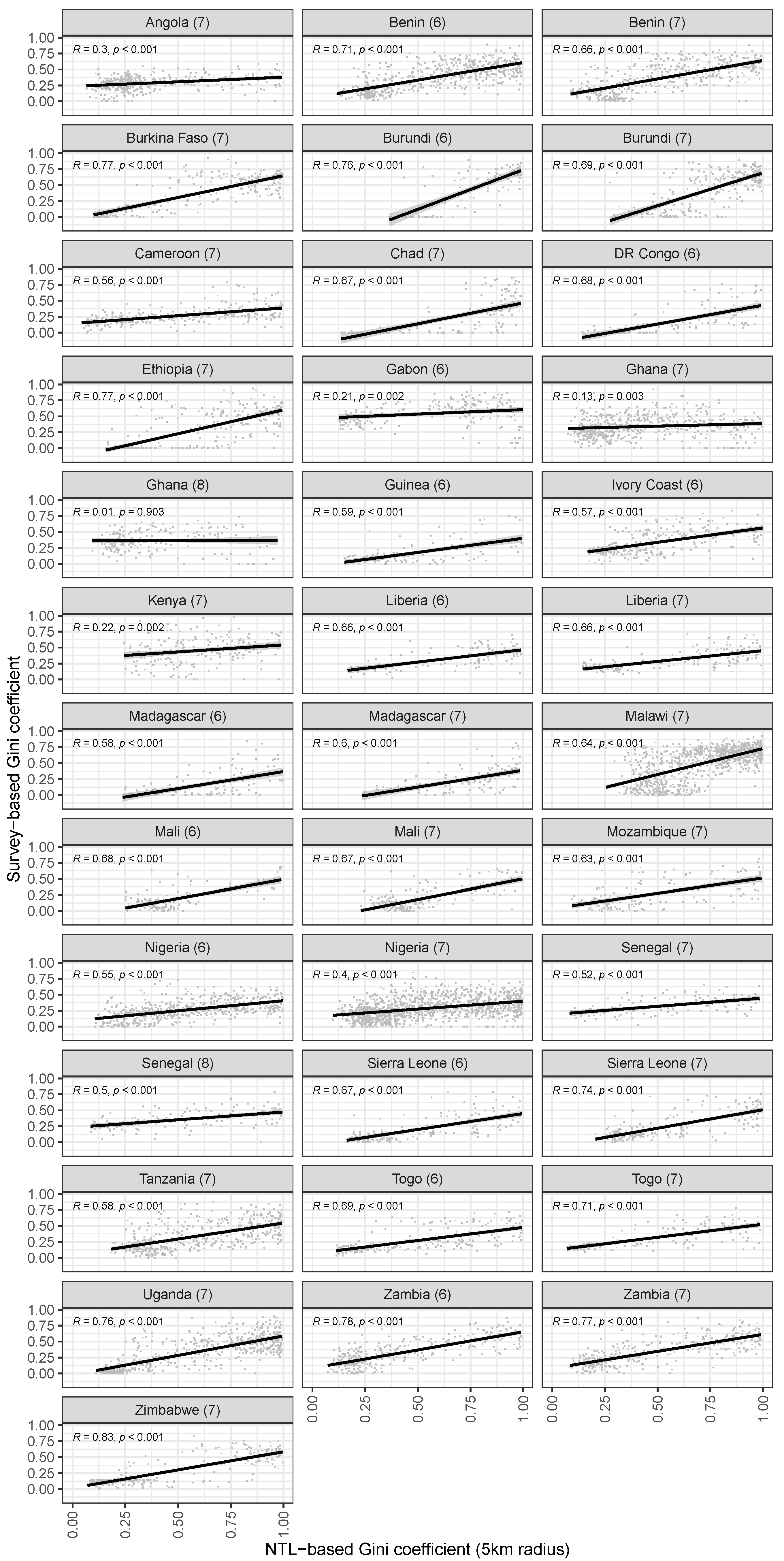
In this article, we have introduced an indicator for local inequality derived from high-resolution night lights data. In addition to the night lights raster data, the computation of this indicator requires only a fine-grained population grid, both of which are freely available. We combine these two data sources to obtain per capita emissions values at the grid cell level, which we use to compute a Gini index of inequality for spatial buffers of a given size. We present two main analyses. In a first validation exercise, we compare the NTL-based indicator to estimates of local inequality derived from survey data. The correlations are positive and significant in almost all countries in our sample, although not surprisingly, the indicator cannot fully capture local inequality as measured by the surveys. This is to be expected: while survey estimates of wealth take into account a variety of household assets, only some of them are related to electricity consumption and are therefore possibly reflected in nightlight emissions. Furthermore, in particular in urban areas, night light emissions are less likely to be attributable to individual households, and rather reflect public infrastructure. This will also reduce the correlation between NTL emissions and individual wealth.
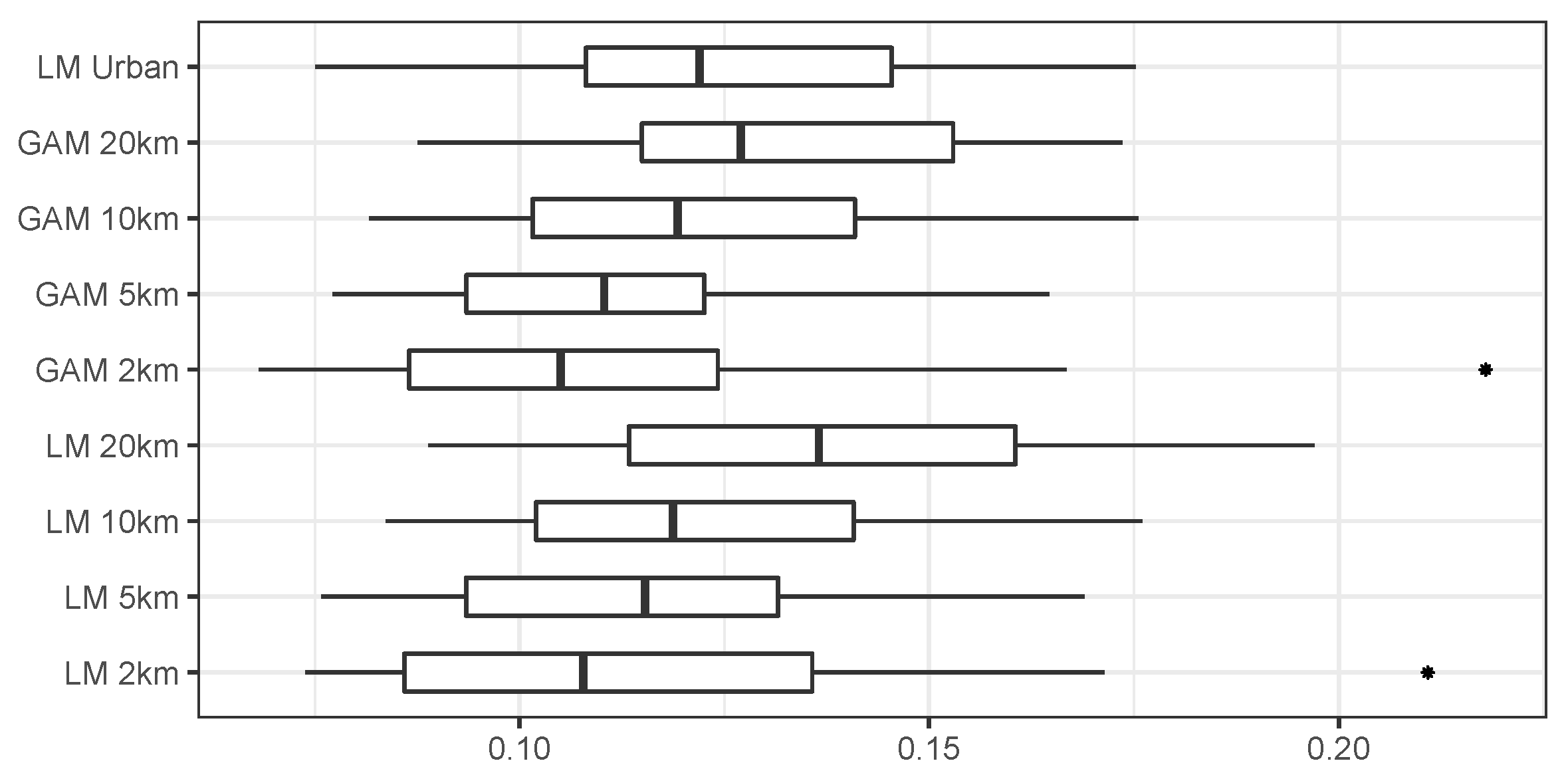
To address the question of whether it is possible to our indicator for locations where no other data are available, we provide a second type of analysis. Here, we generate estimates of local inequality with simple prediction models, and compare these predicted values to the ones measured with the survey data. This analysis shows that prediction errors are generally low. When we predict Gini coefficients of local inequality with our NTL-based indicator, the best predictions have an average error around 0.05 on the 0–1 scale. This is a good result, given that it is derived exclusively from simple spatial datasets (night light emissions and population rasters). Overall, this shows that our approach can be used to generate new estimates of local inequality for locations for which no other data exists.
While our results show that night lights emission can pick up local inequality to a certain extent, they are necessarily weaker as compared to other approaches combining multiple sources of data. For example, Chi et al. [
37] introduce micro-level estimates of wealth that are computed using a variety of input data, including telecommunication coverage maps as well as Facebook connectivity data. This leads to better wealth estimates, which could also be used to estimate local inequality. At the same time, however, the use of proprietary data makes this approach impossible to use for many researchers without access to these data. Furthermore, the coverage of these data may be limited to particular countries, which restricts their applicability to country-specific studies. Our approach, in contrast, uses only publicly available data, is fully replicable using open-source software (PostGIS), and can be used for comparative, cross-national work in the social sciences.
Due to its ability to pick up variation in local inequality and its exclusive reliance on publicly available data, our index enables future research in many different fields. In political science, for example, it helps to better understand how local inequality in an individual’s immediate context affects political preferences and behavior. Sociologists can use these data to study the effect of local inequality on residential choice or personal relationships, and development economists can use it to identify areas in need of particular support.
While the results presented in our article are encouraging, there are several drawbacks associated with the NTL-based estimation of inequality. Due to its reliance on variation in night light emissions, this approach can only work in world regions where no saturation has been reached. For example, in most countries of the Global North, nightly illumination of streets is commonplace, which reduces variation in night light emissions and their correlation with socio-economic variables [
38]. Consequently, we expect our approach to be less applicable to these countries. Furthermore, there are limitations as regards the temporal variation the indicator is able to pick up. Night light emissions change slowly, which is why our indicator will remain relatively stable even in cases of large population shifts, for example due to refugee movements. When relying on night lights as a proxy for wealth or inequality, researchers should be aware of these limitations and carefully consider whether this data source is suitable for their project.