Abstract
Multifarious hyperspectral image (HSI) classification methods based on convolutional neural networks (CNN) have been gradually proposed and achieve a promising classification performance. However, hyperspectral image classification still suffers from various challenges, including abundant redundant information, insufficient spectral-spatial representation, irregular class distribution, and so forth. To address these issues, we propose a novel 2D-3D CNN with spectral-spatial multi-scale feature fusion for hyperspectral image classification, which consists of two feature extraction streams, a feature fusion module as well as a classification scheme. First, we employ two diverse backbone modules for feature representation, that is, the spectral feature and the spatial feature extraction streams. The former utilizes a hierarchical feature extraction module to capture multi-scale spectral features, while the latter extracts multi-stage spatial features by introducing a multi-level fusion structure. With these network units, the category attribute information of HSI can be fully excavated. Then, to output more complete and robust information for classification, a multi-scale spectral-spatial-semantic feature fusion module is presented based on a Decomposition-Reconstruction structure. Last of all, we innovate a classification scheme to lift the classification accuracy. Experimental results on three public datasets demonstrate that the proposed method outperforms the state-of-the-art methods.
1. Introduction
Hyperspectral images (HSI), that is, imaging spectroscopy, are generally obtained by imaging spectrometers or hyperspectral remote sensing sensors [1]. HSI contain massive spectral-spatial information, which reflects the interacted rule between light and materials, as well as the intensity of light reflected, emitted or transmitted by certain objects [2]. Compared with traditional RGB images, HSI has more plentiful and specified spectral information, which is beneficial for classification and recognition tasks [3]. HSI classification aims to assign an accurate land-cover label to each hyperspectral pixel, and has been widely applied in mineral exploitation [4], defense and security [5], environment management [6] and urban development [7].
Despite great progress being realized, HSI classification still struggles with various challenges, which are described as follows: (1) The quantity limitation of labeled samples. In practical applications, hyperspectral images are easily captured by imaging spectrometers, but it is very difficult and time-consuming to label these hyperspectral images; (2) The curse of dimension. In the field of supervised learning, classification accuracy may decline severely with the increment of dimension, due to the imbalance between limited samples and high-dimensional expression [8]; (3) Spatial variability of spectral information. The spectral information of HSI will be influenced by several external factors, such as sensors, surrounding environment, atmospheric conditions, resulting in the phenomenon that the ground feature regions contain diverse categories of pixels. Therefore, more and more researchers are paying attention to tackling the above problems for completing more successful HSI classification.
In the past few years, traditional classification methods mainly include two steps: feature engineering and classifier training [9]. The aim of feature engineering is to reduce the dimension of HSI and extract representative bands or features. There are two primary means to accomplish this task, that is, feature extraction and feature selection. Feature extraction transforms hyperspectral data from a high dimension space into a low dimension space to better distinguish different categories [10]. On the contrary, feature selection discards bands which are useless for classification and preserves expressive spectral information from the original HSI data. The essence of feature extraction and feature selection is dimensionality reduction. The former needs to find the underlying logic between data and the relationship between attributes, so as to change the original feature space. The latter only needs to select some of the most representative features from the original features, without changing the original feature space, and is easy to implement. Meanwhile, most traditional methods usually focus on feature selection [11,12,13,14,15] and classifier design, so it is easy to observe that feature selection is more appropriate. For example, Wang et al., introduce Manifold ranking to eliminate the drawbacks of traditional salient band selection methods [16]. Hidden Markov random field [17] and feature mining techniques [18] can reduce the dimension of HSI and extract the discriminative features or bands. Gu et al., combine the segmentation map of Hidden Markov Random Field with a classification map of SVM to get the final result [19]. Yuan et al., divide bands into several sets with the cluster method and select useful bands to construct tasks [20]. However, these traditional classification methods based on spectral features cannot make full use of spatial features of HSI data. Although some approaches based on spatial or spectral-spatial features are proposed, they only simply integrate spectral and spatial features. In addition, previous methods all rely on hand-crafted features, which are effective only in some certain scenes. As a result, traditional classification methods usually have poor classification performance due to the poor generalization and feature representation abilities [13,21,22,23,24,25,26].
In recent years, all kinds of deep learning models have been carefully explored to further extract more discriminative and richer hierarchical features for HSI classification [10,27,28,29,30,31,32,33,34,35,36], such as auto-encoders (AEs), deep belief networks (DBNs), recurrent neural networks (RNNs) and convolutional neural networks (CNNs). Among these methods, CNNs gradually become more popular since end-to-end CNNs have been proved that have a capability to automatically extract high-level features from HSI data. For example, Hu et al., designed a deep CNN based on the spectral domain to classify HSI data, which contains five 1-D convolutional layers [37]. Li et al., construct a CNN1D model by employing spectral correlation between pixels, which takes pairs of pixels extracted from the original HSI data as the input data [38]. Although these methods have better classification accuracy than traditional classification methods, they only extract spectral features of HSI data and ignore rich two-dimension spatial features.
To solve the above problems, many models based on 2-D CNN are developed, which can simultaneously extract spectral and spatial features from HSI data. Concretely, Cao et al., present a compressed convolutional neural network for HSI classification, which adopts virtual samples to describe the boundary of the teacher network and effectively improves the classification accuracy of the student network [39]. Zhe et al., use two novel mixed link networks to enhance the representative ability of CNNs, which obtains more detailed features from HSI data by utilizing the dense network and the residual network [40]. He et al., employed covariance matrices to train 2-D CNN, which can encode spectral-spatial information and obtain multi-scale covariance maps [41]. Zhong et al., designed an end-to-end spectral-spatial residual network, which learns representative features from HSI data through spectral and spatial residual blocks consecutively [42]. Although these methods try to take full advantage of two-dimension spatial features and one-dimension spectral features, they generally separate joint spectral-spatial features into two independent learning parts and ignore the close correlation between spectral and spatial features. Furthermore, since HSI data are essentially a 3D cube, these methods cannot extract more discriminated features from the spectral dimension.
Naturally, some classification methods based on 3D CNN are proposed to learn the close correlation between spectral and spatial features from raw HSI data. For instance, Zhang et al., propose a novel deep feature aggregation network, which uses a deep feature residual network and a deep feature dense network to obtain the low-level, middle-low and high-level features of HSI data [43]. Zhang et al., describe a multi-scale dense network for HSI classification, which takes full advantage of different scale information and combine them [44]. Zhang et al., design a spectral-spatial fractal residual convolutional neural network to learn spectral-spatial information, which possess a strong ability of categories classification [45]. Lin et al., present an attention-aware pseudo-3-D (AP3D) convolutional network, which acquires intermediate representations of the 3-D input image at different stages [46]. Although have been proved to be more effective, there still exist some unignorable drawbacks in the above methods. First, the useless and distracting information may accumulate drastically, which would restrain the network performance and the classification accuracy [42,47,48,49,50,51,52]. Moreover, they only employ a simple concatenation operation to combine spectral and spatial features, which do not exploit the high-level semantic relation between them.
To solve the above problems, we propose a novel 2D-3D CNN with spectral-spatial multi-scale feature fusion for hyperspectral image classification (SMFFNet), in which multiple functional modules are designed based on CNN. Concretely, we first employ two diverse backbone modules for feature representation, that is, the spectral feature and the spatial feature extraction streams. The former captures multi-scale spectral features by introducing a hierarchical feature extraction module, while the latter utilizes multi-level fusion structure to extract multi-stage spatial features. With these network units, the category attribute information of HSI can be fully excavated. Then, a multi-scale spectral-spatial-semantic feature fusion module is presented based on a Decomposition-Reconstruction structure, which is capable of providing high-level spectral-spatial-semantic fusion features, outputting more complete and robust information for classification. Last of all, to lift the classification accuracy, we innovate a classification scheme to replace the simple combination of two full connected layers.
In summary, the major contributions of this paper are described as follows:
- (1)
- We propose a novel 2D-3D CNN with spectral-spatial multi-scale feature fusion for HSI classification, containing two feature extraction streams, a feature fusion module as well as a classification scheme. It can extract more sufficient and detailed spectral, spatial and high-level spectral-spatial-semantic fusion features for HSI classification;
- (2)
- We design a new hierarchical feature extraction structure to adaptively extract multi-scale spectral features, which is effective at emphasizing important spectral features and suppress useless spectral features;
- (3)
- We construct an innovative multi-level spatial feature fusion module with spatial attention to acquire multi-level spatial features, simultaneously, put more emphasis on the informative areas in the spatial features;
- (4)
- To make full use of both the spectral features and the multi-level spatial features, a multi-scale spectral-spatial-semantic feature fusion module is presented to adaptively aggregate them, producing high-level spectral-spatial-semantic fusion features for classification;
- (5)
- We design a layer-specific regularization and smooth normalization classification scheme to replace the simple combination of two full connected layers, which automatically controls the fusion weights of spectral-spatial-semantic features and thus achieves more outstanding classification performance.
The remainder of this article is organized as follows. Section 2 illustrates the related works. Section 3 presents the details of the overall framework and the individual modules. Then, Section 4 illustrates first experimental datasets and the parameters setting, and then shows the experimental results and analysis. Finally, in Section 5, the conclusions are presented.
2. Related Work
In this section, we introduce some basic knowledge, including convolutional neural networks, residual network and L2 regularization.
2.1. Convolutional Neural Networks
CNNs have made great progress in computer vision problems, due to their the weight-share mechanism and efficiency with local connections. CNNs mainly consist of a stack of alternating convolution layers and pooling layers with a number of fully connected layers. In general, convolutional layers are the most important parts of CNNs. Specifically, let be the input cube, where is the two dimension spatial size and is the number of spectral bands. Suppose there are filters at this convolutional layer and the filter can be characterized by the weight and bias . The output of convolutional layer can be represented as follows:
where, represents the convolutional operation and denotes an activation function, which can improve the nonlinearity of the network. ReLU has been the most used activation function, primarily due to robustness for gradient vanishing and a fast convergence.
2.2. Residual Network
ResNets can be constructed by stacking microblocks sequentially [48]. For each residual block, the input features are element-wisely added to the output features by skip connection, which not only can relieve the training pressure of the network but also contribute to information propagation.
Consider a network with L layers, each of which implements a nonlinear transformation . represents the layer index and consists of several operations, which includes convolution, pooling, batch normalization, activation and linear transformation. is the immediate output of .
Figure 1 shows the connection pattern in the residual network, where introduces skip connection to bypass each transformation . The additional result after skip connection is denoted by , and is equal to . The calculation equation of residual learning process is as follows:

Figure 1.
The structure of residual learning.
Note that is the input of , and is the immediate output of it, that is, . Considering the recursive property of (2), can be rewritten as follows:
Equation (3) shows that is the element-wise sum of the outputs of the preceding layers.
2.3. L2 Regularization
The basic idea of L2 regularization is to add an L2 norm penalty to the loss function as a constraint, which can prevent over-fitting and improve generalization ability. The loss function with L2 regularization is calculated as follows:
where, refers to the original loss function, denotes the L2 norm penalty, stands for the hyperparameter, is the size of training samples and the weights of the model is represented by .
3. Proposed Method
As shown in Figure 2, we give an introduction of the proposed method. The SMFFNet includes spectral feature extraction stream, spatial feature extraction stream, multi-scale spectral-spatial-semantic feature fusion module and classification scheme. The spectral feature extraction stream captures multi-scale spectral features by utilizing a hierarchical feature extraction module. The spatial feature extraction stream introduces a multi-level fusion structure to extract multi-stage spatial features. The two streams that operate in parallel extract simultaneously spectral and spatial features. The former’s input is the size of 7 × 7 × 200 extending over all the spectral bands with 3-D image cube, while the latter takes as input a size of 27 × 27 × 30 with 3-D image cube. The multi-scale spectral-spatial-semantic feature fusion module to map low-level spectral/spatial features to the high-level spectral-spatial-semantic fusion features, which are employed for classification. The classification scheme is used to lift the classification accuracy.
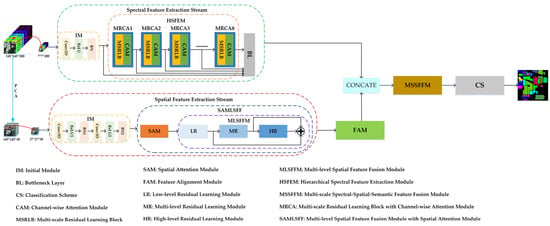
Figure 2.
The overall framework of SMFFNet.
3.1. The Spectral Feature Extraction Stream
The network structure of the spectral feature extraction stream is shown in Figure 2. First, we employ the initial module to capture general spectral features of the training samples. Then, to extract multi-scale spectral features, we design a hierarchical spectral feature extraction module. Finally, we construct a hierarchical spectral feature fusion structure to fuse multi-scale spectral features and effectively obtain global spectral information.
3.1.1. Hierarchical Spectral Feature Extraction Module
To obtain spectral features at different scales, we propose a hierarchical spectral feature extraction module (HSFEM). As shown in Figure 2, the HSFEM consists of several multi-scale residual learning blocks with channel-wise attention modules (MRCA).
Multi-Scale Residual Learning Block (MSRLB): The network structure of MSRLB is shown in Figure 3. The MSRLB is composed of multi-scale spectral feature extraction and local residual learning.
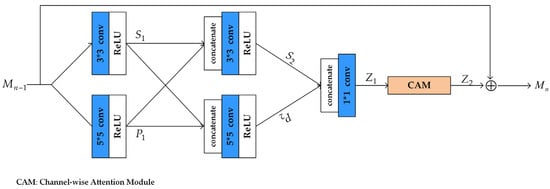
Figure 3.
The structure of multi-scale residual learning block.
Specifically, we construct a two-bypass network and each bypass employs different convolutional kernels. In this way, spectral features at different scales can be detected, simultaneously, the spectral information between all bypasses are able to be shared with each other. The operation can be expressed by:
where the weights and bias are represented by and , respectively. The superscripts refer to the number of layers at which they are located. The subscripts refer to the size of convolutional kernel used in this layer. represents the ReLU activation function. stand for the concatenation operation. denotes spectral feature maps, which are sent to the multi-scale residual learning block.
The first convolutional layer of each bypass not only has the number of channel for input spectral feature maps, but also has the number of channel for output spectral feature maps. Similarly, the second convolutional layer possesses the number of channel for spectral feature maps. The spectral feature maps of all bypasses are concatenated, and then sent to a convolutional layer. Here, the convolutional layer is used as a bottleneck layer, which can reduce the number of channel for spectral feature maps from to .
Each MSRLB adopts residual learning, which can make the network effective. The MSRLB can be described as follows:
where, the input and output of the MSRLB are represented and respectively. Additionally, stands for the output of the channel-wise attention module. The operation is realized by a skip connection and element-wise addition. It is worth noting that the use of the local residual learning can greatly reduce the computational pressure and promote the flow of information.
Channel-Wise Attention Module (CAM): The network structure of CAM is shown in Figure 4. To enhance the important spectral features and suppress the unnecessary spectral features by controlling the weight of each channel, we embed the CAM into the MSRLB. The CAM includes the squeeze process and the excitation process, which consists of a global average pooling layer (GAP), two fully connected layers (FC), and two activation function layers. The 2D global average pooling is used to average the spatial dimension of features maps with a size of H*W*C to form 1*1*C feature maps. The first FC is used to compress C channels into C/r (r is the compressed ratio of spectra channel) channels and the second FC restores the compressed channels to C channels. To guarantee that the input features of the next layer are optimal, the original output features is multiplied by the weight coefficients, which are limited to the [0, 1] range by sigmoid function.

Figure 4.
The structure of channel-wise attention module.
3.1.2. Hierarchical Feature Fusion Structure
It is important to make full use of spectral features and transfer these them to the multi-scale spectral-spatial-semantic feature fusion module (MSSFFM) for classification. However, with the increase of the network depth, these spectral features may gradually disappear. To fully exploit the hierarchical spectral features of each MRCA and improve the classification performance, we propose a hierarchical feature fusion structure (HFFS).
The outputs of each MRCA are sent to the MSSFFM, which can obtain distinct spectral features at different scales. However, these spectral features may not only contain abundant redundant information, but also increase the computational complexity. Thus, we introduce a convolutional layer with kernel as a bottleneck layer, which can adaptively extract critical spectral information from these hierarchical features. The output of HFFS can be formulated as:
where, refers to the output of the initial module for the spectral feature extraction stream, denotes the output of the MRCA, and represents the concatenation operation. The HFFS not only reduces the computational complexity and obtains more representative spectral features, but also improves the classification performance.
3.2. The Spatial Feature Extraction Stream
The network structure of the spatial feature extraction stream is provided in Figure 2. First, we use principal component analysis (PCA) to remove noise and unimportant spectral bands. Second, the initial module is employed to reduce the number of channels and the quantity of calculation. Then, to extract multi-level spatial features, we construct a multi-level spatial feature fusion module with a spatial attention module (SAMLSFF). Finally, a feature alignment module (FAM) is performed, which can reduce the spatial dimension of spatial features to the same as the spectral feature extraction stream.
Spatial Attention Module (SAM): The network structure of SAM is shown in Figure 5. To make full use of the close correlation between hyperspectral pixels and capture more distinguishing spatial features, we embed the SAM into the multi-level spatial feature fusion module.
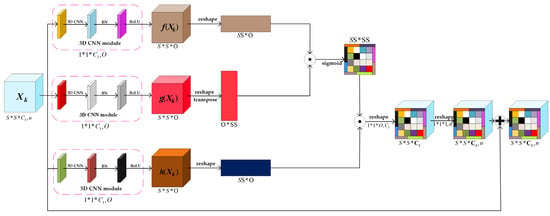
Figure 5.
The structure of spatial attention module.
denotes the input data of the SAM, where and represent the spatial size and the number of spectral channels respectively. First, to simplify computation complexity and reduce the number of channels, the 3-D convolution with kernels is employed to transform the input data into , and from top to bottom. The equation of is as follows:
where, the wight and bias parameters are represented by and respectively. The equations of and are similar to the equation of .
Second, three feature maps obtained in the previous step are reshaped to . The relationship of different hyperspectral pixels is calculated by multiplying by as follows:
Third, a softmax is used to normalize the R by row:
Next, the attention features is produced by multiplying the normalized by , as shown in Equation (16):
Then, two 3-D convolutional layers with and kernels is utilized to convert to , which makes and have the same number of channels.
Finally, to facilitate the convergence of the proposed method, a skip connection is used to add the attention features to the input features .
Multi-Level Spatial Feature Fusion Module (MLSFFM): The network structure of MLSFFM is presented in Figure 2. The spatial features at different levels have a different significance. Shallow spatial features have small receptive fields and can only extract local features, but they have high resolution and richer details. Deep spatial features have low resolution, but they contain more abstract and semantic information. In this work, we design an MLSFFM to fuse different levels of spatial features, which consists of low-level residual block (LR), middle-level residual block (MR) and high-level residual block (HR). The MLSFFM not only obtains the shallow detailed spatial features, but also extracts the deep abstractly semantic spatial features. Each residual block includes two 3-D convolutional layers with kernels. To boost the training speed and improve the ability of nonlinear discrimination, we add a BN layer and a PReLU to the first convolutional layers. Furthermore, to facilitate the convergence of the MLSFFM and avoid over-fitting, we introduce skip connection for each residual block.
We denote the input data and output data of each residual block as and (, i is the residual block index). The process of the MLSFFM is described as follows:
where, stands for the intermediate output of residual block. The weight and bias parameters are represented by and , whose superscripts and subscripts refer to the index of residual block and the number of layers at which they are located. denotes PReLU activation function. The final output of the MLSFFM is realized by element-wise addition. Moreover, to reduce the spatial dimension of spatial features to the same as the spectral feature extraction stream and alleviate feature redundancy to some extent, we propose an FAM. The FAM includes four 3-D convolutional layers with kernels and a 3-D convolutional layer with kernels. The spatial feature extraction stream not only aggregates low-level, middle-level and high-level spatial features, but also pays more attention to the informative areas in the spatial features.
3.3. Multi-Scale Spectral-Spatial-Semantic Feature Fusion Module
After the spectral feature extraction stream and spatial feature extraction stream, we can obtain the multi-scale spectral features and the multi-level spatial features. To extract more representative and discriminating features for HSI classification, we construct a multi-scale spectral-spatial-sematic feature fusion module (MSSFFM). The network structure of MSSFFM is shown in Figure 6. Here, we design a Deconstruction-Reconstruction structure, which not only can map low-level spectral-spatial features to high-level spectral-spatial-semantic features, but also learn multi-scale fusion features at a granular level [53].
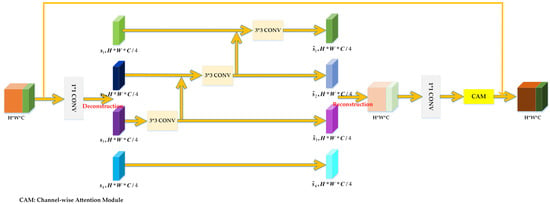
Figure 6.
The structure of Deconstruction-Reconstruction.
First, we adopt a simple concatenation operation to get spectral-spatial features as the input data cube of the Deconstruction-Reconstruction structure. Second, after the convolutional layer, we equally divide the input data into four feature subsets, represented by , , and . The number of channels per feature subset is a quarter of the original input data cube. Except for , each subset contains a corresponding convolution, denoted by . The output of is represented by . The feature subset is added with the output of , and then fed into .To reduce parameters during increasing ,we omit the convolution for . Therefore, can be written as:
Third, is used to generate the first high-level feature subset through the 2-D convolution that contains 18 convolutional filters of size . Then, we use the sum of the first high-level feature subset and the third subset as input to generate the second high-level feature subset . Similarly, we also employ the sum of the second high-level feature subset and the fourth subset as input to generate the second high-level feature subset . Then, to better fuse information at different scales, , , and are concatenated and pass through a convolution. The Deconstruction-Reconstruction structure can make the convolution process features more effectively. Finally, we embed the CAM into the Deconstruction-Reconstruction structure and introduce a skip connection, which can enhance feature extraction ability and promote the flow of spectral-spatial-semantic information.
3.4. Feature Classification Scheme
The current deep learning classification methods employ simple fully connected layers with ReLU activation function [54,55,56,57]. In this work, a smooth normalization and layer-specific regularization classification scheme (CS) is proposed. We define the CS as follows:
where, and refer to convolutional kernels of the two fully connected layers respectively. is the Frobenius norm and denotes the regularization parameter, which controls all the fusion weights. stands for sigmoid activation function. In addition, the input data and output data of the CS are represented by and respectively. Compared with the ReLU activation function, the sigmoid activation function can not only avoid the blow up phenomenon, but also retain a more representative and improved HSI classification performance. To adaptively adjust the fusion weights, we append an L2 regularization term to the CS. Owing to the layer-specific regularization, the novel CS can effectively avoid over-fitting.
Finally, we fed the output into the last fully connected layer with classes following a softmax function to generate the predicted probability vector. The cross entropy objective function is defined as follows:
where represents the total number of training samples, the value of the one-hot encoding ground truth for the train sample is denoted by . and stand for weight and bias in this layer. In addition, refers to the output of the training sample. Our proposed CS can adaptively control the fusion weights of spectral-spatial-semantic features and achieve a better classification performance.
4. Experiments and Results
In this section, we first introduce three public HSI datasets and popular evaluation indexes to evaluate the performance of our proposed SMFFNet method. Second, we discuss the main factors affecting the classification performance. Then, we compare the proposed method with several state-of-the-art HSI classification methods. Finally, to demonstrate the superiority of the proposed SMFFNet method, we perform four ablation experiments on three datasets.
4.1. Experimental Datasets, Classification Evaluation Indexes and Experimental Setup
4.1.1. Experimental Datasets
We employ three commonly available HSI datasets to evaluate the classification performance of the proposed SMFFNet method.
The India Pines (IN) dataset [43] is captured from the pine forest pilot area of Northwest Indiana by an Airborne Visible/Infrared Imaging Spectrometer (AVIRIS ) in 1992. It includes 16 categories with the image sizes of pixels and a spatial resolution of 20 by pixel. There are 224 spectral bands ranging from 0.4 to 2.5 . Because bands 104 to 108, 150 to 163 and 220 cannot be reflected by water, these 20 bands are generally removed, the remaining 200 spectral bands can be used for HSI experiments.
The Kennedy Space Center (KSC) dataset [43] is collected by AVIRIS in 1996 from the Kennedy Space Center, containing 224 spectral bands ranging from 0.4 to 2.5 . It consists of 13 classes with the size of pixels and a spatial resolution of 18 by pixel. After removing water absorption and low signal-to-noise ratio (SNR) bands, the remaining 176 spectral bands can be adopted for HSI experiments.
The Salinas-A scene (SA) dataset [58] is a small subscene of Salinas scene, gathered by AVIRIS in the Salinas Valley of California, with a images sizes of pixels and a spatial resolution 3.7 by pixel, and contains six types of geographic objects. Since 20 bands with high moisture absorption are removed, the remaining 204 spectral bands ranging from 0.4 to 2.5 can be used for HSI experiments.
Table 1, Table 2 and Table 3 show up the total number of samples of each category in each HSI dataset and Figure 7, Figure 8 and Figure 9 list false-color image and ground-truth of three datasets.

Table 1.
Land cover class information for the IN dataset.

Table 2.
Land cover class information for the KSC dataset.

Table 3.
Land cover class information for the SA dataset.

Figure 7.
(a) False-color image, (b) Ground-truth image, and (c) Labels of the IN dataset.

Figure 8.
(a) False-color image, (b) Ground-truth image, and (c) Labels of the KSC dataset.

Figure 9.
(a) False-color image, (b) Ground-truth image, and (c) Labels of the SA dataset.
4.1.2. Classification Evaluation Indexes
In this work, we adopt the overall accuracy (OA), average accuracy (AA) and Kappa coefficient (Kappa) as the HSI classification evaluation indexes. Confusion matrix (CM) can reflect the classification results, which is the basis for people to understand other classification evaluation indexes of HSI. Assuming that there are kinds of ground objects, and the equation of the CM with the size of is as follows:
where element represents that the number of samples in category has been classified as class . and denote the number of samples in category and the number of sample in category respectively.
OA represents the ratio between the number of correctly classified samples and the total number of samples. Although OA reflects the performance of the whole classifier, the unbalanced samples greatly impact it. The equation of OA is as follows:
AA represents the average value of classification accuracy of each category, and reflects each category is equally important, the equation of AA is as follows:
Kappa measures the consistency between the classification results and the ground-truth, which is an indispensable index to evaluate the performance of HSI classification. The equation of Kappa is as follows:
4.1.3. Experimental Setup
In this section, we present the detailed network parameter setting of the proposed SFMMNet for three HSI datasets, as shown in Table 4. All the training and testing results are obtained on the same computer, with the configuration of 16 G of memory, NVIDIA GeForce RTX 2060 SUPER 6G and Intel i-7 9700F. The software platform is based on the Tensorflow 2.3.0, Keras 2.4.3, CUDA 10.1 and Python 3.6.

Table 4.
The network parameter setting of the proposed SFMMNet.
4.2. Experimental Parameters Discussion
4.2.1. Analysis of Different Ratios of the Training, Validation and Test Datasets
To explore the performance of the proposed SMFFNet under different ratios of training samples, we divide the training set, validation set and test dataset into five different ratios {0.5:1:8.5, 1:1:8, 2:1:7, 3:1:6, 4:1:5}. The three evaluation indexes in different ratios of training samples for three HSI datasets are shown in Table 5.

Table 5.
The influence of different sample ratios on three HSI datasets.
From Table 5, we can find that, in general, with the increase of the ratio of training samples, the three evaluation indexes of our proposed method gradually increase. Specifically, when the proportion of training samples is 5%, due to the small total number of samples and the random selection of training samples, some category samples are not selected, which retrains the classification performance, especially the IN dataset. When the proportion of training samples is 30%, we can see that the evaluation indexes of the IN and KSC datasets decrease slightly, while those of the SA dataset reduce significantly. When the proportion of training samples is 40%, the proposed method has already classified the IN and KSC categories with three evaluation indexes close to 100%, and those of the SA dataset are 100%. We may notice that the higher classification accuracy of the proposed method requires a great quantity of training samples. Therefore, we choose the ratio set of 4:1:5 as the final ratios for three HSI datasets.
4.2.2. Analysis of the Patch Size
The patch size greatly affects the classification performance. If the patch size is too small, the information will be lost due to the insufficient receptive filed; while if the patch size is too large, it will introduce much noise and increase interclass interference. Therefore, a suitable patch size is vital for the classification performance. From Figure 10a,b,d and e, we can obviously see that when the spectral patch size is 7 × 7 and the spatial patch size is 27 × 27, the IN and KSC datasets possess best evaluation indexes. As shown in Figure 10c,f, all evaluation indexes are higher than 99.9%, except for the spatial patch size of 21 × 21. To obtain the optimal classification performance and make the proposed SMFFNet universal, we choose the spectral patch size of 7 × 7 and the spatial patch size of 27 × 27 the most suitable size for SA datasets.
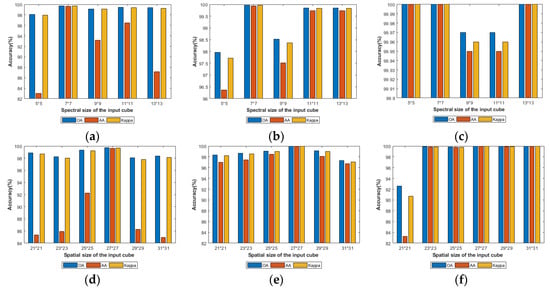
Figure 10.
The influence of different spectral and spatial patch sizes. (a–c) represent the influence of different spectral patch sizes on IN, KSC and SA respectively. (d–f) represent the influence of different spatial sizes patch sizes on IN, KSC and SA respectively.
4.2.3. Analysis of the Principal Components of Spatial Feature Extraction Stream
To analyze the influence of the number of principal components on the classification performance, here, we set the principal components of different ratios to {20, 25, 30, 35, 40}. From Figure 11a, when the number of principal components is 30, the evaluation indexes are the highest and most features of HSI data are retained for the IN dataset. From Figure 11b, we can clearly see that the evaluation indexes with the number of principal components of 30 are significantly superior to other conditions and the classification effect is the most outstanding for the KSC dataset. Therefore, we choose the number of principal components to 30 for the IN and KSC datasets. From Figure 11c, the SA dataset have better evaluation indexes, except the number of principal components of 20. To reserve more feature information and achieve the best classification performance, we set the number of principal components to 30 for the SA dataset.

Figure 11.
The influence of the number of principal components. (a–c) represent the influence of the number of principal components on IN, KSC and SA respectively.
4.2.4. Analysis of Different Ratios of Channel-Wise Attention Module
To explore the sensitivity of the proposed SMFFNet to different compressed ratios of the CAM, we set the version for different . From Figure 12a, when the compressed ratio is 1, the IN dataset has the highest evaluation indexes. Meanwhile, we can find that with the increase of the compressed ratios, the evaluation indexes decrease significantly, especially the AA. From Figure 12b, when the compressed ratio is 4, three evaluation indexes are best for the KSC dataset. Then, with the increase of the compressed ratios, the evaluation indexes decrease slightly. From Figure 12c, compared with the compressed ratio of 4 and 16, three evaluation indexes under other conditions attain 100%. To reduce parameters and relieve the calculation pressure, we set the compressed ratio to 1 for the SA dataset.
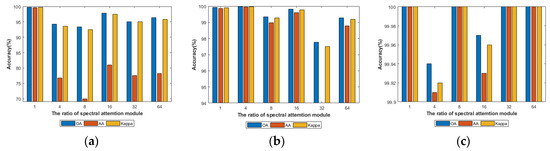
Figure 12.
The influence of different ratios of channel-wise attention module. (a–c) represent the influence of different ratios on IN, KSC and SA, respectively.
4.3. Classification Results Comparison with the State-of-the-Art Methods
To verify the effectiveness of our proposed SSMFFNet method, we compare SMFFNet with several classic methods, including SVM [13], Multinomial Logistic Regression (MLR) [57], Random Forest (RF) [59], 1-D CNN [37], 2-D CNN [60], 3-D CNN [61], Hybrid [62], JSSAN [63], RSSAN [64], TSCNN [65]. Here, SVM, MLR and RF are implemented by scikit learn, other methods are realized by tensorflow frame. We will classify these comparison methods in two ways. On the one hand, SVM, MLR and RF methods belong to the traditional machine learning; nevertheless, 1-D CNN, 2-D CNN, 3-D CNN, Hybrid, JSSAN, RSSAN, TSCNN and our proposed SMFF methods belong to the deep learning. On the other hand, SVM, MLR, RF and 1-D CNN methods are based on spectral information; 2-D CNN method is based on spatial information; nevertheless, 3-D CNN, HybridSN, JSSAN, RSSAN, TSCNN and our proposed SMFF methods are based on spectral and spatial information. For the sake of fair comparison, we choose 40% samples as the training set, 10% samples as the validation set and remaining samples as the test set. The OA, AA, Kappa coefficients, and the classification accuracy of each category for three HSI datasets are shown in Table 6, Table 7 and Table 8.

Table 6.
Classification results of different methods for the IN dataset.

Table 7.
Classification results of different methods for the KSC dataset.

Table 8.
Classification results of different methods for the SA dataset.
- (1)
- From the tables, we can see clearly that compared with other methods, the proposed SMFFNet method has the highest evaluation indexes on three HSI datasets. Specifically, first, compared with three traditional classification methods, deep learning methods achieve generally higher evaluation indexes and better classification performance, except 2-D CNN and RSSAN on the IN data set, 2-D CNN on the KSC data set and 1-D CNN on the SA data set. Because the deep learning methods can automatically extract features from HSI data and have better robustness. Second, compared with classification methods using spectral and spatial information (such as 3D-CNN, HybridSN etc.), classification methods only using spectral information (such as SVM, MLR, RF and 1-D CNN) or spatial information (such as 2-D CNN) obtain lower classification accuracy and worse classification performance, except RSSAN on the IN dataset. It means that these classification methods cannot make full use of spectral and spatial information of HSI. Third, the proposed SMFFNet achieve the highest OA, AA and Kappa with a significant improvement over the above mentioned deep learning methods. For instance, in the Table 6, SMFFN method achieves OA 99.74% with the gains of 17.42%, 41.42%, 1.08%, 5.85%, 4.48%, 32.8% and 0.76% over 1-D CNN, 2-D CNN, 3-D CNN, Hybrid, JSSAN, RSSAN and TSCNN methods, respectively. The other two HSI datasets have semblable classification results. The complexity of 3-D CNN, Hybrid, JSSAN, RSSAN, TSCNN and SMFFNet methods is 0.001717184G, 0.01210803G, 0.000273436G, 0.000261567G, 0.00454323G and 0.010243319G, respectively. Furthermore, compared with these methods, our proposed SMFFNet can classify all categories on three datasets more accurately. It means that the proposed SMFFNet only need fewer training samples to get better classification performance and excellent evaluation indexes.
- (2)
- The TSCCN method consists of a local feature extraction stream and a global feature extraction stream. Nevertheless, our proposed SMFFNet method includes a spectral feature extraction stream, a spatial feature extraction stream and a multi-scale spectral-spatial-semantic feature fusion module. The TSCNN method and the proposed SMFFNet method employ a similar two-stream structure. From the tables, compared with the TSCNN method, the proposed SMFFNet method achieved the highest classification accuracy and a better classification performance. To be specific, on the IN dataset, the OA, AA and Kappa of the SMFFNet method are 0.76%, 5.85% and 3.86% higher than those of the TSCNN method respectively. Moreover, only two classes of our proposed method have lower classification accuracy than those of the TSCCN method. The other two HSI datasets have semblable classification results. This is because that the TSCNN method only uses several ordinary consecutive convolution operations embedded SE modules to extract shallow spectral and spatial features and ignores high-level semantic. However, our proposed SMFFNet not only extracts multi-scale spectral features and multi-level spatial features, but also maps the low-level spectral/spatial features to high-level spectral-spatial-semantic fusion features for improving HSI classification.
- (3)
- The Hybrid method is based on 2D-3D CNN for HSI classification. Nevertheless, our proposed SMFFNet method also employs 2D-3D CNN for HSI classification. The Hybrid method and the proposed SMFFNet method takes 2D-3D CNN as the basic framework. From the tables, compared with the Hybrid method, the evaluation indexes of the proposed SMFFNet method are higher than those of it. Specifically, the OA, AA and Kappa of the SMFFNet method are 5.85%, 5.86% and 5.67% higher than those of the Hybrid method on the IN dataset, respectively. Moreover, only one class of our proposed method has lower classification accuracy than that of the Hybrid method. The other two HSI datasets have semblable classification results. Although the Hybrid method uses 2D-3D convolution to extract spectral and spatial features, it does not extract coarse spectral-spatial fusion features and ignores the close correlation between spectral and spatial information.
- (4)
- The JSSAN, RSSAN, TSCCN and our proposed SMFFNet methods embed an attention mechanism to enhance feature extraction ability. From the tables, we can see that the OA, AA, Kappa and the classification accuracy of each category of our SMFFNet method are the highest. It means that we use channel-wise attention mechanism and spatial attention mechanism to improve the feature extraction capacity, enhance useful feature information and suppress unnecessary ones. These show that the proposed method combined with the attention mechanism can achieve a better classification performance and an excellent classification accuracy.
- (5)
- Figure 13, Figure 14 and Figure 15 show the visualization maps of all categories of all classification methods, along with corresponding ground-truth maps. From the figures, we can find that the classification maps of SVM, MLR, RF, 1-D CNN, 2-D CNN, 3-D CNN, Hybrid, JSSAN, RSSAN and TSCNN have some dot noises in some categories. Compared with these classification methods, the proposed SMFFNet method has smoother classification maps. In addition, the edge of each category is clearer than others and the prediction effect on unlabeled samples is also significantly better, which indicates that the attention mechanism can effectively suppress the distraction of interfering samples. Compared with the proposed SMFFNet method, other methods cause the misclassification of many categories and their classification maps are very rough. Our proposed method not only has fairly smooth classification maps and more higher classification prediction accuracy. Owing to the idiosyncratic structure of SMFFNet method, it can fully extract the spectral-spatial-semantic features of the HSI and achieve more detailed and discriminable fusion features.
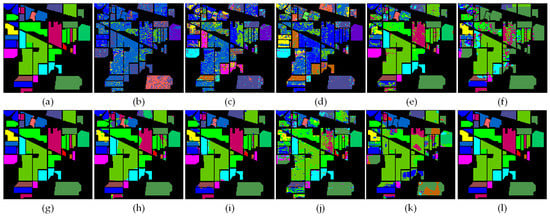 Figure 13. Classification results of the models in comparison with the IN dataset. (a) Ground-truth labels, (b–l) classification results of SVM, MLR, RF, 1D-CNN, 2D-CNN, 3D-CNN, Hybrid, JSSAN, RSSAN, TSCNN and SSMFF, respectively.
Figure 13. Classification results of the models in comparison with the IN dataset. (a) Ground-truth labels, (b–l) classification results of SVM, MLR, RF, 1D-CNN, 2D-CNN, 3D-CNN, Hybrid, JSSAN, RSSAN, TSCNN and SSMFF, respectively. Figure 14. Classification results of the models in comparison with KSC dataset. (a) Ground-truth labels, (b–l) classification results of SVM, MLR, RF, 1D-CNN, 2D-CNN, 3D-CNN, Hybrid, JSSAN, RSSAN, TSCNN and SSMFF, respectively.
Figure 14. Classification results of the models in comparison with KSC dataset. (a) Ground-truth labels, (b–l) classification results of SVM, MLR, RF, 1D-CNN, 2D-CNN, 3D-CNN, Hybrid, JSSAN, RSSAN, TSCNN and SSMFF, respectively. Figure 15. Classification results of the models in comparison with the SA dataset. (a) Ground-truth labels, (b–l) classification results of SVM, MLR, RF, 1D-CNN, 2D-CNN, 3D-CNN, Hybrid, JSSAN, RSSAN, TSCNN and SSMFF respectively.
Figure 15. Classification results of the models in comparison with the SA dataset. (a) Ground-truth labels, (b–l) classification results of SVM, MLR, RF, 1D-CNN, 2D-CNN, 3D-CNN, Hybrid, JSSAN, RSSAN, TSCNN and SSMFF respectively.
4.4. Ablation Experiments
4.4.1. Analysis of Classification Scheme and L2 Regularization Parameter
To prove the validity of the proposed classification scheme and keep other parameters unchanged, we compare four classification schemes: fully connected layers with ReLU activation function (R); fully connected layers with sigmoid activation function (S); ReLU activation function with L2 regularization (R-L2) and our proposed sigmoid activation function with L2 regularization (S-L2).
From Table 9, we can see that, compared with other classification schemes, our proposed classification scheme has the highest evaluation indexes and an excellent classification performance. Specifically, on the IN dataset, compared with the R, the OA, AA and Kappa of the S-L2 improve 0.37%, 0.97% and 0.42% respectively; compared with the S, the OA, AA and Kappa of the S-L2 improve 2.89%, 20.65% and 2.85% respectively; compared with the R-L2, the OA, AA and Kappa of the S-L2 improve 1.64%, 3.39% and 1.87%, respectively. The KSC dataset is similar to the IN dataset, but the evaluation indexes change greatly. The evaluation indexes of the four classification schemes are 100%. These results indicate that our proposed scheme is more robust and effective.

Table 9.
The effect of classification scheme for three HSI datasets.
To explore the sensitivity of the proposed classification scheme to the parameter of L2 regularization, we set different . From Figure 16a,b, we can find that with the increase of the parameter , on the IN and KSC datasets, the curves fluctuate obviously. When the parameter is 0.02, three evaluation indexes are excellent. As shown in Figure 16c, on the SA dataset, the curves decrease slightly at the parameter of 0.0005, then rise to the highest accuracy 100% and remain unchanged, finally decrease sharply at the parameter of 0.2.
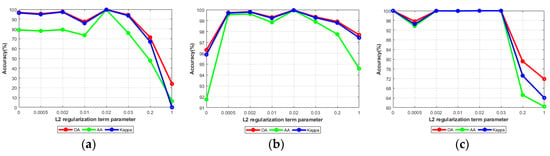
Figure 16.
The influence of L2 regularization parameter. (a–c) represent the influence of L2 regularization parameter on IN, KSC and SA, respectively.
4.4.2. Analysis of Attention Module
To valid the effectiveness of the attention mechanisms embedded in the proposed SMFFNet method, we compared the SMFFNet (CAM+SAM-Net) with the SMFFNet wiuthout the spectral and spatial attention mechanisms (NO-Net); SMFFNet only with a spectral attention mechanism (CAM-Net) and SMFFNet only with a spatial attention mechanism (SAM-Net).
From Table 10, it is obvious that the evaluation indexes of the NO-Net are lowest on three HSI datasets. Specifically, on the IN and KSC datasets, we can see that the evaluation indexes of the SAM-Net are significantly higher than those of the CAM-Net, especially the AA improve 4.46% and 4.62%, respectively. That is probably that the CAM-Net only employs spectral information and ignores rich two dimension spatial information. However, on the SA dataset, the evaluation indexes of the CAM-Net are significantly higher than those of the SAM-Net, the Kappa especially improves by 1.48%. That is probably because the SAM-Net may need more parameters and increase of the training complexity. These results suggest that our proposed CAM+SAM-Net has excellent evaluation indexes and outstanding classification performance.

Table 10.
The effect of attention module for three HSI datasets.
4.4.3. Analysis of Spectral, Spatial and Spectral-Spatial-Semantic Feature Stream
To valid the effectiveness of the spectral feature extraction stream, spatial feature extraction stream and multi-scale spectral-spatial-semantic feature fusion module of the proposed SMFFNet method, we compare the SMFFNet (B+A+S) with other six methods: the SMFFNet only with the spectral feature extraction stream (B); the SMFFNet only with the spatial feature extraction stream (A); the SMFFNet only with the spectral and spatial feature extraction stream (B+A); the SMFFNet only with the multi-scale spectral-spatial-semantic feature fusion module (S); the SMFFNet only with the spectral feature extraction stream and multi-scale spectral-spatial-semantic feature fusion module (B+S); the SMFFNet only with spatial feature extraction stream and multi-scale spectral-spatial-semantic feature fusion module (A+S).
From Figure 17, we can clearly see that the evaluation indexes of the B+A+S are the highest on three HSI datasets. This is because the B+A+S not only fully extracts spectral and spatial features, but also maps low-level spectral/spatial features to high-level spectral-spatial-semantic fusion features so as to improve the classification performance. Specifically, on the IN dataset, the B has the lowest evaluation indexes. That is probably because the B only spectral features and ignores abundant spatial and high-level semantic features. On the KSC dataset, the A has lowest evaluation indexes. That is probably because the A only pays attention to the spatial information and ignores rich spectral and high-level semantic features. On the SA dataset, the B+S has the lowest evaluation indexes. That is probably because, although the B+S employ spectral and semantic information, it introduces much noise and redundancy information, which is harmful to the classification performance. These results illustrate that our proposed method is prime and obtains excellent classification accuracy.
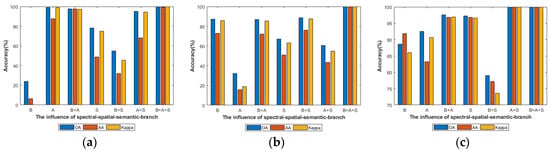
Figure 17.
The influence of spectral, spatial and spectral-spatial-semantic stream. (a–c) represent the influence of spectral, spatial and spectral-spatial-semantic stream on IN, KSC and SA respectively.
4.4.4. Analysis of the Network Depth
The depth of the proposed SMFFNet greatly affects the classification performance. To find the most suitable depth of the spectral feature extraction stream (B), we discuss different depths From Figure 18a,b, we can clearly see that, with the increase of the depth of the B, on the IN and KSC datasets, the evaluation index curves fluctuate greatly, especially the curve of AA. When the depth of the B is 8, three evaluation indexes are the highest on the IN and KSC datasets. From Figure 18c, it is obvious that the evaluation index curves decrease slightly at the depth of 3, and significantly at the depths of 5 and 10 on the SA dataset. The evaluation indexes under other conditions have better accuracy. To make the SMFFNet universal and reduce the network complexity, we set the depth of the B to 8 for SA dataset. In addition, we may notice that the evaluation index curves have a significant increase or decrease on the three datasets, the network depth has great influence on the classification performance. If the network depth is too shallow, the feature extraction is insufficient; if the network depth is too deep, the gradient may disappear. Therefore, the number of MRCA added or removed can not only change the depth of the proposed SMFFNet, but also greatly affect the classification performance.
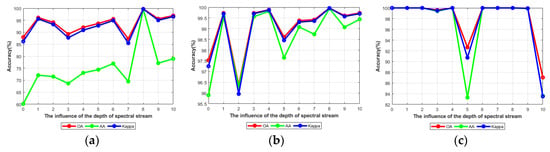
Figure 18.
The influence of the depth of spectral stream. (a–c) represent the influence of the depth of spectral stream on IN, KSC and SA, respectively.
To valid the effectiveness of the multi-level spatial feature fusion module (low+middle+high), we compare it with other three modules: the SMFFNet without the multi-level spatial feature fusion module (no-fusion), the SMFFNet only with low-level residual learning module (low) and the SMFFNet only with the low-level and middle-level residual learning modules (low+middle). From Figure 19, we can find obviously that the evaluation indexes of the low+middle+high are highest on three HSI datasets. Specifically, as shown in Figure 19a, compared with the no-fusion, the OA, AA and Kappa of the evaluation indexes improve 3.27%, 21.32% and 3.73%; compared with the low, the OA, AA and Kappa of the evaluation indexes improve 5.54%, 25.45% and 6.32%; compared with the low+middle, the OA, AA and Kappa of the evaluation indexes improve 3.76%, 21.79% and 4.28%. The results of the KSC dataset are similar to those of the IN dataset. As shown in Figure 19c, the evaluation indexes of the mo-fusion are lowest, those of the other three modules reach 100%. It is probable that the SA dataset containing relatively few label samples and categories train easily. To make the SMFFNet universal, we choose the low+middle+high for our proposed SMFFNet. These results prove that the proposed method has superb classification and more robustness. So, the use of a low-level residual learning module, a middle-level residual learning module and a high-level residual learning module has an effect on the depth of the proposed SMFFNet and classification performance.
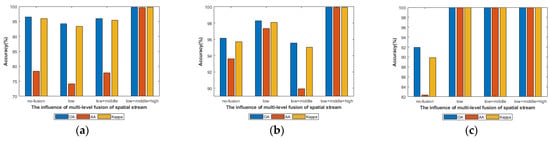
Figure 19.
The influence of multi-level spatial feature fusion structure. (a–c) represent the influence of multi-level spatial feature fusion structure on IN, KSC and SA, respectively.
5. Discussion and Conclusions
In this paper, we propose a novel 2D-3D CNN with spectral-spatial multi-scale feature fusion (SMFFNet) for hyperspectral image classification, which can extract spectral, spatial, and high-level spectral-spatial-semantic fusion features simultaneously. Multiple functional modules of the proposed method are designed based on 2D-3D CNN, in which the 2D convolution is adopted to reduce the training parameters to decrease computation complexity, the 3D convolution is utilized to be more consistent with the 3-D structure of HSI data and extract more discriminating features. The proposed method includes four parts: two features extraction streams, a feature fusion module as well as a classification scheme. First, we use two diverse backbone modules for feature representation, that is, the spectral feature and the spatial feature extraction streams. The spectral feature extraction stream is designed to extract multi-scale spectral features, learn important spectral information, and suppress useless information, which consists of a initial layer, a hierarchical spectral feature extraction module and a hierarchical feature fusion module. The spatial feature extraction stream is constructed to obtain multi-level spatial features, and extract context information to strength the spatial features, which includes an initial module, a multi-level spatial feature fusion module with spatial attention mechanism and a feature alignment module. Two feature extraction streams can fully excavate the category attribute information of HSI. Then, the multi-scale spectral-spatial-semantic feature fusion module is raised based on the Decomposition-Reconstruction structure, which maps low-level spectral/spatial features to the high-level spectral-spatial-semantic fusion features used for classification. Ultimately, to enhance classification performance, we adopt a layer-specific regularization and smooth normalization classification scheme to replace the simple combination of two full connected layers, which can adaptively learn fusion weights of spectral-spatial-semantic features from fusion module.
To prove the effectiveness and advantages of the proposed SMFFNet, lots of comparison experiments are conducted on three popular HSI datasets. The OA, AA, Kappa coefficients, and the classification accuracy of each category on three HSI datasets demonstrate that the proposed SMFFNet outperforms the state-of-the-art methods. Moreover, the above ablation experiments also adequately verify the validity of the proposed hierarchical spectral feature extraction module, the multi-level spatial feature fusion module with the spatial attention module and the multi-scale spectral-spatial-semantic feature fusion module.
However, the proposed method still has some shortcomings. By calculating the computation cost of complex methods, which includes 3-D CNN, Hybrid, JSSAN, RSSAN, TSCNN and SMFFNet methods, we find that the proposed method needs a relatively high computation cost. Since the multi-scale residual block of SSMFFNet contains different blocks, the integrity of information is guaranteed, but the structure of the model is relatively complex and the training parameters are more so. So, future work will focus on how to effectively reduce the complexity of the model while obtaining a high classification. In addition, hyperspectral image classification has been widely used in many fields of computer vision. Therefore, in the future, we will try to apply the proposed classification method to some computer vision tasks, such as target recognition.
Author Contributions
Conceptualization, D.L.; validation, G.H., P.L. and H.Y.; formal analysis, D.L.; investigation, D.L., G.H., P.L. and H.Y.; original draft preparation, D.L.; review and editing, D.L., G.H., P.L., H.Y., X.S., Q.L. and J.W.; funding acquisition, G.H., P.L. and H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant numbers 61602432 and 61401425.
Data Availability Statement
The data presented in this study are available in this article.
Acknowledgments
The authors would like to thank the anonymous reviewers for their constructive comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Landgrebe, D. Hyperspectral image data analysis. IEEE Signal Process. Mag. 2002, 19, 17–28. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Deep learning classifiers for hyperspectral imaging: A review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Generative Adversarial Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5046–5063. [Google Scholar] [CrossRef]
- Yokoya, N.; Chan, J.C.; Segl, K. Potential of Resolution-Enhanced Hyperspectral Data for Mineral Mapping Using Simulated EnMAP and Sentinel-2 Images. Remote Sens. 2016, 8, 172. [Google Scholar] [CrossRef] [Green Version]
- Du, B.; Zhang, Y.; Zhang, L.; Tao, D. Beyond the Sparsity-Based Target Detector: A Hybrid Sparsity and Statistics-Based Detector for Hyperspectral Images. IEEE Trans. Image Process. 2016, 25, 5345–5357. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Chan, J.C.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; Guerriero, L.; Frate, F.D.; Miglietta, F.; Valentini, R. Biodiversity Mapping in a Tropical West African Forest with Airborne Hyperspectral Data. PLoS ONE 2014, 9, e97910. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Wang, Z.; Wang, Z.J.; Ward, R.K.; Wang, X. Deep learning for pixel-level image fusion: Recent advances and future prospects. Inf. Fusion 2018, 42, 158–173. [Google Scholar] [CrossRef]
- Hughes, G. On the Mean Accuracy of Statistical Pattern Recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef] [Green Version]
- Gan, Y.; Luo, F.; Lei, J.; Zhang, T.; Liu, K. Feature Extraction Based Multi-Structure Manifold Embedding for Hyperspectral Remote Sensing Image Classification. IEEE Access 2017, 5, 25069–25080. [Google Scholar] [CrossRef]
- Xu, Y.; Du, B.; Zhang, L. Beyond the Patchwise Classification: Spectral-spatial Fully Convolutional Networks for Hyperspectral Image Classification. IEEE Trans. Big Data 2020, 6, 492–506. [Google Scholar] [CrossRef]
- Cariou, C.; Chehdi, K. Unsupervised Nearest Neighbors Clustering With Application to Hyperspectral Images. IEEE J. Sel. Top. Signal Process. 2015, 9, 1105–1116. [Google Scholar] [CrossRef] [Green Version]
- Haut, J.M.; Paoletti, M.; Plaza, J.; Plaza, A. Cloud implementation of the k-means algorithm for hyperspectral image analysis. J. Supercomput. 2017, 73, 514–529. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of Hyperspectral Remote Sensing Images with Support Vector Machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Xia, J.; Bombrun, L.; Berthoumieu, L.; Germain, C. Spectral-spatial Rotation Forest for Hyprespectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4605–4613. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Semisupervised Hyperspectral Image Segmentation Using Multinomial Logistic Regression With Active Learning. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4085–4098. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Lin, J.; Yuan, Y. Salient Band Selection for Hyperspectral Image Classification via Manifold Ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef] [PubMed]
- Ham, J.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef] [Green Version]
- Jia, X.; Kuo, B.C.; Crawford, M.M. Feature mining for hyperspectral image classification. Proc. IEEE 2013, 101, 676–697. [Google Scholar] [CrossRef]
- Ghamisi, P.; Benediktsson, J.A.; Ulfarsson, M.O. Spectral-spatial hyperspectral image classification via multiscale adaptive sparse representation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2565–2574. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Lin, J.; Wang, Q. Hyperspectral Image Classification via Multitask Joint Sparse Representation and Stepwise MRF Optimization. IEEE Trans. Cybern. 2016, 46, 2966–2977. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification via kernel sparse representation. In Proceedings of the 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 1233–1236. [Google Scholar]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and Spatial Classification of Hyperspectral Data Using SVMs and Morphological Profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef] [Green Version]
- Yin, B.; Cui, B. Multi-feature extraction method based on Gaussian pyramid and weighted voting for hyperspectral image classification. In Proceedings of the 2021 IEEE International Conference on Consumer Electronics and Computer, Guangzhou, China, 15–17 January 2021. [Google Scholar]
- Yu, C.; Xue, B.; Song, M.; Wang, Y.; Li, S.; Chang, C.I. Iterative Target-Constrained Interference-Minimized Classifier for Hyperspectral Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1095–1117. [Google Scholar] [CrossRef]
- Luo, F.; Du, B.; Zhang, L.; Zhang, L.; Tao, D. Feature Learning Using Spatial-Spectral Hypergraph Discriminant Analysis for Hyperspectral Image. IEEE Trans. Cybern. 2019, 49, 2406–2419. [Google Scholar] [CrossRef]
- Li, L.; Khodadadzadeh, M.; Plaza, A.; Jia, X.; Bioucas-Dias, J.M. A Discontinuity Preserving Relaxation Scheme for Spectral-spatial Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 625–639. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, Y.; Zou, S.; Zhang, H.; Bai, Y. Hyperspectral Image Classification with Spatial Consistence Using Fully Convolutional Spatial Propagation Network. IEEE Trans. Geosci. Remote Sens. 2008, 1–13. [Google Scholar] [CrossRef]
- Mei, S.; Ji, J.; Hou, J.; Li, X.; Du, Q. Learning Sensor-Specific Spatial-Spectral Features of Hyperspectral Images via Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4520–4533. [Google Scholar] [CrossRef]
- Gao, H.; Chen, Z.; Li, C. Sandwich Convolutional Neural Network for Hyperspectral Image Classification Using Spectral Feature Enhancement. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3006–3015. [Google Scholar] [CrossRef]
- Yu, C.; Han, R.; Song, M.; Liu, C.; Chang, C. Feedback Attention-Based Dense CNN for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 1–16. [Google Scholar] [CrossRef]
- Ding, W.; Yan, Z.; Deng, R.H. A Survey on Future Internet Security Architectures. IEEE Access 2016, 4, 4374–4393. [Google Scholar] [CrossRef]
- Xu, Q.; Xiao, Y.; Wang, D.; Luo, B. CSA-MSO3DCNN: Multiscale Octave 3D CNN with Channel and Spatial Attention for Hyperspectral Image Classification. Remote Sens. 2020, 12, 188. [Google Scholar] [CrossRef] [Green Version]
- Hang, R.; Li, Z.; Liu, Q.; Ghamisi, P.; Bhattacharyya, S.S. Hyperspectral Image Classification With Attention-Aided CNNs. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2281–2293. [Google Scholar] [CrossRef]
- Xi, B.; Li, J.; Li, Y.; Song, R. Multi-Direction Networks With Attentional Spectral Prior for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 1–16. [Google Scholar] [CrossRef]
- Pantforder, D.; Vogel-Heuser, B.; Gramß, D.; Schweizer, K. Supporting Operators in Process Control Tasks—Benefits of Interactive 3-D Visualization. IEEE Trans. Human-Mach. Syst. 2016, 46, 859–871. [Google Scholar] [CrossRef]
- Qin, A.; Shang, Z.; Tian, J.; Wang, Y.; Zhang, T.; Tang, Y. Spectral-spatial Graph Convolutional Networks for Semisupervised Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2019, 16, 241–245. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral Image Classification Using Deep Pixel-Pair Features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Cao, X.; Ren, M.; Zhao, J.; Li, H.; Jiao, L. Hyperspectral Imagery Classification Based on Compressed Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1583–1587. [Google Scholar] [CrossRef]
- Meng, Z.; Jiao, L.; Liang, M.; Zhao, F. Hyperspectral Image Classification with Mixed Link Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2494–2507. [Google Scholar] [CrossRef]
- He, N.; Paoletti, M.E.; Haut, J.M.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Feature Extraction With Multiscale Covariance Maps for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 755–769. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral-spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Zhang, C.; Li, G.; Lei, R.; Du, S.; Zhang, X.; Zheng, H.; Wu, Z. Deep Feature Aggregation Network for Hyperspectral Remote Sensing Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5314–5325. [Google Scholar] [CrossRef]
- Zhang, C.; Li, G.; Du, S. Multi-Scale Dense Networks for Hyperspectral Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9201–9222. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Zhang, N.; Xu, D.; Luo, H.; Chen, B.; Ben, G. Spectral-spatial Fractal Residual Convolutional Neural Network With Data Balance Augmentation for Hyperspectral Classification. IEEE Trans. Geosci. Remote Sens. 2021, 1–15. [Google Scholar] [CrossRef]
- Lin, J.; Mou, L.; Zhu, X.; Ji, X.; Wang, Z. Attention-Aware Pseudo-3-D Convolutional Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7790–7802. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Wang, W.; Dou, S.; Jiang, Z.; Sun, L. A fast dense spectral-spatial convolution network framework for hyperspectral images classification. Remote Sens. 2018, 10, 1068. [Google Scholar] [CrossRef] [Green Version]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Deep&dense convolutional neural network for hyperspectral image classification. Remote Sens. 2018, 10, 1454. [Google Scholar]
- Fang, B.; Li, Y.; Zhang, H.; Chan, J.C. Hyperspectral images classification based on dense convolutional networks with spectral-wise attention mechanism. Remote Sens. 2019, 11, 159. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Zhang, Q.; Lu, Z.; Zhang, Y. SSDC-DenseNet: A Cost-Effective End-to-End Spectral-spatial Dual-Channel Dense Network for Hyperspectral Image Classification. IEEE Access 2019, 7, 84876–84889. [Google Scholar] [CrossRef]
- Ullah, I.; Manzo, M.; Shah, M.; Madden, M. Graph Convolutional Networks: Analysis, improvements and results. arXiv 2019, arXiv:1912.09592. [Google Scholar]
- Böhning, D. Multinomial logistic regression algorithm. Ann. Inst. Stat. Mathematics 1992, 44, 197–200. [Google Scholar] [CrossRef]
- Gao, S.; Cheng, M.; Zhao, K.; Zhang, X.; Yang, M.; Torr, P. Res2Net: A New Multi-Scale Backbone Architecture. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 652–662. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Hao, S.; Wang, W.; Ye, Y.; Nie, T.; Bruzzone, L. Two-stream deeparchitecture for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2349–2361. [Google Scholar] [CrossRef]
- Zhang, M.; Li, W.; Du, Q. Diverse region-based CNN for hyperspectral image classification. IEEE Trans. Image Process. 2018, 27, 2623–2634. [Google Scholar] [CrossRef]
- Song, W.; Li, S.; Fang, L.; Lu, T. Hyperspectral image classification with deep feature fusion network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3173–3184. [Google Scholar] [CrossRef]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral-spatial classification of hyperspectral imagery using a dual-channel convolutional neural network. Remote Sens. Lett. 2017, 8, 438–447. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhang, H.; Shen, Q. Spectral-spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Zheng, X.; Lu, X.; Wu, S. Spectral-spatial Attention Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3232–3245. [Google Scholar] [CrossRef]
- Zhu, M.; Jiao, L.; Yang, S.; Wang, J. Residual Spectral-spatial Attention Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 449–462. [Google Scholar] [CrossRef]
- Li, X.; Ding, M.; Pižurica, A. Deep Feature Fusion via Two-Stream Convolutional Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2615–2629. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).