Improving Matching Accuracy of Underwater Gravity Matching Navigation Based on Iterative Optimal Annulus Point Method with a Novel Grid Topology
Abstract
:1. Introduction
2. Construction of Iterative Optimal Annulus Point (IOAP) Method with a Novel Grid Topology
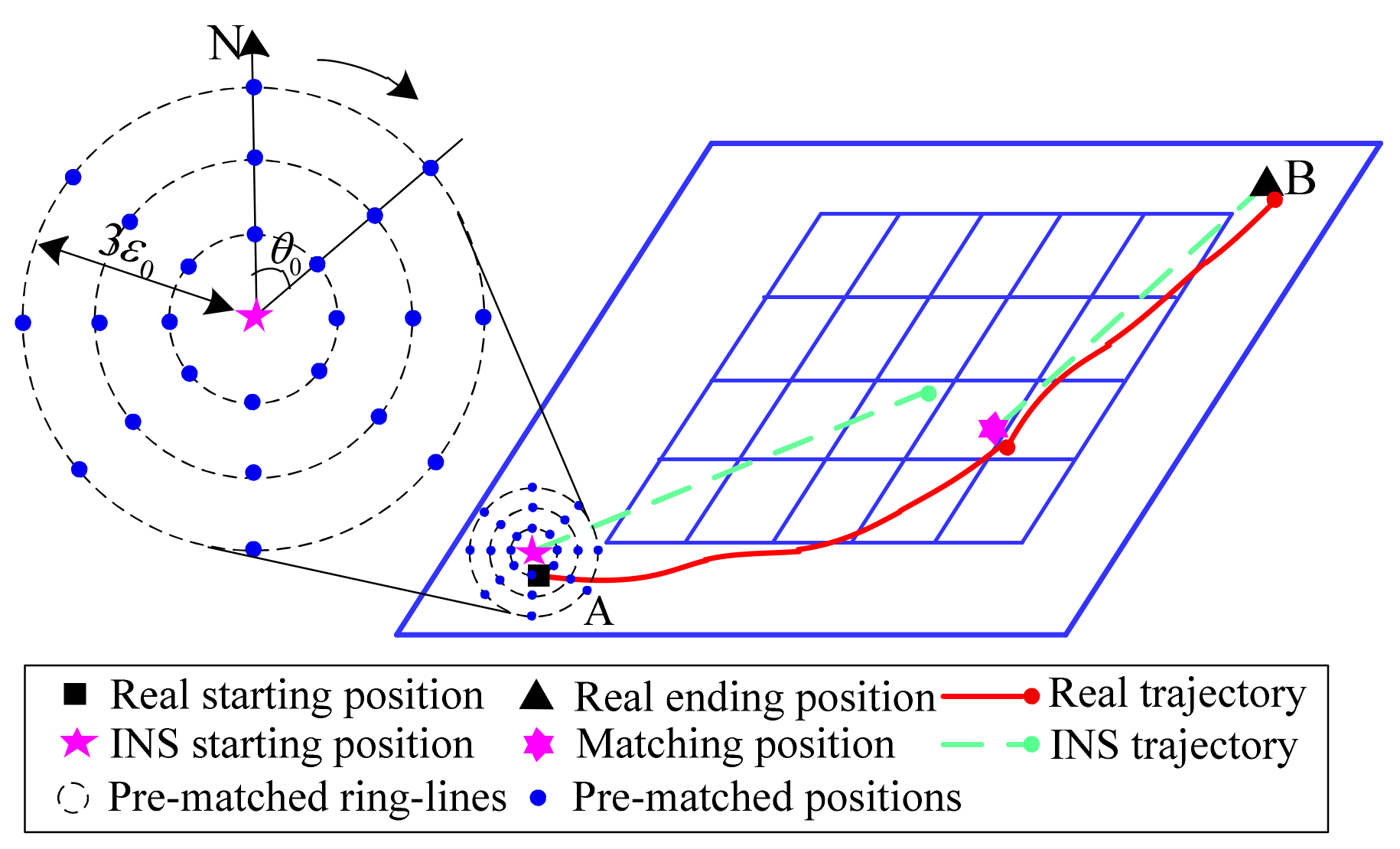
2.1. Matching Positioning Strategy of the Tracking Starting Point in Small Annulus (SPMP)
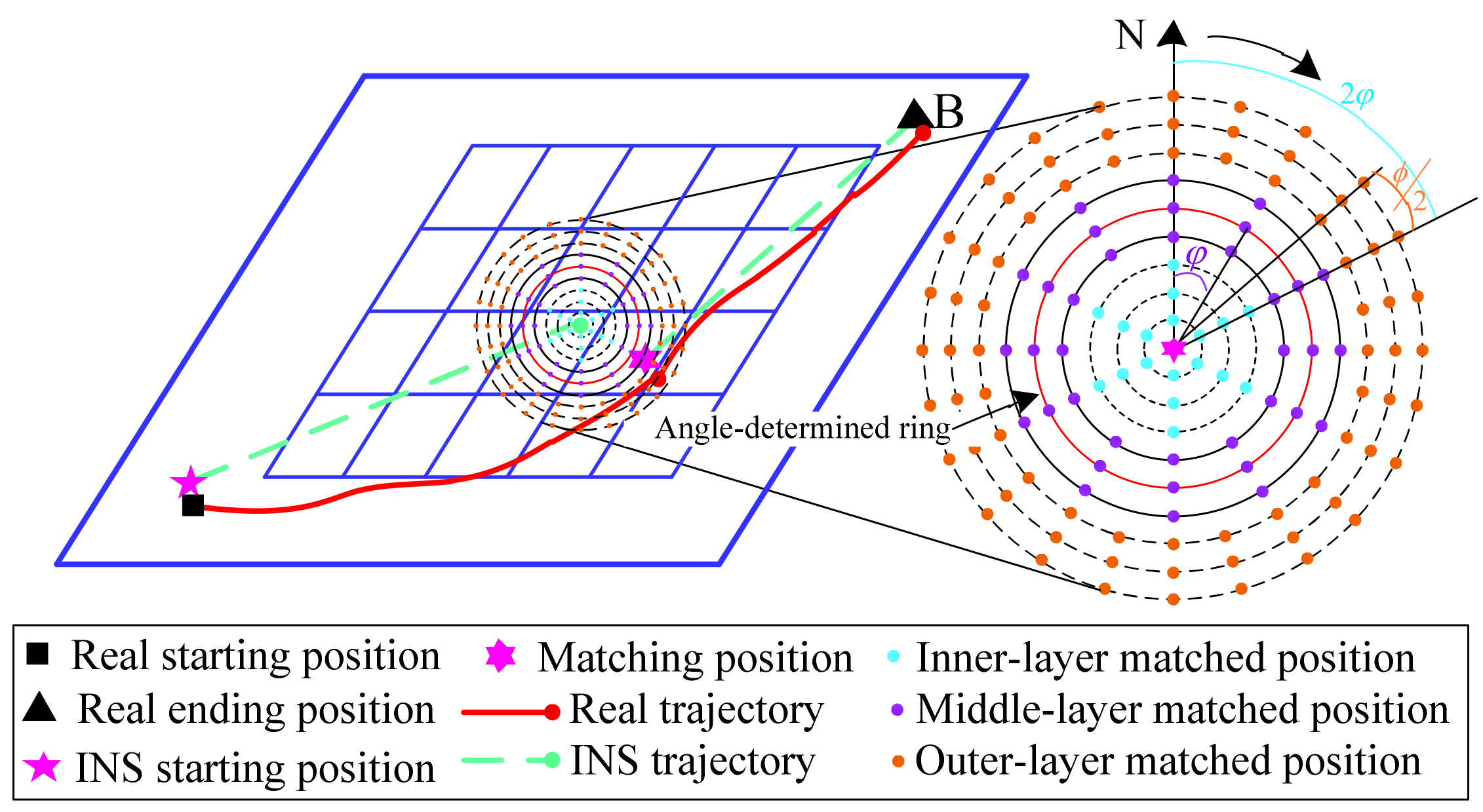
2.2. Matching Positioning Mechanism of the Tracking Ending Point in Three-Layer Annulus (EPMP)
2.3. Implementation Process of Iterative Optimal Annulus Point Algorithm for New Grid Topology
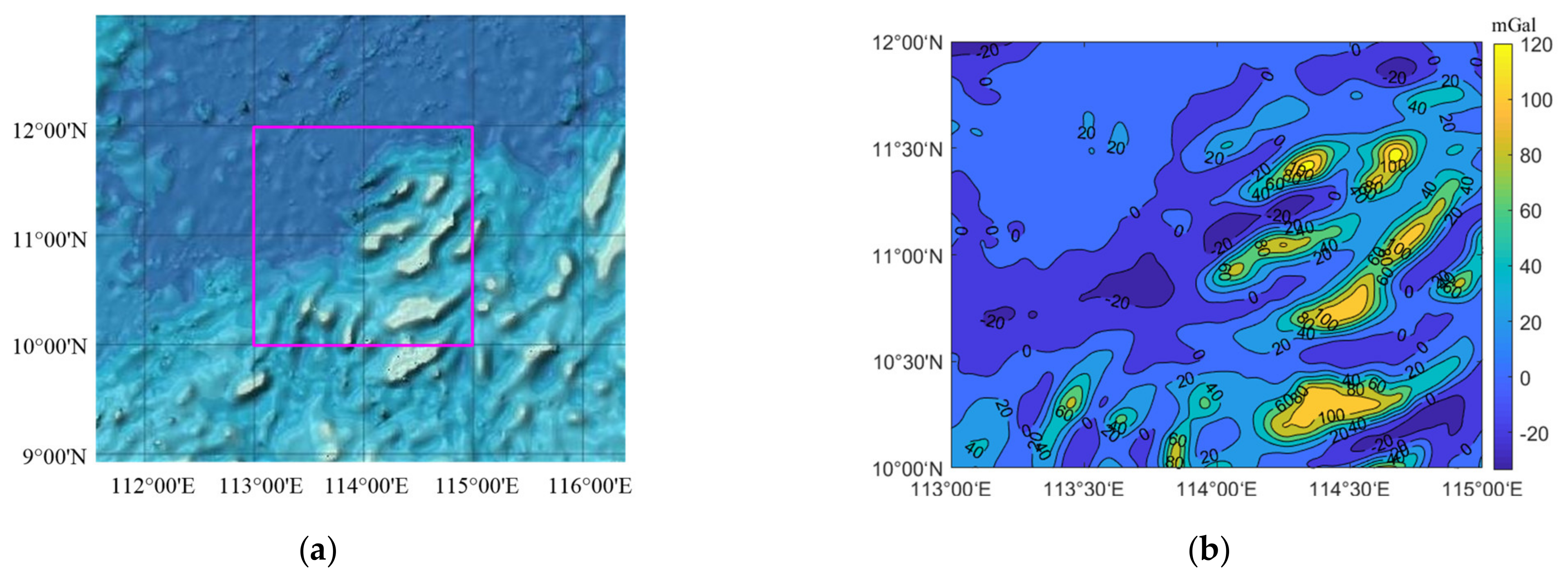
3. Verification and Application of the Proposed IOAP Algorithm
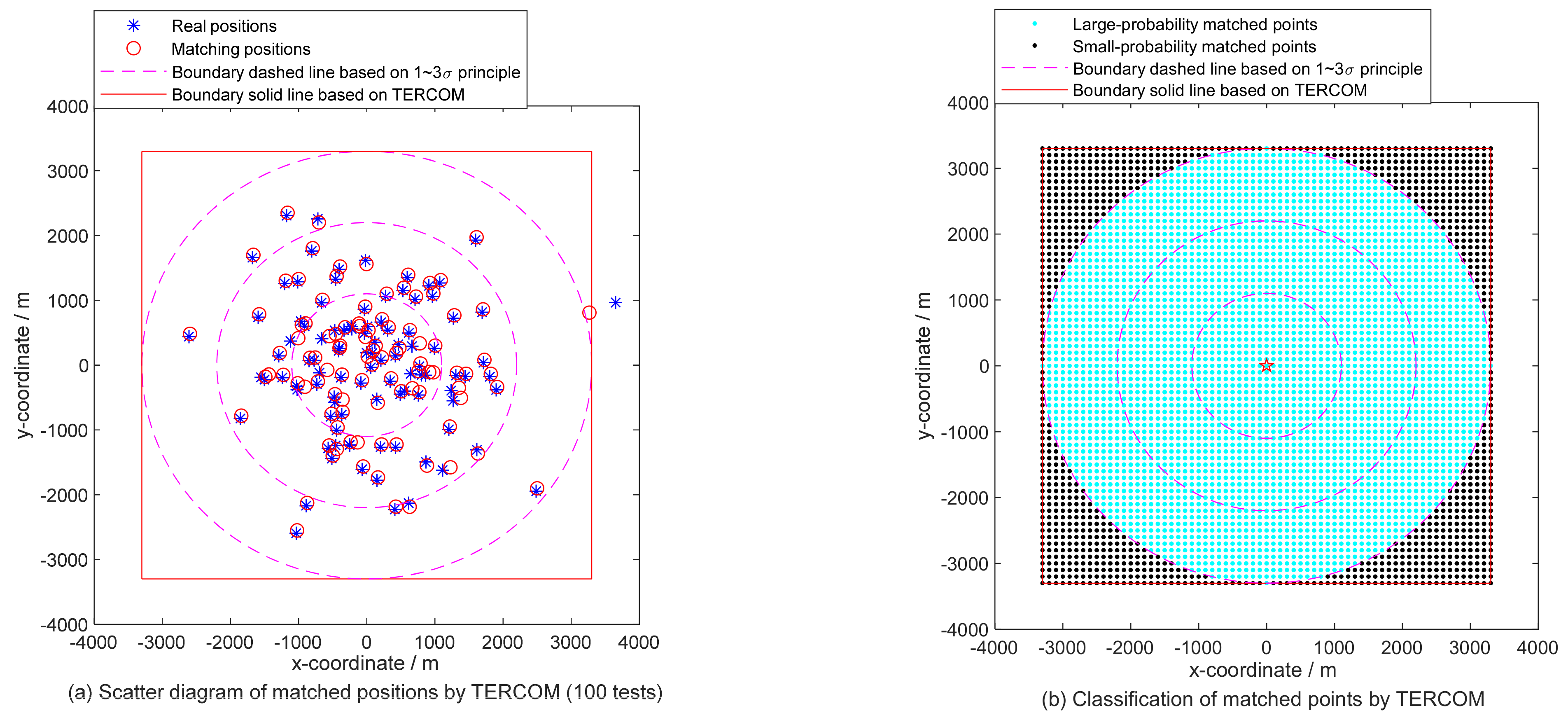
3.1. Verification on the Matched Performance Difference of IOAP with Different Criteria
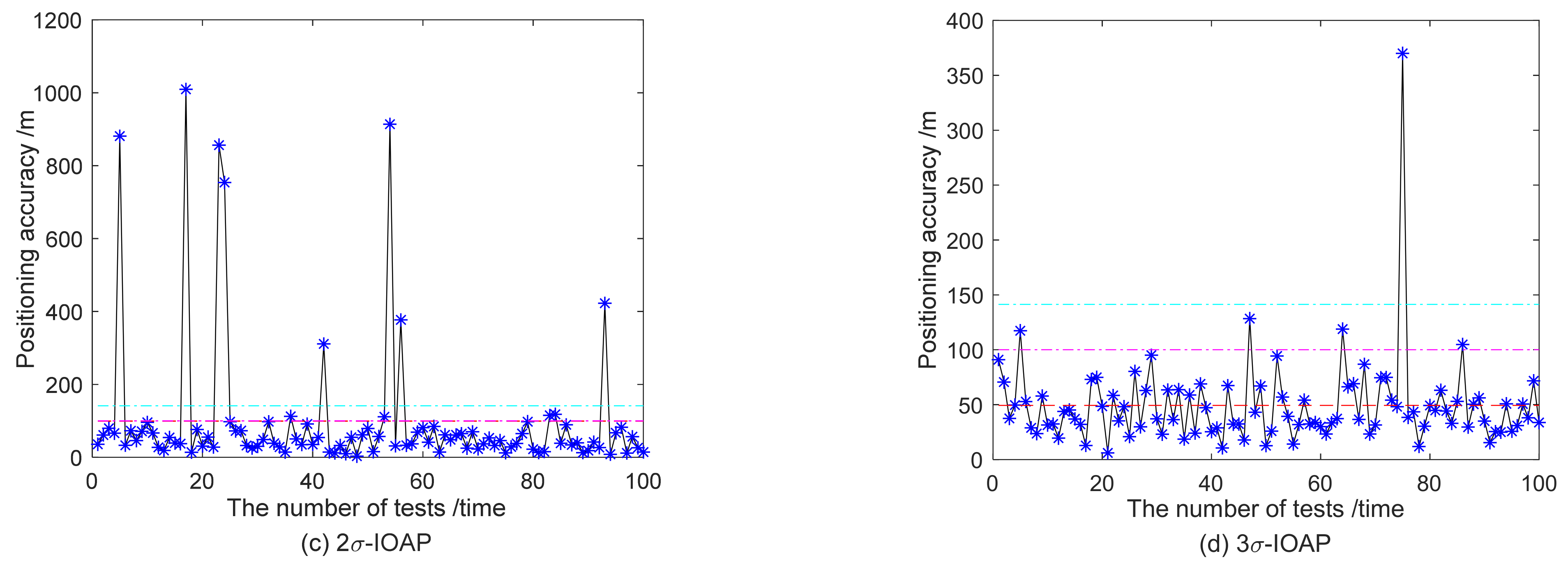
3.2. Verification of the Difference Influence on Matching Performance of IOAPs with Different Ring Radius Reference Angle
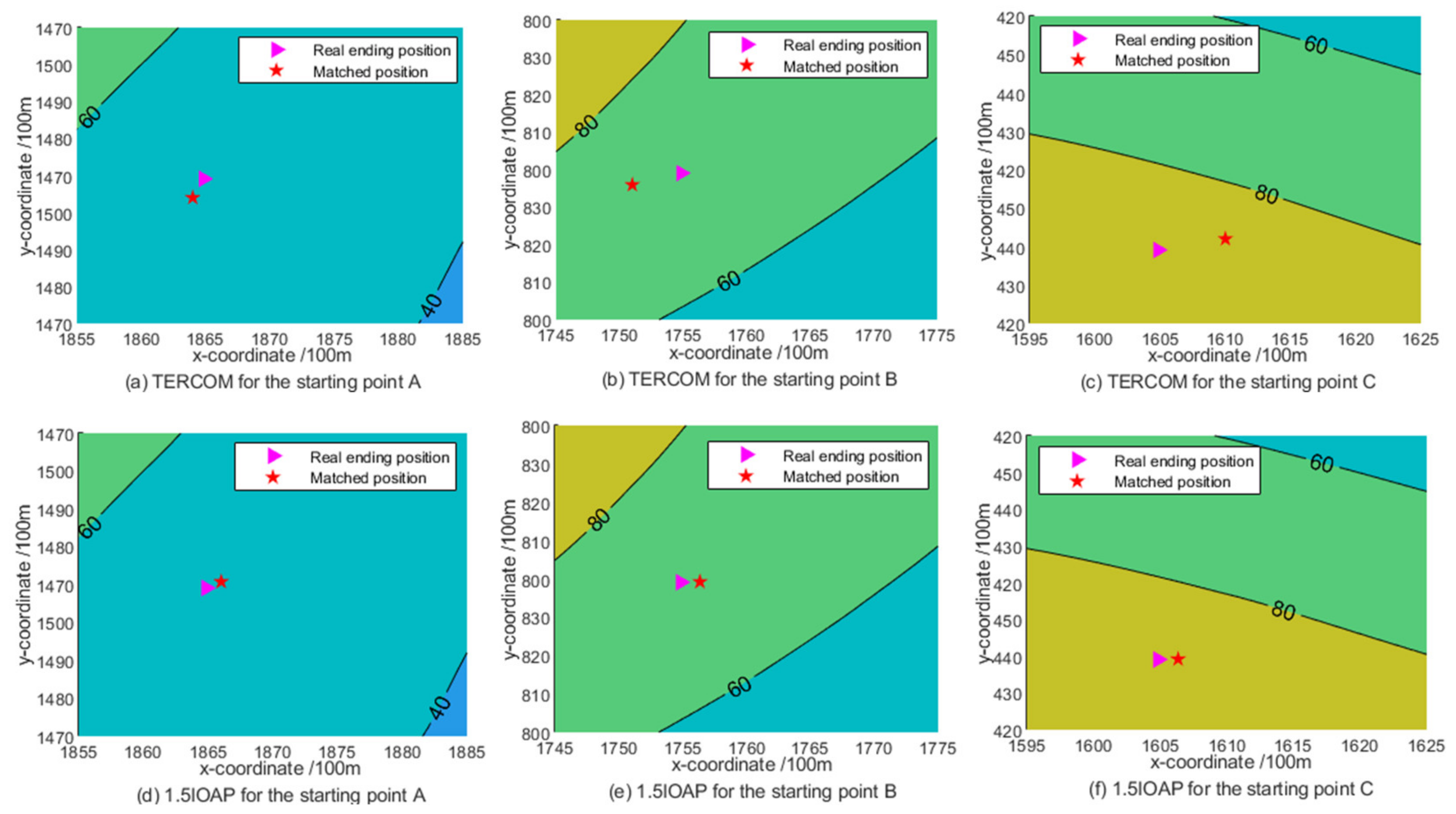
3.3. Verification of the Good Matching Performance of IOAP for Different Tracking Starting Points
4. Conclusions
- (1)
- The construction of an iterative optimal annulus point model with a novel grid topology. On the basis of breaking out from the traditional square-shaped grid topology of the TERCOM, the annulus-shaped topology of the matching grid points was constructed. Then, the Matching Positioning strategy of the tracking Starting Point in small annulus (SPMP) and the Matching Positioning mechanism of the tracking Ending Point in three-layer annulus (EPMP) were proposed by employing the INS sailing direction and distance information. Furthermore, an iterative optimal annulus point model with a novel grid topology was constructed by coupling the SPMP and EPMP.
- (2)
- The optimization selection of the criterion and the reference angular ring radius for the optimal matching navigation in the large annulus at the tracking ending point. In this paper, the matching evaluation indexes, such as the average matching accuracy, matching standard deviation, average matching time and matching success rate, were comprehensively compared. These evaluation indexes were taken as the selection basis of the model parameters, which resulted in verifying the different influences of the parameters on the matching performances of the proposed iterative optimal annulus point algorithm and realizing the selection of good parameters to improve the underwater gravity matching accuracy.
- (3)
- The improvement of the underwater matching navigation accuracy. For the matching performance testing in three regions, the results showed that the iterative optimal annulus point model with a novel grid topology, compared with the TECOM, had little difference of the average matching time. The worst matching accuracies of the proposed model were also improved by up to 47.24%, 63.96% and 72.16%. Simultaneously, the average matching accuracies of the iterative optimal annulus point model were increased by up to 20.37%, 40.39% and 13.88%, respectively. In summary, the iterative optimal annulus point model with a novel grid topology contributed to enhancing the matching accuracy of underwater vehicle gravity matching navigation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, C.; Wang, B.; Deng, Z.; Fu, M. A Delaunay Triangulation-Based Matching Area Selection Algorithm for Underwater Gravity-Aided Inertial Navigation. IEEE/ASME Trans. Mechatron. 2020, 26, 908–917. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, J.; Deng, Z.; Fu, M. A characteristic parameter matching algorithm for gravity-aided navigation of underwater vehicles. IEEE Trans. Ind. Electron. 2018, 66, 1203–1212. [Google Scholar] [CrossRef]
- Jeon, H.C.; Park, W.J.; Park, C.G. Grid design for efficient and accurate point mass filter-based terrain referenced navigation. IEEE Sens. J. 2017, 18, 1731–1738. [Google Scholar] [CrossRef]
- Lee, C.; Oh, J.; Hong, C.; Youn, J. Automated generation of a digital elevation model over steep terrain in Antarctica from high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1186–1194. [Google Scholar] [CrossRef]
- Zheng, W.; Hu, H.Z.; Zhong, M.; Yuan, M.J.; Zhou, X.H.; Bang, B.B. Efficient and rapid estimation of the accuracy of future GRACE Follow-On Earth′s gravitational field using the analytic method. Chin. J. Geophys. 2010, 53, 796–806. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, W.; Wu, F.; Fang, J. Improving the matching efficiency of underwater gravity matching navigation based on a new hierarchical neighborhood threshold method. Chin. J. Geophys. 2019, 62, 2405–2416. [Google Scholar]
- Park, J.; Park, Y.G.; Park, C.G. Parameter Estimation of Radar Noise Model for Terrain Referenced Navigation Using a New EM Initialization Method. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 107–112. [Google Scholar] [CrossRef]
- Golden, J.P. Terrain contour matching (TERCOM): A cruise missile guidance aid. In Image Processing for Missile Guidance; International Society for Optics and Photonics: Bellingham, WA, USA, 1980; Volume 238, pp. 10–18. [Google Scholar]
- Han, Y.; Wang, B.; Deng, Z.; Wang, S.; Fu, M. A mismatch diagnostic method for TERCOM-based underwater gravity-aided navigation. IEEE Sens. J. 2017, 17, 2880–2888. [Google Scholar] [CrossRef]
- Yan, L.; Cui, C. A new algorithm of gravity matching aided navigation. In Second International Conference on Space Information Technology; International Society for Optics and Photonics: Bellingham, WA, USA, 2007; Volume 6795, p. 679529. [Google Scholar]
- Tong, Y.D.; Bian, S.F.; Jiang, D.F.; Xiang, C.B. A new integrated gravity matching algorithm based on approximated local gravity map. Chin. J. Geophys. 2012, 55, 2917–2924. [Google Scholar]
- Zhao, L.; Gao, N.; Huang, B.; Wang, Q.; Zhou, J. A novel terrain-aided navigation algorithm combined with the TERCOM algorithm and particle filter. IEEE Sens. J. 2014, 15, 1124–1131. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, K. Judgement criterion for terrain false matching based on joint probability of multiple reference points. J. Beijing Univ. Aeronaut. Astronaut. 2018, 44, 1562–1568. [Google Scholar]
- Zhang, J.; Xu, Z.; Wang, X. Research on error of underwater terrain aided navigation based on TERCOM algorithm. J. Nav. Univ. Eng. 2020, 32, 44–49. [Google Scholar]
- Han, Y.; Wang, B.; Deng, Z.; Fu, M. An improved TERCOM-based algorithm for gravity-aided navigation. IEEE Sens. J. 2016, 16, 2537–2544. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, W.; Wu, F. Geodesic-based method for improving matching efficiency of underwater terrain matching navigation. Sensors 2019, 19, 2709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, L.; Liu, X.; Jia, S.; Yan, S. A line-surface integrated algorithm for underwater terrain matching. Acta Geod. Cartogr. Sin. 2020, 2, 10–20. [Google Scholar]
- Zhang, J.; Zhang, T.; Shin, H.S.; Wang, J.; Zhang, C. Geomagnetic gradient-assisted evolutionary algorithm for long-range underwater navigation. IEEE Trans. Instrum. Meas. 2020, 70, 1–12. [Google Scholar] [CrossRef]
- Dai, T.; Miao, L.; Shao, H.; Shi, Y. Solving gravity anomaly matching problem under large initial errors in gravity aided navigation by using an affine transformation based artificial bee colony algorithm. Front. Neurorobot. 2019, 13, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Wang, B.; Deng, Z.; Fu, M. A combined matching algorithm for underwater gravity-aided navigation. IEEE/ASME Trans. Mechatron. 2017, 23, 233–241. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, G.; Huang, Z. Study on the Arctic Underwater Terrain-Aided Navigation Based on Fuzzy-Particle Filter. Int. J. Fuzzy Syst. 2021, 23, 1017–1026. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, W.; Fang, J.; Wu, F. Optimizing suitability area of underwater gravity matching navigation based on a new principal component weighted average normalization method. Chin. J. Geophys. 2019, 62, 3269–3278. [Google Scholar]


| Algorithm | Mean/M | Std/M | Max/M | T/S | ||
|---|---|---|---|---|---|---|
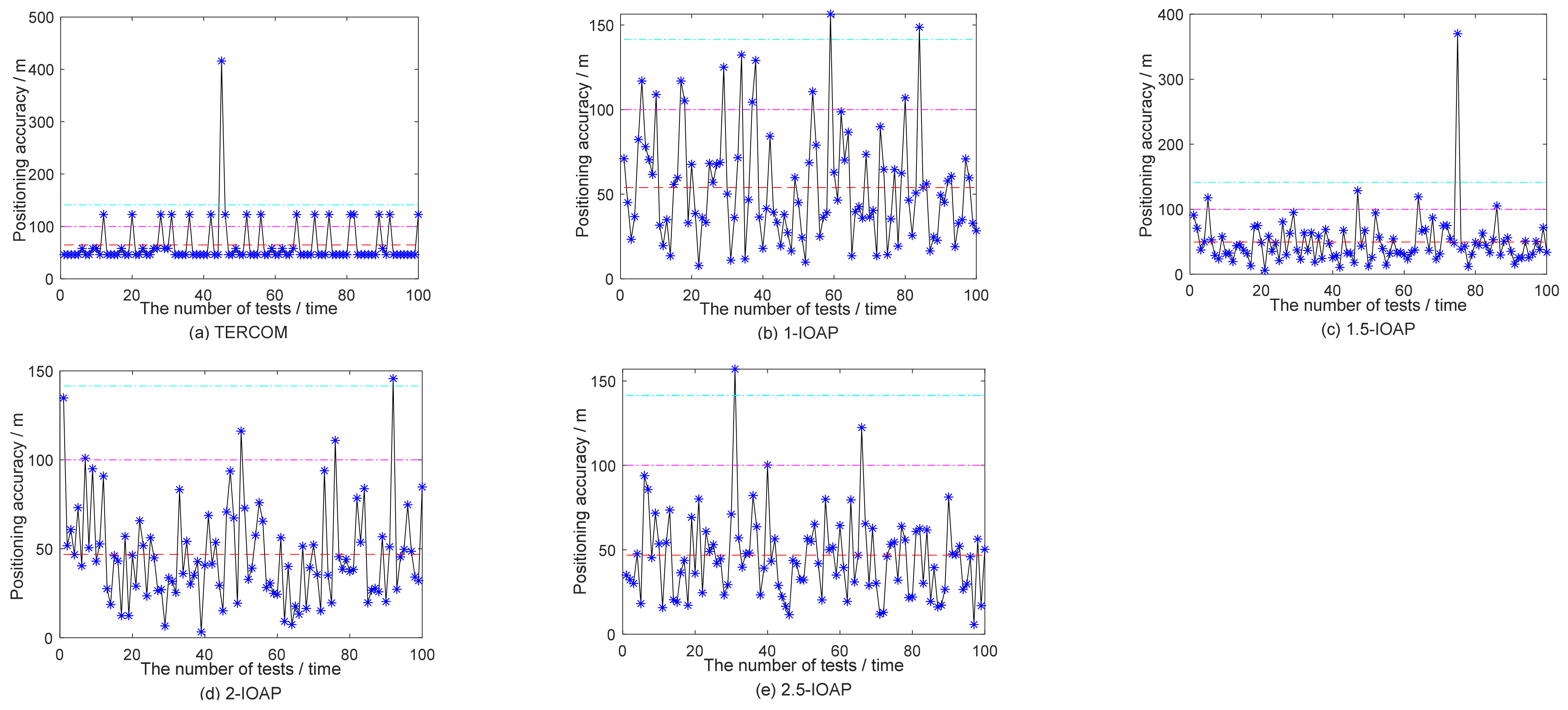
| TERCOM | 64.67 | 45.41 | 415.70 | 2.28 × 10−2 | 82 | 99 |
| 1-IOAP | 394.95 | 518.07 | 2642.07 | 3.90 × 10−3 | 48 | 52 |
| 2-IOAP | 99.23 | 191.91 | 1009.29 | 1.21 × 10−2 | 88 | 92 |
| 3-IOAP | 49.39 | 40.68 | 370.01 | 2.41 × 10−2 | 95 | 99 |
| Algorithm | |||||||
|---|---|---|---|---|---|---|---|
| TERCOM | 0 | 0 | 82 | 82 | 82 | 82 | 99 |
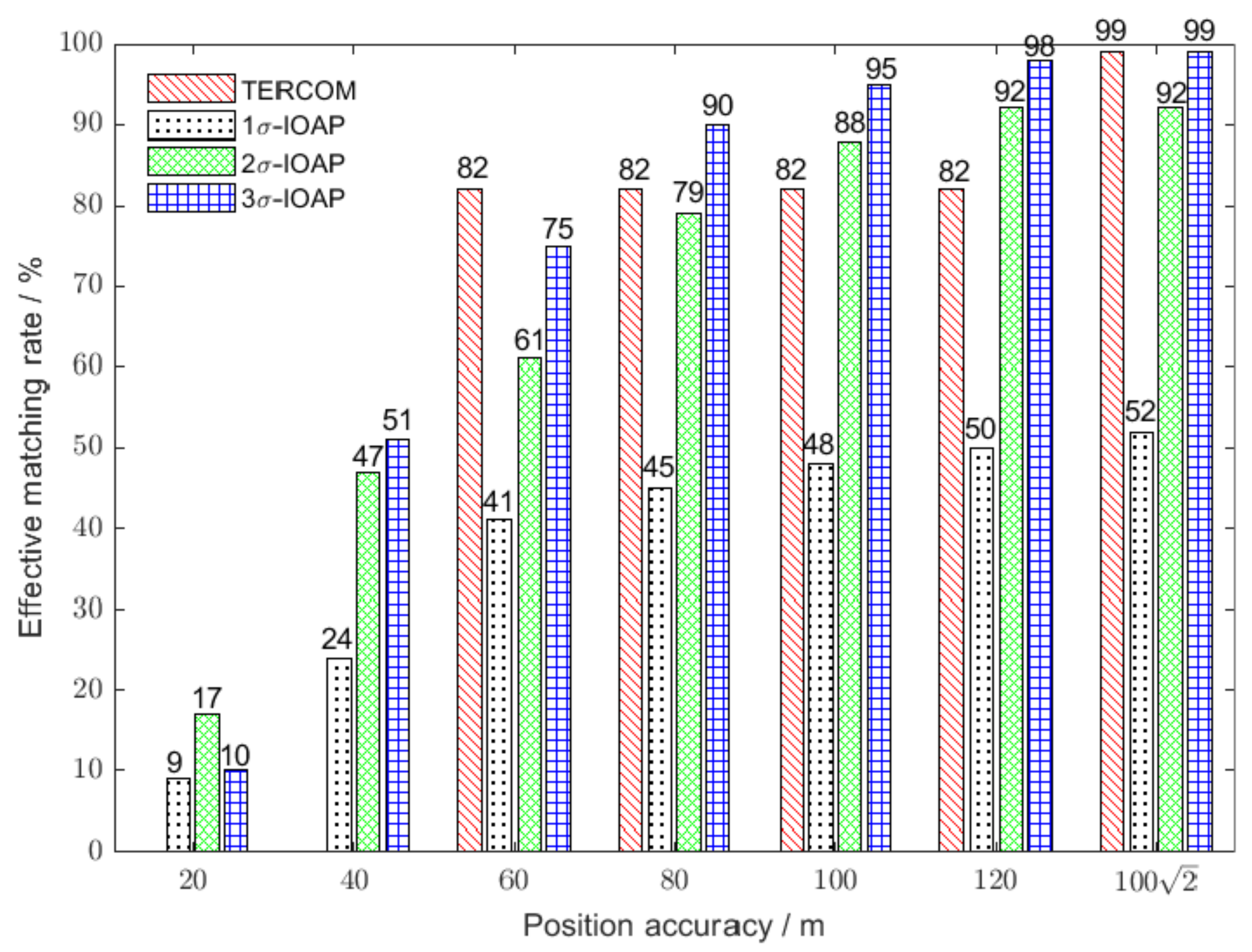
| 1-IOAP | 9 | 24 | 41 | 45 | 48 | 50 | 52 |
| 2-IOAP | 17 | 47 | 61 | 79 | 88 | 92 | 92 |
| 3-IOAP | 10 | 51 | 75 | 90 | 95 | 98 | 99 |
| Algorithm | Mean/M | Std/M | Max/M | T/S | ||
|---|---|---|---|---|---|---|
| TERCOM | 64.67 | 45.41 | 415.70 | 2.28 × 10−2 | 82 | 99 |
| 1-IOAP | 53.93 | 32.85 | 156.43 | 1.77 × 10−2 | 88 | 98 |
| 1.5-IOAP | 49.39 | 40.68 | 370.01 | 2.41 × 10−2 | 95 | 99 |
| 2-IOAP | 46.82 | 27.53 | 145.58 | 3.11 × 10−2 | 95 | 99 |
| 2.5-IOAP | 45.74 | 24.52 | 156.94 | 4.07 × 10−2 | 97 | 99 |
| Algorithm | |||||||
|---|---|---|---|---|---|---|---|
| TERCOM | 0 | 0 | 82 | 82 | 82 | 82 | 99 |
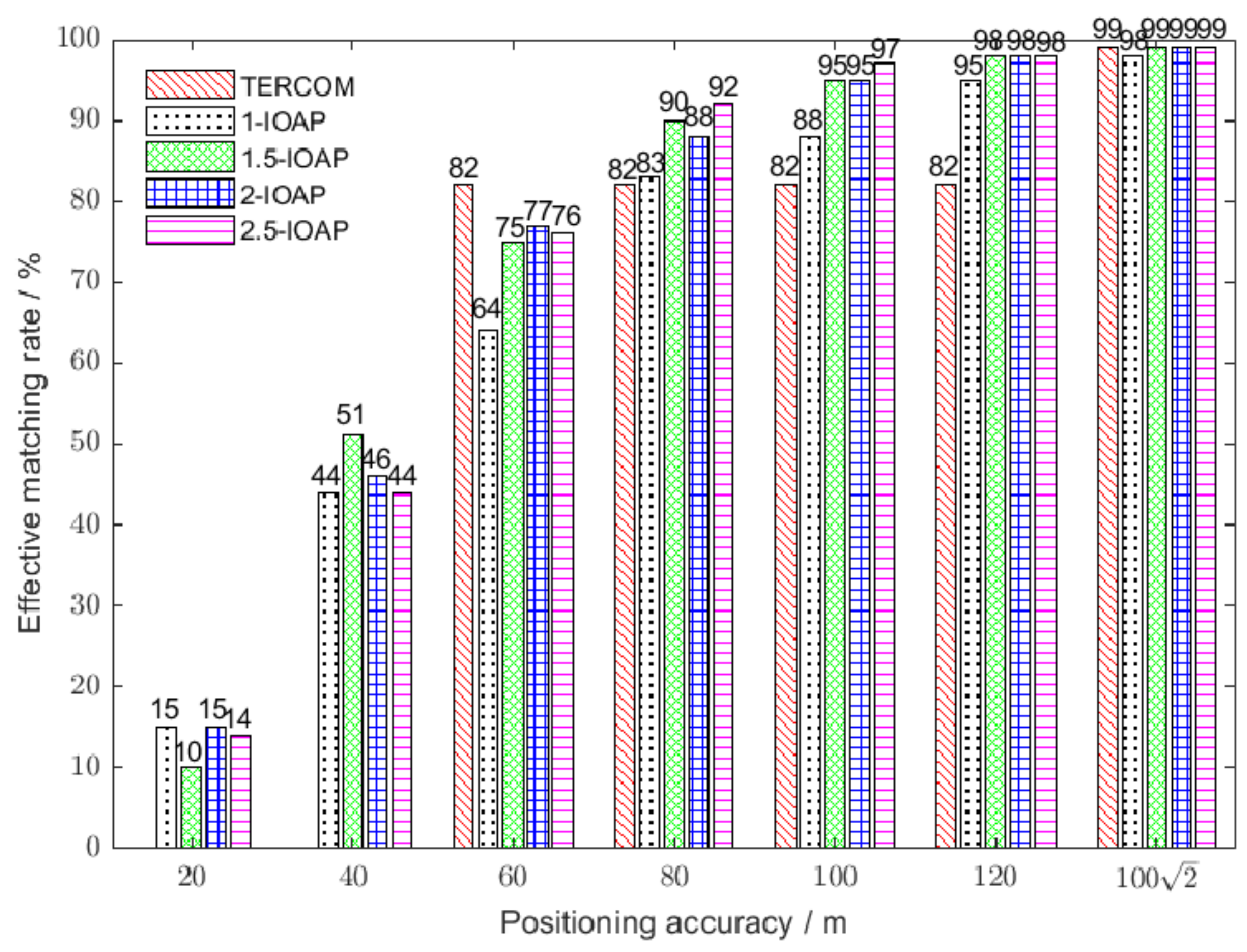
| 1-IOAP | 15 | 44 | 64 | 83 | 88 | 95 | 98 |
| 1.5-IOAP | 10 | 51 | 75 | 90 | 95 | 98 | 99 |
| 2-IOAP | 15 | 46 | 77 | 88 | 95 | 98 | 99 |
| 2.5-IOAP | 14 | 44 | 76 | 92 | 97 | 98 | 99 |
| Starting Point | Algorithm | MEAN/M | STD/M | MAX/M | T/S | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 40 | 60 | 80 | 100 | 120 | |||||||
| A | TERCOM | 78.16 | 41.03 | 269.87 | 2.07 × 10−2 | 0 | 62 | 62 | 62 | 62 | 99 |
| 1.5IOAP | 62.24 | 31.15 | 142.37 | 2.36 × 10−2 | 30 | 47 | 69 | 87 | 97 | 99 | |
| B | TERCOM | 96.82 | 47.78 | 415.70 | 2.03 × 10−2 | 0 | 36 | 36 | 36 | 45 | 99 |
| 1.5IOAP | 57.71 | 34.97 | 149.82 | 2.35 × 10−2 | 33 | 58 | 73 | 84 | 96 | 99 | |
| C | TERCOM | 83.48 | 55.58 | 534.45 | 2.04 × 10−2 | 0 | 66 | 66 | 66 | 66 | 99 |
| 1.5IOAP | 71.89 | 30.07 | 148.78 | 2.39 × 10−2 | 14 | 33 | 60 | 82 | 94 | 99 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Zheng, W.; Li, Z.; Xu, A.; Zhu, H. Improving Matching Accuracy of Underwater Gravity Matching Navigation Based on Iterative Optimal Annulus Point Method with a Novel Grid Topology. Remote Sens. 2021, 13, 4616. https://doi.org/10.3390/rs13224616
Zhao S, Zheng W, Li Z, Xu A, Zhu H. Improving Matching Accuracy of Underwater Gravity Matching Navigation Based on Iterative Optimal Annulus Point Method with a Novel Grid Topology. Remote Sensing. 2021; 13(22):4616. https://doi.org/10.3390/rs13224616
Chicago/Turabian StyleZhao, Shijie, Wei Zheng, Zhaowei Li, Aigong Xu, and Huizhong Zhu. 2021. "Improving Matching Accuracy of Underwater Gravity Matching Navigation Based on Iterative Optimal Annulus Point Method with a Novel Grid Topology" Remote Sensing 13, no. 22: 4616. https://doi.org/10.3390/rs13224616
APA StyleZhao, S., Zheng, W., Li, Z., Xu, A., & Zhu, H. (2021). Improving Matching Accuracy of Underwater Gravity Matching Navigation Based on Iterative Optimal Annulus Point Method with a Novel Grid Topology. Remote Sensing, 13(22), 4616. https://doi.org/10.3390/rs13224616






