1. Introduction
With the rapid development of high-resolution remote sensing sensors, digital stereo image data with large coverage, high precision, and timeliness can be easily obtained. Each pair of overlapping images forms a stereoscopic observation of the ground target, allowing the estimation of its 3D position. An important application of 3D information processing is the extraction of the digital surface model (DSM). DSM can truly reflect the situation on the ground. In addition to terrain elevation, DSM also contains the elevation information of ground objects such as buildings, bridges, and trees, and is widely used in various fields. Dense matching (stereo matching) is a key technology in DSM generation, and it has an important constraint, the epipolar geometry constraint. Using epipolar lines to retrieve conjugate points in image pairs can improve the efficiency and accuracy of stereo matching and it is a development trend to generate high-quality epipolar images from original satellite stereo image pairs [
1]. Currently, optical satellite images are mostly obtained by linear array pushbroom imaging technology. However, unlike frame satellite imagery, linear pushbroom satellite images do not have a strict epipolar relationship and can only generate approximate epipolar images [
2]. Therefore, how to generate epipolar images based on linear pushbroom satellite images has become an ongoing research topic.
As early as the 1980s, Zhang and Zhou proposed a SPOT image approximate epipolar arrangement method, namely, the polynomial fitting method [
3]. This method only needs to use the coordinates of the conjugate points, without knowing other image information. Kim analyzed the epipolar curves generation method of the sensor model based on the collinear equations according to the projection trajectory method [
4]. Morgan et al. proposed an approximate epipolar curves generation method based on a parallel projection model [
2]. This method has certain requirements for the sensor field of view, terrain undulations, and conjugate point matching accuracy and lacks versatility [
5]. Wang et al. proposed a new satellite stereo image epipolar resampling method, which directly establishes the correspondence between original image pixels and epipolar image pixels through a geometric sensor model [
6].
A significant fundamental content of epipolar correction for remote sensing images is to establish the imaging equation between the image coordinates and the spatial coordinates. The general imaging equation is a rigorous model established from the imaging geometric relationship of the sensor, which needs to be calculated by the sensor parameters. However, due to confidentiality and other reasons, the parameters of many sensors cannot be disclosed, so the rational function model (RFM) has emerged. Within a certain elevation range, RFM can replace the rigorous model [
7]. Therefore, we can use the rational polynomial coefficients (RPCs) in the RFM to establish the coordinate conversion relationship without knowing the specific parameters of the sensor. With the widespread application of RPCs, some RPC-based approximate epipolar image generation methods have been proposed. Oh et al. proposed a pushbroom satellite image epipolar resampling method based on RPCs [
8], but for areas with large terrain changes, this method needs further research. Koh et al. proposed a unified piecewise epipolar resampling method that can generate stereo image pairs with near-zero y-parallax [
9].
Since the 20th century, with the development of radar imaging theory, the concept of Synthetic Aperture Radar (SAR) was proposed. Due to the particularity of the SAR imaging mechanism, optical images and SAR images show different appearances and abilities [
10]. Specifically, SAR images obtained by the active sensors reflect the electromagnetic characteristics of the surface targets and provide the ability to view in all-day, all-weather conditions and through clouds. At the same time, the optical images obtained by the passive sensors reflect the radiometric properties of the targets and can provide complementary information. Therefore, methods for generating epipolar images based on optical-SAR image pairs have begun to be proposed. First, Bagheri et al. mathematically proved that there is an epipolar geometry constraint relationship between SAR–optical image pairs, studied the possibility of 3-D reconstruction from very-high-resolution (VHR) SAR–optical image pairs, and indicated that SAR-optical image pairs in urban areas can be used to design a 3-D reconstruction framework [
11]. Moreover, VHR SAR–optical image pairs have great potential for analyzing complex urban areas. If the accuracy of key points detection can be improved and the similarity between SAR images and optical images can be measured, then the accuracy of 3-D reconstruction can also be improved [
12]. Therefore, how to generate high-quality epipolar images based on SAR-optical image pairs needs to be further studied.
In addition to optical image pairs and SAR-optical image pairs, the concept of epipolar geometry is also applicable to the cocircular geometry of SAR image pairs [
13]. Pan et al. proposed an endpoints growing method based on RPCs to generate epipolar images and applied this method to IKONOS image pairs, TerraSAR-X image pairs, and mixture stereo pairs [
14]. However, the feasibility of this method for mixture stereo pairs is subject to RPCs fitting. Karlheinz Gutjahr et al. proposed a method to create the epipolar geometry of a SAR sensor with an arbitrary three-dimensional structure through proper geometric image transformation and applied it to the TerraSAR-X stereo data set [
13].
Although the above-mentioned existing methods have been used to generate approximate epipolar images of satellite stereo images, technical limitations still exist when considering the versatility, applicability, and simplicity of these models. Moreover, due to different viewing conditions and sun angles, in areas with large terrain undulations, nonlinear distortions will appear in the images, and it is difficult to perform image registration [
15]. Moreover, in areas such as mountains and valleys with harsh terrain conditions, the commonly used methods are inefficient and poor in safety [
16]. The existing methods are difficult to be used on multiple types of terrain and multi-sensor images to achieve ideal results at the same time.
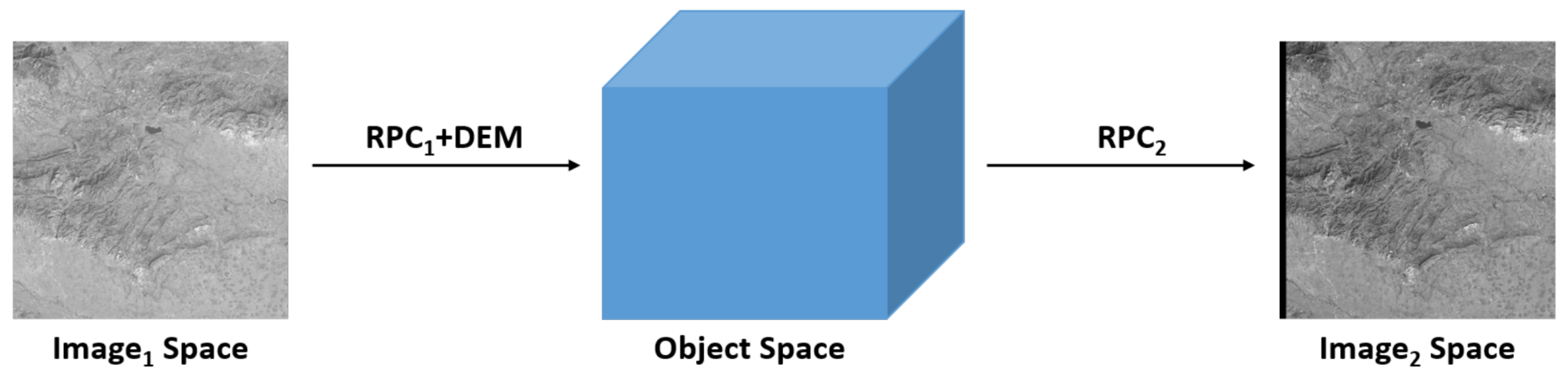
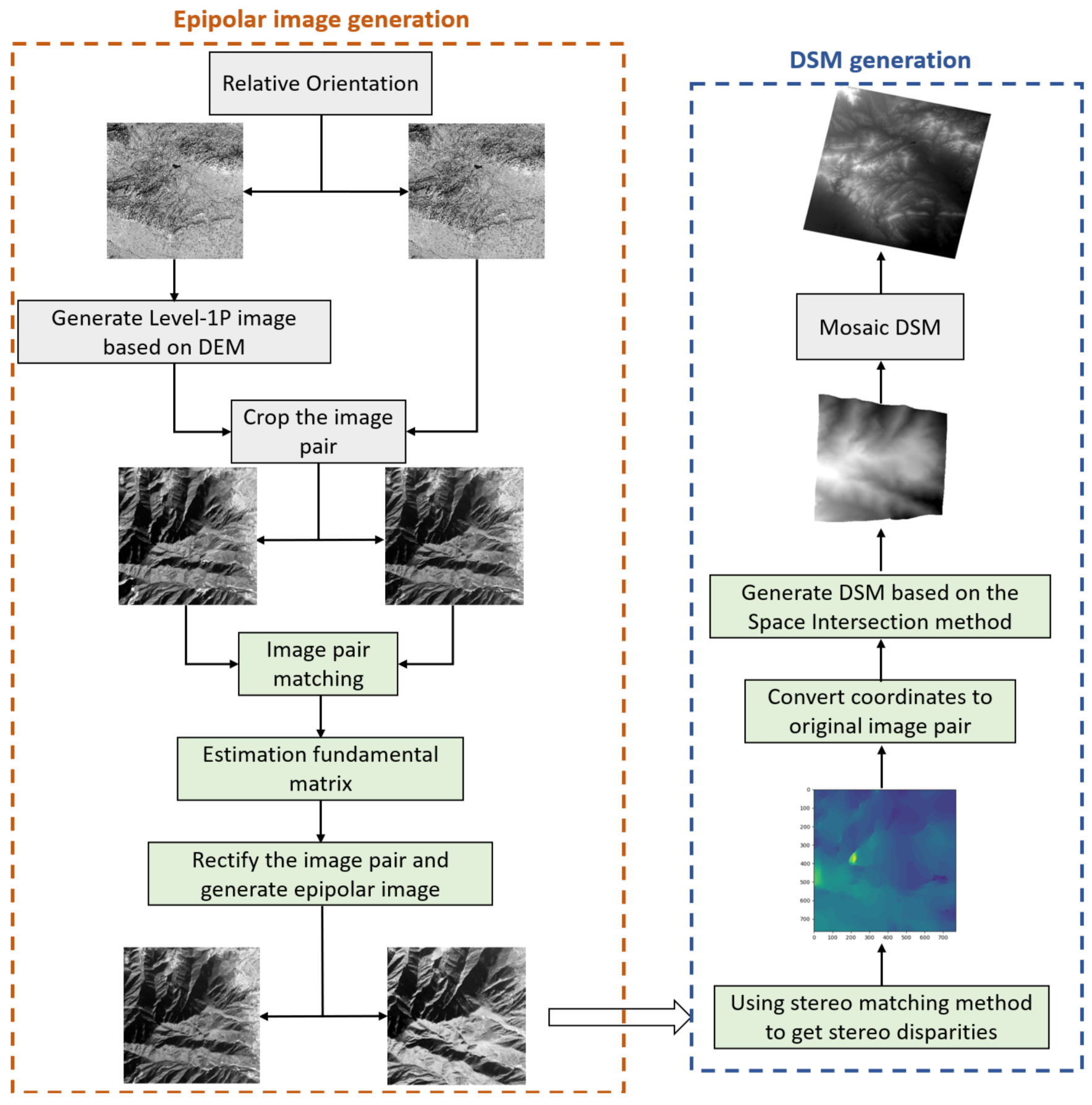
Based on the above analysis, we propose an approximate epipolar image generation framework that can be used for images in areas with large terrain undulations and multi-sensor images, such as SAR-SAR images and SAR-optical images. By generating approximate epipolar images, the two-dimensional stereo matching problem is simplified to one-dimensional stereo matching, thereby improving the accuracy and efficiency of stereo matching [
17]. Among them, the use of the digital elevation model (DEM) can reduce the initial offset of the two stereo images, thereby reducing the impact of terrain elevation changes on the generation of epipolar images. We first process the Level-1 images, which is the radiometric correction products, and use RPCs to project the left image into the image coordinate system of the right image to obtain a new image, which we name as Level-1P images, and then divide the entire image into blocks for parallel processing. Next, we generate approximate epipolar images and DSM for each block. Finally, all DSMs are spliced together to realize the generation of the whole DSM. The stereo satellite data used in this paper can be roughly divided into three categories. They are three-line array satellites, agile stereo satellites, and the general multiple view satellites. Three-line array satellites such as ZY-3 are equipped with three line-array cameras to image the same target from different angles along the direction of the satellite’s flight, to obtain the in-track stereo images [
18]. Agile satellites (e.g., GeoEye) can maneuver in three directions: roll, pitch, and yaw [
19]. By adjusting these three directions in a short period, agile satellites can realize nearly simultaneous multi-angle observations of the same target. The general multiple views satellites collect stereo images by taking images of the ground from different views, such as GF-2 and GF-3, and this kind of stereo image has no rigorous stereo property.
The rest of this paper is organized as follows.
Section 2 first verifies the epipolar constraint relationship of single-sensor and multi-sensor images and then describes the proposed approximate epipolar image generation framework. In
Section 3, the experimental results of epipolar image generation are shown, and their accuracy is qualitatively evaluated and quantitatively analyzed. In
Section 4, DSM generation based on our proposed framework is discussed. Conclusions are drawn in
Section 5.
3. Results
In this section, we first evaluate the performance of the proposed framework by comparing it to the current state-of-the-art algorithms. The first method is an epipolar image generation algorithm based on the PTM [
21]. The second method is the S2P method [
24]. Various scenarios of different sensors, including urban, agriculture, and mountain areas, are used. Then, we explore the applicability of our framework on SAR–optical and SAR–SAR image pairs. In the comparative experiment, the disparities of the matching points are used as the quantitative metric to evaluate the quality of the generated epipolar images. The satellite images used in our experiment include ZY-3, GF-2, GF-3, and GeoEye images. Among them, ZY-3, GF-2, and GeoEye are optical satellites, and GF-3 is a SAR satellite. The coverage area of these image data and their information are shown in
Table 1.
3.1. Experimental Results of Epipolar Images Generation
To verify the performance of the proposed approximate epipolar image generation framework, we first select the ZY-3 satellite images of the Songshan area in China, which is mostly mountainous. The elevation range of Songshan is approximately 67–1472 m. In order to further verify the performance of our framework, the results obtained by our framework are compared to two other methods.
The epipolar images generated by the proposed framework is shown in
Figure 10c. From the results, it can be found that the vertical disparity of the generated epipolar image pair is approximately negligible, which means that satisfactory results can be obtained for areas with large terrain elevation changes that do not satisfy the affine transformation model. In addition, the epipolar images generated by two other comparison methods in the same region are shown in
Figure 10a,b. In order to make the comparison of results more intuitive, we manually select two corresponding points in the epipolar images and display their coordinates
, where
x is the horizontal coordinate and
y is the vertical coordinate. The results show that the y-disparity of the epipolar images generated by these three methods is relatively small and can be approximately ignored. However, in addition to the y-disparity, the x-disparity of the points in
Figure 10c is almost negligible. Therefore, it is clear that compared with the other two methods, the proposed framework can get better epipolar images.
We further calculate the y-disparity of the SIFT matching points in the epipolar image pair to quantitatively evaluate the results. The smaller this y-disparity, the higher the accuracy of the generated epipolar images. Moreover, when performing stereo matching, the reduction of the search range of matching points will improve the accuracy and efficiency of image matching. Therefore, we also calculate the x-disparity of the SIFT matching points at the same time. When the x-disparity is small, the matching efficiency and accuracy during dense matching of epipolar images will be improved. The disparity of matching points is shown in
Table 2. For the sake of comparison, the data in the tables are the statistical results of the absolute value of the disparity.
It can be found that the proposed framework can generate high-quality epipolar images in regions with large terrain undulations according to the image matching results. For the y-disparity, the results obtained by our framework are slightly smaller than the results obtained by the S2P and PTM-based methods. Although the proposed framework only shows a small advantage in y-disparity, it has obvious advantages in x-disparity. The epipolar images obtained by our framework also have higher similarity in the x-direction and the average x-disparity of the matching points can reach the sub-pixel level. The results show that the epipolar images generated by our framework can rearrange the original images better so that the corresponding points of the image pair are approximately on the same horizontal line, thereby reducing the search range of conjugate points in image matching to 1-D space. In addition, the generated epipolar images can also reduce the disparity in the x-direction, which provides a guarantee for the efficiency and accuracy of the dense matching before the subsequent DSM generation.
We also conduct experiments on ZY-3 images in Tianshan, China, which are shown in
Figure 11. Compared with the Songshan area, the terrain changes in this area are more obvious, approximately 24–3091 m. The quality of the epipolar images generated in this area is quantitatively evaluated, and the results are shown in
Table 3. Compared with the Songshan area, the elevation of the Tianshan area has greater fluctuations, so the x-disparity of the generated epipolar image will be greater. However, by comparing the results of the other two methods, it can be found that the x-disparity of the epipolar image generated by the proposed framework is still optimal among the three methods. The results show that in areas with large elevation fluctuations, not only the y-disparity can reach sub-pixels in the epipolar images generated by our framework, but most of the average x-disparity does not exceed 3 pixels. Therefore, our epipolar image generation framework has more obvious advantages for areas with large undulations like Tianshan.
3.2. Verification of the Applicability of the Proposed Framework
It has been verified in
Section 3.1 that the proposed framework can generate good epipolar images for areas with large terrain elevation changes. We select stereo image pairs from other satellites and other regions to generate epipolar images to verify the applicability of the proposed framework.
3.2.1. The Results of Epipolar Image Generation for Different Terrains
We choose the Omaha region of the United States to verify the applicability of the proposed framework in regions with small terrain undulations. The results of the comparative experiment are shown in
Figure 12 and
Table 4. The results show that the proposed framework can still achieve ideal results for urban areas with smaller terrain undulations and larger elevation gradients than mountain areas. Compared with the S2P method, the proposed framework has no obvious advantages for the y-disparity of the epipolar image in the urban area. But the x-disparity is still relatively small. The mean values of the x-disparity of the corresponding points are both about 1 to 2 pixels. Therefore, the proposed epipolar image generation framework is also applicable to areas with small terrain undulations and large terrain undulation gradients.
3.2.2. The Results of Epipolar Image Generation for Different Sensors
We conduct experiments on satellite images from other sources to further verify the universality of the proposed epipolar image generation framework. We choose the stereo image pair consisting of GF-3 satellite image and GF-2 satellite image in Songshan in this experiment. We first generate epipolar images based on the SAR-optical image pair. Due to the particularity of SAR imaging, we adopt different structural features in the matching stage for SAR images [
25]. The epipolar images obtained using the proposed framework are shown in
Figure 13. The average y-disparity of the image matching points can reach approximately 1 pixel, and the average x-disparity is less than 2 pixels (see
Table 5). It can be seen from the comparison results that although the S2P method can generate epipolar images with a small y-disparity, the x-disparity is large. Moreover, the epipolar images are distorted, which is not conducive to subsequent image matching. Therefore, the proposed epipolar images generation framework is also applicable for SAR-optical satellite stereo image pairs.
In addition to the epipolar image generation experiment on the SAR-optical image pairs, we also perform a verification experiment on the SAR–SAR image pair. We choose GF-3 images as our SAR image source and the corresponding area of the images used in Omaha. The epipolar images generated by GF-3 image pairs in the Omaha area are shown in
Figure 14 and the results of the comparative experiment are shown in
Table 6. By comparing with the S2P method, it can be found that the proposed framework has obvious advantages for the generation of epipolar images of SAR–SAR image pairs. The average value of the x-disparity and y-disparity of the epipolar images we generated can reach the sub-pixel level. And the epipolar image pair is not distorted, which is conducive to the dense matching of the epipolar image.
In summary, the proposed epipolar images generation framework can be applied to areas with large and small topographic undulations through the above experiments. Moreover, it can be used not only for the epipolar image generation of optical image pairs but also for the epipolar image generation of SAR–optical image pairs and SAR–SAR image pairs.
4. Discussion
The results in
Section 3 have shown that the proposed framework can generate better quality epipolar images. Next, we evaluate the performance of DSM generation using the generated epipolar images based on the previous experiment.
In the DSM generation experiment, we use the ZY-3 satellite images with a ground sampling distance of 3.5 m. Then, the generated epipolar images of Songshan are tested to obtain the corresponding DSM through the SGM-based stereo matching method and the Space Intersection method, and the result is shown in
Figure 15. We compare the generated DSM with the DSM generated by other methods and the existing DSM to evaluate the accuracy of the DSM generated by our framework, based on the GCPs. We choose AW3D30 DSM and DSM generated by ENVI as comparison data. Among them, AW3D30 (ALOS World 3D-30 m) is a DSM data set released by the Japan Aerospace Exploration Agency(JAXA), with a grid resolution of ~30 m. This DSM data set is obtained by using PRISM on the land observation satellite ALOS to image the same object using three cameras with different perspectives [
34]. In addition, the other DSM for comparison is obtained through the photogrammetry extension module in ENVI-v5.6 [
35]. The ENVI software uses the metadata information of the ZY-3 original image pair to generate DSM.
Comparing the generated DSM with GCPs, the absolute values of the difference between the elevation is mostly within 4 m, and the average absolute difference is 2.33 m. The histogram of the elevation accuracy is shown in
Figure 16.
Table 7 lists the accuracy of DSM at the GCPs marked in
Figure 15. Among them, the vertical precision of AW3D30 DSM in this area is ~20 m. Moreover, the vertical precision of ENVI-DSM and the generated DSM are both about 2 m. Therefore, the results show that the accuracy of the DSM we generated is greatly improved compared to AW3D30 DSM, and it can achieve higher accuracy than the DSM generated by ENVI. Therefore, the proposed framework can generate good quality epipolar images, which can be used to generate high accuracy DSM.