The Use of Remote Sensing-Based ET Estimates to Improve Global Hydrological Simulations in the Community Land Model Version 5.0
Abstract
:1. Introduction
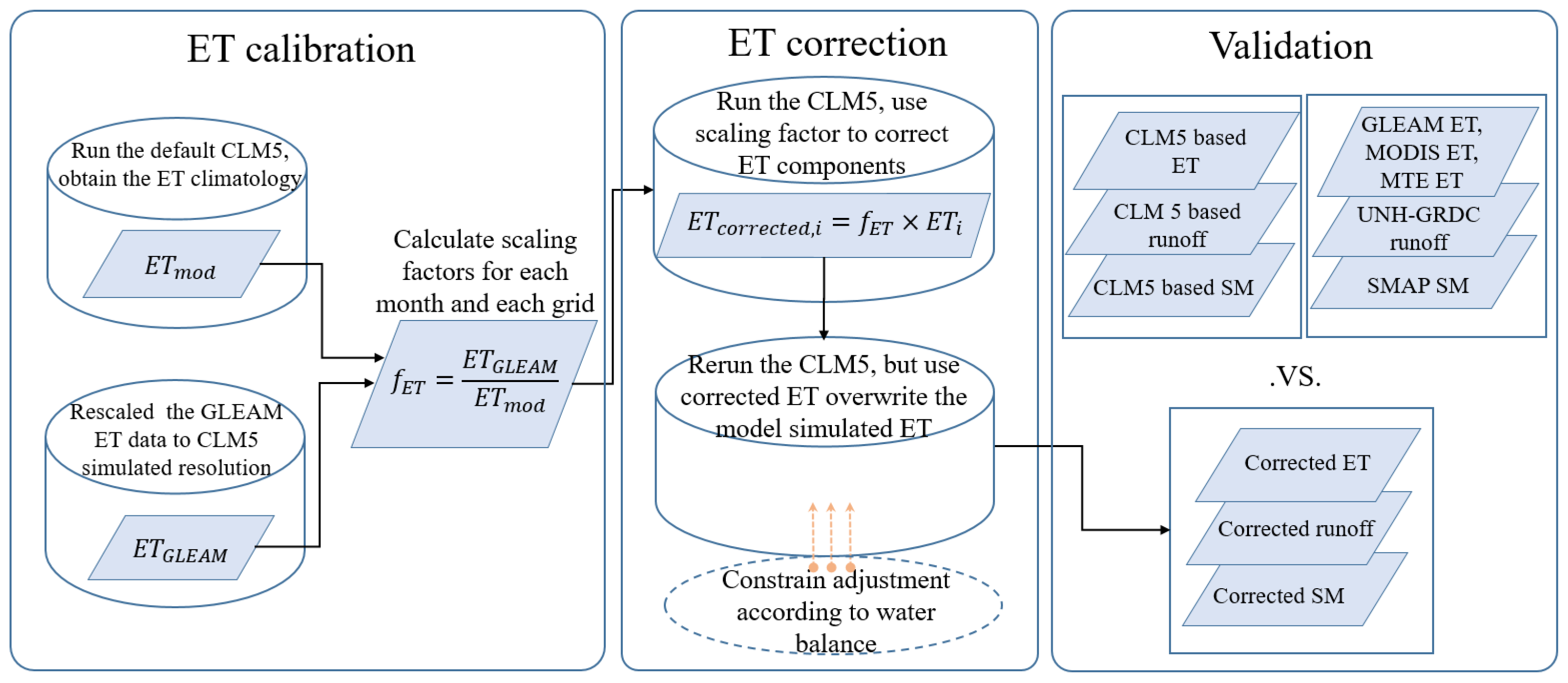
2. Materials and Methods
2.1. Model and Forcing Data
2.2. Methodology
3. Data
3.1. Remote Sensing-Based ET Products
3.1.1. GLEAM ET
3.1.2. MODIS ET and FLUXNET-MTE ET
3.2. University of New Hampshire-GRDC Runoff
3.3. SMAP Soil Moisture
4. Results
4.1. ET Scaling Factor
4.2. Evaluation
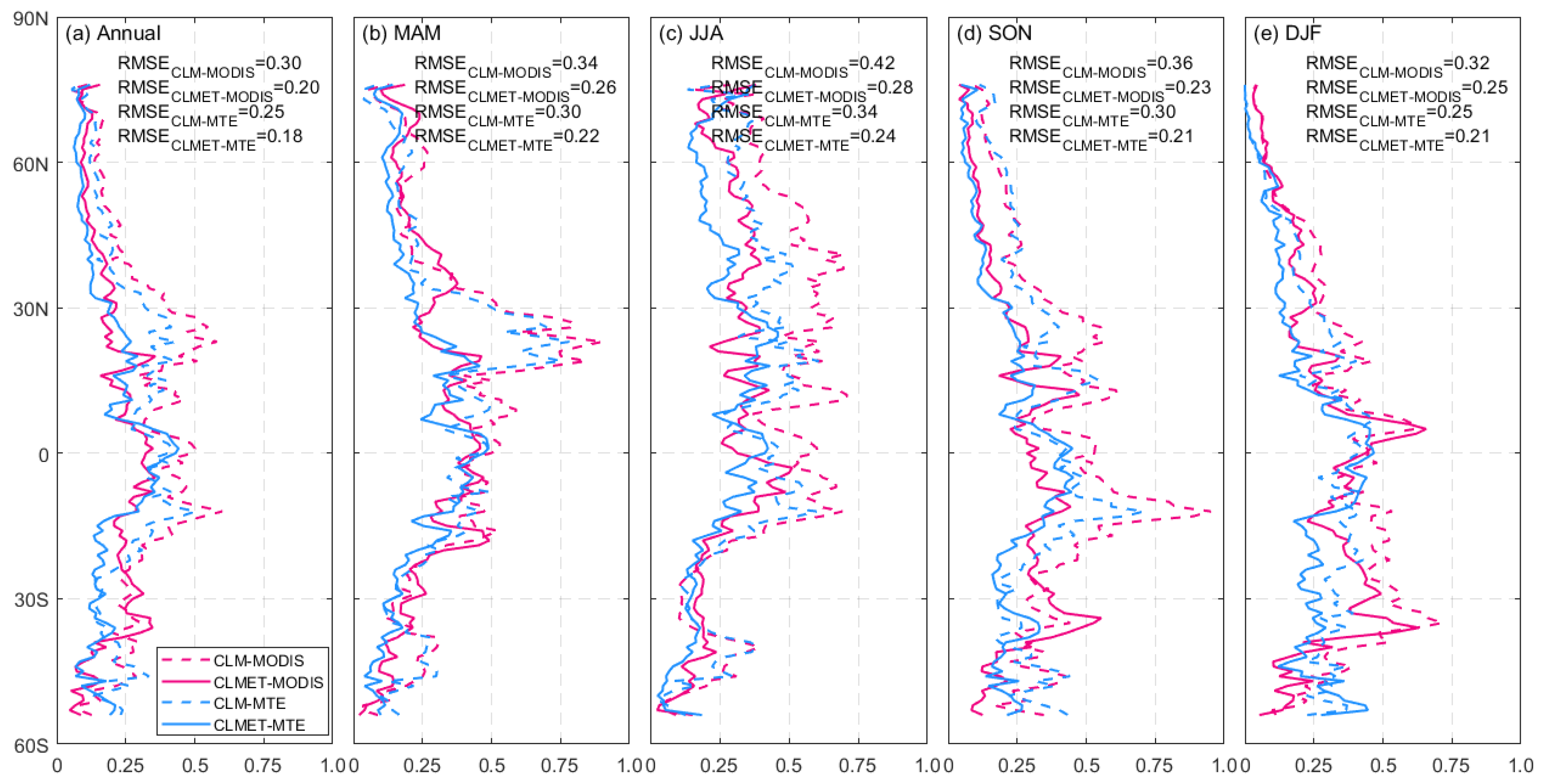
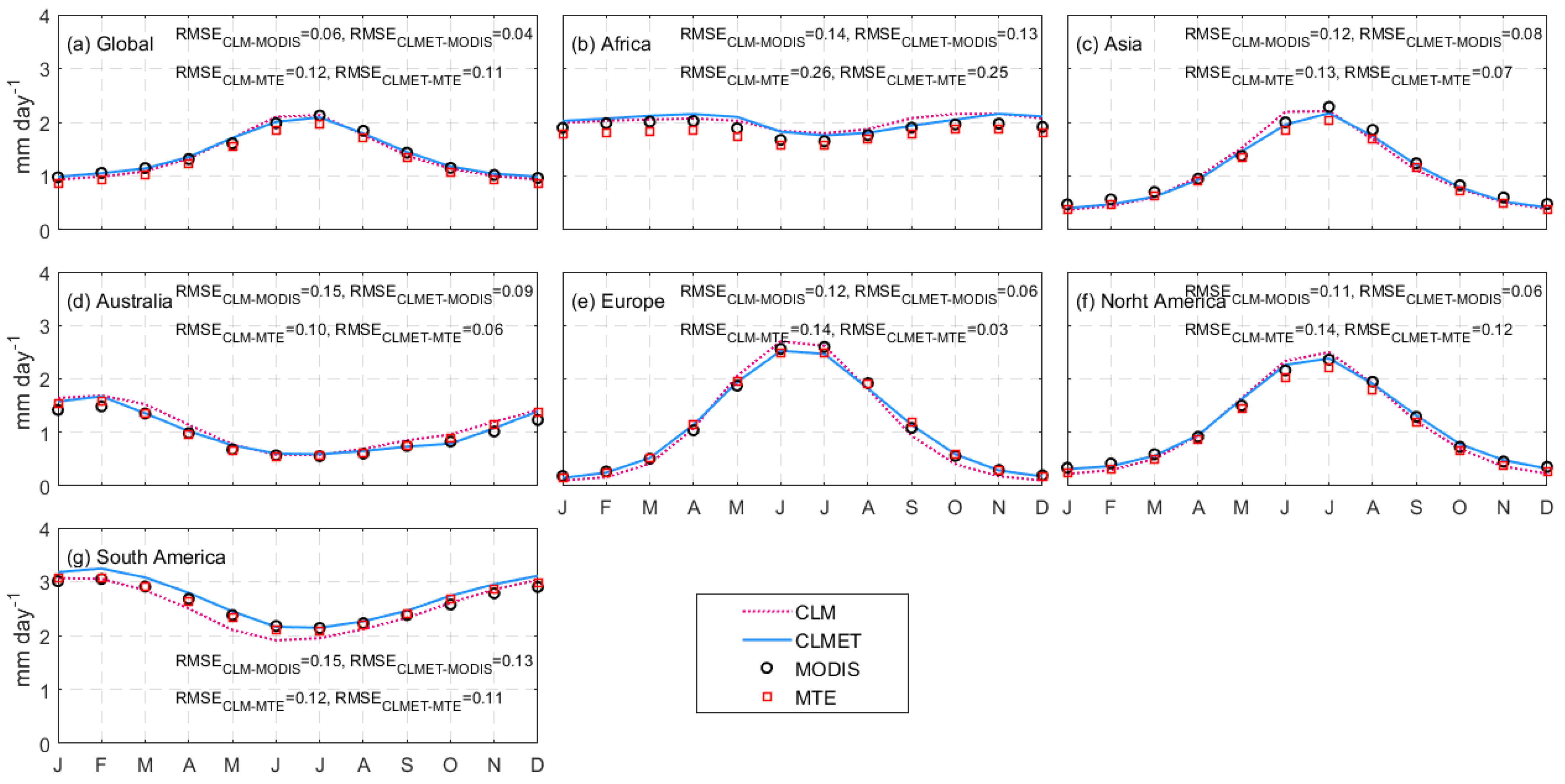
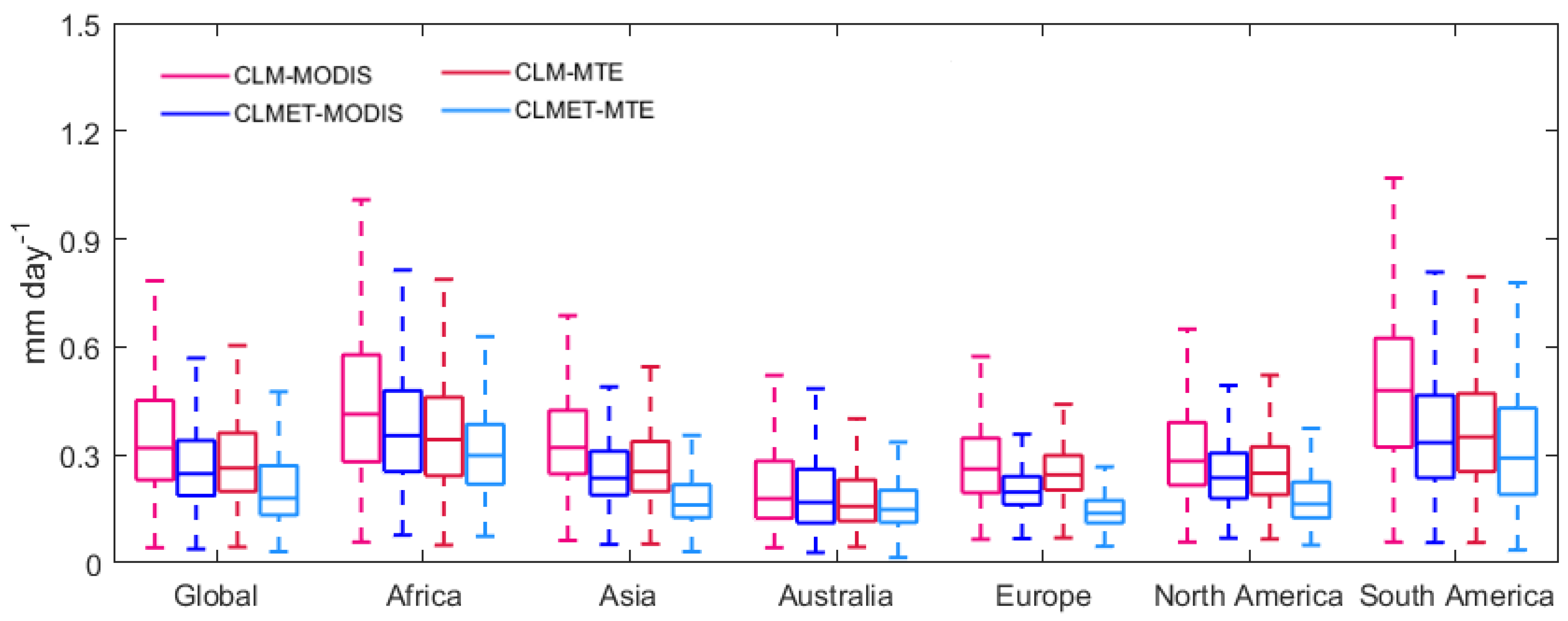
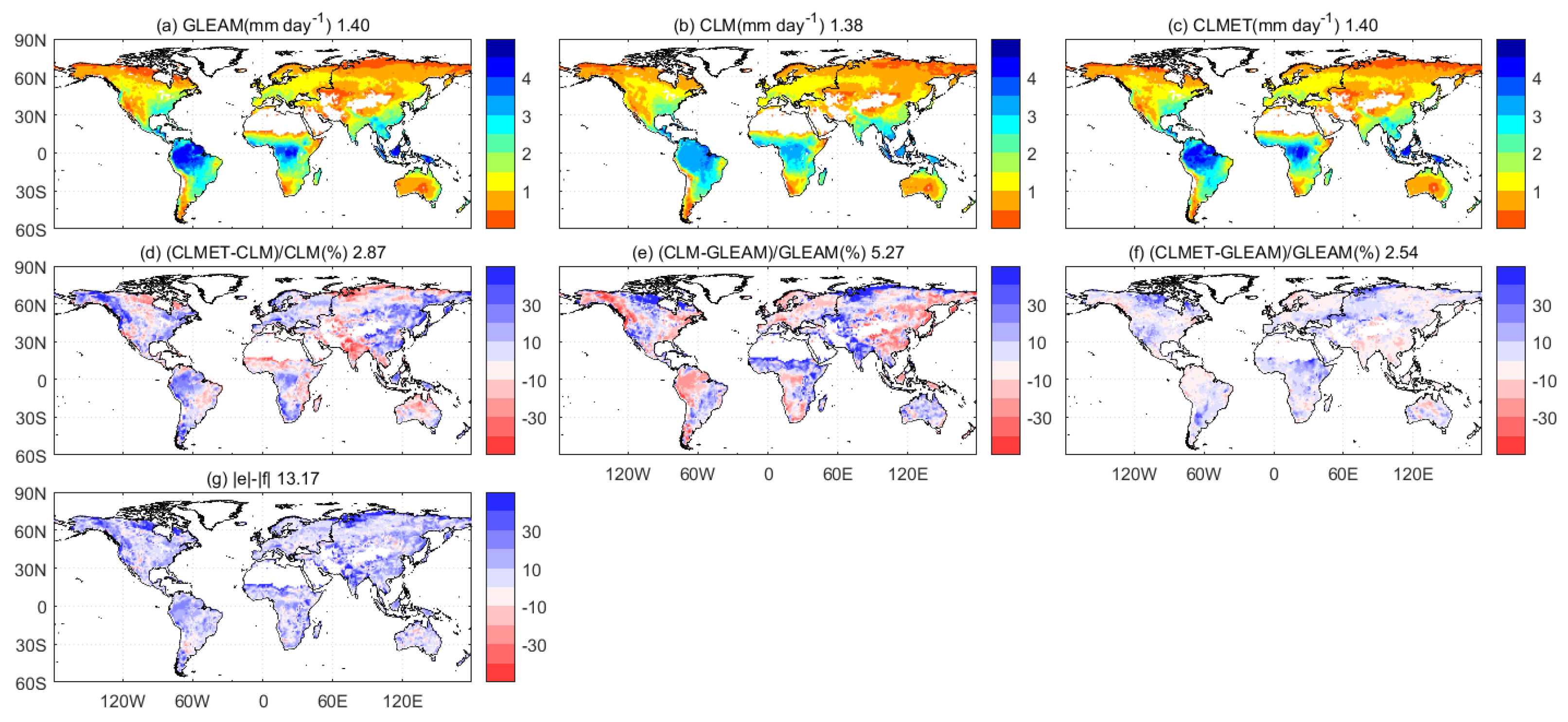
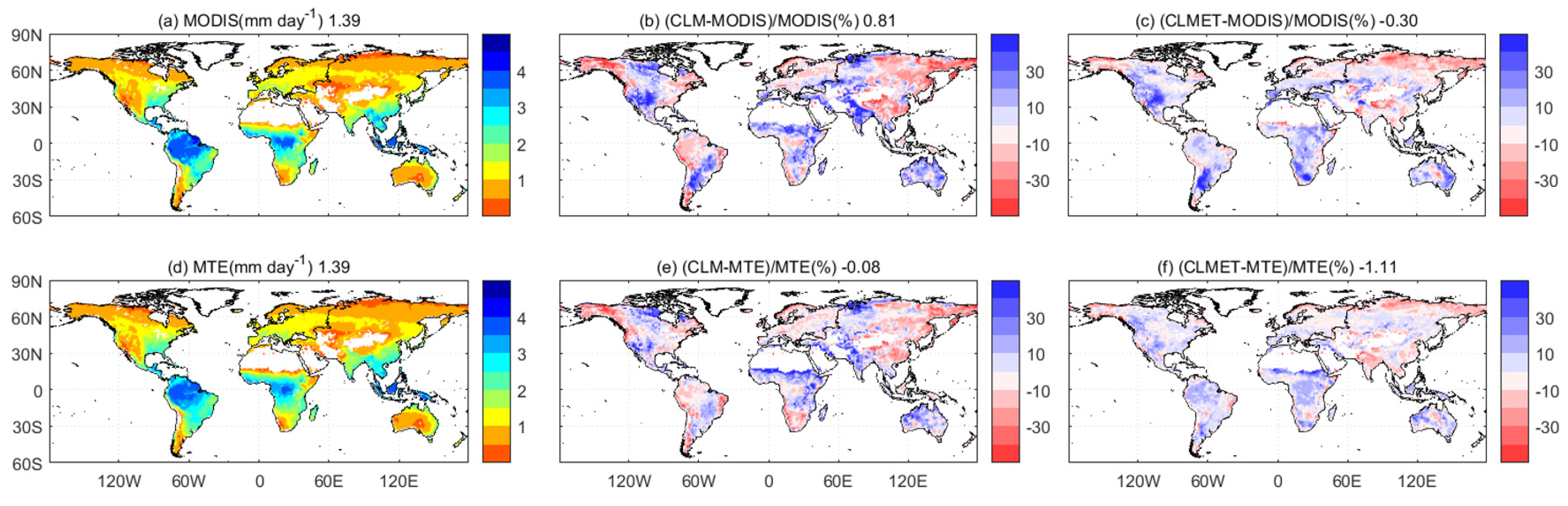
4.2.1. ET
4.2.2. Runoff
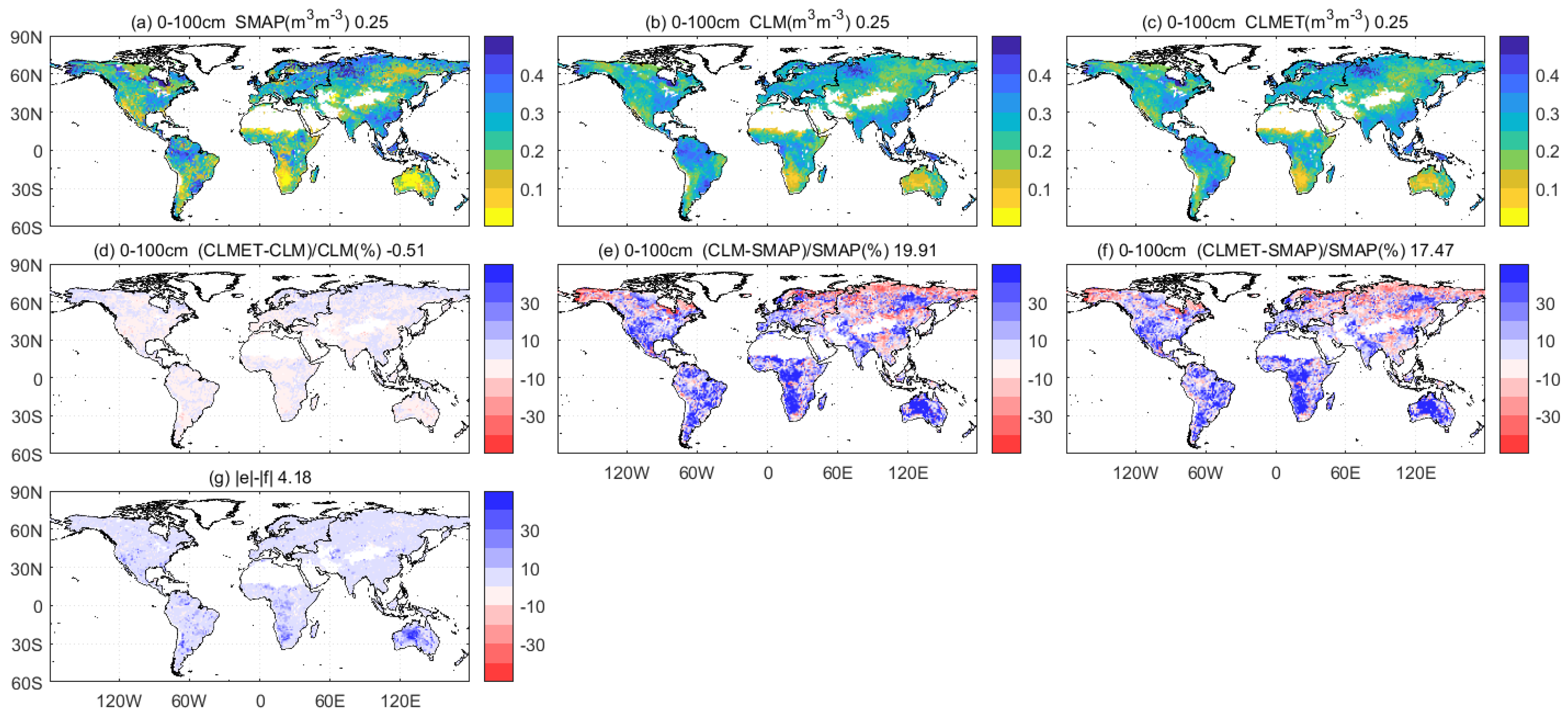
4.2.3. Soil Moisture
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A



| Season | Region | Bias (mm Day−1) | RB (%) | RMSE (mm Day−1) | CC | ||||
|---|---|---|---|---|---|---|---|---|---|
| CLM | CLMET | CLM | CLMET | CLM | CLMET | CLM | CLMET | ||
| MAM | Global | 0.018 | 0.048 | 3.06 | −2.76 | 0.352 | 0.278 | 0.94 | 0.96 |
| Africa | 0.074 | 0.149 | 6.28 | 5.80 | 0.422 | 0.393 | 0.91 | 0.94 | |
| Asia | 0.036 | −0.002 | 1.66 | −9.61 | 0.385 | 0.255 | 0.90 | 0.95 | |
| Australia | 0.138 | 0.036 | 13.91 | 2.07 | 0.244 | 0.176 | 0.93 | 0.93 | |
| Europe | 0.042 | 0.061 | 7.36 | −0.49 | 0.200 | 0.182 | 0.89 | 0.95 | |
| North America | 0.029 | 0.045 | 3.74 | −2.01 | 0.273 | 0.237 | 0.91 | 0.94 | |
| South America | −0.195 | 0.096 | −6.10 | 3.83 | 0.417 | 0.346 | 0.93 | 0.93 | |
| JJA | Global | 0.011 | −0.025 | 6.57 | 1.91 | 0.484 | 0.307 | 0.87 | 0.94 |
| Africa | 0.141 | 0.099 | 9.40 | 7.89 | 0.495 | 0.369 | 0.89 | 0.93 | |
| Asia | −0.020 | −0.091 | 9.85 | −1.94 | 0.506 | 0.308 | 0.80 | 0.92 | |
| Australia | 0.049 | 0.046 | 7.93 | 10.87 | 0.203 | 0.246 | 0.83 | 0.78 | |
| Europe | 0.013 | −0.090 | 4.08 | −1.87 | 0.440 | 0.285 | 0.70 | 0.87 | |
| North America | 0.093 | 0.028 | 8.83 | 3.12 | 0.502 | 0.304 | 0.84 | 0.92 | |
| South America | −0.207 | −0.012 | −8.56 | 5.23 | 0.500 | 0.291 | 0.94 | 0.96 | |
| SON | Global | −0.025 | 0.026 | −4.88 | −0.82 | 0.357 | 0.224 | 0.95 | 0.97 |
| Africa | 0.187 | 0.104 | 13.92 | 4.62 | 0.522 | 0.303 | 0.89 | 0.96 | |
| Asia | −0.089 | −0.041 | −12.93 | −8.88 | 0.287 | 0.166 | 0.95 | 0.98 | |
| Australia | 0.161 | 0.024 | 18.23 | −1.42 | 0.320 | 0.236 | 0.85 | 0.88 | |
| Europe | −0.139 | 0.026 | −21.42 | 3.56 | 0.191 | 0.082 | 0.84 | 0.93 | |
| North America | −0.062 | 0.044 | −5.83 | 3.36 | 0.233 | 0.149 | 0.94 | 0.97 | |
| South America | 0.005 | 0.124 | 3.18 | 7.16 | 0.560 | 0.384 | 0.88 | 0.94 | |
| DJF | Global | −0.037 | 0.017 | −31.65 | −25.85 | 0.310 | 0.258 | 0.97 | 0.98 |
| Africa | 0.105 | 0.143 | 4.29 | 3.80 | 0.413 | 0.390 | 0.92 | 0.94 | |
| Asia | −0.096 | −0.066 | −50.59 | −45.81 | 0.230 | 0.175 | 0.97 | 0.98 | |
| Australia | 0.211 | 0.174 | 16.39 | 11.35 | 0.342 | 0.299 | 0.91 | 0.94 | |
| Europe | −0.096 | −0.025 | −43.58 | −32.95 | 0.140 | 0.108 | 0.74 | 0.69 | |
| North America | −0.115 | −0.030 | −50.57 | −36.00 | 0.181 | 0.168 | 0.95 | 0.92 | |
| South America | 0.049 | 0.175 | 5.15 | 6.38 | 0.551 | 0.423 | 0.84 | 0.91 | |
| Season | Region | Bias (mm Day−1) | RB(%) | RMSE (mm Day−1) | CC | ||||
|---|---|---|---|---|---|---|---|---|---|
| CLM | CLMET | CLM | CLMET | CLM | CLMET | CLM | CLMET | ||
| MAM | Global | −0.003 | 0.026 | 0.48 | −5.51 | 0.305 | 0.232 | 0.95 | 0.97 |
| Africa | 0.107 | 0.182 | 10.23 | 8.08 | 0.359 | 0.314 | 0.94 | 0.97 | |
| Asia | −0.004 | −0.042 | −2.63 | −13.35 | 0.328 | 0.212 | 0.92 | 0.96 | |
| Australia | 0.159 | 0.058 | 18.95 | 6.14 | 0.254 | 0.179 | 0.93 | 0.93 | |
| Europe | −0.044 | −0.025 | −1.25 | −8.23 | 0.190 | 0.146 | 0.91 | 0.97 | |
| North America | −0.025 | −0.008 | −1.28 | −8.03 | 0.246 | 0.173 | 0.93 | 0.96 | |
| South America | −0.131 | 0.161 | −5.05 | 5.14 | 0.352 | 0.327 | 0.94 | 0.97 | |
| JJA | Global | 0.010 | −0.027 | 2.29 | −0.39 | 0.369 | 0.253 | 0.91 | 0.95 |
| Africa | 0.109 | 0.067 | 5.52 | 5.22 | 0.400 | 0.316 | 0.92 | 0.94 | |
| Asia | −0.036 | −0.108 | 2.68 | −5.53 | 0.374 | 0.259 | 0.87 | 0.94 | |
| Australia | 0.046 | 0.044 | 10.11 | 15.05 | 0.189 | 0.259 | 0.81 | 0.81 | |
| Europe | 0.037 | −0.066 | 1.80 | −3.14 | 0.306 | 0.178 | 0.81 | 0.92 | |
| North America | 0.067 | 0.001 | 4.24 | −0.31 | 0.396 | 0.230 | 0.89 | 0.94 | |
| South America | −0.110 | 0.085 | −8.99 | 5.17 | 0.380 | 0.269 | 0.95 | 0.97 | |
| SON | Global | −0.044 | 0.007 | −7.41 | −1.87 | 0.292 | 0.203 | 0.96 | 0.98 |
| Africa | 0.134 | 0.051 | 7.87 | 1.62 | 0.430 | 0.285 | 0.92 | 0.96 | |
| Asia | −0.071 | −0.023 | −10.44 | −3.65 | 0.233 | 0.147 | 0.97 | 0.98 | |
| Australia | 0.078 | −0.059 | 8.75 | −10.44 | 0.226 | 0.191 | 0.90 | 0.92 | |
| Europe | −0.200 | −0.034 | −29.10 | −6.68 | 0.234 | 0.089 | 0.86 | 0.93 | |
| North America | −0.076 | 0.030 | −7.58 | 2.56 | 0.230 | 0.120 | 0.94 | 0.98 | |
| South America | −0.036 | 0.084 | −3.77 | 0.96 | 0.396 | 0.356 | 0.93 | 0.95 | |
| DJF | Global | −0.014 | 0.040 | −7.33 | −0.35 | 0.242 | 0.203 | 0.98 | 0.98 |
| Africa | 0.083 | 0.120 | 9.29 | 6.49 | 0.358 | 0.300 | 0.95 | 0.96 | |
| Asia | −0.032 | −0.002 | −8.97 | 0.06 | 0.172 | 0.123 | 0.98 | 0.99 | |
| Australia | 0.078 | 0.041 | 5.94 | 1.71 | 0.240 | 0.233 | 0.93 | 0.93 | |
| Europe | −0.067 | 0.003 | −17.58 | −8.81 | 0.126 | 0.094 | 0.80 | 0.70 | |
| North America | −0.065 | 0.021 | −18.52 | −3.57 | 0.159 | 0.131 | 0.94 | 0.94 | |
| South America | 0.022 | 0.147 | 0.29 | 2.62 | 0.394 | 0.356 | 0.90 | 0.95 | |
| Season | Region | Soil moisture (m3 m−3) | RB(%) | RMSE(m3 m−3) | CC | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| SMAP | CLM | CLMET | CLM | CLMET | CLM | CLMET | CLM | CLMET | ||
| MAM | Global | 0.241 | 0.242 | 0.237 | 22.53 | 17.66 | 0.142 | 0.121 | 0.27 | 0.44 |
| Africa | 0.169 | 0.223 | 0.211 | 47.91 | 41.01 | 0.095 | 0.078 | 0.70 | 0.76 | |
| Asia | 0.253 | 0.215 | 0.218 | 7.03 | 5.04 | 0.163 | 0.139 | 0.05 | 0.22 | |
| Australia | 0.111 | 0.156 | 0.146 | 70.06 | 57.64 | 0.067 | 0.056 | 0.73 | 0.79 | |
| Europe | 0.322 | 0.300 | 0.295 | 5.00 | 1.27 | 0.159 | 0.134 | −0.26 | 0.04 | |
| North America | 0.256 | 0.244 | 0.240 | 15.14 | 10.88 | 0.149 | 0.127 | 0.18 | 0.37 | |
| South America | 0.249 | 0.321 | 0.302 | 47.74 | 37.67 | 0.115 | 0.094 | 0.65 | 0.73 | |
| JJA | Global | 0.227 | 0.290 | 0.277 | 45.38 | 38.19 | 0.131 | 0.109 | 0.58 | 0.66 |
| Africa | 0.168 | 0.224 | 0.213 | 49.29 | 41.78 | 0.096 | 0.081 | 0.67 | 0.73 | |
| Asia | 0.252 | 0.319 | 0.306 | 38.52 | 32.16 | 0.136 | 0.113 | 0.60 | 0.68 | |
| Australia | 0.110 | 0.161 | 0.150 | 65.35 | 53.94 | 0.072 | 0.058 | 0.74 | 0.80 | |
| Europe | 0.265 | 0.285 | 0.283 | 24.80 | 22.79 | 0.135 | 0.116 | 0.31 | 0.50 | |
| North America | 0.233 | 0.310 | 0.295 | 54.09 | 44.93 | 0.157 | 0.132 | 0.35 | 0.47 | |
| South America | 0.227 | 0.298 | 0.283 | 57.21 | 48.28 | 0.112 | 0.095 | 0.69 | 0.76 | |
| SON | Global | 0.223 | 0.235 | 0.231 | 27.30 | 22.89 | 0.123 | 0.106 | 0.38 | 0.52 |
| Africa | 0.167 | 0.225 | 0.214 | 56.17 | 48.47 | 0.099 | 0.083 | 0.69 | 0.75 | |
| Asia | 0.250 | 0.223 | 0.224 | 2.19 | 0.69 | 0.126 | 0.108 | 0.36 | 0.50 | |
| Australia | 0.089 | 0.139 | 0.132 | 81.98 | 71.81 | 0.067 | 0.057 | 0.76 | 0.81 | |
| Europe | 0.266 | 0.272 | 0.270 | 20.54 | 17.54 | 0.147 | 0.129 | −0.17 | 0.12 | |
| North America | 0.237 | 0.239 | 0.235 | 20.08 | 15.88 | 0.133 | 0.116 | 0.17 | 0.38 | |
| South America | 0.201 | 0.283 | 0.271 | 64.08 | 55.52 | 0.113 | 0.097 | 0.69 | 0.76 | |
| DJF | Global | 0.232 | 0.177 | 0.183 | −3.04 | −3.32 | 0.174 | 0.148 | 0.07 | 0.23 |
| Africa | 0.155 | 0.216 | 0.206 | 55.54 | 48.94 | 0.102 | 0.086 | 0.67 | 0.73 | |
| Asia | 0.248 | 0.135 | 0.150 | −34.59 | −29.96 | 0.195 | 0.166 | 0.06 | 0.22 | |
| Australia | 0.108 | 0.165 | 0.154 | 84.87 | 70.04 | 0.072 | 0.061 | 0.73 | 0.79 | |
| Europe | 0.309 | 0.189 | 0.201 | −30.25 | −27.81 | 0.217 | 0.185 | −0.20 | −0.02 | |
| North America | 0.250 | 0.145 | 0.158 | −26.96 | −24.17 | 0.196 | 0.167 | −0.03 | 0.17 | |
| South America | 0.227 | 0.301 | 0.286 | 50.28 | 41.34 | 0.110 | 0.091 | 0.64 | 0.73 | |
| Season | Region | Soil Moisture (m3 m−3) | RB(%) | RMSE (m3 m−3) | CC | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| SMAP | CLM | CLMET | CLM | CLMET | CLM | CLMET | CLM | CLMET | ||
| MAM | Global | 0.259 | 0.245 | 0.247 | 14.92 | 12.96 | 0.096 | 0.084 | 0.55 | 0.66 |
| Africa | 0.189 | 0.221 | 0.218 | 44.59 | 39.31 | 0.068 | 0.059 | 0.81 | 0.85 | |
| Asia | 0.273 | 0.234 | 0.238 | −4.67 | −4.26 | 0.100 | 0.088 | 0.36 | 0.50 | |
| Australia | 0.138 | 0.178 | 0.173 | 107.34 | 94.17 | 0.063 | 0.056 | 0.84 | 0.88 | |
| Europe | 0.327 | 0.294 | 0.298 | −0.08 | −0.39 | 0.114 | 0.100 | 0.24 | 0.50 | |
| North America | 0.271 | 0.242 | 0.245 | 2.44 | 1.95 | 0.108 | 0.095 | 0.50 | 0.63 | |
| South America | 0.262 | 0.299 | 0.294 | 33.55 | 29.30 | 0.079 | 0.069 | 0.80 | 0.85 | |
| JJA | Global | 0.249 | 0.274 | 0.272 | 30.40 | 26.90 | 0.079 | 0.069 | 0.73 | 0.79 |
| Africa | 0.190 | 0.223 | 0.220 | 42.48 | 37.59 | 0.067 | 0.059 | 0.79 | 0.83 | |
| Asia | 0.275 | 0.295 | 0.294 | 19.16 | 17.16 | 0.076 | 0.067 | 0.73 | 0.79 | |
| Australia | 0.133 | 0.174 | 0.169 | 106.35 | 93.73 | 0.060 | 0.054 | 0.83 | 0.87 | |
| Europe | 0.284 | 0.285 | 0.286 | 13.08 | 12.00 | 0.093 | 0.081 | 0.64 | 0.76 | |
| North America | 0.253 | 0.284 | 0.280 | 28.78 | 25.15 | 0.088 | 0.078 | 0.59 | 0.66 | |
| South America | 0.249 | 0.286 | 0.281 | 35.52 | 31.12 | 0.075 | 0.066 | 0.82 | 0.86 | |
| SON | Global | 0.243 | 0.263 | 0.261 | 30.44 | 26.75 | 0.076 | 0.067 | 0.64 | 0.72 |
| Africa | 0.191 | 0.226 | 0.222 | 49.82 | 44.10 | 0.068 | 0.060 | 0.80 | 0.84 | |
| Asia | 0.269 | 0.279 | 0.278 | 14.37 | 12.67 | 0.071 | 0.063 | 0.61 | 0.70 | |
| Australia | 0.123 | 0.162 | 0.157 | 120.15 | 105.66 | 0.057 | 0.051 | 0.84 | 0.88 | |
| Europe | 0.276 | 0.284 | 0.283 | 16.75 | 14.68 | 0.092 | 0.081 | 0.46 | 0.63 | |
| North America | 0.252 | 0.272 | 0.269 | 23.44 | 20.29 | 0.086 | 0.076 | 0.56 | 0.68 | |
| South America | 0.227 | 0.267 | 0.262 | 41.28 | 36.21 | 0.073 | 0.064 | 0.82 | 0.86 | |
| DJF | Global | 0.249 | 0.229 | 0.232 | 10.34 | 9.00 | 0.095 | 0.084 | 0.35 | 0.48 |
| Africa | 0.184 | 0.219 | 0.216 | 43.81 | 38.92 | 0.069 | 0.061 | 0.78 | 0.82 | |
| Asia | 0.266 | 0.215 | 0.221 | −11.92 | −10.58 | 0.100 | 0.088 | 0.33 | 0.46 | |
| Australia | 0.135 | 0.175 | 0.170 | 100.37 | 87.83 | 0.061 | 0.054 | 0.84 | 0.87 | |
| Europe | 0.309 | 0.270 | 0.274 | −2.83 | −2.77 | 0.114 | 0.100 | 0.12 | 0.29 | |
| North America | 0.263 | 0.222 | 0.227 | −4.04 | −3.76 | 0.109 | 0.095 | 0.32 | 0.48 | |
| South America | 0.243 | 0.282 | 0.277 | 35.15 | 30.79 | 0.075 | 0.066 | 0.79 | 0.84 | |
References
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s global energy budget. Bull. Am. Meteorol. Soc. 2009, 90, 311–323. [Google Scholar] [CrossRef]
- Pascolini-Campbell, M.; Reager, J.T.; Chandanpurkar, H.A.; Rodell, M. A 10 per cent increase in global land evapotranspiration from 2003 to 2019. Nature 2021, 593, 543–547. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50, RG2005. [Google Scholar] [CrossRef]
- Jiménez, C.; Prigent, C.; Mueller, B.; Seneviratne, S.I.; McCabe, M.F.; Wood, E.F.; Rossow, W.B.; Balsamo, G.; Betts, A.K.; Dirmeyer, P.A.; et al. Global intercomparison of 12 land surface heat flux estimates. J. Geophys. Res. Atmos. 2011, 116, D02102. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef] [Green Version]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land-atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; De Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W.; Hong, Y.; Gourley, J.J.; Yu, Z. Vegetation greening and climate change promote multidecadal rises of global land evapotranspiration. Sci. Rep. 2015, 5, 15956. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wires Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- Shuttleworth, W.J. Evaporation models in hydrology. In Land Surface Evaporation: Measurement and Parameterization; Schmugge, T.J., André, J.-C., Eds.; Springer: New York, NY, USA, 1991; pp. 93–120. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Salvucci, G.D.; Bras, R.L. An extremum principle of evaporation. Water Resour. Res. 2004, 40, W09303. [Google Scholar] [CrossRef] [Green Version]
- Luo, Z.; Shao, Q.; Wan, W.; Li, H.; Chen, X.; Zhu, S.; Ding, X. A new method for assessing satellite-based hydrological data products using water budget closure. J. Hydrol. 2021, 594, 125927. [Google Scholar] [CrossRef]
- Huang, S.; Bartlett, P.; Arain, M.A. Assessing nitrogen controls on carbon, water and energy exchanges in major plant functional types across North America using a carbon and nitrogen coupled ecosystem model. Ecol. Model. 2016, 323, 12–27. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Thornton, P.E.; Oleson, K.W.; Bonan, G.B. The partitioning of evapotranspiration into transpiration, soil evaporation, and canopy evaporation in a GCM: Impacts on land-atmosphere interaction. J. Hydrometeorol. 2007, 8, 862–880. [Google Scholar] [CrossRef]
- Bonan, G.B. Land–atmosphere interactions for climate system models: Coupling biophysical, biogeochemical, and ecosystem dynamical processes. Remote Sens. Environ. 1995, 51, 57–73. [Google Scholar] [CrossRef]
- Bonan, G.B.; Oleson, K.W.; Vertenstein, M.; Levis, S.; Zeng, X.; Dai, Y.; Dickinson, R.E.; Yang, Z.L. The land surface climatology of the community land model coupled to the NCAR community climate model. J. Clim. 2002, 15, 3123–3149. [Google Scholar] [CrossRef] [Green Version]
- Parajuli, K.; Jones, S.B.; Tarboton, D.G.; Flerchinger, G.N.; Hipps, L.E.; Allen, L.N.; Seyfried, M.S. Estimating actual evapotranspiration from stony-soils in montane ecosystems. Agric. For. Meteorol. 2019, 265, 183–194. [Google Scholar] [CrossRef] [Green Version]
- Oleson, K.W.; Niu, G.Y.; Yang, Z.L.; Lawrence, D.M.; Thornton, P.E.; Lawrence, P.J.; Stöckli, R.; Dickinson, R.E.; Bonan, G.B.; Levis, S.; et al. Improvements to the community land model and their impact on the hydrological cycle. J. Geophys. Res. Biogeosci. 2008, 113, G01021. [Google Scholar] [CrossRef]
- Oleson, K.; Lawrence, D.M.; Bonan, G.B.; Drewniak, B.; Huang, M.; Koven, C.D.; Levis, S.; Li, F.; Riley, W.J.; Subin, Z.M.; et al. Technical description of version 4.5 of the Community Land Model (CLM). NCAR Tech. Notes 2013. [Google Scholar] [CrossRef]
- Lawrence, D.; Fisher, R.; Koven, C.; Oleson, K.; Swenson, S.; Vertenstein, M. The Community Land Model version 5: Description of new features, benchmarking, and impact of forcing uncertainty. J. Adv. Model. Earth Syst. 2019, 11, 4245–4287. [Google Scholar] [CrossRef] [Green Version]
- Swenson, S.C.; Lawrence, D.M. Assessing a dry surface layer-based soil resistance parameterization for the Community Land Model using GRACE and FLUXNET-MTE data. J. Geophys. Res. Atmos. 2014, 119, 10,299–10,312. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration. Crop Evapotranspiration–Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Liu, M.; Tian, H.; Chen, G.; Ren, W.; Zhang, C.; Liu, J. Effects of land-use and land-cover change on evapotranspiration and water yield in China during 1900–2000. J. Am. Water Resour. Assoc. 2008, 44, 1193–1207. [Google Scholar] [CrossRef]
- Michel, D.; Jiménez, C.; Miralles, D.G.; Jung, M.; Hirschi, M.; Ershadi, A.; Martens, B.; McCabe, M.F.; Fisher, J.B.; Mu, Q.; et al. The WACMOS-ET project—Part 1: Tower-scale evaluation of four remote-sensing-based evapotranspiration algorithms. Hydrol. Earth Syst. Sci. 2016, 20, 803–822. [Google Scholar] [CrossRef] [Green Version]
- Miralles, D.G.; Jiménez, C.; Jung, M.; Michel, D.; Ershadi, A.; McCabe, M.F.; Hirschi, M.; Martens, B.; Dolman, A.J.; Fisher, J.B.; et al. The WACMOS-ET project—Part 2: Evaluation of global terrestrial evaporation data sets. Hydrol. Earth Syst. Sci. 2016, 20, 823–842. [Google Scholar] [CrossRef] [Green Version]
- Mueller, B.; Seneviratne, S.I.; Jimenez, C.; Corti, T.; Hirschi, M.; Balsamo, G.; Ciais, P.; Dirmeyer, P.; Fisher, J.B.; Guo, Z.; et al. Evaluation of global observations-based evapotranspiration datasets and IPCC AR4 simulations. Geophys. Res. Lett. 2011, 38, L06402. [Google Scholar] [CrossRef] [Green Version]
- Tian, H.; Chen, G.; Liu, M.; Zhang, C.; Sun, G.; Lu, C.; Xu, X.; Ren, W.; Pan, S.; Chappelka, A. Model estimates of net primary productivity, evapotranspiration, and water use efficiency in the terrestrial ecosystems of the southern United States during 1895–2007. For. Ecol. Manag. 2010, 259, 1311–1327. [Google Scholar] [CrossRef]
- Wartenburger, R.; Seneviratne, S.I.; Hirschi, M.; Chang, J.; Ciais, P.; Deryng, D.; Elliott, J.; Folberth, C.; Gosling, S.N.; Gudmundsson, L.; et al. Evapotranspiration simulations in ISIMIP2a—Evaluation of spatio-temporal characteristics with a comprehensive ensemble of independent datasets. Environ. Res. Lett. 2018, 13, 075001. [Google Scholar] [CrossRef]
- Haddeland, I.; Clark, D.B.; Franssen, W.; Ludwig, F.; Voß, F.; Arnell, N.W.; Bertrand, N.; Best, M.; Folwell, S.; Gerten, D.; et al. Multimodel estimate of the global terrestrial water balance: Setup and first results. J. Hydrometeorol. 2011, 12, 869–884. [Google Scholar] [CrossRef] [Green Version]
- Pan, S.; Pan, N.; Tian, H.; Friedlingstein, P.; Sitch, S.; Shi, H.; Arora, V.K.; Haverd, V.; Jain, A.K.; Kato, E.; et al. Evaluation of global terrestrial evapotranspiration using state-of-the-art approaches in remote sensing, machine learning and land surface modeling. Hydrol. Earth Syst. Sci. 2020, 24, 1485–1509. [Google Scholar] [CrossRef] [Green Version]
- Lu, H.; Koike, T.; Yang, K.; Hu, Z.; Xu, X.; Rasmy, M.; Kuria, D.; Tamagawa, K. Improving land surface soil moisture and energy flux simulations over the Tibetan plateau by the assimilation of the microwave remote sensing data and the GCM output into a land surface model. Int. J. Appl. Earth Obs. Geoinf. 2012, 17, 43–54. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Jin, R.; Huang, C. Assimilating passive microwave remote sensing data into a land surface model to improve the estimation of snow depth. Remote Sens. Environ. 2014, 143, 54–63. [Google Scholar] [CrossRef]
- Lee, J.S.; Choi, H.I. Improvements to runoff predictions from a land surface model with a lateral flow scheme using remote sensing and in situ observations. Water 2017, 9, 148. [Google Scholar] [CrossRef] [Green Version]
- Marshall, M.; Tu, K.; Funk, C.; Michaelsen, J.; Williams, P.; Williams, C.; Ardo, J.; Boucher, M.; Cappelaere, B.; de Grandcourt, A.; et al. Improving operational land surface model canopy evapotranspiration in Africa using a direct remote sensing approach. Hydrol. Earth Syst. Sci. 2013, 17, 1079–1091. [Google Scholar] [CrossRef] [Green Version]
- Parr, D.; Wang, G.; Bjerklie, D. Integrating remote sensing data on evapotranspiration and leaf area index with hydrological modeling: Impacts on model performance and future predictions. J. Hydrometeorol. 2015, 16, 2086–2100. [Google Scholar] [CrossRef]
- Wang, D.; Wang, G.; Parr, D.T.; Liao, W.; Xia, Y.; Fu, C. Incorporating remote sensing-based ET estimates into the Community Land Model version 4.5. Hydrol. Earth. Syst. Sci. 2017, 21, 3557–3577. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, D.M.; Oleson, K.W.; Flanner, M.G.; Thornton, P.E.; Swenson, S.C.; Lawrence, P.J.; Zeng, X.B.; Yang, Z.L.; Levis, S.; Sakaguchi, K.; et al. Parameterization improvements and functional and structural advances in version 4 of the Community Land Model. J. Adv. Model. Earth Syst. 2011, 3, M03001. [Google Scholar] [CrossRef]
- Lawrence, P.J.; Chase, T.N. Representing a new MODIS consistent land surface in the Community Land Model (CLM 3.0). J. Geophys. Res. Biogeosci. 2007, 112, G01023. [Google Scholar] [CrossRef]
- Verdin, K.L.; Jenson, S.K. Development of continental scale digital elevation models and extraction of hydrographic features. In Proceedings of the Third International Conference/Workshop on Integrating GIS and Environmental Modeling, Santa Fe, NM, USA, 21–26 January 1996. [Google Scholar]
- Cucchi, M.; Weedon, G.P.; Amici, A.; Bellouin, N.; Lange, S.; Müller Schmied, H.; Hersbach, H.; Buontempo, C. WFDE5: Bias-adjusted ERA5 reanalysis data for impact studies. Earth Syst. Sci. Data 2020, 12, 2097–2120. [Google Scholar] [CrossRef]
- Parr, D.; Wang, G.; Fu, C. Understanding evapotranspiration trends and their driving mechanisms over the NLDAS domain based on numerical experiments using CLM4.5. J. Geophys. Res. 2016, 121, 7729–7745. [Google Scholar] [CrossRef] [Green Version]
- Jung, M.; Reichstein, M.; Bondeau, A. Towards global empirical upscaling of FLUXNET eddy covariance observations: Validation of a model tree ensemble approach using a biosphere model. Biogeosciences 2009, 6, 2001–2013. [Google Scholar] [CrossRef] [Green Version]
- Martens, B.; Miralles, D.G.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef] [Green Version]
- Martens, B.; Miralles, D.; Lievens, H.; Fernández-Prieto, D.; Verhoest, N.E.C. Improving terrestrial evaporation estimates over continental Australia through assimilation of SMOS soil moisture. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 146–162. [Google Scholar] [CrossRef]
- Miralles, D.G.; De Jeu, R.A.M.; Gash, J.H.; Holmes, T.R.H.; Dolman, A.J. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef] [Green Version]
- Miralles, D.G.; Gash, J.H.; Holmes, T.R.H.; de Jeu, R.A.M.; Dolman, A.J. Global canopy interception from satellite observations. J. Geophys. Res. Atmos. 2010, 115, D16122. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Cabello, D.; Tomás-Burguera, M.; Martín-Hernández, N.; Beguería, S.; Azorin-Molina, C.; Kenawy, A.E. Drought variability and land degradation in semiarid regions: Assessment using remote sensing data and drought indices (1982–2011). Remote Sens. 2015, 7, 4391–4423. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Zhang, J.; Zhang, S.; Wang, J.; Bai, Y.; Yao, F.; Guo, H. The potential of remote sensing-based models on global water-use efficiency estimation: An evaluation and intercomparison of an ecosystem model (BESS) and algorithm (MODIS) using site level and upscaled eddy covariance data. Agric. For. Meteorol. 2020, 287, 107959. [Google Scholar] [CrossRef]
- Fekete, B.M.; Vörösmarty, C.J.; Grabs, W. High-resolution fields of global runoff combining observed river discharge and simulated water balances. Glob. Biogeochem. Cycles 2002, 16, 15-1–15-10. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; Neill, P.E.O.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Entekhabi, D.; Yueh, S.; O’Neill, P.E.; Kellogg, K.H.; Allen, A.; Bindlish, R.; Brown, M.; Chan, S.; Colliander, A.; Crow, W.T.; et al. SMAP Handbook—Soil Moisture Active Passive: Mapping Soil Moisture and Freeze/Thaw from Space; NASA: Pasadena, CA, USA, 2014. [Google Scholar]
- Reichle, R.; De Lannoy, G.; Koster, R.D.; Crow, W.T.; Kimball., J.S.; Liu, Q. SMAP L4 Global 3-Hourly 9 km EASE-Grid Surface and Root Zone Soil Moisture Analysis Update, Version 5; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2020. [Google Scholar]
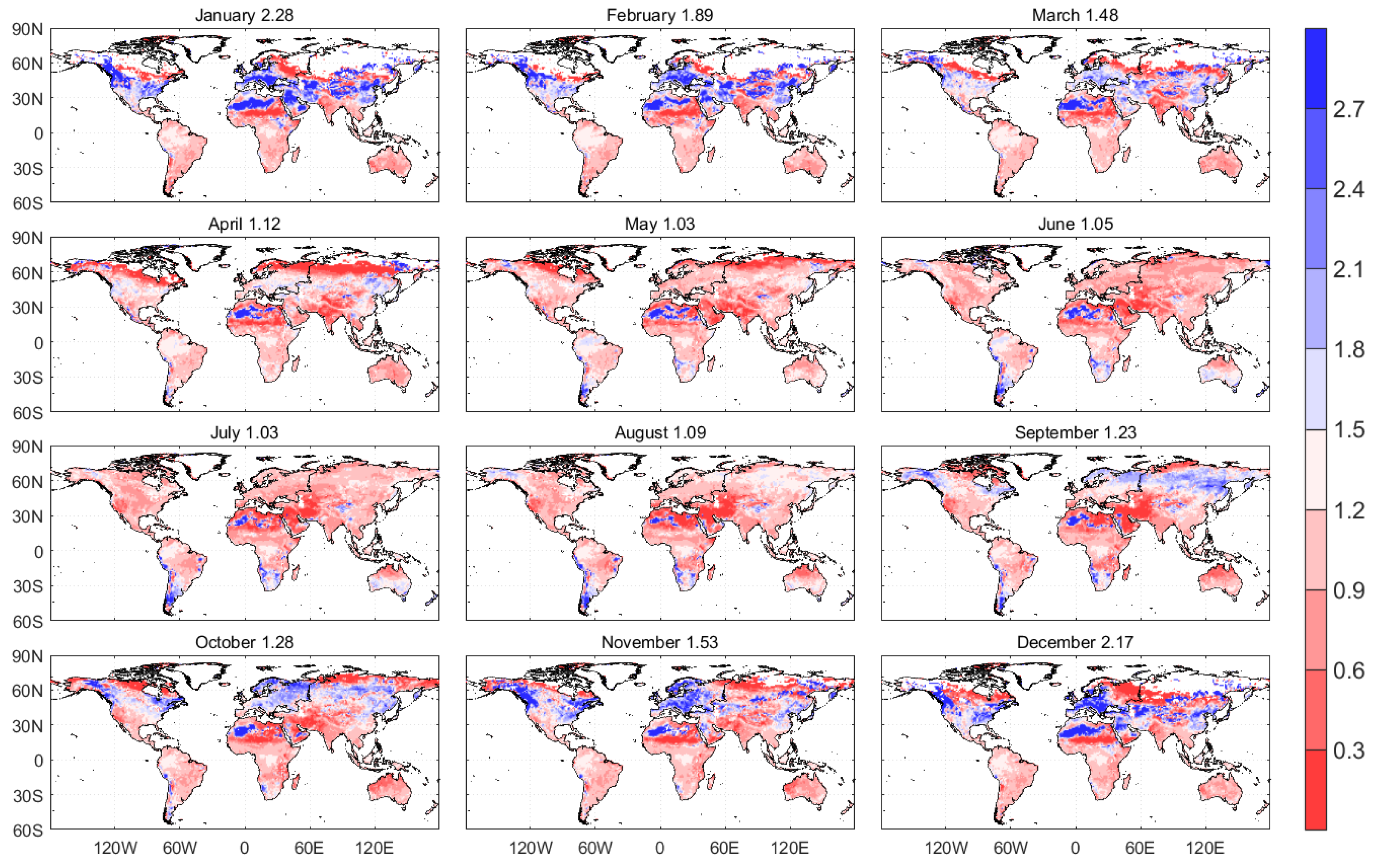



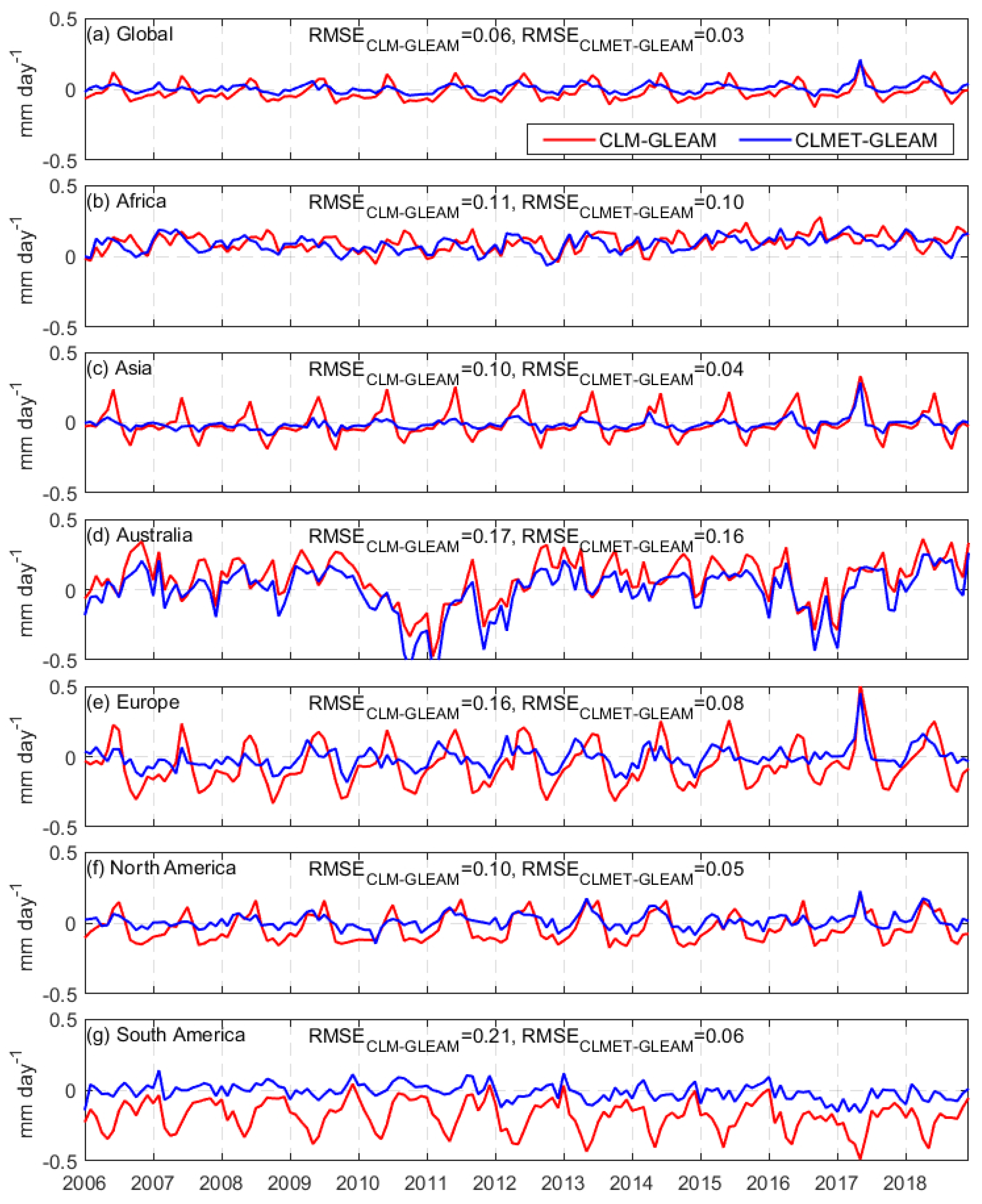
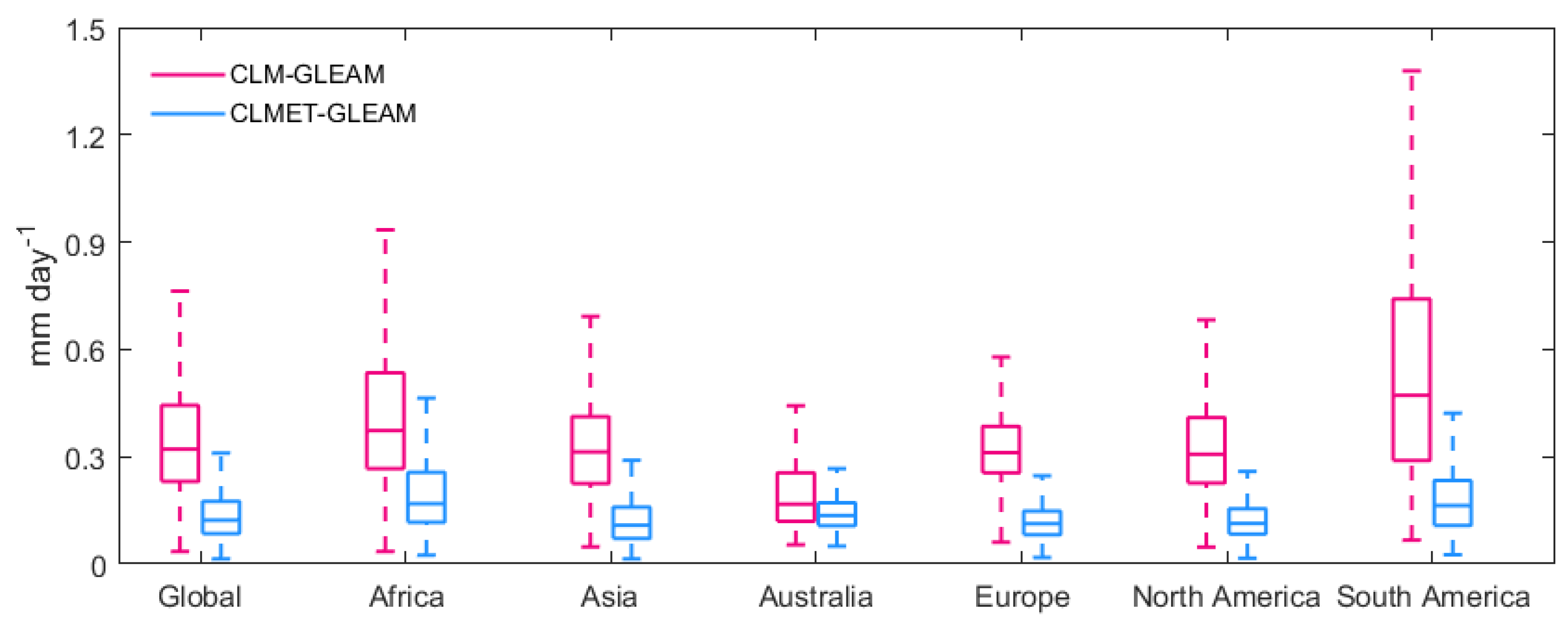
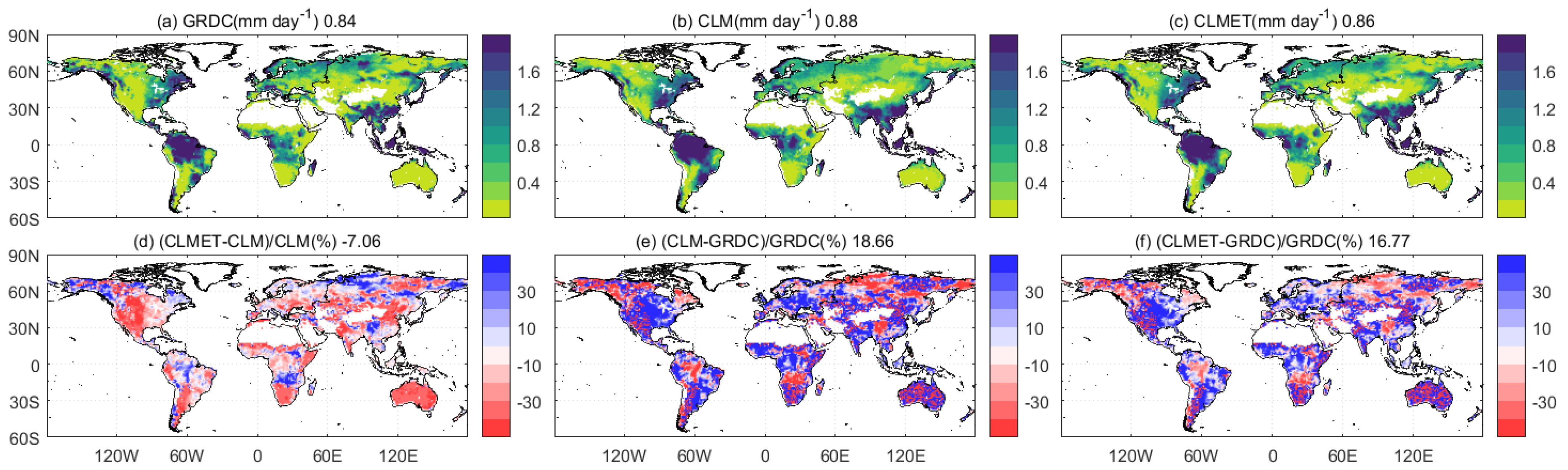

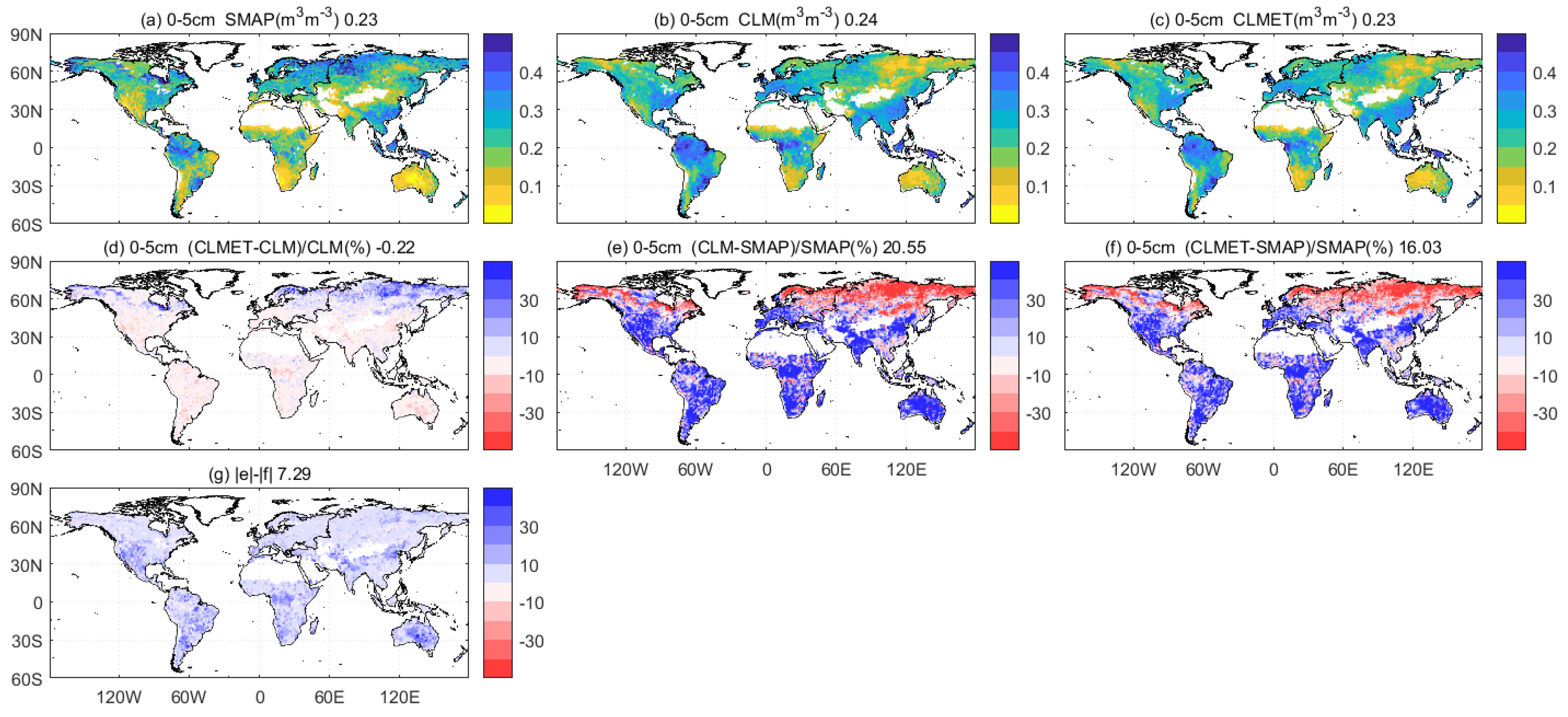
| Region | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Global | 2.28 | 1.89 | 1.48 | 1.12 | 1.03 | 1.05 | 1.03 | 1.09 | 1.23 | 1.28 | 1.53 | 2.17 |
| Africa | 1.50 | 1.33 | 1.45 | 1.31 | 1.35 | 1.22 | 1.11 | 1.16 | 1.53 | 1.65 | 1.65 | 2.01 |
| Asia | 3.30 | 2.56 | 1.71 | 1.11 | 0.88 | 0.88 | 0.94 | 1.02 | 1.18 | 1.09 | 1.28 | 2.51 |
| Australia | 0.90 | 0.94 | 0.87 | 0.88 | 1.05 | 1.19 | 1.17 | 0.99 | 0.83 | 0.80 | 0.85 | 0.93 |
| Europe | 1.99 | 2.00 | 1.39 | 0.99 | 0.95 | 0.97 | 0.96 | 1.05 | 1.36 | 1.73 | 2.04 | 2.31 |
| North America | 3.50 | 2.63 | 1.69 | 1.05 | 0.92 | 1.04 | 0.97 | 1.03 | 1.12 | 1.23 | 2.10 | 2.92 |
| South America | 1.04 | 1.07 | 1.08 | 1.17 | 1.27 | 1.37 | 1.36 | 1.38 | 1.25 | 1.15 | 1.08 | 1.04 |
| Year | Bias (mm Day−1) | RB (%) | RMSE (mm Day−1) | CC | ||||
|---|---|---|---|---|---|---|---|---|
| CLM | CLMET | CLM | CLMET | CLM | CLMET | CLM | CLMET | |
| 2006 | 0.002 | 0.049 | 6.44 | 3.40 | 0.330 | 0.101 | 0.94 | 0.97 |
| 2007 | −0.127 | −0.125 | −2.58 | −4.06 | 0.395 | 0.147 | 0.92 | 0.97 |
| 2008 | −0.019 | 0.018 | 5.22 | 2.42 | 0.343 | 0.110 | 0.93 | 0.97 |
| 2009 | −0.031 | −0.012 | 4.37 | 1.87 | 0.348 | 0.112 | 0.91 | 0.98 |
| 2010 | −0.023 | −0.006 | 5.16 | 2.14 | 0.349 | 0.122 | 0.93 | 0.99 |
| 2011 | −0.028 | 0.012 | 4.39 | 1.69 | 0.344 | 0.123 | 0.93 | 0.99 |
| 2012 | −0.018 | 0.009 | 6.40 | 3.31 | 0.349 | 0.117 | 0.93 | 0.98 |
| 2013 | 0.006 | 0.005 | 6.85 | 3.94 | 0.334 | 0.113 | 0.93 | 0.99 |
| 2014 | −0.011 | 0.026 | 6.20 | 3.11 | 0.340 | 0.112 | 0.93 | 0.96 |
| 2015 | −0.022 | 0.014 | 4.91 | 2.35 | 0.346 | 0.122 | 0.93 | 0.98 |
| 2016 | 0.002 | 0.048 | 5.83 | 3.24 | 0.341 | 0.121 | 0.93 | 0.97 |
| 2017 | −0.014 | 0.013 | 6.22 | 3.61 | 0.351 | 0.125 | 0.93 | 0.98 |
| 2018 | 0.022 | 0.021 | 9.31 | 5.99 | 0.330 | 0.112 | 0.91 | 0.98 |
| Season | Region | Bias (mm Day−1) | RB (%) | RMSE (mm Day−1) | CC | ||||
|---|---|---|---|---|---|---|---|---|---|
| CLM | CLMET | CLM | CLMET | CLM | CLMET | CLM | CLMET | ||
| Annual | Global | −0.019 | 0.007 | 5.27 | 2.54 | 0.346 | 0.118 | 0.93 | 0.98 |
| Africa | 0.097 | 0.086 | 12.33 | 5.70 | 0.404 | 0.175 | 0.90 | 0.98 | |
| Asia | −0.008 | −0.013 | 7.04 | 2.14 | 0.312 | 0.093 | 0.92 | 0.99 | |
| Australia | 0.074 | −0.006 | 8.23 | −0.13 | 0.231 | 0.087 | 0.89 | 0.94 | |
| Europe | −0.059 | −0.010 | −2.41 | −0.57 | 0.188 | 0.074 | 0.85 | 0.95 | |
| North America | −0.035 | 0.013 | 4.69 | 4.54 | 0.286 | 0.092 | 0.89 | 0.98 | |
| South America | −0.180 | −0.014 | −3.88 | 0.76 | 0.538 | 0.176 | 0.89 | 0.98 | |
| MAM | Global | 0.000 | 0.037 | 16.39 | 12.26 | 0.426 | 0.158 | 0.88 | 0.98 |
| Africa | 0.063 | 0.125 | 15.95 | 13.17 | 0.448 | 0.225 | 0.91 | 0.97 | |
| Asia | 0.046 | 0.020 | 23.95 | 15.23 | 0.418 | 0.149 | 0.88 | 0.97 | |
| Australia | 0.106 | 0.014 | 13.01 | 1.57 | 0.227 | 0.096 | 0.90 | 0.93 | |
| Europe | 0.011 | 0.052 | 14.10 | 9.30 | 0.276 | 0.104 | 0.87 | 0.97 | |
| North America | 0.014 | 0.049 | 19.42 | 18.72 | 0.345 | 0.134 | 0.88 | 0.96 | |
| South America | −0.304 | −0.036 | −7.27 | 0.15 | 0.656 | 0.191 | 0.88 | 0.98 | |
| JJA | Global | 0.041 | 0.011 | 6.84 | 3.51 | 0.479 | 0.164 | 0.86 | 0.97 |
| Africa | 0.129 | 0.088 | 8.96 | 6.48 | 0.463 | 0.218 | 0.89 | 0.96 | |
| Asia | 0.046 | −0.018 | 10.22 | 2.92 | 0.478 | 0.158 | 0.79 | 0.96 | |
| Australia | 0.039 | 0.035 | 8.61 | 9.85 | 0.251 | 0.102 | 0.66 | 0.83 | |
| Europe | 0.087 | 0.002 | 6.53 | 1.14 | 0.425 | 0.142 | 0.68 | 0.93 | |
| North America | 0.070 | 0.027 | 7.43 | 2.94 | 0.482 | 0.150 | 0.83 | 0.96 | |
| South America | −0.189 | −0.013 | −8.73 | 2.40 | 0.579 | 0.178 | 0.90 | 0.98 | |
| SON | Global | −0.070 | −0.020 | −4.56 | −1.56 | 0.393 | 0.125 | 0.93 | 0.98 |
| Africa | 0.128 | 0.040 | 12.42 | 3.21 | 0.513 | 0.200 | 0.89 | 0.97 | |
| Asia | −0.087 | −0.041 | −7.83 | −3.87 | 0.322 | 0.098 | 0.94 | 0.99 | |
| Australia | 0.125 | −0.021 | 18.89 | −4.96 | 0.319 | 0.138 | 0.83 | 0.92 | |
| Europe | −0.228 | −0.058 | −28.21 | −7.55 | 0.308 | 0.121 | 0.67 | 0.87 | |
| North America | −0.127 | −0.015 | −6.73 | 1.35 | 0.329 | 0.097 | 0.89 | 0.98 | |
| South America | −0.113 | −0.001 | −1.36 | 1.68 | 0.562 | 0.220 | 0.88 | 0.97 | |
| DJF | Global | −0.048 | −0.002 | −12.68 | −8.27 | 0.338 | 0.132 | 0.96 | 0.99 |
| Africa | 0.069 | 0.090 | 14.65 | 11.43 | 0.409 | 0.208 | 0.93 | 0.97 | |
| Asia | −0.039 | −0.012 | −8.63 | −0.48 | 0.251 | 0.072 | 0.96 | 0.99 | |
| Australia | 0.027 | −0.052 | 4.07 | −5.12 | 0.282 | 0.147 | 0.89 | 0.93 | |
| Europe | −0.107 | −0.038 | −31.44 | −28.60 | 0.190 | 0.101 | 0.71 | 0.72 | |
| North America | −0.098 | −0.010 | −39.87 | −29.74 | 0.258 | 0.095 | 0.88 | 0.94 | |
| South America | −0.112 | −0.005 | 0.17 | 0.33 | 0.598 | 0.212 | 0.81 | 0.95 | |
| Reference | Region | Bias (mm Day−1) | RB (%) | RMSE (mm Day−1) | CC | ||||
|---|---|---|---|---|---|---|---|---|---|
| CLM | CLMET | CLM | CLMET | CLM | CLMET | CLM | CLMET | ||
| MODIS | Global | −0.008 | 0.017 | 0.81 | −0.30 | 0.297 | 0.192 | 0.95 | 0.98 |
| Africa | 0.127 | 0.124 | 9.23 | 6.58 | 0.355 | 0.265 | 0.93 | 0.97 | |
| Asia | −0.042 | −0.050 | −2.35 | −0.98 | 0.286 | 0.155 | 0.93 | 0.98 | |
| Australia | 0.139 | 0.070 | 14.01 | 7.34 | 0.245 | 0.156 | 0.92 | 0.94 | |
| Europe | −0.045 | −0.007 | −3.69 | −1.75 | 0.146 | 0.110 | 0.89 | 0.94 | |
| North America | −0.013 | 0.022 | 0.62 | 1.47 | 0.235 | 0.152 | 0.93 | 0.97 | |
| South America | −0.088 | 0.095 | −1.02 | 5.16 | 0.435 | 0.407 | 0.92 | 0.95 | |
| MTE | Global | −0.013 | 0.012 | −0.08 | −1.11 | 0.243 | 0.179 | 0.96 | 0.96 |
| Africa | 0.108 | 0.105 | 9.95 | 6.02 | 0.332 | 0.246 | 0.93 | 0.97 | |
| Asia | −0.036 | −0.044 | −2.02 | −0.70 | 0.222 | 0.131 | 0.96 | 0.98 | |
| Australia | 0.090 | 0.021 | 9.98 | 3.31 | 0.197 | 0.134 | 0.93 | 0.94 | |
| Europe | −0.068 | −0.031 | −6.30 | −4.27 | 0.127 | 0.097 | 0.92 | 0.96 | |
| North America | −0.024 | 0.011 | −1.11 | −0.19 | 0.202 | 0.120 | 0.94 | 0.98 | |
| South America | −0.064 | 0.119 | −3.19 | 3.32 | 0.320 | 0.288 | 0.94 | 0.97 | |
| Region | Bias (mm Day−1) | RB (%) | RMSE (mm Day−1) | CC | ||||
|---|---|---|---|---|---|---|---|---|
| CLM | CLMET | CLM | CLMET | CLM | CLMET | CLM | CLMET | |
| Global | 0.041 | 0.021 | 18.66 | 16.77 | 0.661 | 0.415 | 0.83 | 0.94 |
| Africa | 0.139 | 0.086 | 24.03 | 21.91 | 0.533 | 0.329 | 0.80 | 0.91 |
| Asia | −0.005 | −0.007 | 13.60 | 13.44 | 0.670 | 0.414 | 0.83 | 0.94 |
| Australia | 0.129 | 0.076 | 12.84 | 12.00 | 0.163 | 0.107 | 0.76 | 0.91 |
| Europe | 0.077 | 0.044 | 25.52 | 17.30 | 0.367 | 0.220 | 0.85 | 0.95 |
| North America | 0.038 | 0.019 | 20.18 | 18.21 | 0.505 | 0.311 | 0.81 | 0.94 |
| South America | −0.009 | −0.016 | 21.53 | 20.06 | 1.144 | 0.743 | 0.80 | 0.94 |
| Soil Layer | Region | Soil Moisture (m3 m−3) | RB (%) | RMSE (m3 m−3) | CC | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| SMAP | CLM | CLMET | CLM | CLMET | CLM | CLMET | CLM | CLMET | ||
| 0–5 cm | Global | 0.231 | 0.236 | 0.232 | 20.6 | 16.0 | 0.119 | 0.101 | 0.64 | 0.73 |
| Africa | 0.165 | 0.222 | 0.211 | 46.8 | 38.6 | 0.095 | 0.079 | 0.75 | 0.80 | |
| Asia | 0.251 | 0.223 | 0.224 | 1.5 | 0.0 | 0.120 | 0.103 | 0.62 | 0.72 | |
| Australia | 0.104 | 0.155 | 0.146 | 72.2 | 59.3 | 0.069 | 0.057 | 0.82 | 0.86 | |
| Europe | 0.291 | 0.261 | 0.262 | 3.3 | 1.5 | 0.150 | 0.129 | 0.39 | 0.60 | |
| North America | 0.244 | 0.234 | 0.232 | 14.4 | 10.6 | 0.128 | 0.110 | 0.61 | 0.73 | |
| South America | 0.226 | 0.301 | 0.286 | 20.55 | 16.03 | 0.110 | 0.091 | 0.80 | 0.84 | |
| 0–100 cm | Global | 0.250 | 0.253 | 0.253 | 46.81 | 38.56 | 0.079 | 0.070 | 0.79 | 0.86 |
| Africa | 0.189 | 0.222 | 0.219 | 1.50 | 0.01 | 0.067 | 0.059 | 0.78 | 0.84 | |
| Asia | 0.271 | 0.256 | 0.258 | 72.17 | 59.32 | 0.076 | 0.066 | 0.79 | 0.86 | |
| Australia | 0.132 | 0.172 | 0.167 | 3.26 | 1.49 | 0.061 | 0.054 | 0.86 | 0.91 | |
| Europe | 0.299 | 0.283 | 0.285 | 14.40 | 10.57 | 0.099 | 0.088 | 0.80 | 0.89 | |
| North America | 0.260 | 0.255 | 0.255 | 51.08 | 41.67 | 0.088 | 0.078 | 0.80 | 0.87 | |
| South America | 0.245 | 0.283 | 0.278 | 19.91 | 17.47 | 0.074 | 0.065 | 0.79 | 0.85 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Wang, D.; Mo, C. The Use of Remote Sensing-Based ET Estimates to Improve Global Hydrological Simulations in the Community Land Model Version 5.0. Remote Sens. 2021, 13, 4460. https://doi.org/10.3390/rs13214460
Wang D, Wang D, Mo C. The Use of Remote Sensing-Based ET Estimates to Improve Global Hydrological Simulations in the Community Land Model Version 5.0. Remote Sensing. 2021; 13(21):4460. https://doi.org/10.3390/rs13214460
Chicago/Turabian StyleWang, Dayang, Dagang Wang, and Chongxun Mo. 2021. "The Use of Remote Sensing-Based ET Estimates to Improve Global Hydrological Simulations in the Community Land Model Version 5.0" Remote Sensing 13, no. 21: 4460. https://doi.org/10.3390/rs13214460
APA StyleWang, D., Wang, D., & Mo, C. (2021). The Use of Remote Sensing-Based ET Estimates to Improve Global Hydrological Simulations in the Community Land Model Version 5.0. Remote Sensing, 13(21), 4460. https://doi.org/10.3390/rs13214460







