A Preliminary Assessment of a Newly-Defined Multispectral Hue Space for Retrieving River Depth with Optical Imagery and In Situ Calibration Data
Abstract
:1. Introduction
2. Principles of Remotely-Sensed Estimation of River Bathymetry Using Passive Optical Measurements
- is the radiance originating from the Lambertian (diffuse) reflection from the bed substrate;
- is the volume radiance of the water column of depth h, which is basically sunlight that has been backscattered upwards before reaching the bottom;
- is the surface radiance due to specular reflections at the air–water interface. can make up a large fraction of for certain geometries or viewing angles (‘sun glints’);
- is a path radiance due to atmospheric scattering.
- The first end-member is the reflectance of bed/substrate, , which depends on both location and wavelength ,
- The second end-member is the reflectance that would be measured over an ‘infinitely deep’ water column.
- First, the reflectance of deep water is assumed to be small compared to the bed reflectance (for any substrate and any wavelength). Deep water reflectance is certainly low if the water is clear, but this assumption breaks down in the presence of sediment, dissolved organic matter, algae, etc. Furthermore, the bed might have a very low reflectance. Quartz sand might be highly reflective, but mud and rocks (especially rocks coated with a microbial film) can be quite dark;
- Second, the ratio of bed reflectances at wavelengths and , is approximated as uniform in space.
3. Beyond Spectral Ratios: A Definition of Multispectral Hue
3.1. Rationale for the Definition of Multispectral Hue
3.1.1. RGB Case: The Color Wheel
- The pure color can be partially desaturated, i.e., mixed with a white component. Such a mixing can occur for example with specular reflections, which will appear nearly white under white illumination if the refractive index of the material is slowly varying with wavelength (this is the case for water, or for an object coated with varnish).
- The overall brightness or value of the color can be decreased. Physically speaking, this other operation is similar to either reducing the intensity of the light source, or changing the orientation of an object’s surface normals so that less light is diffused towards the sensor (‘shaded face’ effect).
3.1.2. Notations
3.1.3. The Reason Why Multispectral Hue Should Have Degrees of Freedom with n Bands
3.2. Multispectral Hue as a Directional Variable
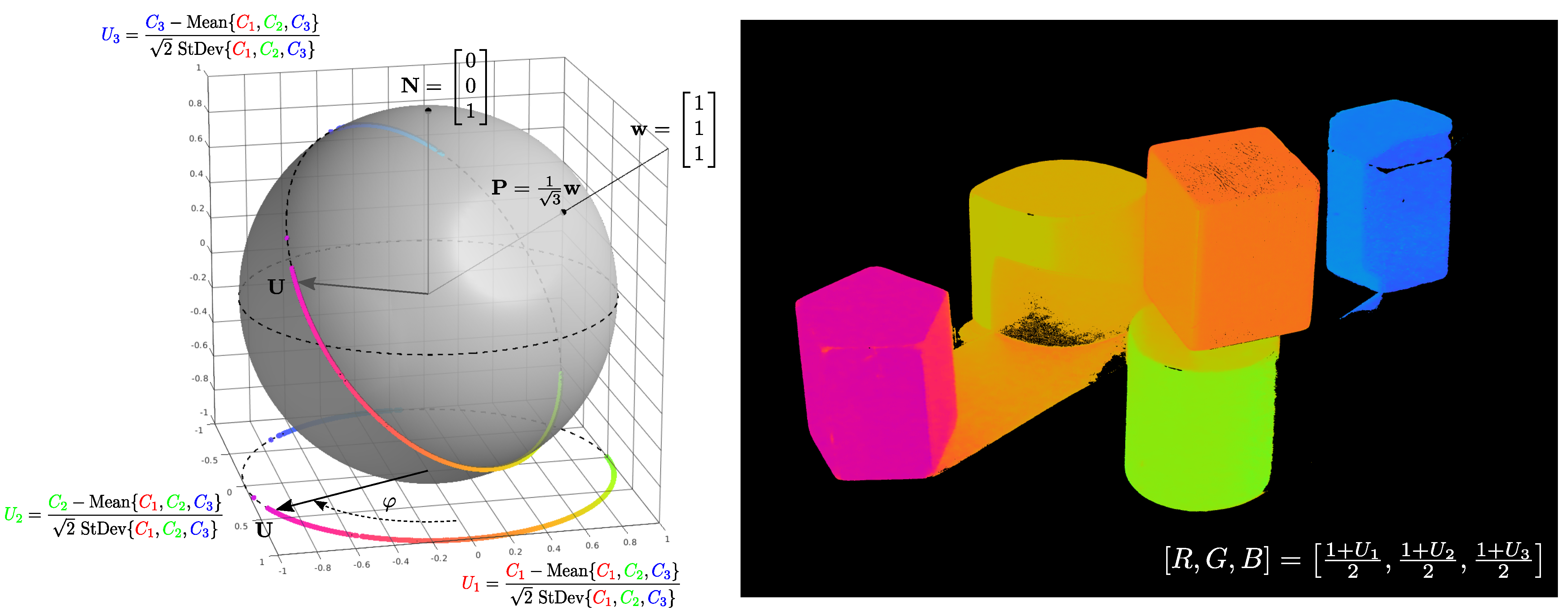
3.2.1. Mathematical Definition
3.2.2. Illustration with the RGB Image
3.2.3. Summary of the Section
- With bands, is on the unit circle in the Euclidean plane : it is closely related to the ‘color wheel’;
- With bands, is on the ‘usual’ unit sphere in the Euclidean space . It has two degrees of freedom, we might call them ‘color latitude’ and ‘color longitude’ as will be seen later;
- With bands, the hypersphere cannot be pictured out. However, it is still a smooth Riemannian manifold, and all familiar properties on and (geodesic distance, Euler angles, rotation group, etc.) can be extended to any dimension.
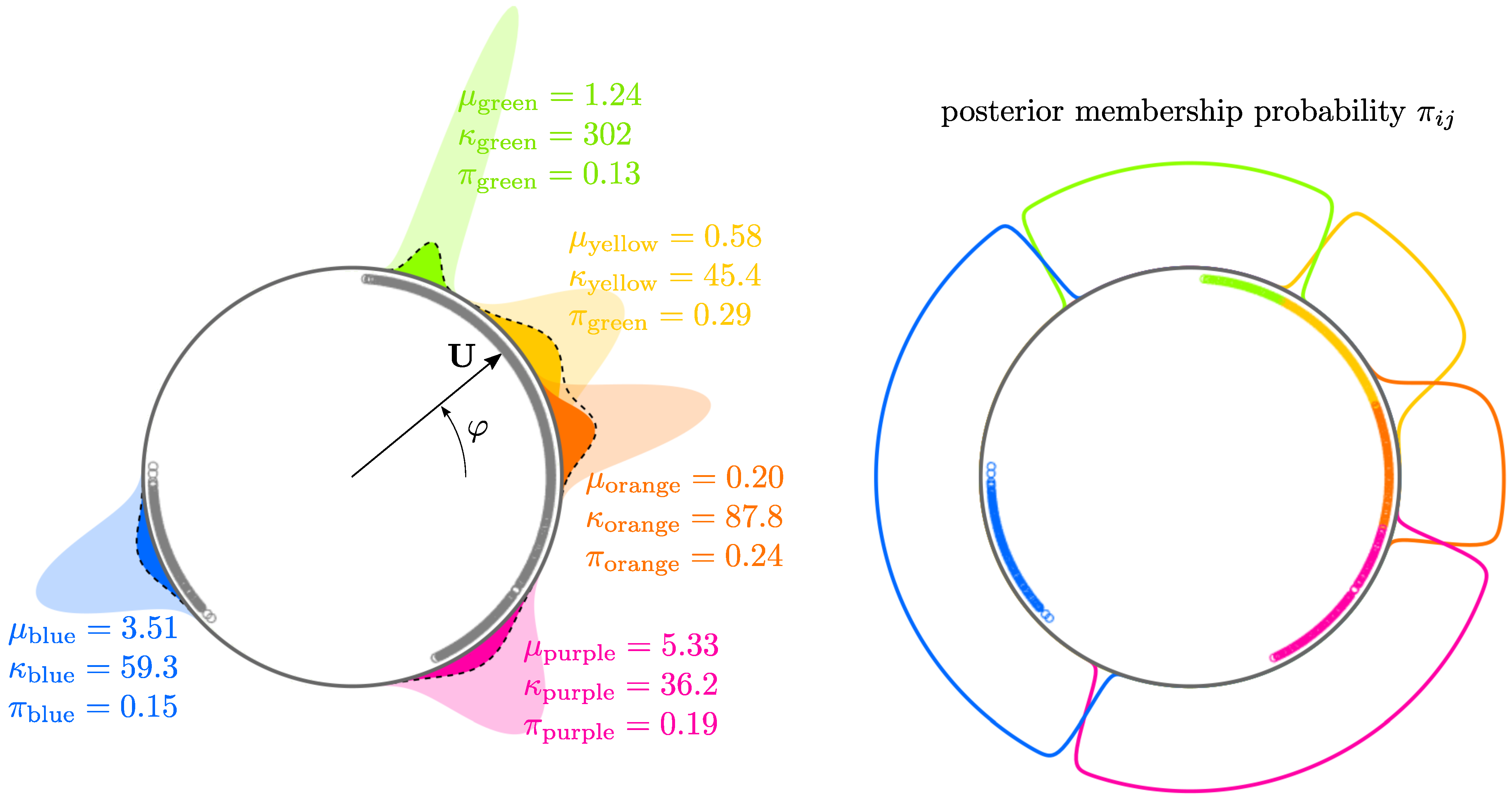
3.3. Mixture Models for the Analysis of Multispectral Hue Distribution
3.3.1. Mixture Density
3.3.2. Parameter Estimation Using Expectation–Maximization Algorithm
- E-step (Expectation): at each iteration , we start with current parameter estimates and we define updated membership probabilities using Bayes formula:where is the estimated probability that pixel i with hue angle comes from component j, with for each pixel;
- M-step (Maximization): given these membership probabilities, the parameters of each component are re-estimated using a slightly modified maximum likelihood method based on the maximization of:We see that the weights in this log-likelihood are the membership probabilities, instead of just 1. can be maximized for each component j independently, leading to updated parameters and
4. Using Multispectral Hue as a Predictor for Depth
4.1. Dataset
4.1.1. High-Resolution Airborne Imagery
4.1.2. In Situ Depth Measurements
4.1.3. LiDAR Data in the Floodplain
4.2. Hue Sphere for Bands
4.3. Masks
- Riparian vegetation as well as floating algae are masked using the classical Normalized Difference Vegetation Index (NDVI) [26], which indicates high chlorophyll content. In practice, the rather low threshold selected (NDVI > −0.3) excludes more than just vegetation pixels: all surfaces with any non-negligible reflectance in the IR will be masked;
- Very dark areas are thoroughly removed: they mainly consist of water pixels in the shadow of riparian vegetation; as these pixels are difficult to characterize spectrally (light has traveled through both leaves and water), the criterion used is simply the mean of the four bands;
- A filter is designed to remove whitewater/white wakes in riffle areas: as these pixels appear in light gray in the visible bands (almost hueless in RGB) but with substantial absorption in the IR (typical digital counts are [0.2 0.6 0.6 0.6]), they are removed on the basis of their low saturation and high brightness in the RGB space along with a threshold in the NIR (). Note that they have nothing to do with specular reflections: the surface of water appears white there for any viewing angle, because of the scattering from the bubbles/air pockets, not from surface reflection;
- A mask for man-made features crossing the river, such as bridges or power lines as well as their casted shadows, is built manually (some of these pixels are already masked by the previous filters, but not all).
4.4. Hue–Depth Visual Correlation on
4.5. Mixture Models on and Higher Dimension, and Depth Predictor
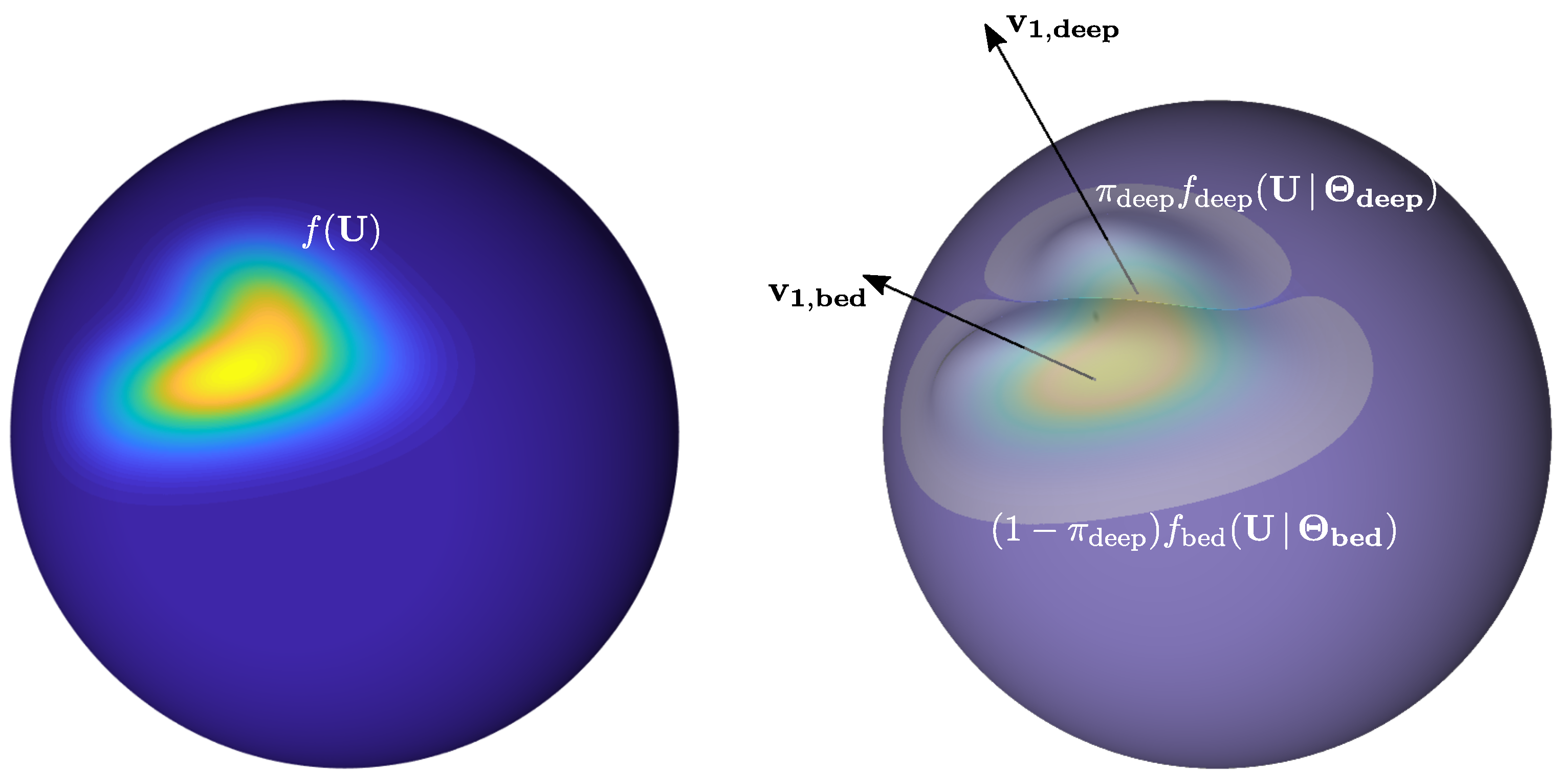
- We assume that the probability density function of multispectral hue in river pixels can be modeled by a two-component mixture density: the first component will represent the statistical distribution of substrate hue, while the second component will represent the statistical distribution of ‘deep water’ hue;
- We will estimate the parameters of the two components so that the membership probability to ‘deep’ component correlates with depth: the probability that pixel i with hue comes from the ‘deep’ component will be the predictor for depth at pixel i.
4.6. Modified EM Algorithm for Depth Estimation
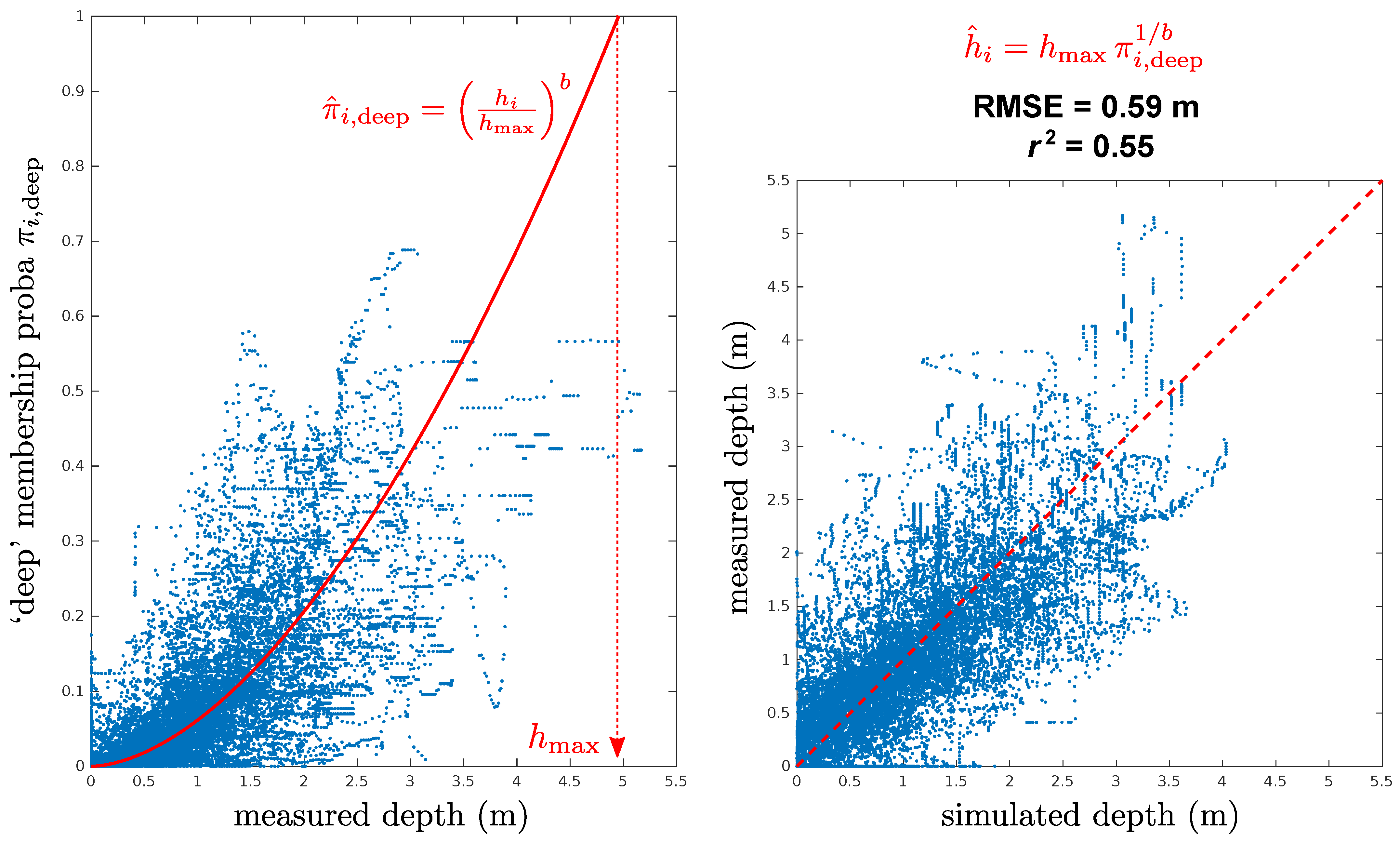
- E-step (Expectation): given current parameter estimates of the mixture at iteration , compute the updated probability that pixel i with multispectral hue comes from a deep component:
- R-step (Regression): regress deep membership probability as a power law function of measured depth so that
- M-step (Maximization): independently maximize the log-likelihood for each componentFinally, we update the prior membership probability (weight of the deep component in the mixture), which is the mathematical expectation of individual (posterior) membership probabilities:
5. Results
5.1. Error Statistics
5.2. Focus on Some Cross-Sections
6. Discussion
6.1. Sources of Error
6.1.1. Radiometric Inhomogeneity
6.1.2. Age and Planar Precision of In Situ Data
6.1.3. Water Surface Elevation
- The first estimate was simply given by the lowest valid elevation at each cross-section in the LiDAR DEM of the floodplain (which also covers the channel through interpolation between the banks). Indeed, the LiDAR survey was conducted during the 2012 low flow period, in hydraulic conditions that we assumed roughly similar to those of the 2016 images;
- The second estimate is the elevation that yields the same width as the one observed in the 2016 images (as defined by the NDWI mask), for each surveyed profile. We then interpolate linearly between the surveyed cross-sections.
6.2. Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. General Expression of the Rotation Matrix Needed for Computing the Multispectral Hue in Any Dimension
Appendix B. Computational Example of the Mapping from to with Four Bands
- We first remove the mean of all bands to each band in order to obtain the vector , and then we normalize it:
- The latter vector is already on a two-sphere, but this sphere is embedded in a three-dimensional subspace of whose axes do not coincide with a triplet of axes of the initial basis (this three-dimensional subspace is orthogonal to the unit ‘white’ vector ). In order to drop one Cartesian coordinate (e.g., the last one), we rotate to the ’North Pole’ of , with the 4D rotation matrix such that:Performing this final rotation and discarding the last, the zero coordinate yields:
- Here we express in Cartesian coordinates of , but we can check that it is indeed in :
Appendix C. Overview of the Fisher–Bingham–Kent (FBK) Distribution
- Degrees of freedom corresponding to the minimum number of rotations (aside from degenerated cases) allowing the change-of-basis from the canonical basis of to the orthonormal basis defined by the ; there are as many such rotations as independent rotation planes in , that is, the number of combinations of two orthogonal directions chosen from among p:
- p degrees of freedom corresponding to the concentration parameter and the asymetry parameters , ,
- 1 degree of freedom removed due to the condition on the
| n Number of Bands | Euclidean Space | Hypersphere | Remark | ||
|---|---|---|---|---|---|
| 3 | 2 | (circle) | 2 | Von Mises distribution | |
| 4 | 3 | (sphere) | 5 | classical Fisher–Bingham “FB5” | |
| 5 | 4 | 9 | |||
| 10 | 9 | 44 | |||
| 50 | 49 | 1224 | |||
| 100 | 99 | 4949 |
References
- Wyrick, J.; Pasternack, G. Geospatial organization of fluvial landforms in a gravel–cobble river: Beyond the riffle–pool couplet. Geomorphology 2014, 213, 48–65. [Google Scholar] [CrossRef] [Green Version]
- Mahdade, M.; Le Moine, N.; Moussa, R.; Navratil, O.; Ribstein, P. Automatic identification of alternating morphological units in river channels using wavelet analysis and ridge extraction. Hydrol. Earth Syst. Sci. 2020, 24, 3513–3537. [Google Scholar] [CrossRef]
- Kinzel, P.J.; Wright, C.W.; Nelson, J.M.; Burman, A.R. Evaluation of an Experimental LiDAR for Surveying a Shallow, Braided, Sand-Bedded River. J. Hydraul. Eng. 2007, 133, 838–842. [Google Scholar] [CrossRef] [Green Version]
- Hilldale, R.C.; Raff, D. Assessing the ability of airborne LiDAR to map river bathymetry. Earth Surf. Process. Landforms 2008, 33, 773–783. [Google Scholar] [CrossRef]
- Nakao, L.; Krueger, C.; Bleninger, T. Benchmarking for using an acoustic Doppler current profiler for bathymetric survey. Environ. Monit. Assess. 2021, 193, 356. [Google Scholar] [CrossRef] [PubMed]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef] [PubMed]
- Marcus, W.A.; Fonstad, M.A. Optical remote mapping of rivers at sub-meter resolutions and watershed extents. Earth Surf. Process. Landforms 2008, 33, 4–24. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Roberts, D.A.; Lawrence, R.L. Spectrally based remote sensing of river bathymetry. Earth Surf. Process. Landforms 2009, 34, 1039–1059. [Google Scholar] [CrossRef]
- Campbell, J.B. Introduction to Remote Sensing, 2nd ed.; The Guilford Press: New York, NY, USA, 1996. [Google Scholar]
- Philpot, W.D. Bathymetric mapping with passive multispectral imagery. Appl. Opt. 1989, 28, 1569–1578. [Google Scholar] [CrossRef]
- Shah, A.; Deshmukh, B.; Sinha, L. A review of approaches for water depth estimation with multispectral data. World Water Policy 2020, 6, 152–167. [Google Scholar] [CrossRef]
- König, M.; Oppelt, N. A linear model to derive melt pond depth from hyperspectral data. Cryosph. Discuss 2019, 2019, 1–17. [Google Scholar]
- König, M.; Birnbaum, G.; Oppelt, N. Mapping the Bathymetry of Melt Ponds on Arctic Sea Ice Using Hyperspectral Imagery. Remote Sens. 2020, 12, 2623. [Google Scholar] [CrossRef]
- Doxani, G.; Papadopoulou, M.; Lafazani, P.; Pikridas, C.; Tsakiri-Strati, M. Shallow-water bathymetry over variable bottom types using multispectral Worldview-2 image. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 159–164. [Google Scholar] [CrossRef] [Green Version]
- Niroumand-Jadidi, M.; Vitti, A.; Lyzenga, D.R. Multiple Optimal Depth Predictors Analysis (MODPA) for river bathymetry: Findings from spectroradiometry, simulations, and satellite imagery. Remote Sens. Environ. 2018, 218, 132–147. [Google Scholar] [CrossRef]
- Montoliu, R.; Pla, F.; Klaren, A.C. Illumination Intensity, Object Geometry and Highlights Invariance in Multispectral Imaging. In Proceedings of the Second Iberian Conference on Pattern Recognition and Image Analysis—Volume Part I; IbPRIA’05. Springer: Berlin/Heidelberg, Germany, 2005; pp. 36–43. [Google Scholar] [CrossRef] [Green Version]
- Kay, S.; Hedley, J.D.; Lavender, S. Sun Glint Correction of High and Low Spatial Resolution Images of Aquatic Scenes: A Review of Methods for Visible and Near-Infrared Wavelengths. Remote Sens. 2009, 1, 697–730. [Google Scholar] [CrossRef] [Green Version]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data via the EM Algorithm. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 1–38. [Google Scholar]
- Jantzi, H.; Carozza, J.M.; Probst, J.L. Les formes d’érosion en lit mineur rocheux: Typologie, distribution spatiale et implications sur la dynamique du lit. Exemple à partir des seuils rocheux molassiques de la moyenne Garonne toulousaine (Sud-Ouest, France). Géomorphologie 2020, 26, 79–96. [Google Scholar] [CrossRef]
- Garambois, P.A.; Biancamaria, S.; Monnier, J.; Roux, H.; Dartus, D. Variationnal data assimilation of AirSWOT and SWOT data into the 2D shallow water model Dassflow, method and test case on the Garonne river (France). In Proceedings of the 20 Years of Progress in Radar Altimetry, Venice, Italy, 24–29 September 2012. [Google Scholar]
- Oubanas, H.; Gejadze, I.; Malaterre, P.O.; Mercier, F. River discharge estimation from synthetic SWOT-type observations using variational data assimilation and the full Saint-Venant hydraulic model. J. Hydrol. 2018, 559, 638–647. [Google Scholar] [CrossRef]
- Goutal, N.; Goeury, C.; Ata, R.; Ricci, S.; Mocayd, N.E.; Rochoux, M.; Oubanas, H.; Gejadze, I.; Malaterre, P.O. Uncertainty Quantification for River Flow Simulation Applied to a Real Test Case: The Garonne Valley. In Advances in Hydroinformatics; Gourbesville, P., Cunge, J., Caignaert, G., Eds.; Springer: Singapore, 2018; pp. 169–187. [Google Scholar]
- Legleiter, C.; Overstreet, B. Hyperspectral image data and field measurements used for bathymetric mapping of the Snake River in Grand Teton National Park, WY. U.S. Geological Survey Data Release, 2018 (accessed 2021-11-02). [CrossRef]
- Institut Géographique National. BD ORTHO® Version 2.0/ORTHO HR® Version 1.0: Descriptif de Contenu, May 2013, Updated July 2018. Available online: https://geoservices.ign.fr/ressources_documentaires/Espace_documentaire/ORTHO_IMAGES/BDORTHO_ORTHOHR/DC_BDORTHO_2-0_ORTHOHR_1-0.pdf (accessed on 14 December 2020).
- Chandelier, L.; Martinoty, G. Radiometric aerial triangulation for the equalization of digital aerial images and orthoimages. Photogramm. Eng. Remote Sens 2009, 75, 193–200. [Google Scholar] [CrossRef]
- Kriegler, F.; Malila, W.; Nalepka, R.; Richardson, W. Preprocessing transformations and their effects on multispectral recognition. Remote Sens. Environ. 1969, 6, 97. [Google Scholar]
- Kent, J.T. The Fisher-Bingham Distribution on the Sphere. J. R. Stat. Soc. Ser. B Methodol. 1982, 44, 71–80. [Google Scholar] [CrossRef]
- Kume, A.; Wood, A.T.A. Saddlepoint Approximations for the Bingham and Fisher-Bingham Normalising Constants. Biometrika 2005, 92, 465–476. [Google Scholar] [CrossRef] [Green Version]
- Kume, A.; Preston, S.P.; Wood, A.T.A. Saddlepoint approximations for the normalizing constant of Fisher-Bingham distributions on products of spheres and Stiefel manifolds. Biometrika 2013, 100, 971–984. [Google Scholar] [CrossRef]
- Amaral, G.J.A.; Dryden, I.L.; Wood, A.T.A. Pivotal Bootstrap Methods for k-Sample Problems in Directional Statistics and Shape Analysis. J. Am. Stat. Assoc. 2007, 102, 695–707. [Google Scholar] [CrossRef]











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le Moine, N.; Mahdade, M. A Preliminary Assessment of a Newly-Defined Multispectral Hue Space for Retrieving River Depth with Optical Imagery and In Situ Calibration Data. Remote Sens. 2021, 13, 4435. https://doi.org/10.3390/rs13214435
Le Moine N, Mahdade M. A Preliminary Assessment of a Newly-Defined Multispectral Hue Space for Retrieving River Depth with Optical Imagery and In Situ Calibration Data. Remote Sensing. 2021; 13(21):4435. https://doi.org/10.3390/rs13214435
Chicago/Turabian StyleLe Moine, Nicolas, and Mounir Mahdade. 2021. "A Preliminary Assessment of a Newly-Defined Multispectral Hue Space for Retrieving River Depth with Optical Imagery and In Situ Calibration Data" Remote Sensing 13, no. 21: 4435. https://doi.org/10.3390/rs13214435
APA StyleLe Moine, N., & Mahdade, M. (2021). A Preliminary Assessment of a Newly-Defined Multispectral Hue Space for Retrieving River Depth with Optical Imagery and In Situ Calibration Data. Remote Sensing, 13(21), 4435. https://doi.org/10.3390/rs13214435







