Abstract
During recent decades East Africa (EA) and Southern Africa (SA) have experienced an intensification of hydrological hazards, such as floods and droughts, which have dramatically affected the population, making these areas two of the regions of the African continent most vulnerable to these hazards. Thus, precipitation monitoring and the evaluation of its variability have become fundamentally important actions through the analysis of long-term data records. In particular, satellite-based precipitation products are often used because they counterbalance the sparsity of the rain gauge networks which often characterize these areas. The aim of this work is to compare and contrast the capabilities of three daily satellite-based products in EA and SA from 1983 to 2017. The selected products are two daily rainfall datasets based on high-resolution thermal infrared observations, TAMSAT version 3 and CHIRPS, and a relatively new global product, MSWEP version 2.2, which merges satellite-based, rain gauge and re-analysis precipitation data. The datasets have been directly intercompared, avoiding the traditional rain gauge validation. This is done by means of pairwise comparison statistics at 0.25° spatial resolution and daily time scale to assess rain–detection and quantitative estimate capabilities. Monthly climatology and spatial distribution of seasonality are analyzed as well. The time evolution of the statistical indexes has been evaluated in order to analyze the stability of the rain detection and estimation performances. Considerable agreement among the precipitation products emerged from the analysis, in spite of the differences occurring in specific situations over complex terrain, such as mountainous and coastal regions and deserts. Moreover, the temporal evolution of the statistical indices has demonstrated that the agreement between the products improved over time, with more stable capabilities in identifying precipitating days and estimating daily precipitation starting in the second half of the 1990s.
1. Introduction
The African continent is one of the most vulnerable places in the world; its population is over a billion people, most of whom live in semi–arid regions heavily prone to droughts, while other regions are plagued by floods. It is an economically and politically unstable continent, where most of the people live below the poverty threshold and social inequalities often make life precarious. African ecosystems are already being affected by climate change, and future impacts are expected to be substantial [1]. A reduction in precipitation is likely in Northern Africa and the southwestern parts of South Africa by the end of the 21st century, whereas in regions of complex topography such as the Ethiopian Highlands, downscaled projections indicate likely increases in rainfall and extreme rainfall [1]. Climate change will amplify the existing stress on water availability, affecting agricultural production and food security. This scenario, characterized by a high dependence on agriculture and a low capacity to adapt to climate change, is expected to contribute to the exasperation of social instability [2,3].
In recent years, Africa has witnessed a series of extreme weather events that have affected the population ranging from extreme droughts to severe floods, highlighting the particular proneness of certain regions to such kind of events. In 2015 Southern Africa was hit by a very severe drought caused by the El Niño episode and intensified by climate change [4]. A strong drought episode during 2011 in Somalia caused the death of tens of thousands of people due to malnutrition and more than eleven million people in East Africa have faced severe food shortages [5]. Conversely, extreme rainfall gave rise to flood events in Ethiopia, Somalia, Kenya, and Uganda during the El Niño-related 1997–1998 episode, and widespread flash and river floods hit the region during the short rainy season in 2019.
With this frame of reference, the relevant role played by precipitation estimates and forecasting at different time scales is clear. On the one hand, proper monitoring and short-time forecasting of precipitation are necessary in order to improve alert systems and damage reduction protocols. On the other hand, knowledge of the climatology of precipitation in terms of analysis of the past events, trends of extreme events, and variability in both can enhance awareness of issues connected to water resources and contribute, together with seasonal and decadal forecasting, to the improvement of water resource management, agricultural planning, and food security. Thus, precious information is contained in long-term datasets of accurate precipitation estimates over the past decades. Although the primary and direct sources of precipitation data come from rain gauges, they are often inadequate tools because of their uneven spatial distribution. This is particularly an issue in Africa, where the density of ground stations can be very scarce with an average station density of just one per 26,000 km2, eight times lower than the World Meteorological Organization (WMO) minimum recommended level [6]. This problem is further aggravated by the high spatial variability of precipitation in many regions of Africa, making the data produced by a rain gauge representative only over a few kilometers’ radius around the station [7]. Finally, the reliability of the data and continuity of station operations cannot be guaranteed due to associated maintenance costs [8]. These limitations have increased the importance of complementing the ground–based measurements with precipitation estimates based on satellite observations. Satellite products have the advantage of providing data sets with global spatial coverage and a long temporal extension, in some cases of more than 30 years [9,10,11].
This is the context of the present analysis, of which the main objective is the intercomparison of different satellite precipitation products taking into consideration both the climate and the precipitation seasonality of the regions of interest, and evaluating their ability to detect and quantify precipitation at different temporal scales. The study is focused on two regions of the African continent, East Africa (EA) and Southern Africa (SA), and covers the time period 1983–2017. Three daily 0.25° gridded satellite datasets were used: the Tropical Application of Meteorology using SATellite and ground based observation version 3 (TAMSAT3); the Climate Hazards group Infrared Precipitation with Stations version 2 (CHIRPS); and the Multi–Source Weighted–Ensemble Precipitation version 2.2 (MSWEP). Long-term satellite products such as those selected for this study are often used to monitor precipitation and evaluate its variability, trends, and linkages with other variables and phenomena able to drive precipitation through teleconnections, all information propaedeutic to a correct planning for water resource management. Nevertheless, results often depend on the specific satellite product under consideration, as demonstrated in [12] for a trend analysis over EA using Africa Rainfall Climatology (ARC) version 2, TAMSAT version 2, and CHIRPS. This is the reason behind this intercomparative study among a selection of the most advanced precipitation products exploited in studies focused on Africa. A correct interpretation of precipitation variability and trend results cannot overlook the differences and peculiarities of the satellite products. On the other hand, the availability of different satellite products must be considered as a powerful source of information that allows us to compare different retrieval methodologies, eventually choosing the most appropriate for the analyzed territory and interpreting the plurality of their estimates and application results as an estimate of the uncertainty range. Moreover, the choice of precipitation products based on different approaches (i.e., thermal infrared (TIR) versus merging of multi–source data including TIR, rain gauges, reanalysis, and passive microwave (PMW) estimates) gives also the opportunity to use a product exploiting PMW.
Numerous studies in literature are focused on satellite product validation over Africa. Recently a pan-African validation of precipitation products (among which were MSWEP 2.1 and CHIRPS) for the period 1981–2016 was carried out by Awange et al. [13], while Dezfuli et al. [14] evaluated the Integrated Multi-satellitE Retrievals for GPM (IMERG) v04A and its predecessor the Tropical Rainfall Measuring Mission (TRMM) Multi-satellite Precipitation Analysis (TMPA). The analyses performed by Dinku et al. [8] for CHIRPS, ARC, and TAMSAT version 2 and 3, and by Ayugi et al. [15], who evaluated ARC, CHIRPS, TMPA, and Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks Climate Data Record (PERSIANN–CDR), were specifically focused on East Africa. Again, TAMSAT3 was evaluated in SA [16] and CHIRPS and TAMSAT version 2 over Mozambique [17]. Among the validation studies on Africa, it is worth mentioning the work of Akinsanola et al. [18] over west Africa involving five gridded precipitation data sets, both ground- and satellite-based. Finally, Satgé et al. [19] validated 23 precipitation products over Western Africa, including those selected for this study, for a short period from 2000 to 2003 at daily and monthly scales. This represents the only example in the literature where the performances of the three selected products in their most recent versions have all been evaluated together to date. Thus, the present work intends to extend this product evaluation to a larger area, considering SA and EA, and to a longer time period, considering 35 years of data. This last aspect allows for obtaining more robust results based on a larger amount of data, and gives more significance and meaning to the analysis of the intercomparative statistics as a function of time.
Unlike the cited validation studies of satellite products, in this work the datasets are not compared with ground-based rain gauge data. In this analysis, two reasons justified the exploitation of direct pairwise comparisons among the satellite products. Rain gauge network density, availability, and reliability is not guaranteed in Africa [20]. Station coverage is not uniform, and there are areas completely lacking rain gauges (e.g., Somalia). Even where ground stations were dense, there is a continuous decrease in their number due to maintenance costs. Moreover, other studies have focused on limited validations over sparsely-gauged African watersheds [21]. Moreover, all the evaluated precipitation products contain a contribution from rain gauge data sets according to their own specific methodologies. This fact makes it very difficult to identify which rain gauge data has not already been used in the satellite products being used for reference.
This paper is organized as follows: In Section 2, the precipitation products and adopted methodologies for the analysis are described. Section 3 focuses on the investigated regions and their precipitation climatology. Section 4 presents the results of cluster analysis and seasonality, statistics from product intercomparisons at daily scales, and the temporal evolution of rain detection and estimation capabilities. Discussion and conclusions are proposed in Section 5 and Section 6, respectively.
2. Materials and Methods
2.1. Precipitation Products: TAMSAT3, CHIRPS, and MSWEP
Three state of the art daily precipitation satellite datasets were used for this study, TAMSAT3, CHIRPS, and MSWEP, remapped on a common 0.25° grid using a local area averaging to interpolate data from their higher native resolution to the common one (function “area_hi2lores” from the NCAR–Command Language—NCL software package [22]). The function accounts for fractional contributions of the input high-resolution grid points to the scope of each low-resolution grid point. This is not a strictly conservative remapping, which represents the most suitable interpolation method used for precipitation fields [23]. Nevertheless, it represents a good compromise between a robust interpolation appropriate for most purposes and a quick approach suitable to be applied to large data sets.
The selection of the datasets was driven by the availability of more than 30 years of data, necessary to give more significance to the regional precipitation climatology of the two regions and to the analysis of inter-product stability. Moreover, the previous use of these precipitation products in African precipitation analysis and monitoring and their operational applications in agriculture and famine early warning systems is another key factor, which calls for the necessity to intercompare them and increase the level of confidence of their users. This is particularly true for TAMSAT3, a product developed mainly for monitoring droughts in Africa [24] and enhancing resilience to agricultural drought [25], and for CHIRPS, with its inclusion in the Famine Early Warning System Network initiative (FEWS NET—https://fews.net, accessed on 21 October 2021) [26]. MSWEP, which uses a completely different approach taking advantage of the complementary strengths of gauge-, satellite- (both TIR and microwave), and reanalysis-based data, was also considered in order to evaluate the behavior of the two TIR-based products against a multi-data source product.
2.1.1. TAMSAT3
TAMSAT3 is a precipitation product based on TIR imagery from geostationary sensors onboard the METEOSAT platforms of the first and second generation (MFG and MSG), providing daily estimates from 1983 to the present on the African continent at a 4 km spatial resolution [7,27]. The algorithm is based on a cloud indexing approach, where the Cold Cloud Duration (CCD) is used as a proxy for precipitation, representing the period of time during which the cloud top temperature is lower than a threshold value selected to identify the precipitating cloud systems. The peculiarity of TAMSAT3 is the exploitation of rain gauge data in the calibration phase, which is climatological and local, i.e., varying monthly and spatially, in order to capture the temporal and geographical variations of precipitation without yearly updates. This eliminates the need to refer to a rain gauge dataset acquired in real time (i.e., simultaneous to satellite acquisitions) in favor of a historical rain gauge dataset. This approach is particularly suitable to the African continent, where the density and availability of real time measurements of precipitation from ground stations varies from area to area, with consequent negative effects on satellite precipitation estimates.
TAMSAT3 provides daily time series of precipitation since 1983, although there are several days with missing data especially in the 1980s and 1990s (the worst years are 1985, 1986, and 1989 with 73, 80, and 71 missing days, respectively). One day is considered missing when it has no TIR data for more than six consecutive hours, while a group of five days is considered missing if more than one day is missing [7]. In the present study, data gaps have been filled in with daily climatological averages obtained from the time series of the TAMSAT3 dataset.
At the time this analysis was being carried out, the available TAMSAT release was the previously described version 3.0, which was replaced by a new version 3.1 now downloadable from TAMSAT archive during the writing of this work. In this new version, changes include an increased number of rain gauges used in the CCD calibration, the extension of minimum threshold temperature to –65°C (as opposed to –60°C), and filling in all missing days so that the rainfall record is temporally complete (no details are provided with respect to the adopted methodology). However, as stated on the TAMSAT v3.1 web page (http://www.tamsat.org.uk/data, accessed on 21 October 2021), there have been no significant algorithmic changes between v3.0 and v3.1; thus, the estimates are very similar and no major differences are expected from v3.0 to v3.1.
2.1.2. CHIRPS
CHIRPS is a precipitation dataset with quasi-global coverage (50S–50N, only over land pixels) and a high space resolution (0.05°), available on a daily, five day, and monthly time scale from 1981 to present [28]. It is designed especially for studying extreme precipitation events, from droughts to floods and climatic trends. Similar to TAMSAT3, CHIRPS is based on TIR observations from the geostationary satellite constellation and uses linear relationships between CCD and precipitation. However, substantial differences among the two products exist in their exploitation of rain gauge data. In this case the calibration of the CCD vs. precipitation relationships is carried out by means of the TMPA 3B42 product [29]. Furthermore, unlike TAMSAT, the temperature threshold chosen to determine the CCDs is fixed and equal to 235 K. The TIR-based estimates are converted into percentage anomalies and subsequently multiplied by the Climate Hazards group Precipitation climatology (CHPClim) dataset to obtain the CHIRP estimates. In this way, the CCD data are used to estimate variations around the CHPclim mean, reducing CHIRP’s systematic bias. In case of a lack of satellite observations, CHIRP estimates are replaced by percentage anomalies calculated using reanalysis data from the Coupled Forecast System (CFS) version 2. The last step in the algorithm involves the merging of CHIRP with precipitation data from ground stations on the basis of a modified inverse distance weighting algorithm. Various rain gauge datasets are used from both private and publicly available archives in order to guarantee the best possible rain gauge spatial coverage.
2.1.3. MSWEP
MSWEP is a relatively new precipitation product, with version 2.2 released in 2018. It is a three-hourly gridded product with global coverage at a 0.1° spatial resolution, available from 1979 to 2017 [30,31]. Since its first release, MSWEP has been exploited in a vast range of applications, among which are modeling of evaporation and soil moisture, evaluation of climatic controls on vegetation, water resource reanalysis, and regional studies of the diurnal variability of precipitation dynamics [31]. Moreover, it provides a consistent precipitation record from 1979 until the near present, enabling trend and drought assessments. MSWEP is the first fully global high–resolution precipitation dataset derived by optimally merging gauge, satellite, and reanalysis estimates through a multi-source weighting procedure. Actually, in addition to TIR-based estimates and precipitation from ground stations, MSWEP integrates PMW estimates from the Climate Prediction Center morphing technique (CMORPH) [32], Global Satellite Mapping of Precipitation_Moving Vector with Kalman (GSMaP_MVK) [33], and TMPA 3B42RT [29] with reanalysis data such as the European Center for Medium-Range Weather Forecast—Interim reanalysis (ERA-Interim) [34] and Japanese 55-year Reanalysis (JRA–55) [35].
2.2. Intercomparison Statistics
As mentioned in the Introduction, direct comparisons of each precipitation product with the others were carried out. Therefore, the present analysis represents more of a comparative analysis among the three products aimed at detecting similarities and differences, rather than an “absolute” validation with respect to an independent reference dataset assumed as “truth”.
Dichotomous statistics was exploited in order to evaluate the precipitation detection capacity. The statistical parameters used to discriminate precipitating and non-precipitating days are summarized in Table 1 according to Ebert’s definitions [36]. A precipitation threshold of 1 mm day–1 was selected to identify precipitating days, as recommended by the Expert Team on Sector-Specific Climate Indices (ET–SCI, https://climpact–sci.org, accessed on 21 October 2021).

Table 1.
Parameters for the dichotomous statistics.
In Table 1, hits (H) is the number of precipitating events (i.e., 0.25° cells with daily precipitation ≥ 1 mm day–1) observed by both products, misses (M) represents the number of precipitating events observed by the product used as a basis for comparison (reference product) but not by the other product (compared product), false alarms (FA) is the number of precipitating events identified by the compared product but not by the reference product, and the correct negatives (CN) is the number of non-precipitating days according to both products. The dichotomous statistics was applied both considering the whole daily precipitation time series from 1983 to 2017 for each 0.25° grid cell, and year by year considering the yearly statistical parameters averaged over each study region. This twofold approach allowed for simultaneously investigating spatial patterns and the temporal evolution (temporal stability) of the products’ capability to discriminate precipitating and non-precipitating events.
For the quantitative evaluation, the exploited statistical parameters were the linear correlation coefficient (CC) measuring the strength of the linear relationship between the two compared products, the mean error (ME) evaluating the tendency toward over- or underestimation of one product compared to the other, and the mean absolute error (MAE) quantifying the average difference between the precipitation estimates of the two compared products. The expressions of these statistical parameters are presented in Table 2, where SPE1 and SPE2 are the satellite precipitation estimates of the two compared products, represent the mean values of the satellite data, and N is the number of considered data pairs. CC, ME, and MAE have been computed at the daily and monthly (only ME and MAE) time scales and year by year, considering the yearly statistical parameters averaged over each study region as for the dichotomous statistics.

Table 2.
Statistical parameters used for the quantitative intercomparisons.
2.3. Cluster Analysis for Identification of Precipitation Seasonality Zones
The marked spatial variability of precipitation seasonality in EA and SA suggested a partition of these regions into sub-areas characterized by a predominant precipitation annual cycle evolution. The adopted approach takes advantage of the procedure already used by Cattani et al. [37] for the EA region. According to that approach, the non-hierarchical k–means clustering algorithm of Hartigan and Wong [38] was applied to the monthly normals of the Global Precipitation Climatology Center data set (GPCC_Clim version 2018) at a 0.25° spatial resolution [39], transforming monthly data into empirical cumulative distribution functions at each grid cell [40]. The use of rain gauge-based climatology to accomplish this task is apparently in contrast with the decision to investigate the intercomparisons among the satellite precipitation products without the direct involvement of rain gauge data as a reference, considering the motivations discussed at the end of the Introduction. However, the availability of a trusted approach already applied to EA and the necessity to have a subdivision of the two regions independent of a specific precipitation product in order to simplify the satellite product intercomparison suggested using the GPCC_Clim data set for the initial partitioning phase. In this way, a single subdivision for each region was determined through the GPCC_Clim data; however, the quantitative evaluation of the monthly climatology for each sub-area was carried out by mutually contrasting only the satellite products and excluding the GPCC data.
The non-hierarchical k–means clustering algorithm allows subdividing of a set of objects, in this case the annual precipitation cycle of each 0.25° grid cell, into k groups based on their characteristics, in this case precipitation seasonality. The goal is to minimize the total intra–cluster variance. The result of the algorithm depends on the number of clusters initially chosen; for this reason, the algorithm is normally executed several times by varying the k value. The analysis of the sum of the squared distances between each member of a cluster and the cluster centroid is the common method to select the appropriate value for k, ending the iterative procedure when increasing k values does not induce any significant decrease in the sum of the squared distances. Thus, a certain degree of subjectivity is involved in the final decision of the cluster number [41], and it is necessary to find a balance between obtaining good homogeneity between the elements belonging to the same cluster without an excessive partition of the regions and consequent reduction in the number of elements in each cluster.
Cluster analysis is instrumental in this work to summarizing the results of the quantitative intercomparisons at the monthly scale and providing statistical scores for sub-areas which are homogeneous in terms of the seasonal cycle (i.e., clusters). The specific choices for EA and SA clustering will be discussed in Section 4.1 and Section 4.2.
3. Regions of Study and Precipitation Climatology
3.1. East Africa
The analyzed region extends from 5S to 20N and from 28E to 52E including Ethiopia, Djibouti, Eritrea, part of Sudan, South Sudan, Somalia, Kenya, Uganda, northern Tanzania, Rwanda, and Burundi (Figure 1). It is a geographically very complex region located on an area of friction between tectonic plates, and therefore mainly characterized by plateaus and mountain chains. The most important geological feature of the region is the presence of the Great Rift Valley extending for 5500 km from the Red Sea’s junction with the Gulf of Aden, then southwest toward Kenya, and finally south to Mozambique. The oldest and best–defined rift, usually referred to as the Ethiopian Rift, is located in the Afar region covering part of Ethiopia, Eritrea, and Djibouti. Then it divides into two branches crossing the equator, the Eastern and Western Rifts, enclosing the large plateau where Lake Victoria lies. The Great Rift Valley is bordered by escarpments with altitudes varying from a few hundred to a few thousand meters, and is surrounded by highlands, the western and eastern Ethiopian Highlands and the East Africa Highlands. The complex geological processes that led to the formation of the Rift Valley are also responsible for the formation of several large lakes, including Lake Victoria, the largest lake in Africa and the second largest in the world. In this region we find the two highest mountains on the entire continent, Mount Kilimanjaro (5895 m) and Mount Kenya (5199 m). Another important geographical feature of EA is the presence of desert areas: the Chalbi desert north-east of Kenya, the Somali desert, the Dancali desert between Eritrea and northeastern Ethiopia, and the Sudan desert.
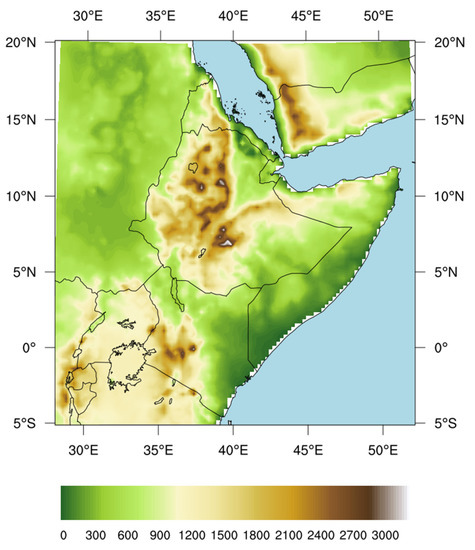
Figure 1.
EA region and elevation map (m).
As a result of the simultaneous presence of various regional factors, i.e., complex topography, maritime influence, and lakes, with large-scale tropical controls, a strong spatial variability characterizes EA’s precipitation intensity and seasonality [42]. Precipitation varies from less than 50 to almost 2000 mm year–1, as obtained by averaging the time series of the three products. The lowest values are found in the region of the Horn of Africa and Sudan, two mainly arid regions, whereas the highest values are located in the mountainous area of western Ethiopia, the area of the Lake Victoria, and the mountain chain of Rwenzori at the border between Uganda and the Democratic Republic of Congo. Likewise, the precipitation seasonality shows a high spatial variability as presented in Figure 2 for the monthly climatology from the average of the three precipitation products. A wide area including Somalia, Eritrea, northeastern Kenya and eastern Ethiopia is characterized by two precipitating seasons, the first one from March to May (the so-called long rain season) and the second one concentrated between October and December (the short rain season). The rain seasons are separated by dry periods (boreal summer and winter) during which the monthly precipitation is lower than 20 mm month–1. In the northern part of Sudan (north of 15N), mainly covered by desert, precipitation is always lower than 20 mm month–1, while central Sudan and South Sudan have a single precipitating season during the boreal summer (June–September) with more intense precipitation up to a maximum of 140 mm month–1. Precipitation is mainly concentrated in a single season in the western mountainous area of Ethiopia, the Ethiopian Highlands, lasting from June to September with precipitation peaks observed in July and exceeding 200 mm month–1. The south-western part of EA (Uganda and Tanzania) has a bimodal precipitation seasonality, from March to May and from October to December, with the more abundant precipitation concentrated in the area surrounding Lake Victoria, where unlike the rest of EA significant precipitation occurs also during January and February.
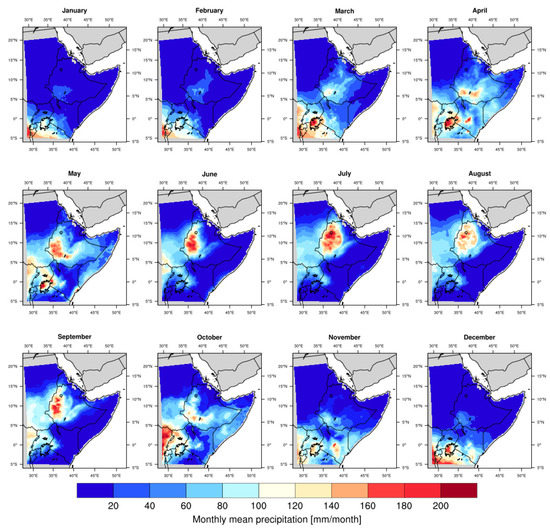
Figure 2.
EA monthly mean precipitation relative to the period 1983–2017. Monthly climatology has been obtained from the ensemble mean of the three precipitation products.
Historically, the explanation of the EA seasonal cycle with rain seasons migrating from south to north and again south was related to the analogous south–north shift from the equator of the Inter Tropical Convergence Zone (ITCZ) [43]. The ITCZ is described over Africa as the area around the equator, where the dry northeast harmattan and the moist southwest monsoon converge. Although this interpretation has been cited many times in the literature, a recent work demonstrated that during the equatorial rainy seasons there is a lack of co-location between the low-level convergence associated with the ITCZ and the regions experiencing precipitation [44]. Rather, the mean static energy, saturation mean static energy, vertically integrated moisture from the Indian Ocean, topography, large-scale phenomena, and vertical cells over the Indian Ocean were identified as the main factors affecting EA rainfall seasonality [45,46,47,48].
3.2. Southern Africa
The second investigated African region is Southern Africa (10–35S, 10–51E) including Madagascar, the Republic of South Africa (RSA), Lesotho, eSwatini, Mozambique, Zimbabwe, Botswana, Namibia, Angola, Zambia, and Malawi (Figure 3).
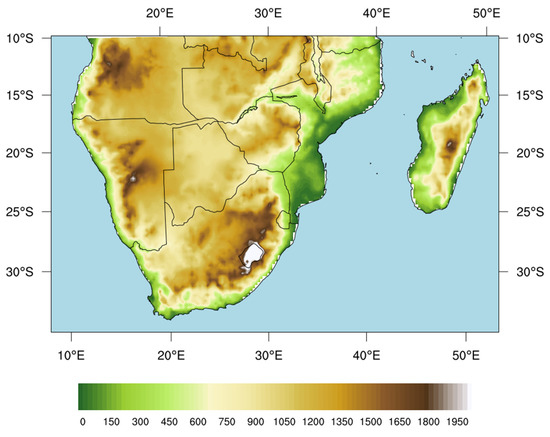
Figure 3.
SA region and elevation map (m).
The Central Plateau covers most of the region. Its altitude is highly variable, from 3000 m in Lesotho and the eastern part of the RSA to 1000 m in Botswana, with the lowest values corresponding to the larger river valleys, and some particularly depressed basins such as that of Kalahari extending into Botswana, Namibia and RSA and encroaching into part of Angola, Zambia and Zimbabwe. The Great Escarpment is the prominent topographical feature of this region and consists of steep slopes from the Central Plateau downward in the direction of the oceans surrounding SA on three sides. The most well–known section of the Great Escarpment and one of the most remarkable mountain range of the region is the Drakensberg, which delimits the edge of the plateau in the south-east of RSA with peaks up to 3500 m of altitude. In the eastern part (i.e., Zambia and Mozambique) the plateau runs along the Rift Valley region (Section 3.1) via a sharp border highlighted by the Lake Malawi. In western SA the Central Plateau runs north to south, bordered by the Skeleton Coast to the northwest, with the Namib Desert and its coastal plains to the southwest. Finally, Madagascar completes the analyzed region, the largest island in the Indian Ocean, separated from the African continent by the Mozambique Channel with a width of 400 km. It is mainly mountainous, crossed latitudinally by a mountain ridge with an average altitude between 1200 and 1500 m and peaks exceeding 2600 m.
Precipitation in this area is characterized by great spatial and temporal variability, mainly attributable to the interaction of multiple factors among which are the geographical location, variations in the regional topography, sea surface temperature, and southward tapering of the subcontinent. Because of the very steep topography of the eastern part, the subtropical easterly flow, and the contrast between the warm Indian Ocean and the cold Atlantic Ocean, SA is characterized by a strong longitudinal precipitation gradient, with more intense precipitation on the eastern side and semi-arid conditions on the western side [16]. The mean annual precipitation obtained by averaging the time series of the three products ranges from less than 200 mm year–1 in the Namib Desert to more than 1000 mm year–1 in northern Mozambique and Angola. In general, northern SA, including Angola, Zambia, Malawi and northern Mozambique, receives more precipitation due to its location within the tropical belt, in an area characterized by the presence of plateaus and escarpments that encourage the development of orographic precipitation. Furthermore, a recent study has attributed 31% of total precipitation in Angola and Zambia to the formation of tropical lows, i.e., synoptic-scale cyclonic vortices that propagate westward across SA during the austral summer with the peculiar tendency to become semi-stationary over Angola, where their aggregation creates a local pressure minimum called the Angola Low [49]. The RSA is characterized by a strong longitudinal precipitation gradient from less than 200 mm year–1 on the west coast up to 1000 mm year–1 on the eastern one, following the profile of the Drakensberg Mountain range. Marked N–S differences are present in Mozambique. Despite its proximity to the Indian Ocean and the prevalence of easterly winds, the high mountains of Madagascar partially prevent the flow of moist air masses toward Mozambique [50]. At the same time, the Madagascan mountains represent a key factor for the spatial distribution of precipitation over the island, leading to orographically enhanced precipitation along the east coast. The easterly trade winds prevail throughout the year such that the eastern part of the island is rainy in all months with the exception of only August and September [51].
The precipitation gradient previously described, a positive gradient from south-west to north-east, is also apparent in Figure 4, where the monthly precipitation climatology is presented using the ensemble mean of the satellite products. Rainy months are characterized by precipitation minima of less than 30 mm month–1 over the Namib desert and peaks up to 300 mm month–1 in the north of Mozambique. Equally evident are the precipitation peaks in January and February in northern Madagascar; this region is often impacted by tropical cyclones responsible for much of the summer precipitation over the island, whereas the south-western part is substantially dryer [51]. Unlike EA, the precipitation seasonality in SA is much more spatially homogeneous, with most of the precipitation concentrated during the austral summer from October to March (Figure 4). A long dry season with rainfall lower than 30 mm month–1 extending from May to September characterizes the whole territory, with the exception of the Cape Town area and the east coast of Madagascar. The Cape Town region receives on average about 100 mm month–1 from May to August, when the track of the temperate weather systems (i.e., extratropical cyclones, cold fronts and cutoff lows) shifts northward. Moreover, the mountains of the Cape Fold Belt surrounding the area affect the precipitation spatial distribution, favoring more abundant rainfall in the coastal zones than inland [52]. Regarding Madagascar, the island’s topography has a role intercepting the easterly moist air masses caused by the anticyclonic tropical belt [53]. However, the precipitation amount on the eastern coast is scarce when compared with that of the other months and does not exceed 100 mm month–1. April and October can be considered transitional months from the rainy to the dry season and vice versa, respectively. In April, most of SA receives rainfall below 30 mm month–1, while in the northern region of Angola and Mozambique and central mountainous region of Madagascar precipitation intensity is still higher than 100 mm month–1. A similar precipitation spatial distribution is also found in October.
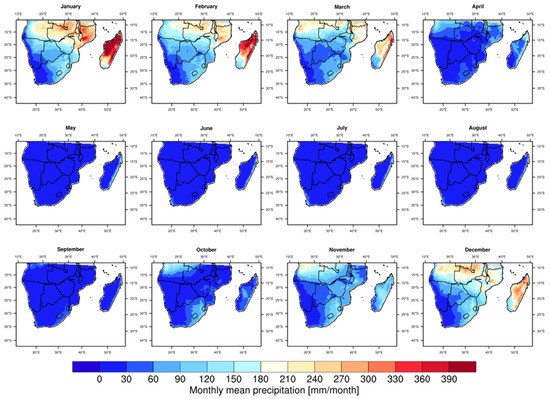
Figure 4.
Same as in Figure 2, but for SA.
4. Results
4.1. Cluster Analysis and Precipitation Seasonality
The k–mean clustering method (Section 2.3) was used to identify homogenous sub–areas with respect to the annual precipitation cycle in the EA and SA regions.
Eight clusters have been adopted for the EA region, as proposed in [37], but without the further subdivision of cluster 1 (see Figure 3a in [37]). Cattani et al. [37] have already demonstrated that the different zones (red zones in Figure 5a) which compose cluster 1 do not imply a variation of the precipitation seasonality but only a variation of precipitation amount. Figure 5a shows the spatial distribution of the clusters obtained from GPCC_Clim, while the corresponding precipitation annual cycles are presented in Figure 5b. As clearly evident in Figure 5 and previously described in Section 3.1, EA is characterized by a spatially highly variable monthly precipitation climatology. Clusters in eastern EA show bimodal annual cycles, with two precipitating seasons well separated by a dry period. This is the case in cluster 1, mainly covering Kenya and other areas around the west coast of Lake Victoria, Rwanda, the tip of the Horn of Africa, and a small coastal portion of Somalia, which is characterized by two precipitating seasons, i.e., with March–April–May (MAM) more intense and lower precipitation values in October–November–December (OND), separated by a dry season in June–July–August–September (JJAS) with precipitation lower than 40 mm month–1. Cluster 3, including central Somalia together with a small area north of Lake Victoria, has an annual cycle similar to the previous one, with lower peak values in MAM and a second rainy season with a peak in October. Cluster 6, a coastal area located on southern Somalia and Kenya, and cluster 8, which includes northern Tanzania and Burundi, show annual cycles analogous to cluster 1 but with more precipitation during the dry season in JJAS (cluster 6) and higher precipitation during January–February (JF) (cluster 8).
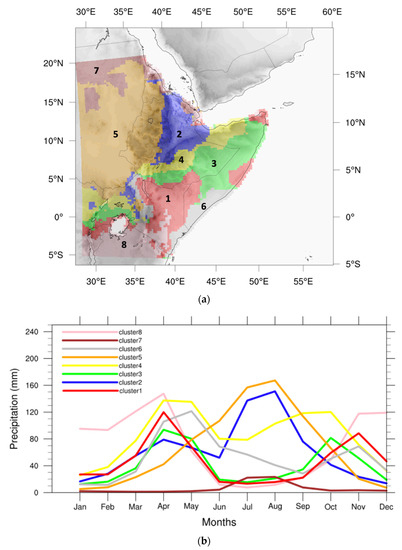
Figure 5.
Map of the EA clusters from GPCC_Clim data (a) and corresponding precipitation annual cycles for each EA cluster (b).
Moving north-west, the dry season during the boreal summer tends to be reduced, with annual cycles characterized by a single precipitating season peaking in July and August, as is the case for clusters 5 (South Sudan and western Ethiopia) and 7 (northern Sudan), this latter with very scarce precipitation not greater than 40 mm month−1. Clusters 2 and 4 represent areas characterized by transitional precipitation annual cycles, where two precipitation peaks develop without a real dry break in MAM and JJAS and in April–May and July–August for cluster 2 and 4, respectively. Cluster 2 encompasses central Ethiopia, the Rift Valley and escarpments of the Ethiopian Highlands, as well as small areas in Uganda and Kenya, whereas cluster 4 encompasses the coast of Somalia on the Gulf of Aden and the eastern range of the Ethiopian Highlands, the central region of Uganda and part of the Democratic Republic of the Congo.
Figure 6 shows the annual cycles for the different precipitation products averaged over each cluster (Figure 5a), depicting the response of the satellite products to EA partitioning on the basis of precipitation seasonality. For each curve, the shaded areas represent the standard deviation associated with the monthly mean values, highlighting the spatial variability of the monthly precipitation within the indicated cluster.
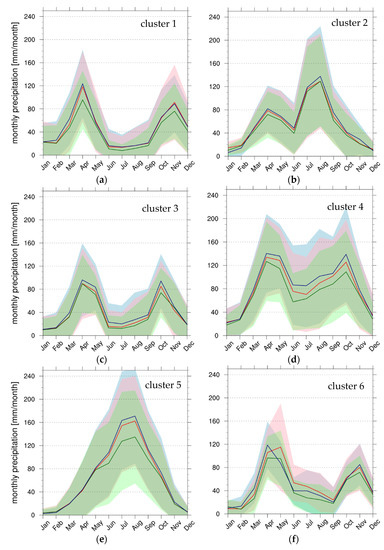
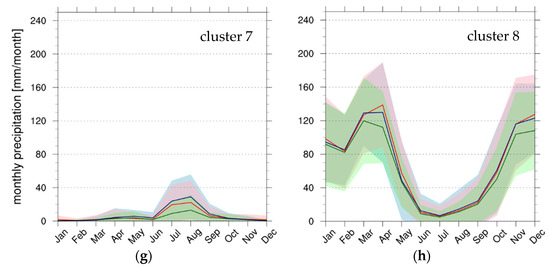
Figure 6.
Mean precipitation annual cycles for each EA cluster, from cluster 1 (a) to cluster 8 (h), and precipitation product: MSWEP (green), CHIRPS (red), and TAMSAT3 (blue). The shaded areas identify the standard deviation (±σ) for each precipitation product, MSWEP (light green), CHIRPS (pink) and TAMSAT3 (light blue).
The verification of the homogeneity of the annual precipitation cycles (homogeneity in terms of precipitation seasonality) within each cluster was carried out for each satellite dataset considering the CCs between the annual precipitation cycle of each pixel of a given cluster and the average annual cycle of the same cluster. For each cluster and dataset, the mean CC value exceeds 0.8 with a p-value ≤ 0.05 (confidence level ≥ 95%).
From a first qualitative analysis of the graphs in Figure 6, it is possible to observe a general tendency of MSWEP to underestimate precipitation compared to the other two datasets, whereas a greater agreement between CHIRPS and TAMSAT3 emerges. The MSWEP underestimation is particularly evident during the precipitation peak months in western EA (cluster 5), but it appears also during the transition between the two rainy seasons, as in clusters 4 and 6. Clusters 2, 4 and 5 are characterized by the greatest intra–cluster variability (i.e., high standard deviation values). The terrain complexity of these areas, with highlands and escarpments, motivates this high variability. To quantify the differences presented in Figure 6, monthly ME and MAE were computed for each cluster, comparing the monthly climatology of the precipitation products pixel by pixel and then spatially averaging monthly ME and MAE on each cluster (Figure 7).
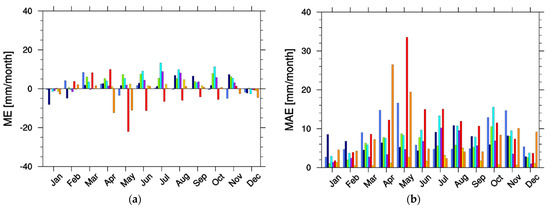
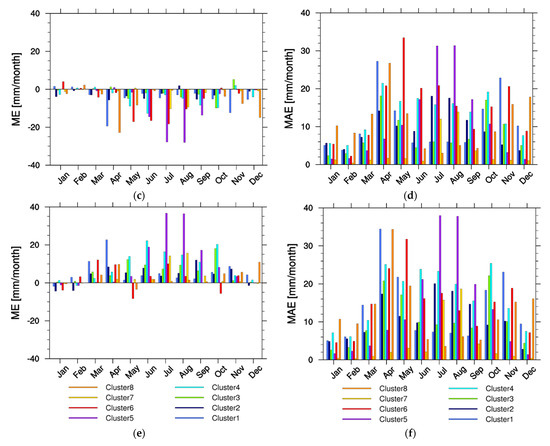
Figure 7.
EA cluster–average monthly ME and MAE values from TAMSAT3 with respect to CHIRPS (a,b), MSWEP with respect to CHIRPS (c,d), and TAMSAT3 with respect to MSWEP (e,f).
The agreement between the TAMSAT3 monthly climatology with CHIRPS is confirmed in Figure 7a,b, with the lowest overestimation of monthly precipitation by TAMSAT3 (ME < 10 mm month–1 except for cluster 4 in July and October) and a more marked underestimation from April to June for clusters 6 and 8. This translates into MAE values generally lower than 10 mm month–1 except for clusters 1, 4, 6 and 8, during the rainy seasons. Looking at the comparisons between MSWEP and CHIRPS (Figure 7c,d) and TAMSAT3 with respect to MSWEP (Figure 7e,f), it is evident how MSWEP systematically underestimates monthly precipitation compared to the other two datasets, with the major MEs found in cluster 5 for the months of July and August. The greatest MAE values come from TAMSAT3 with respect to MSWEP, exceeding 30 mm month–1 in clusters 1 and 8 in April, and cluster 5 in July and August.
The k–mean clustering method was exploited to subdivide the SA territory into homogeneous sub-areas with respect to the annual precipitation cycle. Figure 8a shows the six identified clusters, whereas in Figure 8b the corresponding average annual precipitation cycles from the GPCC_Clim data are presented. Different numbers of clusters were tested in order to obtain the best compromise between the minimization of the intra-cluster variance and excessive fragmentation of the territory. A further increase in the number of clusters out of the six identified resulted only in a further fragmentation of cluster 2, creating two transition zones at the boundary with cluster 3 (i.e., RSA at the boundary with Botswana and Zimbabwe, and northern Angola with the southern Democratic Republic of Congo). Moreover, the corresponding monthly climatology of these transition zones was almost identical to that of cluster 3, with slightly lower quantities in January and February.
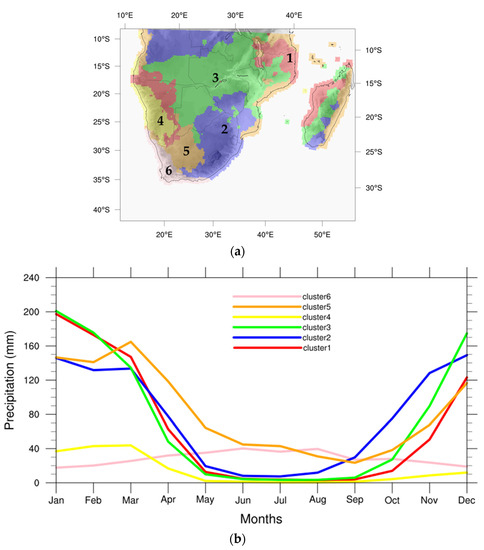
Figure 8.
Same as in Figure 5, but for SA.
SA is characterized by a more homogeneous precipitation seasonality than EA, as shown in Figure 8b, but with variable precipitation amounts. With the exception of cluster 6, which includes the Cape Town region, all clusters show very similar monthly climatology, characterized by a wet season occurring during the austral summer from October to March (ONDJFM) and a dry season coinciding with the austral winter from April to September (AMJJAS). Cluster 1, which includes the pre-desert region in Namibia, northern Mozambique and the northwestern coast of Madagascar, and cluster 3, covering central Madagascar and central SA, are characterized by very similar precipitation annual cycles, with a dry season from May to October with very low precipitation and a rainy season coinciding with the period ONDJFM and culminating during JF. Cluster 3 is slightly more abundant in precipitation than cluster 1 during the early phase of the rainy season in OND. Cluster 2, which includes northern Angola, Eastern RSA at the boundary with Botswana, Zimbabwe, Mozambique, and south-central Madagascar has a shorter dry season from May to August, and is characterized by more abundant rainfall compared to clusters 1 and 3 in the period of September–November. Cluster 5 is characterized by a reduced but still significant amount of precipitation during the austral winter months from May to September, and is mainly located on the east coast of Madagascar, which receives precipitation throughout the year (Figure 4). This cluster also includes the coast of Mozambique and western region of RSA. Cluster 4 occupies the Namib Desert and is therefore characterized by very low rainfall throughout the year, with a precipitating period limited to January, February and March. Finally, cluster 6, covering the coastal region of Cape Town and eastern RSA is the only one with a precipitation annual cycle very different from the rest of SA; precipitation is generally very scarce, with a weak increase from April to September.
The average annual precipitation cycles for each satellite dataset and cluster are shown in Figure 9. The shaded areas represent the corresponding standard deviation values, as in Figure 6. The correlation among the annual cycles belonging to the same cluster has also been explored in this case, with analogous results for the EA cluster analysis. The satellite products responded positively to SA territory clustering, reproducing the annual cycles from GPCC_Clim data in terms of seasonality and precipitation amount. A substantial agreement among the annual cycles of the three precipitation products is evident from Figure 9, except for cluster 5 and 6 characterized by the TAMSAT3 underestimation, particularly marked from January to September in cluster 5 and from April to June in cluster 6. Generally speaking, the variability of the precipitation products’ annual cycles within the clusters is very similar (i.e., σ values are comparable among the products in each cluster, with the exception of cluster 5 in May–September). The significantly high variability seen, for instance, during the austral summer months in cluster 1 and 5 is mainly due to the composite nature of the cluster affecting the precipitation amount even though the seasonality is preserved. As an example, Figure S1 shows the case of cluster 5, with mean annual cycles over the eastern coast of Madagascar (Figure S1a), the coast of Mozambique (Figure S1b), and central RSA (Figure S1b).
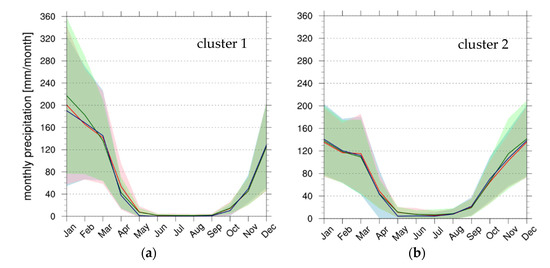
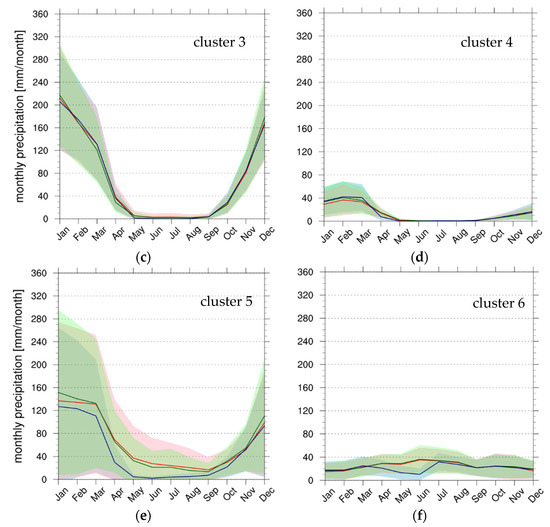
Figure 9.
Same as in Figure 6 but for SA, from cluster 1 (a) to cluster 6 (f).
The agreement among the SA annual cycles for each cluster and the three products has been evaluated through the ME and MAE as previously done for EA (Figure 10). In terms of ME, the highest values (negative) are related to clusters 5 and 6 from April to September, due to TAMSAT3 underestimation of the low intensity precipitation with respect to CHIRPS and MSWEP (Figure 10a,e). The same is not true for the other clusters, where TAMSAT3 exhibits much more limited ME values; thus, this effect does not seem particularly connected to a specific inadequacy of TAMSAT3 for light precipitation estimation, as it is also confirmed by the corresponding MAE values (Figure 10b,d,f). Conversely, substantial agreement is evident between CHIRPS and MSWEP for the same period (Figure 10c,d) and clusters. Considering the precipitating months (ONDJFM, excluding cluster 6), the best ME and MAE values emerge from the TAMSAT3 versus CHIRPS comparison (Figure 10a,b), whereas MSWEP overestimates monthly precipitation with respect to both TAMSAT3 and CHIRPS.
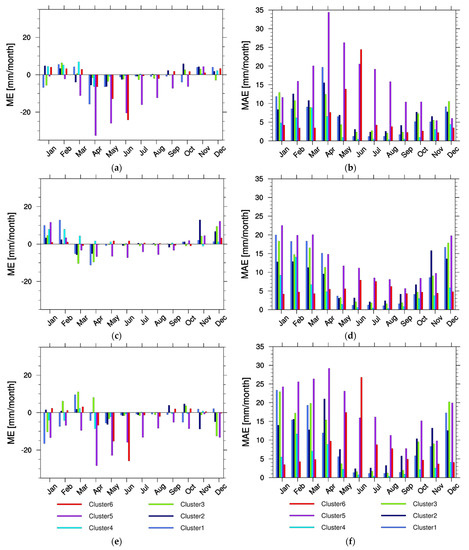
Figure 10.
Same as in Figure 7 but for SA: TAMSAT3 with respect to CHIRPS (a,b), MSWEP with respect to CHIRPS (c,d), and TAMSAT3 with respect to MSWEP (e,f).
4.2. Precipitation Product Intercomparisons at Daily Scale
4.2.1. Dichotomous Statistics: Rain Detection
Dichotomous statistics was applied to verify the products’ respective ability to discriminate between precipitating and non-precipitating days. Starting from the daily time series of TAMSAT3, CHIRPS and MSWEP, contingency tables and the parameters POD, FAR, BIAS and HK (Table 1) were calculated for the two examined regions, by considering one of the datasets as reference. Comparisons between pairs of datasets are presented where the first product represents the reference data set against which the second one is evaluated. According to this scheme, the analyzed couples are: CHIRPS vs. TAMSAT3, with CHIRPS as reference dataset; CHIRPS vs. MSWEP, again with CHIRPS as a reference; and MSWEP vs. TAMSAT3, with MSWEP in the role of reference dataset.
Figure 11 shows the spatial distributions of POD, FAR, BIAS, and HK on EA, whereas Table 3 summarizes the spatially averaged values with the corresponding standard deviations. On average, similar results emerge from the intercomparisons among the various products, assuring substantial agreement among the evaluated products in terms of precipitation detection. Note the best POD value (0.72 ± 0.12) complemented by the best HK (0.62 ± 0.11) from TAMSAT3 with respect to CHIRPS, and the worst results, from TAMSAT3 with respect to MSWEP, relative to FAR (0.45 ± 0.20) and BIAS (1.5 ± 0.89).
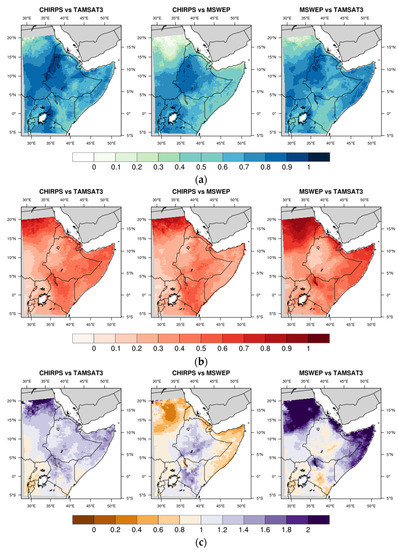
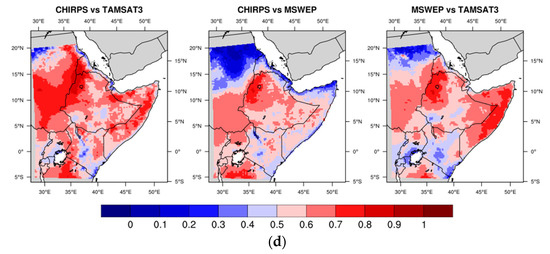
Figure 11.
Maps of POD (a), FAR (b), BIAS (c), and HK (d) for EA.

Table 3.
POD, FAR, BIAS and HK spatially averaged over EA with the corresponding standard deviation values.
Moreover, the analysis of the spatial distribution of the four indices makes possible to identify specific areas where the differences or the agreement among the products are more marked. MSWEP exhibits low POD values (≤0.4) in Somalia, Eritrea, and Sudan compared to CHIRPS (Figure 11a). TAMSAT3 shows similar POD spatial patterns with respect to CHIRPS and MSWEP, with values ≤ 0.4 in central Kenya, Ruanda, and Sudan (lowest values from the MSWEP–TAMSAT3 comparison). In the northern region of Sudan, the low precipitation amounts impact the ability to distinguish precipitating from non-precipitating days, especially in the CHIRPS vs. MSWEP comparison, where POD reaches its minimum. On the other hand, POD > 0.7 are found over the Ethiopian Highlands, South Sudan, Uganda and the entire region surrounding Lake Victoria, together with the lowest FAR values, demonstrating how the high amounts of precipitation typical of these areas “facilitate” the task of precipitation detection. The region with the worst FAR values (~ 1) is northern Sudan, in particular for the MSWEP vs. TAMSAT3 comparison. The tendency of TAMSAT3 to identify more precipitating events in this area is further confirmed by the BIAS, with a wide region exhibiting values ≥ 2 in the MSWEP vs. TAMSAT3 comparison and to a lesser extent for CHIRPS vs. TAMSAT3. Further regions with high FAR and BIAS values are Somalia and Eritrea (FAR > 0.8, BIAS > 1.4) for the MSWEP vs. TAMSAT3 case. In general, a better agreement between CHIRPS and TAMSAT3 emerges from the BIAS maps, with a weak tendency for TAMSAT3 to overestimate the number of precipitating days compared to CHIRPS in a large portion of EA. MSWEP underestimates the occurrence of precipitation compared to the other two products, especially in Somalia, Eritrea, and Sudan, and its behavior deviates more markedly from TAMSAT3 than from CHIRPS. Again, the HK maps confirm the previously described results, with values lower than 0.2 limited to the northern region of Sudan for the CHIRPS vs. MSWEP and MSWEP vs. TAMSAT3 comparisons. This is the area covered by cluster 7 (Figure 6g), with an average daily precipitation of < 0.3 mm day–1, so it is possible that the threshold value of 1 mm day–1 chosen as the discriminant for the precipitating and non-precipitating days is not appropriate. In the rest of EA, HK exceeds 0.4, with large regions characterized by values even higher than 0.6 and 0.8, denoting how the datasets have similar characteristics relative to precipitation detection even with underestimation by MSWEP relative to the other products.
Following the procedure previously described, Figure 12 presents the maps of POD, FAR, BIAS and HK for SA, whereas Table 4 reports the same statistical parameters averaged on the region together with the corresponding standard deviations. Considering the scores in Table 4, an agreement among the products even better than that found in EA emerges, characterized by a general improvement in the scores with lower variability (lower standard deviation). On average, TAMSAT3 and MSWEP give raise to very similar statistical scores when compared to CHIRPS. Looking at the score maps, the coast of Namibia and region of Cape Town, Southern Mozambique, and the east coast of Madagascar are the areas where POD, FAR, BIAS and HK deteriorate with respect to the rest of SA. The higher values of the statistical parameters are found in the northern belt of SA (Angola, Zambia and Northern Mozambique). The coast of Namibia, the region of Cape Town, and southern Mozambique are characterized by HK<0.2 for CHIRPS vs. TAMSAT3 and MSWEP vs. TAMSAT3, demonstrating a different capability of TAMSAT3 with respect to the other products in identifying the precipitating days (Figure 12d). As for the desert of Sudan in EA, the coast of Namibia is a desert area with a low number of precipitating days. The average daily precipitation does not exceed 0.5 mm day–1; therefore, it is reasonable to expect the dichotomous approach be problematic, given 1 mm day–1 as the threshold to discriminate between precipitating and non–precipitating days.
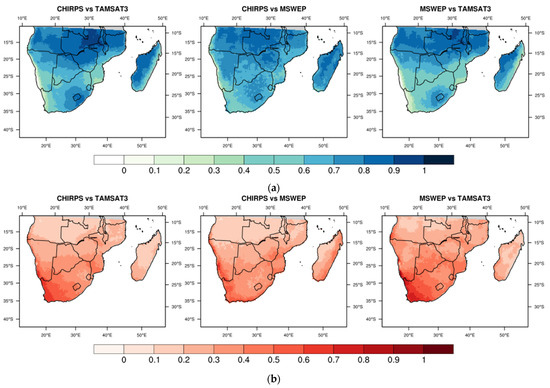
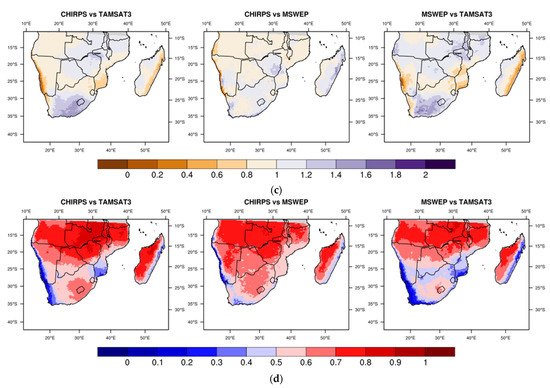
Figure 12.
Maps of POD (a), FAR (b), BIAS (c) and HK (d) for SA.

Table 4.
Same as in Table 3 but for SA.
The presence of a POD latitudinal gradient (Figure 12a) is particularly visible in the CHIRPS vs. TAMSAT3 and MSWEP vs. TAMSAT3 maps, with maximum values close to 1 in northern SA, on the west coast of Madagascar and in the mountain region surrounding Lesotho, decreasing below 0.3 when moving southward on the east coast of Madagascar, Southern Mozambique, Cape Town region and the coast of Namibia, where the index reaches its minimum around 0.1. In Figure 12b the worst FAR values correspond to the zones with low POD values in south-west RSA and improve towards the north. In Figure 12c the spatial distributions of the BIAS values confirm the TAMSAT3 tendency to underestimate the number of precipitating days compared to the other two satellite products on the east coast of Madagascar, southern Mozambique and the Namibian coast, whereas BIAS values very close to 1 come from the comparison of MSWEP to CHIRPS. On the contrary, TAMSAT3 overestimates the occurrence of precipitation in RSA.
4.2.2. Quantitative Intercomparisons at Daily Scale
In Figure 13 the CC, ME, and MAE maps on EA are shown for each pair of intercompared products; the statistical parameters are calculated for each grid cell starting from the daily precipitation time series. The corresponding EA-averaged parameters are reported in Table 5.
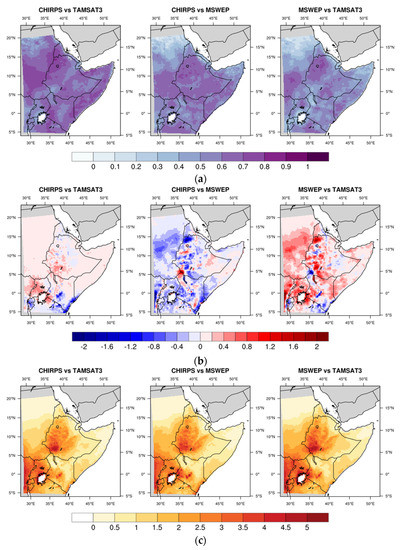
Figure 13.
Maps of CC (a), ME (mm day–1) (b) and MAE (mm day–1) (c) for EA.

Table 5.
CC, ME and MAE spatially averaged over EA with corresponding standard deviations.
In all three maps, the best CC values between 0.7 and 0.8 characterize the Ethiopian Western Highlands and Northern Tanzania (Figure 13a). In the CHIRPS vs. TAMSAT3 map, the lowest values (CC < 0.4) are found in the Sudan desert and the region surrounding Lake Victoria. The CHIRPS vs. MSWEP map presents patterns similar to the previous one but with lower average CC values (0.54 with respect to 0.63). In addition to the areas already mentioned with a decrease in CC, the tip of the Horn of Africa in Somalia, Eritrea, Rwanda and Burundi also show a CC < 0.4. The correlation further deteriorates in the case of the intercomparison of MSWEP vs. TAMSAT3 (CC mean value 0.49), even though the western regions of Ethiopia and South Sudan still exhibit higher CC values.
Systematic differences among the products are identified through the ME maps presented in Figure 13b. A tendency to overestimate daily precipitation characterizes TAMSAT3, more marked with respect to MSWEP, with ME > 0.4 mm day–1, than with respect to CHIRPS. In this case, a wide area of EA exhibits values only up to 0.2 mm day–1, with the exception of Uganda and central Ethiopia (≤ 0.6 mm day–1) and the Kenyan coasts, where on the contrary the underestimation reaches values up to 2 mm day–1 compared to the average daily precipitation of this region of 3 mm day–1. Underestimation is most often present in the CHIRPS vs. MSWEP map, with the exception of small regions mainly concentrated in Ethiopia.
The spatial distributions of MAE are displayed in Figure 13c. MAE spatial patterns are very similar and underline an increase in MAE associated with the areas characterized by the highest precipitation amounts (i.e., Central–Western Ethiopia, Democratic Republic of Congo and Uganda). Again, the MSWEP vs. TAMSAT3 comparison provides slightly higher values, as reported in Table 5.
These results are closely linked with the dichotomous statistics outcomes and also support the results from the analysis of the monthly climatology for the clusters. Even though the three products have a high degree of agreement, generally TAMSAT3 and CHIRPS are the products with more similar behavior at the daily scale in EA in terms of precipitation detection and quantification, whereas the MSWEP results are worse, especially with respect to TAMSAT3, in both aspects. TAMSAT3 tends to underestimate daily precipitation, both quantitatively and in the identification of the precipitating days, in Rwanda and Burundi and on the Kenyan coasts when compared to the other two products; MSWEP shows a tendency to underestimate precipitation, both quantitatively and in the detection of precipitation days, in almost all of EA with the exception of some limited areas, mostly in the mountainous regions of Ethiopia.
In Figure 14, the CC, ME, and MAE spatial patterns for SA are displayed and the corresponding spatially-averaged values are summarized in Table 6.
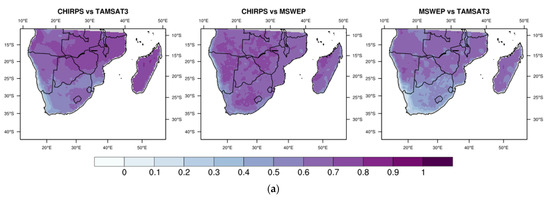
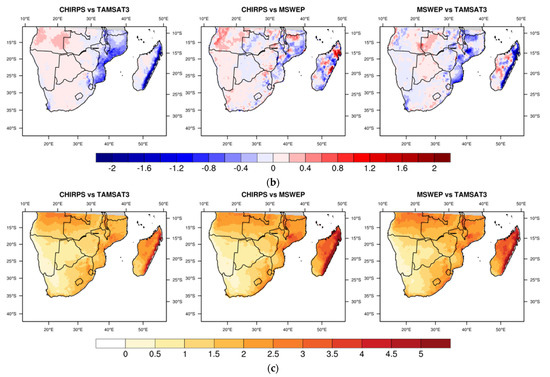
Figure 14.
Maps of CC (a), ME (mm day–1) (b) and MAE (mm day–1) (c) for SA.

Table 6.
CC, ME and MAE spatially averaged over SA, with corresponding standard deviations.
On average, CC values are better in SA than in EA, with a slight decay in the case of MSWEP–TAMSAT3 comparison (Table 6). The best CC results are obtained from the CHIRPS–MSWEP intercomparison, as is apparent from Figure 14a and the low standard deviation associated with the mean CC value in Table 6, which indicates a substantially homogeneous CC spatial pattern. A common aspect of the CHIRPS vs. TAMSAT3 and MSWEP vs. TAMSAT3 intercomparisons is the presence of an area characterized by CC values lower than 0.2 covering the Namibian coast and the area of Cape Town, already highlighted as problematic in the dichotomous statistics for TAMSAT3. Unlike EA, the correlation is much more substantial between the CHIRPS and MSWEP datasets in SA. Mean ME values near 0 are accompanied by high standard deviations (Table 6), demonstrating a more marked ME variability over the region, particularly evident for TAMSAT3 (Figure 14b). TAMSAT3 underestimates the daily precipitation on the east coast of Madagascar compared to the other two products, with ME < –2 mm day–1 and a corresponding MAE ≥ 5 mm day–1 (Figure 14c) with respect to an average daily precipitation ≥ 6 mm day–1, as well as on the coasts of Mozambique and in the Cape Town region, where ME ≅ –1 mm day–1 and MAE > 2 mm day–1 are found associated with a daily precipitation ≅ 3 mm day–1. For the remaining parts of SA, the ME values from the CHIRPS vs. TAMSAT3 and MSWEP vs. TAMSAT3 intercomparisons are much lower, in the range of ± 0.2 mm day–1, with MAE up to 3 mm day–1. As for the CHIRPS vs. MSWEP comparison, the greater differences are limited to Madagascar, where a more pronounced overestimation by MSWEP with respect to CHIRPS is evident, and Mozambique, where CHIRPS overestimates daily precipitation. In any case, the percent MAE values (i.e., the ratio between MAE and mean daily precipitation of the compared product) are always > 50%, due to very low daily totals, especially in Namibia, Angola and RSA (< 2 mm day–1). Finally, note the agreement of the maps shown in Figure 14b with the findings of the BIAS index maps in Figure 12c for the dichotomous statistics.
4.3. Temporal Stability of the Rain Detection and Estimation Capabilities
The temporal evolution of the area-averaged statistical parameters (i.e., dichotomous and quantitative indices) was analyzed in order to evaluate the mutual stability of the precipitation products as a function of time. Starting from the daily time series of the three datasets, the statistical parameters were computed for each year and pixel and then averaged over the EA and SA regions.
Figure 15 presents the annual evolution of dichotomous parameters (i.e., HK, POD, FAR and BIAS) relating to the EA region.
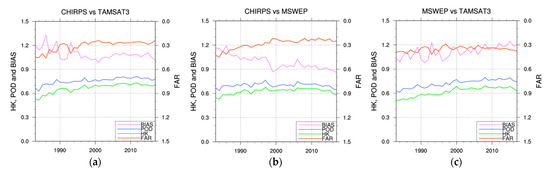
Figure 15.
EA-averaged annual HK, POD, BIAS and FAR (right y-axis) for TAMSAT3 with respect to CHIRPS (a), MSWEP with respect to CHIRPS (b) and TAMSAT3 with respect to MSWEP (c).
Different trends can be seen in Figure 15, with BIAS and FAR being the most variable indices over the 35 years examined. Similar behavior characterizes the intercomparisons of CHIRPS vs. TAMSAT3 and CHIRPS vs. MSWEP (Figure 15a,b), with a decrease in BIAS (from 1.2–1.3 to 0.9–1) and FAR (from 0.4–0.5 to 0.2–0.3) up to the end of the 1990s and a weak increase in the POD, especially for CHIRPS vs. TAMSAT3. This behavior is caused by the TAMSAT3 and MSWEP FA decrease as a function of time with respect to CHIRPS (not shown), followed by a stabilization of values starting in the year 2000. The situation is different for the TAMSAT3–MSWEP intercomparison (Figure 15c), where FAR decreases only slightly, from 0.4 to 0.3, but without the juxtaposition of the pre- and post-2000 behaviors, and BIAS increases up to 1.1–1.2 after an initial phase characterized by high variability, denoting the tendency to overestimate the number of precipitating days by TAMSAT3 with respect to MSWEP already mentioned in Section 4.2.1. In this case, TAMSAT3 misses with respect to MSWEP exhibit a negative trend over the whole period, whereas false alarms substantially decrease during 2000–2017 compared to 1983–1999 (not shown). Generally speaking, the HK index shows an increasing trend in all intercomparisons, indicating an increasing similarity among the three products in discriminating precipitating and non-precipitating days.
An analogous convergence of the quantitative estimation capabilities of the three products with time is shown in Figure 16, with increasing CC and decreasing MAE values, especially for the intercomparisons with respect to CHIRPS (Figure 16a,b). The MAE values for CHIRPS vs. TAMSAT3 and CHIRPS vs. MSWEP intercomparisons, after a first phase characterized by a negative trend, stabilize around 1.5 mm day–1 after 2000, whereas there is not a negative trend with time for the MSWEP vs. TAMSAT3 intercomparison (Figure 16c), but rather a variation in MAE from 1.5 to 2 mm day–1 with a sort of decadal periodicity. MSWEP denotes a permanent underestimation with respect to CHIRPS with ME values in the range of [–0.25, 0.] mm day–1 without any significant evolution with time (Figure 16b). Unlike this case, TAMSAT3 exhibits increasing ME values (Figure 16a,c); the tendency is more pronounced with respect to MSWEP (i.e., a progressing overestimation up to a maximum of 0.5 mm day–1 during the whole period) than to CHIRPS, where TAMSAT3 overestimation takes place only after 2000.
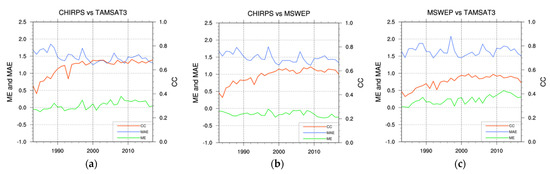
Figure 16.
EA-averaged annual ME (mm day–1), MAE (mm day–1) and CC (right y-axis) for TAMSAT3 with respect to CHIRPS (a), MSWEP with respect to CHIRPS (b), and TAMSAT3 with respect to MSWEP (c).
Considering the dichotomous parameters for SA, again an increasing similarity among the products is evident (see Figure 17). The MSWEP–CHIRPS pair shows the more stable values as a function of time, with only a weak increase in POD and HK and a decrease in FAR supported by a weak decrease in misses and false alarms for MSWEP with respect to CHIRPS (Figure 17b). Both intercomparisons involving TAMSAT3 present the typical decreasing tendency for BIAS and FAR, with the turning point in the year 2000 already observed in EA for CHIRPS vs. TAMSAT3 and CHIRPS vs. MSWEP, mainly due to a decreasing number of false alarms.
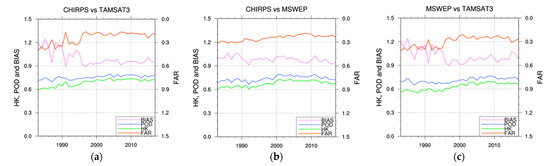
Figure 17.
Same as in Figure 14 but for SA: TAMSAT3 with respect to CHIRPS (a), MSWEP with respect to CHIRPS (b) and TAMSAT3 with respect to MSWEP (c).
As for the quantitative indices, the situation is very similar to that depicted for EA (Figure 18), with increasing CC values reaching 0.7 except for the case of MSWEP vs. TAMSAT3 (Figure 18c). The two products are more dissimilar in this region, as demonstrated by the higher MAE values.
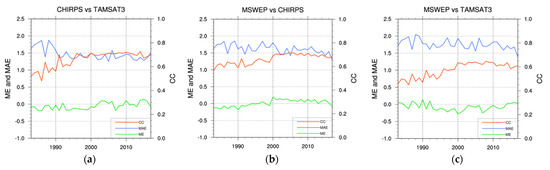
Figure 18.
Same as in Figure 15 but for SA: TAMSAT3 with respect to CHIRPS (a), MSWEP with respect to CHIRPS (b) and TAMSAT3 with respect to MSWEP (c).
In this analysis, the year 2000 often stood out as a turning point in the annual time series of the examined statistical parameters, with a sort of stabilization of the parameters’ variability from 2000 onward. Various factors could have contributed to this pre- and post-2000 change. Before 2000, the days without IR data from geostationary platforms (METEOSAT First Generation satellites) are more numerous with respect to recent decades when the METEOSAT Second Generation satellites entered their operational phase. For example, the TAMSAT3 time series has as many as 80 missing days per year before 2000. These data gaps are filled in using climatological data in TAMSAT3 and CHIRPS according to different methodologies (see Section 2.1.1 and [28] for TAMSAT3 and CHIRPS, respectively), and these procedures can introduce some discontinuities in the time series. In many countries of EA and SA the availability of rain gauges was subject to a drastic decrease, frequently occurring after 2000 (as confirmed on the web page of CHIRPS dignaotics, https://www.chc.ucsb.edu/data/chirps/diagnostics#stationsbycountry, last access 2 July 2021). A similar change around the year 2000 was recently identified for monthly CHIRPS estimates against GPCC data globally [54]. The results indicate that CHIRPS underestimates precipitation before 2000 with respect to GPCC, while this systematic underestimation is effectively removed after 2000. The authors also mention the CHIRPS calibration methodology as a key factor; the algorithm calibrates the CCD regressions using a TMPA 3B42 data set covering the time period 2000–2013. Therefore, it is possible that the CHIRPS CCD–precipitation relationships are more representative of recent decades than they are for 1983–1999. Finally, it is necessary to consider the differences in the input data for the generations of the MSWEP product during the two periods 1983–1999 and 2000–2017. With reference to Figure 4 in [31], where the relative weights assigned to the gauge-, satellite-, and reanalysis-based precipitation estimates are represented, it is clear that in the first period over EA and SA MSWEP is mainly based on rain gauges, with a minor contribution from reanalysis over the rain gauge lacking areas (e.g., Somalia). From 2000 onwards, the merging between satellite precipitation estimates based on passive microwave sensors and reanalysis becomes predominant in EA, except for the area surrounding Lake Victoria where rain gauges are still the main source of input data. On the contrary, in SA rain gauges continue to drive MSWEP estimates, with a minor contribution from the merging between satellite and reanalysis data.
5. Discussion
The most problematic regions for precipitation detection and estimate are located in arid, mountainous and coastal areas. Arid regions are acknowledged as problematic for satellite estimates because of precipitation overestimation with respect to rain gauge measurements due to sub-cloud evaporation [8]. From the dichotomous statistics, differences in the precipitation detection emerged in Northern Sudan, Somalia and the Horn of Africa, and coastal Namibia. The problem is connected with the low daily precipitation values in these areas, usually no more than 1 mm day–1 on average, which is near the threshold value used for precipitation detection. This means that even low estimation errors can determine differences in detection among the products. Moreover, not all mentioned arid areas provided an equal response in this analysis. EA BIAS (Figure 11c) indicates MSWEP as the product with the lowest number of precipitating days, whereas TAMSAT3 overestimates the other two products. On the contrary, TAMSAT3 underestimates precipitation occurrences with respect to both products in the coastal Namib Desert. In this case, the proximity to the coast and presence of non-convective precipitating systems further complicate satellite retrieval [16]. Even coastal and mountain areas are considered among the most demanding contexts for satellite precipitation estimation. In particular, IR-based products can underestimate precipitation over coastal and mountain regions because most of the rain comes from clouds with top temperatures higher than the threshold used by the satellite algorithms [8]. TAMSAT3 tends to underestimate daily precipitation compared to CHIRPS and MSWEP on the eastern coast of Madagascar and Mozambique (Figure 14b), as confirmed by Seyama et al. and Toté et al. at decadal and monthly scales [16,17], and misses precipitation on the coasts of Kenya and southern Somalia with respect to CHIRPS, which exhibits higher precipitation amounts (Figure 13). The coastal region near Cape Town is another emblematic area for the satellite product differences, where TAMSAT3 performance is not aligned with the other two products in terms of detection (HK < 0.3; Figure 12) and to a lesser extent estimation (ME ∈ [–0.6, 0] mm day–1, Figure 14). In the Ethiopian Highlands region, the differences are more limited to precipitation estimation, with MSWEP systematically underestimating precipitation compared to the other two products, which show more similar behavior (Figure 13).
Altogether, the agreement among the three datasets in describing precipitation over EA and SA is considerable, in spite of the specific differences summarized previously. This demonstrates once more the applicability and reliability of IR-based algorithms such as CHIRPS and TAMSAT3 for the evaluation of precipitation long-term variability in Africa with respect to a multi-source precipitation product such as MSWEP, which also exploits passive microwave-based precipitation estimates and reanalyses. Moreover, from the study of the statistical indices as a function of time it is clear that the agreement between the products has generally improved over time, showing more stable capabilities to identify precipitating days and estimate daily precipitation, in particular starting in the late 1990s. Thus, as highlighted by Awange et al. [13], who compared MSWEP v. 2.1 at the monthly scale to various precipitation products including CHIRPS, the results of this analysis do not identify any explicit advantage in using MSWEP rather than CHIRPS and TAMSAT3 in EA and SA, so it is not possible nor appropriate to establish a ranking. Nevertheless, greater similarity between CHIRPS and TAMSAT3 was observed in EA, with MSWEP deviating more, whereas CHIRPS and MSWEP exhibited a higher degree of agreement in SA, with TAMSAT3 showing a tendency to underestimate precipitation. The agreement between CHIRPS and TAMSAT3 was expected; however, a possible explanation for the behavior in SA can be found in the relative weights associated with the various input data in MSWEP, summarized in Section 4.3. Generally, the MSWEP estimates are more based on rain gauges in SA than in EA for the whole analyzed period, and this could contribute to the MSWEP vs. CHIRPS similarity, considering that CHIRPS exploits rain gauges for bias correction of its IR-based precipitation estimates, whereas TAMSAT3 uses only historical rain gauge measurements to calibrate the CCD in a seasonally and spatially varying climatological calibration procedure that does not change from year to year. Moreover, as the climate of SA is strongly influenced by the presence of the Atlantic and Indian Oceans, and by frontal systems, it is possible that TAMSAT3 shows a lower capability to identify non-convective precipitation compared to the other two datasets, given the difficulty in detecting precipitation falling from warm-top clouds, which are not captured by the threshold temperatures adopted for identifying precipitating cloudy systems [16,17].
6. Conclusions
Analogies and differences among TAMSAT3, CHIRPS and MSWEP data sets were evaluated in EA and SA during the period 1983–2017 in terms of precipitation detection and estimation at the daily scale, as well as precipitation monthly climatology and seasonality. Unlike the numerous validation studies available in the literature, in this work we opted for direct pairwise comparisons between the three satellite products, without a rain gauge-based product as reference. The reasons that led to this choice are based on the scarce and uneven spatial coverage of gauge networks in the analyzed regions, in particular East Africa, and the difficulty of obtaining reliable rain gauge data independent from those already used in the generation of the satellite products themselves.
The analysis consisted of several stages. First, applying the k–means clustering method, the study regions were divided into homogeneous sub-areas with respect to the precipitation annual cycle, in order to evaluate the spatial variability of precipitation seasonality and the differences in monthly climatology among the products. Secondly, the spatial distributions of dichotomous parameters (i.e., HK, POD, FAR and BIAS) and their temporal evolution were investigated to evaluate the rain/no rain discrimination capacity of the three satellite products. Finally, the quantitative precipitation estimates were intercompared at the daily scale by means of CC, ME and MAE indices, again with the twofold purpose of evaluating their spatial patterns and temporal variability. The results discussed in the previous section offer a broad picture of the mutual behavior of the three precipitation products in EA and SA. A completing element of this analysis will be the evaluation of the precipitation extremes as perceived by satellite-based products in terms of annual maxima, or high return level events analyzed according to the method exposed in [55,56,57,58]. This kind of research will support the projections of extremes in the vulnerable continent of Africa, providing insights relevant for risk management.
Water resources are a key factor for the development of the African continent and its sociopolitical and economic stability. Their inadequate management and limited access make the survival of local populations closely dependent on precipitation, and its spatial and temporal variations can result in devastating impacts on the territory. Paying attention to these changes and monitoring extreme event trends through high quality satellite-based precipitation products is thus a primary element allowing for resilient development capable of adapting to the evolving environment.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/rs13214419/s1, Figure S1: SA precipitation annual cycles from different zones composing cluster 5: eastern coast of Madagascar (a), coastal Mozambique (b), and central RSA (c).
Author Contributions
Conceptualization, E.C. and V.L.; methodology, E.C., A.M. and V.L.; software, E.C. and A.M.; formal analysis, O.F. and E.C.; investigation, O.F. and E.C.; data curation, E.C. and O.F.; writing—original draft preparation, E.C.; writing—review and editing, all; visualization, O.F., A.M. and E.C.; supervision, E.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
TAMSAT v3.0 and CHIRPS v2.0 are publicly available datasets, which can be found here: http://www.tamsat.org.uk/v3_data_access (accessed on 21 October 2021) and https://www.chc.ucsb.edu/data/chirps# (accessed on 21 October 2021). MSWEP data are available on request from the corresponding author Dr. Hylke Beck at the web page http://www.gloh2o.org/mswep/ (accessed on 21 October 2021).
Acknowledgments
EC and VL acknowledge support from their home institution (CNR–ISAC) for allowing them to carry on the present study. The TAMSAT group at University of Reading provided the TAMSAT v.3 dataset. The Climate Hazards Center of the University of California, Santa Barbara deserves gratitude for making available the CHIRPS dataset. Hylke Beck kindly allowed access to the MSWEP dataset for the present scientific study.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Niang, I.; Ruppel, O.C.; Abdrabo, M.A.; Essel, A.; Lennard, C.; Padgham, J.; Urquhart, P. Africa. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Barros, V.R., Field, C.B., Dokken, D.J., Mastrandrea, M.D., Mach, K.J., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 1199–1265. [Google Scholar]
- Collier, P.; Conway, G.; Venables, T. Climate change and Africa. Oxf. Rev. Econ. Policy 2008, 24, 337–353. [Google Scholar] [CrossRef]
- Scheffran, J.; Brauch, H.G. Conflicts and security risks of climate change in the Mediterranean region. In The Mediterranean Sea: Its History and Present Challenges; Goffredo, S., Dubinsky, Z., Eds.; Springer Nature: Cham, Switzerland, 2014; pp. 625–640. [Google Scholar] [CrossRef]
- Otto, F.E.L.; Wolski, P.; Lehner, F.; Tebaldi, C.; van Oldenborgh, G.J.; Hogesteeger, S.; Singh, R.; Holden, P.; Fučkar, N.S.; Odoulami, R.C.; et al. Anthropogenic influence on the drivers of the Western Cape drought 2015–2017. Environ. Res. Lett. 2018, 13, 124010. [Google Scholar] [CrossRef]
- Nicholson, S.E. A detailed look at the recent drought situation in the Greater Horn of Africa. J. Arid Environ. 2014, 103, 71–79. [Google Scholar] [CrossRef]
- Washington, R.; Harrison, M.; Conway, D.; Black, E.; Challinor, A.; Grimes, D.; Jones, R.; Morse, A.; Kay, G.; Todd, M. African climate change—Taking the shorter route. Bull. Amer. Meteor. Soc. 2006, 87, 1355–1366. [Google Scholar] [CrossRef]
- Maidment, R.; Grimes, D.; Black, E.; Tarnavsky, E.; Young, M.; Greatrex, H.; Allan, R.; Stein, T.; Nkonde, E.; Senkunda, S.; et al. A new, long-term daily satellite-based rainfall dataset for operational monitoring in Africa. Sci. Data 2017, 4, 170063. [Google Scholar] [CrossRef]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS satellite rainfall estimates over eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef]
- Levizzani, V.; Kidd, C.; Kirschbaum, D.B.; Kummerow, C.D.; Nakamura, K.; Turk, F.J. (Eds.) Satellite precipitation measurement: Volume 1. In Advances in Global Change Research; Springer Nature: Cham, Switzerland, 2020; Volume 67, 450p. [Google Scholar] [CrossRef]
- Levizzani, V.; Kidd, C.; Kirschbaum, D.B.; Kummerow, C.D.; Nakamura, K.; Turk, F.J. (Eds.) Satellite precipitation measurement: Volume 2. In Advances in Global Change Research; Springer Nature: Cham, Switzerland, 2020; Volume 69, 712p. [Google Scholar] [CrossRef]
- Roca, R.; Haddad, Z.S.; Akimoto, G.F.; Alexander, L.; Behrangi, A.; Huffman, G.J.; Kato, S.; Kidd, C.; Kirstetter, P.E.; Kubota, T.; et al. The joint IPWG/GEWEX precipitation assessment. WCRP Rep. 2021, 2, 125. [Google Scholar] [CrossRef]
- Cattani, E.; Merino, A.; Guijarro, J.; Levizzani, V. East Africa rainfall trends and variability 1983–2015 using three long-term satellite products. Remote Sens. 2018, 10, 931. [Google Scholar] [CrossRef]
- Awange, J.; Hu, K.; Khaki, M. The newly merged satellite remotely sensed, gauge and reanalysis-based multi-source weighted-ensemble precipitation: Evaluation over Australia and Africa (1981–2016). Sci. Total Environ. 2019, 670, 448–465. [Google Scholar] [CrossRef] [PubMed]
- Dezfuli, A.K.; Ichoku, C.M.; Huffman, G.J.; Mohr, K.I.; Selker, J.S.; van de Giesen, N.; Hochreutener, R.; Annor, F.O. Validation of IMERG precipitation in Africa. J. Hydrometeor. 2017, 18, 2817–2825. [Google Scholar] [CrossRef]
- Ayugi, B.; Tan, G.; Ullah, W.; Boiyo, R.; Ongoma, V. Inter-comparison of remotely sensed precipitation datasets over Kenya during 1998–2016. Atmos. Res. 2019, 225, 96–109. [Google Scholar] [CrossRef]
- Seyama, E.; Masocha, M.; Dube, T. Evaluation of TAMSAT satellite rainfall estimates for Southern Africa: A comparative approach. Phys. Chem. Earth Parts A/B/C 2019, 112, 141–153. [Google Scholar] [CrossRef]
- Toté, C.; Patricio, D.; Boogaard, H.; van der Wijngaart, R.; Tarnavsky, E.; Funk, C. Evaluation of satellite rainfall estimates for drought and flood monitoring in Mozambique. Remote Sens. 2015, 7, 1758–1776. [Google Scholar] [CrossRef]
- Akinsanola, A.A.; Ogunjobi, K.O.; Ajayi, V.O.; Adefisan, E.A.; Omotosho, J.A.; Sanogo, S. Comparison of five gridded precipitation products at climatological scales over West Africa. Meteorol. Atmos. Phys. 2017, 129, 669–689. [Google Scholar] [CrossRef]
- Satgé, F.; Defrance, D.; Sultan, B.; Bonnet, M.P.; Seyler, F.; Rouché, N.; Pierron, F.; Paturel, J.E. Evaluation of 23 gridded precipitation datasets across West Africa. J. Hydrol. 2020, 581, 124412. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Fink, A.H.; Funk, C. Assessing recovery and change in West Africa’s rainfall regime from a 161-year record. Int. J. Climatol. 2018, 38, 3770–3786. [Google Scholar] [CrossRef]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; Levizzani, V.; De Roo, A. Validation of satellite-based precipitation products over sparsely-gauged African river basins. J. Hydrometeorol. 2012, 13, 1760–1783. [Google Scholar] [CrossRef]
- The NCAR Command Language (Version 6.6.2). Boulder, Colorado: UCAR/NCAR/CISL/TDD. 2019. Available online: https://www.ncl.ucar.edu (accessed on 9 July 2020).
- Merino, A.; García-Ortega, E.; Navarro, A.; Fernández-González, S.; Tapiador, F.J.; Sánchez, J.L. Evaluation of gridded rain-gauge-based precipitation datasets: Impact of station density, spatial resolution, altitude gradient and climate. Int. J. Climatol. 2021, 41, 3027–3043. [Google Scholar] [CrossRef]
- Black, E.; Tarnavsky, E.; Maidment, R.; Greatrex, H.; Mookerjee, A.; Quaife, T.; Brown, M. The use of remotely sensed rainfall for managing drought risk: A case study of weather index insurance in Zambia. Remote Sens. 2016, 8, 342. [Google Scholar] [CrossRef]
- Brown, M.; Black, E.; Asfaw, D.; Otu-Larbi, F. Monitoring drought in Ghana using TAMSAT-ALERT: A new decision support system. Weather 2017, 72, 201–205. [Google Scholar] [CrossRef][Green Version]
- Funk, C.; Shukla, S.; Thiaw, W.M.; Rowland, J.; Hoell, A.; McNally, A.; Husak, G.; Novella, N.; Budde, M.; Peters-Lidard, C.; et al. Recognizing the famine early warning systems network: Over 30 years of drought early warning science advances and partnerships promoting global food security. Bull. Amer. Meteorol. Soc. 2019, 100, 1011–1027. [Google Scholar] [CrossRef]
- Maidment, R.I.; Grimes, D.; Allan, R.P.; Tarnavsky, E.; Stringer, M.; Hewison, T.; Roebeling, R.; Black, E. The 30 year TAMSAT African Rainfall Climatology And Time series (TARCAT) data set. J. Geophys. Res. Atmos. 2014, 119, 10–619. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. MSWEP: 3-hourly 0.25° global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef]
- Beck, H.E.; Wood, E.F.; Pan, M.; Fisher, C.K.; Miralles, D.G.; van Dijk, A.I.; McVicar, T.R.; Adler, R.F. MSWEP V2 global 3-hourly 0.1° precipitation: Methodology and quantitative assessment. Bull. Am. Meteorol. Soc. 2019, 100, 473–500. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeor. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Ushio, T.; Sasashige, K.; Kubota, T.; Shige, S.; Okamoto, K.; Aonashi, K.; Inoue, T.; Takahashi, N.; Iguchi, T.; Kachi, M.; et al. A Kalman filter approach to the Global Satellite Mapping of Precipitation (GSMaP) from combined passive microwave and infrared radiometric data. J. Meteorol. Soc. Jpn. 2009, 87, 137–151. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Ebert, E. WWRP/WGNE Joint Working Group on Forecast Verification and Research—Forecast Verification Methods across Time and Space Scales. Available online: https://www.cawcr.gov.au/projects/verification/#Methods_for_dichotomous_forecasts. (accessed on 10 July 2020).
- Cattani, E.; Merino, A.; Levizzani, V. Evaluation of monthly satellite-derived precipitation products over East Africa. J. Hydrometeorol. 2016, 17, 2555–2573. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Meyer-Christoffer, A.; Becker, A.; Finger, P.; Schneider, U.; Ziese, M. GPCC Climatology Version 2018 at 0.25°: Monthly Land-Surface Precipitation Climatology for Every Month and the Total Year from Rain-Gauges Built on GTS-Based and Historical Data. Available online: https://opendata.dwd.de/climate_environment/GPCC/html/gpcc_normals_v2018_doi_download.html (accessed on 13 July 2020).
- DeGaetano, A. A Smirnov test—Based clustering algorithm with application to extreme precipitation data. Water Resour. Res. 1998, 34, 169–176. [Google Scholar] [CrossRef]
- Gong, X.; Richman, M.B. On the application of cluster analysis to growing season precipitation data in North America east of the Rockies. J. Clim. 1995, 8, 897–931. [Google Scholar] [CrossRef]
- Nicholson, S.E. A review of climate dynamics and climate variability in Eastern Africa. In The Limnology, Climatology, and Paleoclimatology of East African Lakes; Johnson, T.C., Odada, E.O., Eds.; Gordon and Breach: London, UK, 1996; pp. 25–56. [Google Scholar]
- Henderson, J.P. Some Aspects of Climate in Uganda: With Special Reference to Rainfall; East African Meteorological Department: Uganda, East Afica, 1949; p. 17.
- Nicholson, S.E. The ITCZ and the seasonal cycle over equatorial Africa. Bull. Am. Meteorol. Soc. 2018, 99, 337–348. [Google Scholar] [CrossRef]
- Yang, W.; Seager, R.; Cane, M.A.; Lyon, B. The annual cycle of East African precipitation. J. Clim. 2015, 28, 2385–2404. [Google Scholar] [CrossRef]
- Berhane, F.; Zaitchik, B. Modulation of daily precipitation over East Africa by the Madden–Julian oscillation. J. Clim. 2014, 27, 6016–6034. [Google Scholar] [CrossRef]
- Hastenrath, S.; Polzin, D.; Mutai, C. Circulation mechanisms of Kenya rainfall anomalies. J. Clim. 2011, 24, 404–412. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Funk, C.; Fink, A.H. Rainfall over the African continent from the 19th through the 21st century. Glob. Planet. Chang. 2018, 165, 114–127. [Google Scholar] [CrossRef]
- Howard, E.; Washington, R.; Hodges, K.I. Tropical lows in Southern Africa: Tracks, rainfall contributions, and the role of ENSO. J. Geophys. Res. Atmos. 2019, 124, 11009–11032. [Google Scholar] [CrossRef]
- Griffiths, J.F. Mozambique. In World Survey of Climatology—Climates of Africa; Landsberg, H.E., Ed.; Elsevier Publishing Company: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 1972; Volume 10, pp. 389–408. ISBN 044440893-2. [Google Scholar]
- Randriamahefasoa, T.; Reason, C. Interannual variability of rainfall characteristics over southwestern Madagascar. Theor. Appl. Climatol. 2017, 128, 421–437. [Google Scholar] [CrossRef]
- Philippon, N.; Rouault, M.; Richard, Y.; Favre, A. The influence of ENSO on winter rainfall in South Africa. Int. J. Climatol. 2012, 32, 2333–2347. [Google Scholar] [CrossRef]
- Griffiths, J.F.; Ranaivoson, R. Madagascar. In World Survey of Climatology—Climates of Africa; Landsberg, H.E., Ed.; Elsevier Publishing Company: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 1972; Volume 10, pp. 461–500. ISBN 044440893-2. [Google Scholar]
- Shen, Z.; Yong, B.; Gourley, J.J.; Qi, W.; Lu, D.; Liu, J.; Ren, L.; Hong, Y.; Zhang, J. Recent global performance of the Climate Hazards group Infrared Precipitation (CHIRP) with Stations (CHIRPS). J. Hydrol. 2020, 591, 125284. [Google Scholar] [CrossRef]
- Marani, M.; Ignaccolo, M. A metastatistical approach to rainfall extremes. Adv. Water Resour. 2015, 79, 121–126. [Google Scholar] [CrossRef]
- Zorzetto, E.; Botter, G.; Marani, M. On the emergence of rainfall extremes from ordinary events. Geophys. Res. Lett. 2016, 43, 8076–8082. [Google Scholar] [CrossRef]
- Marra, F.; Borga, M.; Morin, E. A unified framework for extreme sub-daily precipitation frequency analyses based on ordinary events. Geophys. Res. Lett. 2020, 47, e2020GL090209. [Google Scholar] [CrossRef]
- Miniussi, A.; Marra, F. Estimation of extreme daily precipitation return levels at-site and in ungauged locations using the simplified MEV approach. J. Hydrol. 2021, 603, 126946. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).