GPR Image Noise Removal Using Grey Wolf Optimisation in the NSST Domain
Abstract
:1. Introduction
2. Proposed Method
2.1. Time-Varying Threshold Function
- 1
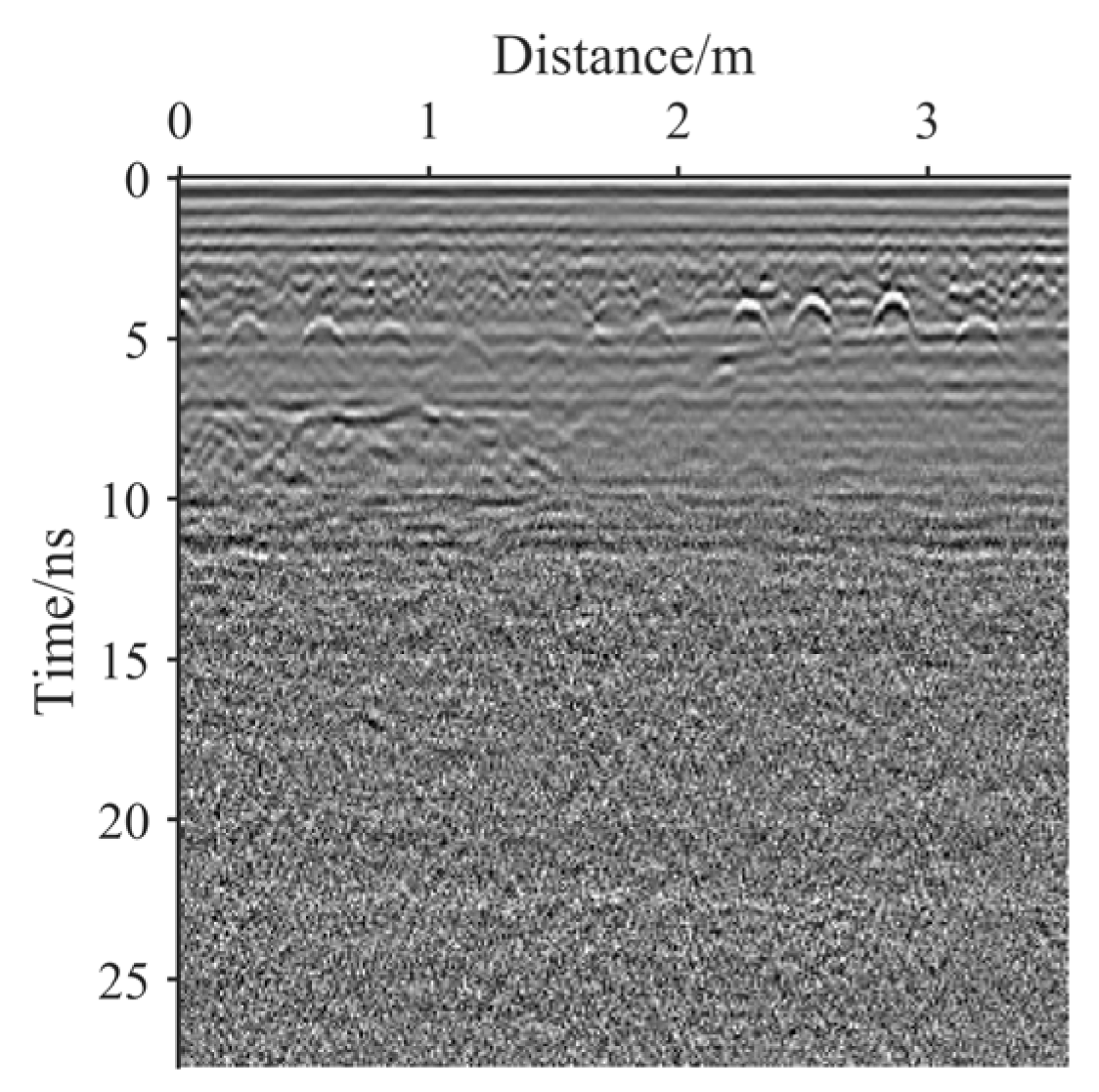
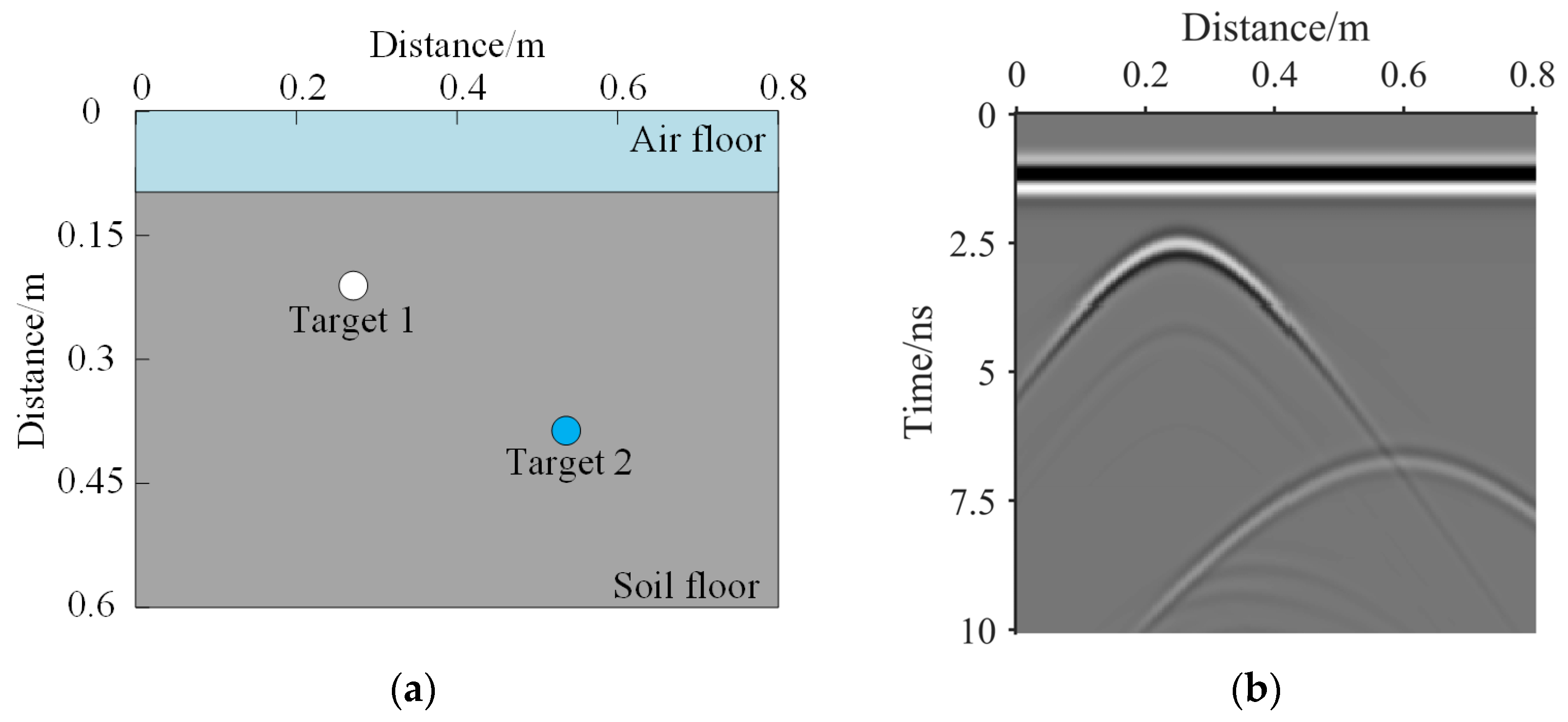
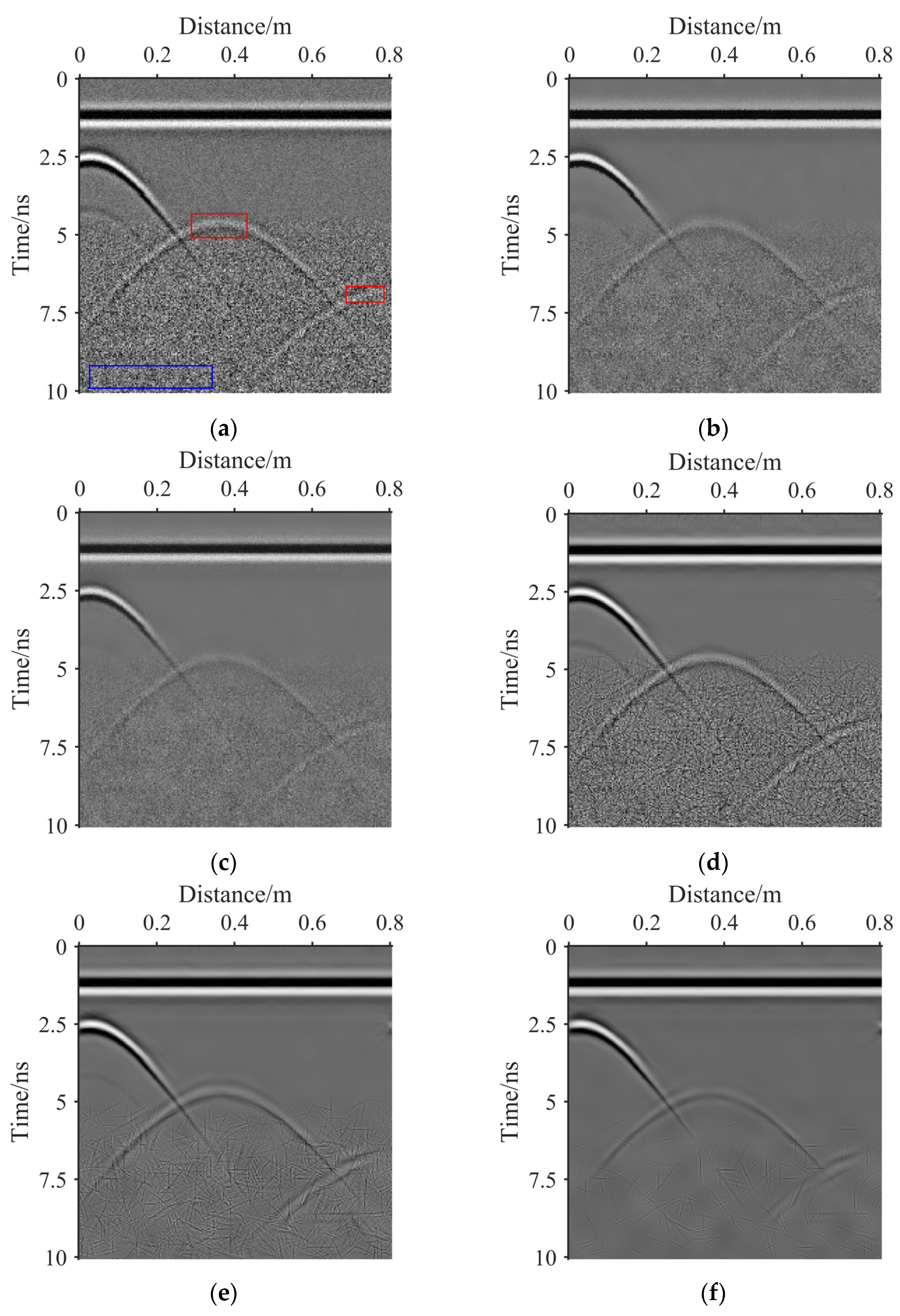
- NSST is used to extract the fourth-scale coefficient of the real GPR image, as shown in Figure 1.
- 2
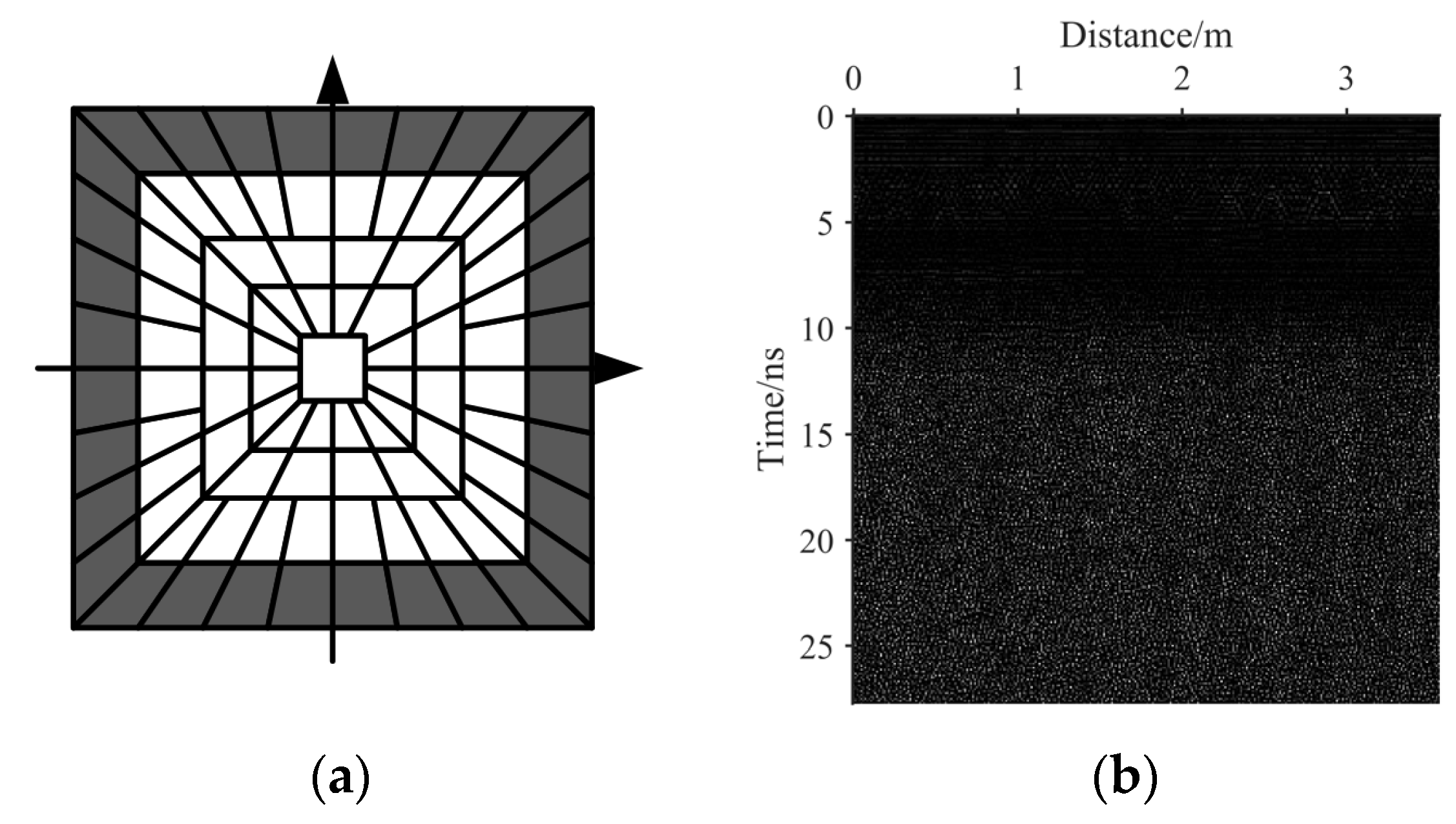
- Second, on the basis of the fourth-scale coefficient, inverse NSST is used to obtain a noise intensity distribution map, as shown in Figure 2b. In combination with Figure 1, it can be seen that the highlight coefficients at a depth of 4 ns are effective reflection signals, not noise information, and thus, this coefficient information is removed. Figure 2b shows that the real GPR image noise is not uniform, and the noise intensity varies with the time axis.
- 3
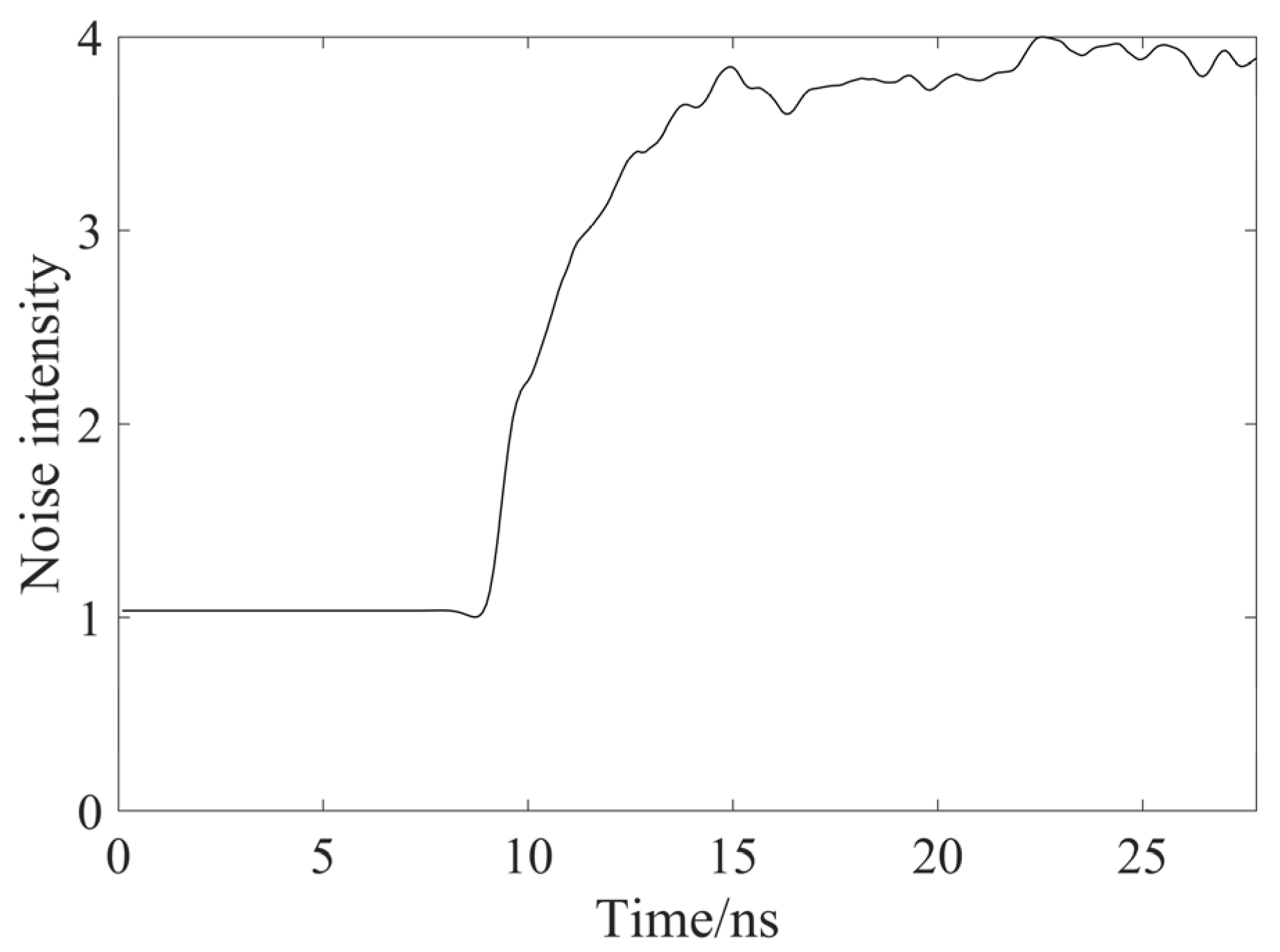
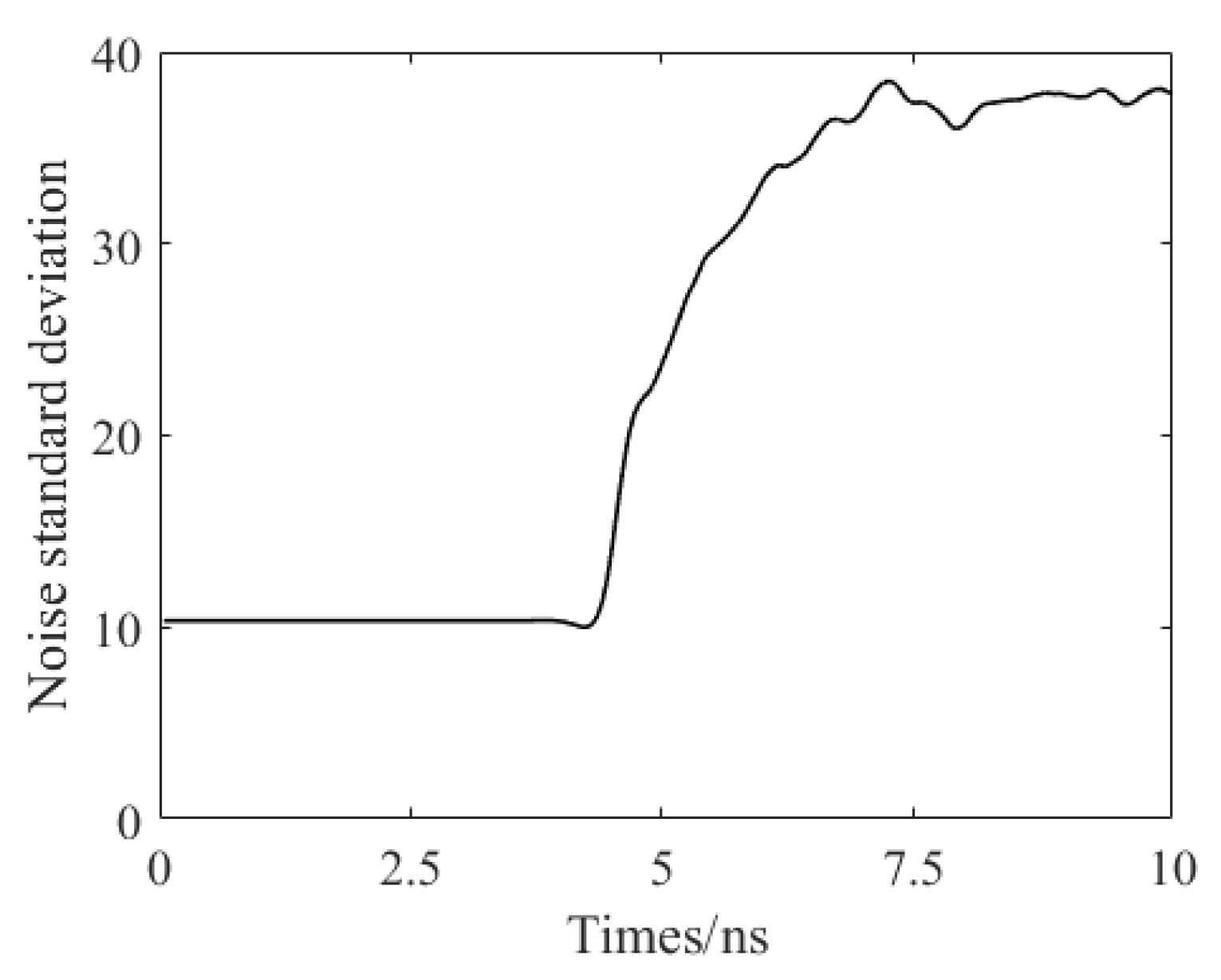
- Finally, each row of the noise intensity distribution map is summed to obtain a column vector, and the fitting function is used for the above column vector to obtain a relative noise intensity trend curve, as shown in Figure 3.
2.2. Edge Area Recognition and PROTECTION
- 1
- The denoised image is obtained from the result of each iteration of the proposed algorithm.
- 2
- The edge area of the denoised image is obtained using the Canny algorithm by employing the threshold .
- 3
- In the edge area, pixel differences between the noisy and denoised images are calculated. These pixel differences are adjusted using threshold . The formula for calculating the denoised image after adjustment is as follows:where is the pixel value of the denoised image after adjustment. is the pixel value of the noisy image. is the pixel difference between the noisy and denoised images before adjustment. and indicate the pixel position of the edge area.
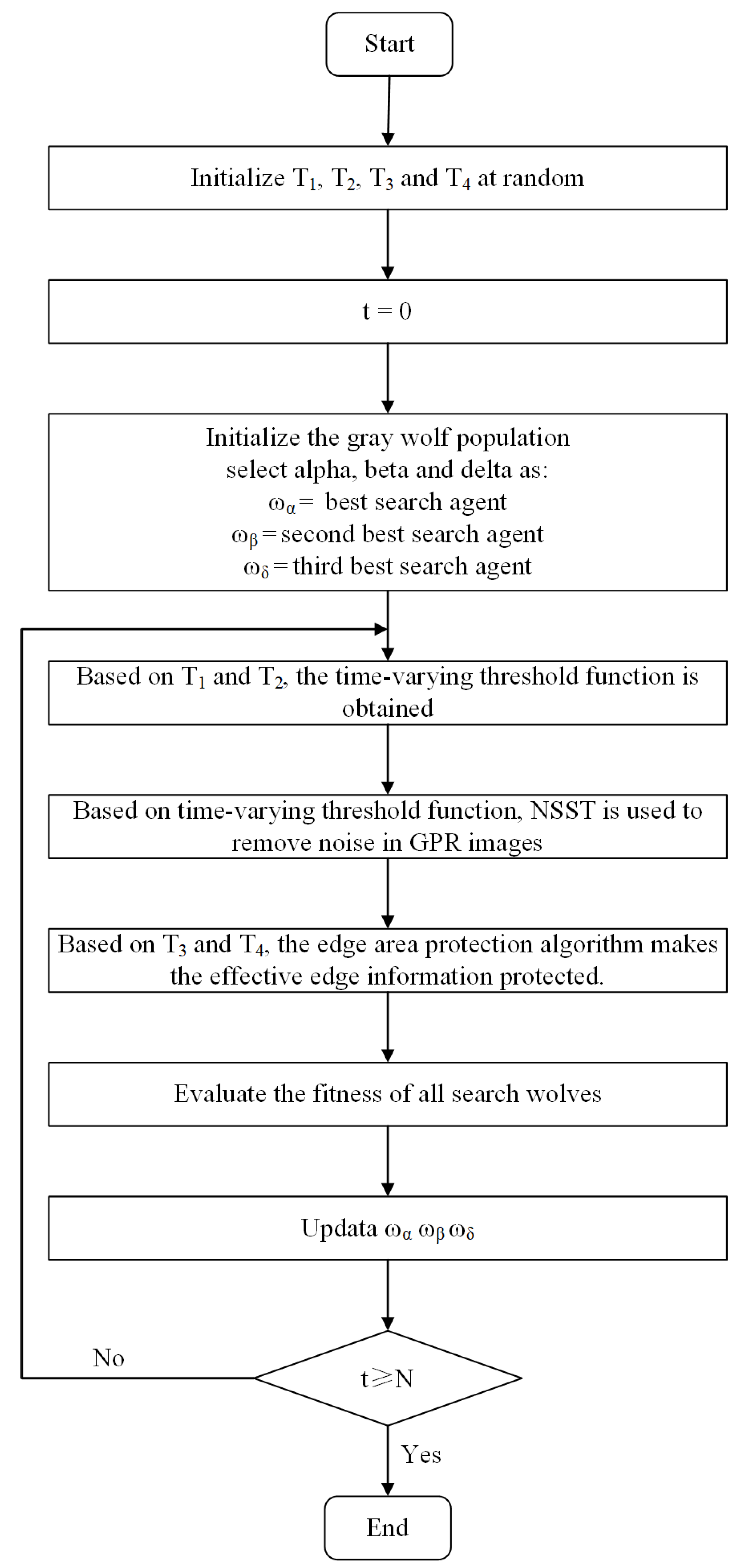
2.3. GWO Framework for GPR Image Denoising
- 1
- All search wolves are randomly initialised in the search space, and grey wolves α, β, and ω are selected according to the degree of fitness.
- 2
- The parameters of the grey wolves α, β, and ω are used to determine and , which are utilised to calculate the time-varying threshold function value.
- 3
- NSST is used to extract the coefficients of each frequency scale of noisy GPR images. Then, the NSST coefficients are denoised using the time-varying threshold function.
- 4
- The parameters of the grey wolves α, β, and ω are used to determine and , which are employed to protect the edge area.
- 5
- On the basis of the denoised GPR image after edge protection adjustment, the fitness of all grey wolves is evaluated. The position parameters of the grey wolves are accordingly updated.
- 6
- Determining whether the end conditions are met is necessary. If the conditions are not met, the grey wolves α, β, and ω are reselected according to the degree of fitness. Multiple iterative calculations are performed until the end conditions are met.
3. Results
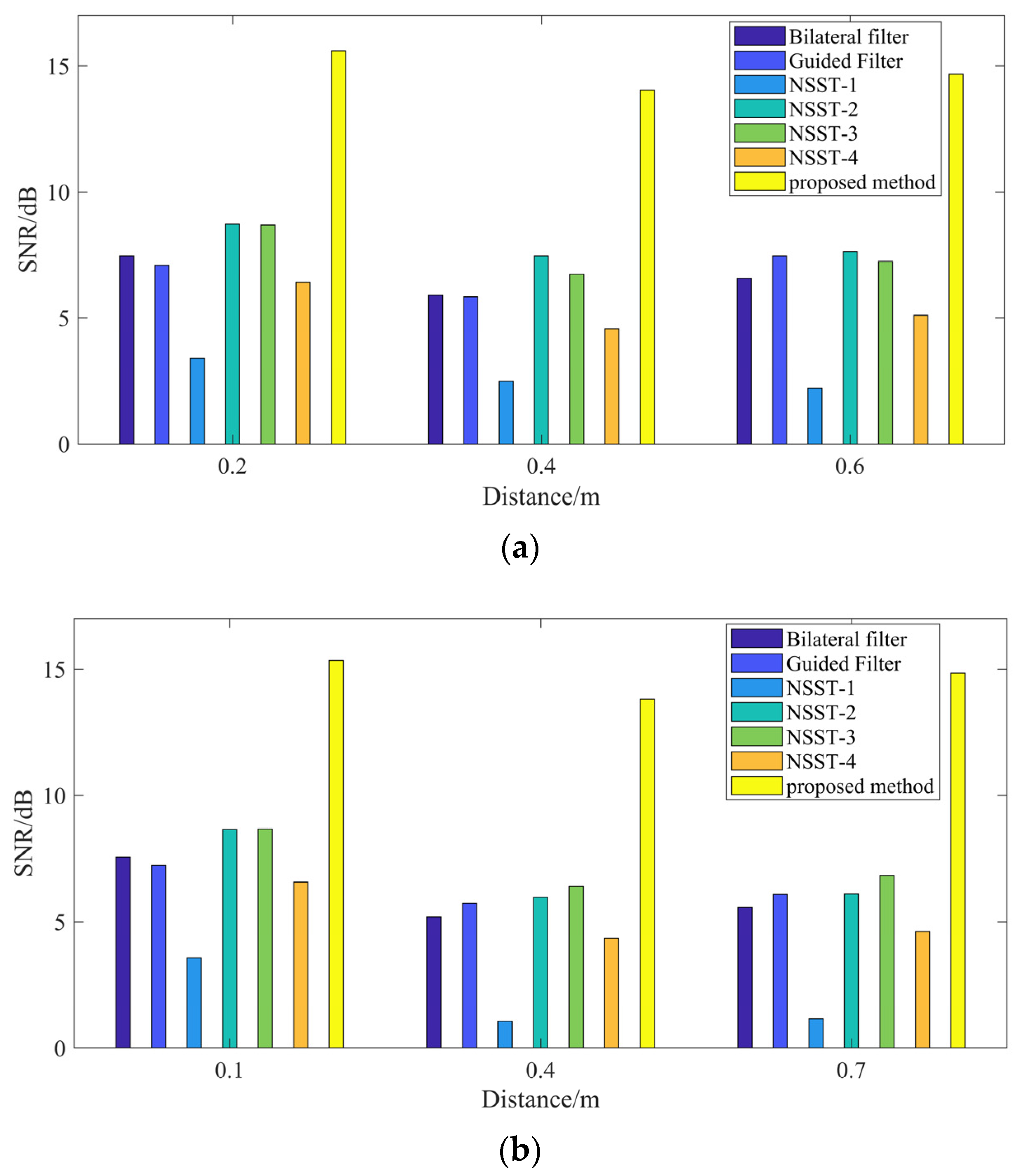
3.1. Simulated GPR Image Results
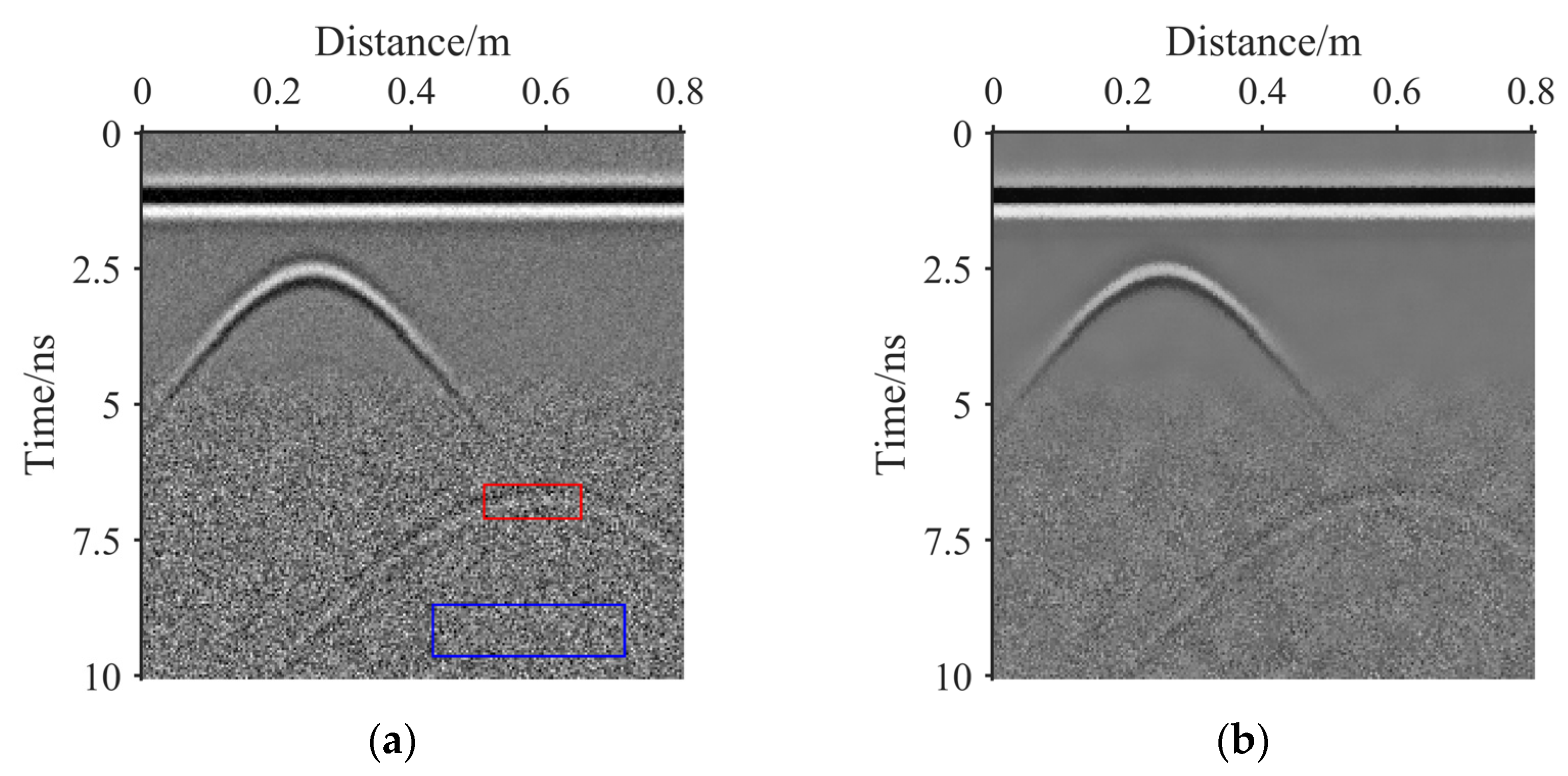
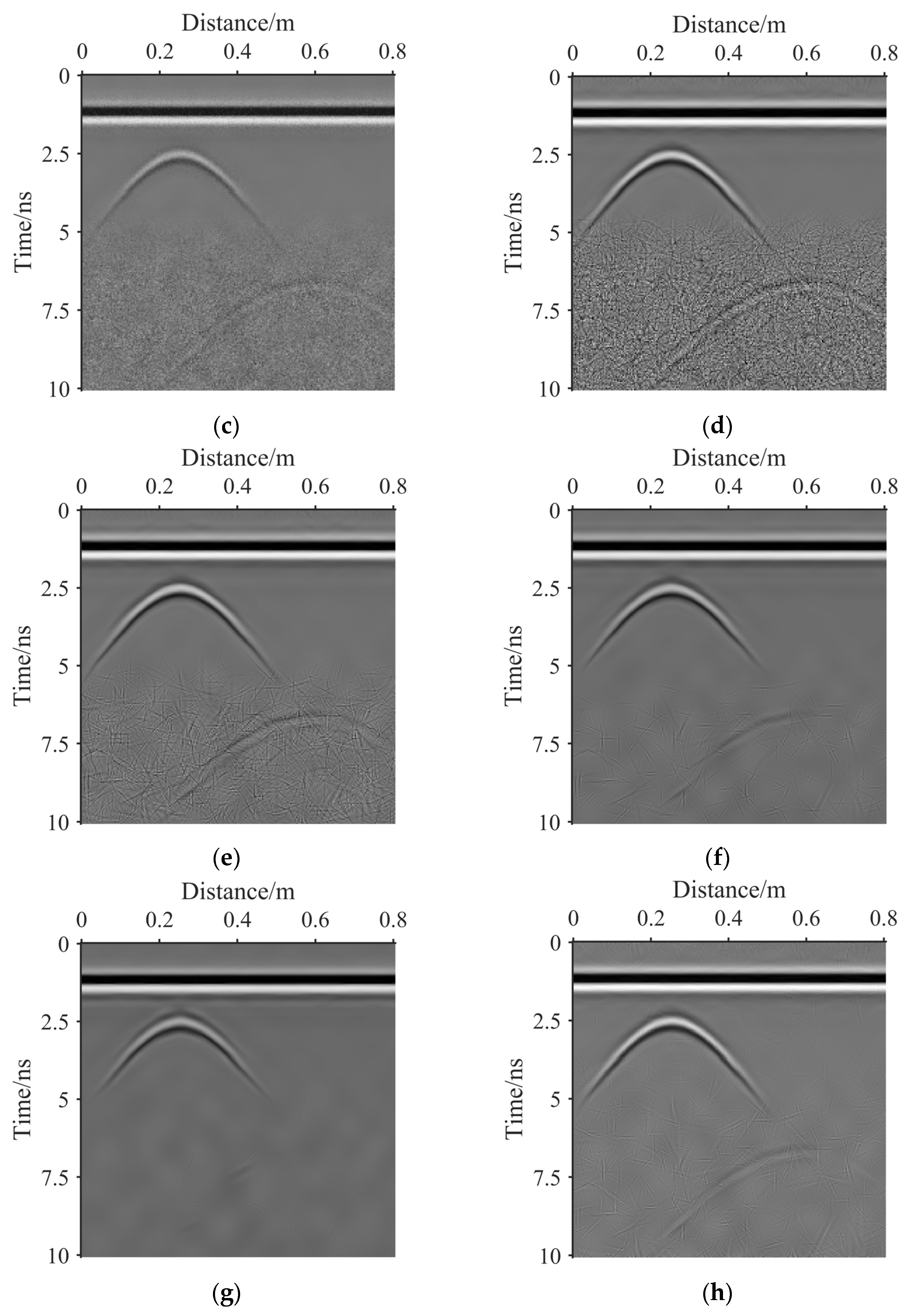
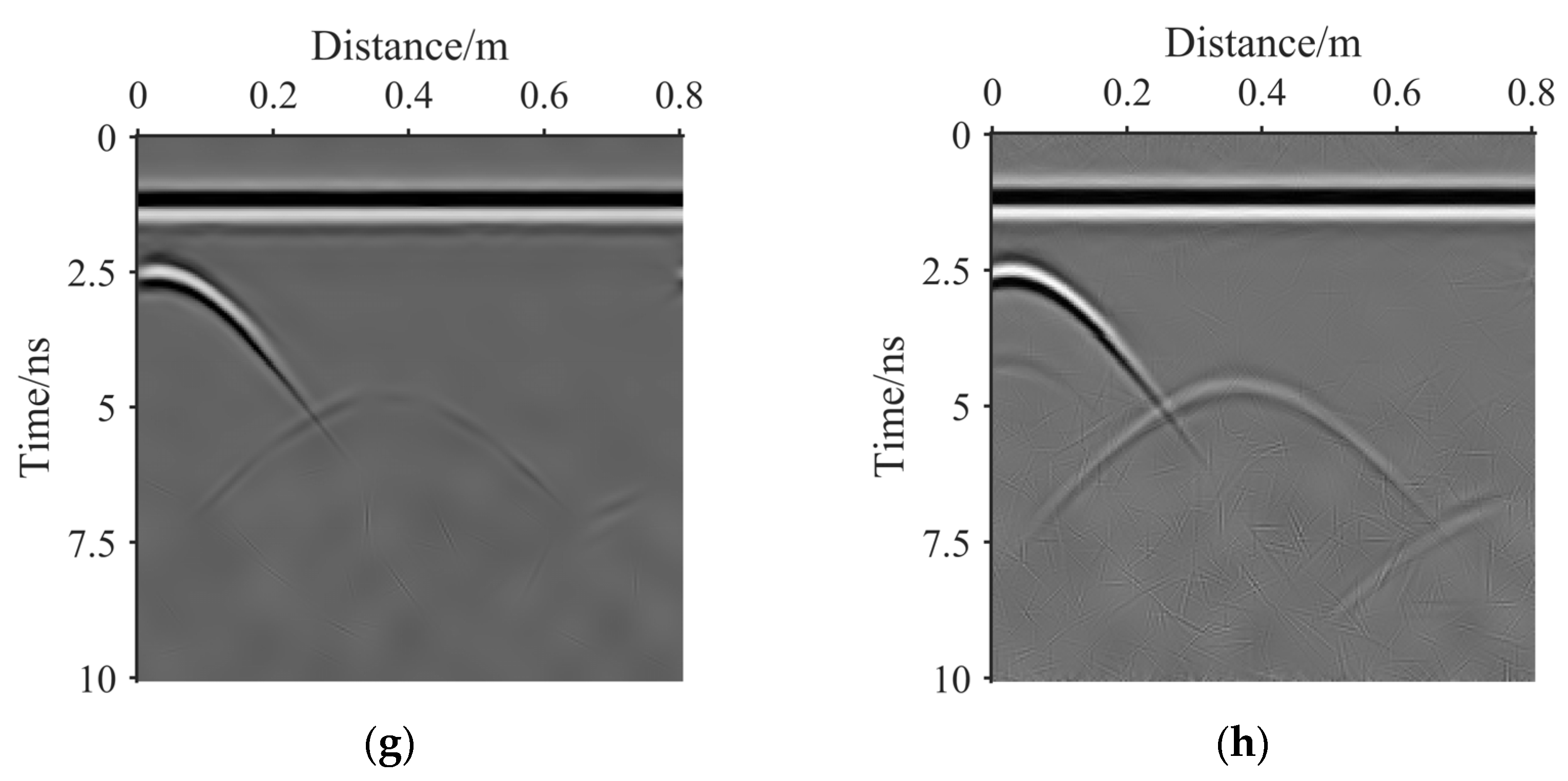
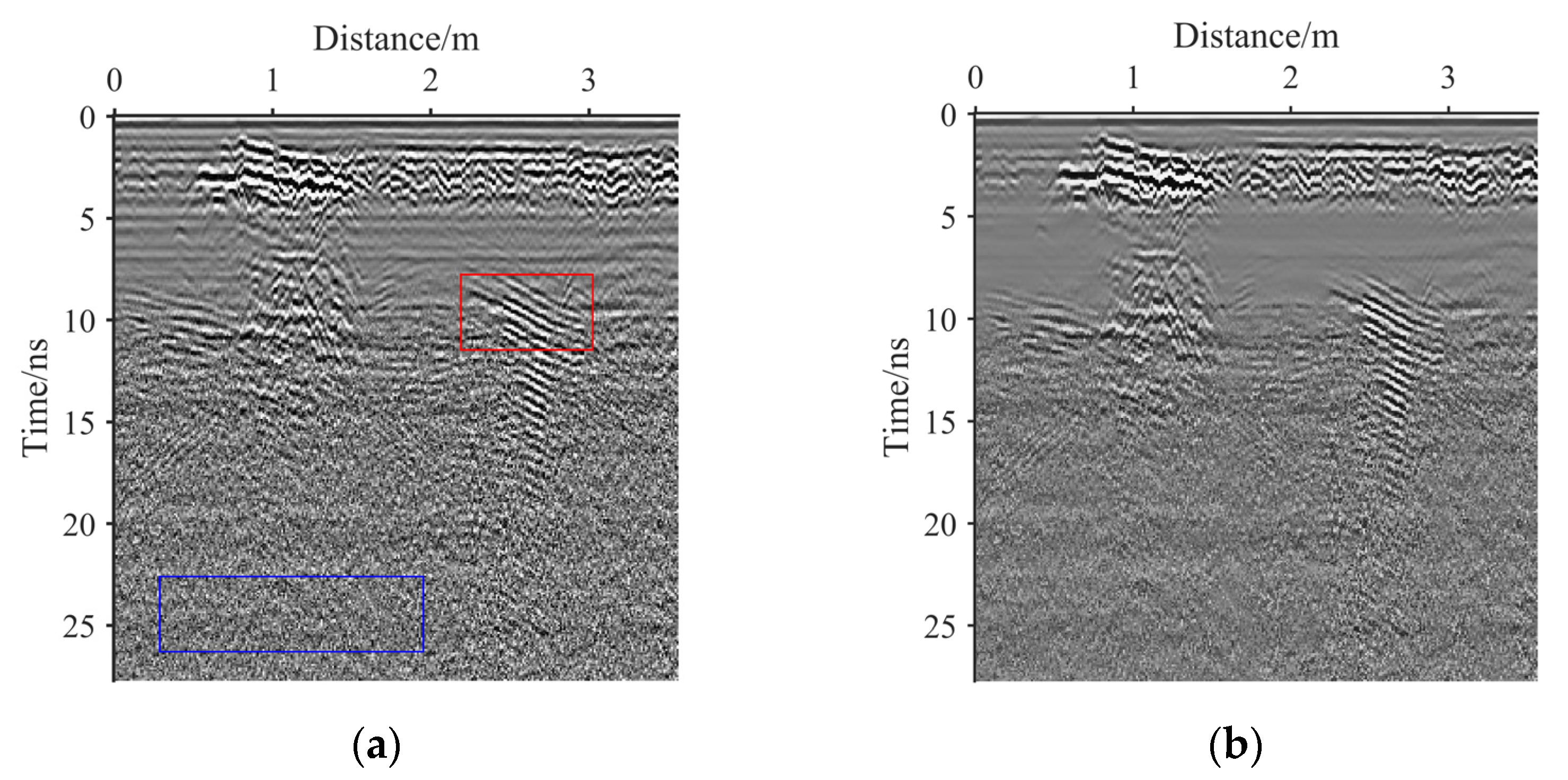
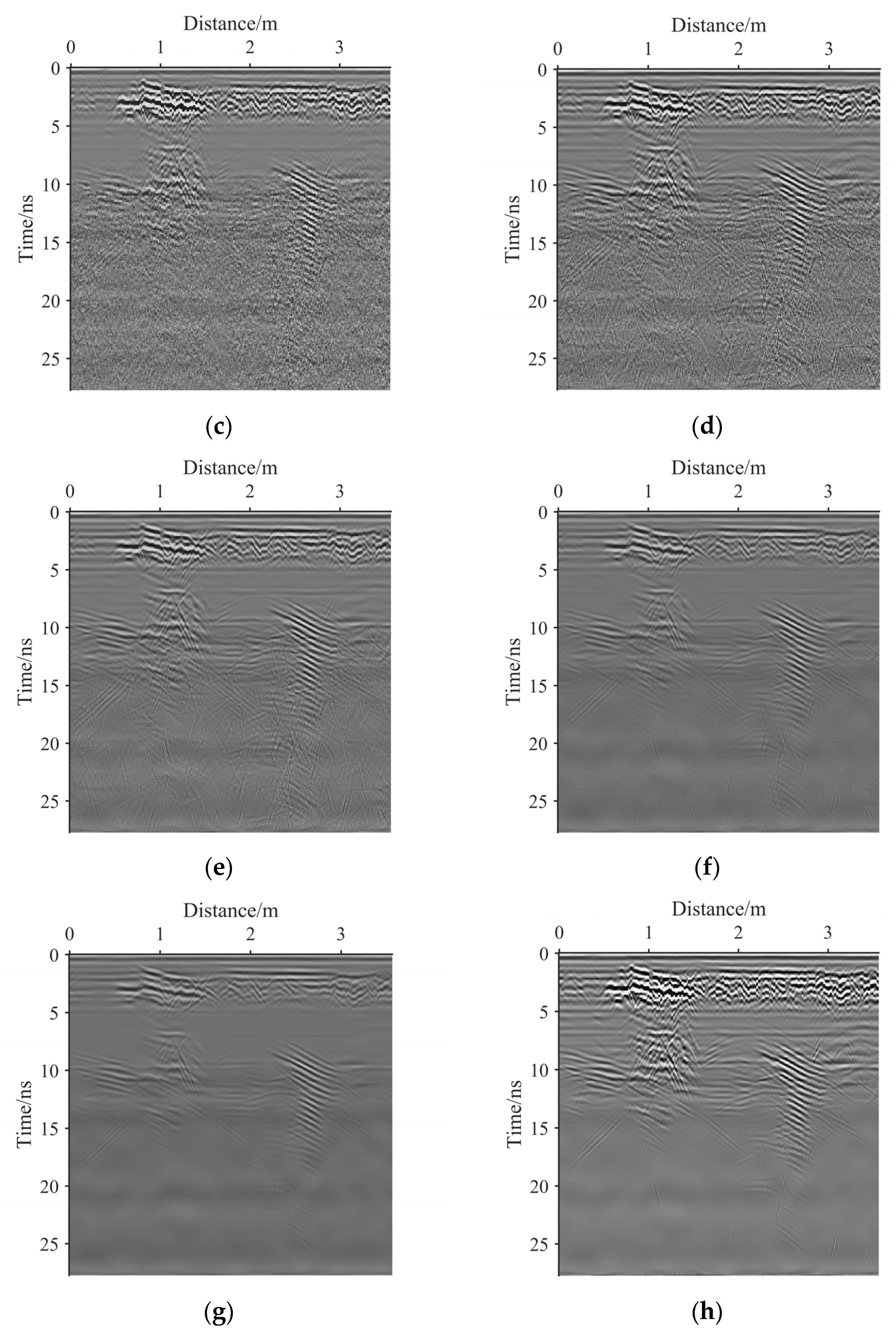
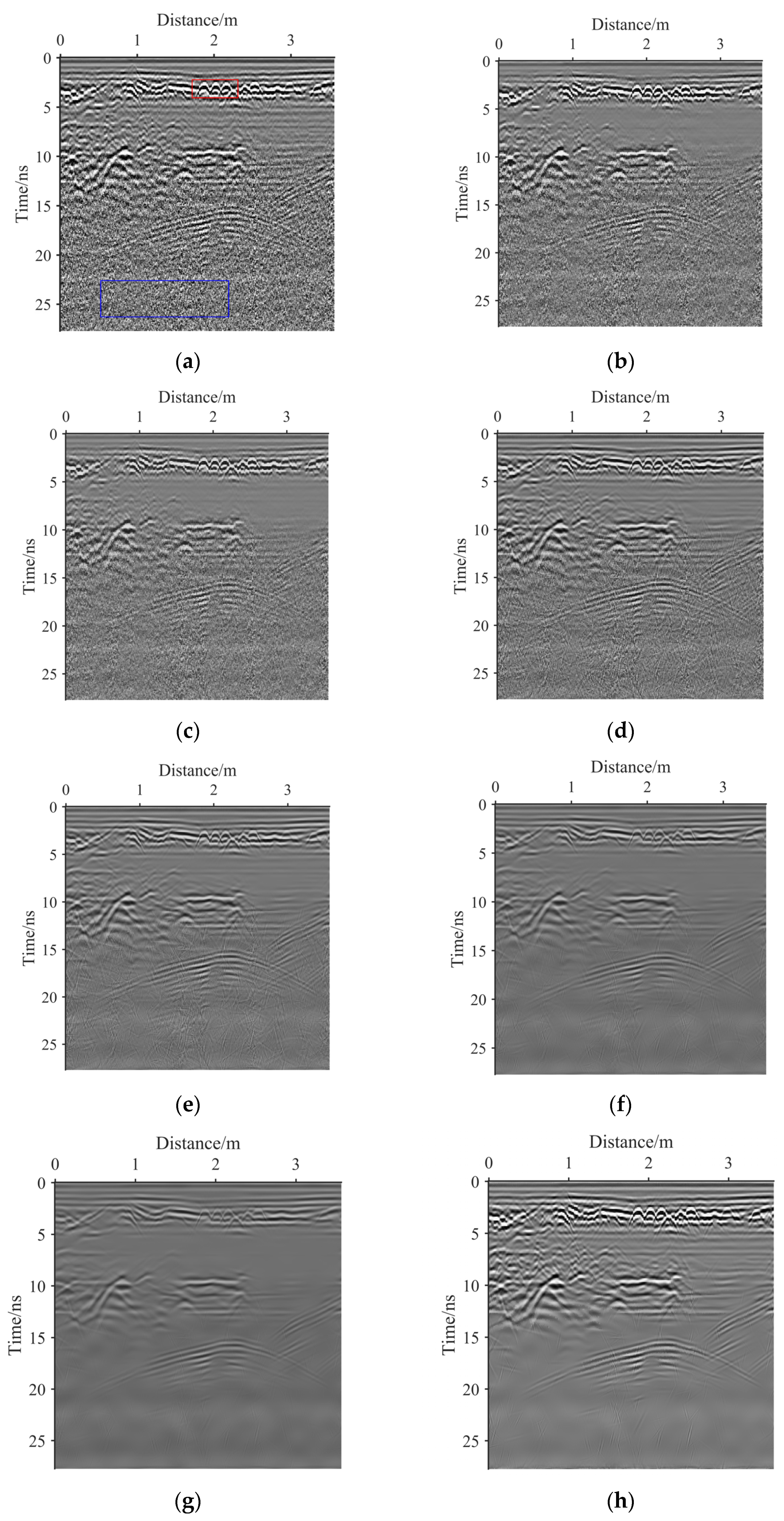
3.2. Real GPR Image Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Utsi, E.C. Ground Penetrating Radar: Theory and Practice; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Jol, H.M. Ground Penetrating Radar Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Diamanti, N.; Annan, A.P.; Jackson, S.R.; Klazinga, D. A GPR-Based Pavement Density Profiler: Operating Principles and Applications. Remote Sens. 2021, 13, 2613. [Google Scholar] [CrossRef]
- Gabler, M.; Uhnér, C.O.J.; Sundet, N.O.; Hinterleitner, A.; Nymoen, P.; Kristiansen, M.; Trinks, I. Archaeological Prospection in Wetlands—Experiences and Observations from Ground-Penetrating Radar Surveys in Norwegian Bogs. Remote Sens. 2021, 13, 3170. [Google Scholar] [CrossRef]
- Cui, X.; Zhang, Z.; Guo, L.; Liu, X.; Quan, Z.; Cao, X.; Chen, X. The Root-Soil Water Relationship Is Spatially Anisotropic in Shrub-Encroached Grassland in North China: Evidence from GPR Investigation. Remote Sens. 2021, 13, 1137. [Google Scholar] [CrossRef]
- Garrido, I.; Solla, M.; Lagüela, S.; Fernández, N. IRT and GPR techniques for moisture detection and characterisation in buildings. Sensors 2020, 20, 6421. [Google Scholar] [CrossRef]
- Šipoš, D.; Gleich, D. A lightweight and low-power UAV-borne ground penetrating radar design for landmine detection. Sensors 2020, 20, 2234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, D.; Liu, S.; Yang, J.; Wang, X.; Wang, X. The Noise Attenuation and Stochastic Clutter Removal of Ground Penetrating Radar Based on the K-SVD Dictionary Learning. IEEE Access 2021, 9, 74879–74890. [Google Scholar] [CrossRef]
- Bi, W.; Zhao, Y.; An, C.; Hu, S. Clutter elimination and random-noise denoising of GPR signals using an SVD method based on the Hankel matrix in the local frequency domain. Sensors 2018, 18, 3422. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Feng, X.; Zhang, Z.; Kang, Z.; Chai, Y.; You, Q.; Ding, L. Dip filter and random noise suppression for GPR B-scan data based on a hybrid method in f-x domain. Remote Sens. 2019, 11, 2180. [Google Scholar] [CrossRef] [Green Version]
- Xue, W.; Luo, Y.; Yang, Y.; Huang, Y. Noise suppression for gpr data based on svd of window-length-optimized hankel matrix. Sensors 2019, 19, 3807. [Google Scholar] [CrossRef] [Green Version]
- Shong, W.; Wu, H. The application of the wavelet transform technique to data processing in GPR. Geophys. Geochem. Explor. 2004, 1, 69–72. [Google Scholar]
- Baili, J.; Lahouar, S.; Hergli, M.; Amimi, A.; Besbes, K. Denoising of GPR Signals Based on the Discrete Wavelet Transform. In Proceedings of the Second International Conference on Machine Intelligence, Tozeur, Tunisia, 5–7 November 2005; pp. 103–134. [Google Scholar]
- Baili, J.; Lahouar, S.; Hergli, M.; Al-Qadi, I.L.; Besbes, K. GPR signal de-noising by discrete wavelet transform. Ndt Int. 2009, 42, 696–703. [Google Scholar] [CrossRef]
- Candès, E.J.; Donoho, D.L. New tight frames of curvelets and optimal representations of objects with piecewise C2 singularities. Commun. Pure Appl. Math. J. Courant Inst. Math. Sci. 2004, 57, 219–266. [Google Scholar] [CrossRef]
- Guo, K.; Kutyniok, G.; Labate, D. Sparse multidimensional representations using anisotropic dilation and shear operators. In Proceedings of the International Conference on the Interaction between Wavelets and Splines, Athens, Greece, 10–14 November 2006. [Google Scholar]
- Easley, G.; Labate, D.; Lim, W.-Q. Sparse directional image representations using the discrete shearlet transform. Appl. Comput. Harmon. Anal. 2008, 25, 25–46. [Google Scholar] [CrossRef] [Green Version]
- Bao, Q.-Z.; Li, Q.-C.; Chen, W.-C. GPR data noise attenuation on the curvelet transform. Appl. Geophys. 2014, 11, 301–310. [Google Scholar] [CrossRef]
- Terrasse, G.; Nicolas, J.-M.; Trouve, E.; Drouet, E. Application of the Curvelet Transform for Clutter and Noise Removal in GPR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4280–4294. [Google Scholar] [CrossRef]
- Wang, X.; Liu, S. Noise suppressing and direct wave arrivals removal in GPR data based on Shearlet transform. Signal Process. 2017, 132, 227–242. [Google Scholar] [CrossRef]
- Wen, J.; Li, Z.; Xiao, J. Noise removal in tree radar B-scan images based on shearlet. Wood Res. 2020, 65, 1–12. [Google Scholar] [CrossRef]
- Goyal, B.; Dogra, A.; Agrawal, S.; Sohi, B.; Sharma, A. Image denoising review: From classical to state-of-the-art approaches. Inf. Fusion 2019, 55, 220–244. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Jin, Z.; Chen, Y. Hybridizing grey wolf optimization with neural network algorithm for global numerical optimization problems. Neural Comput. Appl. 2020, 32, 10451–10470. [Google Scholar] [CrossRef]
- Khairuzzaman, A.K.M.; Chaudhury, S. Multilevel thresholding using grey wolf optimizer for image segmentation. Expert Syst. Appl. 2017, 86, 64–76. [Google Scholar] [CrossRef]
- Marot, J.; Migliaccio, C.; Lantéri, J.; Lauga, P.; Bourennane, S.; Brochier, L. Joint Design of the Hardware and the Software of a Radar System with the Mixed Grey Wolf Optimizer: Application to Security Check. Remote Sens. 2020, 12, 3097. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95 International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Erciyes University: Kayseri, Turkey, 2005. [Google Scholar]
- Yang, X.-S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Kumlu, D.; Erer, I.; Kaplan, N.H. Low complexity clutter removal in GPR images via lattice filters. Digit. Signal Process. 2020, 101, 102724. [Google Scholar] [CrossRef]

| Parameters | Value |
|---|---|
| Number of wolves | 10 |
| Maximum number of iterations | 10–100 |
| cost function | NIQE |
| 0.1–30 | |
| 1–3 | |
| 0.01–0.3 | |
| 0.8–0.95 |
| Methods | Simulated GPR Image 1 | Simulated GPR Image 2 |
|---|---|---|
| bilateral filter | 25.54 | 25.52 |
| guided filter | 25.72 | 25.71 |
| NSST-1 | 21.56 | 21.59 |
| NSST-2 | 26.40 | 26.24 |
| NSST-3 | 26.73 | 26.43 |
| NSST-4 | 24.59 | 24.37 |
| the proposed method | 34.57 | 32.85 |
| Methods | Simulated GPR Image 1 | Simulated GPR Image 2 |
|---|---|---|
| Original noisy image | 1.82 | 5.67 |
| bilateral filter | 2.53 | 6.49 |
| guided filter | 3.19 | 6.04 |
| NSST-1 | 2.33 | 5.65 |
| NSST-2 | 3.85 | 8.51 |
| NSST-3 | 3.00 | 17.03 |
| NSST-4 | 0.14 | 17.52 |
| the proposed method | 6.79 | 20.36 |
| Methods | Real GPR Image 1 | Real GPR Image 2 |
|---|---|---|
| Original noisy image | 5.18 | 8.95 |
| bilateral filter | 4.73 | 9.61 |
| guided filter | 10.92 | 14.59 |
| NSST-1 | 12.73 | 15.06 |
| NSST-2 | 18.27 | 22.48 |
| NSST-3 | 16.77 | 25.37 |
| NSST-4 | 14.05 | 23.01 |
| the proposed method | 28.09 | 40.59 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Wang, C.; Zheng, R.; Li, X. GPR Image Noise Removal Using Grey Wolf Optimisation in the NSST Domain. Remote Sens. 2021, 13, 4416. https://doi.org/10.3390/rs13214416
He X, Wang C, Zheng R, Li X. GPR Image Noise Removal Using Grey Wolf Optimisation in the NSST Domain. Remote Sensing. 2021; 13(21):4416. https://doi.org/10.3390/rs13214416
Chicago/Turabian StyleHe, Xingkun, Can Wang, Rongyao Zheng, and Xiwen Li. 2021. "GPR Image Noise Removal Using Grey Wolf Optimisation in the NSST Domain" Remote Sensing 13, no. 21: 4416. https://doi.org/10.3390/rs13214416
APA StyleHe, X., Wang, C., Zheng, R., & Li, X. (2021). GPR Image Noise Removal Using Grey Wolf Optimisation in the NSST Domain. Remote Sensing, 13(21), 4416. https://doi.org/10.3390/rs13214416






