A Loading Correction Model for GPS Measurements Derived from Multiple-Data Combined Monthly Gravity
Abstract
:1. Introduction
2. Materials and Methods
2.1. GPS Data
2.2. GCM-Based Loading Data
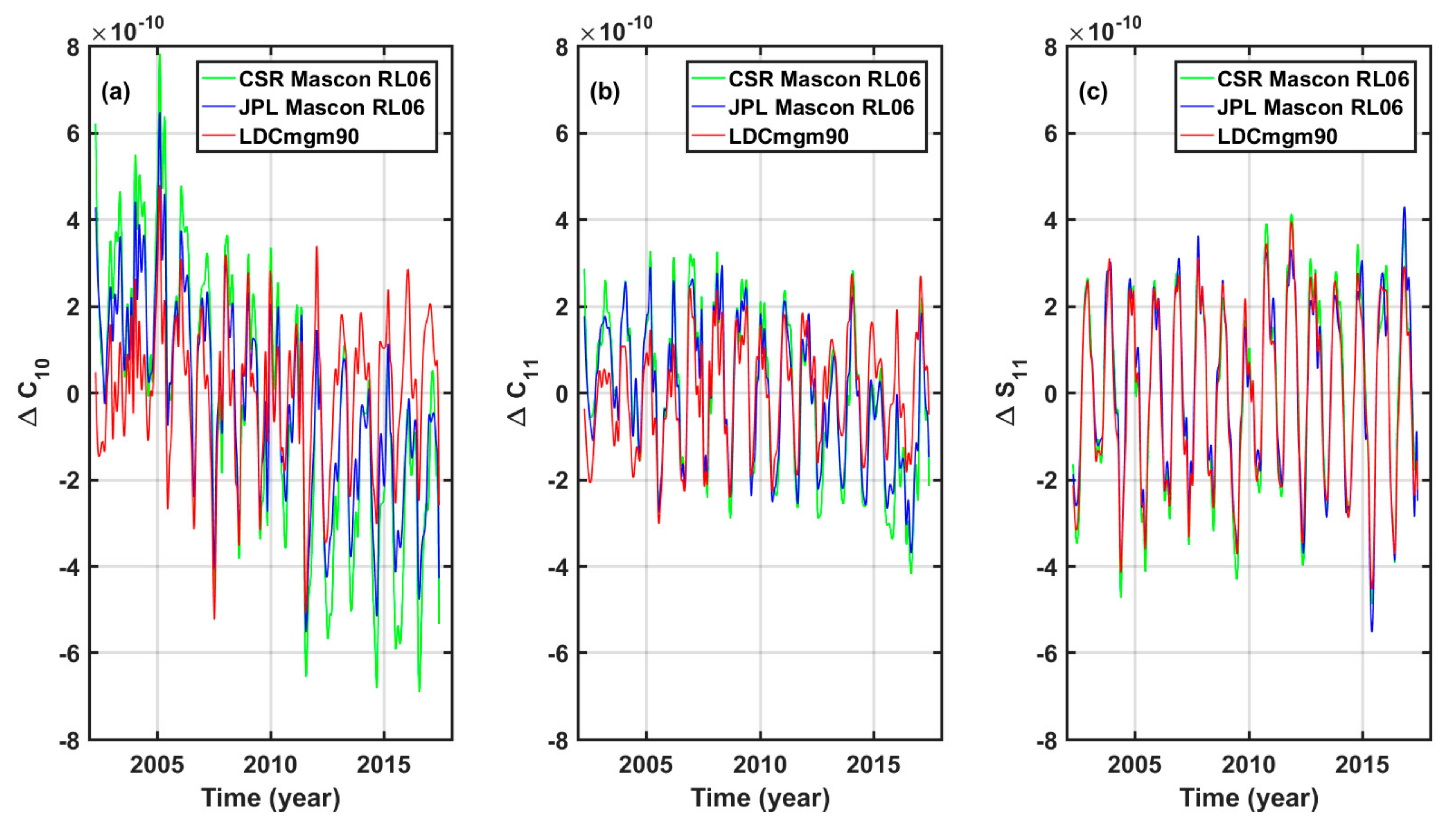
2.3. LDCmgm90-Based Loading Data and Geocenter Motion Correction
2.4. Method to Determine Loading Deformations
3. Results
4. Discussion
4.1. Comparison of Annual Residual
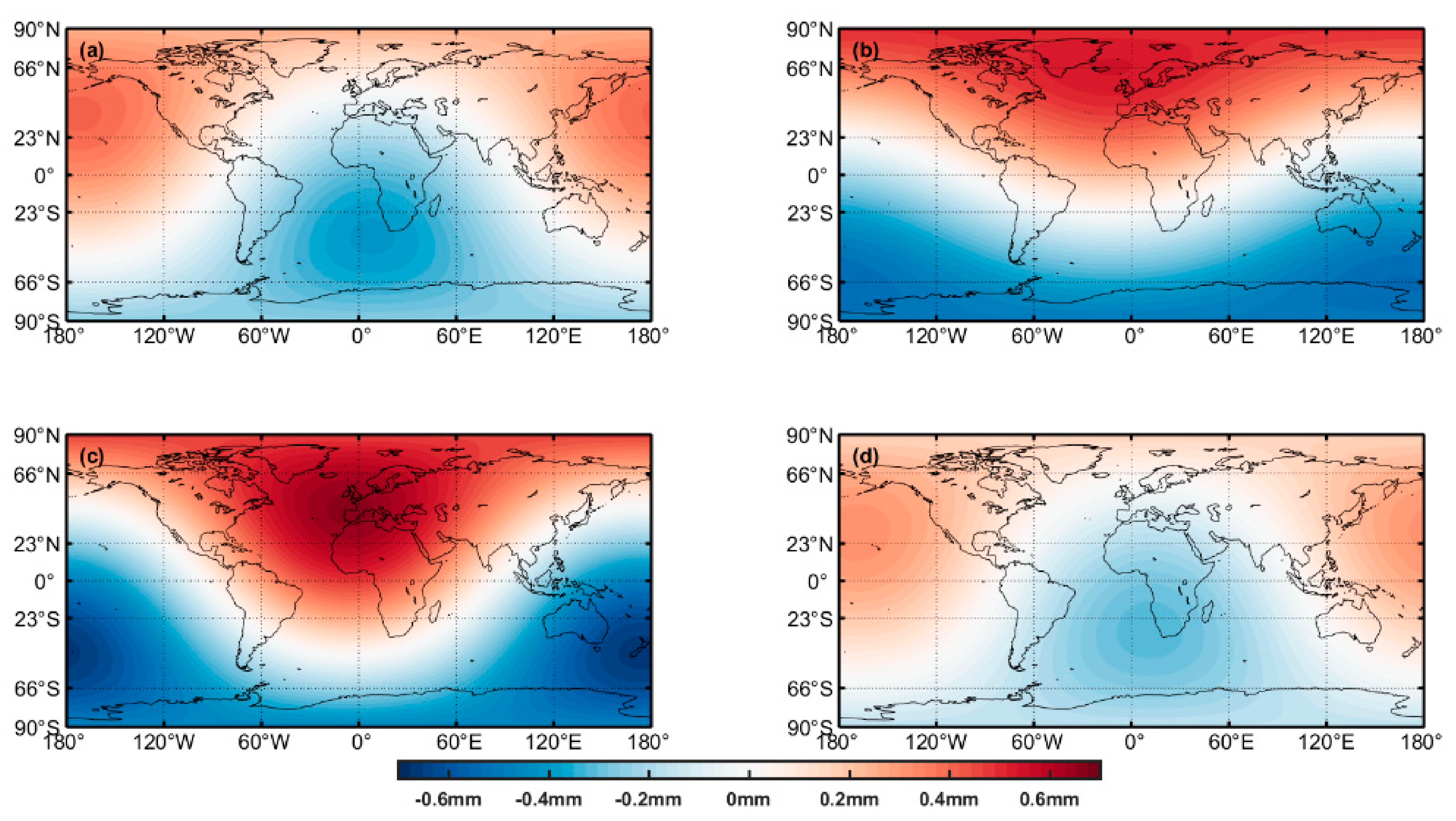
4.2. Loading Due to Seasonal Mass Redistributions
4.3. Contributions of Secular or Long-Term Mass Redistributions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Estimations of Degree-1 Stokes Coefficients and Geocenter Variation of LDCmgm90
| Model | X | σX | Y | σY | Z | σZ |
|---|---|---|---|---|---|---|
| Annual Amplitude (unit: mm) | ||||||
| CSR Mascon | 2.06 | 0.02 | 3.06 | 0.02 | 2.84 | 0.02 |
| JPL Mascon | 1.82 | 0.02 | 2.88 | 0.02 | 1.91 | 0.02 |
| LDCmgm90 | 1.52 | 0.01 | 2.93 | 0.01 | 1.91 | 0.02 |
| Annual Phase (unit: day) 2 | ||||||
| CSR Mascon | 33.88 | 0.48 | 179.56 | 0.30 | 34.47 | 0.42 |
| JPL Mascon | 39.48 | 0.49 | 179.75 | 0.31 | 38.70 | 0.57 |
| LDCmgm90 | 58.95 | 0.50 | 179.70 | 0.26 | 74.57 | 0.58 |
| Linear Trend (unit: mm/year) | ||||||
| CSR Mascon | −0.07 | 0.05 | −0.46 | 0.05 | 1.01 | 0.06 |
| JPL Mascon | −0.05 | 0.04 | 0.03 | 0.04 | 0.58 | 0.05 |
| LDCmgm90 | 0.13 | 0.04 | −0.37 | 0.04 | 0.62 | 0.06 |
Appendix B. Sources of GPS Measurement Errors and Other Systematic Effects
- Draconitic Year Errors
- Temperature Cycle
- Errors in IERS Models
- Antenna-Related Effects
References
- Ray, J. Precision and Accuracy of GNSS Positions; Lecture Presented at School of Geodesy and Geomatics; Wuhan University: Wuhan, China, 4 January 2015. [Google Scholar]
- Petit, G.; Luzum, B. IERS Conventions (2010), IERS Technical Notes 36; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt, Germany, 2010; p. 179. ISBN 3-89888-989-6. [Google Scholar]
- Ray, J.; Altamimi, Z.; Collilieux, X.; van Dam, T. Anomalous harmonics in the spectra of GPS position estimates. GPS Solut. 2008, 12, 55–64. [Google Scholar] [CrossRef]
- Ray, J.; Rebischung, P.; Griffiths, J. IGS polar motion measurement accuracy. Geod. Geodyn. 2017, 8, 413–420. [Google Scholar] [CrossRef]
- van Dam, T.; Wahr, J.; Milly, P.; Shmakin, A.; Blewitt, G.; Lavallee, D.; Larson, K.M. Crustal displacements due to continental water loading. Geophys. Res. Lett. 2001, 28, 651–654. [Google Scholar] [CrossRef] [Green Version]
- Van Dam, T.; Collilieux, X.; Wuite, J.; Altamimi, Z.; Ray, J. Nontidal ocean loading: Amplitudes and potential effects in GPS height time series. J. Geodyn. 2012, 86, 1043–1057. [Google Scholar] [CrossRef] [Green Version]
- Blewitt, G.; Lavallee, D.; Clarke, P.; Nurutdinov, K. A newglobal mode of Earth deformation: Seasonal cycle detected. Science 2001, 294, 2342–2345. [Google Scholar] [CrossRef] [Green Version]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.; Miyazaki, S. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. 2002, 107, 2075. [Google Scholar] [CrossRef] [Green Version]
- Kaniuth, K.; Vetter, S. Estimating atmospheric pressure loading regression coefficients from GPS observations. GPS Solut. 2006, 10, 126–134. [Google Scholar] [CrossRef]
- Grapenthin, R.; Sigmundsson, F.; Geirsson, H.; Árnadóttir, T.; Pinel, V. Icelandic rhythmic: Annual modulation of land elevation and plate spreading by snow load. Geophys. Res. Lett. 2006, 33, L24305. [Google Scholar] [CrossRef] [Green Version]
- Tregoning, P.; Watson, C. Atmospheric effects and spurious signals in GPS analyses. J. Geophys. Res. 2009, 114, B09403. [Google Scholar] [CrossRef] [Green Version]
- King, M.A.; Watson, C.S.; Penna, N.T.; Clarke, P.J. Subdailysignals in GPS observations and their effect at semiannual and annual periods. Geophys. Res. Lett. 2008, 35, L03302. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.; Chen, W.; Zhu, Y.; Zhang, W.; Zhong, M. Contributions of thermal expansion of monuments and nearby bedrock to observed GPS height changes. Geophys. Res. Lett. 2009, 36, L13301. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Dixon, T.; Wdowinski, S. Accelerating uplift in the north Atlantic region as an indicator of ice loss. Nat. Geosci. 2010, 3, 404–407. [Google Scholar] [CrossRef]
- Matsuo, K.; Heki, K. Time-variable ice loss in Asian high mountains from satellite gravimetry. Earth Planet. Sci. Lett. 2010, 290, 30–36. [Google Scholar] [CrossRef]
- Yuan, L.G.; Chao, B.F. Analysis of tidal signals in surface displacement measured by a dense continuous GPS array. Earth Planet. Sci. Lett. 2012, 355–356, 255–261. [Google Scholar] [CrossRef]
- van Dam, T.; Wahr, J. Displacement of the Earth’s surface due to atmospheric loading: Effects on gravity and baseline measurements. J. Geophys. Res. 1987, 92, 1282–1286. [Google Scholar] [CrossRef]
- Mangiarotti, S.; Cazenave, A. Annual vertical crustal motions predicted from surface mass redistribution and observed by space geodesy. J. Geophys. Res. 2001, 106, 4277–4291. [Google Scholar] [CrossRef]
- Blewitt, G. Self-consistency in the reference frames, geocenter definition and surface loading of the solid earth. J. Geophys. Res. 2003, 108, 2103. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Ray, J.; Shen, W.B.; Huang, C.L. Polar motion excitations for an Earth model with frequency-dependent responses: 2 Numerical tests of the meteorological excitations. J. Geophys. Res. Solid Earth 2013, 118, 4995–5007. [Google Scholar] [CrossRef]
- Chen, W.; Li, J.C.; Ray, J.; Cheng, M.K. Improved geophysical excitations constrained by polar motion observations and GRACE/SLR time-dependent gravity. Geod. Geodyn. 2017, 6, 11–22. [Google Scholar] [CrossRef]
- Taplay, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [Green Version]
- Davis, J.; Elósegui, P.; Mitrovica, J.; Tamisiea, M. Climate-driven deformation of the solid Earth from GRACE and GPS. Geophys. Res. Lett. 2004, 31, L24605. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.; Chen, W.; Yuan, L. Crustal vertical deformation response to different spatial scales of GRACE and GCMs surface loading. Geophys. J. Int. 2016, 204, 505–516. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Freymueller, J.T. Seasonal and long-term vertical deformation in Nepal Himalaya constrained by GPS and GRACE measurements. J. Geophys. Res. 2012, 117, B03407. [Google Scholar] [CrossRef]
- Chanard, K.; Fleitout, L.; Calais, E.; Rebischung, P.; Avouac, J.-P. Toward a global horizontal and vertical elastic load deformation model derived from GRACE and GNSS station position time series. J. Geophys. Res. Solid Earth 2018, 123, 3225–3237. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the earth’s gravity field: Hydrological and oceanic effects and their possible detection using grace. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Famiglietti, J.S.; Rodell, M. Spatial sensitivity of GRACE time-variable gravity observations. J. Geophys. Res. 2005, 110, B08408. [Google Scholar]
- Chen, W.; Luo, J.; Ray, J.; Yu, N.; Li, J.C. Multiple-data-based monthly geopotential model set LDCmgm90. Sci. Data 2019, 6, 228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, X.; Heflin, M.B.; Ivins, E.R.; Fukumori, I. Seasonal and interannual global surface mass variations from multisatellite geodetic data. J. Geophys. Res. 2006, 111, B09401. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.K.; Ries, J.C.; Tapley, B.D. Variations of the Earth’s figure axis from satellite laser ranging and GRACE. J. Geophys. Res. 2011, 116, B01409. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.K.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. Solid Earth 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Bar-Sever, Y.E. A new model for GPS yaw attitude. J. Geod. 1996, 70, 714–723. [Google Scholar] [CrossRef]
- Bar-Sever, Y.E.; Kuang, D. New Empirically-Derived Solar Radiation Pressure Model for GPS Satellites; Institute of Navigation: Portland, OR, USA, 2005; pp. 42–160. Available online: http://ipnpr.jpl.nasa.gov/progress_report/42-160/title.htm (accessed on 6 December 2020).
- Bassiri, S.; Hajj, G.A. Higher-order ionospheric effects on the global positioning systems observables and means of modeling them. Manuscr. Geodtica 1993, 18, 280–289. [Google Scholar]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 378–386. [Google Scholar] [CrossRef]
- Blewitt, G. An automatic editing algorithm for GPS data. Geophys. Res. Lett. 1990, 17, 199–202. [Google Scholar] [CrossRef] [Green Version]
- Kedar, S.; Hajj, G.; Wilson, B.; Heflin, M. The effect of the second order GPS ionospheric correction on receiver positions. Geophys. Res. Lett. 2003, 30, 1829. [Google Scholar] [CrossRef]
- Kreemer, C.; Blewitt, G.; Klein, E. A geodetic plate motion and Global Strain Rate Model. Geochem. Geophys. Geosystems 2014, 15, 3849–3889. [Google Scholar] [CrossRef]
- Sibois, A.; Selle, C.; Desai, S.; Sibthorpe, A.; Weiss, J. GSPM13: An updated empirical model for solar radiation pressure forces acting on GPS satellites. In Proceedings of the IGS Workshop 2014, Pasadena, CA, USA, 23–27 June 2014. [Google Scholar]
- Martens, H.R.; Argus, D.F.; Norberg, C.; Blewitt, G.; Herring, T.A.; Moore, A.W.; Hammond, W.C.; Kreemer, C. Atmospheric pressure loading in GPS positions: Dependency on GPS processing methods and effect on assessment of seasonal deformation in the contiguous USA and Alaska. J. Geod. 2020, 94, 115. [Google Scholar] [CrossRef]
- Petrov, L.; Boy, J.-P. Study of the atmospheric pressure loading signal in VLBI observations. J. Geophys. Res. 2004, 109, B03405. [Google Scholar]
- Petrov, L. The International Mass loading Service. arXiv 2015, arXiv:1503.00191. [Google Scholar]
- Carrère, L.; Lyard, F. Modelling the barotropic response of the global ocean to atmospheric wind and pressure forcing—Comparisons with observations. Gephys. Res. Lett. 2003, 30, 1275–1278. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Houser, R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Dill, R.; Dobslaw, H. Numerical simulations of global-scale high-resolution hydrological crustal deformations. J. Geophys. Res. Solid Earth 2013, 118, 5008–5017. [Google Scholar] [CrossRef]
- Dobslaw, H.; Bergmann-Wolf, I.; Dill, R.; Poropat, L.; Thomas, M.; Dahle, C.; Esselborn, S.; König, R.; Flechtner, F. A new high-resolution model of non-tidal atmosphere and ocean mass variability for de-aliasing of satellite gravity observations: AOD1B RL06. Geophys. J. Int. 2017, 211, 263–269. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Yang, S.; Luo, J.; Ray, J.; Huang, Y.; Li, J. Global Glacial Isostatic Adjustment Constrained by GPS Measurements: Spherical Harmonic Analyses of Uplifts and Geopotential Variations. Remote Sens. 2020, 12, 1209. [Google Scholar] [CrossRef] [Green Version]
- Swenson, S.C.; Chambers, D.P.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Solid Earth 2008, 113, B08410. [Google Scholar] [CrossRef] [Green Version]
- Han, D.; Wahr, J. The viscoelastic relaxation of a realistically stratified Earth, and a further analysis of post-glacial rebound. Geophys. J. Int. 1995, 120, 287–311. [Google Scholar] [CrossRef] [Green Version]
- Farrell, W.E. Deformation of the Earth by Surface loads. Rev. Geophys. Space Phys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Chen, J.Y.; Pan, E.; Bevis, M. Accurate computation of the elastic load Love numbers to high spectral degree for a finely layered, transversely isotropic and self-gravitating Earth. Geophys. J. Int. 2018, 212, 827–838. [Google Scholar] [CrossRef]
- Griffiths, J.; Ray, J.R. Sub-daily alias and draconitic errors in the IGS orbits. GPS Solut. 2013, 17, 413–422. [Google Scholar] [CrossRef]
- Yuan, L.; Chao, B.F.; Ding, X.; Zhong, P. The tidal displacement field at Earth’s surface determined using global GPS observations. J. Geophys. Res. Solid Earth 2013, 118, 2618–2632. [Google Scholar] [CrossRef] [Green Version]

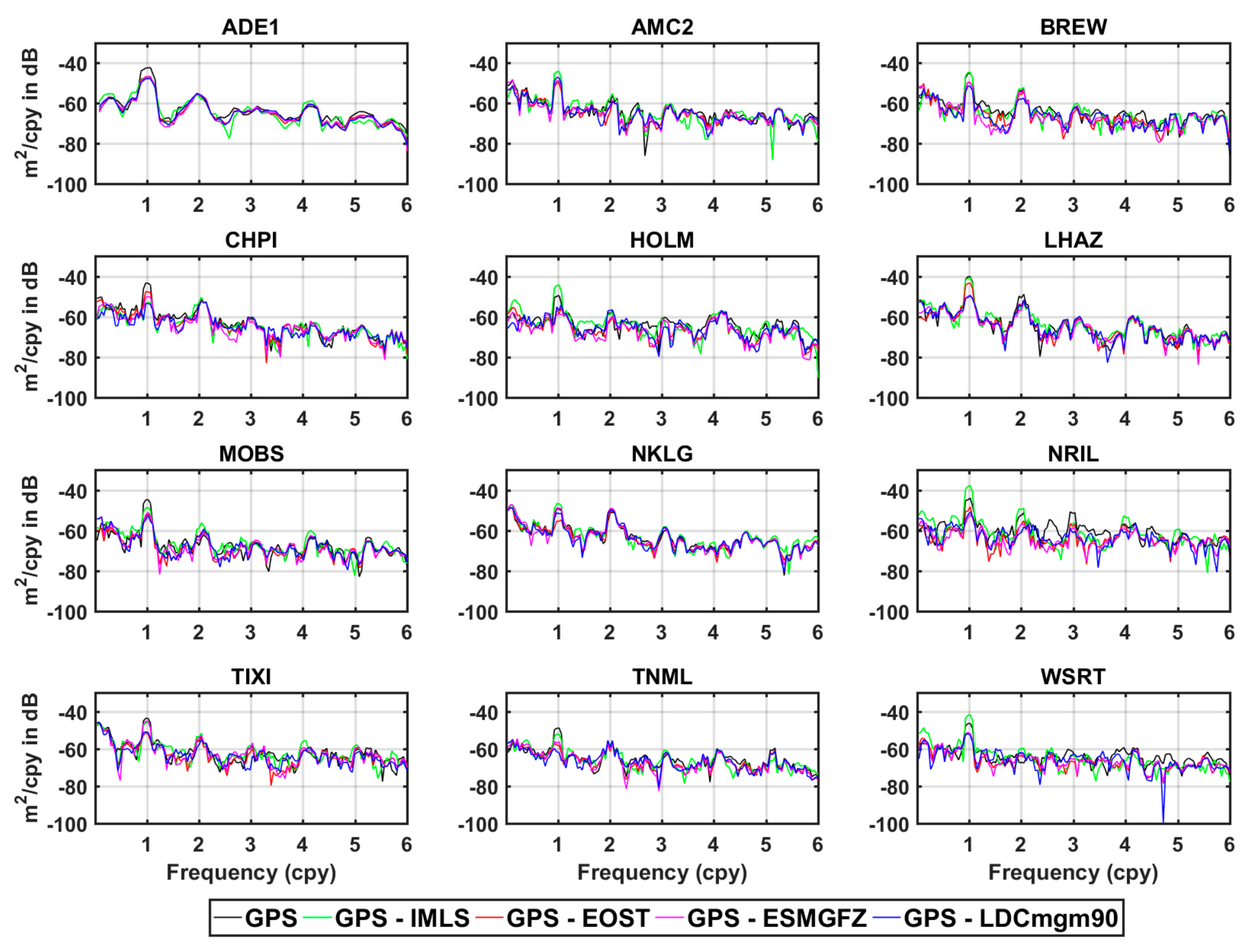
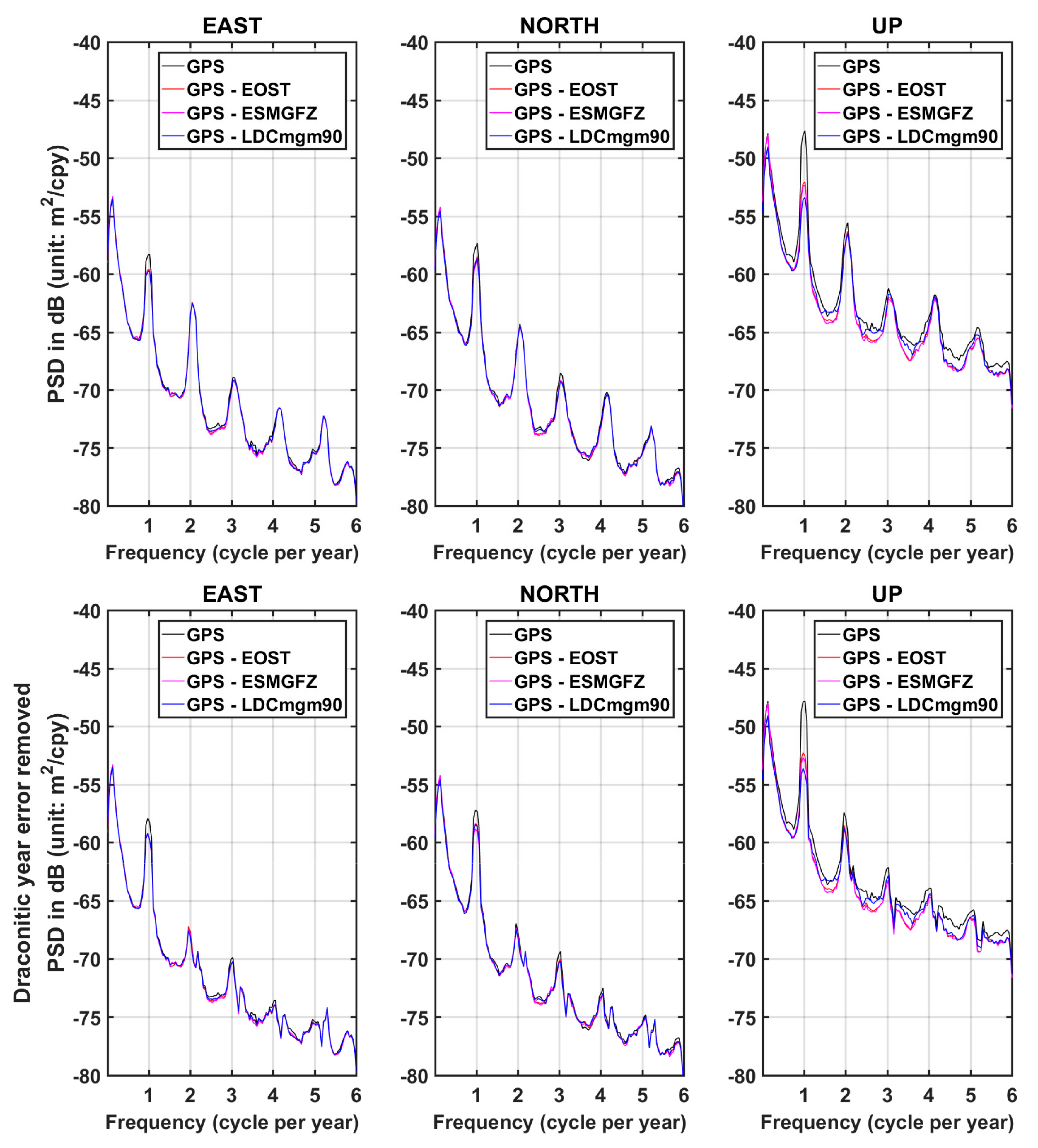
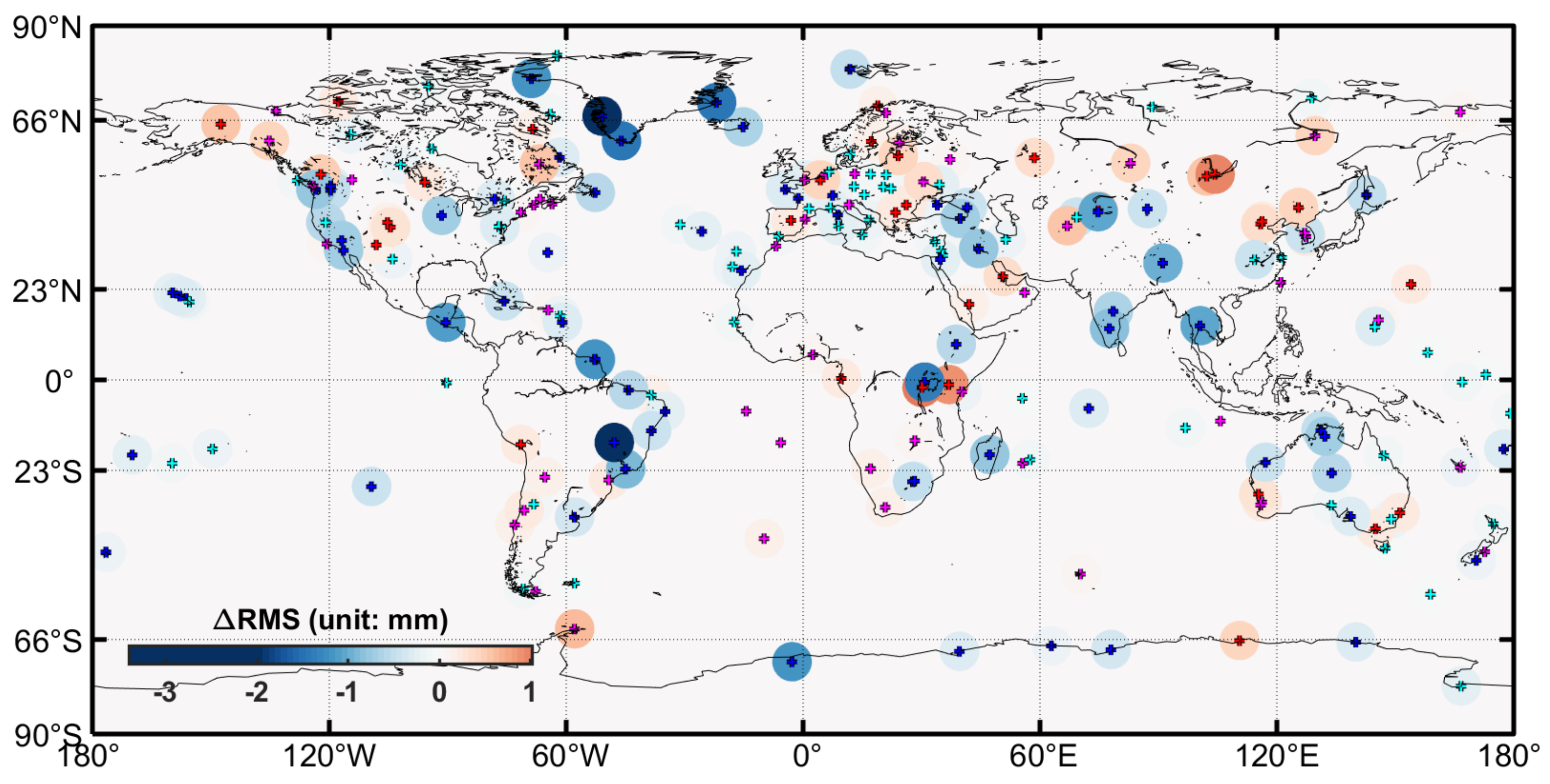
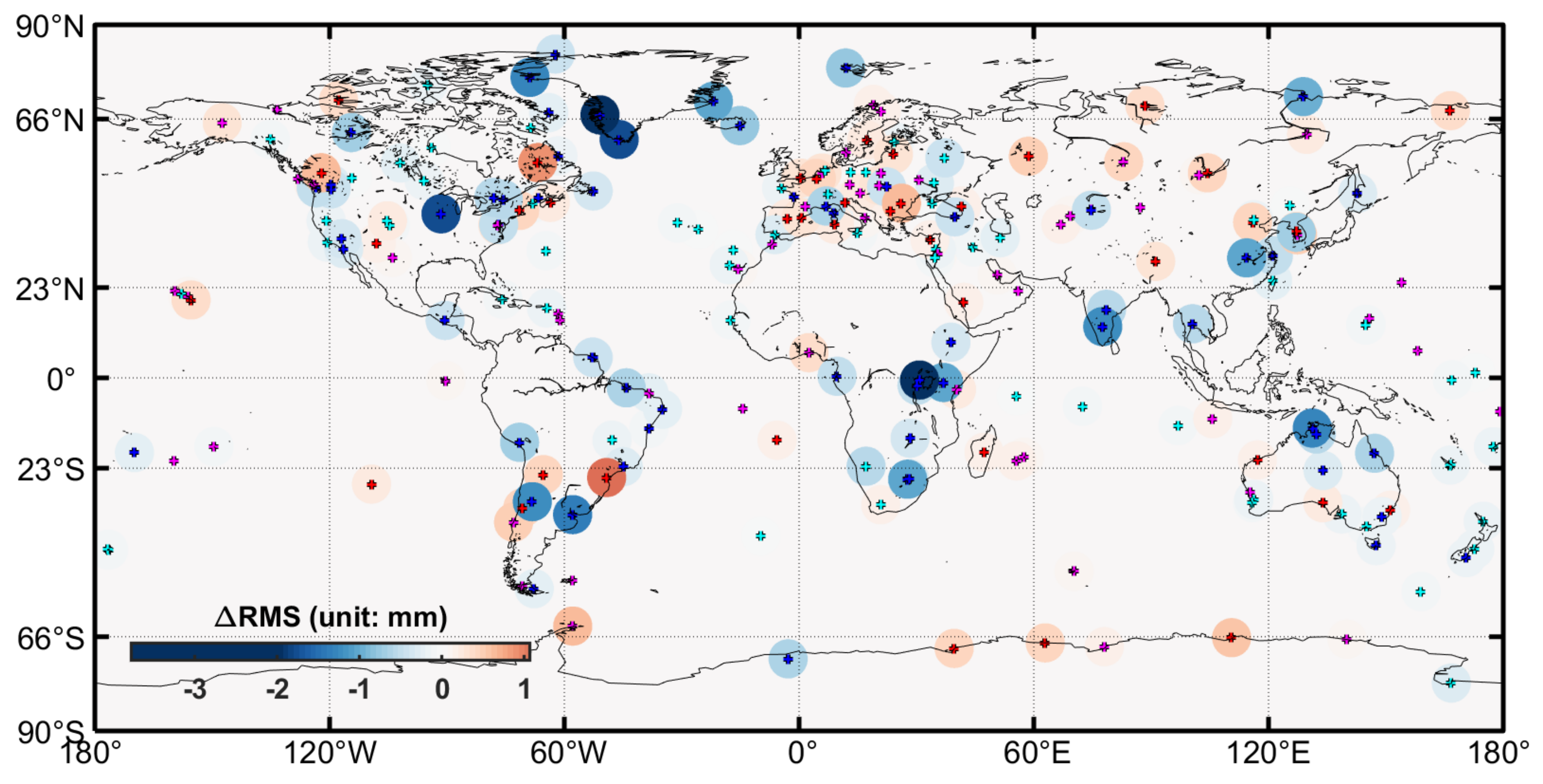
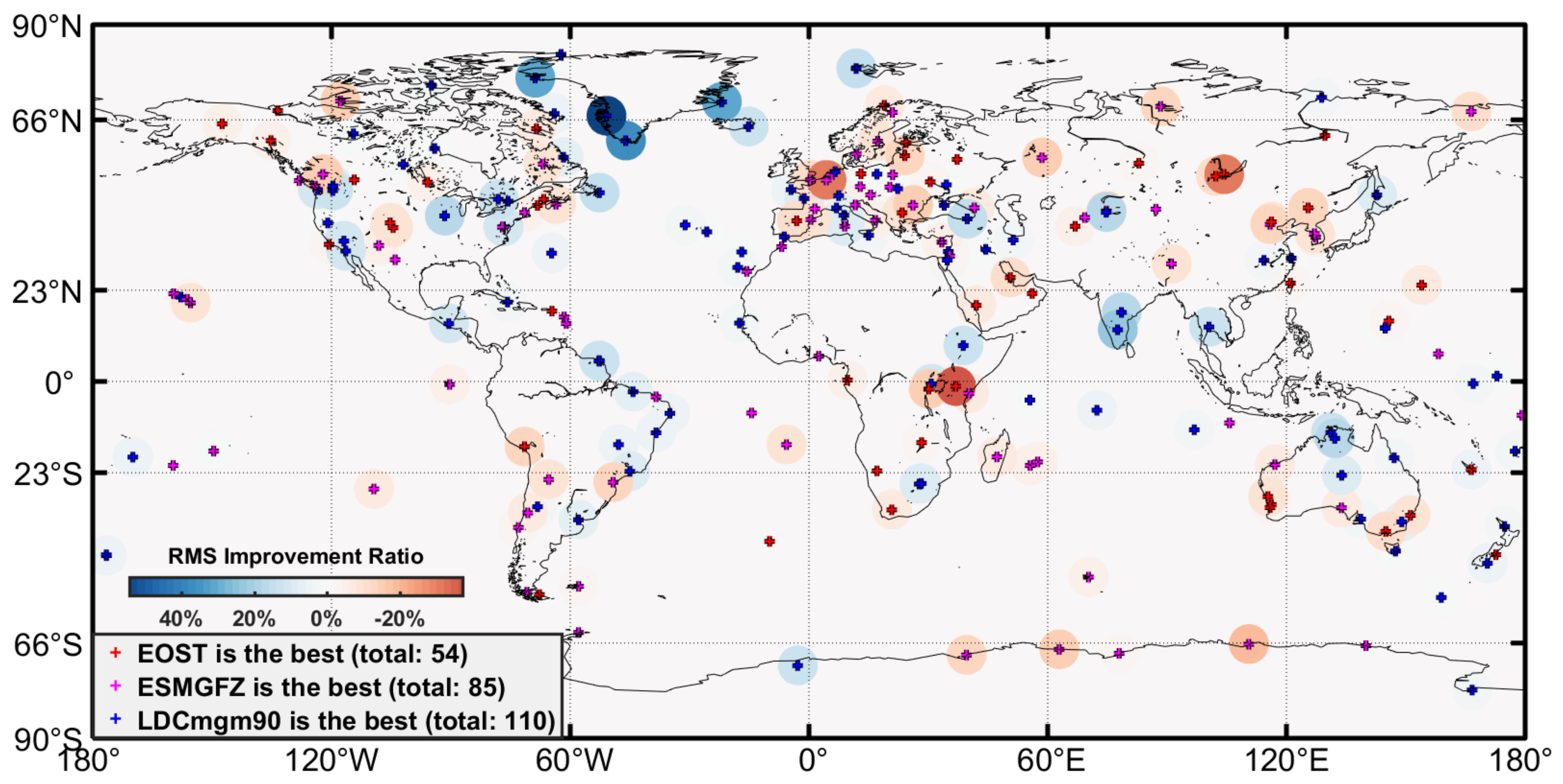
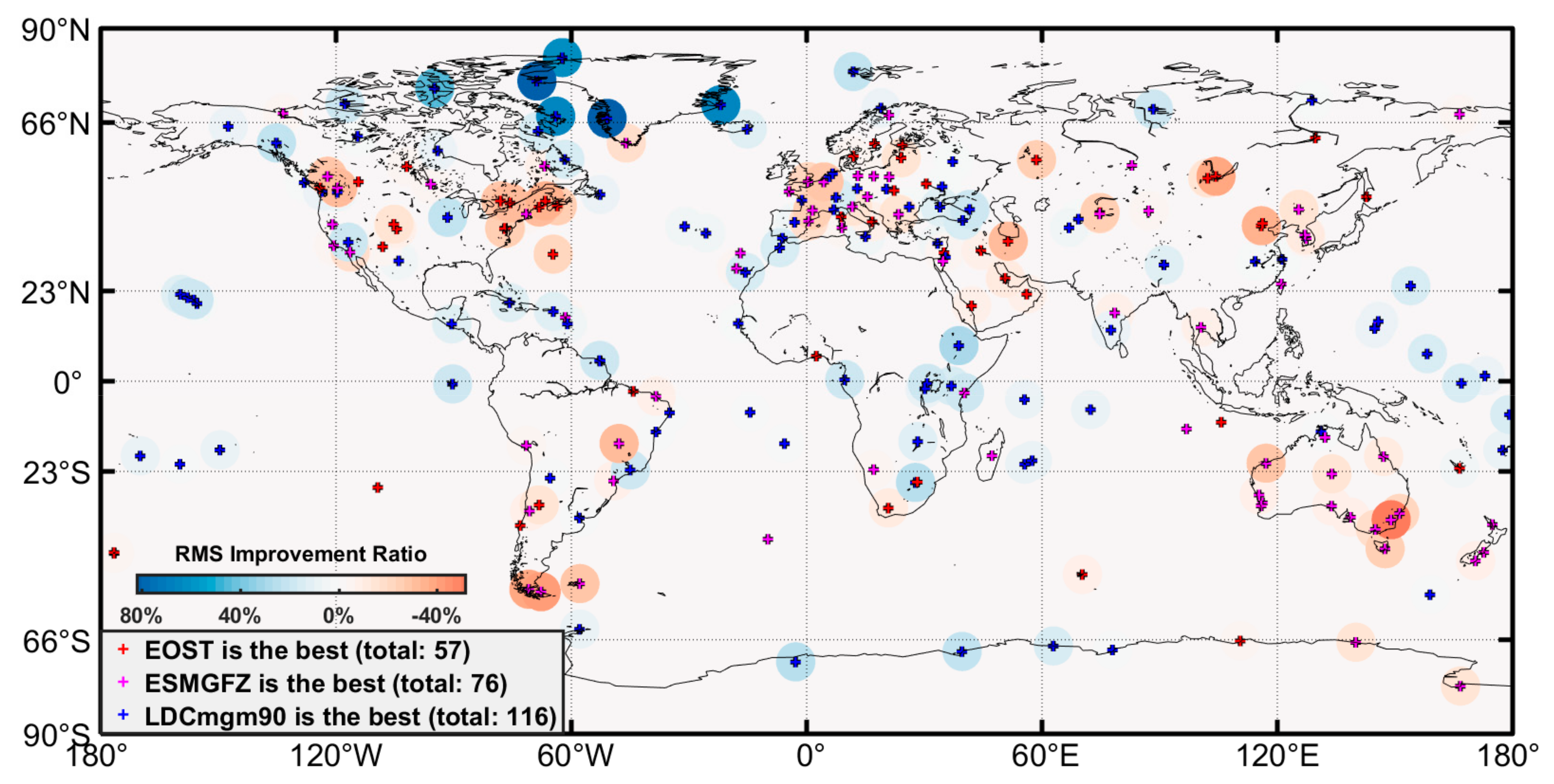
| Dataset | Atmosphere Loading | Ocean Loading | Hydrology Loading | Sea-Level Loading |
|---|---|---|---|---|
| IMLS | GEOS-FPIT | MPIOM06 | GEOS-FPIT | \ |
| EOST | ECMWF reanalysis | TUGO-m | GLDAS/Noah | \ |
| ESMGFZ | ECMWF operational | MPIOM | LSDM | ESMGFZ SLEL |
| LDCmgm90 | LDCmgm90 GAA | LDCmgm90 GAB | LDCmgm90 GSM | \ |
| Station | GPS | GPS—(A + O) 1 | GPS—(A + O + H) 2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| IMLS | EOST | ESMGFZ | LDC 3 | IMLS | EOST | ESMGFZ | LDC | ||
| ADE1 | 7.61 | 4.29 | 5.02 | 4.55 | 4.52 | 4.31 | 4.46 | 4.30 | 3.93 |
| AMC2 | 2.62 | 1.18 | 2.38 | 2.09 | 2.34 | 4.54 | 2.37 | 2.72 | 3.28 |
| BREW | 4.28 | 4.52 | 4.32 | 4.46 | 3.80 | 4.37 | 2.46 | 2.47 | 1.95 |
| CHPI | 5.16 | 4.09 | 4.78 | 4.52 | 4.38 | 1.03 | 2.88 | 1.75 | 0.86 |
| HOLM | 2.33 | 1.44 | 1.43 | 1.44 | 0.64 | 4.36 | 0.52 | 0.21 | 0.78 |
| LHAZ | 7.29 | 8.23 | 6.79 | 7.08 | 6.79 | 6.96 | 5.00 | 2.16 | 2.25 |
| MOBS | 4.32 | 1.95 | 2.64 | 2.33 | 1.91 | 2.47 | 1.44 | 1.65 | 1.30 |
| NKLG | 2.51 | 2.47 | 1.71 | 1.89 | 1.51 | 3.37 | 1.13 | 2.59 | 1.87 |
| NRIL | 4.36 | 5.39 | 3.82 | 4.25 | 3.29 | 9.48 | 2.55 | 1.19 | 1.61 |
| TIXI | 4.75 | 2.64 | 3.08 | 2.62 | 2.07 | 3.75 | 1.93 | 4.24 | 1.96 |
| TNML | 2.79 | 1.93 | 1.70 | 1.52 | 0.81 | 1.86 | 0.94 | 1.15 | 0.51 |
| WSRT | 3.44 | 1.35 | 3.57 | 2.75 | 2.35 | 6.14 | 1.85 | 1.94 | 1.58 |
| Station | GPS | GPS—(A + O) 1 | GPS—(A + O + H) 2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| IMLS | EOST | ESMGFZ | LDC 3 | IMLS | EOST | ESMGFZ | LDC | ||
| ADE1 | 1.36 | 1.55 | 1.57 | 1.56 | 1.48 | 1.18 | 1.50 | 1.43 | 1.51 |
| AMC2 | 0.83 | 0.50 | 0.41 | 0.40 | 0.40 | 0.86 | 0.30 | 0.53 | 0.44 |
| BREW | 1.51 | 1.62 | 1.20 | 1.31 | 1.04 | 1.67 | 1.20 | 1.45 | 0.75 |
| CHPI | 1.16 | 1.04 | 1.05 | 1.02 | 0.99 | 1.50 | 0.85 | 0.46 | 0.81 |
| HOLM | 0.96 | 0.80 | 0.93 | 1.01 | 0.95 | 0.77 | 0.45 | 0.50 | 0.94 |
| LHAZ | 2.35 | 2.47 | 2.36 | 2.44 | 2.34 | 1.34 | 1.53 | 1.07 | 1.46 |
| MOBS | 0.18 | 0.37 | 0.43 | 0.38 | 0.32 | 0.86 | 0.48 | 0.36 | 0.25 |
| NKLG | 0.88 | 0.68 | 0.61 | 0.62 | 0.70 | 1.42 | 1.10 | 1.73 | 1.60 |
| NRIL | 1.61 | 1.80 | 1.88 | 1.82 | 1.71 | 2.51 | 0.87 | 0.67 | 0.43 |
| TIXI | 1.32 | 1.55 | 1.59 | 1.48 | 1.30 | 1.71 | 1.16 | 1.34 | 0.90 |
| TNML | 0.91 | 1.24 | 0.98 | 1.18 | 1.18 | 1.09 | 0.86 | 0.94 | 1.13 |
| WSRT | 0.15 | 0.26 | 0.41 | 0.40 | 0.32 | 0.72 | 0.42 | 0.49 | 0.53 |
| Loading-Removed GPS Signal | RMS Improvement Ratio | Station Improved 2 | |||
|---|---|---|---|---|---|
| >5% | 0~5% | −5~0% | <−5% | ||
| EAST | |||||
| GPS—EOST | 50 (20.08%) | 111 (44.58%) | 72 (28.92%) | 16 (6.43%) | 161 (64.66%) |
| GPS—ESMGFZ | 58 (23.29%) | 94 (37.75%) | 66 (26.51%) | 31 (12.45%) | 152 (61.04%) |
| GPS—LDCmgm90 | 54 (21.69%) | 108 (43.37%) | 73 (29.32%) | 14 (5.62%) | 162 (65.06%) |
| NORTH | |||||
| GPS—EOST | 76 (30.52%) | 117 (46.99%) | 48 (19.28%) | 8 (3.21%) | 193 (77.51%) |
| GPS—ESMGFZ | 92 (36.95%) | 88 (35.34%) | 59 (23.69%) | 10 (4.02%) | 180 (72.29%) |
| GPS—LDCmgm90 | 89 (35.74%) | 102 (40.96%) | 52 (20.88%) | 6 (2.41%) | 191 (76.71%) |
| UP | |||||
| GPS—EOST | 161 (64.66%) | 53 (21.29%) | 28 (11.24%) | 7 (2.81%) | 214 (85.94%) |
| GPS—ESMGFZ | 172 (69.08%) | 44 (17.67%) | 16 (6.43%) | 17 (6.83%) | 216 (86.75%) |
| GPS—LDCmgm90 | 171 (68.67%) | 47 (18.88%) | 25 (10.04%) | 6 (2.41%) | 218 (87.55%) |
| Loading-Removed GPS Signal | RMS Improvement Ratio | Station Improved 2 | |||
|---|---|---|---|---|---|
| >5% | 0~5% | −5~0% | <−5% | ||
| GPS—LDCmgm90 vs. GPS—EOST 3 | |||||
| East | 17 (6.83%) | 111 (44.58%) | 99 (39.76%) | 22 (8.84%) | 128 (51.41%) |
| North | 25 (10.04%) | 111 (44. 58%) | 97 (38.96%) | 16 (6.43%) | 136 (54.62%) |
| Up | 81 (32.53%) | 74 (29.72%) | 59 (23.69%) | 35 (14.06%) | 155 (62.25%) |
| GPS—LDCmgm90 vs. GPS—ESMGFZ | |||||
| East | 27 (10.84%) | 95 (38.15%) | 106 (42.57%) | 21 (8.43%) | 122 (49.00%) |
| North | 21 (8.43%) | 94 (37.75%) | 104 (41.77%) | 30 (12.05%) | 115 (46.18%) |
| Up | 72 (28.92%) | 70 (28.11%) | 62 (24.90%) | 45 (18.07%) | 142 (57.03%) |
| Loading-Removed GPS Signal | RMS Improvement Ratio | Station Improved | |||
|---|---|---|---|---|---|
| >5% | 0~5% | −5~0% | <−5% | ||
| Trend-removed 2 | |||||
| GPS—EOST | 161 (64.66%) | 53 (21.29%) | 28 (11.24%) | 7 (2.81%) | 214 (85.94%) |
| GPS—ESMGFZ | 172 (69.08%) | 44 (17.67%) | 16 (6.43%) | 17 (6.83%) | 216 (86.75%) |
| GPS—LDCmgm90 | 171 (68.67%) | 47 (18.88%) | 25 (10.04%) | 6 (2.41%) | 218 (87.55%) |
| Trend-retained | |||||
| GPS—EOST | 125 (50.20%) | 80 (32.13%) | 37 (14.86%) | 7 (2.81%) | 205 (82.33%) |
| GPS—ESMGFZ | 120 (48.19%) | 51 (20.48%) | 50 (20.08%) | 28 (11.24%) | 171 (68.67%) |
| GPS—LDCmgm90 | 165 (66.27%) | 36 (14.46%) | 28 (11.24%) | 20 (8.03%) | 201 (80.72%) |
| Loading-Removed GPS Signal | RMS Improvement Ratio | Station Improved | |||
|---|---|---|---|---|---|
| >5% | 0~5% | −5~0% | <−5% | ||
| GPS—LDCmgm90 vs. GPS—EOST | |||||
| Trend-removed 2 | 81 (32.53%) | 74 (29.72%) | 59 (23.69%) | 35 (14.06%) | 155 (62.25%) |
| Trend-retained | 108 (43.37%) | 52 (20.88%) | 46 (18.47%) | 43 (17.27%) | 160 (64.26%) |
| GPS—LDCmgm90 vs. GPS—ESMGFZ | |||||
| Trend-removed | 72 (28.92%) | 70 (28.11%) | 62 (24.90%) | 45 (18.07%) | 142 (57.03%) |
| Trend-retained | 111 (44.58%) | 41 (16.47%) | 40 (16.06%) | 57 (22.89%) | 152 (61.04%) |
| Loading-Removed GPS Signal | RMS Improvement Ratio | Station Improved | |||
|---|---|---|---|---|---|
| >5% | 0~5% | −5~0% | <−5% | ||
| Long-term band 1 | |||||
| LDC vs. EOST 2 | 122 (49.00%) | 34 (13.65%) | 31 (12.45%) | 62 (24.90%) | 156 (62.65%) |
| LDC vs. ESMGFZ | 124 (49.80%) | 28 (11.24%) | 22 (8.84%) | 75 (30.12%) | 152 (61.04%) |
| Annual band 3 | |||||
| LDC vs. EOST | 144 (57.83%) | 13 (5.22%) | 16 (6.43%) | 76 (30.52%) | 157 (63.05%) |
| LDC vs. ESMGFZ | 137 (55.02%) | 24 (9.64%) | 22 (8.84%) | 66 (26.51%) | 161 (64.66%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, J.; Chen, W.; Ray, J.; van Dam, T.; Li, J. A Loading Correction Model for GPS Measurements Derived from Multiple-Data Combined Monthly Gravity. Remote Sens. 2021, 13, 4408. https://doi.org/10.3390/rs13214408
Luo J, Chen W, Ray J, van Dam T, Li J. A Loading Correction Model for GPS Measurements Derived from Multiple-Data Combined Monthly Gravity. Remote Sensing. 2021; 13(21):4408. https://doi.org/10.3390/rs13214408
Chicago/Turabian StyleLuo, Jiesi, Wei Chen, Jim Ray, Tonie van Dam, and Jiancheng Li. 2021. "A Loading Correction Model for GPS Measurements Derived from Multiple-Data Combined Monthly Gravity" Remote Sensing 13, no. 21: 4408. https://doi.org/10.3390/rs13214408
APA StyleLuo, J., Chen, W., Ray, J., van Dam, T., & Li, J. (2021). A Loading Correction Model for GPS Measurements Derived from Multiple-Data Combined Monthly Gravity. Remote Sensing, 13(21), 4408. https://doi.org/10.3390/rs13214408






