Abstract
Unmanned aerial vehicle (UAV) and reconfigurable intelligent surface (RIS) methods are promising techniques for improving the energy and spectrum efficiency of Fifth Generation/Beyond Fifth Generation (5G/B5G) networks. In order to take advantage of both techniques, we propose an RIS-assisted UAV secure communication scheme, where an UAV is equipped with RIS to facilitate secure transmission. To maximize the average secrecy rate, we jointly optimize the beamforming power, reflect phase shift, and UAV’s trajectory. For this non-convex problem, we decompose it into the power beamforming problem, the phase shift optimization problem, and the UAV’s trajectory design problem, and proposed an efficient iterative algorithm to solve the problem. The numerical results verify the superiority of the proposed scheme that can improve the average secure transmission rate by about 20% compared to that of Eavesdropping elimination methods.
1. Introduction
The unmanned aerial vehicle (UAV) technique has the advantages of high mobility, line of sight (LOS) transmission and low cost [1,2], which is promising for the Fifth Generation/Beyond Fifth Generation (5G/B5G) networks [3]. Assisted by UAVs, the network coverage can be greatly extended. In addition, by the collaborative optimization of UAV’s trajectory and transmit power, the performances of the wireless networks, such as the throughput, information delay, and energy efficiency, can be improved [4,5]. The reconfigurable intelligent surface (RIS) is composed of a large number of energy-saving and economical reconfigurable reflectors [6,7,8], which can reflect the incident electromagnetic wave by inducing a controlled phase shift [9,10,11,12]. Adjusting the phase shift of all components together and utilizing the coherence of electromagnetic waves, the signals from different transmission paths will be aligned at the desired receiver to improve the achievable rate and energy efficiency. Combining the advantages of UAV and RIS can greatly improve the UAV’s energy efficiency [13,14,15]. Moreover, the RIS is easy to implement, since the hardware cost of RIS is lower and there is no signal forwarding equipment. Currently, there is limited research on the RIS-assisted UAV communications. In [16,17,18,19,20], the RIS relayed the UAV downlink signals to maximize the transmission rate or minimize the bit error rate through optimal power allocation and phase shift designing [21]. In addition, the non-orthogonal multiple access (NOMA) was adopted in [19] to improve the spectrum efficiency, where multiple groups of ground users were serviced. In [22,23], the UAV was equipped with RIS to assist the transmission between the transmitter and receiver.
Due to the openness of the wireless communication environment, the wireless signal is vulnerable to eavesdropping. Recently, physical-layer security (PLS) has become a research hotspot [24], which achieves perfect information security encrypted by the wireless channel characteristic. Assisted by the RIS, the authors in [25] proposed an RIS-aided secure transmission scheme considering the hardware impairments. In [26], the jamming scheme was utilized to further improve the secrecy rate for RIS-aided networks. In [27], the quantized phases were introduced in the secure transmission, where the phase shift was optimized based on the quantized phase. However, to the best of the authors’ knowledge, the secure transmission for the RIS-aided UAV network has not yet been researched in sufficient detail, which will be studied in this paper.
Motivated by the above challenges, we propose an RIS-aided UAV secure transmission scheme, where an UAV carries RIS to assist the secure transmission between the UAV and the ground user (GU). In the proposed scheme, the signals transmitted by BS are reflected to GU through an UAV equipped with RIS, and UAV flies along its optimized trajectory. For this scenario, we maximize the average secure rate by jointly optimizing the UAV trajectory, passive beamforming and phase shift under the constraints of RIS phase shift and actual UAV mobility. Different from the existing works that assumed fixed RIS, we utilize UAV carrying RIS that can utilize the flexibility of RIS and mobility of UAV to further improve the secrecy performance. Moreover, we formulate an average secrecy rate optimization problem to allocate the beamforming power, and design the phase shift and UAV’s trajectory. For this non-convex problem, we decompose it into the power beamforming problem, the phase shift optimization problem, and the UAV’s trajectory design problem, and proposed an efficient iterative algorithm to solve the problem. The numerical results verify the superiority of the proposed scheme, which can improve the average secure transmission rate by about 20% compared to that of the baseline method.
The rest of this paper is organized as follows. Section 2 describes the communication system model of the proposed scheme. In Section 3, we formulate the optimization problem and optimize the transmit power, phase shift and UAV’s trajectory. In Section 4, we present the extensive simulations, and Section 5 concludes the paper.
2. System Model
Figure 1 demonstrates the RIS-aided UAV secure transmission model, which consists of a base station (BS), an RIS-aided UAV (U), an eavesdropper (EVE) and a ground user (GU). In this model, the RIS is equipped on the UAV. The BS securely transmits the confidential information to the GU assisted by the RIS on UAV. Owing to the obstacles blocking the LOS channel, EVE and GU can only obtain the signal from the RIS. The privacy information is threatened by the EVE. Assisted by the RIS, we optimally designed the phase shift, allocated the transmit power and the UAV’s trajectory to maximized the secrecy rate.
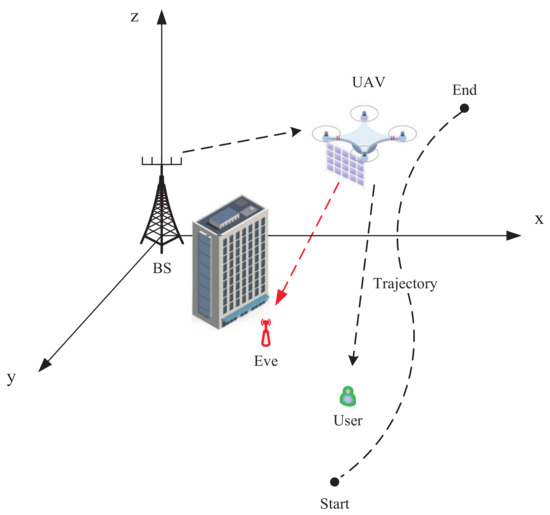
Figure 1.
The RIS-aided UAV secure transmission model.
In the considering model, all channels experience quasi-static Rayleigh flat-fading. The BS is equipped with antennas. GU and the eavesdropper are equipped with only one antenna. Assisted by the RIS, the system can create a programmable wireless environment with reconfigurable passive elements to reduce the signal to interference plus noise ratio (SINR) at the eavesdropping node, and enhance SINR of legitimate receiving users.
It can be seen from [6,28] that in order to optimize the phase shift of RIS, the system needs to obtain high-precision channel state information. This problem was solved by [29] through a large amount of statistical CSI data. Depending on the characteristics of the LoS link, the channel from BS to UAV at nth time slot is denoted as .
where and are the number of antennas for the BS and the GU, respectively; is the fading coefficient of the LoS link [6]; is the corresponding path loss exponent related to the BS to RIS link; denotes the distance between BS and UAV in the nth time slot; is the array steering vector between the azimuth angles from BS to RIS; are the array steering vector between the azimuth angles from RIS to GU. Since we assume that the RIS is parallel to the uniform linear array (ULA) transmitting antenna, the effect of the incident electromagnetic wave on each row of reflected elements on the RIS are the same and . In addition, the array steering vector is denoted as follows:
The array steering vector is defined in the same way as [30], where d is the distance between the antennas at the transmitter and is the electromagnetic wave wavelength.
Due to UAV’s high altitude location, the probability of the LoS path is increased. Since we set the transmitter to use directional beam tracking, and consider the large-scale fading of other paths, the process of electromagnetic wave emission and reflection can be regarded as the LoS link. We assume that the existing channel estimation techniques can allow us to obtain channel state information (CSI) [31]. The channel coefficient between the RIS unit and GU is given by
where and represent the gain of the receiving and reflecting antenna elements; is the fading coefficient between UAV and GU; the distance between UAV and GU is denoted as . We denote the position of UAV as and denote the position of GU as . Then, the array steering vector of RIS is given by
where .
The position of EVE is denoted as . Considering the stability of the system, the UAV flies at a fixed altitude. We denote the horizontal position of UAV at nth time slot as . We denote the position of the GU as . The channels , and are denoted by w, , and , receptively. The transmission signals of the BS can be denoted as
where is the beamforming vector at nth time slot and s is the privacy information transmitted by BS to GU. To reduce the SINR received at the eavesdropper, the average transmit power of the BS is limited by
where I is the maximum permitted transmit power.
The trajectory of UAV should satisfy the following constraints
where and denote the initial and end positions of UAV; V denotes the maximum flight speed of UAV; represents UAV’s maximum flight distance in each time slot.
According to the above discussion, we can derive the transmission rate of GU at the nth slot as
where is the additive white Gaussian noise (AWGN) at GU; is the phase shift of the RIS. Simultaneously, the EVE also receives the confidential information with rate as
where is the channel between UAV and EVE.
3. The RIS-Aided UAV Secure Transmission
Based on PLS, the maximum secure transmission rate over N time slots can be expressed as
To optimize the maximum secure transmission rate, we formulate the problem as
In P1, the first three constraints are associated with the starting, ending and flight velocity of UAV; the last but one constraint is associated with the phase shift; and the last constraint is associated with the power allocation. It can be observed that the objective function and the last constraint are non-convex, which means that they are difficult to solve. In the following, we transform P1 into a convex problem and propose an iterative algorithm to solve it.
In order to solve P1, we propose an iterative algorithm. First, we optimally allocate the beamforming power. Then, the RIS reflect phase shift on the UAV is optimized. Finally, the trajectory optimization is solved. An alternating optimization (AO) algorithm is shown in Algorithm 1.
| Algorithm 1: The AO Algorithm for the Power Allocation and Phase Shift and Trajectory Design |
 |
3.1. BS’s Beamforming Strategy
In this paper, we evaluate the performance of the proposed algorithm against the Eavesdropping elimination method and the situation without beamforming through simulation. In our proposed algorithm, the beamforming of BS will track the channel state to enhance the signal power at UAV as much as possible. There are two strategies in beamforming vector optimization.
- (1)
- Eavesdropping elimination method
The eavesdropping elimination method refers to the utilization of the orthogonality of the transmit signal and the eavesdropping channel to zero out the received signal at the EVE. To simplify the expression of the formulation, we set . For , the beamforming vector can be acquired as
where is the channel between BS and EVE. We suppose that is the projection matrix on the null space of [32] as
To satisfy , we need to satisfy . That is to say, the maximization of is equivalent to the maximization of . We can acquire the beamforming vector as [33]
For the fixed position of UAV and , the optimal passive beamforming reflection elements are given to maximize the nth objective function of the problem. Set
Based on this method, it can be observed that the optimal value of RIS to maximize (14) is given by
- (2)
- Destination aiming method
The eliminate eavesdropping method generally performs well under the unblocked channel. However, when the building blocks the signal, this method does not work well. For the destination aiming method, its main lobe of beam is direct to the destination node. This means that the receiving power of the destination node reaches the maximum, which can improve the communication quality of legitimate channels [30]. In this way, can be denoted as
3.2. Phase Shift Optimization
With the given and , the problem can be represented as RIS’s phase shift optimization problem as
where
It can observe that is a continuously differentiable function, and the constraint set of just forms a complex circle manifold. Therefore, the steady-state solution of can be obtained by the Riemannian conjugate gradient (RCG) algorithm. This algorithm is widely used in the design of the hybrid precoding problem, and it shows good performance in the RIS-aided MISO system. It usually consists of three key steps [34]:
- (1)
- Calculation of Riemannian gradient:Riemannianian gradient is the orthogonal projection of f of Euclidean gradient on the complex field as
- (2)
- Tangent vector of search direction:is the vector transfer function, which is defined as
- (3)
- The tangent vector is projected onto a complex circular manifold:is the size of the Armijo step [35] (We use the Armijo rule for descent in Riemannian manifolds, and provides a detailed description).
3.3. UAV’s Trajectory Optimization
For the given and , the trajectory is need to be optimized. In the following, we adopt the successive convex approximation (SCA) algorithm to transform the non-convex items into convex items for the trajectory optimization [36].
First, we introduce several relaxation variables as follows
Since the above inequality and maximum rate constitute problem are non-convex, we use the first order expansion of Taylor series to transform the trajectory problem as
where is the position of UAV in the mth iteration. Therefore, the trajectory planning optimization problem can be given as
The above optimization problem is convex, and we can effectively solve this problem through the convex optimization algorithm. In this system model, our solution is to maximize the average secure transmission rate. This scheme is composed of two rings: inside and outside. The outer ring is related to AO algorithms for reflection optimization and trajectory optimization. The internal loop is the SCA algorithm itself. Therefore, the proposed optimization problem can be solved through the proposed algorithm.
4. Simulation Results
In this part, we simulate the proposed scheme to validate the proposed scheme through Matlab. The UAV trajectory simulation parameters and information propagation environment parameters are summarized in Table 1. These channel parameters are set according to the 3GPP propagation environment, which are almost consistent with those in [16,37,38].

Table 1.
Simulation parameters.
Figure 2 plots the horizontal locations of the UAV. We can observe that the UAV gradually flies to EVE at the starting node to reflect the signal near EVE and reduces the power that can be received by the EVE. After departure, UAV flies closely to GU to enhance the signal power received at GU. In the straight line among EVE, BS and GU, UAV flies to the closest position of EVE to reflect the signal energy more precisely. At the same time, the RIS reflection reduces the power to the EVE and ensures the SINR of GU.
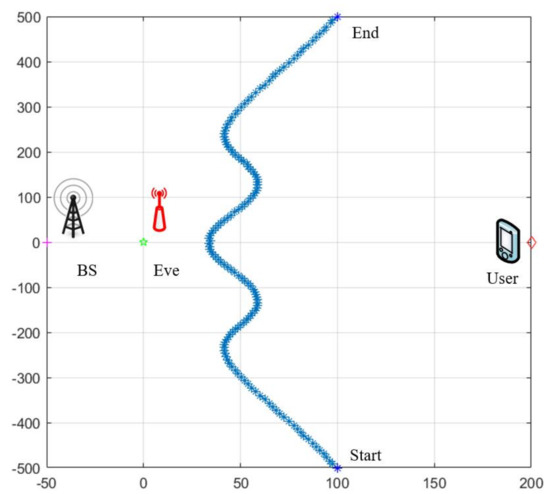
Figure 2.
The trajectory of the UAV.
In Figure 3, it can be observed that the maximum secure transmission rate can be obtained for the proposed algorithm compared with the other schemes. When there is no trajectory optimization and only straight-line flight, the secrecy rate will decrease. When the phase is random and only directional reflection, the secure rate will also decrease. The transmission rate of secure information can be improved by approximately 81% compared to that under the random phase. In addition, we can also observe that the secure transmission rate is lowest when the relay reflection without RIS and the BS transmits the signal directly to GU. We can see that when the BS does not use beamforming, the secure transmission rate is lower than that of the eavesdropping elimination method. The eavesdropping elimination method is correlated with the eavesdropping channel of the RIS, and less correlated with the channel from the BS to the RIS. Therefore, the performance without beamforming is only slightly lower than that of the eavesdropping elimination method.
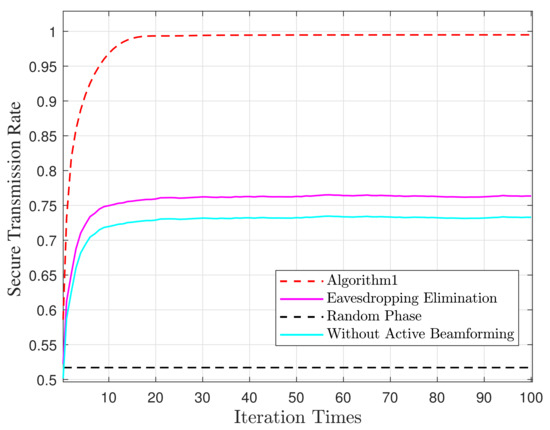
Figure 3.
Maximum secure transmission rate with iteration times.
In Figure 4, it is obvious that the maximum average secure transmission rate increases with the increase in the maximum transmission power and the number of elements. It can be observed that RIS has the greater impact on the secure transmission rate than that of the transmit power. However, when the transmit power is high enough, the average secure transmission rate will increase slowly, limited by the channel power gains. The secrecy rate tends to be flat when the power reaches 2.5 dbm.
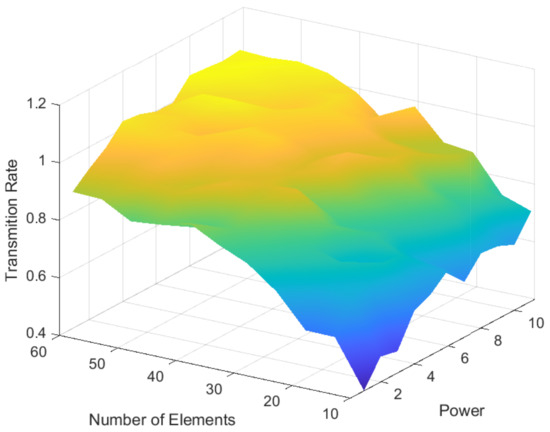
Figure 4.
Maximum secure transmission rate with the power and the number of elements.
Figure 5 shows the secure transmission rate versus the number of reflection units for different methods. It can be seen that the performance of all three methods improves as the number of reflected units increases. The performance of Algorithm 1 is better than the eavesdropping elimination method due to the beamforming enhanced state of the reflection channel. Its performance reaches an upper limit when the number of reflection units reaches 60. The performance of the random phase is worse than that of all the other methods, and its performance improvement is less than that of the other two when the number of reflection units is increased by the same amount.
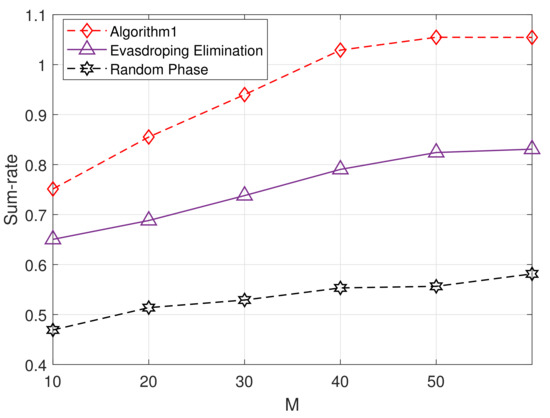
Figure 5.
Maximum average secure transmission rate with the reflective units on each RIS for different methods (P = 2.5 dbm).
5. Conclusions
In this paper, we proposed an RIS-aided UAV secure communication scheme to protect the privacy information. In the proposed scheme, the beamforming is utilized to maximize the signal power at the RIS in motion. The passive targeted reflection of RIS provided a variable channel environment for legitimate users to acquire the light-of-sight transmission model. Therefore, the secure performance can be improved. For the proposed scheme, we formulated a secrecy rate maximization problem and solved it using the SCA and Riemann manifold methods. The simulation shows the secrecy rate improvement of the proposed scheme, which is about 20% higher than that of the eavesdropping elimination method. Moreover, only the optimization of single base station and single user scenarios is considered in this paper. Multiple base stations and multiple users imply a more complex optimization process, which will be studied in depth in the future.
Author Contributions
D.W.: Conceptualization, Methodology, Software, Writing—Original Draft Preparation, Writing—Review and Editing, Visualization, and Funding Acquisition. Y.Z.: Conceptualization, Methodology, Software, and Writing—Original Draft Preparation. Y.H.: Conceptualization, Resources, and Writing—Review and Editing. X.T.: Conceptualization, Resources, Writing—Review and Editing, and Funding Acquisition. L.L.: Conceptualization, Resources, and Funding Acquisition. R.Z.: Conceptualization, Resources, and Funding Acquisition. D.Z.: Conceptualization, Resources, and Funding Acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by Foundation of the Science, Technology, and Innovation Commission of Shenzhen Municipality under Grant JCYJ20190806160218174, in part by the National Natural Science Foundation of China under Grant 61901379, Grant 61941119, Grant 61901378, and Grant 61901366, in part by National Key Research and Development Program of China under Grant 2020YFB1807003, in part by the open research fund of National Mobile Communications Research Laboratory, Southeast University under Grant 2020D04, and in part by the Program of China Scholarships Council under Grant 202006290166.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ding, R.; Gao, F.; Shen, X.S. 3D UAV Trajectory Design and Frequency Band Allocation for Energy-Efficient and Fair Communication: A Deep Reinforcement Learning Approach. IEEE Trans. Wirel. Commun. 2020, 19, 7796–7809. [Google Scholar] [CrossRef]
- Wang, H.; Ding, G.; Gao, F.; Chen, J.; Wang, J.; Wang, L. Power Control in UAV-Supported Ultra Dense Networks: Communications, Caching, and Energy Transfer. IEEE Commun. Mag. 2018, 56, 28–34. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef] [Green Version]
- Zhao, M.; Shi, Q.; Zhao, M. Efficiency Maximization for UAV-Enabled Mobile Relaying Systems With Laser Charging. IEEE Trans. Wirel. Commun. 2020, 19, 3257–3272. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhang, J.; Long, K. Energy Efficiency Optimization for NOMA UAV Network With Imperfect CSI. IEEE J. Sel. Areas Commun. 2020, 38, 2798–2809. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef] [Green Version]
- Di, M.; Zappone, A.; Debbah, M.; Alouini, M.; Yuen, C.; Rosny, J.; Tretyakov, S. Smart Radio Environments Empowered by Reconfigurable Intelligent Surfaces: How It Works, State of Research, and The Road Ahead. IEEE J. Sel. Areas Commun. 2020, 38, 2450–2525. [Google Scholar]
- Liu, Y.; Zhang, S.; Gao, F.; Tang, J.; Dobre, O.A. Cascaded Channel Estimation for RIS Assisted mmWave MIMO Transmissions. IEEE Wirel. Commun. Lett. 2021, 10, 2065–2069. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Towards Smart and Reconfigurable Environment: Intelligent Reflecting Surface Aided Wireless Network. IEEE Commun. Mag. 2020, 58, 106–112. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhang, H.; Liu, W.; Long, K.; Dong, J.; Leung, V.C.M. Energy Efficient User Clustering, Hybrid Precoding and Power Optimization in Terahertz MIMO-NOMA Systems. IEEE J. Sel. Areas Commun. 2020, 38, 2074–2085. [Google Scholar] [CrossRef]
- Liang, Y.; Long, R.; Zhang, Q.; Chen, J.; Cheng, H.V.; Guo, H. Large Intelligent Surface/Antennas (LISA): Making Reflective Radios Smart. J. Commun. Inf. Netw. 2019, 4, 40–50. [Google Scholar]
- Yang, L.; Yang, J.; Xie, W.; Hasna, M.O.; Tsiftsis, T.; Renzo, M.D. Secrecy Performance Analysis of RIS-Aided Wireless Communication Systems. IEEE Trans. Veh. Technol. 2020, 69, 12296–12300. [Google Scholar] [CrossRef]
- He, Y.; Zhai, D.; Jiang, Y.; Zhang, R. Relay selection for UAV-assisted urban vehicular ad hoc networks. IEEE Wirel. Commun. Lett. 2020, 9, 1379–1383. [Google Scholar] [CrossRef]
- He, Y.; Zhai, D.; Huang, F.; Wang, D.; Tang, X.; Zhang, R. Joint task offloading, resource allocation, and security assurance for mobile edge computing-enabled UAV-assisted VANETs. Remote Sens. 2021, 13, 1547. [Google Scholar] [CrossRef]
- Zhang, Q.; Saad, W.; Bennis, M.; Lu, X.; Debbah, M. Predictive Deployment of UAV Base Stations in Wireless Networks: Machine Learning Meets Contract Theory. IEEE Trans. Wirel. Commun. 2021, 20, 637–652. [Google Scholar] [CrossRef]
- Wei, Z.; Cai, Y.; Sun, Z.; Ng, D.W.K.; Yuan, J. Sum-Rate Maximization for IRS-Assisted UAV OFDMA Communication Systems. IEEE Trans. Wirel. Commun. 2020, 20, 2530–2550. [Google Scholar] [CrossRef]
- Hua, M.; Yang, L.; Wu, Q.; Pan, C.; Li, C.; Swindlehurst, A.L. UAV-Assisted Intelligent Reflecting Surface Symbiotic Radio System. IEEE Trans. Wirel. Commun. 2021, 20, 5769–5785. [Google Scholar] [CrossRef]
- Fang, S.; Chen, G.; Li, Y. Joint Optimization for Secure Intelligent Reflecting Surface Assisted UAV Networks. IEEE Wirel. Commun. Lett. 2021, 10, 276–280. [Google Scholar] [CrossRef]
- Mu, X.; Liu, Y.; Guo, L.; Lin, J.; Poor, H.V. Intelligent Reflecting Surface Enhanced Multi-UAV NOMA Networks. IEEE J. Sel. Areas Commun. 2021, 39, 3051–3066. [Google Scholar] [CrossRef]
- Ji, B.; Li, Y.; Cao, D.; Li, C.; Mumtaz, S.; Wang, D. Secrecy Performance Analysis of UAV Assisted Relay Transmission for Cognitive Network With Energy Harvesting. IEEE Trans. Veh. Technol. 2020, 69, 7404–7415. [Google Scholar] [CrossRef]
- Wang, D.; He, Y.; Yu, K.; Srivastava, G.; Nie, L.; Zhang, R. Delay sensitive secure NOMA transmission for hierarchical HAP-LAP medical-care IoT networks. IEEE Trans. Ind. Informat. 2021. [Google Scholar] [CrossRef]
- Shafique, T.; Tabassum, H.; Hossain, E. Optimization of Wireless Relaying With Flexible UAV-Borne Reflecting Surfaces. IEEE Trans. Commun. 2021, 69, 309–325. [Google Scholar] [CrossRef]
- Mahmoud, A.; Muhaidat, S.; Sofotasios, P.; Abualhaol, I.; Dobre, O.A.; Yanikomeroglu, H. Intelligent Reflecting Surfaces Assisted UAV Communications for IoT Networks: Performance Analysis. IEEE Trans. Green Commun. Netw. 2021, 5, 1029–1040. [Google Scholar] [CrossRef]
- Wang, D.; Ren, P.; Cheng, J. Cooperative Secure Communication in Two-Hop Buffer-Aided Networks. IEEE Trans. Commun. 2018, 66, 972–985. [Google Scholar] [CrossRef]
- Zhou, G.; Pan, C.; Ren, H.; Wang, K.; Peng, Z. Secure Wireless Communication in RIS-Aided MISO System With Hardware Impairments. IEEE Wirel. Commun. Lett. 2021, 10, 1309–1313. [Google Scholar] [CrossRef]
- Tang, X.; Lan, X.; Zhai, D.; Zhang, R.; Han, Z. Securing Wireless Transmissions with RIS-Receiver Coordination: Passive Beamforming and Active Jamming. IEEE Trans. Veh. Technol. 2021, 70, 6260–6265. [Google Scholar] [CrossRef]
- Trigui, I.; Ajib, W.; Zhu, W.-P. Secrecy Outage Probability and Average Rate of RIS-Aided Communications Using Quantized Phases. IEEE Commun. Lett. 2021, 25, 1820–1824. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent Reflecting Surface Enhanced Wireless Network: Joint Active and Passive Beamforming Design. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Han, Y.; Tang, W.; Jin, S.; Wen, C.-K.; Ma, X. Large Intelligent Surface-Assisted Wireless Communication Exploiting Statistical CSI. IEEE Trans. Veh. Technol. 2019, 68, 8238–8242. [Google Scholar] [CrossRef] [Green Version]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University, Press: Cambridge, UK, 2005. [Google Scholar]
- Mishra, D.; Johansson, H. Channel Estimation and Low-complexity Beamforming Design for Passive Intelligent Surface Assisted MISO Wireless Energy Transfer. In Proceedings of the ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 4659–4663. [Google Scholar]
- Basilevsky, A. Applied Matrix Algebra in the Statistical Sciences; Courier Corporation: New York, NY, USA, 2013. [Google Scholar]
- Friedlander, B.; Porat, B. Performance analysis of a null-steering algorithm based on direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 461–466. [Google Scholar] [CrossRef]
- Guo, H.; Liang, Y.; Chen, J.; Larsson, E.G. Weighted Sum-Rate Maximization for Reconfigurable Intelligent Surface Aided Wireless Networks. IEEE Trans. Wirel. Commun. 2020, 19, 3064–3076. [Google Scholar] [CrossRef] [Green Version]
- Absil, P.A.; Mahony, R.; Sepulchre, R. Optimization Algorithms on Matrix Manifolds; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Wang, T.; Vandendorpe, L. Successive convex approximation based methods for dynamic spectrum management. In Proceedings of the IEEE International Conference on Communications, Ottawa, ON, Canada, 10–15 June 2012; pp. 4061–4065. [Google Scholar]
- Huang, C.; Zappone, A.; Alexandropoulos, G.C.; Debbah, M.; Yuen, C. Reconfigurable Intelligent Surfaces for Energy Efficiency in Wireless Communication. IEEE Trans. Wirel. Commun. 2019, 18, 4157–4170. [Google Scholar] [CrossRef] [Green Version]
- Björnson, E.; Sanguinetti, L.; Hoydis, J.; Debbah, M. Optimal Design of Energy-Efficient Multi-User MIMO Systems: Is Massive MIMO the Answer? IEEE Trans. Wirel. Commun. 2015, 14, 3059–3075. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).