Performance of BDS-2/3, GPS, and Galileo Time Transfer with Real-Time Single-Frequency Precise Point Positioning
Abstract
:1. Introduction
2. Methods
2.1. Observations
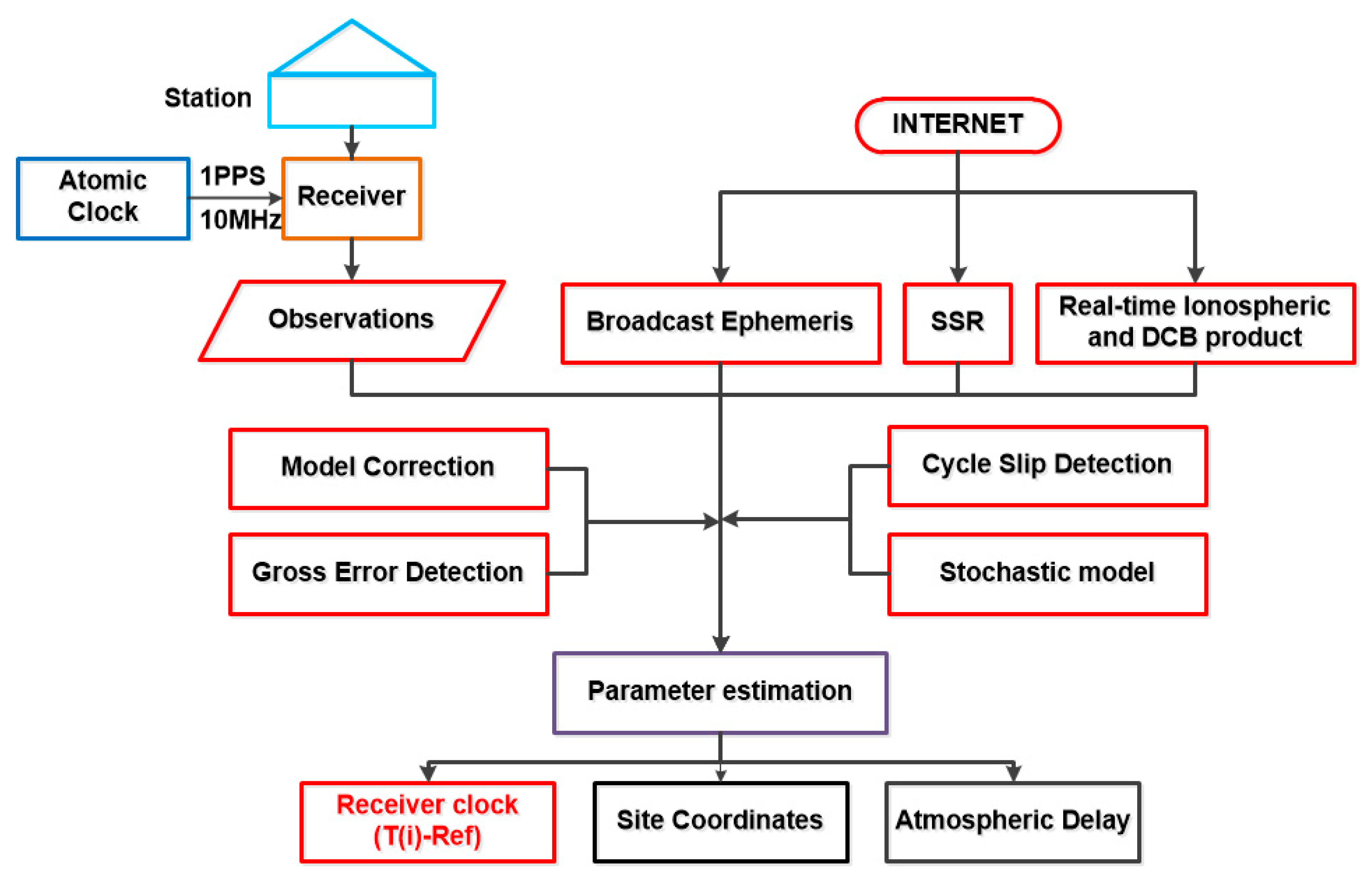
2.2. Time Transfer with Real-Time Single-Frequency PPP
3. Accuracy of Real-Time Precise Product
4. Test Data and Processing Strategies
4.1. Dataset
4.2. Processing Strategies
5. Results
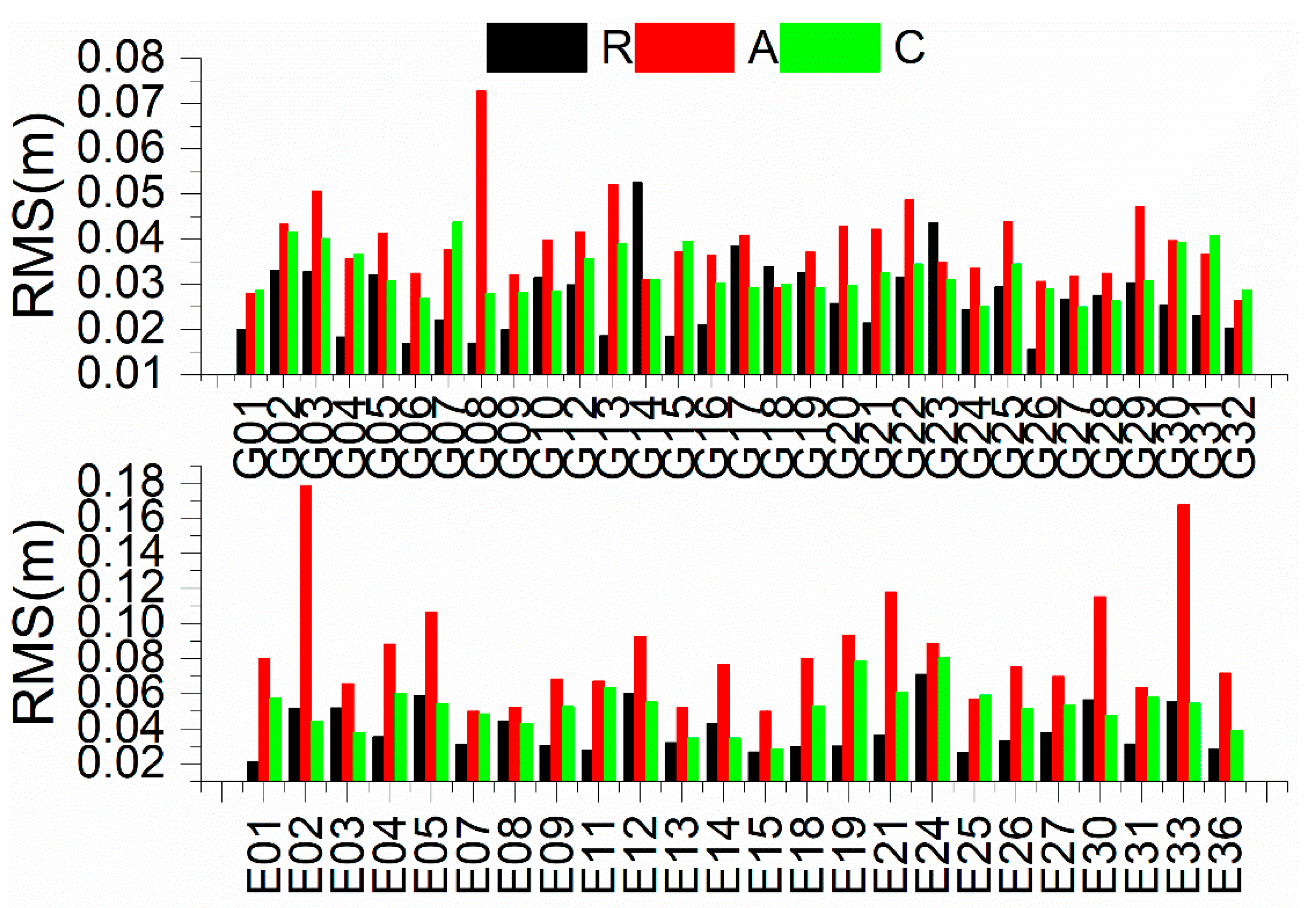
5.1. GPS
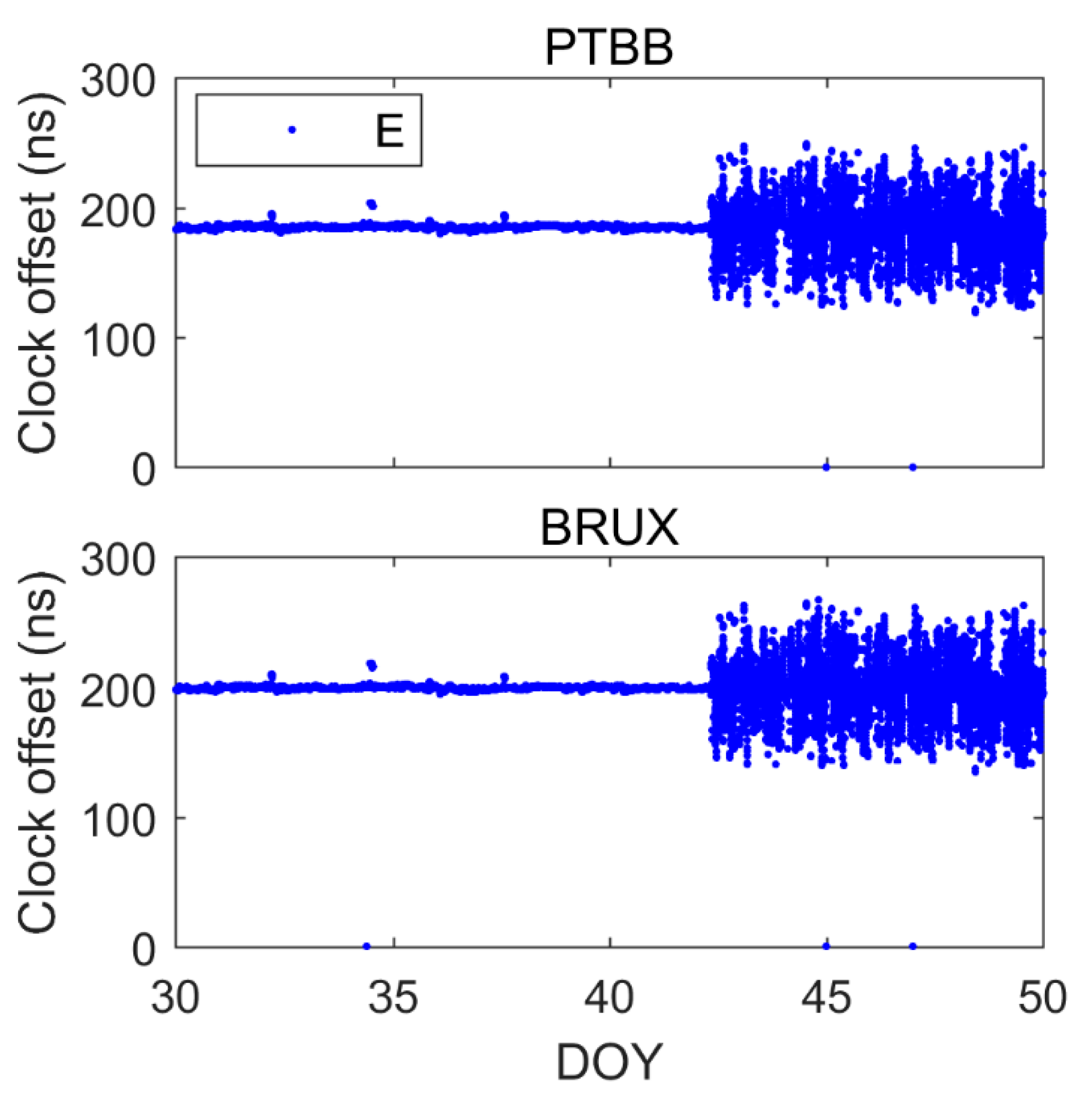
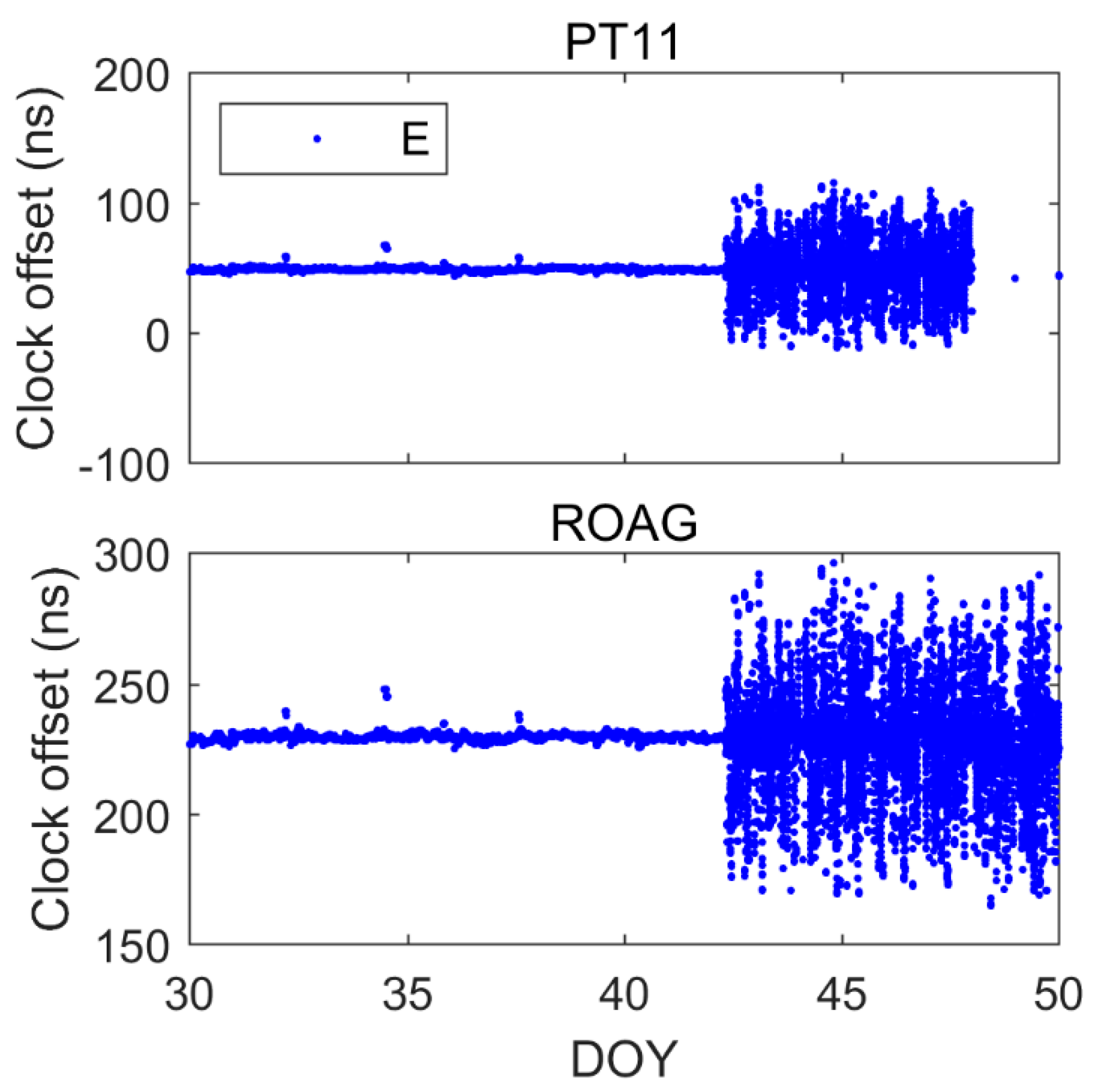
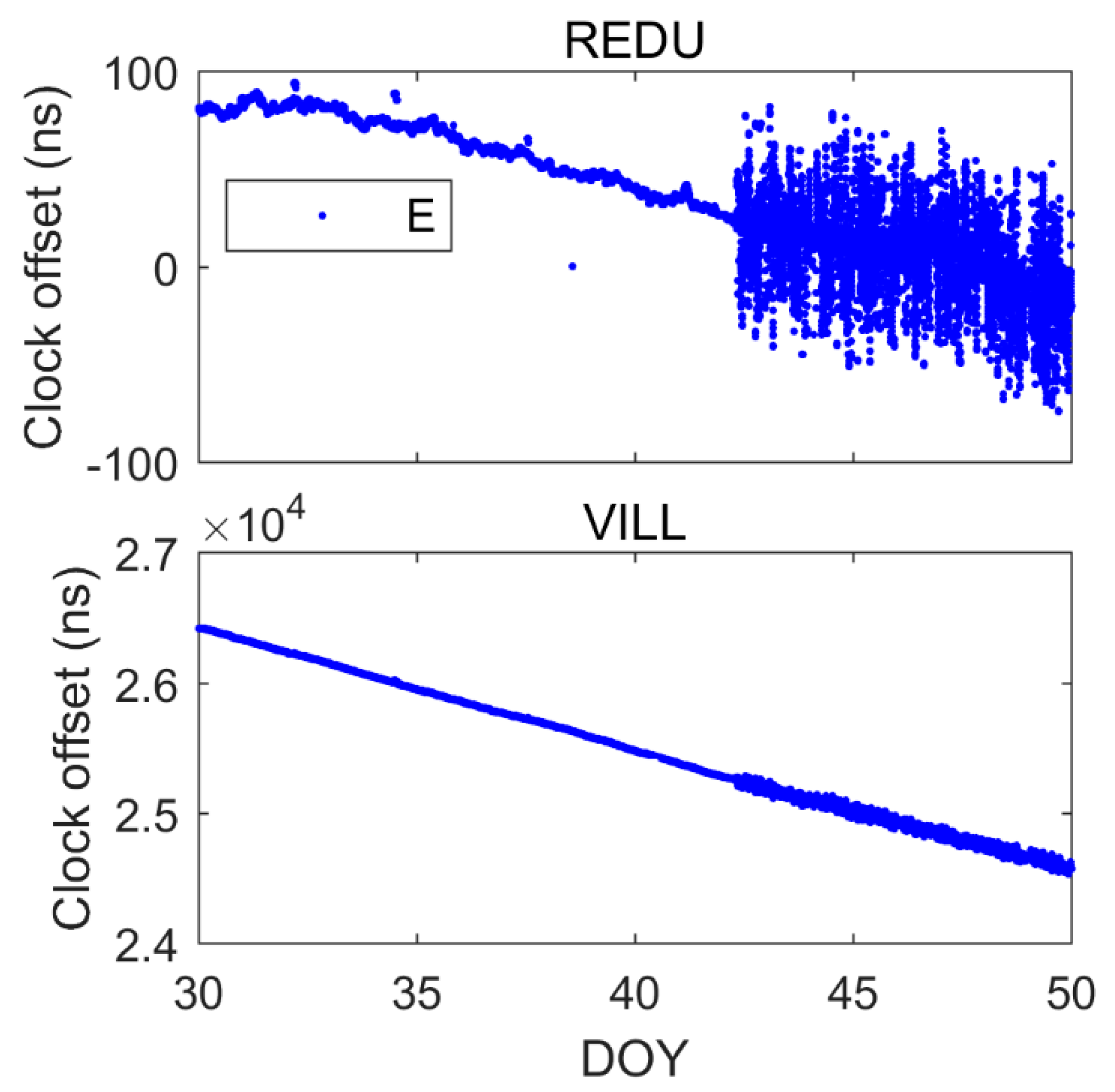
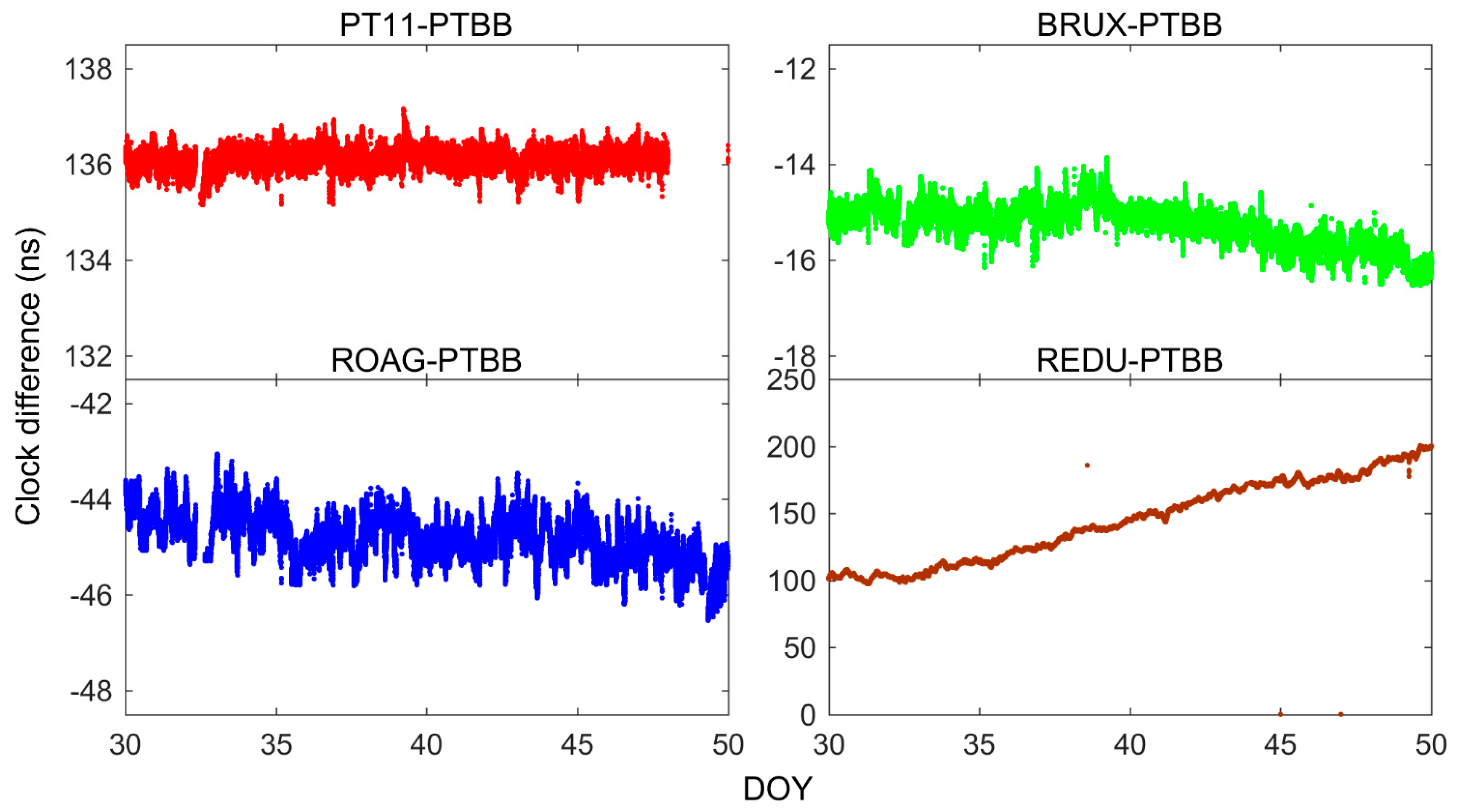
5.2. Galileo
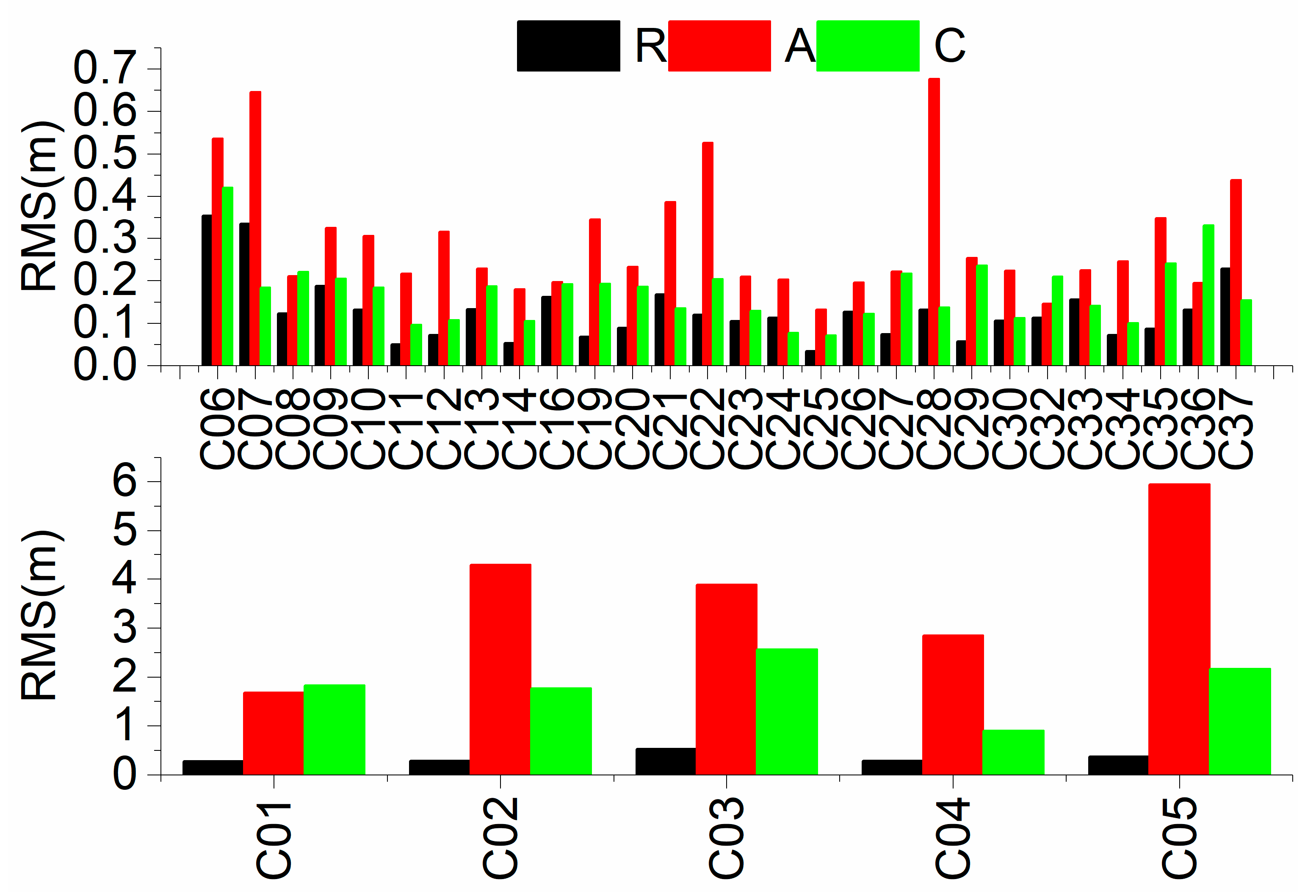
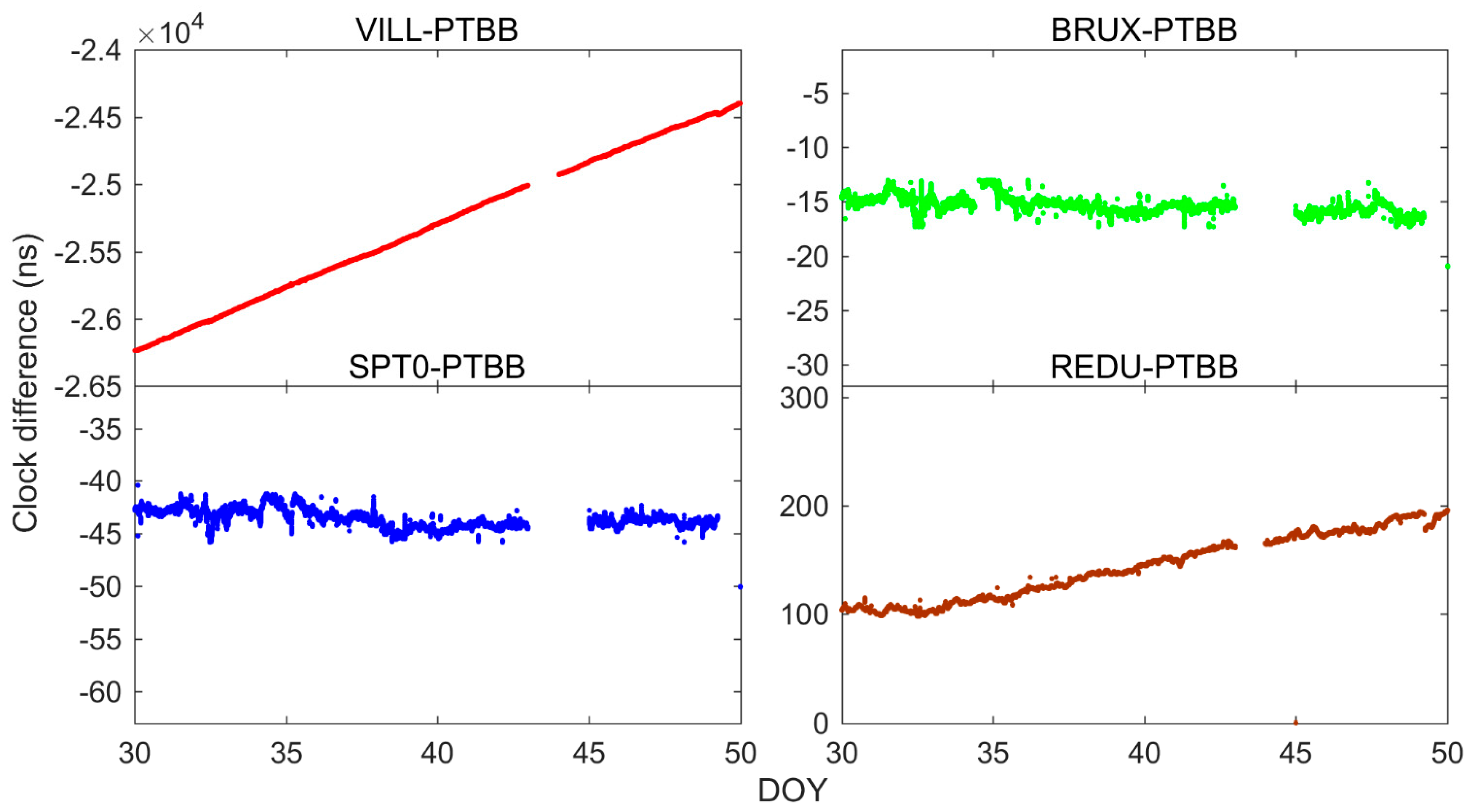
5.3. BDS-2/3
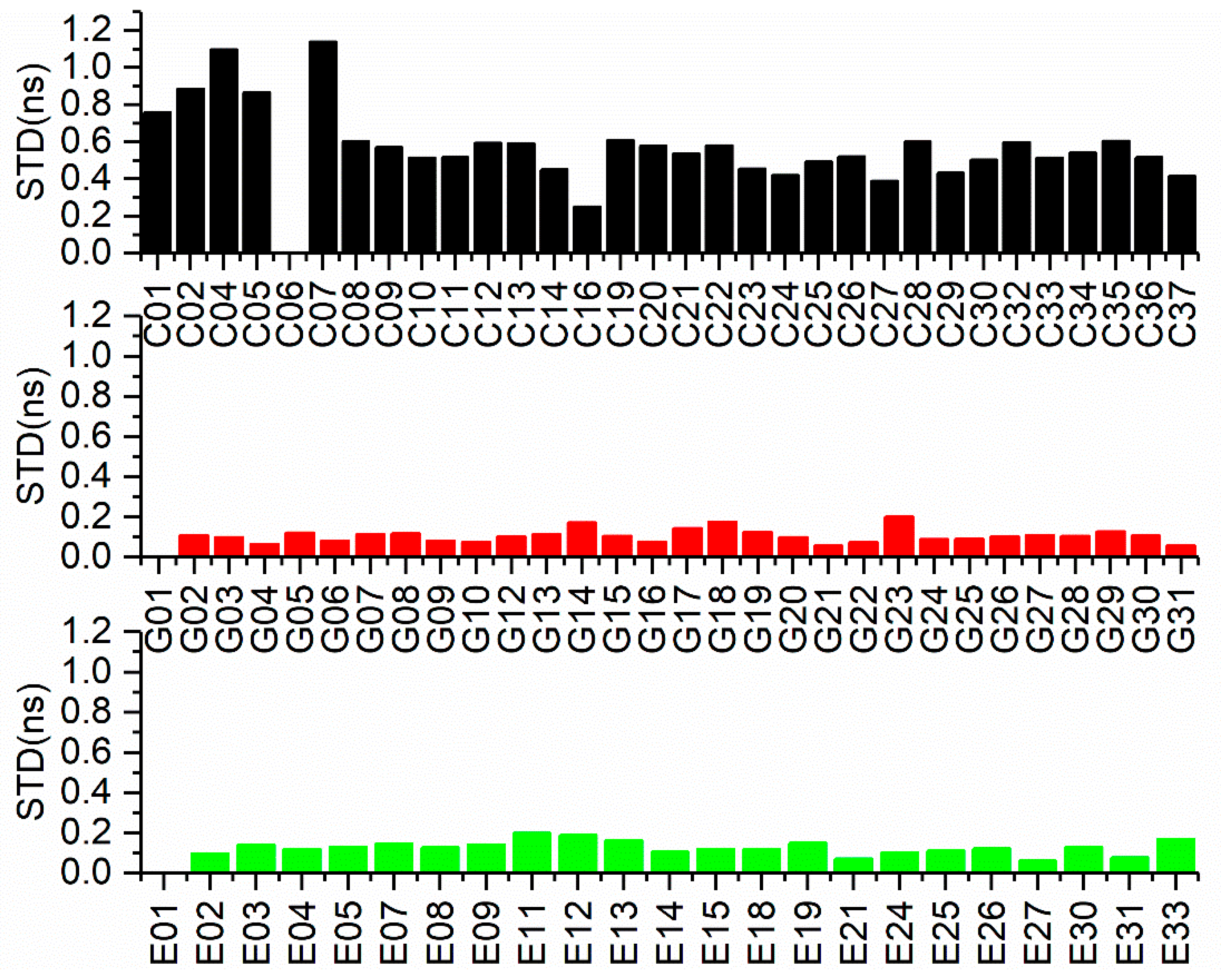
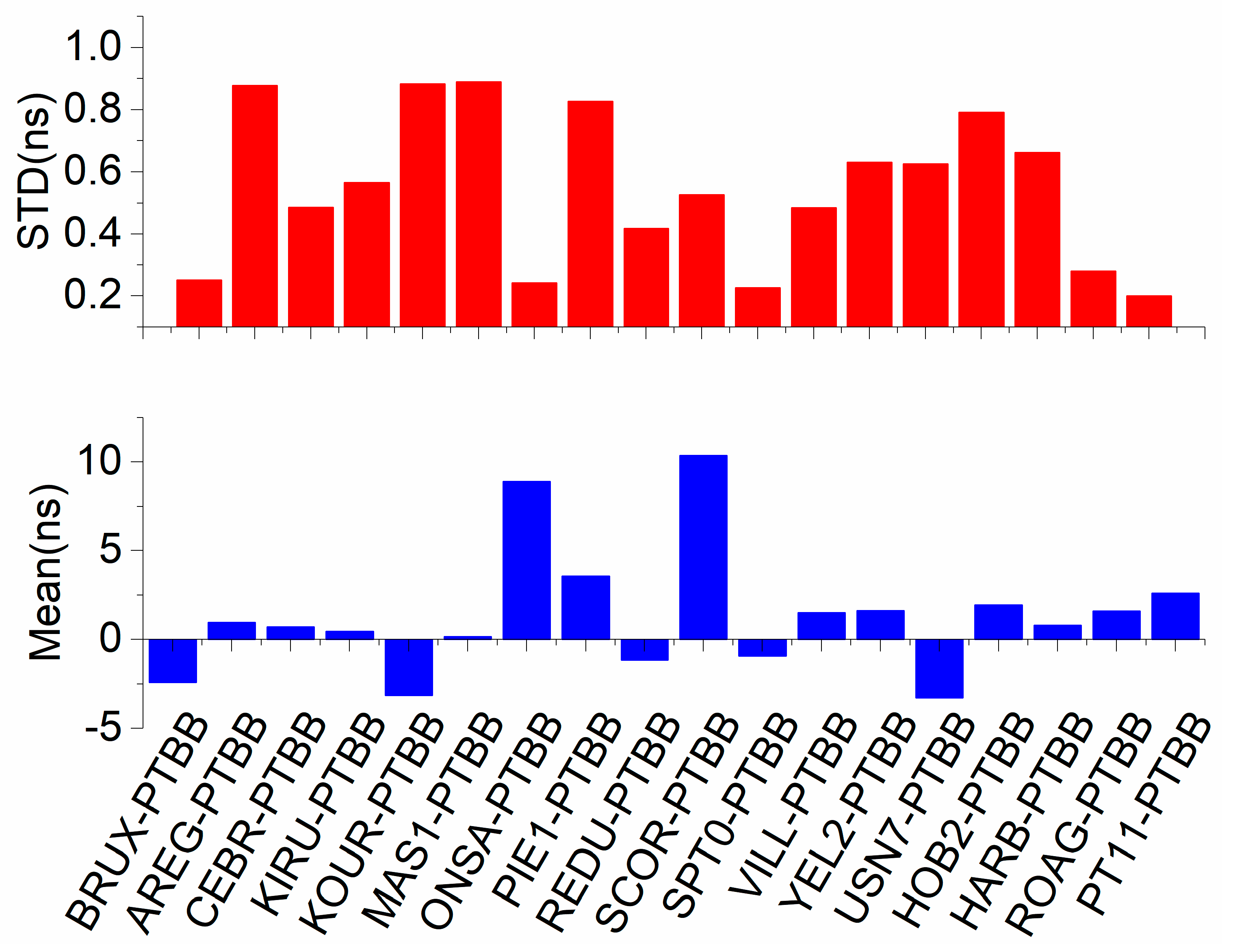
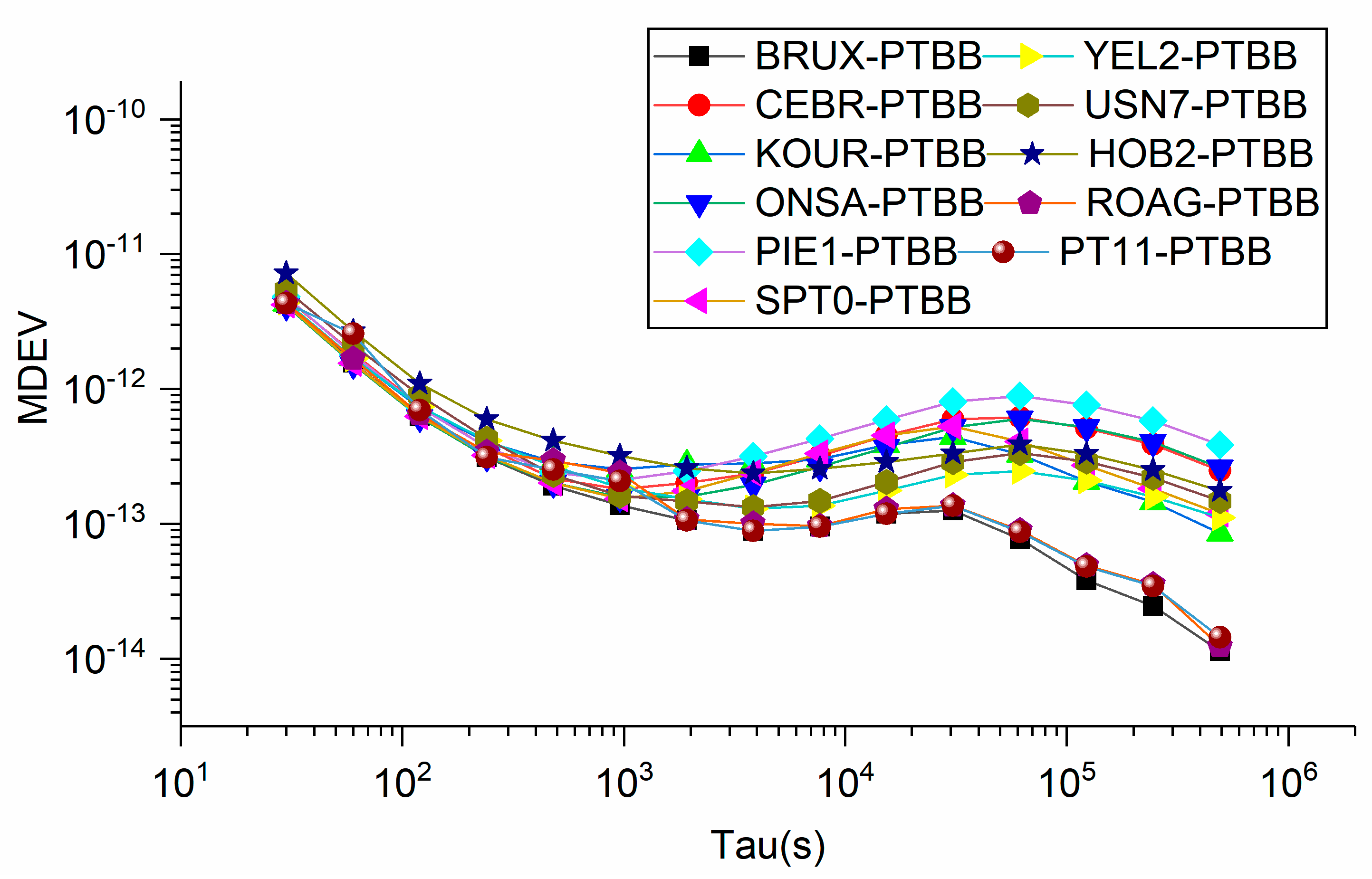
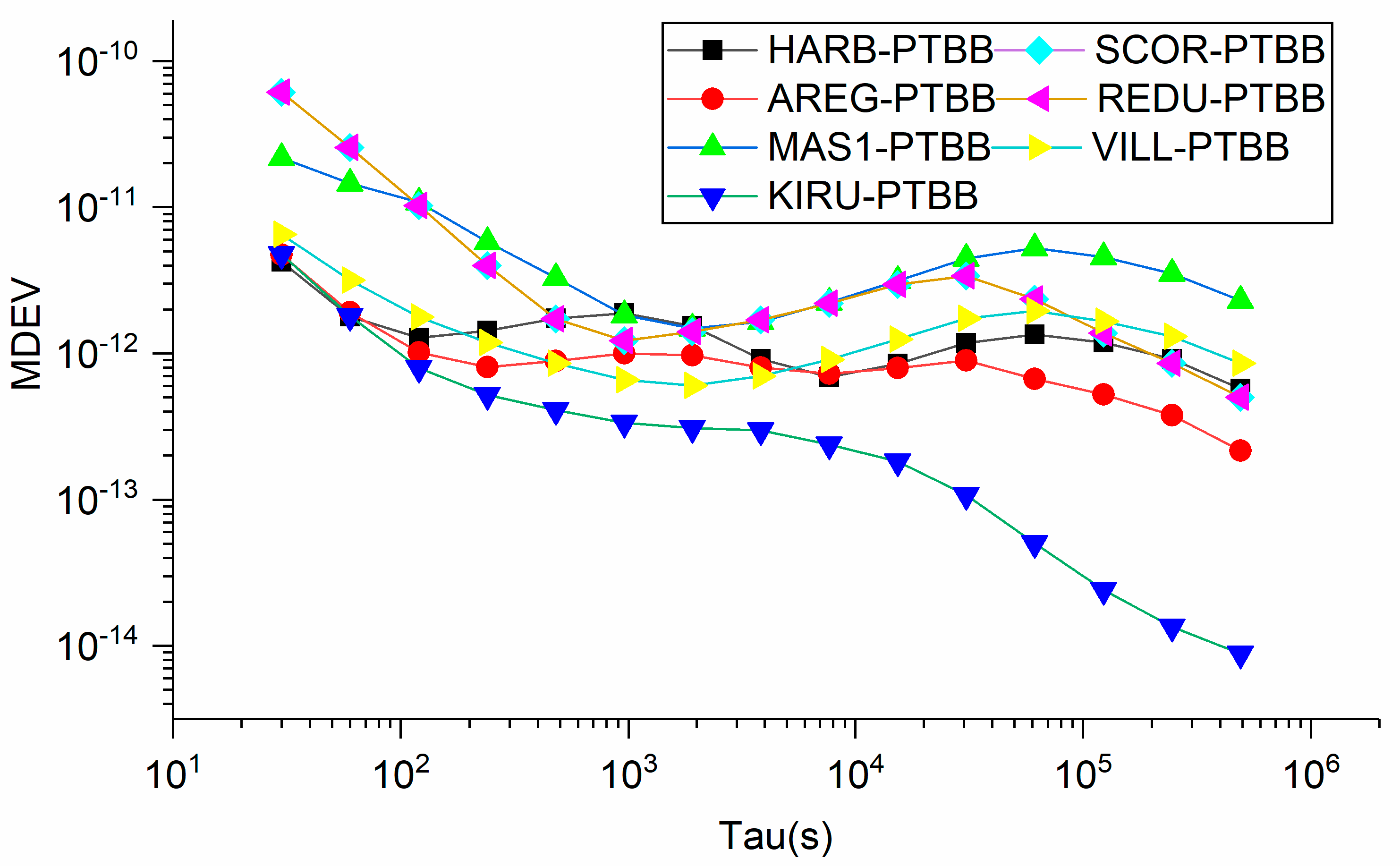
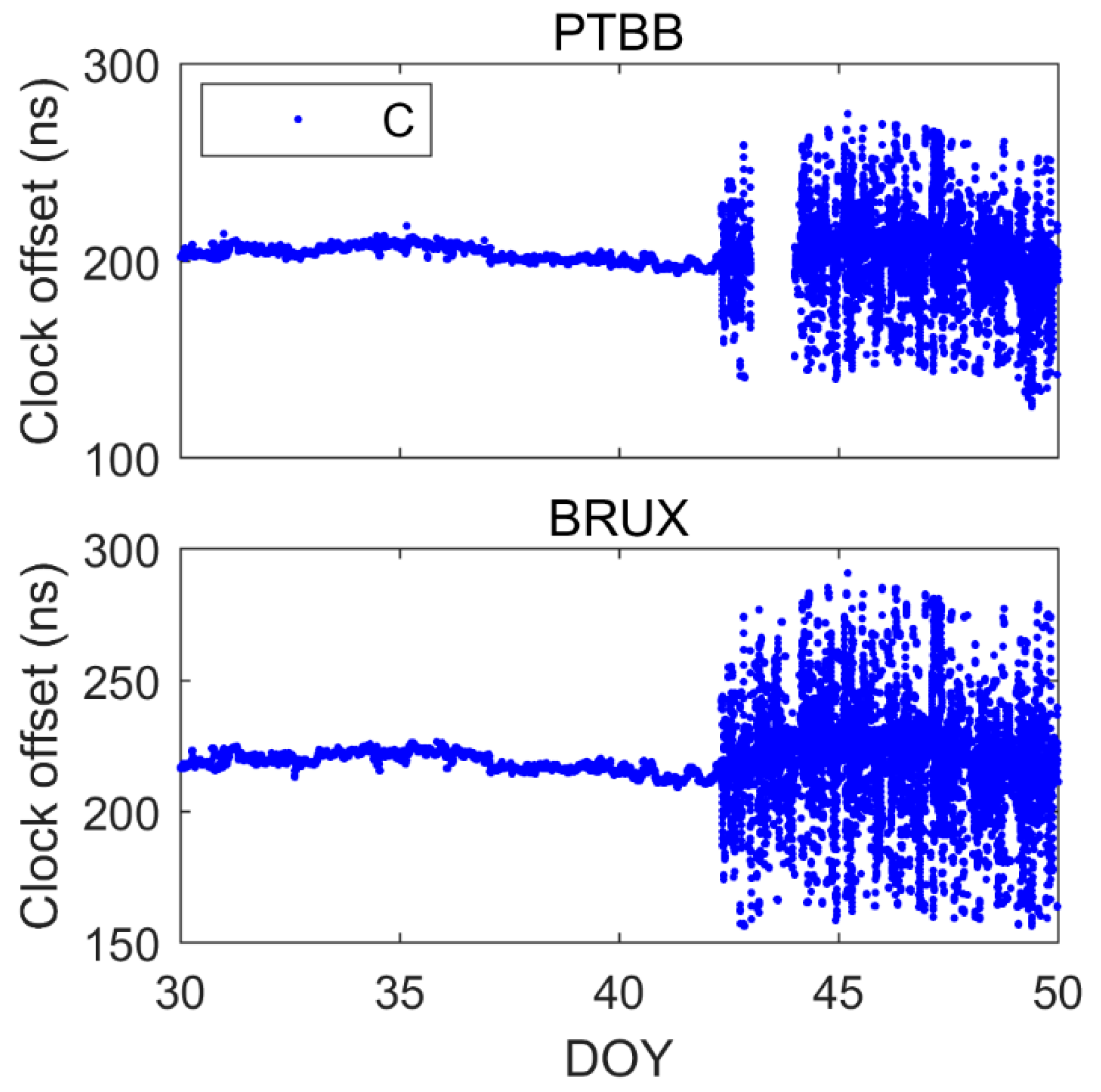
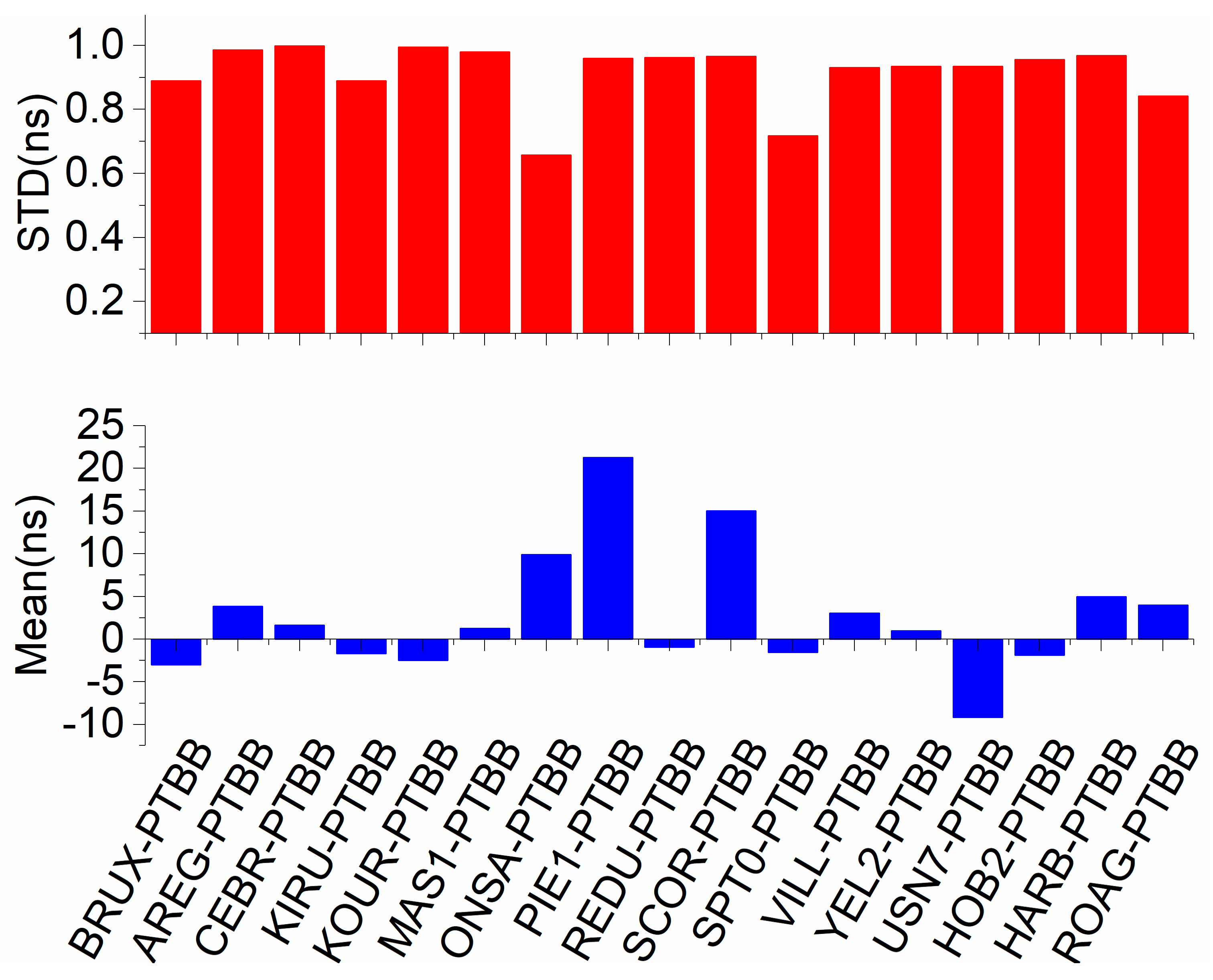
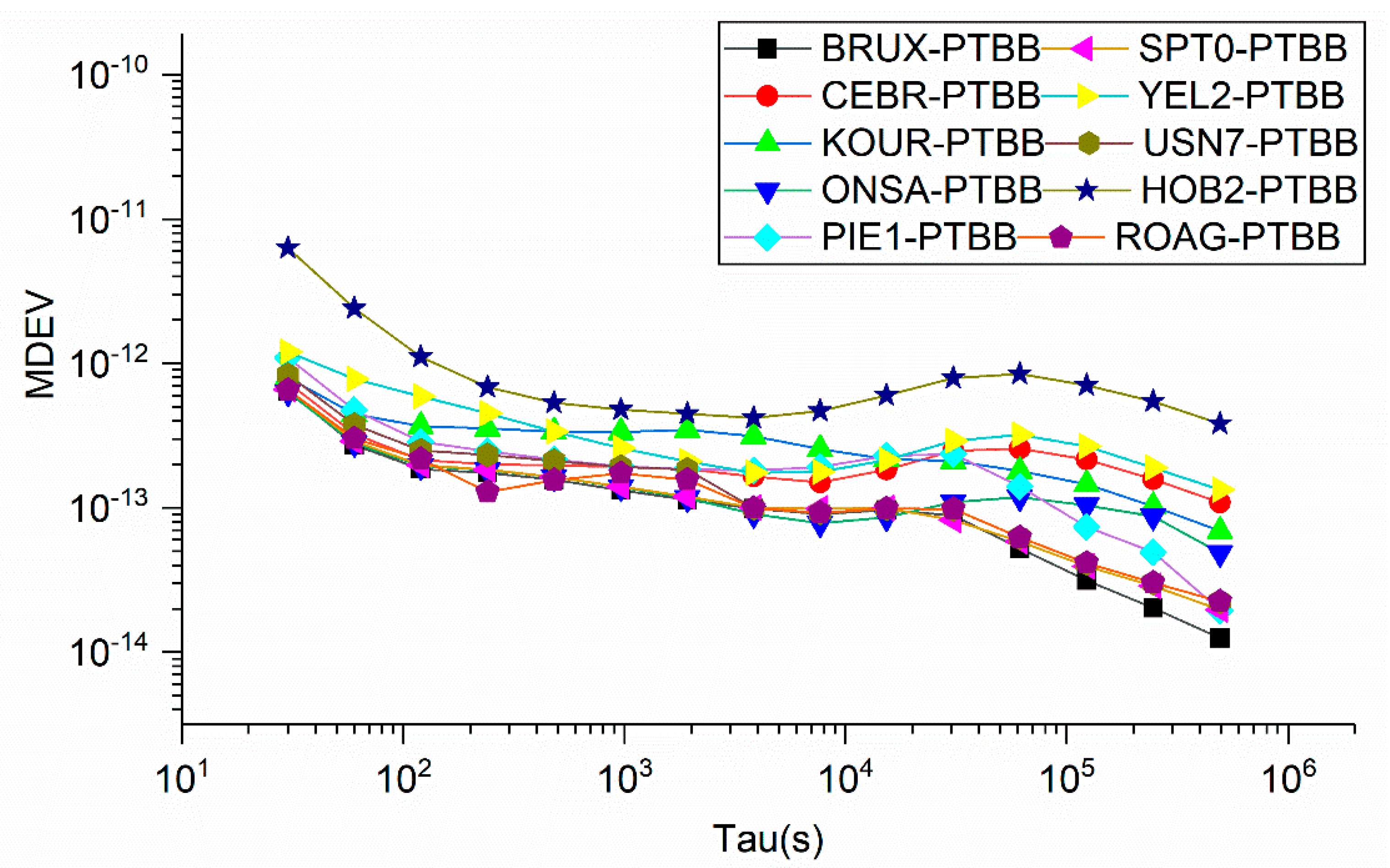
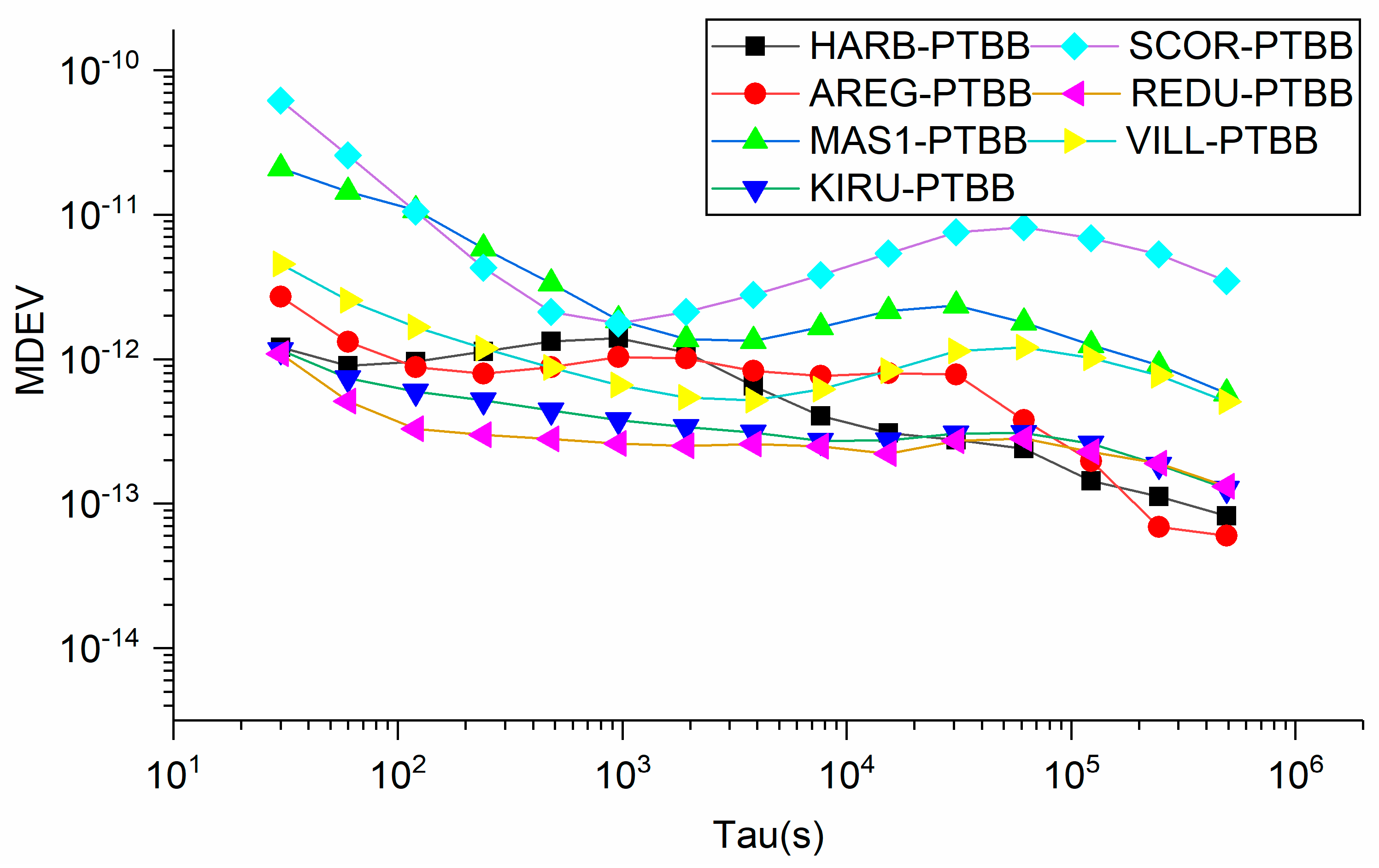
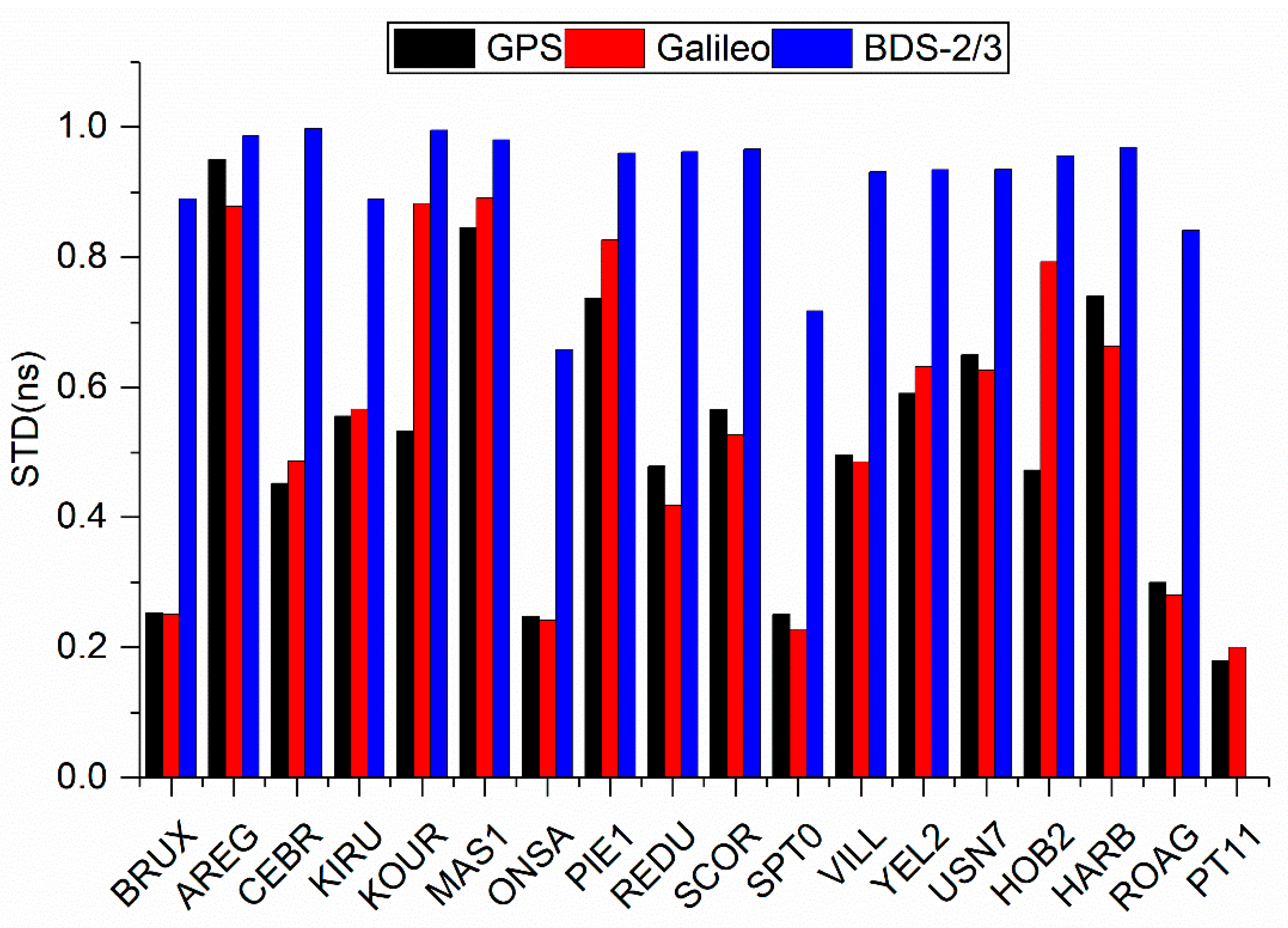
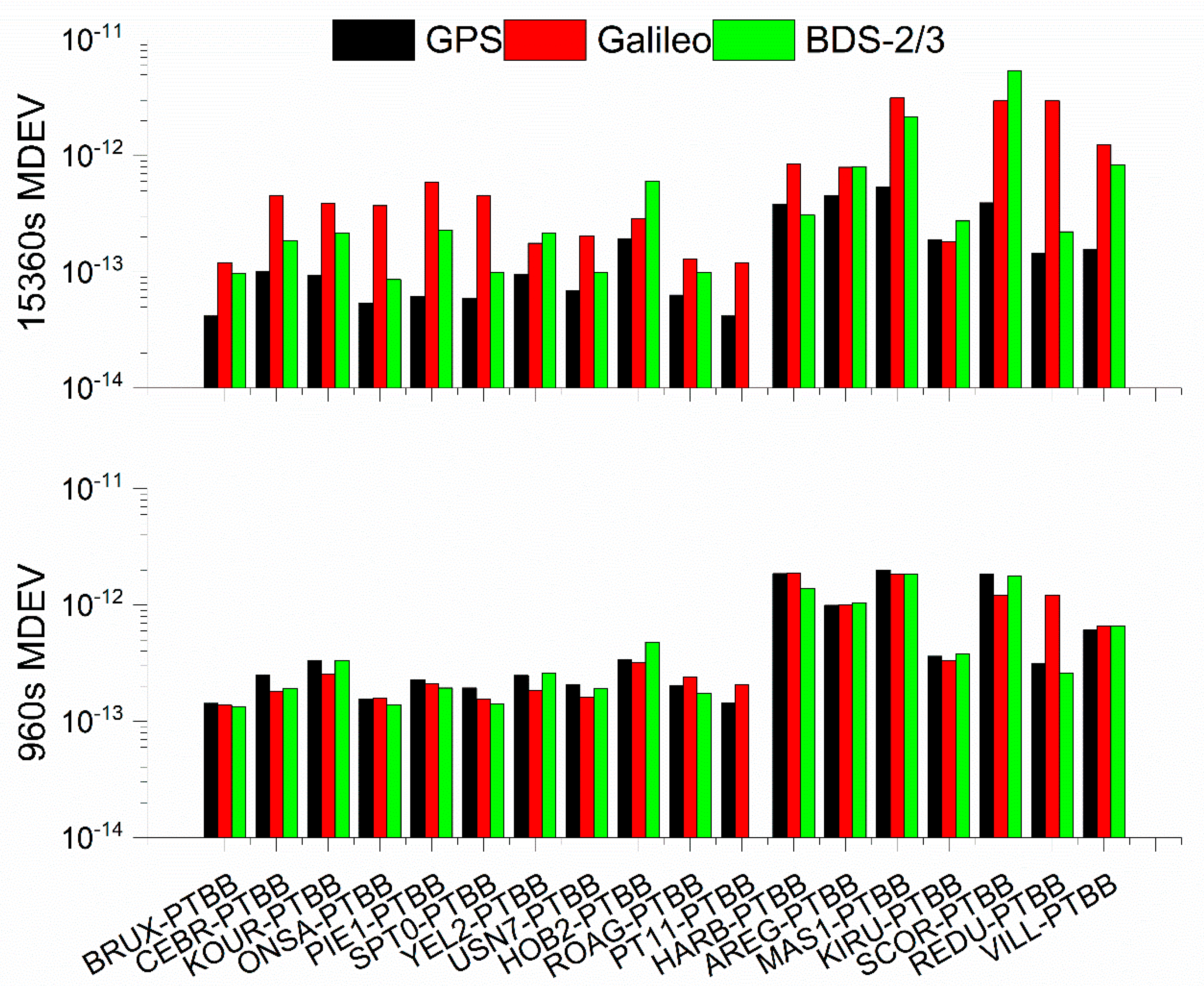
5.4. Comparison of BDS-2/3, GPS and Galileo Single-Frequency PPP Time Transfer
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| AV | All-in-view |
| BDS | BeiDou Navigation Satellite System |
| A | Along |
| R | Radio |
| C | Cross |
| CNES | Centre National d’Etudes Spatiales |
| CV | Common-view |
| DCB | Differential code bias |
| DOY | Day of year |
| GNSS | Global navigation satellite system |
| GEO | Geostationary earth orbit |
| GLONASS | GLObal NAvigation Satellite System |
| IGSO | Inclined geosynchronous orbit |
| TAI | International Atomic Time |
| IFCB | Inter-frequency code biases |
| IPPP | Integer ambiguity PPP techniques |
| IPP | Ionospheric piece point |
| IGS | International GNSS service |
| ISB | Inter system bias |
| OMC | Observed-minus-computed |
| MEO | Medium earth orbit |
| MDEV | Modified Allan deviation |
| MGEX | Multi-GNSS experiment |
| PCO | Phase center offsets |
| PCV | Phase center variations |
| RMS | Root mean squares |
| SSR | State Space Representation |
| STD | Standard deviation |
| 3D | Three dimensions |
| TF | Triple-frequency |
| UCD | Uncalibrated code bias |
| ZWD | Zenith wet delay |
References
- Kirchner, D. Two-way Time Transfer via Communication Satellites. Proc. IEEE 1991, 79, 983–990. [Google Scholar] [CrossRef]
- Defraigne, P.; Bruyninx, C.; Guyennon, N. PPP and Phase-only GPS Time and Frequency transfer. In Proceedings of the IEEE International Frequency Control Symposium Jointly with the 21st European Frequency and Time Forum (EFTF ’07), Geneva, Switzerland, 29 May–1 June 2007; pp. 904–908. [Google Scholar]
- Petit, G.; Jiang, Z. GPS All in View time transfer for TAI computation. Metrologia 2008, 45, 35–45. [Google Scholar] [CrossRef]
- Petit, G.; Jiang, Z. Precise Point Positioning for TAI Computation. Int. J. Navig. Obs. 2008, 2008, 1–8. [Google Scholar] [CrossRef]
- Ge, Y.; Dai, P.; Qin, W.; Yang, X.; Zhou, F.; Wang, S.; Zhao, X. Performance of Multi-GNSS Precise Point Positioning Time and Frequency Transfer with Clock Modeling. Remote Sens. 2019, 11, 347. [Google Scholar] [CrossRef] [Green Version]
- Defraigne, P.; Aerts, W.; Harmegnies, A.; Petit, G.; Rovera, D.; Uhrich, P. Advances in multi-GNSS time transfer. Jt. Eur. Freq. Time Forum Int. Freq. Control Symp. 2013, 508–512. [Google Scholar] [CrossRef]
- Jiang, Z.; Lewandowski, W. Use of GLONASS for UTC time transfer. Metrologia 2012, 49, 57–61. [Google Scholar] [CrossRef]
- Piester, D.; Bauch, A.; Becker, J.; Polewka, T.; McKinley, A.; Breakiron, L.; Smith, A.; Fonville, B.; Matsakis, D. Two-way satellite time transfer between USNO and PTB. In Proceedings of the 2005 IEEE International Frequency Control Symposium and Exposition, Vancouver, BC, Canada, 29–31 August 2005; pp. 316–323. [Google Scholar] [CrossRef]
- Jiang, Z.; Petit, G. Combination of TWSTFT and GNSS for accurate UTC time transfer. Metrologia 2009, 46, 305–314. [Google Scholar] [CrossRef]
- Delporte, J.; Mercier, F.; Laurichesse, D.; Galy, O. GPS Carrier-Phase Time Transfer Using Single-Difference Integer Ambiguity Resolution. Int. J. Navig. Obs. 2008, 2008, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Defraigne, P.; Guyennon, N.; Bruyninx, C. GPS Time and Frequency Transfer: PPP and Phase-Only Analysis. Int. J. Navig. Obs. 2008, 2008, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Guo, W.; Song, W.; Niu, X.; Lou, Y.; Gu, S.; Zhang, S.; Shi, C. Foundation and performance evaluation of real-time GNSS high-precision one-way timing system. GPS Solut. 2019, 23, 23. [Google Scholar] [CrossRef]
- Tu, R.; Zhang, P.; Zhang, R.; Liu, J.; Lu, X. Modeling and performance analysis of precise time transfer based on BDS triple-frequency un-combined observations. J. Geod. 2018, 93, 837–847. [Google Scholar] [CrossRef]
- Tu, R.; Zhang, P.; Zhang, R.; Liu, J.; Lu, X. Modeling and Assessment of Precise Time Transfer by Using BeiDou Navigation Satellite System Triple-Frequency Signals. Sensors 2018, 18, 1017. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiong, J.; Han, F. Positioning performance analysis on combined GPS/BDS precise point positioning. Geod. Geodyn. 2020, 11, 78–83. [Google Scholar] [CrossRef]
- Shi, C.; Wu, X.; Zheng, F.; Wang, X.; Wang, J. Modeling of BDS-2/BDS-3 single-frequency PPP with B1I and B1C signals and positioning performance analysis. Measurement 2021, 178, 109355. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 navigation satellite system. Navigation 2019, 66, 7–18. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Mao, Y.; Sun, B. Basic performance and future developments of BeiDou global navigation satellite system. Satell. Navig. 2020, 1, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Liu, G.; Li, X.; Zhou, F.; Feng, G.; Yuan, Y.; Zhang, K. Galileo PPP rapid ambiguity resolution with five-frequency observations. GPS Solut. 2019, 24, 24. [Google Scholar] [CrossRef]
- Zhao, L.; Václavovic, P.; Douša, J. Performance Evaluation of Troposphere Estimated from Galileo-Only Multi-Frequency Observations. Remote Sens. 2020, 12, 373. [Google Scholar] [CrossRef] [Green Version]
- Petit, G. The TAIPPP pilot experiment. In Frequency Control Symposium, 2009 Joint with the 22nd European Frequency and Time forum. IEEE Int. 2009, 1–2, 116–119. [Google Scholar] [CrossRef]
- Defraigne, P.; Petit, G. Time and frequency transfer combining GLONASS and GPS data. In Proceedings of the 42nd Annual Precise Time and Time Interval Systems and Applications Meeting, San Francisco, CA, USA, 2–5 May 2011; pp. 1–5. [Google Scholar]
- Ge, Y.; Qin, W.; Cao, X.; Zhou, F.; Wang, S.; Yang, X. Consideration of GLONASS Inter-Frequency Code Biases in Precise Point Positioning (PPP) International Time Transfer. Appl. Sci. 2018, 8, 1254. [Google Scholar] [CrossRef] [Green Version]
- Liang, K.; Arias, F.; Petit, G.; Jiang, Z.; Tisserand, L.; Wang, Y.; Yang, Z.; Zhang, A. Evaluation of BeiDou time transfer over multiple inter-continental baselines towards UTC contribution. Metrologia 2018, 55, 513–525. [Google Scholar] [CrossRef]
- Zhang, P.; Tu, R.; Gao, Y.; Zhang, R.; Han, J. Performance of Galileo precise time and frequency transfer models using quad-frequency carrier phase observations. GPS Solut. 2020, 24, 40. [Google Scholar] [CrossRef]
- Lyu, D.; Zeng, F.; Ouyang, X.; Yu, H. Enhancing multi-GNSS time and frequency transfer using a refined stochastic model of a receiver clock. Meas. Sci. Technol. 2019, 30, 125016. [Google Scholar] [CrossRef]
- Zhang, P.; Tu, R.; Zhang, R.; Gao, Y.; Cai, H. Combining GPS, BeiDou, and Galileo Satellite Systems for Time and Frequency Transfer Based on Carrier Phase Observations. Remote Sens. 2018, 10, 324. [Google Scholar] [CrossRef] [Green Version]
- Petit, G. Sub-10–16 accuracy GNSS frequency transfer with IPPP. GPS Solut. 2021, 25, 1–9. [Google Scholar] [CrossRef]
- Petit, G.; Leute, J.; Loyer, S.; Perosanz, F. Sub 10−16 frequency transfer with IPPP: Recent results. In Proceedings of the Frequency and Time Forum and IEEE International Frequency Control Symposium (EFTF/IFC), Joint Conference of the European, Besancon, France, 9–13 July 2017; pp. 784–787. [Google Scholar]
- Defraigne, P.; Aerts, W.; Pottiaux, E. Monitoring of UTC(k)’s using PPP and IGS real-time products. GPS Solut. 2014, 19, 165–172. [Google Scholar] [CrossRef]
- Li, G.; Lin, Y.; Shi, F.; Liu, J.; Yang, Y.; Shi, J. Using IGS RTS Products for Real-Time Subnanosecond Level Time Transfer. In China Satellite Navigation Conference; Springer: Singapore, 2018; Volume 497, pp. 505–518. [Google Scholar] [CrossRef]
- Ge, Y.; Zhou, F.; Liu, T.; Qin, W.; Wang, S.; Yang, X. Enhancing real-time precise point positioning time and frequency transfer with receiver clock modeling. GPS Solut. 2018, 23, 20. [Google Scholar] [CrossRef]
- Qin, W.; Ge, Y.; Wei, P.; Yang, X. An Approach to a Clock Offsets Model for Real-Time PPP Time and Frequency Transfer during Data Discontinuity. Appl. Sci. 2019, 9, 1405. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Qin, W.; Su, K.; Yang, X.; Ouyang, M.; Zhou, F.; Zhao, X. A new approach to real-time precise point-positioning timing with International GNSS Service real-time service products. Meas. Sci. Technol. 2019, 30, 125104. [Google Scholar] [CrossRef]
- Wu, M.; Sun, B.; Wang, Y.; Zhang, Z.; Su, H.; Yang, X. Sub-nanosecond one-way real-time time service system based on UTC. GPS Solut. 2021, 25, 1–9. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.G.; Yuan, Y.; Zhang, H.; Li, M. Joint estimation of vertical total electron content (VTEC) and satellite differential code biases (SDCBs) using low-cost receivers. J. Geod. 2017, 92, 401–413. [Google Scholar] [CrossRef] [Green Version]
- Khodabandeh, A. Single-station PPP-RTK: Correction latency and ambiguity resolution performance. J. Geod. 2021, 95, 1–24. [Google Scholar] [CrossRef]
- Zhao, C.; Yuan, Y.; Zhang, B.; Li, M. Ionosphere Sensing With a Low-Cost, Single-Frequency, Multi-GNSS Receiver. IEEE Trans. Geosci. Remote Sens. 2018, 57, 881–892. [Google Scholar] [CrossRef]
- Ge, Y.; Zhou, F.; Dai, P.; Qin, W.; Wang, S.; Yang, X. Precise point positioning time transfer with multi-GNSS single-frequency observations. Measurement 2019, 146, 628–642. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.; Ge, M.; Li, P.; Wickert, J.; Schuh, H. Simultaneous estimation of GLONASS pseudorange inter-frequency biases in precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22, 19. [Google Scholar] [CrossRef]
- Erol, S.; Alkan, R.M.; Ozulu, İ.M.; İlçi, V. Real-time and post–mission kinematic precise point positioning performance analysis in marine environments. Geod. Geodyn. 2020, 11, 401–410. [Google Scholar] [CrossRef]
- Shi, C.; Gu, S.; Lou, Y.; Ge, M. An improved approach to model ionospheric delays for single-frequency Precise Point Positioning. Adv. Space Res. 2012, 49, 1698–1708. [Google Scholar] [CrossRef]
- Cai, C.; Gong, Y.; Gao, Y.; Kuang, C. An Approach to Speed up Single-Frequency PPP Convergence with Quad-Constellation GNSS and GIM. Sensors 2017, 17, 1302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Li, Z.; Ge, M.; Neitzel, F.; Wang, Z.; Yuan, H. Validation and Assessment of Multi-GNSS Real-Time Precise Point Positioning in Simulated Kinematic Mode Using IGS Real-Time Service. Remote Sens. 2018, 10, 337. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Dong, D.; Li, W.; Jiang, X.; Wickert, J.; Schuh, H. GAMP: An open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22, 33. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions; Bureau International Des Poids Et Mesures Sevres: Sèvres, France, 2010. [Google Scholar]
- Wu, J.T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orienation on GPS carrier phase. Manuscr. Geod. 1992, 18, 91–98. [Google Scholar]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, 10–12. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Ding, S.; Dai, P.; Qin, W.; Yang, X. Modeling and assessment of real-time precise point positioning timing with multi-GNSS observations. Meas. Sci. Technol. 2020, 31, 065016. [Google Scholar] [CrossRef]
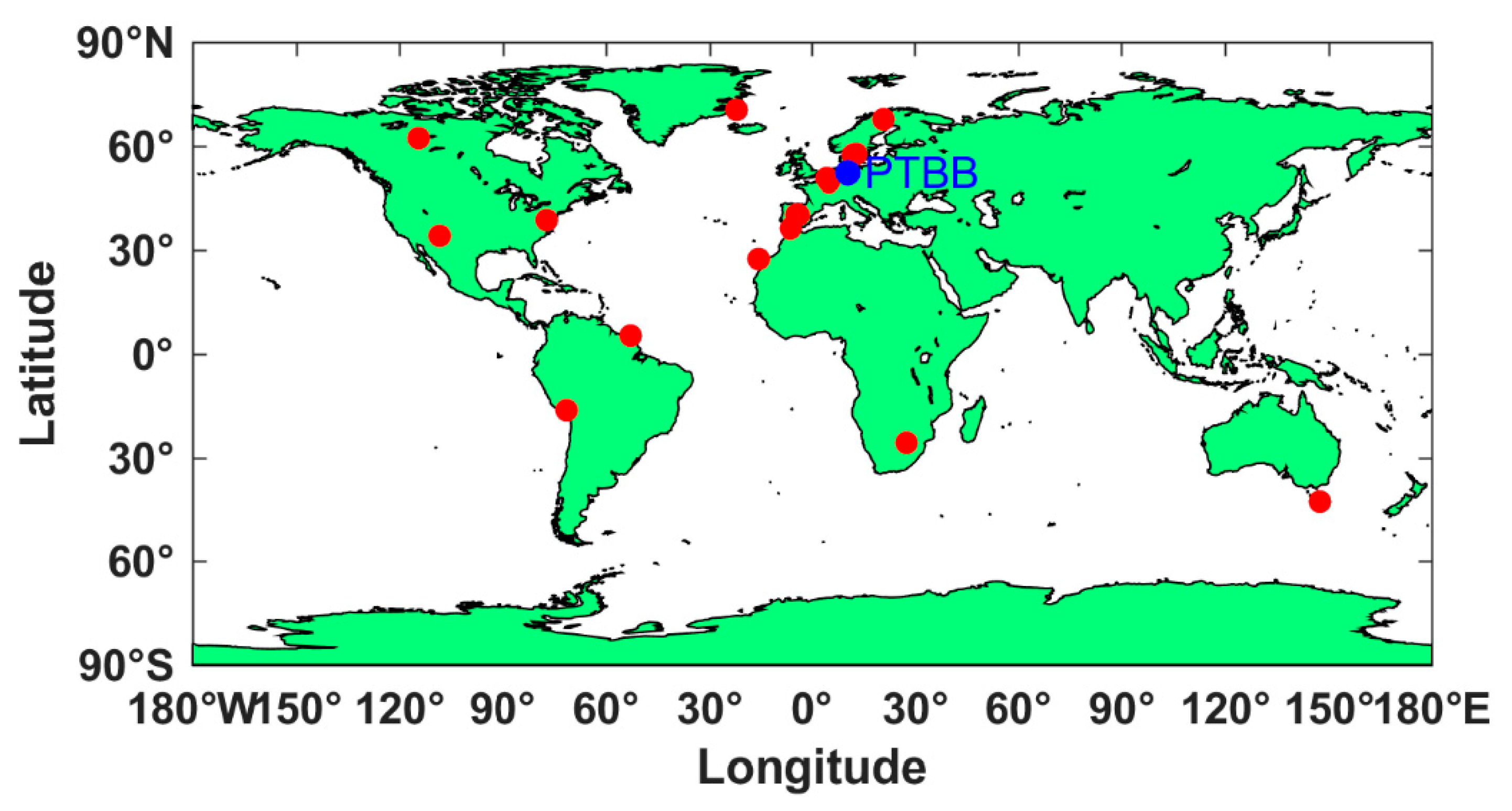
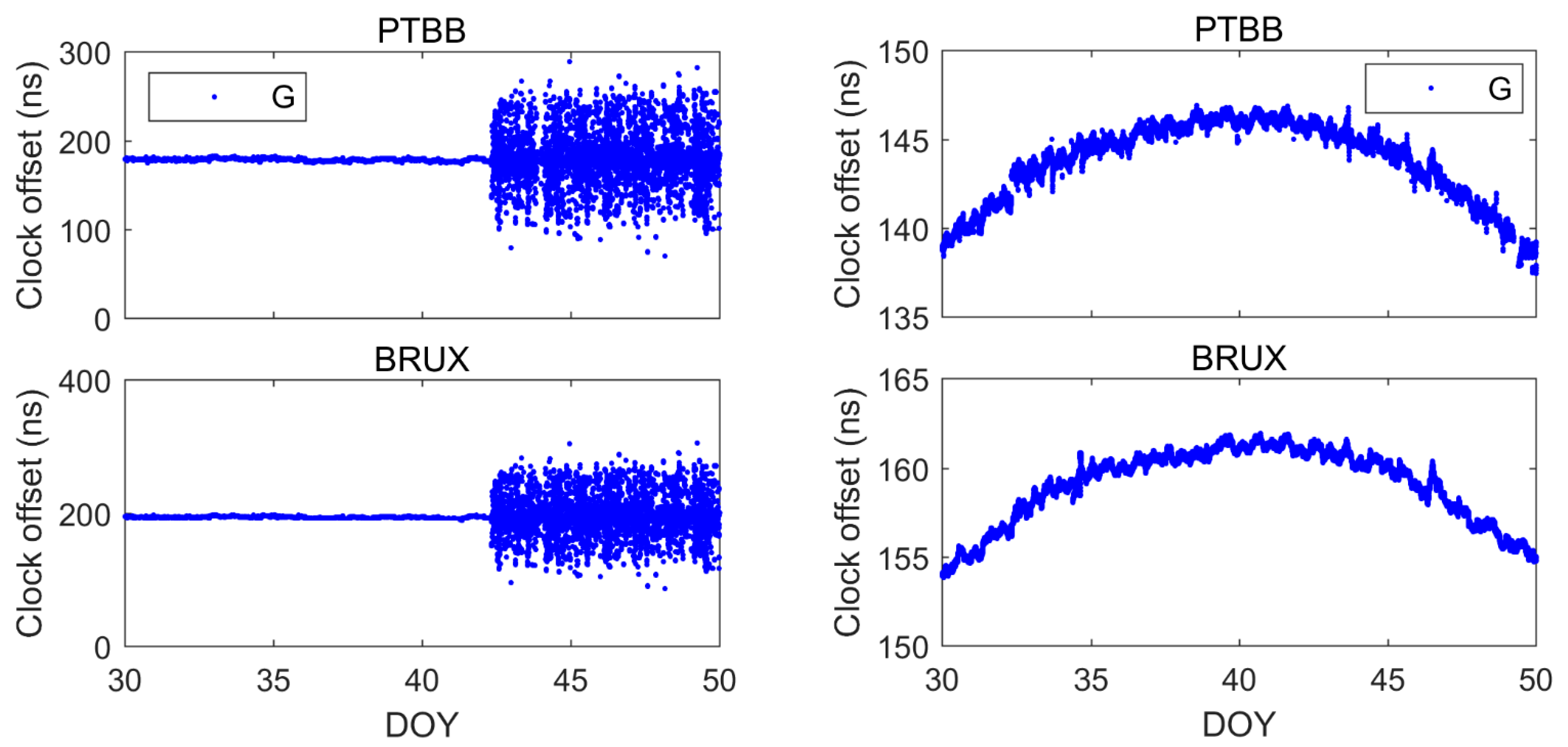




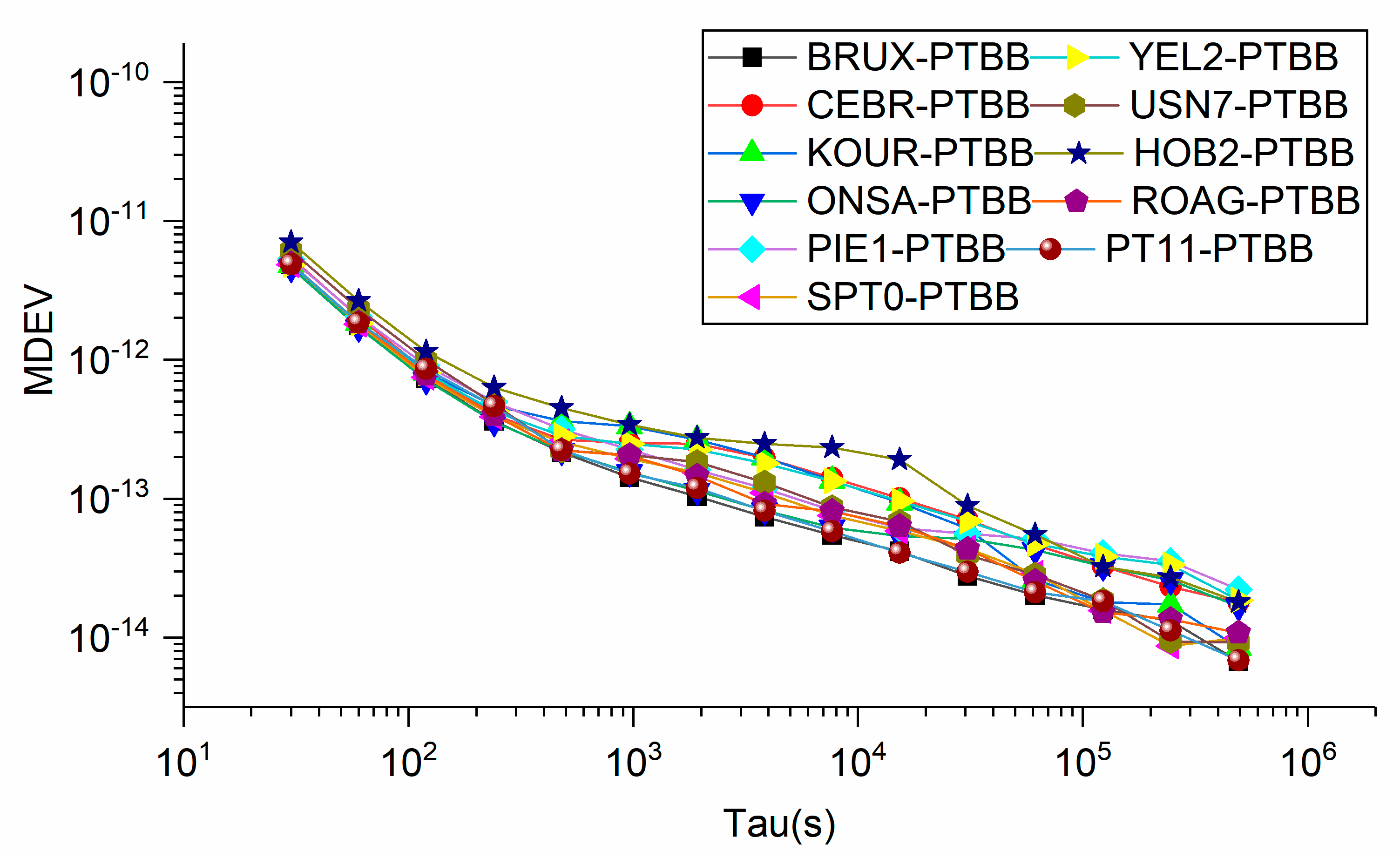
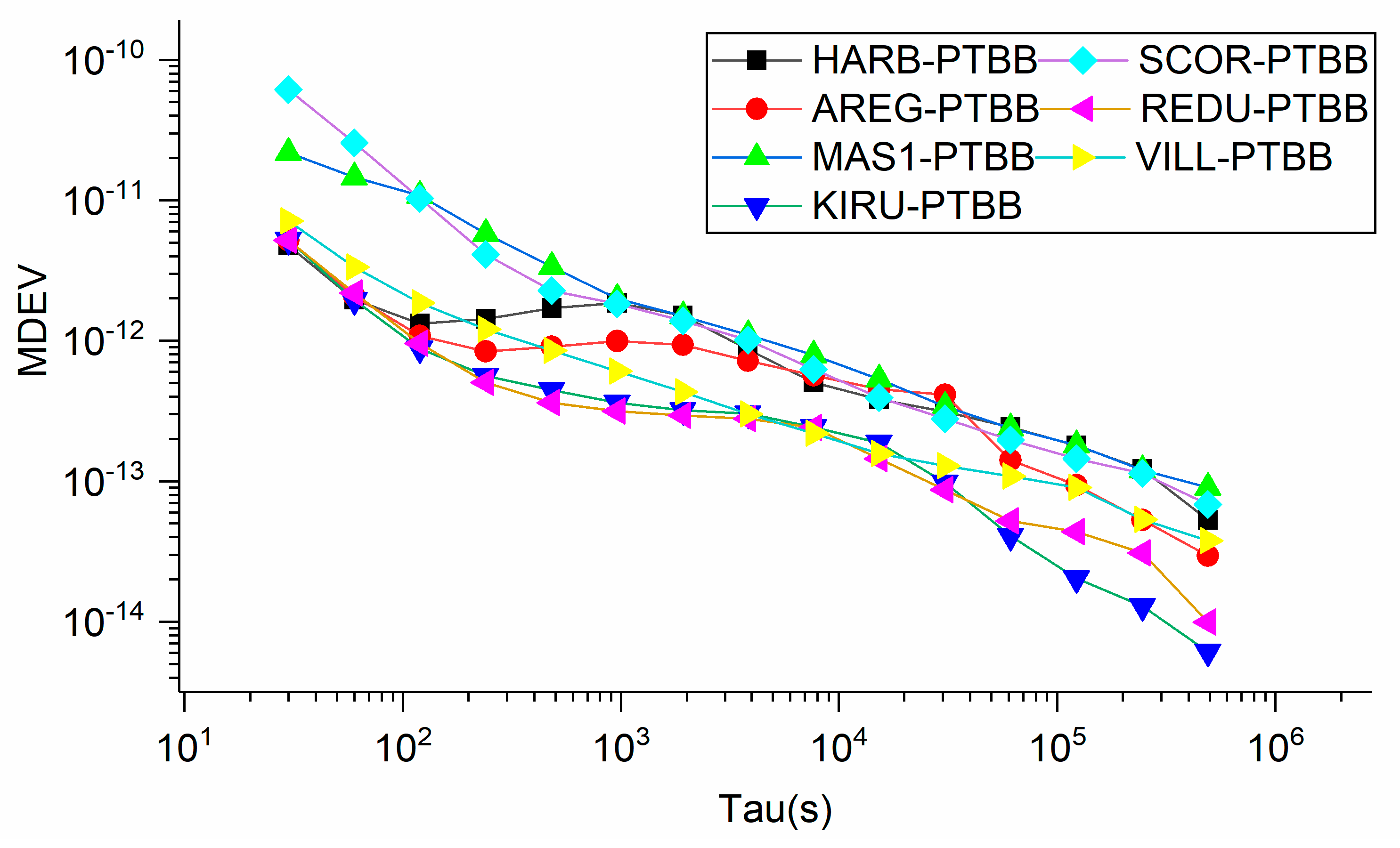



| Station | Receiver | Antenna | Clock |
|---|---|---|---|
| PTBB | SEPT POLARX4TR | LEIAR25.R4 LEIT | UTC(PTB) |
| BRUX | SEPT POLARX4TR | JAVRINGANT_DM | UTC(ROB) |
| PTBB | SEPT POLARX4TR | - | UTC(PTB) |
| AREG | TRIMBLE NETR9 | TRM59800.00 | RUBIDIUM |
| CEBR | SEPT POLARX4 | SEPCHOKE_MC | H-MASER |
| KIRU | SEPT POLARX4 | SEPCHOKE_MC | CESIUM |
| KOUR | SEPT POLARX4 | SEPCHOKE_MC | H-MASER |
| MAS1 | SEPT POLARX4 | LEIAR25.R4 | CESIUM |
| ONSA | JAVAD TRE_G3TH DELTA | AOAD/M_B | H-MASER |
| PIE1 | JAVAD TRE_G3TH DELTA | ASH701945E_M | H-MASER |
| REDU | SEPT POLARX4 | SEPCHOKE_MC | CESIUM |
| SCOR | JAVAD TRE_G3TH SIGMA | ASH701941.B | RUBIDIUM |
| SPT0 | JAVAD TRE_G3TH DELTA | JNSCR_C146-22-1 | H-MASER |
| VILL | SEPT POLARX4 | SEPCHOKE_MC | CESIUM |
| YEL2 | SEPT POLARX4TR | LEIAR25.R4 | H-MASER |
| USN7 | ASHTECH Z-XII3T | TPSCR.G5 | H-MASER |
| ROAG | SEPT POLARX4 | LEIAR25.R4 NONE | H-MASER |
| HOB2 | SEPT POLARX5 | AOAD/M_T | H-MASER |
| HARB | TRIMBLE NETR9 | TRM59800.00 | CESIUM |
| Items | Models |
|---|---|
| Estimate | Kalman filter |
| Cutoff angle | 10° |
| Signal selection | BDS-2/BDS-3: B1I; Galileo: E1; GPS: L1 |
| Sampling rate | 30 s |
| Phase wind-up | Corrected [47] |
| Tropospheric delay | ZHD: corrected by models [48] |
| ZWD: estimated using GMF [49] mapping function | |
| Tidal displacement | Corrected [46] |
| Sagnac effect | Corrected [46] |
| Relativistic effect | Corrected [46] |
| PCO and PCV | Corrected |
| Phase ambiguities | Estimate as constant |
| Receiver clock offset | White noise |
| Station coordinates | Estimated |
| ISB between BDS-2 and BDS-3 | Estimated as white noise |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, X.; Shen, F.; Lu, X.; Shen, P.; Ge, Y. Performance of BDS-2/3, GPS, and Galileo Time Transfer with Real-Time Single-Frequency Precise Point Positioning. Remote Sens. 2021, 13, 4192. https://doi.org/10.3390/rs13214192
Xiao X, Shen F, Lu X, Shen P, Ge Y. Performance of BDS-2/3, GPS, and Galileo Time Transfer with Real-Time Single-Frequency Precise Point Positioning. Remote Sensing. 2021; 13(21):4192. https://doi.org/10.3390/rs13214192
Chicago/Turabian StyleXiao, Xia, Fei Shen, Xiaochun Lu, Pengli Shen, and Yulong Ge. 2021. "Performance of BDS-2/3, GPS, and Galileo Time Transfer with Real-Time Single-Frequency Precise Point Positioning" Remote Sensing 13, no. 21: 4192. https://doi.org/10.3390/rs13214192
APA StyleXiao, X., Shen, F., Lu, X., Shen, P., & Ge, Y. (2021). Performance of BDS-2/3, GPS, and Galileo Time Transfer with Real-Time Single-Frequency Precise Point Positioning. Remote Sensing, 13(21), 4192. https://doi.org/10.3390/rs13214192








