Estimation of Plot-Level Burn Severity Using Terrestrial Laser Scanning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Field Data Collection
2.3. TLS Processing and Metric Generation
2.4. Predictive Modeling and Assessment
3. Results
3.1. Field Data
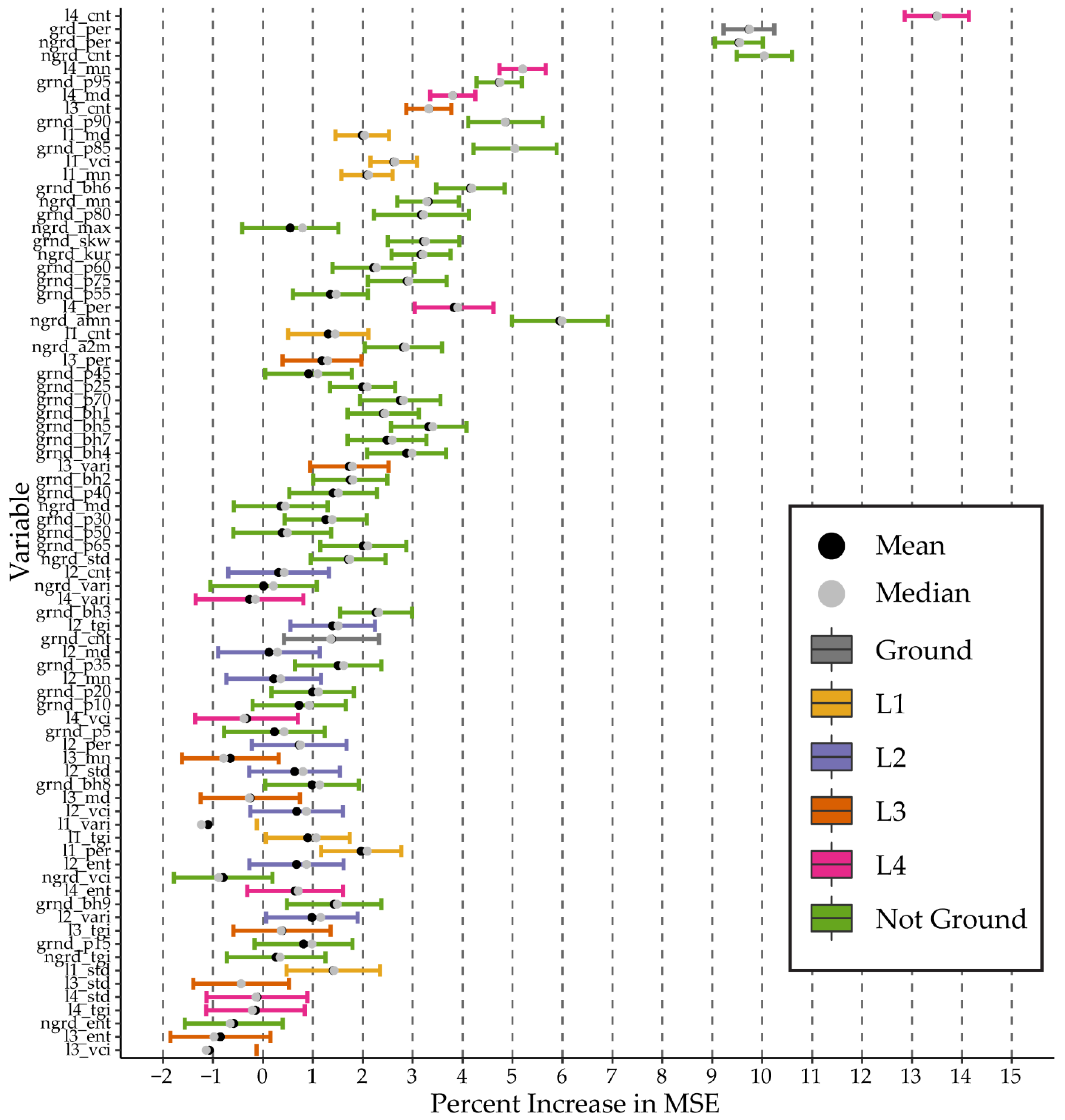
3.2. Variable Importance
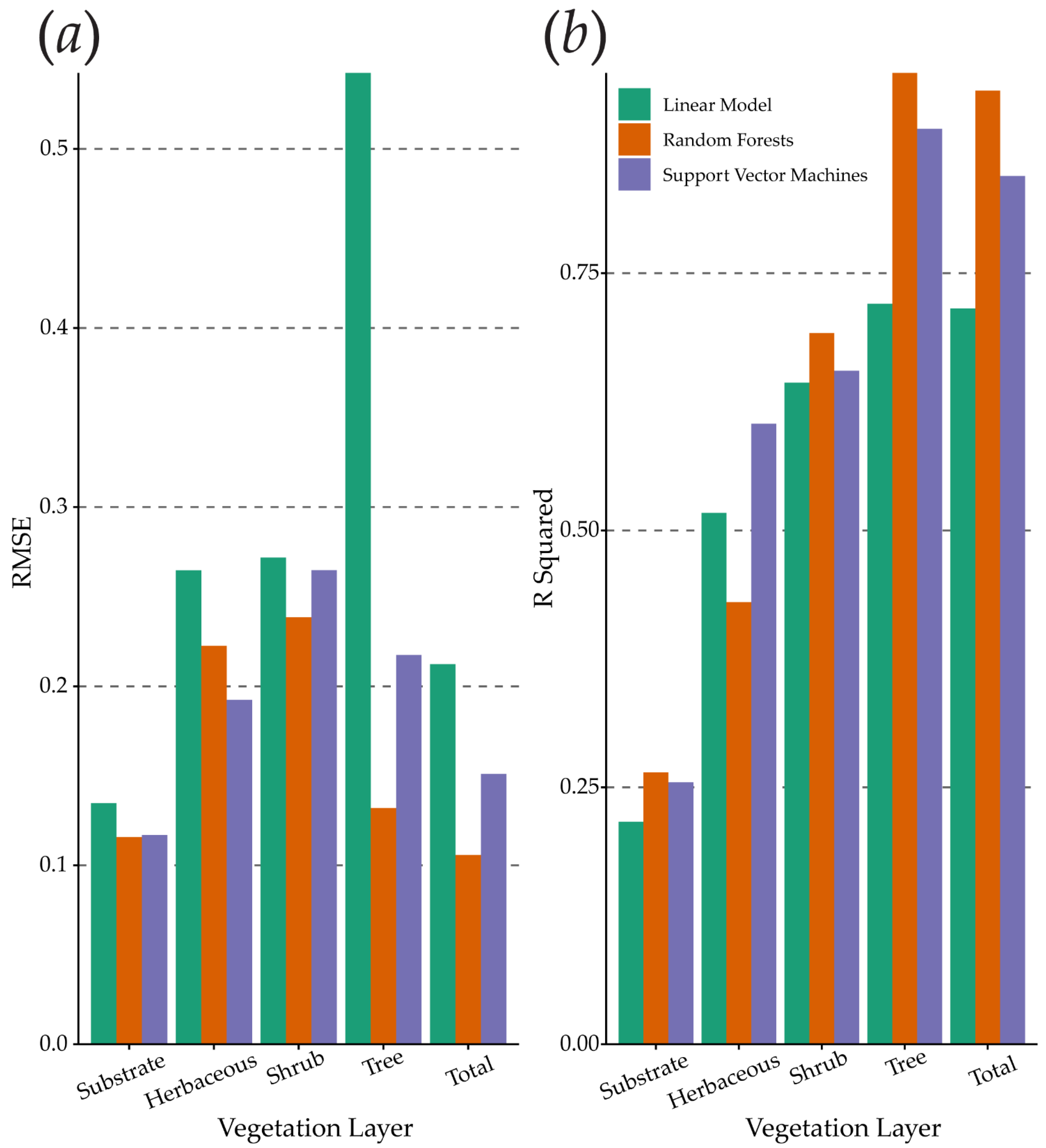
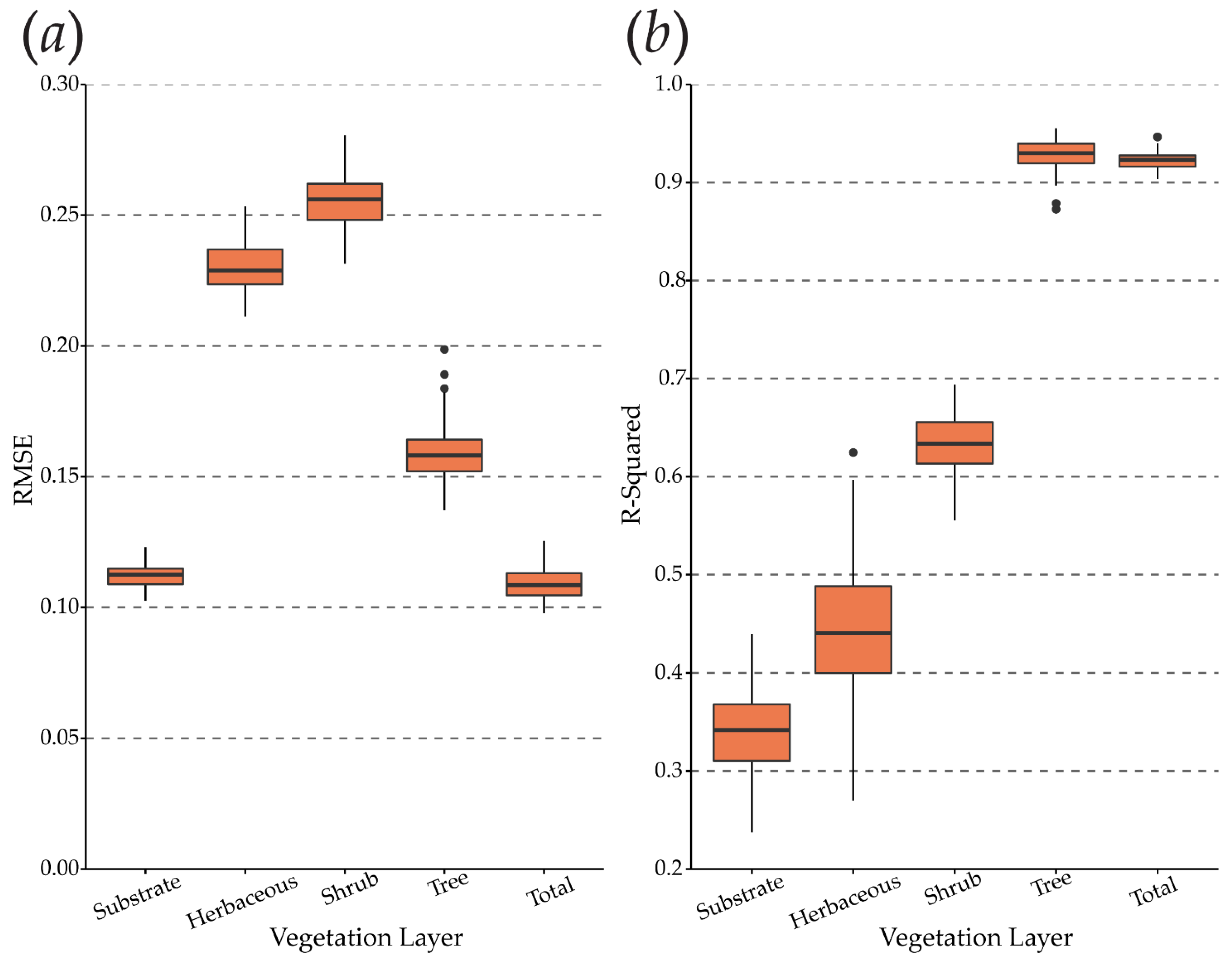
3.3. Model Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Basal Area (m2/ha) | Stems/ha (n) | DBH (cm; Mean ± 1SD) | Height (m; Mean ± 1SD) |
|---|---|---|---|
| 9.7 | 828 | 9.4 ± 8.3 | 4.6 ± 2.9 |
| 15.1 | 2452 | 8.2 ± 3.4 | 4.5 ± 1.6 |
| 17.0 | 2834 | 8.1 ± 3.5 | 4.5 ± 1.6 |
| 17.6 | 2420 | 8.8 ± 3.8 | 4.8 ± 2.0 |
| 18.3 | 2580 | 8.7 ± 3.9 | 4.6 ± 2.0 |
| 19.4 | 2548 | 9.2 ± 3.5 | 4.9 ± 1.8 |
| 19.5 | 541 | 19.1 ± 10.0 | 11.2 ± 4.6 |
| 20.8 | 987 | 14.7 ± 7.5 | 7.5 ± 4.2 |
| 22.2 | 1274 | 12.7 ± 7.9 | 7.7 ± 4.1 |
| 22.6 | 1083 | 13.6 ± 9.1 | 8.7 ± 4.9 |
| 22.8 | 2197 | 10.4 ± 5.0 | 6.5 ± 3.1 |
| 23.7 | 2357 | 10.5 ± 4.2 | 6.4 ± 2.3 |
| 23.9 | 1210 | 13.5 ± 8.3 | 7.6 ± 4.4 |
| 23.9 | 3280 | 8.8 ± 3.9 | 5.2 ± 2.1 |
| 24.7 | 1592 | 12.1 ± 7.2 | 8.2 ± 4.5 |
| 24.9 | 1146 | 13.4 ± 10.0 | 8.7 ± 5.5 |
| 25.0 | 987 | 15.1 ± 9.9 | 8.1 ± 5.1 |
| 26.3 | 1146 | 14.1 ± 9.9 | 8.7 ± 6.2 |
| 26.7 | 1975 | 11.7 ± 6.0 | 7.4 ± 3.5 |
| 26.7 | 1051 | 14.6 ± 10.6 | 9.2 ± 6.1 |
| 26.8 | 1497 | 13.8 ± 6.3 | 8.4 ± 3.6 |
| 26.9 | 2452 | 10.3 ± 5.9 | 6.9 ± 3.3 |
| 27.0 | 1943 | 12.1 ± 5.6 | 7.2 ± 3.1 |
| 27.6 | 1178 | 14.5 ± 9.5 | 9.2 ± 5.4 |
| 27.9 | 1879 | 11.9 ± 6.9 | 8.1 ± 4.3 |
| 28.0 | 987 | 16.9 ± 8.9 | 10.3 ± 4.5 |
| 28.1 | 1783 | 12.6 ± 6.5 | 9.0 ± 4.7 |
| 28.7 | 1274 | 14.6 ± 8.7 | 10.2 ± 4.9 |
| 29.6 | 1051 | 17.0 ± 8.5 | 9.7 ± 4.5 |
| 30.2 | 1274 | 13.9 ± 10.6 | 8.2 ± 4.9 |
| 30.3 | 2229 | 11.7 ± 6.3 | 7.4 ± 3.7 |
| 30.3 | 1083 | 14.8 ± 11.9 | 9.3 ± 6.5 |
| 30.4 | 1401 | 13.7 ± 9.5 | 9.4 ± 5.4 |
| 30.9 | 1943 | 12.8 ± 6.3 | 8.3 ± 3.3 |
| 31.6 | 1752 | 13.1 ± 7.6 | 8.0 ± 4.3 |
| 32.0 | 1815 | 13.2 ± 7.2 | 8.8 ± 4.2 |
| 32.0 | 1975 | 12.2 ± 7.7 | 7.8 ± 4.4 |
| 32.2 | 1401 | 15.1 ± 8.1 | 10.6 ± 4.2 |
| 32.3 | 1656 | 14.1 ± 7.2 | 9.9 ± 4.0 |
| 32.6 | 1178 | 17.5 ± 6.9 | 13.2 ± 4.2 |
| 33.6 | 2070 | 12.7 ± 6.9 | 7.8 ± 4.1 |
| 33.8 | 1656 | 14.4 ± 7.3 | 9.0 ± 4.1 |
| 35.1 | 1783 | 14.0 ± 7.6 | 9.6 ± 4.7 |
References
- Kane, V.R.; Cansler, C.A.; Povak, N.A.; Kane, J.T.; McGaughey, R.J.; Lutz, J.A.; Churchill, D.J.; North, M.P. Mixed severity fire effects within the Rim fire: Relative importance of local climate, fire weather, topography, and forest structure. For. Ecol. Manag. 2015, 358, 62–79. [Google Scholar] [CrossRef] [Green Version]
- McLauchlan, K.K.; Higuera, P.E.; Miesel, J.; Rogers, B.M.; Schweitzer, J.; Shuman, J.K.; Tepley, A.J.; Varner, J.M.; Veblen, T.T.; Adalsteinsson, S.A. Fire as a fundamental ecological process: Research advances and frontiers. J. Ecol. 2020, 108, 2047–2069. [Google Scholar] [CrossRef]
- Simard, S. Fire severity, changing scales, and how things hang together. Int. J. Wildland Fire 1991, 1, 23–34. [Google Scholar] [CrossRef]
- Hardy, C.C. Wildland fire hazard and risk: Problems, definitions, and context. For. Ecol. Manag. 2005, 211, 73–82. [Google Scholar] [CrossRef]
- Keeley, J.E. Fire intensity, fire severity and burn severity: A brief review and suggested usage. Int. J. Wildland Fire 2009, 18, 116–126. [Google Scholar] [CrossRef]
- Bond, W.J.; Keeley, J.E. Fire as a global ‘herbivore’: The ecology and evolution of flammable ecosystems. Trends Ecol. Evol. 2005, 20, 387–394. [Google Scholar] [CrossRef] [PubMed]
- Hardy, C.C.; Schmidt, K.M.; Menakis, J.P.; Sampson, R.N. Spatial data for national fire planning and fuel management. Int. J. Wildland Fire 2001, 10, 353–372. [Google Scholar] [CrossRef]
- Skowronski, N.S.; Gallagher, M.R.; Warner, T.A. Decomposing the Interactions between Fire Severity and Canopy Fuel Structure Using Multi-Temporal, Active, and Passive Remote Sensing Approaches. Fire 2020, 3, 7. [Google Scholar] [CrossRef] [Green Version]
- Meyer, M.D.; Long, J.; Safford, H.; Sawyer, S.; North, M.; White, A. Chapter 1: Principles of postfire restoration in Meyer. In Postfire Restoration Framework for National Forests in California; Gen. Tech. Rep. PSW-GTR-270; Department of Agriculture, Forest Service, Pacific Southwest Research Station: Albany, CA, USA, 2021; pp. 1–30. [Google Scholar]
- Miller, J.D.; Yool, S.R. Mapping forest post-fire canopy consumption in several overstory types using multi-temporal Landsat TM and ETM data. Remote Sens. Environ. 2002, 82, 481–496. [Google Scholar] [CrossRef]
- Key, C.H.; Benson, N.C. Landscape assessment (LA). In FIREMON: Fire effects monitoring and inventory system; Gen. Tech. Rep. RMRS-GTR-164-CD; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; 164, p. LA-1-55. [Google Scholar]
- Garcia, M.J.L.; Caselles, V. Mapping burns and natural reforestation using Thematic Mapper data. Geocarto Int. 1991, 6, 31–37. [Google Scholar] [CrossRef]
- French, N.H.; Kasischke, E.S.; Hall, R.J.; Murphy, K.A.; Verbyla, D.L.; Hoy, E.E.; Allen, J.L. Using Landsat data to assess fire and burn severity in the North American boreal forest region: An overview and summary of results. Int. J. Wildland Fire 2008, 17, 443–462. [Google Scholar] [CrossRef]
- Gallagher, M.R.; Skowronski, N.S.; Lathrop, R.G.; McWilliams, T.; Green, E.J. An Improved Approach for Selecting and Validating Burn Severity Indices in Forested Landscapes. Can. J. Remote Sens. 2020, 46, 100–111. [Google Scholar] [CrossRef]
- Hiers, J.K.; O’Brien, J.J.; Varner, J.M.; Butler, B.W.; Dickinson, M.; Furman, J.; Gallagher, M.; Godwin, D.; Goodrick, S.L.; Hood, S.M. Prescribed fire science: The case for a refined research agenda. Fire Ecol. 2020, 16, 11. [Google Scholar] [CrossRef] [Green Version]
- Kolden, C.A.; Smith, A.M.S.; Abatzoglou, J.T. Limitations and utilisation of Monitoring Trends in Burn Severity products for assessing wildfire severity in the USA. Int. J. Wildland Fire 2015, 24, 1023–1028. [Google Scholar] [CrossRef]
- Picotte, J.J.; Bhattarai, K.; Howard, D.; Lecker, J.; Epting, J.; Quayle, B.; Benson, N.; Nelson, K. Changes to the Monitoring Trends in Burn Severity program mapping production procedures and data products. Fire Ecol. 2020, 16, 16. [Google Scholar] [CrossRef]
- Warner, T.A.; Skowronski, N.S.; La Puma, I. The influence of prescribed burning and wildfire on lidar-estimated forest structure of the New Jersey Pinelands National Reserve. Int. J. Wildland Fire 2020, 29, 1100–1108. [Google Scholar] [CrossRef]
- Pokswinski, S.; Gallagher, M.R.; Skowronski, N.S.; Loudermilk, E.L.; Hawley, C.; Wallace, D.; Everland, A.; Wallace, J.; Hiers, J.K. A simplified and affordable approach to forest monitoring using single terrestrial laser scans and transect sampling. MethodsX 2021, 8, 101484. [Google Scholar] [CrossRef] [PubMed]
- Kato, A.; Moskal, L.M.; Batchelor, J.L.; Thau, D.; Hudak, A.T. Relationships between Satellite-Based Spectral Burned Ratios and Terrestrial Laser Scanning. Forests 2019, 10, 444. [Google Scholar] [CrossRef] [Green Version]
- Philipp, M.B.; Levick, S.R. Exploring the potential of C-Band SAR in contributing to burn severity mapping in tropical savanna. Remote Sens. 2020, 12, 49. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Skidmore, A.K.; Wang, T.; Liu, J.; Darvishzadeh, R.; Shi, Y.; Premier, J.; Heurich, M. Improving leaf area index (LAI) estimation by correcting for clumping and woody effects using terrestrial laser scanning. Agric. For. Meteorol. 2018, 263, 276–286. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Greaves, H.E.; Vierling, L.A.; Eitel, J.U.; Boelman, N.T.; Magney, T.S.; Prager, C.M.; Griffin, K.L. Estimating aboveground biomass and leaf area of low-stature Arctic shrubs with terrestrial LiDAR. Remote Sens. Environ. 2015, 164, 26–35. [Google Scholar] [CrossRef]
- Danson, F.M.; Hetherington, D.; Morsdorf, F.; Koetz, B.; Allgower, B. Forest canopy gap fraction from terrestrial laser scanning. IEEE Geosci. Remote Sens. Lett. 2007, 4, 157–160. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Guo, Q.; Su, Y.; Tao, S.; Zhao, K.; Xu, G. Retrieving the gap fraction, element clumping index, and leaf area index of individual trees using single-scan data from a terrestrial laser scanner. ISPRS J. Photogramm. Remote Sens. 2017, 130, 308–316. [Google Scholar] [CrossRef]
- Disney, M.; Burt, A.; Wilkes, P.; Armston, J.; Duncanson, L. New 3D measurements of large redwood trees for biomass and structure. Sci. Rep. 2020, 10, 16721. [Google Scholar] [CrossRef] [PubMed]
- Ye, W.; Qian, C.; Tang, J.; Liu, H.; Fan, X.; Liang, X.; Zhang, H. Improved 3D stem mapping method and elliptic hypothesis-based DBH estimation from terrestrial laser scanning Data. Remote Sens. 2020, 12, 352. [Google Scholar] [CrossRef] [Green Version]
- Rowell, E.; Loudermilk, E.L.; Hawley, C.; Pokswinski, S.; Seielstad, C.; Queen, L.; O’brien, J.J.; Hudak, A.T.; Goodrick, S.; Hiers, J.K. Coupling terrestrial laser scanning with 3D fuel biomass sampling for advancing wildland fuels characterization. For. Ecol. Manag. 2020, 462, 117945. [Google Scholar] [CrossRef]
- Wilson, N.; Bradstock, R.; Bedward, M. Detecting the effects of logging and wildfire on forest fuel structure using terrestrial laser scanning (TLS). For. Ecol. Manag. 2021, 488, 119037. [Google Scholar] [CrossRef]
- Wilkes, P.; Lau, A.; Disney, M.; Calders, K.; Burt, A.; de Tanago, J.G.; Bartholomeus, H.; Brede, B.; Herold, M. Data acquisition considerations for terrestrial laser scanning of forest plots. Remote Sens. Environ. 2017, 196, 140–153. [Google Scholar] [CrossRef]
- Stovall, A.E.; Atkins, J.W. Assessing low-cost terrestrial laser scanners for deriving forest structure parameters. Preprints 2021. [Google Scholar] [CrossRef]
- Gallagher, M. Monitoring Fire Effects in the New Jersey Pine Barrens Using Burn Severity Indices; Dissertation; Rutgers, The State University of New Jersey: New Brunswick, NJ, USA, 2017. [Google Scholar]
- Skowronski, N.S.; Clark, K.L.; Duveneck, M.; Hom, J. Three-dimensional canopy fuel loading predicted using upward and downward sensing LiDAR systems. Remote Sens. Environ. 2011, 115, 703–714. [Google Scholar] [CrossRef]
- Lutz, H.J. Ecological Relations in the Pitch Pine Plains of Southern New Jersey; Yale University: New Haven, CT, USA, 1934. [Google Scholar]
- Givnish, T.J. Serotiny, geography, and fire in the Pine Barrens of New Jersey. Evolution 1981, 35, 101–123. [Google Scholar] [CrossRef] [Green Version]
- Ledig, F.T.; Hom, J.L.; Smouse, P.E. The evolution of the New Jersey pine plains. Am. J. Bot. 2013, 100, 778–791. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Roussel, J.-R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Meador, A.S.; Bourdon, J.-F.; de Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- De Conto, T.; Olofsson, K.; Görgens, E.B.; Rodriguez, L.C.E.; Almeida, G. Performance of stem denoising and stem modelling algorithms on single tree point clouds from terrestrial laser scanning. Comput. Electron. Agric. 2017, 143, 165–176. [Google Scholar] [CrossRef]
- Roussel, J.; Qi, J. RCSF: Airborne LiDAR Filtering Method Based on Cloth Simulation. R Package Version 2018, 1, 1. [Google Scholar]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Van Ewijk, K.Y.; Treitz, P.M.; Scott, N.A. Characterizing forest succession in Central Ontario using LiDAR-derived indices. Photogramm. Eng. Remote Sens. 2011, 77, 261–269. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Doraiswamy, P.C.; McMurtrey, J.E.; Daughtry, C.S.; Perry, E.M.; Akhmedov, B. A visible band index for remote sensing leaf chlorophyll content at the canopy scale. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 103–112. [Google Scholar] [CrossRef] [Green Version]
- Gitelson, A.; Stark, R.; Grits, U.; Rundquist, D.; Kaufman, Y.; Derry, D. Vegetation and soil lines in visible spectral space: A concept and technique for remote estimation of vegetation fraction. Int. J. Remote Sens. 2002, 23, 2537–2562. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Stoppiglia, H.; Dreyfus, G.; Dubois, R.; Oussar, Y. Ranking a random feature for variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1399–1414. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Lawrence, R.L.; Moran, C.J. The AmericaView classification methods accuracy comparison project: A rigorous approach for model selection. Remote Sens. Environ. 2015, 170, 115–120. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef] [Green Version]
- Gunn, S.R. Support vector machines for classification and regression. ISIS Tech. Rep. 1998, 14, 5–16. [Google Scholar]
- Pal, M.; Mather, P. Support vector machines for classification in remote sensing. Int. J. Remote Sens. 2005, 26, 1007–1011. [Google Scholar] [CrossRef]
- Kuhn, M. Caret: Classification and regression training. Astrophys. Source Code Libr. 2015, ascl: 1505.1003. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Karatzoglou, A.; Smola, A.; Hornik, K.; Zeileis, A. kernlab-an S4 package for kernel methods in R. J. Stat. Softw. 2004, 11, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Clark, K.L.; Gallagher, M.; Aoki, C.; Ayers, M. Southern pine beetle: Damage and consequences in forests of the mid-Atlantic region, USA. Tree Plant Notes 2020, 63, 91–103. [Google Scholar]
- Clark, K.; Renninger, H.; Skowronski, N.; Gallagher, M.; Schäfer, K. Decadal-scale reduction in forest net ecosystem production following insect defoliation contrasts with short-term impacts of prescribed fires. Forests 2018, 9, 145. [Google Scholar] [CrossRef] [Green Version]
- Gallagher, M.R.; Clark, K.L.; Thomas, J.C.; Mell, W.E.; Hadden, R.M.; Mueller, E.V.; Kremens, R.L.; El Houssami, M.; Filkov, A.I.; Simeoni, A.A.; et al. New Jersey Fuel Treatment Effects: Pre- and Post-Burn Biometric Data; Forest Service Research Data Archive: Fort Collins, CO, USA, 2017. [Google Scholar] [CrossRef]
- Good, R.E.; Good, N.F.; Andresen, J.W. The Pine Barren Plains; Pine Barrens: Ecosystem and landscape; Forman, R.T.T., Ed.; Academic Press: New York, NY, USA, 1998; pp. 283–294. [Google Scholar]
- Debeer, D.; Strobl, C. Conditional permutation importance revisited. BMC Bioinform. 2020, 21, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Nicodemus, K.K.; Malley, J.D.; Strobl, C.; Ziegler, A. The behaviour of random forest permutation-based variable importance measures under predictor correlation. BMC Bioinform. 2010, 11, 110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Strobl, C.; Boulesteix, A.-L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Strobl, C.; Boulesteix, A.-L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 1–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fox, J.; Weisberg, S. An R Companion to Applied Regression, 3rd ed.; Sage Publications: Los Angeles, CA, USA, 2019. [Google Scholar]
- He, H.; Garcia, E.A. Learning from imbalanced data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef] [Green Version]
- Rorie, R.L.; Purcell, L.C.; Karcher, D.E.; King, C.A. The assessment of leaf nitrogen in corn from digital images. Crop. Sci. 2011, 51, 2174–2180. [Google Scholar] [CrossRef] [Green Version]
- Putra, B.T.W.; Soni, P. Improving nitrogen assessment with an RGB camera across uncertain natural light from above-canopy measurements. Precis. Agric. 2020, 21, 147–159. [Google Scholar] [CrossRef]




| Stratification | Definition |
|---|---|
| Ground | Points classified as ground |
| Not Ground | Points not classified as ground |
| L1 | Substrate (height > 0.001 m & height ≤ 0.3 m) |
| L2 | Herbs and low shrubs (height > 0.3 m & height ≤ 1 m) |
| L3 | Tall shrubs (height > 1 m & height ≤ 3 m) |
| L4 | Pole-size trees and tall trees (height > 3 m) |
| Strata | Sensor | Variable | Abbreviation | Count |
|---|---|---|---|---|
| Ground | TLS | Number of returns | grnd_cnt | 1 |
| Percent of total returns | grd_per | 1 | ||
| Not Ground | TLS | Number of returns | ngrnd_cnt | 1 |
| Percent of total returns | ngrnd_per | 1 | ||
| Mean of z 1 | ngrnd_mn | 1 | ||
| Median of z | ngrnd_md | 1 | ||
| Standard deviation of z | ngrnd_std | 1 | ||
| Entropy of z | ngrnd_ent | 1 | ||
| Vertical complexity index (VCI) of z | ngrnd_vci | 1 | ||
| Skewness of z | ngrnd_skw | 1 | ||
| Kurtosis of z | ngrnd_kur | 1 | ||
| Percent above mean z | ngrnd_amn | 1 | ||
| Percent more than 2 m above ground | ngrnd_a2m | 1 | ||
| Maximum not ground z | ngrnd_max | 1 | ||
| z percentiles for not ground 2 | ngrnd_px | 19 | ||
| Percent of points below height 3 | ngrnd_bhx | 9 | ||
| RGB | Triangular greenness index (TGI) | ngrnd_tgi | 1 | |
| Visible atmospherically resistant index (VARI) | ngrnd_vari | 1 | ||
| Not Ground in L1, L2, L3, L4 | TLS | Number of total not ground returns in strata | lx_cnt 4 | 4 |
| Percent of total not ground returns in strata | lx_per | 4 | ||
| Mean of z | lx_mn | 4 | ||
| Median of z | lx_md | 4 | ||
| Standard deviation of z | lx_std | 4 | ||
| Entropy of z | lx_ent | 4 | ||
| Vertical Complexity Index (VCI) of z | lx_vci | 4 | ||
| RGB | Triangular greenness index (TGI) | lx_tgi | 4 | |
| Visible atmospherically resistant index (VARI) | lx_vari | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallagher, M.R.; Maxwell, A.E.; Guillén, L.A.; Everland, A.; Loudermilk, E.L.; Skowronski, N.S. Estimation of Plot-Level Burn Severity Using Terrestrial Laser Scanning. Remote Sens. 2021, 13, 4168. https://doi.org/10.3390/rs13204168
Gallagher MR, Maxwell AE, Guillén LA, Everland A, Loudermilk EL, Skowronski NS. Estimation of Plot-Level Burn Severity Using Terrestrial Laser Scanning. Remote Sensing. 2021; 13(20):4168. https://doi.org/10.3390/rs13204168
Chicago/Turabian StyleGallagher, Michael R., Aaron E. Maxwell, Luis Andrés Guillén, Alexis Everland, E. Louise Loudermilk, and Nicholas S. Skowronski. 2021. "Estimation of Plot-Level Burn Severity Using Terrestrial Laser Scanning" Remote Sensing 13, no. 20: 4168. https://doi.org/10.3390/rs13204168
APA StyleGallagher, M. R., Maxwell, A. E., Guillén, L. A., Everland, A., Loudermilk, E. L., & Skowronski, N. S. (2021). Estimation of Plot-Level Burn Severity Using Terrestrial Laser Scanning. Remote Sensing, 13(20), 4168. https://doi.org/10.3390/rs13204168