CryoSat-2 Significant Wave Height in Polar Oceans Derived Using a Semi-Analytical Model of Synthetic Aperture Radar 2011–2019
Abstract
:1. Introduction
2. Data and Methods
2.1. CryoSat-2 Altimetry Data
2.2. Addtional Accompanying Data
2.3. Semi-Analytical Model
2.4. Operational Retrieval of Significant Wave Height
3. Results
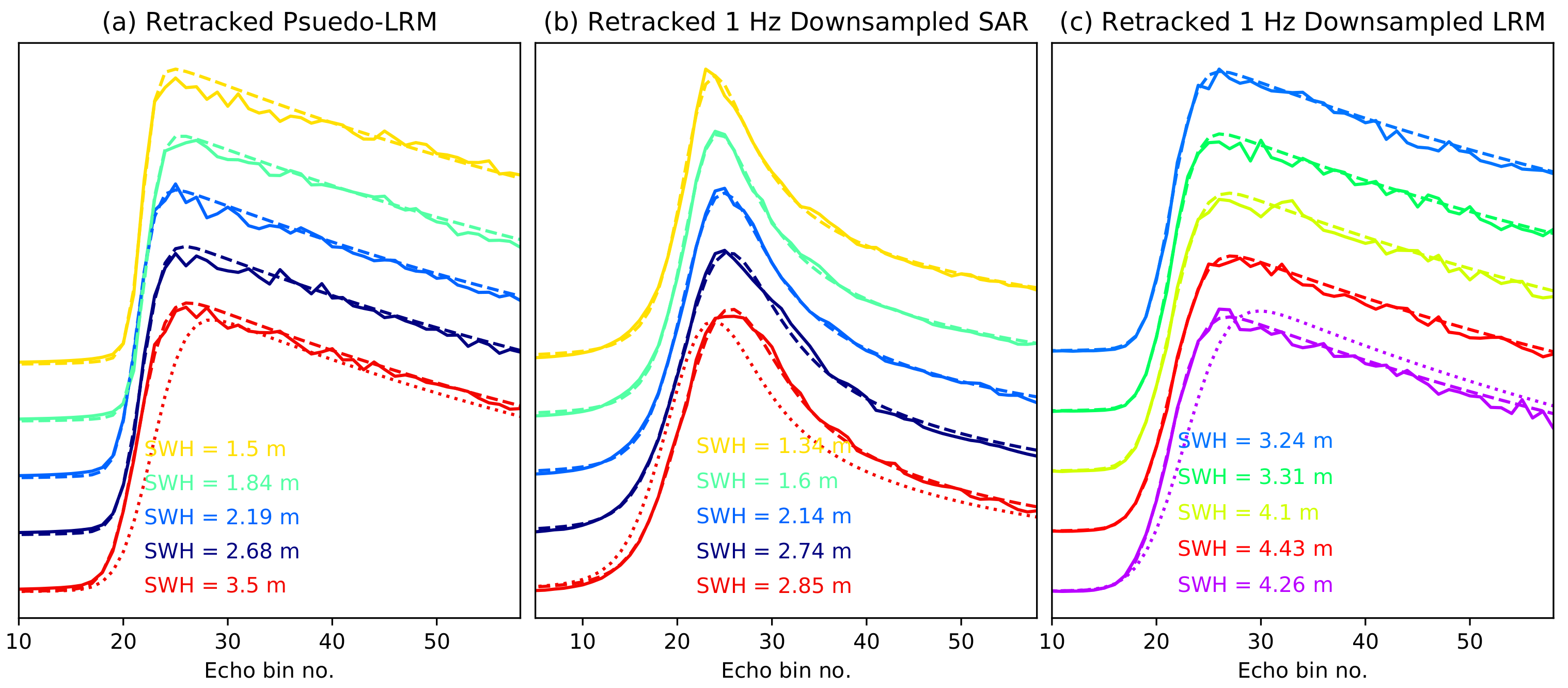
3.1. Echo Fit Examples
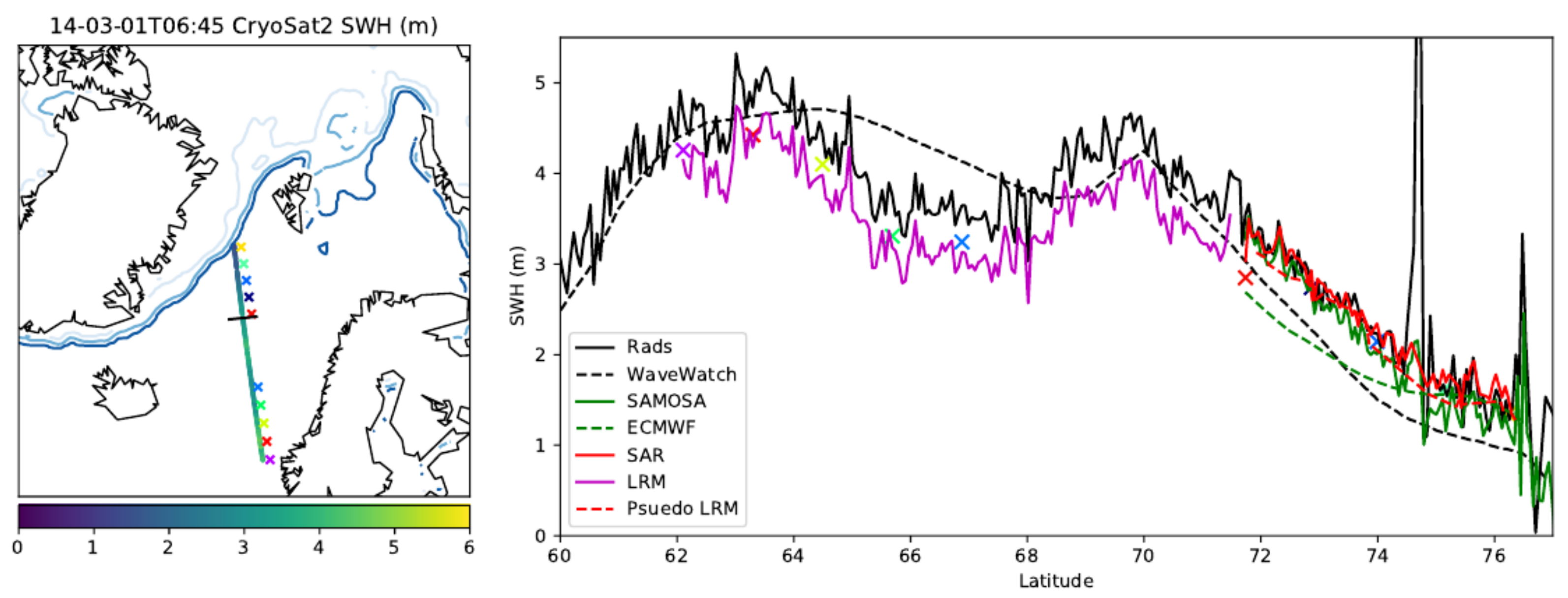
3.2. North Atlantic 2014-03-01
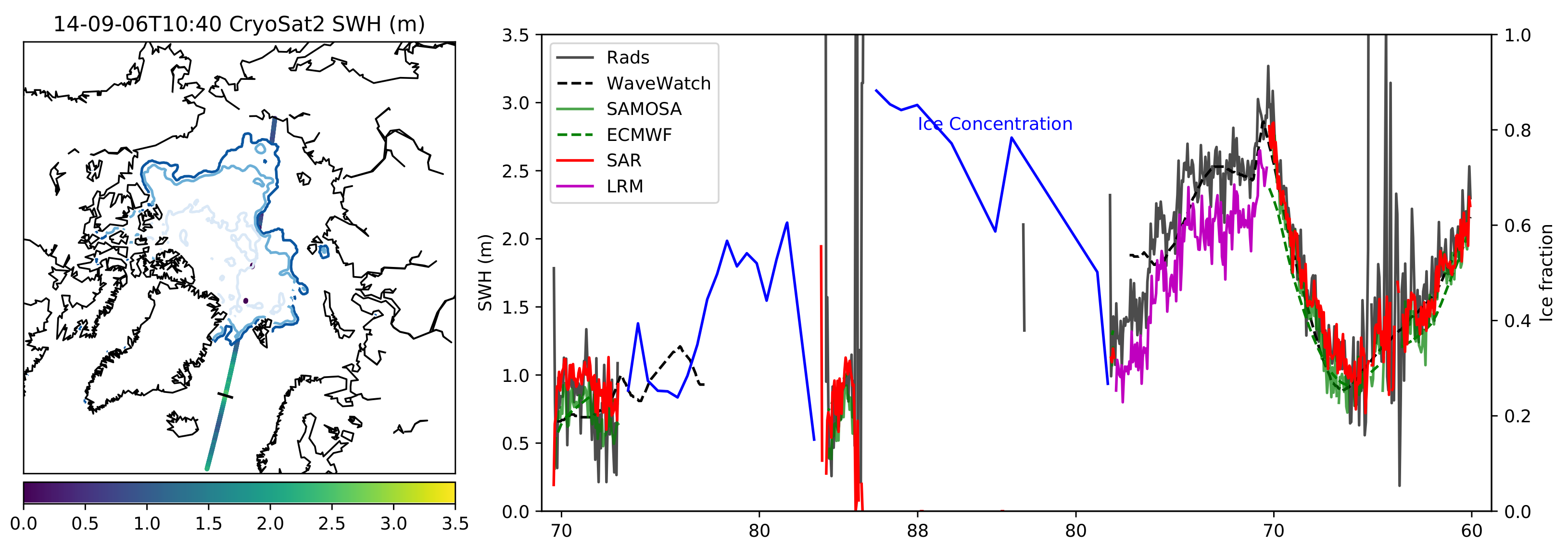
3.3. Central Arctic 2014-09-12
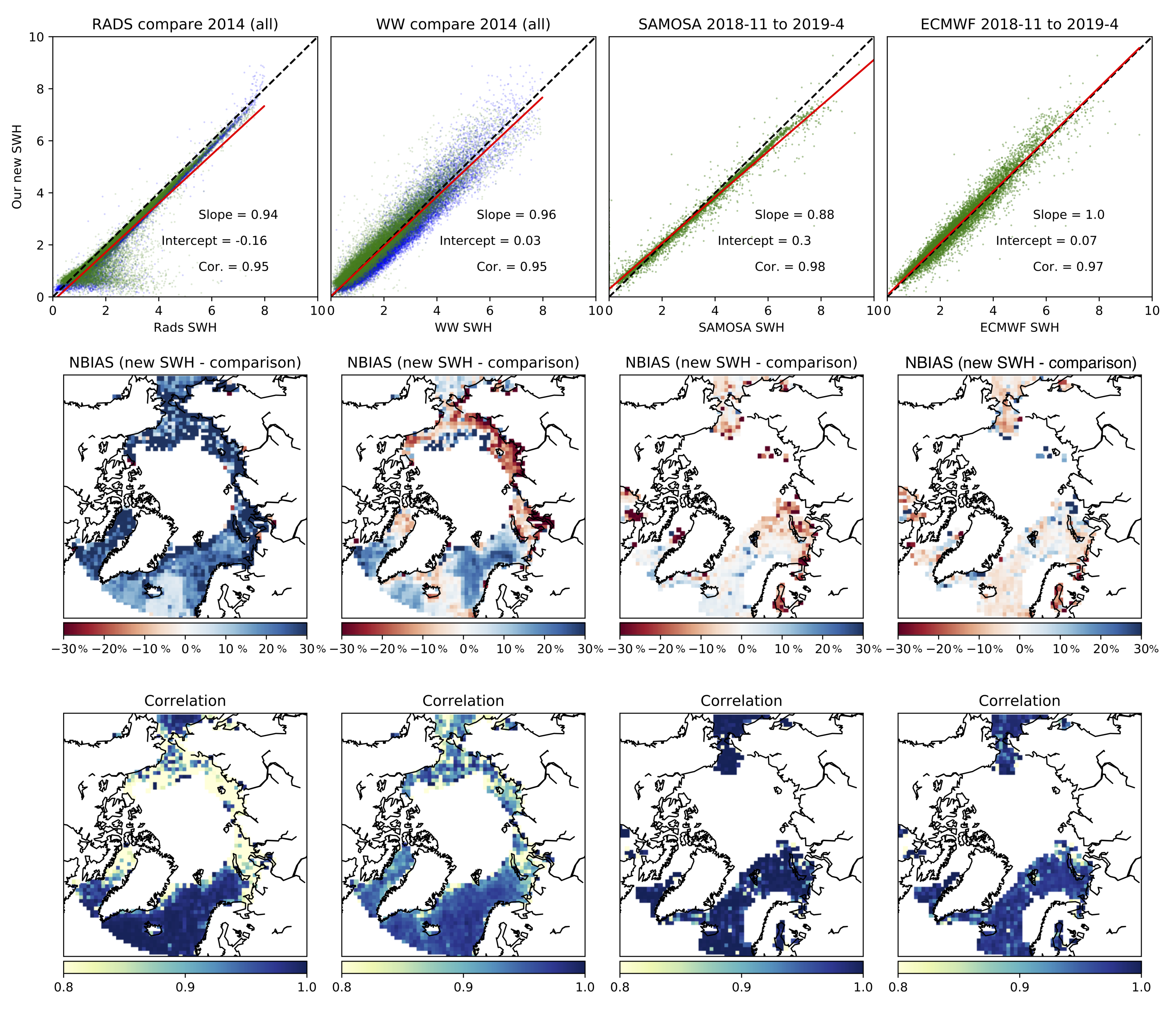
3.4. Alternate CS2 SWH Data Comparison
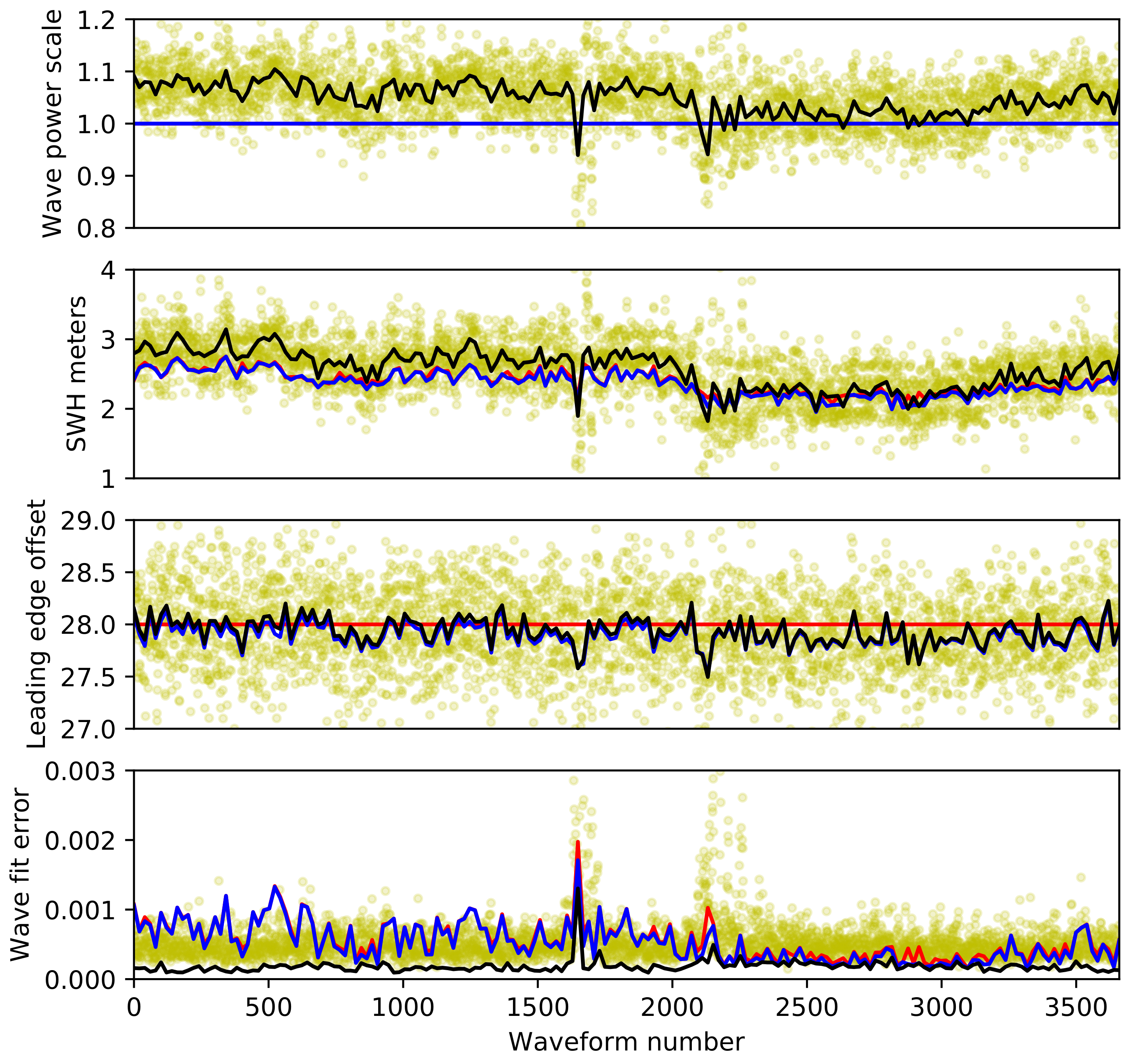
3.5. Buoy SWH Observational Validation
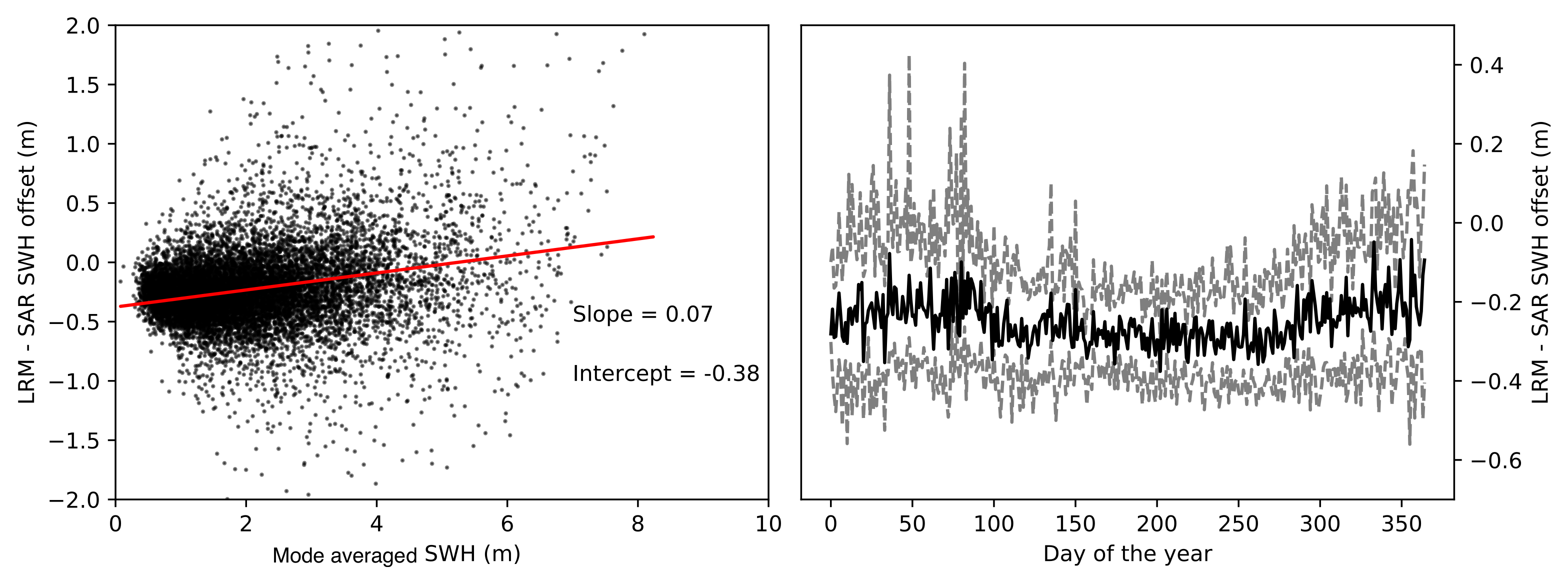
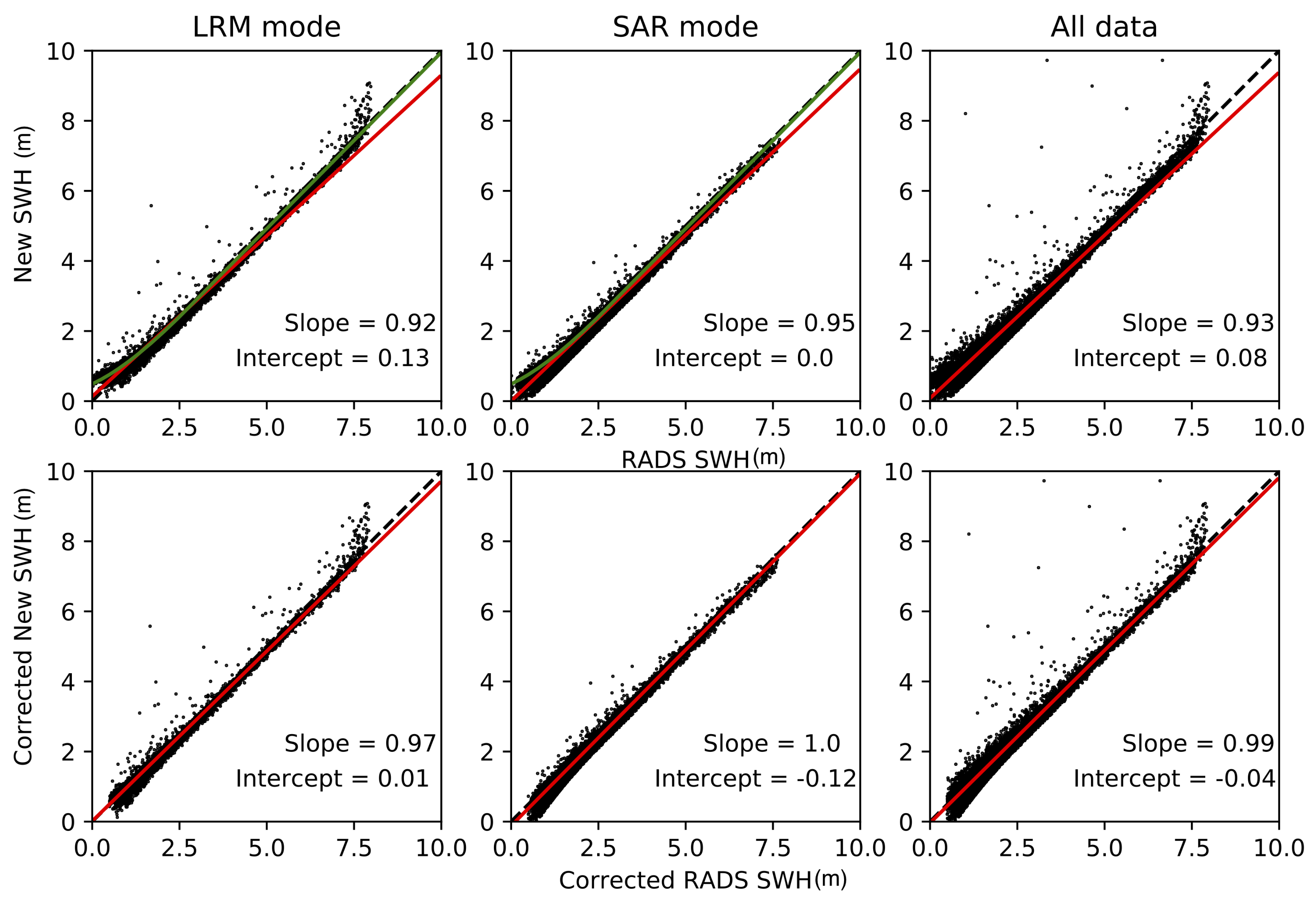
3.6. Mode Bias Corrections
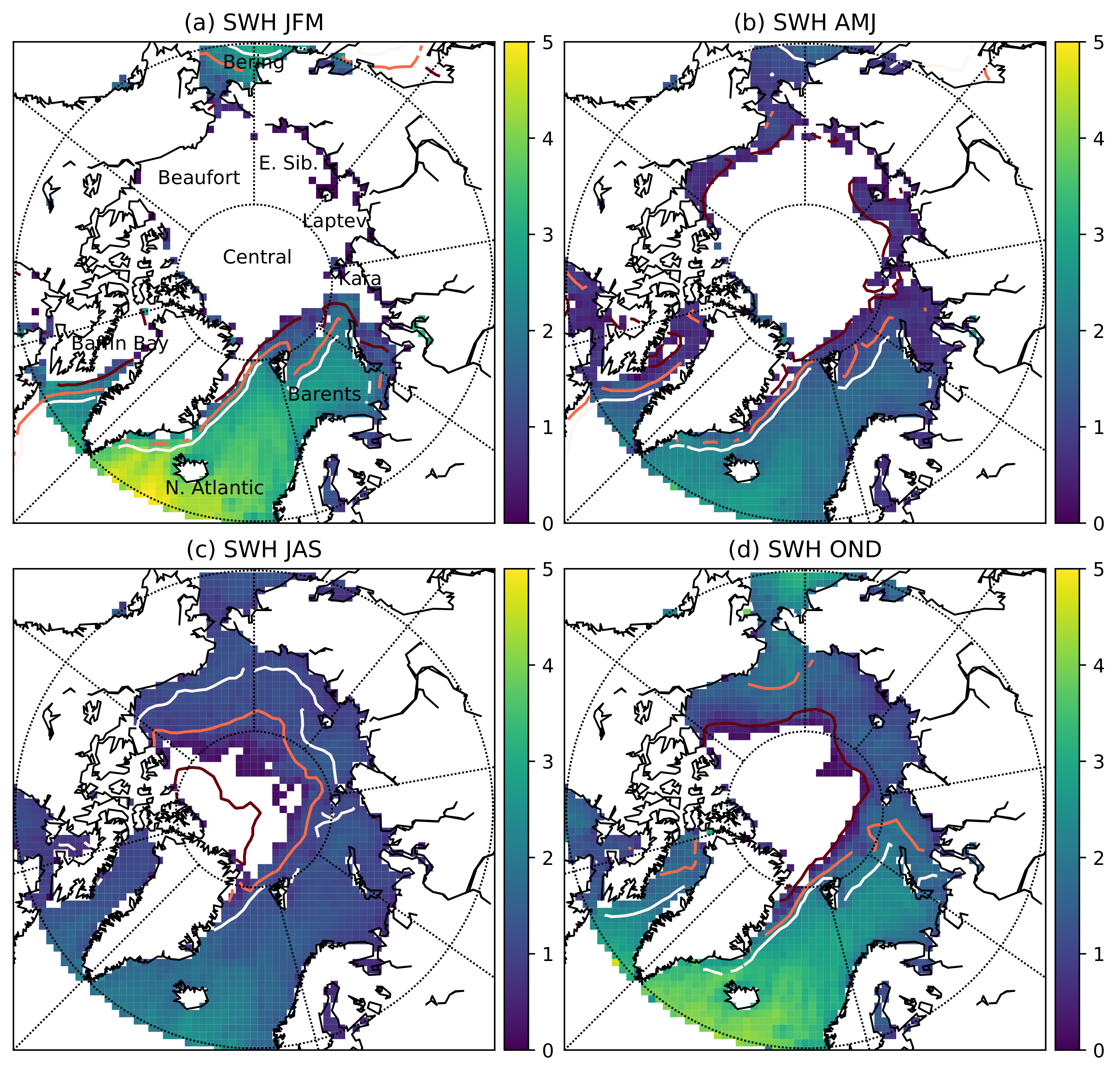
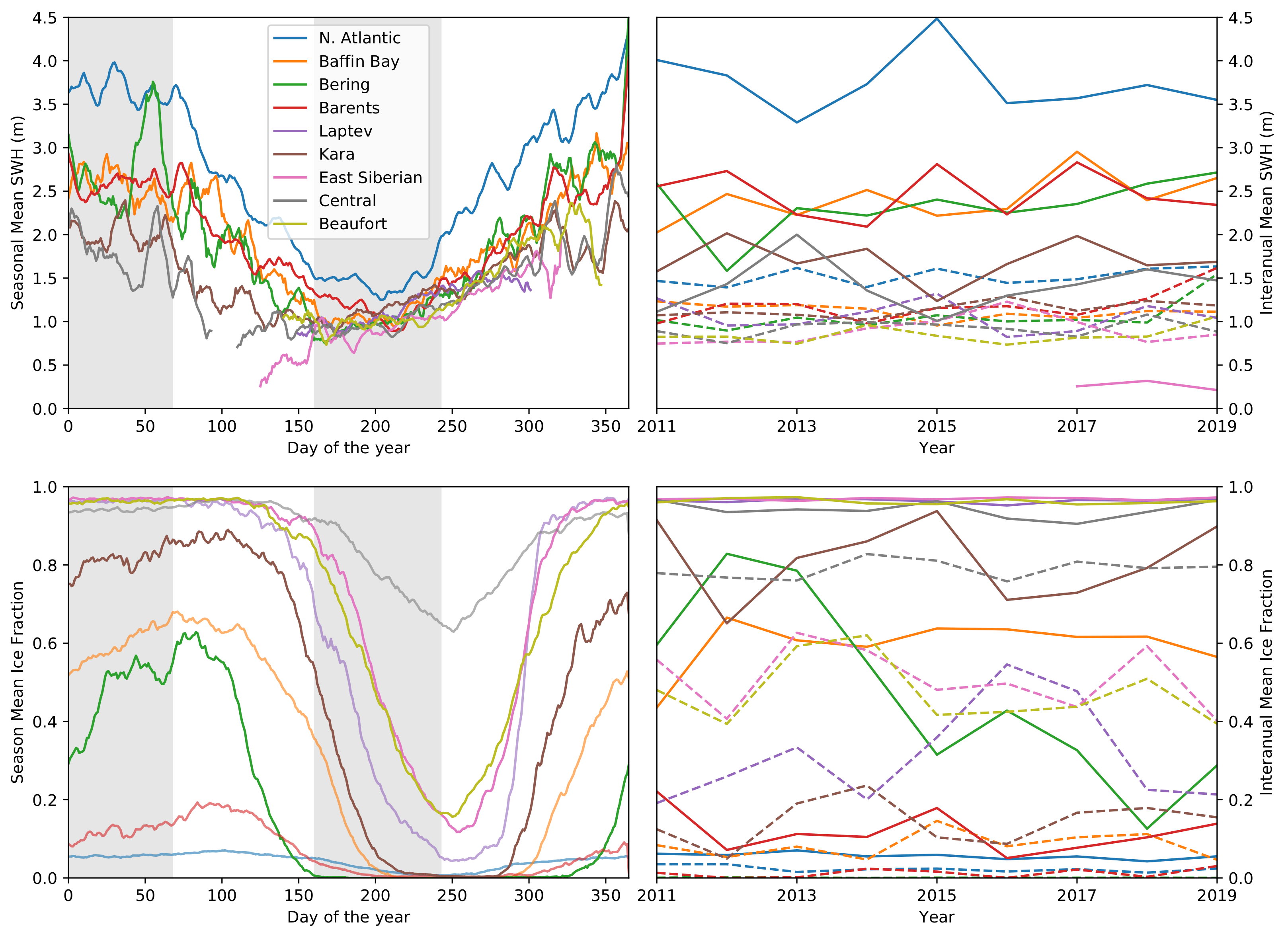
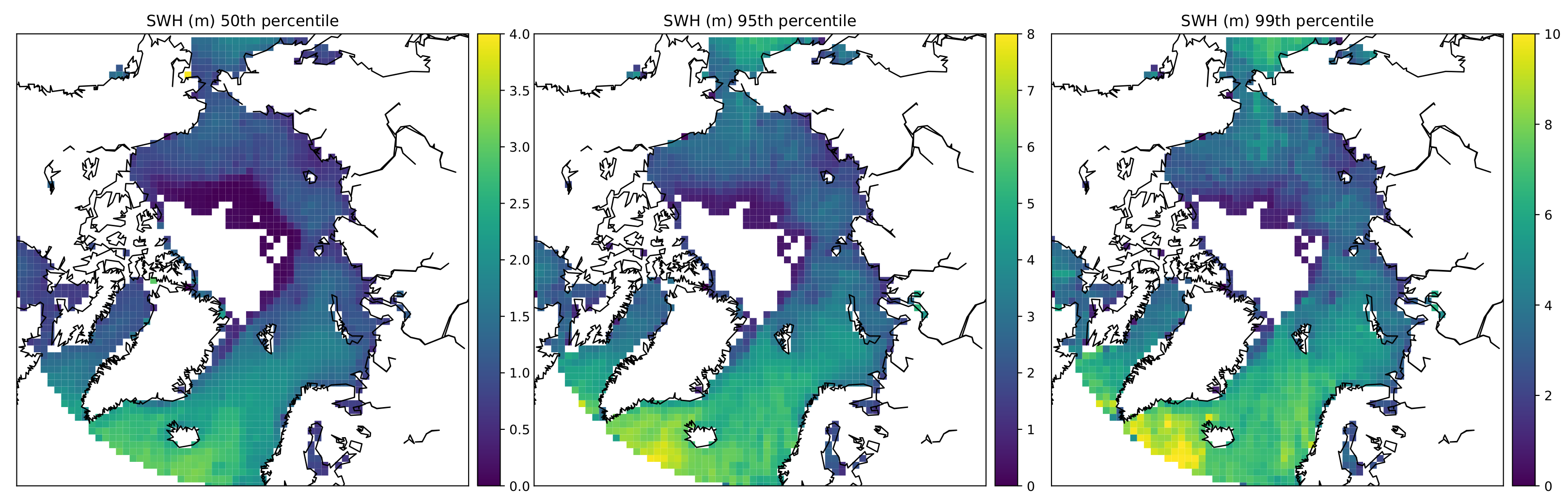
3.7. Full Arctic Data Set
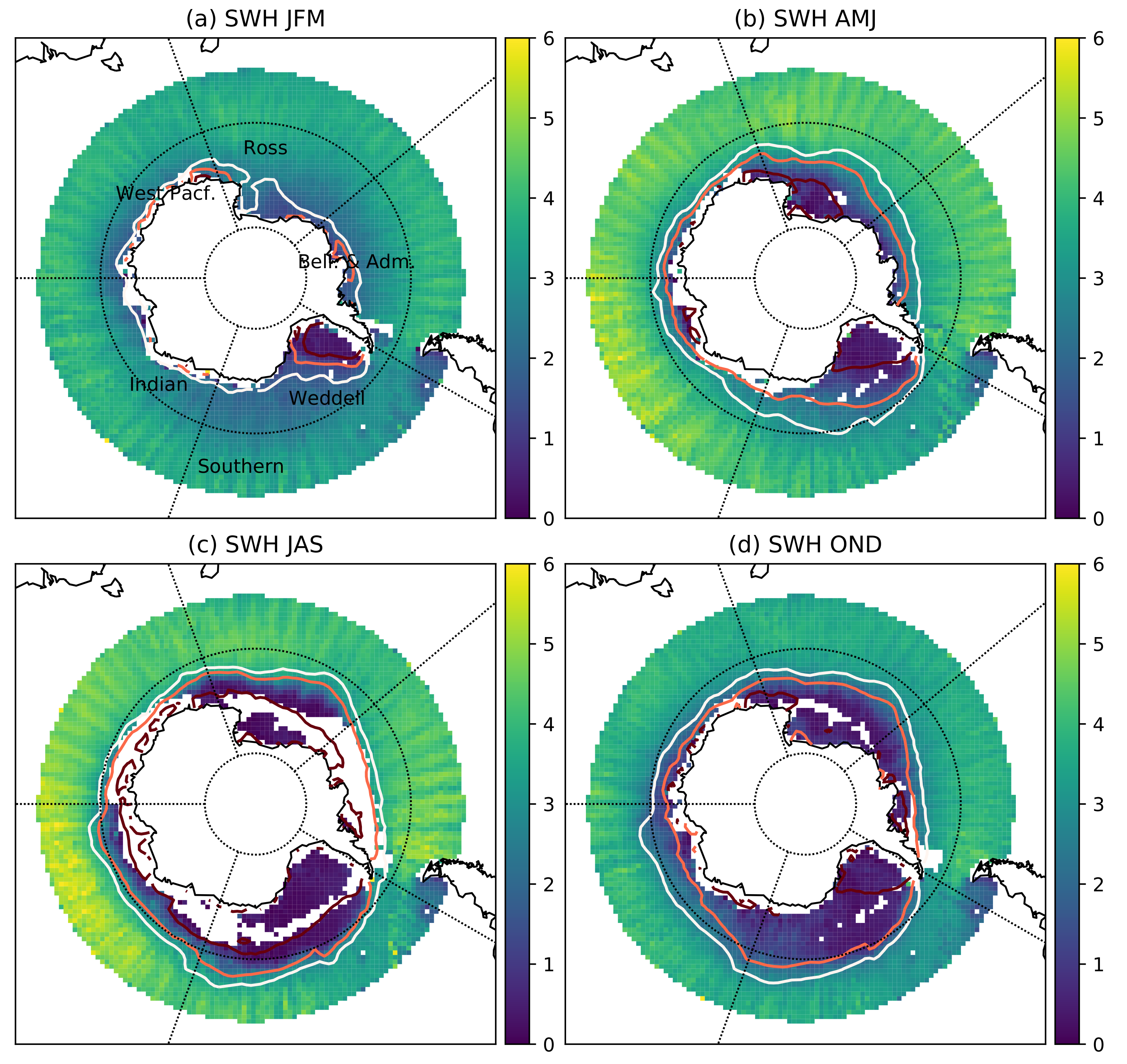
3.8. Full Antarctic Data Set
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stroeve, J.C.; Kattsov, V.; Barrett, A.; Serreze, M.; Pavlova, T.; Holland, M.; Meier, W.N. Trends in Arctic sea ice extent from CMIP5, CMIP3 and observations. Geophys. Res. Lett. 2012, 39, L16502. [Google Scholar] [CrossRef]
- Comiso, J.C.; Parkinson, C.L.; Gersten, R.; Stock, L. Accelerated decline in the Arctic sea ice cover. Geophys. Res. Lett. 2008, 35, L01703. [Google Scholar] [CrossRef]
- Squire, V.A.; Dugan, J.P.; Wadhams, P.; Rottier, P.J.; Liu, A.K. Of Ocean Waves and Sea Ice. Annu. Rev. Fluid Mech. 1995, 27, 115–168. [Google Scholar] [CrossRef]
- Wadhams, P.; Squire, V.A.; Goodman, D.J.; Cowan, A.M.; Moore, S.C. The attenuation rates of ocean waves in the marginal ice zone. J. Geophys. Res. Ocean. 1988, 93, 6799–6818. [Google Scholar] [CrossRef]
- Kohout, A.L.; Williams, M.J.M.; Dean, S.M.; Meylan, M.H. Storm-induced sea-ice breakup and the implications for ice extent. Nature 2014, 509, 604–607. [Google Scholar] [CrossRef] [PubMed]
- Kohout, A.L.; Meylan, M.H. An elastic plate model for wave attenuation and ice floe breaking in the marginal ice zone. J. Geophys. Res. 2008, 113, C09016. [Google Scholar] [CrossRef]
- Montiel, F.; Squire, V.A.; Doble, M.; Thomson, J.; Wadhams, P. Attenuation and Directional Spreading of Ocean Waves During a Storm Event in the Autumn Beaufort Sea Marginal Ice Zone. J. Geophys. Res. Ocean. 2018, 123, 5912–5932. [Google Scholar] [CrossRef]
- Stopa, J.E.; Ardhuin, F.; Thomson, J.; Smith, M.M.; Kohout, A.; Doble, M.; Wadhams, P. Wave Attenuation Through an Arctic Marginal Ice Zone on 12 October 2015: 1. Measurement of Wave Spectra and Ice Features From Sentinel 1A. J. Geophys. Res.-Ocean. 2018, 123, 3619–3634. [Google Scholar] [CrossRef]
- Stopa, J.E.; Ardhuin, F.; Girard-Ardhuin, F. Wave climate in the Arctic 1992–2014: Seasonality and trends. Cryosphere 2016, 10, 1605–1629. [Google Scholar] [CrossRef]
- Cheng, S.; Stopa, J.; Ardhuin, F.; Shen, H.H. Spectral attenuation of ocean waves in pack ice and its application in calibrating viscoelastic wave-in-ice models. Cryosphere 2020, 14, 2053–2069. [Google Scholar] [CrossRef]
- Lin, S.; Sheng, J.; Xing, J. Performance Evaluation of Parameterizations for Wind Input and Wave Dissipation in the Spectral Wave Model for the Northwest Atlantic Ocean. Atmos.-Ocean 2020, 58, 258–286. [Google Scholar] [CrossRef]
- Nose, T.; Waseda, T.; Kodaira, T.; Inoue, J. Satellite-retrieved sea ice concentration uncertainty and its effect on modelling wave evolution in marginal ice zones. Cryosphere 2020, 14, 2029–2052. [Google Scholar] [CrossRef]
- Rascle, N.; Ardhuin, F. A global wave parameter database for geophysical applications. Part 2: Model validation with improved source term parameterization. Ocean Model. 2013, 70, 174–188. [Google Scholar] [CrossRef]
- Zhang, J.; Rothrock, D.A. Modeling global sea ice with a thickness and enthalpy distribution model in generalized curvilinear coordinates. Mon. Weather Rev. 2003, 131, 845–861. [Google Scholar] [CrossRef]
- Young, I.R.; Zieger, S.; Babanin, A.V. Global Trends in Wind Speed and Wave Height. Science 2011, 332, 451–455. [Google Scholar] [CrossRef] [PubMed]
- Marsh, J.G.; Martin, T.V. The SEASAT altimeter mean sea surface model. J. Geophys. Res. Ocean. 1982, 87, 3269–3280. [Google Scholar] [CrossRef]
- Queffeulou, P.; Croizé-Fillon, D. Global Altimeter SWH Data Set; Technical Report; IFREMER, Laboratoire d’Océanographie Physique Spatiale: Plouzané, France, 2017. [Google Scholar]
- Ribal, A.; Young, I.R. 33 years of globally calibrated wave height and wind speed data based on altimeter observations. Sci. Data 2019, 6, 1–15. [Google Scholar]
- Wingham, D.; Francis, C.; Baker, S.; Bouzinac, C.; Brockley, D.; Cullen, R.; de Chateau-Thierry, P.; Laxon, S.; Mallow, U.; Mavrocordatos, C.; et al. CryoSat: A mission to determine the fluctuations in Earth’s land and marine ice fields. Adv. Space Res. 2006, 37, 841–871. [Google Scholar] [CrossRef]
- Thomsen, K. Offshore Wind: A Comprehensive Guide to Successful Offshore Wind Farm Installation; Elsevier: Waltham, MA, USA, 2011. [Google Scholar]
- Scharroo, R.; Leuliette, E.; Lillibridge, J.; Byrne, D.; Naeije, M.; Mitchum, G. Rads: Consistent multi-mission products. In 20 Years of Progress in Radar Altimatry; ESA: Venice, Italy, 2012; p. 4. [Google Scholar]
- Scagliola, M.; Recchia, L.; Maestri, L.; Giudici, D. Evaluating the impact of range walk compensation in delay/Doppler processing over open ocean. Adv. Space Res. 2021, 68, 937–946. [Google Scholar] [CrossRef]
- Wingham, D.J.; Giles, K.A.; Galin, N.; Cullen, R.; Armitage, T.W.K.; Smith, W.H.F. A Semianalytical Model of the Synthetic Aperture, Interferometric Radar Altimeter Mean Echo, and Echo Cross-Product and Its Statistical Fluctuations. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2539–2553. [Google Scholar] [CrossRef]
- Tolman, H.L.; The WAVEWATCH III® Development Group. User manual and system documentation of WAVEWATCH III TM version 5.16. In NOAA Technical Note; Marine Modeling and Analysis Branch: College Park, MD, USA, 2016; p. 361. [Google Scholar]
- Cavalieri, D.J.; Parkinson, C.L.; Gloersen, P.; Zwally, H.J. Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS Passive Microwave Data, Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 1996. [Google Scholar] [CrossRef]
- Orzech, M.D.; Shi, F.; Veeramony, J.; Bateman, S.; Calantoni, J.; Kirby, J.T. Incorporating floating surface objects into a fully dispersive surface wave model. Ocean Model. 2016, 102, 14–26. [Google Scholar] [CrossRef]
- Brown, G. The average impulse response of a rough surface and its applications. IEEE Trans. Antennas Propag. 1977, 25, 67–74. [Google Scholar] [CrossRef]
- Wingham, D.; Phalippou, L.; Mavrocordatos, C.; Wallis, D. The mean echo and echo cross product from a beamforming interferometric altimeter and their application to elevation measurement. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2305–2323. [Google Scholar] [CrossRef]
- Armitage, T.W.K. Studies of the Arctic Ocean from Satellite Radar Altimetry. Ph.D. Thesis, UCL (University College London), London, UK, 2016. [Google Scholar]
- Amarouche, L.; Thibaut, P.; Zanife, O.Z.; Dumont, J.P.; Vincent, P.; Steunou, N. Improving the Jason-1 Ground Retracking to Better Account for Attitude Effects. Mar. Geod. 2004, 27, 171–197. [Google Scholar] [CrossRef]
- Ray, C.; Martin-Puig, C.; Clarizia, M.P.; Ruffini, G.; Dinardo, S.; Gommenginger, C.; Benveniste, J. SAR Altimeter Backscattered Waveform Model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 911–919. [Google Scholar] [CrossRef]
- Recchia, L.; Scagliola, M.; Giudici, D.; Kuschnerus, M. An Accurate Semianalytical Waveform Model for Mispointed SAR Interferometric Altimeters. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1537–1541. [Google Scholar] [CrossRef]
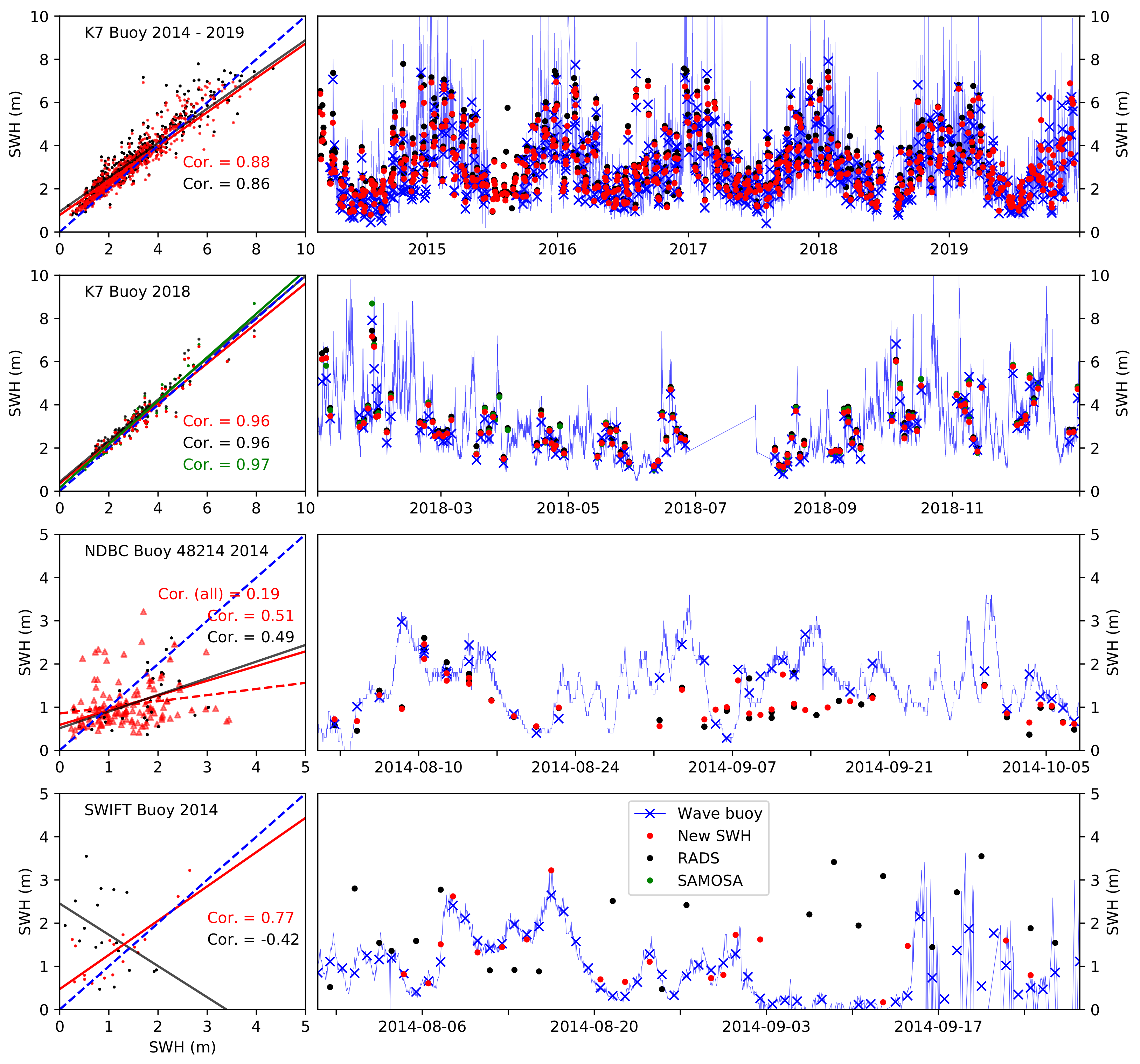
| Buoy Name | Period | Location | Correlation |
|---|---|---|---|
| Swift array | 28 July 2014 to 28 September 2014 | −144.5E, 70.9N | 0.77 |
| −159.9E, 74.6N | |||
| Met Office K7 | 2014 | −4.5E, 60.7N | 0.89 |
| 2015 | 0.91 | ||
| 2016 | 0.97 | ||
| 2017 | 0.96 | ||
| 2018 | 0.96 | ||
| 2019 | 0.96 | ||
| 48,213 | 1 September 2012 to 7 October 2012 | 164.1E, 71.5N | −0.43 |
| 1 August 2013 to 31 October 2013 | 0.14 | ||
| 48,214 | 1 September 2014 to 11 October 2014 | 165.2E, 70.9N | −0.35 |
| 1 August 2014 to 8 October 2014 | 0.51 | ||
| 14 July 2015 to 12 October 2015 | 0.5 |
| Description | Value | |
|---|---|---|
| Pulse duration | 3.52 ms | |
| Antenna gain | 42 dB | |
| SAR synthetic beam gain | 36.12 dB | |
| beam look angles | 51 | |
| c | Speed of light | |
| Earth radius | m | |
| Carrier wavelength | ||
| Carrier wave number | ||
| Antenna shape parameter | 0.0122 | |
| Antenna shape parameter | 0.0382 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heorton, H.; Tsamados, M.; Armitage, T.; Ridout, A.; Landy, J. CryoSat-2 Significant Wave Height in Polar Oceans Derived Using a Semi-Analytical Model of Synthetic Aperture Radar 2011–2019. Remote Sens. 2021, 13, 4166. https://doi.org/10.3390/rs13204166
Heorton H, Tsamados M, Armitage T, Ridout A, Landy J. CryoSat-2 Significant Wave Height in Polar Oceans Derived Using a Semi-Analytical Model of Synthetic Aperture Radar 2011–2019. Remote Sensing. 2021; 13(20):4166. https://doi.org/10.3390/rs13204166
Chicago/Turabian StyleHeorton, Harold, Michel Tsamados, Thomas Armitage, Andy Ridout, and Jack Landy. 2021. "CryoSat-2 Significant Wave Height in Polar Oceans Derived Using a Semi-Analytical Model of Synthetic Aperture Radar 2011–2019" Remote Sensing 13, no. 20: 4166. https://doi.org/10.3390/rs13204166
APA StyleHeorton, H., Tsamados, M., Armitage, T., Ridout, A., & Landy, J. (2021). CryoSat-2 Significant Wave Height in Polar Oceans Derived Using a Semi-Analytical Model of Synthetic Aperture Radar 2011–2019. Remote Sensing, 13(20), 4166. https://doi.org/10.3390/rs13204166







