Abstract
Optical flow is a vision-based approach that is used for tracking the movement of objects. This robust technique can be an effective tool for determining the source of failures on slope surfaces, including the dynamic behavior of rockfall. However, optical flow-based measurement still remains an issue as the data from optical flow algorithms can be affected by the varied photographing environment, such as weather and illuminations. To address such problems, this paper presents an optical flow-based tracking algorithm that can be employed to extract motion data from video records for slope monitoring. Additionally, a workflow combined with photogrammetry and the optical flow technique has been proposed for producing highly accurate estimations of rockfall motion. The effectiveness of the proposed approach has been evaluated with the dataset obtained from a photogrammetry survey of field rockfall tests performed by the authors in 2015. The results show that the workflow adopted in this study can be suitable to identify rockfall events overtime in a slope monitoring system. The limitations of the current approach are also discussed.
1. Introduction
In the slope monitoring of open pit mines, real-time monitoring techniques such as ground-based radar [1], Lidar [2,3], IoT sensors [4] and vision-based technology [5,6,7] have been rapidly developed to investigate the instability of rock slopes. Among these techniques, vision-based technology, which includes inspection using captured records, image analysis, photogrammetry and real-time computer vision, has been regarded as the most effective and economical way to identify areas where inactive rock slopes have started to move [5,6,7,8,9,10]. Furthermore, current applications of the vision-based techniques have expanded to obtain quantitative measurements in distance, displacements and the sizes of objects in images. Additionally, the vision-based technique combined with deep learning has significant potential as a leader of the next generation in monitoring technology. Sets of images can provide a source of data to detect a failure on slope surface using deep learning algorithms such as convolutional neural networks (CNNs) [11]. Although these techniques have the drawbacks of using optics due to various external factors such as weather and dust, the vision-based approaches have the potential to continuously inspect the structural instability of rock slopes in real time.
Image processing has proven to be valuable for the monitoring of slope conditions and rockfall detection [12]. Firstly, a change detection analysis has been successfully employed to detect rockfall motions, and this approach has also been successful in rockfall simulation [5,13,14]. Comparing sequential time-lapsed image sets, the image change detection techniques can be employed to identify the true changes by considering the differences in images in real time. Similarly, at a close distance, falling rocks in a field test have been identified by using an image quality assessment (IQA) method [13]. Generally, the objective of IQA is to measure the quality of an image by comparing the pixels of an image to those of the original. Thus, this approach allows to quantify the changed area in pairs of images in percentage. Many algorithms have been developed to identify changes in image pairs and they all have some advantages [14]. However, it is still hard to select an optimal image processing method that will produce accurate change detection for any specific purpose.
Optical flow techniques provide a simple description of both the area of the image experiencing motion and the velocity of motion. This method can calculate the motion of each pixel between two successive frames, and it thus provides a feasible way to obtain the trajectory of objects. For natural ground material such as soil and rocks, optical flow methods have successfully tracked changes ranging from a small to a large scale. An optical flow technique was employed to measure small displacements of soil specimens in a series of triaxial compressive tests [15]. Additionally, the occurrence of landslide has been surveyed and predicted with optical flow techniques by analyzing video records and time-lapse image processing [16,17,18]. These studies showed that optical flow methods can be useful to identify natural changes such as the motion of rockfall and to detect relative or absolute movement of objects occurring during the time elapsed between the available videos. However, optical flow using two-dimensional images requires spatial information to ensure true quantities such as the sizes of objects, changes and displacement for measurement.
Photogrammetry has also been employed for periodically repeated slope mapping and determining slope deformations. Through photogrammetry surveys, rockfall has been explored and analyzed using 3D models obtained [19,20]. Generally, 3D analysis requires accurate topography of the slope surfaces, and unmanned aerial vehicle (UAV) techniques are popularly employed to obtain high-density and accurate images. This technique can provide more accurate data supported by precise positioning systems such as the global navigation satellite system (GNSS) in real time [21]. In connection with the phases for a slope monitoring system, photogrammetry is suitable for a preparation phase which is used to detect possible signals with respect to a potential failure. Thus, image processing can respond more or less timely to the function of early warning. With the development of photogrammetry, the current research has progressed toward more fused forms which combine photogrammetry and image processing techniques. Recently, the applications of 3D optical flow combined with photogrammetry have been explored regarding geospatial information [22]. Likewise, further studies on the application of 3D photogrammetric models are required.
This study estimates the potential of an early warning system supported by image processing with a focus on the use of change detection methods and optical flow algorithms. Image quality assessment and optical flow algorithms were tested to identify rockfall events using a dataset of field rockfall tests. Differences in motion vectors between two images of falling rocks were detected and visualized using OpenCV and Python scripts and then used to create error maps and vector maps.
2. Methods
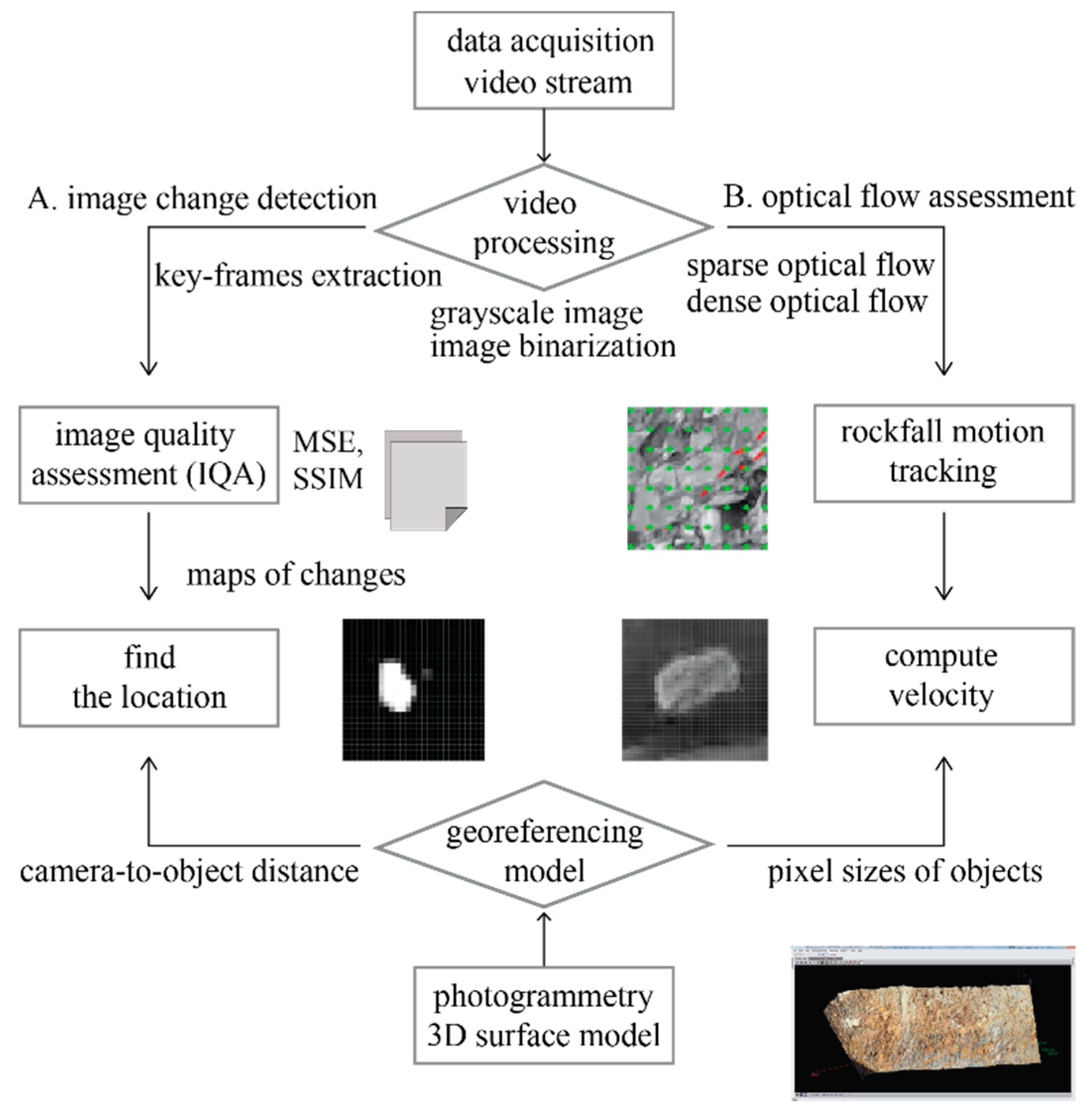
The methodology of this study comprises two steps. The first step is video processing, which includes image change detection and optical flow procedures. The next procedure for the proposed workflow is construction of a 3D surface model using photogrammetry. This section describes the key explanations of the video processing. The workflow is shown in Figure 1.
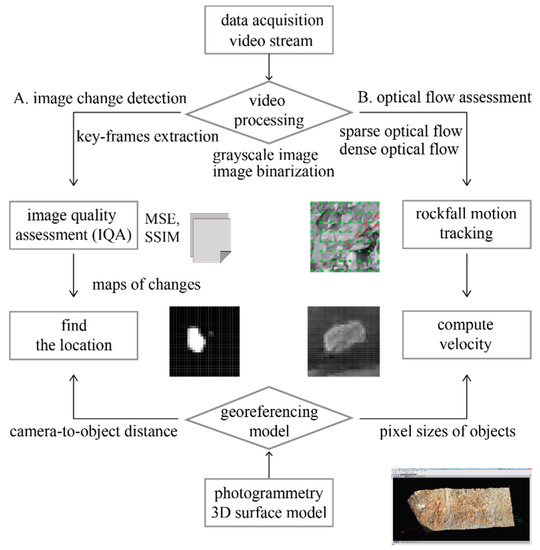
Figure 1.
Flow chart of proposed method.
2.1. Image Change Detection Using Time-Lapse Image
Time-lapse photography is a technique where a target is captured over regular time intervals. The idea of this technique is to capture the changes that allow researchers to view what had happened over a period of hours, days and even years [23]. When using time-lapsed image data, the values of image pixels at a previous time are compared with the values of the corresponding image pixels at a later time in order to determine the degree of change. In this process, it can be quite difficult to identify the pixels of significant change by controlling negligible changes due to camera motion, sensor noise, illumination variation, etc. Li and Leung [24] noted that this pixel-based method can be sensitive to noise and illumination changes because it does not exploit local structural information. On the other hand, the change detection at pixel level is intuitive and requires a lower computational cost. Thus, the pixel-based method can be suitable for applications in an environment where there is little change in illumination during the time interval.
To detect an object in image analysis, the selection of a suitable algorithm for a given condition is extremely important. If time-lapsed images are captured at a fixed position without any changes in photographing conditions, image quality assessment (IQA) can be selected as the most applicable method for change detection. Originally, this technique was developed to monitor and modify the image quality. It has also been employed to detect the differences between similar images that were compared to each other. Numerous algorithms and image quality metrics for image quality assessments have been proposed such as the mean squared error (MSE) [25] and the structural similarity index (SSIM) [26]. These methods estimate the locations and magnitudes of the changes in photographs, and the results can be visualized by means of an error map.
As a feature on images, rock blocks on slopes exhibit diverse colors, shapes and textures. Based on the features, detection of the movement of rocks in images can be approached by methods that detect objects using their differences in shadows and contrast. [27,28]. In this study, the detection of rocks was performed by using the change in contrast between the time-lapsed images. Then, the difference between the images was calculated by IQA.
• MSE: Mean Squared Error
In statistics, mean squared error (MSE) is a well-known measure of the quality of an estimator. As defined in Equation (1), this simple formulation has been applied to various fields due to its clear interpretation. For a pair of n-dimensional image vectors, MSE calculates the average squared distance between two vectors (x and y).
• SSIM: A Structural Similarity Measure
Automatic detection of the similarity between images was conducted using the structural similarity (SSIM) index. This approach has been widely used for image quality assessment. This algorithm considers image distortion as a combination of three factors: luminance, contrast and structure errors. If x and y are two non-negative image signals, the relevant index for luminance comparison is expressed by the following equation:
where C1 is the constant related to pixel values, and are the mean intensity of the two image signals. The contrast comparison function is in Equation (3), and and represent the standard deviation of intensity. C2 is the constant related to pixel values as defined in Equations (4) and (5).
where L is the range of pixel values (in an 8-bit greyscale image, L is 255), and and are small constants. In the SSIM algorithm, structure comparison is followed by luminance comparison and constant subtraction. The structure comparison function is defined as follows:
Then, the final step is the combination of the above three comparisons. The SSIM index is expressed by Equation (6), where are parameters to adjust the relative importance of the three components.
2.2. Optical Flow
Optical flow is defined as the apparent motion of objects, surfaces and edges in a visual scene caused by the relative motion between an observer and a scene. This technique can show the distribution of apparent velocities of movement of brightness patterns in an image. For example, in a condition of illumination, the surface of an object presents a certain spatial distribution which is called a grayscale pattern, and optical flow refers to the motion of the grayscale pattern. It is a 2D vector field where each vector is a displacement vector showing the movement of points from the first frame to the second. In practice, optical flow applications have mainly been approached by using video compression aspects. This technique uses sequential images to estimate the motion of objects in the image sets.
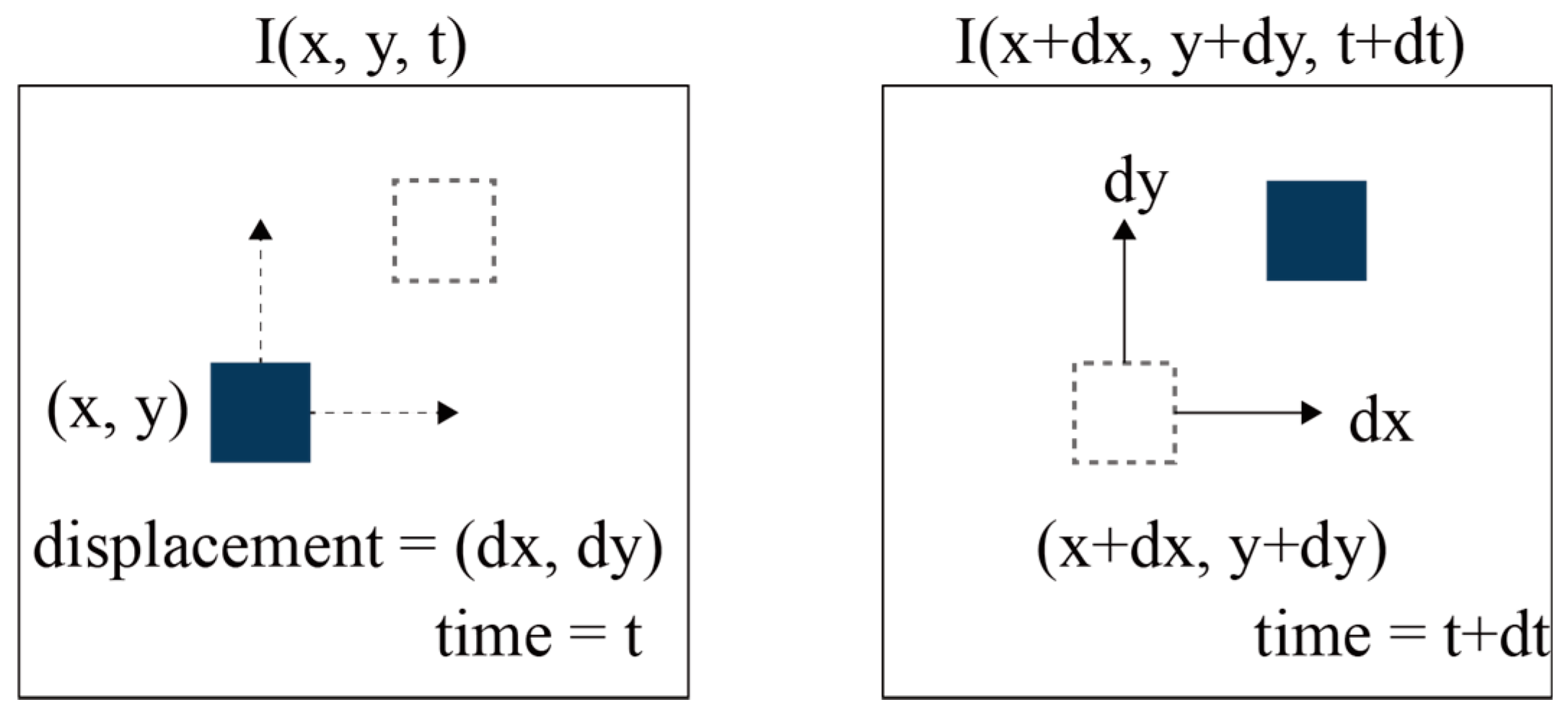
Considering the pixel I (x, y, t) within a frame of an image, the pixel has moved by a certain distance (dx, dy) in the next frame, taken in the time increment dt, as shown in Figure 2. It is assumed that the intensity of the pixels is the same, and the pixels should satisfy the following equation.
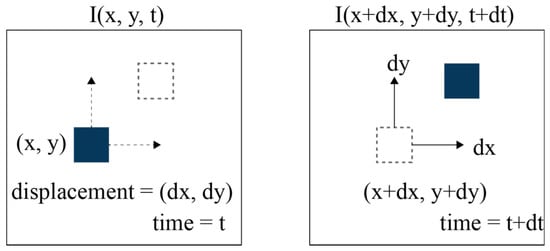
Figure 2.
Illustration of motion estimation using optical flow.
Then, Taylor series approximation can be estimated as follows:
where fx and fy are the image gradients and ft is the gradient along time;
where the local image flow vectors u and υ are unknown. To solve this problem, optical flow has been estimated by various methods such as the Horn–Schunck [29], Buxton–Buxton [30], Black–Jepson [31], Lucas–Kanade [32] and Farnebäck [33] methods. In this paper, the Lucas–Kanade method and Farnebäck’s method are tested for the application of rockfall surveillance using images from a video camera. These two methods were chosen because they have been successfully applied in OpenCV, which is an open-source computer vision library [34,35]. Their availability in OpenCV makes it easy for users to analyze the video data.
• Lucas–Kanade method
The Lucas–Kanade method is a widely used differential method for optical flow estimation which can provide an estimation of the movement of interesting features in successive images [32]. This method employs two important assumptions. Firstly, the two successive images are separated by a small time increment , and the objects undergo small changes. Secondly, the textured objects in the images are exhibited by shades of gray, so the changes can be depicted by intensity levels. This method is known as a sparse method that processes the points detected by corner detection algorithms. Considering a pixel, the Lucas–Kanade method uses a 3 × 3 kernel around the pixel. Thus, all 9 pixels have the same motion as described in Equation (11). Detailed solutions have been presented and discussed in relevant scholarly works [32].
• Farnebäck method
Gunner Farnebäck introduced a methodology to estimate the optical flow for all the points in the frame [33]. Compared to the Lucas–Kanade approach, this method is a dense optical flow. The computation is slower but it gives more accurate and denser results, which can be suitable for applications such as video segmentation. This method approximates the windows of image frames by quadratic polynomial expansion transform. This method approximates the neighborhood of both frames at times t1 and t2 using a polynomial function. The intensity of a pixel is expressed as follows:
where A is the symmetric matrix, b is the vector and c is the scalar. Considering these quadratic polynomials, a new signal is constructed by a global displacement (d). Then, the global displacement is calculated by equating the coefficients in the quadratic polynomials’ yields.
Equations (13) and (14) can be equated at every pixel, while the solution may be obtained iteratively.
3. Data Collection
3.1. Video Capturing and Data Sampling
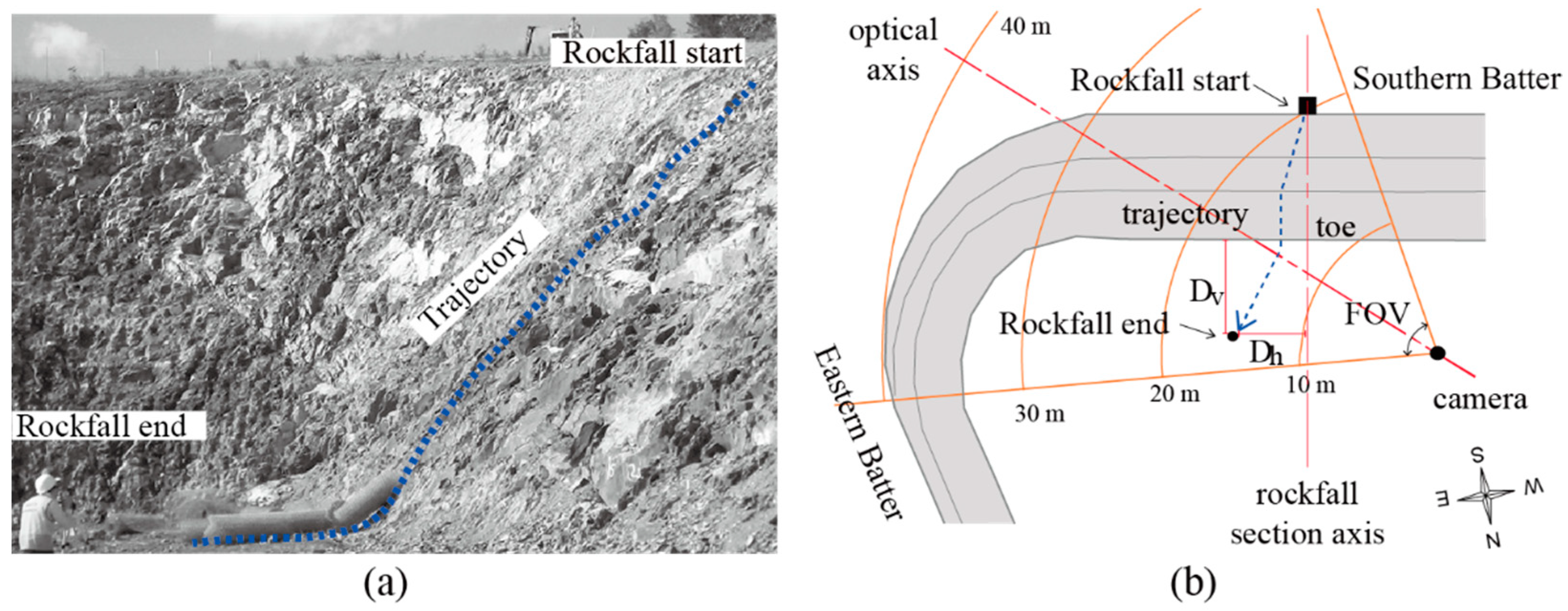
The applicability of the image processing technique to rockfall identification was tested by analyzing the image data obtained from field rockfall tests. The field tests were carried out at a position near the toe-cut slope by the authors [21]. The study area was an excavated slope located in Brisbane, Australia. The slope was prepared for the installation of a drapery system for rockfall protection. The slope was approximately 10 m in height. The slope geology comprised weathered metasiltstone and metasandstone from the Neranleigh-Fernvale beds [36]. The weathered rock can range from a moderately to slightly weathered grade based on Schmidt hammer rebounds according to the weathering classification system suggested by Arikan et al. [37]. A total of ten rocks, which were collected from the site, were manually thrown from the top position of the slope. During the field test, horizontal and vertical falling distances from the toe of the slope were measured based on the rockfall section axis, and each rockfall test was carefully recorded by a video camera which was positioned in front of the slope with an appropriate optical axis to include the entire rockfall paths. The final positions of falling rocks were located at the left side from the center line, including the falling point ranging from 0.6 to 6.3 m. These left-biased rockfall paths were explained by the orientation of dominant joint sets dipping to a northeastern direction [21]. The overview of the field test is shown in Figure 3.
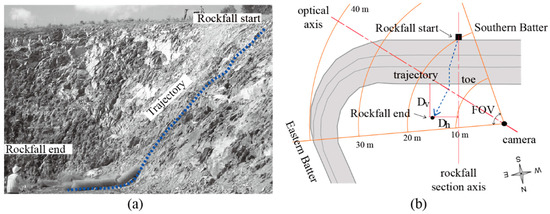
Figure 3.
Overview of the study area with the rockfall test location: (a) a captured image from Zoom Q2 HD handy video at the test location; (b) illustration of the plan view of field test.
A Zoom Q2 HD handy video recorder was employed to acquire images at a spatial resolution of 1920 × 1080 pixels per frame with an operating speed of 30 frames per second (fps). This camera employs a fixed 3.2F focal length lens, and its FOV is approximately 80 degrees. The trajectories and elapsed time of each rockfall event were obtained by analyzing the results from the video recording. For video processing, each rockfall test was extracted from the video record using Adobe Premiere Pro (Adobe Inc., San Francisco, CA, USA). To create datasets for image processing, still images were saved in TIFF data format to avoid losing image quality.
3.2. Dataset Evaluation
• Variation of object’s size
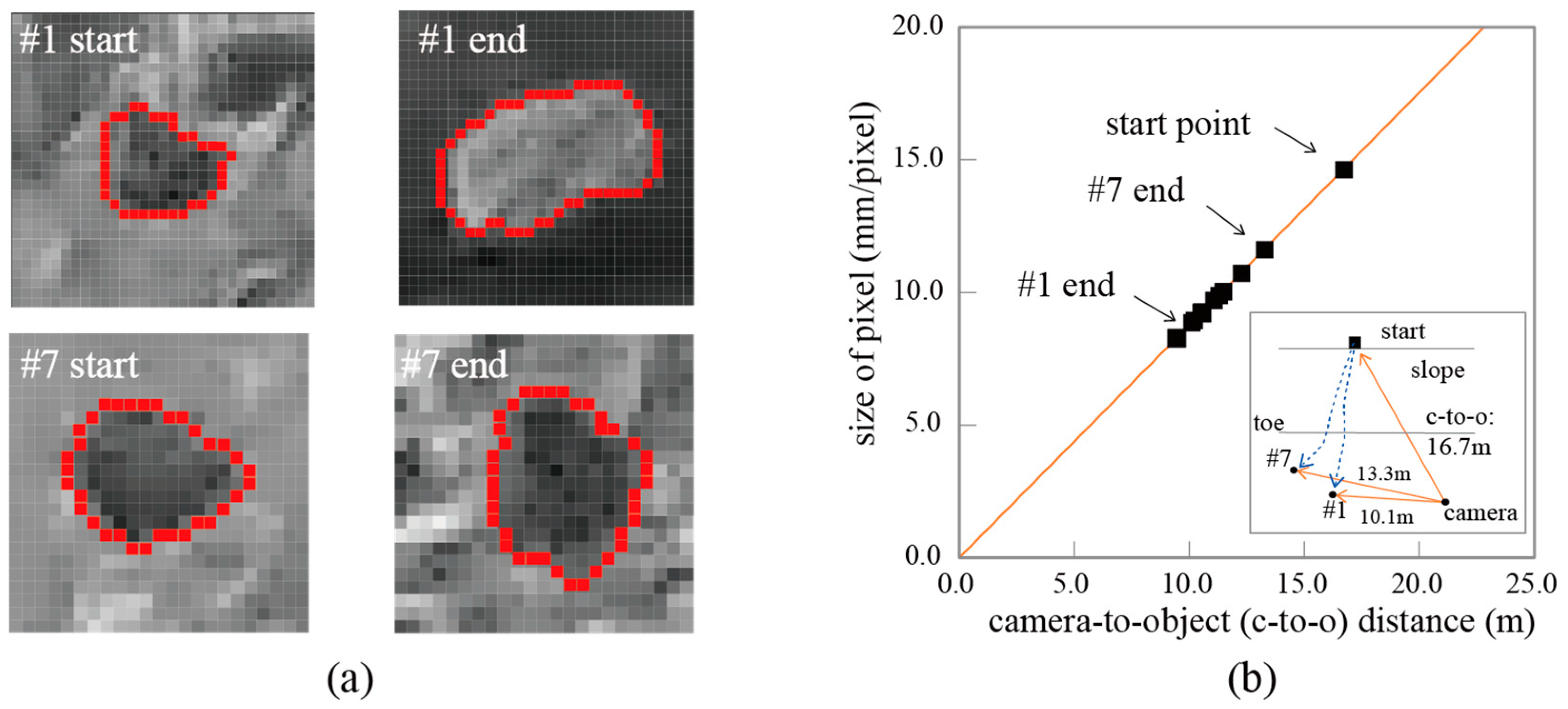
In this study, the main challenge for rockfall detection through image processing was that the camera resolution could be insufficient to detect the small rock blocks. Furthermore, due to the camera-to-object distance in the field tests, the rock moving occupied only a small area in each frame that consisted of a limited number of pixels. Additionally, the sizes of rockfall objects varied with the changes in camera-to-object distances frame by frame due to the changes of rockfall paths in three-dimensional space. As presented in Figure 3b, it is evident that the captured size of the thrown rock decreased on the video clip from the start point to the end based on the geometrical relationship between the camera axis and the rockfall paths. Figure 4 illustrates the variation in the size of rock objects with the changes in camera-to-object distances. The size of objects in pixels depends primarily on the camera-to-object distance as shown in Figure 4b. It was estimated from the analyzed pictures that a pixel represents a size of 8 × 8 mm2 at the 10-m distance. In practice, diameters of 20- and 30-mm rock fragments were visible to the naked eye in the field tests [21].
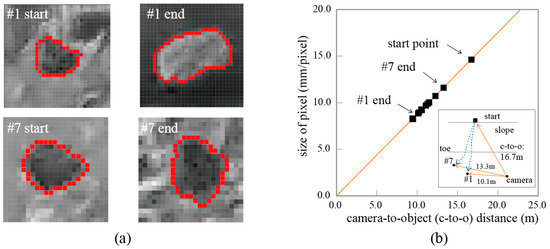
Figure 4.
Variation in object size through rockfall test in this study: (a) clipped images of the rocks at start and end points of test #1, test #7 and bounded edges with red color; (b) pixel size as a function of camera-to-object distance.
• Frame rate
To identify the motion of rocks, image processing needs to consider important factors that can degrade the resolution and quality of video images. The first quality factor in temporal sampling is the frame rate, which is defined as the number of images per second. A low frame rate value indicates that the camera captures objects at a low speed. By estimating the distance that the rock moves between two successive frames, it is possible to estimate the appropriate range of fps. In the field tests, the thrown rock arrival time ranged from 2.5 to 4.5 s. Accordingly, the rock traveled along the slope at 5.4 m/s on average. Then, the travel distance per frame can be estimated using Equations (15) and (16).
Table 1 indicates that the object moved 18.1 cm on average in each frame, which means an image of the rock movement was sampled every 18.1 cm on average. Thus, the frame speed of 30 fps can be low to accurately capture the details of rock movement such as rotation and rolling.

Table 1.
Results of rockfall tests [21].
• Motion blur
The second factor is the shutter speed, which has a strong influence on motion blur. Motion blur is the blur seen in moving objects in a photograph or a single frame of a video. In the field tests, the shutter speed of the video recorder was approximately 1/60th of a second. Using a simple relationship equation (Equation (14)) between the shutter speed and the travel velocity, the approximate range of motion blur can be estimated. As presented in Table 1, the rockfalls were blurred around 9.0 cm on average for the low shutter speed. Considering the size of the rocks thrown, the motion blur may not be a minor range at the travel velocity. For example, Figure 5 shows a set of successive frames of a video sequence for test #4. The motion of rocks can be found by determining the pixel intensity variation between the successive frames. The location of rockfall is sequentially indicated by observation using red bounds per frame. It is difficult to estimate the locations with the naked eye because of the motion blur. It is also difficult to estimate the amount of motion blur due to the variation in travel velocity combined with complex movements such as falling, rotating, bounce and sliding. However, it was observed that there are pronounced changes of intensity within the red bounds between the successive frames. It can then be assumed that the location of falling rocks along the trajectories can be tracked by using the pixel intensity variation with a certain amount of error.

Figure 5.
A clipped frame of the video record for test #4 and the rock block used for test #4. The red bounds highlight the detected rocks and fragments that arrived at the bottom with blur.
3.3. Photogrammetry
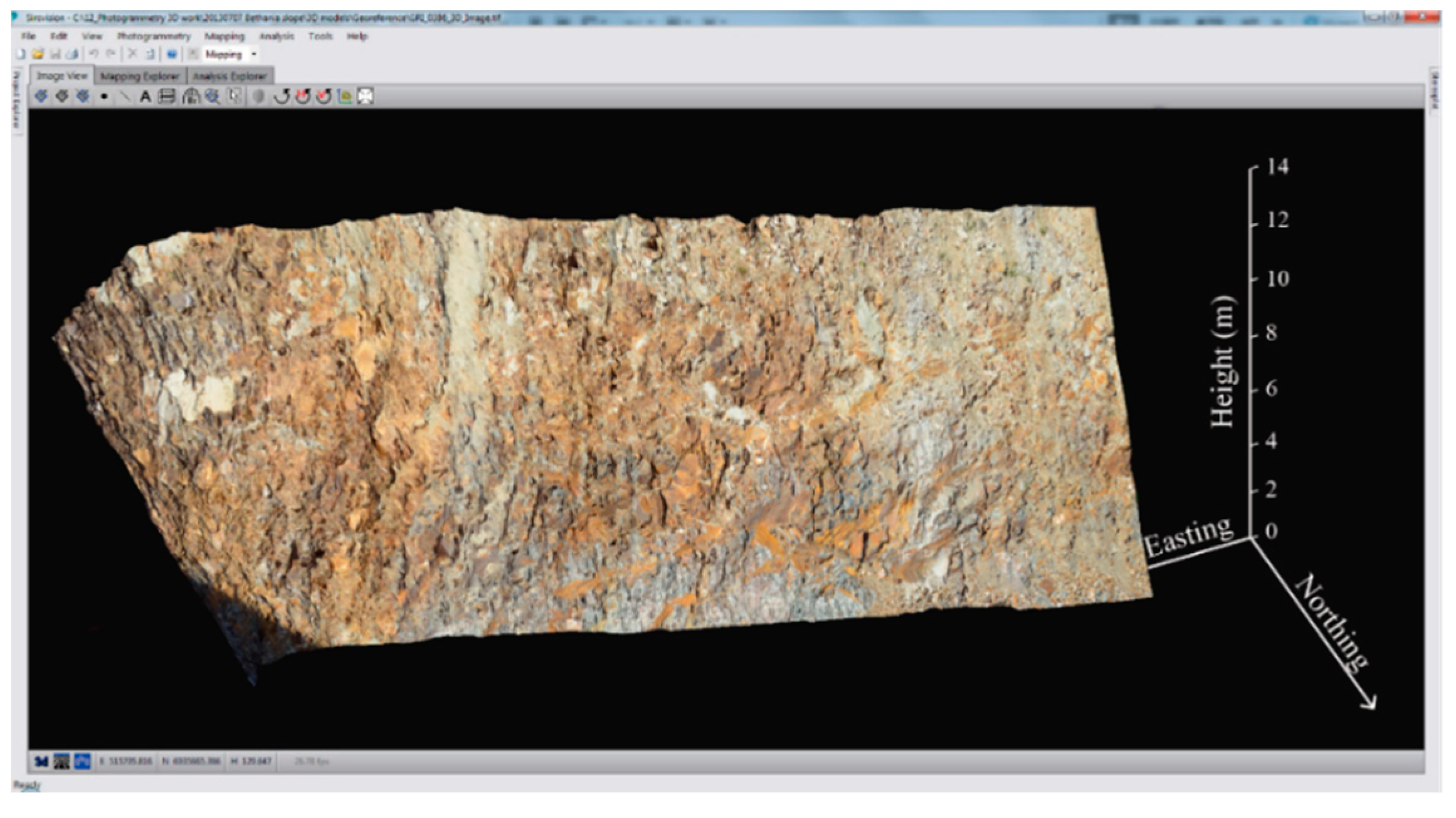
To evaluate rockfall paths in accordance with the topography of the slope, a georeferenced 3D surface model was derived from the photogrammetry field survey (Figure 6).
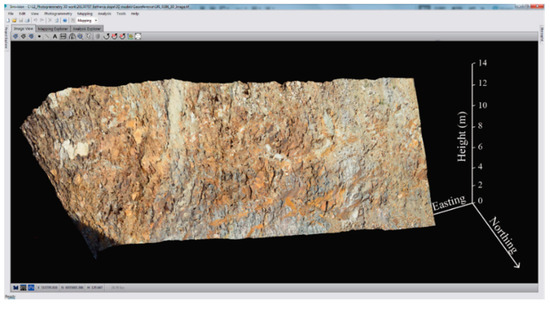
Figure 6.
Three-dimensional slope surface model obtained from Sirovision [21].
A single-lens reflex digital camera (Nikon D7000) which has a high-resolution CCD sensor (4924 × 3264 pixels) with a 24-mm focal length lens was employed to capture images of the rock slope. Two pictures were taken at a distance of 30 m from the slope to create 3D slope sections including the entire rockfall paths. The computer program Sirovision was then used to build a 3D model [38]. This computer code produced a high-resolution 3D slope surface model (1620 pixels/m2) for the slope of the rockfall tests.
4. Results
4.1. Image Quality Assessment
4.1.1. Visualization by Error Map
An error map visualizes the areas of an image which are associated with disparities between two images. In this study, the pairs of images which are the start-to-middle point and the start-to-end point of each test were analyzed. These images were manually selected from each rockfall test video clip. For seven rockfall tests, the image quality assessment was carried out. Fourteen pairs of images were extracted from the video clip and used for the image quality assessment. To perform IQA, the MSE and SSIM techniques from Section 2.1 were applied using a Python script.
In the field tests, the motions created collisions and consequential rock fragments along trajectories on the slope surface. The IQA highlighted the locations of rocks in motion and magnitudes of changes as shown in Figure 7. In the threshold images (Figure 7a,c), black-colored sections of the map represent areas in which there are few discernible errors. The bright white portions of the threshold images indicate more noticeable changes. As shown in Figure 7a,c, the falling rock and rolling rock fragments were clearly detected in the threshold images at the moments when the rock reached a midpoint on the rockfall path. When considering the motion blur, the images used are of relatively good quality, and the shape of the rock in motion is still recognizable even though the image is slightly blurry. The enlarged windows in Figure 7 give a further explanation of how the motion of rock is shown within the structured rock surface composition.

Figure 7.
Threshold and highlighted images illustrating rock fragments’ movements along the rockfall trajectory of test #2: (a) threshold image; (b) moment (1″29th frame) reached to midpoint; (c) enlarged portion of the white box on threshold image; (d) enlarged portion of the white box on the original image before rockfall; (e) enlarged portion of the white box on the original image at the rockfall moment.
A Python script was written to place rectangles around the regions identified as “disparity”. Figure 8 shows the rock detection results with red boxes around differences and the threshold image. The SSIM maps in Figure 8 indicate that SSIM can successfully detect the motion of rocks and even small fragments from the complex geological features. Interestingly, the SSIM algorithm inevitably detected slight movements of clouds in the sky, plants and the movements of the person in an orange safety vest as well.

Figure 8.
Contextual images—examples of detection results from the SSIM algorithm: (a) detected rock fragments inside red boxes along the rockfall path; (b) zoomed regions.
4.1.2. MSE and SSIM
The MSE and SSIM indices obtained from the IQA are presented in Table 2. If an image is at 8-bit color depth, the values of MSE range from 0 (no difference) to 65,025 (maximum difference). In the case of SSIM, the acceptable values are from 0 (maximum difference) to 1 (no difference). The rockfall tests created similar falling, rolling and bouncing patterns with 2 to 4 times of collision. It is noted that the objects, rock blocks and fragment features are relatively small in the whole region of each picture. Consequently, it seems acceptable that the values of both the MSE and SSIM indices in Table 2 are within a minor change region.

Table 2.
Image quality assessment results.
As discussed by Dosselmann and Yang [39], the SSIM index provides more accurate results than MSE does when it comes to the image quality assessment. Additionally, in this experiment, SSIM gave a better performance in terms of consistency. The range from 0.912 to 0.939 represents the consistent rockfall patterns well. Generally, it is known that MSE has shown an inconsistent performance for distorted images with different visual quality [26]. However, in this study, the quality of the images extracted from the video record was nearly equivalent, so the range of MSE values is not significantly different from that of SSIM.
4.2. Optical Flow Assessment
4.2.1. Sparse Optical Flow
The optical flow algorithms described in Section 2.2 were tested to evaluate the performance of optical flow for rockfall monitoring using sets of video sequences, as well as to examine the differences between the optical flow and observation outputs from the field. Since the sets of video clips were recorded by a normal speed video camera (30 fps), the point of interest was whether the optical flow can track the motion of rocks at a high speed over time by locating their positions in every frame of the video. Furthermore, it was quite questionable whether optical flow can describe the objects in different modes of motion of falling rocks. Two individual rockfall tests (tests #4 and #5 in Table 2) were chosen to evaluate the performance according to the modes of rockfall motion.
The Lucas–Kanade method and the Farnebäck method were implemented in this study using the code of the OpenCV Python library with the computer module of a Jetson Xavier NX developer kit (384-core GPU, NVIDIA). Optical flow is a computationally intensive task that employs embedded systems. The running speed of optical flow algorithms can be influenced by the performance of the hardware and the size of the optical flow field. Prior to video processing, the original video clip of each rockfall test was shortened, while the video sequences were cropped to remove irrelevant regions from the periphery of the original frame. Table 3 summarizes some influential factors used for the optical flow method.

Table 3.
Comparison of processing time between sparse and dense optical flow methods.
4.2.2. Dense Optical Flow
Dense optical flow is based on the motion estimation of all pixels in two adjacent frames. The Farnebäck method enables dense visualization of the flow field and a better visual perception of detailed differences between the neighboring pixels. The motion of rocks can be identified with the sizes and directions of flow vectors, while the velocity of rockfall is computed in a grid-based optical flow field. The density of grid points was determined by the size of the falling rocks; then, the nodes of a regularly sampled grid were generated in one of every ten pixels as shown in Figure 9a,b. The process of optical flow computation continued incorporating the changes that occurred during iterations. Figure 9 shows an example of a frame with the results obtained for the dense optical flow in tests #4 and #5.

Figure 9.
Results of dense optical flow analysis using Farnebäck method: (a) generated grid points (green cross) and optical flow paths (red) of test #4; (b) test #5; (c) enlarged image of test #4; (d) test #5; (e) tracked rock in an enlarged color map of test #4; (f) test #5.
Figure 9c,d show an enlarged zone of the dense vector field with the grid feature detections and the corresponding motion vectors. The estimated flow vectors are depicted as red lines, showing the apparent displacements and their directions in a frame and creating a vector map around the tracked rock. This study focuses on the performance of a dense optical flow that can be employed to estimate the rockfall velocity and detect rockfalls. By calculating the distance and the length of vectors travelled by each pixel and knowing the time between the successive frames, the velocity of rockfall per frame can be simply estimated. In this study, two different modes of motion are considered. As shown in Table 3, the rockfall motion mostly comprised bouncing, whereas in test #5, it was closer to a sliding mode. Consequently, the direction and velocity of rockfall were well detected by the Farnebäck algorithm. During bouncing of rocks, test #4 clearly showed the marked flow vectors near the falling object. Additionally, it was observed that the vectors caused by sliding motion in test #5 were parallel to the sliding area, as seen in Figure 9c,d. In addition, for easy observations, the position and direction of the detected rocks can be displayed using different color information, as shown in Figure 9e,f.
5. Discussion
5.1. Tracking of Rockfall by Sparse Optical Flow
The sparse optical flow was applied to two (tests #4 and #5) rockfall field test video sequences. The tracking points (i.e., rock features) were defined using the Shi–Tomasi corner detection technique, which is part of the Lucas–Kanade algorithm. As shown in Figure 10a, 30,000 red points were generated by the Shi–Tomasi algorithm [40] on the cropped area of the slope. The algorithm performed well by detecting the angular points and rock edges on the slope surface. After the rockfall began, the tracking points were consistently monitored in every frame. It is evident that the Lucas–Kanade algorithm can trace the falling rocks and the trajectories with the direction of optical flow. The tracked paths are indicated by the connected pixels in pink in Figure 10b,c. The falling rocks were detected in the early stage of each test and then tracked until the end. During the analysis, the rocks could change to an “inactive” state, which indicated that the tracked rocks were lost in their trajectories, or they went back to the “tracked” state again.

Figure 10.
Results of sparse optical flow analysis using Lucas–Kanade method: (a) points generated (red spots) by Shi–Tomasi corner detection method in the cropped slope area used for optical flow; (b) enlarged picture of optical flow lines and the position of tracked rock for test #4 in the region ‘A’; (c) for test #5.
The reason for these transitions can be explained by changes in the brightness of the tracked objects. The brightness of the falling rocks varied due to the light refraction. The Lucas–Kanade method assumes that the brightness of pixels in a moving object remains fixed in the consecutive frames. Accordingly, the tracking line of rockfall was disconnected because of illumination variation. It was also observed that the generated tracking points at irregular intervals had a strong influence on the tracking process. Considering the size of rocks in the field test, the tracking points were too sparsely distributed in some areas, which resulted in tracked rocks being lost in their trajectories. The results show that the sparse optical flow using the Lucas–Kanade method can lead to insufficient tracking for rockfall monitoring if the target is lost. However, the flow lines directly represent the direction of movement and can offer an excellent intuitive perception of the physical motion. Therefore, this method can be sufficient to provide the rockfall path with reliable directions if the algorithm is processed using a sufficient number of tracking points.
5.2. Estimation of Rockfall Motion from Dense Optical Flow
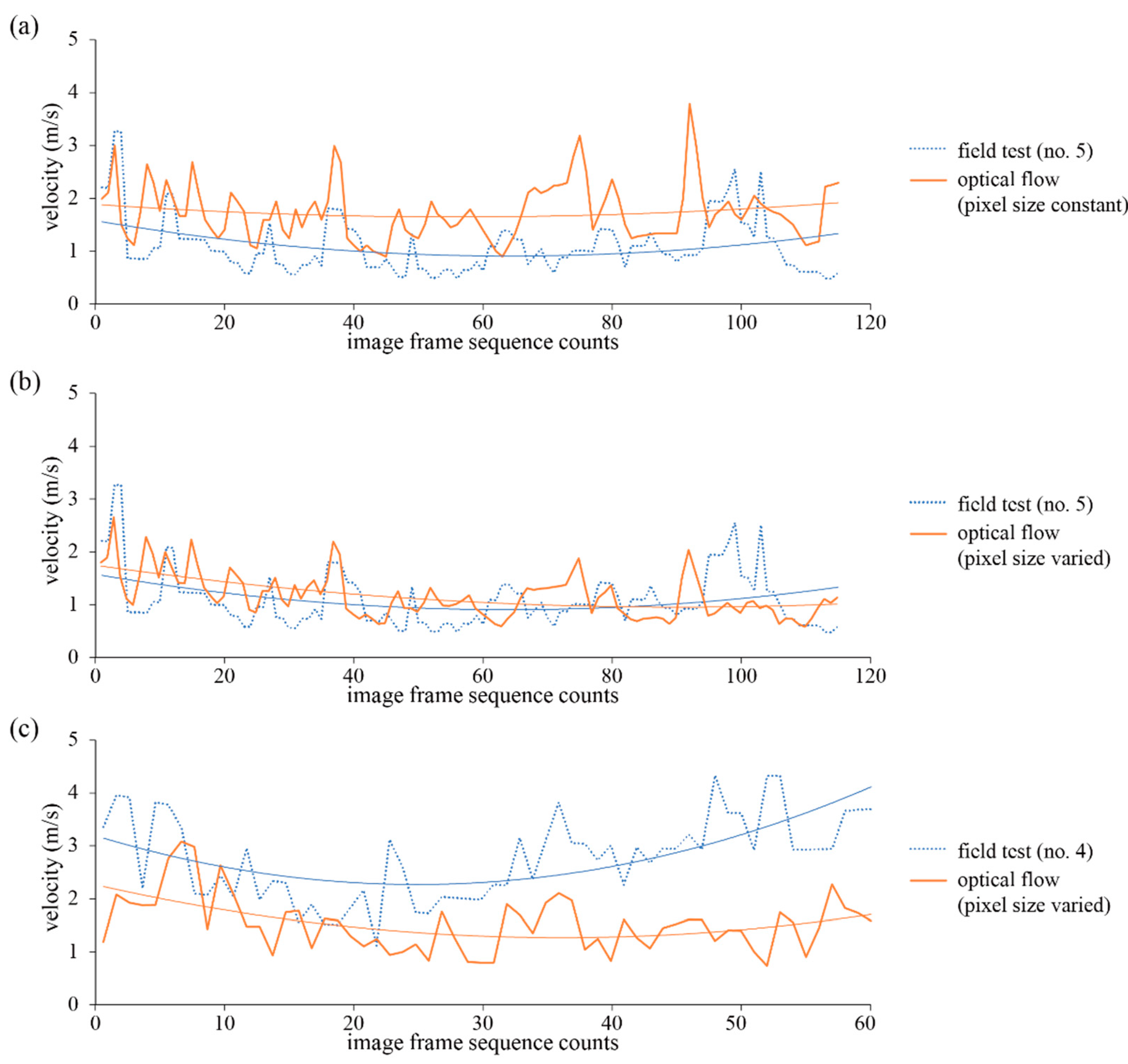
To study the feasibility of optical flow, the outcomes of the velocity estimation using the dense optical flow were compared with the observed velocity using slow sequences of video. The challenge was the practical limitations of two-dimensional images. It was assumed that the trajectories were orthogonal to the camera axis and that the sizes of pixels in an image frame were identical to each other. The results of the estimation are demonstrated in Figure 11a. Since the motion field of optical flow was projected from three-dimensional space into a two-dimensional plane, the measurement of distance using pixel-based calculations introduced errors in the estimation of velocity.
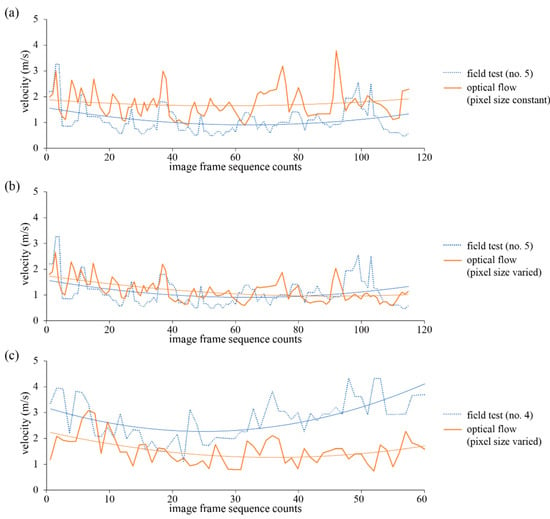
Figure 11.
Comparison between optical flow results and calculation by observation with regard to the velocity of rockfalls: (a) for test #5 (sliding mode) using constant pixel size; (b) for test #5 using pixel sizes obtained from photogrammetric 3D topography; (c) for test #4 (bouncing mode).
To overcome this limitation and to minimize the measurement errors, three-dimensional coordinates of the georeferenced 3D surface model generated from Sirovision were employed to obtain more precise camera-to-object distances. Using the pixel sizes in accordance with the three-dimensional distances obtained from the photogrammetric topography, the velocity data were calculated and are plotted in Figure 11b. For test #5, the distribution of velocity obtained from optical flow was similar to the observed data, with an estimated mean value of 1.13 m/s compared to the observed value of 1.09 m/s.
In contrast, in the case of test #4, there was an underestimation of the optical flow data regarding the velocity, which may be due to the low frame rate and shutter speed of the camera. It was observed that the current frame rate was too slow to capture the rapid rock object between successive frames. As shown in Table 1, test #4 comprised bouncing with fast falling, and the rockfall was faster than in test #5. As discussed in Section 3.2, the frame rate and shutter speed of a video recording can affect the quality of images, resulting in about 12 cm of blurring in test #4. These observations indicate that a high-speed camera with a high frame rate and fast shutter speed is required for assessing fast rockfall motions. Consequently, combination of dense optical flow and three-dimensional depth information can provide real-time rockfall data on the rock trajectories as well as the location and velocity of rockfalls at a regional scale.
6. Conclusions
In this study, the image processing, optical flow and photogrammetry methods were assessed for application to rockfall monitoring. Based on the obtained results, the following conclusions can be drawn.
SSIM maps can successfully detect the motion of rocks. The MSE and SSIM techniques can produce consistent and favorable results for the diverse morphologies and textures of rock slopes based on images obtained from field rockfall tests.
As a sparse optical flow algorithm, the Lucas–Kanade method successfully tracked the rockfall using video sequences. The flow lines directly indicated the direction of rockfall movement. However, the change in illumination of the tracked objects was a main factor influencing the maintenance of the tracking in rockfall trajectories. Additionally, it was found that the sparse optical flow could lead to insufficient tracking for rockfall monitoring if the target was lost.
The dense optical flow using grid points revealed that the direction and velocity of rockfall were well identified by the Farnebäck algorithm. However, it was found that the low frame rate and shutter speed of the camera underestimated the rockfall velocity. The results indicate that a high-speed camera with a high frame rate and a fast shutter speed is required to detect rockfall motions.
Furthermore, the dense optical flow more accurately estimated rockfall velocity when accompanied by three-dimensional camera-to-object distances from photogrammetry.
Author Contributions
Conceptualization, D.-H.K. and I.G.; methodology, D.-H.K. and I.G.; software, D.-H.K.; validation, D.-H.K. and I.G.; formal analysis, D.-H.K.; investigation, D.-H.K. and I.G.; resources, I.G.; data curation, D.-H.K.; writing—original draft preparation, D.-H.K.; writing—review and editing, I.G.; visualization, D.-H.K.; supervision, I.G.; project administration, I.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dick, D.J.; Eberhardt, E.; Stead, D.; Rose, N.D. Early detection of impending slope failure in open pit mines using spatial and temporal analysis of real aperture radar measurements. In Proceedings of the Slope Stability 2013, Brisbane, QLD, Australia, 25–27 September 2013; Australian Centre for Geomechanics: Crawley, Australia, 2013; pp. 949–962. [Google Scholar]
- Intrieri, E.; Gigli, G.; Mugnai, F.; Fanti, R.; Gasagli, N. Design and implementation of a landslide early warning system. Eng. Geol. 2012, 147–148, 124–136. [Google Scholar] [CrossRef] [Green Version]
- Brideau, M.A.; Sturzenegger, M.; Stead, D.; Jaboyedoff, M.; Lawrence, M.; Roberts, N.; Ward, B.; Millard, T.; Clague, J. Stability analysis of the 2007 Chehalis Lake landslide based on long-range terrestrial photogrammetry and airborne LiDAR data. Landslides 2012, 9, 75–91. [Google Scholar] [CrossRef]
- Park, S.; Lim, H.; Tamang, B.; Jin, J.; Lee, S.; Chang, S.; Kim, Y. A study on the slope failure monitoring of a model slope by the application of a displacement sensor. J. Sens. 2019, 2019, 7570517. [Google Scholar] [CrossRef]
- Donovan, J.; Raza Ali, W. A change detection method for slope monitoring and identification of potential rockfall using three-dimensional imaging. In Proceedings of the 42nd US Rock Mechanics Symposium and 2nd U.S.-Canada Rock Mechanics Symposium, San Francisco, CA, USA, 29 June–2 July 2008. [Google Scholar]
- Kim, D.H.; Gratchev, I.; Balasubramaniam, A.S. Determination of joint roughness coefficient (JRC) for slope stability analysis: A case study from the Gold Coast area. Landslides 2013, 10, 657–664. [Google Scholar] [CrossRef] [Green Version]
- Fantini, A.; Fiorucci, M.; Martino, S. Rock falls impacting railway tracks: Detection analysis through an artificial intelligence camera prototype. Wirel. Commun. Mob. Comput. 2017, 2017, 9386928. [Google Scholar] [CrossRef] [Green Version]
- Kromer, R.; Walton, G.; Gray, B.; Lato, M.; Group, R. Development and optimization of an automated fixed-location time lapse photogrammetric rock slope monitoring system. Remote Sens. 2019, 11, 1890. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Min, G.; Chen, P.; Liu, Y.; Tian, S.; Zhang, D.; Zhang, W. Computer vision-based techniques and path planning strategy in a slope monitoring system using unmanned aerial vehicle. Int. J. Adv. Robot. Syst. 2020, 17. [Google Scholar] [CrossRef]
- Voumard, J.; Abellán, A.; Nicolet, P.; Penna, I.; Chanut, M.-A.; Derron, M.-H.; Jaboyedoff, M. Using street view imagery for 3-D survey of rock slope failures. Nat. Hazards Earth Syst. Sci. 2017, 17, 2093–2107. [Google Scholar] [CrossRef] [Green Version]
- Ghorbanzadeh, O.; Meena, S.R.; Blaschke, T.; Aryal, J. UAV-based slope failure detection using deep-learning convolutional neural networks. Remote Sens. 2019, 11, 2046. [Google Scholar] [CrossRef] [Green Version]
- McHuge, E.L.; Girard, J.M. Evaluating techniques for monitoring rockfalls and slope stability. In Proceedings of the 21st International Conference on Ground Control in Mining, Morgantown, WV, USA, 6–8 August 2002; West Virginia University: Monongalia County, WV, USA, 2002; pp. 335–343. [Google Scholar]
- Kim, D.; Balasubramaniam, A.S.; Gratchev, I.; Kim, S.R.; Chang, S.H. Application of image quality assessment for rockfall investigation. In Proceedings of the 16th Asian Regional Conference on Soil Mechanics and Geotechnical Engineering, Taipei, Taiwan, 14–18 October 2019. [Google Scholar]
- Lu, D.; Mausel, P.; Brondizizio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2407. [Google Scholar] [CrossRef]
- Srokosz, P.E.; Bujko, M.; Bochenska, M.; Ossowski, R. Optical flow method for measuring deformation of soil specimen subjected to torsional shearing. Measurement 2021, 174, 109064. [Google Scholar] [CrossRef]
- Kenji, A.; Teruo, Y.; Hiroshi, H. Landslide occurrence prediction using optical flow. In Proceedings of the 2019 19th International Conference on Control, Automation and Systems (ICCAS), Jeju, Korea, 15–18 October 2019; pp. 1311–1315. [Google Scholar]
- Rosin, P.L.; Hervás, J. Remote sensing image thresholding methods for determining landslide activity. Int. J. Remote Sens. 2005, 26, 1075–1092. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.W.; Dunning, S.; Bainbridge, R.; Martin, J.; Diaz-Moreno, A.; Torun, H.; Jin, N.; Woodward, J.; Lim, M. Low-cost automatic slope monitoring using vector tracking analyses on live-streamed time-lapse imagery. Remote Sens. 2021, 13, 893. [Google Scholar] [CrossRef]
- Vanneschi, C.; Camillo, M.D.; Aiello, E.; Bonciani, F.; Salvini, R. SfM-MVS photogrammetry for rockfall analysis and hazard assessment along the ancient Roman via Flaminia road at the Furlo Gorge (Italy). ISPRS Int. J. Geo-Inf. 2019, 8, 325. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.H.; Gratchev, I.; Berends, J.; Balasubramaniam, A.S. Calibration of restitution coefficients using rockfall simulations based on 3D photogrammetry model: A case study. Nat. Hazards. 2015, 78, 1931–1946. [Google Scholar] [CrossRef] [Green Version]
- Štroner, M.; Urban, R.; Reindl, T.; Seidl, J.; Broucek, J. Evaluation of the georeferencing accuracy of a photogrammetric model using a quadrocopter with onboard GNSS RTK. Sensors 2020, 20, 2318. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuan, W.; Yuan, X.; Xu, S.; Gong, J.; Shibasaki, R. Dense image-matching via optical flow field estimation and fast-guided filter refinement. Remote Sens. 2019, 11, 2410. [Google Scholar] [CrossRef] [Green Version]
- Nones, M.; Archetti, R.; Guerrero, M. Time-Lapse photography of the edge-of-water line displacements of a sandbar as a proxy of riverine morphodynamics. Water 2018, 10, 617. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Leung, M. Integrating intensity and texture differences for robust change detection. IEEE Trans. Image Process. 2002, 11, 105–112. [Google Scholar]
- Chandler, D.; Hemami, S.S. VSNR: A wavelet-based visual signal-to-noise ratio for natural images. IEEE Trans. Image Process. 2007, 16, 2284–2298. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Thompson, D.; Castano, R. Performance comparison of rock detection algorithms for autonomous planetary geology. In Proceedings of the 2007 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2007. [Google Scholar]
- Thompson, D.; Niekum, S.; Smith, T.; Wettergreen, D. Automatic detection and classification of features of geologic interest. In Proceedings of the 2005 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2005. [Google Scholar]
- Horn, B.K.P.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef] [Green Version]
- Buxton, B.F.; Buxton, H. Computation of optic flow from the motion of edge features in image sequences. Image Vis. Comput. 1984, 2, 59–75. [Google Scholar] [CrossRef]
- Jepson, A.; Black, M.J. Mixture models for optical flow computation. In Proceedings of the IEEE Computer Vision and Pattern Recognition, CVPR-93, New York, NY, USA, 15–17 June 1993; pp. 760–761. [Google Scholar]
- Lucas, B.D.; Kanade, T. An image registration technique with an application to stereo vision. In Proceedings of the 7th International Joint Conference on Artificial Intelligence (IJCAI ’81), Vancouver, BC, Canada, 24–28 August 1981; pp. 121–130. [Google Scholar]
- Farnebäck, G. Two-frame motion estimation based on polynomial expansion. In Proceedings of the Scandinavian Conference on Image Analysis, SCIA 2003: Image Analysis, Lecture Notes in Computer Science, Halmstad, Sweden, 29 June–2 July 2003; Bigun, J., Gustavsson, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2749, pp. 363–370. [Google Scholar]
- Bai, J.; Huang, L. Research on LK optical flow algorithm with Gaussian pyramid model based on OpenCV for single target tracking. IOP Conf. Ser. Mater. Sci. Eng. 2018, 435, 012052. [Google Scholar] [CrossRef]
- Akehi, K.; Matuno, S.; Itakura, N.; Mizuno, T.; Mito, K. Improvement in eye glance input interface using OpenCV. In Proceedings of the 7th International Conference on Electronics and Software Science (ICESS2015), Takamatsu, Japan, 20–22 July 2015; pp. 207–211. [Google Scholar]
- Willmott, W. Rocks and Landscape of the Gold Coast Hinterland: Geology and Excursions in the Albert and Beaudesert Shires; Geological Society of Australia, Queensland Division: Brisbane, QLD, Australia, 1986. [Google Scholar]
- Arikan, F.; Ulusay, R.; Aydin, N. Characterization of weathered acidic volcanic rocks and a weathering classification based on a rating system. Bull. Eng. Geol. Environ. 2007, 66, 415–430. [Google Scholar] [CrossRef]
- CSIRO. Siro3D-3D Imaging System Manual, Version 5.0; © CSIRO Exploration & Mining: Canberra, Australia, 2014.
- Dosselmann, R.; Yang, X.D. A comprehensive assessment of the structural similarity index. Signal Image Video Process. 2011, 5, 81–91. [Google Scholar] [CrossRef]
- Shi, J.; Tomasi, C. Good features to track. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR-94, Seattle, WD, USA, 21–23 June 1994; pp. 593–600. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).