Estimating Snowpack Density from Near-Infrared Spectral Reflectance Using a Hybrid Model
Abstract
1. Introduction
2. Materials and Methods
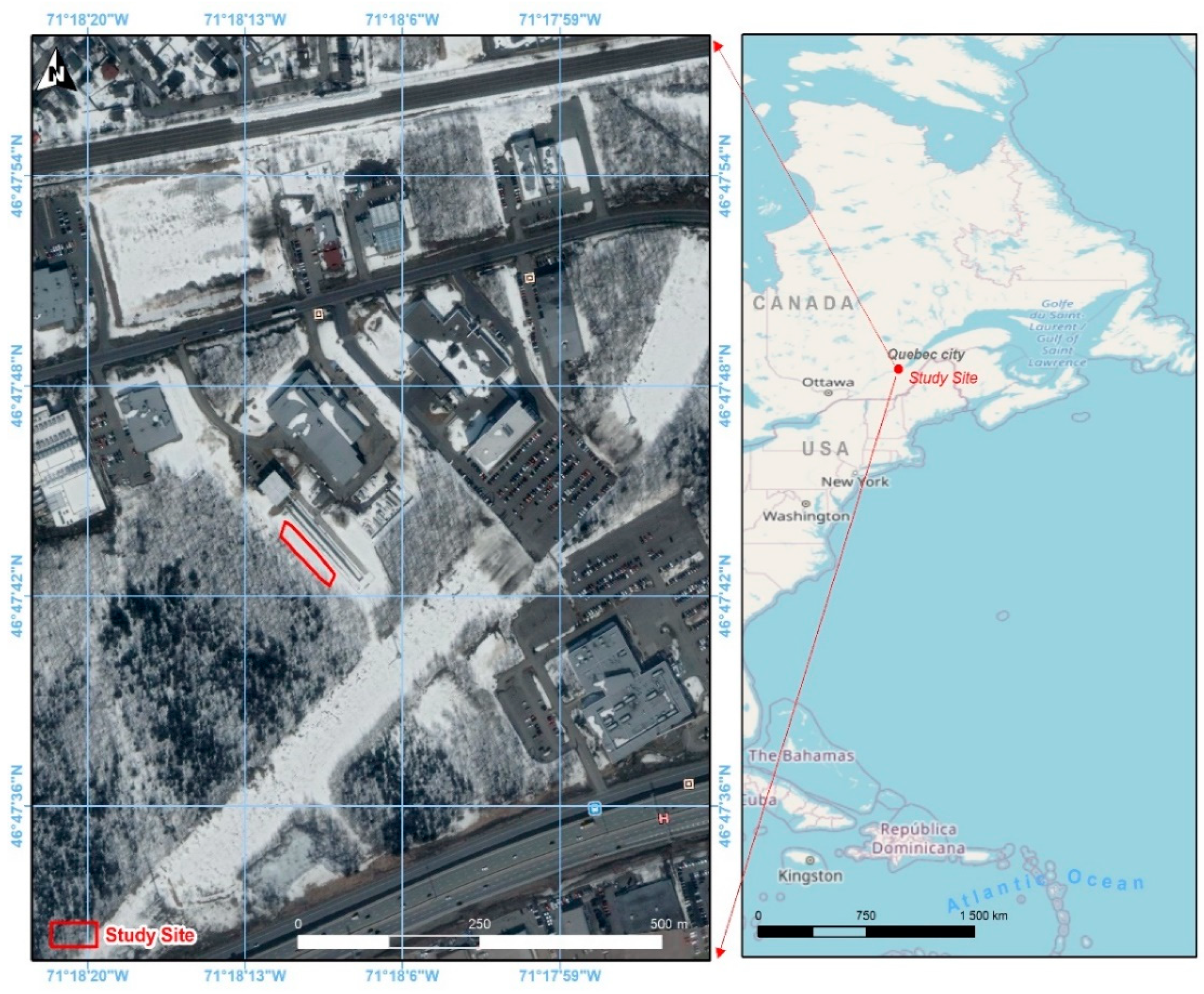
2.1. Study Area
2.2. In-Situ Data Collection
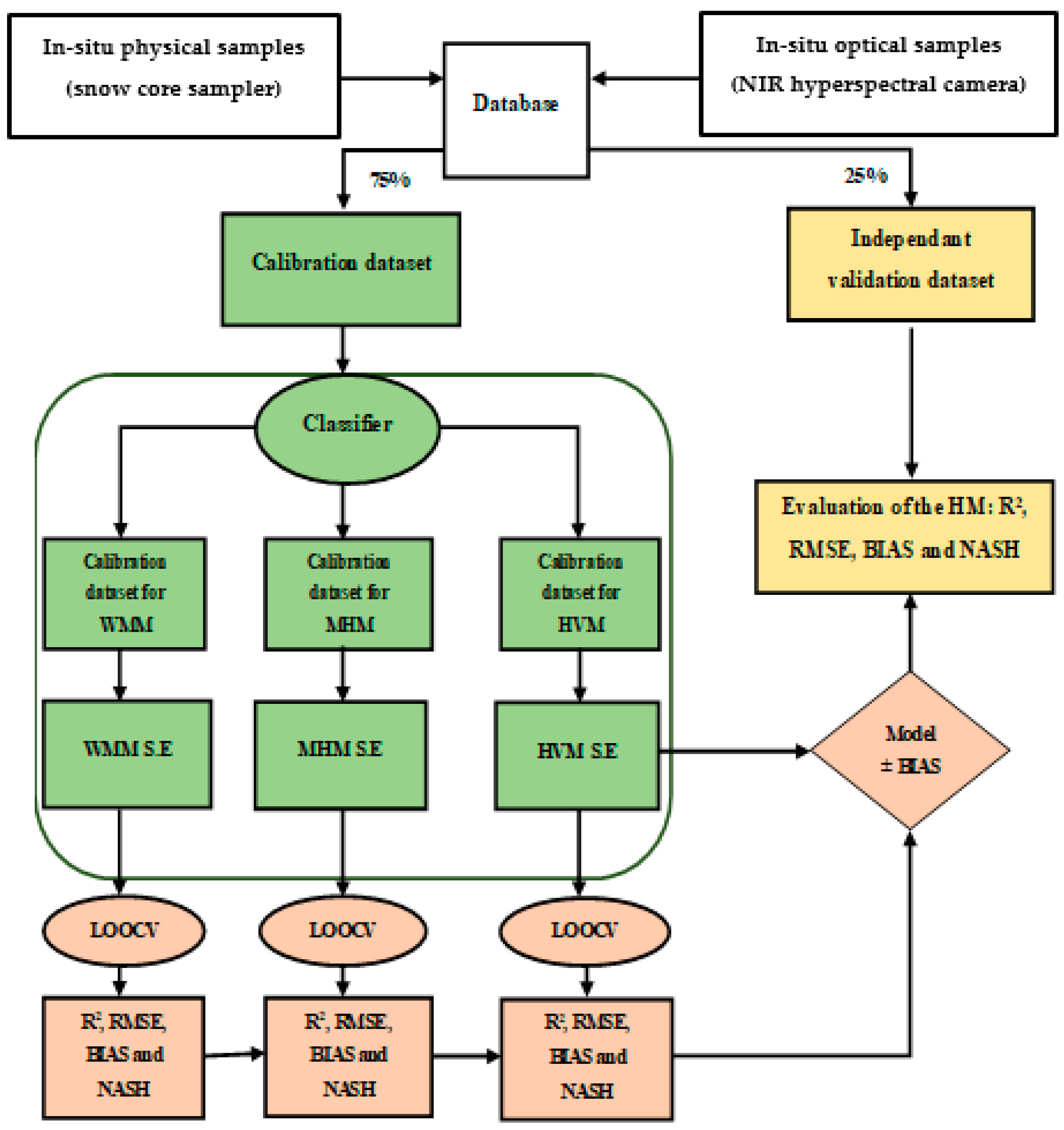
2.3. Methodological Approach
- ❖
- The calibration of the classifier and the specific estimation of the HM
- ❖
- Evaluation of the specific estimators using the leave-one-out cross-validation (LOOCV) algorithm [42];
- ❖
- HM evaluation using independent data selected using the systematic split validation (SSV) technique.
3. Results and Discussion
3.1. Descriptive Analysis of Data
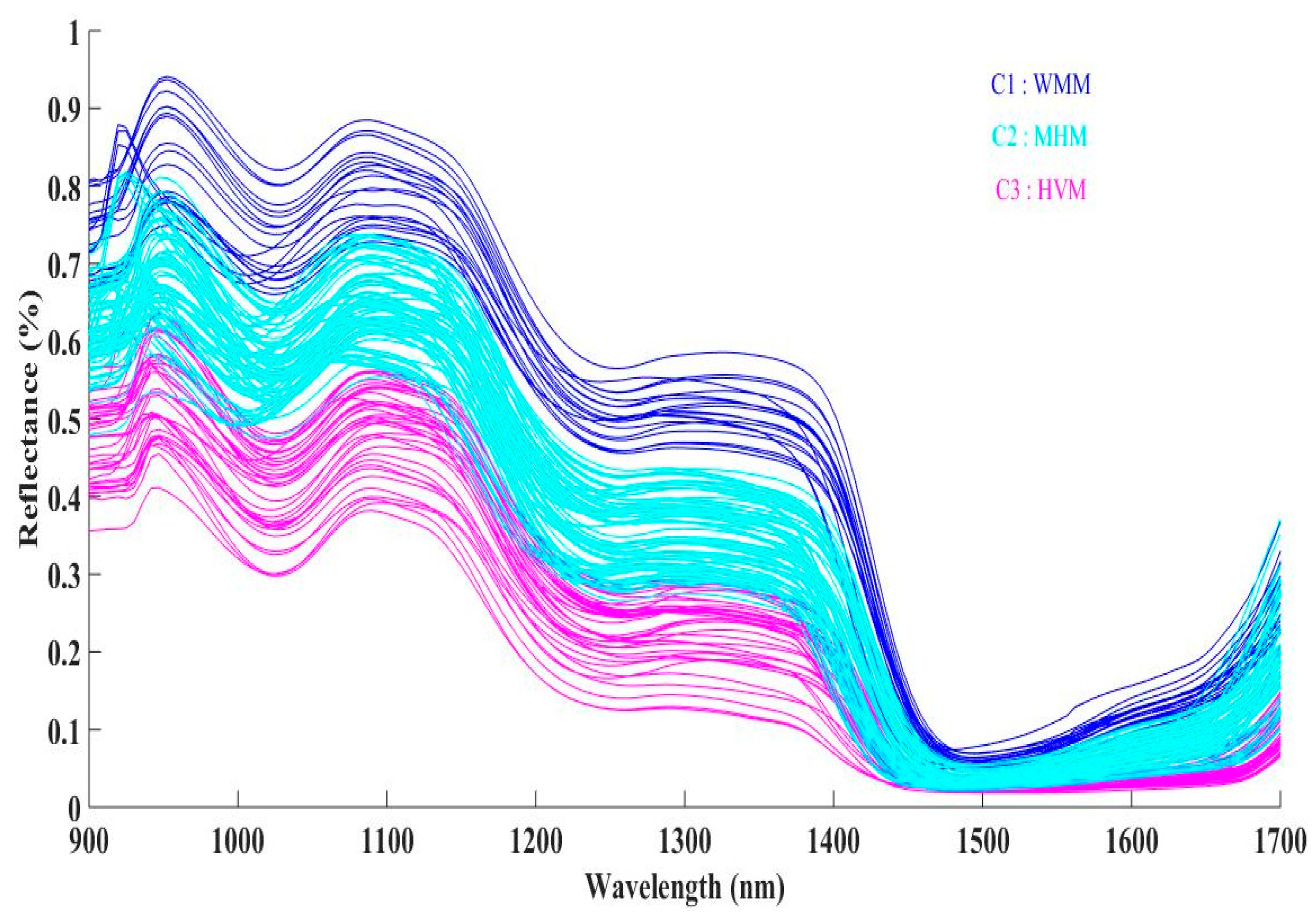
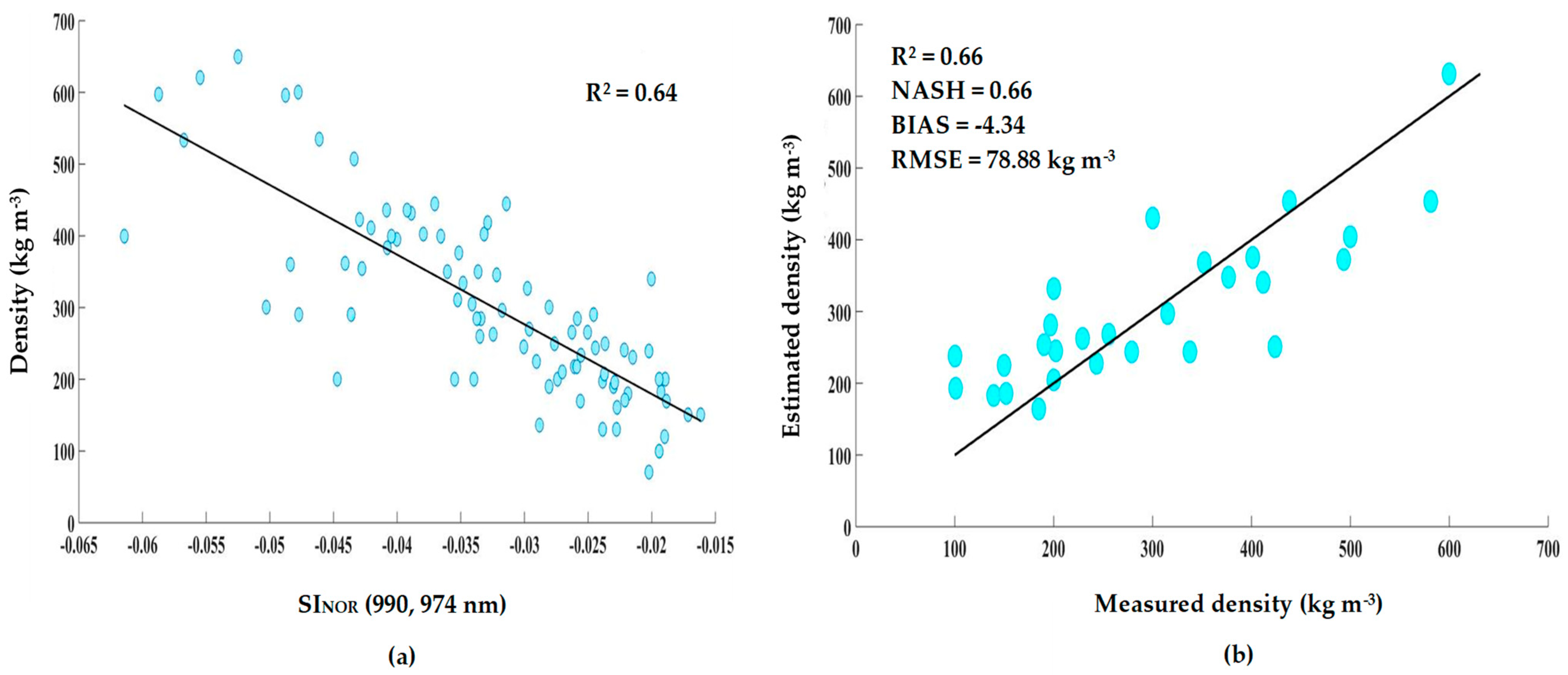
3.2. Statistical Dependence between Density and Spectral Reflectance
3.3. Calibration of the Hybrid Model
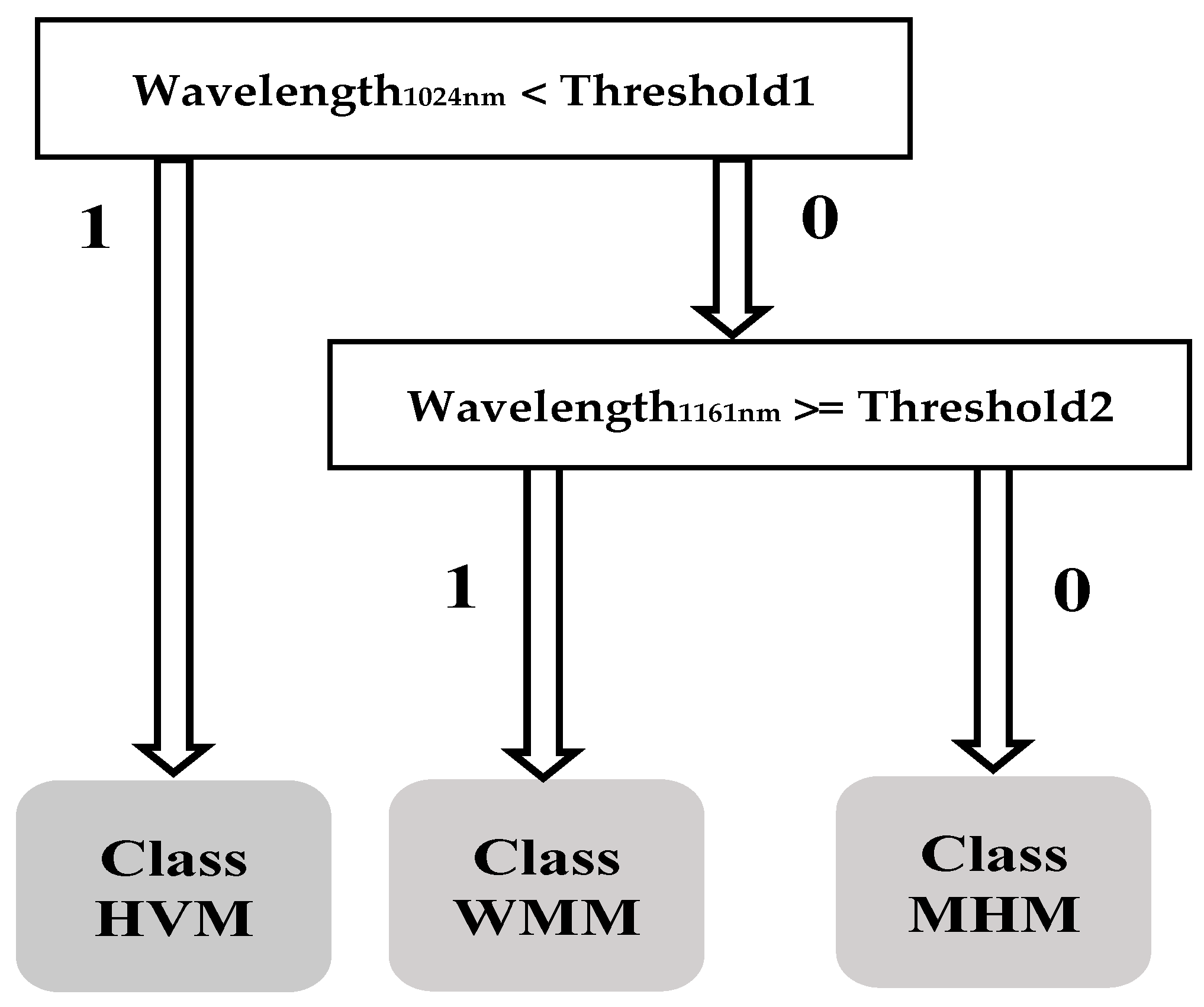
3.3.1. HM Classifier Calibration
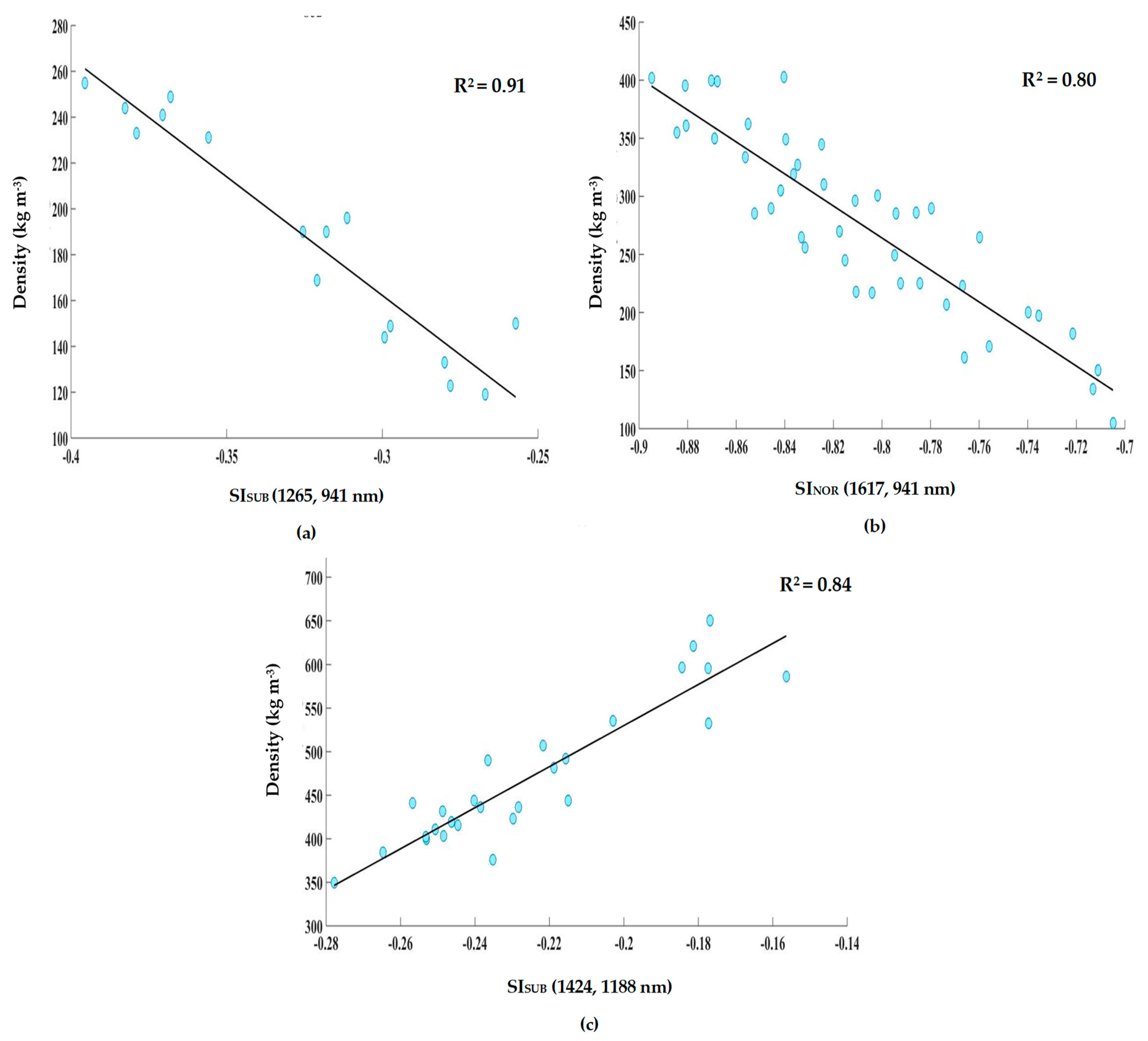
3.3.2. Calibration of the Specific Models
3.4. Evaluation and Validation of the Hybrid Model
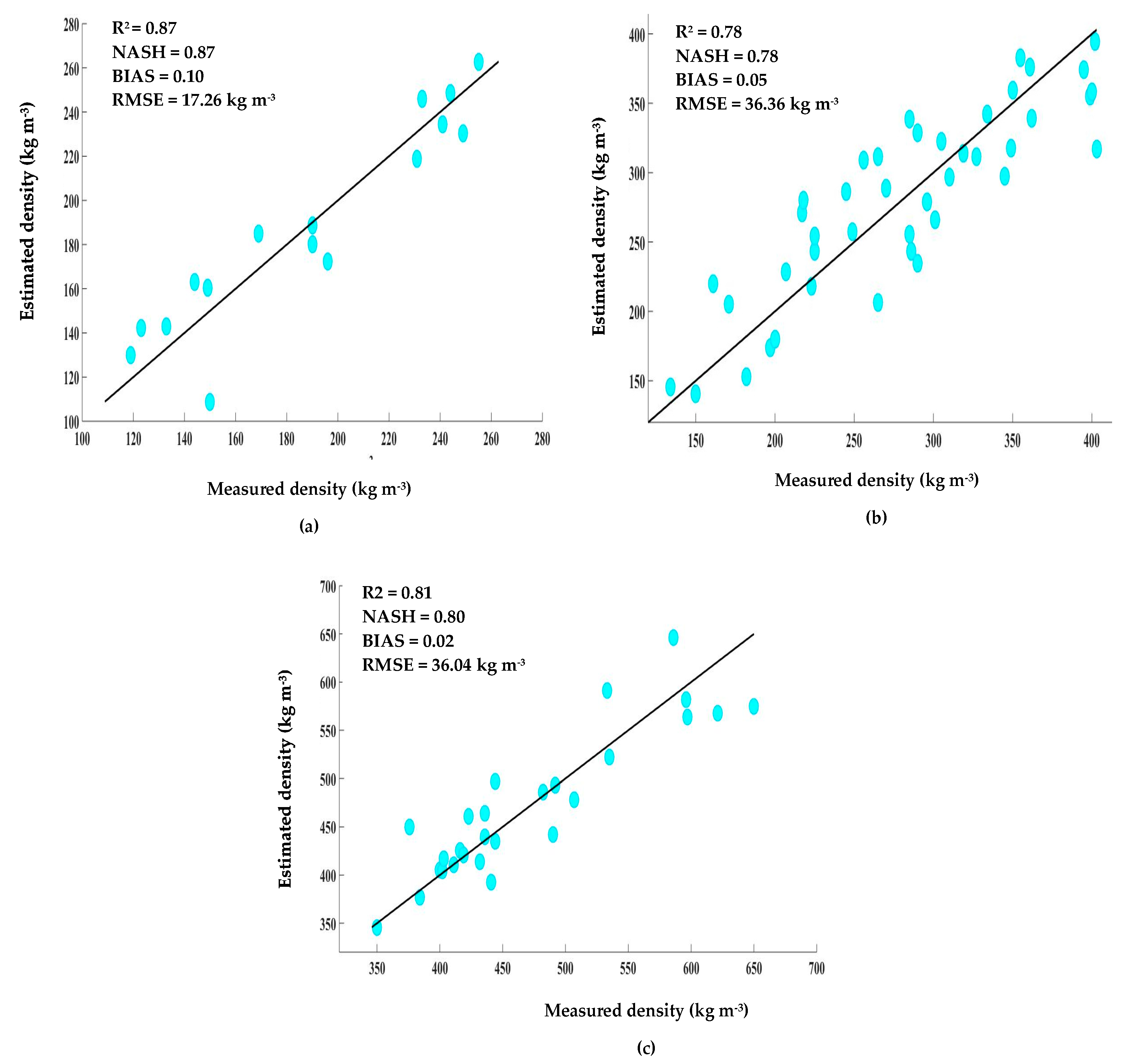
3.4.1. Evaluation of the Specific Estimators Using the LOOCV Algorithm
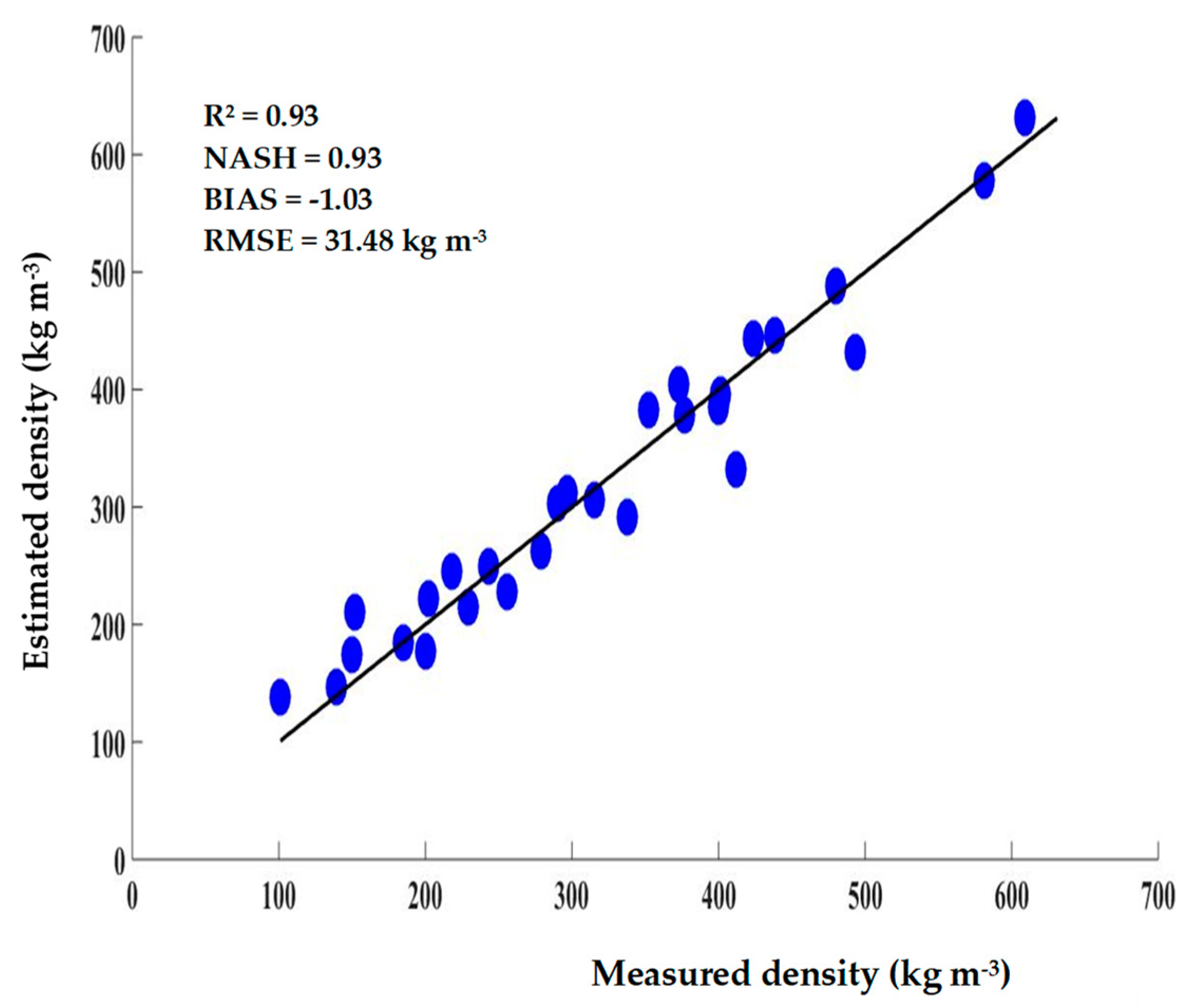
3.4.2. Evaluation of the Hybrid Model Using SSV
- ❖
- Assign a given class using the HM classifier;
- ❖
- Estimate the density using the specific estimators corresponding to the preassigned class;
- ❖
- Correct the estimates’ BIAS;
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kropacek, J.; Feng, C.; Alle, M.; Kang, S.; Hochschild, V. Temporal and spatial aspects of snow distribution in the Nam Co Basin on the Tibetan Plateau from MODIS data. Remote Sens. 2010, 2, 2700–2712. [Google Scholar] [CrossRef]
- Marbouty, D. Les propriétés physiques de la neige. Houille Blanche 1984, 557–567. [Google Scholar] [CrossRef][Green Version]
- Davis, R.; Pangburn, T.; Daly, S.; Ochs, E.; Hardy, J.; Bryant, E.; Pugner, P. Can satellite snow maps, ground measurements, and modeling improve water management and control in the Kings River Basin, California. In Proceedings of the Efforts toward finding the answer—67th Annual Western Snow Conference, South Lake Tahoe, CA, USA, 19–22 April 1999; pp. 54–61. [Google Scholar]
- Fassnacht, S.; Helfrich, S.; Lampkin, D.; Dressler, K.; Bales, R.; Halper, E.; Reigle, D.; Imam, B. Snowpack modelling of the Salt Basin with water management implications. In Proceedings of the Annual Western Snow Conference, Sun Valley, ID, USA, 17–19 April 2001; pp. 65–76. [Google Scholar]
- Brown, R.; Armstrong, R. Snow-cover data: Measurement, products, and sources. In Snow and Climate; Armstrong, R.L., Brun, E., Eds.; Cambridge University Press: Cambridge, UK, 2008; pp. 181–216. [Google Scholar]
- Dutra, E.; Viterbo, P.; Miranda, P.M.; Balsamo, G. Complexity of snow schemes in a climate model and its impact on surface energy and hydrology. J. Hydrometeorol. 2012, 13, 521–538. [Google Scholar] [CrossRef]
- Castebrunet, H.; Eckert, N.; Giraud, G.; Durand, Y.; Morin, S. Projected changes of snow conditions and avalanche activity in a warming climate: The French Alps over the 2020–2050 and 2070–2100 periods. Cryosphere 2014, 8, 1673–1697. [Google Scholar] [CrossRef]
- Lehning, M.; Bartelt, P.; Brown, B.; Russi, T.; Stöckli, U.; Zimmerli, M. SNOWPACK model calculations for avalanche warning based upon a new network of weather and snow stations. Cold Reg. Sci. Technol. 1999, 30, 145–157. [Google Scholar] [CrossRef]
- Langham, E.J. Physics and properties of snowcover. In Handbook of Snow, Principles, Processes, Management and Use; Gray, D.M., Male, D.H., Eds.; Pergamon Press: Toronto, ON, USA, 1981; pp. 275–337. [Google Scholar]
- Pomeroy, J.W.; Hanson, S.; Faria, D. Small-scale variation in snowmelt energy in a boreal forest: An additional factor controlling depletion of snow cover. In Proceedings of the Eastern Snow Conference, Ottawa, ON, Canada, 17–19 May 2001; pp. 85–96. [Google Scholar]
- Roy, V.; Goïta, K.; Royer, A.; Walker, A.E.; Goodison, B.E. Snow water equivalent retrieval in a Canadian boreal environment from microwave measurements using the HUT snow emission model. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1850–1859. [Google Scholar] [CrossRef]
- Sturm, M.; Taras, B.; Liston, G.E.; Derksen, C.; Jonas, T.; Lea, J. Estimating snow water equivalent using snow depth data and climate classes. J. Hydrometeorol. 2010, 11, 1380–1394. [Google Scholar] [CrossRef]
- Farnes, P.; Goodison, B.; Peterson, N.; Richards, R. Proposed metric snow samplers. In Proceedings of the 48th Western Snow Conference, Laramie, WY, USA, 15–17 April 1980; pp. 107–119. [Google Scholar]
- Farnes, P. Criteria for determining mountain snow pillow sites. In Proceedings of the 35th Western Snow Conference, Boise, ID, USA, 18–20 April 1967; pp. 59–62. [Google Scholar]
- Kinar, N.; Pomeroy, J. Measurement of the physical properties of the snowpack. Rev. Geophys. 2015, 53, 481–544. [Google Scholar] [CrossRef]
- Zuanon, N. IceCube, a portable and reliable instruments for snow specific surface area measurement in the field. In Proceedings of the International Snow Science Workshop Grenoble-Chamonix Mont-Blance—2013 Proceedings, Grenoble, France, 7–11 October 2013; pp. 1020–1023. [Google Scholar]
- Wright, M.; Kavanaugh, J.; Labine, C. Performance analysis of GMON3 snow water equivalency sensor. In Proceedings of the Western Snow Conference, Stateline, NV, USA, 18–21 April 2011; pp. 105–108. [Google Scholar]
- Cui, Y.; Xiong, C.; Lemmetyinen, J.; Shi, J.; Jiang, L.; Peng, B.; Li, H.; Zhao, T.; Ji, D.; Hu, T. Estimating snow water equivalent with backscattering at X and Ku band based on absorption loss. Remote Sens. 2016, 8, 505. [Google Scholar] [CrossRef]
- Negi, H.; Jassar, H.; Saravana, G.; Thakur, N.; Snehmani; Ganju, A. Snow-cover characteristics using Hyperion data for the Himalayan region. Int. J. Remote Sens. 2013, 34, 2140–2161. [Google Scholar] [CrossRef]
- Gergely, M.; Schneebeli, M.; Roth, K. First experiments to determine snow density from diffuse near-infrared transmittance. Cold Reg. Sci. Technol. 2010, 64, 81–86. [Google Scholar] [CrossRef]
- Chauchard, F.; Cogdill, R.; Roussel, S.; Roger, J.; Bellon-Maurel, V. Application of LS-SVM to non-linear phenomena in NIR spectroscopy: Development of a robust and portable sensor for acidity prediction in grapes. Chemom. Intell. Lab. Syst. 2004, 71, 141–150. [Google Scholar] [CrossRef]
- Osborne, B.G. Near-infrared spectroscopy in food analysis. In Encyclopedia of Analytical Chemistry: Applications, Theory and Instrumentation; John Wiley and Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Lu, G.; Fei, B. Medical hyperspectral imaging: A review. J. Biomed. Opt. 2014, 19, 010901. [Google Scholar] [CrossRef]
- Gallet, J.-C. La Neige du Plateau Antarctique. Surface Spécifique et Applications. Ph.D. Thesis, Université Joseph-Fourier-Grenoble I, Saint-Martin-d’Hères, France, 2010. [Google Scholar]
- ElMasry, G.; Sun, D.-W.; Allen, P. Near-infrared hyperspectral imaging for predicting colour, pH and tenderness of fresh beef. J. Food Eng. 2012, 110, 127–140. [Google Scholar] [CrossRef]
- Lorente, D.; Aleixos, N.; Gómez-Sanchis, J.; Cubero, S.; García-Navarrete, O.L.; Blasco, J. Recent advances and applications of hyperspectral imaging for fruit and vegetable quality assessment. Food Bioprocess Technol. 2012, 5, 1121–1142. [Google Scholar] [CrossRef]
- Haq, M.A.; Ghosh, A.; Rahaman, G.; Baral, P. Artificial neural network-based modeling of snow properties using field data and hyperspectral imagery. Nat. Resour. Model. 2019, 32, e12229. [Google Scholar] [CrossRef]
- Nolin, A.W.; Dozier, J. A hyperspectral method for remotely sensing the grain size of snow. Remote Sens. Environ. 2000, 74, 207–216. [Google Scholar] [CrossRef]
- Negi, H.S.; Singh, S.; Kulkarni, A.; Semwal, B. Field-based spectral reflectance measurements of seasonal snow cover in the Indian Himalaya. Int. J. Remote Sens. 2010, 31, 2393–2417. [Google Scholar] [CrossRef]
- Kulkarni, A.; Srinivasulu, J.; Manjul, S.; Mathur, P. Field based spectral reflectance studies to develop NDSI method for snow cover monitoring. J. Indian Soc. Remote Sens. 2002, 30, 73–80. [Google Scholar] [CrossRef]
- Dozier, J. Spectral signature of alpine snow cover from the Landsat Thematic Mapper. Remote Sens. Environ. 1989, 28, 9–22. [Google Scholar] [CrossRef]
- Warren, S.G.; Wiscombe, W.J. A model for the spectral albedo of snow. II: Snow containing atmospheric aerosols. J. Atmos. Sci. 1980, 37, 2734–2745. [Google Scholar] [CrossRef]
- Eppanapelli, L.K.; Lintzén, N.; Casselgren, J.; Wåhlin, J. Estimation of liquid water content of snow surface by spectral reflectance. J. Cold Reg. Eng. 2018, 32, 05018001. [Google Scholar] [CrossRef]
- Warren, S.G.; Brandt, R.E. Optical constants of ice from the ultraviolet to the microwave: A revised compilation. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Dozier, J.; Painter, T.H. Multispectral and hyperspectral remote sensing of alpine snow properties. Annu. Rev. Earth Planet. Sci. 2004, 32, 465–494. [Google Scholar] [CrossRef]
- Domine, F.; Taillandier, A.S.; Simpson, W.R. A parameterization of the specific surface area of seasonal snow for field use and for models of snowpack evolution. J. Geophys. Res. Earth Surf. 2007, 112. [Google Scholar] [CrossRef]
- Li, H.; Wang, A.; Guan, D.; Jin, C.; Wu, J.; Yuan, F.; Shi, T. Empirical model development for ground snow sublimation beneath a temperate mixed forest in Changbai mountain. J. Hydrol. Eng. 2016, 21, 04016040. [Google Scholar] [CrossRef]
- Bohren, C.F.; Beschta, R.L. Snowpack albedo and snow density. Cold Reg. Sci. Technol. 1979, 1, 47–50. [Google Scholar] [CrossRef]
- El Oufir, M.K.; Chokmani, K.; El Alem, A.; Agili, H.; Bernier, M. Seasonal snowpack classification based on physical properties using near-infrared proximal hyperspectral data. Sensors 2021, 21, 5259. [Google Scholar] [CrossRef]
- Fierz, C.; Armstrong, R.L.; Durand, Y.; Etchevers, P.; Greene, E.; McClung, D.M.; Nishimura, K.; Satyawali, P.K.; Sokratov, S.A. The International Classification for Seasonal Snow on the Ground; UNESCO/IHP: Paris, France, 2009; Volume 25. [Google Scholar]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Wadsworth Statistics/Probability Series; Wadsworth: Monterey, CA, USA, 1984. [Google Scholar]
- Vehtari, A.; Gelman, A.; Gabry, J. Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Stat. Comput. 2017, 27, 1413–1432. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Libois, Q. Evolution des propriétés physiques de neige de surface sur le plateau Antarctique. Observations et Modélisation du Transfert Radiatif et du Métamorphisme. Thèse de Doctorat, Université de Grenoble, Grenoble, France, 2014. [Google Scholar]
- Pahaut, E. Les Cristaux de Neige et Leurs Métamorphoses; Centre d’étude de la neige. St-martin d’hérés: Grenoble, France, 1975. [Google Scholar]
- ElMasry, G.; Sun, D.-w. Principles of hyperspectral imaging technology. In Hyperspectral Imaging for Food Quality Analysis and Control; Elsevier: Amsterdam, The Netherlands, 2010; pp. 3–43. [Google Scholar]
- Ling, F.; Zhang, T. A numerical model for surface energy balance and thermal regime of the active layer and permafrost containing unfrozen water. Cold Reg. Sci. Technol. 2004, 38, 1–15. [Google Scholar] [CrossRef]
- Roy, V.; Goita, K.; Granberg, H.; Royer, A. On the use of reflective hyperspectral remote sensing for the detection of compacted snow. In Proceedings of the Geoscience and Remote Sensing Symposium, 2006—IGARSS 2006, Denver, CO, USA, 31 July–4 August 2006; pp. 3263–3266. [Google Scholar]
- Wilkinson, L. Tests of significance in stepwise regression. Psychol. Bull. 1979, 86, 168. [Google Scholar] [CrossRef]
- Gallet, J.-C.; Domine, F.; Dumont, M. Measuring the specific surface area of wet snow using 1310 nm reflectance. Cryosphere 2014, 8, 1139–1148. [Google Scholar] [CrossRef]




| Snow Class | Grain Size (mm) | Grain Type | Number of Samples | Density (kg m−3) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <100 | 100–150 | 150–200 | 200–250 | 250–300 | 300–350 | 350–400 | 400–450 | 450–500 | >500 | ||||
| WMM | + λ | < 1 mm | 19 | 5 | 6 | 5 | 3 | ||||||
| MHM | □ • | 1–2 mm | 59 | 9 | 6 | 15 | 12 | 12 | 5 | ||||
| VHM | ˄ ᴼ | > 2 mm | 36 | 7 | 10 | 7 | 12 | ||||||
| Snow Class | Specific Estimator |
|---|---|
| WMM | Density = −1035 × SISUB (1265 nm, 941 nm) − 148 |
| MHM | Density = −1377 × SINOR (1617 nm, 941 nm) − 838 |
| HVM | Density = 2357 × SISUB (1424 nm, 1188 nm) + 1002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Oufir, M.K.; Chokmani, K.; El Alem, A.; Bernier, M. Estimating Snowpack Density from Near-Infrared Spectral Reflectance Using a Hybrid Model. Remote Sens. 2021, 13, 4089. https://doi.org/10.3390/rs13204089
El Oufir MK, Chokmani K, El Alem A, Bernier M. Estimating Snowpack Density from Near-Infrared Spectral Reflectance Using a Hybrid Model. Remote Sensing. 2021; 13(20):4089. https://doi.org/10.3390/rs13204089
Chicago/Turabian StyleEl Oufir, Mohamed Karim, Karem Chokmani, Anas El Alem, and Monique Bernier. 2021. "Estimating Snowpack Density from Near-Infrared Spectral Reflectance Using a Hybrid Model" Remote Sensing 13, no. 20: 4089. https://doi.org/10.3390/rs13204089
APA StyleEl Oufir, M. K., Chokmani, K., El Alem, A., & Bernier, M. (2021). Estimating Snowpack Density from Near-Infrared Spectral Reflectance Using a Hybrid Model. Remote Sensing, 13(20), 4089. https://doi.org/10.3390/rs13204089







