A Novel Method to Discriminate Active from Residual Whitecaps Using Particle Image Velocimetry
Abstract
:1. Introduction
2. Materials and Methods
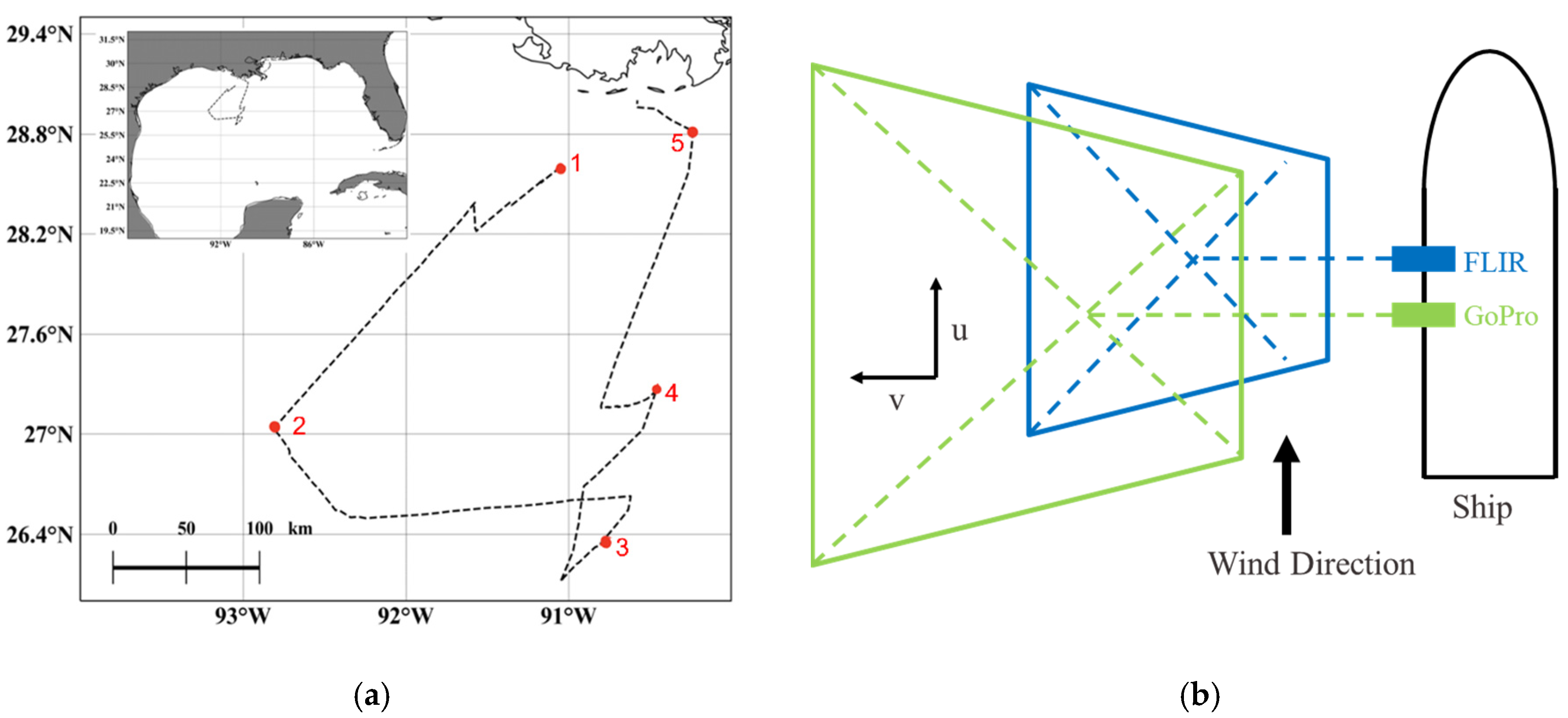
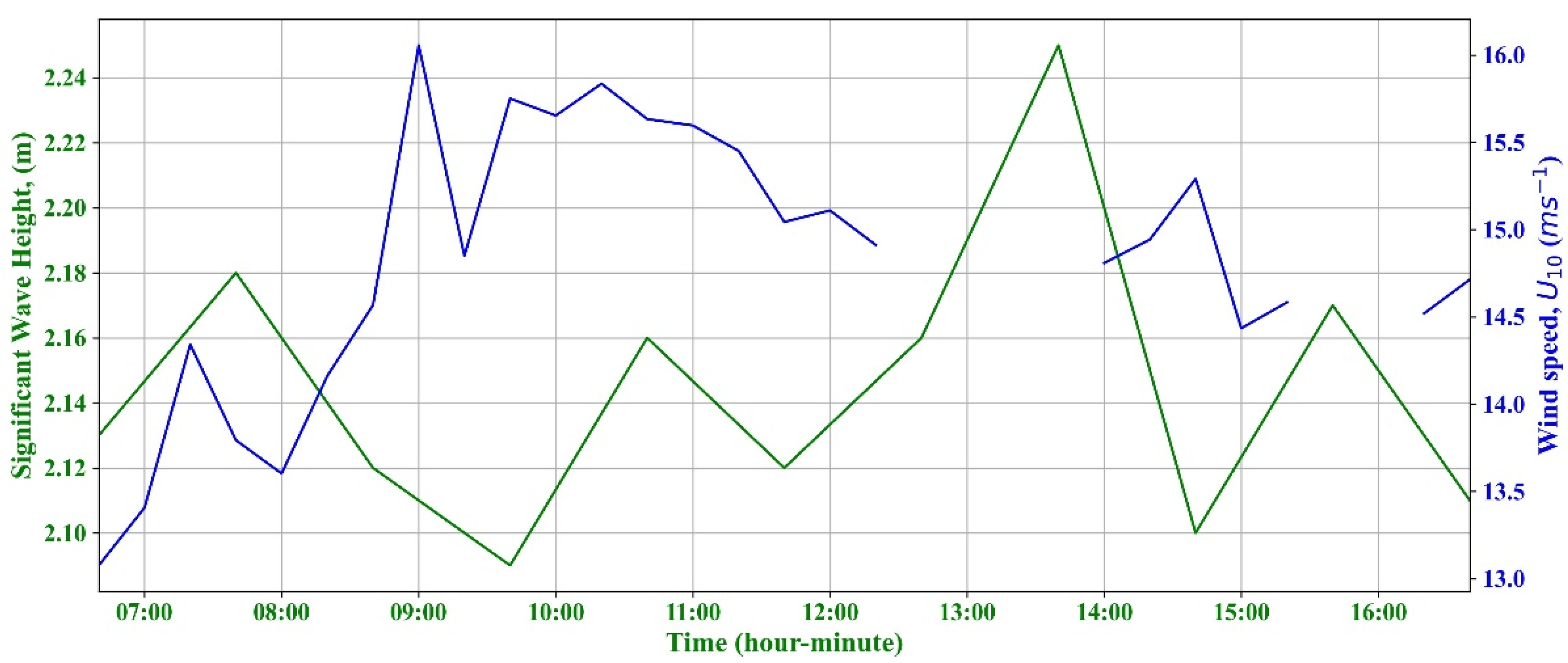
2.1. Instrumentation
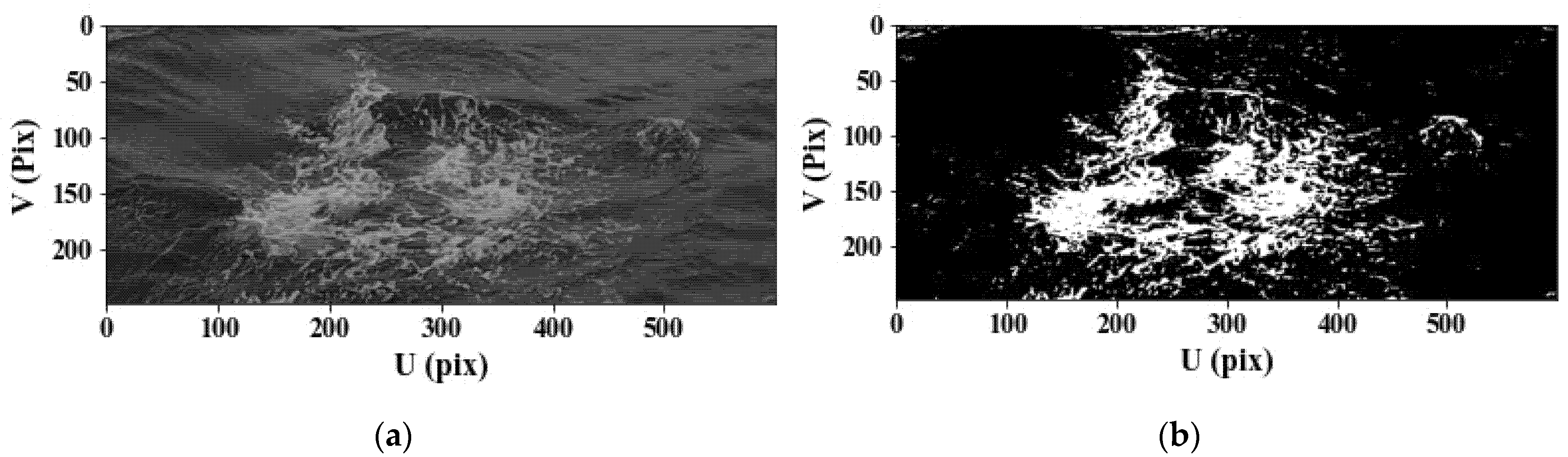
2.2. Image Processing
2.3. PIV Method
3. Results and Discussion
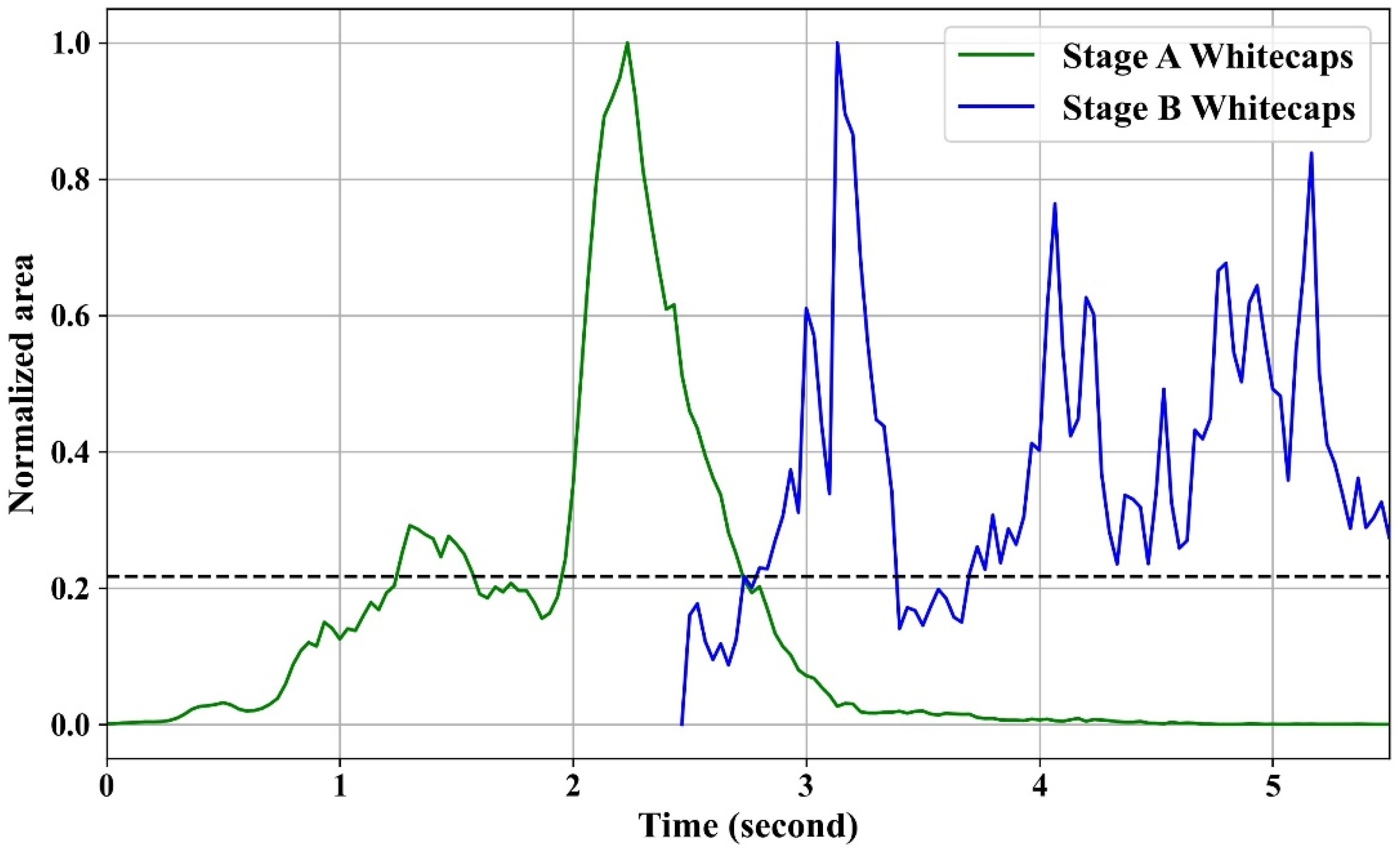
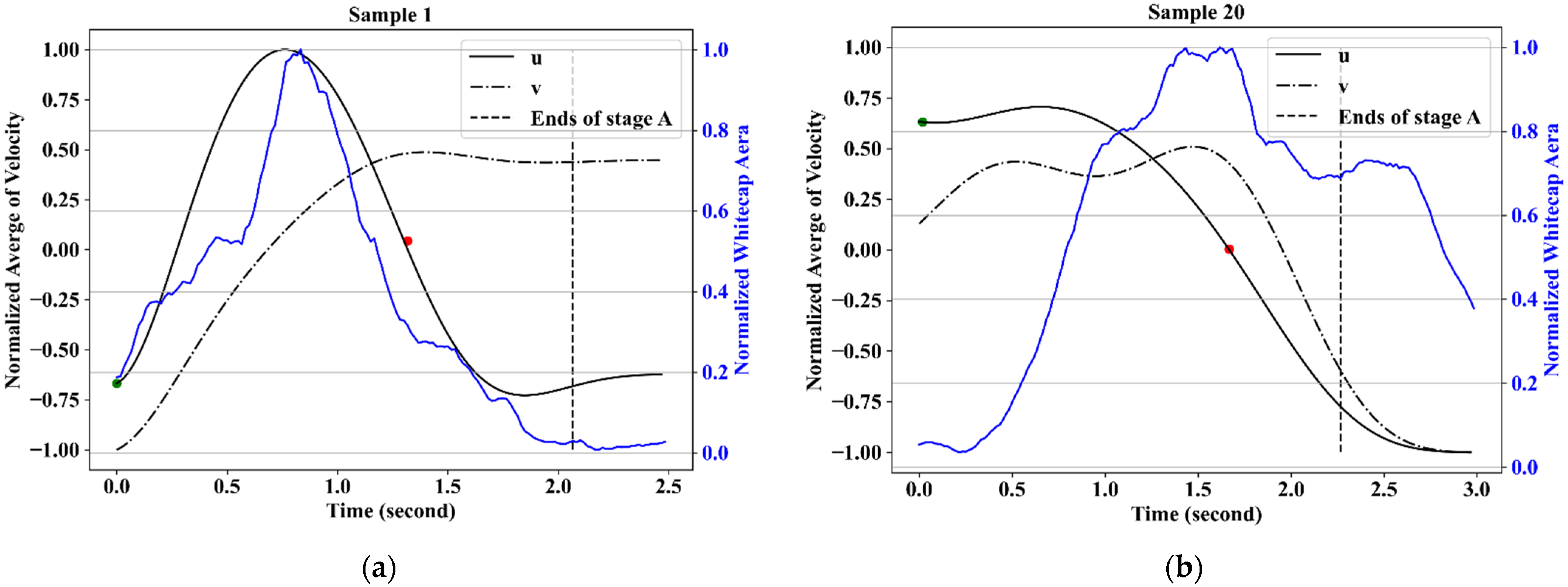
3.1. Signatures of Whitecap Lifetime Stages in PIV Results
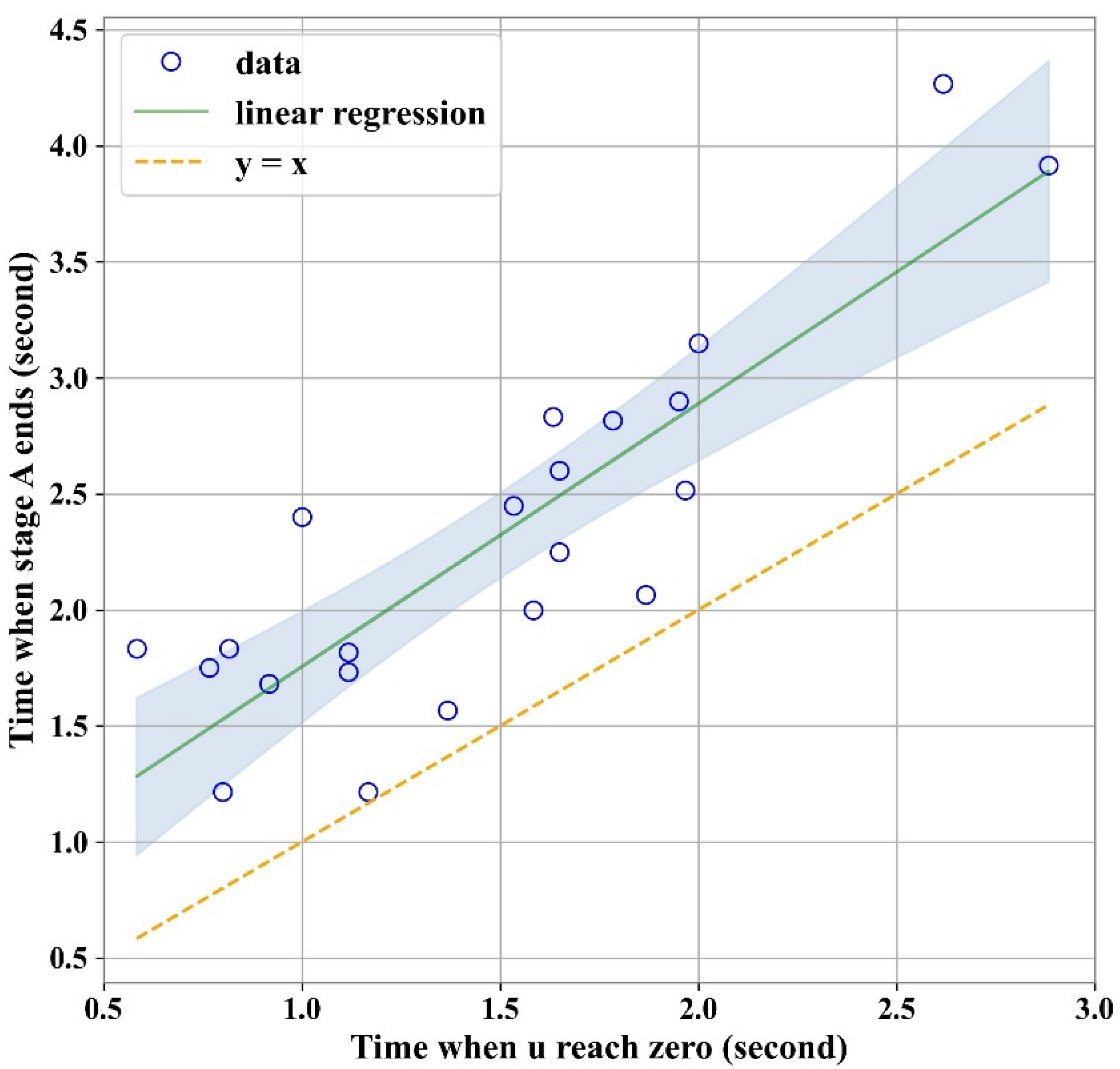
3.2. Linear Regression Model
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Monahan, E.C.; Woolf, D.K. Comments on “Variations of whitecap coverage with wind stress and water temperature”. J. Phys. Oceanogr. 1989, 19, 706–709. [Google Scholar] [CrossRef] [Green Version]
- Monahan, E.C.; Lu, M. Acoustically Relevant Bubble Assemblages and Their Dependence on Meteorological Parameters. IEEE J. Ocean. Eng. 1990, 15, 340–349. [Google Scholar] [CrossRef]
- Padmanabhan, S.; Rose, L.A.; Gaiser, P.W. Effects of foam on ocean surface microwave emission inferred from radiometric observations of reproducible breaking waves. IEEE Trans. Geosci. Remote Sens. 2006, 44, 569–582. [Google Scholar] [CrossRef]
- Andreas, E.L.; Emanuel, K.A. Effects of sea spray on tropical cyclone intensity. J. Atmos. Sci. 2001, 58, 3741–3751. [Google Scholar] [CrossRef] [Green Version]
- Blanchard, D.C. The production, distribution, and bacterial enrichment of the sea-salt aerosol. In Air-Sea Exchange of Gases and Particles; Springer: Dordrecht, The Netherlands, 1983; pp. 407–454. [Google Scholar]
- Lewis, E.R.; Lewis, R.; Lewis, E.R.; Schwartz, S.E. Sea Salt Aerosol Production: Mechanisms, Methods, Measurements, and Models; American Geophysical Union: Washington, DC, USA, 2004; Volume 152, ISBN 0875904173. [Google Scholar]
- Monahan, E.C. Oceanic whitecaps. J. Phys. Oceanogr. 1971, 1, 139–144. [Google Scholar] [CrossRef]
- Brumer, S.E.; Zappa, C.J.; Brooks, I.M.; Tamura, H.; Brown, S.M.; Blomquist, B.W.; Fairall, C.W.; Cifuentes-Lorenzen, A. Whitecap coverage dependence on wind and wave statistics as observed during SO GasEx and HiWinGS. J. Phys. Oceanogr. 2017, 47, 2211–2235. [Google Scholar] [CrossRef]
- Callaghan, A.H.; White, M. Automated processing of sea surface images for the determination of whitecap coverage. J. Atmos. Ocean. Technol. 2009, 26, 383–394. [Google Scholar] [CrossRef]
- Monahan, E.C.; O’Muircheartaigh, I.G. Whitecaps and the passive remote sensing of the ocean surface. Int. J. Remote Sens. 1986, 7, 627–642. [Google Scholar] [CrossRef]
- Wu, J. Variations of whitecap coverage with wind stress and water temperature. J. Phys. Oceanogr. 1988, 18, 1448–1453. [Google Scholar] [CrossRef] [Green Version]
- Xu, D.; Liu, X.; Yu, D. Probability of wave breaking and whitecap coverage in a fetch-limited sea. J. Geophys. Res. Oceans 2000, 105, 14253–14259. [Google Scholar] [CrossRef]
- Asher, W.; Edson, J.; McGillis, W.; Wanninkhof, R.; Ho, D.T.; Litchendorf, T. Fractional area whitecap coverage and air-sea gas transfer velocities measured during GasEx-98. Geophys. Monogr. Ser. 2001, 127, 199–203. [Google Scholar] [CrossRef]
- Anguelova, M.D.; Webster, F. Whitecap coverage from satellite measurements: A first step toward modeling the variability of oceanic whitecaps. J. Geophys. Res. Oceans 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Lafon, C.; Piazzola, J.; Forget, P.; Despiau, S. Whitecap coverage in coastal environment for steady and unsteady wave field conditions. J. Mar. Syst. 2007, 66, 38–46. [Google Scholar] [CrossRef]
- Salisbury, D.J.; Anguelova, M.D.; Brooks, I.M. On the variability of whitecap fraction using satellite-based observations. J. Geophys. Res. Oceans 2013, 118, 6201–6222. [Google Scholar] [CrossRef] [Green Version]
- Scanlon, B.; Ward, B. Oceanic wave breaking coverage separation techniques for active and maturing whitecaps. Methods Oceanogr. 2013, 8, 1–12. [Google Scholar] [CrossRef]
- Hanson, J.L.; Phillips, O.M. Wind sea growth and dissipation in the open ocean. J. Phys. Oceanogr. 1999, 29, 1633–1648. [Google Scholar] [CrossRef]
- Mironov, A.S.; Dulov, V.A. Detection of wave breaking using sea surface video records. Meas. Sci. Technol. 2008, 19, 015405. [Google Scholar] [CrossRef]
- Kleiss, J.M. Airborne Observations of the Kinematics and Statistics of Breaking Waves. Ph.D. Thesis, UC San Diego, San Diego, CA, USA, 2009. [Google Scholar]
- Kleiss, J.M.; Melville, W.K. Observations of wave breaking kinematics in fetch-limited seas. J. Phys. Oceanogr. 2010, 40, 2575–2604. [Google Scholar] [CrossRef]
- Anguelova, M.D.; Hwang, P.A. Using energy dissipation rate to obtain active whitecap fraction. J. Phys. Oceanogr. 2016, 46, 461–481. [Google Scholar] [CrossRef]
- Anguelova, M.D.; Gaiser, P.W.; Raizer, V. Foam emissivity models for microwave observations of oceans from space. Int. Geosci. Remote Sens. Symp. 2009, 2, 274–277. [Google Scholar] [CrossRef]
- Anguelova, M.D.; Gaiser, P.W. Skin depth at microwave frequencies of sea foam layers with vertical profile of void fraction. J. Geophys. Res. Oceans 2011, 116, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Potter, H.; Smith, G.B.; Snow, C.M.; Dowgiallo, D.J.; Bobak, J.P.; Anguelova, M.D. Whitecap lifetime stages from infrared imagery with implications for microwave radiometric measurements of whitecap fraction. J. Geophys. Res. Oceans 2015, 120, 7521–7537. [Google Scholar] [CrossRef]
- Jessup, A.T.; Zappa, C.J.; Loewen, M.R.; Hesany, V. Infrared remote sensing of breaking waves. Nature 1997, 385, 52–55. [Google Scholar] [CrossRef]
- Marmorino, G.O.; Smith, G.B. Bright and dark ocean whitecaps observed in the infrared. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Russmeier, N.; Hahn, A.; Zielinski, O. Ocean surface water currents by large-scale particle image velocimetry technique. In Proceedings of the OCEANS 2017—Aberdeen, Aberdeen, UK, 19–22 June 2017; pp. 1–10. [Google Scholar] [CrossRef]
- Melville, W.K.; Matusov, P. Distribution of breaking waves at the ocean surface. Nature 2002, 417, 58–63. [Google Scholar] [CrossRef]
- Bakhoday-Paskyabi, M.; Reuder, J.; Flügge, M. Automated measurements of whitecaps on the ocean surface from a buoy-mounted camera. Methods Oceanogr. 2016, 17, 14–31. [Google Scholar] [CrossRef]
- Zack, G.W.; Rogers, W.E.; Latt, S.A. Automatic measurement of sister chromatid exchange frequency. J. Histochem. Cytochem. 1977, 25, 741–753. [Google Scholar] [CrossRef] [PubMed]
- Westerweel, J. Fundamentals of digital particle image velocimetry. Meas. Sci. Technol. 1997, 8, 1379–1392. [Google Scholar] [CrossRef] [Green Version]
- Fujita, I.; Muste, M.; Kruger, A. Large-scale particle image velocimetry for flow analysis in hydraulic engineering applications. J. Hydraul. Res. 1998, 36, 397–414. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Kinzel, P.J.; Nelson, J.M. Remote measurement of river discharge using thermal particle image velocimetry (PIV) and various sources of bathymetric information. J. Hydrol. 2017, 554, 490–506. [Google Scholar] [CrossRef]
- Jessup, A.T.; Phadnis, K.R. Measurement of the geometric and kinematic properties of microscale breaking waves from infrared imagery using a PIV algorithm. Meas. Sci. Technol. 2005, 16, 1961–1969. [Google Scholar] [CrossRef]
- Techet, A.H.; McDonald, A.K. High Speed PIV of Breaking Waves on Both Sides of the Air-Water Interface. In Proceedings of the 6th International Symposium on Particle Image Velocimetry, Pasadena, CA, USA, 21–23 September 2005; pp. 1–14. [Google Scholar]
- Siddiqui, M.H.K.; Loewen, M.R.; Richardson, C.; Asher, W.E.; Jessup, A.T. Simultaneous particle image velocimetry and infrared imagery of microscale breaking waves. Phys. Fluids 2001, 13, 1891–1903. [Google Scholar] [CrossRef]
- Grant, I. Particle image velocimetry: A review. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1997, 211, 55–76. [Google Scholar] [CrossRef]
- Thielicke, W.; Stamhuis, E.J. PIVlab-time-resolved digital particle image velocimetry tool for MATLAB. Publ. BSD Licens. Program. MATLAB 2014, 7, R14. [Google Scholar]
- Callaghan, A.H.; Deane, G.B.; Stokes, M.D.; Ward, B. Observed variation in the decay time of oceanic whitecap foam. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Callaghan, A.H.; Deane, G.B.; Stokes, M.D. Two regimes of laboratory whitecap foam decay: Bubble-plume controlled and surfactant stabilized. J. Phys. Oceanogr. 2013, 43, 1114–1126. [Google Scholar] [CrossRef]
- Callaghan, A.H.; Deane, G.B.; Stokes, M.D. Laboratory air-entraining breaking waves: Imaging visible foam signatures to estimate energy dissipation. Geophys. Res. Lett. 2016, 43, 11320–11328. [Google Scholar] [CrossRef]
- Masnadi, N.; Chickadel, C.C.; Jessup, A.T. On the Thermal Signature of the Residual Foam in Breaking Waves. J. Geophys. Res. Oceans 2021, 126, e2020JC016511. [Google Scholar] [CrossRef]


| Lifetime of Active Whitecaps (s) | Number |
|---|---|
| 1–2 | 10 |
| 2–3 | 9 |
| >3 | 3 |
| Coefficient | 95% CI 1 | t | p | |
|---|---|---|---|---|
| Intercept | 0.621 | [0.118 1.125] | 2.575 | 0.018 |
| slope | 1.134 | [0.819 1.448] | 7.515 | 0.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Potter, H. A Novel Method to Discriminate Active from Residual Whitecaps Using Particle Image Velocimetry. Remote Sens. 2021, 13, 4051. https://doi.org/10.3390/rs13204051
Yang X, Potter H. A Novel Method to Discriminate Active from Residual Whitecaps Using Particle Image Velocimetry. Remote Sensing. 2021; 13(20):4051. https://doi.org/10.3390/rs13204051
Chicago/Turabian StyleYang, Xin, and Henry Potter. 2021. "A Novel Method to Discriminate Active from Residual Whitecaps Using Particle Image Velocimetry" Remote Sensing 13, no. 20: 4051. https://doi.org/10.3390/rs13204051
APA StyleYang, X., & Potter, H. (2021). A Novel Method to Discriminate Active from Residual Whitecaps Using Particle Image Velocimetry. Remote Sensing, 13(20), 4051. https://doi.org/10.3390/rs13204051






