Using Microwave Profile Radar to Estimate Forest Canopy Leaf Area Index: Linking 3D Radiative Transfer Model and Forest Gap Model
Abstract
1. Introduction
2. Material and Methods
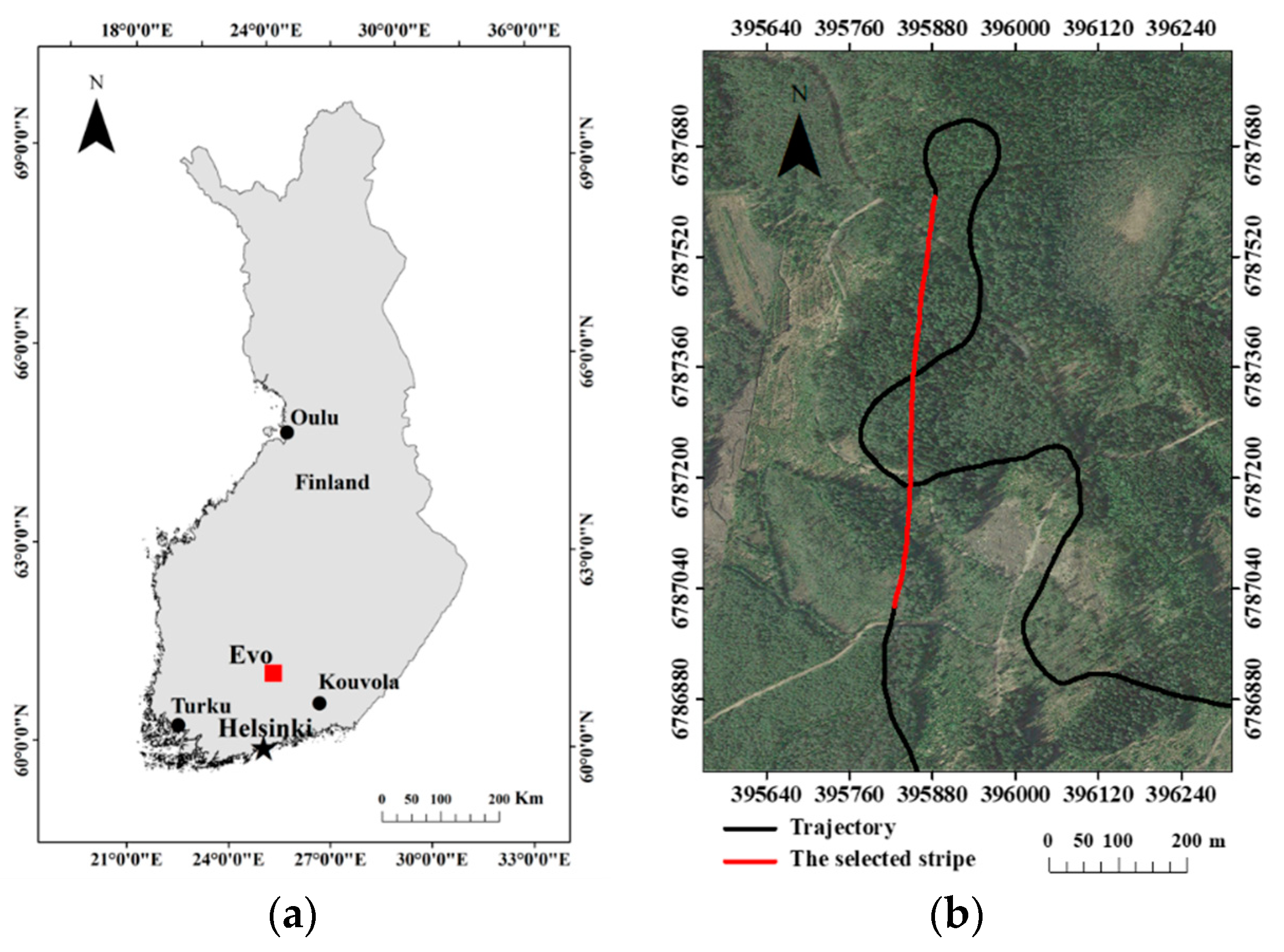
2.1. Study Site and Data Collection
2.2. Tomoradar Data
2.3. Lidar Data
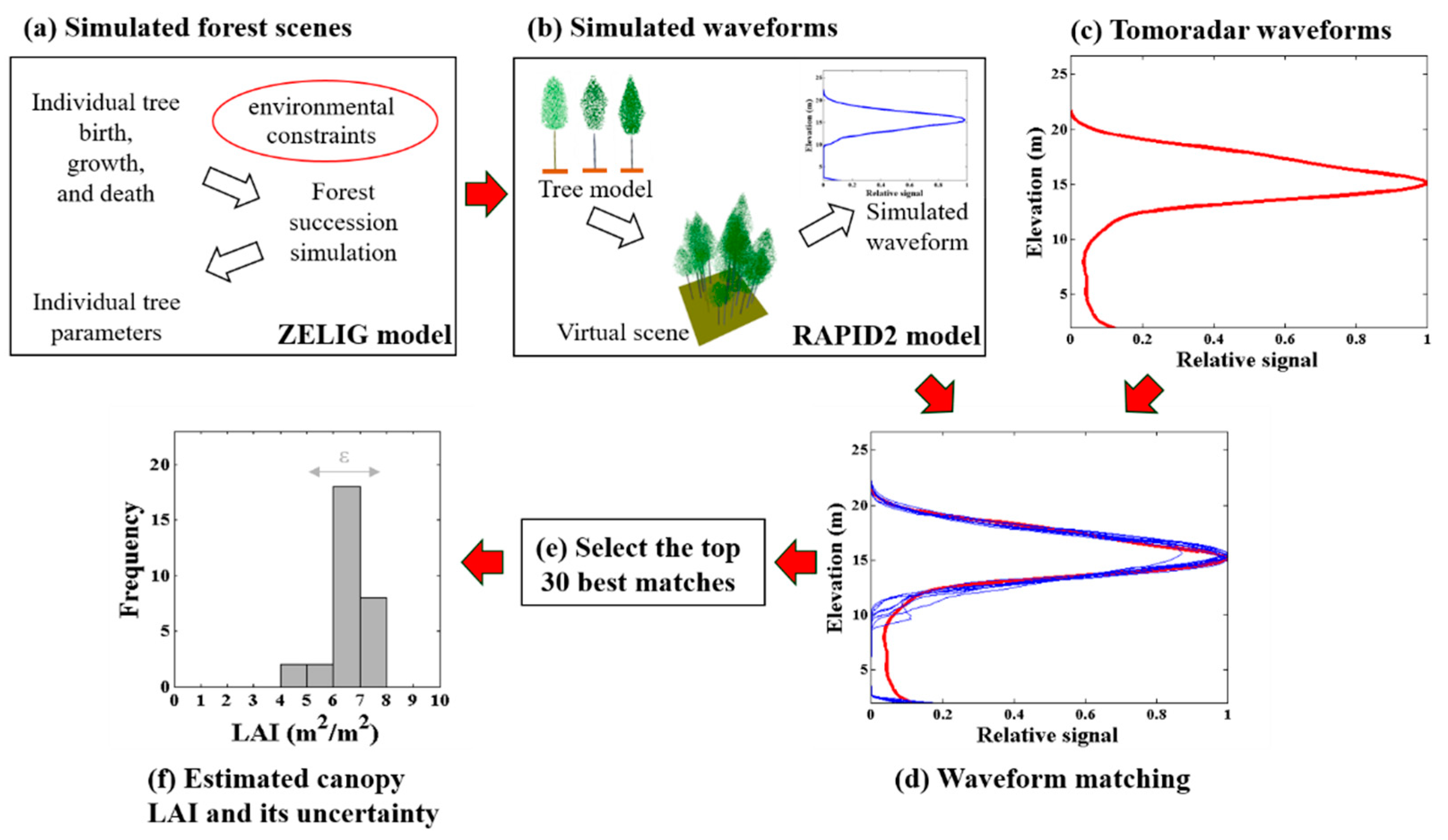
2.4. Forest Canopy LAI Estimation by Waveform Matching
2.4.1. Forest Gap Model and Forest Succession Simulation
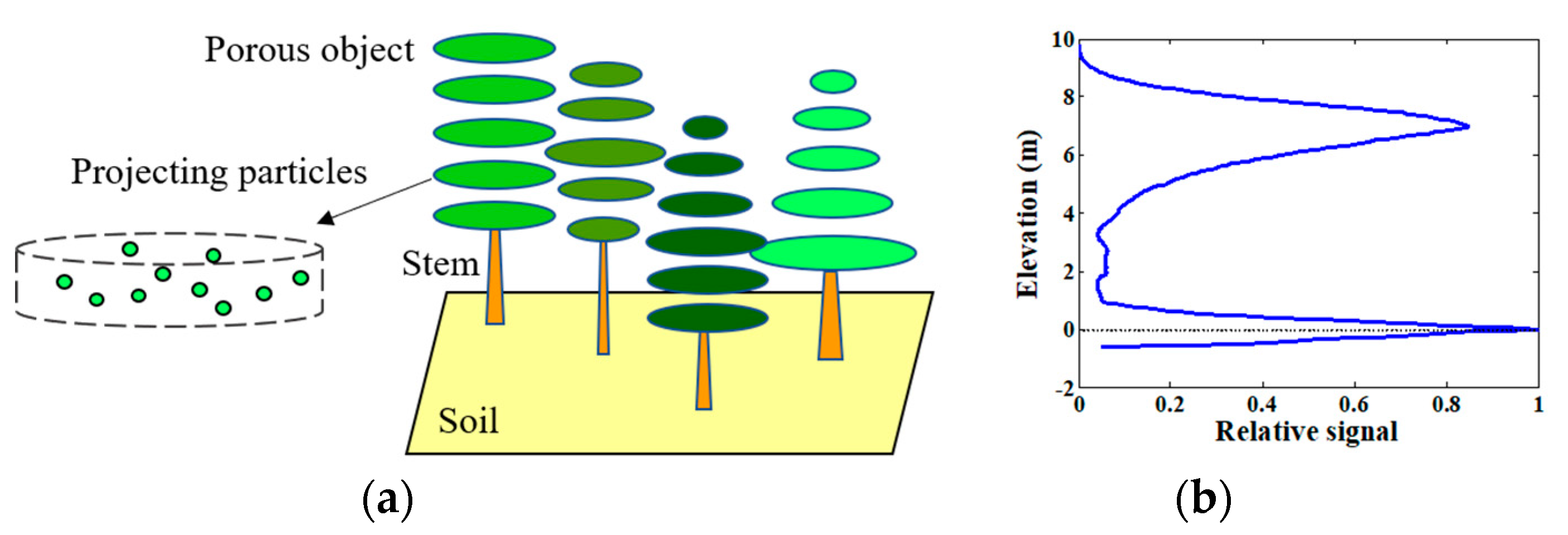
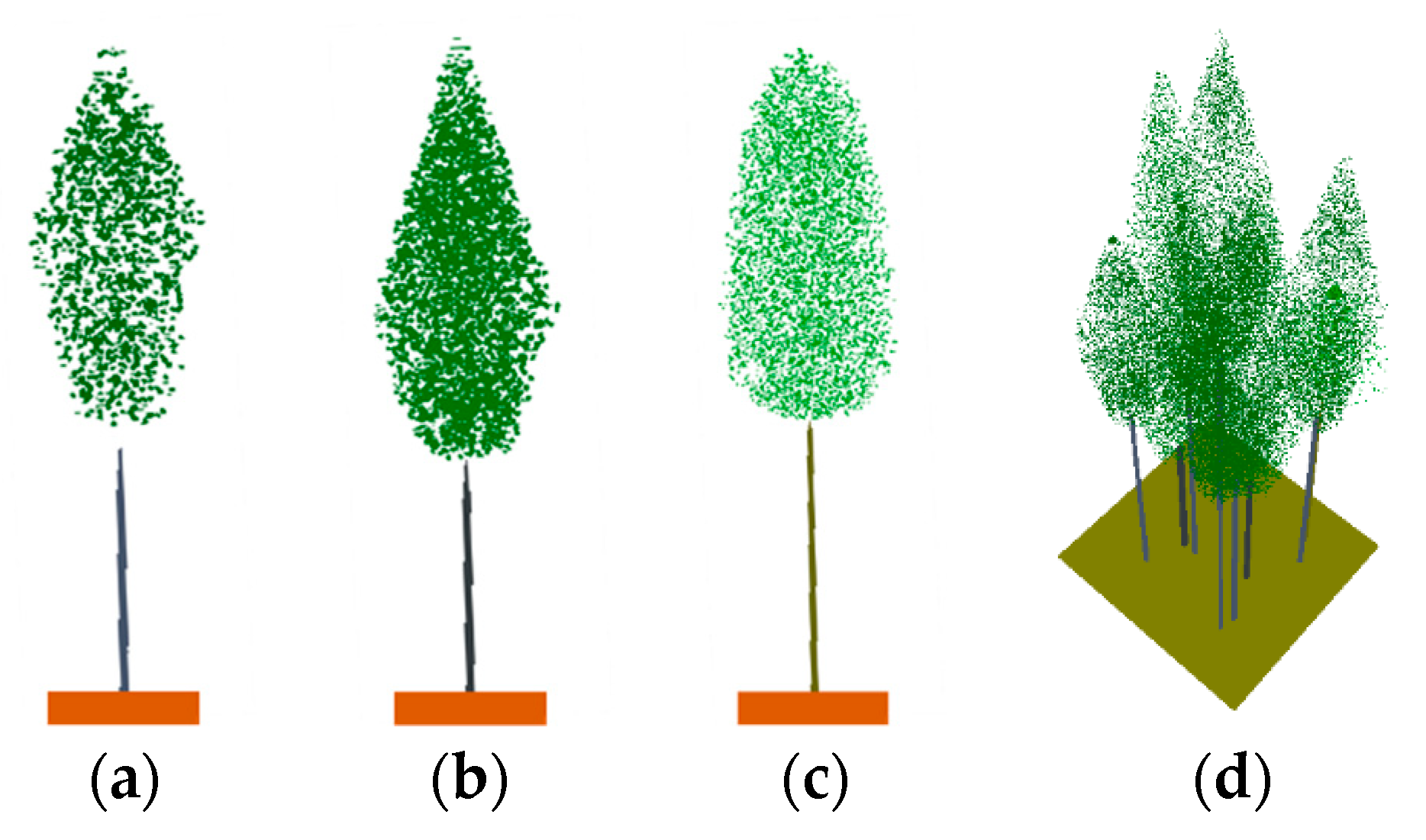
2.4.2. RAPID2 Model and Waveform Simulation
2.4.3. Waveform Matching and Canopy LAI Estimation
3. Results
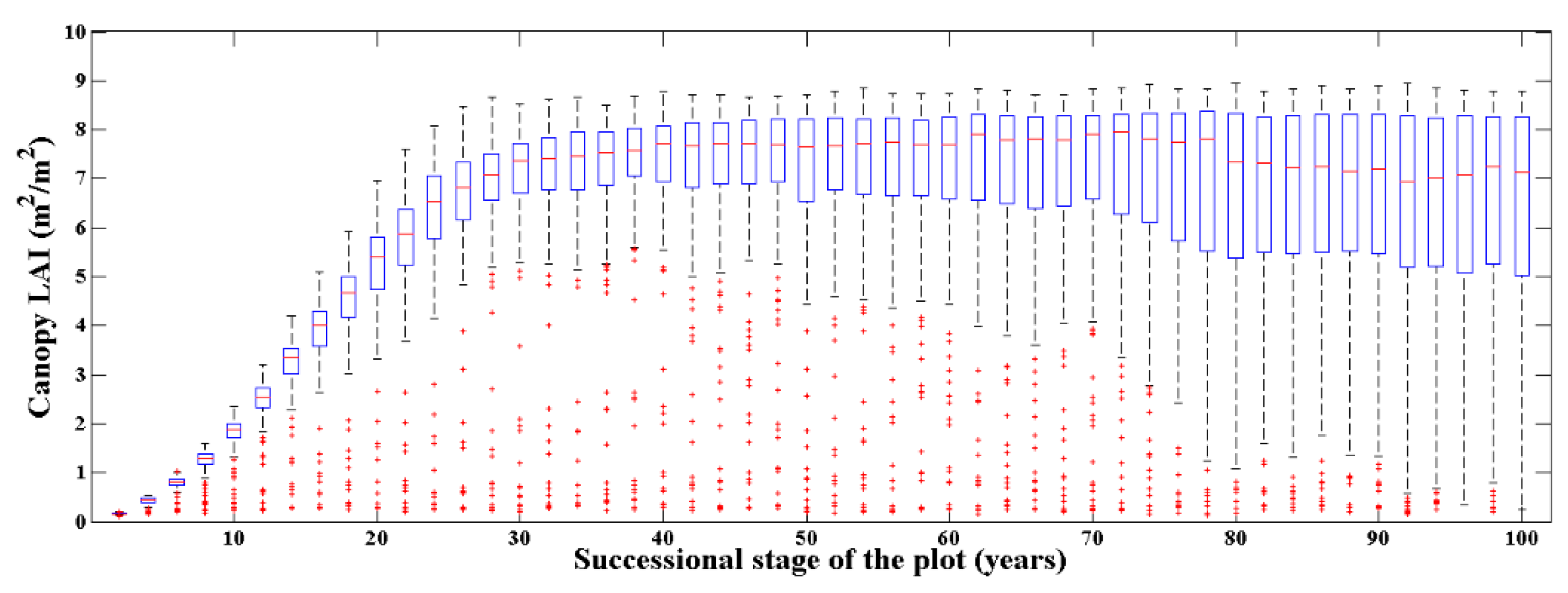
3.1. Forest Scenes Simulation
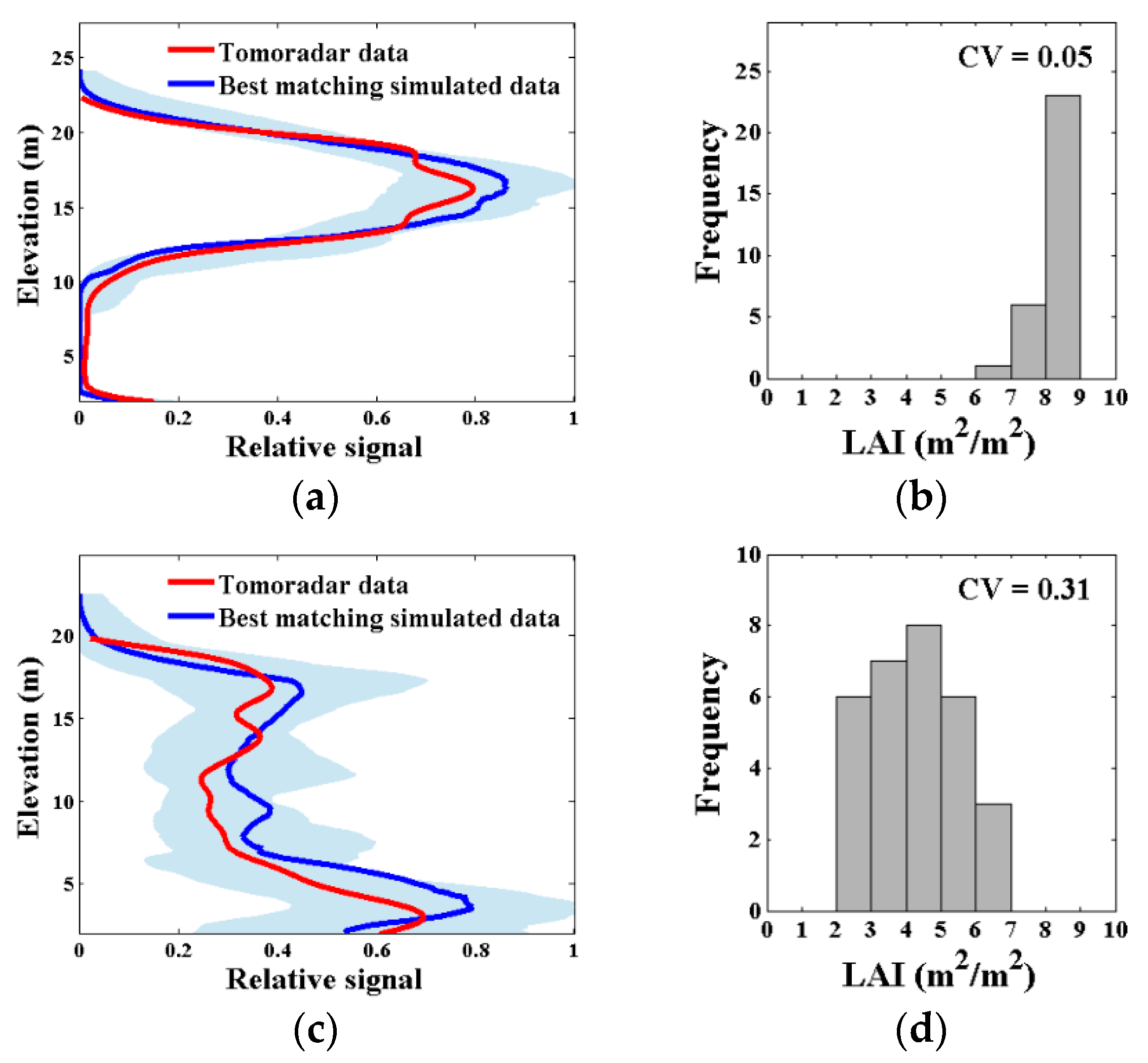
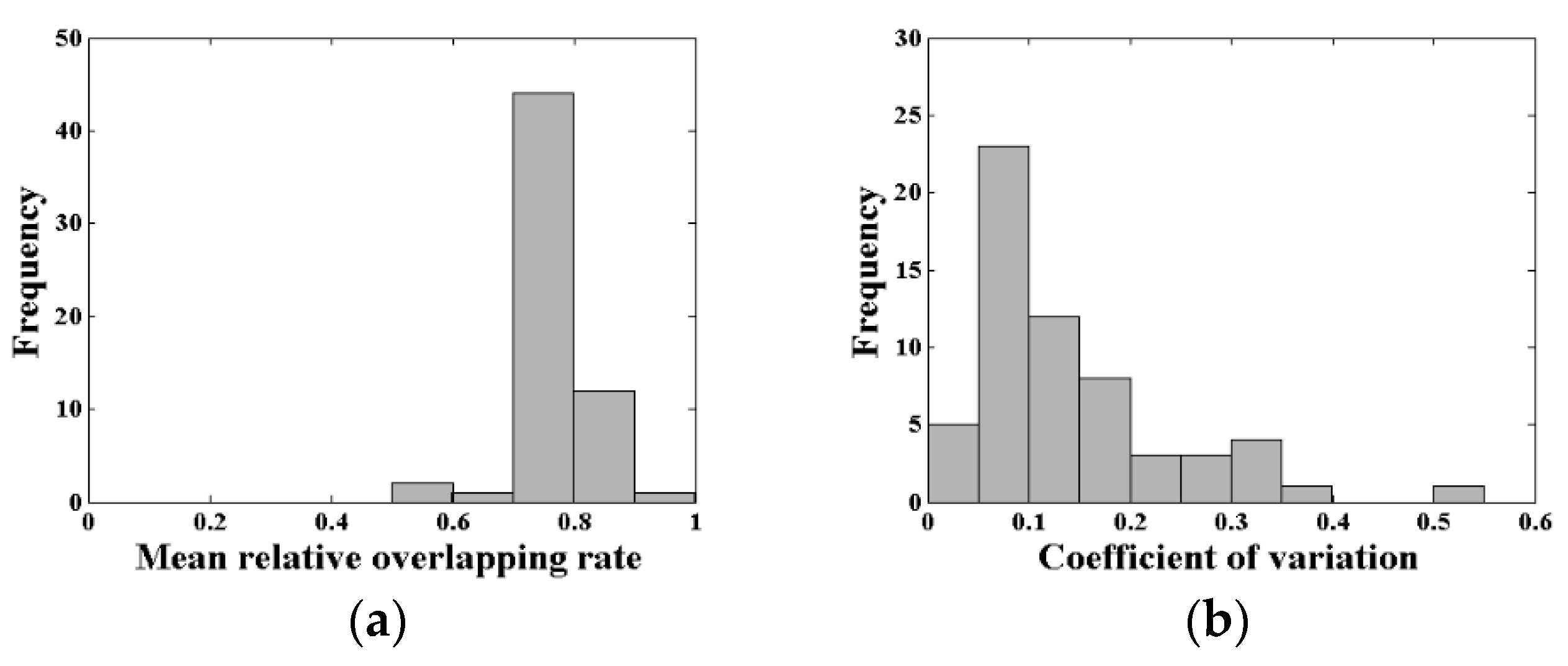
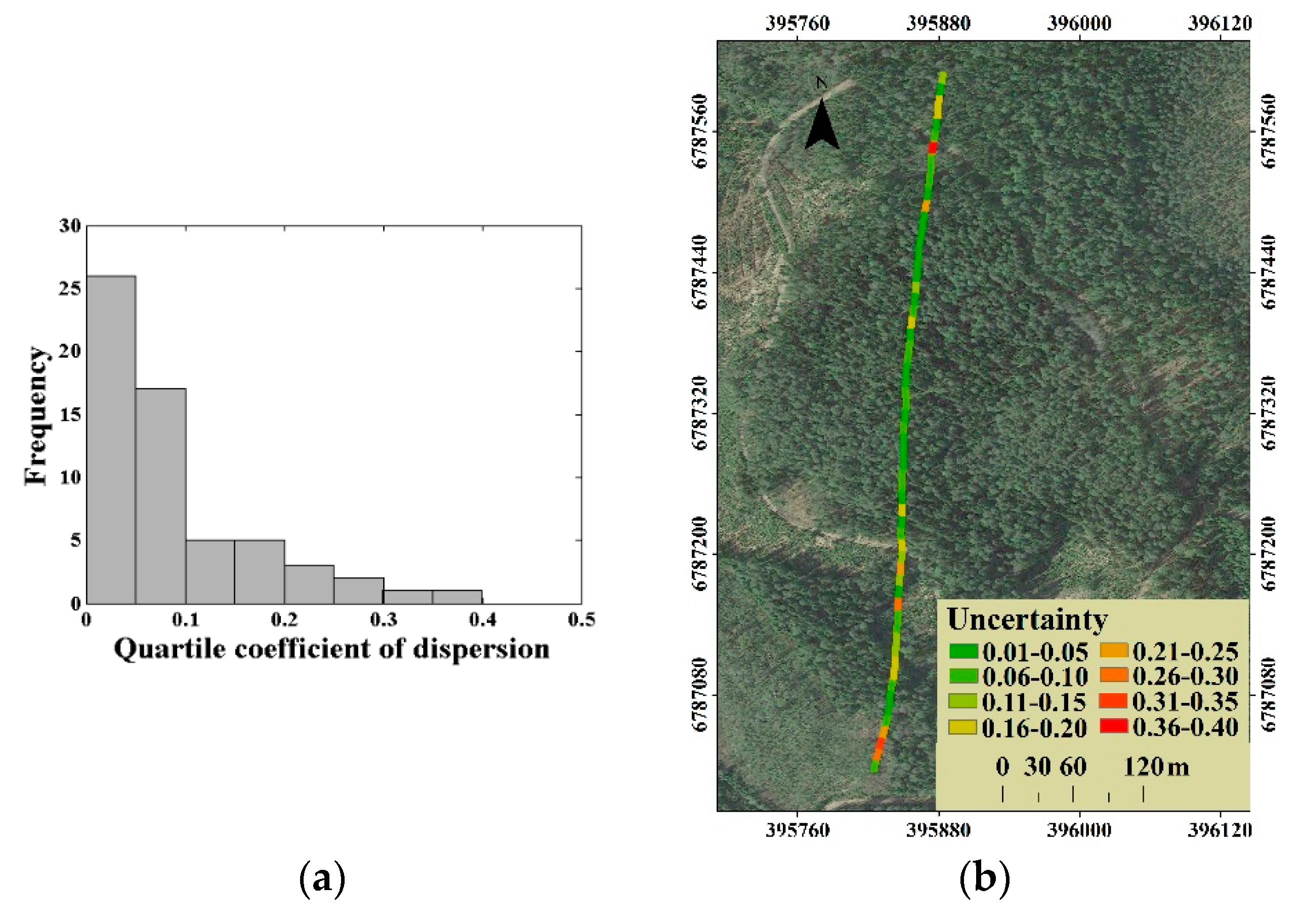
3.2. The Relative Overlapping Rate and Uncertainty
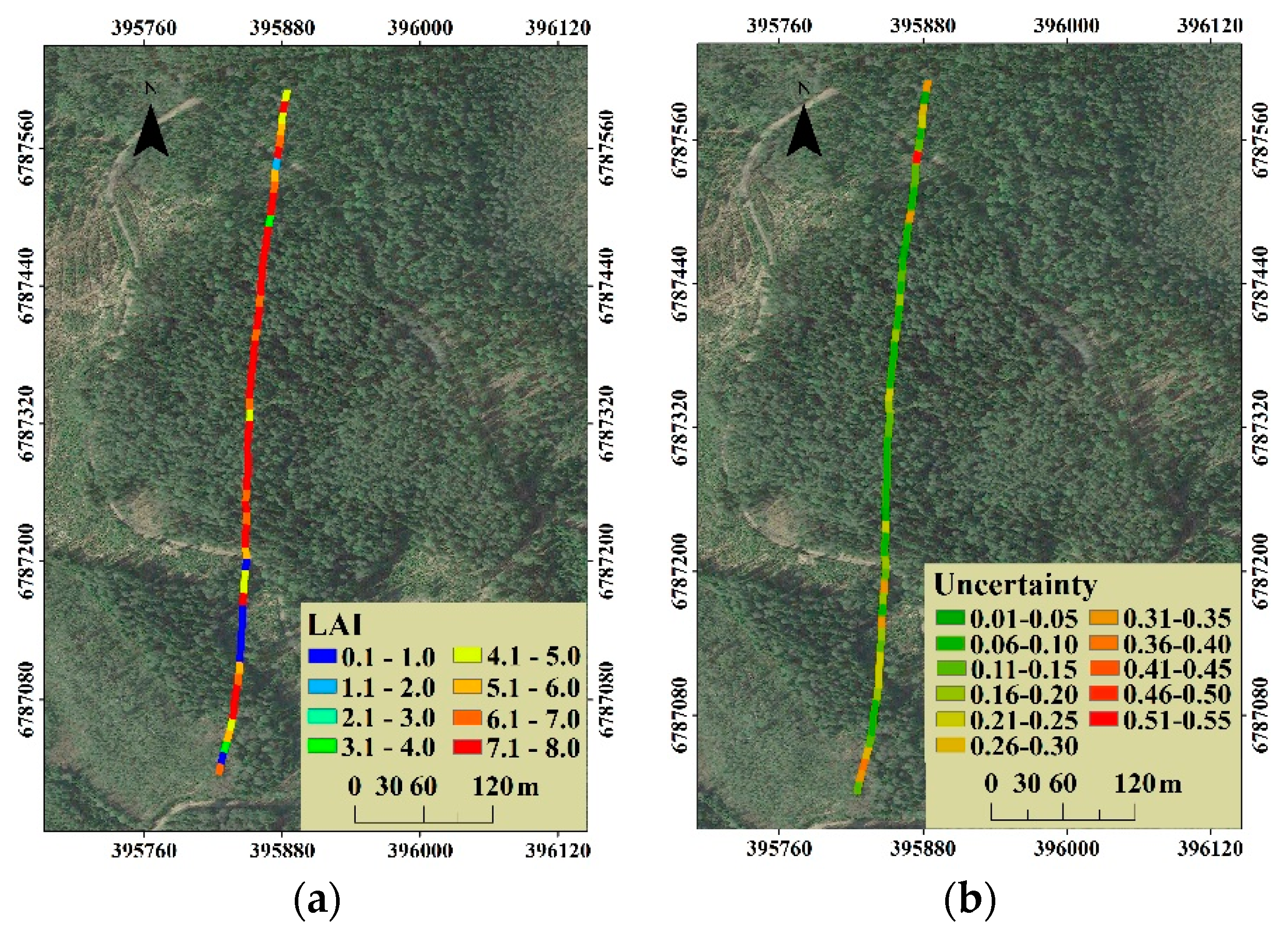
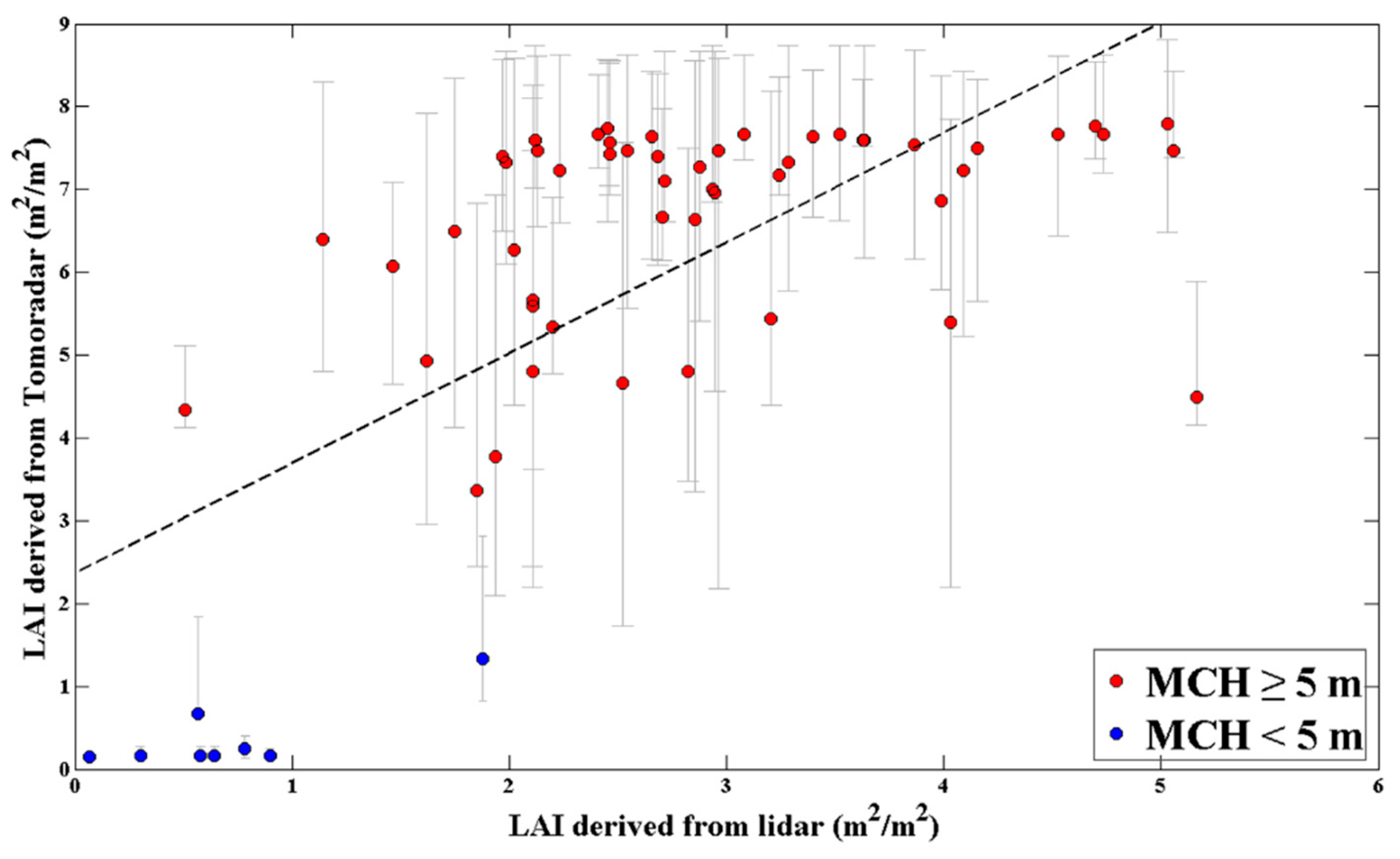
3.3. Canopy LAI Estimation
4. Discussion
4.1. Uncertainty of the Canopy LAI Estimation
4.2. Comparison of Accuracy in Canopy LAI Estimation
4.3. Advantage of the Approach
4.4. Limitation of the Approach
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.M.; Black, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. Retrieving leaf area index of boreal conifer forests using Landsat TM images. Remote Sens. Environ. 1996, 55, 153–162. [Google Scholar] [CrossRef]
- Gordon, B. Importance of leaf area index and forest type when estimating photosynthesis in boreal forests. Remote Sens. Environ. 1993, 43, 303–314. [Google Scholar]
- Tian, Y.; Dickinson, R.E.; Zhou, L.; Myneni, R.B.; Friedl, M.; Schaaf, C.B.; Carroll, M.; Gao, F. Land boundary conditions from MODIS data and consequences for the albedo of a climate model. Geophys. Res. Lett. 2004, 31, 179–211. [Google Scholar] [CrossRef]
- Jin, M.L.; Shepherd, J.M.; Peters-Lidard, C. Development of a parameterization for simulating the urban temperature hazard using satellite observations in climate model. Nat. Hazards 2007, 43, 257–271. [Google Scholar] [CrossRef]
- Xiao, Z.Q.; Liang, S.L.; Wang, J.D.; Chen, P.; Yin, X.; Zhang, L.; Song, J.L. Use of General Regression Neural Networks for Generating the GLASS Leaf Area Index Product from Time Series MODIS Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Fassnacht, K.S.; Gower, S.T.; Mackenzie, M.D.; Nordheim, E.V.; Lillesand, T.M. Estimating the leaf area index of North Central Wisconsin forests using the landsat thematic mapper. Remote Sens. Environ. 1997, 61, 229–245. [Google Scholar] [CrossRef]
- Gonsamo, A.; Chen, J.M. Continuous observation of leaf area index at Fluxnet-Canada sites. Agric. For. Meteorol. 2014, 189–190, 168–174. [Google Scholar] [CrossRef]
- Fernandes, R.; Butson, C.; Leblanc, S.; Latifovic, R. Landsat-5 TM and Landsat-7 ETM+ based accuracy assessment of leaf area index products for Canada derived from SPOT-4 VEGETATION data. Can. J. Remote Sens. 2014, 29, 241–258. [Google Scholar] [CrossRef]
- Solberg, S.; Brunner, A.; Hanssen, K.H.; Lange, H.; Naesset, E.; Rautiainen, M.; Stenberg, P. Mapping LAI in a Norway spruce forest using airborne laser scanning. Remote Sens. Environ. 2009, 113, 2317–2327. [Google Scholar] [CrossRef]
- Peduzzi, A.; Wynne, R.H.; Fox, T.R.; Nelson, R.F.; Thomas, V.A. Estimating leaf area index in intensively managed pine plantations using airborne laser scanner data. For. Ecol. Manag. 2012, 270, 54–65. [Google Scholar] [CrossRef]
- Moeser, D.; Roubinek, J.; Schleppi, P.; Morsdorf, F.; Jonas, T. Canopy closure, LAI and radiation transfer from airborne LiDAR synthetic images. Agric. For. Meteorol. 2014, 197, 158–168. [Google Scholar] [CrossRef]
- Hirosawa, H.; Matsuzaka, Y.; Kobayashi, O. Measurement of microwave backscatter from a cypress with and without leaves. IEEE Trans. Geosci. Remote Sens. 1989, 27, 698–701. [Google Scholar] [CrossRef]
- Manninen, T.; Stenberg, P.; Rautiainen, M.; Voipio, P.; Smolander, H. Leaf area index estimation of boreal forest using ENVISAT ASAR. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2627–2635. [Google Scholar] [CrossRef]
- Manninen, T.; Stenberg, P.; Rautiainen, M.; Voipio, P. Leaf Area Index Estimation of Boreal and Subarctic Forests Using VV/HH ENVISAT/ASAR Data of Various Swaths. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3899–3909. [Google Scholar] [CrossRef]
- Tanase, M.A.; Villard, L.; Pitar, D.; Apostol, B.; Petrila, M.; Chivulescu, S.; Leca, S.; Borlaf-Mena, I.; Pascu, I.; Dobre, A. Synthetic aperture radar sensitivity to forest changes: A simulations-based study for the Romanian forests. Sci. Total Environ. 2019, 689, 1104–1114. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Hakala, T.; Karjalainen, M.; Feng, Z.; Tang, J.; Litkey, P.; Kukko, A.; Jaakkola, A.; Hyyppa, J. UAV-Borne Profiling Radar for Forest Research. Remote Sens. 2017, 9, 58. [Google Scholar] [CrossRef]
- Hallikainen, M.; Hyyppä, J.; Haapanen, J.; Tares, T.; Ahola, P.; Pulliainen, J.; Toikka, M. A Helicopter-Borne Eight-Channel Ranging Scatterometer for Remote Sensing: Part I: System Description. IEEE Trans. Geosci. Remote Sens. 1993, 31, 161–169. [Google Scholar] [CrossRef]
- Hyyppa, J.; Hallikainen, M. Applicability of Airborne Profiling Radar to Forest Inventory. Remote Sens. Environ. 1996, 57, 39–57. [Google Scholar] [CrossRef]
- Hyyppa, J.; Pulliainen, J.; Hallikainen, M.; Saatsi, A. Radar-derived standwise forest inventory. IEEE Trans. Geosci. Remote Sens. 1997, 35, 392–404. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, Y.; Feng, Z.; Li, F.; Hyyppa, J.; Hakala, T.; Karjalainen, M.; Jiang, C.; Pei, L. The Comparison of Canopy Height Profiles Extracted from Ku-band Profile Radar Waveforms and LiDAR Data. Remote Sens. 2018, 10, 701. [Google Scholar] [CrossRef]
- Du, K.; Huang, H.; Zhu, Y.; Feng, Z.; Hakala, T.; Chen, Y.; Hyyppa, J. Simulation of Ku-Band Profile Radar Waveform by Extending Radiosity Applicable to Porous Individual Objects (RAPID2) Model. Remote Sens. 2020, 12, 684. [Google Scholar] [CrossRef]
- Monsi, M.; Saeki, T. On the Factor Light in Plant Communities and its Importance for Matter Production. Ann. Bot. 2005, 95, 549–567. [Google Scholar] [CrossRef]
- Zhu, Y. Study on Microwave Signal Penetration in Finland Boreal Forest Based on Airborne Profiling Radar. Master’s Thesis, Beijing Forestry University, Beijing, China, 2018. [Google Scholar]
- Rödig, E.; Knapp, N.; Fischer, R.; Bohn, F.J.; Dubayah, R.; Tang, H.; Huth, A. From small-scale forest structure to Amazon-wide carbon estimates. Nat. Commun. 2019, 10, 5088. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Huug, V. A global monthly land surface air temperature analysis for 1948-present. J. Geophys. Res. 2008, 113, D1103. [Google Scholar] [CrossRef]
- Xie, P.; Arkin, P.A. Global Precipitation: A 17-Year Monthly Analysis Based on Gauge Observations, Satellite Estimates, and Numerical Model Outputs. Bull. Am. Meteorol. Soc. 1997, 78, 2539–2558. [Google Scholar] [CrossRef]
- Feng, Z.; Chen, Y.; Hyyppa, J.; Hakala, T.; Zhou, H.; Wang, Y.; Karjalainen, M. Estimating Ground Level and Canopy Top Elevation with Airborne Microwave Profiling Radar. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2283–2294. [Google Scholar] [CrossRef]
- Urban, D.L.; Bonan, G.B.; Smith, T.M.; Shugart, H.H. Spatial applications of gap models. For. Ecol. Manag. 1991, 42, 95–110. [Google Scholar] [CrossRef]
- Shugart, H.H. A theory of forest dynamics. Springer, New York. Soil Sci. Soc. Am. J. 1984, 64, 681–689. [Google Scholar]
- Botkin, D.B.; Janak, J.F.; Wallis, J.R. Some Ecological Consequences of a Computer Model of Forest Growth. J. Ecol. 1972, 60, 849–872. [Google Scholar] [CrossRef]
- Yang, H.; Liu, D.; Sun, G.; Guo, Z.; Zhang, Z. Simulation of Interferometric SAR Response for Characterizing Forest Successional Dynamics. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1529–1533. [Google Scholar] [CrossRef]
- Wang, Q.; Pang, Y.; Li, Z.; Sun, G.; Chen, E.; Ni-Meister, W. The Potential of Forest Biomass Inversion Based on Vegetation Indices Using Multi-Angle CHRIS/PROBA Data. Remote Sens. 2016, 8, 891. [Google Scholar] [CrossRef]
- Wang, X.Y.; Qin, W.H.; Sun, G.Q.; Zhu, J. Estimation of forest LAI by inverting canopy reflectance models and multi-angle imagery. Geocarto Int. 2019, 34, 959–976. [Google Scholar] [CrossRef]
- Larocque, G.R.; Archambault, L.; Delisle, C. Modelling forest succession in two southeastern Canadian mixedwood ecosystem types using the ZELIG model. Ecol. Model. 2006, 199, 350–362. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, Z.; Ni, W.; Chai, L.; Qin, W.; Liu, G.; Xie, D.; Jiang, L.; Liu, Q. Extending RAPID model to simulate forest microwave backscattering. Remote Sens. Environ. 2018, 217, 272–291. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Verstraete, M.; Pinty, B.; Gobron, N. Allometric Relationships of Selected European Tree Species; European Commission Joint Research Centre: Ispra, Italy, 2003. [Google Scholar]
- Ulaby, F. Microwave Dielectric Spectrum of Vegetation Part II: Dual-Dispersion Model. IEEE Trans. Geosci. Remote Sens. 1987, 25, 550–557. [Google Scholar] [CrossRef]
- Knapp, N.; Fischer, R.; Huth, A. Linking lidar and forest modeling to assess biomass estimation across scales and disturbance states. Remote Sens. Environ. 2018, 205, 199–209. [Google Scholar] [CrossRef]
- Richardson, J.J.; Moskal, L.M.; Kim, S. Modeling approaches to estimate effective leaf area index from aerial discrete-return LIDAR. Agric. For. Meteorol. 2009, 149, 1152–1160. [Google Scholar] [CrossRef]
- Mattos, E.M.; Binkley, D.; Campoe, O.C.; Alvares, C.A.; Stape, J.L. Variation in canopy structure, leaf area, light interception and light use efficiency among Eucalyptus clones. For. Ecol. Manag. 2020, 463, 118038. [Google Scholar] [CrossRef]
- Rödig, E.; Cuntz, M.; Heinke, J.; Rammig, A.; Huth, A. Spatial heterogeneity of biomass and forest structure of the Amazon rain forest: Linking remote sensing, forest modelling and field inventory. Glob. Ecol. Biogeogr. 2017, 26, 1292–1302. [Google Scholar] [CrossRef]


| Parameters | Specified Values |
|---|---|
| Modulation type | FM-CW |
| Center frequency (GHz) | 14 |
| Modulation frequency (Hz) | 163 |
| Polarization modes | HH, HV, VH, VV |
| Field of view (°) | 6 |
| Range resolution (m) | 0.15 |
| Data rate (Mbits/s) | 2.5 |
| Parameters | Specified Values |
|---|---|
| Laser line number | 16 |
| Measurement point output (pts/s) | 300,000 |
| Wavelength (nm) | 905 |
| Measuring range (m) | 100 |
| measurement accuracy (m) | ±0.03 |
| Species | Amax (year) | Dmax (cm) | Hmax (cm) | G | DDmin | DDmax | Light | Drt | Nutri |
|---|---|---|---|---|---|---|---|---|---|
| Scots pine | 150 | 100 | 3500 | 260 | 500 | 1800 | 4 | 4 | 3 |
| Norway spruce | 300 | 130 | 5500 | 240 | 550 | 1800 | 1 | 3 | 2 |
| birch | 140 | 40 | 2500 | 310 | 700 | 2500 | 4 | 2 | 2 |
| Species | Crown Model | Allometric Relationships |
|---|---|---|
| Scots pine | 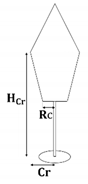 | [m] |
| [m] | ||
| [m] | ||
| Norway spruce | 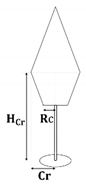 | [m] |
| [m] | ||
| [m] | ||
| birch | 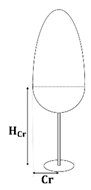 | [m] |
| [m] | ||
| Parameters | Scots Pine | Norway Spruce | Birch |
|---|---|---|---|
| leaf/needle length (cm) | 4 | 2 | 3 |
| leaf/needle thickness (cm) | 0.2 | 0.2 | 0.05 |
| Twig length (m) | 0.52 | 0.52 | 0.52 |
| Twig diameter (cm) | 1.28 | 1.28 | 1.28 |
| Twig density (number/m3) | 3.48 | 3.48 | 3.48 |
| Branch length (m) | 2.10 | 2.10 | 2.10 |
| Branch diameter (cm) | 2.60 | 2.60 | 2.60 |
| Branch density (number/m3) | 0.27 | 0.27 | 0.27 |
| Components | Dielectric Constants |
|---|---|
| Soil | 6.65-j0.88 |
| Trunk | 13.97-j4.31 |
| Twig/branch | 17.75-j4.37 |
| Leaf/needle | 21.75-j8.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, K.; Huang, H.; Feng, Z.; Hakala, T.; Chen, Y.; Hyyppä, J. Using Microwave Profile Radar to Estimate Forest Canopy Leaf Area Index: Linking 3D Radiative Transfer Model and Forest Gap Model. Remote Sens. 2021, 13, 297. https://doi.org/10.3390/rs13020297
Du K, Huang H, Feng Z, Hakala T, Chen Y, Hyyppä J. Using Microwave Profile Radar to Estimate Forest Canopy Leaf Area Index: Linking 3D Radiative Transfer Model and Forest Gap Model. Remote Sensing. 2021; 13(2):297. https://doi.org/10.3390/rs13020297
Chicago/Turabian StyleDu, Kai, Huaguo Huang, Ziyi Feng, Teemu Hakala, Yuwei Chen, and Juha Hyyppä. 2021. "Using Microwave Profile Radar to Estimate Forest Canopy Leaf Area Index: Linking 3D Radiative Transfer Model and Forest Gap Model" Remote Sensing 13, no. 2: 297. https://doi.org/10.3390/rs13020297
APA StyleDu, K., Huang, H., Feng, Z., Hakala, T., Chen, Y., & Hyyppä, J. (2021). Using Microwave Profile Radar to Estimate Forest Canopy Leaf Area Index: Linking 3D Radiative Transfer Model and Forest Gap Model. Remote Sensing, 13(2), 297. https://doi.org/10.3390/rs13020297








