Matching Large Baseline Oblique Stereo Images Using an End-to-End Convolutional Neural Network
Abstract
1. Introduction
- complex geometric and radiometric distortions inhibit these algorithms to extract sufficient invariant features with a good repetition rate, and thus it would increase the probability of outliers;
- Universally repetitive textures in images may result in numerous non-matching descriptors with very similar Euclidean distances, due to the fact that the minimized loss functions only consider the matching descriptor and the closest non-matching descriptor;
- Because of the fact that feature detection and matching are carried out independently, the feature points to be matched using above methods can only achieve pixel-level accuracy.
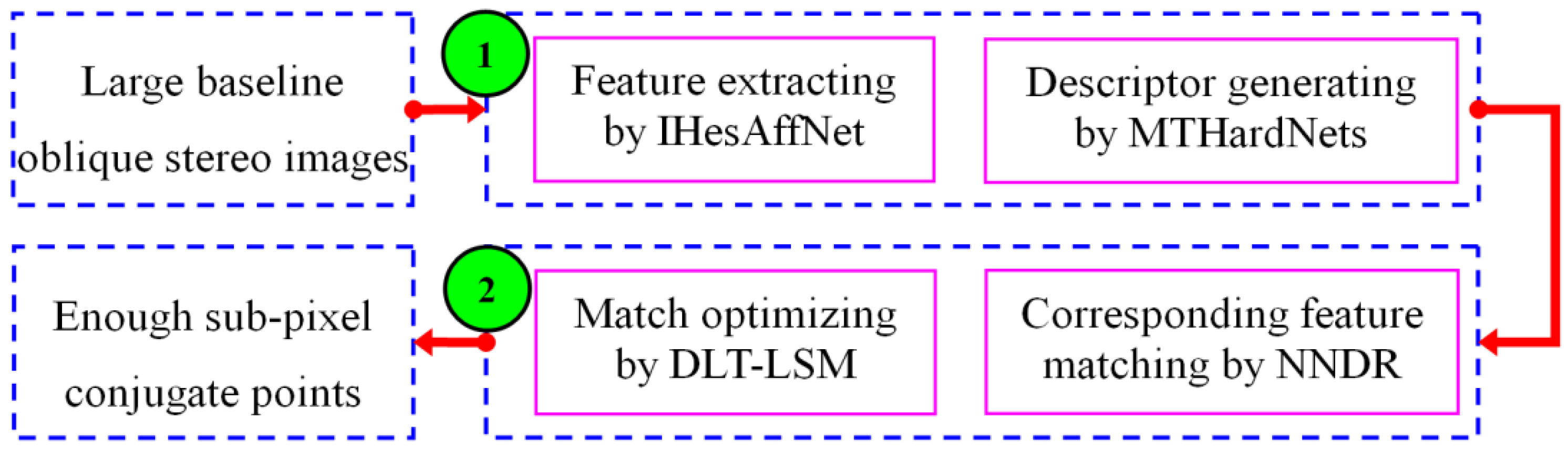
2. Methodology
2.1. IHesAffNet for Feature Extraction
| Algorithm 1. IHesAffNet Region Extraction. |
| Begin (1) Divide image into grids. (2) For one grid, extract Hessian points. Compute the average information entropy of the grid by Equation (1). (3) Set the threshold to be , and remove all the Hessian points that lower than . (4) Go to Step (2) and (3), until all the grids are processed. Then, save the Hessian points. (5) For one Hessian point, use AffNet6 to extract affine invariant region, until all the Hessian points are processed. Then, save the Hessian affine invariant regions. (6) Select the stable regions by dual criteria as and . End |
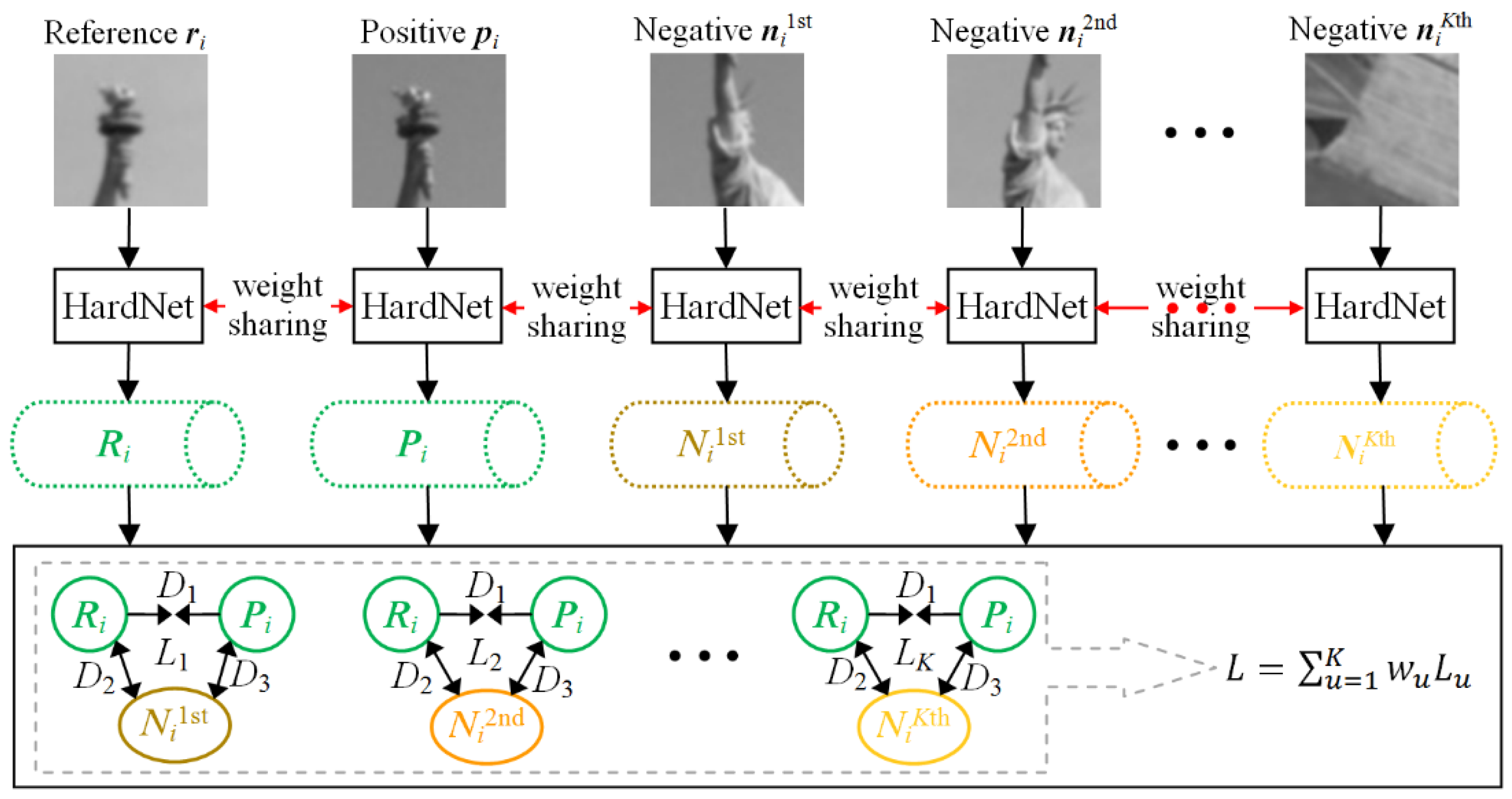
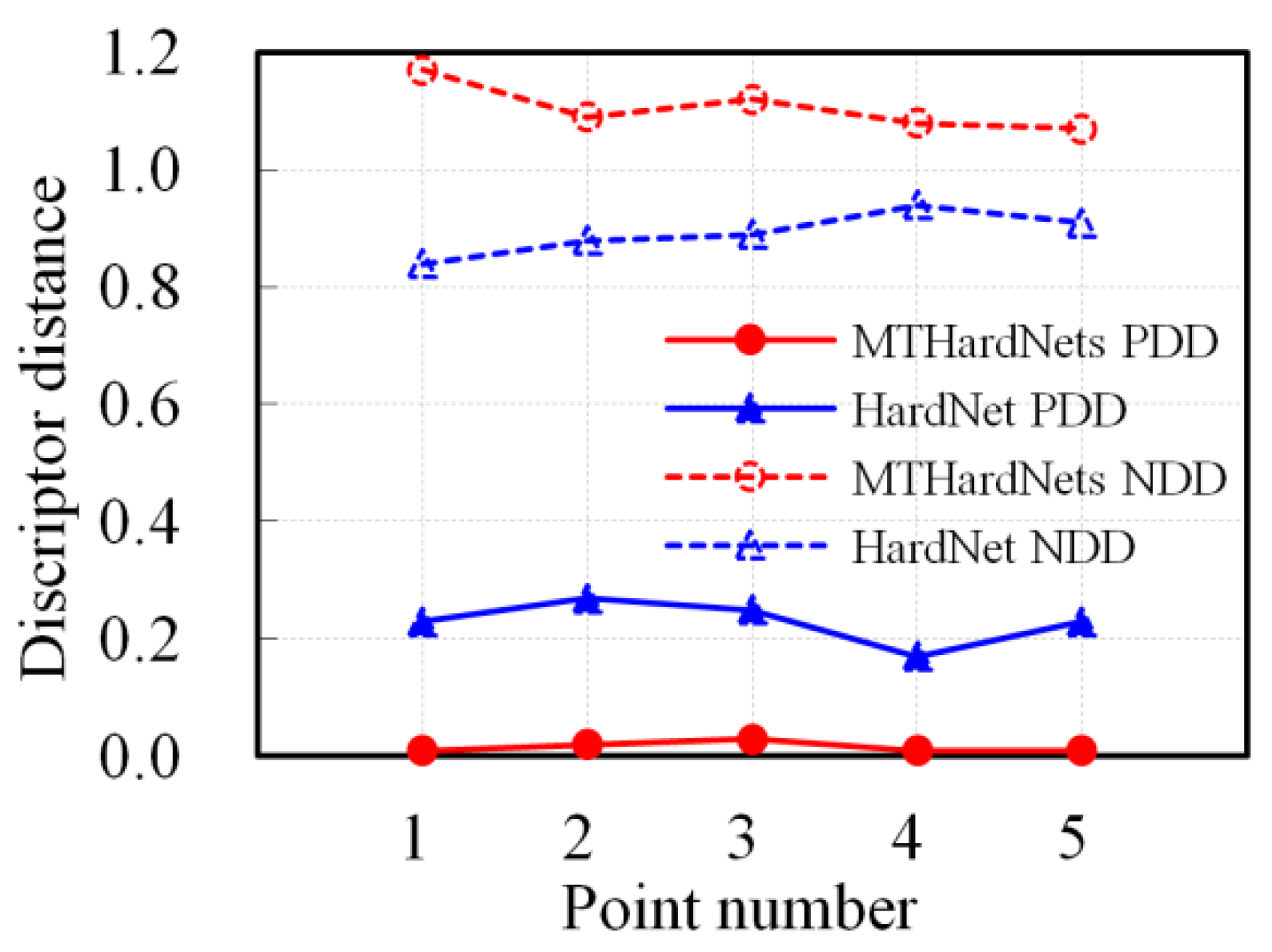
2.2. Descriptor Generating by MTHardNets
| Algorithm 2. MTHardNets Descriptor. |
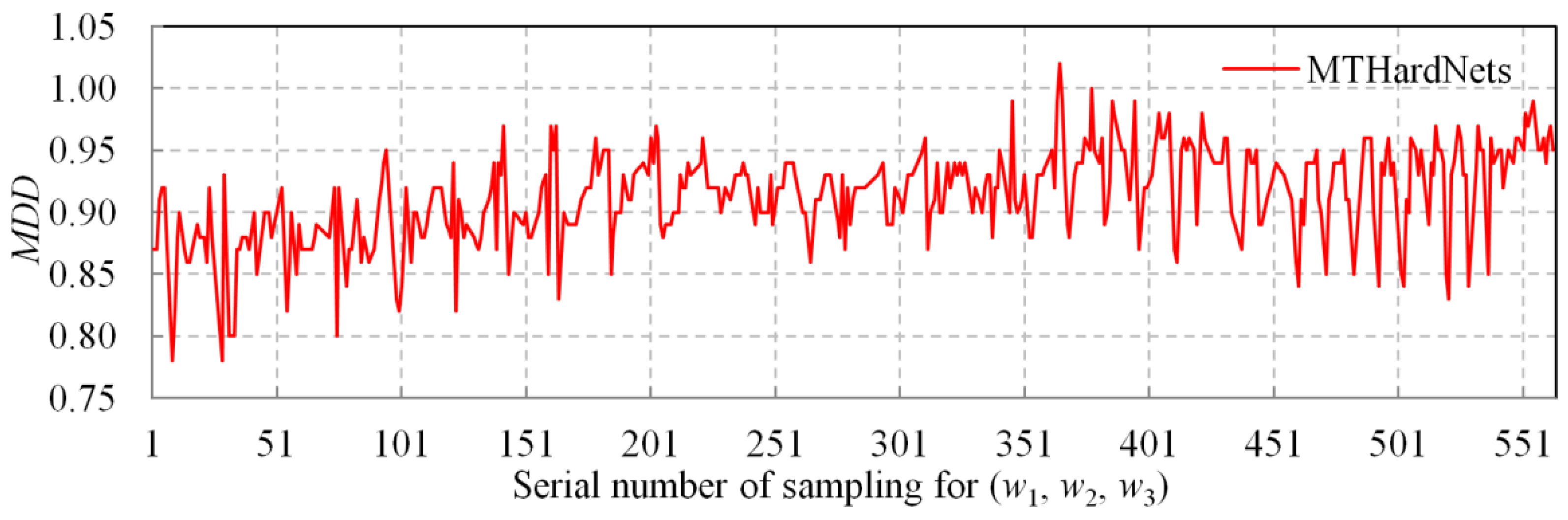
| Begin (1) Given , then select closest non-matching patches for . (2) Transform current patches into unit descriptors with 128-D, and compute distance D1 by Equation (3). Similarly, compute distances D2 and D3. (3) Estimate a distance matrix D by Equation (4), then generate by Equation (5). (4) Generate EWLF by using and Equation (6), and build EWLF model by Equation (7). (5) For each weight group, train the MTHardNets and compute MDD by Equation (8). (6) Use the highest MDD to simplify EWLF model as Equation (9). End |
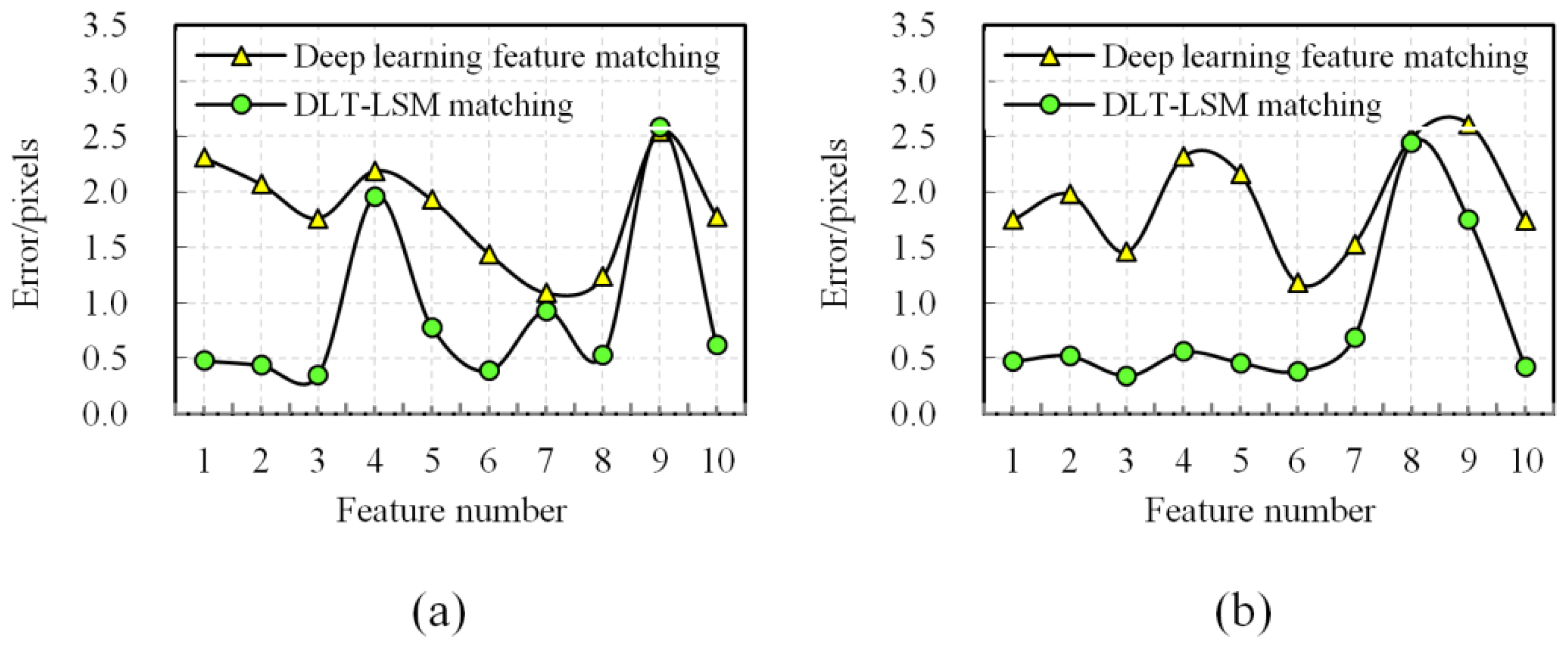
2.3. Match Optimizing by DLT-LSM
| Algorithm 3. DLT-LSM. |
| Begin (1) For one correspondence and , determine the initial affine transform by Equation (10). Initialize using . Set the threshold of maximum iterations to be . (2) Build correlation windows and by Equations (11) and (12), and then compute by Equation (13). (3) Build LSM error equation as Equation (14), then compute and update . If the number of iterations is less than , then go to Step (2); otherwise, correct by Equation (15). End |
2.4. Training Dataset and Implementation Details
3. Results
3.1. Test Data and Evaluation Criteria
- Number of correct correspondences (the unit is pair): The matching error is calculated using and Equation (16). If the error of a corresponding point is less than the given threshold (1.5 pixels in our experiment), it was regarded as a inlier and used to compute .
- Correct ratio β (in percentage, %) of matches: It is computed by , where num (the unit is pair) is the number of total matches.
- Root mean square error (the unit is pixel) of matches: It is calculated by
- Matching distribution quality MDQ: Lower MDQ value indicates the geometric homogeneity of the Delaunay triangles, which are generated based on matched points. Thus, the MDQ can be a uniform distribution metric of matches. This index is estimated by previous Equation (2).
- Matching efficiency η (the unit is second per pair of matching points): We compute the η according to average run time for one pair of corresponding points, namely , where t (the unit is second) denotes the total test time of the algorithm.
3.2. Experimental Results of the Key Steps of the Proposed Method
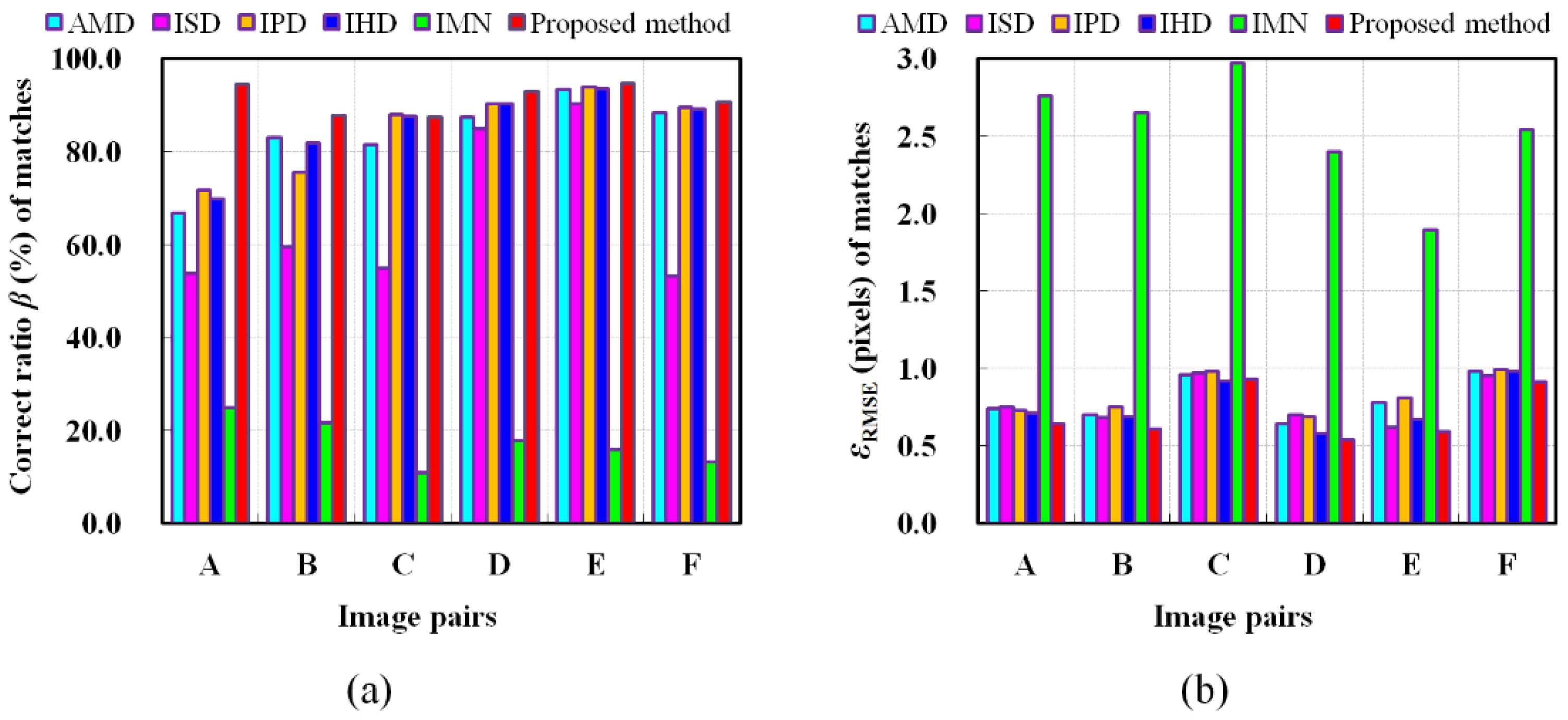
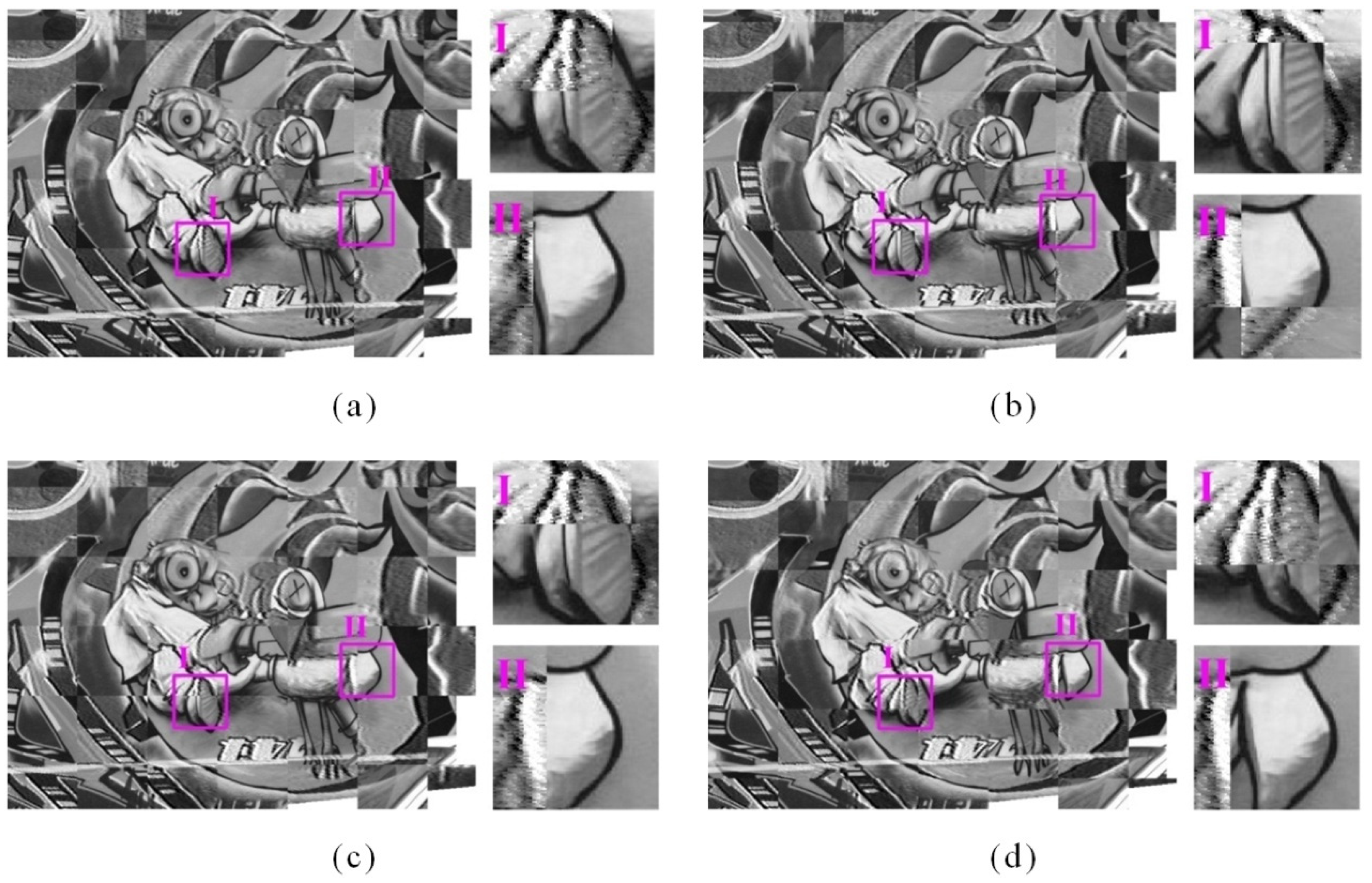
3.3. Experimental Results of Comparison Methods
- The proposed method.
- Detone’s method [26]: This approach uses a fully convolutional neural network (MagicPoint) trained on an extensive synthetic dataset which poses a liability to real scenarios. The homographic adaptation (HA) strategy is employed to transform MagicPoint into SuperPoint, which boosts the performance of the detector and generate repeatable feature points. This method also combines SuperPoint with a descriptor subnetwork that generates 256 dimensional descriptors. Matching is achieved using NNDR metric. While the use of HA outperforms classical detectors, the random nature of the HA step limits the invariance of this technique to geometric deformations.
- Morel’s method [10]: This method samples stereo images by simulating discrete poses in the 3D affine space. It uses SIFT algorithm to simulated image pairs and transforms all matches to the original image pair. This method was shown to find correspondences from image pairs with large viewpoint changes. However, false positives often occur for repeating patterns.
- Matas’s method [12]: The approach extracts features using MSER and estimates SIFT descriptors after normalizing the feature points. It uses the NNDR metric to obtain matching features.
4. Discussion
4.1. Discussion on Experimental Results of the Key Steps of the Proposed Method
4.2. Discussion on Experimental Results of Comparison Methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qin, R. A critical analysis of satellite stereo pairs for digital surface model generation and a matching quality prediction model. ISPRS J. Photogramm. Remote Sens. 2019, 154, 139–150. [Google Scholar] [CrossRef]
- Liu, W.; Wu, B. An integrated photogrammetric and photoclinometric approach for illumination-invariant pixel-resolution 3D mapping of the lunar surface. ISPRS J. Photogramm. Remote Sens. 2020, 159, 153–168. [Google Scholar] [CrossRef]
- Zhang, H.; Ni, W.; Yan, W.; Xiang, D.; Bian, H. Registration of multimodal remote sensing image based on deep fully convolutional neural network. IEEE J. Stars 2019, 12, 3028–3042. [Google Scholar] [CrossRef]
- Gruen, A. Development and status of image matching in photogrammetry. Photogramm. Rec. 2012, 27, 36–57. [Google Scholar] [CrossRef]
- Song, W.; Jung, H.; Gwak, I.; Lee, S. Oblique aerial image matching based on iterative simulation and homography evaluation. Pattern Recognit. 2019, 87, 317–331. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Gool, L. Speeded-Up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Murartal, R.; Montiel, J.; Tardos, J. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Ma, W.; Wen, Z.; Wu, Y.; Jiao, L.; Gong, M.; Zheng, Y.; Liu, L. Remote sensing image registration with modified SIFT and enhanced feature matching. IEEE Geosci. Remote Sens. Lett. 2017, 14, 3–7. [Google Scholar] [CrossRef]
- Morel, J.M.; Yu, G.S. ASIFT: A new framework for fully affine invariant image comparison. SIAM J. Imaging Sci. 2009, 2, 438–469. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. Scale & affine invariant interest point detectors. Int. J. Comput. Vis. 2004, 60, 63–86. [Google Scholar] [CrossRef]
- Matas, J.; Chum, O.; Urban, M.; Pajdla, T. Robust wide-baseline stereo from maximally stable extremal regions. Image Vis. Comput. 2004, 22, 761–767. [Google Scholar] [CrossRef]
- Liu, X.; Samarabandu, J. Multiscale Edge-Based Text Extraction from Complex Images. In Proceedings of the IEEE International Conference on Multimedia and Expo, Toronto, ON, Canada, 9–12 July 2006; pp. 1721–1724. [Google Scholar] [CrossRef]
- Tuytelaars, T.; Gool, L. Matching widely separated views based on affine invariant regions. Int. J. Comput. Vis. 2004, 59, 61–85. [Google Scholar] [CrossRef]
- Yao, G.; Man, X.; Zhang, L.; Deng, K.; Zheng, G. Registrating oblique SAR images based on complementary integrated filtering and multilevel matching. IEEE J. Stars. 2019, 12, 3445–3457. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Tuytelaars, T.; Schmid, C.; Zisserman, A.; Matas, J.; Schaffalitzky, F.; Kadir, T.; Gool, L. A comparison of affine region detectors. Int. J. Comput. Vis. 2005, 65, 43–72. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. A performance evaluation of local descriptors. IEEE Trans. Pattern Anal. 2005, 27, 1615–1630. [Google Scholar] [CrossRef] [PubMed]
- Lenc, K.; Vedaldi, A. Learning covariant feature detectors. In Proceedings of the ECCV Workshop on Geometry Meets Deep Learning, Amsterdam, The Netherlands, 31 August–1 September 2016; pp. 100–117. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, F.X.; Karaman, S. Learning discriminative and transformation covariant local feature detectors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4923–4931. [Google Scholar] [CrossRef]
- Doiphode, N.; Mitra, R.; Ahmed, S. An improved learning framework for covariant local feature detection. In Proceedings of the Asian Conference on Computer Vision (ACCV), Perth, Australia, 2–6 December 2018; pp. 262–276. [Google Scholar] [CrossRef]
- Yi, K.M.; Verdie, Y.; Fua, P.; Lepetit, V. Learning to assign orientations to feature points. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar] [CrossRef]
- Detone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Self-supervised interest point detection and description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 224–236. [Google Scholar] [CrossRef]
- Tian, Y.; Fan, B.; Wu, F. L2-Net: Deep Learning of Discriminative Patch Descriptor in Euclidean Space. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6128–6136. [Google Scholar] [CrossRef]
- Mishchuk, A.; Mishkin, D.; Radenovic, F. Working hard to know your neighbor’s margins: Local descriptor learning loss. In Proceedings of the Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4826–4837. [Google Scholar]
- Mishkin, D.; Radenovic, F.; Matas, J. Repeatability is not Enough: Learning Affine Regions via Discriminability. In European Conference on Computer Vision (ECCV); Springer: Cham, Switzerland, 2018; pp. 287–304. [Google Scholar] [CrossRef]
- Wan, J.; Yilmaz, A.; Yan, L. PPD: Pyramid patch descriptor via convolutional neural network. Photogramm. Eng. Remote Sens. 2019, 85, 673–686. [Google Scholar] [CrossRef]
- Han, X.; Leung, T.; Jia, Y.; Sukthankar, R. MatchNet: Unifying feature and metric learning for patch-based matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3279–3286. [Google Scholar] [CrossRef]
- Hoffer, E.; Ailon, N. Deep metric learning using triplet network. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 84–92. [Google Scholar] [CrossRef]
- Tian, Y.; Yu, X.; Fan, B. SOSNet: Second order similarity regularization for local descriptor learning. In Proceedings of the Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 11016–11025. [Google Scholar] [CrossRef]
- Ebel, P.; Trulls, E.; Yi, K.M.; Fua, P.; Mishchuk, A. Beyond Cartesian Representations for Local Descriptors. In Proceedings of the International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 253–262. [Google Scholar] [CrossRef]
- Luo, Z.; Shen, T.; Zhou, L.; Zhu, S.; Zhang, R.; Yao, Y.; Fang, T.; Quan, L. GeoDesc: Learning local descriptors by integrating geometry constraints. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 170–185. [Google Scholar] [CrossRef]
- Luo, Z.; Shen, T.; Zhou, L.; Zhu, S.; Zhang, R.; Yao, Y.; Fang, T.; Quan, L. ContextDesc: Local descriptor augmentation with cross-modality context. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 2527–2536. [Google Scholar] [CrossRef]
- Yi, K.; Trulls, E.; Lepetit, V.; Fua, P. LIFT: Learned invariant feature transform. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; pp. 467–483. [Google Scholar] [CrossRef]
- Ono, Y.; Trulls, E.; Fua, P. LF-Net: Learning local features from images. In Proceedings of the Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 6234–6244. [Google Scholar]
- Revaud, J.; Weinzaepfel, P.; De, S. R2D2: Repeatable and reliable detector and descriptor. arXiv 2019, arXiv:1906.06195. [Google Scholar]
- Jin, Y.; Mishkin, D.; Mishchuk, A.; Matas, J.; Fua, P.; Yi, F.; Trulls, E. Image matching across wide baselines: From paper to practice. Int. J. Comput. Vis. 2020, 1–31. [Google Scholar] [CrossRef]
- Sedaghat, A.; Mokhtarzade, M.; Ebadi, H. Uniform robust scale-invariant feature matching for optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4516–4527. [Google Scholar] [CrossRef]
- Zhu, Q.; Wu, B.; Xu, Z.X. Seed point selection method for triangle constrained image matching propagation. IEEE Geosci. Remote Sens. Lett. 2006, 3, 207–211. [Google Scholar] [CrossRef]
- Brown, M.; Lowe, D.G. Automatic panoramic image stitching using invariant features. Int. J. Comput. Vis. 2007, 74, 59–73. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.S.; Chintala, G.; Chanan, E.; Yang, Z.; DeVito, Z.; Lin, A.; Desmaison, L.; Lerer, A. Automatic differentiation in pytorch. In Proceedings of the Advances in Neural Information Processing Systems Workshop, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Podbreznik, P.; Potočnik, B. A self-adaptive ASIFT-SH method. Adv. Eng. Inform. 2013, 27, 120–130. [Google Scholar] [CrossRef]
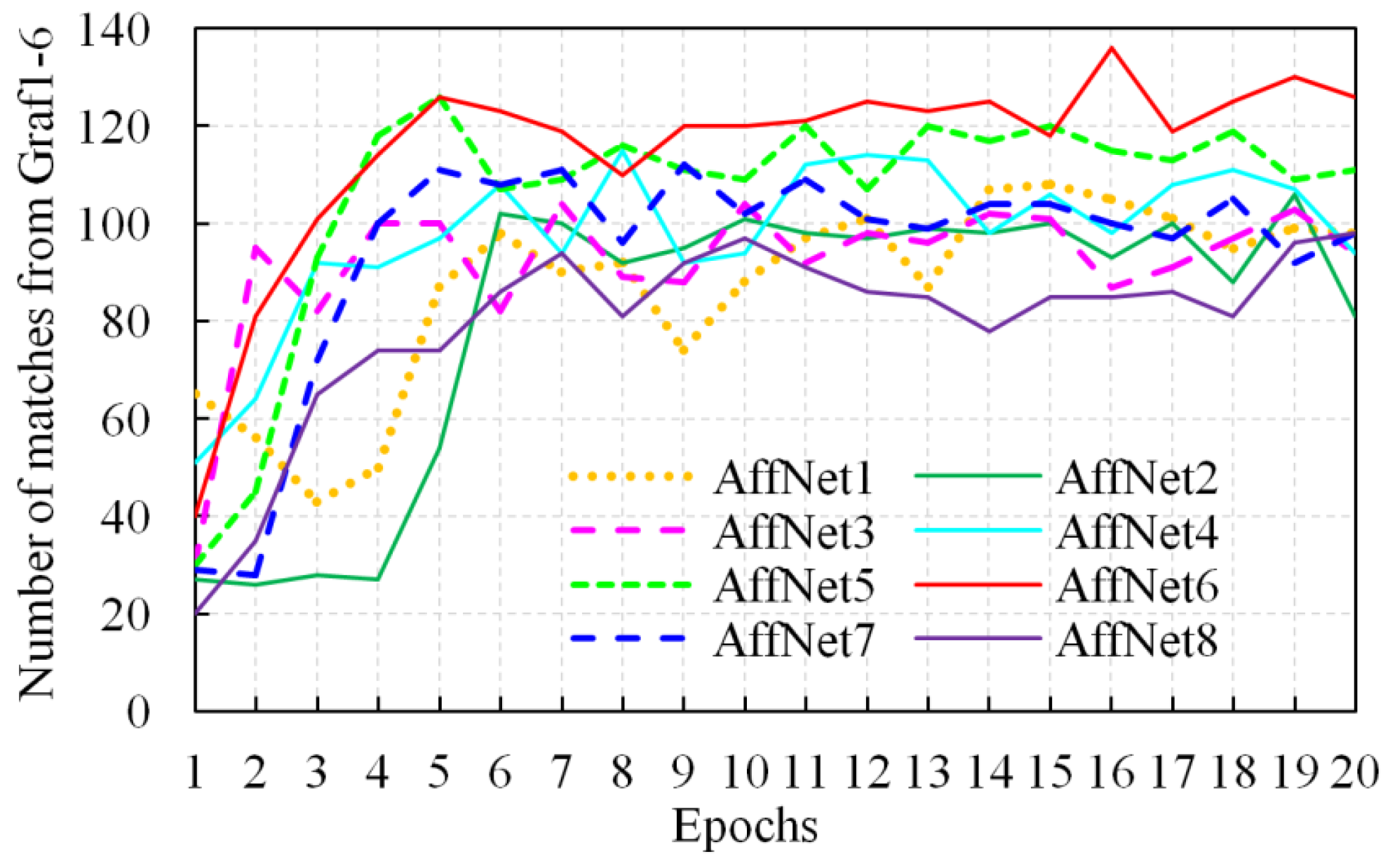






| AffNet Version | Number of Dimensions in Each Layer | ||||||
|---|---|---|---|---|---|---|---|
| 1st Layer | 2nd Layer | 3rd Layer | 4th Layer | 5th Layer | 6th Layer | 7th Layer | |
| AffNet1 | 32 | 32 | 64 | 64 | 128 | 128 | 3 |
| AffNet2 | 28 | 28 | 56 | 56 | 112 | 112 | 3 |
| AffNet3 | 24 | 24 | 48 | 48 | 96 | 96 | 3 |
| AffNet4 | 20 | 20 | 40 | 40 | 80 | 80 | 3 |
| AffNet5 | 16 | 16 | 32 | 32 | 64 | 64 | 3 |
| AffNet6 | 12 | 12 | 24 | 24 | 48 | 48 | 3 |
| AffNet7 | 8 | 8 | 16 | 16 | 32 | 32 | 3 |
| AffNet8 | 4 | 4 | 8 | 8 | 16 | 16 | 3 |
| Method | Left MDQ | Right MDQ | Matched Features |
|---|---|---|---|
| The HesAffNet | 1.19 | 1.32 | 93 |
| Our IHesAffNet | 0.84 | 0.89 | 136 |
| Left Neighborhood | Initial Right Neighborhood | First Iteration | Second Iteration | Third Iteration | Fourth Iteration | |
|---|---|---|---|---|---|---|
| Window border |  |  |  | 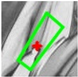 | 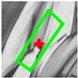 |  |
| ε = 2.635 | ε = 2.244 | ε = 1.290 | ε = 0.837 | ε = 0.516 | ||
| Correlation windows |  |  |  |  |  |  |
| ρ = 0.569 | ρ = 0.638 | ρ = 0.805 | ρ = 0.919 | ρ = 0.957 | ||
| Window border |  |  |  |  |  | 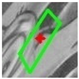 |
| ε = 1.278 | ε = 0.860 | ε = 0.553 | ε = 0.375 | ε = 0.241 | ||
| Correlation windows |  |  |  |  |  |  |
| ρ = 0.832 | ρ = 0.915 | ρ = 0.949 | ρ = 0.957 | ρ = 0.965 |
| Steps | AMD | ISD | IPD | IHD | IMN | Proposed Method |
|---|---|---|---|---|---|---|
| Feature extracting | AffNet [25] | IHesAffNet | IHesAffNet | IHesAffNet | IHesAffNet | IHesAffNet |
| Descriptor generating | MTHardNets | SIFT [6] | PPD [26] | HardNet [24] | MTHardNets | MTHardNets |
| Match optimizing | DLT-LSM | DLT-LSM | DLT-LSM | DLT-LSM | Null | DLT-LSM |
| Image Pair | AMD | ISD | IPD | IHD | IMN | Proposed Method |
|---|---|---|---|---|---|---|
| A | 78 | 21 | 86 | 92 | 41 | 152 |
| B | 219 | 35 | 203 | 235 | 87 | 349 |
| C | 313 | 85 | 409 | 402 | 164 | 662 |
| D | 329 | 90 | 339 | 348 | 97 | 397 |
| E | 912 | 120 | 937 | 921 | 196 | 972 |
| F | 375 | 42 | 401 | 398 | 93 | 408 |
| Image Pair | AMD | ISD | IPD | IHD | IMN | Proposed Method |
|---|---|---|---|---|---|---|
| A | 29.02 | 24.09 | 29.36 | 30.45 | 29.14 | 31.49 |
| B | 32.79 | 27.49 | 33.45 | 34.58 | 33.20 | 36.55 |
| C | 39.60 | 36.52 | 43.10 | 42.70 | 39.05 | 45.73 |
| D | 40.14 | 35.60 | 42.08 | 41.83 | 40.57 | 44.61 |
| E | 47.05 | 41.65 | 48.74 | 49.06 | 43.74 | 52.32 |
| F | 40.33 | 35.94 | 40.16 | 41.63 | 40.92 | 43.80 |
| Method | Indexes | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|
| Proposed | 152 | 349 | 662 | 397 | 972 | 408 | |
| β | 94.43 | 87.70 | 87.45 | 92.98 | 94.71 | 90.66 | |
| 0.64 | 0.61 | 0.93 | 0.54 | 0.59 | 0.91 | ||
| MDQ | 0.893 | 1.021 | 1.130 | 0.988 | 0.764 | 1.104 | |
| t | 31.49 | 36.55 | 45.73 | 44.61 | 52.32 | 43.80 | |
| η | 0.196 | 0.092 | 0.060 | 0.105 | 0.051 | 0.097 | |
| Detone’s | 6 | 56 | 0 | 0 | 0 | 0 | |
| β | 46.15 | 43.75 | 0 | 0 | 0 | 0 | |
| 3.32 | 2.28 | 221.83 | 53.62 | 50.25 | 247.41 | ||
| MDQ | 1.706 | 1.290 | 3.379 | 2.561 | 3.027 | 2.643 | |
| t | 16.84 | 20.33 | 27.89 | 24.30 | 30.95 | 25.19 | |
| η | 1.295 | 0.159 | 3.984 | 3.038 | 3.095 | 1.679 | |
| Morel’s | 257 | 408 | 86 | 66 | 532 | 31 | |
| β | 36.25 | 41.17 | 23.50 | 21.71 | 38.89 | 13.78 | |
| 0.91 | 0.92 | 1.80 | 0.96 | 0.88 | 0.98 | ||
| MDQ | 0.974 | 1.083 | 1.384 | 1.920 | 1.005 | 1.766 | |
| t | 31.38 | 33.20 | 33.90 | 29.13 | 32.07 | 33.85 | |
| η | 0.044 | 0.034 | 0.093 | 0.096 | 0.023 | 0.150 | |
| Matas’s | 10 | 48 | 7 | 6 | 4 | 0 | |
| β | 34.48 | 78.69 | 41.18 | 42.86 | 66.67 | 0 | |
| 2.74 | 1.39 | 3.61 | 8.35 | 1.93 | 25.26 | ||
| MDQ | 1.562 | 1.495 | 2.279 | 1.981 | 1.596 | 2.885 | |
| t | 2.78 | 3.82 | 5.99 | 6.72 | 6.37 | 6.38 | |
| η | 0.095 | 0.063 | 0.352 | 0.480 | 1.062 | 0.798 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, G.; Yilmaz, A.; Zhang, L.; Meng, F.; Ai, H.; Jin, F. Matching Large Baseline Oblique Stereo Images Using an End-to-End Convolutional Neural Network. Remote Sens. 2021, 13, 274. https://doi.org/10.3390/rs13020274
Yao G, Yilmaz A, Zhang L, Meng F, Ai H, Jin F. Matching Large Baseline Oblique Stereo Images Using an End-to-End Convolutional Neural Network. Remote Sensing. 2021; 13(2):274. https://doi.org/10.3390/rs13020274
Chicago/Turabian StyleYao, Guobiao, Alper Yilmaz, Li Zhang, Fei Meng, Haibin Ai, and Fengxiang Jin. 2021. "Matching Large Baseline Oblique Stereo Images Using an End-to-End Convolutional Neural Network" Remote Sensing 13, no. 2: 274. https://doi.org/10.3390/rs13020274
APA StyleYao, G., Yilmaz, A., Zhang, L., Meng, F., Ai, H., & Jin, F. (2021). Matching Large Baseline Oblique Stereo Images Using an End-to-End Convolutional Neural Network. Remote Sensing, 13(2), 274. https://doi.org/10.3390/rs13020274







