Individual Sick Fir Tree (Abies mariesii) Identification in Insect Infested Forests by Means of UAV Images and Deep Learning
Abstract
1. Introduction
2. Methodology
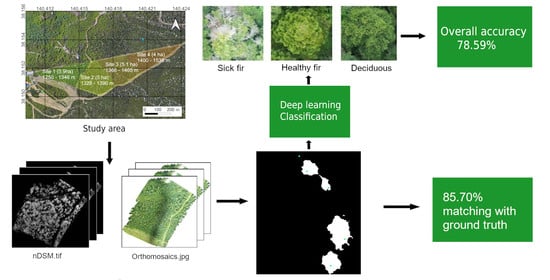
2.1. Study Sites, Data Acquisition and Problem Definition
2.1.1. Study Sites
2.1.2. UAV Data Acquisition
2.1.3. Problem Definition
2.1.4. Dense Point Cloud, DSM and Orthomosaic Generation
2.2. Data Pre-Processing
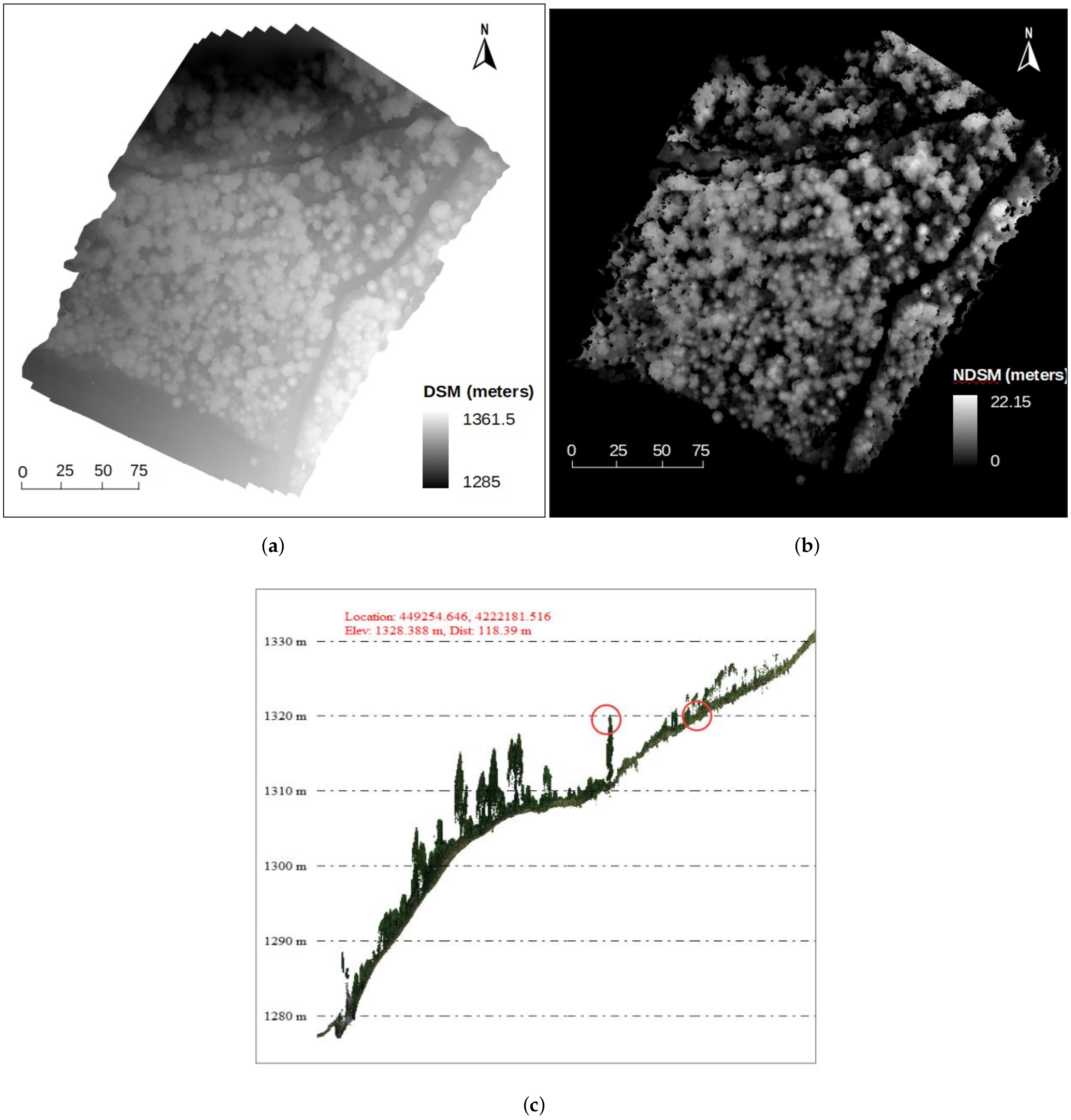
2.2.1. Normalized Digital Surface Model (nDSM) Generation and Validation
2.2.2. Data Annotation
2.3. Treetop Detection
2.3.1. Treetop Detection Algorithm
- Two-step algorithm: a large concentration of treetops at the higher intensity pixels was observed, for example in the first orthomosaic 50% of the treetops are contained in the 10% higher pixels and 90% of the treetops are contained in the 40% higher pixels. Consequently, the algorithm runs in two main steps (which we refer to as “bands”). The first considers only pixel intensities of the nDSM from a certain threshold up and the second one considers all intensities.
- Sliding window: for each of these two steps, a sliding window is passed over the nDSM. The positions of the window have a 100-pixel overlap. For each position of the window (Figure 5), a list of candidate treetops is initialised to an empty list and a threshold value is set. Then at each iteration:
- Only the upper band of intensities (larger than ) is considered.
- Connected components are computed in the image limited to the current window and band of pixel intensities. Each newly appearing component (if it is large enough) is assigned a new treetop that is added to the list of treetop candidates. Connected components already containing a candidate treetop do not add new candidate treetops to the list. If two connected components contain one treetop then they are fused and both treetops are kept.
- is updated and the process continues until reaches the minimum intensity present in the window.
- Refinement: once all the treetops are computed, they are refined to eliminate those that are too close to each other, specifically, a circle is drawn around each candidate treetop (with radius = 50 pixels) to exclude pixels higher than the candidate top (with a difference of more than 1.5 meters with the top). Then, the top point in each of the connected components is chosen as a predicted treetop. Thus, the highest treetops among those whose regions intersect are selected and the lower are discarded. An initial refinement step is done over the candidate tops resulting from considering all pixel intensities. Then, the treetop candidates corresponding to the high intensity bands is performed. As the treetops detected in the higher-intensity band are considered more reliable, this second refinement step is less strict (the value for = 35).

2.3.2. Treetop Detection Validation
2.4. Treetop Classification
2.4.1. Treetop Classification Algorithm
- Alexnet [24] is one of the first widely used convolutional neural networks, composed of eight layers (five convolutional layers sometimes followed by max-pooling layers and three fully connected layers). This network was the one that started the current DL trend after outperforming the current state-of-the-art method on the ImageNet data set by a large margin.
- Squeezenet [25] uses so-called squeeze filters, including point-wise filter to reduce the number of necessary parameters. A similar accuracy to Alexnet was claimed with fewer parameters.
- Vgg [26] represents an evolution of the Alexnet network that allowed for an increased number of layers (16 in the version considered in our work) by using smaller convolutional filters.
- Resnet [27] is one of the first DL architectures to allow higher number of layers (and, thus, “deeper” networks) by including blocks composed of convolution, batch normalization and ReLU. In the current work a version with 50 layers was used.
- Densenet [28] is another evolution of the resnet network that uses a larger number of connections between layers to claim increased parameter efficiency and better feature propagation that allows them to work with even more layers (121 in this work).
2.4.2. Data Augmentation
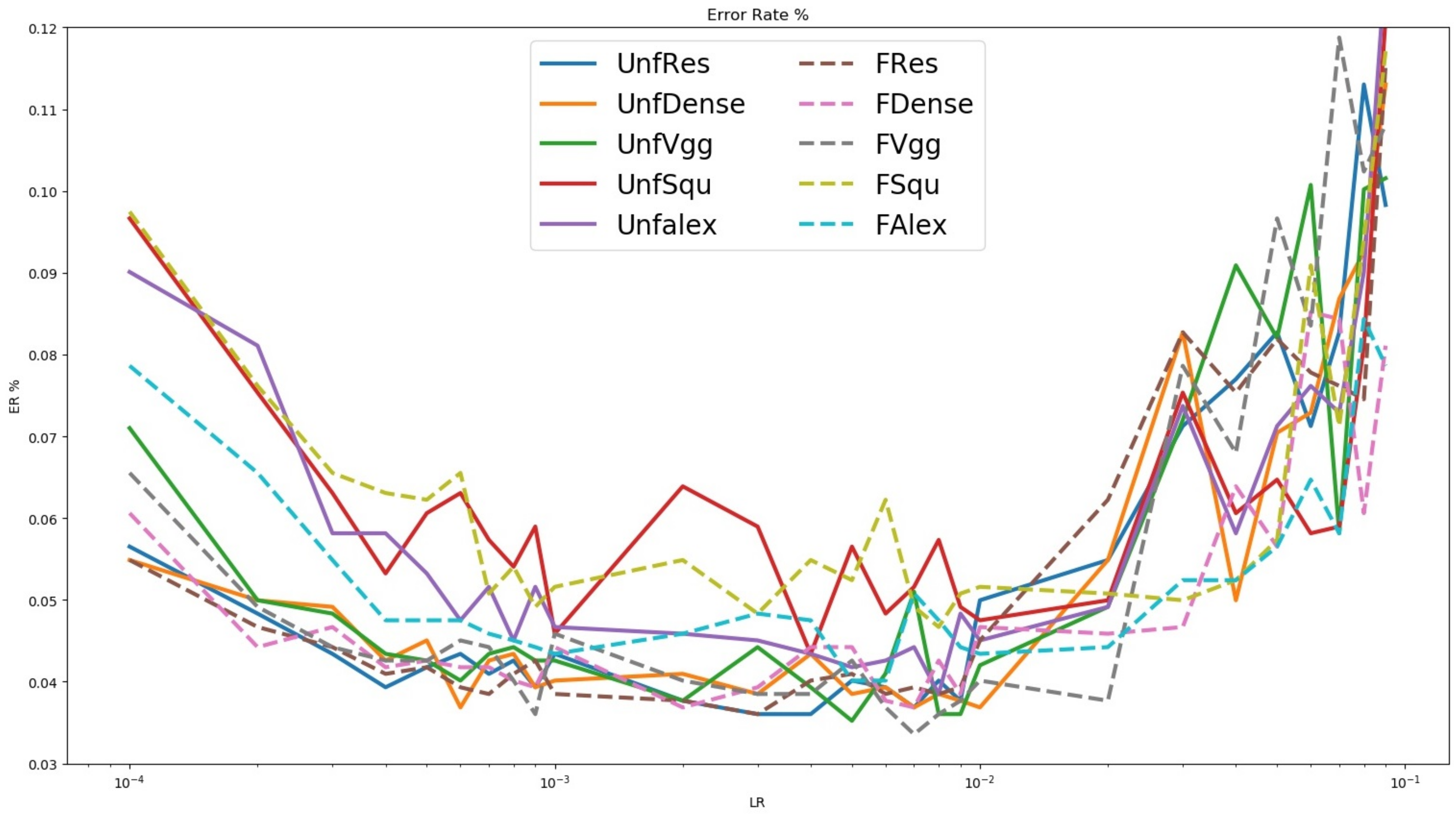
2.4.3. Treetop Classification Algorithm Training and Validation
- Checked to which of the classes it belonged.To do so it checked the manually annotated class binary masks (See Section 2.2 for details on the annotation process).
- Cut a small patch of the orthomosaic around each treetop (of 100 × 100 RGB pixels, amounting approximately to a 2 m sided square).
- Once the correct class had been identified and the patch built, the patch was stored as an image with the class name in its file name.
- First fold, testing: Site 1 (mosaics 1,2,3) training/validation Sites 2,3,4 (mosaics 4–9)
- Second fold, testing: Site 2 (mosaics 4,5,6) training/validation Sites 1,3,4 (mosaics 1–3,7–9)
- Third fold, testing: Site 3 (mosaics 7,8) training/validation Sites 1,2,4 (mosaics 1–6,9)
- Fourth fold, testing: Site 4 (mosaic 9) training/validation Sites 1,2,3 (mosaics 1–8)
3. Results
3.1. nDSM Validation
3.2. Treetop Detection
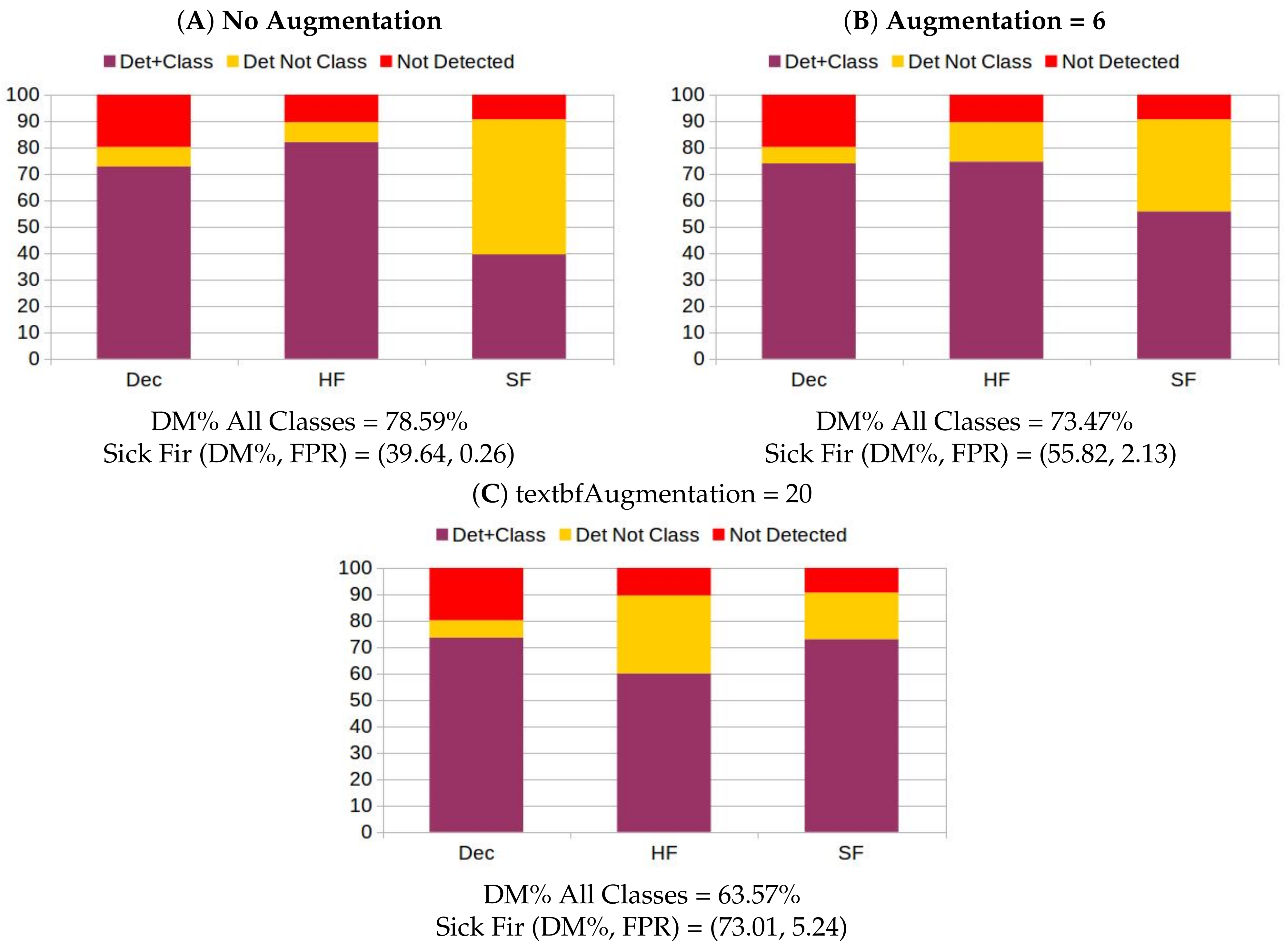
3.3. Classification of Ground Truth Treetops Using Deep Learning
3.4. Automatic Detection and Classification of Sick Fir trees
4. Discussion
4.1. Data Challenges
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jactel, H.; Koricheva, J.; Castagneyrol, B. Responses of forest insect pests to climate change: Not so simple. Curr. Opin. Insect Sci. 2019, 35, 103–108. [Google Scholar] [CrossRef] [PubMed]
- Agne, M.C.; Beedlow, P.A.; Shaw, D.C.; Woodruff, D.R.; Lee, E.H.; Cline, S.P.; Comeleo, R.L. Interactions of predominant insects and diseases with climate change in Douglas-fir forests of western Oregon and Washington, USA. For. Ecol. Manag. 2018, 409, 317–332. [Google Scholar] [CrossRef] [PubMed]
- Przepióra, F.; Loch, J.; Ciach, M. Bark beetle infestation spots as biodiversity hotspots: Canopy gaps resulting from insect outbreaks enhance the species richness, diversity and abundance of birds breeding in coniferous forests. For. Ecol. Manag. 2020, 473, 118280. [Google Scholar] [CrossRef]
- Krokene, P.; Solheim, H. Pathogenicity of four blue-stain fungi associated with aggressive and nonaggressive bark beetles. Phytopathology 1998, 88, 39–44. [Google Scholar] [CrossRef]
- Rice, A.V.; Thormann, M.N.; Langor, D.W. Mountain pine beetle associated blue-stain fungi cause lesions on jack pine, lodgepole pine, and lodgepole× jack pine hybrids in Alberta. Botany 2007, 85, 307–315. [Google Scholar] [CrossRef]
- Six, D.; Paine, T. Effects of mycangial fungi and host tree species on progeny survival and emergence of Dendroctonus ponderosae (Coleoptera: Scolytidae). Environ. Entomol. 1998, 27, 1393–1401. [Google Scholar] [CrossRef]
- Näsi, R.; Honkavaara, E.; Lyytikäinen-Saarenmaa, P.; Blomqvist, M.; Litkey, P.; Hakala, T.; Viljanen, N.; Kantola, T.; Tanhuanpää, T.; Holopainen, M. Using UAV-based photogrammetry and hyperspectral imaging for mapping bark beetle damage at tree-level. Remote Sens. 2015, 7, 15467–15493. [Google Scholar] [CrossRef]
- Smigaj, M.; Gaulton, R.; Barr, S.; Suárez, J. UAV-borne thermal imaging for forest health monitoring: Detection of disease-induced canopy temperature increase. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2015, 40, 349. [Google Scholar] [CrossRef]
- Safonova, A.; Tabik, S.; Alcaraz-Segura, D.; Rubtsov, A.; Maglinets, Y.; Herrera, F. Detection of fir trees (Abies sibirica) damaged by the bark beetle in unmanned aerial vehicle images with deep learning. Remote Sens. 2019, 11, 643. [Google Scholar] [CrossRef]
- Pulido, D.; Salas, J.; Rös, M.; Puettmann, K.; Karaman, S. Assessment of tree detection methods in multispectral aerial images. Remote Sens. 2020, 12, 2379. [Google Scholar] [CrossRef]
- Diez, Y., Kentsch, S., Lopez-Caceres, M.L., Nguyen, H.T., Serrano, D., Roue, F., Eds.; Comparison of Algorithms for Tree-top Detection in Drone Image Mosaics of Japanese Mixed Forests. Proceeding of the 9th International Conference on Pattern Recognition Applications and Methods, INSTICC, Valletta, Malta, 22–24 February 2020; SciTePress: Setúbal, Portugal, 2020. [Google Scholar]
- Kentsch, S.; Lopez Caceres, M.L.; Serrano, D.; Roure, F.; Diez, Y. Computer Vision and Deep Learning Techniques for the Analysis of Drone-Acquired Forest Images, a Transfer Learning Study. Remote Sens. 2020, 12, 1287. [Google Scholar] [CrossRef]
- Krisanski, S.; Taskhiri, M.S.; Turner, P. Enhancing methods for under-canopy unmanned aircraft system based photogrammetry in complex forests for tree diameter measurement. Remote Sens. 2020, 12, 1652. [Google Scholar] [CrossRef]
- Brovkina, O.; Cienciala, E.; Surovỳ, P.; Janata, P. Unmanned aerial vehicles (UAV) for assessment of qualitative classification of Norway spruce in temperate forest stands. Geo-Spat. Inf. Sci. 2018, 21, 12–20. [Google Scholar] [CrossRef]
- Michez, A.; Piégay, H.; Lisein, J.; Claessens, H.; Lejeune, P. Classification of riparian forest species and health condition using multi-temporal and hyperspatial imagery from unmanned aerial system. Environ. Monit. Assess. 2016, 188, 146. [Google Scholar] [CrossRef] [PubMed]
- Vastaranta, M.; Holopainen, M.; Yu, X.; Hyyppä, J.; Mäkinen, A.; Rasinmäki, J.; Melkas, T.; Kaartinen, H.; Hyyppä, H. Effects of individual tree detection error sources on forest management planning calculations. Remote Sens. 2011, 3, 1614–1626. [Google Scholar] [CrossRef]
- Bennett, G.; Hardy, A.; Bunting, P.; Morgan, P.; Fricker, A. A transferable and effective method for monitoring continuous cover forestry at the individual tree level using UAVs. Remote Sens. 2020, 12, 2115. [Google Scholar] [CrossRef]
- Dash, J.P.; Watt, M.S.; Pearse, G.D.; Heaphy, M.; Dungey, H.S. Assessing very high resolution UAV imagery for monitoring forest health during a simulated disease outbreak. ISPRS J. Photogramm. Remote Sens. 2017, 131, 1–14. [Google Scholar] [CrossRef]
- Sylvain, J.D.; Drolet, G.; Brown, N. Mapping dead forest cover using a deep convolutional neural network and digital aerial photography. ISPRS J. Photogramm. Remote. Sens. 2019, 156, 14–26. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, J.; Ao, Z.; Lao, D.; Xin, Q. Deep Learning Approaches for the Mapping of Tree Species Diversity in a Tropical Wetland Using Airborne LiDAR and High-Spatial-Resolution Remote Sensing Images. Forests 2019, 10, 1047. [Google Scholar] [CrossRef]
- McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; US Department of Agriculture, Forest Service, Pacific Northwest Research Station: Seattle, WA, USA, 2009; Volume 123. [Google Scholar]
- Pleșoianu, A.I.; Stupariu, M.S.; Șandric, I.; Pătru-Stupariu, I.; Drăguț, L. Individual Tree-Crown Detection and Species Classification in Very High-Resolution Remote Sensing Imagery Using a Deep Learning Ensemble Model. Remote Sens. 2020, 12, 2426. [Google Scholar] [CrossRef]
- Dupret, G.; Koda, M. Bootstrap re-sampling for unbalanced data in supervised learning. Eur. J. Oper. Res. 2001, 134, 141–156. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Volume 1, pp. 1097–1105. [Google Scholar]
- Iandola, F.N.; Moskewicz, M.W.; Ashraf, K.; Han, S.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50× fewer parameters and <1MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2016; pp. 2261–2269. [Google Scholar]
- Cabezas, M.; Kentsch, S.; Tomhave, L.; Gross, J.; Caceres, M.L.L.; Diez, Y. Detection of Invasive Species in Wetlands: Practical DL with Heavily Imbalanced Data. Remote Sens. 2020, 12, 3431. [Google Scholar] [CrossRef]
- Shiferaw, H.; Bewket, W.; Eckert, S. Performances of machine learning algorithms for mapping fractional cover of an invasive plant species in a dryland ecosystem. Ecol. Evol. 2019, 9, 2562–2574. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Yu, R. Pest Recognition System Based on Bio-Inspired Filtering and LCP Features. In Proceedings of the 2015 12th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP), Chengdu, China, 18–20 December 2015; pp. 202–204. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, J.; Tian, J.; Zhuo, L.; Zhang, J. Residual Dense Network Based on Channel-Spatial Attention for the Scene Classification of a High-Resolution Remote Sensing Image. Remote Sens. 2020, 12, 1887. [Google Scholar] [CrossRef]
- Masarczyk, W.; Głomb, P.; Grabowski, B.; Ostaszewski, M. Effective Training of Deep Convolutional Neural Networks for Hyperspectral Image Classification through Artificial Labeling. Remote Sens. 2020, 12, 2653. [Google Scholar] [CrossRef]
- Onishi, M.; Ise, T. Automatic classification of trees using a UAV onboard camera and deep learning. arXiv 2018, arXiv:1804.10390. [Google Scholar]
- Natesan, S.; Armenakis, C.; Vepakomma, U. Resnet-Based Tree Species Classification Using Uav Images. ISPRS Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2019, 42, 475–481. [Google Scholar] [CrossRef]
- 3.10 Q QGIS Geographic Information System. Open Source Geospatial Foundation Project. Available online: http://qgis.org/ (accessed on 7 December 2019).
- Schomaker, M. Crown-Condition Classification: A Guide to Data Collection and Analysis; US Department of Agriculture, Forest Service, Southern Research Station: Asheville, NC, USA, 2007; Volume 102. [Google Scholar]
- Agisoft, L. Agisoft Metashape, Professional Edition, Version 1.5.5. Available online: http://agisoft.com/ (accessed on 19 March 2020).
- Team, T.G. GNU Image Manipulation Program. Available online: http://gimp.org (accessed on 19 August 2019).
- Van Rossum, G.; Drake, F.L., Jr. Python Tutorial; Centrum voor Wiskunde en Informatica: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS J. Photogramm. Remote. Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Geographics, B.M. Global Mapper Version 21.1. Available online: https://www.bluemarblegeo.com/ (accessed on 24 June 2020).
- Howard, J.; Thomas, R.; Gugger, S. Fastai. Available online: https://github.com/fastai/fastai (accessed on 18 April 2020).
- Jung, A.B.; Wada, K.; Crall, J.; Tanaka, S. Imgaug. 2020. Available online: https://github.com/aleju/imgaug (accessed on 1 July 2020).




| nDSM | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| % treetop lost | 1.12 | 1.57 | 0.17 | 6.90 | 3.08 | 2.25 | 0.00 | 1.00 | 3.20 | 2.14 |
| nDSM | 1 | 2 | 3 | 4 | 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Method | m% | cnt | m% | cnt | m% | cnt | m% | cnt | m% | cnt |
| OUR Approach | 89.61 | 9.87 | 80.14 | 14.51 | 90.47 | 5.67 | 82.97 | 14.15 | 85.61 | 8.73 |
| Dawkins [9] | 70.54 | 2.18 | 54.61 | 13.79 | 73.41 | 6.92 | 59.79 | 16.32 | 51.12 | 19.35 |
| GM [11] | 71.17 | −9.21 | 60.75 | −11.11 | 78.35 | −9.82 | 70.09 | −8.12 | 69.81 | −9.76 |
| FCM [11] | 66.22 | −9.74 | 61.68 | −12.37 | 73.56 | −12.25 | 73.21 | −7.25 | 69.49 | −9.05 |
| nDSM | 6 | 7 | 8 | 9 | AVERAGE | |||||
| Method | m% | cnt | m% | cnt | m% | cnt | m% | cnt | m% | cnt |
| Our Approach | 85.71 | 8.37 | 80.52 | 7.74 | 80 | 9.24 | 96.29 | 8.78 | 85.70 | 9.67 |
| Dawkins [9] | 50.06 | 22.43 | 70.69 | 1.27 | 71.36 | 8.79 | 92.61 | 3.31 | 66.02 | 10.48 |
| GM [11] | 68.85 | −14.82 | 63.27 | −9.44 | 72.82 | −12.27 | 87.67 | −7.41 | 71.42 | 10.22 |
| FCM [11] | 72.2 | −10.18 | 64.71 | −17.87 | 72.3 | −7.76 | 90.14 | −5.71 | 71.50 | 10.24 |
| Sensitivity | Specificity | Accuracy | |
|---|---|---|---|
| Deciduous | 0.982 | 0.999 | 0.995 |
| Healthy Fir | 0.995 | 0.926 | 0.976 |
| Sick Fir | 0.513 | 0.996 | 0.980 |
| DenseNet | ResNet | VGG | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Sens | Spec | Acc | Sens | Spec | Acc | Sens | Spec | ||
| no augm | 0.4109 | 0.9959 | 0.9771 | 0.4422 | 0.9912 | 0.9738 | 0.4001 | 0.9931 | 0.9761 |
| augm 2 | 0.6772 | 0.9948 | 0.9763 | 0.7199 | 0.9941 | 0.9782 | 0.6576 | 0.9921 | 0.9752 |
| aumg 6 | 0.9382 | 0.9875 | 0.9796 | 0.9407 | 0.9863 | 0.9788 | 0.9391 | 0.9877 | 0.9787 |
| augm 10 | 0.9806 | 0.9839 | 0.9834 | 0.9794 | 0.9810 | 0.9809 | 0.9792 | 0.981 | 0.9794 |
| augm 20 | 0.9936 | 0.9769 | 0.9836 | 0.9972 | 0.9822 | 0.9880 | 0.9868 | 0.9805 | 0.9791 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, H.T.; Lopez Caceres, M.L.; Moritake, K.; Kentsch, S.; Shu, H.; Diez, Y. Individual Sick Fir Tree (Abies mariesii) Identification in Insect Infested Forests by Means of UAV Images and Deep Learning. Remote Sens. 2021, 13, 260. https://doi.org/10.3390/rs13020260
Nguyen HT, Lopez Caceres ML, Moritake K, Kentsch S, Shu H, Diez Y. Individual Sick Fir Tree (Abies mariesii) Identification in Insect Infested Forests by Means of UAV Images and Deep Learning. Remote Sensing. 2021; 13(2):260. https://doi.org/10.3390/rs13020260
Chicago/Turabian StyleNguyen, Ha Trang, Maximo Larry Lopez Caceres, Koma Moritake, Sarah Kentsch, Hase Shu, and Yago Diez. 2021. "Individual Sick Fir Tree (Abies mariesii) Identification in Insect Infested Forests by Means of UAV Images and Deep Learning" Remote Sensing 13, no. 2: 260. https://doi.org/10.3390/rs13020260
APA StyleNguyen, H. T., Lopez Caceres, M. L., Moritake, K., Kentsch, S., Shu, H., & Diez, Y. (2021). Individual Sick Fir Tree (Abies mariesii) Identification in Insect Infested Forests by Means of UAV Images and Deep Learning. Remote Sensing, 13(2), 260. https://doi.org/10.3390/rs13020260