Abstract
Human pose reconstruction has been a fundamental research in computer vision. However, existing pose reconstruction methods suffer from the problem of wall occlusion that cannot be solved by a traditional optical sensor. This article studies a novel human target pose reconstruction framework using low-frequency ultra-wideband (UWB) multiple-input multiple-output (MIMO) radar and a convolutional neural network (CNN), which is used to detect targets behind the wall. In the proposed framework, first, we use UWB MIMO radar to capture the human body information. Then, target detection and tracking are used to lock the target position, and the back-projection algorithm is adopted to construct three-dimensional (3D) images. Finally, we take the processed 3D image as input to reconstruct the 3D pose of the human target via the designed 3D CNN model. Field detection experiments and comparison results show that the proposed framework can achieve pose reconstruction of human targets behind a wall, which indicates that our research can make up for the shortcomings of optical sensors and significantly expands the application of the UWB MIMO radar system.
1. Introduction
Computer vision sensing technologies, such as visible light and structured light, have drawn more and more attention in the fields of anti-terrorism, stability maintenance, emergency rescue, and scene monitoring [1,2,3,4,5]. Human pose reconstruction is a hot topic of computer vision that has been explored by researchers in recent years, which can be applied in the healthcare industry by automating patient monitoring [6], and used in automatic teaching for fitness, sports and dance, motion capture, augmented reality in film production, and training a robot to follow a human pose doing specific actions [7,8,9].
During the last decade, various human pose reconstruction methods have been proposed. At present, the main pose reconstruction approaches can be divided into traditional methods and deep learning-based methods. The traditional methods are generally designed two-dimensional (2D) human body parts detectors based on the graph structure and deformation part model, which use the graph model to establish the connectivity of each part, and then combine the relevant constraints of human kinematics to continuously optimize the graph structure model to reconstruct the human body pose. Although traditional methods have high efficiency, the extracted features are mainly artificially set and cannot make full use of image information [10]. As a result, the algorithm is subject to different appearances, viewing angles, occlusions, and inherent geometric ambiguities in the image. The pose reconstruction methods are based on the deep learning method and mainly use the convolutional neural network (CNN) [11] to extract human pose features from the image. Compared with traditional methods of artificial design features, CNN can obtain more abundant semantic information, and can obtain the multiscale multi-type human key points under different receptive fields. Furthermore, human pose reconstruction methods have developed from 2D to three-dimensional (3D), and deep learning has achieved remarkable success in both fields. For the 2D pose reconstruction field, DeepPose is the first method for single-person human pose reconstruction based on deep learning [12], which uses multistage regression to design CNN, and uses coordinates as the optimization goal to directly return to the 2D coordinates of human bone joint points. OpenPose is one of the most popular pose reconstruction methods [13], it proposed a part affinity fields (PAFs) theory to describe the degree of connection between the joints while estimating the confidence probability maps; the combination of the two operation results has higher pose reconstruction accuracy. Mask-RCNN is a very popular semantic and instance segmentation architecture [14,15], which uses a Faster R-CNN as the human detector and a full convolution network (FCN) as the basic network structure of a single person pose detector, which can simultaneously predict the position of candidate frames and human pose of multiple objects. At the same time, DeepCut [16], CPN [17], and RMPE [18] have also achieved good pose reconstruction results.
Concerning 3D pose reconstruction, there are mainly two existing methods, i.e., one method directly predicts the 3D pose from the image and the other method is a two-step approach that, first, predicts the 2D pose, and then lifts the 2D pose to the 3D pose. As compared with the first method, the second method reduces the complexity of the entire task, which is easier for the network to learn the 2D to 3D pose mapping, and it is better to introduce reprojection for semi-supervision. Tome et al. [19] proposed a typical end-to-end model with a multistage CNN architecture to reconstruct 3D pose from a single image and used the knowledge of plausible 3D landmark locations to refine the search for better 2D locations, which provided a simple and efficient method. Pavlakos et al. [20] proposed a multistage hourglass architecture to reconstruct human 3D pose from a single image, which improved the spatial resolution of the heatmap through continuous coarse-to-fine operation, and finally obtained a 3D heatmap to reconstruct human pose. Zhou et al. [21] designed a weakly-supervised human pose reconstruction method. Their network structure is similar to hourglass architecture, where the input image, first, extracts the features through the convolution layer, and then predicts the 2D heatmap of joints through the hourglass architecture. These heatmaps are added to the feature maps generated in the hourglass architecture, and input to the depth module for 3D pose prediction. Wandt et al. [22] proposed a training method for generating confrontation, using a discriminator for weak supervision, thereby obtaining more accurate prediction results from the 2D pose to the 3D pose. Additionally, the discriminator introduced constraints such as bone length and motion angle. Other than reconstructing human pose from a single image or 2D pose, many approaches have been proposed based on RGB and depth data [23], RGB image sequences data [24], and multiple perspectives data [25].
Human pose reconstruction has developed rapidly [26,27], and has made breakthroughs in computer vision. However, most of the research has been based on visual sensors that are unable to cope with shaded and dark environments, especially complex urban environments. Visual sensors also face the privacy leakage problem, which limits their applications. A radar system with electromagnetic waves as the information carrier is an active detection sensor, which is different from vision system technology and can complement visual information. In terms of the technical principle, it solves the detection problems caused by the complex environment such as no light, shielding, and non-line-of-sight [28]. Existing studies on radar sensors mainly use the micro-Doppler effect of radar to classify the movement of human targets [29,30]. However, these studies can only judge the motion state of human targets, and cannot obtain the spatial location information of different body parts of human targets. There are few studies on human pose reconstruction based on radar sensors, which is a new and urgent research. Zhao Mingming and others proposed a pose reconstruction method based on radio frequency signals called “RF-Pose” [31,32]. This method used a “T” shaped radar system with a bandwidth of 1.8 GHz (5.4–7.2 GHz) and used a teacher-student network to reconstruct the pose of human targets. Arindam Sengupta et al. designed a real-time human skeletal posture estimation method based on millimeter-wave radar and CNN called “mm-Pose” [33]. This method converted 77 GHz radar data into point cloud data, and then used CNN to reconstruct the pose of the human target from the projection image of the point cloud data. Those methods further expanded the application range and greatly improved the practicality of radar technology. However, although the sensors used in these methods have higher resolution to ensure detection accuracy, they have limited penetrability and can only be used in unobstructed scenes or scenes obstructed by better penetrating material.
In this paper, a low-frequency 3D ultra-wideband (UWB) multiple-input multiple-output (MIMO) radar is used as the detect sensor, where low frequency refers to the frequency band below 3 GHz, which has better penetrability of the brick wall. The 3D radar can provide 3D information of the distance, azimuth, and height of the detected target. As compared with the conventional narrow-band microwave system, the UWB radar has higher range resolution. As compared with the one-dimensional (1D) radar used to measure the distance of the target and the 2D radar used to measure the distance and azimuth of the target [34], the 3D MIMO radar has wider detection range [35,36,37], and can obtain more abundant target scattering information, which has significant advantages in target imaging, target recognition, and through wall target detection.
Villanova University was the first institute to carry out theoretical research on 3D UWB radar imaging technology. In 2008, they proposed a 3D radar imaging method based on time-delay summation beamforming [38]. In the same year, Cameron company developed a 3D UWB radar imaging system called “xaver800”, it proved that the combination of large MIMO plane arrays and ultra-wideband signals could achieve 3D imaging of targets behind walls. Li et al. used a array to detect a 2 m target behind a wall [39]. The experimental results showed that low-frequency signals also had the ability to image human targets in three dimensions, but the imaging results of the trunk, limbs, and other structures were still relatively fuzzy. Therefore, more and more scholars have begun to study the super-resolution method of 3D radar imaging. For example, Zhao D et al. introduced deconvolution super-resolution in 3D radar imaging and verified it with simulation and measured data [40]. Fadel et al. proposed an imaging method named “RF-capture” for the contour of human targets behind the wall [41]. This method studied the scattering point alignment technology based on common human models, and finally obtained a high-resolution and accurate human contour image. However, limited by the portability and cost of the radar system, radar images, especially 3D radar images have been abstract and difficult to understand, even though scholars have designed various methods to improve the resolution of radar images.
Taking into consideration the advantages and disadvantages of the approaches mentioned above, we propose a pose reconstruction framework to detect the pose of targets behind walls. In our framework, the low-frequency UWB MIMO radar is used to detect the target, and then sequentially performs 2D imaging, constant false alarm rate (CFAR) detection, tracking, and 3D imaging processing of the radar echo. Then, the trained 3D CNN is used to reconstruct the root-relative 3D pose of the human target from the radar 3D images, and the final absolute 3D pose is obtained by fusing the human pose with the target root joint position. Our research transforms traditional abstract UWB radar images into the easy-to-understand 3D pose, and it greatly improves the visualization ability of UWB radar. The main contributions of the proposed approach are summarized as follows:
- A novel pose reconstruction framework is developed to solve the 3D pose reconstruction problem of occluded human targets.
- It is the first pose reconstruction approach that uses low-frequency UWB MIMO radar as the detect sensor, which has better penetrating performance; it can penetrate many materials such as curtain, wood, plastic board, brick wall and so on, making it applicable to more complex indoor scenes.
- We adopt the sequence of large-scale 2D imaging, and then fine 3D imaging to process radar signals. As compared with the method of direct 3D imaging to radar signal, our method ensures imaging efficiency and imaging quality simultaneously.
- A special 3D CNN is designed to reconstruct 3D poses from 3D images. Taking the type and characteristics of the input data into consideration, an end-to-end 3D CNN is contrived to operate supervised learning.
The remainder of the paper is organized as follows: In Section 2, we describe the supporting materials for our method design; in Section 3, we demonstrate the process of the UWB MIMO radar pose reconstruction framework; in Section 4, we present the network test results and field experimental results; in Section 5, we include a discussion; followed by the conclusions, in Section 6.
2. Materials
2.1. Multiple-Input Multiple-Output (MIMO) Radar through-Wall Imaging
2.1.1. MIMO Radar
In this subsection, we mainly describe MIMO radar. Since the MIMO radar system has multiple transmitting antennas and multiple receiving antennas, it has more equivalent channels, thereby obtaining a larger detection range and higher signal gain, which is widely used for target detection and identification. At present, there are two kinds of MIMO arrays, i.e., line array and plane array, in which a line array can obtain 2D information of the target, such as distance-azimuth information or distance-height information. As compared with the line array, the plane array adds the array in height dimension to obtain the height dimension information of the human target, which can simultaneously obtain the distance-azimuth-height information. Therefore, the plane array is considered in this article, which can receive more abundant information about targets.
The MIMO radar system adopts a stepped frequency continuous wave (SFCW) as the transmitted signal in this article [42]. Compared with the radar system with a narrow pulse signal, the SFCW signal is easier to realize high transmission power [43], with good bandwidth expansion and long operating distance, which is more conducive to through-wall detection. The UWB radar transmits the electromagnetic wave signal, penetrates the shielding, irradiates the human target, and then reflects the radar echo. After preprocessing such as mixing frequency and digital demodulation, the expression of the echo signal is defined in (1) [44]. Suppose the MIMO array has transmitting antennas and receiving antennas, there are a total of channels as follows:
where denotes the complex amplitude of point , is the speed of point , is the number of frequency points, denotes the frequency corresponding to the th frequency point, and is the round-trip propagation delay from the pixel to the th transmitting antenna and the th receiving antenna, where , . The MIMO radar human target detection sketch map as shown in Figure 1a; it can be seen from Figure 1a that the MIMO radar has a wide detection range and can obtain the reflection echo of all parts of the human body.
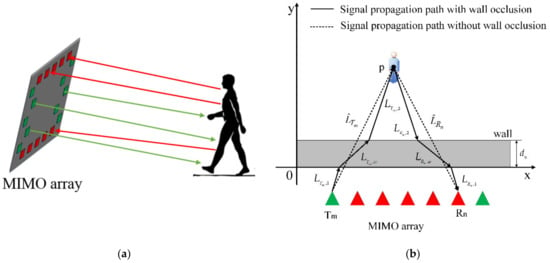
Figure 1.
(a) Sketch map of multiple-input multiple-output (MIMO) radar human detection; (b) Geometric schematic diagram of MIMO radar through-wall imaging.
However, in the actual application scene, the human target will reflect echo, and other furniture and walls in the detection scene will also reflect echo. Since the human target cannot be completely stationary, even if the human target is stationary, its respiration and heartbeat will modulate the radar signal. Therefore, the moving target indication (MTI) [45] algorithm is usually used in radar signal processing to filter out the stationary clutter and extract the echo of the moving target, which greatly improves the detection ability of the moving target in the background of clutter and improves the anti-interference ability of radar system.
2.1.2. Back-Projection Imaging of MIMO Radar
In this article, the back-projection (BP) algorithm is used as the imaging method, which is a typical and widely used time-domain image formation, applicable for almost any antenna array layout; it is the most commonly used method for through-wall imaging [46]. The basic idea of the BP algorithm is to calculate the time delay between a point in the imaging area and the receiving and transmitting antennas, and then coherently stack the contributions of all echoes to obtain the corresponding pixel value of the point in the image. In this way, the image of the imaging area can be obtained by coherently stacking the whole imaging area point by point. As for the point, , in the imaging space, its 3D BP imaging formation of MIMO radar can be represented as:
where is the total frequency points, is the total channels, is the radar echo as defined in (1), and is the round-trip propagation delay.
As for the human target, it is an extended target that contains many scattering points of various parts of the body. We use (2) to calculate these scattering points of all channels to focus the energy at the position of the limbs, and then obtain the morphological distribution of the human target in space, which is the 3D imaging result of the human target containing distance-azimuth-height information. However, due to the limitation of the radar aperture, the resolution of 3D imaging is low, and it is hard to observe the shape of the human target. Therefore, we consider using a neural network to further reconstruct the pose of the human target.
Furthermore, 2D imaging and 3D imaging techniques are both used in this article, where the 2D imaging range is set as the azimuth-distance plane at a fixed height in detect space to achieve the azimuth and distance information of the target, and the 3D imaging is adopted to capture the azimuth, distance, and height 3D information of human targets. Notably, 2D imaging and 3D imaging use the same radar system and imaging principle, except the imaging dimension is different. In a sense, the 2D imaging result is a slice of the 3D imaging result.
2.1.3. Through-Wall Target Imaging
As for the through-wall target imaging, except power attenuation, the propagation speed of the electromagnetic wave in the wall is also lower than that in free space, the round-trip delay will be lengthened when the electromagnetic wave propagates through the wall [47]. The working processing of MIMO radar through-wall imaging is shown in Figure 1b, which presents the transmission path between th transmitting antenna and th receiving antenna to detect the point . Therefore, the time delay in (2) can be expressed as:
where is the speed of light and is the relative dielectric constant of the wall. and are related to the thickness and relative dielectric constant of the wall, respectively. If the wall penetration is not considered, the transmission path as the dotted line in Figure 1b, therefore, the time delay corresponding to the point is calculated as:
obviously, , the locations of the target in the result of BP imaging will be farther than the real locations of the target. Therefore, in the process of through-wall target imaging, we perform wall compensation according to the different wall materials to ensure the target is in the correct position.
2.2. Convolutional Neural Network (CNN) for Pose Reconstruction
As a hierarchical network structure, CNN can separate and abstract the input data layer-by-layer through stacked convolutional layers to realize the integration of feature extraction and classification recognition. The first successful commercial CNN was LeNet proposed by Yann LeCun, in 1998 [48], which was used for handwritten digital recognition in emails; it laid the foundation for the basic structure of CNN. After that, AlexNet [49], VGGNet [50], ResNet [51], and other convolutional network models have constantly refreshed the performance ceiling in multiple tasks of computer vision. However, the composition and structure of various convolutional networks are not much different, except that the size design of the convolution kernel and the information transmission line of the convolution kernel have been improved.
The typical convolutional neural network consists of the following three parts: convolutional layer, pooling layer, and nonlinear activation function. The components of the convolutional neural network stack with each other, and hierarchical data analysis is carried out through forwarding propagation, and error conduction and network parameter optimization are carried out through backward propagation. The forward propagation is the process of first inputting a sample vector to the network, then, each element of the sample vector goes through the step-by-step weighted summation and nonlinear activation of each hidden layer, and finally outputs a prediction vector from the output layer. The backward propagation is the opposite of the forwarding propagation, which uses the gradient descent method to obtain model parameters layer-by-layer from the last layer to the first layer of the neural network model to minimize the loss function of the neural network model on the training data. Notably, the forward propagation and backward propagation are the basic structures of convolution neural network design [52].
The CNN network is widely used in the optical image field for the pose reconstruction task, the general structure mainly includes the feature extraction module and pose reconstruction module, as shown in Figure 2. Firstly, the feature extraction module extracts the intensity and location information of the human body in the input image through multilayer convolution operations, and then obtains the depth feature matrix. Secondly, the pose reconstruction module transforms the feature matrix into probability confidence maps through multilayer deconvolution operations. Finally, the joint location information of the human target is reconstructed from the probability confidence maps using the softmax function. Furthermore, the pooling layer and nonlinear activation function layer are after each convolutional and deconvolutional layer.
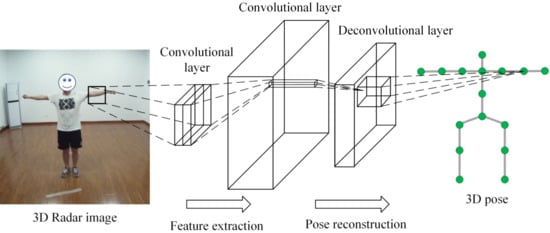
Figure 2.
Schematic diagram of human pose reconstruction based on convolutional neural network (CNN).
The difference between an optical image and a 3D radar image is that an optical image has better resolution, and a 3D radar image can obtain the 3D spatial information of a human target body. The common point is that both contain the body structure information of a human target, which is the feature extracted by a deep learning network to reconstruct human pose, as described in Figure 2. Considering that the 3D radar image contains the 3D structure information of a human target, although the resolution is low, it is still possible to reconstruct human pose from a 3D radar image using CNN.
3. Methods
In this section, we present a detailed description of the flowchart and the implementation of our proposed framework. First, the dataset preparation is introduced, which is the basis of the network training. Then, the network architecture, loss function and training details are described in turn. Since there are many kinds of research on radar target detection, clustering, and tracking, and these technologies are relatively mature, this article will not specifically introduce their implementation process.
3.1. The Proposed Framework
On the basis of the development of UWB MIMO radar 3D imaging and deep learning technology, we designed a framework for through-wall human target pose reconstruction. The whole flowchart of our proposed pose reconstruction framework is shown in Figure 3. The proposed framework covers two stages, i.e., training process and application. In the training process stage, the 3D radar image from the dataset is translated into a 3D pose by the designed 3D CNN model. The training loss is obtained by calculating the error between the reconstructed pose and the ground truth, and then the network parameters are optimized by backward propagation.
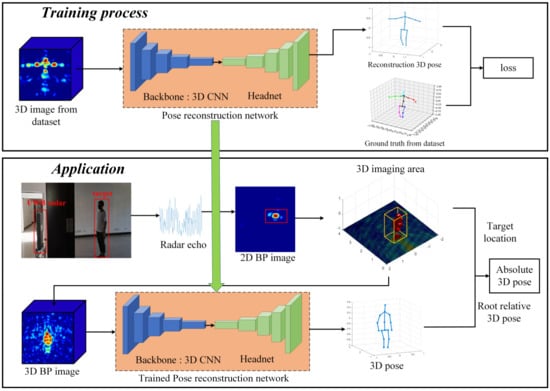
Figure 3.
The whole flowchart of our proposed pose reconstruction framework.
In the application stage, we use the UWB radar system to obtain the radar echo of the hidden target, and then carry out the 2D BP imaging in the azimuth-range plane to get the 2D images of the detection scene. The 2D images are processed by CFAR detection, clustering, and tracking to lock the location of the target on the azimuth-range plane. After that, a small-scale fine 3D BP imaging is performed on the area where the target is located, and the 3D image of the human target is obtained. Next, we input the 3D radar image into the trained pose reconstruction network obtained from the training process stage to reconstruct the root-relative 3D pose of the target. Finally, the detected target root joint location is fused with the estimated 3D pose to obtain the final absolute 3D pose. For multiple target detection scenes, we only consider the targets that can be distinguished in the 2D BP imaging results, that is the spatial position of the targets is greater than the resolution of our radar system. CFAR was used to extract the region of interest of each target, and then 3D imaging was conducted for each target separately, where the motion state of multiple targets does not affect our detection. For targets with relatively close spatial positions, some super-resolution algorithms can be used to distinguish them, which will be explored in future studies.
3.2. Implementation
3.2.1. Dataset
The dataset, in this paper, is jointly recorded by the UWB radar system and optical camera, the data collection scenario is shown in Figure 4. It can be seen from Figure 4 that the data collection system includes UWB radar, camera, and personal computer (PC), in which the UWB radar collects radar data, the camera collects image data, and the PC controls the data synchronization of the two sensors.
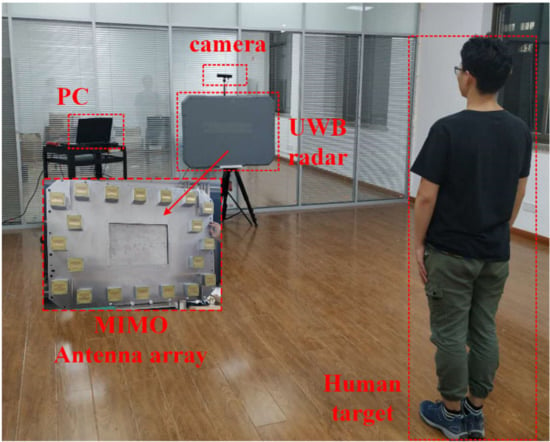
Figure 4.
Dataset collection scenario.
We deployed a UWB MIMO system with 10 transmitting antennas and 10 receiving antennas. As shown in Figure 4, the 10 transmitting antennas are located on the left and right sides of the array, and the 10 receiving antennas are located on the top and bottom sides of the array, where the arrangement of the antenna array ensures that the imaging result has a lower side lobe. The size of the antenna array is . The UWB radar transmits SFCW signals in 1.78–2.78 GHz at a step of 4 MHz, and the pulse repetition frequency is set at 10 Hz. The working frequency band and bandwidth ensure that our system has better penetration and range resolution, making the resolution smaller than the width of body parts of the human target, so that the body contour information of the human target can be obtained [53]. The pulse repetition frequency is obtained by taking the system cost and algorithm operation into account comprehensively. Moreover, 10 Hz was able to meet the requirements of unambiguous detection to conventional indoor actions [54].
The dataset preparation flowchart is presented in Figure 5, where the process of generating 3D radar images is the same as that in Figure 3. The optical camera captures the image of human target, and then inputs the image into the trained optical image pose reconstruction network to reconstruct the 3D pose of the human target, where the 3D pose contains 16 joint points, namely head, thorax, spine, shoulder (left and right), elbow (left and right), wrist (left and right) and, hip (left, right, and center), knee (left and right) and foot (left and right), the details are shown in Figure 6. Finally, the 3D radar image and 3D pose are stored in the dataset as samples and labels, respectively.
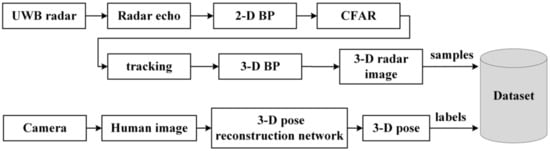
Figure 5.
Flowchart of the dataset preparation.
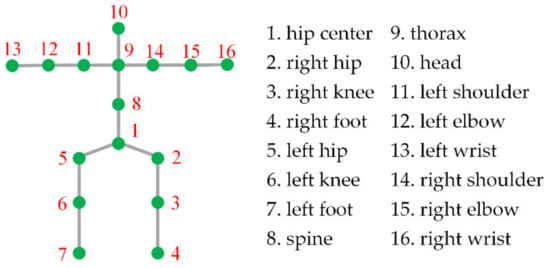
Figure 6.
Distribution of human joint points.
For more detail about the optical image 3D pose reconstruction network used in this article please refer to [19]. It should be noted that the 3D pose obtained by this network is not completely accurate, it just provides an approximate pose label for our model. Meanwhile, the 3D pose label acquisition method adopted in this article is not the only one, it can also be obtained through the multiview camera system or Microsoft Kinect. This is not the focus of this paper, and therefore we will not introduce it in detail.
The dataset contains multiple people, multiple scenes, and multiple action data, where the types of actions include walking, boxing, clapping, waving, calling, sitting, raising hands, etc., which ensures the diversity of training data. We collected 120,000 frames of data and all of the data were recorded in the visual scenes.
3.2.2. Network Architecture
The overall pose reconstruction network architecture is shown in Figure 7. It is an end-to-end full convolutional network, where the backbone network is designed based on 3D Resnet [48], and the head network is composed of multiple deconvolution modules. It takes the 3D radar image as the input data, and each image data contains three-dimensions, namely azimuth, distance, and height. The human body features of the input radar image are first extracted by a Conv3D module, and then aggregated by a max-pooling operation. The output features are processed by eight Resnet 3D blocks to extract the deep features, and then after five deConv3D operations, the location confidence probability maps of the human pose are obtained. Each location map represents the possible 3D location for every pixel, where the confidence probability of the joint location is higher than other pixels. Finally, the confidence probability maps are converted into 3D pose coordinates of human targets through the soft-argmax operation. As compared with the commonly used argmax function, the soft-argmax function is differentiable, which can provide a higher precision coordinates estimation result. We also give the detailed overall 3D CNN network structure parameters, as shown in Table 1, where the size of the input radar image is , the size of the output pose is , which represents the 3D coordinates of the 16 joint points.
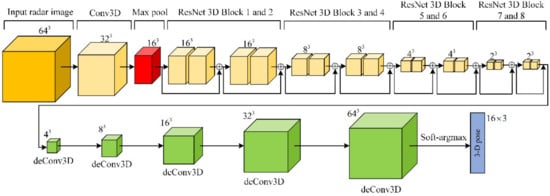
Figure 7.
Pose reconstruction three-dimensional (3D) CNN network architecture.

Table 1.
Overall 3D CNN network structure parameters.
3.2.3. Loss Function
In our model, we train the network by minimizing the distance between the ground truth value and the predicted value of the joint point locations. The loss is defined in the following equation:
where is the batch size during training and is the total number of joint points, donates the ground truth position of the th joint point, and donates the predicted position of the th joint point. The loss is also the most commonly used evaluation index of 3D pose reconstruction accuracy, which is called mean per joint position error (MPJPE).
3.2.4. Training Details
For the training process, 80% of the samples were in the training set, and 20% of the samples were in the testing set, where the training data and testing data are from different experimental human targets and scenes. We use the adaptive moment estimation (Adam) as the optimization method [55], it combines the advantages of AdaGrad and RMSProp. Adam comprehensively considers the first-moment estimation and second-moment estimation of the gradient to calculate the update step size, which overcomes the problem of the sharp decrease of AdaGrad gradient and has shown excellent adaptive learning rate ability in many applications. The rectified linear unit (Relu) [56] is utilized as the activation function in the training process, which is most commonly used at present. As compared with the sigmoid function, the Relu takes less computation and does not have the vanishing gradient problem, which makes the convergence rate of the model maintain a stable state. Meanwhile, the sparsity of the Relu can alleviate the over-fitting problem. The training initial learning rate is and reduced by a factor of 10 at the 20th and the 30th epoch. The training batch size is 10. The total training epoch is set as 50, and our networks are implemented in PyTorch deep learning framework.
4. Results
In this section, first, we evaluate the network through the test results analysis and the feature analysis, and then the field detection performance is verified by multiple scene experiments, comparison experiments, and through-wall detection performance analysis.
4.1. Network Evaluation
4.1.1. Test Results and Analysis
We evaluate the root-relative pose reconstruction accuracy of our proposed framework on the test dataset by comparing it with the ground truth predicted from the optical images, where the test set contains the targets at different distances. The training loss and evaluation error are shown in Figure 8a,b, where the blue line in Figure 8a is the training loss and the red line is the motion average of the training loss. It can be seen from Figure 8a that the training error gradually decreases with an increase in training iterations. At the same time, with an increase in training epochs, the fitting ability of our network becomes better, and therefore the evaluation error decreases and gradually converges to the minimum value, where the minimum mean average evaluation error is 37.87 mm, which is obtained in the 23th epoch, as shown in Figure 8b.
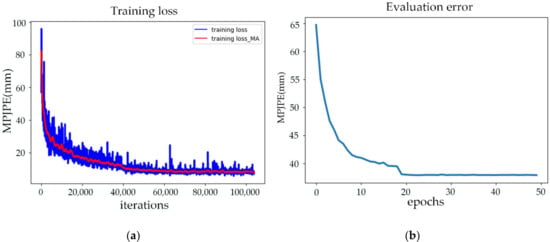
Figure 8.
(a) The training loss of our network; (b) The evaluation loss on the test set.
The different joints reconstruction error in the 23th epoch is shown in Figure 9, it reports the MPJPE of 16 different joints, where the joint names correspond to the numbers referred to in Figure 6. Figure 9 shows that the main body parts, such as the hip center and spine, achieve less reconstruction error than the average error, while the elbows and wrists achieve higher reconstruction error. The main reason for this phenomenon is that the small size of the elbow and wrist leads to weak reflected signal strength. When the distance of the target is relatively far, the size of the elbow and wrists may be smaller than the resolution of the UWB radar system, which makes it impossible to capture these body parts. Furthermore, the elbow and wrist have a higher degree of freedom and a range of motion than the hip-center and spine, resulting in higher joint reconstruction error. Overall, it can be seen from Figure 8 and Figure 9 that our framework achieves excellent pose reconstruction accuracy.
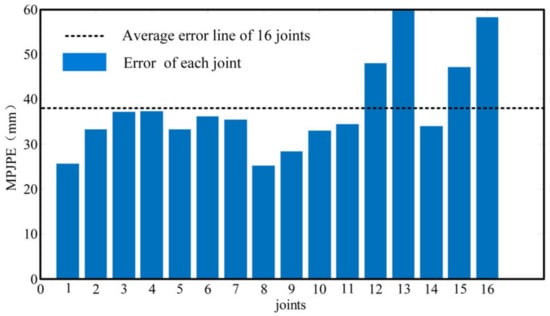
Figure 9.
Joints reconstruction error.
4.1.2. Feature Analysis
In this subsection, we design an experiment to analyze the feature extracted by the neural network and show the working process of our 3D CNN network, the detect scene as shown in Figure 10a. The 3D radar image of the human target is obtained through the detection and imaging operation, and then the azimuth-height projection is carried out to the 3D radar image to get a more intuitive visualization result; the project result is shown in Figure 10b.
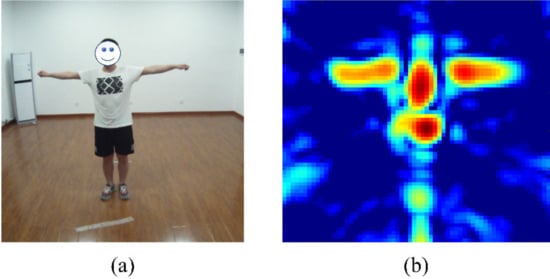
Figure 10.
(a) Human target; (b) Azimuth-height projection image of the 3D radar image.
The 3D radar image is input into the trained network, and then the features extracted by the first layer of the network are visualized. The visualization results are presented in Figure 11. The output of the first layer is a tensor of size , where 64 represents the number of features, represents the feature matrix, the 64 feature matrixes are projected, sequentially, and then the results are obtained, as shown in Figure 11. It can be seen from Figure 11 that the first layer of the network extracts the human body contour features from the 3D radar image as the first image in Figure 11, which are the most important features for human pose reconstruction. Notably, not all the features are useful or can be understood intuitively, so there will be some incomprehensible images in the feature visualization results, which are normal phenomena in the deep learning field.

Figure 11.
Feature visualization of the first layer of 3D CNN network.
We also give the visualization results of the features extracted by the last layer of our 3D CNN network, as shown in Figure 12, which are the projection of the confidence probability maps of 16 joints. It represents the probability of the position of the joint point in the azimuth-height plane, where the point with the largest value is considered to be the joint coordinate, which can be obtained by using the soft-argmax function. By comparing the positions of the 16 joints with the reference optical image in Figure 10a, it is found that the positions of the joints are reconstructed by our network. Therefore, the feature visualization results verify the effectiveness of our trained network.
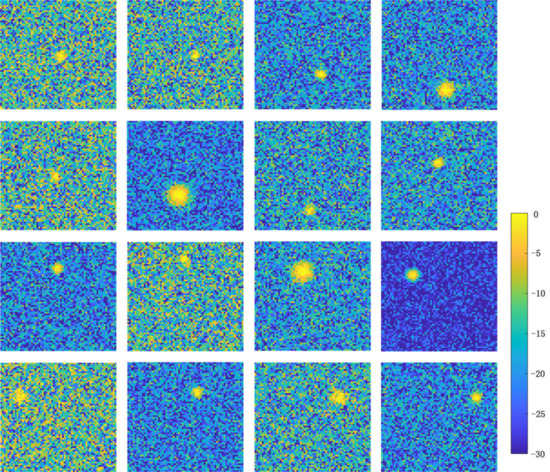
Figure 12.
Feature visualization of the last layer of 3D CNN network.
4.2. Field Experiments
4.2.1. Experimental Setup
The field experiment scene is shown in Figure 13. Considering the size of a single room, the detection area is set as , where the azimuth range is from −2 to 2 m, and the distance range is from 1 to 6 m, all the experimental targets move in this area. In the experiment, the azimuth range of 2D imaging is (−2, 2), the distance range is (1, 6), the height of the 2D imaging is 0 m, and the 2D imaging matrix is . For the range of 3D imaging, considering the height of the general human target and the length of the open arms, we set the azimuth range to (x − 1, x + 1), the distance range is (y − 1, y + 1), the height range is (−1, 1.5), where (x, y) is the center coordinate of the target in the 2D image plane, and the 3D imaging matrix is . Furthermore, the UWB MIMO radar system parameters are as described in Section 3.2.1. and all the field application processing algorithms were implemented in the Linux system using the python programming language.
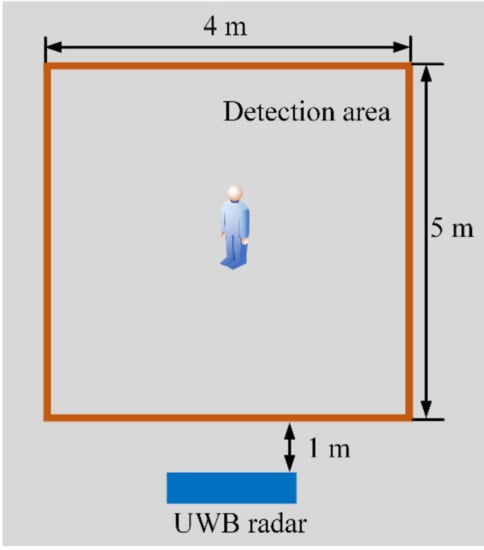
Figure 13.
Experiment scene.
In this section, we also constructed some simulation experiments to analyze the computational methods of our framework and other methods, where the simulation software is MATLAB (Mathwork Inc., Natick, MA, USA), the system memory is 64 GB, and the GPU memory is 6 GB.
4.2.2. Multiple Scene Experiments
To validate the measured performance of our approach under different numbers of human targets and different occlusion materials, we designed two field experiments with different scenes, which were single target scene and two targets scene. For the single target scene, as shown in Figure 14a, the UWB radar is placed in room B, while the human target is blocked by a brick wall in room A. For the two targets scene, as shown in Figure 15a, two human targets are in the detection area, where one target is blocked by the plastic board, and the other is not.
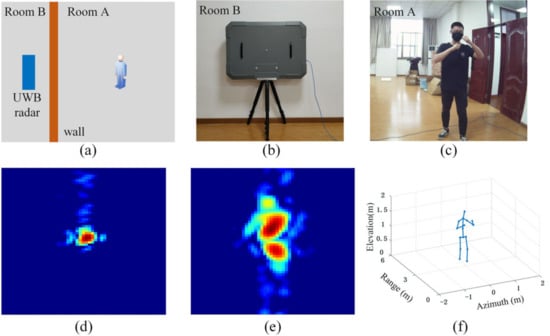
Figure 14.
(a) Sketch map of the single target scene; (b) Scene of room B;(c) Scene of room A for visual reference; (d) 2D back-projection (BP) imaging result of the whole detection scene; (e) Azimuth-height projection image of 3D BP imaging result; (f) Pose reconstruction results from our framework.
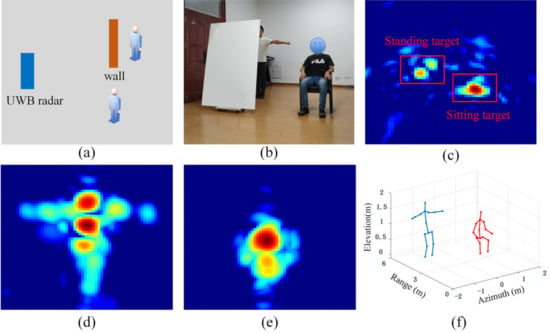
Figure 15.
(a) Sketch map of the two targets scene; (b) Detection scene for visual reference; (c) 2D BP imaging result of the whole detection scene; (d) Azimuth-height projection image of the 3D BP imaging result of the standing target; (e) Azimuth-height projection image of the 3D BP imaging result of the sitting target; (f) Pose reconstruction results from our framework.
As for the single target experiment, Figure 14c shows the detection scene for visual reference, where the human target holds the boxing pose behind the brick wall with a thickness of 24 cm. The UWB radar system is placed in room B, as shown in Figure 14b. Figure 14d is the 2D imaging result of the detection area, which takes CFAR detection to lock the target position in the 2D image, which contains the distance and azimuth information of the target. Then, the 3D imaging is performed on the area where the target is located. To see the 3D images more intuitively, we made a maximum projection towards the azimuth-height direction in the 3D images, the projection image is shown in Figure 14e, which represents the azimuth-height information of the human body structure. Figure 14f is the final absolute pose calculated by our framework, it shows that our framework produces convincing results even for the target behind the brick wall, which proves that our system has strong penetrability.
For the two targets experiment, Figure 15b shows the detection scene with two human targets, one of them is sitting, the other is standing behind the plastic wall with arms open. Figure 15c is the 2D BP imaging result of the whole detection scene, the locations of the two targets are locked by the CFAR detection processing. Then, 3D BP imaging was performed on the two targets, sequentially. The azimuth-height projection images of two targets are shown in Figure 15d,e. It can be seen from Figure 15d,e that the projection images reflect the scattering information of the human body in the azimuth and height direction, and the scattering center height of standing and sitting targets are also different. Input the 3D radar image into our trained pose reconstruction network to obtain the root-relative 3D pose of the two targets, and then fuse with the target location to get the absolute 3D pose, as shown in Figure 15f. As compared with the reference image in Figure 15b, we can see that the poses reconstructed from the radar images are the same as the real pose of the targets.
4.2.3. Comparison with Optical Method
In this subsection, we construct some field measured experiments to compare the pose reconstruction performance of our framework and the optical method. The experiments include the scene without occlusion, the scene partially occluded by the plastic board, and the scene completely occluded by smoke, as shown in Figure 16a,d,g, where all the targets are in moving state. Figure 16b,e,h is the 3D poses of the three scenes predicted from the optical images by [19], where the different colors represent different limbs, Figure 16c,f,i is the 3D pose reconstructed from 3D radar images by our framework. As can be seen from Figure 16a–c, both methods can effectively reconstruct human pose for the free space scene. However, for the partially occluded scene in Figure 16d, since the lower body of the target is occluded by the board, the optical sensor cannot obtain the structure information of the lower body. Therefore, the 3D pose can only be reconstructed by the random estimation method, which leads to poor pose reconstruction results, as shown in Figure 16e. However, our system is not affected by occlusion and obtains the pose reconstruction result in Figure 16f, which is consistent with the actual situation. For the smoke occluding scene in Figure 16g, the optical sensor cannot capture the human target, so the pose reconstruction output is empty in Figure 16h, but our framework can still work normally to obtain the target location and 3D pose, as shown in Figure 16i.
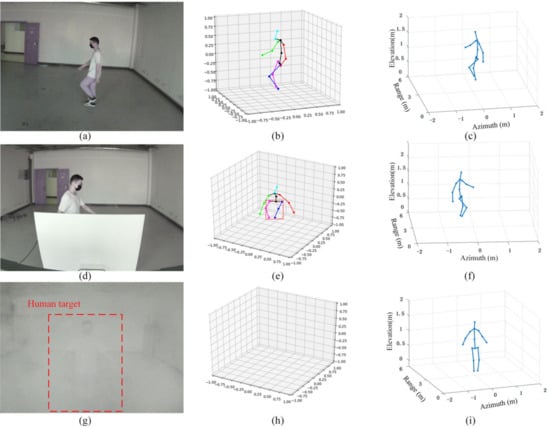
Figure 16.
Comparison with the optical sensor. (a,d,g) The optical images captured by camera; (b,e,h) The 3D poses predicted by [19]; (c,f,i) The 3D poses reconstructed by our framework.
4.2.4. Performance Comparison
Since there are few kinds of research on human pose reconstruction based on the radar system, especially for low-frequency UWB MIMO radar with low resolution, and there is a lack of public datasets and network structures, therefore, we compare the final pose reconstruction accuracy with the existing two radar pose reconstruction methods of different systems, namely RF-Pose3D [32] and mm-Pose [33]. The pose reconstruction average errors of different methods are shown in Table 2, where it can be seen from Table 2 that the pose reconstruction accuracy of our method is better than the other two methods. As compared with the RF-Pose3D method, for our system with low working frequency and narrow signal bandwidth, the imaging resolution is lower than RF-Pose3D. However, in terms of imaging acquisition, we adopt 2D imaging first, and then carry out high grid density 3D imaging of the target area after detecting the target. As compared with the 3D imaging of the whole detection scene directly by RF-Pose3D, our method does not need to image the non-target area, which avoids the waste of calculation, and the high grid density 3D imaging operation can ensure the quality of 3D imaging, thereby ensuring better pose reconstruction accuracy. The millimeter-wave radar adopted by mm-Pose has high frequency and large bandwidth, therefore, it has better resolution. However, the system is a 2D radar sensor, although 3D human body data is constructed through 3D fast Fourier transform (FFT), and therefore the information provided in the third dimension is limited, and it cannot achieve high pose reconstruction accuracy. Meanwhile, RF-Pose3D and mm-Pose both take some measures to reduce the dimensionality of the network input data, which also cause information loss.

Table 2.
Detection performance comparison.
4.2.5. Computation Time Analysis
As for the computation analysis, we focus on the comparison with RF-Pose3D, which is the most similar to our processing method. Since the deep learning processing part is relatively fast, we do not make a specific comparison, and therefore only compare the radar imaging time. The computation time comparisons are shown in Table 3, which are the simulation results for the same detect scene, where the size of the detection area and the imaging parameters are as described in Section 4.2.1., and the imaging grid densities of two methods are the same. It can be seen from [31,32] that RF-Pose3D directly constructs 3D imaging of the entire detection scene, therefore, the imaging time is fixed no matter how many targets are in the detect scene. As shown in Table 3, the imaging time is 2.641 s. As for our method, the total imaging time is the sum of 2D imaging time and 3D imaging time, and the calculation formula is as follow:
where is the 2D imaging time, is the 3D imaging time, and is the number of targets. Obviously, as the number of targets increases, the total imaging time will gradually increase. From Table 3, we can see that when the number of targets is less than eight, the imaging time of our method is less, and when the number of targets is more than or equal to eight, the imaging time exceeds the RF-Pose3D method, which proves that our method has faster processing speed in the scene with fewer targets. However, due to the limitation of the resolution, the low-frequency UWB radar system is usually used in the scene with low target density. In the experiments, the scene with more than eight targets in the range of is a high target density scene, which is no longer suitable for the low-frequency UWB radar detection. Therefore, our method is more efficient than RF-Pose3D in practical applications.

Table 3.
Computation time comparisons.
4.2.6. Through-Wall Detection Performance
To evaluate the pose reconstruction performance of our system through different wall materials, we conducted some experiments. The wall materials are air, smoke, plastic board, wooden board, and 24 cm thick brick wall, where their relative dielectric constants increase sequentially. The pose reconstruction errors through different wall materials are shown in Table 4. It can be seen from Table 4 that with an increase in the relative dielectric constant of the wall materials, the average error of pose reconstruction gradually increases. The main reason is that the larger the relative dielectric constant, the more severe the reduction of the radar signal, resulting in a decrease in the signal-to-noise ratio of the system, which in turn leads to a decrease in the accuracy of pose reconstruction. As a whole, our system has good pose reconstruction performance through different wall materials.

Table 4.
Pose reconstruction error through the different wall material.
5. Discussion
We constructed several experiments to validate our framework in Section 4. First,we use the test dataset to verify the trained network, where the test error curve of the pose reconstruction network and the errors of each joint point show that our network can achieve good root-relative pose reconstruction accuracy. Meanwhile, we visualized the features extracted from the first layer and the confidence probability maps in the last layer to show the working process of our network and prove the effectiveness of our network. To investigate the performance of our framework, in the real environment, we designed multiple scenes experiments and comparison experiments. The multiple scenes experimental results proved that our framework can work in multiple scenes such as single target scene, multiple targets scene, plastic board occluded scene, and brick wall occluded scene. Furthermore, the through brick wall detection experiment also proved that our system has good penetration. The comparison results with the pose reconstruction method based on optical images showed that our system is more effective than optical sensors in dark and occluded environments. Then, we made a comparison with the existing methods about the pose reconstruction performance and computational; the comparison results demonstrated that our method had better pose reconstruction accuracy and faster processing speed in practical applications. Finally, we evaluated the pose reconstruction performance of our system through different material walls, which had different relative dielectric constants. The experimental results show that our system has good pose reconstruction performance in the common wall material occlusion environment.
Generally, the experimental results prove that our framework can reconstruct human pose from 3D radar image, and that it can achieve good reconstruction performance, which solves the problem of weak penetration of RF-Pose3D and mm-Pose and the lack of penetration of the optical sensor, and it has a broader application scene. Furthermore, the imaging process of first 2D imaging and then 3D imaging, is more efficient than direct 3D imaging, which is more suitable for the actual measurement applications. Meanwhile, the signal processing flow is a general framework, where the dataset preparation method, the faster imaging process, and the network structure in the framework can also be used in other radar systems to reconstruct human pose, and it can provide a reference for research on the combination of radar image and deep learning.
6. Conclusions
In this article, we developed a novel through-wall 3D pose reconstruction framework for hidden target detection using UWB MIMO radar and 3D CNN. To improve the visualization ability of the radar system and to obtain more abundant information of the hidden target, we construct 2D BP imaging and 3D imaging processing of radar echo captured by the UWB MIMO radar system, and then input the 3D radar image into the trained pose reconstruction network based on 3D CNN to predict the 3D pose of the human target. The obtained pose is finally fused with the human root joint location detected from the 2D BP imaging result. The field experiment and comparison results show that our framework can be used for position sensing and pose reconstruction of occluded targets, which cannot be achieved by traditional visual sensors, proving that our framework can work in more complex scenes, especially useful for the urban environments. Our framework enriches the existing detection and sensing means, and provides information complementary with visual sensors and other technologies. Moreover, based on the location and 3D pose of concealed targets, it can be further expanded to the fields of target behavior intention analysis.
As for the application of our system, it can be used in low-visibility fire scenes to perform position detection and pose reconstruction of human targets blocked by smoke or flames, and therefore assist firefighters in formulating appropriate rescue plans. Due to the good penetrability of our system, it can detect human targets buried in buildings after an earthquake disaster and obtain 3D pose information of human targets, which can help rescuers save unnecessary digging and buy more rescue time for the trapped. Meanwhile, our system can also be used in urban anti-terrorism scenarios to detect the location and 3D pose of indoor terrorists, which can provide reference information for counter-terrorism fighters to avoid unnecessary casualties.
Although the proposed method acquired satisfying results and outperformed other similar methods, there are still some limitations to overcome. For example, limited by the azimuth resolution of low-frequency UWB radar, we did not experiment with distances larger than 6 m. Furthermore, due to the limitations of the experimental site and experimental equipment, we still have many wall materials that have not been evaluated, and the next step will be completed gradually. In addition, there is also motion clutter introduced by fans and air conditioners in radar echo of indoor detection, but its Doppler effect is quite different from the motion of human targets. We can use CNN for identification and plan to verify it in future experiments. Future work will focus on increasing the pose reconstruction range of our system and optimizing the proposed framework for more complex detection environments.
Author Contributions
Conceptualization, Y.S. (Yongkun Song), T.J., and Y.D.; Formal analysis, Y.S. (Yongkun Song); Funding acquisition, T.J.; Investigation, Y.S. (Yongkun Song); Methodology, Y.S. (Yongkun Song), Y.S. (Yongping Song) and Y.D.; Project administration, T.J.; Resources, Y.S. (Yongkun Song) and Y.S. (Yongping Song); Supervision, T.J., and X.Z.; Validation, Y.D. and X.Z.; Writing—original draft, Y.S. (Yongkun Song) and Y.D.; Writing—review and editing, Y.S. (Yongkun Song), Y.S. (Yongping Song) and Y.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China, grant number 61971430 entitled, “Study on ultra-wideband radar gait recognition technique”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors thank anonymous reviewers and academic editors for their valuable comments and helpful suggestions. The authors would also be grateful to assistant editor for her meticulous work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Poppe, R.W. A survey on vision-based human action recognition. Image Vis. Comput. 2010, 28, 976–990. [Google Scholar] [CrossRef]
- Guo, Y.; He, D.; Chai, L. A Machine Vision-Based Method for Monitoring Scene-Interactive Behaviors of Dairy Calf. Animals 2020, 10, 190. [Google Scholar] [CrossRef] [PubMed]
- Costa, D.G. Visual Sensors Hardware Platforms: A Review. IEEE Sens. J. 2020, 20, 4025–4033. [Google Scholar] [CrossRef]
- Muhammad, K.; Rodrigues, J.J.P.C.; Kozlov, S.; Piccialli, F.; De Albuquerque, V.H.C. Energy-Efficient Monitoring of Fire Scenes for Intelligent Networks. IEEE Netw. 2020, 34, 108–115. [Google Scholar] [CrossRef]
- Oghaz, M.M.D.; Razaak, M.; Kerdegari, H.; Argyriou, V.; Remagnino, P. Scene and Environment Monitoring Using Aerial Imagery and Deep Learning. In Proceedings of the 2019 15th International Conference on Distributed Computing in Sensor Systems (DCOSS), Santorini, Greece, 29–31 May 2019; pp. 362–369. [Google Scholar]
- Oulton, J.A. The Global Nursing Shortage: An Overview of Issues and Actions. Policy Politics Nurs. Pract. 2006, 7, 34S–39S. [Google Scholar] [CrossRef]
- Liu, H.; Wang, L. Gesture recognition for human-robot collaboration: A review. Int. J. Ind. Ergon. 2018, 68, 355–367. [Google Scholar] [CrossRef]
- Zhang, F.; Zhu, X.; Ye, M. Fast Human Pose Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 3512–3521. [Google Scholar]
- Gilbert, A.; Trumble, M.; Malleson, C.; Hilton, A.; Collomosse, J. Fusing Visual and Inertial Sensors with Semantics for 3D Human Pose Estimation. Int. J. Comput. Vis. 2019, 127, 381–397. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–26 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Toshev, A.; Szegedy, C. DeepPose: Human Pose Estimation via Deep Neural Networks. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1653–1660. [Google Scholar]
- Cao, Z.; Simon, T.; Wei, S.-E.; Sheikh, Y. Realtime Multi-person 2D Pose Estimation Using Part Affinity Fields. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1302–1310. [Google Scholar]
- He, K.; Gkioxari, G.; Dollar, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Couteaux, V.; Si-Mohamed, S.; Nempont, O.; Lefevre, T.; Popoff, A.; Pizaine, G.; Villain, N.; Bloch, I.; Cotten, A.; Boussel, L. Automatic knee meniscus tear detection and orientation classification with Mask-RCNN. Diagn. Interv. Imaging 2019, 100, 235–242. [Google Scholar] [CrossRef]
- Pishchulin, L.; Insafutdinov, E.; Tang, S.; Andres, B.; Andriluka, M.; Gehler, P.; Schiele, B. DeepCut: Joint Subset Partition and Labeling for Multi Person Pose Estimation. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4929–4937. [Google Scholar]
- Chen, Y.; Wang, Z.; Peng, Y.; Zhang, Z.; Yu, G.; Sun, J. Cascaded Pyramid Network for Multi-person Pose Estimation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7103–7112. [Google Scholar]
- Fang, H.-S.; Xie, S.; Tai, Y.-W.; Lu, C. RMPE: Regional Multi-person Pose Estimation. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2353–2362. [Google Scholar]
- Tome, D.; Russell, C.; Agapito, L. Lifting from the Deep: Convolutional 3D Pose Estimation from a Single Image. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5689–5698. [Google Scholar]
- Pavlakos, G.; Zhou, X.; Derpanis, K.G.; Daniilidis, K. Coarse-to-Fine volumetric prediction for single-image 3d human pose. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1263–1272. [Google Scholar]
- Zhou, X.; Huang, Q.; Sun, X.; Xue, X.; Wei, Y. Towards 3D Human Pose Estimation in the Wild: A Weakly-Supervised Ap-proach. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 398–407. [Google Scholar]
- Wandt, B.; Rosenhahn, B. RepNet: Weakly Supervised Training of an Adversarial Reprojection Network for 3D Human Pose Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 7774–7783. [Google Scholar]
- Buys, K.; Cagniart, C.; Baksheev, A.; De Laet, T.; De Schutter, J.; Pantofaru, C. An adaptable system for RGB-D based human body detection and pose estimation. J. Vis. Commun. Image Represent. 2014, 25, 39–52. [Google Scholar] [CrossRef]
- Pavllo, D.; Feichtenhofer, C.; Grangier, D.; Auli, M. 3D Human Pose Estimation in Video With Temporal Convolutions and Semi-Supervised Training. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 7745–7754. [Google Scholar]
- Mitra, R.; Gundavarapu, N.B.; Sharma, A.; Jain, A. Multiview-Consistent Semi-Supervised Learning for 3D Human Pose Estimation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 6906–6915. [Google Scholar]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in neural information processing systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Li, J.; Zeng, Z.; Sun, J.; Liu, F. Through-Wall Detection of Human Being’s Movement by UWB Radar. IEEE Geosci. Remote Sens. Lett. 2012, 9, 1079–1083. [Google Scholar] [CrossRef]
- Du, H.; Jin, T.; Song, Y.; Dai, Y.; Li, M. A Three-Dimensional Deep Learning Framework for Human Behavior Analysis Using Range-Doppler Time Points. IEEE Geosci. Remote Sens. Lett. 2020, 17, 611–615. [Google Scholar] [CrossRef]
- Qi, F.; Lv, H.; Liang, F.; Li, Z.; Yu, X.; Wang, J. MHHT-Based Method for Analysis of Micro-Doppler Signatures for Human Finer-Grained Activity Using Through-Wall SFCW Radar. Remote Sens. 2017, 9, 260. [Google Scholar] [CrossRef]
- Zhao, M.M.; Li, T.H.; Mohammad, A.A. Through-Wall Human Pose Estimation Using Radio Signals. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Zhao, M.; Tian, Y.; Zhao, H.; Abu Alsheikh, M.; Li, T.; Hristov, R.; Kabelac, Z.; Katabi, D.; Torralba, A. RF-based 3D skeletons. In Proceedings of the 2018 Conference of the ACM Special Interest Group on Data Communication, Budapest, Hungary, 20–25 August 2018; pp. 267–281. [Google Scholar]
- Sengupta, A.; Jin, F.; Zhang, R.; Cao, S. mm-Pose: Real-Time Human Skeletal Posture Estimation Using mmWave Radars and CNNs. IEEE Sens. J. 2020, 20, 10032–10044. [Google Scholar] [CrossRef]
- Nag, S.; Barnes, M.A.; Payment, T.; Holladay, G. Ultrawideband through-wall radar for detecting the motion of people in real time. In Proceedings of the Radar Sensor Technology and Data Visualization, Orlando, FL, USA, 30 July 2002. [Google Scholar]
- Yarovoy, A.; Ligthart, L.; Matuzas, J.; Levitas, B. UWB radar for human being detection [same as "UWB radar for human being detection", ibid., vol. 21, n. 11, 06]. IEEE Aerosp. Electron. Syst. Mag. 2008, 23, 36–40. [Google Scholar] [CrossRef]
- Ma, Y.; Liang, F.; Wang, P.; Lv, H.; Yu, X.; Zhang, Y.; Wang, J. An Accurate Method to Distinguish Between Stationary Hu-man and Dog Targets Under Through-Wall Condition Using UWB Radar. Remote Sens. 2019, 11, 2571. [Google Scholar] [CrossRef]
- Lv, H.; Qi, F.; Zhang, Y.; Jiao, T.; Liang, F.; Li, Z.; Wang, J. Improved Detection of Human Respiration Using Data Fusion Basedon a Multistatic UWB Radar. Remote Sens. 2016, 8, 773. [Google Scholar] [CrossRef]
- Ahmad, F.; Zhang, Y.; Amin, M.G. Three-Dimensional Wideband Beamforming for Imaging Through a Single Wall. IEEE Geosci. Remote Sens. Lett. 2008, 5, 176–179. [Google Scholar] [CrossRef]
- Kong, L.; Cui, G.; Yang, X.; Yang, J. Three-dimensional human imaging for through-the-wall radar. In Proceedings of the 2009 IEEE Radar Conference, Pasadena, CA, USA, 4–8 May 2009; pp. 1–4. [Google Scholar]
- Zhao, D.; Jin, T.; Dai, Y.; Song, Y.; Su, X. A Three-Dimensional Enhanced Imaging Method on Human Body for Ultra-Wideband Multiple-Input Multiple-Output Radar. Electronics 2018, 7, 101. [Google Scholar] [CrossRef]
- Adib, F.; Hsu, C.-Y.; Mao, H.; Katabi, D.; Durand, F. Capturing the human figure through a wall. ACM Trans. Graph. 2015, 34, 1–13. [Google Scholar] [CrossRef]
- Hu, Z.; Zeng, Z.; Wang, K.; Feng, W.; Zhang, J.; Lu, Q.; Kang, X. Design and Analysis of a UWB MIMO Radar System with Miniaturized Vivaldi Antenna for Through-Wall Imaging. Remote Sens. 2019, 11, 1867. [Google Scholar] [CrossRef]
- Lu, B.; Song, Q.; Zhou, Z.; Wang, H. A SFCW radar for through wall imaging and motion detection. In Proceedings of the 2011 8th European Radar Conference, Manchester, UK, 12–14 October 2011; pp. 325–328. [Google Scholar]
- Xiong, J.; Cheng, L.; Ma, D.; Wei, J. Destination-Aided Cooperative Jamming for Dual-Hop Amplify-and-Forward MIMO Untrusted Relay Systems. IEEE Trans. Veh. Technol. 2016, 65, 7274–7284. [Google Scholar] [CrossRef]
- Martone, A.F.; Ranney, K.; Le, C. Noncoherent Approach for Through-the-Wall Moving Target Indication. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 193–206. [Google Scholar] [CrossRef]
- Setlur, P.; Alli, G.; Nuzzo, L. Multipath Exploitation in Through-Wall Radar Imaging Via Point Spread Functions. IEEE Trans. Image Process. 2013, 22, 4571–4586. [Google Scholar] [CrossRef]
- Song, Y.; Hu, J.; Chu, N.; Jin, T.; Zhang, J.; Zhou, Z. Building Layout Reconstruction in Concealed Human Target Sensing via UWB MIMO Through-Wall Imaging Radar. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1199–1203. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Neapolitan, R.E. Neural Networks and Deep Learning. In Artificial Intelligence; Sterling Publishing Co., Inc.: New York, NY, USA, 2018; pp. 389–411. [Google Scholar]
- Liu, J.; Jia, Y.; Kong, L.; Yang, X.; Liu, Q.H. MIMO through-wall radar 3-D imaging of a human body in different postures. J. Electromagn. Waves Appl. 2016, 30, 849–859. [Google Scholar] [CrossRef]
- Chen, V.C. The Micro-Doppler Effect in Radar; Artech House: Norwood, MA, USA, 2011; ISBN 9781608070572. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. J. Mach. Learn. Res. 2011, 15, 315–323. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).