A Constrained Graph-Based Semi-Supervised Algorithm Combined with Particle Cooperation and Competition for Hyperspectral Image Classification
Abstract
1. Introduction
- (1)
- A novel constrained affinity matrix construction method is introduced for initial graph construction, which has the powerful ability to excavate the proficiency and complicated structure in the data.
- (2)
- For the purpose of preventing the performance deterioration of graph-based SSL caused by the label noise of predicted labels, the PCC mechanism was adopted to mitigate the adverse impact of label noise in LPA.
- (3)
- Aiming at the high costs to gain labeled samples and a rich supply of unlabeled samples in real-world hyperspectral datasets, we applied our semi-supervised CLPPCC algorithm to HSIs classification by only using a small number of labeled samples and the results demonstrated our proposal was superior to alternatives.
2. Related Work
2.1. Label Propagation
2.2. Particle Cooperation and Competition
3. The Proposed Method
3.1. Graph Construction
3.2. Label Propagation
| Algorithm 1 Constrained Label Propagation Algorithm |
| Input: Data set , where are labeled dataset and its labels, are unlabeled dataset. 1: Initialization: compute the affinity matrix though Equation (10); 2: Compute probability transition matrix based on the affinity matrix using Equation (11); 3: Define a labeled matrix using Equation (12) and ; 4: repeat 5: Propagate labels: update Y by using Equation (13): ; 6: Clamp the labeled data: Update by using Equation (14); 7: until the converges; 8: Calculate the label yi of unlabeled data by Equation (15); Output: The predicted label set of unlabeled dataset |
3.3. The Proposed Graph-Based Semi-Supervised Model Combined with Particle Cooperation and Competition
- Initial configuration
- Nodes and particles dynamics
- Random-Greedy walk
- Stop Criterion
4. Experiments and Analysis
4.1. Experimental Setup
4.1.1. Hyperspectral Images
- Indian Pines image
- Pavia University scene
- Salinas image
4.1.2. Evaluation Criteria
- Overall Accuracy, OA
- Average Accuracy, AA
- Kappa Coefficient
4.1.3. Comparative Algorithms
- TSVM: Transductive Support Vector Machine algorithm [3].
- LGC: The Local and Global Consistency graph-based algorithm [50].
- LPA: the original Label Propagation Algorithm [5].
- LPAPCC: the original Label Propagation Algorithm combined with Particle Cooperation and Competition without the novel graph construction mentioned in Section 3.1.
4.2. Classification of Hyperspectral Images
4.3. Running time
4.4. Robustness of the Proposed Method
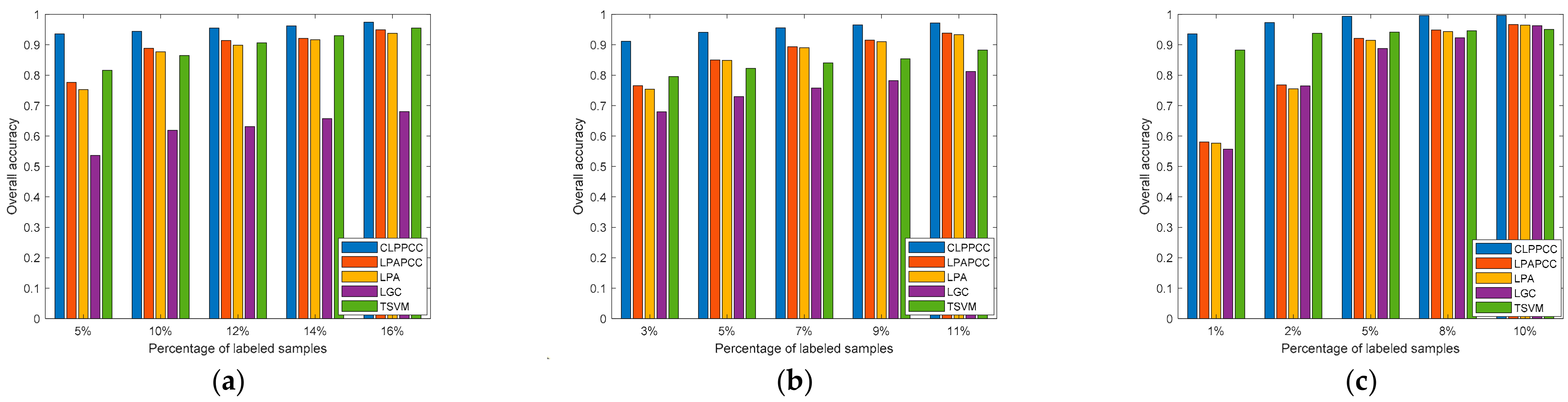
4.4.1. Labeled Size Robustness
4.4.2. Noise Robustness
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deng, C.; Ji, R.; Liu, W.; Tao, D.; Gao, X. Visual Reranking through Weakly Supervised Multi-graph Learning. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2600–2607. [Google Scholar]
- Vanegas, J.A.; Escalante, H.J.; González, F.A. Scalable multi-label annotation via semi-supervised kernel semantic embedding. Pattern Recognit. Lett. 2019, 123, 97–103. [Google Scholar] [CrossRef]
- Joachims, T. Transductive inference for text classification using support vector machines. In Proceedings of the Sixteenth International Conference on Machine Learning, Bled, Slovenia, 27–30 June 1999; pp. 200–209. [Google Scholar]
- Blum, A.; Mitchell, T. Combining labeled and unlabeled data with co-training. In Proceedings of the 11th Annual Conference on Computational Learning Theroy, Madison, WI, USA; 1998; pp. 92–100. [Google Scholar]
- Zhu, X.J.; Zoubin, Z. Learning from Labeled and Unlabeled Data with Label Propagation; Carnegie Mellon Univerisity: Pittsburgh, PA, USA, 2002. [Google Scholar]
- Berthelot, D.; Carlini, N.; Goodfellow, L.; Oliver, A.; Papernot, N.; Raffel, C. Mixmatch: A holistic approach to semi-supervised learning. arXiv 2020, arXiv:1905.02249. [Google Scholar]
- Sohn, K.; Berthelot, D.; Li, C.; Zhang, Z.; Carlini, N.; Cubuk, E.; Kurakin, A.; Zhang, H.; Raffel, C. Fixmatch: Simplifying semi-supervised learning with consistency and confidence. arXiv 2020, arXiv:2001.07685. [Google Scholar]
- Igor, S. Semi-supervised neural network training method for fast-moving object detection. In Proceedings of the 2018 14th Symposium on Neural Networks and Applications (NEUREL), Belgrade, Serbia, 20–21 November 2018; pp. 1–6. [Google Scholar]
- Hoang, T.; Engin, Z.; Lorenza, G.; Paolo, D. Detecting mobile traffic anomalies through physical control channel fingerprinting: A deep semi-supervised approach. IEEE Access 2019, 7, 152187–152201. [Google Scholar]
- Tokuda, E.K.; Ferreira, G.B.A.; Silva, C.; Cesar, R.M. A novel semi-supervised detection approach with weak annotation. In Proceedings of the 2018 IEEE Southwest Symposium on Image Analysis and Interpretation (SSIAI), Las Vegas, NV, USA, 8–10 April 2018; pp. 129–132. [Google Scholar]
- Chen, G.; Liu, L.; Hu, W.; Pan, Z. Semi-Supervised Object Detection in Remote Sensing Images Using Generative Adversarial Networks. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2018; pp. 2503–2506. [Google Scholar]
- Zu, B.; Xia, K.; Du, W.; Li, Y.; Ali, A.; Chakraborty, S. Classification of Hyperspectral Images with Robust Regularized Block Low-Rank Discriminant Analysis. Remote Sens. 2018, 10, 817. [Google Scholar] [CrossRef]
- Liu, C.; Li, J.; He, L. Superpixel-Based Semisupervised Active Learning for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 1–14. [Google Scholar] [CrossRef]
- Shi, C.; Lv, Z.; Yang, X.; Xu, P.; Bibi, I. Hierarchical Multi-View Semi-supervised Learning for Very High-Resolution Remote Sensing Image Classification. Remote Sens. 2020, 12, 1012. [Google Scholar] [CrossRef]
- Zhou, S.; Xue, Z.; Du, P. Semisupervised Stacked Autoencoder With Cotraining for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3813–3826. [Google Scholar] [CrossRef]
- Ahmadi, S.; Mehreshad, N. Semisupervised classification of hyperspectral images with low-rank representation kernel. J. Opt. Soc. Am. A 2020, 37, 606–613. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, S.; Cui, M.; Prasad, S. Spatially Constrained Semisupervised Local Angular Discriminant Analysis for Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 1203–1212. [Google Scholar] [CrossRef]
- Mohanty, R.; Happy, S.L.; Routray, A. A Semisupervised Spatial Spectral Regularized Manifold Local Scaling Cut with HGF for Dimensionality Reduction of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3423–3435. [Google Scholar] [CrossRef]
- Wu, Y.; Mu, G.; Qin, C.; Miao, Q.-G.; Ma, W.; Zhang, X. Semi-Supervised Hyperspectral Image Classification via Spatial-Regulated Self-Training. Remote Sens. 2020, 12, 159. [Google Scholar] [CrossRef]
- Hu, Y.; An, R.; Wang, B.; Xing, F.; Ju, F. Shape Adaptive Neighborhood Information-Based Semi-Supervised Learning for Hyperspectral Image Classification. Remote Sens. 2020, 12, 2976. [Google Scholar] [CrossRef]
- Triguero, I.; García, S.; Herrera, F. Self-labeled techniques for semi-supervised learning: Taxonomy, software and empirical study. Knowl. Inf. Syst. 2015, 42, 245–284. [Google Scholar] [CrossRef]
- Wang, D.; Nie, F.; Huang, H. Large-scale adaptive semi-supervised learning via unified inductive and transductive model. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 482–491. [Google Scholar]
- Abu-Aisheh, Z.; Raveaux, R.; Ramel, J.-Y. Efficient k-nearest neighbors search in graph space. Pattern Recognit. Lett. 2020, 134, 77–86. [Google Scholar] [CrossRef]
- Yang, X.; Deng, C.; Liu, X.; Nie, F. New -norm relaxation of multi-way graph cut for clustering. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Nie, F.; Wang, X.; Jordan, M.; Huang, H. The constrained Laplacian rank algorithm for graph-based clustering. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; AAAI Press: New Orleans, LA, USA, 2016. [Google Scholar]
- Breve, F.; Zhao, L.; Quiles, M.; Pedrycz, W.; Liu, C.-M. Particle Competition and Cooperation in Networks for Semi-Supervised Learning. IEEE Trans. Knowl. Data Eng. 2011, 24, 1686–1698. [Google Scholar] [CrossRef]
- Breve, F.A.; Zhao, L. Particle Competition and Cooperation to Prevent Error Propagation from Mislabeled Data in Semi-supervised Learning. In Proceedings of the 2012 Brazilian Symposium on Neural Networks, Curitiba, Brazil, 20–25 October 2012; pp. 79–84. [Google Scholar]
- Breve, F.A.; Zhao, L.; Quiles, M.G. Particle competition and cooperation for semi-supervised learning with label noise. Neurocomputing 2015, 160, 63–72. [Google Scholar] [CrossRef]
- Tan, K.; Zhang, J.; Du, Q.; Wang, X. GPU Parallel Implementation of Support Vector Machines for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4647–4656. [Google Scholar] [CrossRef]
- Gao, L.; Plaza, L.; Khodadadzadeh, M.; Plaza, J.; Zhang, B.; He, Z.; Yan, H. Subspace-Based Support Vector Machines for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2014, 12, 349–353. [Google Scholar] [CrossRef]
- Liu, L.; Huang, W.; Liu, B.; Shen, L.; Wang, C. Semisupervised Hyperspectral Image Classification via Laplacian Least Squares Support Vector Machine in Sum Space and Random Sampling. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4086–4100. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Plaza, J.; Plaza, L.; Plaza, A. Active Learning with Convolutional Neural Networks for Hyperspectral Image Classification Using a New Bayesian Approach. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6440–6461. [Google Scholar] [CrossRef]
- Priya, T.; Prasad, S.; Wu, H. Superpixels for Spatially Reinforced Bayesian Classification of Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1071–1075. [Google Scholar] [CrossRef]
- Ham, J.; Chen, Y.; Crawford, M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, G.; Li, X.; Wang, B. Cascaded Random Forest for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1082–1094. [Google Scholar] [CrossRef]
- Peerbhay, K.Y.; Mutanga, O.; Ismail, R. Random Forests Unsupervised Classification: The Detection and Mapping of Solanum mauritianum Infestations in Plantation Forestry Using Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3107–3122. [Google Scholar] [CrossRef]
- Tu, B.; Huang, S.; Fang, L.; Zhang, G.; Wang, J.; Zheng, B. Hyperspectral Image Classification via Weighted Joint Nearest Neighbor and Sparse Representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4063–4075. [Google Scholar] [CrossRef]
- Blanzieri, E.; Melgani, F. Nearest Neighbor Classification of Remote Sensing Images with the Maximal Margin Principle. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1804–1811. [Google Scholar] [CrossRef]
- Zhao, Y.; Su, F.; Fengqin, Y. Novel Semi-Supervised Hyperspectral Image Classification Based on a Superpixel Graph and Discrete Potential Method. Remote Sens. 2020, 12, 1528. [Google Scholar] [CrossRef]
- Jamshidpour, N.; Safari, A.; Homayouni, S. A GA-Based Multi-View, Multi-Learner Active Learning Framework for Hyperspectral Image Classification. Remote Sens. 2020, 12, 297. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, G.; Li, X.; Wang, B.; Fu, P. Active Semi-Supervised Random Forest for Hyperspectral Image Classification. Remote Sens. 2019, 11, 2974. [Google Scholar] [CrossRef]
- Ou, D.; Tan, K.; Du, Q.; Zhu, J.; Wang, X.; Chen, Y. A Novel Tri-Training Technique for the Semi-Supervised Classification of Hyperspectral Images Based on Regularized Local Discriminant Embedding Feature Extraction. Remote Sens. 2019, 11, 654. [Google Scholar] [CrossRef]
- Cui, B.; Xie, X.; Hao, S.; Cui, J.; Lu, Y. Semi-Supervised Classification of Hyperspectral Images Based on Extended Label Propagation and Rolling Guidance Filtering. Remote Sens. 2018, 10, 515. [Google Scholar] [CrossRef]
- Xue, Z.; Du, P.; Su, H.; Zhou, S. Discriminative Sparse Representation for Hyperspectral Image Classification: A Semi-Supervised Perspective. Remote Sens. 2017, 9, 386. [Google Scholar] [CrossRef]
- Xia, J.; Liao, W.; Du, P. Hyperspectral and LiDAR Classification with Semisupervised Graph Fusion. IEEE Geosci. Remote Sens. Lett. 2020, 17, 666–670. [Google Scholar] [CrossRef]
- Cao, Z.; Li, X.; Zhao, L. Semisupervised hyperspectral imagery classification based on a three-dimensional convolutional adversarial autoencoder model with low sample requirements. J. Appl. Remote Sens. 2020, 14, 024522. [Google Scholar] [CrossRef]
- Zhao, W.; Chen, X.; Bo, Y.; Chen, J. Semisupervised Hyperspectral Image Classification with Cluster-Based Conditional Generative Adversarial Net. IEEE Geosci. Remote Sens. Lett. 2020, 17, 539–543. [Google Scholar] [CrossRef]
- Fahime, A.; Mohanmad, K. Improving semisupervised hyperspectral unmixing using spatial correlation under a polynomial postnonlinear mixing model. J. Appl. Remote Sens. 2019, 13, 036512. [Google Scholar]
- Kang, X.; Li, S.; Benediktsson, J.A. Feature Extraction of Hyperspectral Images with Image Fusion and Recursive Filtering. IEEE Trans. Geosci. Remote Sens. 2013, 52, 3742–3752. [Google Scholar] [CrossRef]
- Zhou, D.; Olivier, B.; Thomas, N. Learning with Local and Global Consistency; MIT Press: Cambridge, MA, USA, 2003; pp. 321–328. [Google Scholar]










| Class | Indian Pines Image | Pavia University Scene | Salinas Image | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Sample No. | Train | Test | Sample No. | Train | Test | Sample No. | ||||
| L | U | L | U | L | U | |||||||
| C1 | 5 | 8 | 33 | 46 | 99 | 1890 | 4642 | 6631 | 12 | 590 | 1407 | 2009 |
| C2 | 42 | 386 | 1000 | 1428 | 279 | 5315 | 13,055 | 18,649 | 22 | 1095 | 2609 | 3726 |
| C3 | 24 | 225 | 581 | 830 | 31 | 598 | 1470 | 2099 | 11 | 581 | 1384 | 1976 |
| C4 | 7 | 64 | 166 | 237 | 45 | 874 | 2145 | 3064 | 8 | 410 | 976 | 1394 |
| C5 | 14 | 130 | 339 | 483 | 20 | 383 | 942 | 1345 | 16 | 787 | 1875 | 2678 |
| C6 | 21 | 198 | 511 | 730 | 75 | 1433 | 3521 | 5029 | 23 | 1164 | 2772 | 3959 |
| C7 | 5 | 3 | 20 | 28 | 19 | 380 | 931 | 1330 | 21 | 1052 | 2506 | 3579 |
| C8 | 14 | 129 | 335 | 478 | 55 | 1049 | 2578 | 3682 | 67 | 3314 | 7890 | 11,271 |
| C9 | 5 | 1 | 14 | 20 | 14 | 270 | 663 | 947 | 37 | 1823 | 4343 | 6203 |
| C10 | 29 | 262 | 681 | 972 | - | - | - | - | 19 | 964 | 2295 | 3278 |
| C11 | 73 | 663 | 1719 | 2455 | - | - | - | - | 6 | 314 | 748 | 1068 |
| C12 | 17 | 160 | 416 | 593 | - | - | - | - | 11 | 567 | 1349 | 1927 |
| C13 | 6 | 55 | 144 | 205 | - | - | - | - | 5 | 269 | 642 | 916 |
| C14 | 37 | 342 | 886 | 1265 | - | - | - | - | 6 | 315 | 749 | 1070 |
| C15 | 11 | 104 | 271 | 386 | - | - | - | - | 43 | 2137 | 5088 | 7268 |
| C16 | 5 | 22 | 66 | 93 | - | - | - | - | 10 | 532 | 1265 | 1807 |
| Total | 315 | 2752 | 7182 | 10,249 | 637 | 12,192 | 29,947 | 42,776 | 317 | 15,914 | 37,898 | 54,129 |
| Method | TSVM | LGC | LPA | LPAPCC | CLPPCC | LPA | LPAPCC | CLPPCC |
|---|---|---|---|---|---|---|---|---|
| C1 | 0.7251 | 0.4371 | 0.0478 | 0.0547 | 0.6310 | 0.8030 | 0.8126 | 0.9512 |
| C2 | 0.8698 | 0.5140 | 0.9421 | 0.9587 | 0.9357 | 0.9290 | 0.9062 | 0.9200 |
| C3 | 0.7214 | 0.5599 | 0.9326 | 0.9228 | 0.9492 | 0.8795 | 0.8828 | 0.9569 |
| C4 | 0.8806 | 0.4205 | 0.9310 | 0.9574 | 0.8955 | 0.9246 | 0.9313 | 0.9700 |
| C5 | 0.9737 | 0.8059 | 0.9955 | 0.9851 | 0.9729 | 0.9693 | 0.9906 | 0.9783 |
| C6 | 0.9440 | 0.7727 | 0.9758 | 0.9870 | 0.9758 | 0.9671 | 0.9700 | 0.9765 |
| C7 | 0.3597 | 0.4289 | 0.6609 | 0.5325 | 0.6898 | 0.4356 | 0.4244 | 0.5610 |
| C8 | 0.9983 | 0.9413 | 1 | 1 | 1 | 1 | 1 | 1 |
| C9 | 0.5356 | 0.1723 | 0.8180 | 0.8862 | 0.7085 | 0.7788 | 0.9028 | 0.9375 |
| C10 | 0.8255 | 0.5348 | 0.9337 | 0.9360 | 0.8943 | 0.9166 | 0.9192 | 0.9466 |
| C11 | 0.8613 | 0.5228 | 0.9599 | 0.9634 | 0.9607 | 0.9404 | 0.9447 | 0.9656 |
| C12 | 0.6773 | 0.4165 | 0.9214 | 0.9344 | 0.9069 | 0.8932 | 0.8835 | 0.9121 |
| C13 | 0.9806 | 0.8050 | 0.9965 | 0.9970 | 0.9990 | 0.9950 | 0.9955 | 1 |
| C14 | 0.9867 | 0.8388 | 0.9977 | 0.9936 | 0.9799 | 0.9840 | 0.9894 | 0.9984 |
| C15 | 0.9345 | 0.4765 | 0.9511 | 0.9522 | 0.9592 | 0.9520 | 0.9582 | 0.9012 |
| C16 | 0.9757 | 0.9906 | 0.9871 | 0.9780 | 0.9457 | 0.9853 | 0.9874 | 0.9886 |
| OA | 0.8648 | 0.6188 | 0.8768 | 0.8886 | 0.9439 | 0.9342 | 0.9350 | 0.9571 |
| AA | 0.8281 | 0.6023 | 0.8682 | 0.8776 | 0.9002 | 0.8971 | 0.9062 | 0.9353 |
| Kappa | 0.8458 | 0.5534 | 0.8607 | 0.8741 | 0.9361 | 0.9249 | 0.9258 | 0.9511 |
| Method | TSVM | LGC | LPA | LPAPCC | CLPPCC | LPA | LPAPCC | CLPPCC |
|---|---|---|---|---|---|---|---|---|
| C1 | 0.7126 | 0.5135 | 0.5332 | 0.5335 | 0.8723 | 0.8943 | 0.8982 | 0.9077 |
| C2 | 0.9123 | 0.9198 | 0.9917 | 0.9915 | 0.9886 | 0.9859 | 0.9868 | 0.9905 |
| C3 | 0.6837 | 0.6265 | 0.8954 | 0.9297 | 0.8833 | 0.8702 | 0.8607 | 0.8473 |
| C4 | 0.8198 | 0.4756 | 0.9695 | 0.9777 | 0.8823 | 0.9749 | 0.9610 | 0.9071 |
| C5 | 0.9572 | 0.8932 | 0.9960 | 0.9977 | 0.9853 | 0.9964 | 0.9981 | 0.9960 |
| C6 | 0.8869 | 0.9445 | 0.9949 | 0.9960 | 0.9932 | 0.9839 | 0.9851 | 0.9894 |
| C7 | 0.7080 | 0.6068 | 0.9251 | 0.9059 | 0.8782 | 0.8297 | 0.8551 | 0.8651 |
| C8 | 0.6626 | 0.5431 | 0.8738 | 0.8851 | 0.8676 | 0.8291 | 0.8224 | 0.8543 |
| C9 | 0.4501 | 0.2614 | 0.8894 | 0.9443 | 0.8652 | 0.8439 | 0.8440 | 0.8632 |
| OA | 0.8227 | 0.7295 | 0.8488 | 0.8499 | 0.9407 | 0.9420 | 0.9425 | 0.9454 |
| AA | 0.7548 | 0.6427 | 0.8966 | 0.9068 | 0.9129 | 0.9120 | 0.9124 | 0.9134 |
| Kappa | 0.7626 | 0.6502 | 0.8005 | 0.8020 | 0.9213 | 0.9230 | 0.9237 | 0.9276 |
| Method | TSVM | LGC | LPA | LPAPCC | CLPPCC | LPA | LPAPCC | CLPPCC |
|---|---|---|---|---|---|---|---|---|
| C1 | 0.9378 | 0.1983 | 0.2134 | 0.2174 | 0.7418 | 0.8827 | 0.8830 | 0.9975 |
| C2 | 0.9750 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| C3 | 0.9747 | 0.9877 | 0.9971 | 0.9979 | 0.9977 | 0.9918 | 0.9952 | 0.9740 |
| C4 | 0.8457 | 0.9349 | 0.9922 | 0.9900 | 0.9708 | 0.9782 | 0.9837 | 0.9943 |
| C5 | 0.9696 | 0.9384 | 0.9989 | 0.9978 | 1 | 0.9871 | 0.9957 | 0.9621 |
| C6 | 0.9947 | 1 | 1 | 1 | 0.9957 | 0.9999 | 1 | 0.9962 |
| C7 | 0.9649 | 0.9783 | 0.9933 | 0.9956 | 0.9930 | 0.9891 | 0.9880 | 0.9972 |
| C8 | 0.9250 | 0.9944 | 0.9994 | 0.9996 | 0.9998 | 0.9993 | 0.9993 | 0.9945 |
| C9 | 0.9940 | 0.6112 | 0.5211 | 0.5459 | 0.9421 | 0.9640 | 0.9704 | 0.9915 |
| C10 | 0.9827 | 0.9916 | 0.9974 | 0.9948 | 0.9955 | 0.9923 | 0.9899 | 0.9558 |
| C11 | 0.9859 | 1 | 1 | 1 | 0.9797 | 1 | 1 | 1 |
| C12 | 0.9731 | 0.9761 | 0.9937 | 0.9972 | 1 | 0.9876 | 0.9784 | 0.9675 |
| C13 | 0.8525 | 0.9619 | 0.9970 | 0.9927 | 0.9360 | 0.9370 | 0.9618 | 0.9718 |
| C14 | 0.9383 | 0.9082 | 0.9684 | 0.9815 | 0.8646 | 0.9781 | 0.9847 | 0.9777 |
| C15 | 0.8584 | 0.9978 | 0.9992 | 0.9991 | 0.9931 | 0.9974 | 0.9979 | 0.9917 |
| C16 | 0.9796 | 0.9606 | 1 | 1 | 1 | 0.9998 | 0.9980 | 1 |
| OA | 0.9380 | 0.7646 | 0.7555 | 0.7681 | 0.9727 | 0.9854 | 0.9868 | 0.9881 |
| AA | 0.9470 | 0.9025 | 0.9169 | 0.9193 | 0.9631 | 0.9803 | 0.9829 | 0.9857 |
| Kappa | 0.9310 | 0.7418 | 0.7269 | 0.7433 | 0.9696 | 0.9837 | 0.9983 | 0.9867 |
| Method | TSVM | LGC | LPA | LPAPCC | CLPPCC | LPA | LPAPCC | CLPPCC |
|---|---|---|---|---|---|---|---|---|
| Indian Pines images | 4.51 | 6.40 | 28.41 | 36.78 | 32.07 | 30.39 | 39.18 | 49.82 |
| Pavia University scene | 14.49 | 132.65 | 640.89 | 807.4 | 884.61 | 651.20 | 828.54 | 958.87 |
| Salinas image | 29.34 | 213.57 | 1086.87 | 1897.48 | 1321.87 | 1352.86 | 2069.80 | 1432.51 |
| Images | TSVM | LGC | LPA | LPAPCC | CLPPCC | |
|---|---|---|---|---|---|---|
| Indian Pines image | OA | 0.8269 | 0.5993 | 0.8638 | 0.8822 | 0.9404 |
| AA | 0.7740 | 0.5756 | 0.8736 | 0.8733 | 0.8941 | |
| Kappa | 0.8026 | 0.5310 | 0.8465 | 0.8669 | 0.9321 | |
| Pavia University scene | OA | 0.7884 | 0.7106 | 0.8245 | 0.8414 | 0.9363 |
| AA | 0.7667 | 0.6339 | 0.8880 | 0.8918 | 0.9047 | |
| Kappa | 0.7120 | 0.6195 | 0.7688 | 0.7908 | 0.9156 | |
| Salinas image | OA | 0.9093 | 0.7481 | 0.7420 | 0.7601 | 0.9700 |
| AA | 0.9191 | 0.8901 | 0.9166 | 0.9174 | 0.9597 | |
| Kappa | 0.8997 | 0.7239 | 0.7146 | 0.7343 | 0.9666 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Xia, K.; Li, T.; Zu, B.; Yin, Z.; Zhang, J. A Constrained Graph-Based Semi-Supervised Algorithm Combined with Particle Cooperation and Competition for Hyperspectral Image Classification. Remote Sens. 2021, 13, 193. https://doi.org/10.3390/rs13020193
He Z, Xia K, Li T, Zu B, Yin Z, Zhang J. A Constrained Graph-Based Semi-Supervised Algorithm Combined with Particle Cooperation and Competition for Hyperspectral Image Classification. Remote Sensing. 2021; 13(2):193. https://doi.org/10.3390/rs13020193
Chicago/Turabian StyleHe, Ziping, Kewen Xia, Tiejun Li, Baokai Zu, Zhixian Yin, and Jiangnan Zhang. 2021. "A Constrained Graph-Based Semi-Supervised Algorithm Combined with Particle Cooperation and Competition for Hyperspectral Image Classification" Remote Sensing 13, no. 2: 193. https://doi.org/10.3390/rs13020193
APA StyleHe, Z., Xia, K., Li, T., Zu, B., Yin, Z., & Zhang, J. (2021). A Constrained Graph-Based Semi-Supervised Algorithm Combined with Particle Cooperation and Competition for Hyperspectral Image Classification. Remote Sensing, 13(2), 193. https://doi.org/10.3390/rs13020193







