Tighten the Bolts and Nuts on GPP Estimations from Sites to the Globe: An Assessment of Remote Sensing Based LUE Models and Supporting Data Fields
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Existing GPP Models Used in this Study and the New Models
2.2. Description of the LUE-EF Model
- FPAR is in practice approximated by EVI [11], since photosynthetically active vegetation is estimated as a ratio α of EVI, set to be α = 1:
- Most previous models underestimates of GPP on cloudy days mainly because photosynthesis can be increased by diffuse radiation under cloudy conditions [6,32]. The regulating effect of cloud cover on GPP was expressed by a cloudiness index (CI) as follow:where CI is the ratio of PAR to potential PAR (PPAR) [6], and PPAR is PAR that reaches the upper atmosphere. Using the FLUXNET2015 dataset, the coefficients were determined to be a (= 2.9) and b (= 1.2);
- For calculating the influence of atmospheric CO2 on GPP, we employed the algorithm in the Frankfurt Biosphere Model (FBM):where CCL is the internal CO2 concentration of leaves, and it assumed to be 70% of atmospheric CO2 concentration [33]. Δ(T) is the CO2 compensation point for gross photosynthesis and photorespiration at temperature T (°C) [34]:
- The regulation scalar of water on GPP, WS, was expressed as the evaporative fraction (EF) of the total sensible and latent heat [9]:where LE is latent heat flux (W m−2), and H is sensible heat flux (W m−2).
2.3. Description of the LUE-NDWI Model
2.4. Data for Evaluation of Models and Spatial Data Products
2.5. Evaluation of Spatial Data Products and Model Performance
3. Results
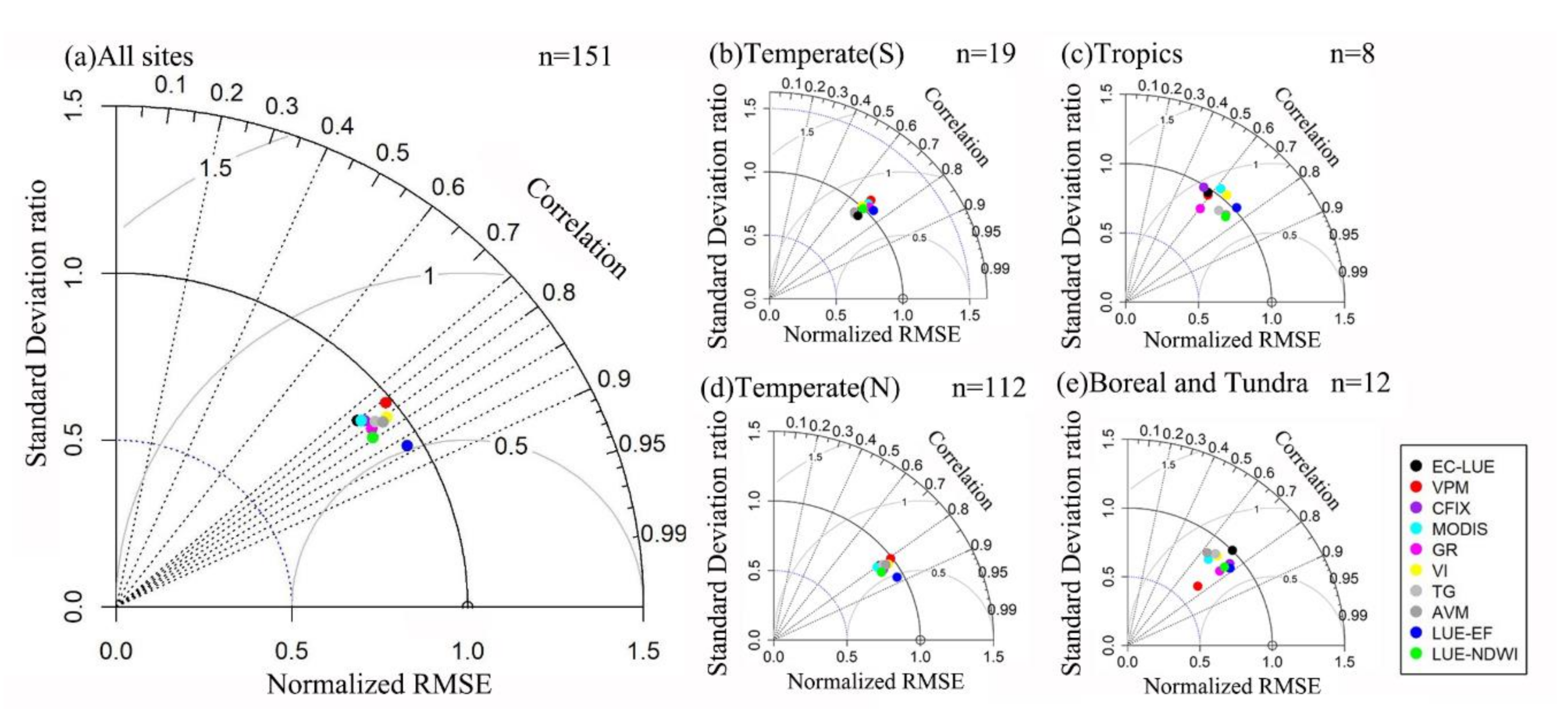
3.1. Comparison of Model Performance at the Site Scale
3.2. Biases in Remote Sensing Data Products and Consequences on Global GPP Estimation
3.3. Comparison of 24 Global GPP Products
4. Discussion
4.1. Adequacy of Model Structure in Representing Processes
4.2. Input Data Biases and Possible Impacts on GPP Simulations
4.3. Improving GPP Simulation Capability: The Ways Forward
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| ID | SITE | LAT | LON | BIO |
|---|---|---|---|---|
| 1 | BE-Lon | 50.5516 | 4.7461 | CRO * |
| 2 | DE-Seh | 50.8706 | 6.4497 | CRO |
| 3 | FI-Jok | 60.8986 | 23.5135 | CRO |
| 4 | IT-CA2 | 42.3772 | 12.026 | CRO * |
| 5 | US-CRT | 41.6285 | −83.347 | CRO * |
| 6 | US-Lin | 36.3566 | −119.84 | CRO |
| 7 | US-Tw3 | 38.1159 | −121.65 | CRO |
| 8 | US-Twt | 38.1087 | −121.65 | CRO * |
| 9 | US-ARM | 36.6058 | −97.489 | CRO * |
| 10 | US-Ne2 | 41.1649 | −96.47 | CRO |
| 11 | US-Ne3 | 41.1797 | −96.44 | CRO |
| 12 | DE-Kli | 50.8931 | 13.5224 | CRO |
| 13 | FR-Gri | 48.8442 | 1.9519 | CRO * |
| 14 | US-Ne1 | 41.1651 | −96.477 | CRO * |
| 15 | IT-Noe | 40.6062 | 8.1512 | CSH |
| 16 | US-KS2 | 28.6086 | −80.672 | CSH * |
| 17 | CA-Oas | 53.6289 | −106.2 | DBF |
| 18 | CA-TPD | 42.6353 | −80.558 | DBF |
| 19 | DE-Hai | 51.0792 | 10.453 | DBF * |
| 20 | DK-Sor | 55.4859 | 11.6446 | DBF * |
| 21 | FR-Fon | 48.4764 | 2.7801 | DBF |
| 22 | IT-CA1 | 42.3804 | 12.0266 | DBF * |
| 23 | IT-CA3 | 42.38 | 12.0222 | DBF |
| 24 | IT-Col | 41.8494 | 13.5881 | DBF |
| 25 | IT-Isp | 45.8126 | 8.6336 | DBF * |
| 26 | IT-Ro1 | 42.4081 | 11.93 | DBF |
| 27 | IT-Ro2 | 42.3903 | 11.9209 | DBF |
| 28 | PA-SPn | 9.3181 | −79.635 | DBF * |
| 29 | US-Ha1 | 42.5378 | −72.172 | DBF * |
| 30 | US-MMS | 39.3232 | −86.413 | DBF * |
| 31 | US-Oho | 41.5545 | −83.844 | DBF |
| 32 | US-UMB | 45.5598 | −84.714 | DBF * |
| 33 | US-UMd | 45.5625 | −84.698 | DBF |
| 34 | US-WCr | 45.8059 | −90.08 | DBF |
| 35 | ZM-Mon | −15.438 | 23.2528 | DBF * |
| 36 | RU-SkP | 62.255 | 129.168 | DNF |
| 37 | AU-Cum | −33.615 | 150.724 | EBF * |
| 38 | AU-Tum | −35.657 | 148.152 | EBF |
| 39 | AU-Wac | −37.426 | 145.188 | EBF * |
| 40 | AU-Whr | −36.673 | 145.029 | EBF * |
| 41 | AU-Wom | −37.422 | 144.094 | EBF |
| 42 | BR-Sa1 | −2.8567 | −54.959 | EBF |
| 43 | BR-Sa3 | −3.018 | −54.971 | EBF * |
| 44 | FR-Pue | 43.7413 | 3.5957 | EBF * |
| 45 | GF-Guy | 5.2788 | −52.925 | EBF |
| 46 | IT-Cp2 | 41.7043 | 12.3573 | EBF |
| 47 | IT-Cpz | 41.7053 | 12.3761 | EBF |
| 48 | MY-PSO | 2.973 | 102.306 | EBF |
| 49 | AU-ASM | −22.283 | 133.249 | ENF * |
| 50 | CA-NS1 | 55.8792 | −98.484 | ENF |
| 51 | CA-NS2 | 55.9058 | −98.525 | ENF |
| 52 | CA-NS3 | 55.9117 | −98.382 | ENF * |
| 53 | CA-NS4 | 55.9144 | −98.381 | ENF |
| 54 | CA-NS5 | 55.8631 | −98.485 | ENF |
| 55 | CA-Obs | 53.9872 | −105.12 | ENF * |
| 56 | CA-Qfo | 49.6925 | −74.342 | ENF |
| 57 | CA-SF1 | 54.485 | −105.82 | ENF |
| 58 | CA-SF2 | 54.2539 | −105.88 | ENF * |
| 59 | CA-TP1 | 42.6609 | −80.56 | ENF |
| 60 | CA-TP2 | 42.7744 | −80.459 | ENF * |
| 61 | CA-TP3 | 42.7068 | −80.348 | ENF |
| 62 | CA-TP4 | 42.7102 | −80.357 | ENF * |
| 63 | CH-Dav | 46.8153 | 9.8559 | ENF * |
| 64 | CZ-BK1 | 49.5021 | 18.5369 | ENF |
| 65 | DE-Lkb | 49.0996 | 13.3047 | ENF * |
| 66 | FI-Let | 60.6418 | 23.9595 | ENF |
| 67 | FR-LBr | 44.7171 | −0.7693 | ENF * |
| 68 | IT-La2 | 45.9542 | 11.2853 | ENF |
| 69 | IT-Ren | 46.5869 | 11.4337 | ENF * |
| 70 | IT-SR2 | 43.732 | 10.291 | ENF * |
| 71 | RU-Fyo | 56.4615 | 32.9221 | ENF |
| 72 | US-Blo | 38.8953 | −120.63 | ENF |
| 73 | US-GBT | 41.3658 | −106.24 | ENF * |
| 74 | US-GLE | 41.3665 | −106.24 | ENF * |
| 75 | US-Me2 | 44.4523 | −121.56 | ENF |
| 76 | US-Me3 | 44.3154 | −121.61 | ENF |
| 77 | US-Me5 | 44.4372 | −121.57 | ENF * |
| 78 | US-Me6 | 44.3233 | −121.61 | ENF |
| 79 | US-NR1 | 40.0329 | −105.55 | ENF * |
| 80 | US-Prr | 65.1237 | −147.49 | ENF * |
| 81 | US-Wi4 | 46.7393 | −91.166 | ENF |
| 82 | US-Wi9 | 46.6188 | −91.081 | ENF * |
| 83 | AT-Neu | 47.1167 | 11.3175 | GRA * |
| 84 | AU-DaP | −14.063 | 131.318 | GRA * |
| 85 | AU-Emr | −23.859 | 148.475 | GRA * |
| 86 | AU-Rig | −36.65 | 145.576 | GRA |
| 87 | CH-Cha | 47.2102 | 8.4104 | GRA * |
| 88 | CH-Fru | 47.1158 | 8.5378 | GRA |
| 89 | CH-Oe1 | 47.2858 | 7.7319 | GRA |
| 90 | CN-Cng | 44.5934 | 123.509 | GRA * |
| 91 | CN-Dan | 30.4978 | 91.0664 | GRA * |
| 92 | CN-Du2 | 42.0467 | 116.284 | GRA |
| 93 | CN-HaM | 37.37 | 101.18 | GRA |
| 94 | CZ-BK2 | 49.4944 | 18.5429 | GRA * |
| 95 | DE-Gri | 50.95 | 13.5126 | GRA |
| 96 | DK-Eng | 55.6905 | 12.1918 | GRA * |
| 97 | DK-ZaH | 74.4733 | −20.55 | GRA |
| 98 | IT-Tor | 45.8444 | 7.5781 | GRA |
| 99 | PA-SPs | 9.3138 | −79.631 | GRA * |
| 100 | RU-Ha1 | 54.7252 | 90.0022 | GRA * |
| 101 | RU-Tks | 71.5943 | 128.888 | GRA |
| 102 | US-AR1 | 36.4267 | −99.42 | GRA |
| 103 | US-AR2 | 36.6358 | −99.598 | GRA * |
| 104 | US-ARb | 35.5497 | −98.04 | GRA |
| 105 | US-ARc | 35.5465 | −98.04 | GRA * |
| 106 | US-Cop | 38.09 | −109.39 | GRA |
| 107 | US-Goo | 34.2547 | −89.874 | GRA |
| 108 | US-IB2 | 41.8406 | −88.241 | GRA * |
| 109 | US-SRG | 31.7894 | −110.83 | GRA * |
| 110 | US-Var | 38.4133 | −120.95 | GRA |
| 111 | US-Wkg | 31.7365 | −109.94 | GRA * |
| 112 | BE-Bra | 51.3076 | 4.5198 | MF |
| 113 | BE-Vie | 50.305 | 5.9981 | MF * |
| 114 | CA-Gro | 48.2167 | −82.156 | MF |
| 115 | CN-Cha | 42.4025 | 128.096 | MF * |
| 116 | US-Syv | 46.242 | −89.348 | MF |
| 117 | CA-NS6 | 55.9167 | −98.964 | OSH * |
| 118 | CA-NS7 | 56.6358 | −99.948 | OSH * |
| 119 | CA-SF3 | 54.0916 | −106.01 | OSH |
| 120 | ES-Amo | 36.8336 | −2.2523 | OSH |
| 121 | ES-LgS | 37.0979 | −2.9658 | OSH * |
| 122 | US-SRC | 31.9083 | −110.84 | OSH * |
| 123 | US-Whs | 31.7438 | −110.05 | OSH |
| 124 | AU-Dry | −15.259 | 132.371 | SAV |
| 125 | AU-GWW | −30.191 | 120.654 | SAV * |
| 126 | CG-Tch | −4.2892 | 11.6564 | SAV * |
| 127 | SD-Dem | 13.2829 | 30.4783 | SAV |
| 128 | SN-Dhr | 15.4028 | −15.432 | SAV * |
| 129 | ZA-Kru | −25.02 | 31.4969 | SAV * |
| 130 | AU-Fog | −12.545 | 131.307 | WET |
| 131 | CN-Ha2 | 37.6086 | 101.327 | WET * |
| 132 | CZ-wet | 49.0247 | 14.7704 | WET |
| 133 | DE-Akm | 53.8662 | 13.6834 | WET |
| 134 | DE-SfN | 47.8064 | 11.3275 | WET * |
| 135 | DE-Spw | 51.8923 | 14.0337 | WET |
| 136 | DE-Zrk | 53.8759 | 12.889 | WET |
| 137 | DK-NuF | 64.1308 | −51.386 | WET * |
| 138 | DK-ZaF | 74.4814 | −20.555 | WET |
| 139 | FI-Lom | 67.9972 | 24.2092 | WET * |
| 140 | SE-St1 | 68.3542 | 19.0503 | WET |
| 141 | US-Atq | 70.4696 | −157.41 | WET * |
| 142 | US-Ivo | 68.4865 | −155.75 | WET * |
| 143 | US-Los | 46.0827 | −89.979 | WET |
| 144 | US-Myb | 38.0498 | −121.77 | WET |
| 145 | US-Tw1 | 38.1074 | −121.65 | WET * |
| 146 | US-WPT | 41.4646 | −82.996 | WET |
| 147 | AU-Gin | −31.376 | 115.714 | WSA |
| 148 | AU-How | −12.494 | 131.152 | WSA * |
| 149 | AU-RDF | −14.564 | 132.478 | WSA |
| 150 | US-SRM | 31.8214 | −110.87 | WSA * |
| 151 | US-Ton | 38.4316 | −120.97 | WSA * |
| Slope | Intercept | R2 | Slope | Intercept | R2 | Slope | Intercept | R2 | |
|---|---|---|---|---|---|---|---|---|---|
| site_daily | site_year | site_years | |||||||
| EC-LUE | 0.76 ** | 0.25 ** | 0.61 | 0.83 * | 0.87 * | 0.74 | 0.95 * | 0.79 * | 0.81 |
| VPM | 0.8 ** | −0.18 ** | 0.60 | 0.93 * | −0.27 ** | 0.71 | 0.98 ** | −0.67 * | 0.81 |
| CFIX | 0.71 | 0.77 | 0.48 | 0.77 | 0.53 | 0.69 | 0.84 | 0.17 | 0.79 |
| MODIS | 0.69 * | 0.83 * | 0.57 | 0.76 * | 0.58 | 0.78 | 0.82 | 0.23 | 0.82 |
| GR | 0.73 | 0.89 | 0.54 | 0.81 * | 0.55 | 0.73 | 0.89 | 0.18 | 0.82 |
| VI | 0.77 * | 0.25 ** | 0.53 | 0.76 | 0.32 | 0.72 | 0.8 * | 0.13 * | 0.85 |
| TG | 0.73 * | 0.58 * | 0.48 | 0.87 ** | −0.01 ** | 0.73 | 0.96 | −0.39 | 0.8 |
| AVM | 0.75 | 0.44 | 0.46 | 0.87 * | −0.03 ** | 0.72 | 0.94 * | −0.38 * | 0.79 |
| LUE-NDWI | 0.79 ** | 0.94 * | 0.68 | 1 ** | 0.3 ** | 0.75 | 1 ** | 0.38 * | 0.82 |
| LUE-EF | 0.82 ** | 0.84 * | 0.74 | 1 ** | 0.32 ** | 0.85 | 1.06 ** | 0.06 ** | 0.97 |
| biome_daily | biome_year | biome_years | |||||||
| EC-LUE | 0.84 ** | −0.05 ** | 0.73 | 0.84 * | −0.07 * | 0.83 | 0.97 ** | 0.72 * | 0.94 |
| VPM | 0.86 ** | −0.58 * | 0.77 | 0.96 ** | −0.68 * | 0.77 | 1.03 * | −0.87 * | 0.96 |
| CFIX | 0.76 * | 0.45 * | 0.76 | 0.79 * | 0.45 * | 0.76 | 0.83 * | 0.2 * | 0.92 |
| MODIS | 0.75 * | 0.49 * | 0.75 | 0.79 * | 0.49 * | 0.75 | 0.82 * | 0.23 ** | 0.91 |
| GR | 0.79 * | 0.57 * | 0.81 | 0.79 * | 0.58 * | 0.81 | 0.87 * | 0.27 ** | 0.89 |
| VI | 0.82 | 0.03 | 0.8 | 0.88 | 0.33 | 0.8 | 0.79 | 0.17 | 0.87 |
| TG | 0.82 ** | 0.19 ** | 0.78 | 0.88 * | 0.29 ** | 0.78 | 0.93 ** | −0.15 ** | 0.89 |
| AVM | 0.85 * | 0.06 * | 0.79 | 0.9 * | 0.26 ** | 0.79 | 0.91 * | −0.14 * | 0.84 |
| LUE-NDWI | 0.98 ** | 0.38 ** | 0.76 | 1.04 ** | 0.11 ** | 0.84 | 1.09 ** | 0.1 ** | 0.94 |
| LUE-EF | 0.96 * | 0.49 * | 0.84 | 1.03 * | 0.15 ** | 0.88 | 1.08 ** | 0.02 ** | 0.97 |



References
- Campbell, J.E.; Berry, J.A.; Seibt, U.; Smith, S.J.; Montzka, S.A.; Launois, T.; Belviso, S.; Bopp, T.L.S.B.L.; Laine, M. Large historical growth in global terrestrial gross primary production. Nature 2017, 544, 84–87. [Google Scholar] [CrossRef]
- Schaefer, K.; Schwalm, C.R.; Williams, C.; Arain, M.A.; Barr, A.; Chen, J.M.; Davis, K.J.; Dimitrov, D.; Hilton, T.W.; Hollinger, D.Y.; et al. A model-Data comparison of gross primary productivity: Results from the North American Carbon Program site synthesis. J. Geophys. Res. Space Phys. 2012, 117, 1–15. [Google Scholar] [CrossRef]
- Yi Zheng, Y.; Shen, R.; Wang, Y.; Li, X.; Liu, S.; Liang, S.; Chen, J.M.; Ju, W.; Hang, L.; Yuan, W. Improved estimate of global gross primary production for reproducing its long-Term variation, 1982–2017. Earth Syst. Sci. Data Discuss. 2019, 12, 2725–2746. [Google Scholar] [CrossRef]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Chevallier, F.; Gomez, C.; Guanter, L.; Hicke, J.A.; Huete, A.R.; Ichii, K.; Ni, W.; Pang, Y.; Rahman, A.F. Remote sensing of the terrestrial carbon cycle: A review of advances over 50 years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
- Wang, H.; Prentice, I.C.; Keenan, T.F.; Davis, T.W.; Wright, I.J.; Cornwell, W.K.; Evans, B.J.; Peng, C. Towards a universal model for carbon dioxide uptake by plants. Nat. Plants 2017, 3, 734–741. [Google Scholar] [CrossRef]
- Yuan, W.; Cai, W.; Xia, J.; Chen, J.; Liu, S.; Dong, W.; Merbold, L.; Law, B.; Arain, A.; Beringer, J.; et al. Global comparison of light use efficiency models for simulating terrestrial vegetation gross primary production based on the LaThuile database. Agric. For. Meteorol. 2014, 192–193, 108–120. [Google Scholar] [CrossRef]
- Wagle, P.; Gowda, P.H.; Xiao, X.; Anup, K.C. Parameterizing ecosystem light use efficiency and water use efficiency to estimate maize gross primary production and evapotranspiration using MODIS EVI. Agric. For. Meteorol. 2016, 222, 87–97. [Google Scholar] [CrossRef]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B. Satellite-Based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Zhou, G.; Zhou, G.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Xiang, Y.; Zhao, X.; Song, J. Long-Time-Series global land surface satellite leaf area index product derived from MODIS and AVHRR Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5301–5318. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, Q.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Moore, B.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, L.; Xiao, J.; Yuan, W.; Yan, M.; Li, T.; Zhang, Z. Sources of uncertainty in gross primary productivity simulated by light use efficiency models: Model structure, parameters, input data, and spatial resolution. Agric. For. Meteorol. 2018, 263, 242–257. [Google Scholar] [CrossRef]
- Yuan, W.; Chen, Y.; Xia, J.; Dong, W.; Magliulo, V.; Moors, E.; Olesen, J.E.; Zhang, H. Estimating crop yield using a satellite-Based light use efficiency model. Ecol. Indic. 2016, 60, 702–709. [Google Scholar] [CrossRef]
- Xie, X.; Li, A.; Tan, J.; Jin, H.; Nan, X.; Zhang, Z.; Bian, J.; Lei, G. Assessments of gross primary productivity estimations with satellite data-Driven models using eddy covariance observation sites over the northern hemisphere. Agric. For. Meteorol. 2020, 280, 107771. [Google Scholar] [CrossRef]
- Yuan, W.; Cai, W.; Nguy-Robertson, A.L.; Fang, H.; Suyker, A.E.; Chen, Y.; Dong, W.; Liu, S.; Zhang, H. Uncertainty in simulating gross primary production of cropland ecosystem from satellite-Based models. Agric. For. Meteorol. 2015, 207, 48–57. [Google Scholar] [CrossRef]
- Wang, H.; Jia, G.; Fu, C.; Feng, J.; Zhao, T.; Ma, Z. Deriving maximal light use efficiency from coordinated flux measurements and satellite data for regional gross primary production modeling. Remote Sens. Environ. 2010, 114, 2248–2258. [Google Scholar] [CrossRef]
- Xiao, J.; Davis, K.J.; Urban, N.M.; Keller, K.; Saliendra, N.Z. Upscaling carbon fluxes from towers to the regional scale: Influence of parameter variability and land cover representation on regional flux estimates. J. Geophys. Res. 2011, 116, 1–15. [Google Scholar] [CrossRef]
- Badgley, G.; Anderegg, L.D.L.; Berry, J.A.; Field, C.B. Terrestrial gross primary production: Using NIRV to scale from site to globe. Glob. Chang. Biol. 2019, 25, 3731–3740. [Google Scholar] [CrossRef]
- Majasalmi, T.; Stenberg, P.; Rautiainen, M. Comparison of ground and satellite-Based methods for estimating stand-Level fPAR in a boreal forest. Agric. For. Meteorol. 2017, 232, 422–432. [Google Scholar] [CrossRef]
- Sasai, T.; Okamoto, K.; Hiyama, T.; Yamaguchi, Y. Comparing terrestrial carbon fluxes from the scale of a flux tower to the global scale. Ecol. Model. 2007, 208, 135–144. [Google Scholar] [CrossRef]
- Gomis-cebolla, J.; Jimenez, J.C.; Sobrino, J.A. Remote Sensing of Environment LST retrieval algorithm adapted to the Amazon evergreen forests using MODIS data. Remote Sens. Environ. 2017, 204, 401–411. [Google Scholar] [CrossRef]
- Foga, S.; Scaramuzza, P.L.; Guo, S.; Zhu, Z.; Dilley, R.D.; Beckmann, T.; Schmidt, G.L.; Dwyer, J.L.; Hughes, M.J.; Laue, B. Cloud detection algorithm comparison and validation for operational Landsat data products. Remote Sens. Environ. 2017, 194, 379–390. [Google Scholar] [CrossRef]
- Stillinger, T.; Roberts, D.A.; Collar, N.M.; Dozier, J. Cloud masking for Landsat 8 and MODIS Terra over snow covered terrain: Error analysis and spectral similarity between snow and cloud. Water Resour. Res. 2019, 55, 6169–6184. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Chen, J.M.; Desai, A.R.; Hollinger, D.Y.; Arain, M.A.; Margolis, H.A.; Gough, C.; Staebler, R.M. Remote sensing of canopy light use efficiency in temperate and boreal forests of North America using MODIS imagery. Remote Sens. Environ. 2012, 118, 60–72. [Google Scholar] [CrossRef]
- Sims, D.A.; Rahman, A.F.; Cordova, V.D.; El-Masri, B.Z.; Baldocchi, D.D.; Bolstad, P.V.; Flanagan, L.B.; Goldstein, A.H.; Hollinger, D.Y.; Misson, L.; et al. A new model of gross primary productivity for North American ecosystems based solely on the enhanced vegetation index and land surface temperature from MODIS. Remote Sens. Environ. 2008, 112, 1633–1646. [Google Scholar] [CrossRef]
- Veroustraete, F.; Sabbe, H.; Eerens, H. Estimation of carbon mass fluxes over Europe using the C-Fix model and Euroflux data. Remote Sens. Environ. 2002, 83, 376–399. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Verma, S.B.; Rundquist, D.; Arkebauer, T.J.; Keydan, G.; Leavitt, B.; Ciganda, V.; Burba, G.G.; Suyker, A.E. Relationship between gross primary production and chlorophyll content in crops: Implications for the synoptic monitoring of vegetation productivity. J. Geophys. Res. 2006, 111, 1–13. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, L.; Wang, S. Comparison of different GPP models in China using MODIS image and ChinaFLUX data. Remote Sens. Sens. 2014, 6, 10215–10231. [Google Scholar] [CrossRef]
- Running, S.T.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M. A Continuous Satellite-Derived Measure of Global Terrestrial Primary Production. Bioscience 2006, 54, 547–560. [Google Scholar] [CrossRef]
- Wu, C.; Munger, J.W.; Niu, Z.; Kuang, D. Comparison of multiple models for estimating gross primary production using MODIS and eddy covariance data in Harvard Forest. Remote Sens. Environ. 2010, 114, 2925–2939. [Google Scholar] [CrossRef]
- Gu, L.; Baldocchi, D.D.; Wofsy, S.C.; Munger, J.W.; Michalsky, J.J.; Urbanski, S.P.; Boden, T.A. Response of a Deciduous Forest to the Mount Pinatubo Eruption: Enhanced Photosynthesis. Science 2003, 299, 2035–2038. [Google Scholar] [CrossRef] [PubMed]
- Kicklighter, D.W. A first-Order analysis of the potential rôle of CO2 fertilization to affect the global carbon budget: A comparison of four terrestrial biosphere models. Tellus B: Chem. Phys. Meteorol. 1999, 51, 343–366. [Google Scholar] [CrossRef]
- Raich, J.W.; Rastetter, E.B.; Melillo, J.M.; Kicklighter, D.W.; Steudler, P.A.; Peterson, B.J.; Grace, A.L.; Moore, B.; Vorosmarty, C.J. Potential Net Primary Productivity in South America: Application of a Global Model. Ecol. Appl. 2013, 1, 399–429. [Google Scholar] [CrossRef] [PubMed]
- Murphy, R.J.; Whelan, B.; Chlingaryan, A.; Sukkarieh, S. Quantifying leaf scale variations in water absorption in lettuce from hyperspectral imagery: A laboratory study with implications for measuring leaf water content in the context of precision agriculture. Precis. Agric. 2018, 767–787. [Google Scholar] [CrossRef]
- Ding, C.; Liu, X.; Huang, F.; Li, Y.; Zou, X. Onset of drying and dormancy in relation to water dynamics of semi-arid grasslands from MODIS NDWI. Agric. For. Meteorol. 2017, 234–235, 22–30. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Frank, J.; Frank, J.; Massman, M.; Urbanski, S. The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef]
- Baty, F.; Ritz, C.; Charles, S.; Brutsche, M. A toolbox for nonlinear regression in R: The package nls tools. J. Stat. Softw. 2015, 66, 1–21. [Google Scholar] [CrossRef]
- Zhang, F.; Shi, X.; Zeng, C.; Wang, L.; Xiao, X.; Wang, G.; Chen, Y.; Zhang, H.; Lu, X.; Immerzeel, W. Recent stepwise sediment flux increase with climate change in the Tuotuo River in the central Tibetan Plateau. Sci. Bull. 2020, 65, 410–418. [Google Scholar] [CrossRef]
- Carroll, R.J.; Ruppert, D. The Use and Misuse of Orthogonal Regression in Linear Errors-in-Variables Models. General 2014, 50, 1–6. [Google Scholar]
- Piñeiro, G.; Perelman, S.; Guerschman, J.P.; Paruelo, J.M. How to evaluate models: Observed vs. predicted or predicted vs. observed? Ecol. Model. 2008, 216, 316–322. [Google Scholar] [CrossRef]
- Leng, L.; Zhang, T.; Kleinman, L.; Zhu, W. Ordinary least square regression, orthogonal regression, geometric mean regression and their applications in aerosol science. J. Phys. Conf. Ser. 2007, 78, 24–28. [Google Scholar] [CrossRef]
- Valbuena, R.; Hernando, A.; Manzanera, J.; Görgens, E.; Almeida, D.; Mauro, F.; García-Abril, A.; Coomes, D. Enhancing of accuracy assessment for forest above-Ground biomass estimates obtained from remote sensing via hypothesis testing and overfitting evaluation. Ecol. Model. 2017, 366, 15–26. [Google Scholar] [CrossRef]
- Forzieri, G. Increased control of vegetation on global terrestrial energy fluxes. Nat. Clim. Chang. 2020, 10, 356–362. [Google Scholar] [CrossRef]
- Running, S.W.; Zhao, M. Daily GPP and Annual NPP (MOD17A2/A3) products NASA Earth Observing System MODIS Land Algorithm-User’s guide V3. General 2015, 28, 1–6. [Google Scholar]
- Keenan, T.F.; Prentice, I.C.; Canadell, J.G.; Williams, A.C.; Wang, H.; Raupach, M.; Collatz, G.J. Recent pause in the growth rate of atmospheric CO2 due to enhanced terrestrial carbon uptake. Nat. Commun. 2016, 7, 1–9. [Google Scholar] [CrossRef]
- Jung, M.; Schwalm, C.; Migliavacca, M.; Walther, S.; Camps-Valls, G.; Koirala, S.; Anthoni, P.; Besnard, S.; Bodesheim, P.; Carvalhais, N.; et al. Scaling carbon fluxes from eddy covariance sites to globe: Synthesis and evaluation of the FLUXCOM approach. Biogeosciences 2020, 17, 1343–1365. [Google Scholar] [CrossRef]
- Kondo, M.; Ichii, K.; Takagi, H.; Sasakawa, M. Comparison of the data-Driven top-Down and bottom-Up global terrestrial CO2 exchanges: GOSAT CO2 inversion and empirical eddy flux upscaling. J. Geophys. Res. Biogeosci. 2015, 120, 1226–1245. [Google Scholar] [CrossRef]
- Jiang, C.; Ryu, Y. Remote Sensing of Environment Multi-Scale evaluation of global gross primary productivity and evapotranspiration products derived from Breathing Earth System Simulator (BESS). Remote Sens. Environ. 2016, 186, 528–547. [Google Scholar] [CrossRef]
- Upadhyaya, S.A.; Kirstetter, P.-E.; Gourley, J.J.; Kuligowski, R.J. On the Propagation of Satellite Precipitation Estimation Errors: From Passive Microwave to Infrared Estimates. Estimates. J. Hydrometeorol. 2020, 21, 1367–1381. [Google Scholar] [CrossRef]
- Cheng, S.J.; Butterfield, Z.; Keppel-Aleks, G.; Steiner, A.L. The Global Influence of Cloud Optical Thickness on Terrestrial Carbon Uptake. Earth Interact. 2019, 23, 1–22. [Google Scholar]
- Haverd, V.; Smith, B.; Canadell, J.G.; Cuntz, M.; Mikaloff-Fletcher, S.; Farquhar, G.D.; Woodgate, W.; Briggs, P.R.; Trudinger, C.M. Higher than expected CO 2 fertilization inferred from leaf to global observations. Glob. Chang. Biol. 2020, 26, 2390–2402. [Google Scholar] [CrossRef] [PubMed]
- Smith, W.K.; Reed, S.C.; Cleveland, C.C.; Ballantyne, A.P.; Anderegg, W.R.L.; Wieder, W.R.; Liu, Y.Y.; Running, S.W. Large divergence of satellite and Earth system model estimates of global terrestrial CO2 fertilization. Nat. Clim. Chang. 2016, 6, 306–310. [Google Scholar] [CrossRef]
- Chen, Y.; Xia, J.; Liang, S.; Feng, J.; Fisher, J.B.; Li, X.; Li, X.; Liu, S.; Ma, Z.; Miyata, A.; et al. Comparison of satellite-based evapotranspiration models over terrestrial ecosystems in China. Remote Sens. Environ. 2014, 140, 279–293. [Google Scholar] [CrossRef]
- Ma, H.Y. CAUSES: On the Role of Surface Energy Budget Errors to the Warm Surface Air Temperature Error Over the Central United States. J. Geophys. Res. Atmos. 2018, 123, 2888–2909. [Google Scholar] [CrossRef]
- Gao, B.-C. NDWI—A normalized difference Water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 266, 257–266. [Google Scholar] [CrossRef]
- Keppel-Aleks, G.; Washenfelder, R.A. The effect of atmospheric sulfate reductions on diffuse radiation and photosynthesis in the United States during 1995–2013. Geophys. Res. Lett. 2016, 43, 9984–9993. [Google Scholar] [CrossRef]
- Lee, M.S.; Hollinger, D.Y.; Keenan, T.F.; Ouimette, A.P. Agricultural and Forest Meteorology Model-based analysis of the impact of di ff use radiation on CO 2 exchange in a temperate deciduous forest. Agric. For. Meteorol. 2018, 249, 377–389. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, X.; Zhang, X.; Tani, H.; Engliang, G.; Shuai, Y.; Zhang, T. Science of the Total Environment Evaluating and comparing remote sensing terrestrial GPP models for their response to climate variability and CO2 trends. Sci. Total Environ. 2019, 668, 696–713. [Google Scholar] [CrossRef]
- Xie, X.; Li, A. Development of a topographic-Corrected temperature and greenness model (TG) for improving GPP estimation over mountainous areas. Agric. For. Meteorol. 2020, 295, 108193. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Zhang, Y.; Chen, J.M. Correcting Clear-Sky Bias in Gross Primary Production Modeling From Satellite Solar-Induced Chlorophyll Fluorescence Data. J. Geophys. Res. Biogeosci. 2020, 125, e2020JG005822. [Google Scholar] [CrossRef]
- Flack-Prain, S.; Meir, P.; Malhi, Y.; Smallman, T.; Williams, M. The importance of physiological, structural and trait responses to drought stress in driving spatial and temporal variation in GPP across Amazon forests. Biogeosciences 2019, 16, 4463–4484. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, F.; Kung, H.-T.; Johnson, V.C.; Wang, J.; Zhang, Y.; Yu, H.; Yushanjiang, A. Using the vegetation-solar radiation (VSr) model to estimate the short-term gross primary production (GPP) of vegetation in Jinghe county, XinJiang, China. Ecol. Eng. 2017, 107, 208–215. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Liu, S.; Wang, Y.-P.; Valbuena, R.; Wu, Y.; Kutia, M.; Zheng, Y.; Lu, W.; Zhu, Y.; Zhao, M.; et al. Tighten the Bolts and Nuts on GPP Estimations from Sites to the Globe: An Assessment of Remote Sensing Based LUE Models and Supporting Data Fields. Remote Sens. 2021, 13, 168. https://doi.org/10.3390/rs13020168
Wang Z, Liu S, Wang Y-P, Valbuena R, Wu Y, Kutia M, Zheng Y, Lu W, Zhu Y, Zhao M, et al. Tighten the Bolts and Nuts on GPP Estimations from Sites to the Globe: An Assessment of Remote Sensing Based LUE Models and Supporting Data Fields. Remote Sensing. 2021; 13(2):168. https://doi.org/10.3390/rs13020168
Chicago/Turabian StyleWang, Zhao, Shuguang Liu, Ying-Ping Wang, Ruben Valbuena, Yiping Wu, Mykola Kutia, Yi Zheng, Weizhi Lu, Yu Zhu, Meifang Zhao, and et al. 2021. "Tighten the Bolts and Nuts on GPP Estimations from Sites to the Globe: An Assessment of Remote Sensing Based LUE Models and Supporting Data Fields" Remote Sensing 13, no. 2: 168. https://doi.org/10.3390/rs13020168
APA StyleWang, Z., Liu, S., Wang, Y.-P., Valbuena, R., Wu, Y., Kutia, M., Zheng, Y., Lu, W., Zhu, Y., Zhao, M., Peng, X., Gao, H., Feng, S., & Shi, Y. (2021). Tighten the Bolts and Nuts on GPP Estimations from Sites to the Globe: An Assessment of Remote Sensing Based LUE Models and Supporting Data Fields. Remote Sensing, 13(2), 168. https://doi.org/10.3390/rs13020168







