Abstract
Small unmanned aerial systems (sUAS) are becoming increasingly popular due to their affordability and logistical ease for repeated surveys. While sUAS-based remote sensing has many applications in water resource management, their applicability and limitations in fluvial settings is not well defined. This study uses a combined thermal-optic sUAS to monitor the seasonal geothermal influence of a 1-km-long reach of the Yellowstone River, paired with in-situ streambed temperature profiles to evaluate geothermal seep interactions with Yellowstone River in Montana, USA. Accurate river water surface elevation along the shoreline was estimated using structure from motion (SfM) photogrammetry digital surface models (DSMs); however, water surface elevations were unreliable in the main river channel. Water temperature in thermal infrared (TIR) orthomosaics was accurate in temperature ranges of tens of degrees (>≈30 °C), but not as accurate in temperature ranges of several degrees (>≈15 °C) as compared to in-situ water temperature measurements. This allowed for identification of geothermal features but limited the ability to identify small-scale temperature changes due to river features, such as pools and riffles. The study concludes that rivers with an average width greater than or equal to 123% of the ground area covered by a TIR image will be difficult to study using structure from motion photogrammetry, given Federal Aviation Administration (FAA) altitude restrictions and sensor field of view. This study demonstrates the potential of combined thermal-optic sUAS systems to collect data over large river systems, and when combined with in-situ measurements, can further increase the sUAS utility in identifying river characteristics.
1. Introduction
Small unmanned aerial systems (sUAS) are increasingly being used for scientific applications such as water level detection [1,2] hydromorphological characterization [3,4,5], bathymetric observation [6,7], groundwater–surface water (GW–SW) interactions [8,9,10] and thermal analysis of fisheries habitat [11]. As opposed to other remote sensing platforms such as satellite and manned aircraft, sUAS allows for inexpensive, high resolution data collection, and repeated surveys for assessing temporal variation.
The utility of structure from motion (SfM) photogrammetry [12] products, such as orthomosaics and digital surface models (DSM), is well documented in the literature with applications for fluvial systems [3,4,5,13,14,15]. SfM photogrammetry processing of RGB-images and thermal infrared (TIR) images has become widely available through a variety of software packages, such as Pix4D Mapper, Drone Deploy and Agisoft Metashape among others. SfM photogrammetry relies on identifying objects, or unique pixels, in consecutive 2-D photographs to generate a 3-D point cloud model. Homogenous surfaces such as deep water can result in low density point clouds and data gaps. The presence of low-density regions and gaps in the point cloud can result in poor 3-D elevation model construction. Despite demonstrations of quantifying water level from SfM photogrammetry [1,2], loss of elevational accuracy due to low point cloud densities is seldom acknowledged in the literature [6,7].
Geothermal systems in and near Yellowstone National Park (YNP), USA, are part of the world’s highest concentration of active geothermal features. Numerous studies have investigated spatial and temporal heterogeneity of hydrothermal features [16,17], their seasonal variation in discharge [18], and their effect on river water quality [19] and ecology [20]. Continued monitoring of geothermal systems and the rivers into which they discharge will require continuous improvements in methodology for evaluating seasonal and spatial patterns. There is also the continuing need to establish baseline conditions considering increased interest in geothermal development. The Yellowstone River, MT, exhibits large seasonal variation in flow and distinct geothermal inputs making it ideal for assessing potential of sUAS-based RGB-imagery and thermal imagery to observe river physical properties over a range of hydrologic conditions.
sUAS-based TIR imagery has been successfully used for fluvial environments [8,9,10,21,22,23]. SfM photogrammetry using TIR imagery generally requires much greater image overlap due to low sensor resolution compared to traditional RGB-images. Low sensor resolution in combination with narrower field of view (FOV) make SfM photogrammetry processing with TIR imagery more difficult and could limit the scale over which sUAS-based TIR imagery is appropriate. Given current TIR camera technology and FAA restrictions on sUAS flight altitude (122 m), river width could be a limiting factor for sUAS TIR imagery and associated SfM photogrammetry processing. While TIR imaging is frequently used to quantify GW–SW interactions [23,24,25,26,27], volumetric groundwater discharge into rivers has not been quantified using sUAS TIR imagery.
Streambed temperature profiles can be used to solve the heat transport equation for seepage flux (one-dimensional vertical flow of water through the shallow riverbed) [28]. Analytical solutions to the heat transport equation [29,30] and the development of the VFLUX, a toolbox in MATLAB (MathWorks Inc.) [31,32], have simplified seepage flux calculations. Seepage flux is a point-in-space measurement and can be paired with area from TIR imagery to evaluate volumetric groundwater discharge.
The goal of this research is to evaluate the effectiveness of SfM photogrammetry using sUAS-based RGB and TIR imaging techniques to assess geothermal seepage into a small reach of Yellowstone River, MT. Specifically, the study aims to evaluate (a) sUAS-based RGB and TIR image SfM photogrammetry techniques to estimate river stage and delineate geothermally influenced areas, respectively, (b) seasonal variation of geothermal seepage into the study reach, and (c) seepage flux variation with respect to depth of water. This work has significant implications for using sUAS-based high-resolution, low-cost, remote sensing data collection methods to evaluate GW–SW interactions.
2. Methods
2.1. Study Site
La Duke Hot Springs (LDHS) lies within a complex fault system and surfaces near the intersection of Reese Creek normal fault, Gardiner reverse fault, and several other smaller normal faults [32]. Faults can act as hydraulic connections between deep geothermal water and the surface. LDHS is a hot spring complex consisting of a developed main geothermal spring and a series of hot seeps that flow into the Yellowstone River. LDHS is located in southwestern Montana in the known geothermal resource area of the Yellowstone Controlled Groundwater Area [33]. The unenhanced flow at the LDHS spring box is approximately 9.15 L/s and is routed approximately 2 miles downstream to a commercial pool [34]. There are other smaller, undeveloped hot springs and seeps associated with LDHS that flow directly into the Yellowstone River. A two-year study conducted by the USGS evaluated the effects of the development of LDHS in relation to Mammoth Hot Spring in Yellowstone National Park (YNP) [35]. Concerns regarding potential connections between features such as LDHS and YNP geothermal features led to the inception of the Yellowstone Controlled Groundwater Area, within which geothermal groundwater resource development is restricted.
The study site (Figure 1) is located approximately 2 miles upstream from USGS 06191500 Yellowstone River at Corwin Springs gauging station (https://waterdata.usgs.gov/nwis/uv?site_no=06191500) and covers an area of approximately 45 ha. The Yellowstone River at Corwin Springs Station drains 6775 square kilometers, with low and high mean monthly flowrates of 11.9 and 135 cubic meters per second, respectively [36]. In Montana’s late spring/early summer snowmelt dominated river systems, low flows generally occur from December through February and high flows generally occur in late May/early June during spring runoff. The peak discharge over the past 5 years has in some cases exceeded 30 times the baseflow discharge.
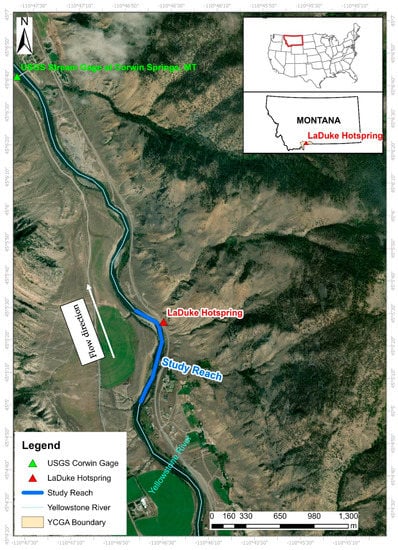
Figure 1.
Map showing the study area and key features. “YCGA Boundary” refers to Yellowstone Controlled Groundwater Area. Credits for the background service layer: United States Department of Agriculture Farm Service Agency (USDA FSA), GeoEye Inc., and Maxar.
The yearly ambient temperature dynamic is characterized by low humidity year-round with winter lows of −14.5 °C and summer highs of 24.6 °C. The river water temperature fluctuates between nearly 0 °C in the winter and nearly 20 °C in the summer, while ground water temperatures fluctuated between 12.0 °C and 19.1 °C depending on well location and time of year.
2.2. Field Methods and Data Acquisition
A combination of sUAS-based remote sensing and in-situ data collection methods were used in the study (Figure 2). sUAS-based remote sensing was used for RGB and TIR image acquisition. In-situ data (temperature sensors, streambed temperature profiles, global navigation satellite system (GNSS) data) was collected to ground truth remote sensing data and to calculate seepage flux rate.
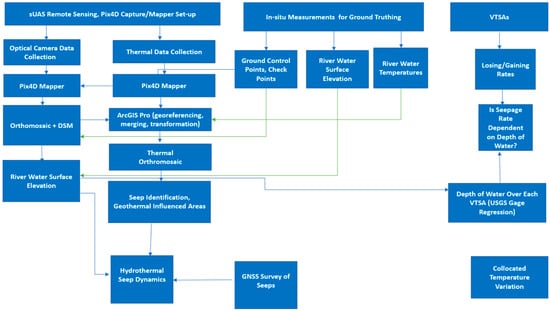
Figure 2.
Overview of the data collection and processing workflow. Green lines represent remote sensing data accuracy verification using ground truthing data.
2.2.1. RGB and TIR Image Acquisition
The sUAS system consisted of the DJI Matrice 600 Pro platform mounted with the FLIR Vue Pro R (stabilized with the Tarot Metal 3 Axis Thermal Imaging Gimbal), which outputs calibrated radiometric temperature measurements, (25° field of view (FOV), 336 × 256 pixels, 7.5–13.5 µm spectral band, with an uncooled VOx microbolometer thermal imager) and DJI Zenmuse Z3 optical camera (92° FOV, 4000 × 3000 pixels, 22–77 mm equivalent focal length).
Automated flights were created in Pix4D Capture (https://www.pix4d.com/product/pix4dcapture) software for RGB and TIR image acquisition independently (Figure 3) so that identical flight paths could be covered on multiple dates. Flights for RGB image acquisition were planned with 80% overlap in across and along-track directions, with the camera angle set at 60°, and a flight speed of 7.6 m/s. For the RGB acquisition, we obtained oblique imagery because there were steep sided riverbanks and large canopy cover that obscured the shoreline in places. To cover the study area, two flights were flown consecutively with duration of approximately 16:24 MM:SS and 16:30 MM:SS for the northern and southern flight plans, respectively. Flights for TIR image acquisition were planned with 87% overlap in across and along-track directions, with the camera positioned at nadir, and a flight speed of 4.8 m/s. To cover the study area, three flights were flown consecutively with duration of approximately 16:29 MM:SS, 16:29 MM:SS and 16:15 MM:SS for the northern, middle and southern flights, respectively. Conservative flight times (less than 20 min) were employed to avoid complications from shorter battery life during winter months. To avoid interferences with solar irradiance and ensure maximum temperature difference (ΔT) between geothermal seepage and river temperature TIR image acquisition took place at sunrise before the sun rose above mountains to the east; with the exception of march, where colder atmospheric temperatures forced the flight duration to 1:00–2:38 pm. Flight duration to collect the entire TIR-image data sets were between 1 h 7 min and 1 h 38 min, during these time periods the variation in river temperature was between 0.1 and 0.9 °C according to the downstream USGS gauging station 06191500.TIR image quality was verified visually after each flight. Both RGB and TIR images were taken from an altitude of 106 m Above Ground Level (AGL). Flights were conducted on 5 November 2018; 10 March 2019; 1 June 2019; 14 July 2019, and 23 September 2019. To evaluate collocated temperature variation, on 24 September 2019, the northern TIR flight survey was carried out two additional times, first flying east-to-west then flying west-to-east.

Figure 3.
Flight paths generated in Pix4D Capture to conduct repeated surveys. Left figure (a) shows the two flight paths used to acquire RGB-imagery; the right figure (b) shows the three flight paths used to acquire thermal infrared (TIR) imagery. Credits for the background service layer: United States Department of Agriculture Farm Service Agency (USDA FSA), GeoEye Inc. and Maxar.
2.2.2. Ground Truth and Water Elevation Data
Ground control points (GCPs) and check points (CPs), were used for ground truthing RGB images. GCPs and CPs were marked on the ground using five-gallon bucket lids (30 cm in diameter). The GCPs were used during SfM photogrammetry processing to increase spatial accuracy, and CPs were used for unbiased check for spatial accuracy in SfM photogrammetry products. Prior to each RGB flight, 8 to 10 GCPs were staked to the ground throughout the study area, four or five on each side of the river. GCPs were left on the ground between flight dates and replaced as needed. Prior to flights in June, July and September an additional 9 or 10 targets were staked to the ground throughout the study area to be used as check points (CP). Each target was surveyed using a centimeter-level accuracy Trimble Geo 7X Handheld Data Collector with Trimble Zephyr 2 Antenna. Expected accuracy of GNSS measurements, based on the nearest base station (https://www.ngs.noaa.gov/CORS_Map/) 14.34 km from the study site, was 2.4 cm horizontally and 6.4 cm vertically. All GNSS measurements were post-processed in Trimble Pathfinder Office and were exported in WGS84 (2011) (horizontal) and EGM 96 (vertical) datum.
Prior to each flight, six HOBO TidbiT MX Temperature 400’ Data Loggers (TidbiT) were placed in the river throughout the study area and programmed to log temperature every five minutes. Each TidbiT was given a unique I.D. and surveyed using the GNSS equipment. The TidbiT has a range of −20 °C to 50 °C in water, accuracy of ±0.2 °C between 0 °C and 70 °C, resolution of 0.01 °C and drift of 0.1 °C per year.
Within one hour of the sUAS RGB-image acquisition flights, water level elevations were surveyed on each side of the river using Trimble Geo 7X Handheld Data Collector with a Trimble Zephyr 2 Antenna. Between 10 and 20 GNSS measurements were gathered at the shoreline throughout the study area. To verify the accuracy of estimated river stage from SfM photogrammetry, DSM elevation values were compared to GNSS measurements of the river shoreline elevation.
2.2.3. Stream Bed Vertical Temperature Profiles
A total of nine Vertical Temperature Sensing Assemblies (VTSAs) were constructed to measure streambed temperature profiles. Thermocon iButton DS 1922L were used in the VTSAs. Thermocon iButtons have a range of −40 °C to 85 °C, accuracy of ±0.5 °C between −10 °C and 65 °C, resolution of 0.0625 °C and are capable of recording 4096 measurements in 16-bit format. Each VTSA was built from a 91 cm segment of 1.9 cm diameter steel pipe with foam inserted the length of the pipe. Four Thermocon iButtons were inserted in the pipe at depths corresponding to 0, 3, 7 and 12 cm below the streambed (Figure 4). The VTSA set-up was adopted from Briggs [37], with minor modifications, due to its ability to detect both strong gaining (water flow moving from the subsurface sediments to the river) and losing (water flowing from the river to the subsurface) conditions. All Thermocon iButtons were programmed to log temperature every 60 min in 16-bit format.

Figure 4.
Vertical temperature sensing assembly with Thermocon iButtons temperature sensors removed from the pipe for visualization. The foam and Thermocon iButton assembly was inserted into the pipe, sealed and then driven into the riverbed to the red tape. Thermocon iButton sensors are 0, 3, 7 and 12 cm bellow the riverbed.
Three VTSAs were installed on 18 February 2019. The Thermocon iButtons contained in this group of VTSAs were encased in small plastic bags to prevent water damage. In addition, one VTSA was installed on 2 June 2019 and five others were installed on 13 July 2019. The Thermocon iButtons contained in the six VTSAs that were installed in June and July were sealed using Plasti Dip® to prevent water damage [38]. Of the nine VTSAs installed, eight of them were recovered on 24 September 2019. 75% of Thermocon iButtons placed in plastic bags failed due to water exposure and the iButtons placed in Plastic Dip logged data successfully without any failures. VTSAs were placed to target geothermally influenced and nongeothermally influenced streambed areas (Figure 5). VTSAs field locations were surveyed using the GNSS instrument.
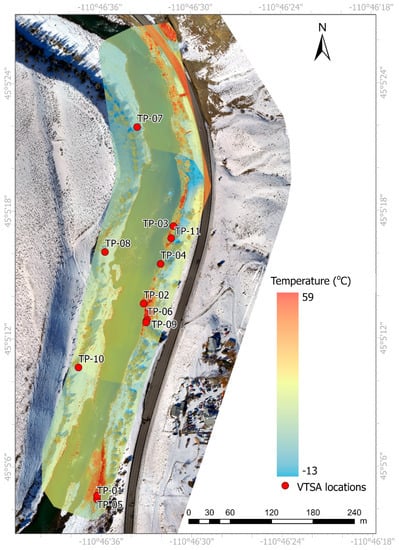
Figure 5.
Map showing placement of Vertical Temperature Sensing Assemblies (VTSAs) in the study area. The RGB orthomosaic and TIR orthomosaic correspond to the flight data from March 2019.
A 470 mL sample of streambed sediment was collected on 24 September 2019 to measure bulk density and porosity. Dispersivity, thermal conductivity and the volumetric heat capacity of the sediment were obtained from Lapham [39] and are listed in Table 1. Sediment thermal properties typically vary less than hydraulic conductivity [39], though these properties can have a significant impact on seepage flux calculations.

Table 1.
Yellowstone River study area sediment properties.
2.3. Data Analysis
2.3.1. SfM Photogrammetry
SfM photogrammetry products from RGB (RGB-orthomosaics and DSMs) and TIR imagery (TIR orthomosaics) were produced using Pix4D Mapper version 4.3.31 (Pix4D). Between 430 and 488 images were taken during RGB image acquisition and between 2866 and 3028 images were taken during TIR image acquisition. The average ground sampling distance was 4.72 cm for RGB images and 14.63 cm for TIR images.
All RGB images were processed simultaneously in Pix4D, and GCPs were used during SfM photogrammetry processing. Check points were used to validate accuracy of RGB-image SfM photogrammetry products collected during June, July and September 2019 surveys. Images, GCP and CP coordinates were entered into Pix4D using the WGS84 (2011) and EGM96 datum, and the processed orthomosaics were obtained in WGS84/ UTM Zone 12N, EGM96 coordinate system.
Each of the three flights carried out for TIR image acquisition had to be processed in Pix4D separately, with approximately 900–1000 images per flight. Due to the low resolution of the thermal camera, generating an optimal amount of tie points was challenging. TIR orthomosaics were processed several times, altering the initial focal length value within Pix4D’s Camera Model Parameters between runs, until the relative difference in initial and optimized values were less than 5% difference and key points per image, calibrated images and matches per calibrated image were in an acceptable range, according to Pix4D, (500–10,000, 60%–95% and 100–1000, respectively). GCPs and CPs were not used during the SfM thermal photogrammetry processing, instead TIR orthomosaics were georeferenced using the spline method in ArcGIS Pro (v2.2.0) by identifying common features in the corresponding RGB orthomosaic.
2.3.2. TIR Image Temperature Data Transformation, Accuracy, and Feature Identification
FLIR Vue Pro R camera uses an algorithm to convert each pixel’s thermal energy into radiometric temperature values using user entered (pre-flight) emissivity, air temperature, sky condition, humidity, and target range. Prior to TIR image acquisition the internal FLIR Vue Pro R value for emissivity was set to 0.94 and settings for air temperature, sky condition, humidity, and target range were set to match field conditions. Emissivity of water is typically in the range of 0.92 to 0.96 [40,41], so, a 0.94 value has been used for all the flights as we are only interested in water surface temperatures. TIR orthomosaics produced from FLIR Vue Pro R TIR imagery contains radiometric temperature values in every pixel, however, TIR orthomosaic radiometric temperature accuracy is variable and must be validated using in-situ temperature measurements. TIR orthomosaic radiometric temperatures were first validated and then, transformed using in-situ temperature measurements. In order to compensate for TIR-image acquisition time and potential spatial inaccuracy, in-situ temperature measurements were averaged over the TIR-image acquisition period (approximately one hour) and radiometric temperature was averaged over nine pixels (pixel with the in-situ temperature measurement location and surrounding the eight pixels). Radiometric temperature data was transformed using the best fit equation generated from plotting radiometric temperature vs. kinetic temperature using all the data points (nongeothermally influenced and geothermally influenced). It should be noted, we have not applied external atmospheric corrections to the thermal camera output (radiometric temperatures in each pixel); hence, thermal orthomosaic data presented in this study should be considered as radiometric temperatures and not kinetic temperatures.
In ArcGIS Pro, a temperature value of 15 °C above the background river water temperature was selected to identify areas that were geothermally influenced for November and December. For March, a single threshold value of 30 °C was used instead of 15 °C above background water temperature identified, as rocks and ground at a few places were warmer than the 15 °C above background water temperature value. Geothermally influenced raster areas were converted into polygons in each TIR orthomosaic for a comparative metric between seasons. Consecutive automated TIR flights plans in Pix4D capture were identical for each season, so the GSD, altitude, fight speed, and other parameters were comparable through time.
2.3.3. DSM Water Surface Elevation Accuracy and Water Depth Rating Curve
Flights conducted in June, July and September of 2019 were used to assess the accuracy of river water elevation obtained from DSMs. DSM outputs from Pix4D were produced using inverse distance weighting method. The accuracy of DSMs water surface elevation was evaluated via linear regression with in-situ water surface elevation measurements. The elevation of each VTSA was subtracted from the water surface elevation to obtain depth of water over each VTSA. River depth at USGS Yellowstone River gage station at Corwin Springs was used to build rating curves to predict continuous water depth above each VTSA. This continuous water depth was then used to evaluate the effect of depth of water on the geothermal seepage rates.
2.3.4. Seepage Flux
Temperature time series data from the VTSAs were used to calculate seepage flux using the VFLUX toolbox [31,32] in MATLAB. VFLUX tool solves the one-dimensional vector of fluid flow (seepage flux) using amplitude and phase shift equations [29,30]. Temperature time series data from two adjacent Thermocron iButtons are used to solve for seepage flux and the seepage flux measurement is reported at the center of pair depth. To simplify comparisons, only seepage flux rates calculated using the Hatch [29] amplitude ratio method was used. Seepage flux changes temporally, spatially and with depth below riverbed [32]. In order to be consistent for spatial and temporal comparison, only seepage flux calculated at 5 cm below the stream bed was used. Five cm depth was chosen as it returned the greatest number of successful seepage flux calculations across all VTSAs.
3. Results
3.1. SfM Photogrammetry
3.1.1. RGB Orthomosaic and DSM Accuracy
The Root Means Square Error (RMSE) for GCPs were 5.6, 3.4, 3.3, 5.3 and 3.1 cm for November, March, June, July and September surveys, respectively. Only RGB-Orthomosaic and DSMs from June, July and September surveys were validated with CPs (Table 2).

Table 2.
Sample size (n) and RMSE (x, y and z directions) in geolocation of RGB SfM products for GCPs and CPs.
3.1.2. Thermal Orthomosaic Accuracy and Feature Identification
TIR orthomosaics of the entire reach were produced for November, March and September TIR image data sets (Figure 6). For Pix4D to calibrate an image, enough key points are required to accurately match with at least two other images (https://support.pix4d.com/hc/en-us/articles/202560189-How-to-manually-calibrate-uncalibrated-Cameras-in-the-rayCloud; https://support.pix4d.com/hc/en-us/articles/202558689-Quality-Report-Help). The June flights had a range of 2 to 33% calibrated images and the July flights had a range of 36 to 50% calibrated images. Therefore, TIR orthomosaics of the entire reach could not be generated for June and July flight surveys (Table 3). A partial reach TIR orthomosaic was generated for July by significantly altering the SfM photogrammetry workflow. Rather than processing every image from a flight, only a subset (approximately 200 images from each flight) of images that represented the east bank of the river were used. Using this smaller data set, 98%, 49% and 88% calibrated images was achieved for the north, middle and south flight plans, respectively. Flight duration to collect the entire TIR-image data sets were between 1 h 7 min and 1 h 38 min, during these time periods the variation in river temperature was between 0.1 and 0.9 °C according to USGS gauging station 06191500.

Figure 6.
Orthomosaics generated from RGB images with survey date and Yellowstone River flow rate.

Table 3.
Summary of number of images processed, area covered, median keypoints per image, percent calibrated images and median matches per image for every thermal orthomosaic SfM model. Median values are calculated for full flight image processing.
To evaluate the accuracy of original and transformed TIR orthomosaics, radiometric temperature data was verified with in-situ kinetic measurements using linear regression and RMSE. A plot of radiometric temperatures (from TIR orthomosaics) and kinetic temperatures (in-situ measurements) should produce a best fit line with a slope of one and intercept of zero. Both R2 and RMSE values have improved after transformation compared to original data (Figure A1 and Figure 7) for November, March, and September data sets. For pre-transformed July data, the R2 value was negative due to lower number of in-situ measurements, the lower temperature range covered with in-situ measurements, and the relatively higher depth of water which might have masked geothermal signal. Due to this negative R2 value, July data was not transformed and not analyzed further. For transformed data, in November, March, and September the linear regression slopes were 0.95, 0.98, and 0.97, respectively. Over large temperature gradients (T ≥ 30 °C) the R2 values for radiometric temperature vs kinetic temperature were between 0.85 and 0.94 (Figure 7). RMSE values for predicted vs observed radiometric temperatures were 6.09, 3.85, and 4.78 °C for November, March, and September, respectively (Table 4).
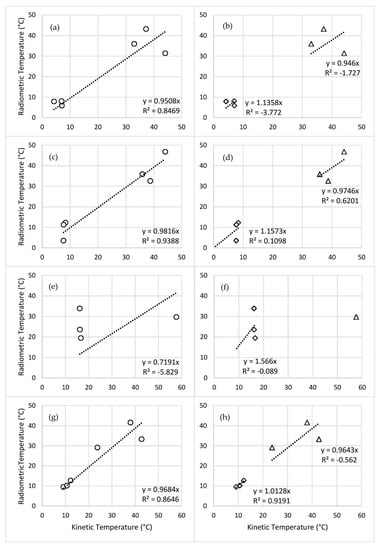
Figure 7.
Transformed radiometric temperature from TIR orthomosaics vs. kinetic temperature from TidbiTs. Left column (a,c,e,g) is combined data and right column (b,d,f,h) is data separated into geothermally influenced (triangles) and nongeothermally influenced (diamonds). From top to bottom are November 2018 (a,b), March 2019 (c,d), July 2019 (e,f) and September 2019 (g,h) survey data.

Table 4.
RMSE values for original radiometric temperature and transformed radiometric temperature data.
This large temperature gradient, as opposed to typical GW–SW temperature conditions in rivers, was only possible due to the geothermal influence in the study area. When the data were broken into smaller temperature ranges (i.e., geothermally influenced and nongeothermally influenced), R2 values were generally low or negative, suggesting the trend lines were only useful in differentiating between geothermal and nongeothermal regions (Figure 8). Temperature accuracy was determined to be satisfactory to identify geothermally influenced areas, which occur only on the eastern bank of the study reach. Geothermal seeps surveyed in March match well with elevated temperature regions in March TIR orthomosaics (Figure 8). Similarly, as expected, elevated temperature regions in November and September TIR orthomosaics plot near surveyed seeps in March (Figure A2 and Figure A3). The background river temperatures for November, March and September are 6.07 °C (n = 3), 7.89 °C (n = 3), and 10.66 °C (n = 3), respectively. Threshold temperatures used for November and September are 21.07 °C and 25.66 °C, respectively (15 °C higher than corresponding background river water temperature). For March, an arbitrary value of 30 °C was used instead of 22.89 °C (which is 15 °C higher than corresponding background river water temperature), as rocks and bare ground at a few places were warmer than 22.89 °C. The geothermally influenced areas were estimated in November, March, and September to be 1234, 781, and 333 m2, respectively.

Figure 8.
Thermal orthomosaics using transformed thermal data generated in Pix4D Mapper and Georeferenced in ArcPro for March. Seep locations that were surveyed in March 2019 were also included for reference. TIR orthomosaics correspond to the flight data from March 2019.
Evaluation of Collocated Temperature Variation
The northernmost TIR flight in the study area was flown back-to-back on 24 September 2019 to assess the collocated temperature variation during transposed flight plans under nearly identical environmental conditions. The first flight was flown from east-to-west, between 7:13–7:30 am and the second flight was flown from west-to-east, between 7:37–7:53 am. Temperature data for three cross sections was compared from these two consecutive flights (Figure 9). The temperature difference at any point in the three cross sections was between 0 to 2.1 °C (Figure 9). It should be noted that at USGS Yellowstone River gage station at Corwin Springs, the water temperature ranged between 13.3–13.4 °C from the start of the first flight to the end of the second flight.
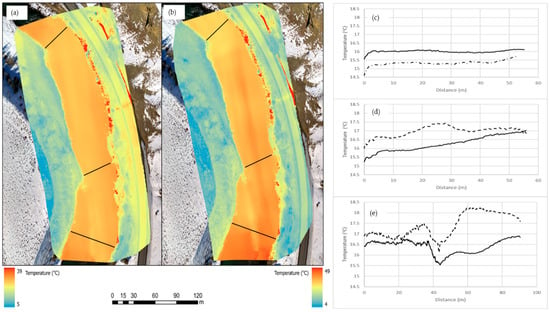
Figure 9.
Back-to-back flights thermal imagery (a,b) to assess the collocated temperature variation. River flow direction is from south to north. Black lines represent the temperature cross sections. Temperature profiles on the right from top to bottom are the northern most (c), middle (d) and south (e) cross sections, respectively. The dashed and solid lines are east-to-west and west-to-east flights, respectively. Temperature cross sections run from the west to east bank of the river.
3.2. DSM Water Surface Elevation Accuracy
Water surface elevations obtained from three of the four DSMs agreed well with the GNSS survey measurements. For June, July and September the linear regression R2 values were 0.94, 0.91, and 0.98, respectively (Figure 10). While the R2 values were universally satisfactory, the RMSE value for June was significantly higher than in July or September with a value of 63.4 cm (n = 10) compared to 11.1 cm (n = 10) and 10.08 cm (n = 18) respectively. June water surface elevations were found to be biased at 99% confidence using the Wilcoxon signed rank test (p-value = 0.0051), while both July and September were found to be unbiased at 99% confidence (p-values were 0.57 and 0.012, respectively).
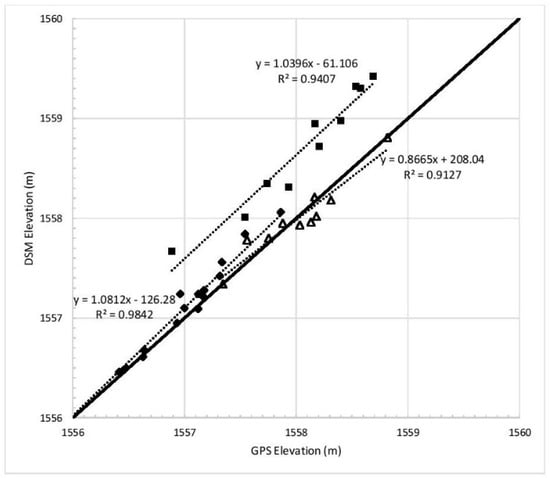
Figure 10.
Water surface elevation from SfM DSM vs GNSS measurement elevation. Squares, diamonds and triangles represent June, July and September flight surveys, respectively.
River water surface should be relatively smooth in natural settings, in the absence of waterfalls, boulders, etc. Therefore, presence of outliers in the water surface elevation data can be used as a proxy for misrepresentation of water surface elevation. DSMs were transformed to triangular irregular networks (TINs) and then the “Locate Outlier” tool was used to identify inconsistent elevation data points. For November, March, June, July and September surveys, 580; 4189; 43,701; 21,875; and 5957 outliers were detected, respectively. The most outliers were detected during peak flows in the Yellowstone River when the water was deep and had high turbidity. Outliers were generally located in areas where the riverbed is not visible in orthomosaics. This indicates that elevation data in the deeper channels of rivers from DSMs is potentially erroneous during high flows.
3.3. Seepage Flux
The successes of seepage flux calculation varied with depth and from sensor to sensor. Unreliable calculations result from an amplitude ratio that is equal to one or zero. Between 83% and 100% of seepage flux calculations were successful among all VTSAs. In geothermally influenced areas, VTSAs collected data from 14 July 2019 to 24 September 2019. The seepage flux rates varied from losing (downward flow of water from the river to the sediments) at 1.4 m/day at the TP-09 location to gaining (upward flow of water from the subsurface to the river) at 1.5 m/day at location TP-03. It should be noted that TP-03 was installed directly in a geothermal pool that is inundated by the river for a portion of the year while TP-09 was installed in a more generally geothermally altered discharge zone with no obvious flow path. The average seepage rate for all VTSAs placed in geothermally influenced areas was gaining at 0.18 m/day. VTSAs in nongeothermally influenced areas had a seepage flux that was both strongly losing at 2.9 m/day and gaining at 1.4 m/day through 14 July and 14 September. The average seepage rate for all VTSAs placed in nongeothermally influenced areas was losing at 0.11 m/day.
To evaluate the variation of seepage flux with depth, depth of water over each VTSA was estimated. Rating curves were developed to estimate depth of water over each VTSA using the USGS gauge station stage data. Regression was generally acceptable with regression coefficients ranging from 0.71 to 0.98. These regression equations were used to estimate depth of water over each VTSA, to account for variability in how the hydraulic surface of the river interacts with fine scale channel topography. Slopes varied from just over four to slightly less than 2 and intercepts varied from about negative one to nearly negative four (Table 5). Seepage flux is highly variable in both space and time, related to local hydraulic conductivities, relative stages of the river, and the water table elevation. When observed over short periods of no precipitation, seepage flux is highly correlated with water depth above the VTSAs (Figure 11). Over short time periods change in aquifer water table is likely negligible compared to changes in river stage. Over longer periods of time, when the change in aquifer water table can no longer be assumed negligible the correlation between seepage flux and water level decreases significantly.

Table 5.
List of equations and R2 values for each VTSA generated from water level rating curves. S is the river stage observed at USGS 06191500 and WD is the depth of water of the riverbed at each VTSA.
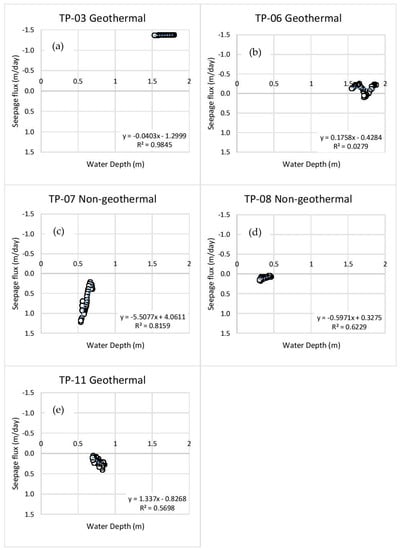
Figure 11.
Seepage flux vs. depth of water above VTSA from 20 July to 22 July (three days after a rain event). Negative slopes indicate increased seepage flux with river stage. Figures (a–e) correspond to TP-03, TP-06, TP-07, TP-08, TP-11 VTSA locations as marked in Figure 5.
4. Discussion
4.1. RGB and TIR SfM Photogrammetry Utility and Limitations for Fluvial Environments
Fluvial geomorphology and temperature heterogeneity are important characteristics for management in the context of flood mitigation, ecology and geochemical processes. sUAS-based remote sensing is rapidly gaining in popularity for quantifying various parameters for fluvial systems. It is important to understand both their utility and limitations in terms of data precision, accuracy, and the environmental constraints that affect results.
This study demonstrated the use of sUAS-based remote sensing to conduct repeated surveys over a 1 km reach of the Yellowstone River, MT. In the present study, the river surface elevation was successfully estimated near the river’s shoreline with R2 values universally above 0.90, indicating good predictability. In all three DSMs, the RMSE for water surface elevation (near shoreline) was comparable (within 3.5 cm) to the RMSE observed for CPs. It is noteworthy that in June, the RMSE for both river surface elevation and CPs were approximately 50 cm larger than in July and September. While the RMSE was large in June, there was still a good fit (R2 = 0.94) between DSM and in-situ elevation data revealing the utility of water surface elevation extraction from remotely sensed DSMs, though highlighting the importance of ground control points to check and correct data.
Previous studies have leveraged the ability to determine water surface elevation near the rivershore line to create a TIN surface profile of the river water body in order to determine river bathymetry [6,7]. The accuracy of shoreline water surface elevation lends itself to the ability to create TINs from the river shoreline elevation. However, it should be noted that the study areas presented in Bagheri [6] and Woodget [7] are narrow channels (<10 m). As the river width increases, so does the interpolation distanced in the TIN, so the accuracy would decrease in the mid channel regions. Also, it should be noted that, point cloud density from SfM photogrammetry greatly decreases or is entirely void over deep water, therefore elevation measurements from DSM could be relatively inaccurate over deep water. High prevalence of irregularities observed in the DSMs within the river channel suggest that SfM photogrammetry is inappropriate for characterizing continuous water surface elevation over a wider river channel. Despite this limitation, Ridolfi & Manciola [2] successfully extracted water elevation at a dam site in Italy, which may have been possible due to calm, clear water and the ability to detect submerged features for SfM. Further, quantifying water surface elevation using SfM photogrammetry has been addressed in laboratory settings by artificially “seeding” the water and/or applying specific lighting conditions [42,43]. Techniques outlined by Ferreira [42] and Rupnik [43]; however, would be hard to replicate in the field for wider rivers, as they rely on several photos taken simultaneously to mitigate the dynamic nature of water (i.e., a study site would be limited to one photograph frame). Niedzielski [1] documented that river surface area can be correlated with river stage, which would make identification of stage possible if sufficient in-situ data is obtainable. The reliability of quantifying terrestrial topography paired with river stage extraction also makes it possible to calculate volumes for short term changes in storage during peak flows or in retention ponds. When research questions and timing allow, surveys of large river systems would have the highest rate of success during low flow and turbidity conditions when the water has the highest clarity.
Researchers have used sUAS-based thermal imaging to determine thermal anomalies for both terrestrial and fluvial landscapes [23,44,45] and noted several limitations. The current study notes that reach and river scale considerations are very important for successful sUAS remote sensing applications. Uncooled, miniaturized, radiometric TIR cameras are subject to thermal drift, which can result in inconsistent temperature measurements between images and can cause inconsistencies in SfM photogrammetry TIR orthomosaics. Slight surface temperature variations between adjacent TIR orthomosaics can be identified visually by sharp lines between consecutive flight paths or flight plans. This may be due to slight variations in the dynamic surface temperature of the river or temporal variations in solar radiation. Future work will investigate the temperature differences between individual TIR images and TIR orthomosaics.
In this study, the collocated temperature variations in the TIR orthomosaics did not appear to be time dependent or consistent between flights (in some cross sections, the east-west flight had consistently higher temperature and in other areas the west-east were warmer). Temperatures in consecutive flights followed a similar pattern and the difference was within 2.1 °C. In a comparison between the TIR orthomosaic temperatures and in-situ temperatures, the linear fit was good (R2 > 0.8), when both geothermally and nongeothermally influenced data are included, indicating that large water temperatures (>≈ 30 °C) differences lead to reasonable agreement in temperature. However, the temperature accuracy over smaller water temperature difference range (<≈ 15 °C) have a poor linear fit with in-situ temperatures. In addition, in some cases, the temperature difference between radiometric orthomosaic and in-situ measurements was over 5 °C. There are a few potential reasons for the poor linear fit: (a) TIR orthomosaics provide “skin” temperature, whereas Tidbits measure bulk temperatures, (b) TIR image acquisition conditions and post-processing, and (c) slight spatial inaccuracies in the generally cooler portion of the river (mainly in the middle of the river, introduced during the mosaicking) whereas the geothermally influenced areas are generally close to the shoreline and may have higher spatial accuracy. These results may be improved by image pre-processing and camera pre-calibration [14] and/or analysis of individual TIR images, because the SfM orthomosaicing may introduce additional uncertainty. Caldwell et al. [46], and Dugdale et al. [23] while noting limitations of absolute temperature measurements, suggested that TIR imagery can be used to develop products that can evaluate variations like discrete thermal inputs. If greater temperature precision in data is required, such as to determine seepage rates, then more expensive cooled TIR cameras, post-processing algorithms such as that in Abolt [9], or external shutters are required. Future work should investigate the differences between in-situ temperature and the individual geolocated TIR images and the TIR orthomosaics, with and without an external shutter and calibration or post-processing algorithms.
The present study produced three complete thermal orthomosaics out of five sUAS flight surveys of the river, which highlights the importance of considering river width when conducting sUAS-based thermal surveys. Pix4D recommends a minimum coverage of 30% land in images to generate an orthomosaic of water surfaces having an acceptable percentage of calibrated images. The percentage of calibrated images was inversely related with the fraction of river width to frame width (Figure A4). Pix4D Mapper suggests that a minimum of 60% of calibrated images are needed for the generation SfM photogrammetry outputs and that greater than 95% is ideal. Results from the present study suggest that it will be difficult to develop a TIR orthomosaic when the river width is 123% or more of the ground area covered by a TIR image. Considering FAA flight regulations (restrictions at heights above the ground of >122 m in the US), sUAS mounted with a FLIR Vue Pro R with a 25° FOV is limited to surveying rivers up to 65.2 m wide. Wider rivers could be observed using a TIR camera with a wider FOV. For instance, the widest FOV available for FLIR Vue Pro R cameras is 69° and could be used to model a river up to 205 m wide. For ideal SfM photogrammetry reconstruction, the maximum river widths are 44 and 139 m for 25° and 69° FOV FLIR cameras, respectively. Wider FOV’s increase ground sampling distance for a given pixel and flight altitude. They also increase potential for inter-image bias from solar reflection as pointed out by Dugdale [23].
4.2. Hydrothermal Seep Dynamics
The geothermally influenced area near La Duke Hot Spring varies seasonally in response to the river stage (Figure 12). The maximum geothermally influenced area occurred in November, while the Yellowstone River was at its annual low flow, but the maximum geothermally influenced seepage flux occurred in June while the Yellowstone River approached the annual high flow. An increase in geothermally influenced seepage flux during spring agrees with patterns observed by Ingebritsen [18], who proposed that hydrothermal discharge increased due to spring snowmelt recharging geothermally influenced aquifers. TIR cameras capture only the “skin” temperature of an object, therefore any seepage that is occurring deep underwater will be difficult to detect unless the geothermal discharge to the river is sufficient and/or buoyant enough to reach the water surface. During high flows in the Yellowstone River substantial sediment deposition occurs, which could act to bury geothermally influenced seeps. During low flows, geothermally influenced seeps continue to percolate through sediments, eventually creating a flow path. Similarly, as the river stage and width increase it is more likely for the river water to mask thermal signature from geothermally influenced areas.

Figure 12.
Temporal variation of geothermally influenced area for a seep. From left to right—November 2018, July 2019, September 2019. The top row (a–c) is a segment of the thermal orthomosaics and the bottom row (d–f) is a segment of the RGB orthomosaics. The seep locaiton is marked in the Figure A5.
In the project area, there were a series of about 30 small geothermal seeps that generally occurred in a line extending from LaDuke hot spring above the riverbank to the south for several hundred meters where they descend to the shoreline. In March, the majority of seeps were above the river shoreline elevation, and as the river stage increased through the summer, many of the seeps in the south were inundated (Figure 8). Several geothermally influenced seeps occurred in the same location before and after high flows (Figure 12) while others, as identified using GNSS surveys and TIR orthomosaics, move up and down slope based on river stage (Figure 13). Of the seeps that were transient, they generally shifted up-gradient when the Yellowstone River stage was high. The complex interaction of these geothermal seeps with the river stage is likely a result of fluctuations in hydraulic head, seasonal changes in geothermal discharge, and heterogeneity of geology in the shallow subsurface.
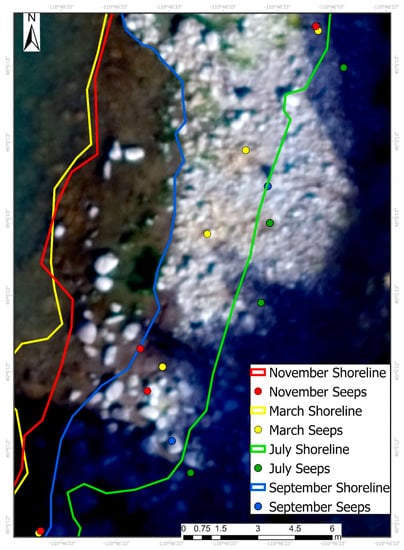
Figure 13.
Location of geothermal seeps. The river edge through time is shown as colored lines. The colored dots show corresponding geothermal seep locations through time. The background image is from September 2019 when the discharge was 53.5 m3/s.
The Yellowstone River reach upstream of LaDuke Hot Springs is extensively geothermally influenced and has a naturally high mineral content. Due to naturally high mineral content of Yellowstone River and the disparity of flow between geothermally influenced areas surrounding LDHS and Yellowstone River, traditional solute mass balance techniques would be unreliable. Sorey [33] estimated a combined flow from LaDuke and surrounding features to be approximately 60 L/s based on sulfate solute balance, however later investigations by the Montana Bureau of Mines and Geology, Butte, MT, proved unable to repeat this finding. The authors believe the presented techniques are a reasonable alternative for estimating discharge when the incoming groundwater has a distinct thermal signature and is less than the margin of error produced from stream gaging.
4.3. Limitations
In this study, we have used an emissivity value of 0.94, as per documentation provided by FLIR camera manufacturer [40,41]. However, in the literature a range of emissivity values (0.96–0.98) were used for streams and rivers [46,47]. Future studies might consider a range of emissivity values and perform sensitivity analysis. In this study, For November and September, geothermally influenced areas were delineated using a threshold temperature which is 15 °C higher than background river water temperature. 15 °C is arbitrarily selected and needs further investigation. For March, a single threshold temperature value of 30 °C was used. A major limitation of this approach is not accounting for depth of water and mixing. Further studies are required to accurately identify the geothermally influenced streambed areas using TIR images. Future studies may also consider pre-calibration of thermal camera and the use of individual images instead of mosaics, as mosaics introduce errors due to interpolation. This will facilitate better estimation of spatially distributed seepage areas in the river, which can then be integrated with spatially distributed seepage rates, to accurately estimate the reach scale geothermal seepage rates. Also, it should be noted that in this study, only one streambed sample was analyzed for bulk density and porosity. This does not characterize the sediment heterogeneity, which is likely present throughout the study’s reach. However, the use of a single streambed sample is sufficient for comparison over time at a location. The current approach used in this study is sufficient to evaluate the spatial and temporal variation of geothermal-influenced areas using sUAS-based thermal remote sensing products.
5. Conclusions
This study demonstrates the successful application of sUAS-based remote sensing (optical and thermal) to monitor the seasonality of a geothermally influenced section of the Yellowstone River, MT. The present study suggests that monitoring rivers using TIR imagery with an average river width greater than 123% of the ground area covered by a TIR image will be difficult while adhering to FAA regulations; therefore survey planning should consider the total river width, discharge and stage. SfM photogrammetry had the ability to mosaic TIR images even over the total survey flight time of one hour (3 flights). The collocated temperature, as observed with consecutive transposed flight plans, did not appear to be time dependent or consistent between flights, but temperatures in consecutive flights followed a similar pattern and actual temperature differences were within 2 °C. The accuracy of the thermal TIR orthomosaics compared to in-situ measured temperature within the hour flight time is low when comparing values within several degrees; however, if objects of interest are several tens of degrees different (as in the present study) the accuracy is adequate to identify geothermal sources without image correction. If greater accuracy is desired, such as for quantifying seepage rate using TIR imagery, a cooled TIR camera, image post-processing [9], or an external shutter may improve TIR image accuracy.
RGB-image orthomosaics and DSMs were successful at estimating the river shoreline water surface elevation. The RMSE of water surface elevation data near the shoreline was only marginally larger than the RMSE for terrestrial data for two out of the three flights. Only one DSM out of three DSMs (from three flights) that were used to estimate water surface elevation had a higher RMSE (60 cm) but still a good linear fit, which emphasizes the importance of ground control data to calibrate remote sensing data. While water surface elevation can be estimated near shoreline, the water surface elevation for mid-channel regions was not accurately predicted by SfM photogrammetry DSMs.
Author Contributions
Data curation, J.B., R.M.N., and J.C.; Formal analysis, J.B., J.C., and R.M.N.; Funding acquisition, R.M.N. and J.C.; Writing—original draft, J.B. R.M.N., and J.C.; Writing—review & editing, R.M.N., J.C. and J.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partly supported by Montana Water Center [grant number 526171, 2018; grant number 62828, 2019], Montana Space Grant Consortium (grant number G106-20-W5472, 2019), and Montana Association of Geographic Information Professionals [grant number 790-803908, 2019].
Data Availability Statement
Acknowledgments
Montana Bureau of Mines and Geology and Montana Technological University have made significant contributions in equipment and data collection. We would like to thank Church Universal Triumphant and Sandy Bierle for granting land access to pilot the sUAS and install equipment. We would also like to thank Allan English, Jeanne Larson, John LaFave, Lantana Clark, Oliver Crowley and Cara McKee for assistance with equipment acquisition and data collection. The authors are grateful to the three anonymous reviewers and associate editor for their helpful feedback that significantly improved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
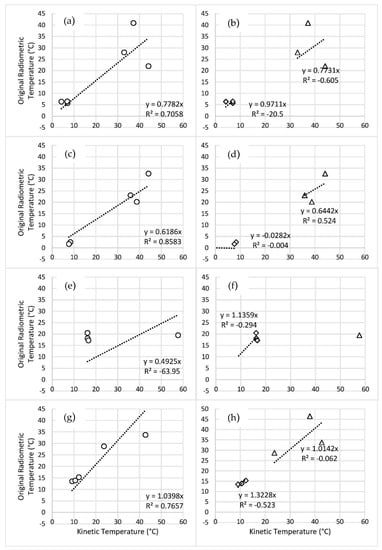
Figure A1.
Pre-transformed radiometric temperature from TIR orthomosaics vs. kinetic temperature from TidbiTs. Left column (a,c,e,g) is combined data and right column (b,d,f,h) is data separated into geothermally influenced (triangles) and nongeothermally influenced (diamonds). From top to bottom are November 2018 (a,b), March 2019 (c,d), July 2019 (e,f) and September 2019 (g,h) survey data.

Figure A2.
Thermal orthomosaics using transformed thermal data generated in Pix4D Mapper and Georeferenced in ArcPro for November. RGB orthomosaic corresponds to the flight data from March 2019.
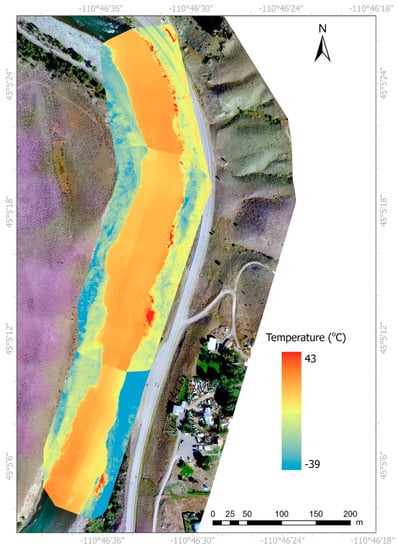
Figure A3.
Thermal orthomosaics using transformed thermal data generated in Pix4D Mapper and Georeferenced in ArcPro for September. RGB orthomosaic corresponds to the flight data from September 2019.
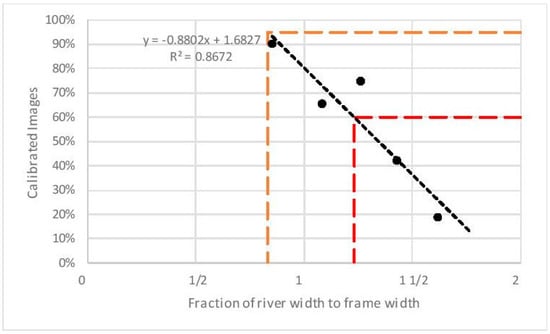
Figure A4.
Relationship between calibrated images during Pix4D Mapper processing and the associated fractional value of river width to ground area covered by a TIR image. Acceptable SfM outputs require at least 60% calibrated images, the best fit line suggests that scenes in which the river width is 123% or more of the ground area covered by a TIR image cannot be rendered using sUAS thermal imagery.

Figure A5.
Study area RGB orthomosaic (November 2018) with Figure 12 location.
References
- Niedzielski, T.; Witek, M.; Spallek, W. Observing river stages using unmanned aerial vehicles. Hydrol. Earth Syst. Sci. 2016, 20, 3193–3205. [Google Scholar] [CrossRef]
- Ridolfi, E.; Manciola, P. Water Level Measurements from Drones: A Pilot Case Study at a Dam Site. Water 2018, 10, 297. [Google Scholar] [CrossRef]
- Rivas Casado, M.; Ballesteros Gonzalez, R.; Wright, R.; Bellamy, P. Quantifying the effect of aerial imagery resolution in automated hydromorphological river characterization. Remote Sens. 2016, 8, 650. [Google Scholar] [CrossRef]
- Woodget, A.S.; Visser, F.; Maddock, I.P.; Carbonneau, P.E. The Accuracy and Reliability of Traditional Surface Flow Type Mapping: Is it Time for a New Method of Characterizing Physical River Habitat? River Res. Appl. 2016, 32, 1902–1914. [Google Scholar] [CrossRef]
- Woodget, A.S.; Austrums, R.; Maddock, I.P.; Habit, E. Drones and digital photogrammetry: From classifications to continuums for monitoring river habitat and hydromorphology. Wiley Interdiscip. Rev. Water 2017, 4, e1222. [Google Scholar] [CrossRef]
- Bagheri, O.; Ghodsian, M.; Saadatseresht, M. Reach scale application of UAV+ SfM method in shallow rivers hy-perspatial bathymetry. The International Archives of Photogrammetry. Remote Sens. Spatial Inform. Sci. 2015, 40, 77. [Google Scholar]
- Woodget, A.S.; Carbonneau, P.E.; Visser, F.; Maddock, I.P. Quantifying submerged fluvial topography using hy-perspatial resolution UAS imagery and structure from motion photogrammetry. Earth Surf. Process. Landf. 2015, 40, 47–64. [Google Scholar] [CrossRef]
- Aicardi, I.; Chiabrando, F.; Lingua, A.M.; Noardo, F.; Piras, M.; Vigna, B. A methodology for acquisition and pro-cessing of thermal data acquired by UAVs: A test about subfluvial springs’ investigations. Geomatics. Nat. Hazards Risk 2017, 8, 5–17. [Google Scholar] [CrossRef]
- Abolt, C.; Caldwell, T.; Wolaver, B.; Pai, H. Unmanned aerial vehicle-based monitoring of groundwater inputs to surface waters using an economical thermal infrared camera. Opt. Eng. 2018, 57, 053113. [Google Scholar] [CrossRef]
- Briggs, M.A.; Dawson, C.B.; Holmquist-Johnson, C.; Williams, K.H.; Lane, J.W., Jr. Efficient hydrogeological char-acterization of remote stream corridors using drones. Hydrol. Process. 2019, 33, 316–319. [Google Scholar] [CrossRef]
- Chacon, D.C. Thermal Infrared Remote Sensing for Water Temperature Assessment along the Santa Ana River Using an Unmanned Aerial Vehicle (UAV) System. Ph.D. Thesis, California State University, Fullerton, CA, USA, 2019. [Google Scholar]
- Ullman, S. The interpretation of structure from motion. Proceedings of the Royal Society of London. Ser. B Biol. Sci. 1979, 203, 405–426. [Google Scholar]
- Kalacska, M.; Chmura, G.; Lucanus, O.; Bérubé, D.; Arroyo-Mora, J. Structure from motion will revolutionize analyses of tidal wetland landscapes. Remote. Sens. Environ. 2017, 199, 14–24. [Google Scholar] [CrossRef]
- Döpper, V.; Gränzig, T.; Kleinschmit, B.; Förster, M. Challenges in UAS-Based TIR Imagery Processing: Image Alignment and Uncertainty Quantification. Remote. Sens. 2020, 12, 1552. [Google Scholar] [CrossRef]
- Dugdale, S.J.; Malcolm, I.A.; Hannah, D.M. Drone-based Structure-from-Motion provides accurate forest canopy data to assess shading effects in river temperature models. Sci. Total Environ. 2019, 678, 326–340. [Google Scholar] [CrossRef] [PubMed]
- Jaworowski, C.; Heasler, H.; Neale, C.M.U.; Saravanan, S.; Masih, A. Temporal and Seasonal Variations of the Hot Spring Basin Hydrothermal System, Yellowstone National Park, USA. Remote Sens. 2013, 5, 6587–6610. [Google Scholar] [CrossRef]
- Neale, C.M.U.; Jaworowski, C.; Heasler, H.; Sivarajan, S.; Masih, A. Hydrothermal monitoring in Yellowstone National Park using airborne thermal infrared remote sensing. Remote Sens. Environ. 2016, 184, 628–644. [Google Scholar] [CrossRef]
- Ingebritsen, S.; Galloway, D.L.; Colvard, E.; Sorey, M.; Mariner, R. Time-variation of hydrothermal discharge at selected sites in the western United States: Implications for monitoring. J. Volcanol. Geotherm. Res. 2001, 111, 1–23. [Google Scholar] [CrossRef]
- Boylen, C.W.; Brock, T.D. Effects of Thermal Additions from the Yellowstone Geyser Basins on the Benthic Algae of the Firehole River. Ecology 1973, 54, 1282–1291. [Google Scholar] [CrossRef]
- Garrott, R.A.; Eberhardt, L.L.; Otton, J.K.; White, P.J.; Chaffee, M.A. A geochemical trophic cascade in Yellow-stone’s geothermal environments. Ecosystems 2002, 5, 0659–0666. [Google Scholar] [CrossRef]
- Jensen, A.M.; Neilson, B.T.; McKee, M.; Chen, Y. Thermal remote sensing with an autonomous unmanned aerial remote sensing platform for surface stream temperatures. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5049–5052. [Google Scholar]
- Wawrzyniak, V.; Piégay, H.; Allemand, P.; Vaudor, L.; Grandjean, P. Prediction of water temperature heterogeneity of braided rivers using very high resolution thermal infrared (TIR) images. Int. J. Remote. Sens. 2013, 34, 4812–4831. [Google Scholar] [CrossRef]
- Dugdale, S.J.; Kelleher, C.; Malcolm, I.A.; Caldwell, S.; Hannah, D.M. Assessing the potential of drone-based thermal infrared imagery for quantifying river temperature heterogeneity. Hydrol. Process. 2019, 33, 1152–1163. [Google Scholar] [CrossRef]
- Loheide, S.P.; Gorelick, S.M. Quantifying Stream—Aquifer Interactions through the Analysis of Remotely Sensed Thermographic Profiles and In Situ Temperature Histories. Environ. Sci. Technol. 2006, 40, 3336–3341. [Google Scholar] [CrossRef]
- Schuetz, T.; Weiler, M. Quantification of localized groundwater inflow into streams using ground-based infrared thermography. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Hare, D.K.; Briggs, M.A.; Rosenberry, D.O.; Boutt, D.F.; Lane, J.W. A comparison of thermal infrared to fiber-optic distributed temperature sensing for evaluation of groundwater discharge to surface water. J. Hydrol. 2015, 530, 153–166. [Google Scholar] [CrossRef]
- Liu, C.; Liu, J.; Hu, Y.; Wang, H.; Zheng, C. Airborne Thermal Remote Sensing for Estimation of Groundwater Discharge to a River. Ground Water 2015, 54, 363–373. [Google Scholar] [CrossRef] [PubMed]
- Stallman, R.W. Steady one-dimensional fluid flow in a semi-infinite porous medium with sinusoidal surface temperature. J. Geophys. Res. 1965, 70, 2821–2827. [Google Scholar] [CrossRef]
- Hatch, C.E.; Fisher, A.T.; Revenaugh, J.S.; Constantz, J.; Ruehl, C. Quantifying surface water-groundwater interactions using time series analysis of streambed thermal records: Method development. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Keery, J.; Binley, A.; Crook, N.; Smith, J.W.N. Temporal and spatial variability of groundwater–surface water fluxes: Development and application of an analytical method using temperature time series. J. Hydrol. 2007, 336, 1–16. [Google Scholar] [CrossRef]
- Gordon, R.P.; Lautz, L.; Briggs, M.A.; McKenzie, J.M. Automated calculation of vertical pore-water flux from field temperature time series using the VFLUX method and computer program. J. Hydrol. 2012, 420, 142–158. [Google Scholar] [CrossRef]
- Irvine, D.J.; Lautz, L.K.; Briggs, M.A.; Gordon, R.P.; McKenzie, J.M. Experimental evaluation of the applicability of phase, amplitude, and combined methods to determine water flux and thermal diffusivity from temperature time series using VFLUX 2. J. Hydrol. 2015, 531, 728–737. [Google Scholar] [CrossRef]
- Lonn, J.D.; Porter, K.W.; Metesh, J.J. Geology of the Yellowstone Controlled Ground-Water Area, South-Central Montana; Open-File Report 557; Montana Bureau of Mines and Geology: Butte, MT, USA, 2007; 36p. [Google Scholar]
- LaFave, J.; Metesh, J. La Duke Spring Drawdown Test—Technical Memo. Unpublished data. 2010. [Google Scholar]
- Sorey, M.L. Effects of Potential Geothermal Development in the Corwin Springs Known Geothermal Resources Area, Montana, on the Thermal Features of Yellowstone National Park; (No. 91-4052); US Geological Survey: Reston, VA, USA, 1991.
- Chase, K.J. Streamflow Statistics for Unregulated and Regulated Conditions for Selected Locations on the Upper Yel-lowstone and Bighorn Rivers, Montana and Wyoming, 1928–2002; United States Geological Survey: Reston, VA, USA, 2014.
- Briggs, M.A.; Lautz, L.K.; Buckley, S.F.; Lane, J.W. Practical limitations on the use of diurnal temperature signals to quantify groundwater upwelling. J. Hydrol. 2014, 519, 1739–1751. [Google Scholar] [CrossRef]
- Roznik, E.A.; Alford, R.A. Does waterproofing Thermochron iButton dataloggers influence temperature readings? J. Therm. Biol. 2012, 37, 260–264. [Google Scholar] [CrossRef]
- Lapham, W.W. Use of temperature profiles beneath streams to determine rates of vertical ground-water flow and vertical hydraulic conductivity. In Use of Temperature Profiles Beneath Streams to Determine Rates of Vertical Ground-Water Flow and Vertical Hydraulic Conductivity; United States Geological Survey: Reston, VA, USA, 1989. [Google Scholar] [CrossRef]
- FLIR Systems. Personal communication, 2020.
- FLIR Systems. SUAS Radiometry Technical Note. 2016. Available online: https://dl.djicdn.com/downloads/zenmuse_xt/en/sUAS_Radiometry_Technical_Note.pdf (accessed on 15 November 2020).
- Ferreira, E.; Chandler, J.; Wackrow, R.; Shiono, K. Automated extraction of free surface topography using SfM-MVS photogrammetry. Flow Measur. Instrum. 2017, 54, 243–249. [Google Scholar] [CrossRef]
- Rupnik, E.; Jansa, J.; Pfeifer, N. Sinusoidal Wave Estimation Using Photogrammetry and Short Video Sequences. Sensors 2015, 15, 30784–30809. [Google Scholar] [CrossRef] [PubMed]
- Harvey, M.; Rowland, J.; Luketina, K. Drone with thermal infrared camera provides high resolution georeferenced imagery of the Waikite geothermal area, New Zealand. J. Volcanol. Geotherm. Res. 2016, 325, 61–69. [Google Scholar] [CrossRef]
- Nishar, A.; Richards, S.; Breen, D.; Robertson, J.; Breen, B. Thermal infrared imaging of geothermal environments and by an unmanned aerial vehicle (UAV): A case study of the Wairakei—Tauhara geothermal field, Taupo, New Zealand. Renew. Energy 2016, 86, 1256–1264. [Google Scholar] [CrossRef]
- Caldwell, S.H.; Kelleher, C.; Baker, E.A.; Lautz, L.K. Relative information from thermal infrared imagery via un-occupied aerial vehicle informs simulations and spatially-distributed assessments of stream temperature. Sci. Total Environ. 2019, 661, 364–374. [Google Scholar] [CrossRef]
- Torgersen, C.E.; Faux, R.N.; McIntosh, B.A.; Poage, N.J.; Norton, D.J. Airborne thermal remote sensing for water temperature assessment in rivers and streams. Remote. Sens. Environ. 2001, 76, 386–398. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).