Abstract
Lakes in direct contact with glaciers (ice-marginal lakes) are found across alpine and polar landscapes. Many studies characterize ice-marginal lake behavior over multi-decadal timescales using either episodic ~annual images or multi-year mosaics. However, ice-marginal lakes are dynamic features that experience short-term (i.e., day to year) variations in area and volume superimposed on longer-term trends. Through aliasing, this short-term variability could result in erroneous long-term estimates of lake change. We develop and implement an automated workflow in Google Earth Engine to quantify monthly behavior of ice-marginal lakes between 2013 and 2019 across south-central Alaska using Landsat 8 imagery. We employ a supervised Mahalanobis minimum-distance land cover classifier incorporating three datasets found to maximize classifier performance: shortwave infrared imagery, the normalized difference vegetation index (NDVI), and spatially filtered panchromatic reflectance. We observe physically-meaningful ice-marginal lake area variance on sub-annual timescales, with the median area fluctuation of an ice-marginal lake found to be 10.8% of its average area. The median signal (slow lake growth) to noise (physically-meaningful short-term area variability) ratio is 1.5:1, indicating that short-term variability is responsible for ~33% of observed area change in the median ice-marginal lake. The magnitude of short-term area variability is similar for ice-marginal and nonglacial lakes, suggesting that the cause of observed variations is not of glacial origin. These data provide a new context for interpreting behaviors observed in multi-decadal studies and encourage attention to sub-annual behavior of ice-marginal lakes even in long-term studies.
1. Introduction
Through the 20th and 21st centuries, lakes in direct contact with glacier ice (ice-marginal lakes) have undergone rapid change [1]. Ice-marginal lakes can be subdivided into two groups: (1) proglacial lakes: those found downstream from a glacier terminus and dammed by bedrock or moraine (Figure 1a) [2,3]; and (2) ice-dammed lakes: those found on a glacier’s lateral margins and dammed by glacier ice (Figure 1b) [2,4,5]. As glaciers change in a warming world, they perturb the hydrologic systems at their peripheries. The associated evolution of ice-marginal lakes has impacts both upstream and downstream, affecting glacier dynamics [5], stream ecology [6], and natural hazards [7].
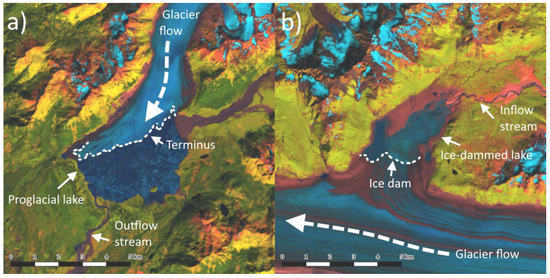
Figure 1.
Example false-color satellite images of a typical proglacial lake (a) and ice-dammed lake (b). False color image is using bands 6 (short-wave infrared), 5 (near infrared), and 4 (visible red). Proglacial lakes reside beyond the terminus of the glacier, while ice-dammed lakes are dammed on the side of a glacier. Note the iceberg presence in both examples.
Proglacial lakes provide a body of water into which a glacier may calve [5,8,9] and can enhance glacier mass loss by subaqeuous melt [5]. These effects have a negative impact on glacial mass balance [10,11], but the magnitude of the impact is unclear [12]. Further, proglacial lakes trap sediment that would otherwise be transported through outflow streams into the proglacial environment [3,5], which impacts downstream biological processes [6]. Finally, ice-dammed lakes can source repeat glacial lake outburst floods (GLOFs) when the pressure of rising impounded water overwhelms that of the dam, draining the lake through subglacial channels [2,4,5,7,13,14], posing a threat to downstream lives and infrastructure. Therefore, understanding ice-dammed lake dynamics is important for flood hazards preparedness.
Like many other elements in cryospheric systems, ice-marginal lakes are changing rapidly in the modern era, increasing in both number and area (e.g., [1,15,16,17,18]). Their long-term behavior is closely tied to glacier change; ice-marginal lake area and volume typically expand as glaciers retreat [2,19]. Globally, median glacial lake area has increased about 3% over the past two decades (this figure includes both ice-marginal lakes and those very near but not in direct contact with glacier ice [16]). However, interactions between glaciers and ice-marginal lakes can drive complex lake behavior that varies on monthly timescales [2]. For example, a well-documented mechanism for sudden changes in lake area is the GLOF cycle, a cyclic process in which an ice-dammed lake slowly fills and catastrophic drains through subglacial channels [2,4,5]. In studies using infrequent temporal sampling (e.g., a single image taken to be representative of a multi-year period), such short-term variability could alias with longer-term trends, resulting in erroneous estimates of ice-marginal lake area change.
Here, we seek to characterize the magnitude of short-term (month to year) variability in ice-marginal lake area in comparison to longer-term behavior (two to eight years). We undertake this investigation in south-central Alaska (Figure 2), a region with abundant ice-marginal lakes [16] that has received relatively little study [15,17,18,20] compared to other areas (e.g., Himalayas [11,21,22,23], or Patagonia [24]). We implement and optimize a spectral land cover classifier to digitally map ice-marginal lakes from Landsat 8 satellite imagery at monthly time resolution. This high temporal resolution allows quantification of the magnitude of short-term variability in ice-marginal lake area. This work provides context and uncertainty estimates for long-term surveys of ice-marginal lake area change by describing lake behavior on a short timescale that multidecadal-scale studies cannot fully capture.
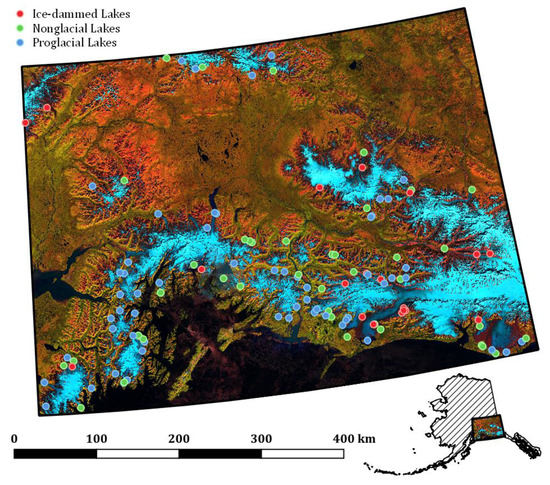
Figure 2.
Study area, including much of the Alaska, Wrangell, St Elias, and Chugach ranges. Inset shows study area extent in the state of Alaska. False color image is from Landsat 8 using bands 6/5/4 (short-wave infrared/near infrared/red). Dots show locations of lakes included in final dataset. Proglacial lakes (blue) are distributed evenly across glaciated regions of the study area. Multiple ice-dammed lakes (red) tend to occur along the lateral margins of a single glacier. Nonglacial lakes (green) are only used as a “control” for comparison with ice-marginal lakes.
2. Methodology
2.1. Classifier Optimization
We developed an automated land cover classification and post-processing routine to map ice-marginal lakes in Alaska. We utilized a supervised classifier, thereby requiring a manually-delineated land cover classification dataset for training. In Google Earth Engine (GEE), we hand-delineated training classes from a Landsat 8 three-month composite (July through September, 2018) to represent the following broad types of land cover: glacier ice, water, vegetation, and bare rock. Where possible, we broke expansive land cover classes into multiple, descriptive smaller classes (e.g., debris-covered glacier ice, “clean” glacier ice) to improve the quality of the classification. In all, we designated 14 land cover classes (Supplemental Table S1) for classification.
We sought to optimize our routine for accurate freshwater identification, possibly at the expense of accuracy in other types of land cover identification. We did not know a priori which input bands or post-processing steps would produce the best ice-marginal lake delineations. Therefore, we systematically varied our data processing steps in each run: i.e., changing classifier type, classifier input data, and post-processing parameters. We then evaluated the accuracy of each run against a hand-delineated validation dataset produced using Landsat 8 imagery from June-September 2018. By systemically varying these classifier parameters, we optimized the performance of the classifier and find those parameter values that were best-suited to our application of delineating Alaskan ice-marginal lakes.
We evaluated a range of input data, including land surface slope derived from the ALOS digital elevation model (DEM [25]); several band ratios including the normalized difference vegetation index (NDVI [26,27]) and the modified normalized difference water index (MNDWI [28]); Landsat 8 bands 5 (near infrared), 6 (shortwave infrared), 8 (panchromatic visible), and 10 (thermal infrared); and the variance of the aforementioned Landsat 8 bands using a variety of kernel sizes (e.g., 1 to 5). This preliminary selection of input data was chosen from all Landsat 8 bands and several other band ratios, based upon a manual review of the contrast between water, ice, and other land cover types in the respective datasets.
Post-processing parameters included a terrain slope cutoff value (tested from 0°–30°) and the size of morphological processes (tested from a 0 to 7 pixel radius) which were sampled randomly from a uniform distribution. Finally, we tested both types of minimum-distance classifier available to us in GEE: Euclidean and Mahalanobis classifiers (see Section 2.3). Overall, we systematically tested over 200 different classifiers, each with a different combination of input data, post-processing parameters, and classifier method.
We used an F-score metric to assess the performance of each of these classifiers. The F-score is a performance metric commonly used for quantifying the power of binary classification methods [29]. The F-score combines measures of precision (the ratio of true positives to false positives) and recall (the ratio of true positives to false negatives). The closer the F-score is to 1, the better the performance of the classifier. The F-score, F, is given by
where tp is the number of true positive pixels, fp is the number of false positive pixels, and fn is the number of false negatives. The classification designation (e.g., true positive) of each pixel is determined relative to the manually delineated ground-truth validation dataset. This dataset is composed of 257 ice-marginal and near-glacial lakes (nonglacial lakes within 3 km of a glacier) in three test regions (Supplemental Figure S1). After calculation of F-scores for each set of input parameters, we manually reviewed the classification results of the best few classifiers to verify satisfactory performance and subsequently selected a final image classification routine by expert inspection of the results.
We note that because we ultimately manually verify the accuracy of all lake classifications (Section 2.4), the performance of our classifier does not directly affect the quality of the data used in our study. However, we seek to develop an accurate classifier because the more accurate delineations we obtain, the larger the size of our final manually-reviewed dataset. Nevertheless, the F-score of the classifier should not be taken as a measure of the physical accuracy of the final curated dataset.
2.2. Lake Cover Classification
We found that the best-performing ice-marginal lake identification was obtained from a classifier using input data from Landsat 8 band 6 (shortwave infrared reflectance), NDVI, and the local variance (i.e., standard deviation) of Landsat band 8 (panchromatic reflectance). The optimal post-processing routine was achieved through a 15° DEM slope threshold and a 3 × 3 pixel (90 × 90 m) kernel for morphological opening followed by morphological closing. This classification and post-processing routine produced an F-score of 0.77 in the best-performing test region and 0.33 in the most challenging. This process succeeded for the following reasons:
- Short wave infrared (SWIR) reflectance (Landsat 8 band 6) is useful for water classification because soil and bare rock are reflective in SWIR, while water is highly absorptive. SWIR provides the classifier with powerful discriminatory ability between water and soil/bare rock.
- NDVI describes the relationship between visible reflectance in red wavelengths and near-infrared reflectance. It returns a positive value in the presence of vegetation, a zero value for bare ground, and a negative value for water [27,30]. We find the NDVI is a better discriminator than the normalized difference water index (NDWI [31]) in distinguishing ice-marginal lakes from spectrally similar land cover types (e.g., wet supraglacial debris).
- Local variance of Landsat 8 band 8 (panchromatic visible reflectance) allows us to differentiate between land cover types that have similar spectral properties but are texturally different (i.e., visually smooth/homogeneous vs. visually rough/heterogeneous surfaces). Debris-mantled glacier ice is spectrally similar to sediment-laden cold water. However, the rough texture of rocky debris is much more visually heterogeneous than the smooth surface of a lake. A surface with a homogeneous appearance will have low local variance due to adjacent pixels having similar values, while a heterogeneous surface (e.g., crevassed glacier) will have high local variance.
- Although surface water and wet ice or supraglacial debris may appear spectrally similar, water features are physically flat and glaciers are typically sloped. The 15° slope threshold strikes a balance between exclusion of sloped terrain while being large enough to accommodate error in the DEM and slope due to iceberg presence. This slope threshold also removes false positives in shadowed areas.
- Morphological opening removes pixel level noise, which tends to appear in the unprocessed classification result in regions of heterogeneous terrain that are spectrally similar to water, such as regions of wet supraglacial debris or shadowed bare rock. Morphological closing removes pixel-level holes, which tend to appear in lakes with small icebergs or sediment plumes. These morphological operations perform best using a 3-by-3-pixel kernel.
2.3. Implementation of Land Cover Classification Using Google Earth Engine
Land cover classification with high temporal resolution is both a data- and processing-heavy task. We utilized Google Earth Engine, a cloud-computing service, to quickly process large amounts of remote sensing data without the need to download or store input or intermediate data. Additionally, long-running tasks may be submitted to the GEE cloud servers to complete in parallel, greatly reducing overall processing time. Use of GEE streamlined our workflow (Figure 3) by condensing the majority of our land cover classification routine to a single GEE script. However, Google limits which processes are permitted to run on their servers (https://developers.google.com/earth-engine/apidocs, accessed on 30 June 2021), and at the time of our research, maximum-likelihood classifiers were not implemented in GEE. Thus, we chose to employ a Mahalanobis minimum-distance land cover classifier, a type of minimum-distance classifier which produces results that closely resemble those of maximum-likelihood classifiers [32,33].
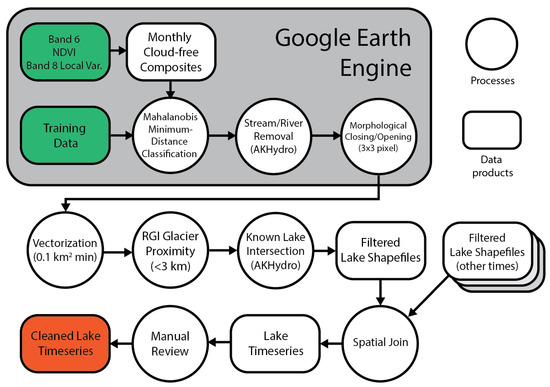
Figure 3.
Flowchart of land cover classification workflow. Processes are represented by circular nodes, while input, output, and intermediate data products are represented by rectangles. Steps completed in Google Earth Engine (GEE) are enclosed in the larger gray box. Input data product importing, land cover classification, and two post-processing processes are completed within GEE. Several post-processing steps are then completed outside of GEE, including a manual review of preliminary lake data.
A standard (Euclidean) minimum-distance classifier minimizes the Euclidean (straight-line) distance between a pixel’s spectral values and those of its land cover class centroid. Conversely, a Mahalanobis classifier essentially normalizes for intraclass spectral variance, classifying pixels by minimizing the number of standard deviations between a data point and the centroid of a class with a potentially irregular shape in spectral space [30]. Through our search process (Section 2.1), we found the Mahalanobis minimum-distance method to be the best performing classifier within the limited selection of classifiers implemented in GEE.
For each year spanning 2013–2019, we produced a monthly, mostly cloud-free composite image for June through September over our study area (Figure 2) using the GEE simpleComposite() function. We fed our input raster data into the Mahalanobis minimum distance classifier to obtain an output logical raster of water presence. Our raster post-processing steps were as follows:
- Remove pixel-level noise by a 3 × 3 morphological opening process (erosion followed by dilation). Next, we close small holes in our water identifications by a 3 × 3 morphological closing process (dilation followed by erosion).
- Exclude all pixels which are above a 15° slope threshold, using elevation data from the ALOS Global Digital Surface Model [25]. This removes false positives associated with shaded slopes and glacier surfaces.
- Remove streams and rivers from water identifications by masking against the AKHydro stream product. Proglacial streams are as much water as ice-marginal lakes, but we seek to exclude these non-lake water features from later analyses. To do this, we use the National Hydrography Dataset’s AKHydro map of Alaskan stream channels (available at http://akhydro.uaa.alaska.edu/data/nhd/, accessed on 30 June 2021) to exclude all pixels which may be in a river or floodplain from the binary water presence map. AKHydro provides a highly accurate snapshot of water bodies but lacks temporal resolution and the frequently but partially updated dataset does not present a consistent snapshot in time.
After post-processing, we vectorized the lake water raster to generate multitemporal shapefiles of lake perimeters. Our study focuses specifically on ice-marginal lakes, so we removed lakes further than 3 km from glaciers in the Randolph Glacier Inventory (RGI [34]; available at http://www.glims.org/RGI/, accessed on 30 June 2021). Note that this retains a number of nonglacial lakes within this 3 km glacial buffer. These lakes are included in our study but are not necessarily the focus of our analyses.
Additionally, we intersected automated lake delineations with AKHydro lake polygons to further remove false positives. Our dataset has much higher temporal resolution than AKHydro, but this intersection verifies that some part of each automated lake delineation was classified as a lake in AKHydro. Thus, we only included lakes which to some degree intersect the AKHydro dataset, although they may be a different size and/or shape than their AKHydro representation. Lastly, we excluded lakes smaller than 0.1 km2 in area, following Post and Mayo [7]. Below this threshold, it is difficult to reliably observe changes in lake area without using higher-resolution imagery, as lakes below 0.1 km2 in area appear as no more than eleven pixels in Landsat 8 (30 m resolution) imagery.
Generating multitemporal delineations of a single lake can be complicated due to the lake splitting into several smaller lakes during the low stage, or multiple small lakes combining into one lake during the higher stage. We used a spatial join to aggregate lakes that appear separate at one snapshot in time, but merge into a larger lake at another time. This spatial join prevents apparent rapid changes in a lake’s area due to the merging and splitting of smaller water bodies.
2.4. Manual Data Review
The process described above (Section 2.3) identified 216 lakes in our study area with 2676 monthly observations in total. Of the possible 28 images over the 2013–2019 study period (4 composites of each summer month over the course of 7 years), no lake was able to be identified in every image. We obtained an average of 12.3 observations per lake over the 2013–2019 study period. Lakes may not be observed in a given image due to physical obstructions (e.g., clouds) or classifier area, discussed in greater detail in Section 4.3.
Even minor errors in lake delineation could obscure physically-meaningful short-term variations in the proglacial lake area we seek to characterize. To ensure we were not interpreting noise, we manually reviewed each delineation of every study lake. We did not edit the automatically-produced lake delineations or supplement them with hand-drawn delineations; we simply rejected all imperfect classifications. Lakes which had only unsatisfactory delineations were discarded entirely from the final dataset. This review minimizes error associated with classifier performance, image quality, and obstructions (e.g., cloud or iceberg cover). During the process, lakes were manually classified as proglacial, ice-dammed, or nonglacial.
2.5. Identification of Multi-Annual Trends
Using the manually-reviewed data, we estimated the long-term lake area behavior by smoothing individual lake area timeseries using locally weighted scatterplot smoothing (LOESS [30]). LOESS smoothing is a non-parametric method that is robust to outliers and uses tri-cube weights to value close points more than those farther away. The number of points used for smoothing varies slightly due to the missing data associated with rejected lake delineations, but we used no more than 9 (±4) points for smoothing.
These smoothed timeseries represent multi-annual lake behavior. We used criteria based on the time rate of change of the smoothed lake area (Supplemental Table S2) to automatically classify each lake as growing or shrinking, which we then subdivided into accelerating, constant, decelerating, or reversing change. To avoid over-interpreting the data, we denoted a neutral “no change” category in which observed change in the smoothed timeseries falls below the detection limit of Landsat 8 imagery. Lakes were classified as unchanging if their area change was less than that associated with ±0.5 pixel (±15 m) variation along the entire lake perimeter. We simplified calculations by estimating each lake’s perimeter to be that of a circle of equal area. A lake was classified as unchanging if its area at the end of the record was within this margin of error from that of its first delineation.
2.6. Characterization of Short-Term Variability
We defined short-term variability as lake behavior unaccounted for by the LOESS smoothed multi-annual trends. Physically, this short-term variability is driven by processes occurring on monthly to annual timescales, such as glacier and/or water balance fluctuations or glacier lake outburst floods. We quantified a lake’s absolute magnitude of short-term area variability as the range of the residuals about the smoothed lake area time series. We defined a relative metric to describe short-term area variability by normalizing the absolute variability by the lake’s maximum size.
To assess the contributions of short-term variability and long-term trends to observed variations in a lake’s area time series, we calculated a signal-to-noise ratio. We defined the signal-to-noise ratio as the ratio of the standard deviation of the signal magnitude to the standard deviation of the noise magnitude [35]. In our analysis, we considered long-term area changes of the lake to be the signal. Accordingly, we considered the short-term variability of the lake to be physically meaningful noise that obscures the long-term signal. We obtained the signal-to-noise ratio by dividing the standard deviation of signal-driven variation (signal strength) over the standard deviation of noise-generated variation (noise strength). Note that “noise” in this context is not synonymous with “error”. Manual review ensures that lakes are correctly mapped; thus, short-term area changes reflect physical “noise” (e.g., dry months, brief glacier advances, rapid partial draining) obscuring multi-annual trends.
3. Results
Following manual review of automated lake delineations, we obtain a final dataset of 119 lakes, including 70 ice-marginal lakes (14 ice-dammed and 56 proglacial), and 39 nonglacial lakes. We stress that this dataset does not sample every single ice-marginal lake in the study region. Some lakes, particularly ice-dammed lakes, were difficult to consistently delineate accurately and so are omitted from the study.
To quantify the completeness of our dataset, we compare it with hand-delineated inventories of ice-marginal lakes in the same region. The Field et al. dataset [17] contains timeseries of 38 lakes in our study area. Twenty-seven of these lakes are also identified by our method, while 11 are not. The Field et al. dataset [17] does not attempt to describe every lake in the region however, and 92 of our lakes were not included in that study. While we do detect many of these lakes at least one time during our study period, most are discarded after manual review due to a low number of high-quality delineations and/or imagery. While perfect classifier performance would be ideal, our study goals do not require a complete inventory of every lake in our study area, just a representative sample sufficient to characterize typical values of short-term lake area variability. For this goal, our dataset is adequate, although we later discuss the potential impact of lake omission upon our results (Section 4.4).
In the study area, nonglacial and ice-dammed lakes are predominately between 0.1 and 1 km2 in area. Proglacial lakes are both larger and exhibit a greater diversity of sizes, generally between 0.3 and 20 km2 in area (Figure 4). Our methodology excludes lakes <0.1 km2, so our estimates of average lake area do not include the many very small lakes present in the region.
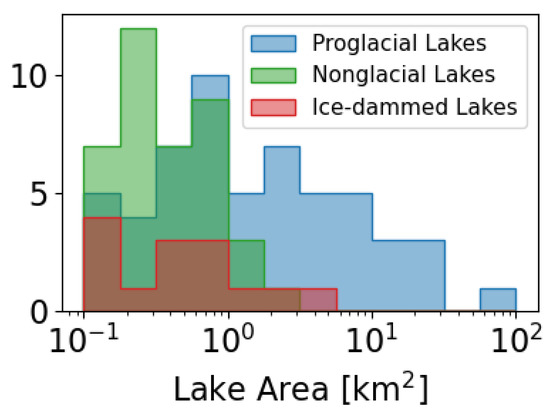
Figure 4.
Distribution of maximum observed lake areas. Ice-dammed (red) and nonglacial (green) lakes are generally smaller than proglacial lakes (blue). Note the logarithmic binning for the horizontal axis.
Though substantial variation exists in the long-term area trends (Figure 5), of the 119 studied lakes, 58 grew, 12 shrank, and 39 changed less than the detection limit over the 2013–2019 period (Supplemental Figure S3b). Lake area change is quantified as the difference between the starting and ending values of the LOESS smoothed area time series. Lake area change behavior varies both by lake type as well as a lake’s starting area. Generally, proglacial lakes experienced greater area change than ice-dammed or nonglacial lakes (Figure 6). Smaller lakes, on average, underwent greater relative area change than larger lakes. For lakes <1 km2, the median proglacial lake grew by 27.3% (interquartile range (IQR) of 11.8% to 46.7% growth), while the median ice-dammed lake grew by 11.2% with less variation between growth rates of individual lakes (IQR of 1.7% to 28.6% growth). Nonglacial lakes smaller than 1 km2 did grow, but much less so than ice-marginal lakes. The median small non-glacier lakes grew by 3.8% (IQR of −2.6% to 12.4% growth).
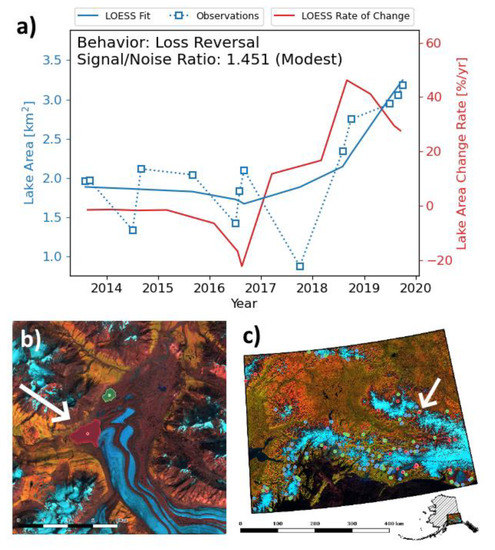
Figure 5.
An example timeseries (a) for a studied ice-dammed lake (Supplemental Figure S2). Location is indicated with white arrows identifying the red lake (b), and the location in our study area (c). Delineations which were manually reviewed and confirmed to be accurate are plotted in blue squares. These observations were smoothed using LOESS to form an estimate representation of multi-annual behavior (blue line). The discrete rate of change of this fit is indicated in red. This example lake was initially losing area at about 5% per year, but over the study period reversed this loss pattern and began gradually gaining area at a rate of up to 40% per year.
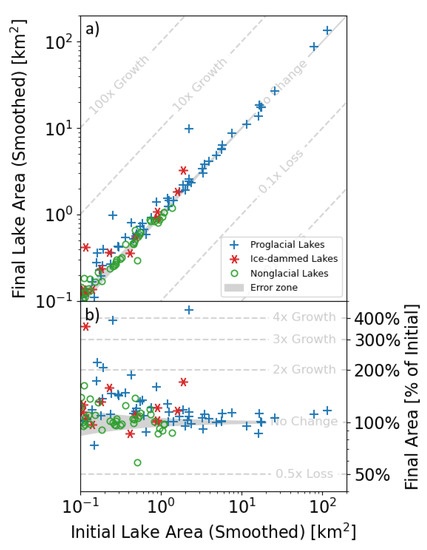
Figure 6.
Final lake areas plotted against initial lake areas where final lake area is plotted in absolute terms (i.e., km2) (a) and relative terms (%) (b). Note log-log axes. The gray zone depicts the area uncertainty due to sub-pixel border error, which defines the “no change” lake area category (Section 2.5). Both ice-dammed (red stars) and proglacial lakes (blue crosses) are growing, generally, while the majority of nonglacial lakes (green circles) lie within the gray “no change” zone. Smaller lakes are growing faster in relative terms.
Proglacial lakes larger than 1 km2 dominate area change in absolute terms (i.e., km2), with 41.0 km2 of cumulative proglacial lake growth. The median >1 km2 proglacial lake grew by 0.184 km2 (IQR of 0.013 km2 to 0.490 km2 growth). Larger lakes are growing slower in relative terms, with the median lake larger than 1 km2 growing by 5.5% (IQR of −0.2% to 14.7% growth). In comparison, the median lake smaller than 1 km2 grew by 10.7% (IQR of 0.6 to 31.5% growth). Note that these values include the relatively unchanging nonglacial lakes, which themselves are mostly smaller than 1 km2 (Figure 4). Excluding nonglacial lakes, the median ice-marginal lake smaller than 1 km2 is growing by 21.8% (IQR of 9.2 to 43.5% growth).
Overall, proglacial lakes grew in cumulative area by 11.8%, ice-dammed lakes by 29.5%, and nonglacial lakes stayed nearly constant with an overall increase of just 0.9% in cumulative lake area. The majority of ice-marginal lakes are growing, a behavior which distinguishes them from nonglacial lakes. Of proglacial lakes, 21% are changing less than the detection limit, 57% are growing, and 21% are shrinking. These multi-annual trends provide the longer-term context upon which we analyze short-term variability.
Short-term lake area variability is similar between different lake types and generally scales with lake size, although relative short-term variability is slightly more pronounced in smaller lakes (Figure 7). The median short-term variability about the long-term area trend for <1 km2 lakes is 0.040 km2 (IQR of 0.024 km2 to 0.073 km2) while it is 0.204 km2 (IQR of 0.128 km2 to 0.627 km2) for >1 km2 lakes. Expressed in relative terms, the median short-term variability about the long-term area trend for <1 km2 lakes is 11.2% of the total lake area (IQR of 7.9% to 18.2%), while the median short-term variability for larger lakes is 8.6% the total lake area (IQR of 4.5% to 11.7%) (Figure 7). The median short-term area variability for ice-marginal lakes is 10.8% of the lake size (IQR of 6.4% to 19.0%), and the median variability of nonglacial lakes is 10.5% (IQR of 7.6% to 15.9%). Over lakes of all sizes and types, the median relative short-term variability is 10.6% (IQR of 6.9% to 17.7%).
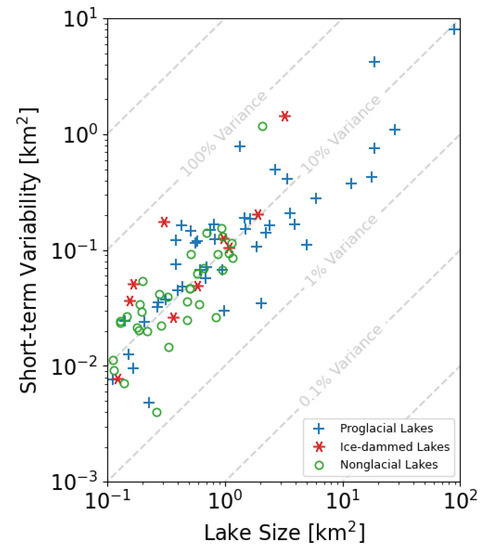
Figure 7.
Short-term variability in lake area plotted against lake area. Note log-log axes. Lines of equal relative variability (Section 2.6) are indicated by gray lines. While nonglacial lakes tend to be smaller than proglacial lakes (Figure 4) and exhibit less absolute variability, they closely follow the same relative variability trends as proglacial lakes.
Signal-to-noise (S:N) ratios compare the relative magnitudes of multi-annual trends (signal) and short-term variability (noise) in the area timeseries of a given lake (Section 2.6, Figure 8). Lakes with strong S:N ratios show clear changes in lake area that persist over multiple years, while lakes with weak S:N ratios have area change dominated by sub-annual variation that are not attributable to multi-annual trends. Lakes in the “no change” category (Section 2.5, Figure 6) generally have low S:N (Figure 8). These lakes have no discernible multi-annual trends in lake area, and changes in lake area are driven solely by sub-annual processes.
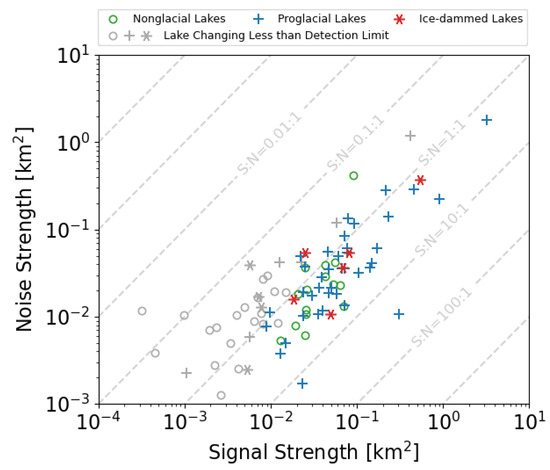
Figure 8.
The relation of long-term trends (signal strength) in lake area to short-term variability (noise strength) in the studied lakes. Note the log-log axes. Lakes which fall in the “no change” (Section 2.5) category are shown in gray. The ratio of signal strength to noise strength is the signal-to-noise ratio (S:N) and lines of equal S:N are shown in dashed gray. The majority of S:N<1:1 lakes fall into the “no change” category. Most nonglacial lakes (circles) fall further to the upper left than proglacial lakes (crosses), indicating that they have weaker signal strength and poorer signal-to-noise ratios than proglacial lakes.
Generally, proglacial lakes have a greater S:N ratio (median 1.52:1, IQR 0.86:1 to 2.94:1) than that of nonglacial lakes (median 0.80:1, IQR 0.38:1 to 1.84:1). Physically, this means that the multi-annual behavioral trends of proglacial lakes are more confidently identified than nonglacial lakes. This does not mean proglacial lakes experience less sub-annual variability than nonglacial lakes (Figure 7). Instead, proglacial lakes generally show large multi-annual change, while nonglacial lakes are more stable. This observation agrees with earlier analyses that showed that the majority of nonglacial lakes are changing less than the detection limit (Figure 6, Supplemental Figure S3) while showing that the majority of proglacial lakes display quantifiable long-term growth behavior (Supplemental Figure S3). The small sample size of ice-dammed lakes in our dataset prevents a comparable assessment for this lake type, although they generally appear to overlap with proglacial lakes in S:N space (Figure 8).
4. Discussion and Conclusions
4.1. Comparison with Previous Work
Our results document an overall growth in the cumulative area of lakes in our study region driven by the growth of individual proglacial lakes (Figure 7 and Figure 8). This finding agrees with Field et al. [17] and Rick et al. [18], but disagrees with the findings of Wolfe et al. [15]. Wolfe et al. [15], who focused primarily on ice-dammed lakes in southern Alaska, found the numbers of such lakes to have decreased since the 1970s. Our study is biased towards proglacial lakes, which possibly explains some of the discrepancy with Wolfe et al. [15], though closer inspection suggests treatment of short-term variability may also underlie differences. Field et al. [17] found proglacial lakes in the region grew in cumulative area by 59%, while ice-dammed lakes shrank by 17% overall. Our estimate of proglacial lake area change (11.8% growth) agrees in sign with Field et al. (2021) but not in magnitude. Our estimate of ice-dammed lake area change (29.5% growth) does not show the same area decrease as Field et al. [17], Rick et al. [18], nor Wolfe et al. [15]. Unlike these studies, our estimates of lake area change account for sub-annual variation by smoothing the lake area timeseries before calculating percent change. This reduces our sensitivity to lake fluctuations and will produce more conservative estimates of area change, but it is unlikely that such accounting for short-term variation explains the sign difference between our work and the earlier studies. We likely do not discern the draining behavior of many shrinking ice-dammed lakes due to the automated method’s poor delineation performance in small iceberg-filled lakes, particularly when they are partially or completely drained (discussed further in Section 4.3 and Section 4.4). Further, it is possible that our results, obtained entirely from the last decade, do not agree with those of earlier studies utilizing the entire Landsat record due to different temporal intervals studied. If that were true, it would suggest a slowing in the rates of proglacial lake growth over time, as well as a recent reversal in the multi-decadal trend of ice-dammed lake shrinkage.
4.2. Impact of Short-Term Variability on Ice-Marginal Lake Area Estimates
The ice-marginal lakes we study exhibit substantial short-term variability in lake area (Figure 5), with an individual observation differing from the smoothed lake area at the time by 10% on average (and up to 80%; Figure 8). After manual review of all lake delineations and the input imagery used for classification, we are confident that this variation is physically meaningful and does not simply reflect classifier error. Potential causes for these variations might be: brief periods of glacier advance or retreat, prevalence of local warm and wet versus cold and dry weather, or variations in sediment transport processes. We do not find temporally synchronous lake behavior over the study area (Supplemental Figure S4), suggesting that regional-scale weather forcings have limited influence on lake behavior at this scale. Rather, microclimate and/or glacial-basin-scale processes possibly drive the short-term area variations observed in this study.
While proglacial lakes display greater absolute area variability due to their larger average size, proglacial and nonglacial lakes show similar amounts of relative variability, with the median short-term variation of a given lake found to be about 10.6% of a lake’s total area, regardless of glacial context (Figure 7). This suggests that these short-term variations are due to non-glacial factors shared by all lake types, such as the regional water balance (e.g., Wendler et al. [36]). Our high temporal resolution timeseries allow characterization of this sub-annual variability, while studies using single images to represent lake area for a longer period may identify an area that is significantly different from the lake’s mean area over the representative time. The estimates of sub-annual lake area variability we present here may be used in future work to characterize the uncertainty in their observations due to undersampling in time. We emphasize that these errors are associated purely with aliasing due to physical sub-annual variability. The true error of automated lake area estimates may be higher due to classifier error (see Section 4.3).
The use of signal-to-noise ratios (S:N) allows us to distill the relative impact of long-term trends and short-term variability on an individual lake’s area timeseries down to a single number (Figure 8). We find that nonglacial lakes have a median S:N of less than 1:1, indicating that variation in their area is primarily driven by sub-annual forces. Proglacial lakes have a median S:N between 1:1 and 2:1, indicating that, while area change in proglacial lakes is primarily due to multi-annual trends, sub-annual variations still strongly impact proglacial lake area. A median S:N of 1.5:1 in proglacial lakes tells us that only two-thirds of observed lake area change in proglacial lakes is likely to be representative of long-term behavior. Studies using a limited number of images to represent lake area for long periods must be cautious that observed lake area at any given point in time may not be representative of long-term trends.
4.3. Physical Challenges of Remote Sensing Ice-Marginal Lake Area
The manual review of 2676 individual images containing an automated lake observation and 1461 additional images of the same scenes at times when a lake was not delineated provides insight into the difficulties of automated delineation of ice-marginal lakes. Despite the overall success of the automated method in images without physical obstructions, it frequently produced inaccurate delineations in low quality imagery. During manual review, we removed any inaccurate lake delineations (Section 2.4), so they do not affect the results presented above. However, it is worthwhile discussing the sources of classifier error because they highlight general challenges of remote sensing investigations of ice-marginal lakes. The majority (2362 of 3192, 74%) of missing or incorrect delineations were due to cloud cover and the presence of icebergs within the lake (Supplemental Figure S6). These physical obstructions pose fundamental limitations on how well a pixel-based spectral image classifier can delineate ice-marginal lakes.
Pixel-based spectral image classifiers operate with minimal spatial context, with each pixel classified independent of its neighboring pixels. As a result, pixel-based classifiers are incapable of distinguishing a pixel of intact glacial ice from that of icebergs floating within the lake. In summer, calving events distribute icebergs across the lake surface, often resulting in underestimation of the true lake area. We observe that some icebergs persist for multiple years, and frequently have spatial distributions that are difficult to filter out algorithmically. While morphological filtering can remove isolated small icebergs, large aggregates of icebergs that raft together at a lake’s outlet are more difficult to distinguish and remove. Finally, clouds often partially or entirely obscure the lake surface, even in composite imagery, resulting in underestimates of lake area at those times (Supplemental Figure S6a–d).
Beyond these physical obstructions, cold sediment-laden lake water is very similar in spectral appearance to thinly debris-mantled glacier ice (Supplementary Table S1). This spectral similarity poses a challenge to spectral pixel-based image classifiers, and can result in erroneously high estimates of lake area if terminal portions of the glacier are classified as part of the ice-marginal lake. These issues make accurate automated delineation of ice-marginal lake change from remotely-sensed data challenging, and most frequently result in overestimation of a lake’s true area (Supplemental Figure S6e).
Mosaicking multiple images to produce cloud-free composite imagery can mitigate some, but not all of these issues. Composite imagery simply “smears” floating icebergs across the lake surface and does not change the spectral similarity of ice-marginal lake water and debris-mantled glacier ice. Further, the long temporal intervals required to produce high quality cloud-free imagery fundamentally limit the temporal resolution of Alaskan ice-marginal lake studies and may conceal important short-term dynamics. As observed in our monthly composites, short time span composites cannot effectively eliminate all clouds or ice cover. Thus, the impact of physical obstruction upon automated lake delineation processes increases in severity as the temporal resolution of the study becomes finer, even if mosaicking is used. Recent advances in smallsat earth imaging technology may facilitate daily coverage and even higher temporal resolution studies [37,38], particularly in regions of high cloud cover like the Gulf of Alaska.
Without manual review, as was conducted in this study, physical obstruction causes erroneous variations in lake area estimates that are difficult to distinguish from real fluctuation in lake area. Such erroneous variations confound estimates of physically meaningful lake area change. These classifier errors will be in addition to the physical sub-annual variability in lake area discussed in Section 4.2. Therefore, our suggestion of error bounds for a single observation of lake area should be taken as a minimum estimate, upon which classifier error (due to physical obstruction and resulting misclassification) will further increase the uncertainty of true lake area.
4.4. Potential Biases in Estimates of Short-Term Lake Area Variability
Ice-marginal lakes included in the final dataset are predominantly proglacial (80%; 56 proglacial lakes of 70 ice-marginal lakes), with less representation from ice-dammed lakes. Ice-dammed lakes can feature periodic outburst floods [7], making their area especially variable. Ice-dammed lakes that undergo regular outburst flooding often feature dense iceberg cover: rapid lake stage reduction during drainage cause serac falls from the ice dam, which then float across the lake’s surface as stage rises again. Due to our encountered difficulty in automated delineation of iceberg-filled lakes (Section 4.3), our study likely undersamples ice-dammed lakes that undergo regular drain-and-fill sequences (e.g., Hidden Creek Lake dammed by Kennicott Glacier, Alaska [39,40]). This undersampling of active ice-dammed lakes means that we likely underestimate the true magnitude of short-term area variability for ice-dammed lakes. Therefore, the results we present in Section 3 are likely more reliable for proglacial lakes, and should be taken as a minimum estimate of the short-term area variability for ice-dammed lakes, and then only for the largest and least iceberg-filled ice-dammed lakes.
5. Conclusions
We find that ice-marginal lakes in south-central Alaska have increased in area over the 2013–2019 period; in contrast, near-glacial but nonglacial lakes demonstrate very little change. All study lakes exhibit a substantial amount of variability on sub-annual timescales, with an individual observation of lake area differing from the lake’s average lake area at that time by about 10.6% in median, regardless of whether the lake is ice-marginal or nonglacial. This variability can obscure identification of lake change trends if the lake is sampled too infrequently. Even in proglacial lakes, which show a strong growth signal over the study period, only 66% of lake area variation (in median) can be attributed to long-term patterns, with the remainder caused by sub-annual fluctuations. The magnitude of short-term variations for lakes of a similar size is similar between ice-marginal and nonglacial lakes, suggesting that a non-glacial process such as regional water balance fluctuations may drive the variations. We encourage future studies to critically evaluate the impact of short-term variability, and associated processes, upon long-term estimates of ice-marginal lake area change.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/rs13193955/s1.
Author Contributions
Conceptualization, W.A. and A.M.H.; Methodology, W.A. and A.M.H.; Software, A.M.H. and W.A.; Validation, W.A., A.M.H., D.M. and B.R.; Formal Analysis, A.M.H.; Investigation, A.M.H. and W.A.; Resources, W.A.; Data Curation, A.M.H.; Writing–Original Draft Preparation, A.M.H. and W.A.; Writing–Review & Editing, W.A., D.M. and B.R.; Visualization, A.M.H.; Supervision, W.A.; Project Administration, W.A.; Funding Acquisition, W.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funding by the National Science Foundation, grant number OPP-1821002.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
These data are freely available on arcticdata.io at https://arcticdata.io/catalog/view/urn:uuid:c8a627b0-3d69-4743-bbc5-2d77081bb959, accessed on 30 June 2021. The portion of the workflow implemented through Google Earth Engine is accessible at https://github.com/armstrwa/proglacialLakes/blob/master/anton_earth_engine_classify.txt, accessed on 30 June 2021.
Acknowledgments
This research was supported by NSF award OPP-1821002. We thank Hannah Field for constructive discussions and review of an earlier draft of this manuscript. We thank editor Miloš Mirić and two anonymous reviewers, whose comments improved the clarity and rigor of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tweed, F.S.; Carrivick, J. Deglaciation and proglacial lakes. Geol. Today 2015, 31, 96–102. [Google Scholar] [CrossRef]
- Carrivick, J.; Tweed, F. Proglacial lakes: Character, behaviour and geological importance. Quat. Sci. Rev. 2013, 78, 34–52. [Google Scholar] [CrossRef]
- Bogen, J.; Xu, M.; Kennie, P. The impact of pro-glacial lakes on downstream sediment delivery in Norway. Earth Surf. Process. Landf. 2015, 40, 942–952. [Google Scholar] [CrossRef]
- Tweed, F.S.; Russell, A.J. Controls on the formation and sudden drainage of glacier-impounded lakes: Implications for jokulhlaup characteristics. Prog. Phys. Geogr. 1999, 23, 79–110. [Google Scholar] [CrossRef]
- Otto, J.-C. Proglacial Lakes in High Mountain Environments. In The Physical Geography of Hungary; Springer: Berlin/Heidelberg, Germany, 2019; pp. 231–247. [Google Scholar]
- Dorava, J.M.; Milner, A.M. Role of lake regulation on glacier-fed rivers in enhancing salmon productivity: The Cook Inlet watershed, south-central Alaska, USA. Hydrol. Process. 2000, 14, 3149–3159. [Google Scholar] [CrossRef]
- Post, A.; Mayo, L.R. Glacier Dammed Lakes and Outburst Floods in Alaska; US Geological Survey: Washington, DC, USA, 1971. [Google Scholar]
- Walder, J.S.; Trabant, D.C.; Cunico, M.; Fountain, A.G.; Anderson, S.P.; Anderson, R.S.; Malm, A. Local response of a glacier to annual filling and drainage of an ice-marginal lake. J. Glaciol. 2006, 52, 440–450. [Google Scholar] [CrossRef][Green Version]
- Chernos, M.; Koppes, M.; Moore, R.D. Ablation from calving and surface melt at lake-terminating Bridge Glacier, British Columbia, 1984–2013. Cryosphere 2016, 10, 87–102. [Google Scholar] [CrossRef]
- Larsen, C.F.; Burgess, E.; Arendt, A.A.; O’Neel, S.; Johnson, A.J.; Kienholz, C. Surface melt dominates Alaska glacier mass balance. Geophys. Res. Lett. 2015, 42, 5902–5908. [Google Scholar] [CrossRef]
- King, O.; Bhattacharya, A.; Bhambri, R.; Bolch, T. Glacial lakes exacerbate Himalayan glacier mass loss. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef]
- Truffer, M.; Motyka, R.J. Where glaciers meet water: Subaqueous melt and its relevance to glaciers in various settings. Rev. Geophys. 2016, 54, 220–239. [Google Scholar] [CrossRef]
- Jacquet, J.; McCoy, S.W.; McGrath, D.; Nimick, D.A.; Fahey, M.; O’Kuinghttons, J.; Friesen, B.A.; Leidich, J. Hydrologic and geomorphic changes resulting from episodic glacial lake outburst floods: Rio Colonia, Patagonia, Chile. Geophys. Res. Lett. 2017, 44, 854–864. [Google Scholar] [CrossRef]
- Falatkova, K.; Sobr, M.; Neureiter, A.; Schoner, W.; Jansky, B.; Hausler, H.; Engel, Z.; Benes, V. Development of proglacial lakes and evaluation of related outburst susceptibility at the Adygine ice-debris complex, northern Tien Shan. Earth Surf. Dyn. 2019, 7, 1–29. [Google Scholar] [CrossRef]
- Wolfe, D.F.; Kargel, J.S.; Leonard, G.J. Glacier-dammed ice-marginal lakes of Alaska. In Global Land Ice Measurements from Space; Springer: Berlin/Heidelberg, Germany, 2014; pp. 263–295. [Google Scholar]
- Shugar, D.H.; Burr, A.; Haritashya, U.K.; Kargel, J.S.; Watson, C.S.; Kennedy, M.C.; Bevington, A.R.; Betts, R.A.; Harrison, S.; Strattman, K. Rapid worldwide growth of glacial lakes since 1990. Nat. Clim. Chang. 2020, 10, 939–945. [Google Scholar] [CrossRef]
- Sutherland, J.; Field, H.R.; Armstrong, W.H.; Huss, M. Topography exerts primary control on the rate of Gulf of Alaska ice-marginal lake area change over the Landsat record. Cryosphere Discuss. 2021, 1–34. [Google Scholar]
- Rick, B.; McGrath, D.; Armstrong, W.; McCoy, S.W. Dam type and topological position govern ice-marginal lake area change in Alaska and NW Canada between 1984 and 2019. Cryosphere Discuss. 2021, 1–28. [Google Scholar]
- Buckel, J.; Otto, J.; Prasicek, G.; Keuschnig, M. Glacial lakes in Austria—Distribution and formation since the Little Ice Age. Glob. Planet. Chang. 2018, 164, 39–51. [Google Scholar] [CrossRef]
- Anderson, L.S.; Armstrong, W.H.; Anderson, R.S.; Buri, P. Debris cover and the thinning of Kennicott Glacier, Alaska: In situ measurements, automated ice cliff delineation and distributed melt estimates. Cryosphere 2021, 15, 265–282. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, M.; Tian, B.; Li, Z. Extraction of Glacial Lake Outlines in Tibet Plateau Using Landsat 8 Imagery and Google Earth Engine. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4002–4009. [Google Scholar] [CrossRef]
- Zhang, M.-M.; Chen, F.; Tian, B.-S. An automated method for glacial lake mapping in High Mountain Asia using Landsat 8 imagery. J. Mt. Sci. 2018, 15, 13–24. [Google Scholar] [CrossRef]
- Brun, F.; Treichler, D.; Shean, D.; Immerzeel, W.W. Limited Contribution of Glacier Mass Loss to the Recent Increase in Tibetan Plateau Lake Volume. Front. Earth Sci. 2020, 8, 495. [Google Scholar] [CrossRef]
- Barcaza, G.; Nussbaumer, S.U.; Tapia, G.; Valdés, J.; García, J.-L.; Videla, Y.; Albornoz, A.; Arias, V. Glacier inventory and recent glacier variations in the Andes of Chile, South America. Ann. Glaciol. 2017, 58, 166–180. [Google Scholar] [CrossRef]
- Tadono, T.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Precise global DEM generation by ALOS PRISM. Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 71. [Google Scholar] [CrossRef]
- Rouse, J.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Pettorelli, N. The Normalized Difference Vegetation Index; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Dembczynski, K.; Waegeman, W.; Cheng, W.; Hullermeier, E. An exact algorithm for f-measure maximization. Adv. Neural Inf. Process. Syst. 2011, 24, 1404–1412. [Google Scholar]
- Gong, P.; Howarth, P. An assessment of some factors influencing multispectral land-cover classification. Photogramm. Eng. Remote Sens. 1990, 56, 597–603. [Google Scholar]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Cohen, R.A. An introduction to proc loess for local regression. In Proceedings of the Twenty-Fourth Annual SAS Users Group International Conference, Miami Beach, FL, USA, 11–14 April 1999. [Google Scholar]
- Wacker, A.; Landgrebe, D. Minimum distance classification in remote sensing. LARS Tech. Rep. 1972, 25. [Google Scholar]
- Pfeffer, W.T.; Arendt, A.A.; Bliss, A.; Bolch, T.; Cogley, J.G.; Gardner, A.; Hagen, J.-O.; Hock, R.; Kaser, G.; Kienholz, C.; et al. The Randolph Glacier Inventory: A globally complete inventory of glaciers. J. Glaciol. 2014, 60, 537–552. [Google Scholar] [CrossRef]
- Trenberth, K.E. Signal Versus Noise in the Southern Oscillation. Mon. Weather. Rev. 1984, 112, 326–332. [Google Scholar] [CrossRef]
- Wendler, G.; Gordon, T.; Stuefer, M. On the Precipitation and Precipitation Change in Alaska. Atmosphere 2017, 8, 253. [Google Scholar] [CrossRef]
- Bhushan, S.; Shean, D.; Alexandrov, O.; Henderson, S. Automated digital elevation model (DEM) generation from very-high-resolution Planet SkySat triplet stereo and video imagery. ISPRS J. Photogramm. Remote Sens. 2021, 173, 151–165. [Google Scholar]
- Kääb, A.; Altena, B.; Mascaro, J. River-ice and water velocities using the Planet optical cubesat constellation. Hydrol. Earth Syst. Sci. 2019, 23, 4233–4247. [Google Scholar] [CrossRef]
- Anderson, S.P.; Walder, J.S.; Anderson, R.S.; Kraal, E.R.; Cunico, M.; Fountain, A.G.; Trabant, D.C. Integrated hydrologic and hydrochemical observations of Hidden Creek Lake jökulhlaups, Kennicott Glacier, Alaska. J. Geophys. Res. Space Phys. 2003, 108. [Google Scholar] [CrossRef]
- Bartholomaus, T.; Anderson, R.S.; Anderson, S. Response of glacier basal motion to transient water storage. Nat. Geosci. 2007, 1, 33–37. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).