A Remote Sensing and Machine Learning-Based Approach to Forecast the Onset of Harmful Algal Bloom
Abstract
1. Introduction
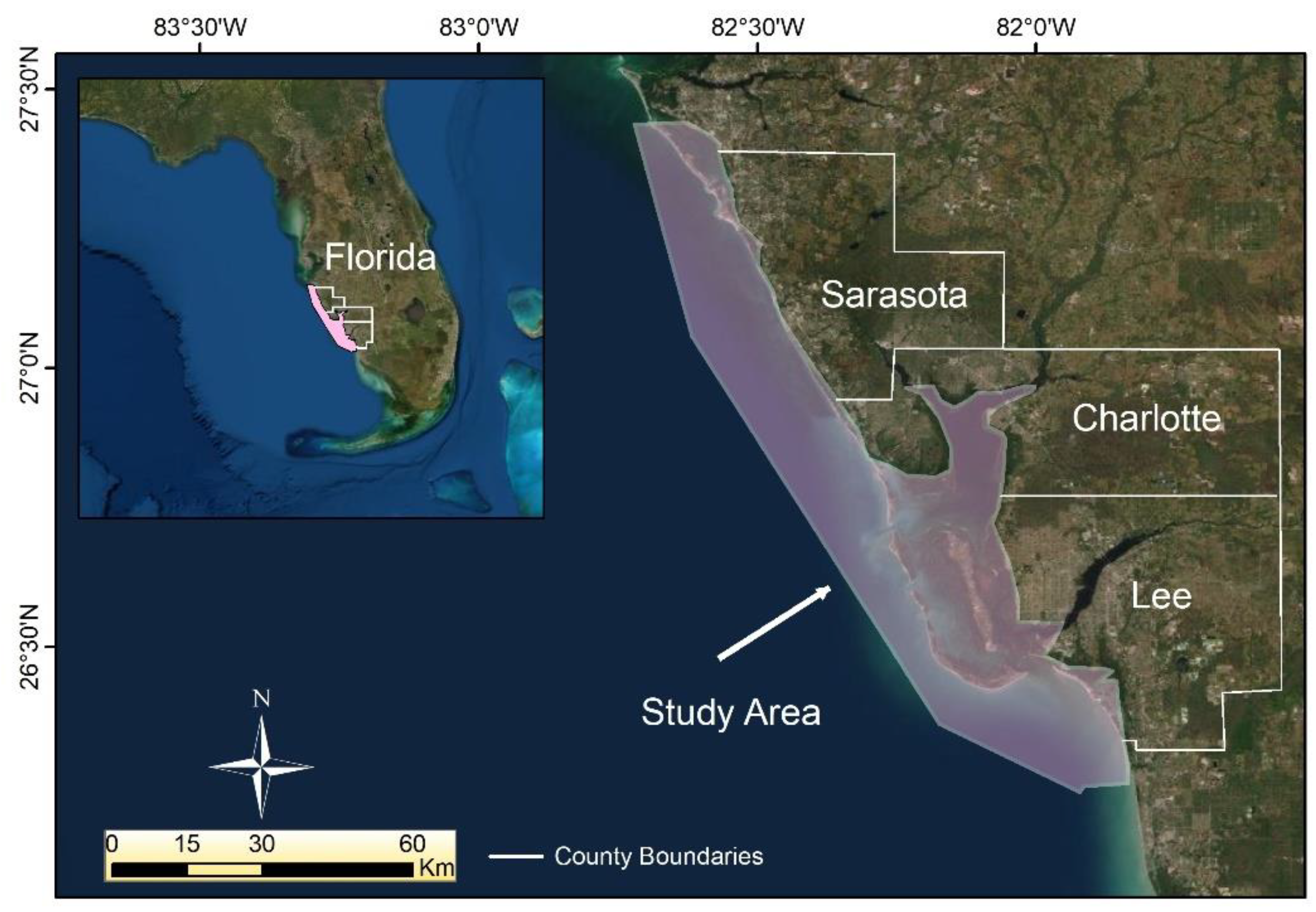
2. Study Area
3. Data and Methods
3.1. Data
3.1.1. Independent Variables
- Euphotic depth (m) and Secchi disk depth
- Chlorophyll-a (mg/m3)
- Diffuse attenuation coefficient (Kd_490; m−1)
- Sea surface temperature (°C)
- Fluorescence line height
- Particulate backscattering coefficient
- Turbidity index
3.1.2. Target Variable
3.1.3. Data Preparation
3.2. Machine Learning Modeling
3.2.1. Linear Models
3.2.2. Tree-Based Models (Non-Linear)
- Extreme gradient boosting
- Random forest
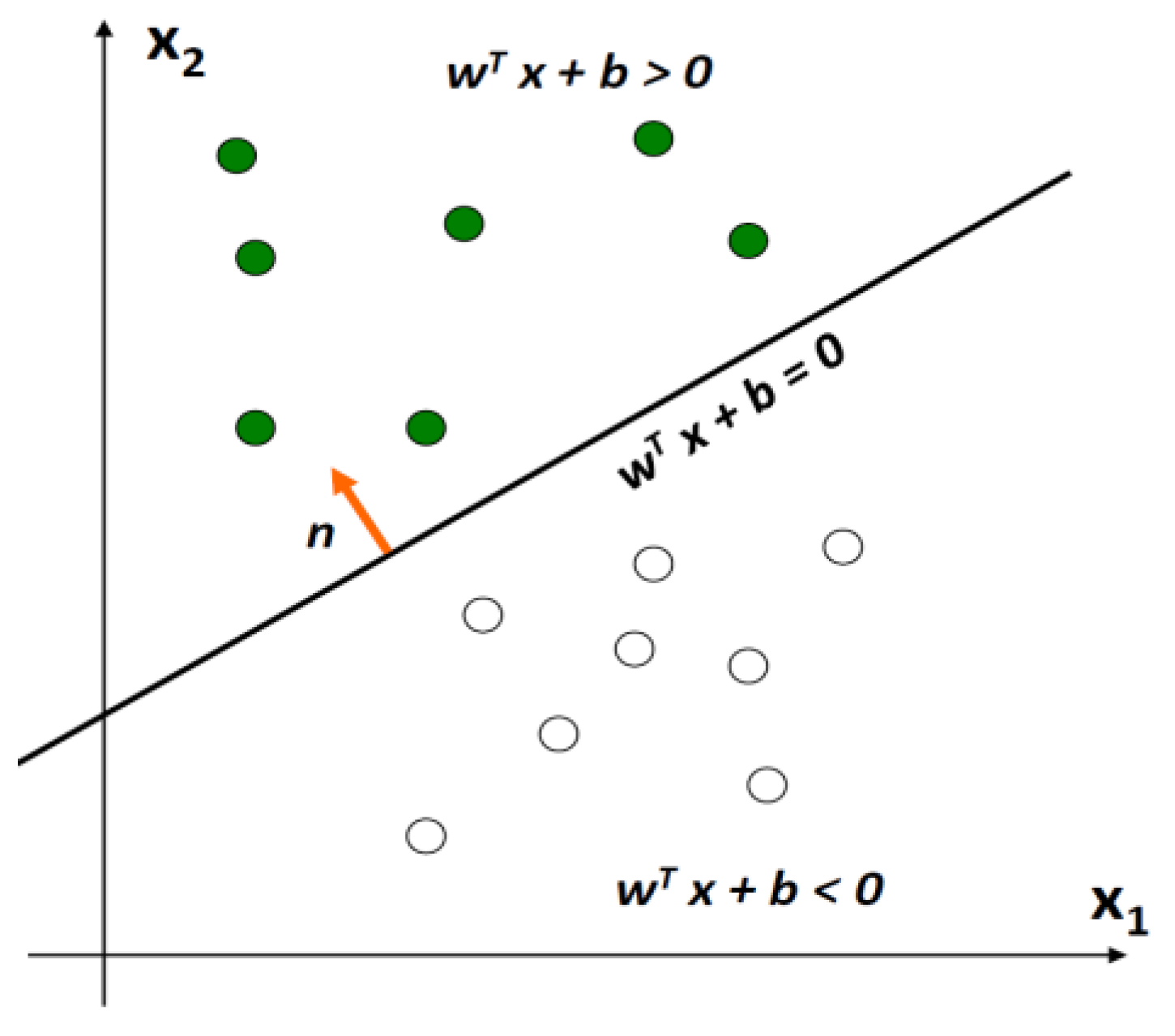
- Support vector machines
3.2.3. Assessment of Models
4. Results
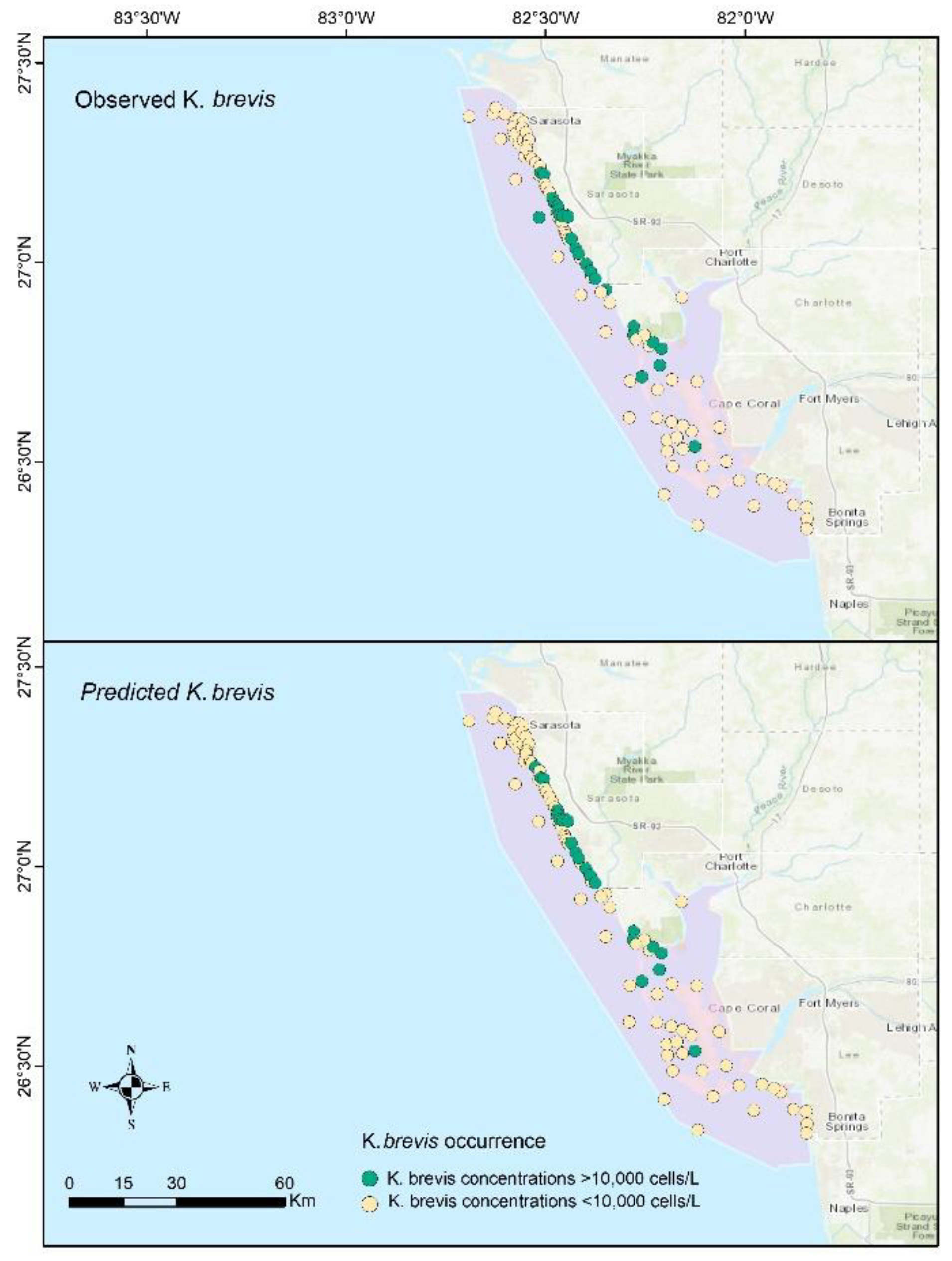
4.1. Model Structure Comparison and Selection of Optimum Model Structure
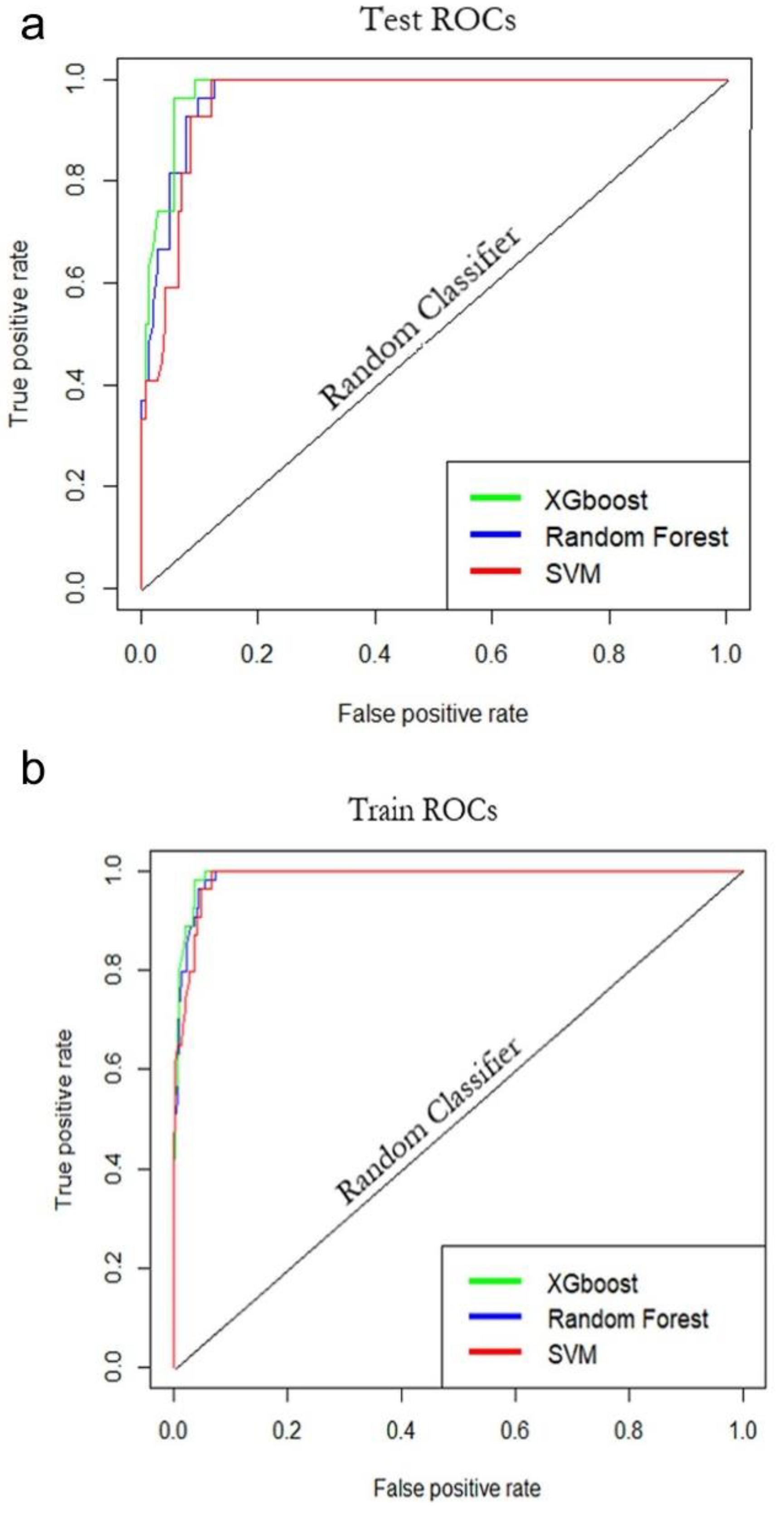
4.2. Comparison of the Performance of Statistical Models and Selection of the Optimum Model
4.3. Comparison of Lag Times and Selection of Optimum Lag Time
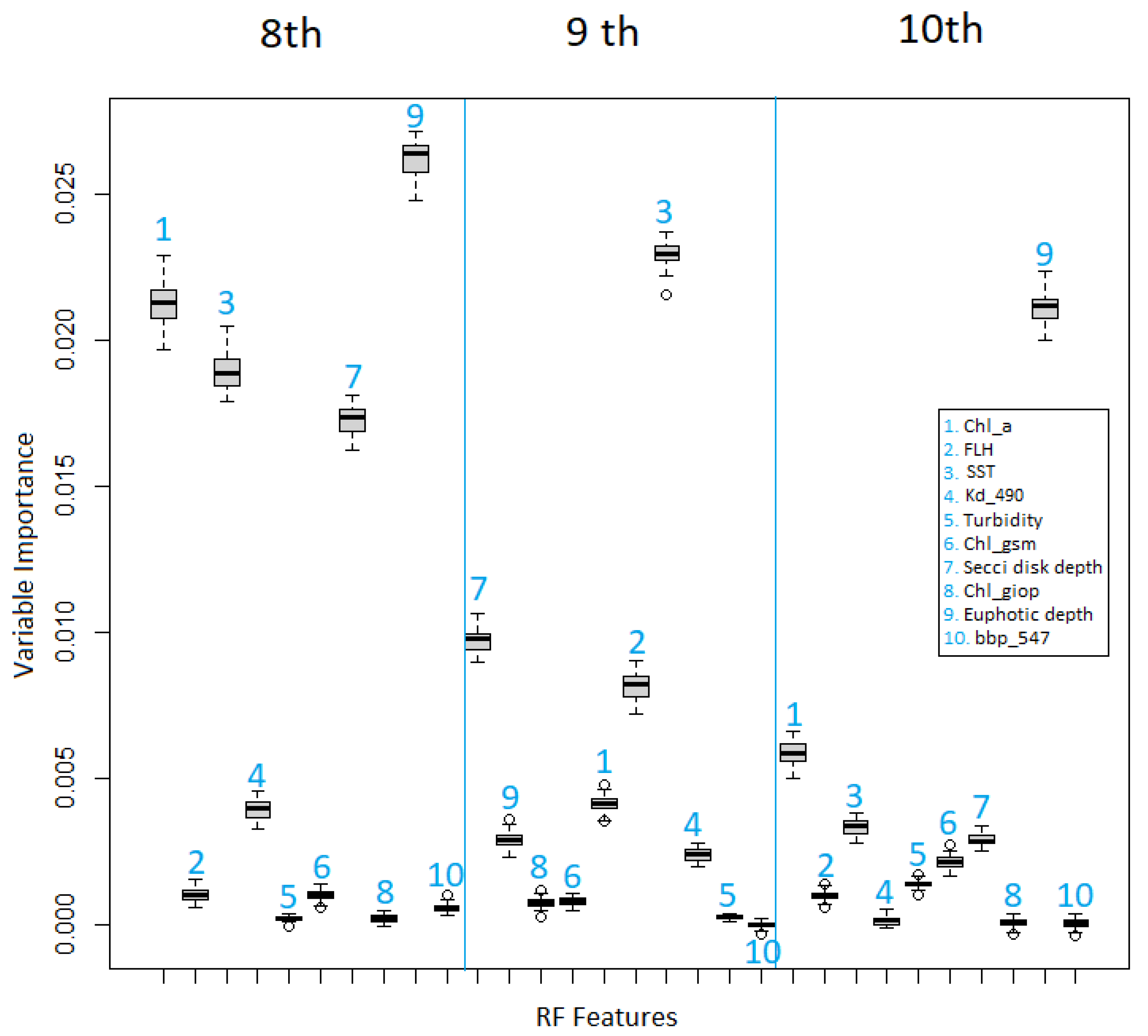
4.4. Identification of Controlling Factor Importance
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fuentes-Yaco, C.; Vézina, A.F.; Larouche, P.; Gratton, Y.; Gosselin, M. Phytoplankton pigment in the Gulf of St. Lawrence, Canada, as determined by the Coastal Zone Color Scanner Part II: Multivariate analysis. Cont. Shelf Res. 1997, 17, 1441–1459. [Google Scholar] [CrossRef]
- Chari, N.V.H.K.; Keerthi, S.; Sarma, N.S.; Pandi, S.R.; Chiranjeevulu, G.; Kiran, R.; Koduru, U. Fluorescence and absorption characteristics of dissolved organic matter excreted by phytoplankton species of western Bay of Bengal under axenic laboratory condition. J. Exp. Mar. Biol. Ecol. 2013, 445, 148–155. [Google Scholar] [CrossRef]
- Gohin, F.; Lampert, L.; Guillaud, J.F.; Herbland, A.; Nézan, E. Satellite and in situ observations of a late winter phytoplankton bloom, in the northern Bay of Biscay. Cont. Shelf Res. 2003, 23, 1117–1141. [Google Scholar] [CrossRef][Green Version]
- Kahru, M.; Mitchell, B.G.; Diaz, A.; Miura, M. MODIS detects a devastating algal bloom in Paracas Bay, Peru. Eos 2004, 85, 465–472. [Google Scholar] [CrossRef]
- Oliveira, P.B.; Moita, T.; Silva, A.; Monteiro, I.T.; Sofia Palma, A. Summer diatom and dinoflagellate blooms in Lisbon Bay from 2002 to 2005: Pre-conditions inferred from wind and satellite data. Prog. Oceanogr. 2009, 83, 270–277. [Google Scholar] [CrossRef]
- Ryan, J.P.; Fischer, A.M.; Kudela, R.M.; Gower, J.F.R.; King, S.A.; Marin, R.; Chavez, F.P. Influences of upwelling and downwelling winds on red tide bloom dynamics in Monterey Bay, California. Cont. Shelf Res. 2009, 29, 785–795. [Google Scholar] [CrossRef]
- Tilstone, G.H.; Angel-Benavides, I.M.; Pradhan, Y.; Shutler, J.D.; Groom, S.; Sathyendranath, S. An assessment of chlorophyll-a algorithms available for SeaWiFS in coastal and open areas of the Bay of Bengal and Arabian Sea. Remote Sens. Environ. 2011, 115, 2277–2291. [Google Scholar] [CrossRef]
- Moradi, M.; Kabiri, K. Red tide detection in the Strait of Hormuz (east of the Persian Gulf) using MODIS fluorescence data. Int. J. Remote Sens. 2012, 33, 1015–1028. [Google Scholar] [CrossRef]
- Blondeau-Patissier, D.; Gower, J.F.R.; Dekker, A.G.; Phinn, S.R.; Brando, V.E. A review of ocean color remote sensing methods and statistical techniques for the detection, mapping and analysis of phytoplankton blooms in coastal and open oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef]
- Song, H.; Ji, R.; Stock, C.; Wang, Z. Phenology of phytoplankton blooms in the Nova Scotian Shelf-Gulf of Maine region: Remote sensing and modeling analysis. J. Plankton Res. 2010, 32, 1485–1499. [Google Scholar] [CrossRef]
- Nezlin, N.P.; Li, B.L. Time-series analysis of remote-sensed chlorophyll and environmental factors in the Santa Monica-San Pedro Basin off Southern California. J. Mar. Syst. 2003, 39, 185–202. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Minnett, P.J.; Fleming, L.E.; Banzon, V.F.; Baringer, W. Satellite remote sensing of harmful algal blooms: A new multi-algorithm method for detecting the Florida Red Tide (Karenia brevis). Harmful Algae 2010, 9, 440–448. [Google Scholar] [CrossRef]
- Magaña, H.A.; Contreras, C.; Villareal, T.A. A historical assessment of Karenia brevis in the western Gulf of Mexico. Harmful Algae 2003, 2, 163–171. [Google Scholar] [CrossRef]
- Kutser, T. Passive optical remote sensing of cyanobacteria and other intense phytoplankton blooms in coastal and inland waters. Int. J. Remote Sens. 2009, 17, 4401–4425. [Google Scholar] [CrossRef]
- Dierssen, H.M.; Kudela, R.M.; Ryan, J.P.; Zimmerman, R.C. Red and black tides: Quantitative analysis of water-leaving radiance and perceived color for phytoplankton, colored dissolved organic matter, and suspended sediments. Limnol. Oceanogr. 2006, 51, 2646–2659. [Google Scholar] [CrossRef]
- Amin, R.; Zhou, J.; Gilerson, A.; Gross, B.; Moshary, F.; Ahmed, S. Novel optical techniques for detecting and classifying toxic dinoflagellate Karenia brevis blooms using satellite imagery. Opt. Express 2009, 17, 9126–9144. [Google Scholar] [CrossRef]
- Haywood, A.J.; Steidinger, K.A.; Truby, E.W.; Bergquist, P.R.; Bergquist, P.L.; Adamson, J.; MacKenzie, L. Comparative morphology and molecular phylogenetic analysis of three new species of the genus Karenia (Dinophyceae) from New Zealand. J. Phycol. 2004, 40, 165–179. [Google Scholar] [CrossRef]
- Kirkpatrick, B.; Fleming, L.E.; Squicciarini, D.; Backer, L.C.; Clark, R.; Abraham, W.; Benson, J.; Cheng, Y.S.; Johnson, D.; Pierce, R.; et al. Literature review of Florida red tide: Implications for human health effects. Harmful Algae 2004, 3, 99–115. [Google Scholar] [CrossRef]
- Ross, C.; Ritson-Williams, R.; Pierce, R.; Bullington, J.B.; Henry, M.; Paul, V.J. Effects of the Florida red tide dinoflagellate, Karenia brevis, on oxidative stress and metamorphosis of larvae of the coral Porites astreoides. Harmful Algae 2010, 9, 173–179. [Google Scholar] [CrossRef]
- Landsberg, J.H. The effects of harmful algal blooms on aquatic organisms. Rev. Fish. Sci. 2002, 2, 113–390. [Google Scholar] [CrossRef]
- Fleming, L.E.; Kirkpatrick, B.; Backer, L.C.; Walsh, C.J.; Nierenberg, K.; Clark, J.; Reich, A.; Hollenbeck, J.; Benson, J.; Cheng, Y.S.; et al. Review of Florida red tide and human health effects. Harmful Algae 2011, 10, 224–233. [Google Scholar] [CrossRef]
- Fleming, L.E.; McDonough, N.; Austen, M.; Mee, L.; Moore, M.; Hess, P.; Depledge, M.H.; White, M.; Philippart, K.; Bradbrook, P.; et al. Oceans and human health: A rising tide of challenges and opportunities for Europe. Mar. Environ. Res. 2014, 99, 16–19. [Google Scholar] [CrossRef]
- Dyson, K.; Huppert, D.D. Regional economic impacts of razor clam beach closures due to harmful algal blooms (HABs) on the Pacific coast of Washington. Harmful Algae 2010, 9, 264–271. [Google Scholar] [CrossRef]
- Stauffer, B.A.; Bowers, H.A.; Buckley, E.; Davis, T.W.; Johengen, T.H.; Kudela, R.; McManus, M.A.; Purcell, H.; Smith, G.J.; Vander Woude, A.; et al. Considerations in harmful algal bloom research and monitoring: Perspectives from a consensus-building workshop and technology testing. Front. Mar. Sci. 2019, 6. [Google Scholar] [CrossRef]
- Thomas, A.C.; Townsend, D.W.; Weatherbee, R. Satellite-measured phytoplankton variability in the Gulf of Maine. Cont. Shelf Res. 2003, 23, 971–989. [Google Scholar] [CrossRef]
- Vargo, G.A. A brief summary of the physiology and ecology of Karenia brevis Davis (G. Hansen and Moestrup comb. nov.) red tides on the West Florida Shelf and of hypotheses posed for their initiation, growth, maintenance, and termination. Harmful Algae 2009, 8, 573–584. [Google Scholar] [CrossRef]
- Howarth, R.W.; Billen, G.; Swaney, D.; Townsend, A.; Jaworski, N.; Lajtha, K.; Downing, J.A.; Elmgren, R.; Caraco, N.; Jordan, T.; et al. Regional nitrogen budgets and riverine N & P fluxes for the drainages to the North Atlantic Ocean: Natural and human influences. Biogeochemistry 1996, 35, 75–139. [Google Scholar] [CrossRef]
- Boesch, D.F.; Boynton, W.R.; Crowder, L.B.; Diaz, R.J.; Howarth, R.W.; Mee, L.D.; Nixon, S.W.; Rabalais, N.N.; Rosenberg, R.; Sanders, J.G.; et al. Nutrient enrichment drives Gulf of Mexico hypoxia. Eos 2009, 90, 117–118. [Google Scholar] [CrossRef]
- Pinet, P.R. Invitation to Oceanography; Jones & Bartlett Publishers: Burlington, MA, USA, 2009; ISBN 1449667988. [Google Scholar]
- Tomlinson, M.C.; Wynne, T.T.; Stumpf, R.P. An evaluation of remote sensing techniques for enhanced detection of the toxic dinoflagellate, Karenia brevis. Remote Sens. Environ. 2009, 113, 598–609. [Google Scholar] [CrossRef]
- Hu, C.; Muller-Karger, F.E.; Vargo, G.A.; Neely, M.B.; Johns, E. Linkages between coastal runoff and the Florida Keys ecosystem: A study of a dark plume event. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Anderson, D.M. Approaches to monitoring, control and management of harmful algal blooms (HABs). Ocean Coast. Manag. 2009, 52, 342–347. [Google Scholar] [CrossRef]
- Lee, J.H.W.; Hodgkiss, I.J.; Wong, K.T.M.; Lam, I.H.Y. Real time observations of coastal algal blooms by an early warning system. Estuar. Coast. Shelf Sci. 2005, 65, 172–190. [Google Scholar] [CrossRef]
- Kamangir, H.; Collins, W.; Tissot, P.; King, S.A.; Dinh, H.T.H.; Durham, N.; Rizzo, J. FogNet: A multiscale 3D CNN with double-branch dense block and attention mechanism for fog prediction. Mach. Learn. Appl. 2021, 5, 100038. [Google Scholar] [CrossRef]
- Park, S.; Lee, S.R. Red tides prediction system using fuzzy reasoning and the ensemble method. Appl. Intell. 2014, 40, 244–255. [Google Scholar] [CrossRef]
- Craig, S.E.; Lohrenz, S.E.; Lee, Z.; Mahoney, K.L.; Kirkpatrick, G.J.; Schofield, O.M.; Steward, R.G. Use of hyperspectral remote sensing reflectance for detection and assessment of the harmful alga, Karenia brevis. Appl. Opt. 2006, 45, 5414–5425. [Google Scholar] [CrossRef]
- Kislik, C.; Dronova, I.; Kelly, M. UAVs in support of algal bloom research: A review of current applications and future opportunities. Drones 2018, 2, 35. [Google Scholar] [CrossRef]
- Sakuno, Y.; Maeda, A.; Mori, A.; Ono, S.; Ito, A. A simple red tide monitoring method using sentinel-2 data for sustainable management of Brackish Lake Koyama-ike, Japan. Water 2019, 11, 1044. [Google Scholar] [CrossRef]
- Klemas, V. Remote sensing of algal blooms: An overview with case studies. J. Coast. Res. 2012, 278, 34–43. [Google Scholar] [CrossRef]
- Seydi, S.T.; Akhoondzadeh, M.; Amani, M.; Mahdavi, S. Wildfire damage assessment over Australia using Sentinel-2 imagery and modis land cover product within the Google Earth engine cloud platform. Remote Sens. 2021, 13, 220. [Google Scholar] [CrossRef]
- Ghannadi, M.A.; Alebooye, S.; Izadi, M.; Moradi, A. A method for Sentinel-1 DEM outlier removal using 2-D Kalman filter. Geocarto Int. 2020, 35, 1–15. [Google Scholar] [CrossRef]
- Ghannadi, M.A.; SaadatSeresht, M.; Izadi, M.; Alebooye, S. Optimal texture image reconstruction method for improvement of SAR image matching. IET Radar Sonar Navig. 2020, 14, 1229–1235. [Google Scholar] [CrossRef]
- Gower, J.; King, S.; Goncalves, P. Global monitoring of plankton blooms using meris MCI. Int. J. Remote Sens. 2008, 29, 6209–6216. [Google Scholar] [CrossRef]
- Xing, X.G.; Zhao, D.Z.; Liu, Y.G.; Yang, J.H.; Xiu, P.; Wang, L. An overview of remote sensing of chlorophyll fluorescence. Ocean Sci. J. 2007, 42, 49–59. [Google Scholar] [CrossRef]
- Matthews, M.W.; Bernard, S.; Robertson, L. An algorithm for detecting trophic status (chlorophyll-a), cyanobacterial-dominance, surface scums and floating vegetation in inland and coastal waters. Remote Sens. Environ. 2012, 129, 637–652. [Google Scholar] [CrossRef]
- Siswanto, E.; Ishizaka, J.; Tripathy, S.C.; Miyamura, K. Detection of harmful algal blooms of Karenia mikimotoi using MODIS measurements: A case study of Seto-Inland Sea, Japan. Remote Sens. Environ. 2013, 129, 185–196. [Google Scholar] [CrossRef]
- Bernard, S.; Balt, C.; Pitcher, G.; Probyn, T.; Fawcett, A.; Du Randt, A. The use of MERIS for harmful algal bloom monitoring in the Southern Benguela. In Proceedings of the MERIS (A)ATSR Workshop 2005 (ESA SP-597), Frascati, Italy, 26–30 September 2005. [Google Scholar]
- Cao, Z.; Ma, R.; Duan, H.; Pahlevan, N.; Melack, J.; Shen, M.; Xue, K. A machine learning approach to estimate chlorophyll-a from Landsat-8 measurements in inland lakes. Remote Sens. Environ. 2020, 248, 111974. [Google Scholar] [CrossRef]
- Moore, T.S.; Campbell, J.W.; Dowell, M.D. A class-based approach to characterizing and mapping the uncertainty of the MODIS ocean chlorophyll product. Remote Sens. Environ. 2009, 113, 2424–2430. [Google Scholar] [CrossRef]
- Elkadiri, R.; Manche, C.; Sultan, M.; Al-Dousari, A.; Uddin, S.; Chouinard, K.; Abotalib, A.Z. Development of a coupled spatiotemporal algal bloom model for coastal areas: A remote sensing and data mining-based approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5159–5171. [Google Scholar] [CrossRef]
- Song, W.; Dolan, J.M.; Cline, D.; Xiong, G. Learning-based algal bloom event recognition for oceanographic decision support system using remote sensing data. Remote Sens. 2015, 7, 13564–13585. [Google Scholar] [CrossRef]
- Gokaraju, B.; King, R.L.; Durbha, S.S.; Younan, N.H. A Machine Learning Based Spatio-Temporal Data Mining Approach for Detection of Harmful Algal Blooms in the Gulf of Mexico. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 710–720. [Google Scholar] [CrossRef]
- Lee, M.S.; Park, K.A.; Chae, J.; Park, J.E.; Lee, J.S.; Lee, J.H. Red tide detection using deep learning and high-spatial resolution optical satellite imagery. Int. J. Remote Sens. 2020, 41, 5838–5860. [Google Scholar] [CrossRef]
- Hill, P.R.; Kumar, A.; Temimi, M.; Bull, D.R. HABNet: Machine learning, remote sensing-based detection of harmful algal blooms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3229–3239. [Google Scholar] [CrossRef]
- Karki, S.; Sultan, M.; Elkadiri, R.; Elbayoumi, T. Mapping and forecasting onsets of harmful algal blooms using MODIS data over coastalwaters surrounding charlotte county, Florida. Remote Sens. 2018, 10, 1656. [Google Scholar] [CrossRef]
- Franks, P.J.S. Models of harmful algal blooms. Limnol. Oceanogr. 1997, 42, 1273–1282. [Google Scholar] [CrossRef]
- Trombetta, T.; Vidussi, F.; Mas, S.; Parin, D.; Simier, M.; Mostajir, B. Water temperature drives phytoplankton blooms in coastal waters. PLoS ONE 2019, 14, e0214933. [Google Scholar] [CrossRef]
- Lotliker, A.A.; Baliarsingh, S.K.; Samanta, A.; Varaprasad, V. Growth and decay of high-biomass algal bloom in the Northern Arabian Sea. J. Indian Soc. Remote Sens. 2020, 48, 465–471. [Google Scholar] [CrossRef]
- Izadi, M.; Sultan, M.; Elkadiri, R.; Ghannadi, M.A.; Nikraftar, Z.; Namjoo, F. Remote sensing and statistical learning approach to harmful algal bloom forecasting using MODIS ocean colour parameters. In Proceedings of the AGU Fall Meeting Abstracts; 2020. Available online: https://ui.adsabs.harvard.edu/abs/2020AGUFMIN011..09I/abstract (accessed on 5 September 2021).
- Zolfaghari, A.; Izadi, M. Burst Pressure Prediction of Cylindrical Vessels Using Artificial Neural Network. J. Press. Vessel Technol. Trans. ASME 2020, 142, 1–7. [Google Scholar] [CrossRef]
- Izadi, M.; Mohammadzadeh, A.; Haghighattalab, A. A new neuro-fuzzy approach for post-earthquake road damage assessment using GA and SVM classification from QuickBird satellite images. J. Indian Soc. Remote Sens. 2017, 45, 965–977. [Google Scholar] [CrossRef]
- Recknagel, F.; Michener, W. Ecological Informatics: Data Management and Knowledge Discovery; Springer: Berlin, Germany, 2017. [Google Scholar]
- Kim, D.; Jeong, K.; McKay, R.; Chon, T.; Joo, G. Machine learning for predictive management: Short and long term prediction of phytoplankton biomass using genetic algorithm based recurrent neural networks. Int. J. Environ. Res. 2012, 6, 95–108. [Google Scholar]
- Kim, S. A multiple process univariate model for the prediction of chlorophyll-a concentration in river systems. Int. J. Limnol. 2016, 56, 137–150. [Google Scholar] [CrossRef]
- Cho, H.; Choi, U.; Park, H. Deep learning application to time-series prediction of daily chlorophyll-a concentration. Wit. Trans. Ecol. Environ. 2018, 215, 163–175. [Google Scholar] [CrossRef]
- Lee, S.; Lee, D. Improved prediction of harmful algal blooms in four Major South Korea’s Rivers using deep learning models. Int. J. Environ. Res. Public Health 2018, 15, 1322. [Google Scholar] [CrossRef]
- Malek, S.; Salleh, A.; Milow, P.; Baba, M.; Sharifah, S. Applying artificial neural network theory to exploring diatom abundance at tropical Putrajaya lake, Malaysia. J. Freshw. Ecol. 2012, 27, 211–227. [Google Scholar] [CrossRef]
- Daghighi, A. Harmful Algae Bloom Prediction Model for Western Lake Erie Using Stepwise Multiple Regression and Genetic Programming. Master’s Thesis, Cleveland State University, Cleveland, OH, USA, 2017. [Google Scholar]
- Qin, M.; Li, Z.; Du, Z. Red tide time series forecasting by combining ARIMA and deep belief network. Knowl.-Based Syst. 2017, 125, 39–52. [Google Scholar] [CrossRef]
- McGowan, J.A.; Deyle, E.R.; Ye, H.; Carter, M.L.; Perretti, C.T.; Seger, K.D.; Verneil, A.; Sugihara, G. Predicting coastal algal blooms in Southern California. Ecology 2017, 98, 1419–1433. [Google Scholar] [CrossRef]
- Sheykhmousa, M.; Mahdianpari, M.; Ghanbari, H.; Mohammadimanesh, F.; Ghamisi, P.; Homayouni, S. Support vector machine versus random forest for remote sensing image classification: A meta-analysis and systematic review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6308–6325. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2000; ISBN 978-1-4614-7137-0. [Google Scholar]
- Lee, Z.P.; Weidemann, A.; Kindle, J.; Arnone, R.; Carder, K.L.; Davis, C. Euphotic zone depth: Its derivation and implication to ocean-color remote sensing. J. Geophys. Res. Ocean. 2007, 112. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Falkowski, P.G. A consumer’s guide to phytoplankton primary productivity models. Limnol. Oceanogr. 1997, 42, 1479–1491. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Boss, E.; Siegel, D.A.; Shea, D.M. Carbon-based ocean productivity and phytoplankton physiology from space. Glob. Biogeochem. Cycles 2005, 19. [Google Scholar] [CrossRef]
- Anderson, D.M.; Glibert, P.M.; Burkholder, J.M. Harmful algal blooms and eutrophication: Nutrient sources, composition, and consequences. Estuaries 2002, 25, 704–726. [Google Scholar] [CrossRef]
- Morel, A.; Huot, Y.; Gentili, B.; Werdell, P.J.; Hooker, S.B.; Franz, B.A. Examining the consistency of products derived from various ocean color sensors in open ocean (Case 1) waters in the perspective of a multi-sensor approach. Remote Sens. Environ. 2007, 111, 69–88. [Google Scholar] [CrossRef]
- Wang, G.; Lee, Z.; Mouw, C. Multi-spectral remote sensing of phytoplankton pigment absorption properties in cyanobacteria bloom waters: A regional example in the western basin of Lake Erie. Remote Sens 2017, 9, 1309. [Google Scholar] [CrossRef]
- Hoepffner, N.; Sathyendranath, S. Effect of pigment composition on absorption properties of phytoplankton. Mar. Ecol. Prog. Ser. 1991, 73, 11–23. [Google Scholar] [CrossRef]
- O’Reilly, J.; Maritorena, S. Ocean color chlorophyll a algorithms for SeaWiFS, OC2, and OC4: Version 4. In SeaWiFS Postlaunch Calibration and Validation Analyses, Part 3; NASA Center for AeroSpace Information: Mountain View, CA, USA, 2000. [Google Scholar]
- Maritorena, S.; Siegel, D.A.; Peterson, A.R. Optimization of a semianalytical ocean color model for global-scale applications. Appl. Opt. 2002, 41, 2705–2714. [Google Scholar] [CrossRef]
- Lacava, T.; Ciancia, E.; Di Polito, C.; Madonia, A.; Pascucci, S.; Pergola, N.; Piermattei, V.; Satriano, V.; Tramutoli, V. Evaluation of MODIS-Aqua chlorophyll-a algorithms in the Basilicata Ionian Coastal waters. Remote Sens. 2018, 10, 987. [Google Scholar] [CrossRef]
- Shang, S.L.; Dong, Q.; Hu, C.M.; Lin, G.; Li, Y.H.; Shang, S.P. On the consistency of MODIS chlorophyll products in the northern South China Sea. Biogeosciences 2014, 11, 269–280. [Google Scholar] [CrossRef]
- Mishra, D.R.; Narumalani, S.; Rundquist, D.; Lawson, M. Characterizing the vertical diffuse attenuation coefficient for downwelling irradiance in coastal waters: Implications for water penetration by high resolution satellite data. ISPRS J. Photogramm. Remote Sens. 2005, 60, 48–64. [Google Scholar] [CrossRef]
- Chen, J.; Cui, T.; Tang, J.; Song, Q. Remote sensing of diffuse attenuation coefficient using MODIS imagery of turbid coastal waters: A case study in Bohai Sea. Remote Sens. Environ. 2014, 140, 78–93. [Google Scholar] [CrossRef]
- Ghanea, M.; Moradi, M.; Kabiri, K. A novel method for characterizing harmful algal blooms in the Persian Gulf using MODIS measurements. Adv. Space Res. 2016, 58, 1348–1361. [Google Scholar] [CrossRef]
- Lee, Z.P.; Du, K.P.; Arnone, R. A model for the diffuse attenuation coefficient of downwelling irradiance. J. Geophys. Res. C Ocean. 2005, 110. [Google Scholar] [CrossRef]
- Goldman, J.C.; Carpenter, E.J. A kinetic approach to the effect of temperature on algal growth. Limnol. Oceanogr. 1974, 19, 756–766. [Google Scholar] [CrossRef]
- Hallegraeff, G.M. Ocean climate change, phytoplankton community responses, and harmful algal blooms: A formidable predictive challenge. J. Phycol. 2010, 46, 220–235. [Google Scholar] [CrossRef]
- Bricaud, A.; Bosc, E.; Antoine, D. Algal biomass and sea surface temperature in the Mediterranean Basin: Intercomparison of data from various satellite sensors, and implications for primary production estimates. Remote Sens. Environ. 2002, 81, 163–178. [Google Scholar] [CrossRef]
- Errera, R.M.; Yvon-Lewis, S.; Kessler, J.D.; Campbell, L. Reponses of the dinoflagellate Karenia brevis to climate change: PCO2 and sea surface temperatures. Harmful Algae 2014, 37, 110–116. [Google Scholar] [CrossRef]
- Sarma, Y.V.B.; Al-Hashmi, K.; Smith, S.L. Sea surface warming and its implications for harmful algal blooms off oman. Int. J. Mar. Sci. 2013, 3, 65–71. [Google Scholar] [CrossRef]
- Hu, C.; Muller-Karger, F.E.; Taylor, C.; Carder, K.L.; Kelble, C.; Johns, E.; Heil, C.A. Red tide detection and tracing using MODIS fluorescence data: A regional example in SW Florida coastal waters. Remote Sens. Environ. 2005, 97, 311–321. [Google Scholar] [CrossRef]
- El-habashi, A.; Ioannou, I.; Tomlinson, M.C.; Stumpf, R.P.; Ahmed, S. Satellite retrievals of Karenia brevis harmful algal blooms in the West Florida Shelf using neural networks and comparisons with other techniques. Remote Sens. 2016, 8, 377. [Google Scholar] [CrossRef]
- Neville, R.A.; Gower, J.F.R. Passive remote sensing of phytoplankton via chlorophyll α fluorescence. J. Geophys. Res. 1977, 82, 3487–3493. [Google Scholar] [CrossRef]
- Zhao, J.; Hu, C.; Lenes, J.M.; Weisberg, R.H.; Lembke, C.; English, D.; Wolny, J.; Zheng, L.; Walsh, J.J.; Kirkpatrick, G. Three-dimensional structure of a Karenia brevis bloom: Observations from gliders, satellites, and field measurements. Harmful Algae 2013, 29, 22–30. [Google Scholar] [CrossRef]
- Cannizzaro, J.P.; Hu, C.; English, D.C.; Carder, K.L.; Heil, C.A.; Müller-Karger, F.E. Detection of Karenia brevis blooms on the west Florida shelf using in situ backscattering and fluorescence data. Harmful Algae 2009, 8, 898–909. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef]
- Davies-Colley, R.J.; Smith, D.G. Turbidity, suspended sediment, and water clarity: A review. J. Am. Water Resour. Assoc. 2001, 37, 1085–1101. [Google Scholar] [CrossRef]
- Roelke, D.; Buyukates, Y. The diversity of harmful algal bloom-triggering mechanisms and the complexity of bloom initiation. Hum. Ecol. Risk Assess. 2001, 7, 1347–1362. [Google Scholar] [CrossRef]
- May, C.L.; Koseff, J.R.; Lucas, L.V.; Cloern, J.E.; Schoellhamer, D.H. Effects of spatial and temporal variability of turbidity on phytoplankton blooms. Mar. Ecol. Prog. Ser. 2003, 254, 111–128. [Google Scholar] [CrossRef]
- Morel, A.; Bélanger, S. Improved detection of turbid waters from ocean color sensors information. Remote Sens. Environ. 2006, 102, 237–249. [Google Scholar] [CrossRef]
- Brand, L.E.; Compton, A. Long-term increase in Karenia brevis abundance along the Southwest Florida coast. Harmful Algae 2007, 6, 232–252. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Chen, T.; He, T.; Benesty, M. Xgboost: eXtreme Gradient Boosting, R Package version 0.71-2; Grin Verlag: München, Germnay, 2018; pp. 1–4. [Google Scholar]
- Hastie, T.; Tibshirani, R.; James, G.; Witten, D. An Introduction to Statistical Learning, Springer Texts; Springer: Berlin, Germany, 2006; ISBN 9780387781884. [Google Scholar]
- Klusowski, J.M. Complete analysis of a random forest model. arXiv 2018, arXiv:1005.0208. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. Proc. Int. Conf. Doc. Anal. Recognit. 1995, 1, 278–282. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Kim, T.-J. Prevention of harmful algal blooms by control of growth parameters. Adv. Biosci. Biotechnol. 2018, 09, 613–648. [Google Scholar] [CrossRef][Green Version]
- Zhang, M.; Niu, Z.; Cai, Q.; Xu, Y.; Qu, X. Effect of water column stability on surface chlorophyll and time lags under different nutrient backgrounds in a deep reservoir. Water 2019, 11, 1504. [Google Scholar] [CrossRef]
- Jones, M. Forecasting algal bloom lags and stability in a watershed. SIAM Undergrad. Res. Online 2018, 11, 352–368. [Google Scholar] [CrossRef]

| Combination (7th XGB) | −7 | −8 | −9 | −7, −8 | −8, −9 | −7, −8, −9 |
| Kappa | 0.77 | 0.76 | 0.76 | 0.74 | 0.76 | 0.80 |
| F-score | 0.89 | 0.88 | 0.88 | 0.85 | 0.88 | 0.96 |
| Precision | 0.84 | 0.88 | 0.88 | 0.92 | 0.88 | 0.94 |
| B. accuracy | 87.0 | 86.0 | 86.0 | 83.0 | 86.0 | 88.0 |
| Combination (2nd SVM) | −2 | −3 | −4 | −2, −3 | −3, −4 | −2, −3, −4 |
| Kappa | 0.35 | 0.4 | 0.37 | 0.4 | 0.4 | 0.50 |
| F-score | 0.51 | 0.52 | 0.48 | 0.52 | 0.52 | 0.60 |
| Precision | 0.56 | 0.72 | 0.81 | 0.73 | 0.73 | 0.82 |
| B. accuracy | 66.0 | 66.0 | 64.0 | 67.0 | 66.0 | 71.0 |
| Days (2000–2020) < 10% Cloud | Scenes | Frequency |
|---|---|---|
| Total | 2905 | |
| single days | 1039 | 36% |
| 2 consecutive days | 562 | 20% |
| 3 consecutive days | 260 | 9.0% |
| 4 consecutive days | 57 | 1.9% |
| 5 consecutive days | 29 | 0.9% |
| 6 consecutive days | 21 | 0.7% |
| 7 consecutive days | 14 | 0.4% |
| 8 consecutive days | 6 | 0.2% |
| 9 consecutive days | 1 | 0.03% |
| 10 consecutive days | 0 | 0% |
| 3 Day Models | |||||||||||||
| −13 | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | Day |
| X | X | X | Bloom | ||||||||||
| X | X | X | Bloom | ||||||||||
| X | X | X | Bloom | ||||||||||
| X | X | X | Bloom | ||||||||||
| X | X | X | Bloom | ||||||||||
| X | X | X | Bloom | ||||||||||
| X | X | X | Bloom | ||||||||||
| X | X | X | Bloom | ||||||||||
| X | X | X | Bloom | ||||||||||
| X | X | X | Bloom | ||||||||||
| X | X | X | Bloom | ||||||||||
| 2 Day Models | |||||||||||||
| −13 | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | Day |
| X | X | Bloom | |||||||||||
| X | X | Bloom | |||||||||||
| X | X | Bloom | |||||||||||
| X | X | Bloom | |||||||||||
| X | X | Bloom | |||||||||||
| X | X | Bloom | |||||||||||
| X | X | Bloom | |||||||||||
| X | X | Bloom | |||||||||||
| X | X | Bloom | |||||||||||
| X | X | Bloom | |||||||||||
| X | X | Bloom | |||||||||||
| XGBoost | Model Performance | |||||||||||||||
| −13 | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | Accuracy | Kappa | F-Score | AUC |
| X | X | X | 73.1 | 0.52 | 0.64 | 0.74 | ||||||||||
| X | X | X | 73.9 | 0.65 | 0.82 | 0.85 | ||||||||||
| X | X | X | 58.0 | 0.27 | 0.63 | 0.67 | ||||||||||
| X | X | X | 76.4 | 0.58 | 0.78 | 0.84 | ||||||||||
| X | X | X | 83.9 | 0.0.7 | 0.87 | 0.88 | ||||||||||
| X | X | X | 92.0 | 0.86 | 0.95 | 0.97 | ||||||||||
| X | X | X | 87.6 | 0.81 | 0.96 | 0.98 | ||||||||||
| X | X | X | 96.2 | 0.93 | 0.98 | 0.98 | ||||||||||
| X | X | X | 87.4 | 0.76 | 0.92 | 0.91 | ||||||||||
| X | X | X | 83.6 | 0.71 | 0.88 | 0.81 | ||||||||||
| X | X | X | 79.6 | 0.68 | 0.80 | 0.80 | ||||||||||
| RF | Model Performance | |||||||||||||||
| −13 | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | Accuracy | Kappa | F-Score | AUC |
| X | X | X | 65.6 | 0.40 | 0.74 | 0.73 | ||||||||||
| X | X | X | 77.2 | 0.63 | 0.71 | 0.86 | ||||||||||
| X | X | X | 54.7 | 0.13 | 0.20 | 0.74 | ||||||||||
| X | X | X | 76.1 | 0.60 | 0.73 | 0.87 | ||||||||||
| X | X | X | 83.5 | 0.67 | 0.80 | 0.83 | ||||||||||
| X | X | X | 89.2 | 0.82 | 0.84 | 0.95 | ||||||||||
| X | X | X | 91.4 | 0.75 | 0.84 | 0.96 | ||||||||||
| X | X | X | 95.2 | 0.92 | 0.95 | 0.96 | ||||||||||
| X | X | X | 78.3 | 0.73 | 0.88 | 0.80 | ||||||||||
| X | X | X | 81.7 | 0.67 | 0.78 | 0.87 | ||||||||||
| X | X | X | 80.7 | 0.62 | 0.71 | 0.79 | ||||||||||
| SVM | Model Performance | |||||||||||||||
| −13 | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | Accuracy | Kappa | F-score | AUC |
| X | X | X | 62.4 | 0.35 | 0.72 | 0.69 | ||||||||||
| X | X | X | 71.2 | 0.50 | 0.60 | 0.80 | ||||||||||
| X | X | X | 56.3 | 0.20 | 0.27 | 0.79 | ||||||||||
| X | X | X | 73.7 | 0.63 | 0.75 | 0.84 | ||||||||||
| X | X | X | 83.6 | 0.67 | 0.81 | 0.81 | ||||||||||
| X | X | X | 87.0 | 0.66 | 0.77 | 0.94 | ||||||||||
| X | X | X | 91.1 | 0.72 | 0.79 | 0.90 | ||||||||||
| X | X | X | 88.2 | 0.83 | 0.86 | 0.93 | ||||||||||
| X | X | X | 74.1 | 0.62 | 0.63 | 0.82 | ||||||||||
| X | X | X | 63.0 | 0.32 | 0.74 | 0.80 | ||||||||||
| X | X | X | 61.0 | 0.59 | 0.70 | 0.80 | ||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izadi, M.; Sultan, M.; Kadiri, R.E.; Ghannadi, A.; Abdelmohsen, K. A Remote Sensing and Machine Learning-Based Approach to Forecast the Onset of Harmful Algal Bloom. Remote Sens. 2021, 13, 3863. https://doi.org/10.3390/rs13193863
Izadi M, Sultan M, Kadiri RE, Ghannadi A, Abdelmohsen K. A Remote Sensing and Machine Learning-Based Approach to Forecast the Onset of Harmful Algal Bloom. Remote Sensing. 2021; 13(19):3863. https://doi.org/10.3390/rs13193863
Chicago/Turabian StyleIzadi, Moein, Mohamed Sultan, Racha El Kadiri, Amin Ghannadi, and Karem Abdelmohsen. 2021. "A Remote Sensing and Machine Learning-Based Approach to Forecast the Onset of Harmful Algal Bloom" Remote Sensing 13, no. 19: 3863. https://doi.org/10.3390/rs13193863
APA StyleIzadi, M., Sultan, M., Kadiri, R. E., Ghannadi, A., & Abdelmohsen, K. (2021). A Remote Sensing and Machine Learning-Based Approach to Forecast the Onset of Harmful Algal Bloom. Remote Sensing, 13(19), 3863. https://doi.org/10.3390/rs13193863







