Figure 1.
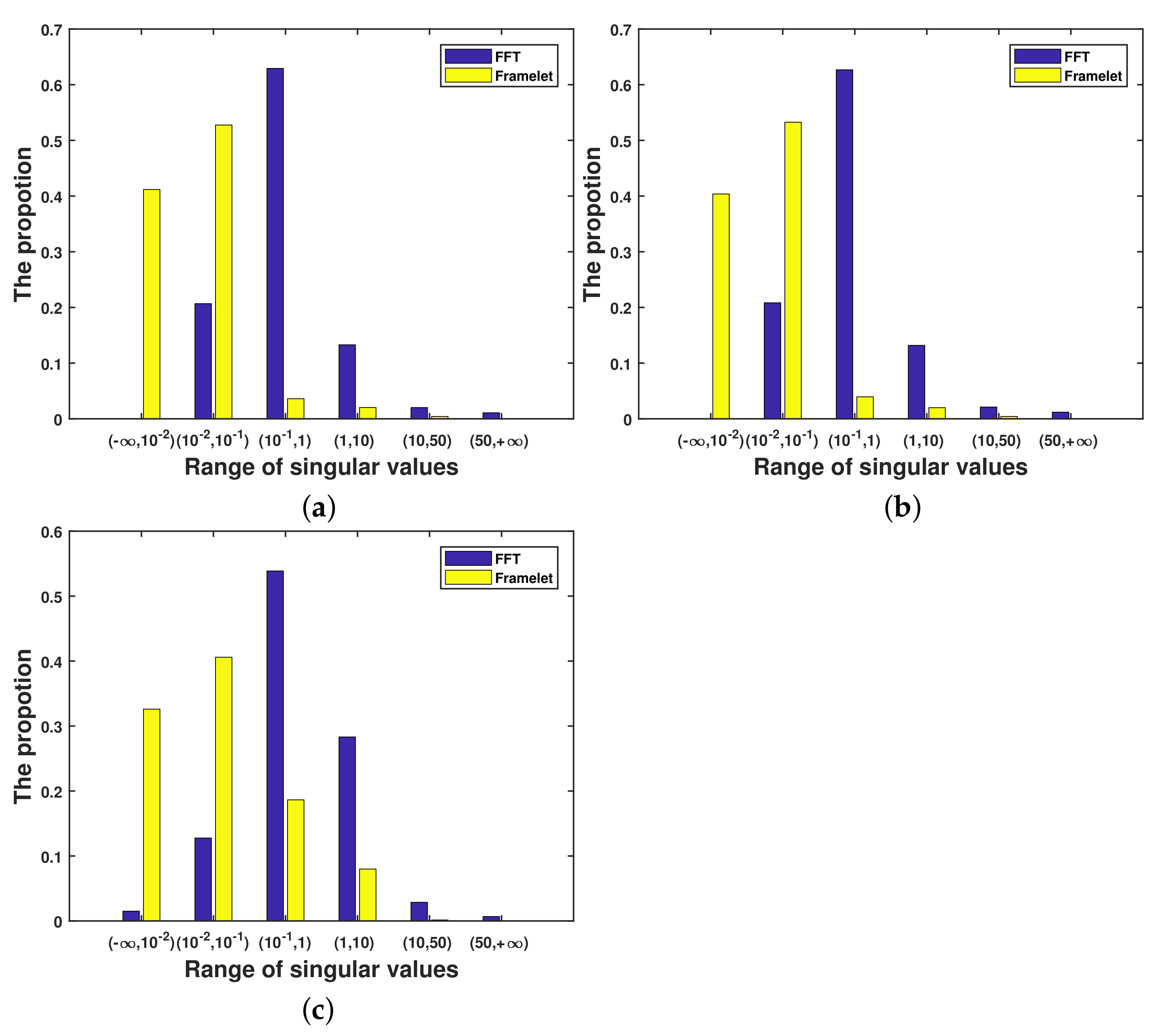
The distribution of singular values on each frontal slice of the two different transformed tensors. (a) The first mode, (b) the second mode, (c) the third mode.
Figure 1.
The distribution of singular values on each frontal slice of the two different transformed tensors. (a) The first mode, (b) the second mode, (c) the third mode.
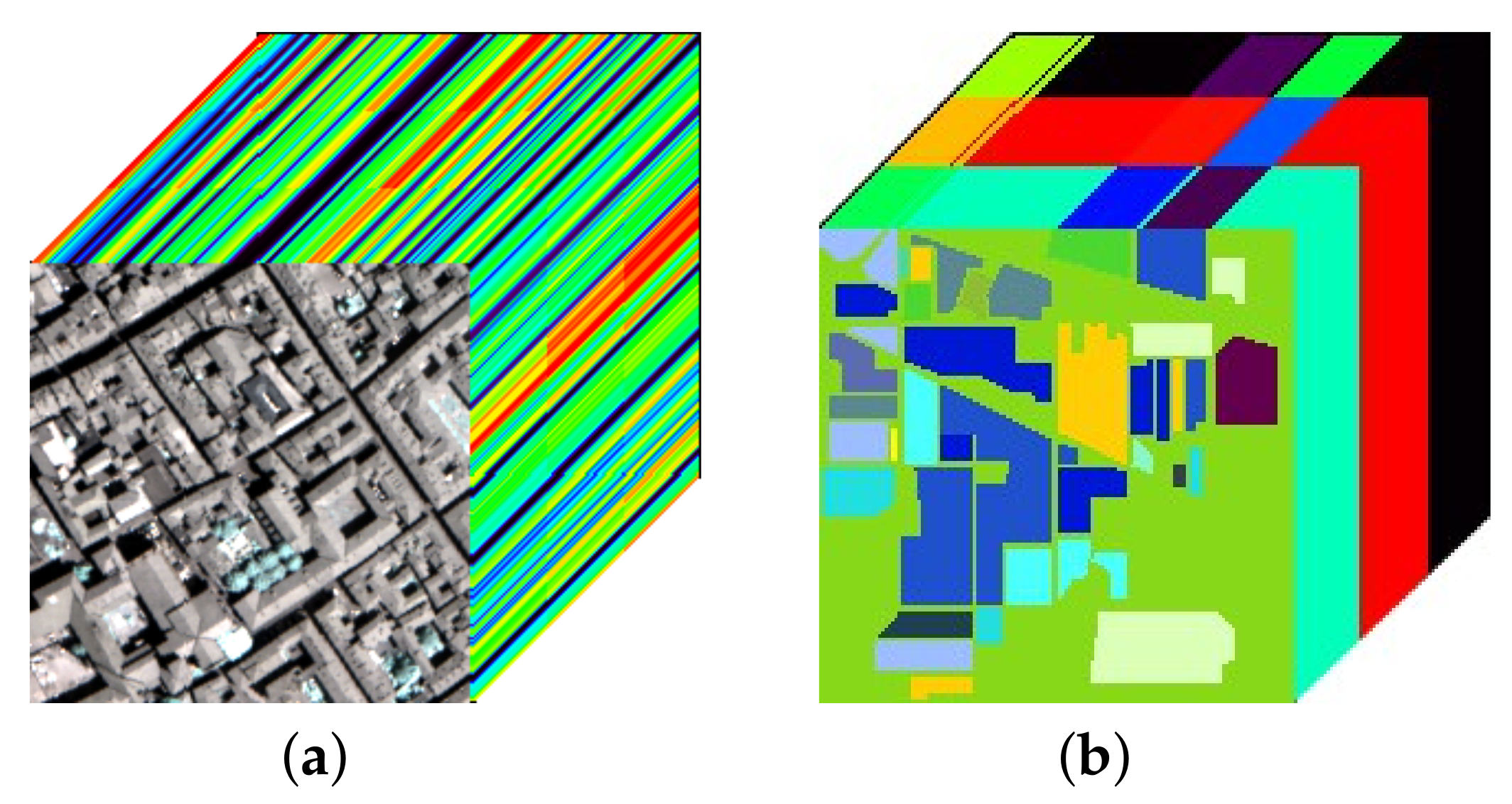
Figure 2.
(a) Pavia City Center dataset, (b) USGS Indian Pines dataset.
Figure 2.
(a) Pavia City Center dataset, (b) USGS Indian Pines dataset.
Figure 3.
(a) Original image, (b) noisy image, image denoised by (c) LRTA, (d) BM4D, (e) LRMR, (f) LRTDTV, (g) L1HyMixDe, (h) LRTDGS, (i) 3DTNN, (j) ours of band 65 in dataset-1, noise case 3.
Figure 3.
(a) Original image, (b) noisy image, image denoised by (c) LRTA, (d) BM4D, (e) LRMR, (f) LRTDTV, (g) L1HyMixDe, (h) LRTDGS, (i) 3DTNN, (j) ours of band 65 in dataset-1, noise case 3.
Figure 4.
(a) Original image, (b) noisy image, image denoised by (c) LRTA, (d) BM4D, (e) LRMR, (f) LRTDTV, (g) L1HyMixDe, (h) LRTDGS, (i) 3DTNN, (j) ours of band 60 in dataset-1, noise case 8.
Figure 4.
(a) Original image, (b) noisy image, image denoised by (c) LRTA, (d) BM4D, (e) LRMR, (f) LRTDTV, (g) L1HyMixDe, (h) LRTDGS, (i) 3DTNN, (j) ours of band 60 in dataset-1, noise case 8.
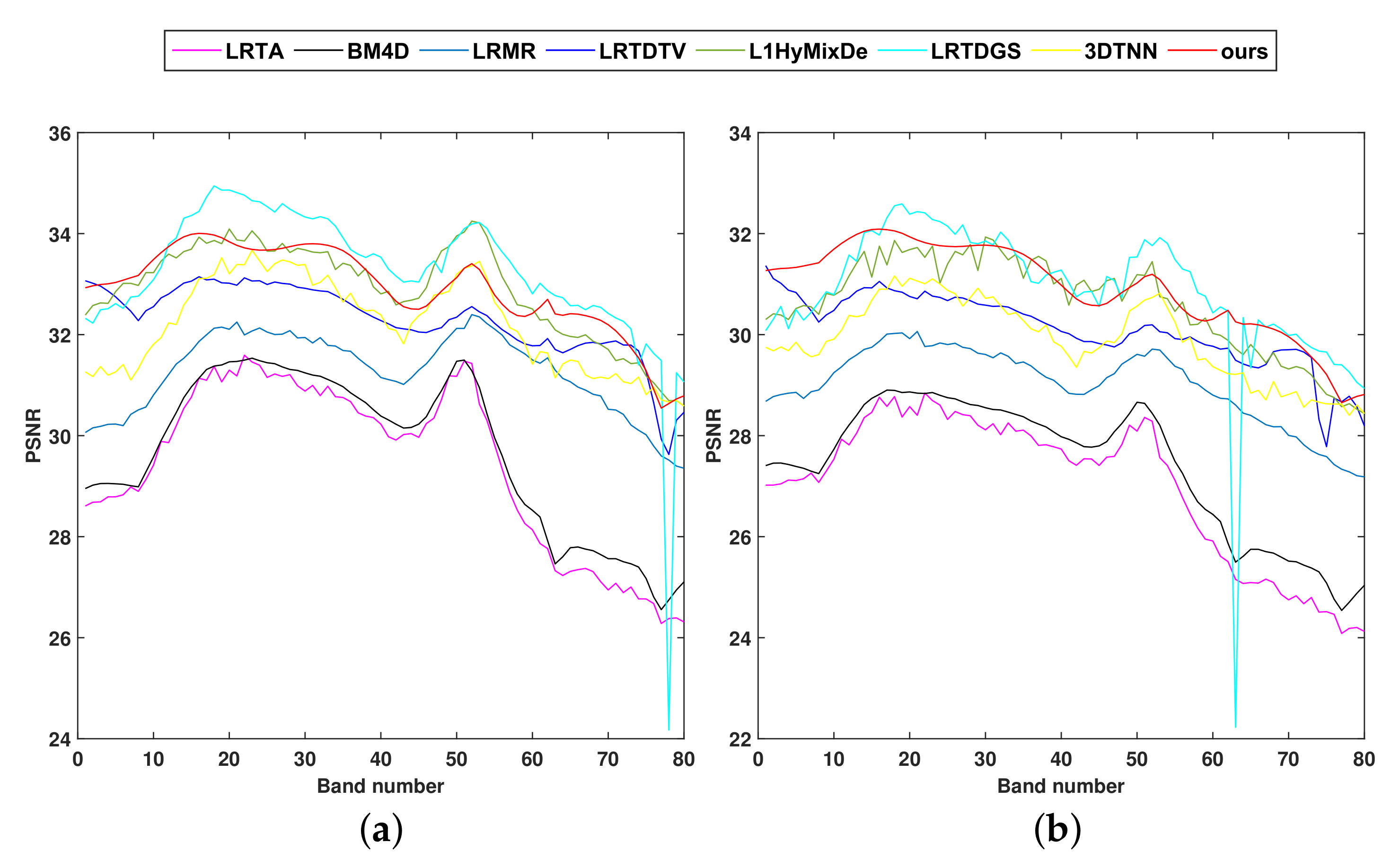
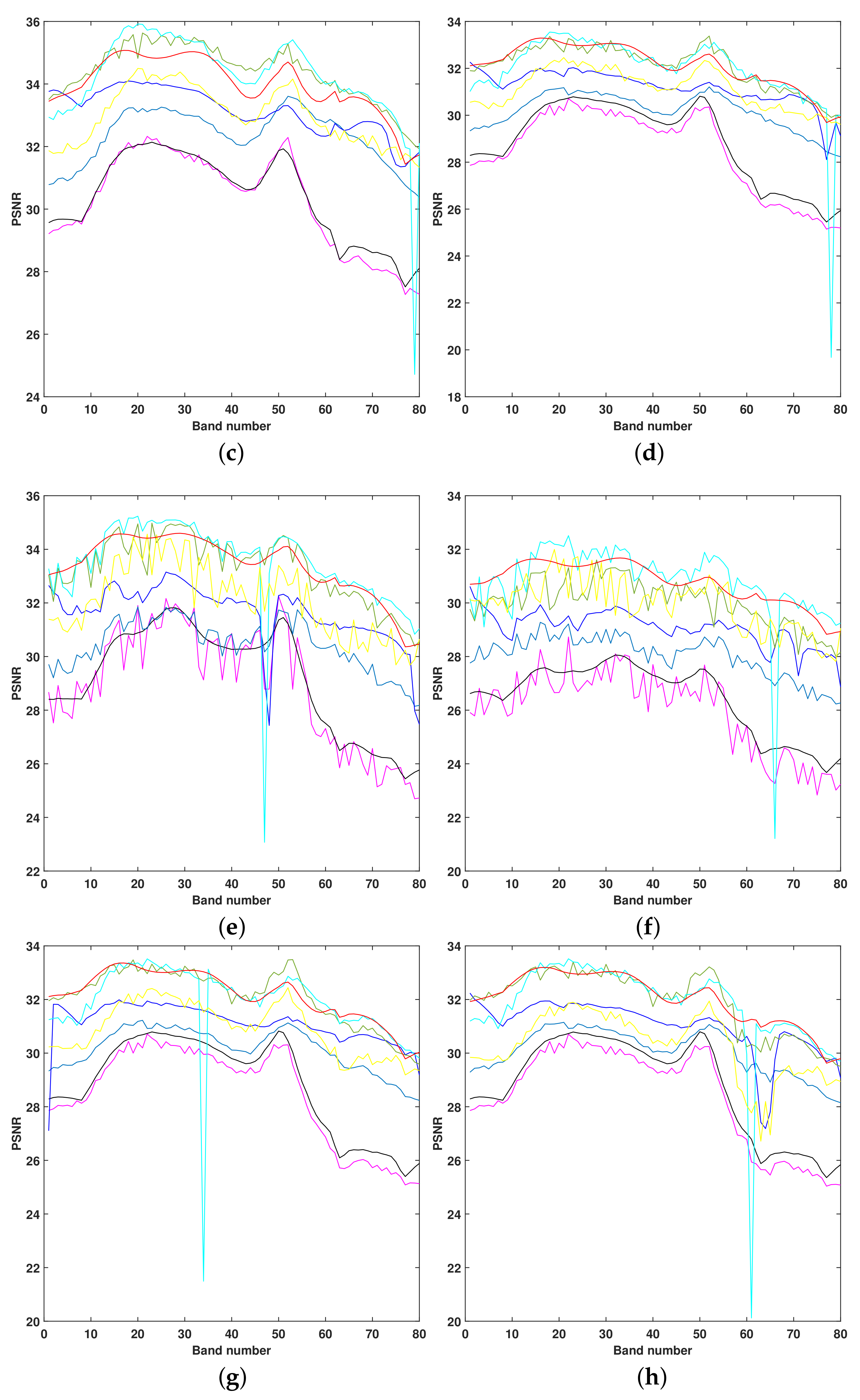
Figure 5.
The PSNR values of each band in dataset-1 after denoising by eight different methods under (a) case 1, (b) case 2, (c) case 3, (d) case 4, (e) case 5, (f) case 6, (g) case 7, (h) case 8.
Figure 5.
The PSNR values of each band in dataset-1 after denoising by eight different methods under (a) case 1, (b) case 2, (c) case 3, (d) case 4, (e) case 5, (f) case 6, (g) case 7, (h) case 8.
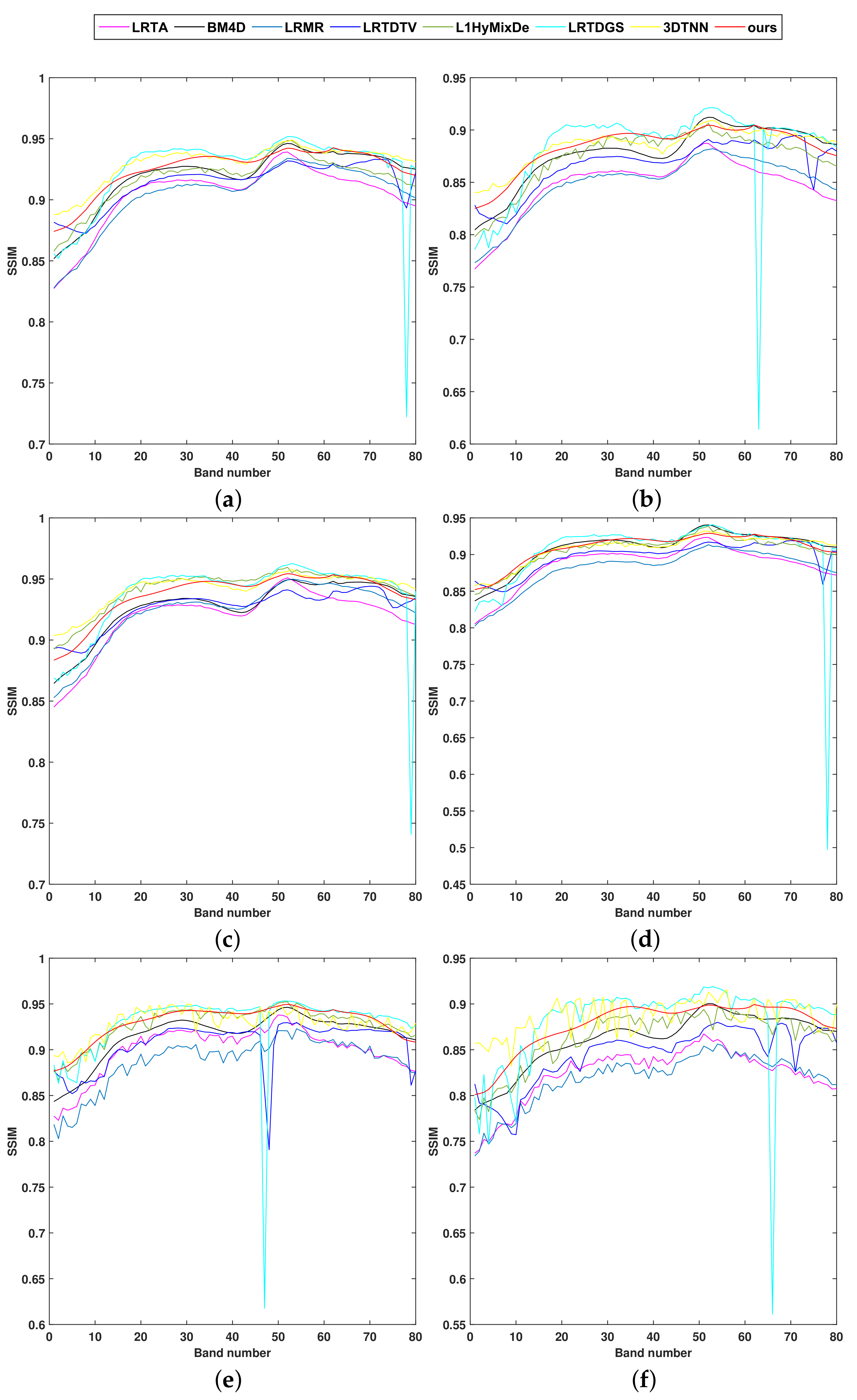
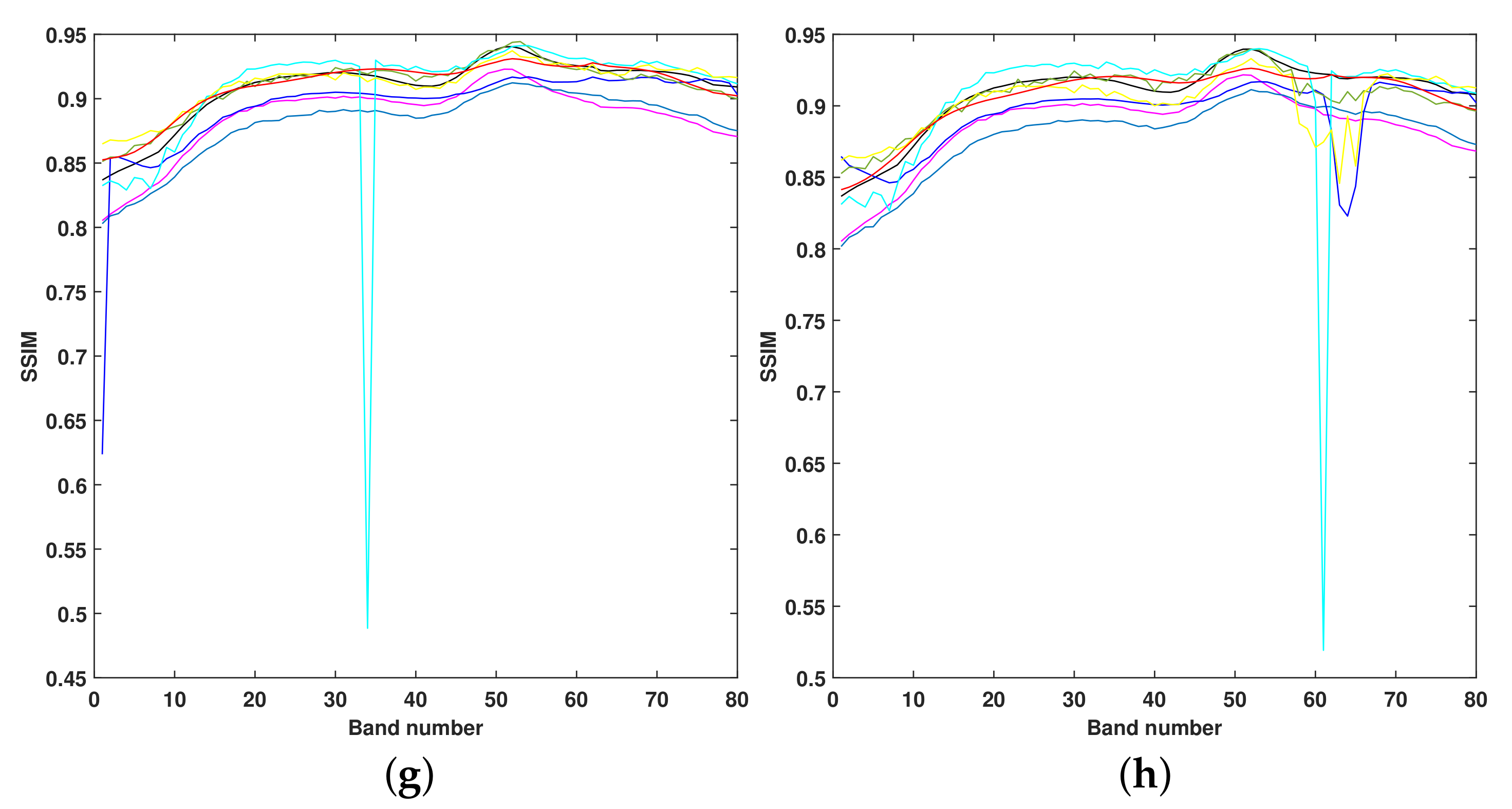
Figure 6.
The SSIM values of each band in dataset-1 after denoising by eight different methods under (a) case 1, (b) case 2, (c) case 3, (d) case 4, (e) case 5, (f) case 6, (g) case 7, (h) case 8.
Figure 6.
The SSIM values of each band in dataset-1 after denoising by eight different methods under (a) case 1, (b) case 2, (c) case 3, (d) case 4, (e) case 5, (f) case 6, (g) case 7, (h) case 8.
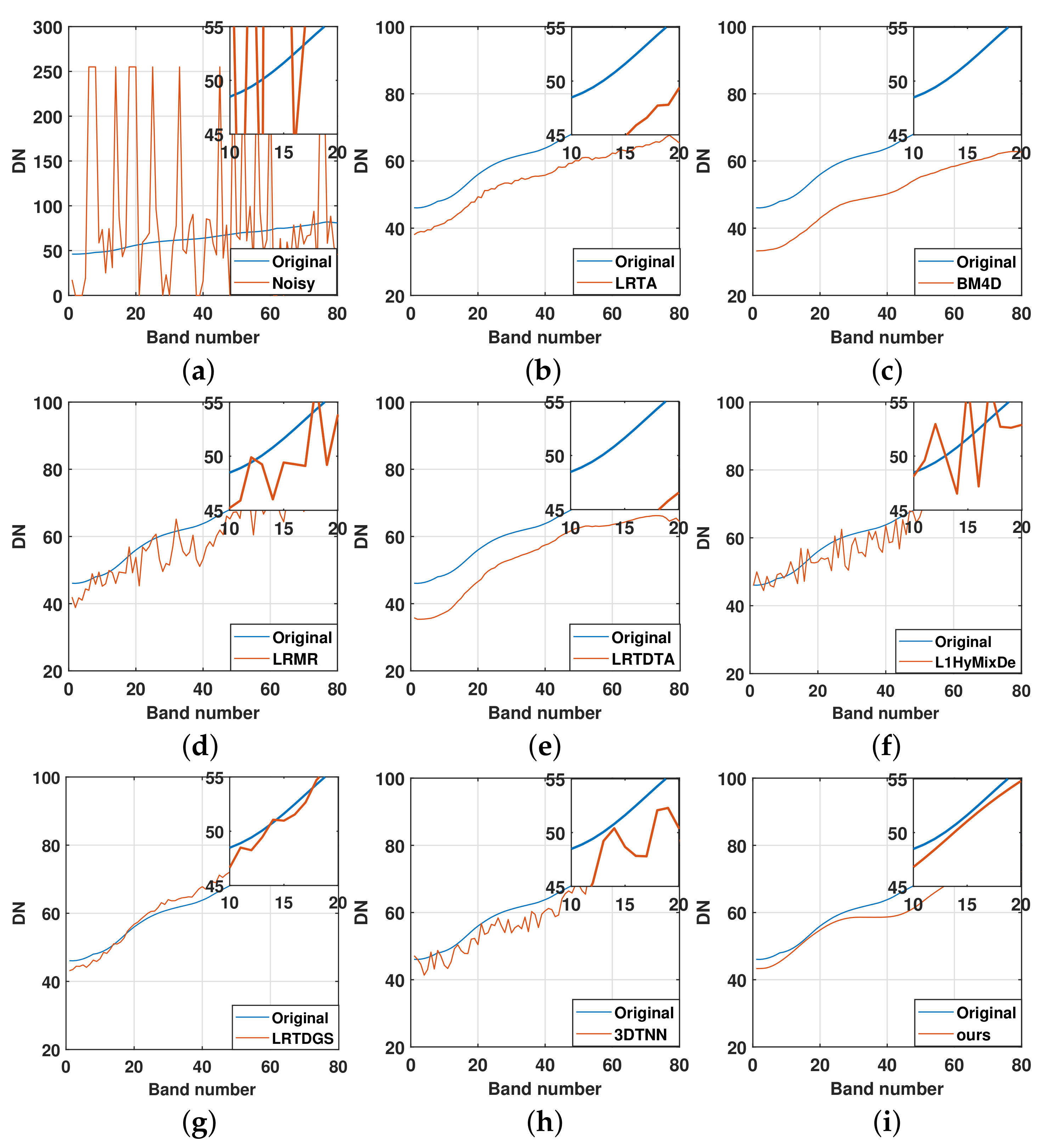
Figure 7.
The reflectance of pixel (30, 30) in (a) noisy dataset-1, dataset-1 denoised by (b) LRTA, (c) BM4D, (d) LRMR, (e) LRTDTV, (f) L1HyMixDe, (g) LRTDGS, (h) 3DTNN, (i) ours under noise case 4.
Figure 7.
The reflectance of pixel (30, 30) in (a) noisy dataset-1, dataset-1 denoised by (b) LRTA, (c) BM4D, (d) LRMR, (e) LRTDTV, (f) L1HyMixDe, (g) LRTDGS, (h) 3DTNN, (i) ours under noise case 4.
Figure 8.
(a) Original image, (b) noisy image, image denoised by (c) 3DTNN, (d) ours of band 26 in the dataset-2, noise case 2.
Figure 8.
(a) Original image, (b) noisy image, image denoised by (c) 3DTNN, (d) ours of band 26 in the dataset-2, noise case 2.
Figure 9.
(a) Original image, (b) noisy image, image denoised by (c) 3DTNN, (d) ours of band 4 in the dataset-2, noise case 5.
Figure 9.
(a) Original image, (b) noisy image, image denoised by (c) 3DTNN, (d) ours of band 4 in the dataset-2, noise case 5.
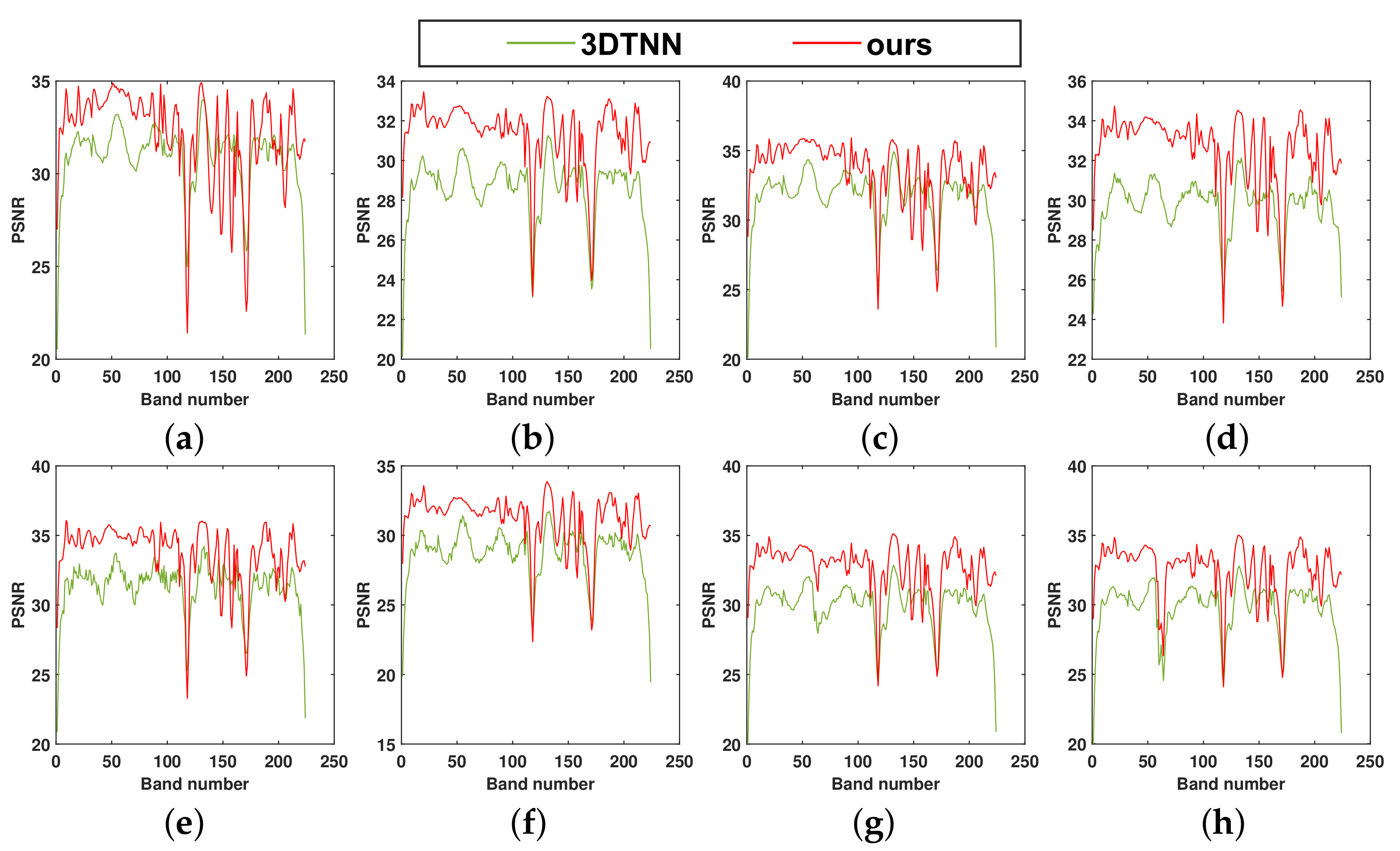
Figure 10.
The PSNR values of each band in the dataset-2 after denoising by 3DTNN and our model under (a) case 1, (b) case 2, (c) case 3, (d) case 4, (e) case 5, (f) case 6, (g) case 7, (h) case 8.
Figure 10.
The PSNR values of each band in the dataset-2 after denoising by 3DTNN and our model under (a) case 1, (b) case 2, (c) case 3, (d) case 4, (e) case 5, (f) case 6, (g) case 7, (h) case 8.
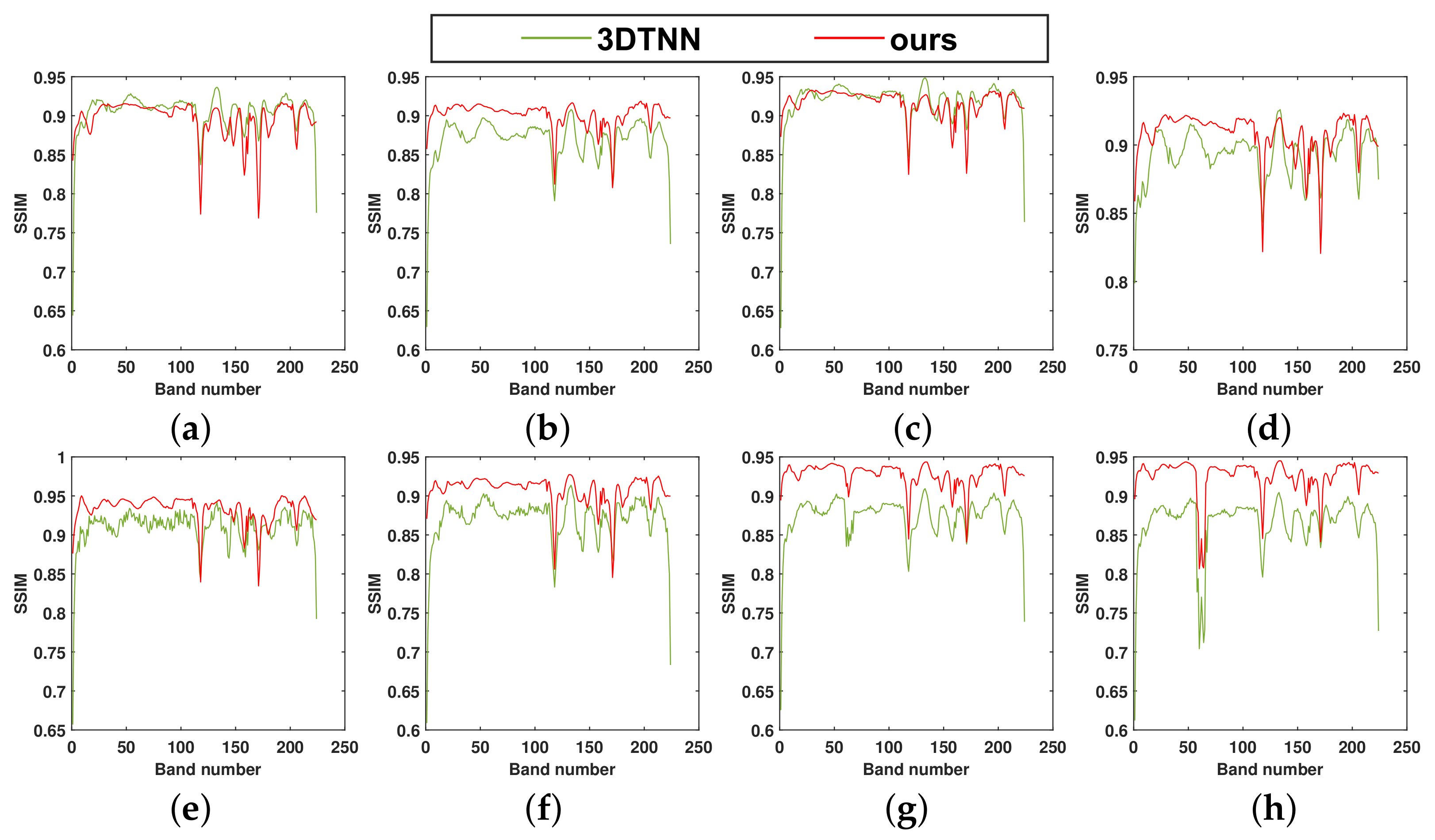
Figure 11.
The SSIM values of each band in the dataset-2 after denoising by 3DTNN and our model under (a) case 1, (b) case 2, (c) case 3, (d) case 4, (e) case 5, (f) case 6, (g) case 7, (h) case 8.
Figure 11.
The SSIM values of each band in the dataset-2 after denoising by 3DTNN and our model under (a) case 1, (b) case 2, (c) case 3, (d) case 4, (e) case 5, (f) case 6, (g) case 7, (h) case 8.
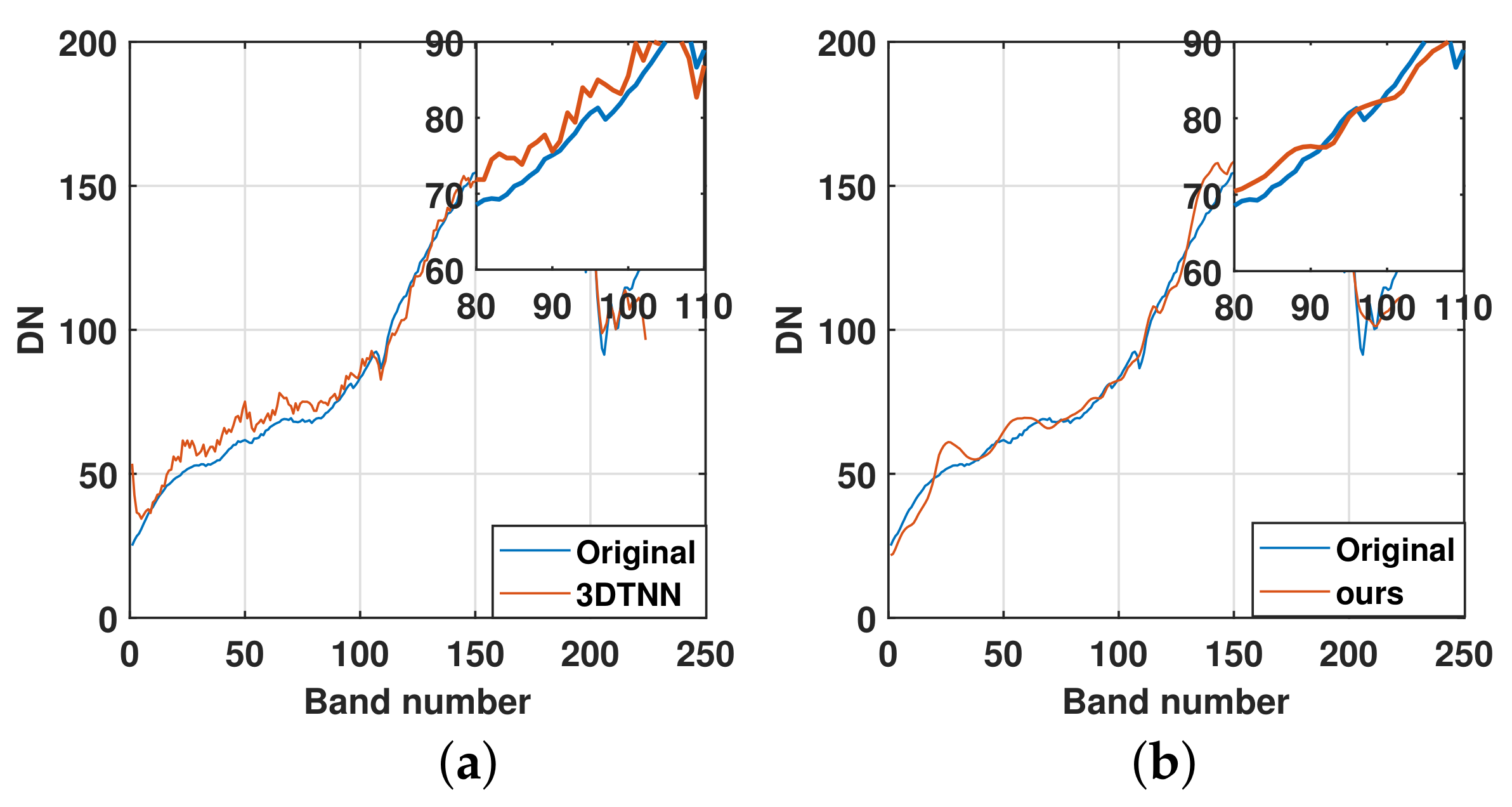
Figure 12.
The reflectance of pixel (100,30) in the dataset-2 denoised by (a) 3DTNN and (b) ours under noise case 3.
Figure 12.
The reflectance of pixel (100,30) in the dataset-2 denoised by (a) 3DTNN and (b) ours under noise case 3.
Figure 13.
(a) AVIRIS Indian Pines dataset, (b) HYDICE Urban dataset.
Figure 13.
(a) AVIRIS Indian Pines dataset, (b) HYDICE Urban dataset.
Figure 14.
(a) Original image, image denoised by (b) LRTA, (c) BM4D, (d) LRMR, (e) LRTDTV, (f) L1HyMixDe, (g) LRTDGS, (h) 3DTNN, (i) ours of band 106 in dataset-3.
Figure 14.
(a) Original image, image denoised by (b) LRTA, (c) BM4D, (d) LRMR, (e) LRTDTV, (f) L1HyMixDe, (g) LRTDGS, (h) 3DTNN, (i) ours of band 106 in dataset-3.
Figure 15.
(a) Original image, image denoised by (b) LRTA, (c) BM4D, (d) LRMR, (e) LRTDTV, (f) L1HyMixDe, (g) LRTDGS, (h) 3DTNN, (i) ours of band 163 in dataset-3.
Figure 15.
(a) Original image, image denoised by (b) LRTA, (c) BM4D, (d) LRMR, (e) LRTDTV, (f) L1HyMixDe, (g) LRTDGS, (h) 3DTNN, (i) ours of band 163 in dataset-3.
Figure 16.
(a) Original image, image denoised by (b) LRTA, (c) BM4D, (d) LRMR, (e) LRTDTV, (f) L1HyMixDe, (g) LRTDGS, (h) 3DTNN, (i) ours of band 104 in dataset-4.
Figure 16.
(a) Original image, image denoised by (b) LRTA, (c) BM4D, (d) LRMR, (e) LRTDTV, (f) L1HyMixDe, (g) LRTDGS, (h) 3DTNN, (i) ours of band 104 in dataset-4.
Figure 17.
(a) Original image, image denoised by (b) LRTA, (c) BM4D, (d) LRMR, (e) LRTDTV, (f) L1HyMixDe, (g) LRTDGS, (h) 3DTNN, (i) ours of band 109 in dataset-4.
Figure 17.
(a) Original image, image denoised by (b) LRTA, (c) BM4D, (d) LRMR, (e) LRTDTV, (f) L1HyMixDe, (g) LRTDGS, (h) 3DTNN, (i) ours of band 109 in dataset-4.
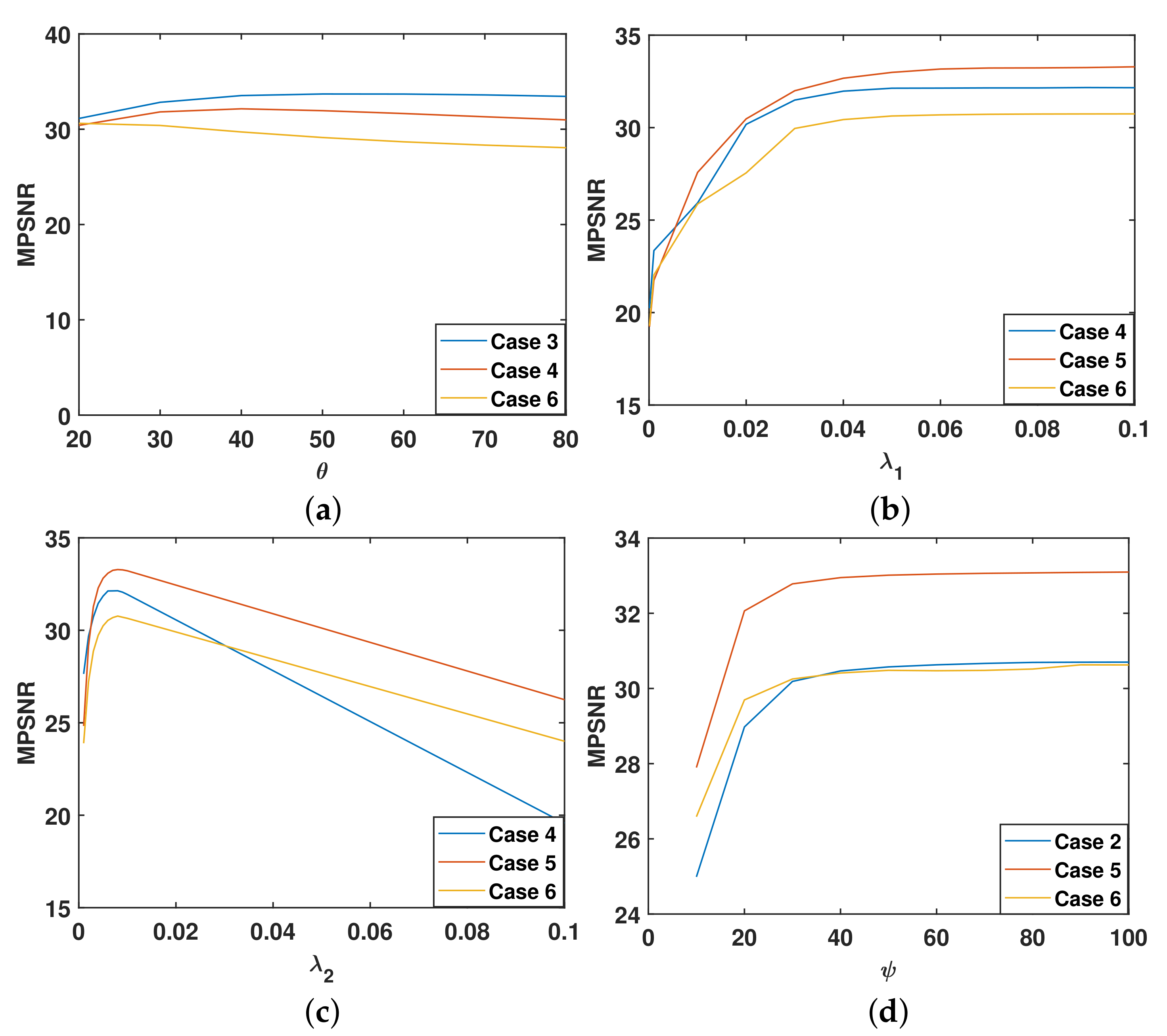
Figure 18.
PSNR values concerning different values of (a) (controls ), (b) , (c) and (d) (controls ).
Figure 18.
PSNR values concerning different values of (a) (controls ), (b) , (c) and (d) (controls ).
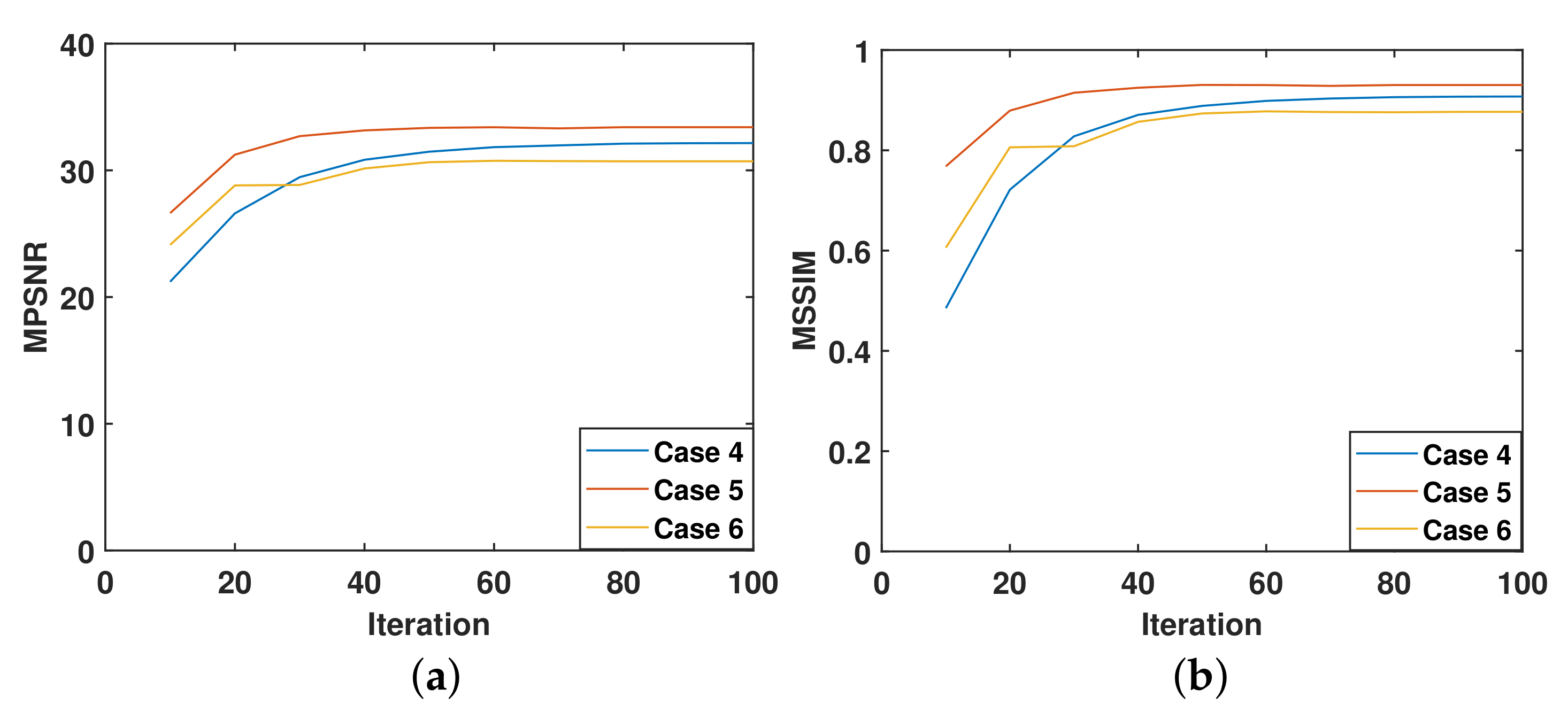
Figure 19.
The change of (a) MPSNR value, (b) MSSIM value with the iteration.
Figure 19.
The change of (a) MPSNR value, (b) MSSIM value with the iteration.
Table 1.
The mean value of fibered rank for three orders by using a different transform.
Table 1.
The mean value of fibered rank for three orders by using a different transform.
| Data | | Transformation | The First Mode | The Second Mode | The Third Mode |
|---|
| Pavia | 0.04 | FFT | 78 | 78 | 188 |
| Framelet | 13 | 13 | 70 |
| 0.05 | FFT | 75 | 75 | 185 |
| Framelet | 10 | 10 | 65 |
| Indian | 0.04 | FFT | 16 | 16 | 106 |
| Framelet | 3 | 3 | 42 |
| 0.05 | FFT | 16 | 16 | 105 |
| Framelet | 3 | 3 | 40 |
Table 2.
The details of the eight noise cases.
Table 2.
The details of the eight noise cases.
| Noise | Gaussian Noise | Impulse Noise | Deadline Noise | Stripe Noise |
|---|
| Case 1 | mean value = 0, variance = 0.1 | percentage = 0.2 | \ | \ |
| Case 2 | mean value = 0, variance = 0.15 | percentage = 0.2 | \ | \ |
| Case 3 | mean value = 0, variance = 0.1 | percentage = 0.1 | \ | \ |
| Case 4 | mean value = 0, variance = 0.1 | percentage = 0.3 | \ | \ |
| Case 5 | mean value = 0, variance ∼ U(0.05, 0.15) | percentage = 0.2 | \ | \ |
| Case 6 | mean value = 0, variance ∼ U(0.1, 0.2) | percentage = 0.2 | \ | \ |
| Case 7 | mean value = 0 | percentage = 0.3 | 10% of the bands | \ |
| variance = 0.1 | number ∼ U(1, 4) | \ |
| Case 8 | mean value = 0 | percentage = 0.3 | 10% of the bands | 10% of the bands |
| variance = 0.1 | number ∼ U(1, 4) | number ∼ U(20, 40) |
Table 3.
The value of quantitative indices in the dataset-1.
Table 3.
The value of quantitative indices in the dataset-1.
| Noise Case | Level | Evaluation Index | LRTA | BM4D | LRMR | LRTDT | L1HyMixDe | LRTDGS | 3DTNN | Our |
|---|
| Case 1 | | MPSNR | 29.4396 | 29.7014 | 31.2593 | 32.2970 | 32.9077 | 33.2535 | 32.1996 | 32.9243 |
| G = 0.1 | MSSIM | 0.9048 | 0.9203 | 0.9045 | 0.9138 | 0.9177 | 0.9253 | 0.9307 | 0.9256 |
| P = 0.2 | SAM | 6.8049 | 5.8404 | 6.8244 | 4.9305 | 4.4064 | 4.3546 | 3.4856 | 3.7368 |
| Case 2 | | MPSNR | 27.0258 | 27.4204 | 29.0133 | 30.1107 | 30.6235 | 30.9044 | 29.8947 | 30.9274 |
| G = 0.15; | MSSIM | 0.8480 | 0.8787 | 0.8494 | 0.8669 | 0.8745 | 0.8833 | 0.8854 | 0.8857 |
| P = 0.2 | SAM | 7.8247 | 6.6710 | 7.6899 | 5.8480 | 4.9587 | 5.4792 | 4.2935 | 4.4098 |
| Case 3 | | MPSNR | 30.2658 | 30.3936 | 32.3389 | 33.1557 | 34.3770 | 34.2453 | 32.9942 | 33.9806 |
| G = 0.1 | MSSIM | 0.9190 | 0.9281 | 0.9237 | 0.9267 | 0.9421 | 0.9374 | 0.9423 | 0.9477 |
| P = 0.1 | SAM | 6.4482 | 5.5052 | 6.4019 | 4.6077 | 3.5472 | 4.0836 | 3.1475 | 3.6220 |
| Case 4 | | MPSNR | 28.4836 | 28.8640 | 30.1731 | 31.1878 | 32.1109 | 31.9825 | 31.1434 | 32.1440 |
| G = 0.1 | MSSIM | 0.8868 | 0.9098 | 0.8814 | 0.8972 | 0.9068 | 0.9057 | 0.9088 | 0.9099 |
| P = 0.3 | SAM | 7.2045 | 6.2362 | 7.2500 | 5.3489 | 4.7865 | 5.4171 | 4.3108 | 4.1209 |
| Case 5 | | MPSNR | 28.9336 | 29.1991 | 30.4432 | 31.6456 | 33.2988 | 33.5211 | 32.1036 | 33.8946 |
| G = (0.05,0.15) | MSSIM | 0.9003 | 0.9161 | 0.8880 | 0.9062 | 0.9283 | 0.9293 | 0.9293 | 0.9302 |
| P = 0.2 | SAM | 7.1954 | 6.0548 | 7.1967 | 5.2504 | 4.2118 | 4.2629 | 3.6644 | 3.8739 |
| Case 6 | | MPSNR | 26.0073 | 26.4507 | 28.0358 | 29.0656 | 30.0129 | 30.8340 | 29.9707 | 30.7688 |
| G = (0.1,0.2) | MSSIM | 0.8239 | 0.8621 | 0.8188 | 0.8452 | 0.8640 | 0.8808 | 0.8859 | 0.8777 |
| P = 0.2 | SAM | 8.3887 | 6.9711 | 8.1535 | 6.4062 | 5.5859 | 5.5074 | 4.5080 | 4.2183 |
| Case 7 | G = 0.1 | MPSNR | 28.4375 | 28.8168 | 30.1479 | 31.1278 | 32.1303 | 31.9213 | 30.9232 | 32.1686 |
| P = 0.3 | MSSIM | 0.8863 | 0.9095 | 0.8812 | 0.8951 | 0.9108 | 0.9079 | 0.9123 | 0.9167 |
| +deadline | SAM | 7.2212 | 6.2393 | 7.2828 | 5.3694 | 6.6968 | 6.7940 | 5.2777 | 4.1205 |
| Case 8 | G = 0.1 P = 0.3 | MPSNR | 28.3902 | 28.7718 | 30.0586 | 31.0073 | 31.9432 | 31.8225 | 30.2764 | 32.0232 |
| +deadline | MSSIM | 0.8852 | 0.9088 | 0.8798 | 0.8939 | 0.9075 | 0.9068 | 0.9027 | 0.9063 |
| +stripe | SAM | 7.2192 | 6.2496 | 7.3609 | 5.6445 | 6.9130 | 7.1390 | 5.7186 | 4.3586 |
Table 4.
The value of quantitative indices in the dataset-2.
Table 4.
The value of quantitative indices in the dataset-2.
| Noise Case | Level | MPSNR | 3DTNN MSSIM | SAM | MPSNR | Our MSSIM | SAM |
|---|
| Case 1 | G = 0.1 | 30.9073 | 0.9050 | 2.7583 | 32.1435 | 0.8964 | 2.7254 |
| P = 0.2 |
| Case 2 | G = 0.15 | 28.5602 | 0.8697 | 3.5259 | 31.3247 | 0.9013 | 2.5945 |
| P = 0.2 |
| Case 3 | G = 0.1 | 31.6945 | 0.9185 | 2.5888 | 33.6358 | 0.9170 | 2.2334 |
| P = 0.1 |
| Case 4 | G = 0.1 | 29.7186 | 0.8931 | 2.8884 | 32.5633 | 0.9080 | 2.3556 |
| P = 0.3 |
| Case 5 | G = (0.05,0.15) | 31.2729 | 0.9089 | 2.6462 | 33.7245 | 0.9329 | 2.1341 |
| P = 0.2 |
| Case 6 | G = (0.1,0.2) | 28.7189 | 0.8699 | 3.5476 | 31.2484 | 0.9076 | 2.6554 |
| P = 0.2 |
| Case 7 | G = 0.1 P = 0.3 | 29.9070 | 0.8747 | 3.1159 | 32.7050 | 0.9274 | 2.2178 |
| +deadline |
| Case 8 | G = 0.1 P = 0.3 | 29.7521 | 0.8653 | 3.2478 | 32.5152 | 0.9256 | 2.3006 |
| +deadline +stripe |
Table 5.
The ablation experiment of F-3MTNN.
Table 5.
The ablation experiment of F-3MTNN.
| Spatial Information | Spectral Information | PSNR | SSIM |
|---|
| ✓ | | 21.7398 | 0.3938 |
| | ✓ | 25.8850 | 0.7504 |
| ✓ | ✓ | 30.9274 | 0.8857 |
Table 6.
The running time (in seconds) of the different methods in the real HSI dataset experiments.
Table 6.
The running time (in seconds) of the different methods in the real HSI dataset experiments.
| HSI Data | LRTA | BM4D | LRMR | LRTDTV | L1HyMixDe | LRTDGS | 3DTNN | Our |
|---|
| AVIRIS Indian Pines | 35 | 261 | 412 | 131 | 4 | 123 | 87 | 1259 |
| HYDICE Urban | 143 | 4076 | 6132 | 960 | 7 | 811 | 1503 | 6602 |