Bathymetric-Based Band Selection Method for Hyperspectral Underwater Target Detection
Abstract
:1. Introduction
- We develop a novel unsupervised spectral representation learning scheme to generate the physically meaningful subspace as the reference for band selection, which is devoted to tackling the issue of insufficient labelled samples and the interference of water environment in hyperspectral underwater detection task.
- Considering the diversity of band selection result, we establish an iteration-based band subset generation strategy to select out the distinct band subsets based on different subspaces. Meanwhile, this strategy also contributes greatly to making full use of spectral information.
- To decrease the redundancy in band subsets, we design a sparse representation method to pick out the representative bands. Then, all of these representative bands are utilized to generate the final band selection result with specific band sequence.
2. Preliminaries
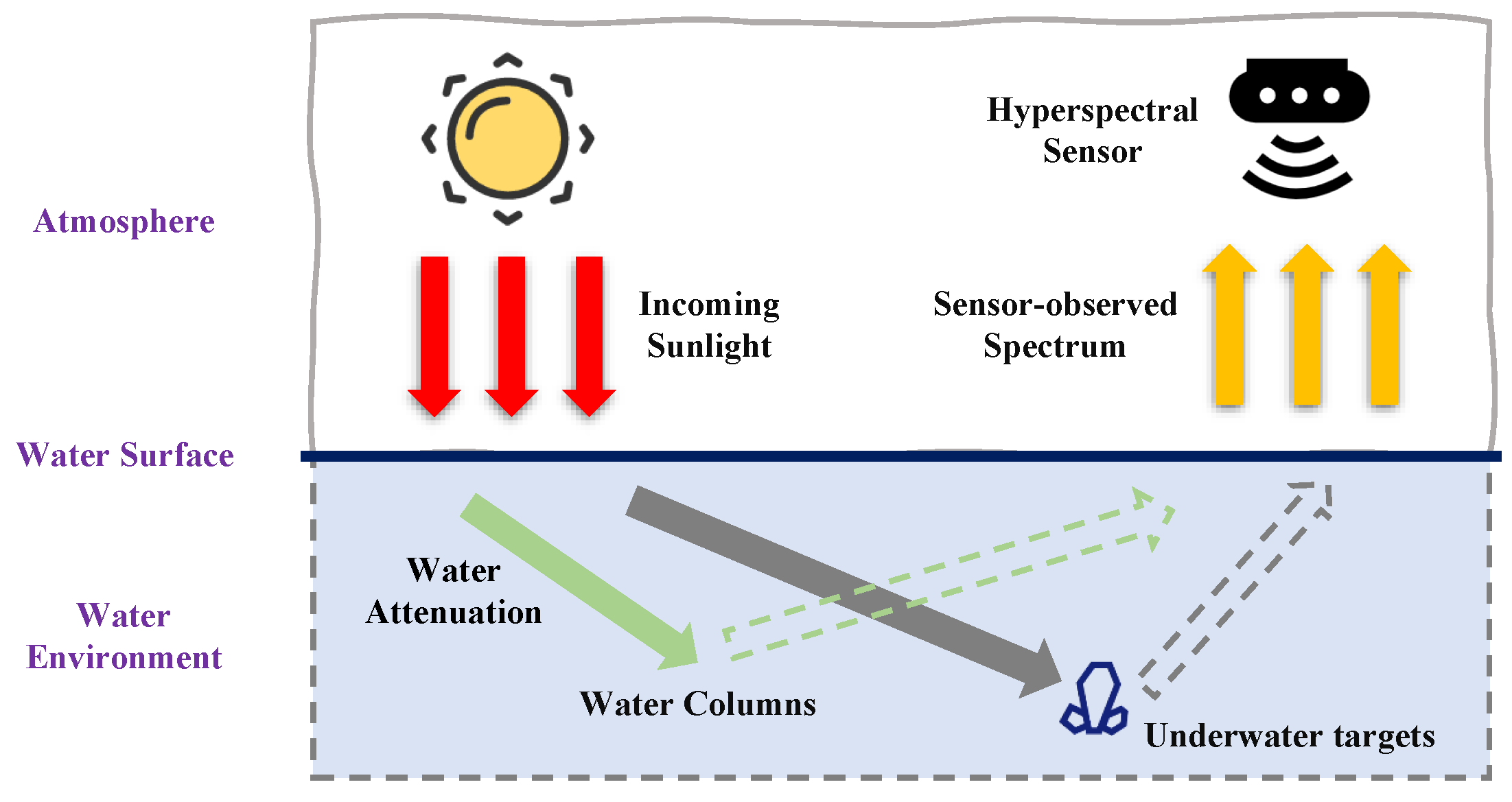
2.1. Bathymetric Model
2.2. Autoencoder
3. Methodology
3.1. Bathymetric Latent Spectral Representation Learning
3.2. Diversified Band Subsets Generation
3.3. Representative Bands Selection
| Algorithm 1 The total process of the proposed method |
| Input: HSI , band subset size control factor and sparse degree control factor q |
| Output: Band selection result for hyperspectral underwater target detection |
| 1: Establish an autoencoder with bathymetric model according to Equation (5). |
| 2: Train autoencoder with HSI to minimize Equation (6). |
| 3: Exploit the encoder part of to generate the bathymetric-based subspace . |
| 4: Transform the HSI into a hyperspectral bands set . |
| 5: . |
| 6: while the terminal condition in Equation (8) is not satisfied do |
| 7: Produce the t-th band subset from with subspace with Equation (7); |
| 8: Update the hyperspectral bands set based on:
|
| 9: |
| 10: Train autoencoder with hyperspectral bands set to minimize Equation (6). |
| 11: Use the encoder part of to yield a new bathymetric-based subspace from hyperspectral bands set ; |
| 12: end while |
| 13: for do |
| 14: Compute the sparse form of band subset according to Equation (13); |
| 15: Select out the bands whose sparse coefficients are nonzero values as representative bands for band subset . |
| 16: end for |
| 17: Concatenate the representative bands of all the band subsets with the original band sequence to generate final band selection result. |
4. Experiments
4.1. Dataset Description
| Algorithm 2 The process of generating experimental datasets |
| Input: Real-world underwater HSI set , water attenuation coefficient |
| Output: Underwater target detection data sets |
| 1: for real-world underwater HSI do |
| 2: Acquire the water column spectrum by calculating the mean vector of real-world underwater HSI ; |
| 3: Select the spectra of one specific material from USGS spectral library [37] as the desired target spectrum ; |
| 4: Produce the four distinct underwater target spectra with the water column spectrum , desired target spectrum and four different depth information H according to Equation (1); |
| 5: Embed the generated target spectra into the real-world underwater HSI at different spatial locations. |
| 6: end for |
4.2. Experimental Details
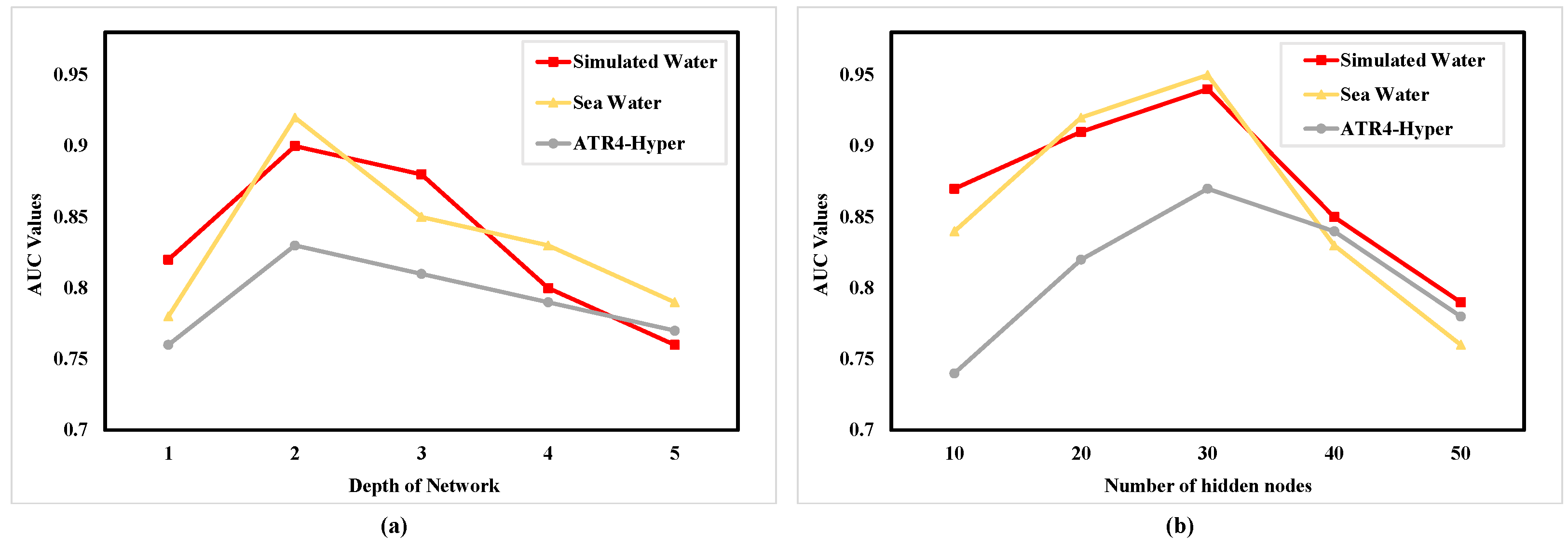
4.3. Ablation Study
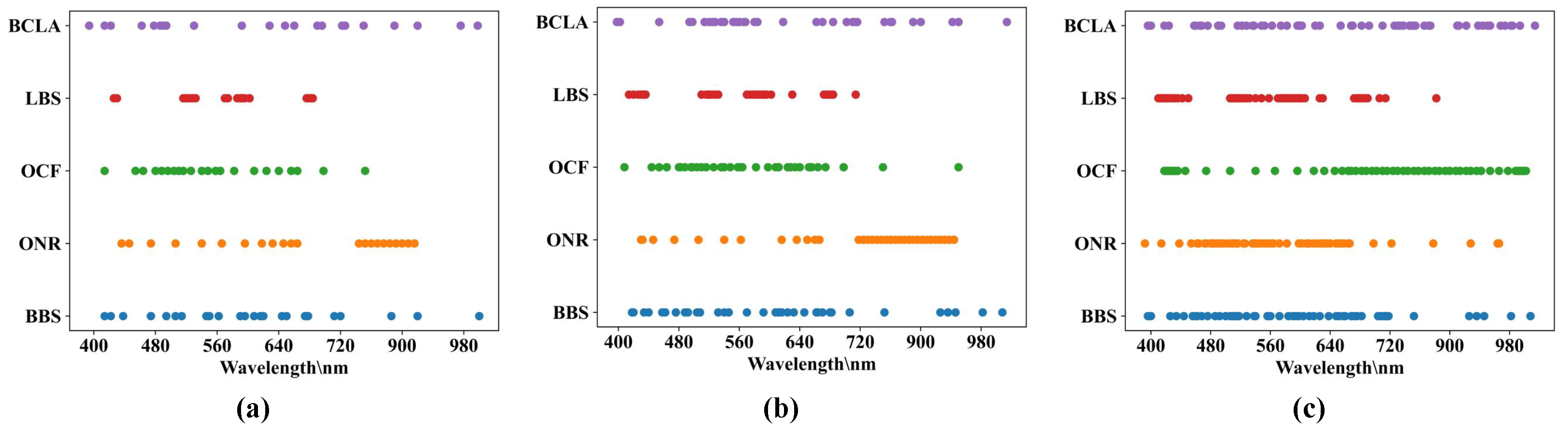
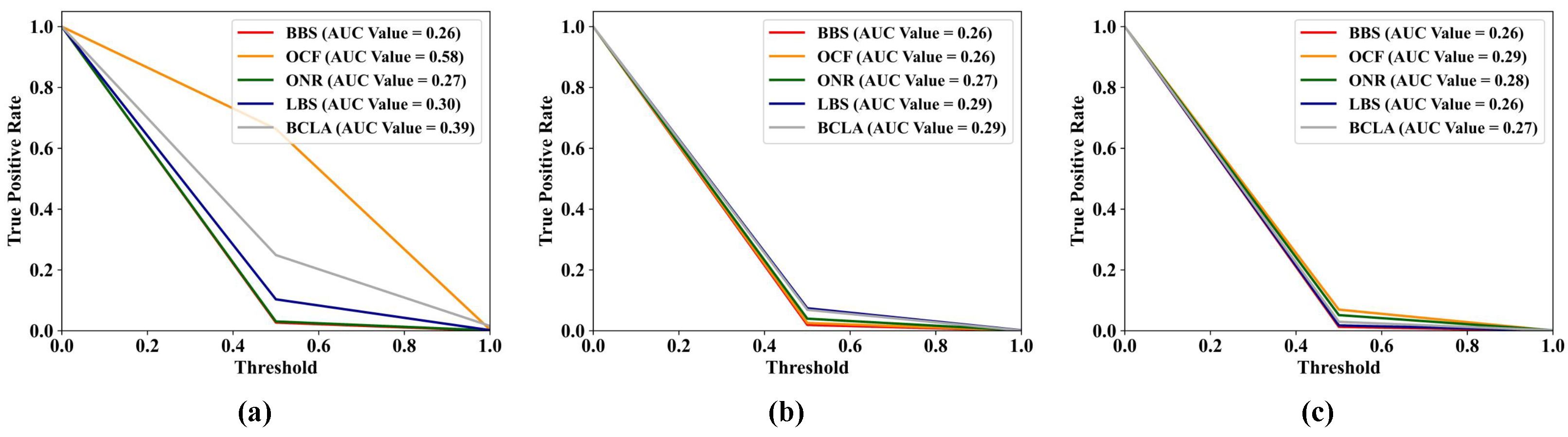
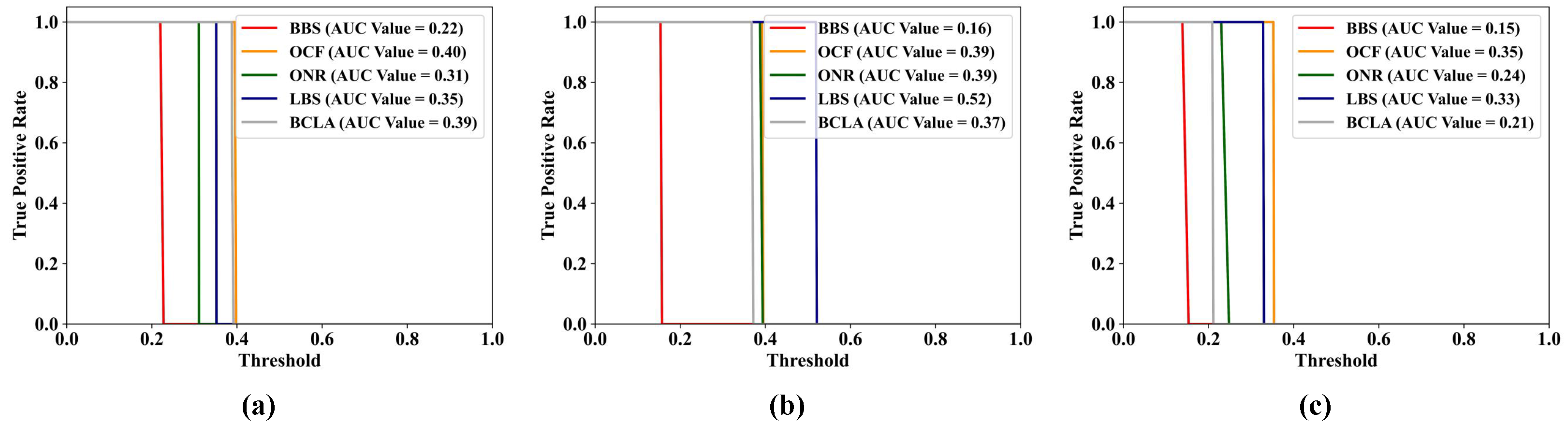
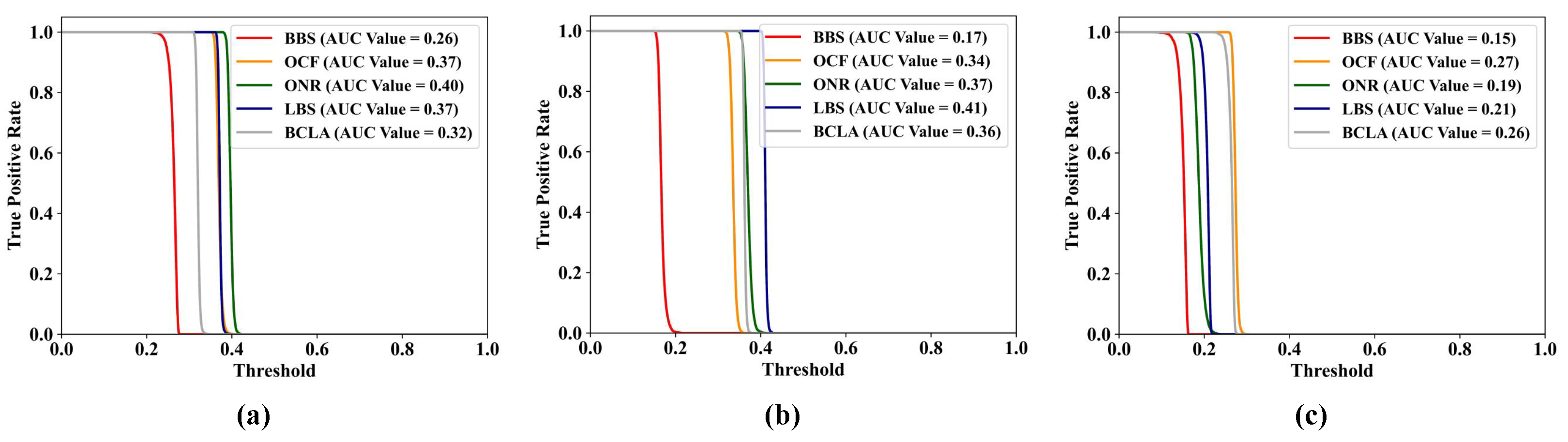
4.4. Band Selection Performances and Discussion
4.5. The Limitation of Our Study
- 1.
- The proposed method can only be applied in deep-water scenarios. The employed physical model (underwater bathymetric model in Equation (1)) in this paper is based on the assumption that the hyperspectral sensor will capture the reflectance deprived by the sea bottom. Thus, our proposed method does not consider the effects of the sea bottom and is proposed for deep-underwater scenarios. Consequently, the practical application scenario of our proposed method is limited, and we will attempt to modify the physical model to improve the generalization of our proposed method in future research.
- 2.
- The proposed method leads to more burden on time and memory. Based on Table 8, we can find that the time burden of BBS refers to the heaviest one among all the comparison methods, since an iteration-based strategy is designed to promote the performance of the band selection results. Deep learning methodology is also exploited in our research work, and the method requires more computational memory and resource.
- 3.
- The proposed method refers to a two-stage band selection method. The process of our proposed method can be divided into two stages: diversified band subset generation and representative band selection. There is no doubt that the performance of diversified band subset generation will affect the the performance of representative band selection, which might eventually undermine the final band selection results.
5. Conclusions
- , the product of depth information and water attenuation coefficient, comes to be an excellent metric for designing band selection criterion. First of all, target pixels and background pixels possess different values, then can be regarded as a preeminent feature to differentiate these two kinds of pixels. Furthermore, compared with the depth information and water attenuation coefficient, our research found that it was easy to determine in an unsupervised manner. In other words, performed well in real-world applications.
- Making full use of the unselected bands contributes greatly to the diversify and the performance of band selection result. Most of the existing band selection methods merely select the bands from input HSI at a time and then discard the unselected bands. In our research, the experimental results in Table 3 confirm that iteratively selecting out bands from the input HSI had a better performance than selecting the bands from the input HSI at a time. More generally, it is more rational to select a few bands many times instead of picking out plenty of bands only once. Therefore, we believe that designing the band selection method in a iteration manner can be a useful trick to promote band selection performance.
- Representative band selection helps to reduce the redundancy of band selection result. Due the high spectral resolution of HSI, the band selection results always contain plentiful redundant information, which leads to long processing times and bad band selection performance. To tackle this issue, we proposed a representative band selection strategy based on the detection results, and the relevant experimental results in Table 4 and Table 5 validate the effectiveness of this proposed strategy. On the basis of the above results, it is necessary to exploit the representative band selection method to post-processing the band selection results, especially for cluster-based band selection methods. It remains an interesting research topic regarding how to merge the band selection process and the redundant information reduction process into an entire whole.
- Compared with other testing methods, our proposed method can take full advantage of the target spectrum information. In the representative band selection strategy, we employed the prior target information as guidance to determine the proper representative bands. Prior target information makes the selected bands more appropriate for underwater target detection task. Moreover, since the band selection method is proposed to promote the performance of underwater target detection results, prior target information may play a more important role than other prior information.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral Imaging: A Review on UAV-Based Sensors, Data Processing and Applications for Agriculture and Forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Li, W.; Su, H.; Liu, K. Spectral-Spatial Classification of Hyperspectral Image Based on Kernel Extreme Learning Machine. Remote Sens. 2014, 6, 5795–5814. [Google Scholar] [CrossRef] [Green Version]
- Liang, H.; Li, Q. Hyperspectral Imagery Classification Using Sparse Representations of Convolutional Neural Network Features. Remote Sens. 2016, 8, 99. [Google Scholar] [CrossRef] [Green Version]
- Gong, Z.; Zhong, P.; Hu, W. Statistical Loss and Analysis for Deep Learning in Hyperspectral Image Classification. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 322–333. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, K.; Geng, X.; Ji, L.; Lu, Y. A New Band Selection Method for Hyperspectral Image Based on Data Quality. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2014, 7, 2697–2703. [Google Scholar] [CrossRef]
- Su, P.; Tarkoma, S.; Pellikka, P.K.E. Band Ranking via Extended Coefficient of Variation for Hyperspectral Band Selection. Remote Sens. 2020, 12, 3319. [Google Scholar] [CrossRef]
- Jiao, C.; Chen, C.; McGarvey, R.G.; Bohlman, S.; Jiao, L.; Zare, A. Multiple instance hybrid estimator for hyperspectral target characterization and sub-pixel target detection. ISPRS J. Photogramm. Remote Sens. 2018, 146, 235–250. [Google Scholar] [CrossRef] [Green Version]
- Xie, W.; Lei, J.; Yang, J.; Li, Y.; Du, Q.; Li, Z. Deep Latent Spectral Representation Learning-Based Hyperspectral Band Selection for Target Detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2015–2026. [Google Scholar] [CrossRef]
- Luo, G.; Chen, G.; Tian, L.; Qin, K.; Qian, S.-E. Minimum Noise Fraction versus Principal Component Analysis as a Preprocessing Step for Hyperspectral Imagery Denoising. Can. J. Remote Sens. 2016, 42, 106–116. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Nascimento, J.M.P. Hyperspectral Subspace Identification. IEEE Trans. Geosci. Remote Sens. 2008, 46, 435–2445. [Google Scholar] [CrossRef] [Green Version]
- Jing, W.; Chein, I.C. Independent component analysis-based dimensionality reduction with applications in hyperspectral image analysis. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1586–1600. [Google Scholar] [CrossRef]
- Bruce, L.M.; Koger, C.H.; Jiang, L. Dimensionality reduction of hyperspectral data using discrete wavelet transform feature extraction. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2331–2338. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Benediktsson, J.A. Feature Extraction of Hyperspectral Images With Image Fusion and Recursive Filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3742–3752. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Q.; Li, X. An Efficient Clustering Method for Hyperspectral Optimal Band Selection via Shared Nearest Neighbor. Remote Sens. 2019, 11, 350. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Song, M.; Chang, C.-I. Band Subset Selection for Hyperspectral Image Classification. Remote Sens. 2018, 10, 113. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Jiang, M.; Li, W.; Liu, Y. A Symmetric Sparse Representation Based Band Selection Method for Hyperspectral Imagery Classification. Remote Sens. 2016, 8, 238. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Lin, J.; Wang, Q. Dual-Clustering-Based Hyperspectral Band Selection by Contextual Analysis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1431–1445. [Google Scholar] [CrossRef]
- Jia, S.; Tang, G.; Zhu, J.; Li, Q. A Novel Ranking-Based Clustering Approach for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 88–102. [Google Scholar] [CrossRef]
- Li, W.; Prasad, S.; Fowler, J.E.; Bruce, L.M. Locality-Preserving Dimensionality Reduction and Classification for Hyperspectral Image Analysis. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1185–1198. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; He, Y.; Zhou, N.; Zheng, Y. Semisupervised Dimensionality Reduction of Hyperspectral Images via Local Scaling Cut Criterion. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1547–1551. [Google Scholar] [CrossRef]
- MartÍnez-UsÓMartinez-Uso, A.; Pla, F.; Sotoca, J.M.; GarcÍa-Sevilla, P. Clustering-Based Hyperspectral Band Selection Using Information Measures. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4158–4171. [Google Scholar] [CrossRef]
- Cao, X.; Xiong, T.; Jiao, L. Supervised Band Selection Using Local Spatial Information for Hyperspectral Image. IEEE Geosci. Remote Sens. Lett. 2016, 13, 329–333. [Google Scholar] [CrossRef]
- Yang, H.; Du, Q.; Su, H.; Sheng, Y. An Efficient Method for Supervised Hyperspectral Band Selection. IEEE Geosci. Remote Sens. Lett. 2011, 8, 138–142. [Google Scholar] [CrossRef]
- Feng, J.; Jiao, L.; Liu, F.; Sun, T.; Zhang, X. Mutual-Information-Based Semi-Supervised Hyperspectral Band Selection With High Discrimination, High Information, and Low Redundancy. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2956–2969. [Google Scholar] [CrossRef]
- Gong, M.; Zhang, M.; Yuan, Y. Unsupervised Band Selection Based on Evolutionary Multiobjective Optimization for Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 544–557. [Google Scholar] [CrossRef]
- Chein, I.C.; Su, W. Constrained band selection for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1575–1585. [Google Scholar] [CrossRef]
- Geng, X.; Sun, K.; Ji, L.; Zhao, Y. A Fast Volume-Gradient-Based Band Selection Method for Hyperspectral Image. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7111–7119. [Google Scholar] [CrossRef]
- Qi, J.; Gong, Z.; Xue, W.; Liu, X.; Yao, A.; Zhong, P. An Unmixing-Based Network for Underwater Target Detection From Hyperspectral Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5470–5487. [Google Scholar] [CrossRef]
- Wei, X.; Zhu, W.; Liao, B.; Cai, L. Matrix-Based Margin-Maximization Band Selection With Data-Driven Diversity for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7294–7309. [Google Scholar] [CrossRef]
- Jay, S.; Guillaume, M.; Blanc-Talon, J. Underwater Target Detection With Hyperspectral Data: Solutions for Both Known and Unknown Water Quality. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1213–1221. [Google Scholar] [CrossRef]
- Gillis, D.B. An Underwater Target Detection Framework for Hyperspectral Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1798–1810. [Google Scholar] [CrossRef]
- Qi, J.; Xue, W.; Gong, Z.; Zhang, S.; Yao, A.; Zhong, P. Hybrid Sequence Networks for Unsupervised Water Properties Estimation From Hyperspectral Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3830–3845. [Google Scholar] [CrossRef]
- Gong, M.; Liu, J.; Li, H.; Cai, Q.; Su, L. A Multiobjective Sparse Feature Learning Model for Deep Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 3263–3277. [Google Scholar] [CrossRef] [PubMed]
- Chein, I.C. An information-theoretic approach to spectral variability, similarity, and discrimination for hyperspectral image analysis. IEEE Trans. Geosci. Remote Sens. 2000, 46, 1927–1932. [Google Scholar]
- Harsanyi, J.C. Detection and Classification of Subpixel Spectral Signatures in Hyperspectral Image Sequences. Ph.D. Dissertation, University of Maryland, College Park, MD, USA, 1993. [Google Scholar]
- Clark, R.; Swayze, G.; Wise, R.; Livo, E.; Hoefen, T.; Kokaly, R.; Sutley, S. USGS Digital Spectral Library splib06a: Us Geological Survey, Digital Data Series 231. Available online: http://speclab.cr.usgs.gov/spectral-lib.html (accessed on 1 July 2021).
- Albert, A.; Mobley, C.D. An analytical model for subsurface irradiance and remote sensing reflectance in deep and shallow case-2 waters. Opt. Express 2003, 11, 2873–2890. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Wu, Z.; Du, Q.; Du, P. Hyperspectral Anomaly Detection Using Collaborative Representation With Outlier Removal. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2018, 11, 5029–5038. [Google Scholar] [CrossRef]
- Richter, R.; Schläpfer, D. Geo-atmospheric processing of airborne imaging spectrometry data. Part 2: Atmospheric/topographic correction. Remote Sens. Lett. 2002, 23, 2631–2649. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, F.; Li, X. Optimal Clustering Framework for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5910–5922. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Zhang, F.; Li, X. Hyperspectral Band Selection via Optimal Neighborhood Reconstruction. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8465–8476. [Google Scholar] [CrossRef]
- Sun, K.; Geng, X.; Ji, L. A New Sparsity-Based Band Selection Method for Target Detection of Hyperspectral Image. IEEE Geosci. Remote Sens. Lett. 2015, 12, 329–333. [Google Scholar]





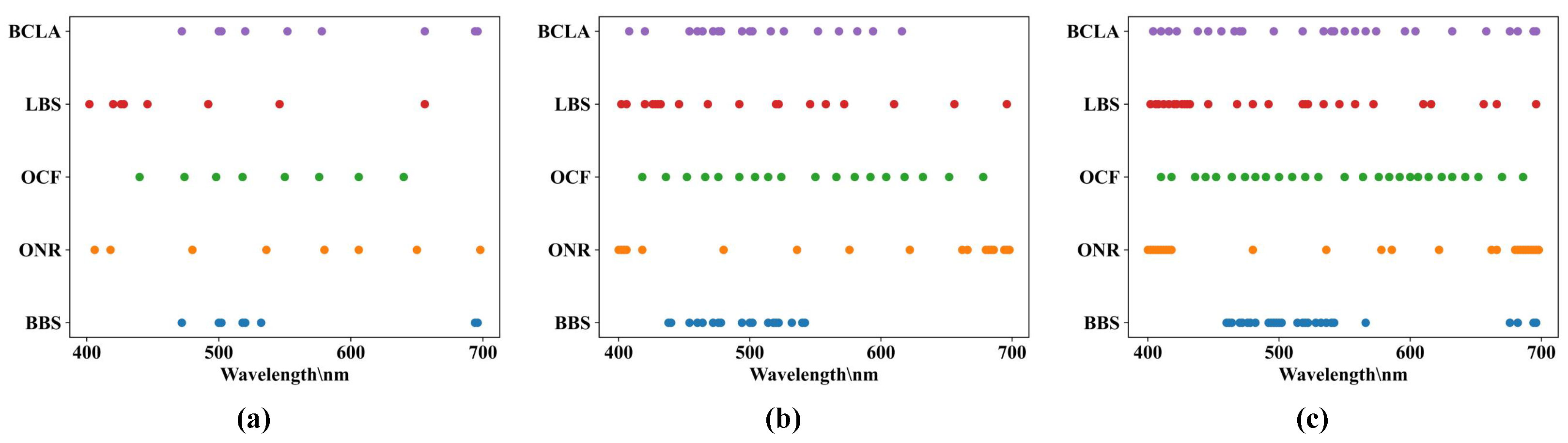
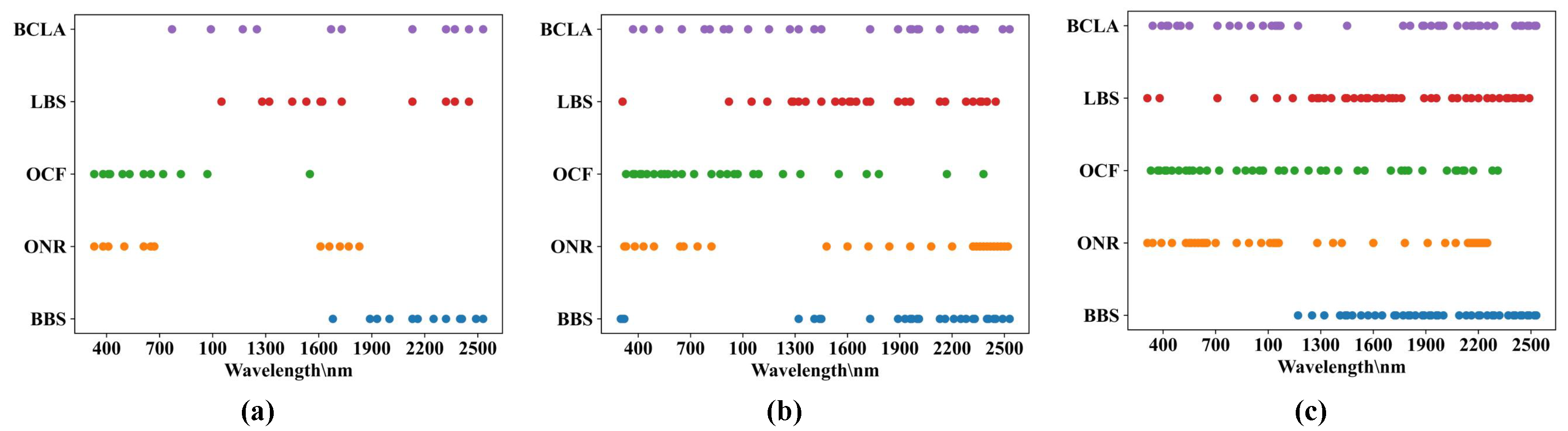





| Dataset | Spatial Solution | Band Numbers | Target Material | Depth Information |
|---|---|---|---|---|
| Nano-Hyper | 270 | Metal plates | 1 m and 1.5 m | |
| Turbid water | 150 | Sheet metal material | 0.1 m, 1 m, 2 m and 3 m | |
| Sea water | 224 | Alunite material | 0.5 m, 1 m, 2.5 m, and 5 m |
| Dataset | Hyper-Parameter | Hyper-Parameter | Hyper-Parameter q | Selected Band Amount |
|---|---|---|---|---|
| Nano-Hyper | 0.005 | 0.1 | 0.1 | 22 |
| 0.01 | 0.2 | 0.2 | 34 | |
| 0.02 | 0.3 | 0.3 | 58 | |
| Turbid water | 0.02 | 0.1 | 0.1 | 8 |
| 0.03 | 0.2 | 0.2 | 18 | |
| 0.05 | 0.3 | 0.3 | 27 | |
| Sea water | 0.01 | 0.1 | 0.1 | 17 |
| 0.02 | 0.2 | 0.2 | 27 | |
| 0.04 | 0.3 | 0.3 | 42 |
| Number of Selected Bands | Nano-Hyper | Turbid Water | Sea Water | |||
|---|---|---|---|---|---|---|
| BBS (N) | BBS (Y) | BBS (N) | BBS (Y) | BBS (N) | BBS (Y) | |
| 10 | 0.68 | 0.73 | 0.81 | 0.85 | 0.91 | 0.93 |
| 20 | 0.74 | 0.79 | 0.84 | 0.91 | 0.92 | 0.96 |
| 30 | 0.76 | 0.83 | 0.86 | 0.95 | 0.94 | 0.98 |
| Average | 0.727 | 0.783 | 0.834 | 0.903 | 0.923 | 0.957 |
| Number of Selected Bands | Nano-Hyper | Turbid Water | Sea Water | |||
|---|---|---|---|---|---|---|
| BBS (N) | BBS (Y) | BBS (N) | BBS (Y) | BBS (N) | BBS (Y) | |
| 10 | 0.14 | 0.41 | 0.17 | 0.54 | 0.08 | 0.33 |
| 20 | 0.25 | 0.63 | 0.31 | 0.62 | 0.27 | 0.57 |
| 30 | 0.43 | 0.71 | 0.46 | 0.77 | 0.41 | 0.62 |
| Average | 0.273 | 0.583 | 0.313 | 0.643 | 0.253 | 0.507 |
| Number of Selected Bands | Nano-Hyper | Turbid Water | Sea Water | |||
|---|---|---|---|---|---|---|
| BBS (N) | BBS (Y) | BBS (N) | BBS (Y) | BBS (N) | BBS (Y) | |
| 10 | 0.59 | 0.73 | 0.69 | 0.85 | 0.71 | 0.93 |
| 20 | 0.62 | 0.79 | 0.73 | 0.91 | 0.78 | 0.96 |
| 30 | 0.71 | 0.83 | 0.77 | 0.95 | 0.84 | 0.98 |
| Average | 0.64 | 0.783 | 0.73 | 0.903 | 0.776 | 0.957 |
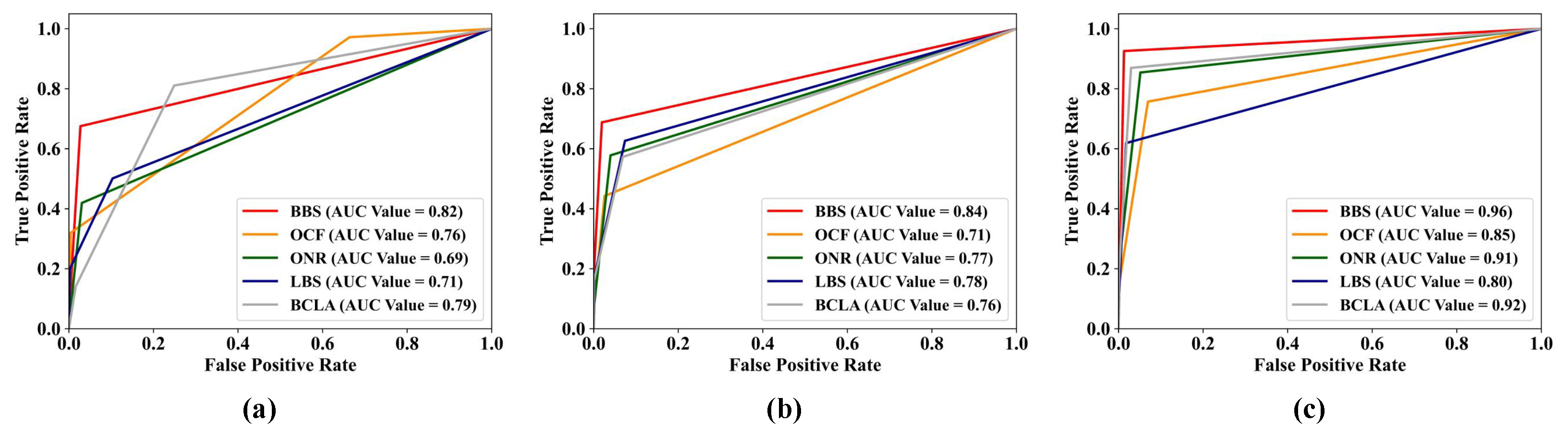
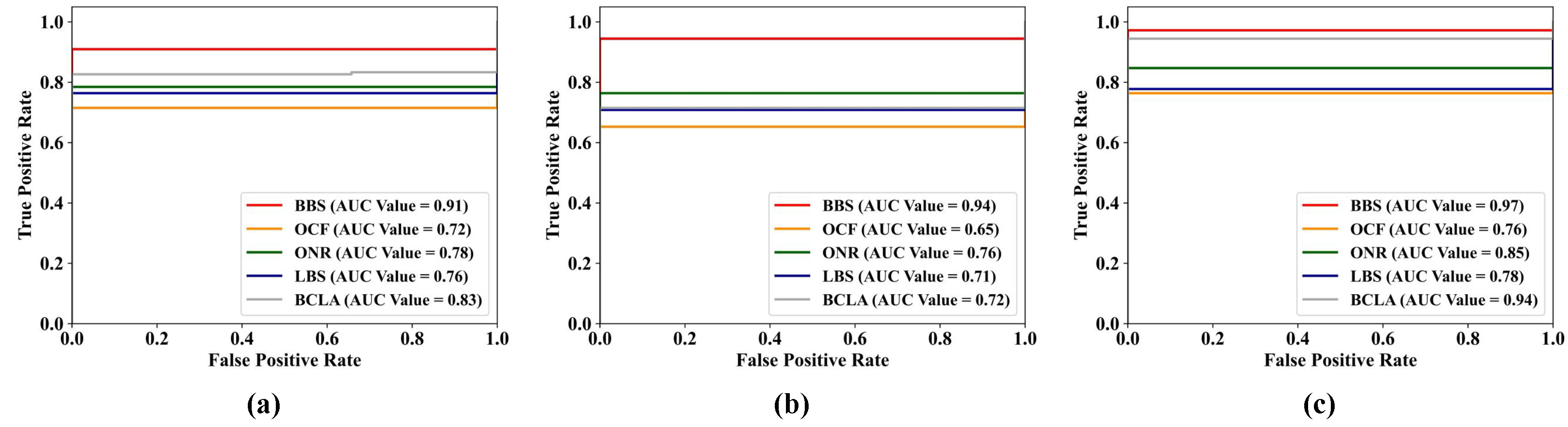
| Number of Selected Bands | AUC Values for Nano-Hyper Data Set | ||||
|---|---|---|---|---|---|
| LBS | OCF | ONR | BCLA | BBS | |
| 22 | 0.71 | 0.76 | 0.69 | 0.79 | 0.82 |
| 34 | 0.78 | 0.71 | 0.77 | 0.76 | 0.84 |
| 58 | 0.80 | 0.85 | 0.91 | 0.92 | 0.96 |
| Average | 0.76 | 0.77 | 0.79 | 0.82 | 0.87 |
| Number of Selected Bands | AUC Values for Turbid Water Data Set | ||||
| LBS | OCF | ONR | BCLA | BBS | |
| 8 | 0.76 | 0.72 | 0.78 | 0.83 | 0.91 |
| 18 | 0.71 | 0.65 | 0.76 | 0.72 | 0.94 |
| 27 | 0.78 | 0.76 | 0.85 | 0.94 | 0.97 |
| Average | 0.75 | 0.71 | 0.80 | 0.83 | 0.94 |
| Number of Selected Bands | AUC Values for Sea Water Data Set | ||||
| LBS | OCF | ONR | BCLA | BBS | |
| 17 | 0.88 | 0.73 | 0.76 | 0.85 | 0.91 |
| 27 | 0.93 | 0.84 | 0.92 | 0.94 | 0.95 |
| 42 | 0.88 | 0.79 | 0.87 | 0.89 | 0.98 |
| Average | 0.90 | 0.79 | 0.85 | 0.89 | 0.95 |
| Number of Selected Bands | AUC Values for Nano-Hyper Data Set | ||||
|---|---|---|---|---|---|
| LBS | OCF | ONR | BCLA | BBS | |
| 22 | 0.35 | 0.40 | 0.31 | 0.39 | 0.22 |
| 34 | 0.52 | 0.39 | 0.39 | 0.37 | 0.16 |
| 58 | 0.33 | 0.35 | 0.24 | 0.21 | 0.15 |
| Average | 0.40 | 0.38 | 0.31 | 0.32 | 0.18 |
| Number of Selected Bands | AUC Values for Turbid Water Data Set | ||||
| LBS | OCF | ONR | BCLA | BBS | |
| 8 | 0.39 | 0.58 | 0.27 | 0.30 | 0.26 |
| 18 | 0.29 | 0.26 | 0.27 | 0.29 | 0.26 |
| 27 | 0.26 | 0.29 | 0.28 | 0.27 | 0.26 |
| Average | 0.31 | 0.38 | 0.27 | 0.29 | 0.26 |
| Number of Selected Bands | AUC Values for Sea Water Data Set | ||||
| LBS | OCF | ONR | BCLA | BBS | |
| 17 | 0.37 | 0.37 | 0.40 | 0.32 | 0.26 |
| 27 | 0.41 | 0.34 | 0.37 | 0.36 | 0.17 |
| 42 | 0.21 | 0.27 | 0.19 | 0.26 | 0.15 |
| Average | 0.33 | 0.33 | 0.32 | 0.31 | 0.19 |
| Dataset | Execution Time (in Seconds) | ||||
|---|---|---|---|---|---|
| BBS | LBS | ONR | OCF | BCLA | |
| Nano-Hyper | 36.7081 | 3.8713 | 11.7812 | 19.6337 | 29.4203 |
| Turbid water | 27.7148 | 2.8456 | 8.7495 | 15.1754 | 23.7893 |
| Sea water | 42.4982 | 5.3969 | 14.8247 | 22.7496 | 37.4817 |
| Average | 35.6404 | 4.0199 | 11.7851 | 19.1862 | 30.2304 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, J.; Gong, Z.; Yao, A.; Liu, X.; Li, Y.; Zhang, Y.; Zhong, P. Bathymetric-Based Band Selection Method for Hyperspectral Underwater Target Detection. Remote Sens. 2021, 13, 3798. https://doi.org/10.3390/rs13193798
Qi J, Gong Z, Yao A, Liu X, Li Y, Zhang Y, Zhong P. Bathymetric-Based Band Selection Method for Hyperspectral Underwater Target Detection. Remote Sensing. 2021; 13(19):3798. https://doi.org/10.3390/rs13193798
Chicago/Turabian StyleQi, Jiahao, Zhiqiang Gong, Aihuan Yao, Xingyue Liu, Yongqian Li, Yichuang Zhang, and Ping Zhong. 2021. "Bathymetric-Based Band Selection Method for Hyperspectral Underwater Target Detection" Remote Sensing 13, no. 19: 3798. https://doi.org/10.3390/rs13193798
APA StyleQi, J., Gong, Z., Yao, A., Liu, X., Li, Y., Zhang, Y., & Zhong, P. (2021). Bathymetric-Based Band Selection Method for Hyperspectral Underwater Target Detection. Remote Sensing, 13(19), 3798. https://doi.org/10.3390/rs13193798







