Kinematic ZTD Estimation from Train-Borne Single-Frequency GNSS: Validation and Assimilation

Abstract

Water vapour is one of the most important parameters utilized for the description of state and evolution of the Earth’s atmosphere. It is the most effective greenhouse gas and shows high variability, both in space and time. Thus, detailed knowledge of its distribution is of immense importance for weather forecasting, and therefore high resolution observations are crucial for accurate precipitation forecasts, especially for the short-term prediction of severe weather. Although not intentionally built for this purpose, Global Navigation Satellite Systems (GNSS) have proven to meet those requirements. The derivation of water vapour content from GNSS observations is based on the fact that electromagnetic signals are delayed when travelling through the atmosphere. The most prominent parameterization of this delay is the Zenith Total Delay (ZTD), which has been studied extensively as a major error term in GNSS positioning. On the other hand, the ZTD has also been proven to provide substantial benefits for atmospheric research and especially Numerical Weather Prediction (NWP) model performance. Based on these facts, the scientific area of GNSS Meteorology has emerged. The present study goes beyond the current status of GNSS Meteorology, showing how reasonable estimates of ZTD can be derived from highly-kinematic, single-frequency (SF) GNSS data. This data was gathered from trains of the Austrian Federal Railways (ÖBB) and processed using the Precise Point Positioning (PPP) technique. The special nature of the observations yields a number of additional challenges, ranging from appropriate pre-processing and parameter settings in PPP to more sophisticated validation and assimilation methodologies . The treatment of the ionosphere for SF-GNSS data represents one of the major challenges of this study. Two test cases (train travels) were processed using different strategies and validated using ZTD calculated from ERA5 reanalysis data. The validation results indicate a good overall agreement between the GNSS-ZTD solutions and ERA5-derived ZTD, although substantial variability between solutions was still observed for specific sections of the test tracks. The bias and standard deviation values ranged between 1 mm and 8 cm, heavily depending on the utilized processing strategy and investigated train route. Finally, initial experiments for the assimilation of GNSS-ZTD estimates into a NWP model were conducted, and the results showed observation acceptance rates of 30–100% largely depending on the test case and processing strategy.

1. Introduction

Water vapour, accounting for only roughly 0.25% of the mass of the atmosphere, is a highly variable constituent [1]. Large spatial and temporal variations characterize both its global and regional distribution, making its observation at suitable resolutions a demanding task. At the same time, it denotes the most important greenhouse gas impacting global warming, a key component of the hydrological cycle and the basic prerequisite for all forms of precipitation. Thus, observations of atmospheric water vapour are of key importance for weather forecasting and climate studies. Therefore, a multitude of observation systems were developed, but all of them are subject to systematic errors and usability constraints in different environmental conditions. Utilized sensors range from classical radiosonde measurements to ground-based microwave radiometers and modern satellite missions specifically designed for the retrieval of water vapour.

Global Navigation Satellite Systems (GNSS) belong to the latter category, although they were originally built up for different purposes. In addition to their typical applications, such as positioning and navigation, GNSS have become a feasible alternative for remote sensing of the troposphere over the last decades, in particular for atmospheric water vapour. The derivation of the atmospheric water vapour content from GNSS is based on the fact that GNSS signals transmitted between the satellites and the ground-based receivers are affected by the atmosphere [2].

This fact has given rise to the scientific field of GNSS Meteorology, whose basic concept was outlined by Bevis et al. [3]. The GNSS signal experiences a delay, which depends on the amount of water vapour contained in the atmosphere along the signal path. This delay is typically estimated for the zenith direction and, therefore, called the Zenith Total Delay (ZTD).

The ZTD is related to the weather conditions in the vicinity of the GNSS station (pressure, temperature, and humidity) and, therefore, carries valuable meteorological information [4], which can be exploited by means of data assimilation (DA) in numerical weather prediction (NWP). Unfortunately, the ZTD denotes an integral measurement along the vertical and, therefore, does not provide a suitable vertical resolution that can be easily mapped to meteorological conditions in various height layers.

For beneficial usage in NWP, high accuracy requirements (∼1 cm [5]) have to be met for ZTD estimates. Therefore, typically double-difference (DD) processing of static reference station networks is applied in GNSS analysis. Nevertheless, using alternative approaches, such as Precise Point Positioning (PPP) for GNSS Meteorology have been investigated over the recent years (e.g., [5,6,7,8]), due to the manifold benefits of the technique. These include independence of reference station data and, therefore, smaller data amounts for processing, reducing latency time of resulting products, which is crucial in particular for near-real time NWP operation (Nowcasting).

However, most studies and operational products still use only dual-frequency (DF) observations from fixed stations, due to the easier data processing and more controllable environmental conditions. Thus, SF-PPP processing for troposphere monitoring has yet been explored by only a limited number of studies (e.g., [9,10,11]). Deng et al. [12] densified an already existing station network with SF receivers and retrieved tropospheric delays using static PPP in post-processing mode.

In order to deal with the ionospheric influence, they developed the Satellite-specific Epoch-differenced Ionospheric Delay (SEID) model, which uses information from the surrounding reference stations to generate synthetic observations on a second frequency for the SF receiver. This approach was also investigated in the course of this study for kinematic observations. Krietemeyer et al. [10] studied the feasibility of using low-cost receivers to increase the density of GNSS networks for retrieval of the Precipitable Water Vapour (PWV).

They processed one year of GNSS data from an IGS station and two co-located SF stations by using the SEID algorithm to correct for the ionospheric influence. Mendez Astudillo et al. [13] carried out a performance assessment of three PPP online services and three software packages concerning ZTD estimation. In this context, they compared ZTD estimates from PPP processing to those obtained from the IGS tropospheric products.

The results indicate that the online PPP service performance was better than those of selected PPP software packages in all cases. Zhao et al. [14] estimated both PWV from low-cost multi-GNSS receivers in static mode. They retrieved ZTDs with an accuracy better than 10 mm compared with tropospheric products published by IGS and about 3 mm for PWV compared to radiosonde results.

The possibility of monitoring tropospheric parameters from kinematic platforms has been investigated by only a small number of studies. Most of them concentrated on maritime environments, such as ship-borne [15,16,17,18] and buoy data [19,20]. ZTD estimation from airborne data was initially investigated by Skone et al. [21].

Up until now, the only investigation on train-borne GNSS data was carried out by Webb et al. [22], who analysed Zenith Wet Delay (ZWD) for over a decade of continuous DF observations over a range of altitudes on the Snowdon Mountain Railway, located in Snowdonia National Park, North Wales. Their multi-system GNSS solutions yielded an improvement of about 5 mm in ZWD estimated in kinematic PPP mode, compared to the GPS-only solution. The overall agreement in ZWD with NWP-based reference data was 11.6 mm for the multi-GNSS solution and 16.2 mm for the GPS-only solution.

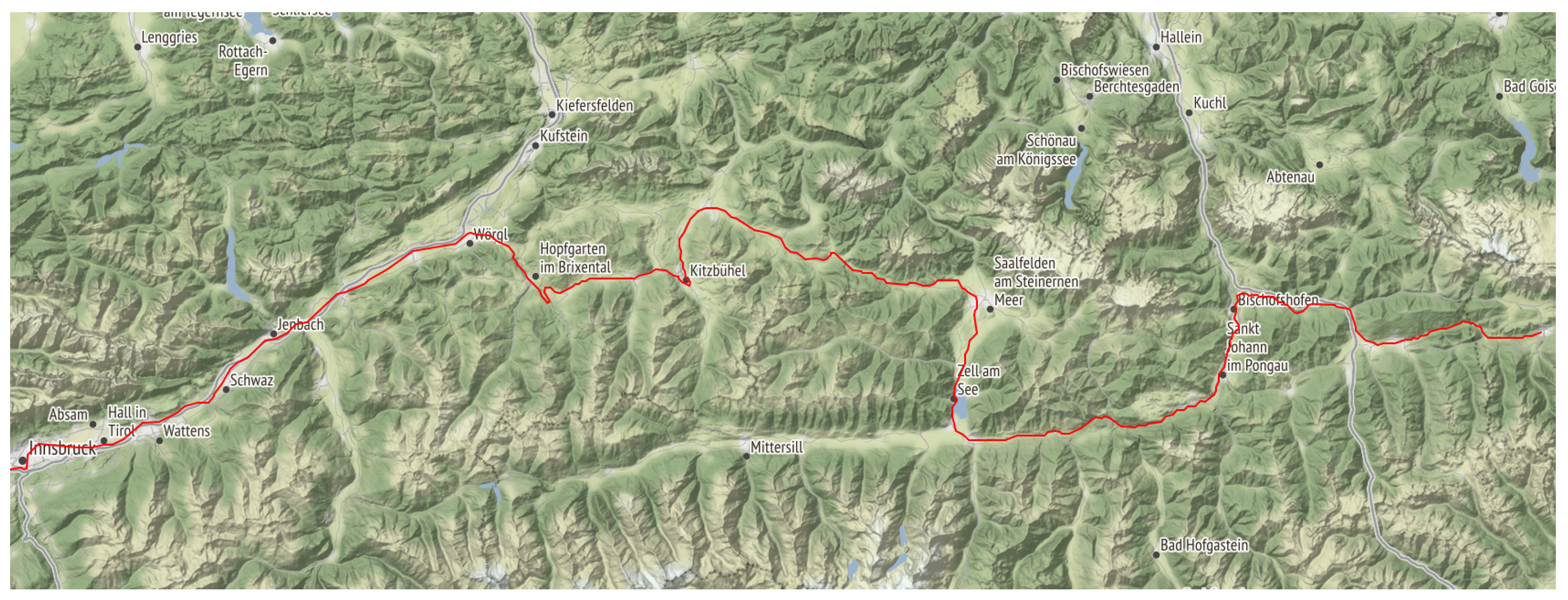
Our present study goes beyond the investigations outlined above by applying kinematic PPP processing on SF-GNSS data gathered by receivers, which are mounted on trains. The study, therefore, represents an initial assessment of the usability of train-borne SF-GNSS data for meteorological purposes and the challenges associated with this approach. The underlying idea is to use trains travelling on rail-tracks in the federal reserve of Austria as permanently moving meteorological sensors. Currently, a large number of trains (∼1400) are equipped with dual-system SF receivers, which are currently able to track GPS and GLONASS signals. Data is gathered on different railway tracks over Austria in the course of the project Greenlight, led by ÖBB.

The main motivation of using train-borne data for GNSS Meteorology is the much denser spatial resolution due to the large number of sensors that are possibly available. These travel through different height regions and weather systems and, therefore, are predestined to investigate small-scale phenomena that are currently hard to represent in NWP [23]. On the other hand, a significantly higher number of challenges is experienced due to the specific nature of the data set.

This concerns problems, such as high kinematics (travel speeds of over 200 km/h), ionospheric mitigation (SF data) and a large variety of critical environments encountered along the tracks. Nevertheless, first investigations have already shown the feasibility of this specific dataset for tropospheric monitoring [24]. This study aims to establish some of the basic knowledge on data processing and estimation of tropospheric parameters from highly-kinematic sensors with sufficient accuracy.

The results shown here concentrate on ZTD estimation and validation using independent, NWP-based reference data as well as first tests of assimilation into an NWP model. Further case studies and detailed analysis concerning other aspects and results of the PPP processing of these data sets can be found in Aichinger-Rosenberger [25].

2. Data and Methodology

2.1. GNSS Data Sources

The analysed train-borne GNSS data stem from two different railway tracks. The GNSS observations were gathered on diverse days on trains operated by ÖBB in the course of the Greenlight project. In the course of this project, ÖBB began to equip their fleet of trains with multi-GNSS receivers capable of logging GPS and GLONASS L1 observations at an update rate of 1 Hz. Today, more than 1400 vehicles are already equipped with such single-frequency receivers, providing decimetre localisation of the fast-moving traction vehicles as well as access to raw GNSS data stored on the receivers on-board. These data, acquired for two full days, form the foundation of all results shown in the following.

Furthermore, DF observations of a regional GNSS station network operated by EPOSA (Echtzeit Positionierung Austria) and partners were utilized to generate the parameters for the SEID model in the course of this study. The network consists of 38 stations distributed all over Austria as visualized in Figure 1.

2.2. Tropospheric Delays from GNSS

As already outlined in the introduction, the retrieval of atmospheric information from GNSS observations is based on the fact that electromagnetic signals are delayed by the presence of the Earth’s atmosphere. The non-dispersive, tropospheric part of the atmospheric delay is most commonly given as the ZTD—the delay experienced by signals in the zenith direction. The ZTD can be split up into a hydrostatic part (the Zenith Hydrostatic Delay, ZHD) and a wet part (the ZWD):

$$\mathrm{ZTD}=\mathrm{ZHD}+\mathrm{ZWD}.$$

(1)

ZHD accounts for the major part of the total delay and is largely determined by the atmospheric pressure. Therefore, it can be modelled with sufficient accuracy from surface pressure observations using, e.g., the formula of Saastamoinen [26]:

$$\mathrm{ZHD}=\frac{0.0022767·p_s}{1-0.00266·cos(2·\theta )-0.00028·H}$$

(2)

where $p_s$ is the surface pressure, $\theta$ the station latitude, and H is the station height above the geoid.

ZWD is directly related to the water vapour content in the air, representing the signal of interest for meteorological purposes. Therefore, it also shows a high temporal and spatial variability (just as water vapour), making precise modelling from meteorological surface observations impossible. Thus, ZWD is commonly estimated as an unknown in GNSS parameter estimation alongside of station coordinates and the receiver clock error.

2.3. GNSS Processing Strategy

The following section introduces the basic strategies used for processing of the train-borne GNSS data, from pre-processing to specific approaches utilized for ionospheric mitigation and parameter estimation in PPP.

2.3.1. Pre-Processing

The special nature of the utilized data requires extended pre-processing in order to use code and phase measurements in PPP processing. Along with common strategies for outlier detection such as outlined by Blewitt [27], this mostly concerns the detection and correction of cycle slips present in the raw phase observations. Uncorrected, they can significantly degrade the performance of PPP solutions.

The detection and correction of cycle slips is especially challenging for SF data, since classical methods, such as the geometry-free (GF) or the Melbourne-Wübenna (MW) linear combination (LC) [28] require observations on two carrier frequencies. Therefore, second-order time-differencing of $L_1$ phase observations was utilized, in order to detect and exclude affected observations from processing.

2.3.2. Ionospheric Mitigation for SF Observations

The second major error source in GNSS processing attached to the Earth’s atmosphere is the influence of the ionosphere. This atmospheric layer, located between ∼50–1500 km in height above the surface, is characterized by ionization through solar radiation. A high concentration of free electrons is existent especially within the F2-layer located about 350–450 km above the surface, which influences the propagation speed of electromagnetic waves and, therefore, causes a delay of GNSS signals.

Since the ionosphere is a dispersive medium for microwaves, the actual delay experienced depends on the signal frequency. This fact is typically exploited in GNSS processing to remove the ionospheric delay, by forming an adequate linear combination of observations taken on two frequencies. This Ionosphere-Free Linear Combination (IF-LC) serves as the basis of typical PPP and other GNSS-processing algorithms.

For SF data, however, the ionospheric delay cannot be eliminated by forming linear combinations and, thus, remains a major challenge for SF-GNSS processing. One common approach for mitigation is to assume all electrons to be contained in a single (shell) layer and estimate the Total Electron Content (TEC) of this layer using empirical models [29,30]. Another approach is to use range corrections given by regional or global maps of TEC (as generated by the Center for Orbit determination in Europe (CODE) ), which are derived from geodetic reference station networks.

As another alternative to these approaches, the Satellite-specific Epoch-differenced Ionospheric Delay model (SEID) was introduced by Deng et al. [12]. It allows for processing data from a SF receiver embedded in a network of DF reference stations. The model makes use of the geometry-free linear combination (GF-LC) $L_4$, given by

$$L_4=L_1-L_2,$$

(3)

and corresponds to the difference between carrier phase observations on the $L_1$ and $L_2$ frequency, which is mainly governed by the ionospheric refraction.

Unfortunately, $L_4$ still contains the phase ambiguity parameter, whose estimation is still a major obstacle in GNSS processing. Therefore, the algorithm uses epoch-differences of $L_4$, $\delta L_4$, in order to eliminate the influence of the phase ambiguities. For two consecutive time steps, i and $i+1$, this quantity reads

$$\delta L_4\left(i\right)=L_4(i+1)-L_4\left(i\right).$$

(4)

The spatial change of the delay can be expressed by the positions of the intercept pierce points (IPP) of the signal path and the layer [12]. The basic assumption now is that this epoch-difference of a specific satellite, derived from DF stations, can be fitted to a linear function, e.g., a plane. Using the notation of Deng et al. [12], this linear fit reads

$$\delta L_4={\alpha }_0+{\alpha }_1\lambda +{\alpha }_2\theta ,$$

(5)

where $\theta$ is the latitude, $\lambda$ is the longitude of their IPPs, and ${\alpha }_0$, ${\alpha }_1$ and ${\alpha }_2$ are the model parameters to be determined.

From Equation (5), it becomes obvious that a minimum of three reference stations is required to derive those model parameters. In general, a higher number of stations is beneficial to derive more accurate results and deal with possible data gaps at certain stations. In the case of four or more reference stations, the parameters are estimated by means of a least-squares adjustment for each satellite at each epoch. This results in a different plane model for each satellite-epoch combination, which gives a hint on the high computational demand of the approach for larger datasets.

Analysing the magnitudes of the computed $\delta L_4$ values can be used for detection of outliers and cycle slips affecting the utilized satellites at each epoch. In the processing carried out in this study, a threshold of ±0.5 m is applied for $\delta L_4$. If this threshold is exceeded, the corresponding satellite is excluded from the further processing.

Using the generated model parameters at epoch i, the epoch-differenced ionospheric correction of any SF receiver inside the reference network can be calculated. The correction for a specific epoch k, $\widetilde{L_4}(i_0,k)$, is the sum of the epoch-differenced corrections between an initial epoch $i_0$ and epoch k,

$$\widetilde{L_4}(i_0,k)=\sum _{i=i_0}^{k-1}\widetilde{\delta L_4}(i,i+1).$$

(6)

The ionospheric delay at the initial epoch $i_0$ is unknown and, thus, set to zero by definition. This has the disadvantage of destroying the integer nature of the phase ambiguity, which cannot be fixed to integer in PPP processing afterwards. By means of $\widetilde{L_4}(i_0,k)$ , a converted $L_2$ observation ($\widetilde{L_2}$) can be derived using

$$\widetilde{L_2}\left(k\right)=L_1\left(k\right)-\widetilde{L_4}(i_0,k).$$

(7)

Although pseudorange observations are usually significantly down-weighted or not used at all in PPP processing, they can be treated using the same procedure. However, it is no longer necessary to operate on epoch-differences since no ambiguity parameter is present. For a detailed formulation of the SEID-algorithm for pseudorange observations, we refer to [12] or [25].

The original SF dataset can then be extended by the converted $L_2$ and $P_2$ observations and can be used for DF processing (using the IF-LC) in a software package of choice.

2.3.3. PPP Processing

In order to estimate ZTD from the train-borne GNSS observations, the PPP technique is used. The PPP technique is characterized through the use of precise satellite products (e.g., orbits, clocks, and biases), accurate observation models, and sophisticated algorithms, which all are applied on the observation of a single GNSS receiver [31]. For a detailed discussion of the entire PPP algorithm, we refer to Zumberge et al. [32] or Kouba and Héroux [33].

GNSS data for processing were provided by ÖBB as raw observations available every second in binary format. These were converted to RINEX 2.11 format [34] and fed to the PPP processing engines. Three different software packages were utilized for PPP processing in SF or DF mode:

• CSRS-PPP [35]
• GAMP [36]
• PPP-Wizard [37,38]

All processing schemes outlined were applied at least for one test case. In the following, these schemes are referred to as:

• CSRS-PPP: CSRS-PPP
• GAMP using SEID model: SGAMP (used only for CS1)
• PPP-Wizard: PPPW
• PPP-Wizard with height-constraint: PPPW-HC

3D-coordinates, receiver clock error, and ZWD were estimated every second using those processing schemes.

Depending on the actual scheme either SF- or DF-PPP for GPS and GLONASS observations were used. IGS final products were utilized for satellite orbit and clock corrections. Ionospheric corrections are applied for CSRS-PPP through IGS GIM broadcast TEC models and for PPPW by obtaining EGNOS (European Geostationary Navigation Overlay Service) corrections. Since the SGAMP scheme operates in DF-PPP mode, the IF-LC is applied here. The hydrostatic part of the tropospheric delay (i.e., ZHD) is modelled by means of grids of the Vienna Mapping Function 1 (VMF1) [39] for CSRS-PPP and using the Saastamoinen model [26] for PPPW and SGAMP.

VMF1 (CSRS-PPP) and the Global Mapping Function (GMF) [40] (SGAMP and PPPW) serve as tropospheric mapping functions. We chose 7.5${}^{\circ }$ as the default setting for the cut-off observation angle. Measurements from elevation angles below this value were not considered in the processing. For a priori noise estimates in the Kalman Filter (${\sigma }_L$,${\sigma }_P$,${\sigma }_{\mathrm{ZWD}}$,${\sigma }_{Position}$) a range of different setups were tried out, and the optimal settings were found to vary significantly between the test tracks.

Both the code and phase range noise (${\sigma }_P$,${\sigma }_L$) were set to significantly higher values compared to typically magnitude to account for rather low quality of the raw GNSS data and difficult environmental conditions (e.g., multipath). ZWD was modelled as a random walk process with a standard deviation (${\sigma }_{\mathrm{ZWD}}$) of 5 mm/$\sqrt{s}$.

A number of different settings were tested for this parameter and the presented one were found to provide the best average solution for GNSS-ZTD with respect to validation results. The chosen setting might represent a tight constraint on ZWD in the first place, but this is relativized by the fact that the ZWD is estimated every second above the fast moving sensor.

Furthermore, for almost all test cases, the trains spent a significant amount of time at fairly high altitude where the influence of water vapour is decreasing, especially in stable and dry weather situations. An overview of the settings applied for the different processing schemes can be found in

Table 1. General PPP settings used for the test cases.

Parameter	Setting
Mode	Kinematic SF-PPP (CSRS-PPP/PPPW)/DF-PPP (SGAMP)
GNSS	GPS + GLONASS
Phase Ambiguities	Float
Observation weighting	Elevation-dependent
Orbits	IGS final
Clocks	IGS final
Ionosphere	IGS GIM (CSRS-PPP)/EGNOS (PPPW)/SEID (SGAMP)
ZHD (a priori)	VMF1 (CSRS-PPP)/Saastamoinen (PPPW, SGAMP)
Mapping function	VMF1 (CSRS-PPP)/GMF (PPPW, SGAMP)
Elevation cut-off	7.5${}^{\circ }$
${\sigma }_L$	0.1 m
${\sigma }_P$	1 m
${\sigma }_{\mathrm{ZWD}}$	5 mm/$\sqrt{s}$
${\sigma }_{Position}$	10 m

.

2.3.4. Height-Constrained PPP

Parameter constraints have been extensively used in GNSS processing (e.g., [41,42]) as well as sensor fusion algorithms [43,44]. In this study, we make use of a state constraint on the height coordinate to support ZTD estimation. The idea behind this approach is to decorrelate ZTD and height estimates by using precise height information from a GNSS-independent source. Therefore, height coordinates from an existing database of railway tracks (RDB) all over Austria were used. The database was thankfully provided by ÖBB.

The followed approach represents a simple correction of the height estimate in the Kalman Filter, by using the height provided at the nearest point in the RDB. For the following approach, two remarks have to be considered:

• RDB heights are given above the mean sea level and, thus, have to be converted to geodetic heights using interpolated geoid undulations from the Austrian Geoid model GEOnAUT [45].
• As the coordinates of the RDB points do not refer to the GNSS antenna but to (reference) pylons along the railway tracks, a height offset has to be applied. A median offset of four meters (between pylon heights and an average of all PPP height solutions available) was calculated over both tracks (i.e., the same train type travelling in both test cases) and applied to the RDB heights for both cases analysed here.

The PPP height coordinate then is set to the corresponding geodetic height of the track database and eliminated from the state vector in the Kalman filter. This corresponding (geodetic) DB height then refers to the point in the RDB whose 2D-coordinates are nearest to the PPP solution. The constraint (i.e., fixing of the height coordinate to RDB value) is applied when the following condition is met:

$$|H_{\mathrm{GNSS}}-(H_{\mathrm{RDB}}+dH)|>0.1\mathrm{m}$$

(8)

where $H_{\mathrm{GNSS}}$ and $H_{\mathrm{RDB}}$ are geodetic heights from GNSS-PPP and the track database (converted as described above), respectively, and $dH$ is the applied offset between pylon and antenna and equals four meters for this study (as described above).

This simple implementation of the height-constraint has the drawback of not providing uncertainty estimates for the eliminated height coordinate. Thus, the approach strongly relies on the quality of the RDB heights and the geoid model. The quality of the RDB heights is generally in the mm range for each pylon reference point, at a maximum distance between pylons of five metres [46]. As no large height differences will be covered by the train track within this distance, the uncertainty introduced by the interpolation will not exceed that of the kinematic SF-PPP estimates. GEOnAUT provides geoid undulations with a standard deviation of about 2 cm [45], which is also significantly lower than the typical kinematic SF-PPP performance.

The approach described above was implemented in the PPP-Wizard software and operated as a separate processing scheme (PPPW-HC). Utilized PPP settings for the test cases are exactly the same as for PPPW, outlined in Table 1.

2.4. GNSS-ZTD Validation Using ERA5

GNSS-ZTD estimates derived from PPP processing have to be validated using independent reference data in order to make sure that quality standards for NWP usage can be met. This was accomplished by computing reference ZTD values from atmospheric reanalysis fields using ray-tracing methods. The utilized reanalysis data stems from the ERA5-reanalysis [47]—the newest atmospheric reanalysis data set from the European Centre for Mid-Range Weather Forecasts (ECMWF).

4D-fields of pressure, temperature, and specific humidity were used for the computation of reference ZTD values (in following referred to as ERA-ZTD). The data-set, which has a horizontal and temporal resolution of 31 km and one hour, respectively, is provided at https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-pressure-levels?tab=overview, accessed on 20 November 2020. The detailed procedure of ZTD computation follows the approach presented by Wilgan and Geiger [48] and is outlined in the following.

Using the formulation of Essen and Froome [49], the total refractivity $N_{tot}$ is computed by

$$N_{tot}=k_1\frac{p}{T}-k_2\frac{e}{T}+k_3\frac{e}{T^2},$$

(9)

where p denotes the pressure, T is the temperature, e is the partial water vapour pressure, and $k_1=77.689\mathrm{KhPa}{}^{-1}$, $k_2=71.2952\mathrm{KhPa}{}^{-1}$, and $k_3=375,463\mathrm{K}{}^2\mathrm{hPa}{}^{-1}$ are the optimal average refractivity coefficients from Rüeger [50], empirically determined for the L-band frequencies.

With Equation (9), 4D-fields of $N_{tot}$ were calculated from the ERA5 data. These allow for the computation of 3D-fields of ZTD (${\mathrm{ZTD}}_{ERA}$) through the vertical integration given by Equation (10)

$${\mathrm{ZTD}}_{ERA}={10}^{-6}{\int }_{H_{\mathrm{GNSS}}}^{H_{NL}}{N}_{tot},$$

(10)

where $H_{\mathrm{GNSS}}$ and $H_{NL}$ denote the heights of the GNSS receiver and the ERA5 top model level, respectively. For discrete data as used here in the form of ERA5 grids, Equation (10) can be approximated by Equation (11):

$${\mathrm{ZTD}}_{ERA}={10}^{-6}\sum _{i=1}^{NL-1}\frac{N_i+N_{i+1}}{2}·\delta s_i,$$

(11)

where $N_i$ is the total refractivity at the i-th vertical level, $NL$ is the number of vertical levels of ERA5, and $\delta s_i$ denotes the geometric distance between the i-th and the (i+1)-th layer. Furthermore, the delay at the top level NL is derived using Equation (12) following [26]:

$${\mathrm{ZTD}}_{NL}=0.002277·(p_{NL}+(\frac{1255}{T_{NL}}+0.05)·e_{NL}),$$

(12)

where $p_{NL}$, $T_{NL}$, and $e_{NL}$ represent the respective parameters at the highest vertical level of ERA5. The total ZTD is then given by Equation (13)

$${\mathrm{ZTD}}_{total}={\mathrm{ZTD}}_{NL}+{\mathrm{ZTD}}_{ERA}.$$

(13)

The actual ZTD value for a given point on the train-trajectory is determined via linear interpolation of the 3D ${\mathrm{ZTD}}_{total}$ field and referred to as ERA-ZTD in the following.

In order to assess the performance of the different processing schemes outlined in Section 2.3, deviations between ERA-ZTD and GNSS-ZTD were computed for all test cases and are presented in Section 3.1.2 and Section 3.2.1. These differences in ZTD are analysed by visual comparison and in terms of the following statistical performance metrics:

• Bias
• Standard deviation ($\sigma$)
• Root Mean Square Error (RMS)
• Correlation coefficient (R)

2.5. Assimilation Experiments

Furthermore, initial experiments for assimilation of train-borne GNSS-ZTD were carried out in the course of this study. Therefore, we introduce the main setup and objectives of these assimilation tests in the following section. These tests should not be equated with full impact studies for ZTD assimilation as found in various literature (e.g., [51,52,53,54]). A rather reduced setup was used and investigations concentrate fully on an assessment of the required quality of the GNSS-ZTD estimates and their ability to enter the DA system. Therefore, a few considerations have to be noted here before the results are presented:

• Due to both time and computational resources, the results of this study focus on the actual DA procedure. This means that only the WRFDA module was run, and an assessment of the quantity of GNSS-ZTD observations entering the procedure (and therefore the models initial state) is presented.
• No actual forecast was produced due to reasons mentioned above and also due to the unlucky coincidence that almost no precipitation was observed over Austria on the investigated days. This would make it difficult to verify an (beneficial) impact on precipitation/moisture forecasts, even if the computational resources would have been available.
• Furthermore, the impact of GNSS-ZTD gathered from just one railway track per analysed case study on actual forecasts is assumed to be very limited. In a future state, this might change as soon as data from multiple tracks can be obtained simultaneously. Nevertheless, comparisons of model output with independently-derived GNSS-ZTD at surrounding reference stations were carried out to obtain a first impression on the impact using only a small data set (i.e., one hour on one track).

Model and Setup

The Weather Research and Forecasting (WRF) model [55] was utilized for the assimilation tests. The different model domains used for the tests are shown in Figure 2, respectively, for the first test case.

The parent domain with a 30 km horizontal resolution, shown in black (d01), essentially covers Central Europe and the first nested domain, shown in blue (d02), with a 10 km resolution fitted to the Austrian borders. Furthermore, a third, very small domain with a 3 km resolution (green, d03) was added in order to adequately represent the mountainous terrain that is encountered on the train routes.

The general settings for the assimilation tests are summarized in

Table 2. Overview of the WRFDA settings chosen for the assimilation tests.

Parameter	Setting
Horizontal resolution (d01,d02,d03)	30/10/3 km
Boundary conditions	ERA5
Observation interval (GNSS-ZTD)	60 s
Assimilation method	4D-Var
Assimilation window	1 h
Observation operator	GPSZTD
Observation error (pre-defined in WRFDA)	0.5 cm
Error threshold	2.5 cm

.

Under special conditions, such as mountainous terrain in combination with moderate or unknown quality of the observation data, the most important parameter in the DA setup is the horizontal resolution of the model domain. It determines the quality of the background/model topography, which is crucial for the calculation of ZTD values in the model domain (referred to as WRF-ZTD from now on). Since the quality check is based on the deviation between GNSS-ZTD and WRF-ZTD, the accuracy of WRF-ZTD directly influences the results of the check and, therefore, the decision of which GNSS-ZTD observations are accepted by WRFDA.

3. Results

In the following, the results of two test cases are provided in the form of estimated GNSS-ZTD and comparison with ERA-ZTD. All presented ZTD time series were post-processed using a moving-average filter with a time window of five minutes, in order to smooth out noise components still present in the PPP solutions. Each of the processing schemes outlined before was utilized for at least one of the presented case studies. Furthermore, initial assimilation tests using the WRF model are presented in a separate section for each test case. A detailed overview of those case studies is given in

Table 3. Overview of the conducted case studies. Indicated are the route and date of travel.

Test Case	Date	Route
CS1	28 September 2017	Salzburg–Klagenfurt
CS2	29 November 2019	Innsbruck-Wörgl-Schwarzach/St.Veit-Liezen

.

3.1. Case Study 1: 28 September 2017

The first case study (CS1) investigates a train travel on the route Salzburg–Klagenfurt on 28 September 2017. The actual train track (as derived from CSRS-PPP processing) is visualized in Figure 3. The route includes a large variety of difficult environments for GNSS positioning, from urban areas at the beginning and end (corresponding to Salzburg and Klagenfurt/Villach) to extended sections of alpine terrain (narrow valleys), where large amounts of multipath effects and signal obstructions are present. The latter can be seen from Figure 4, which shows the number of observed satellites and Geometric Dilution Of Precision (GDOP) values along the track.

Substantial variations in both the number of satellites and GDOP indicate a large variability of environmental conditions and sections of distorted geometry are visible as a drop in available satellites and an increase in GDOP. These sections correspond to the passage of the most complex terrain along the track (narrow valleys and passing of the main alpine ridge). Furthermore, large differences in absolute height are covered by the track, with the highest points reaching over 1000 m above sea level (a.s.l.).

3.1.1. CS1: Kinematic SEID Model

For this first case study, the application of the SEID model is tested for ionospheric mitigation. As the SEID model relies on DF data from nearby reference stations, the EPOSA network was utilized for the provision of DF observations. The chosen seven stations are listed in

Table 4. Reference stations chosen for SEID processing for CS1.

Station	Distance from Reference Point [km]
Gummern	47.6
Oching Süd	4.9
Rötenkogel	55.2
Saalfelden	66.0
Salzburg	62.4
Sillian	66.2
Schladming	62.4

, and the track map with the station locations indicated is shown in Figure 3. The decision of which and how many stations were selected was based on the distance from a defined reference point, which was determined in a static way as the midpoint (median) of the trajectory, and all stations within an 80 km distance from this reference point (indicated by the blue circle in Figure 3) were selected.

The actual threshold value was based on former studies and was variable under different circumstances (e.g., a higher/lower number of stations available within a shorter distance, i.e., a more or less dense reference station network). This clearly represents a simplified approach for a kinematic application, which should be extended for follow-up studies to test the usage of a moving reference point, which was chosen as a suitable time step.

3.1.2. CS1: ZTD Validation

For this test case, ZTD estimation was carried out using all four processing schemes introduced before. Furthermore, ERA-ZTDs were calculated along the entire track according to the outlined methodology and used for the validation of GNSS-ZTDs. Figure 5 shows a comparison of GNSS-ZTDs and ERA-ZTDs in terms of ZTD values and ZTD differences of the different processing schemes for CS1. In addition, histograms of ZTD differences with respect to ERA-ZTD for each GNSS-ZTD solution are shown in Figure 6.

A number of key features can be spotted from the resulting time series. First prominent feature is the high correlation between all solutions of GNSS-ZTD and ERA-ZTD. Temporal patterns of all solutions only differ marginally for the utilized processing schemes and the reference values derived from ERA5. Nevertheless, an (approximately constant) offset to ERA-ZTD is present for essentially all GNSS-ZTD solutions. The largest offset shows up in the PPPW solution, resulting in a significant underestimation of ZTD along the track compared to ERA-ZTD (a negative bias of 8.8 cm). This is also visible in the distributions of ZTD differences, shown in the respective histograms (see Figure 6).

However, the PPPW-HC version actually performs best in comparison to ERA-ZTD, showing very low bias (0.1 cm) and RMS (1.2 cm) values as also visible in

Table 5. The performance metrics for the ZTD validation against ERA-ZTD for the processing results of CSRS-PPP, SGAMP, PPPW, and PPPW-HC for CS1.

Processing Scheme	Bias [cm]	$\mathit{\sigma }$ [cm]	RMS [cm]	R
CSRS-PPP	2.4	1.2	2.7	0.99
SGAMP	1.3	2.5	2.8	0.95
PPPW	−8.8	1.8	8.9	0.97
PPPW-HC	0.1	1.3	1.3	0.99

. Therefore, at least the bias is comparable to the values typically provided by DF solutions from geodetic equipment, which is commonly used for troposphere monitoring (see, e.g., [4]). Although the standard deviations are higher than for geodetic solutions, the results from this type of processing are still very promising. The pronounced advantage of the PPPW-HC over the standard version might indicate a height offset introduced in PPPW, which diminishes by applying a constraint as described in Section 2.3.4.

The SGAMP solution also shows low values for bias and RMS (1.3/2.8 cm), but an increased standard deviation (by a factor ∼2) compared to the other schemes. Nevertheless, these results are able to indicate the potential of the SEID model for SF-GNSS processing and applications, such as GNSS Meteorology.

The results from CSRS-PPP are comparable to those of SGAMP in terms of bias (2.4 cm) and similar for RMS (2.7 cm). This scheme provides the lowest standard deviation of all solutions (1.2 cm). A detailed summary of the performance metrics for the ZTD validation is given in Table 5.

Overall, the results of the CS1 ZTD validation outline the potential of the newly introduced processing schemes (SGAMP and PPPW-HC), which both are able to outperform the “standard” PPP solutions from CSRS-PPP and PPPW. In particular, the good performance of PPPW-HC encourages its usage for the second test case (CS2) shown as well as for future studies.

3.1.3. CS1: Assimilation Test

This section provides results of the first initial assimilation tests for CS1. The GNSS-ZTD solutions validated in the prior section are introduced in the WRFDA procedure using the setup outlined in Section 2.5. Before discussing this test case in detail, it should be noted here that the chosen time slot for assimilation (from 9–10 UTC) corresponds to the most challenging part of the track, the actual passing of the alpine ridge. This was chosen on purpose in order to investigate the DA procedure and observation usability in the most challenging conditions possible.

An overview of the acceptance rates for the utilized schemes is given in

Table 6. The acceptance rates for GNSS-ZTD results of CSRS-PPP, SGAMP, PPPW, and PPPW-HC for CS1.

Processing Scheme	Acceptance Rate [%]
CSRS-PPP	0.0
SGAMP	37.5
PPPW	25.0
PPPW-HC	51.8

. The overall performance of most schemes is reasonable but significantly degraded in comparison to the second test case (see Section 3.2.2). This holds especially for the CSRS-PPP solution, as no single observation is accepted by WRFDA. This fact seems particularly anomalous when revisiting the validation results from the prior section. However, there appears to be a distinctive bias introduced by the coarse representation of topography within WRF, not only to the real-world but also with respect to ERA5. This might explain the good performance of CSRS-PPP in the validation (also with a low standard deviation) but weak results in the assimilation test.

The other solutions will be affected as well by this bias, although the observation errors (with respect to WRF-ZTD) of their estimates seem to fall below the cut-off (see Table 2) more frequently. For PPPW-HC, approximately half of the derived GNSS-ZTD was accepted (29/56, ∼52%), which represents promising results under the given conditions. For SGAMP 21 (37.5%) and for PPPW 14 (25%), the observations still passed the quality check. Another interesting feature of those results is the areal distribution of assimilated observations for each processing scheme.

Some major differences in agreement with the model state/background forecast show up when looking at different sections along the investigated track. SGAMP and PPPW-HC appear to fit better in the first part of the track (first half hour), whereas all accepted observations from PPPW were gathered at the end of the track. This behaviour is likely also attached to the model topography and the biases introduced by it, as discussed above.

3.1.4. CS1: Assimilation Impact at Nearby GNSS Sites

In order to make an initial assessment of the impact of GNSS-ZTD assimilation on the model performance, WRF-ZTD calculations (both with/without assimilation of train-borne GNSS-ZTD) were compared with ZTD estimates from nine EPOSA stations near the train track. For CS1, all available processing schemes were used in WRFDA and, therefore, can be considered in the following comparison. However, since no CSRS-PPP observations passed the quality check in WRFDA (see prior section), its results are left out for this test case. The chosen EPOSA stations are visualized along with the covered train track and the WRF domain in Figure 7.

Estimates from these stations are derived operationally together with whole network shown in Figure 1 from DD processing using the Bernese GNSS software 5.2 [56] and serve as a reference for the different WRF-ZTD results. Furthermore, ERA-ZTDs were also calculated at the respective station locations in order to add another data source for comparison. The ZTD results from all nine analysed stations and for each type of derivation are summarized in

Table 7. Differences between the ZTD estimates from EPOSA stations against WRF-ZTD without (WRF) and with the assimilation of train-borne GNSS-ZTD (WRF-SGAMP, WRF-PPPW-HC, and WRF-PPPW) and ERA-ZTD calculated at the respective stations.

dZTD-Type	KIBG	ROET	SILL	SAAL	SALZ	OCHS	SHLA	LIEZ	SHEI
ERA5 [mm]	−18.9	−10.5	−8.5	−12.8	−25.8	−9.5	−22.7	−27.6	−24.8
WRF [mm]	−10.5	−0.4	6.0	−0.4	−9.7	−6.2	−9.9	−10.4	−16.1
WRF-SGAMP [mm]	−18.4	−5.3	0.1	−9.6	−19.5	−13.5	−18.3	−17.8	−22.7
WRF-PPPW-HC [mm]	−5.3	1.5	11.3	4.2	−4.5	−1.1	−3.9	−4.4	−11.4
WRF-PPPW [mm]	3.7	8.9	16.2	16.4	8.2	6.5	5.1	2.8	−4.4

.

In general, te results show deviations between EPOSA-ZTD and different WRF-ZTD solutions from the mm range up to 1–3 cm at certain stations. Monitoring the stations along the railway track (SALZ and OCHS) the assimilated WRF-SGAMP solution showed an improvement in consistency with EPOSA-ZTDs compared to the sole WRF solution. On the other hand, for more distant stations, the PPPW solution appears to provide ZTD estimates closer to the EPOSA-ZTD estimates.

Furthermore, looking at the ERA-ZTD values derived at the EPOSA sites, a consistent overestimation of ZTD can be noticed. This might explain why PPPW (always negative bias with respect to ERA-ZTD, see Section 3.1.2) performed the best for most stations in this comparison.

3.2. Case Study 2: 29 November 2019

The second test case (CS2) investigates data gathered on 29 November 2019 along the route Innsbruck–Liezen. The exact train track, again derived from CSRS-PPP processing, is shown in Figure 8.

This route again provides very diverse conditions along the track with some prominent features, such as major cities (Innsbruck), major (Inn Valley and Enns Valley), and very narrow alpine valleys (Brixen Valley, i.e., Wörgl-Kitzbühel) as well as mountain passes (Grießen pass, and Mandling pass). Therefore, environmental conditions (multipath, signal obstruction, and atmospheric conditions) are very different along different sections of the route, which is, again, reflected in the number of visible satellites and GDOP values visualized in Figure 9. The first section (corresponding to the Inn Valley) provides better geometry (GDOP between 2 and 4) and visibility of satellites (number of visible satellites constantly over 10), whereas a significant degradation of these parameters is observed when entering more mountainous environments afterwards.

3.2.1. CS2: ZTD Validation

Similar to CS1, the results of the ZTD validation using the ERA-ZTD reference values are shown here for CS2. Figure 10 shows the comparison of GNSS-ZTD estimations from three different processing schemes (CSRS-PPP, PPPW, and PPPW-HC) and ERA-ZTD (top), as well as deviations of all schemes from ERA-ZTD (bottom part). Furthermore, Figure 11 shows histograms of ZTD differences with respect to ERA-ZTD for each GNSS-ZTD solution.

In general, the results show similar features as already observed for CS1. Correlation is, again, very high between GNSS-ZTD solutions and ERA-ZTD for large parts of the analysed track, with correlation coefficients between 0.97 and 0.98 for PPPW and CSRS-PPP, respectively. The results show an excellent performance of CSRS-PPP, with differences to ERA5 often in the mm range and very high correlation between the respective time series. The overall bias is only around 2.7 mm, the median is in the sub-millimetre range, and the standard deviation is the lowest of all schemes (6.1 mm). PPPW-HC provides comparable results for a large part of the route; however, some distinct deviations to ERA-ZTD are visible around 13:30 to 14:30, which corresponds to the time with the worst geometry (Figure 9).

These issues more likely originate from interpolation errors made in the constraining process (wrong point/height stored in database is chosen). This becomes more intuitive by looking at the PPPW solution, which shows a similar pattern to ERA-ZTD in this section. Overall, the PPPW standard version shows an increased bias and RMS compared to CSRS-PPP and PPPW-HC, although this bias is generally lower than for the prior test case.

The correlation with ERA-ZTD is, again, very high for most schemes, only the PPPW-HC results are distorted by the deviations around 13:30–14:30 (R = 0.72 for PPPW-HC compared to R = 0.97/0.98 for CSRS-PPP/PPPW). Detailed statistics for the ZTD validation of CS2 can be found in

Table 8. Performance metrics for the ZTD validation against ERA-ZTD for processing results of CSRS-PPP, PPPW and PPPW-HC for CS2.

Processing Scheme	Bias [cm]	$\mathit{\sigma }$ [cm]	RMS [cm]	R
CSRS-PPP	−0.27	0.61	0.66	0.98
PPPW	−2.87	1.64	2.95	0.97
PPPW-HC	0.57	0.80	1.68	0.72

. Overall, the results are very promising, especially for CSRS-PPP and PPPW-HC, considering the challenging conditions of the route.

3.2.2. CS2: Assimilation Test

Similar to CS1, we present the results of some initial assimilation tests here for CS2. The utilized DA settings can again be found in Table 2. For CS2, only CSRS-PPP and PPPW results were introduced in WRFDA. The acceptance rates for those two schemes are given in

Table 9. Acceptance rates for the GNSS-ZTD results of CSRS-PPP and PPPW for CS2.

Processing Scheme	Acceptance Rate [%]
CSRS-PPP	100.0
PPPW	81.6

.

Overall, the CS2 tests showed very promising results for both investigated GNSS-ZTD solutions. All observations of CSRS-PPP were assimilated (60/60 points, right part) and showed comparable or sometimes even smaller deviations to WRF-ZTD than to ERA-ZTD. The performance of PPPW is also on a high level with 49/60, i.e., ∼82% of observations entering WRFDA. Contrary to CS1, the biases introduced to the model topography appear to be less present for this test case, resulting in an unexpectedly large number of accepted observations as well as in a much better performance from the CSRS-PPP solution.

This might be explained by slightly less mountainous terrain along the train track, where at least half of the route covers a major valley (Inn Valley), which might be represented more accurately in the WRF topography. Overall, these are promising results showing the feasibility of using such GNSS-ZTD estimates for DA and backing up the results derived in the validation.

3.2.3. CS2: Assimilation Impact at Nearby GNSS Sites

Similar to CS1, WRF-ZTD (again, with/without ZTD assimilation) were compared with ZTD estimates from six EPOSA stations near the train track. The chosen stations, along with the covered train track and the WRF domain, can be seen in Figure 12. ERA-ZTD was also calculated at the respective station locations as another data source for comparison. The results from all six analysed stations and for each type of derivation are summarized in

Table 10. Differences between ZTD estimates from EPOSA stations against WRF-ZTD without (WRF) and with assimilation of train-borne GNSS-ZTD (WRF-CSRS and WRF-PPPW) and ERA-ZTD calculated at the respective stations.

dZTD-Type	KIBG	ROET	MATR	SALZ	OCHS	JENB
ERA5 [mm]	−4.1	−5.0	−10.7	−10.4	−13.1	−11.3
WRF [mm]	1.2	−2.7	−5.2	−0.3	−3.6	−3.2
WRF-CSRS [mm]	−1.6	−3.7	−7.6	−3.1	−6.1	−6.3
WRF-PPPW [mm]	18.0	6.6	7.6	19.0	9.2	15.3

.

The results indicate only a small influence (compared to CS1) of ZTD assimilation for the CSRS-PPP solution (1–3 mm). In the case of PPPW, the deviations were significantly larger (1–2 cm). In comparison to CS1, none of the two investigated processing solutions showed a positive impact on the WRF model state. Rather, a slight increase of the bias can be observed for CSRS-PPP estimates (due to overestimation) as well as a cm-range increase for PPPW (underestimation in all cases). As already visible for CS1, ERA5-based estimates tend to overestimate ZTD at all stations compared to the reference values.

4. Discussion and Conclusions

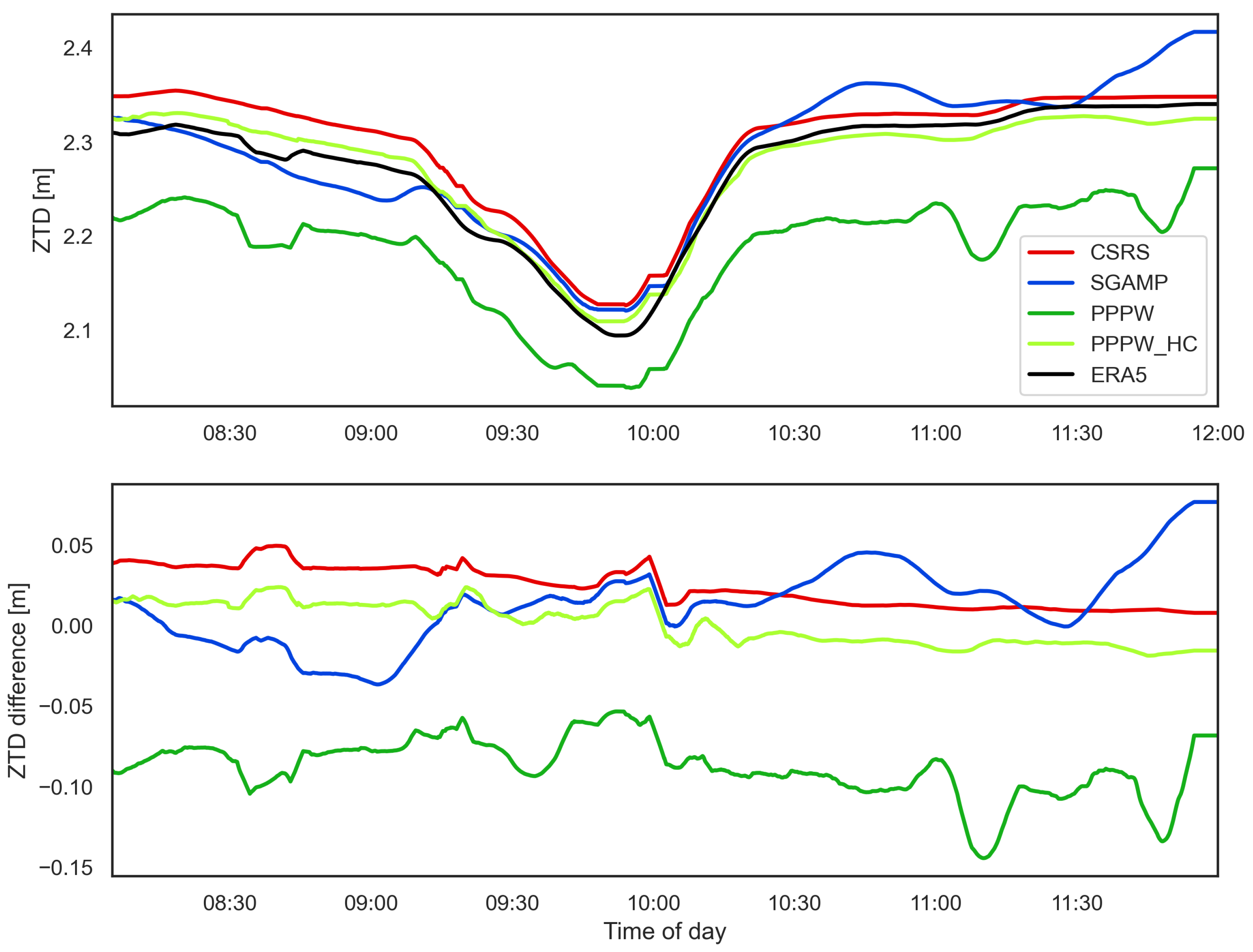
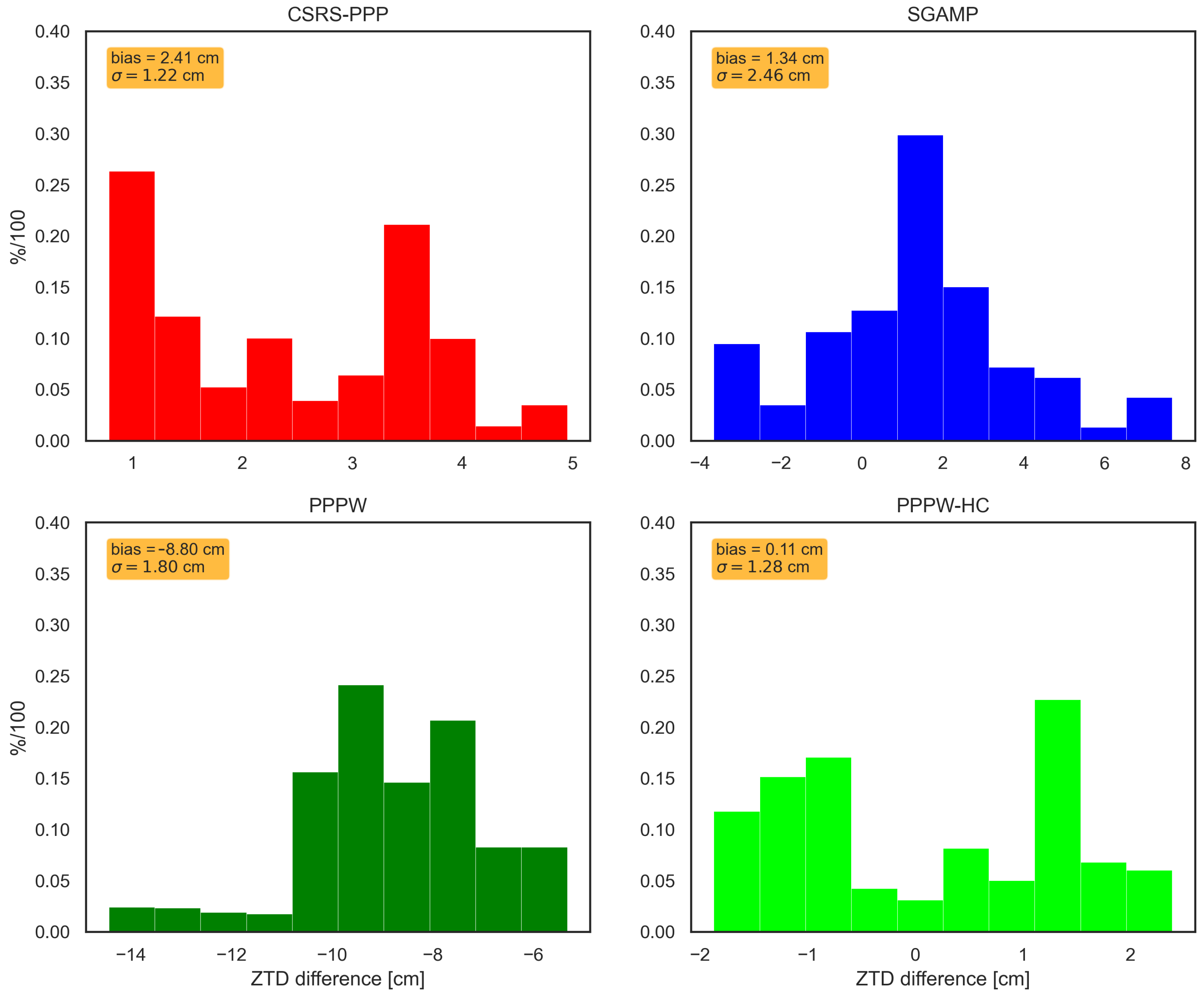
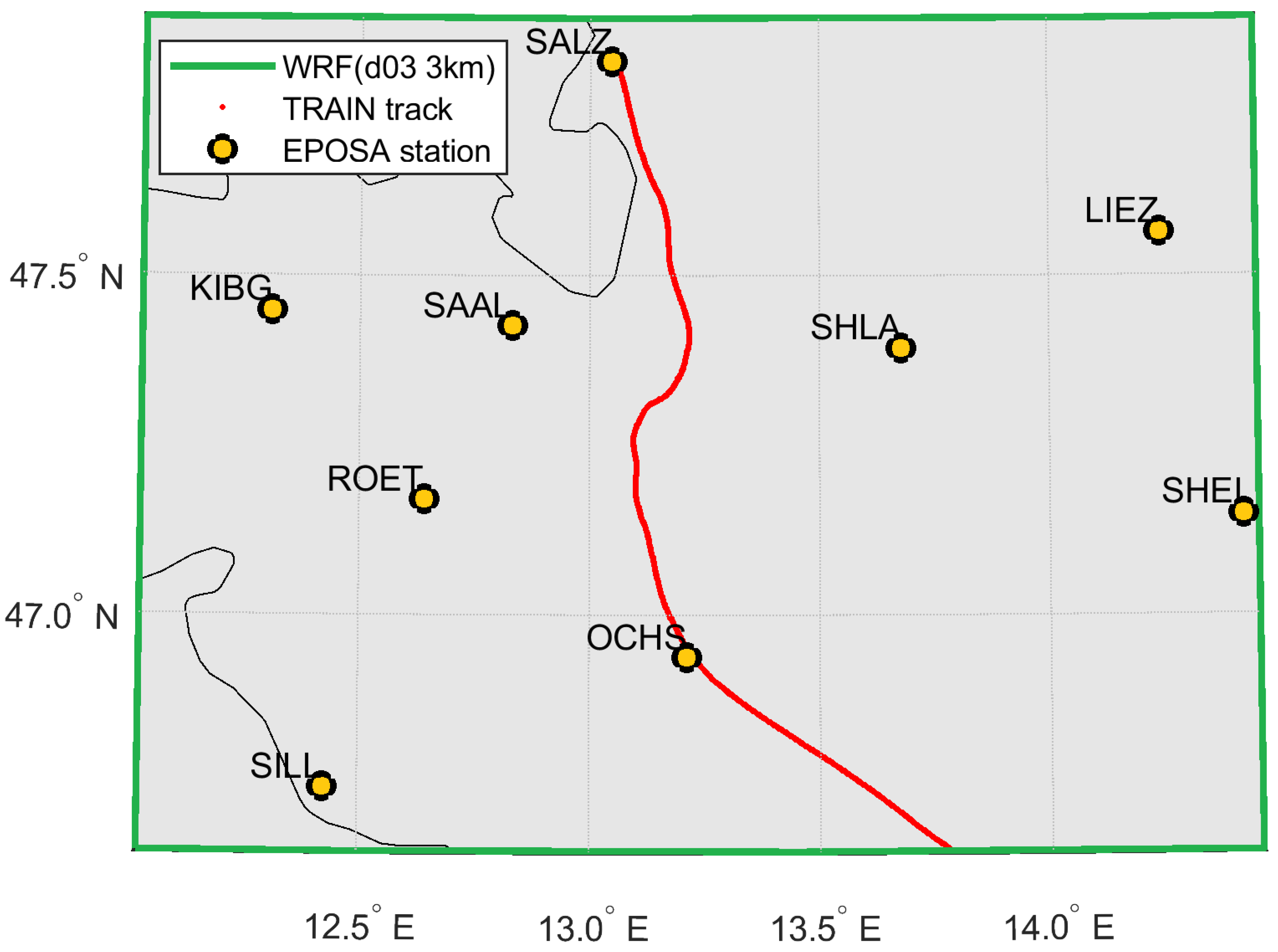
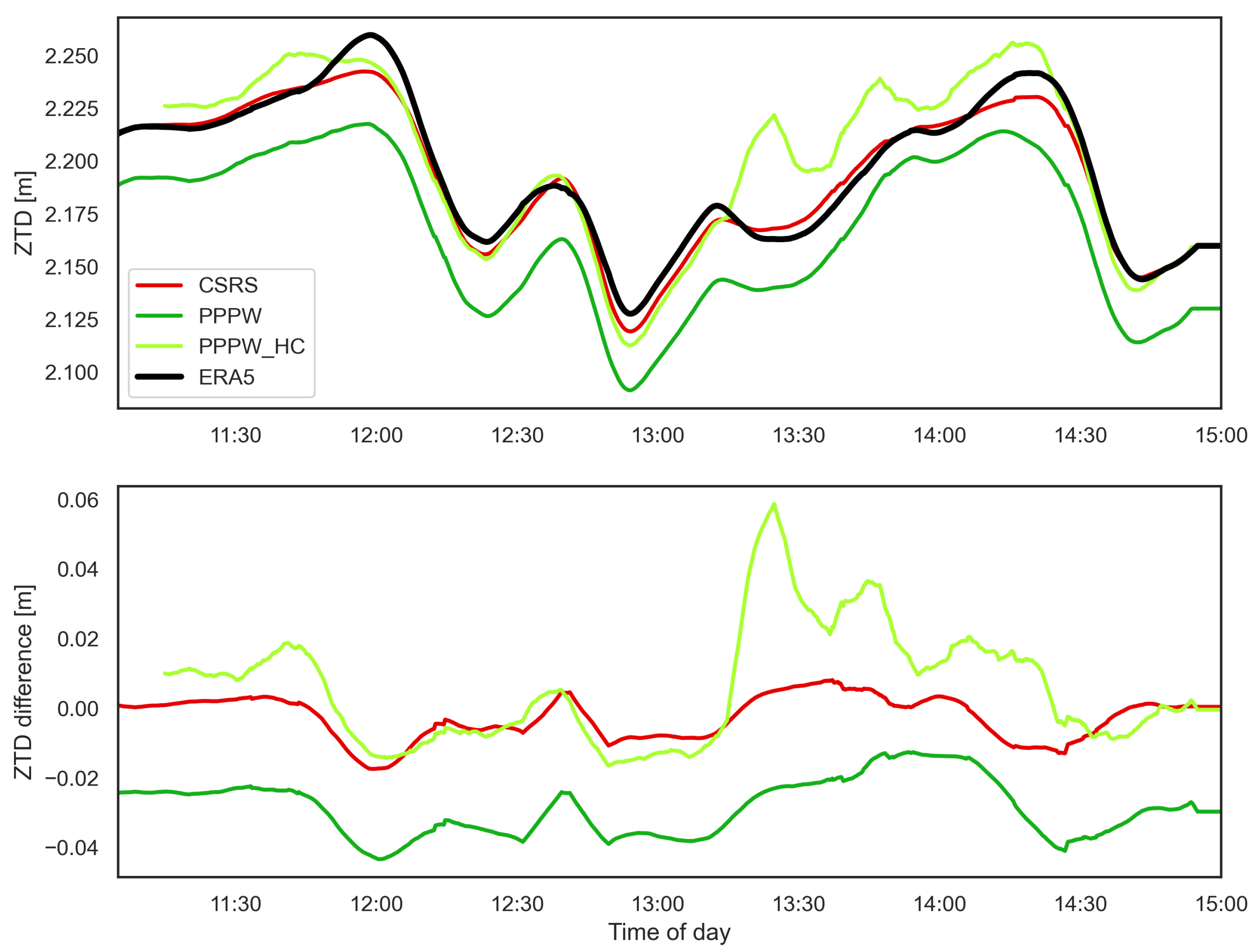
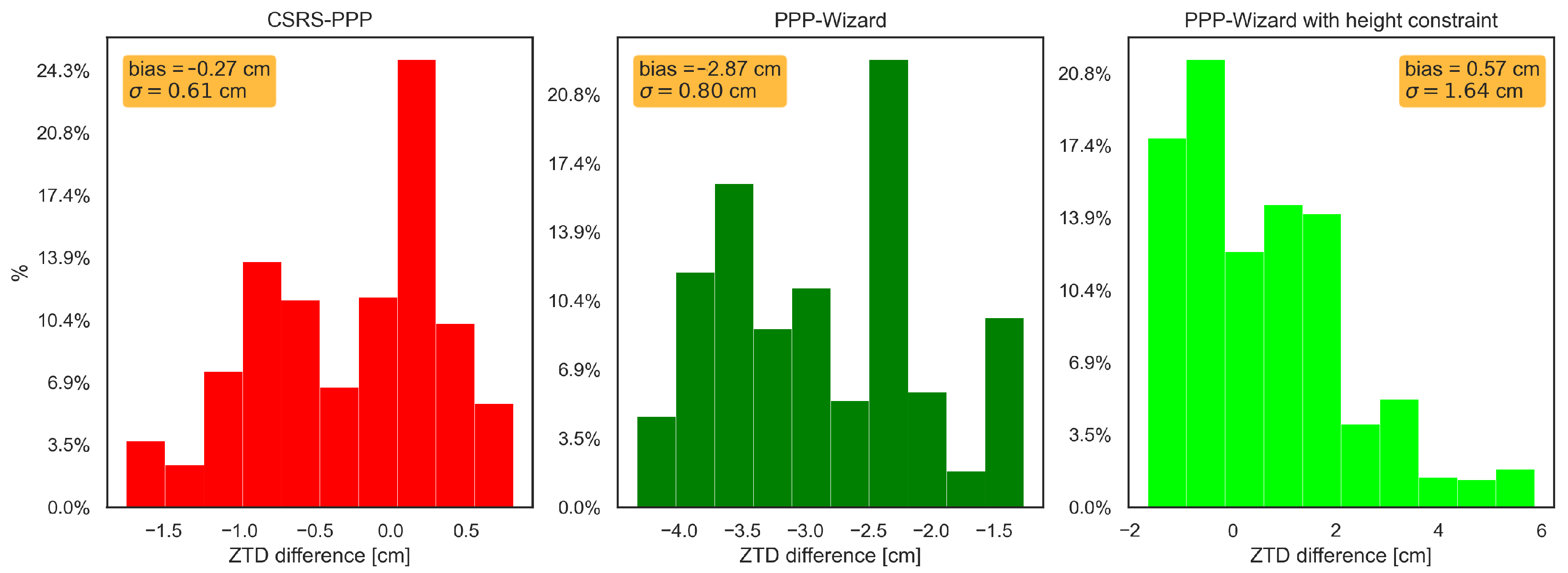
This study assessed the feasibility of deriving tropospheric parameters from GNSS receivers operated on trains and their usability for assimilation in NWP models. GNSS-ZTD estimates were produced by kinematic PPP processing using four different processing schemes based on different software packages (CSRS-PPP, SGAMP, PPPW, and PPPW-HC). The derived GNSS-ZTD estimates were validated using reference ZTD computed using ERA5-reanalysis data (ERA-ZTD) for two test cases (specific days and train travelling routes).

Although the initial results indicated a good overall agreement between GNSS-ZTD and ERA-ZTD, significant differences between processing schemes and test cases were visible. On average, the GNSS-ZTD solutions agreed at the low cm to mm level with ERA-ZTD. No distinctive superiority of one processing scheme over the others was recognized, although certain strengths and weaknesses of different schemes were visible.

As an alternative approach of ionospheric mitigation for SF data, the SEID model was modified to a kinematic mode and tested for CS1. The corresponding processing scheme (SGAMP) showed promising results, especially for highly challenging applications, such as presented here. SGAMP had a significantly lower bias (1.34 cm) compared to CSRS-PPP/PPPW (2.4/8.8 cm), and the correlation with ERA-ZTD was as high as for the other solutions. This makes the SGAMP processing scheme a promising candidate for future investigations on this topic, although further experience and tests are definitely required.

Furthermore, the performance of GNSS-ZTD estimation can be improved by applying a state constraint on the height coordinate in parameter estimation. With the aid of height coordinates of the investigated railway tracks, stored in the official track database of ÖBB, the Kalman filter module of the PPPW software was extended for such a height-constraint option. Solutions derived using this implementation showed medium to large improvements compared to the standard PPPW version and the other solutions. Overall, this provided the most accurate validation results for CS1 (bias ∼1 mm) and reasonable performance for CS2, although some problems were still found for certain periods.

In addition to the validation, the first assimilation tests for GNSS-ZTD data derived from trains were conducted for the presented test cases using the WRF model. A 4D-Var data assimilation scheme (WRFDA) was used for the assimilation of one hour GNSS-ZTD using a temporal resolution of one minute, i.e., 60 observations each case. Overall, the tests showed very promising results; however, (as for the validation results) distinctive differences between the test cases and processing schemes were evident. This is outlined by the comparison between both test cases.

For test case CS2, almost all GNSS-ZTD observations (CSRS-PPP: 100%, PPPW: 81%) passed the quality check of the WRFDA module, which performs the assimilation procedure within the WRF. On the other hand, the results for test case CS1 were significantly worse, as for most of the four tested processing schemes, not even half of the observations were accepted.

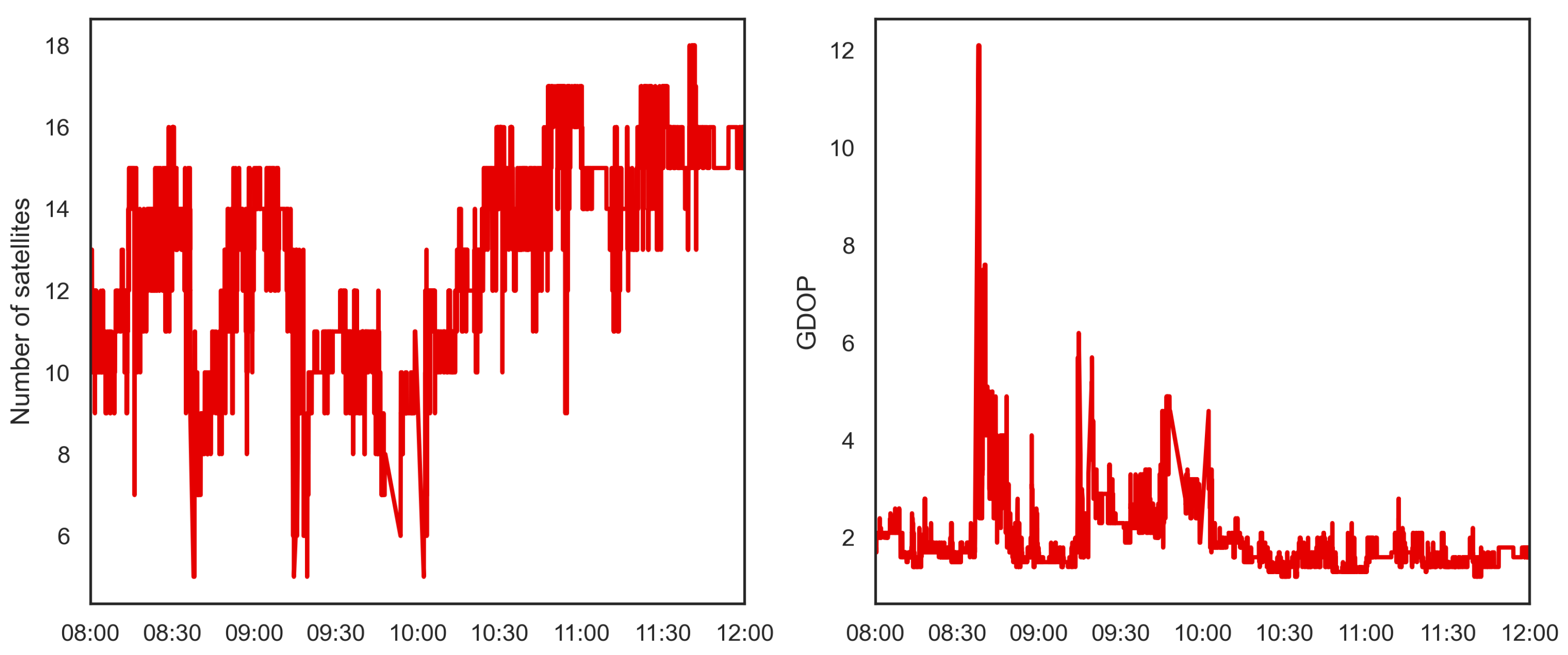
These differences most likely stem from the highly variable complexity of the environmental conditions (mountainous terrain and GNSS-denied areas, such as tunnels and urban areas), which might degrade both the NWP and GNSS performance. The major part of the experienced degradation for CS1 might be linked to the rather coarse representation of the topography in WRF (at 3 km in high mountainous regions) introducing the observed biases. This would also explain the local differences in the acceptance rate of GNSS-ZTD observations between the processed solutions.

For three out of four schemes (CSRS-PPP, PPPW-HC, and SGAMP) only observations in the first part of the investigated track were assimilated and, for PPPW, only observations from the end of the track. GNSS-specific error sources (e.g., multipath) will also still influence the results, but rather show in an increase of noise in the solutions, which has already been reduced by the moving-average filtering carried out in post-processing of the PPP solutions.

Furthermore, comparisons to independent GNSS-ZTD from geodetic reference stations were carried out for an initial assessment of the impact of train-borne ZTD on the WRF model state. The comparisons revealed differences from the mm range to 1–3 cm with respect to the independent ZTD estimates depending on the test case and processing scheme. These results indicate that further improvements in terms of quality of train-borne GNSS-ZTD are needed and to be tackled for in future studies.

However, the observed deviations (and even increases in bias) compared to the original model state were relatively small in most cases (few mm—1 cm) and could also be attached to other factors of uncertainty still present in this comparison, such as:

• Bias correction: Typically, a bias correction is applied to all GNSS-ZTD estimates from static stations used in NWP data assimilation. This is done to correct for inconsistencies between model and real-world topography, which could lead to errors in the mm to cm range, especially in mountainous areas. For static data, different approaches, including static or variational techniques, have been developed. However, no typical procedure exists for kinematic data up until now, and even simple averaging over a number of collected time series along the same track was not possible in this study due to the limited data resources.
• Formal errors of EPOSA-ZTD: Smaller deviations (in the mm range) between results with/without ZTD assimilation are often covered by the formal errors of the EPOSA-ZTD estimates.

Therefore, no solid conclusion on the impact of assimilating train-borne GNSS can be given for the present study. Moreover, as this investigation did not include the production of an actual (precipitation) forecast, it can only serve as a first indication of the usability of the GNSS-ZTD estimates in NWP. Therefore, the actual benefit of such data sets on a NWP forecast cannot yet be determined through verification of forecast products.

Overall, the presented study shows that reasonable ZTD estimates can be derived from train-borne SF-GNSS data. Although specific (pre-) processing has to be applied and the results are very sensitive to the chosen PPP setup, they are able to reach the desired quality for NWP applications. Although their actual impact on NWP forecasts is still uncertain and, therefore, a major topic for subsequent studies, chances for beneficial usage are high as data quality is expected to increase further with the planned installation of new-generation, low-cost (but DF) equipment on train fleets and more sophisticated processing approaches.

The initial idea of having a large fleet of trains (up to 1000 vehicles) and using each one of them as a meteorological sensor for atmospheric water vapour is expected to draw interest in the atmospheric science and NWP community, since the achievable horizontal and temporal resolution cannot be provided by any other sensor at the moment. Furthermore, a possible extension to near real-time ZTD estimation will be of great benefit for operational weather forecasting, particularly nowcasting applications.