Abstract
Entomological radar is an effective means of monitoring insect migration, and can realize long-distance and large-scale rapid monitoring. The stable tracking of individual insect targets is the basic premise underlying the identification of insect species and the study of insect migration mechanisms. However, the complex motion trajectory and large number of false measurements decrease the performance of insect target tracking. In this paper, an insect target tracking algorithm in clutter was designed based on the multidimensional feature fusion strategy (ITT-MFF). Firstly, multiple feature parameters of measurements were fused to calculate the membership of measurements and target, thereby improving the data association accuracy in the presence of clutter. Secondly, a distance-correction factor was introduced to the probabilistic data association (PDA) algorithm to accomplish multi-target data association with a low computational cost. Finally, simulation scenarios with different target numbers and clutter densities were constructed to verify the effectiveness of the proposed method. The tracking result comparisons of the experimental data acquired from a Ku-band entomological radar also indicate that the proposed method can effectively reduce computational cost while maintaining high tracking precision, and is suitable for engineering implementation.
1. Introduction
Insects are the most abundant and economically important group of terrestrial migrants [1]. They transfer enormous quantities of parasites, propagules, nutrients, and energy between regions, with substantial effects on the essential ecosystem [2]. However, some migratory pests can cause serious plant diseases [3] and virus transmission [4], creating great losses for human society. According to statistics, in China, pests cause an average of 17.5 billion kilograms of lost crop production annually [5]. Observations of migratory flight have utility for crop protection that aim to predict damaging pests and reduce their impacts [6]. Radar, having the advantages of a wide detection range all-time, is an effective technology to realize the large-scale and rapid monitoring of flying insects [7]. Meanwhile, the tracking of insect targets via high-resolution radar is of great significance for the study of insect migration mechanisms [8]. However, for the insect target tracking in cluttered environments [9], complex flight trajectories (such as parallel and crossing trajectories) and large numbers of false measurements not only make it difficult to accurately determine the sources of the measurements but also increase the calculation burden.
The Bayesian multi-target probability data association algorithm is widely used in engineering due to its superior tracking performance [10]. Multiple hypothesis tracking (MHT) is recognized theoretically as the optimal approach in Bayesian tracking, in which the hypotheses are propagated into the future in anticipation that subsequent data will resolve the uncertainty [11]; however, this process requires high computational complexity. Furthermore, the joint probabilistic data association algorithm (JPDA), where a track is updated by a weighted sum of all measurements in its gate, can maintain excellent performance in the case of dense clutter and missed detections [12]. Nevertheless, the intensive computations limit its practical applications.
In terms of reducing computational complexity, in [13], a cheap JPDA algorithm was designed using an ad hoc formula to simplify association probability calculations. On this basis, a suboptimal JPDA algorithm was developed [14], in which joint event probability is simplified by assuming that the probability of detection is one, or very nearly one, using partial joint events. Although cheap JPDA and suboptimal JPDA can greatly reduce computational complexity, the tracking performance degrades in the presence of dense clutter. Furthermore, from the perspective of fuzzy mathematics theory, a joint probabilistic data association algorithm based on all-neighbor fuzzy clustering (ANFCJPDA) was developed [15]. In this algorithm, the predicted position of the target is set as a cluster center, and the association probabilities are calculated according to fuzzy clustering. In [16], a rough set probabilistic data association (RS-PDA) algorithm was presented, in which rough set theory is introduced to judge the origination of measurements in the validation regions, and the measurements in the intersection region can then be processed discriminatingly. The above two algorithms can maintain a good tracking performance in the presence of clutter, but their time consumption is only slightly less than that of JPDA. Therefore, it is difficult to achieve a balance between computational cost and tracking performance in the existing optimized JPDA algorithm, which makes it difficult to ensure excellent performance in insect target tracking scenarios.
Another challenging problem for multitarget tracking is differentiating between measurements arising from the target of interest and measurements originating from other target returns or clutter. As a result, accurate judgments of measurement origin would help enhance tracking accuracy. In addition to target position measurements, the Doppler component [17] is widely used in combination with kinetic information as an additional discriminant of measurement origin. However, when target Doppler is included in the measurement vector, a nonlinear filter process is required to deal with the nonlinearity between the target’s kinematic state and Doppler measurement, which brings additional computation. Moreover, in many studies, several non-kinematic features were utilized to assist in determining the measurement source. In [18,19], four different types of sensor data were introduced for target tracking: kinematic measurements (target position and velocity), features (such as radar cross section (RCS), signal strength, and wing span), attributes (such as the number of aircraft engines and type of radar), and categorical features (such as wing span, with only a few types of targets). In [20], target class information was integrated into the data association process, and the association results was improved when the kinematic likelihoods were similar for different targets. However, for migrating insect groups, the individuals in the group are usually of the same category, potentially invalidating the class information. Moreover, amplitude is also a vital information to discriminate against false measurements and further improve tracking performance. In [21], the target RCS was used to track multiple Rayleigh targets. Further, in [22], based on the probabilistic data association filter with amplitude information [23], appropriate amplitude likelihoods were specified to cope with K-distributed clutter. Nevertheless, in the above algorithm, only a single-dimensional feature is utilized, making it difficult to achieve excellent performance in complex insect target tracking scenarios.
For a rotating-polarization radar [24], which is generally used to observe insect migration, many feature parameters related to the insect target characteristics can be measured, besides the RCS parameters. Therefore, in this paper, an insect target tracking algorithm in clutter was designed based on the multidimensional feature fusion strategy, which is mainly aimed at data association processing, one of the most important aspects of tracking. For the echo data collected by high resolution and fully polarimetric entomological radar, multidimensional feature parameters of the measurements are extracted, and then these features are fused based on the proposed multidimensional feature fusion strategy. The obtained membership of the multidimensional feature fusion can effectively improve the accuracy of measurement-to-track associations. Further, in this work, a distance-correction factor was introduced to PDA to modify the association probability of the measurements falling into the crossing gate, thereby avoiding the split of association probability matrix in JPDA and ensuring the multitarget tracking performance under the premise of low computation.
The remainder of this paper is organized as follows. In Section 2, the multiple target tracking problem is described and the problems in the insect target tracking scenario are analyzed. Section 3 presents the principles of the proposed insect target tracking algorithm based on the multidimensional feature fusion strategy. Section 4 introduces comparisons of simulations and experimental data results between the proposed method and traditional methods. The discussion and future work are presented in Section 5, and the conclusions are given in Section 6.
2. Multiple Target Tracking Problem Formation
Assume that the number of targets in the surveillance is , and the dynamic and measurement models for target , , are defined as
where denotes the state vector of target at time , and denotes the measurement vector. is the state transition matrix and is the measurement transition matrix. is the process noise distribution matrix. and are zero-mean mutually dependent white Gaussian noise vectors with covariance matrices and , respectively.
Suppose the number of validated measurements at time is . The validated measurement set at time is denoted as . Generally, JPDA [12] is the preferred method to handle multitarget tracking in clutter. The following is a brief introduction to the process of multi-target tracking based on JPDA.
The state prediction and the measurement prediction at time are defined as
The predicted covariance is defined as
The innovation covariance is
The filter gain is
A validation gate is designed to select the validated measurements of the target , and is represented as
where the value of parameter can be obtained from tables of chi-square distribution based on the probability that the true measurements will fall in the elliptical gate. On this basis, the following validation matrix can be defined as follows:
where refers to the binary elements that indicate whether measurement lies in the validation gate for target . Index indicates “no target” and the corresponding column of has all units, which represents each measurement may originate from clutter or a false alarm.
The state estimation for target is
is combined innovation and defined as
where . is the association probability that the validated measurement originates from target at time and is calculated by
where is the th feasible event, and is the event that the measurement originates from target in the th feasible event. denotes the cumulative measurement set up to time , and is the number of the feasible events.
For multi-target tracking based on JPDA, the probabilities of all feasible joint events should be calculated. As the number of targets and clutter density increase, the joint events also increase exponentially, which result in huge amounts of calculations. Moreover, only the position distribution is considered in . Consequently, it is difficult to achieve excellent tracking performance for insect target tracking in a cluttered background.
3. Insect Target Tracking Algorithm Based on Multidimensional Feature Fusion
To improve the tracking accuracy of insect targets in cluttered environments with low computational cost, we designed an insect target tracking algorithm based on the multidimensional feature fusion strategy. The flow diagram is shown in Figure 1. Based on the framework of the probabilistic data association algorithm, two key modules are added to better deal with insect target tracking scenarios, as shown in the grey boxes in Figure 1. On the one hand, a multidimensional feature fusion strategy based on fuzzy logic synthesis is proposed to calculate the membership of multi-dimensional feature fusion between the measurements and the existing target track, thereby improving the accuracy of measurement-to-track associations. On the other hand, a distance correction factor is introduced to correct the association probability of the measurements falling into the crossing gate, enabling the PDA [23] to handle multitarget tracking with a low computational load. Finally, the association probability of PDA is modified based on the membership of multidimensional feature fusion and the distance correction factor.
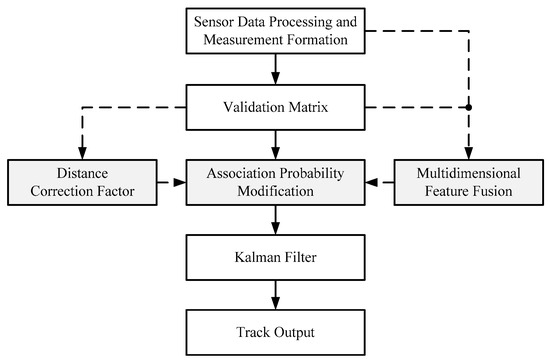
Figure 1.
Flow diagram of the proposed insect target tracking algorithm.
3.1. Multidimensional Feature Fusion Strategy
A key problem of multitarget tracking in cluttered environments is the uncertainty of measurement-to-track data associations, which means it is difficult to correctly determine the sources of measurements by only relying on kinematic information (target position and velocity). According to the previous literature [24,25], it can be concluded that an insect’s polarization pattern and scattering matrix (SM) are closely related to the insect’s geometry and composition, which can be measured using a fully polarimetric radar. This type of radar can measure all four linear-polarization receive–transmit (HH, HV, VH, VV) backscattering combinations. The corresponding feature parameters reflect the inherent characteristics of the insect target and are beneficial to distinguish the target and clutter measurements.
Therefore, a multidimensional feature fusion strategy based on fuzzy logic synthesis theory is proposed to obtain the membership of the multidimensional feature fusion. The flow diagram of this strategy is shown in Figure 2. It mainly includes four key modules, as shown in the grey boxes. Firstly, the feature parameters of measurements are extracted in real time. Secondly, a new membership function, the fitting probability distribution function (PDF) ratio of the target and clutter feature parameters, is designed to adapt to the characteristics of insect targets. Meanwhile, the analytic hierarchy process (AHP) is employed to calculate the weight of each feature. In the end, multidimensional feature fusion is realized by fuzzy logic synthesis.
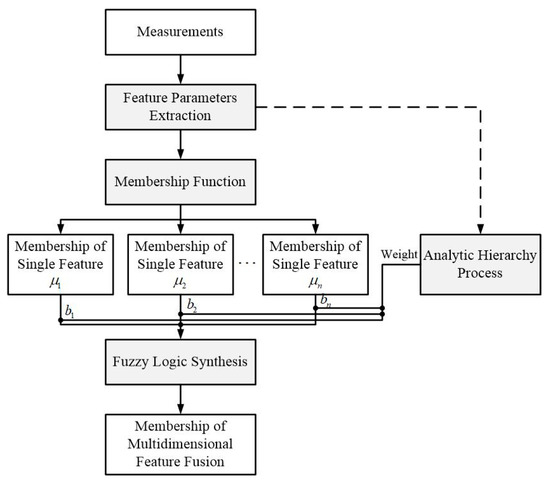
Figure 2.
Principle diagram of the multidimensional feature fusion strategy.
3.1.1. Feature Parameter Exaction
The feature parameters extracted by the polarization pattern and SM are represented as , , and , and their definitions and physical meanings are as follows.
According to [26], the insect’s polarization pattern can be expressed as
where is the direction of linear polarization, and represents the average of the RCS over all polarization angles (360°). and are parameters of theoretical model in natural coordinates. and are magnitudes of harmonic modulations representing elongated component and cruciform component respectively.
The backscatter of a target is defined by the scattering matrix. For monostatic radar, the general form of the insect SM is modeled as follows [26,27]:
where , , and represent the square roots of the RCSs, , , and (unit: ), respectively. and are the maximum of the copolar polarization pattern and the value in the orthogonal direction, respectively, and is the cross polarisation element magnitudes. They can be calculated from , , and [26]. and are the phases related to target properties. The eigenvalue of is defined as and . For fully polarimetric radar, by transmitting orthogonally polarized signals, the inset SM elements can be measured from the echo signals of different polarization directions.
According to [26], and are the invariant target parameters of SM, which can be calculated by the Graves matrix. The Graves matrix [28] is defined as
where superscript represents combined conjugate and transpose operations.
and are the two eigen values of the Graves matrixDet [29,30]. Assuming that , then
where
The determinant of the Graves matrix can be expressed as the product of its two eigenvalues
The determinant is represented by variable :
An “eigen parameter” is defined as
where, represents the phase difference between and .
3.1.2. Membership Function Definition
The membership function [31] is the core element when using fuzzy synthesis theory to solve practical problems. Commonly used membership functions include normal distribution and distribution. Considering the characteristics of insect targets, a new membership function is proposed. For each feature, the ratio of the target and the clutter feature parameter’s fitting PDF is defined as the membership function. Correspondingly, the membership of the th feature is expressed as
where, is the target PDF of the th feature, is the clutter PDF of the th feature, and is the feature parameter value calculated by the measurement information.
As a result, the statistical models for the target and clutter measurement feature parameters need to be known a priori to achieve multi-dimensional feature fusion. For this reason, the PDF of the feature parameters defined in Section 3.1.1 was modeled based on the experimental data collected by the fully polarimetric entomological radar in Ku-band in August 2019 in Lancang, Yunnan province, China. The experimental scenario and parameters are detailed in Section 4.3.1. The measurements, after undertaking constant false alarm rate (CFAR) detection process, included not only kinetic information but also the feature parameters extracted in Section 3.1.1. Here, the number of target trajectory samples is 5000, and the number of measurements of each trajectory is greater than 100. The ground clutter data were collected by the radar at different elevation angles and distances.
Next, based on the least squares fitting criterion and Kolmogorov–Smirnov (K–S) fitting goodness test methods [32], four typical distribution models (Lognormal, Weibull, Gamma, and Normal distribution) were employed to fit the statistical characteristics of the four feature parameters. The least squares fitting error and K–S test parameters are shown in Figure 3 and Figure 4, respectively. Then, on the basis of the fitting results, the fitting model of the four feature parameters was selected, as shown in Table 1. Furthermore, Figure 5 shows the PDF fitting curves for the different feature parameters of insect targets and clutter. It can be seen that the extracted features present obvious distinction between the target and clutter measurements.
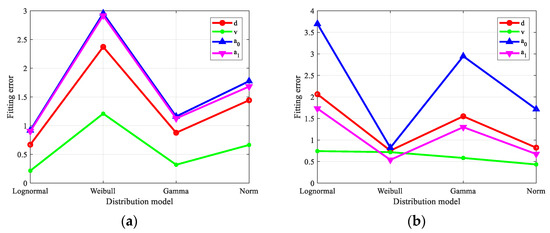
Figure 3.
The least squares fitting error: (a) target, (b) clutter.
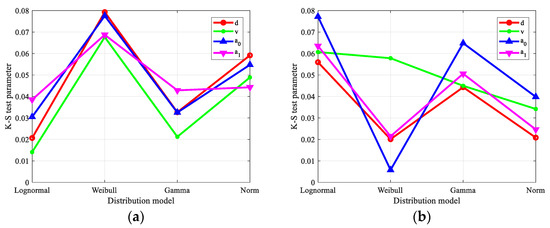
Figure 4.
K–S test parameter: (a) target, (b) clutter.

Table 1.
The selected statistical model for different feature parameters.
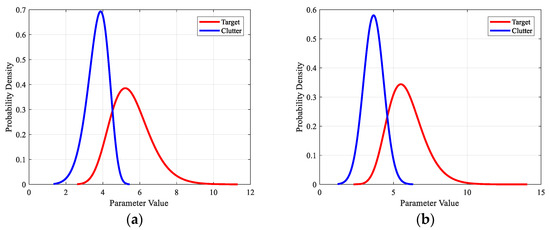
Figure 5.
PDF fitting curves for the different feature parameters of insect targets and clutter: (a) , (b) , (c) , (d) .
3.1.3. Feature Weight Assignment
As shown in Figure 5, the overlapping areas of target and clutter PDF are different for different features. The smaller the overlap area is, the better the distinction. Therefore, it is necessary to define a scheme to achieve feature weight assignment.
The analytic hierarchy process is an effective way to determine the weight assignment [33,34] and is widely employed to quantitatively describe the weight value of each feature. The first step of the AHP method is to evaluate the relative importance of each pair of factors and to build a pairwise comparison matrix. In this section, the overlapping area of the PDF fitting model of the target and clutter feature parameters is used to measure the discrimination of those features, expressed as , , , and . Then the ratios of the PDF overlapping areas between multiple features are taken as the corresponding elements of the comparison matrix, as shown in Table 2.

Table 2.
Pairwise comparison matrix of multiple factors.
Based on the comparison matrix, an arithmetic mean method is adopted to calculate the assigned weight of each feature. Specifically, we use the arithmetic mean value of all column vectors to calculate the weight vector. The expression is as follows:
where is the element in the comparison matrix, and is the dimension of matrix, i.e., the number of feature parameters.
3.1.4. Fuzzy Logic Synthesis
Fuzzy logic synthesis [35] is implemented using the weighted average method. Consequently, the multidimensional feature fusion membership of each measurement that falls into the target validation gate at time can be obtained, as follows:
where is the number of measurements in the target validation gate, and is the normalization factor. is the th feature membership of measurement and target , which can be calculated by (22).
3.2. Distance-Correction Factor Calculation
For the scenario of insect target tracking, the JPDA, due to its combinatorial nature, comprises the bulk of the computational load in multitarget tracking processing. The PDA uses all of the validated measurements with different probabilities to update the target states, but it does not take into account the measurements in the crossing gate and is also not suitable for multitarget tracking. Therefore, here, we introduce a distance-correction factor into PDA to modify the association probability of the measurement in the crossing gate, enabling the algorithm to better handle multiple target tracking and achieve a compromise between the quantity of calculations and the tracking performance. The calculation steps for the distance-correction factor are described as follows:
Firstly, the target set is divided based on the validation matrix defined in (9). Assume that is the number of validation gates that measurement lies in, i.e., . indicates that measurement might have originated from multiple targets. In this case, the corresponding target index set is defined as
Then, the Mahalanobis distance [36] is employed to measure the distance between measurement and the center of the validation gate , the size of which measures the competition degree between multiple crossing gates and the involved measurements. The mathematical expression is
Here, the smaller the distance, the higher the relevance degree between measurement and target . Therefore, the distance-correction factor between measurement and target is defined as
3.3. Association Probability Matrix Modification
The number of candidate measurements of target is denoted as , and the validation measurement set originating from target at time can be obtained based on the validation matrix denoted as :
The association probability that measurement originated from target , as calculated by the PDA algorithm [23], is defined as
where, is the feasible event that the measurement originates from target , and denotes the measurement set up to frame .
However, in a cluttered environment, the number of measurements is usually greater than the number of targets. Thus, the source of measurements within the crossing gate needs to be considered. Moreover, only the position distribution is considered in (28). It is, therefore, difficult to deal with complex insect target tracking.
Thus, in the proposed ITT-MFF, the association probability , defined in (28), is modified by the multidimensional feature fusion membership in (24) and the distance-correction factor in (26). The utilization of more dimensional features is beneficial to improving the accuracy of measurement-to-track associations, and the introduction of the distance-correction factor can realize multi-target tracking under the premise of a low computational cost. The modified expression is defined as
4. Simulations and Experimental Results
In this section, the tracking performance of the proposed insect target tracking algorithm is first evaluated in the simulation scenarios with different target numbers and clutter densities. Then, based on the real observational data acquired from the Ku-band entomological radar, the tracking results in a cluttered environment also verify the effectiveness of the proposed method.
4.1. Tracking Performance Evaluation Criteria
Three evaluation criteria were considered to evaluate the tracking performance of the algorithms.
- Success Tracking Ratio (STR)
If a track can maintain more than frames and ensure that the mean of the tracking error is less than the standard deviation of measurement noise , the trajectory is considered to be tracked successfully, thereby satisfying:
where is the state estimation at time , and is the real value. is the number of scan frames.
- Optimal Subpattern Assignment (OSPA) Statistic
The OSPA statistic [37] gives an evaluation of the performance of a tracking algorithm. The metric includes two parameters, and , where limits the penalty assigned for false or lost tracks, and determines the penalty assigned for estimates that are not close to any true target.
The OSPA statistic between the set of estimated state vectors and the set of true target states can be expressed as
where ; represents the distance between and ; is the -th state of ; represents the set of all permutations of the true target states; is the number of measurements; and is the number of targets. In the following simulation, we set the values as and .
After times Monte Carlo simulation runs, the mean OSPA (MOSPA) is defined by taking the average of the errors, which is expressed as
- Running Time
To assess the computational requirements of the proposed method, the running time (denoted by ) is obtained by computing the average CPU time in MATLAB 2017 on an Intel Core 2.40 GHz two-CPU computer operating under Windows 10.
4.2. Simulations
4.2.1. Simulation Scenarios
In this section, a crossing target scenario is simulated. The number of targets is set to two, four, and six, as shown in Figure 6. The targets move towards each other, cross at a certain moment, and then move away from each other. In each simulation scenario, the three clutter density values are set to 10−5, 10−4, and 10−3, respectively. The tracking filter parameters are shown in Table 3. The PDF of the target and the clutter feature parameters satisfy the statistical model in Section 3.1.2.
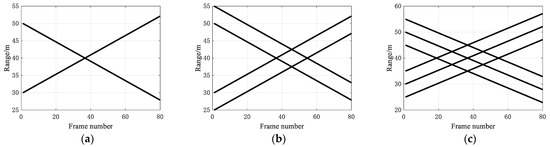
Figure 6.
Cross trajectory scenarios with different numbers of targets: (a) two targets; (b) four targets; (c) six targets.

Table 3.
Simulation Parameters.
4.2.2. Result Comparisons
Based on the performance evaluation criteria listed in Section 4.1, the proposed ITT-MFF algorithm is compared with several probability data association algorithms (JPDA [12], cheap JPDA [13] and suboptimal JPDA [14]) in different simulation scenarios. At the same time, for fairness, a comparison with the ITT-NoMFF (only the distance-correction factor is introduced) algorithm is added to verify the performance in the absence of multidimensional feature fusion. In addition, when the clutter density is 10−3 and the number of targets is six, the result of the JPDA algorithm is not shown due to the high memory requirements and time-consuming.
- STR
The comparison results of the algorithm’s STR in different simulation scenarios are shown in Table 4. For JPDA, suboptimal JPDA, cheap JPDA, and ITT-NoMFF, without the aid of multidimensional features, the STR decreases with an increase of clutter density. With an increase in the number of targets, the magnitude of this decline increases. Notably, when the clutter density is 10−3 and the number of targets is greater than four, the STR drops to less than 50%. However, the ITT-NoMFF algorithm is superior to cheap JPDA and suboptimal JPDA, and is basically the same as the JPDA algorithm, which verifies the validity of the distance-correction factor. Besides, the proposed ITT-MFF algorithm is robust in cluttered background due to the use of multidimensional feature fusion. Moreover, when the clutter density is 10−3, the successful tracking ratio of ITT-MFF can still be guaranteed as greater than 90%. Therefore, compared to other algorithms, ITT-MFF offers more stable tracking performance.

Table 4.
STR comparisons.
- MOSPA
The MOPSA metric is an effective means to evaluate the algorithm’s tracking precision. To avoid the impact of unsuccessful tracking results on the evaluation in the process of multiple Monte Carlo simulations, only the tracking accuracy of successful tracking is evaluated. The MOPSA distance comparison results in different simulation scenarios are shown in Figure 7, Figure 8 and Figure 9. It can be seen that with an increase in clutter density, the MOSPA distances of JPDA, suboptimal JPDA, Cheap JPDA, and ITT-NoMFF gradually increase. However, ITT-NoMFF outperforms the other three methods.
Figure 7.
MOSPA comparisons of the two target scenarios with different clutter densities: (a) ; (b) ; (c) .
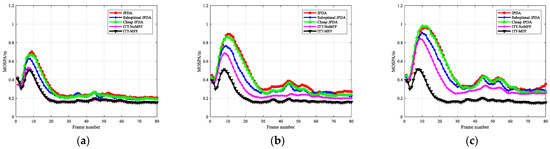
Figure 8.
MOSPA comparisons of the four target scenarios with different clutter densities: (a) ; (b) ; (c) .
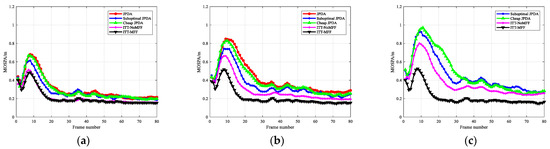
Figure 9.
MOSPA comparisons of the six target scenarios with different clutter densities. (a) ; (b) ; (c) .
When the multi-dimensional feature fusion strategy is introduced, the proposed ITT-MFF algorithm still guarantees high tracking accuracy with an increase in clutter density, which indicates that the extracted features can effectively improve the distinction between the target and clutter measurements.
- Running Time
Running time comparisons of different algorithms are shown in Table 5. For the JPDA algorithm, as the number of targets increases, the running time increases rapidly. Moreover, the greater the clutter density is, the larger the growth rate. Such increases are unacceptable in practical applications. Since cheap JPDA and suboptimal JPDA simplify the calculations of association probability, the running time is reduced greatly. However, the tracking precision in dense clutter is difficult to meet the demand. Although the running time of the proposed ITT-MFF algorithm increased slightly compared to the two simplified algorithms, it will not, like JPDA, increase rapidly with an increase in clutter density or number of targets. Moreover, compared to ITT-NoMFF, the multidimensional feature fusion processing does not entail much extra computation.

Table 5.
Running time comparisons (unit: s).
4.3. Experiment Data Validation
4.3.1. Experiment Scenarios
The engineering practicability of the proposed ITT-MFF algorithm is verified based on experimental field data. In August 2019, the echo data were collected using a Ku-band high resolution and fully polarimetric entomological radar (shown in Figure 10) in Lancang, Yunnan province, China. The experimental scene is shown in Figure 11. The basic parameters of the radar system are shown in Table 6.

Figure 10.
Ku-band entomological radar.

Figure 11.
Experimental scene.

Table 6.
The basic parameters of the radar system.
After CFAR detection processing, the target measurement sets were acquired, as shown in Figure 12. For this study, we selected six insect target trajectories, including parallel and crossing situations. To evaluate the algorithm’s tracking performance in different clutter densities, a semi-physical simulation experiment [38] was adopted. We assumed that the positions of the clutter measurements were uniformly distributed around the target measurements, and set the clutter density to 10−3. The target feature parameters were obtained in real time based on the theoretical formulas in Section 3.1.1, and the clutter feature parameters were subjected to the PDF distribution model obtained in Section 3.1.2.
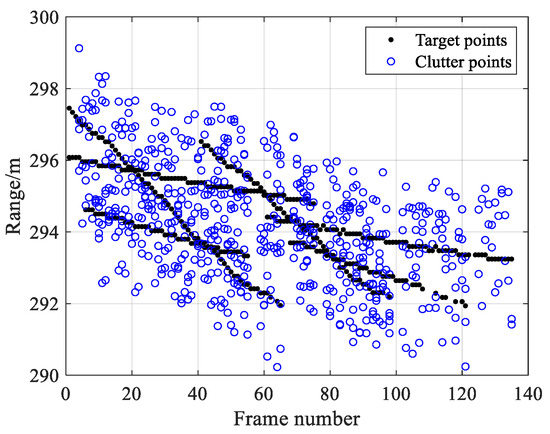
Figure 12.
Measurements after CFAR detection.
4.3.2. Result Comparisons
Based on the practical measurements of insect targets, a comparative analysis of various algorithms was conducted based on the filter result diagram and running time.
The filtering results are shown in Figure 13. It can be seen that because of the interference of the clutter points, the cheap JPDA, suboptimal JPDA, JPDA, and ITT-NoMFF algorithms all have false associations. Especially around the 70th frame, when the target trajectory crosses and the distance is small, the performance significantly degrades. However, the proposed ITT-MFF algorithm can effectively distinguish target and clutter measurements based on multidimensional feature fusion, thereby reducing the number of false associations and achieving stable tracking in a cluttered environment.
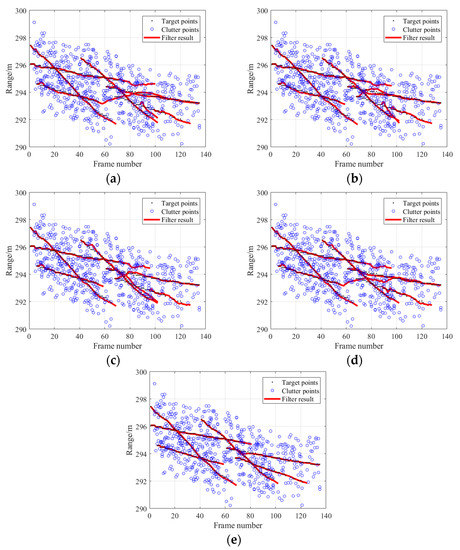
Figure 13.
Filtering result comparisons: (a) cheap JPDA, (b) suboptimal JPDA, (c) JPDA, (d) ITT-NoMFF, (e) ITT-MFF.
Correspondingly, the running time comparison results are shown in Table 7. It can be seen that, although the running time of ITT-MFF is slightly higher than that of cheap JPDA and suboptimal JPDA, it is still much lower than that of JPDA.

Table 7.
Running time comparison (Unit: s).
5. Discussion
For insect target tracking in a cluttered environment, complex flight trajectories (such as parallel and crossing trajectories) and large numbers of false measurements not only make it difficult to accurately determine the origins of the measurements but also increase the calculation burden. The JPDA algorithm can maintain an excellent performance in the case of dense clutter, but the expensive computational cost is a critical problem in applying the algorithm. Therefore, determining how to achieve a tradeoff between computation and tracking accuracy is a primary problem in achieving insect target tracking. To this end, we designed an insect target tracking algorithm based on multidimensional feature fusion strategy.
The simulation experiments show that the time consumption of JPDA algorithm increases exponentially with an increase in the number of targets. Although the suboptimal JPDA and cheap JPDA offer high computing efficiency, their performance degrades seriously in crossing trajectory and densely cluttered environments. The main reason for this decrease in tracking performance is the difficulty in achieving the correct discrimination of measurement sources in clutter. The method proposed in this paper fully considers the scattering characteristics of insect targets and improves the data association accuracy in cluttered environments based on multidimensional feature fusion strategy. A distance-correction factor was also introduced into the PDA algorithm to ensure the effectiveness of multi-target tracking processing. The experimental data processing results further show that, compared to other algorithms, this method can realize the stable tracking of insect targets with a low computational cost.
The accurate extraction of insect target trajectories is of great significance to the study of insect migration mechanisms. However, the research in this paper mainly focuses on the tracking algorithm for individual insect targets. In future research, we will consider using the movement characteristics of group targets to track larger numbers of insects. In addition, multi-sensor tracking systems will be employed to obtain more target information and deal with more complex tracking scenarios.
6. Conclusions
In this paper, an insect target tracking algorithm in clutter based on the multidimensional feature fusion strategy was proposed. Based on the simulation results under different scenarios, this method achieved a higher successful tracking rate and tracking accuracy, which means that multidimensional feature fusion can effectively improve the accuracy of data association. In addition, compared to the JPDA algorithm, the running time was greatly reduced and there was no exponential explosion in computations, which indicates that introducing the distance-correction factor avoided splitting the confirmation matrix, and also provided excellent performance in the crossing track. To summarize, the proposed method can guarantee an excellent tracking performance in cluttered background with a low computing cost and is suitable for insect target tracking scenarios.
Author Contributions
Conceptualization, L.F. and W.T.; methodology, L.F. and W.T.; software, L.F.; validation, L.F. and R.W.; formal analysis, R.W.; investigation, R.W.; resources, C.Z.; data curation, L.F.; writing—original draft preparation, L.F. and W.T.; writing—review and editing, R.W. and L.F.; visualization, C.Z.; supervision, C.H.; project administration, C.H.; funding acquisition, C.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 31727901) and the National Natural Science Foundation of China (Grant No. 61971037).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chapman, J.W.; Reynolds, D.R.; Wilson, K. Long-range seasonal migration in insects: Mechanisms, evolutionary drivers and ecological consequences. Ecol. Lett. 2015, 18, 287–302. [Google Scholar] [CrossRef] [Green Version]
- Hu, G.; Lim, K.S.; Horvitz, N.; Clark, S.J.; Reynolds, D.R.; Sapir, N.; Chapman, J.W. Mass seasonal bioflows of high-flying insect migrants. Science 2016, 354, 1584–1587. [Google Scholar] [CrossRef] [Green Version]
- Hunter, D.; Deveson, T. Forecasting and management of migratory pests in Australia. Insect Sci. 2002, 9, 13–25. [Google Scholar] [CrossRef]
- Reynolds, D.R.; Chapman, J.W.; Harrington, R. The migration of insect vectors of plant and animal viruses. Adv. Virus Res. 2006, 67, 453–517. [Google Scholar] [CrossRef] [PubMed]
- The Ministry of Agriculture of the People’s Republic of China. China Agricultural Statistics 2013; China Agriculture Press: Beijing, China, 2014.
- Drake, V.A.; Wang, H. Recognition and characterization of migratory movements of Australian plague locusts, Chortoicetes terminifera, with an insect monitoring radar. J. Appl. Remote Sens. 2013, 7, 075095. [Google Scholar] [CrossRef] [Green Version]
- Drake, V.A.; Wang, H. Ascent and descent rates of high-flying insect migrants determined with a non-coherent vertical-beam entomological radar. Int. J. Remote Sens. 2019, 40, 883–904. [Google Scholar] [CrossRef]
- Long, T.; Hu, C.; Wang, R.; Zhang, T.; Kong, S.; Li, W.; Cai, J.; Tian, W.; Zeng, T. Entomological radar overview: System and signal processing. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 20–32. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, Y.; Tian, W.; Cai, J.; Hu, C.; Zhang, T. Fast implementation of insect multi-target detection based on multimodal optimization. Remote Sens. 2021, 13, 594. [Google Scholar] [CrossRef]
- Li, S.; Xu, Y. Joint probabilistic data association algorithm based on adaptive cluster probability matrix. J. Southwest Jiaotong Univ. 2017, 52, 340–347. [Google Scholar] [CrossRef]
- Blackman, S.S. Multiple hypothesis tracking for multiple target tracking. IEEE Aerosp. Electron. Syst. Mag. 2009, 19, 5–18. [Google Scholar] [CrossRef]
- Fortmann, T.; Bar-Shalom, Y.; Scheffe, M. Sonar tracking of multiple targets using joint probabilistic data association. IEEE J. Ocean. Eng. 2003, 8, 173–184. [Google Scholar] [CrossRef] [Green Version]
- Fitzgerald, R.J. Development of practical PDA logic for multitarget tracking by microprocessor. In Proceedings of the American Control Conference, Seattle, WA, USA, 18–20 June 1986; pp. 889–898. [Google Scholar] [CrossRef]
- Roecker, J.A.; Phillis, G.L. Suboptimal joint probabilistic data association. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 510–517. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; He, Y.; Sun, S. Joint probabilistic data association algorithm based on all-neighbor fuzzy clustering in clutter. J. Electron. Inf. Technol. 2016, 38, 1438–1445. [Google Scholar] [CrossRef]
- Ni, L.; Gao, S.; Feng, P.; Zhao, K. Rough sets probabilistic data association algorithm and its application in multi-target tracking. Def. Technol. 2013, 9, 208–216. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Musicki, D.; Ellem, R.; Fletcher, F. Efficient and enhanced multi-target tracking with doppler measurements. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1400–1417. [Google Scholar] [CrossRef]
- Drummond, O.E. Feature, attribute, and classification aided target tracking. Proc. SPIE 2001, 4473, 542–558. [Google Scholar] [CrossRef]
- Drummond, O.E. Attributes in tracking and classification with incomplete data. Signal Data Process. Small Targets 2004, 5428, 476–496. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Kirubarajan, T.; Gokberk, C. Tracking with classification-aided multiframe data association. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 868–878. [Google Scholar] [CrossRef]
- Ehrman, L.M.; Blair, W.D. Using target RCS when tracking multiple rayleigh targets. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 701–716. [Google Scholar] [CrossRef]
- Edmund, B.; Oddvar, H.; John, G. Tracking small targets in heavy-tailed clutter using amplitude information. IEEE J. Ocean. Eng. 2010, 35, 314–329. [Google Scholar] [CrossRef]
- Lerro, D.; Bar-Shalom, Y. Automated tracking with target amplitude information. In Proceedings of the American Control Conference, San Diego, CA, USA, 23–25 May 1990; pp. 2875–2880. [Google Scholar] [CrossRef]
- Hu, C.; Li, W.; Wang, R.; Long, T.; Liu, C.; Drake, V.A. Insect biological parameter estimation based on the invariant target parameters of the scattering matrix. IEEE Trans. Geosci. Electron. 2019, 57, 6212–6225. [Google Scholar] [CrossRef]
- Hu, C.; Kong, S.; Wang, R.; Zhang, F. Radar measurements of morphological parameters and species identification analysis of migratory insects. Remote Sens. 2019, 11, 1977. [Google Scholar] [CrossRef] [Green Version]
- Aldhous, A.C. An Investigation of the Polarisation Dependence of Insect Radar Cross Sections at Constant Aspect. Ph.D. Thesis, Cranfield Institute of Technology, Cranfield, UK, 1989. [Google Scholar]
- Hobbs, S.E.; Aldhous, A.C. Insect ventral radar cross-section polarisation dependence measurements for radar entomology. IEE Proc.-Radar Sonar Navig. 2007, 153, 502–508. [Google Scholar] [CrossRef] [Green Version]
- Graves, C.D. Radar polarization power scattering matrix. Proc. IRE 1956, 44, 248–252. [Google Scholar] [CrossRef]
- Boerner, W.M.; Yan, W. On the basic principles of radar polarimetry: The target characteristic polarization state theory of Kennaugh, Huynen’s polarization fork concept, and its extension to the partially polarized case. Proc. IEEE 1991, 79, 1538–1550. [Google Scholar] [CrossRef]
- Li, W.; Hu, C.; Wang, R.; Kong, S.; Zhang, F. Comprehensive analysis of polarimetric radar cross-section parameters for insect body width and length estimation. Sci. China Inf. Sci. 2021, 64, 122302. [Google Scholar] [CrossRef]
- He, Y.; Wang, G.; Lu, D.; Peng, Y. Multisensor Information Fusion with Applications; Publishing House of Electronics Industry: Beijing, China, 2007. [Google Scholar]
- Dowdy, P.C. RCS probability distribution function modeling of a fluctuating target. In Proceedings of the Radar Conference, Los Angeles, CA, USA, 12–13 March 1991. [Google Scholar] [CrossRef]
- Mordeson, J.N.; Wierman, M.J.; Clark, T.D.; Pham, A.; Redmond, M.A. The Analytic Hierarchy Process; Springer Science and Business Media LLC: Berlin, Germany, 2013; Volume 463, pp. 93–117. [Google Scholar] [CrossRef]
- Mario, E.; Tommaso, P. Project selection by constrained fuzzy AHP. Fuzzy Optim. Decis. Mak. 2004, 3, 39–62. [Google Scholar] [CrossRef]
- Horton, M.J.; Jones, R.A. Fuzzy logic extended rule set for multitarget tracking. In Proceedings of the Acquisition, Tracking, and Pointing IX, Orlando, FL, USA, 26 May 1995; pp. 106–117. [Google Scholar] [CrossRef]
- Maesschalck, R.D.; Jouan-Rimbaud, D.; Massart, D.L. The Mahalanobis distance. Chemom. Intell. Lab. Syst. 2000, 50, 1–18. [Google Scholar] [CrossRef]
- Schuhmacher, D.; Vo, B.T.; Vo, B.N. A consistent metric for performance evaluation of multi-object filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Xiu, J.; Guan, X. Radar Data Processing with Applications; Publishing House of Electronics Industry: Beijing, China, 2013. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).