Deep Learning for Chlorophyll-a Concentration Retrieval: A Case Study for the Pearl River Estuary
Abstract
:1. Introduction
2. Materials and Methods
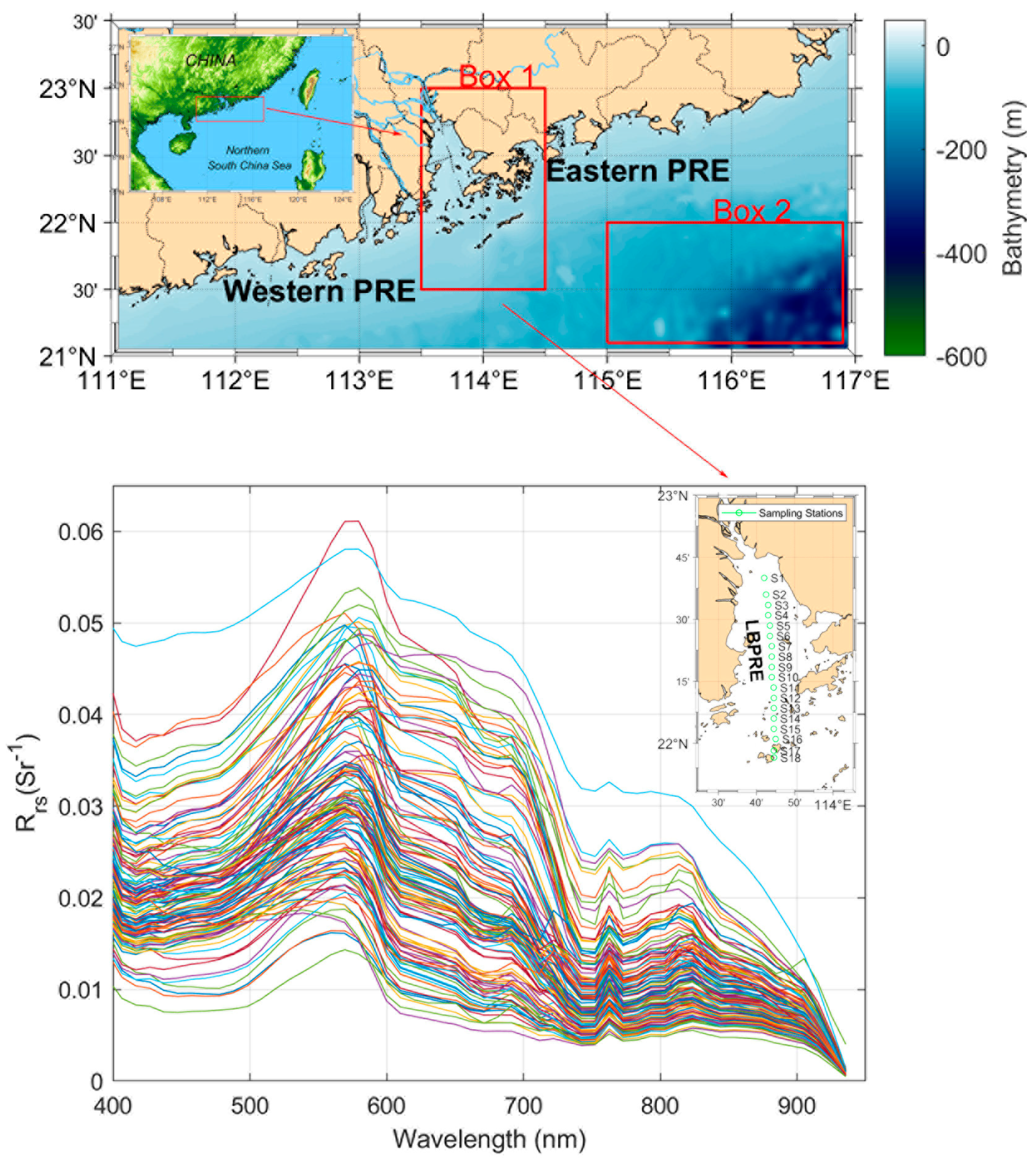
2.1. Study Area
2.2. Data Sources
2.2.1. In-Situ Dataset
2.2.2. MODIS Imagery
3. Algorithm Development
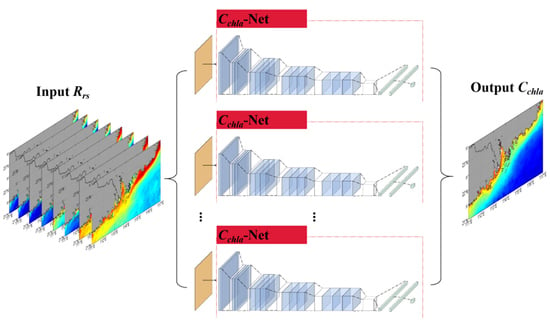
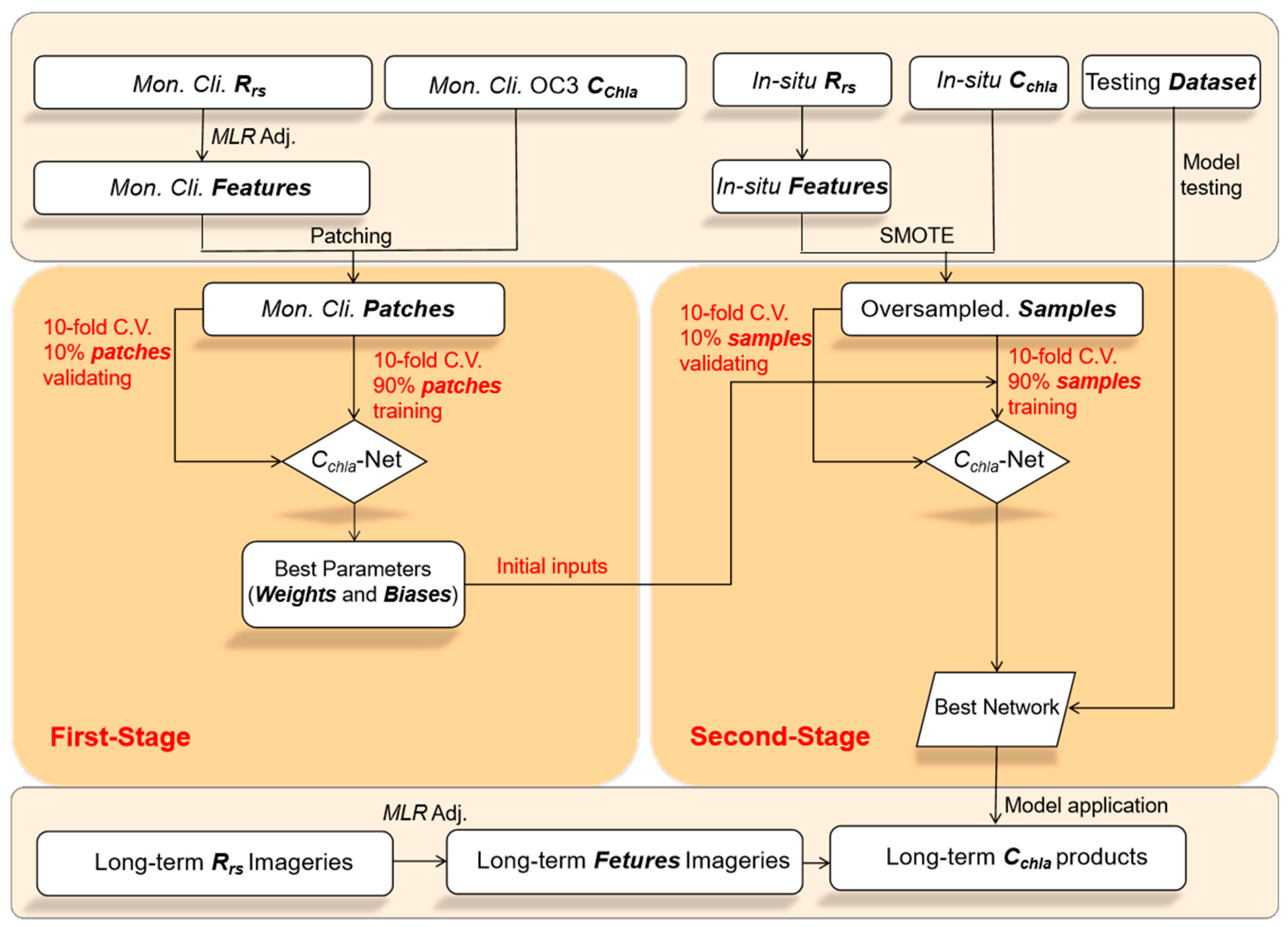
3.1. Overall Framework
3.2. Feature Generation and Data Preprocessing
3.3. Oversampling In-Situ Dataset
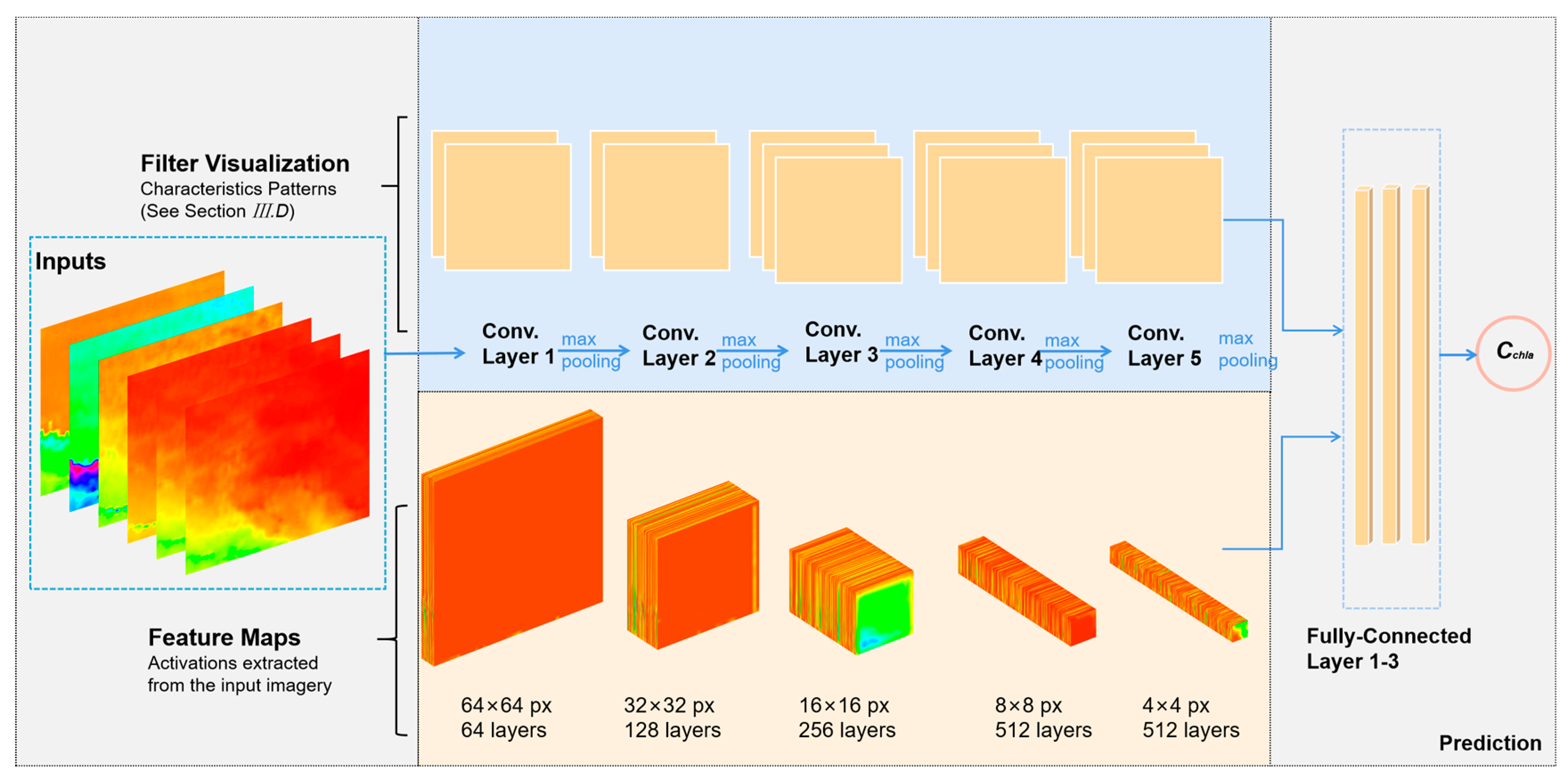
3.4. Cchla-Net Structure
4. Results and Discussion
4.1. MLR Adjustment
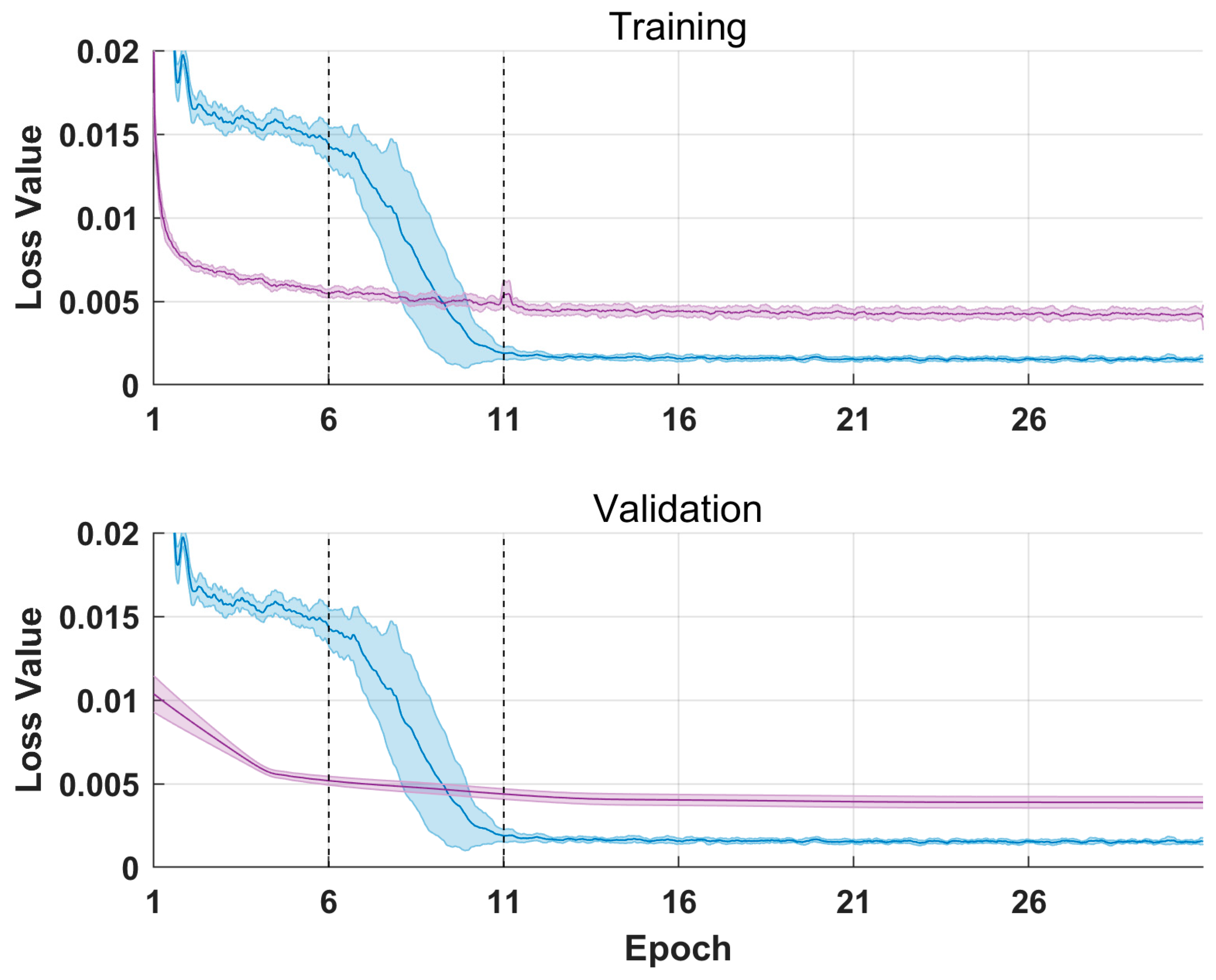
4.2. K-Fold Cross-Validation
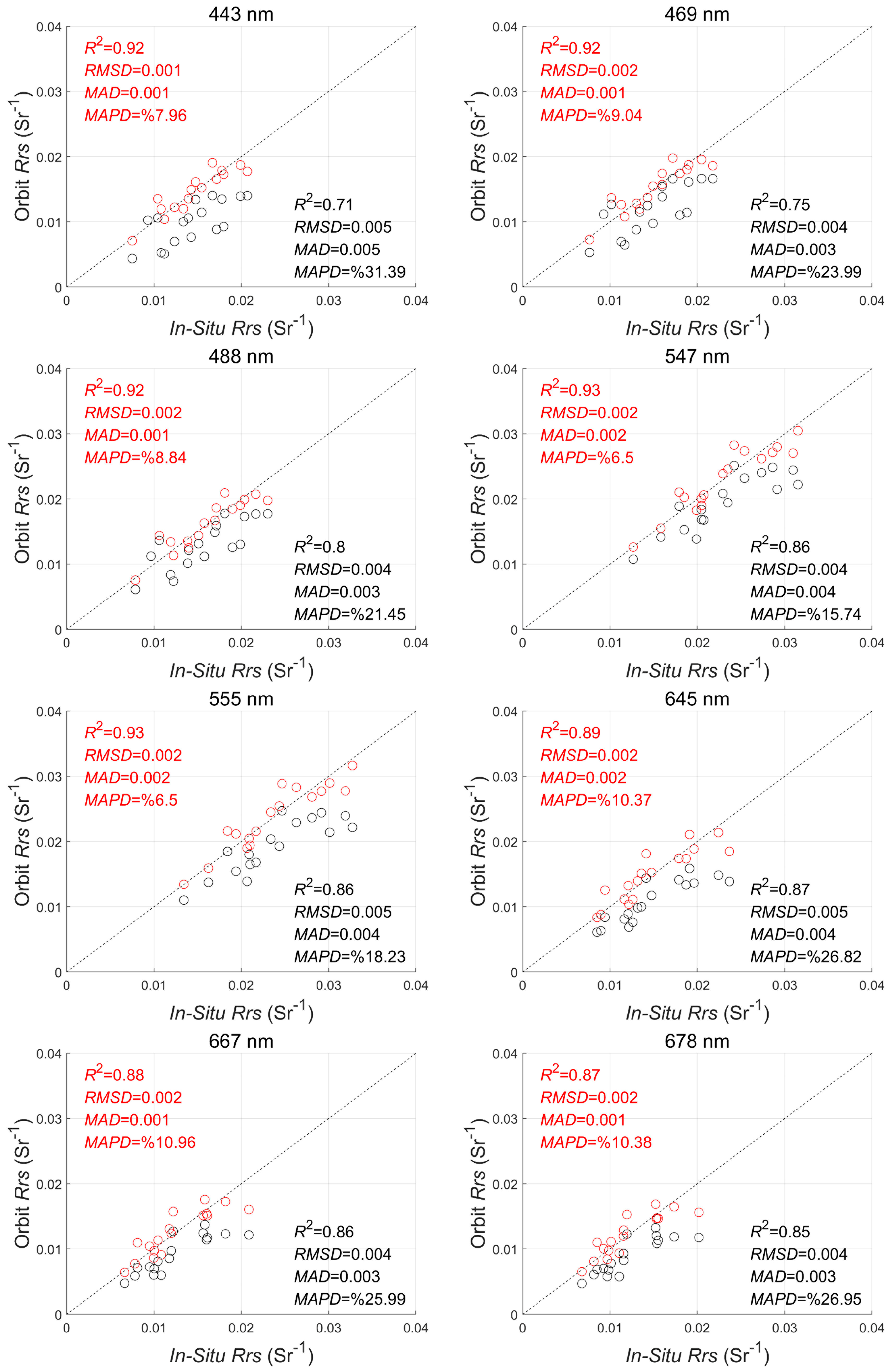
4.3. Model Performances
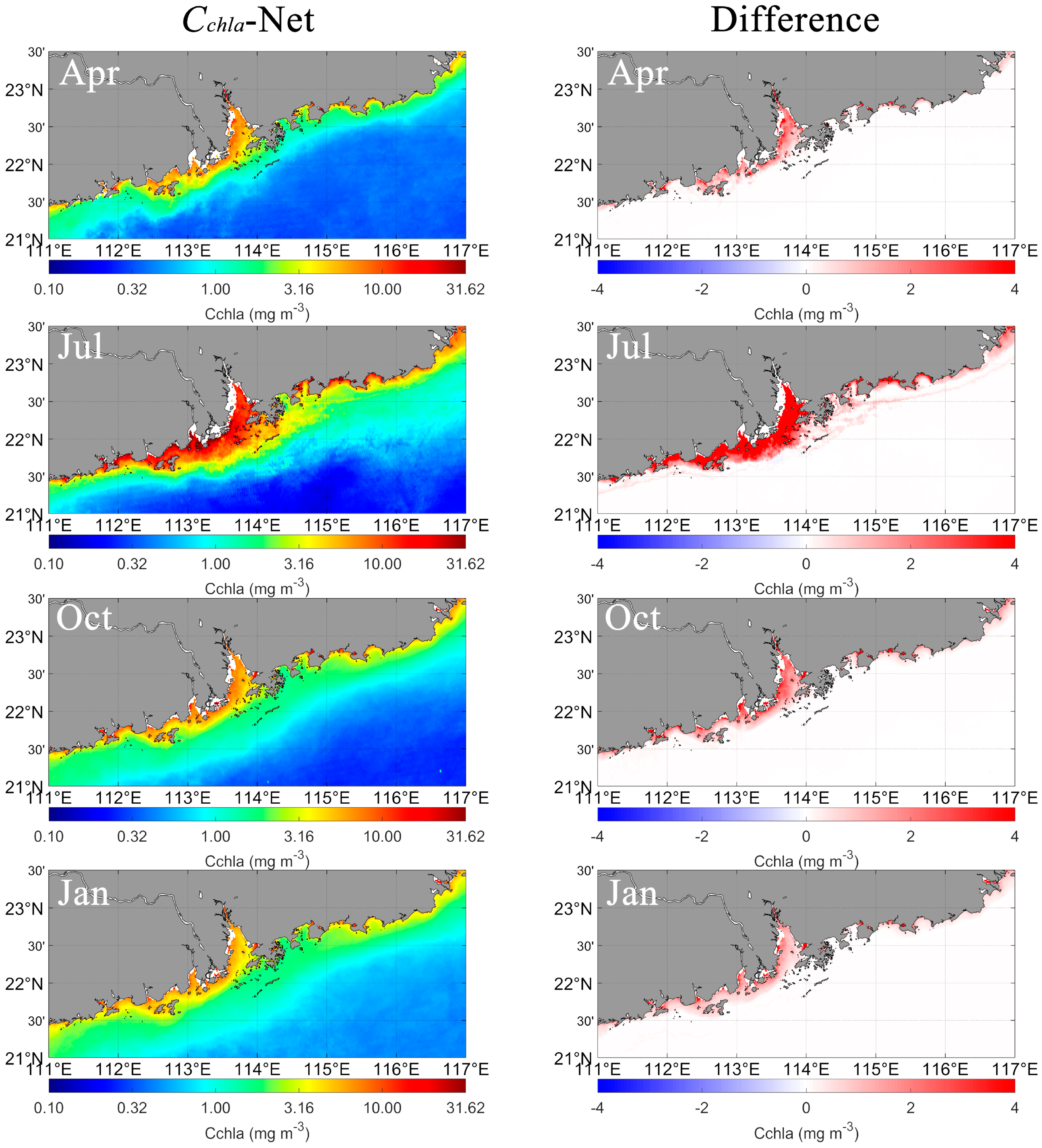
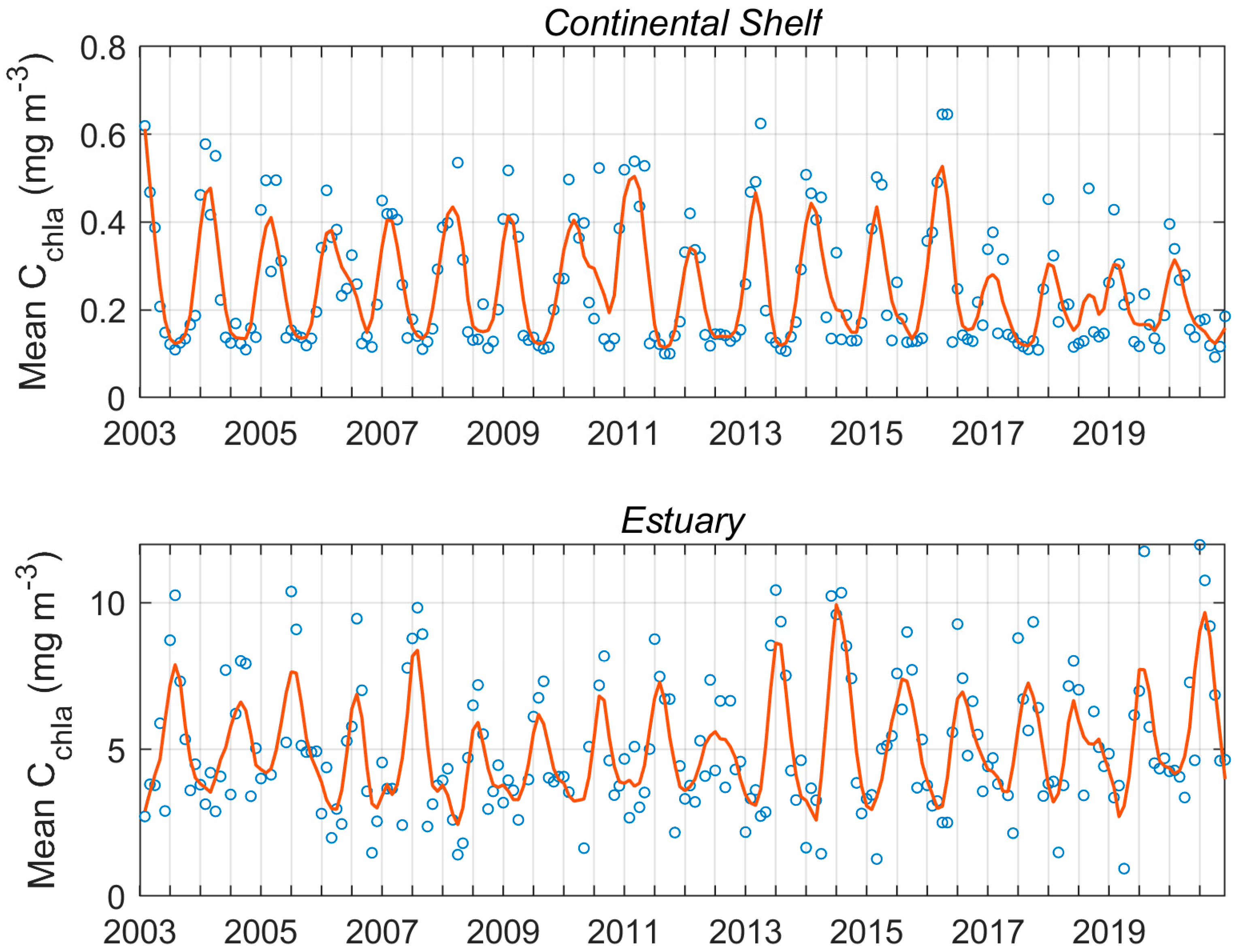
4.4. Model Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, C.; Shi, P.; Larson, M.; Jonsson, L. Estimation of chlorophyll-a concentration in the Zhujiang estuary from SeaWiFS data. Acta Oceanol. Sin. 2002, 21, 55–65. [Google Scholar]
- Zheng, G.; DiGiacomo, P.M. Uncertainties and applications of satellite-derived coastal water quality products. Prog. Oceanogr. 2017, 159, 45–72. [Google Scholar] [CrossRef]
- Son, Y.; Kim, H. Empirical ocean color algorithms and bio-optical properties of the western coastal waters of Svallbard Arctic. ISPRS J. Photogram. Remote Sens. 2018, 139, 272–283. [Google Scholar] [CrossRef]
- Reilly, J.E.O. SeaWiFS Postlaunch Calibration and Validation Analyses, Part 3. In NASA Technical Memorandum; Hooker, S.B., Firestone, E.R., Eds.; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2000; Volume 11, p. 49. [Google Scholar]
- Morel, A.; Prieur, L. Analysis of variations in ocean color. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Gordon, H.R.; Morel, A. Remote Assessment of Ocean Color for Interpretation of Satellite Visible Imagery, A Review; Springer: New York, NY, USA, 1983; Volume 4. [Google Scholar]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. 1998, 103, 24937–24953. [Google Scholar] [CrossRef] [Green Version]
- Garver, S.A.; Siegel, D.A. Inherent optical property inversion of ocean color spectra and its biogeochemical interpretation. I. Time series from the Sargasso Sea. J. Geophys. Res. 1997, 102, 18607–18625. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef] [PubMed]
- Maritorena, S.; Siegel, D.A.; Peterson, A.R. Optimization of a semianalytical ocean color model for global-scale applications. Appl. Opt. 2002, 41, 2705–2714. [Google Scholar] [CrossRef]
- Kampel, M.; Frouin, J.R.; Gaeta, A.S.; Lorenzzetti, J.A.; Pompeu, M. Satellite estimates of chlorophyll-a concentration in the Brazilian Southeastern continental shelf and slope waters, Southwestern Atlantic. In Coastal Ocean Remote Sensing; International Society for Optics and Photonics: Bellingham, WA, USA, 2007; Volume 6680. [Google Scholar]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N.S.; Singh, R. Evaluation of variable-infiltration capacity model and MODIS-terra satellite-derived grid-scale evapotranspiration estimates in a River Basin with Tropical Monsoon-Type climatology. J. Irrig. Drain. Eng. 2017, 143, 04017028. [Google Scholar] [CrossRef] [Green Version]
- Elbeltagi, A.; Kumari, N.; Dharpure, J.K.; Mokhtar, A.; Alsafadi, K.; Kumar, M.; Kuriqi, A. Prediction of combined terrestrial evapotranspiration index (CTEI) over large river basin based on machine learning approaches. Water 2021, 13, 547. [Google Scholar] [CrossRef]
- Liu, H.Z.; Li, Q.Q.; Bai, Y.; Yang, C.; Wang, J.J.; Zhou, Q.M.; Hu, S.B.; Shi, T.Z.; Liao, X.M.; Wu, G.F. Improving satellite retrieval of oceanic particulate organic carbon concentrations using machine learning methods. Remote Sens. Environ. 2021, 256, 112316. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems NIPS, Lake Taho, NV, USA, 3–6 December 2012; Curran Associates Inc.: Red Hook, NY, USA, 2012; Volume 25. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE International Conference Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Region-based convolutional networks for accurate object detection and semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 142–158. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE International Conference Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Nazeer, M.; Nichol, J.E. Development and application of a remote sensing-based Chlorophyll-a concentration prediction model for complex coastal waters of Hong Kong. J. Hydrol. 2016, 532, 80–89. [Google Scholar] [CrossRef]
- Ye, H.B.; Yang, C.Y.; Tang, S.L.; Chen, C.Q. The phytoplankton variability in the Pearl River estuary based on VIIRS imagery. Cont. Shelf Res. 2020, 207, 104228. [Google Scholar] [CrossRef]
- Gan, J.P.; Li, H.; Curchitser, E.N.; Haidvogel, D.B. Modeling South China Sea circulation: Response to seasonal forcing regimes. J. Geophys. Res. 2006, 111, C06034. [Google Scholar] [CrossRef]
- Xie, S.P.; Xie, Q.; Wang, D.X.; Liu, W.T. Summer upwelling in the South China Sea and its role in regional climate variations. J. Geophys. Res. 2003, 108, 3261. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.Y.; Ye, H.B.; Tang, S.L. Seasonal variability of diffuse attenuation coefficient in the Pearl River Estuary from Long-Term Remote Sensing Imagery. Remote Sens. 2020, 12, 2269. [Google Scholar] [CrossRef]
- Li, M.G.; Yan, Y.; Han, X.J.; Li, W.D. Physical model study for effects of the HongKong-Zhuhai-Macao Bridge on harbors and channels in Lingdingyang Bay of the Pearl River Estuary. Ocean Coast. Manag. 2019, 177, 76–86. [Google Scholar]
- Chen, C.; Tang, S.; Pan, Z.; Zhan, H.; Larson, M.; Jonsson, L. Remotely sensed assessment of water quality levels in the Pearl River Estuary, China. Mar. Pollut. Bull. 2007, 54, 1267–1272. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Cao, W.; Wang, G.; Yang, D.; Yang, Y.; Sun, Z.; Zhou, W.; Liang, S. The variations in optical properties of CDOM throughout an algal bloom event. Estuar. Coast. Shelf Sci. 2009, 82, 225–232. [Google Scholar] [CrossRef]
- Mueller, J.L. Radiometric Measurements and Data Analysis Protocols; Goddard Space Flight Center: Greenbelt, MD, USA, 2003.
- Welschmeyer, N. Fluorometric analysis of chlorophyll a in the presence of chlorophyll b and pheopigments. Limnol. Oceanogr. 1994, 38, 1985–1992. [Google Scholar] [CrossRef]
- Ruddick, K.G.; Ovidio, F.; Rijkeboer, M. Atmospheric correction of SeaWiFS imagery for turbid coastal and inland waters. Appl. Opt. 2000, 39, 897–912. [Google Scholar] [CrossRef] [Green Version]
- Evers-King, H.; Martinez-Vicente, V.; Brewin, R.J.W.; Dall’Olmo, G.; Hickman, A.E.; Jackson, T.; Kostadinov, T.S.; Krasemann, H.; Loisel, H.; Röttgers, R.; et al. Validation and Intercomparison of ocean color algorithms for estimating particulate organic carbon in the oceans. Front. Mar. Sci. 2017, 4, 251. [Google Scholar] [CrossRef]
- D’Alimonte, D.; Zibordi, G.; Melin, F. A statistical method for generating Cross-Mission consistent normalized water-leaving radiances. IEEE Trans. Geosci. Remote Sens. 2008, 46, 4075–4093. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the IEEE International Joint Conference on Neural Networks, Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar]
- Morel, A.; Maritorena, S. Bio-optical properties of oceanic waters: A reappraisal. J. Geophys. Res. 2001, 106, 7163–7180. [Google Scholar] [CrossRef] [Green Version]



| No. | Date | N | Range of Cchla (mg·m−3) |
|---|---|---|---|
| 1 | 6 January 2003 | 18 | 7.82 ± 10.79 |
| 2 | 6 January 2004 | 18 | 14.48 ± 11.45 |
| 3 | 18 May 2004 | 17 | 15.17 ± 13.03 |
| 4 | 15 August 2009 | 16 | 6.10 ± 4.65 |
| 5 | 22 October 2009 | 16 | 5.55 ± 4.85 |
| 6 | 22 November 2009 | 16 | 2.43 ± 1.83 |
| 7 | 13 December 2009 | 16 | 4.40 ± 1.51 |
| 8 | 1 February 2010 | 16 | 3.24 ± 1.38 |
| 9 | 4 July 2010 | 16 | 13.73 ± 6.29 |
| 10 | 5 June 2012 | 16 | 3.77 ± 2.02 |
| R2 | RMSD | MAD | MAPD (%) | |
|---|---|---|---|---|
| Cchla-Net | 0.85 | 0.15 | 0.13 | 14.34 |
| GSM | 0.63 | 0.25 | 0.22 | 25.61 |
| OC3M | 0.77 | 0.32 | 0.26 | 22.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, H.; Tang, S.; Yang, C. Deep Learning for Chlorophyll-a Concentration Retrieval: A Case Study for the Pearl River Estuary. Remote Sens. 2021, 13, 3717. https://doi.org/10.3390/rs13183717
Ye H, Tang S, Yang C. Deep Learning for Chlorophyll-a Concentration Retrieval: A Case Study for the Pearl River Estuary. Remote Sensing. 2021; 13(18):3717. https://doi.org/10.3390/rs13183717
Chicago/Turabian StyleYe, Haibin, Shilin Tang, and Chaoyu Yang. 2021. "Deep Learning for Chlorophyll-a Concentration Retrieval: A Case Study for the Pearl River Estuary" Remote Sensing 13, no. 18: 3717. https://doi.org/10.3390/rs13183717
APA StyleYe, H., Tang, S., & Yang, C. (2021). Deep Learning for Chlorophyll-a Concentration Retrieval: A Case Study for the Pearl River Estuary. Remote Sensing, 13(18), 3717. https://doi.org/10.3390/rs13183717