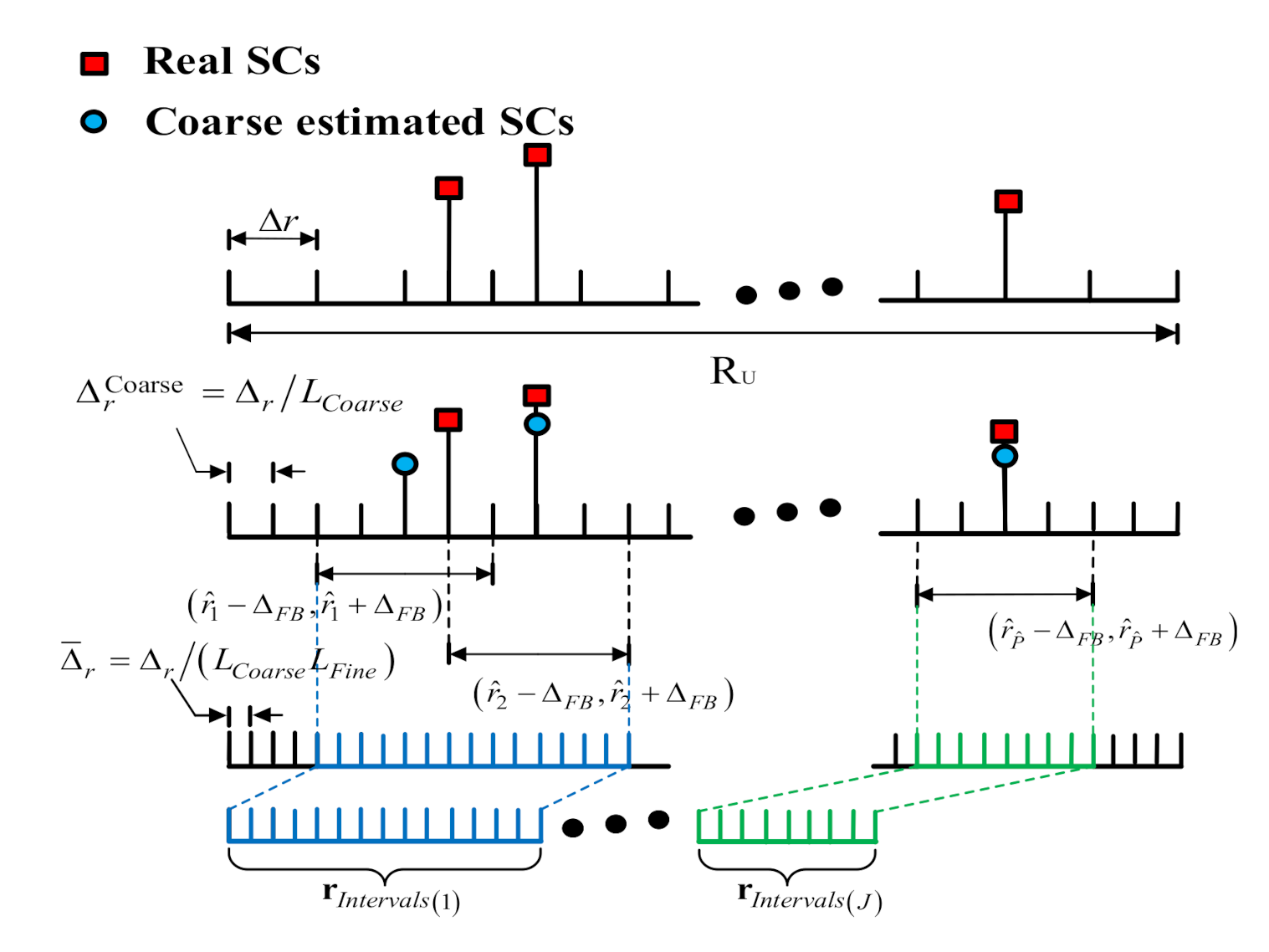
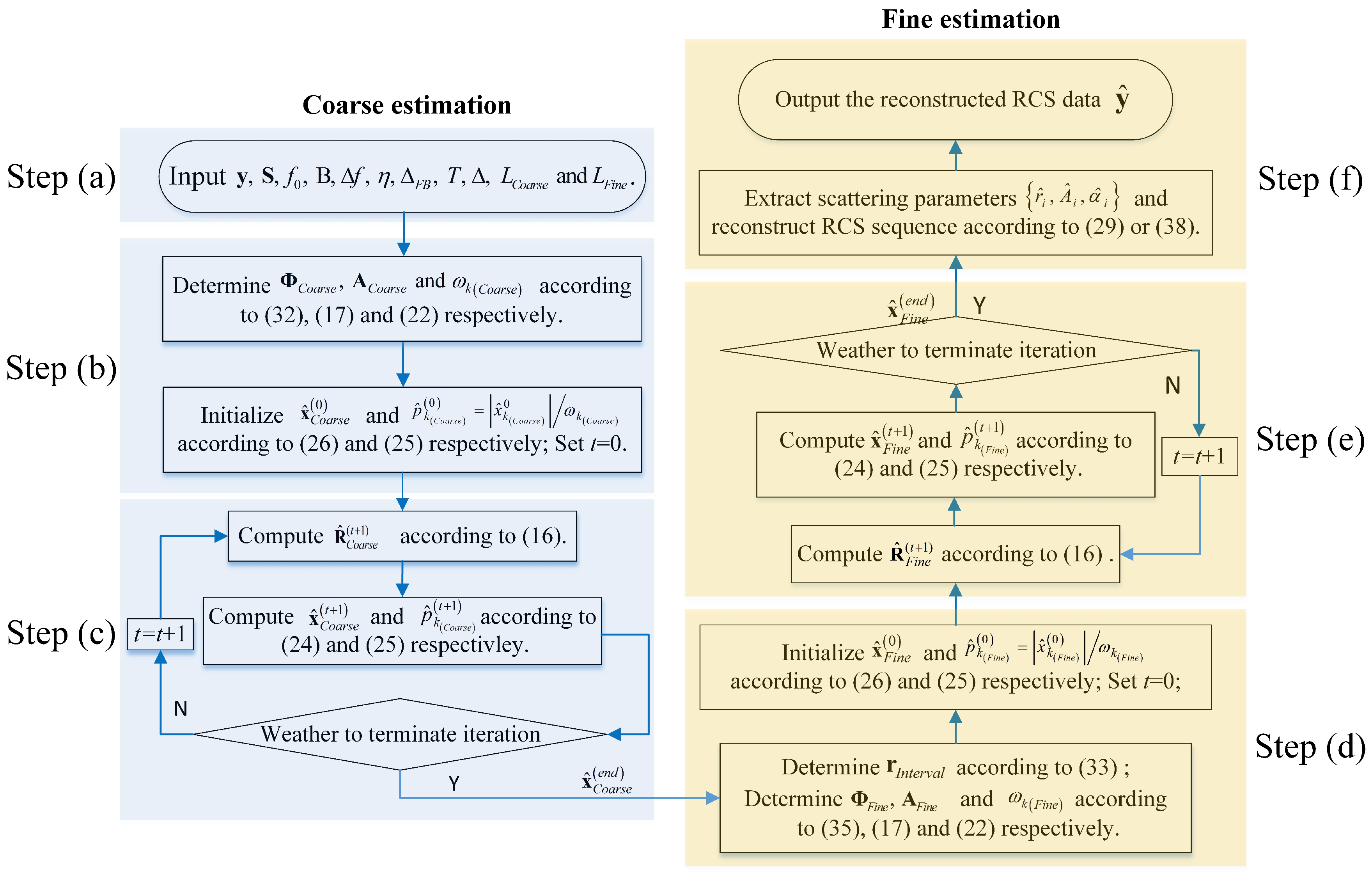
Assume that the radar target consists of five SCs, and the scattering parameters are set according to
Table 1. In this case, the parameters of the radar system are set as follows:
,
, and
. Accordingly, the number of stepped frequency points is
, the normal range resolution is
, and the maximum unambiguous range is
. The subsampling range interval
is set to
(
L = 4). For easy reference, the radar parameters are listed in
Table 2. The simulated data is obtained based on (2). In order to provide a benchmark, the GTD–CVX method and GTD–IRLS method are used. Therefore, the GTD–SPICE method, the DE–GTD–SPICE method, the GTD–IRLS method and the GTD–CVX method are included in the following experiments.
5.2.1. Validation of the Proposed Methods
First, let us validate the effectiveness of the proposed methods under different SNR conditions. In this experiment, the FHR is fixed to 60%, and the SNR is set to 25 dB and 5 dB, respectively. Note that the auxiliary parameter of the GTD–CVX method is chosen as
and
, respectively.
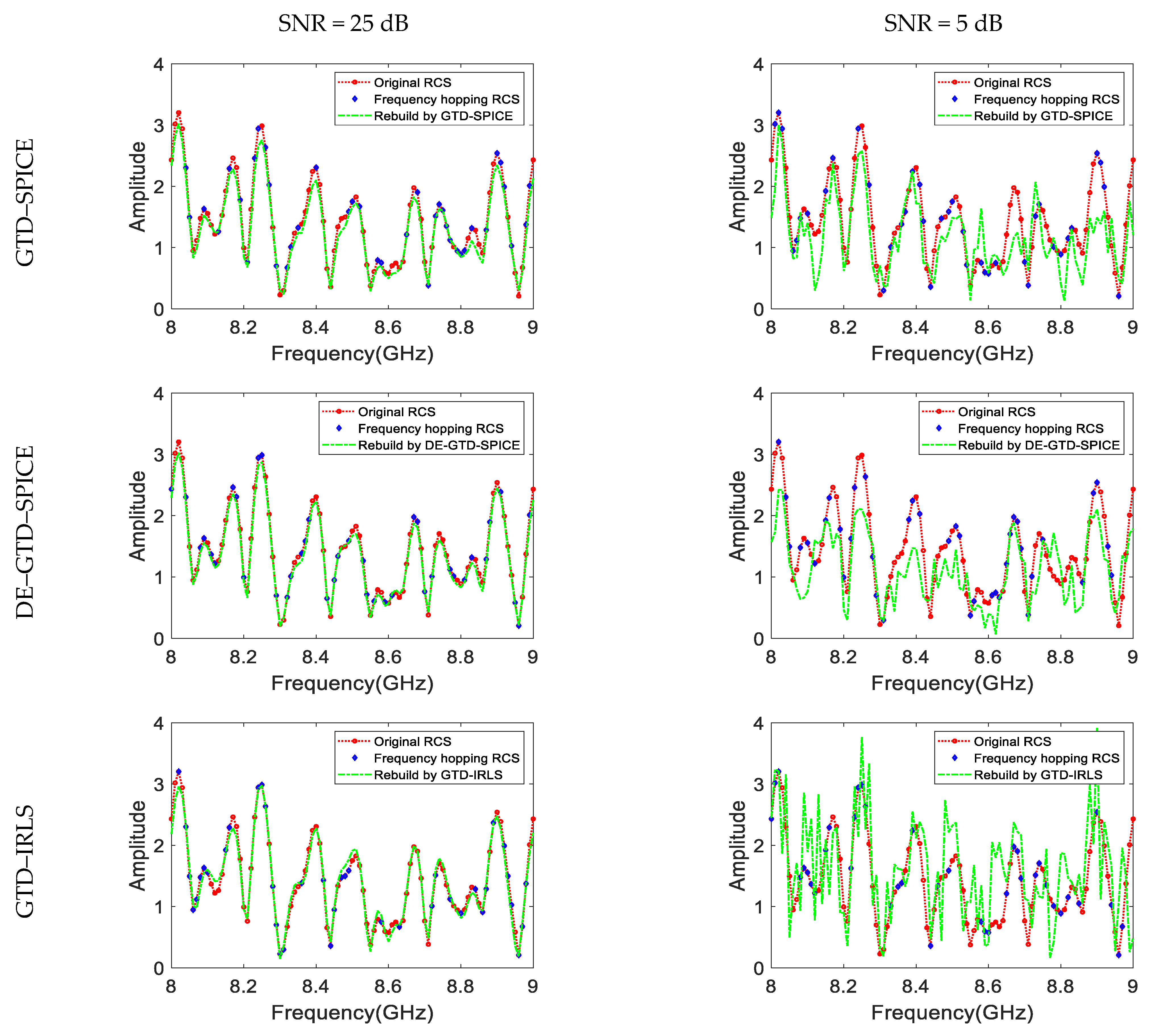
Figure 5 shows the SPE results of the GTD–SPICE, DE–GTD–SPICE, the GTD–IRLS, and the GTD–CVX method at 25 dB and 5 dB, respectively.
It is seen in
Figure 5 that the SPE results of the four methods at 25 dB are more precise than those at 5 dB. When SNR = 25 dB, the parameters extracted by the GTD–SPICE method and the DE–GTD–SPICE method are consistent with their true values. The scattering locations and scattering types of the five SCs are all estimated correctly. As shown in the first column of
Figure 5, the intensities of the five SCs obtained by the DE–GTD–SPICE method are closer to their true values than those obtained by the GTD–SPICE method. The mean error of the scattering intensities of the five SCs of the DE–GTD–SPICE method is 0.09, whereas the mean error of the GTD–SPICE method is 0.13. In particular, the scattering intensity of S3 (0.99) estimated by the DE–GTD–SPICE method is quite close to its true value (1.00), and it has the least deviation.
In contrast, the SPE results of the other two methods are less accurate. Though the parameters of S2, S3, S4, and S5 are extracted correctly by the GTD–IRLS method, the scattering intensity and scattering type of S1 are misestimated as and , respectively. Also, there is a little deviation in the scattering location of S1, and there is also a fake scattering center near S1. The results of the GTD–CVX method are sensitive to the auxiliary parameter . When , the SPE results of S1, S2, S3, and S4 are all correct, and only the scattering type and scattering intensity of S1 are inaccurate. The scattering type of S1 is misjudged as , and there is a deviation of about 0.09 in the scattering intensity of S1. When , the SPE results are the poorest. The maximum deviation of the scattering intensity occurs at S2, and its relative error is over 80%. In addition, S5 is not contained in its results.
Compared with the case of SNR = 25 dB, the SPE results of the four methods under SNR = 5 dB are poorer. The SPE results of the five SCs by the GTD–SPICE method are basically consistent with the true values. It is seen that the scattering locations of the five SCs are correctly extracted. The scattering types of S2, S3, S4, and S5 are correctly judged, except that the scattering type of S1 is misjudged as . The scattering intensities of S2, S3, S4, and S5 are also close to their true values. The deviation of the estimated scattering intensity of S1 is up to 0.31, which is the maximum deviation among all SCs. In addition, there are four fake estimated SCs whose intensities are smaller than 0.1. The SPE results obtained by the DE–GTD–SPICE method are less accurate than that of the GTD–SPICE method. The scattering locations and scattering types of the five SCs are correctly estimated; however, the deviations of the scattering intensities of the five SCs are all larger than 0.1, and the maximum deviation of the estimated scattering intensity reaches 0.34. Also, there are four fake estimated SCs.
The scattering locations and scattering intensity of the five SCs extracted by the GTD.IRLS method are basically consistent with their true values, and the mean error of their scattering intensities is 0.15. Also, the scattering type of S1 and S2 is misjudged as and , respectively. When , the GTD–CVX method correctly estimates S2, whereas the scattering types of S1, S3, S4, and S5 are misjudged as , , and , respectively. The maximum deviation of the scattering intensity of the five SCs occurs at S3, up to 0.52. In addition, the result contains eighteen wrong SCs. When , due to strong noise, the method can only extract two SCs whose locations may be correct. However, the estimated scattering intensities are far from their true values. This indicates that the estimated results are totally wrong.
Based on the estimated scattering parameters, the RCS sequence can be reconstructed.
Figure 6 shows the amplitude of the reconstructed RCS sequence of the four methods. It is seen that the reconstruction results at 25 dB are more accurate than those at 5 dB. When SNR = 25 dB, the performance of the GTD–SPICE method, DE–GTD–SPICE method, GTD–IRLS method, and the GTD–CVX (
) method are comparable, and the reconstructed RCS sequences are close to the true RCS sequence. In contrast, the GTD–CVX (
) method cannot reconstruct the RCS sequence well. The amplitude of the reconstructed sequence has a large deviation from the true RCS sequence. These results are consistent with the poor SPE results of the GTD–CVX (
) method in
Figure 5.
When SNR = 5 dB, the reconstruction results of the four methods are poorer. As shown in the second column of
Figure 6, the performance of the GTD–SPICE method, DE–GTD–SPICE method, GTD–IRLS method, and GTD–CVX (
) method seems to be comparable as well. It is seen that there are large deviations near the peak position of the reconstructed RCS sequence by the four methods. Similarly, the reconstructed RCS sequence by the GTD–CVX (
) method is greatly deviated from the true RCS sequence. It is the poorest result.
To quantitatively compare the performance of the four methods,
,
,
, and the computational time are given in
Table 3. Since the GTD–SPICE (
) method has the poorest results, its metrics are not provided. When SNR = 25 dB, the
,
,
of the GTD–SPICE method, DE–GTD–SPICE method, and GTD–CVX (
) method are almost equal to each other, respectively. Although the GTD–IRLS method has the minimum
, i.e.,
, it has the maximum
, i.e.,
, and minimum
, i.e.,
. This indicates that the accuracy of the reconstructed RCS sequence by the GTD–SPICE method, the DE–GTD–SPICE method, and the GTD–CVX (
) method is basically similar, and the accuracy of the reconstructed RCS sequence by the GTD–IRLS method is slightly lower. When SNR = 5 dB, the GTD–SPICE method has the minimum
, i.e.,
, the minimum
, i.e.,
, and the maximum
, i.e.,
. In contrast, the GTD–IRLS method has the maximum
, i.e.,
, the maximum
, i.e.,
, and the minimum
, i.e.,
. These metrics show that in this case, the GTD–SPICE method has the best reconstructed RCS sequence, whereas the GTD–IRLS method has the poorest reconstruction results.
Then, let us compare the computational time. The GTD–SPICE method has the longest computational time of about 30 s under the two SNR conditions. In contrast, the DE–GTD–SPICE method has the shortest time of 2.2969 s at 25 dB. Compared with the GTD–SPICE method, the computational time is reduced by more than 26 s (larger than 90%). This validates the effectiveness of the DE–GTD–SPICE method in reducing the computational time compared to the GTD–SPICE method. Moreover, it is more than 4 s and 6 s faster than the GTD–CVX () method and the GTD–IRLS method, respectively. When SNR = 5 dB, though the computational time of the DE–GTD–SPICE method increases to 18.5156 s, it is still faster than the GTD–SPICE method. The GTD–SPICE method takes almost three times as long as the GTD–CVX () method. Therefore, the computational time of the DE–GTD–SPICE method may be related to SNR, and the computational time of the GTD–SPICE algorithm may be independent of the SNR.
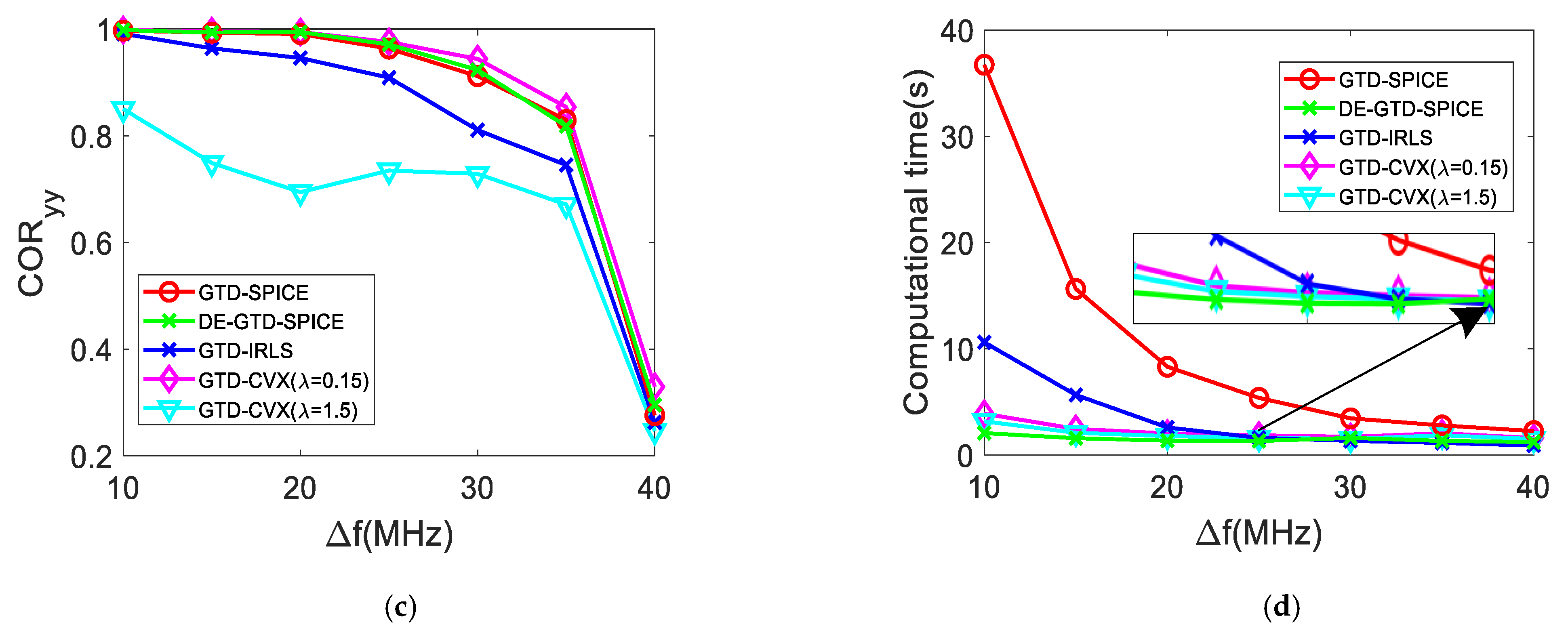
5.2.2. Performance Versus
The frequency-sweeping interval determines the maximum unambiguous distance () and the number of stepped frequency points . Thus, plays a role in the accuracy of RCS reconstruction.
First, let us compare the performance of the four methods under different
. In this experiment, the SNR and FHR are fixed to 30 dB and 60%, respectively. The Monte Carlo simulation with 50 trials is used. The
ranges from 10 MHz to 40 MHz with an interval of 5 MHz. The averages of the
,
,
, and computational time versus
are shown in
Figure 7a–d, respectively.
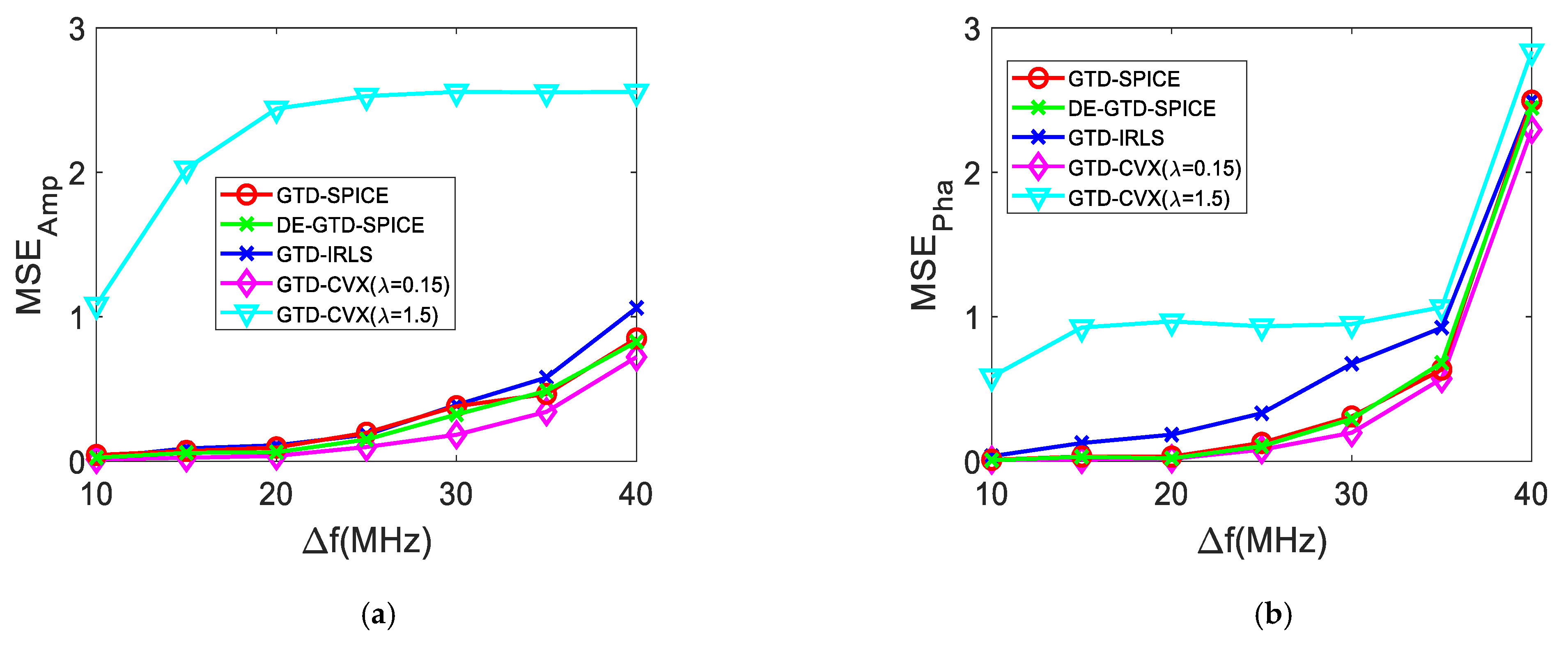
It can be seen in
Figure 7a–c that the
and
increase with the increase of
, and the
of the four methods decreases with the increase of
. It is seen that the GTD–CVX (
) method is more accurate than the GTD–CVX (
) method, due to the fact that it has much smaller
,
, and larger
. This indicates that the selection of auxiliary parameter
is the key to the performance of the GTD–CVX method. For simplicity, unless specifically illustrated, the GTD–CVX method refers to the GTD–CVX (
) method in the following.
When
, the
,
, and
of the four methods are almost the same, respectively, which indicates the comparable performance in RCS reconstruction. It is seen in
Figure 7a that when
, the
of the GTD–SPICE method and the DE–GTD–SPICE method is slightly less than that of the GTD–IRLS method, and a little bigger than that of the GTD–CVX method.
Figure 7b shows that the
of the GTD–SPICE method, the DE–GTD–SPICE method, and the GTD–CVX method is quite close, and it is less than that of the GTD–IRLS method. As shown in
Figure 7c, the
of the GTD–SPICE method, the DE–GTD–SPICE method, and the GTD–CVX method is almost the same, and it is larger than that of the GTD–IRLS method. Therefore, it can be inferred that the GTD–SPICE method, the DE–GTD–SPICE method, and the GTD–CVX method can have a comparable performance at all
, and a better performance than the GTD–IRLS method when
is large.
As shown in
Figure 7d, with the increase of
, the computational time of the GTD–SPICE method, the GTD–IRLS method, and the GTD–CVX method gradually decreases. This is due to their computational complexity decreases with the decrease of
, which is consistent with (40). The GTD–SPICE method requires the longest computational time of about 37s when
. It is more than three times and six times of that of the GTD–IRLS method and the GTD–CVX method, respectively. When
ranges from 10 MHz to 30 MHz, the maximum computational time of the DE–GTD–SPICE method is about 3 s, which is only around 8.12% of that of the GTD–SPICE method, which indicates that the DE–GTD–SPICE method can reduce computational time compared with the GTD–SPICE method. It is also seen that when
, the computational time of the DE-GTD method has a slight increase as the increase of
. The reason for this phenomenon will be explained in
Section 5.2.4.
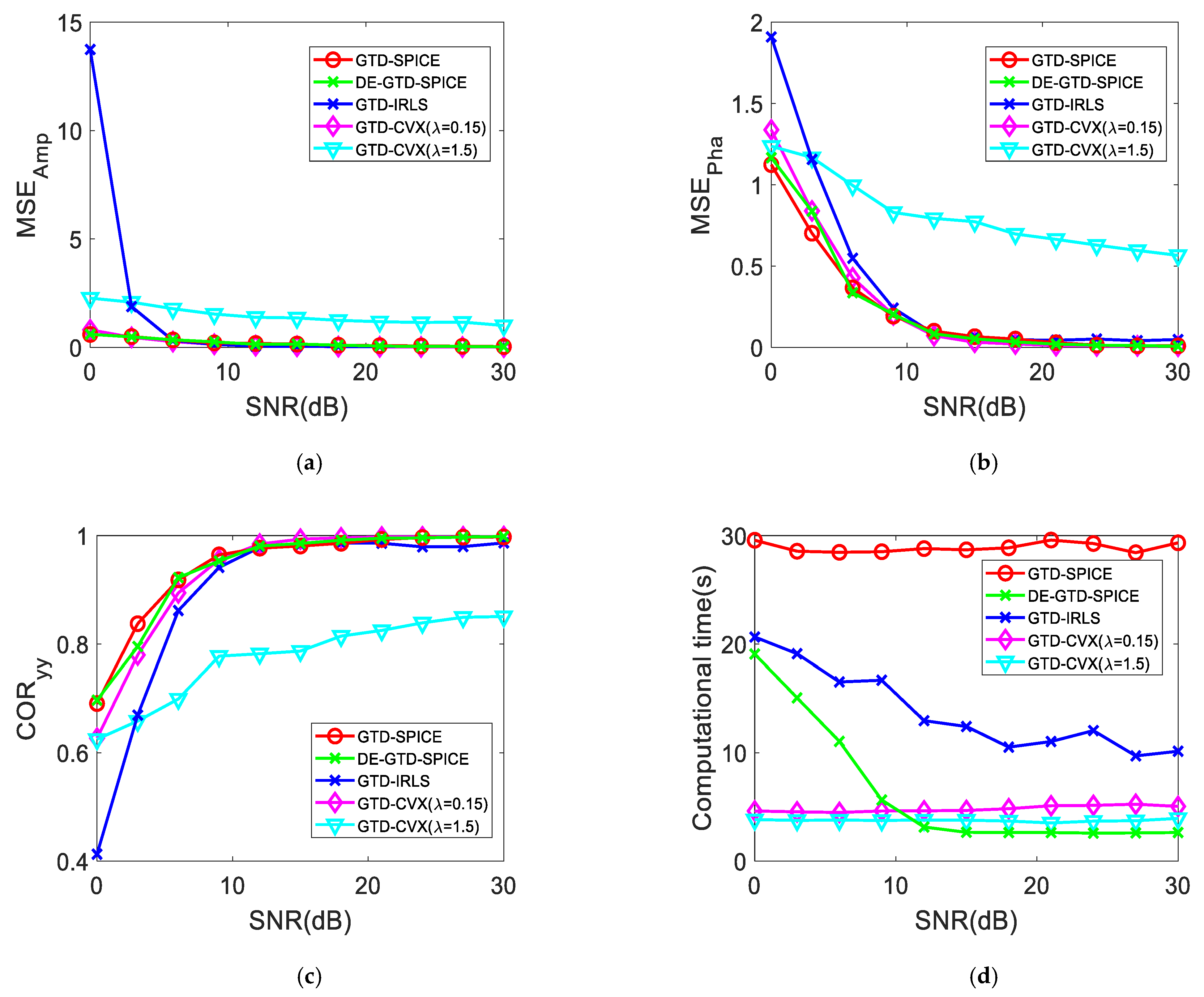
5.2.3. Performance Versus SNR
Let us further compare the performance of the four methods under different SNRs. In this experiment, the
and the FHR are fixed to 10 MHz and 60%, respectively. The Monte Carlo simulation with 50 trials is used. The SNR ranges from 0 dB to 30 dB with an interval of 3 dB. The averages of the
,
,
, and computational time versus SNR are shown in
Figure 8a–d, respectively.
As shown in
Figure 8a–c, the
and
decrease with the increase of SNR, and the
of the four methods increases with the increase of SNR. It can be seen that the performance of the GTD–CVX (
) method is worse than that of the GTD–CVX (
) method due to it has larger
,
, and smaller
. This also means that the GTD–CVX method is sensitive to the auxiliary parameter
.
As can be seen in
Figure 8a, when SNR < 6 dB, the
of the GTD–SPICE method, the DE–GTD–SPICE method, and the GTD–CVX method is much smaller than that of the GTD–IRLS method. When SNR > 6 dB, the
of the four methods is almost the same. As shown in
Figure 8b, when SNR < 12 dB, the
of both the GTD–SPICE method and DE–GTD–SPICE method is slightly smaller than that of the GTD–CVX method and much smaller that of the GTD–IRLS method. In contrast, when SNR > 12 dB, the
of the four methods is quite close and tends to be 0, except that the
of the GTD–IRLS method is slightly larger than 0 when SNR is from 20 to 30 dB. It is seen in
Figure 8c that when SNR < 10 dB, the
of the GTD–SPICE method and the DE–GTD–SPICE method is slightly larger than that of the GTD–CVX method and much larger than that of the GTD–IRLS method. When SNR > 10 dB, the
of the four methods is almost equal and quite close to 1, except that the
of the GTD–IRLS methods is a little smaller than 1 when SNR is from 20 to 30 dB.This indicates that the two proposed methods outperform both the GTD–CVX method and the GTD–IRLS method under low SNR conditions, and have a slight advantage under high SNR conditions.
As shown in
Figure 8d, when SNR ranges from 0 dB to 30 dB, the computational time of the GTD–SPICE method and the GTD–CVX method is almost a constant. The GTD–SPICE method has the longest computational time of approximately 30 s, and the GTD–CVX method has a computational time of about 6s. The computational time of the GTD–IRLS method is in the middle and decreases with the increase of SNR. Also, it can be seen that the computational time of the DE–GTD–SPICE method decreases with the increase of the SNR under the condition of SNR being 0~13 dB. Since severe noise affects the accuracy of the coarse estimation, the estimation of the number of SCs, i.e.,
, becomes larger. Accordingly,
also becomes larger, which increases the computational complexity of the fine estimation. This is consistent with (46). Although the computational time of the DE–GTD–SPICE method has the maximum, around 20 s at SNR = 0 dB, it is only about 66.7% of that of the GTD–SPICE method. When SNR > 13 dB, its computational time tends to be stable and approaches 3 s, which is only about 10% of that of the GTD–SPICE method (30 s). Substituting
and
into (47), we can have
. This is basically consistent with 10%, which validates the effectiveness of the DE–GTD–SPICE method in reducing the computational cost.
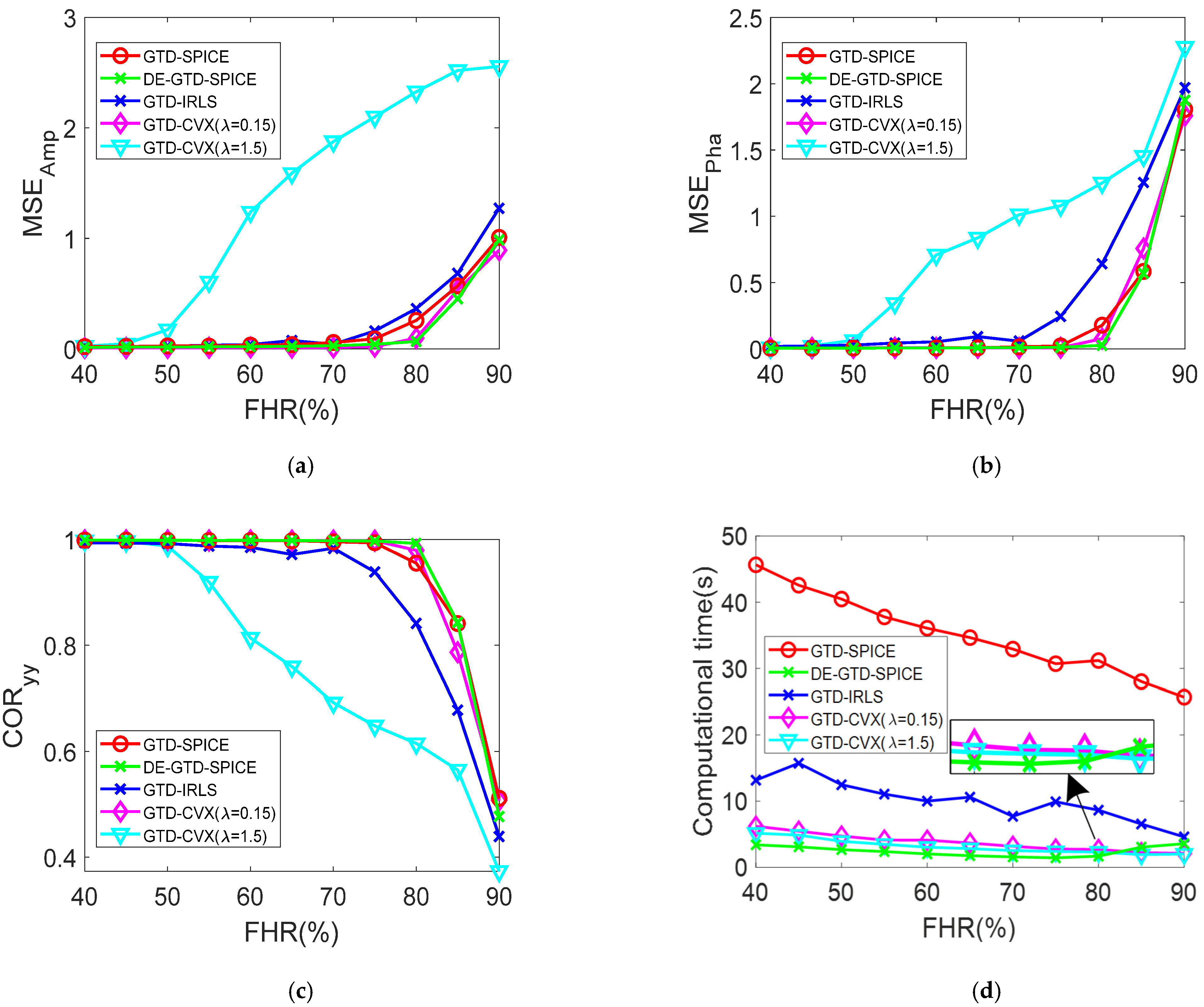
5.2.4. Performance Versus FHR
Next, we compare the performance of the four methods in different FHRs. The
and SNR are fixed to 10 MHz and 30 dB, respectively. Similarly, the Monte Carlo simulation with 50 trials is used. The FHR ranges from 40% to 90% with an interval of 5%. The averages of the
,
,
, and computational time are shown in
Figure 9a–d, respectively.
It can be seen in
Figure 9a–c that the
and
increase with the increase of FHR, and the
of the four methods decreases with the increase of the FHR. It is seen that the GTD–CVX (
) method is much more accurate than the GTD–CVX (
) method. This also shows that the selection of the auxiliary parameter
is the key to the performance of the GTD–CVX method.
When
, the
,
, and
of the four methods are quite close, respectively, which indicates the comparable performance in RCS reconstruction. It is seen in
Figure 9a when
that the
of the GTD–SPICE method, the DE–GTD–SPICE method, and the GTD–CVX method is close and slightly smaller than that of the GTD–IRLS method.
Figure 9b also shows the similar relation of the
of the four methods. When
, the
of the GTD–SPICE method, the DE–GTD–SPICE method, and the GTD–CVX method is basically close, and is smaller to that of the GTD–IRLS method. As shown in
Figure 9c, when
, the
of the GTD–SPICE method, the DE–GTD–SPICE method, and the GTD–CVX method is almost the same, whereas the
of the GTD–IRLS method is smaller than that of the other three methods. Therefore, the four methods have comparable performance in low FHRs, while the proposed methods outperform the GTD–IRLS method under high FHR conditions.
It can be also found that when
, the
,
, and
of the four methods all change dramatically, which is due to the destruction of RIP conditions. According to [
40], the minimum number of scattering measurement points
can be determined theoretically. According to [
41], for a reliable recovery,
can be calculated as
. As shown in
Figure 9a–c, the low boundary of FHR is approximately 80%. Hence, the number of frequency-hopping points in actual is
, i.e.,
, which is basically consistent with the theoretical low boundary
.
As shown in
Figure 9d, with the increase of FHR, the computational time of the GTD–SPICE method, the GTD–IRLS method, and the GTD–CVX method gradually decreases. This is due to the fact that their computational complexity decreases with the decrease of
, which is consistent with (39). The GTD–SPICE method requires the longest computational time of about 30 s at FHR = 40% among the four methods. When FHR ranges from 40% to 75%, the computational time of DE–GTD–SPICE method decreases with the decrease of FHR, on the premise of guaranteeing the accuracy of RCS reconstruction. This is also due to the complexity of the DE–GTD–SPICE method, which decreases with the decrease of
. Moreover, it has the least computational time of about 3 s at FHR = 75%, which is about 10% of that of the GTD–SPICE method (about 30 s). This is also consistent with (47). In contrast, when FHR > 75%, its computational time begins to increase, whose phenomenon also occurs at
Figure 7d. This is the result of the FHR approaching the RIP condition. In this case, the coarse estimation obtains a larger number of SCs than that of the true value and
becomes larger, which increases the computational complexity of the fine estimation. This is consistent with (46), in which the increase of
will increase the computational complexity.
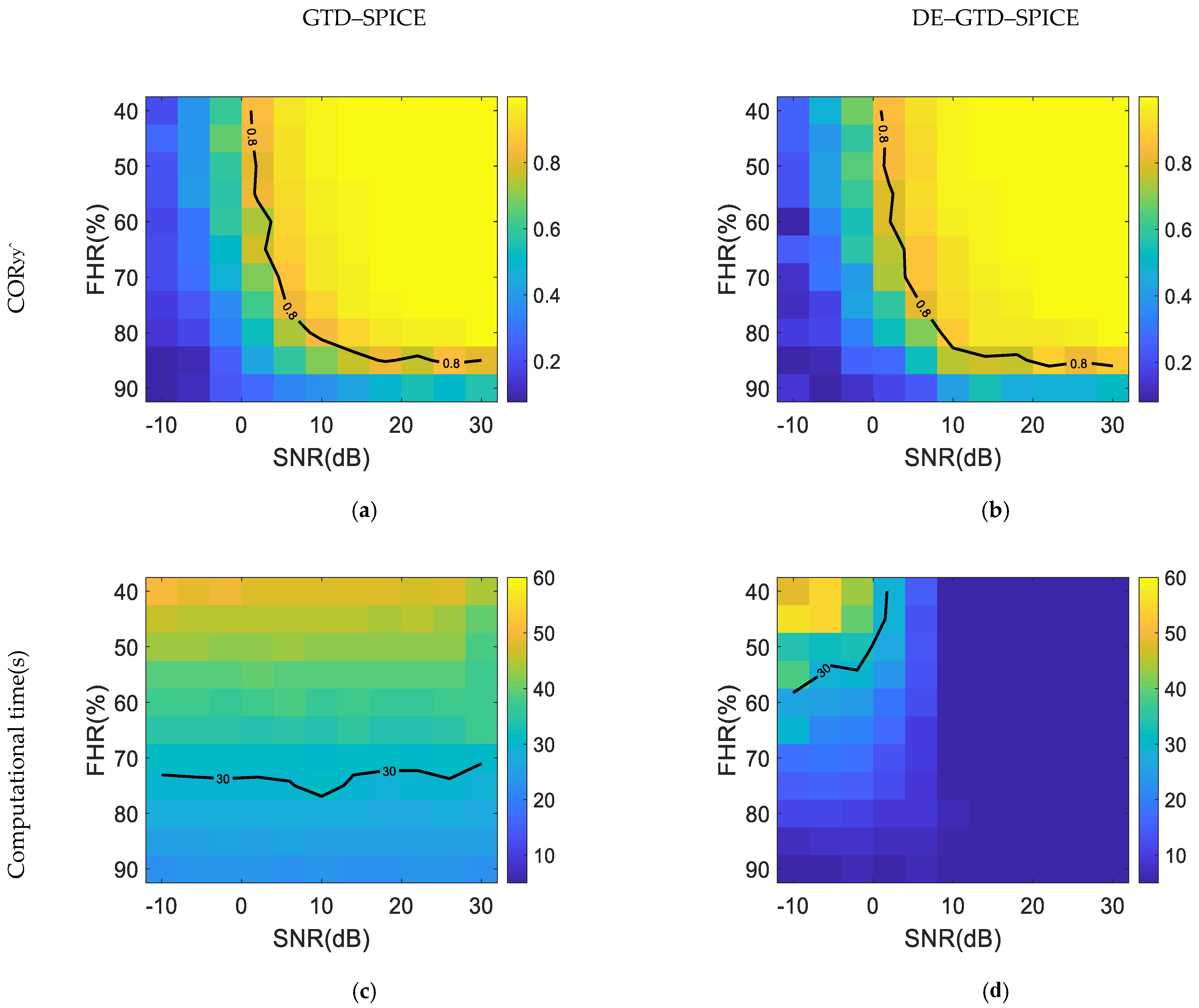
5.2.5. Joint Experiment on Different SNRs and FHRs
Lastly, the joint impacts of
, SNR, and FHR on the proposed methods in RCS reconstruction are analyzed. Since the performance of the GTD–SPICE method and the DE–GTD–SPICE method in RCS reconstruction is related to
, SNR, and FHR, it is difficult to determine which
, SNR, and FHR are more efficient. Considering the above findings that the performance of the proposed method has similar trends in terms of
and FHR, only the SNR and FHR are performed jointly in this experiment. The SNR ranges from 10 dB to 30 dB with an interval of 4 dB, and the FHR ranges from 40% to 90% with an interval of 5%. Similarly, the Monte Carlo simulation with 50 trials is used. The averages of the
and the computational time of the two proposed methods are shown in
Figure 10a–d, respectively.
As shown in
Figure 10a–b, the
of the two proposed methods is quite close under the same SNR and FHR. When SNR > 8 dB and FHR < 80%, the
of the two methods is larger than 0.8, which shows superior performance in RCS reconstruction. Then, let us further compare its computational time. It can be seen in
Figure 10c that the computational time of the GTD–SPICE method significantly depends on FHR. When FHR < 75%, its computational time is larger than 30 s. In contrast, the computational time of the DE–GTD–SPICE method is affected by both the SNR and FHR. It is seen in
Figure 10d that only when SNR < 0 dB and FHR < 50%, the computational time of the DE–GTD–SPICE method is larger than 30s. From
Figure 10c–d, it can be found that the DE–GTD–SPICE method has a shorter time and a higher efficiency than the GTD–SPICE method. Therefore, it can be concluded that both the methods are reliable and effective for RCS reconstruction. In particular, the DE–GTD–SPICE method requires less computational time.