A Comprehensive Evaluation of Near-Real-Time and Research Products of IMERG Precipitation over India for the Southwest Monsoon Period
Abstract
:1. Introduction
- (1)
- To quantify error characteristics of V06B near-real-time (IMERG-E and IMERG-L) and research (IMERG-F) products;
- (2)
- To assess the changes in error characteristics of the IMERG-F product from V05B to V06B;
- (3)
- To assess the consistency of error characteristics of IMERG-F V06B for pre-GPM and GPM periods.
2. Data and Methods
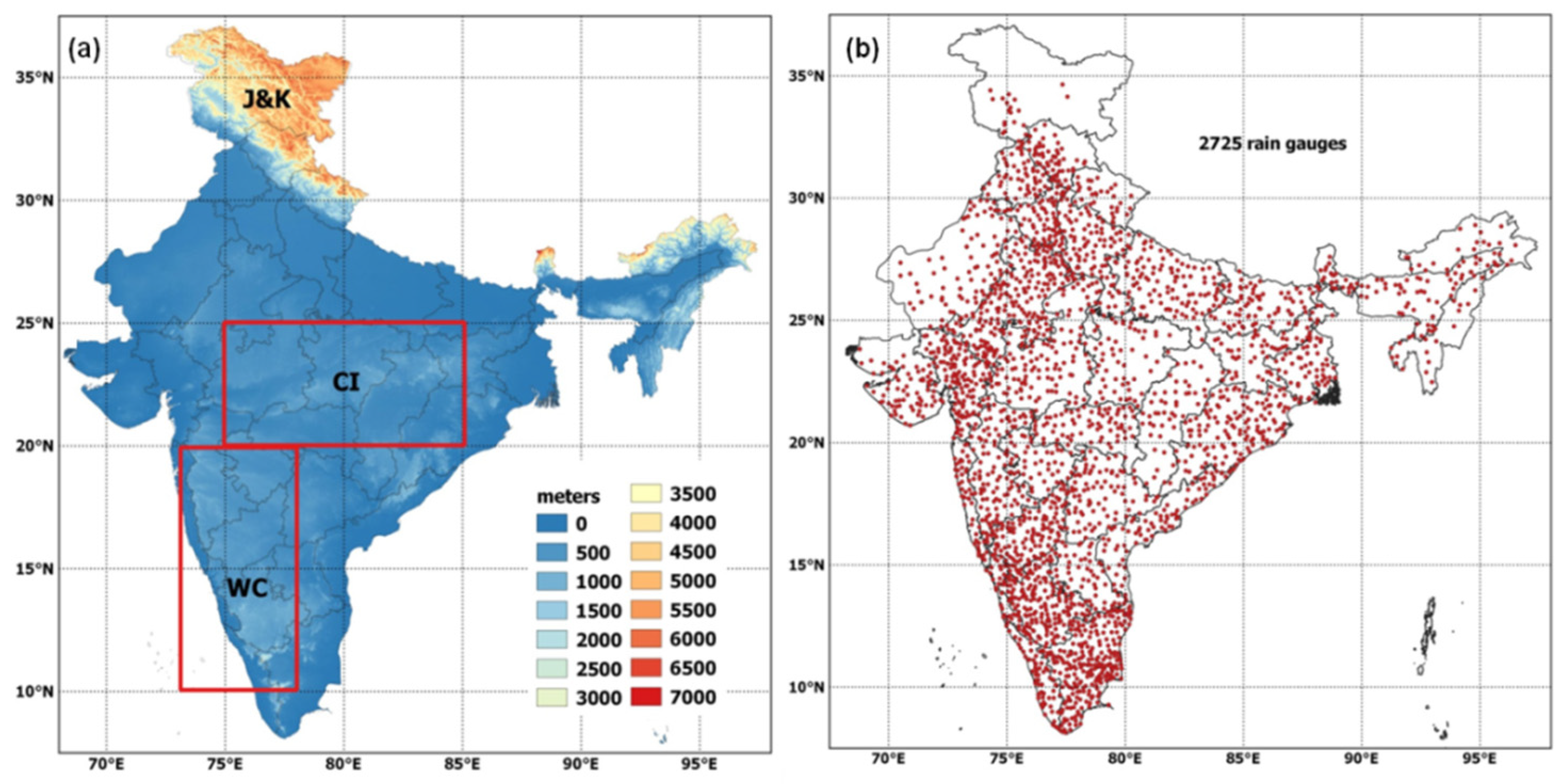
2.1. Rain Gauge Data
2.2. IMERG Data
2.3. Evaluation Methodology
3. Results and Discussion
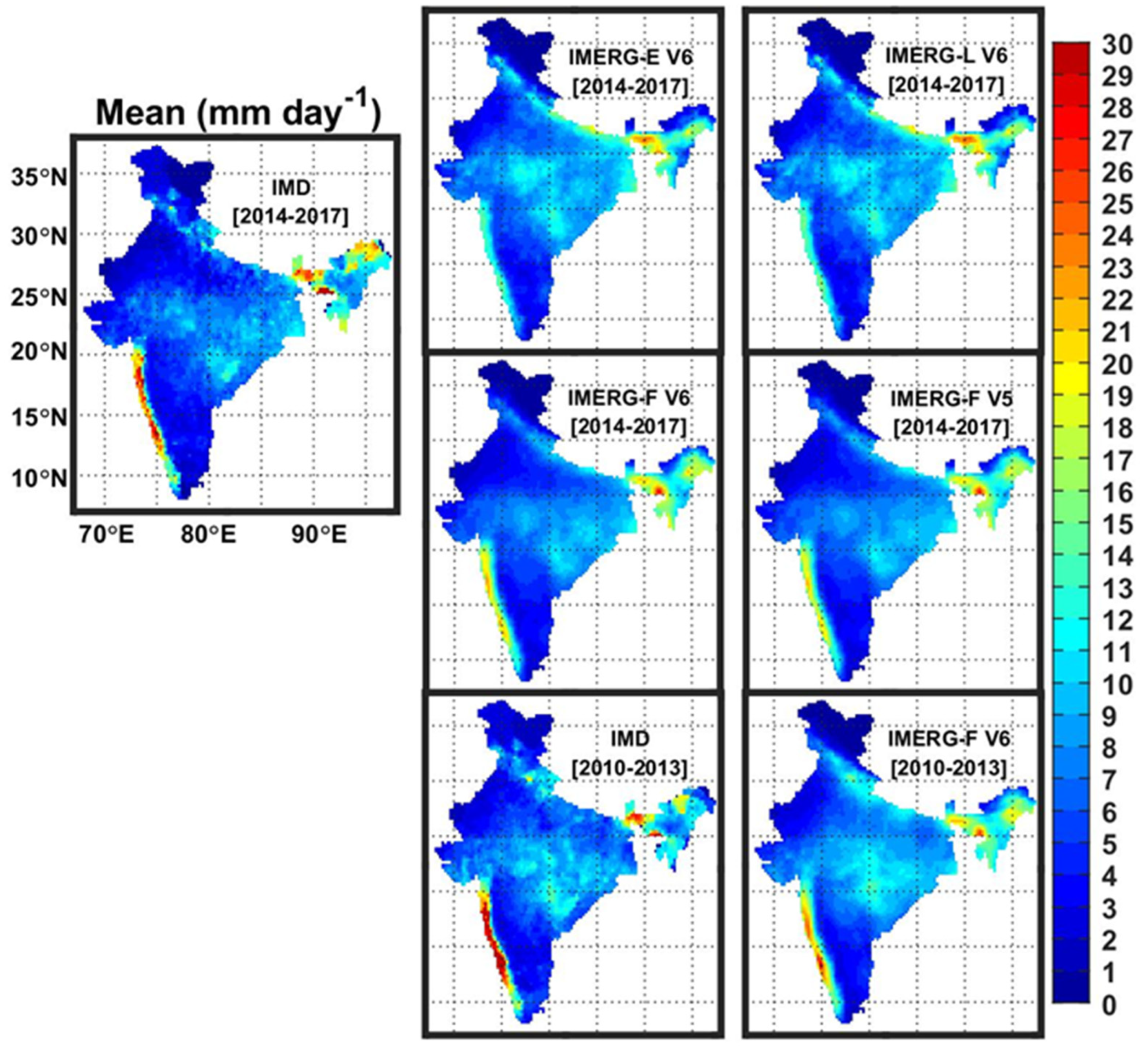
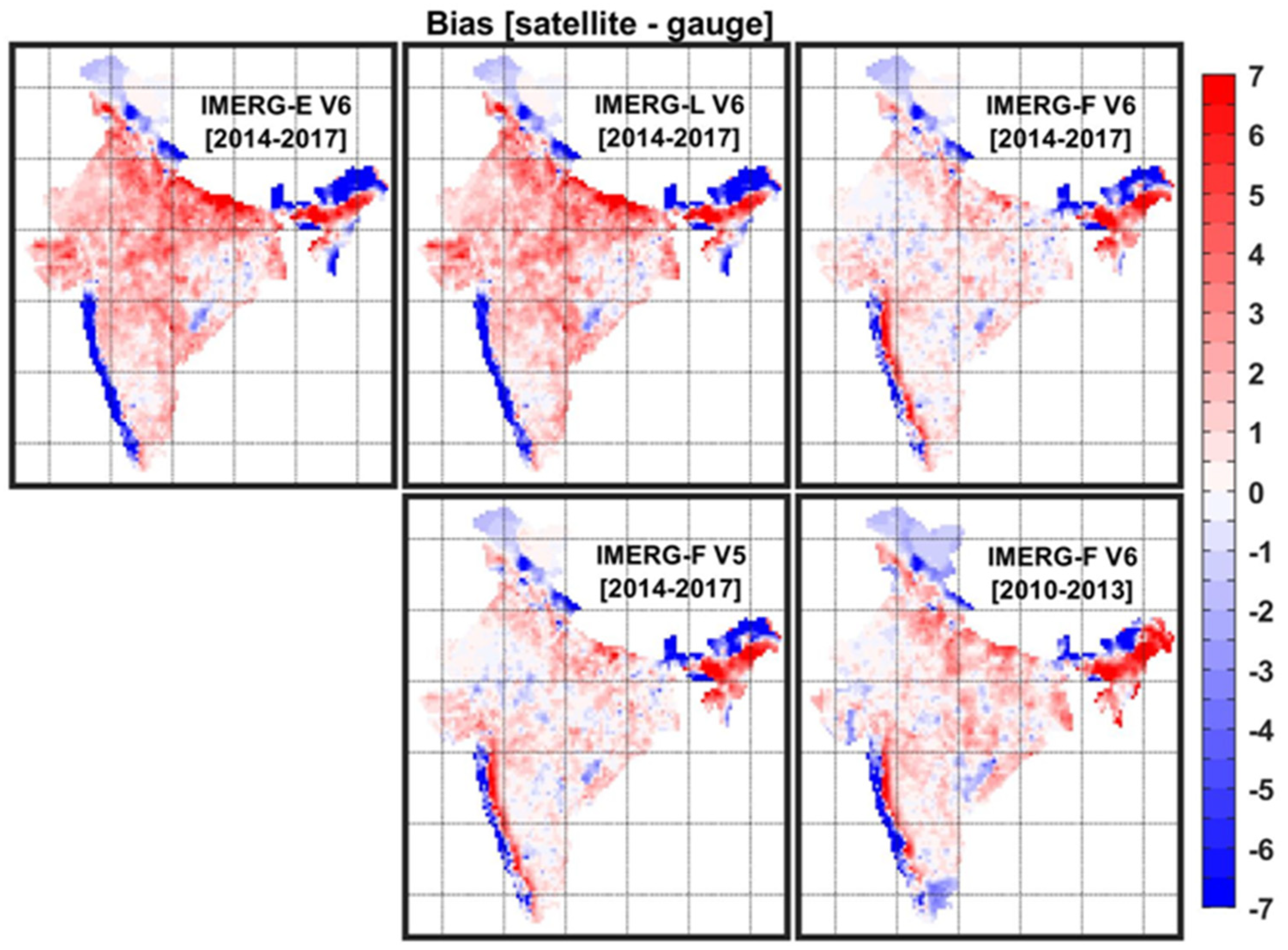
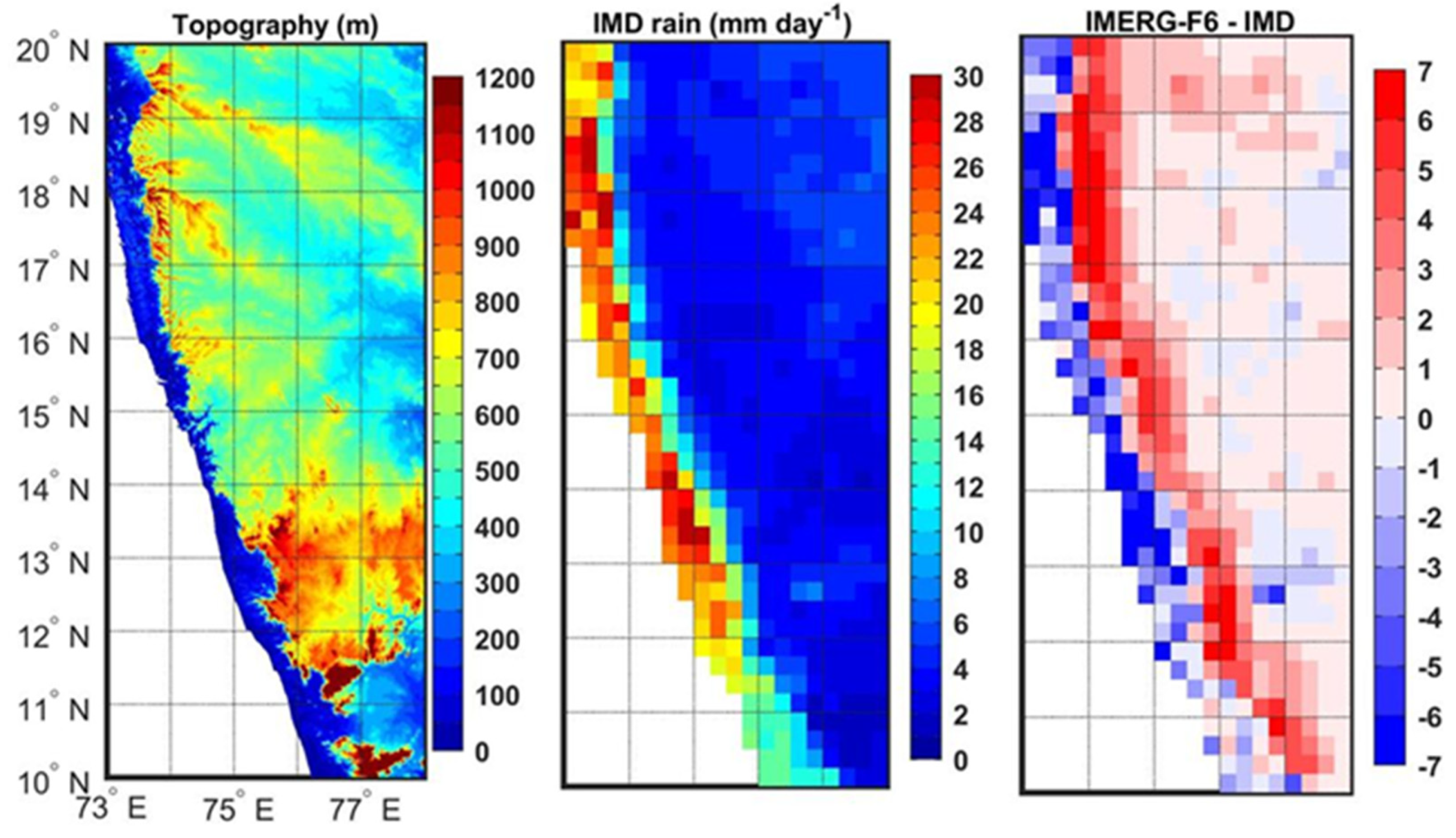
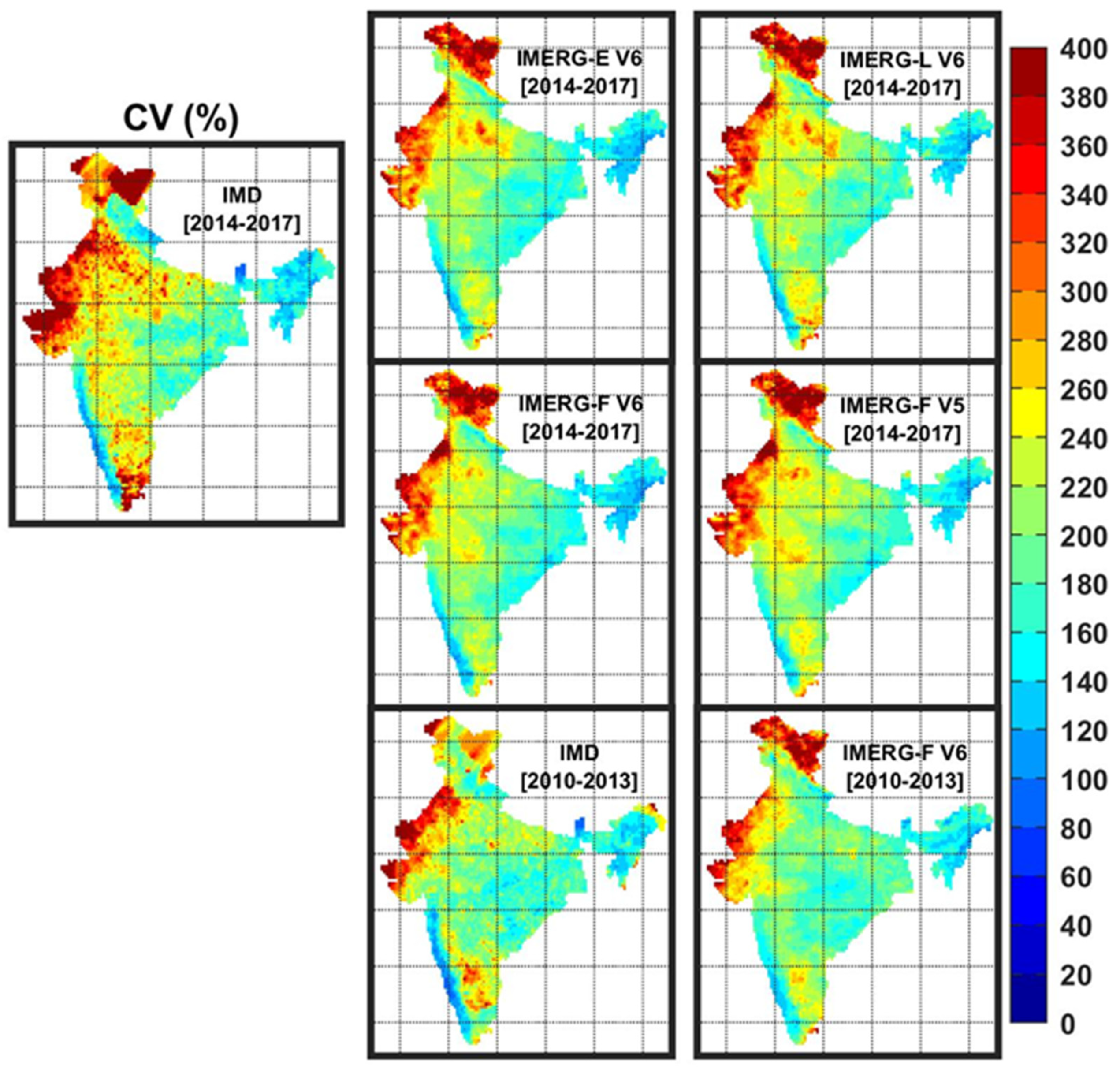
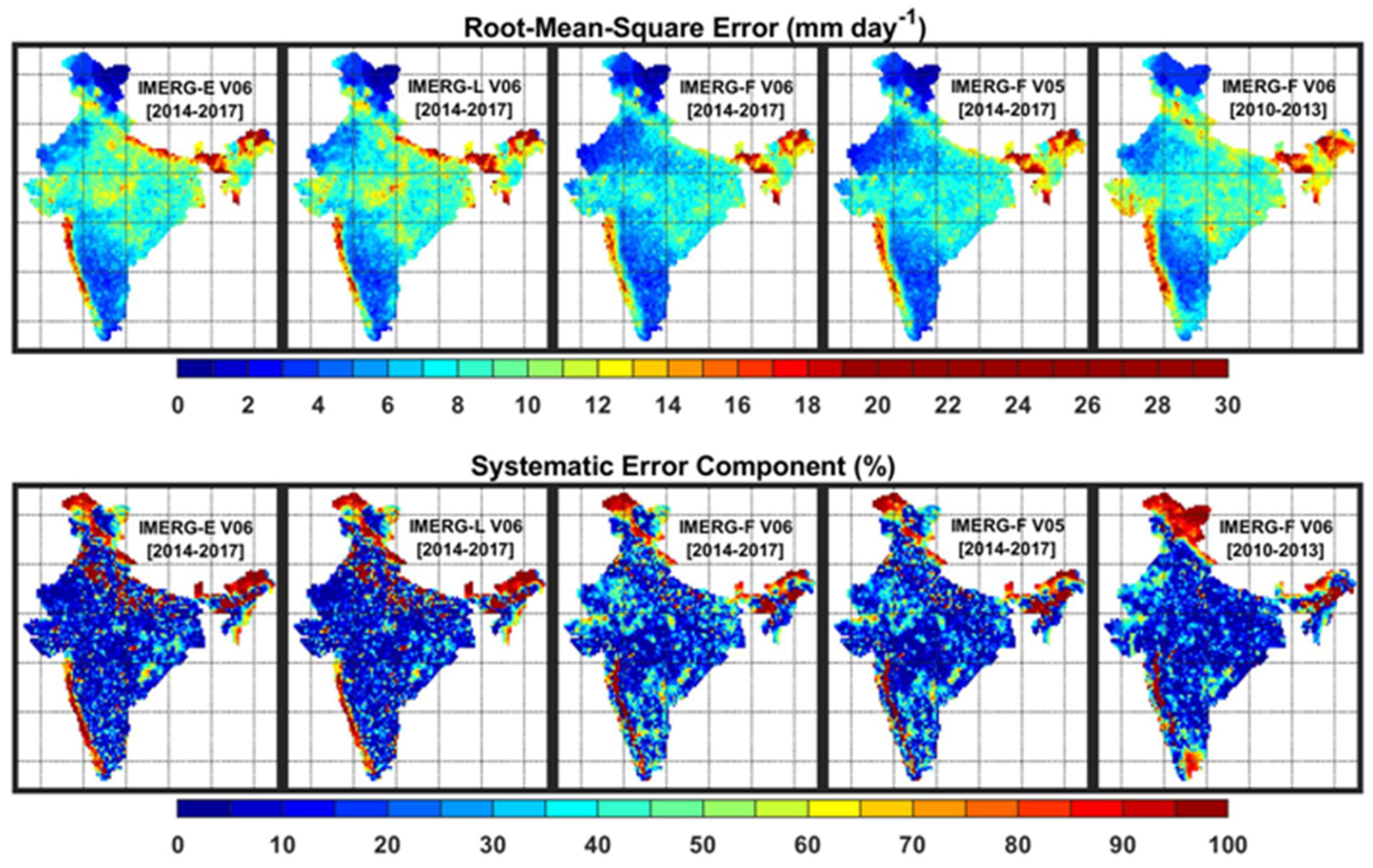
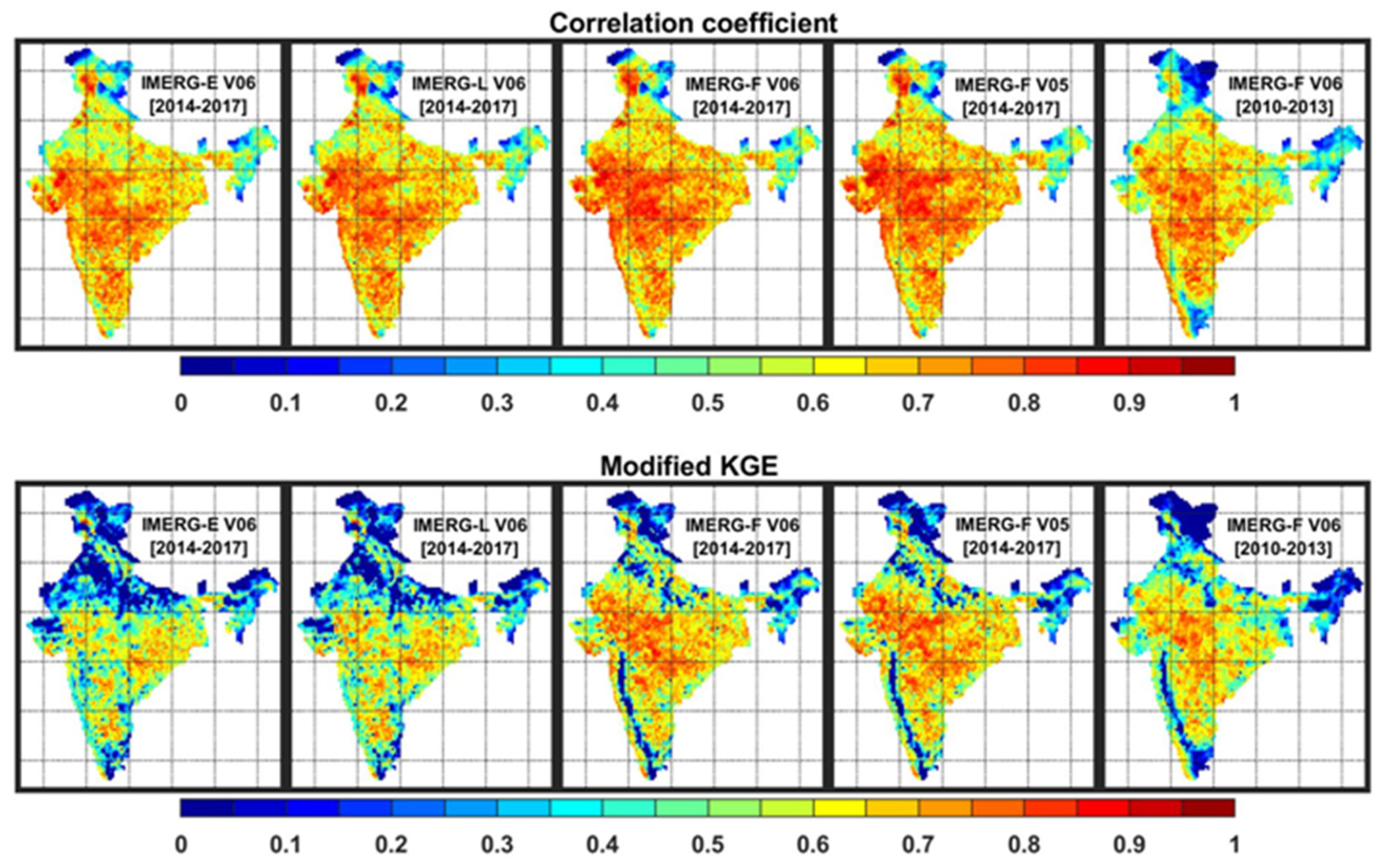
3.1. Spatial Distributions of Continuous Error Metrics
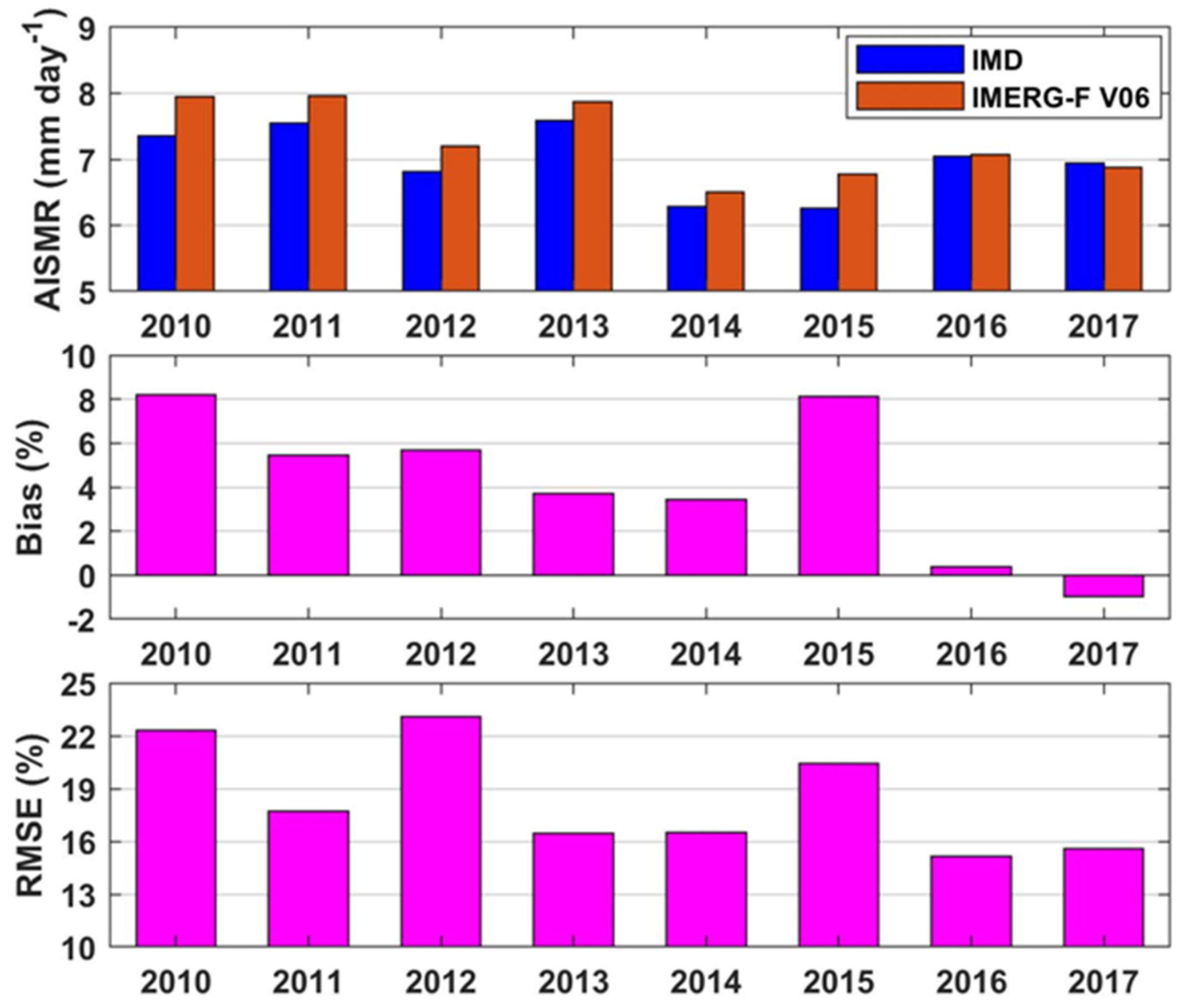
3.2. Error Metrics at the All-India Scale
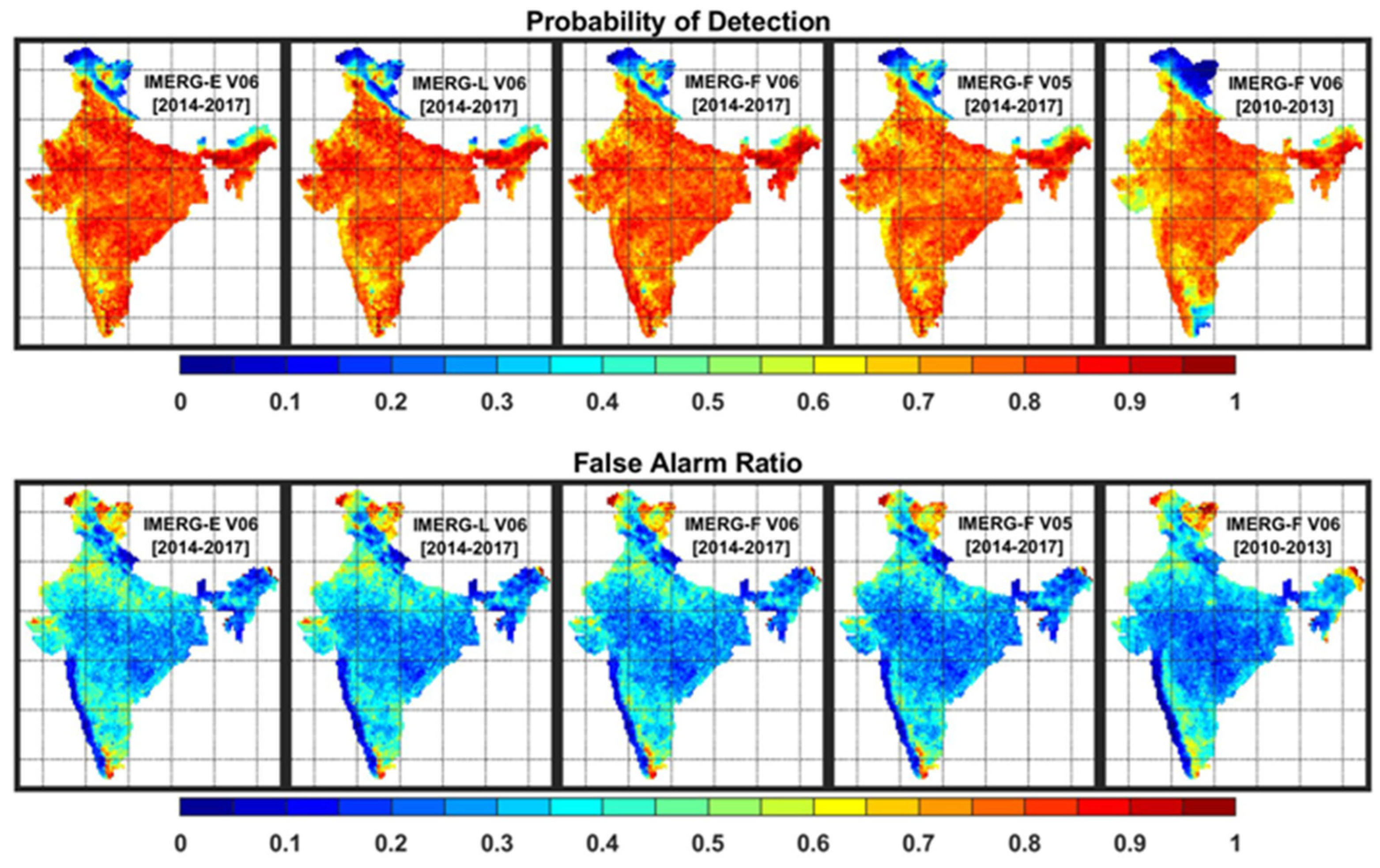
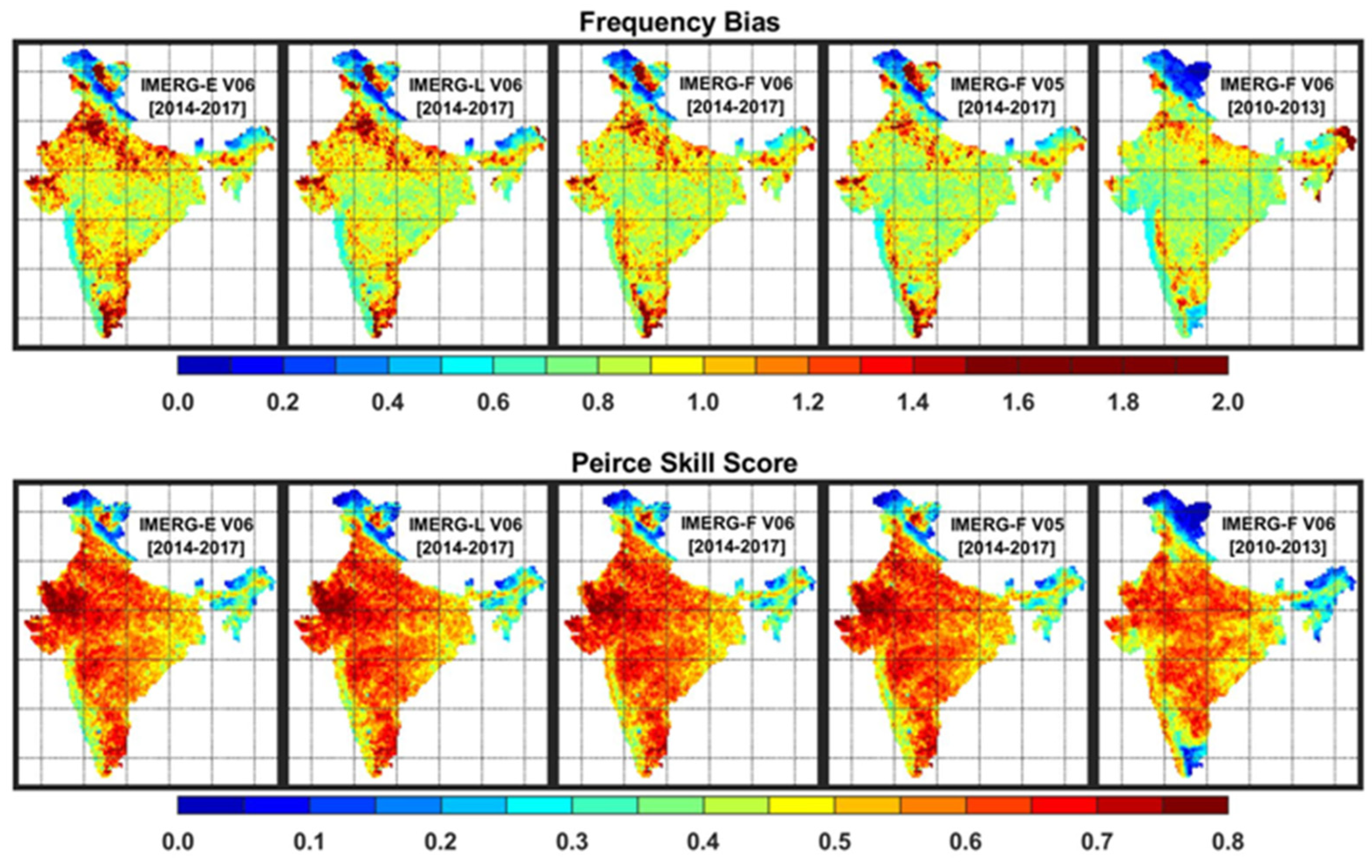
3.3. Spatial Distributions of Categorical Skill Metrics
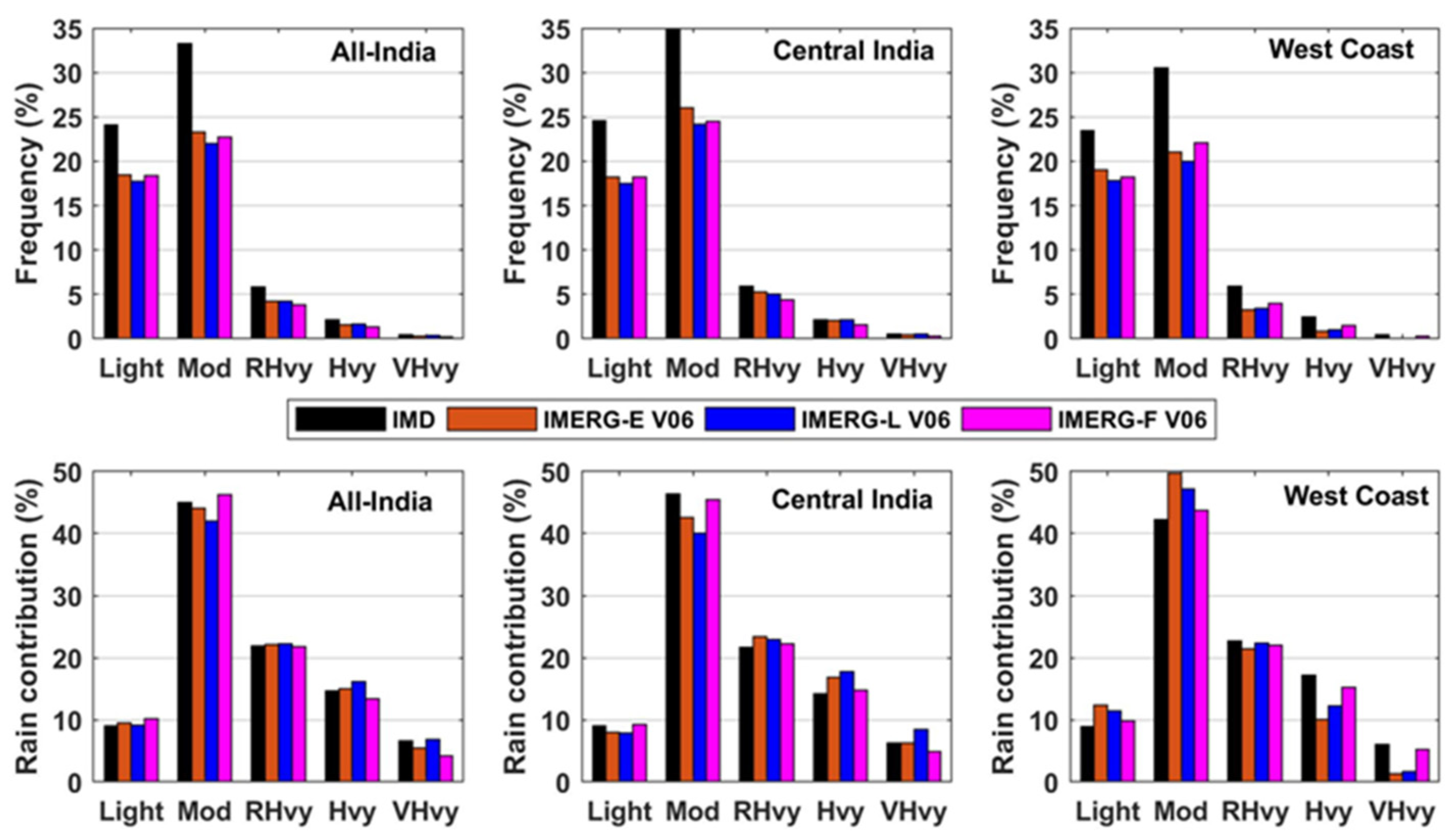
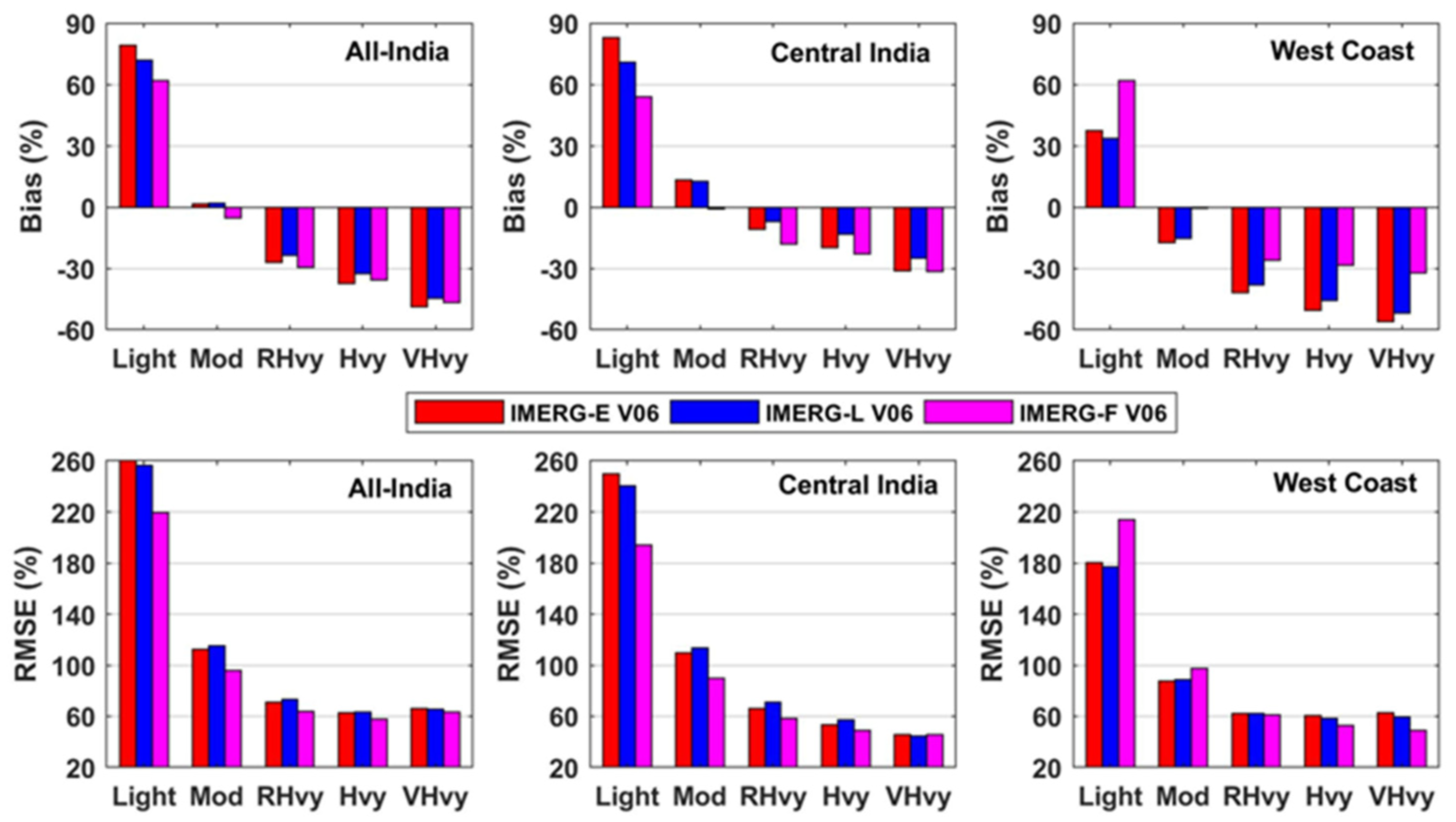
3.4. Error Metrics for Different Rainfall Intensity Intervals
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schlosser, C.A.; Houser, P.R. Assessing a satellite-era perspective of the global water cycle. J. Clim. 2007, 20, 1316–1338. [Google Scholar] [CrossRef] [Green Version]
- Levizzani, V.; Cattani, E. Satellite remote sensing of precipitation and the terrrestrial water cycle in a changing climate. Remote Sens. 2019, 11, 2301. [Google Scholar] [CrossRef] [Green Version]
- Kidd, C.; Huffman, G.; Maggioni, V.; Chambon, P.; Oki, R. The global satellite precipitation constellation: Current status and future requirement. Bull. Amer. Meteorol. Soc. 2021, 1–47. [Google Scholar] [CrossRef]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The Tropical Rainfall Measuring Mission (TRMM) sensor package. J. Atmos. Ocean. Tecnol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Hong, Y.; Tang, G.; Ma, Y.; Huang, Q.; Han, Z.; Zeng, Z.; Yang, Y.; Wang, C.; Guo, X. Remote sensing precipitation: Sensors, retrievals, validations, and applications. In Observation and Measurement of Ecohydrological Processes; Li, X., Vereecken, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–23. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A review of global precipitation data sets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef] [Green Version]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, how much of the Earth’s surface is covered by rain gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The TRMM Multi-satellite Precipitation Analysis (TMPA). In Satellite Precipitation for Surface Hydrology; Hossain, F., Gebremichael, M., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 3–22. [Google Scholar] [CrossRef] [Green Version]
- Joyce, R.; Xie, P.; Janowiak, J.E. Kalman filter-based CMORPH. J. Hydrometeorol. 2011, 12, 1547–1563. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.L.; Sorooshian, S.; Gao, X. Precipitation estimation from remotely sensed imagery using an artificial neural network cloud classification system. J. Appl. Meteorol. 2004, 43, 1834–1852. [Google Scholar] [CrossRef] [Green Version]
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Nakagawa, K.; Iwanami, K.; et al. Global precipitation map using satelliteborne microwave radiometers by the GSMaPproject: Production and validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Maggioni, V.; Meyers, P.C.; Robinson, M.D. A review of merged high-resolution satellite precipitation product accuracy during the Tropical Rainfall Measuring Mission (TRMM) era. J. Hydrometeorol. 2016, 17, 1101–1117. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Gairola, R.M.; Norouzi, H.; Pai, D.S. Status of high-resolution multisatellite precipitation products across India. In Remote Sensing of Aerosols, Clouds, and Precipitation; Islam, T., Hu, Y., Kokhanovsky, A., Wang, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 301–314. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Kirschbaum, D.; Petersen, W.; Huffman, G.; Kidd, C.; Stocker, E.; Kakar, R. The Global Precipitation Measurement (GPM) mission’s scientific achievements and societal contributions: Reviewing four years of advanced rain and snow observations. Q. J. R. Meteorol. Soc. 2018, 144, 27–47. [Google Scholar] [CrossRef] [Green Version]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG). Algorithm Theoretical Basis Document (ATBD) Version 5.2. 2018; p. 35. Available online: https://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V5.2.pdf (accessed on 12 February 2021).
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.-L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J.; et al. Integrated Multi-satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG). In Satellite Precipitation Measurement; Springer: Berlin/Heidelberg, Germany, 2020; Volume 1, pp. 343–353. [Google Scholar] [CrossRef]
- Fang, J.; Yang, W.; Luan, Y.; Du, J.; Lin, A.; Zhao, L. Evaluation of the TRMM 3B42 and GPM IMERG products for extreme precipitation analysis over China. Atmos. Res. 2019, 223, 24–38. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Pai, D.S.; AghaKouchak, A. From TRMM to GPM: How well can heavy rainfall be detected from space? Adv. Water Resour. 2016, 88, 1–7. [Google Scholar] [CrossRef]
- Sharma, S.; Khadka, N.; Hamal, K.; Shrestha, D.; Talchabhadel, R.; Chen, Y. How accurately can satellite products (TMPA and IMERG) detect precipitation patterns, extremities, and drought across the Nepalese Himalaya? Earth Space Sci. 2020, 7, e2020EA001315. [Google Scholar] [CrossRef]
- Tan, J.; Petersen, W.A.; Kirstetter, P.-E.; Tian, Y. Performance of IMERG as a function of spatiotemporal scale. J. Hydrometeorol. 2017, 18, 307–319. [Google Scholar] [CrossRef]
- Sunilkumar, K.; Yatagai, A.; Masuda, M. Preliminary evaluation of GPM-IMERG rainfall estimates over three distinct climate zones with APHRODITE. Earth Sapce Sci. 2019, 6, 1321–1335. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z. Comparison of Integrated Multisatellite Retrievals for GPM (IMERG) and TRMM Multisatellite Precipitation Analysis (TMPA) monthly precipitation products: Initial results. J. Hydrometeorol. 2016, 17, 777–790. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Liu, Z.; Norouzi, H.; Pai, D.S. A preliminary assessment of GPM-based multi-satellite precipitation estimates over a monsoon dominated region. J. Hydrol. 2018, 556, 865–876. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Guo, B.; Xing, W.; Zhou, J.; Xu, F.; Xu, Y. Comprehensive evaluation of latest GPM era IMERG and GSMaP precipitation products over mainland China. Atmos. Res. 2020, 246, 105132. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Soe, K.M.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Applications of TRMM- and GPM-era multiple-satellite precipitation products for flood simulations at sub-daily scales in a sparsely gauged watershed in Myanmar. Remote Sens. 2019, 11, 140. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.J.; Wang, D.H.; Qin, Z.; Zheng, Y.; Guo, J. Assessment of the GPM and TRMM precipitation products using the rain gauge network over the Tibetan Plateau. J. Meteorol. Res. 2018, 32, 324–336. [Google Scholar] [CrossRef]
- Cui, W.; Dong, X.; Xi, B.; Feng, Z.; Fan, J. Can the GPM IMERG Final product accurately represent MCSs’ precipitation characterstics over the Central and Eastern United States? J. Hydrometeorol. 2020, 21, 39–57. [Google Scholar] [CrossRef]
- Afonso, J.M.S.; Vila, D.A.; Gan, M.A.; Quispe, D.P.; Barreto, N.J.C.; Chinchay, J.H.H.; Palharini, R.S.A. Precipitation diurnal cycle assessment of satellite-based estimates over Brazil. Remote Sens. 2020, 12, 2339. [Google Scholar] [CrossRef]
- Li, X.; Sungmin, O.; Wang, N.; Liu, L.; Huang, Y. Evaluation of the GPM IMERG V06 products for light rain over Mainland China. Atmos. Res. 2021, 253, 105510. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.; He, J.; Ge, F.; Chen, Q.; Tang, S.; Yao, S. Can the GPM IMERG hourly products replicate the variation in precipitation during the wet season over the Sichuan Basin, China? Earth Space Sci. 2020, 7, e2020EA001090. [Google Scholar] [CrossRef] [Green Version]
- Hosseini-Moghari, S.-M.; Tang, Q. Validation of GPM IMERG V05 and V06 precipitation products over Iran. J. Hydrometeorol. 2020, 21, 1011–1037. [Google Scholar] [CrossRef] [Green Version]
- Mahmoud, M.T.; Hamouda, M.A.; Mohamed, M.M. Spatiotemporal evaluation of the GPM satellite precipitation products over the United Arab Emirates. Atmos. Res. 2019, 219, 200–212. [Google Scholar] [CrossRef]
- Sakib, S.; Ghebreyesus, D.; Sharif, H.O. Performance evaluation of IMERG GPM products during tropical storm Imelda. Atmosphere 2021, 12, 687. [Google Scholar] [CrossRef]
- Derin, Y.; Anagnostou, E.; Berne, A.; Borga, M.; Boudevillain, B.; Buytaert, W.; Chang, C.-H.; Chen, H.; Delrieu, G.; Hsu, Y.C.; et al. Evaluation of GPM-era global satellite precipitation products over multiple complex terrain regions. Remote Sens. 2019, 11, 2936. [Google Scholar] [CrossRef] [Green Version]
- Hamza, A.; Anjum, M.N.; Cheema, M.J.M.; Chen, X.; Afzal, A.; Azam, M.; Shafi, M.K.; Gulakhmadov, A. Assessment of IMERG-V06, TRMM-3B42V7, SM2RAIN-ASCAT, and PERSIANN-CDR precipitation products over the Hindu Kush mountains of Pakistan, South Asia. Remote Sens. 2020, 12, 3871. [Google Scholar] [CrossRef]
- Beria, H.; Nanda, T.; Bisht, D.S.; Chatterjee, C. Does the GPM mission improve the systematic error component in satellite rainfall estimates over TRMM? An evaluation at a pan-India scale. Hydrol. Earth Syst. Sci. 2017, 21, 6117–6134. [Google Scholar] [CrossRef] [Green Version]
- Murali Krishna, U.V.; Das, S.K.; Deshpande, S.M.; Doiphode, S.L.; Pandithurai, G. The assessment of Global Precipitation Measurement estimates over the Indian subcontinent. Earth Space Sci. 2017, 4, 540–553. [Google Scholar] [CrossRef]
- Reddy, M.V.; Mitra, A.K.; Momin, I.M.; Mitra, A.K.; Pai, D.S. Evaluation and inter-comparison of high-resolution multi-satellite rainfall products over India for the southwest monsoon period. Int. J. Remote Sens. 2019, 40, 4577–4603. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Stocker, E.F.; Tan, J. V06 IMERG Release Notes. 2020; p. 15. Available online: https://gpm.nasa.gov/sites/default/files/2020-10/IMERG_V06_release_notes_201006_0.pdf (accessed on 12 February 2021).
- Pai, D.S.; Sridhar, L.; Rajeevan, M.; Sreejith, O.P.; Satbhai, N.S.; Mukhopadhyay, B. Development of a new high spatial resolution (0.25° × 0.25°) long period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region. Mausam 2014, 65, 1–18. [Google Scholar]
- Bharti, V.; Singh, C. Evaluation of error in TRMM 3B42V7 precipitation estimates over the Himalayan region. J. Geophys. Res. Atmos. 2015, 120, 12458–12473. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Pai, D.S. Error characterization of TRMM Multisatellite Precipitation Analysis (TMPA-3B42) products over India for different seasons. J. Hydrol. 2015, 529, 1302–1312. [Google Scholar] [CrossRef]
- Vinnarasi, R.; Dhanya, C.T. Changing characteristics of extreme wet and dry spells of Indian monsoon rainfall. J. Geophys. Res. Atmos. 2016, 121, 2146–2160. [Google Scholar] [CrossRef]
- Sharma, S.; Mujumdar, P. Increasing frequency and spatial extent of concurrent meteorological droughts and heatwaves in India. Sci. Rep. 2017, 7, 15582. [Google Scholar] [CrossRef] [Green Version]
- Barik, B.; Ghosh, S.; Sahana, A.S.; Pathak, A.; Sekhar, M. Water-food-energy nexus with changing agricultural scenarios in India during recent decades. Hydrol. Earth Syst. Sci. 2017, 21, 3041–3060. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, S.; Aadhar, S.; Stone, D.; Mishra, V. Increase in extreme precipitation events under anthropogenic warming in India. Weather Clim. Extrem. 2018, 20, 45–53. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Mehran, A.; Norouzi, H.; Behrangi, A. Systematic and random error components in satellite precipitation data sets. Geophys. Res. Lett. 2012, 39, L09406. [Google Scholar] [CrossRef] [Green Version]
- Gadgil, S. The Indian monsoon and its variability. Annu. Rev. Earth Planet. Sci. 2003, 31, 429–467. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Tang, G.; Hong, Z.; Chen, M.; Gao, S.; Kirstetter, P.; Gourley, J.J.; Wen, Y.; Yami, T.; Nabih, S.; et al. Two-decades of GPM IMERG Early and Final run products intercomparison: Similarity and difference in climatology, rates, and extremes. J. Hydrol. 2021, 594, 125975. [Google Scholar] [CrossRef]
- Francis, P.A.; Gadgil, S. Intense rainfall events over the west coast of India. Meteorol. Atmos. Phys. 2006, 94, 27–42. [Google Scholar] [CrossRef]
- Konduru, R.T.; Mrudula, G. Effect of offshore troughs on the South India erratic summer monsoon rainfall in June 2017. Dyn. Atmos. Oceans 2021, 93, 101187. [Google Scholar] [CrossRef]
- Kumar, S.; Hazra, A.; Goswami, B.N. Role of interaction between dynamics, thermodynamics and cloud microphysics on summer monsoon precipitation clouds over the Myanmar Coast and Western Ghats. Clim. Dyn. 2014, 43, 911–924. [Google Scholar] [CrossRef]
- Rojas, Y.; Minder, J.R.; Campbell, L.S.; Massmann, A.; Garreaud, R. Assessment of GPM IMERG satellite precipitation estimation and its dependence on microphysical rain regimes over the mountains of south-central Chile. Atmos. Res. 2021, 253, 105454. [Google Scholar] [CrossRef]
- Guo, J.; Zhai, P.; Wu, L.; Cribb, M.; Li, Z.; Ma, Z.; Wang, F.; Chu, D.; Wang, P.; Zhang, J. Diurnal variation and the influential factors of precipitation from surface and satellite measurements in Tibet. Int. J. Climatol. 2014, 34, 2940–2956. [Google Scholar] [CrossRef]
- Chiaravalloti, F.; Brocca, L.; Prcopio, A.; Massari, C.; Gabriele, S. Assessment of GPM and SM2RAIN-ASCAT rainfall products over complex terrain in southern Italy. Atmos. Res. 2018, 206, 64–74. [Google Scholar] [CrossRef]
- Wehbe, Y.; Temimi, M.; Ghebreyesus, D.T.; Milewski, A.; Norouzi, H.; Ibrahim, E. Consistency of precipitation products over the Arabian Peninsula and interactions with soil moisture and water storage. Hydrol. Sci. J. 2018, 63, 408–425. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.-P.; Willems, P.; Onof, C. A review of radar-rain gauge data merging methods and their potential for urban hydrological applications. Water Resour. Res. 2019, 55, 6356–6391. [Google Scholar] [CrossRef]
- Wehbe, Y.; Temimi, M.; Adler, R.F. Enhancing precipitation estimates through the fusion of weather radar, satellite retrievals, and surface parameters. Remote Sens. 2020, 12, 1342. [Google Scholar] [CrossRef] [Green Version]
- Tan, J.; Petersen, W.A.; Tokay, A. A novel approach to identify sources of errors in IMERG for GPM ground validation. J. Hydrometeorol. 2016, 17, 2477–2491. [Google Scholar] [CrossRef]
- Rajagopal, M.; Zipser, E.; Huffman, G.; Russell, J.; Tan, J. Comparison of IMERG version 06 precipitation at and between passive microwave overpasses in the tropics. J. Hydrometeorol. 2021, 22, 2117–2130. [Google Scholar] [CrossRef]
- Ayat, H.; Evans, J.P.; Behrangi, A. How do different sensors impact IMERG precipitation estimates during hurricane days? Remote Sens. Environ. 2021, 259, 112417. [Google Scholar] [CrossRef]
- Prakash, S.; Seshadri, A.; Srinivasan, J.; Pai, D.S. A new parameter to assess impact of rain gauge density on uncertainty in the estimates of monthly rainfall over India. J. Hydrometeorol. 2019, 20, 821–832. [Google Scholar] [CrossRef]
| Error Metrics | Formulae |
|---|---|
| Bias (mm day−1) | where, and |
| Correlation coefficient | |
| Coefficient of variation (%) | |
| Root mean square error (mm day−1) | |
| Modified Kling–Gupta efficiency |
| Formulae | Range | Perfect Score | |
|---|---|---|---|
| Probability of Detection | 0 to 1 | 1 | |
| False Alarm Ratio | 0 to 1 | 0 | |
| Frequency Bias Index | 0 to ∞ | 1 | |
| Peirce′s Skill Score | −1 to 1 | 1 |
| 2014–2017 | 2010–2013 | ||||||
|---|---|---|---|---|---|---|---|
| IMD | IMERG-E V6 | IMERG-L V6 | IMERG-F V6 | IMERG-F V5 | IMD | IMERG-F V6 | |
| Mean(mm/day) | 6.63 | 7.34 | 7.29 | 6.80 | 6.78 | 7.32 | 7.74 |
| Bias (%) | – | 10.70 | 9.88 | 2.59 | 2.18 | – | 5.73 |
| CV (%) | 46.52 | 51.13 | 50.63 | 47.73 | 49.01 | 42.66 | 45.47 |
| Correlation | – | 0.89 | 0.92 | 0.94 | 0.93 | – | 0.92 |
| RMSE (%) | – | 28.65 | 24.91 | 16.89 | 18.26 | – | 19.91 |
| KGE | – | 0.81 | 0.84 | 0.93 | 0.91 | – | 0.88 |
| Rain Category | Daily Rainfall Range (mm) |
|---|---|
| Light | 2.5–7.5 mm |
| Moderate (Mod) | 7.5–35.5 mm |
| Rather heavy (RHvy) | 35.5–64.5 mm |
| Heavy (Hvy) | 64.5–124.5 mm |
| Very heavy (VHvy) | ≥124.5 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prakash, S.; Srinivasan, J. A Comprehensive Evaluation of Near-Real-Time and Research Products of IMERG Precipitation over India for the Southwest Monsoon Period. Remote Sens. 2021, 13, 3676. https://doi.org/10.3390/rs13183676
Prakash S, Srinivasan J. A Comprehensive Evaluation of Near-Real-Time and Research Products of IMERG Precipitation over India for the Southwest Monsoon Period. Remote Sensing. 2021; 13(18):3676. https://doi.org/10.3390/rs13183676
Chicago/Turabian StylePrakash, Satya, and Jayaraman Srinivasan. 2021. "A Comprehensive Evaluation of Near-Real-Time and Research Products of IMERG Precipitation over India for the Southwest Monsoon Period" Remote Sensing 13, no. 18: 3676. https://doi.org/10.3390/rs13183676
APA StylePrakash, S., & Srinivasan, J. (2021). A Comprehensive Evaluation of Near-Real-Time and Research Products of IMERG Precipitation over India for the Southwest Monsoon Period. Remote Sensing, 13(18), 3676. https://doi.org/10.3390/rs13183676






