Multiple Images Improve Lake CDOM Estimation: Building Better Landsat 8 Empirical Algorithms across Southern Canada
Abstract
:1. Introduction
2. Materials and Methods
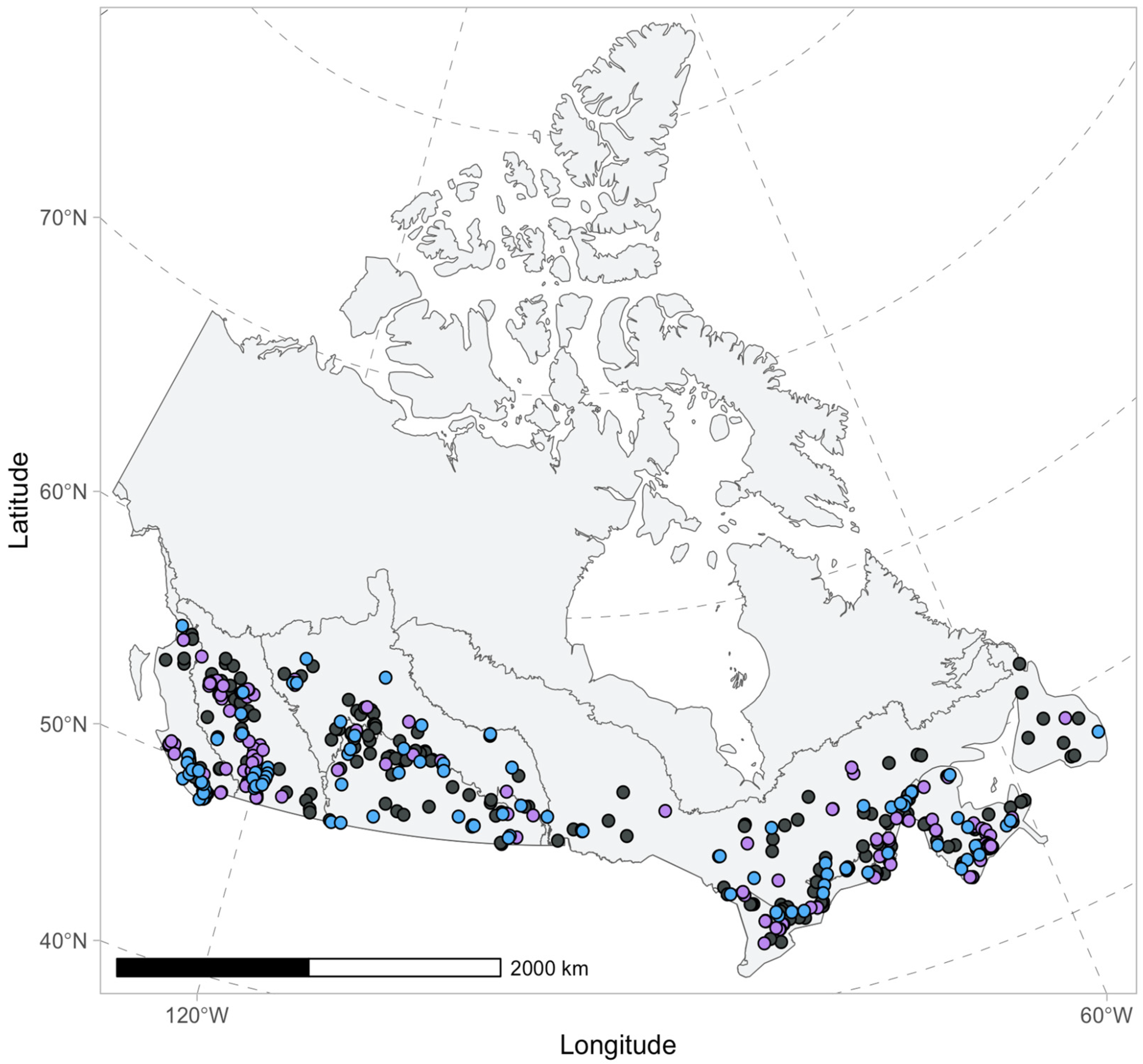
2.1. Study Site
2.2. In Situ Data Collection
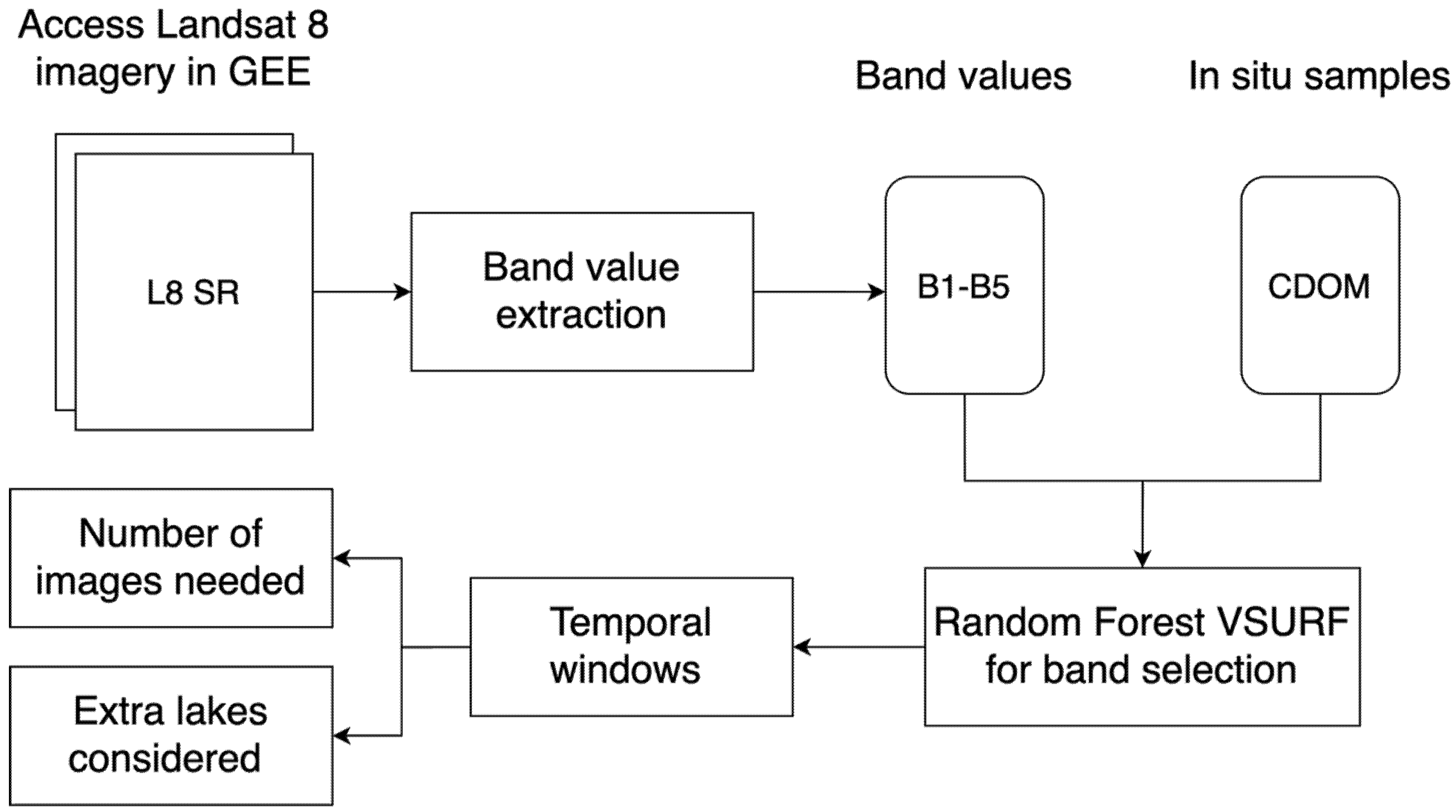
2.3. Image Collection and Processing
2.4. Coloured Dissolved Organic Matter Modelling
2.4.1. Predictor Selection
2.4.2. Time Windows
- Thirty-day Window Median: median image reflectance within ±30 days of the in situ sample date for each sample station (242 images, average 2.2 images per lake).
- Same Summer Median: median image reflectance within the same summer (20 June–20 September); the in situ sample was taken for each sample station (305 images, average 3.2 images per lake).
- All Summers Median: median image reflectance of all available summer images (20 June–20 September) throughout the Landsat record (2013–2019) for each sample station (2290 images, average 23.8 images per lake).
2.4.3. Effects of Adding Imagery
2.4.4. Extra Lakes Considered when the Time Window Was Expanded
2.4.5. Overall Workflow
3. Results
3.1. CDOM Model Results
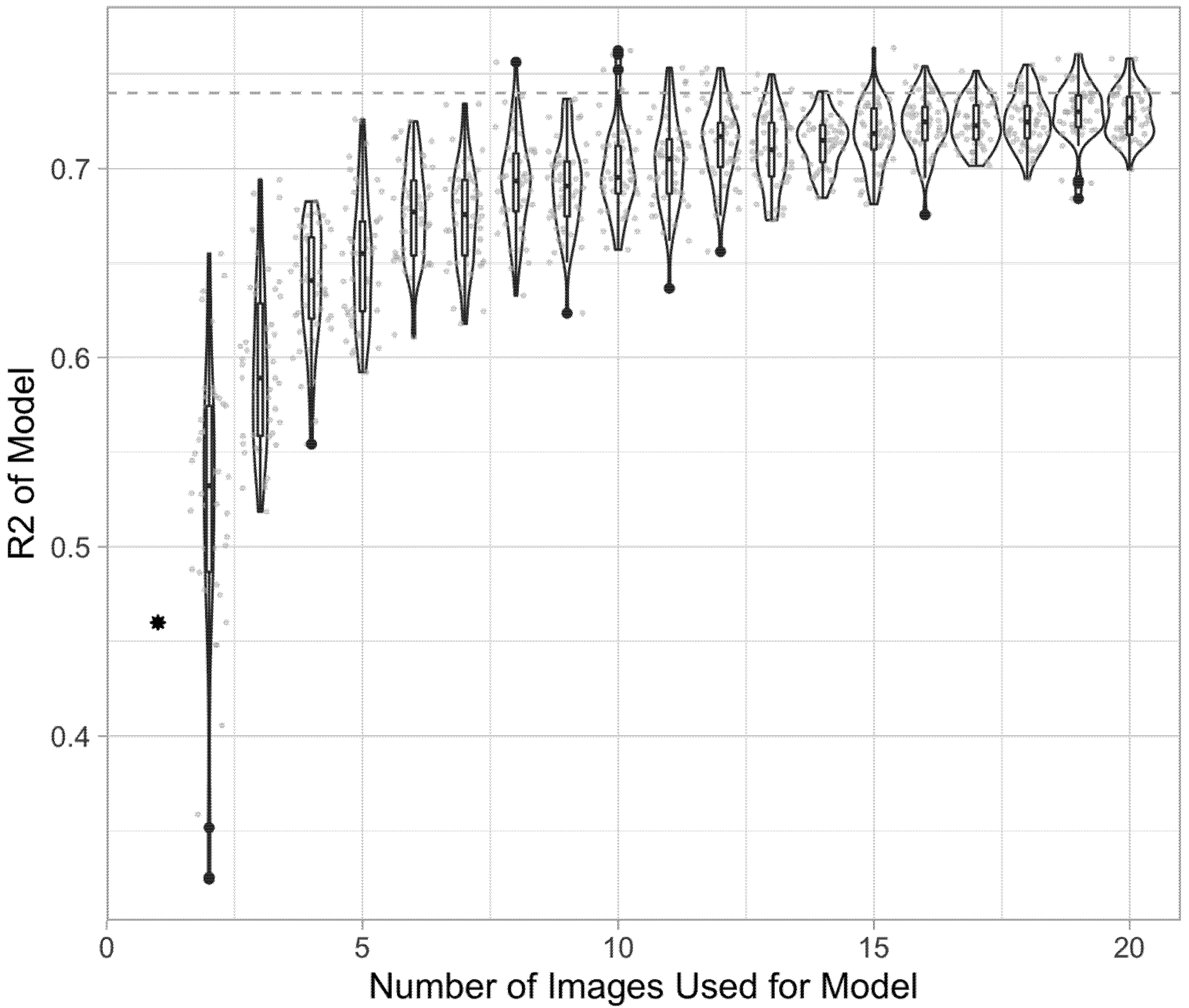
3.2. Using More Than One Image for Model Development
3.3. Model Validation
3.4. Effects of Adding Imagery
3.5. Extra Lakes Considered When the Time Window Was Expanded
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Creed, I.F.; Bergström, A.-K.; Trick, C.G.; Grimm, N.B.; Hessen, D.O.; Karlsson, J.; Kidd, K.A.; Kritzberg, E.; McKnight, D.M.; Freeman, E.C.; et al. Global Change-Driven Effects on Dissolved Organic Matter Composition: Implications for Food Webs of Northern Lakes. Glob. Chang. Biol. 2018, 24, 3692–3714. [Google Scholar] [CrossRef]
- Solomon, C.T.; Jones, S.E.; Weidel, B.C.; Buffam, I.; Fork, M.L.; Karlsson, J.; Larsen, S.; Lennon, J.T.; Read, J.S.; Sadro, S.; et al. Ecosystem Consequences of Changing Inputs of Terrestrial Dissolved Organic Matter to Lakes: Current Knowledge and Future Challenges. Ecosystems 2015, 18, 376–389. [Google Scholar] [CrossRef]
- Hudson, N.; Baker, A.; Reynolds, D. Fluorescence Analysis of Dissolved Organic Matter in Natural, Waste and Polluted Waters—A Review. River Res. Appl. 2007, 23, 631–649. [Google Scholar] [CrossRef]
- Brezonik, P.; Arnold, W.A. Water Chemistry: An Introduction to the Chemistry of Natural and Engineered Aquatic Systems; Oxford University Press: New York, NY, USA, 2011; ISBN 978-0-19-973072-8. [Google Scholar]
- Chen, Y.; Arnold, W.A.; Griffin, C.G.; Olmanson, L.G.; Brezonik, P.L.; Hozalski, R.M. Assessment of the Chlorine Demand and Disinfection Byproduct Formation Potential of Surface Waters via Satellite Remote Sensing. Water Res. 2019, 165, 115001. [Google Scholar] [CrossRef]
- Gaiser, E.E.; Deyrup, N.D.; Bachmann, R.W.; Battoe, L.E.; Swain, H.M. Effects of Climate Variability on Transparency and Thermal Structure in Subtropical, Monomictic Lake Annie, Florida. Fundam. Appl. Limnol. 2009, 175, 217–230. [Google Scholar] [CrossRef]
- Heijerick, D.G.; Janssen, C.R.; Coen, W.M.D. The Combined Effects of Hardness, PH, and Dissolved Organic Carbon on the Chronic Toxicity of Zn to D. Magna: Development of a Surface Response Model. Arch. Environ. Contam. Toxicol. 2003, 44, 210–217. [Google Scholar] [CrossRef] [PubMed]
- Houser, J.N. Water Color Affects the Stratification, Surface Temperature, Heat Content, and Mean Epilimnetic Irradiance of Small Lakes. Can. J. Fish. Aquat. Sci. 2006, 63, 2447–2455. [Google Scholar] [CrossRef]
- Pilla, R.M.; Williamson, C.E.; Zhang, J.; Smyth, R.L.; Lenters, J.D.; Brentrup, J.A.; Knoll, L.B.; Fisher, T.J. Browning-Related Decreases in Water Transparency Lead to Long-Term Increases in Surface Water Temperature and Thermal Stratification in Two Small Lakes. J. Geophys. Res. Biogeosci. 2018, 123, 1651–1665. [Google Scholar] [CrossRef]
- Thrane, J.-E.; Hessen, D.O.; Andersen, T. The Absorption of Light in Lakes: Negative Impact of Dissolved Organic Carbon on Primary Productivity. Ecosystems 2014, 17, 1040–1052. [Google Scholar] [CrossRef] [Green Version]
- Lapierre, J.-F.; Guillemette, F.; Berggren, M.; del Giorgio, P.A. Increases in Terrestrially Derived Carbon Stimulate Organic Carbon Processing and CO2 Emissions in Boreal Aquatic Ecosystems. Nat. Commun. 2013, 4, 2972. [Google Scholar] [CrossRef]
- Song, G.; Li, Y.; Hu, S.; Li, G.; Zhao, R.; Sun, X.; Xie, H. Photobleaching of Chromophoric Dissolved Organic Matter (CDOM) in the Yangtze River Estuary: Kinetics and Effects of Temperature, PH, and Salinity. Environ. Sci. Process. Impacts 2017, 19, 861–873. [Google Scholar] [CrossRef] [PubMed]
- Blewett, T.A.; Dow, E.M.; Wood, C.M.; McGeer, J.C.; Smith, D.S. The Role of Dissolved Organic Carbon Concentration and Composition on Nickel Toxicity to Early Life-Stages of the Blue Mussel Mytilus Edulis and Purple Sea Urchin Strongylocentrotus Purpuratus. Ecotoxicol. Environ. Saf. 2018, 160, 162–170. [Google Scholar] [CrossRef]
- Schwartz, M.L.; Curtis, P.J.; Playle, R.C. Influence of Natural Organic Matter Source on Acute Copper, Lead, and Cadmium Toxicity to Rainbow Trout (Oncorhynchus Mykiss). Environ. Toxicol. Chem. 2004, 23, 2889. [Google Scholar] [CrossRef] [PubMed]
- Grünwald, A.; Šťastný, B.; Slavíčková, K.; Slavíček, M. Formation of Haloforms during Chlorination of Natural Waters. Acta Polytech. 2002, 42. [Google Scholar] [CrossRef]
- Minear, R.A.; Amy, G.L. Disinfection By-Products in Water Treatment: The Chemistrg of Their Formation and Control; CRC Press: Boca Raton, FL, USA, 1996; ISBN 978-1-315-14135-0. [Google Scholar]
- Olmanson, L.G.; Page, B.P.; Finlay, J.C.; Brezonik, P.L.; Bauer, M.E.; Griffin, C.G.; Hozalski, R.M. Regional Measurements and Spatial/Temporal Analysis of CDOM in 10,000+ Optically Variable Minnesota Lakes Using Landsat 8 Imagery. Sci. Total Environ. 2020, 724, 138141. [Google Scholar] [CrossRef] [PubMed]
- Ross, M.R.V.; Topp, S.N.; Appling, A.P.; Yang, X.; Kuhn, C.; Butman, D.; Simard, M.; Pavelsky, T.M. AquaSat: A Data Set to Enable Remote Sensing of Water Quality for Inland Waters. Water Resour. Res. 2019, 55, 10012–10025. [Google Scholar] [CrossRef]
- Stanley, E.H.; Powers, S.M.; Lottig, N.R.; Buffam, I.; Crawford, J.T. Contemporary Changes in Dissolved Organic Carbon (DOC) in Human-Dominated Rivers: Is There a Role for DOC Management? Freshw. Biol. 2012, 57, 26–42. [Google Scholar] [CrossRef]
- Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the Volume and Age of Water Stored in Global Lakes Using a Geo-Statistical Approach. Nat. Commun. 2016, 7, 13603. [Google Scholar] [CrossRef]
- Mannino, A.; Russ, M.E.; Hooker, S.B. Algorithm Development and Validation for Satellite-Derived Distributions of DOC and CDOM in the U.S. Middle Atlantic Bight. J. Geophys. Res. 2008, 113, C07051. [Google Scholar] [CrossRef]
- Klein, I.; Gessner, U.; Dietz, A.J.; Kuenzer, C. Global WaterPack—A 250 m Resolution Dataset Revealing the Daily Dynamics of Global Inland Water Bodies. Remote Sens. Environ. 2017, 198, 345–362. [Google Scholar] [CrossRef]
- Kutser, T.; Pierson, D.C.; Kallio, K.Y.; Reinart, A.; Sobek, S. Mapping Lake CDOM by Satellite Remote Sensing. Remote Sens. Environ. 2005, 94, 535–540. [Google Scholar] [CrossRef]
- Mishra, D.R.; Ogashawara, I.; Gitelson, A.A. (Eds.) Bio-Optical Modelling and Remote Sensing of Inland Waters; Elsevier: Amsterdam, The Netherlands, 2017; ISBN 978-0-12-804644-9. [Google Scholar]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary Analysis of the Performance of the Landsat 8/OLI Land Surface Reflectance Product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef] [PubMed]
- Brezonik, P.; Olmanson, L.G.; Finlay, J.C.; Bauer, M.E. Factors Affecting the Measurement of CDOM by Remote Sensing of Optically Complex Inland Waters. Remote Sens. Environ. 2015, 157, 199–215. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, W.-N.; Tian, Y.Q.; Yu, Q. Estimation of Colored Dissolved Organic Matter From Landsat-8 Imagery for Complex Inland Water: Case Study of Lake Huron. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2201–2212. [Google Scholar] [CrossRef]
- Kutser, T.; Casal Pascual, G.; Barbosa, C.; Paavel, B.; Ferreira, R.; Carvalho, L.; Toming, K. Mapping Inland Water Carbon Content with Landsat 8 Data. Int. J. Remote Sens. 2016, 37, 2950–2961. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Brezonik, P.L.; Finlay, J.C.; Bauer, M.E. Comparison of Landsat 8 and Landsat 7 for Regional Measurements of CDOM and Water Clarity in Lakes. Remote Sens. Environ. 2016, 185, 119–128. [Google Scholar] [CrossRef]
- Tyler, A.N.; Hunter, P.D.; Spyrakos, E.; Groom, S.; Constantinescu, A.M.; Kitchen, J. Developments in Earth Observation for the Assessment and Monitoring of Inland, Transitional, Coastal and Shelf-Sea Waters. Sci. Total Environ. 2016, 572, 1307–1321. [Google Scholar] [CrossRef] [Green Version]
- Bonansea, M.; Rodriguez, M.C.; Pinotti, L.; Ferrero, S. Using Multi-Temporal Landsat Imagery and Linear Mixed Models for Assessing Water Quality Parameters in Río Tercero Reservoir (Argentina). Remote Sens. Environ. 2015, 158, 28–41. [Google Scholar] [CrossRef]
- Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-Based Remote Sensing of Lake Water Quality Characteristics, Including Chlorophyll and Colored Dissolved Organic Matter (CDOM). Lake Reserv. Manag. 2005, 21, 373–382. [Google Scholar] [CrossRef]
- Cardille, J.A.; Leguet, J.-B.; del Giorgio, P. Remote Sensing of Lake CDOM Using Noncontemporaneous Field Data. Can. J. Remote Sens. 2013, 39, 118–126. [Google Scholar] [CrossRef]
- Dekker, A.G.; Vos, R.J.; Peters, S.W.M. Analytical Algorithms for Lake Water TSM Estimation for Retrospective Analyses of TM and SPOT Sensor Data. Int. J. Remote Sens. 2002, 23, 15–35. [Google Scholar] [CrossRef]
- Deutsch, E.S.; Cardille, J.A.; Koll-Egyed, T.; Fortin, M.-J. Landsat 8 Lake Water Clarity Empirical Algorithms: Large-Scale Calibration and Validation Using Government and Citizen Science Data from across Canada. Remote Sens. 2021, 13, 1257. [Google Scholar] [CrossRef]
- Griffin, C.G.; McClelland, J.W.; Frey, K.E.; Fiske, G.; Holmes, R.M. Quantifying CDOM and DOC in Major Arctic Rivers during Ice-Free Conditions Using Landsat TM and ETM+ Data. Remote Sens. Environ. 2018, 209, 395–409. [Google Scholar] [CrossRef]
- Kallio, K.; Attila, J.; Härmä, P.; Koponen, S.; Pulliainen, J.; Hyytiäinen, U.-M.; Pyhälahti, T. Landsat ETM+ Images in the Estimation of Seasonal Lake Water Quality in Boreal River Basins. Environ. Manag. 2008, 42, 511–522. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, C.; de Matos Valerio, A.; Ward, N.; Loken, L.; Sawakuchi, H.O.; Kampel, M.; Richey, J.; Stadler, P.; Crawford, J.; Striegl, R.; et al. Performance of Landsat-8 and Sentinel-2 Surface Reflectance Products for River Remote Sensing Retrievals of Chlorophyll-a and Turbidity. Remote Sens. Environ. 2019, 224, 104–118. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Yu, Q.; Tian, Y.Q.; Becker, B.L.; Siqueira, P.; Torbick, N. Spatio-Temporal Variations of CDOM in Shallow Inland Waters from a Semi-Analytical Inversion of Landsat-8. Remote Sens. Environ. 2018, 218, 189–200. [Google Scholar] [CrossRef]
- Lin, S.; Novitski, L.N.; Qi, J.; Stevenson, R.J. Landsat TM/ETM+ and Machine-Learning Algorithms for Limnological Studies and Algal Bloom Management of Inland Lakes. J. Appl. Remote Sens. 2018, 12, 026003. [Google Scholar] [CrossRef]
- McCullough, I.M.; Loftin, C.S.; Sader, S.A. Combining Lake and Watershed Characteristics with Landsat TM Data for Remote Estimation of Regional Lake Clarity. Remote Sens. Environ. 2012, 123, 109–115. [Google Scholar] [CrossRef]
- Page, B.P.; Olmanson, L.G.; Mishra, D.R. A Harmonized Image Processing Workflow Using Sentinel-2/MSI and Landsat-8/OLI for Mapping Water Clarity in Optically Variable Lake Systems. Remote Sens. Environ. 2019, 231, 111284. [Google Scholar] [CrossRef]
- Matthews, M.W. A Current Review of Empirical Procedures of Remote Sensing in Inland and Near-Coastal Transitional Waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Chen, T.; Ma, K.-K.; Chen, L.-H. Tri-State Median Filter for Image Denoising. IEEE Trans. Image Process. 1999, 8, 1834–1838. [Google Scholar] [CrossRef] [Green Version]
- Gupta, G. Algorithm for Image Processing Using Improved Median Filter and Comparison of Mean, Median and Improved Median Filter. Int. J. Soft Comput. Eng. 2011, 1, 304–311. [Google Scholar]
- Axelsson, A.; Lindberg, E.; Reese, H.; Olsson, H. Tree Species Classification Using Sentinel-2 Imagery and Bayesian Inference. Int. J. Appl. Earth Obs. Geoinform. 2021, 100, 102318. [Google Scholar] [CrossRef]
- Huot, Y.; Brown, C.A.; Potvin, G.; Antoniades, D.; Baulch, H.M.; Beisner, B.E.; Bélanger, S.; Brazeau, S.; Cabana, H.; Cardille, J.A.; et al. The NSERC Canadian Lake Pulse Network: A National Assessment of Lake Health Providing Science for Water Management in a Changing Climate. Sci. Total Environ. 2019, 695, 133668. [Google Scholar] [CrossRef]
- American Fisheries Society. Hubert, W.A., Quist, M.C., Eds.; Inland Fisheries Management in North America, 3rd ed.; American Fisheries Society: Bethesda, MD, USA, 2010; ISBN 978-1-934874-16-5. [Google Scholar]
- U.S. Geological Survey. Landsat 8 (L8) Data Users Handbook; Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA, 2019.
- Mobley, C.; Boss, E.; Roesler, C. Ocean Optics Web Book. 2020. Available online: http://www.oceanopticsbook.info (accessed on 1 September 2021).
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems, 3rd ed.; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-1-139-16821-2. [Google Scholar]
- Langford, V.S.; McKinley, A.J.; Quickenden, T.I. Temperature Dependence of the Visible-Near-Infrared Absorption Spectrum of Liquid Water. J. Phys. Chem. A 2001, 105, 8916–8921. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Slonecker, E.T.; Jones, D.K.; Pellerin, B.A. The New Landsat 8 Potential for Remote Sensing of Colored Dissolved Organic Matter (CDOM). Mar. Pollut. Bull. 2016, 107, 518–527. [Google Scholar] [CrossRef]
- Zhu, W.; Yu, Q.; Tian, Y.Q.; Becker, B.L.; Zheng, T.; Carrick, H.J. An Assessment of Remote Sensing Algorithms for Colored Dissolved Organic Matter in Complex Freshwater Environments. Remote Sens. Environ. 2014, 140, 766–778. [Google Scholar] [CrossRef]
- Foga, S.; Scaramuzza, P.L.; Guo, S.; Zhu, Z.; Dilley, R.D.; Beckmann, T.; Schmidt, G.L.; Dwyer, J.L.; Joseph Hughes, M.; Laue, B. Cloud Detection Algorithm Comparison and Validation for Operational Landsat Data Products. Remote Sens. Environ. 2017, 194, 379–390. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and Expansion of the Fmask Algorithm: Cloud, Cloud Shadow, and Snow Detection for Landsats 4–7, 8, and Sentinel 2 Images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. Variable Selection Using Random Forests. Pattern Recognit. Lett. 2010. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Neill, S.P.; Hashemi, M.R. Ocean Modelling for Resource Characterization. In Fundamentals of Ocean Renewable Energy; Elsevier: Amsterdam, The Netherlands, 2018; pp. 193–235. ISBN 978-0-12-810448-4. [Google Scholar]
- Willmott, C.; Matsuura, K. Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in Assessing Average Model Performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Hamner, B.; Frasco, M.; LeDell, E. Metrics: Evaluation Metrics for Machine Learning; CRAN: Vienna, Austria, 2018. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Rubin, H.J.; Lutz, D.A.; Steele, B.G.; Cottingham, K.L.; Weathers, K.C.; Ducey, M.J.; Palace, M.; Johnson, K.M.; Chipman, J.W. Remote Sensing of Lake Water Clarity: Performance and Transferability of Both Historical Algorithms and Machine Learning. Remote Sens. 2021, 13, 1434. [Google Scholar] [CrossRef]
- Al-Kharusi, E.S.; Tenenbaum, D.E.; Abdi, A.M.; Kutser, T.; Karlsson, J.; Bergström, A.-K.; Berggren, M. Large-Scale Retrieval of Coloured Dissolved Organic Matter in Northern Lakes Using Sentinel-2 Data. Remote Sens. 2020, 12, 157. [Google Scholar] [CrossRef] [Green Version]
- Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of Constituent Retrieval in Optically Deep and Complex Waters from Satellite Imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef] [Green Version]
- Shang, Y.; Liu, G.; Wen, Z.; Jacinthe, P.-A.; Song, K.; Zhang, B.; Lyu, L.; Li, S.; Wang, X.; Yu, X. Remote Estimates of CDOM Using Sentinel-2 Remote Sensing Data in Reservoirs with Different Trophic States across China. J. Environ. Manag. 2021, 286, 112275. [Google Scholar] [CrossRef]
- Wang, D.; Ma, R.; Xue, K.; Loiselle, S. The Assessment of Landsat-8 OLI Atmospheric Correction Algorithms for Inland Waters. Remote Sens. 2019, 11, 169. [Google Scholar] [CrossRef] [Green Version]
- Shao, T.; Song, K.; Du, J.; Zhao, Y.; Ding, Z.; Guan, Y.; Liu, L.; Zhang, B. Seasonal Variations of CDOM Optical Properties in Rivers Across the Liaohe Delta. Wetlands 2016, 36, 181–192. [Google Scholar] [CrossRef]
- Toming, K.; Arst, H.; Paavel, B.; Laas, A.; Tiina, N. Spatial and Temporal Variations in Coloured Dissolved Organic Matter in Large and Shallow Estonian Waterbodies. Boreal Environ. Res. 2009, 14, 959–970. [Google Scholar]
- Erm, A.; Arst, H.; Nõges, P.; Nõges, T.; Reinart, A.; Sipelgas, L. Temporal Variations in Bio-Optical Properties of Four North Estonian Lakes in 1999–2000. Geophysica 2002, 38, 89–111. [Google Scholar]
- Evans, C.D.; Chapman, P.J.; Clark, J.M.; Monteith, D.T.; Cresser, M.S. Alternative Explanations for Rising Dissolved Organic Carbon Export from Organic Soils. Glob. Chang Biol. 2006, 12, 2044–2053. [Google Scholar] [CrossRef]
- Haaland, S.; Hongve, D.; Laudon, H.; Riise, G.; Vogt, R.D. Quantifying the Drivers of the Increasing Colored Organic Matter in Boreal Surface Waters. Environ. Sci. Technol. 2010, 44, 2975–2980. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L. Novel Spectra-Derived Features for Empirical Retrieval of Water Quality Parameters: Demonstrations for OLI, MSI, and OLCI Sensors. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10285–10300. [Google Scholar] [CrossRef]
- Neil, C.; Spyrakos, E.; Hunter, P.D.; Tyler, A.N. A Global Approach for Chlorophyll-a Retrieval across Optically Complex Inland Waters Based on Optical Water Types. Remote Sens. Environ. 2019, 229, 159–178. [Google Scholar] [CrossRef]
- Reinart, A.; Herlevi, A.; Arst, H.; Sipelgas, L. Preliminary Optical Classification of Lakes and Coastal Waters in Estonia and South Finland. J. Sea Res. 2003, 49, 357–366. [Google Scholar] [CrossRef]
- Spyrakos, E.; O’Donnell, R.; Hunter, P.D.; Miller, C.; Scott, M.; Simis, S.G.H.; Neil, C.; Barbosa, C.C.F.; Binding, C.E.; Bradt, S.; et al. Optical Types of Inland and Coastal Waters. Limnol. Oceanogr. 2018, 63, 846–870. [Google Scholar] [CrossRef] [Green Version]


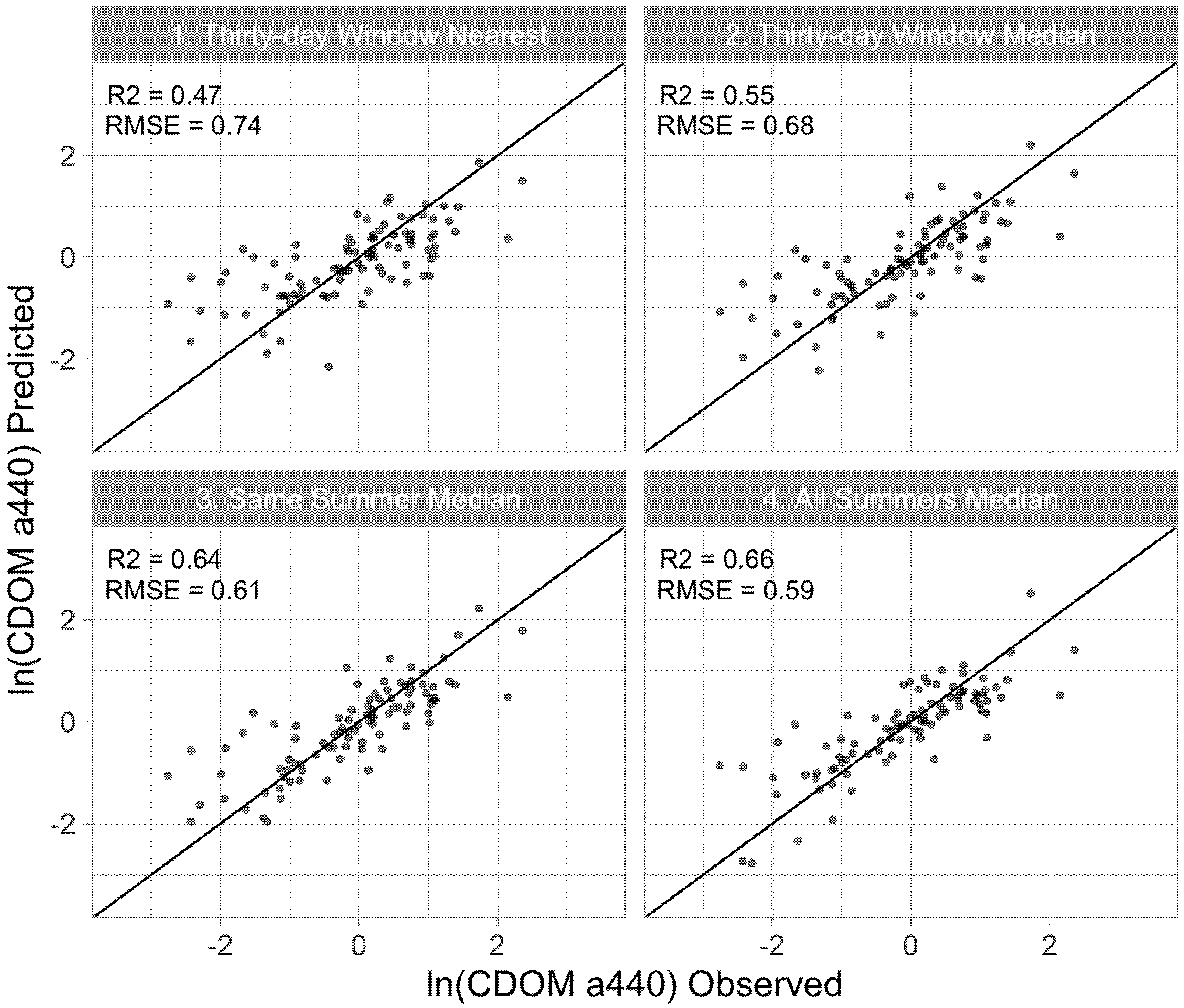

| Time Window | Sample Size | Intercept | Coefficient (G/R) | Coefficient (B) | RMSE | MAE | Bias | Adj. R2 | Valid-ation Adj. R2 | Extra Lakes Adj R2 |
|---|---|---|---|---|---|---|---|---|---|---|
| Thirty-day Window Nearest | 233 | 3.96 | −2.91 | −0.46 | 0.73 | 0.55 | 0.31 | 0.45 | 0.47 | n/a |
| Thirty-day Window Median | 233 | 4.04 | −3.1 | −0.46 | 0.72 | 0.54 | 0.29 | 0.46 | 0.55 | n/a |
| Median of Same Summer | 233 | 5 | −3.89 | −0.58 | 0.59 | 0.49 | 0.235 | 0.63 | 0.64 | 0.49 |
| Median of All Summers | 233 | 4.41 | −4.14 | −0.46 | 0.54 | 0.43 | 0.19 | 0.7 | 0.66 | 0.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koll-Egyed, T.; Cardille, J.A.; Deutsch, E. Multiple Images Improve Lake CDOM Estimation: Building Better Landsat 8 Empirical Algorithms across Southern Canada. Remote Sens. 2021, 13, 3615. https://doi.org/10.3390/rs13183615
Koll-Egyed T, Cardille JA, Deutsch E. Multiple Images Improve Lake CDOM Estimation: Building Better Landsat 8 Empirical Algorithms across Southern Canada. Remote Sensing. 2021; 13(18):3615. https://doi.org/10.3390/rs13183615
Chicago/Turabian StyleKoll-Egyed, Talia, Jeffrey A. Cardille, and Eliza Deutsch. 2021. "Multiple Images Improve Lake CDOM Estimation: Building Better Landsat 8 Empirical Algorithms across Southern Canada" Remote Sensing 13, no. 18: 3615. https://doi.org/10.3390/rs13183615
APA StyleKoll-Egyed, T., Cardille, J. A., & Deutsch, E. (2021). Multiple Images Improve Lake CDOM Estimation: Building Better Landsat 8 Empirical Algorithms across Southern Canada. Remote Sensing, 13(18), 3615. https://doi.org/10.3390/rs13183615






