Evaluation of a Method for Calculating the Height of the Stable Boundary Layer Based on Wind Profile Lidar and Turbulent Fluxes
Abstract
:1. Introduction
2. Sites, Synoptic Condition, Instruments, and Data Processing
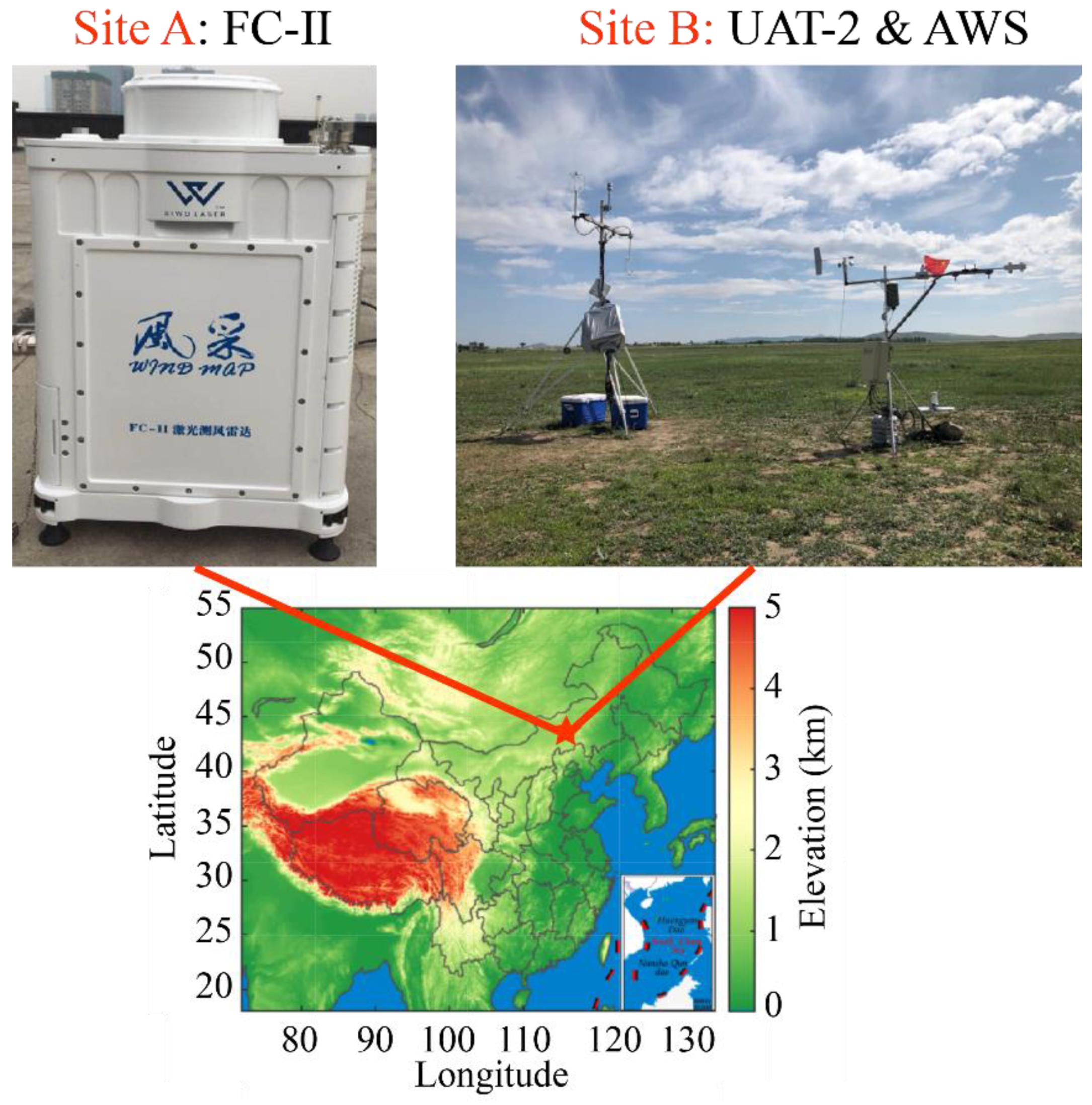
2.1. Sites, Synoptic Condition
2.2. Instruments
2.2.1. Portable Doppler Wind Lidar
2.2.2. Ultrasonic Anemometer Thermometer
2.2.3. Other Observational Data
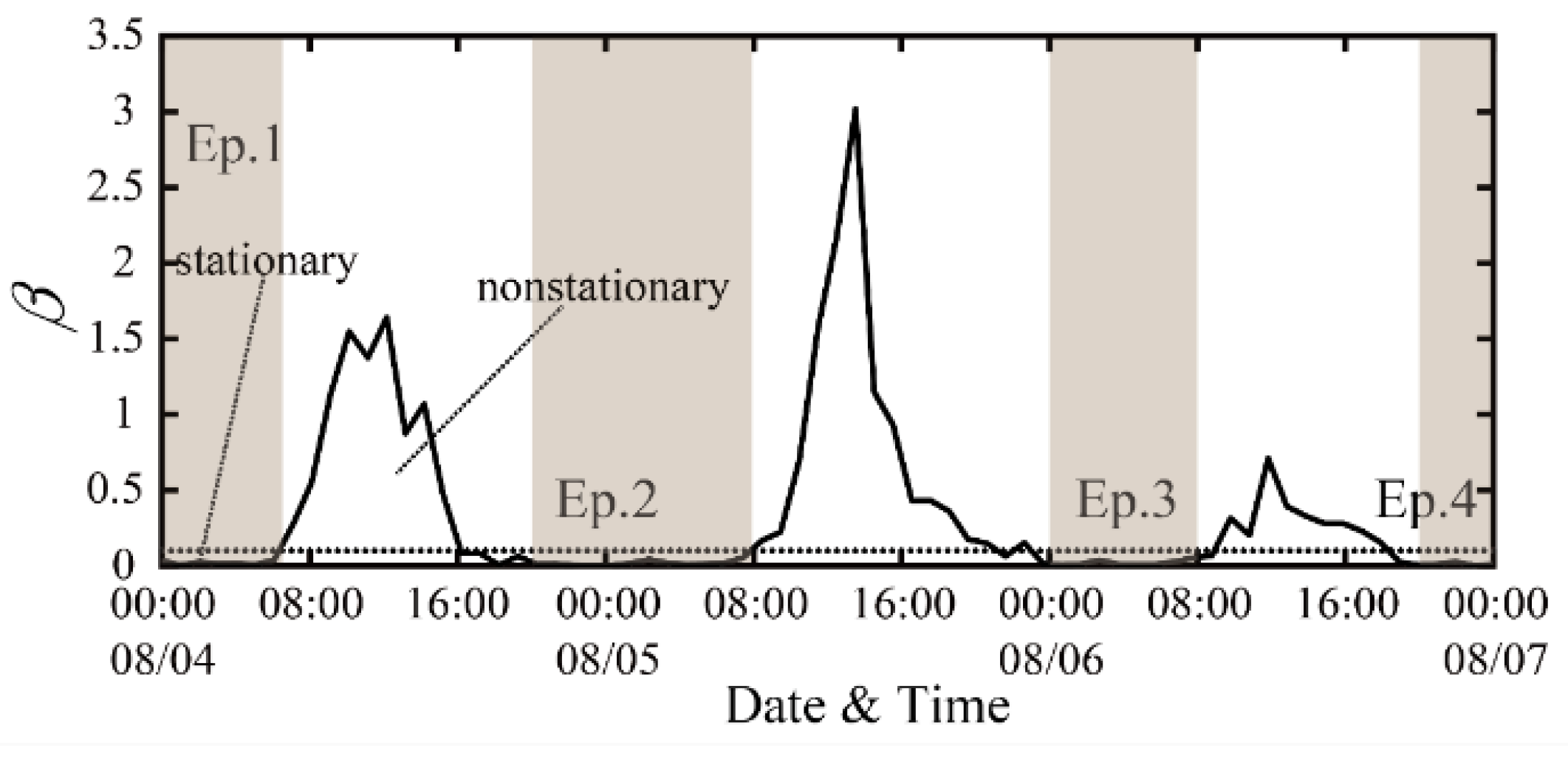
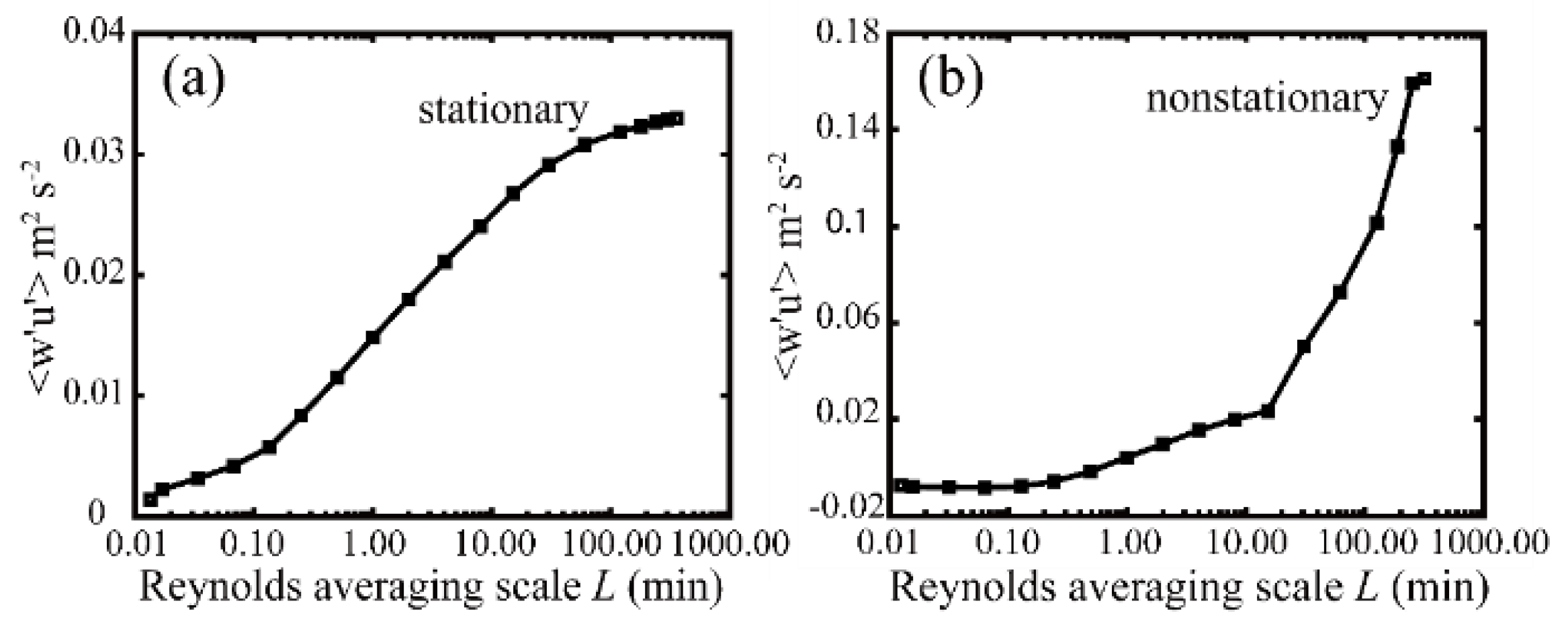
2.3. Determination of Stationary and Nonstationary Conditions
3. Calculation Method and Comparison Results
3.1. Using fluxes and Wind Profiles to Calculate
3.2. Compared with Other Predicted SBL Heights
3.3. Comparison with the Observation-Derived SBL Heights
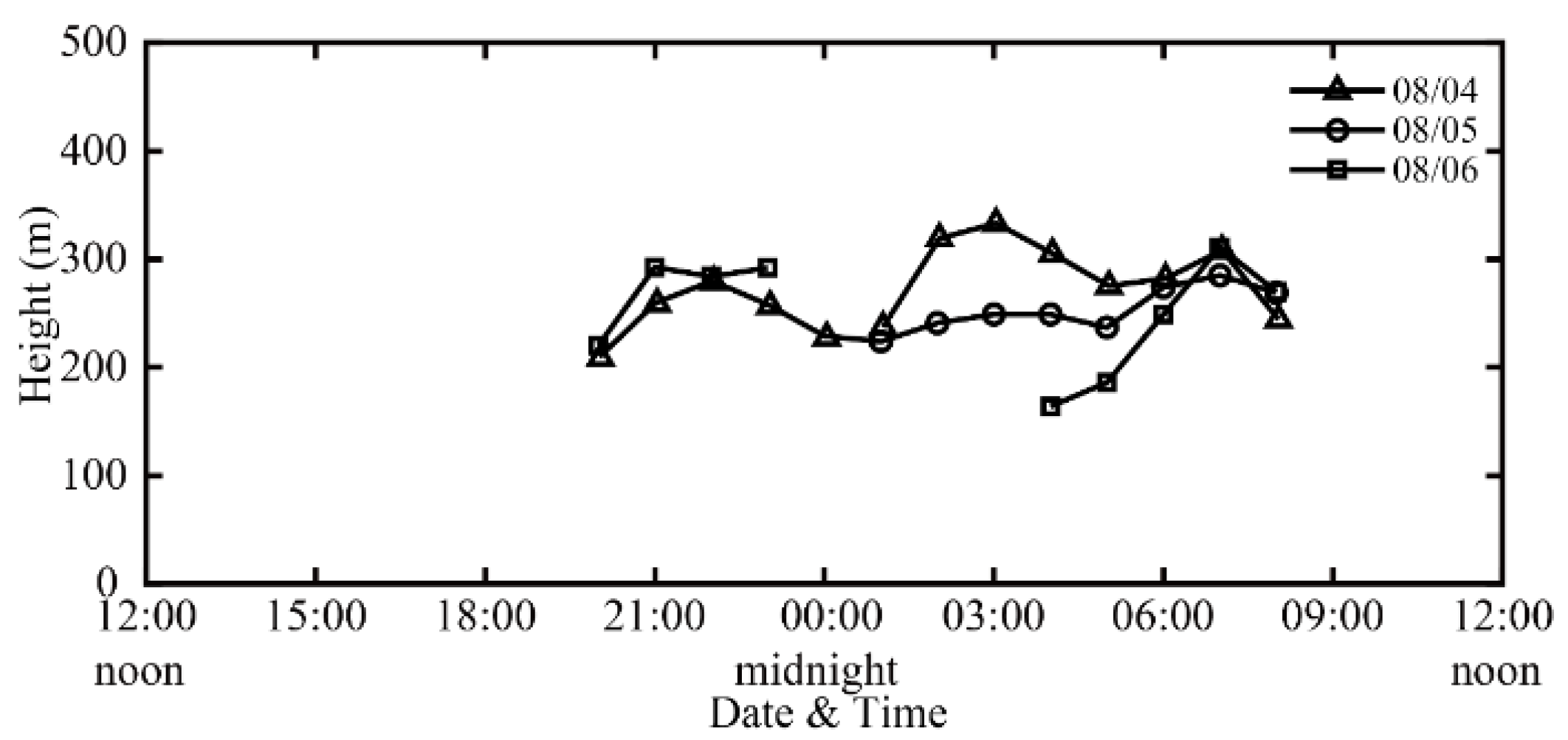
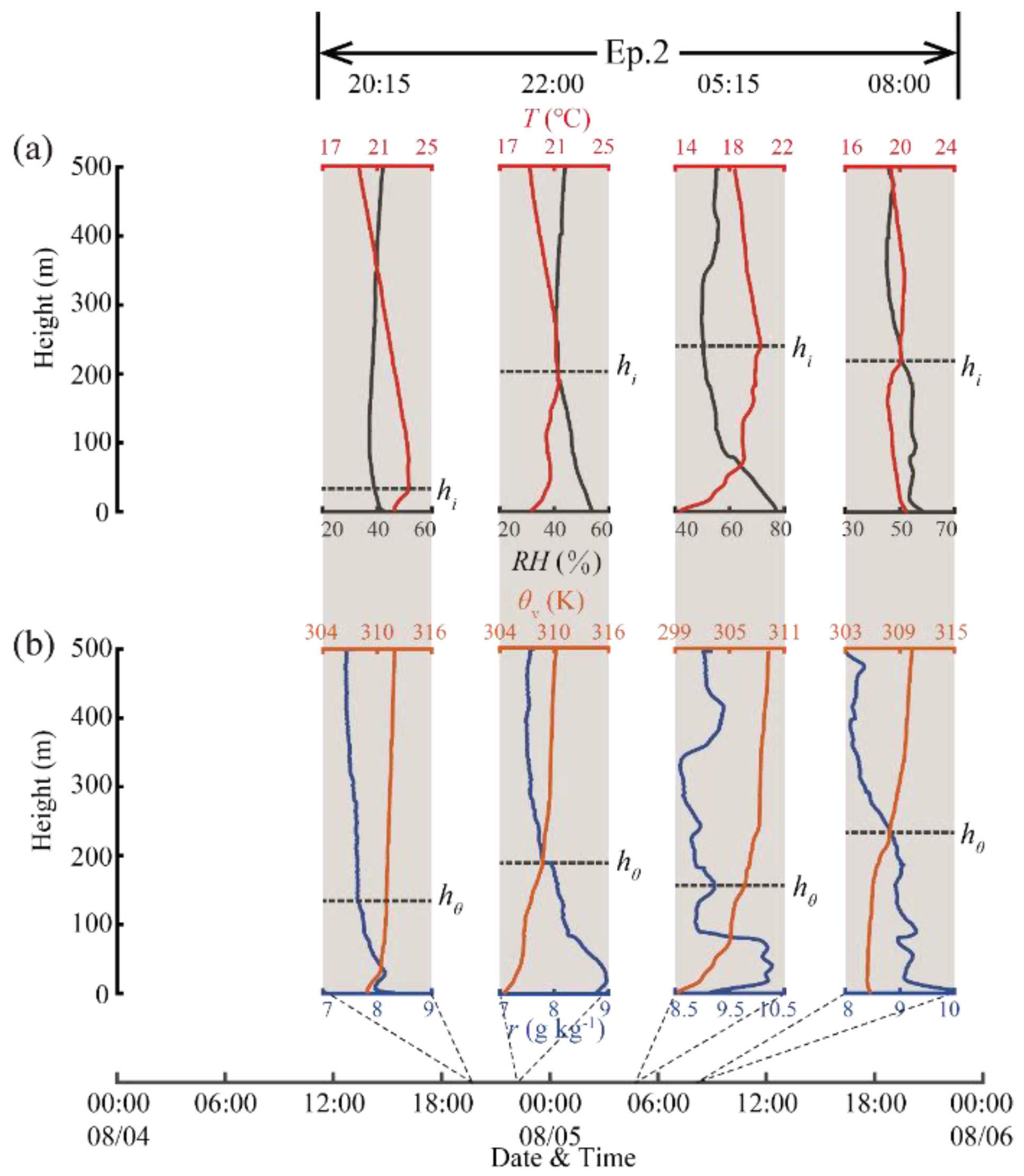
3.3.1. SBL Heights Derived from Wind Profiles
3.3.2. SBL Heights Derived from Radiosonde Data
4. Conclusions
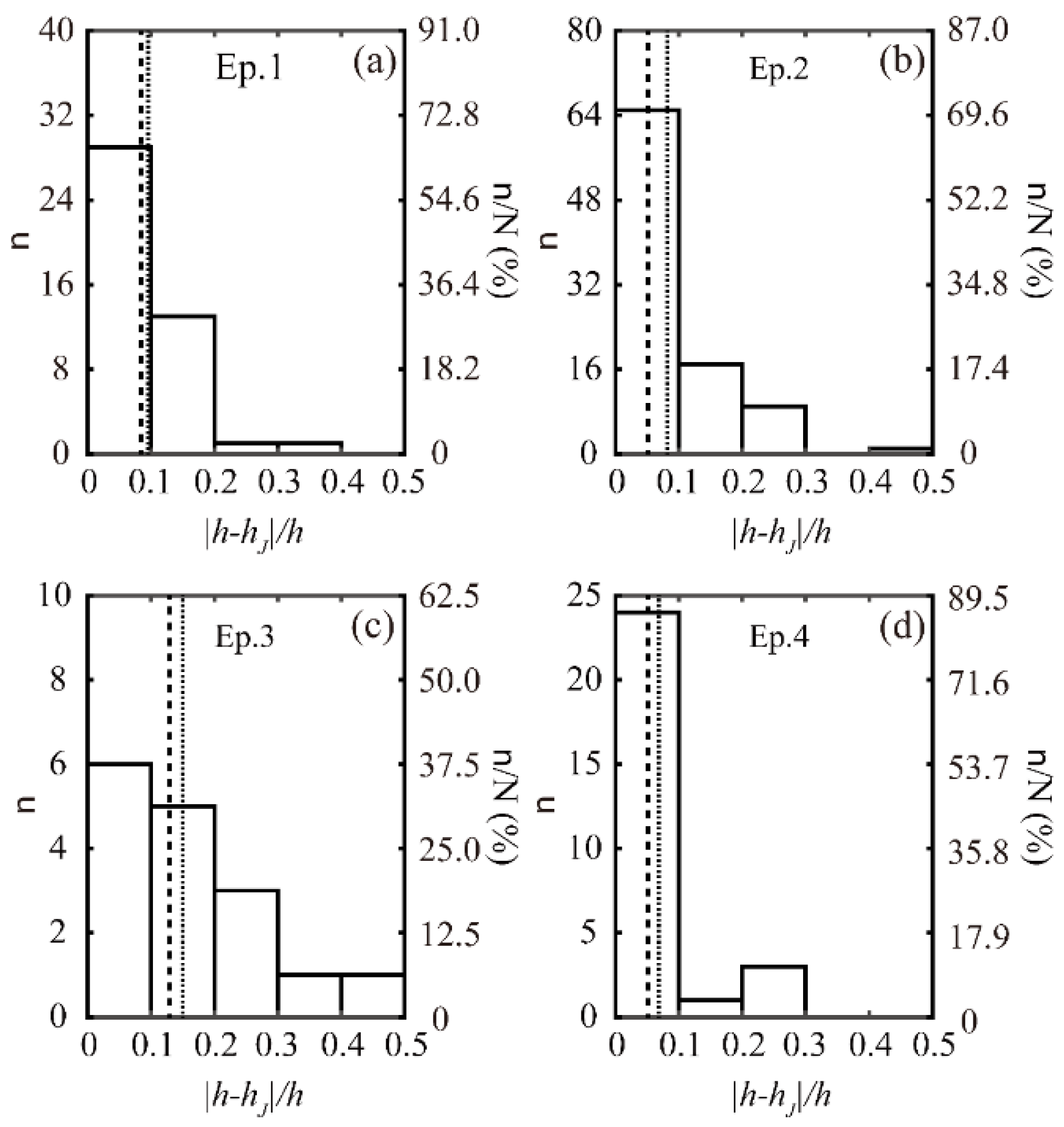
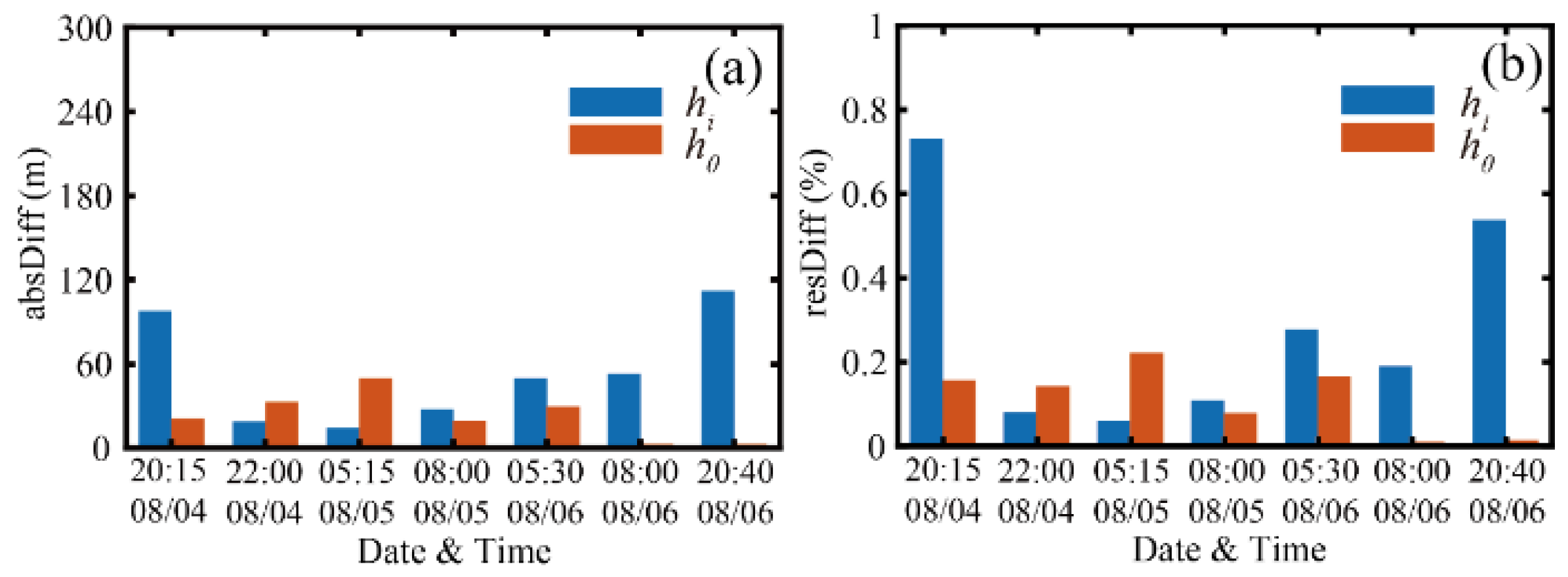
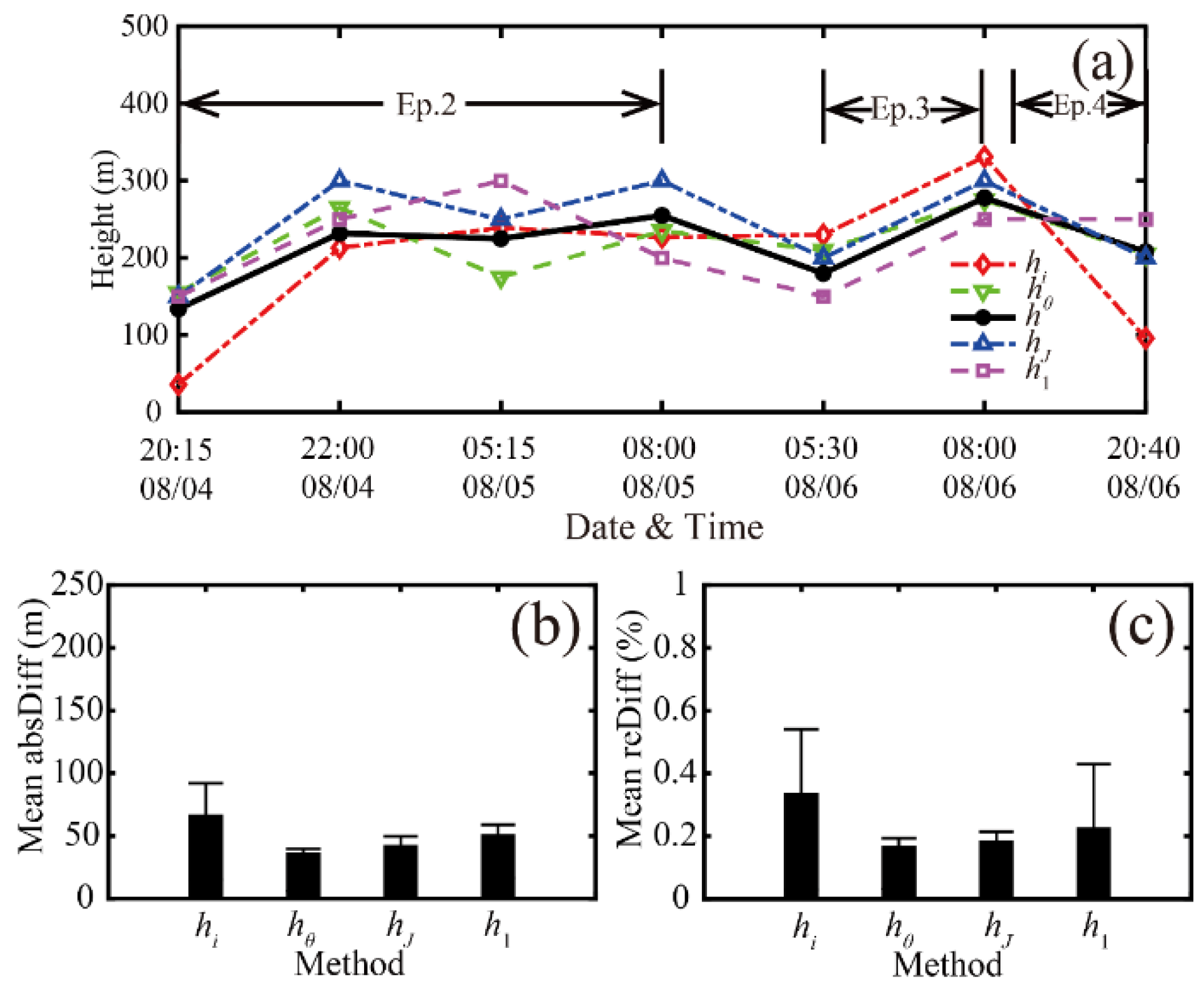
- is in good agreement with and obtained by radiosonde data, especially for . A comparison of with the radiosonde-derived estimates demonstrates that presents a relatively poor result with mean absDiff and reDiff values of 72 m and 36%, respectively. and may be satisfactory but have minor differences. In addition, shows the smallest mean absDiff and reDiff values (below 48 m and 22%, respectively). Moreover, with regard to the one standard deviation, shows the smallest values.
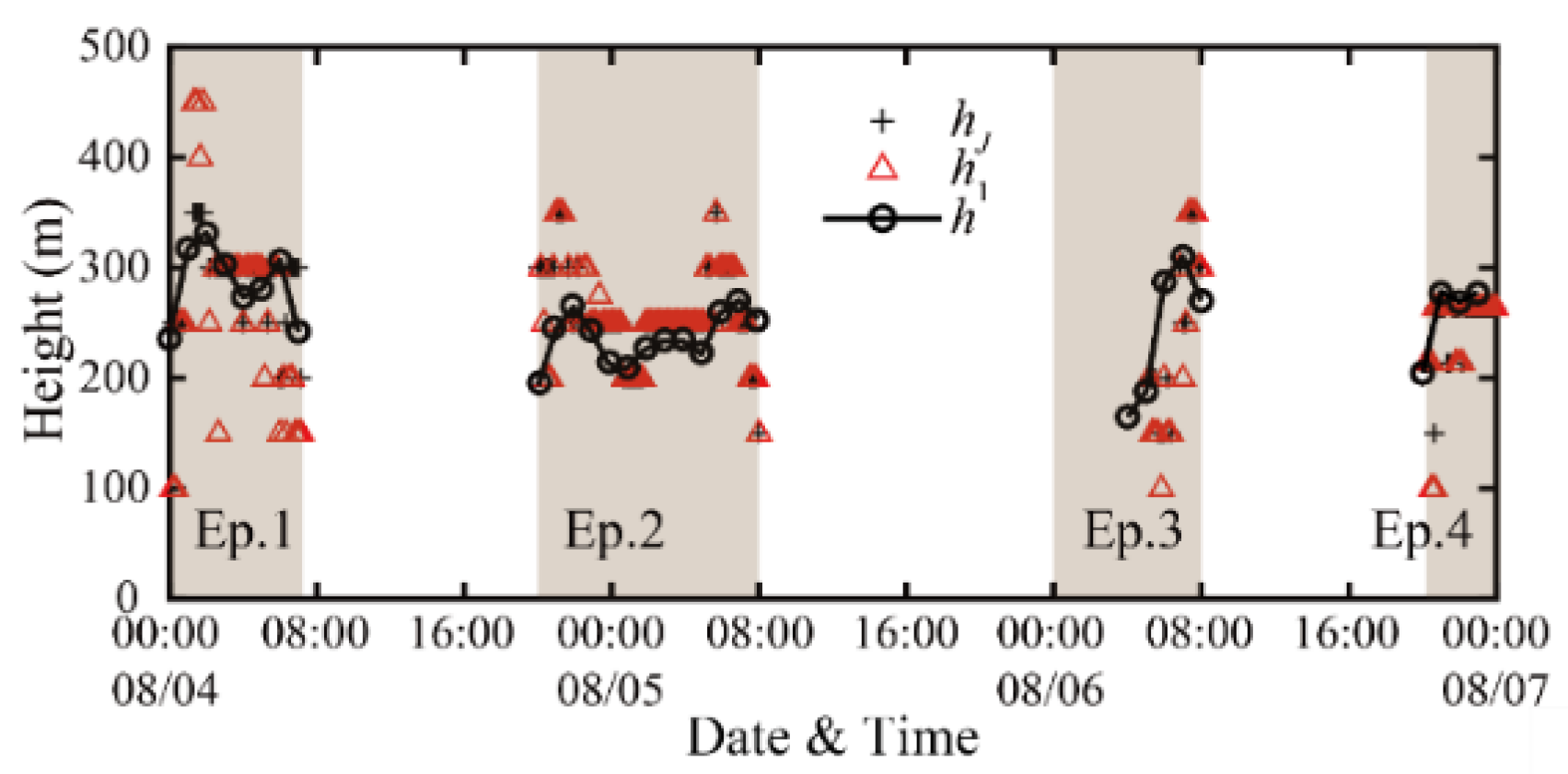
- The heights derived from wind profiles ( and ) also show good agreement with . The SBL height derived from shows low absDiff and reDiff values below 50 m and 23%, respectively. However, for , the mean relative error (46.0%) is twice as large as that for .
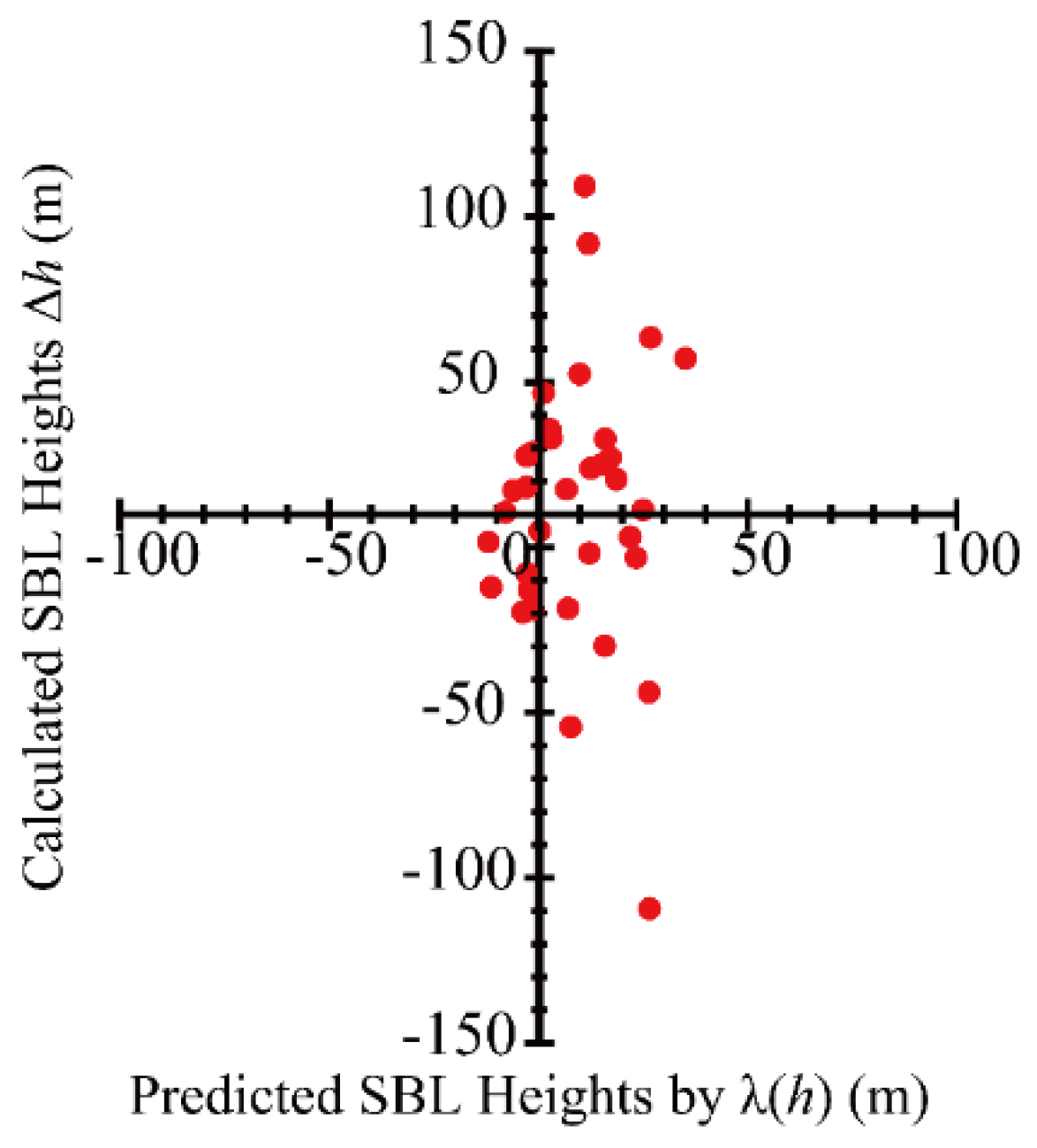
- The diagnostic formula of fits the best with among the three diagnostic formulas, whereas the prediction equation is not applicable. Nevertheless, the diagnostic formulas of and are found to be appropriate, especially under extremely and moderately stable conditions. Furthermore, the performance of presents the best results among all the dimensional scale height parameters. shows less consistency with , but under extremely stable conditions, all three diagnostic formulas provide good fits with , especially those of and . However, the prognostic equation of in our study is very unsatisfactory.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer: Dordrecht, The Netherlands, 1988; pp. 167–171. [Google Scholar]
- Zhang, H.; Zhang, X.; Li, Q.; Cai, X.; Fan, S.; Song, Y.; Hu, F.; Che, H.; Quan, J.; Kang, L.; et al. Research Progress on Estimation of the Atmospheric Boundary Layer Height. J. Meteorol. Res. 2020, 34, 482–498. [Google Scholar] [CrossRef]
- Krishnamurthy, R.; Newsom, R.K.; Berg, L.K.; Xiao, H.; Ma, P.-L.; Turner, D.D. On the estimation of boundary layer heights: A machine learning approach. Atmos. Meas. Tech. 2020, 14, 4403–4424. [Google Scholar] [CrossRef]
- Compton, J.C.; Delgado, R.; Berkoff, T.A.; Hoff, R.M. Determination of Planetary Boundary Layer Height on Short Spatial and Temporal Scales: A Demonstration of the Covariance Wavelet Transform in Ground-Based Wind Profiler and Lidar Measurements. J. Atmos. Ocean. Technol. 2013, 30, 1566–1575. [Google Scholar] [CrossRef]
- Schmid, P.; Niyogi, D. A Method for Estimating Planetary Boundary Layer Heights and Its Application over the ARM Southern Great Plains Site. J. Atmos. Ocean. Technol. 2012, 29, 316–322. [Google Scholar] [CrossRef] [Green Version]
- Zilitinkevich, S.; Baklanov, A. Calculation of the Height of the Stable Boundary Layer in Practical Applications. Bound. Layer Meteorol. 2002, 105, 389–409. [Google Scholar] [CrossRef]
- Beyrich, F.; Gryning, S.-E.; Joffre, S.; Rasmussen, A.; Seibert, P.; Tercier, P. Mixing Height Determination for Dispersion Modelling—A Test of Meteorological Pre-Processors. In Air Pollution Modeling and Its Application XII; Springer: Boston, MA, USA, 1998; Volume 17, pp. 541–549. [Google Scholar]
- Elperin, T.; Kleeorin, N.; Rogachevskii, I.; Zilitinkevich, S. Formation of large-scale semiorganized structures in turbulent convection. Phys. Rev. E 2002, 66, 066305. [Google Scholar] [CrossRef] [Green Version]
- James, O.; Richard, W.; Timothy, B.; Harry, S.; Marc, S. Profiling the Surface Layer of Optical Turbulence with Slodar. Mon. Not. R. Astron. Soc. 2010, 406, 1405–1408. [Google Scholar] [CrossRef]
- Shikhovtsev, A.Y.; Kiselev, A.V.; Kovadlo, P.G.; Kolobov, D.Y.; Lukin, V.P.; Tomin, V.E. Method for Estimating the Altitudes of Atmospheric Layers with Strong Turbulence. Atmos. Ocean. Opt. 2020, 33, 295–301. [Google Scholar] [CrossRef]
- Lenschow, D.; Li, X.S.; Zhu, C.J.; Stankov, B.B. The stably stratified boundary layer over the great plains. In Topics in Micrometeorology; Springer: Dordrecht, The Netherlands, 1988; Volume 42, pp. 95–121. [Google Scholar] [CrossRef]
- Caughey, S.J.; Wyngaard, J.C.; Kaimal, J.C. Turbulence in the Evolving Stable Boundary Layer. J. Atmos. Sci. 1979, 36, 1041–1052. [Google Scholar] [CrossRef]
- Banta, R.M.; Pichugina, Y.L.; Brewer, W.A. Turbulent Velocity-Variance Profiles in the Stable Boundary Layer Generated by a Nocturnal Low-Level Jet. J. Atmos. Sci. 2006, 63, 2700–2719. [Google Scholar] [CrossRef] [Green Version]
- Banta, R.M.; Newsom, R.K.; Lundquist, J.K.; Pichugina, Y.L.; Coulter, R.L.; Mahrt, L. Nocturnal Low-Level Jet Characteristics Over Kansas During Cases-99. Bound. Layer Meteorol. 2002, 105, 221–252. [Google Scholar] [CrossRef]
- Moreira, G.D.A.; Marques, M.T.A.; Nakaema, W.; Moreira, A.C.D.C.A.; Landulfo, E. Detecting the planetary boundary layer height from low-level jet with Doppler lidar measurements. In Lidar Technologies, Techniques, and Measurements for Atmospheric Remote Sensing XI; International Society for Optics and Photonics: Bellingham, DC, USA, 2015; Volume 96450, p. F–96450F. [Google Scholar] [CrossRef]
- Banta, R.M. Stable-boundary-layer regimes from the perspective of the low-level jet. Acta Geophys. 2008, 56, 58–87. [Google Scholar] [CrossRef]
- Businger, J.A.; Arya, S.P.S. Height of the Mixed Layer in the Stably Stratified Planetary Boundary Layer. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 1975; pp. 73–92. [Google Scholar] [CrossRef]
- Mahrt, L.; Heald, R.C. Comments on “Determining Height of the Nocturnal Boundary Layer”. J. Appl. Meteorol. 2010, 18, 383. [Google Scholar] [CrossRef] [Green Version]
- Lange, B.; Larsen, S.; Højstrup, J.; Barthelmie, R. The Influence of Thermal Effects on the Wind Speed Profile of the Coastal Marine Boundary Layer. Bound. Layer Meteorol. 2004, 112, 587–617. [Google Scholar] [CrossRef]
- Mahrt, L.; Andre, J.C.; Heald, R.C. On the Depth of the Nocturnal Boundary Layer. J. Appl. Meteorol. 1982, 21, 90–92. [Google Scholar] [CrossRef] [Green Version]
- Yu, T.-W. Determining Height of the Nocturnal Boundary Layer. J. Appl. Meteorol. 1978, 17, 28–33. [Google Scholar] [CrossRef] [Green Version]
- Hanna, S.R. The thickness of the planetary boundary layer. Atmos. Environ. 1969, 3, 519–536. [Google Scholar] [CrossRef]
- Kim, D.-K.; Lee, D.-I. Atmospheric thickness and vertical structure properties in wintertime precipitation events from microwave radiometer, radiosonde and wind profiler observations. Meteorol. Appl. 2015, 22, 599–609. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, W.; Feng, G.; Liao, K.; Liu, Y. Effect of off-zenith observations on reducing the impact of precipitation on ground-based microwave radiometer measurement accuracy. Atmos. Res. 2014, 140–141, 85–94. [Google Scholar] [CrossRef]
- Coen, M.C.; Praz, C.; Haefele, A.; Ruffieux, D.; Kaufmann, P.; Calpini, B. Determination and climatology of the planetary boundary layer height above the Swiss plateau by in situ and remote sensing measurements as well as by the COSMO-2 model. Atmos. Chem. Phys. Discuss. 2014, 14, 13205–13221. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Gao, Z.; Miao, S.; Chen, F.; LeMone, M.A.; Li, J.; Hu, F.; Wang, L. Estimate of Boundary-Layer Depth Over Beijing, China, Using Doppler Lidar Data During SURF-2015. Bound. Layer Meteorol. 2017, 162, 503–522. [Google Scholar] [CrossRef] [Green Version]
- Seibert, P.; Beyrich, F.; Gryning, S.-E.; Joffre, S.; Rasmussen, A.; Tercier, P. Review and intercomparison of operational methods for the determination of the mixing height. Atmos. Environ. 2002, 1, 569–613. [Google Scholar] [CrossRef]
- Smedman, A.-S. Observations of a multi-level turbulence structure in a very stable atmospheric boundary layer. Bound. Layer Meteorol. 1988, 44, 231–253. [Google Scholar] [CrossRef]
- Godowitch, J.M.; Ching, J.K.S.; Clarke, J.F. Evolution of the Nocturnal Inversion Layer at an Urban and Nonurban Location. J. Clim. Appl. Meteorol. 1985, 24, 791–804. [Google Scholar] [CrossRef] [Green Version]
- Koračin, D.; Berkowicz, R. Nocturnal boundary-layer height: Observations by acoustic sounders and predictions in terms of surface-layer parameters. Bound. Layer Meteorol. 1988, 43, 65–83. [Google Scholar] [CrossRef]
- Nieuwstadt, F.T.M. Some aspects of the turbulent stable boundary layer. Bound. Layer Meteorol. 1984, 30, 31–55. [Google Scholar] [CrossRef]
- Arya, S.P.S. Parameterizing the Height of the Stable Atmospheric Boundary Layer. J. Appl. Meteorol. 1981, 20, 1192–1202. [Google Scholar] [CrossRef] [Green Version]
- Mahrt, L. Modelling the depth of the stable boundary-layer. Bound. Layer Meteorol. 1981, 21, 3–19. [Google Scholar] [CrossRef]
- Zilitinkevich, S.S. On the determination of the height of the Ekman boundary layer. Bound. Layer Meteorol. 1972, 3, 141–145. [Google Scholar] [CrossRef]
- Dai, C.; Wang, Q.; Kalogiros, J.A.; Lenschow, D.H.; Gao, Z.; Zhou, M. Determining Boundary Layer Height from Aircraft Measurements. Bound. Layer Meteorol. 2014, 152, 277–302. [Google Scholar] [CrossRef]
- Richardson, H.; Basu, S.; Holtslag, A.A.M. Improving Stable Boundary-Layer Height Estimation Using a Stability-Dependent Critical Bulk Richardson Number. Bound. Layer Meteorol. 2013, 148, 93–109. [Google Scholar] [CrossRef]
- Syrakov, E. General diagnostic equations and regime analysis for the height of the planetary boundary layer. Q. J. R. Meteorol. Soc. 2015, 141, 2869–2879. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Shi, H.; Jin, L.; Chen, H.; Wen, H. Measuring boundary-layer height under clear and cloudy conditions using three instruments. Particuology 2016, 28, 15–21. [Google Scholar] [CrossRef]
- Garratt, J.R. Surface Fluxes and the Nocturnal Boundary Layer Height. J. Appl. Meteorol. 2010, 21, 725–729. [Google Scholar] [CrossRef]
- Garratt, J.R. Observations in the nocturnal boundary layer. Bound. Layer Meteorol. 1982, 22, 21–48. [Google Scholar] [CrossRef]
- Nieuwstadt, F.T.M. The steady-state height and resistance laws of the nocturnal boundary layer: Theory compared with cabauw observations. Bound. Layer Meteorol. 1981, 20, 3–17. [Google Scholar] [CrossRef]
- Zilitinkevich, S.; Esau, I.; Baklanov, A. Further comments on the equilibrium height of neutral and stable planetary boundary layers. Q. J. R. Meteorol. Soc. 2006, 133, 265–271. [Google Scholar] [CrossRef]
- Aitken, M.L.; Rhodes, M.E.; Lundquist, J.K. Performance of a Wind-Profiling Lidar in the Region of Wind Turbine Rotor Disks. J. Atmos. Ocean. Technol. 2012, 29, 347–355. [Google Scholar] [CrossRef]
- Sun, H.J.; Shi, Y.; Liu, L.; Ding, W.C.; Zhang, Z.; Hu, F. Impacts of Atmospheric Boundary Layer Vertical Structure on Haze Pollution Observed by Tethered Balloon and Lidar. J. Meteorol. Res. 2021, 35, 209–223. [Google Scholar] [CrossRef]
- Cheng, X.L.; Peng, Z.; Hu, F.; Zeng, Q.C.; Luo, W.D.; Zhao, Y.J.; Hong, Z.X. Measurement errors and correction of the UAT-2 ultrasonic anemometer. Sci. China Ser. E Technol. Sci. 2015, 58, 677–686. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Li, G.X. Fundamentals of Temperature and Fluid Parameters Measurement; CRC Press: Boka Raton, FL, USA, 1986; pp. 82–86. (In Chinese) [Google Scholar]
- Wang, Q.; Sun, Y.; Xu, W.; Du, W.; Zhou, L.; Tang, G.; Chen, C.; Cheng, X.; Zhao, X.; Ji, D.; et al. Vertically resolved characteristics of air pollution during two severe winter haze episodes in urban Beijing, China. Atmos. Chem. Phys. 2018, 18, 2495–2509. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Ling, C.; Chen, H.; Zhang, J.; Peng, L.; Yu, Y.U. Comparison of Two Reanalysis Data with the RS92 Radiosonde Data. Clim. Environ. Res. 2012, 17, 381–391. [Google Scholar]
- Mahrt, L.; Vickers, D.; Howell, J.; Højstrup, J.; Wilczak, J.M.; Edson, J.; Hare, J. Sea surface drag coefficients in the Risø Air Sea Experiment. J. Geophys. Res. Space Phys. 1996, 101, 14327–14335. [Google Scholar] [CrossRef] [Green Version]
- Zilitinkevich, S.S.; Esau, I.N. Similarity theory and calculation of turbulent fluxes at the surface for the stably stratified atmospheric boundary layer. Bound. Layer Meteorol. 2007, 125, 193–205. [Google Scholar] [CrossRef] [Green Version]
- Zilitinkevich, S.S.; Esau, I.N. Resistance and heat-transfer laws for stable and neutral planetary boundary layers: Old theory advanced and re-evaluated. Q. J. R. Meteorol. Soc. 2005, 131, 1863–1892. [Google Scholar] [CrossRef] [Green Version]
- Esau, I.N.; Byrkjedal, Ø. Application of a Large Eddy Simulation Database to Optimization of First Order Closures for Neutral and Stably Stratified Boundary Layers. Bound. Layer Meteorol. 2007, 125, 207–225. [Google Scholar] [CrossRef]
- Rossby, C.-G.; Montgomery, R.B. The Layer of Frictional Influence in Wind and Ocean Currents; Massachusetts Institute of Technology: Cambridge, MA, USA; Woods Hole Oceanographic Institution: Falmouth, MA, USA, 1935. [Google Scholar] [CrossRef] [Green Version]
- Pollard, R.T.; Rhines, P.B.; Thompson, R.O.R.Y. Wind Driven Mixing and deepening of the wind-Mixed layer. Geophys. Astrophys. Fluid Dyn. 1973, 4, 381. [Google Scholar] [CrossRef]
- Clarke, R.H. Observational studies in the atmospheric boundary layer. Q. J. R. Meteorol. Soc. 1972, 98, 231–235. [Google Scholar] [CrossRef]
- Deardorff, J.W. Parameterization of the Planetary Boundary layer for Use in General Circulation Models. Mon. Weather Rev. 1972, 100, 93–106. [Google Scholar] [CrossRef] [Green Version]
- Monin, A.S.; Obukhov, A.M. Basic Laws ofTurbulent Mixing in the Surface Layer of the Atmosphere. Trudy Geophys. Inst. AN SSSR 1954, 24, 153–187. [Google Scholar]
- Pichugina, Y.L.; Banta, R.M. Stable Boundary Layer Depth from High-Resolution Measurements of the Mean Wind Profile. J. Appl. Meteorol. Clim. 2010, 49, 20–35. [Google Scholar] [CrossRef]
- Hyun, Y.-K.; Kim, K.-E.; Ha, K.-J. A comparison of methods to estimate the height of stable boundary layer over a temperate grassland. Agric. For. Meteorol. 2005, 132, 132–142. [Google Scholar] [CrossRef]

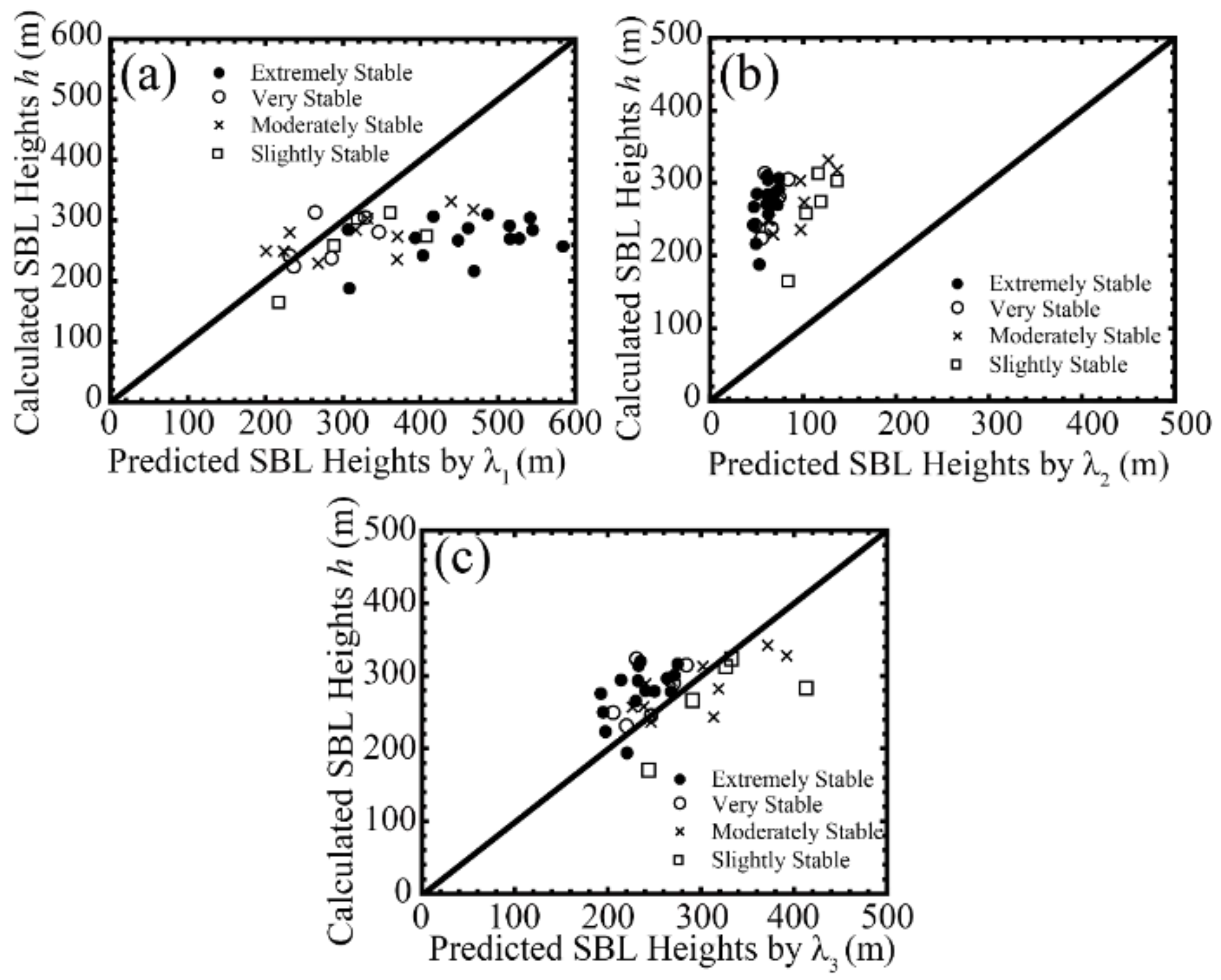
| Correlation Coefficients | |||
|---|---|---|---|
| (I) Slightly stable | 0.36 (1.31) | 0.45 (2.14) | 0.53 (2.04) |
| (II) Moderately stable | 0.56 (1.10) | 0.66 (1.10) | 0.54 (1.10) |
| (III) Very stable | 0.65 (1.47) | 0.74 (1.97) | 0.61 (2.35) |
| (IV) Extremely stable | 0.78 (2.04) | 0.88 (1.98) | 0.65 (2.12) |
| (V) Total cases | 0.36 (2.17) | 0.41 (2.50) | 0.46 (2.86) |
| Episode | (m s−1) | Type I, II (% & n) | |||
|---|---|---|---|---|---|
| Ep. 1 | 3.49 | 95 42 | 154.73 | 0.47 | 0.66 (5.08) |
| Ep. 2 n = 92 | 3.29 | 89 82 | 160.52 | 0.39 | 0.64 (7.15) |
| Ep. 3 n = 16 | 7.78 | 94 15 | 142.09 | 0.51 | 0.76 (3.59) |
| Ep. 4 n = 28 | 4.40 | 96 27 | 373.55 | −0.27 | 0.72 (4.54) |
| Total n = 180 | 4.74 | 92 166 | 140.08 | 0.50 | 0.68 (11.03) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Shi, H.; Chen, H.; Tang, G.; Sheng, C.; Che, K.; Chen, H. Evaluation of a Method for Calculating the Height of the Stable Boundary Layer Based on Wind Profile Lidar and Turbulent Fluxes. Remote Sens. 2021, 13, 3596. https://doi.org/10.3390/rs13183596
Sun H, Shi H, Chen H, Tang G, Sheng C, Che K, Chen H. Evaluation of a Method for Calculating the Height of the Stable Boundary Layer Based on Wind Profile Lidar and Turbulent Fluxes. Remote Sensing. 2021; 13(18):3596. https://doi.org/10.3390/rs13183596
Chicago/Turabian StyleSun, Haijiong, Hongrong Shi, Hongyan Chen, Guiqian Tang, Chen Sheng, Ke Che, and Hongbin Chen. 2021. "Evaluation of a Method for Calculating the Height of the Stable Boundary Layer Based on Wind Profile Lidar and Turbulent Fluxes" Remote Sensing 13, no. 18: 3596. https://doi.org/10.3390/rs13183596
APA StyleSun, H., Shi, H., Chen, H., Tang, G., Sheng, C., Che, K., & Chen, H. (2021). Evaluation of a Method for Calculating the Height of the Stable Boundary Layer Based on Wind Profile Lidar and Turbulent Fluxes. Remote Sensing, 13(18), 3596. https://doi.org/10.3390/rs13183596







