Hyperspectral Image Classification Based on Sparse Superpixel Graph
Abstract
:1. Introduction
- An efficient HSI classification scheme is suggested based on sparse superpixel graph.
- A computationally simple but effective distance between superpixels is newly defined.
- A sparse superpixel graph is constructed by using spectral-spatial connection strategy.
- The use of CGDM in the proposal speeds up the process of label propagation on graph.
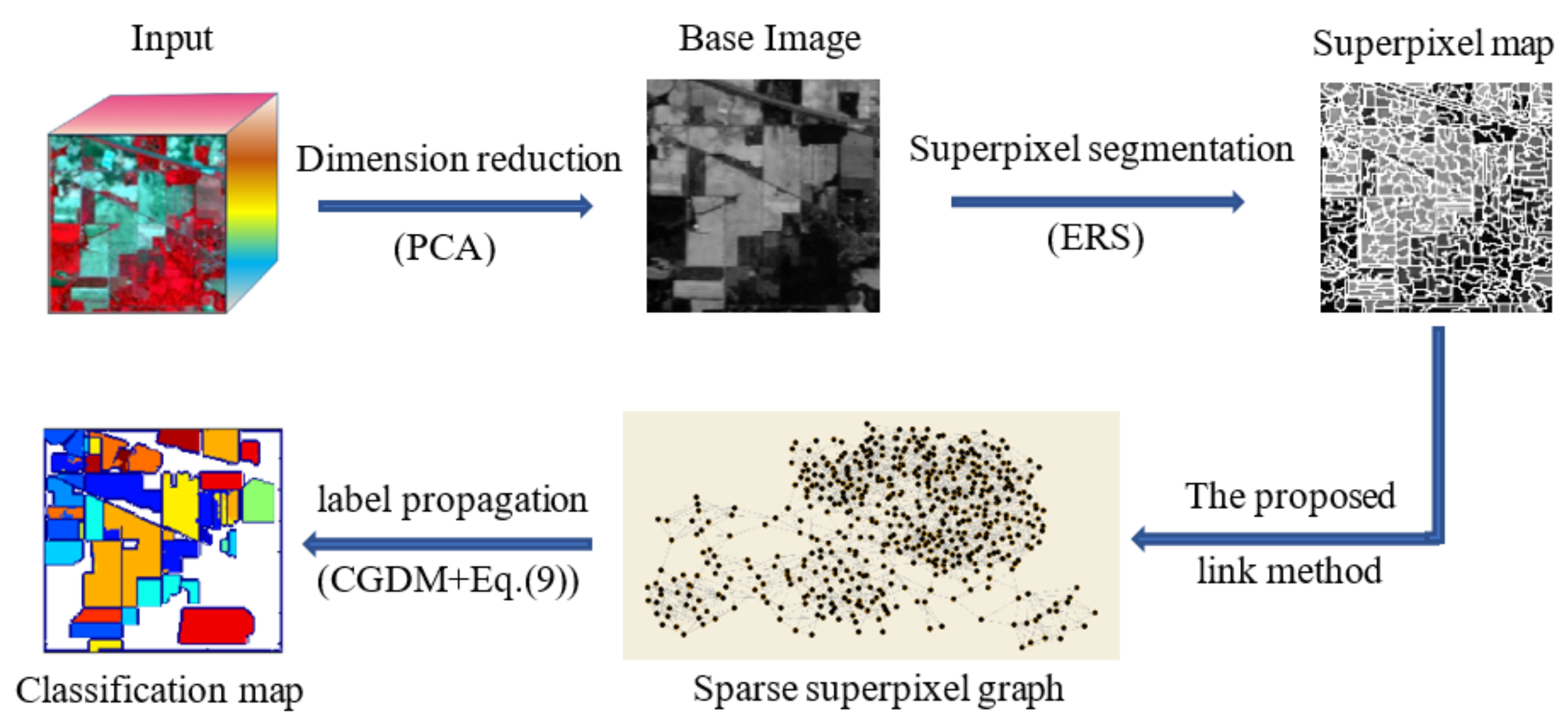
2. Methods
2.1. Superpixel Segmentation
2.2. Distance between Superpixels
2.3. The Construction of Sparse Superpixel Graph
2.4. Label Propagation on Graph
| Algorithm 1. SSG |
| procedure (, , , C)
Initialize A |
| Assign parameters to variables
Call for PCA to generate the base image Execute ERS to segment the base image into superpixels for i = 1 to |
| for j = 1 to |
| Compute if belongs to the first nearest neighbors of then |
| the number of spatial neighbors of for h = 1 to |
| Compute if belongs to the first nearest neighbors of then Compute D LD − A for m = 1 to C Derive Equation (8) from the m-EF Execute CGDM to solve Equation (8) Use Equation (9) to assign the class label to each unlabeled vertex |
| end procedure |
3. Experiments
3.1. Description of Three Datsets
3.2. Experimental Setup
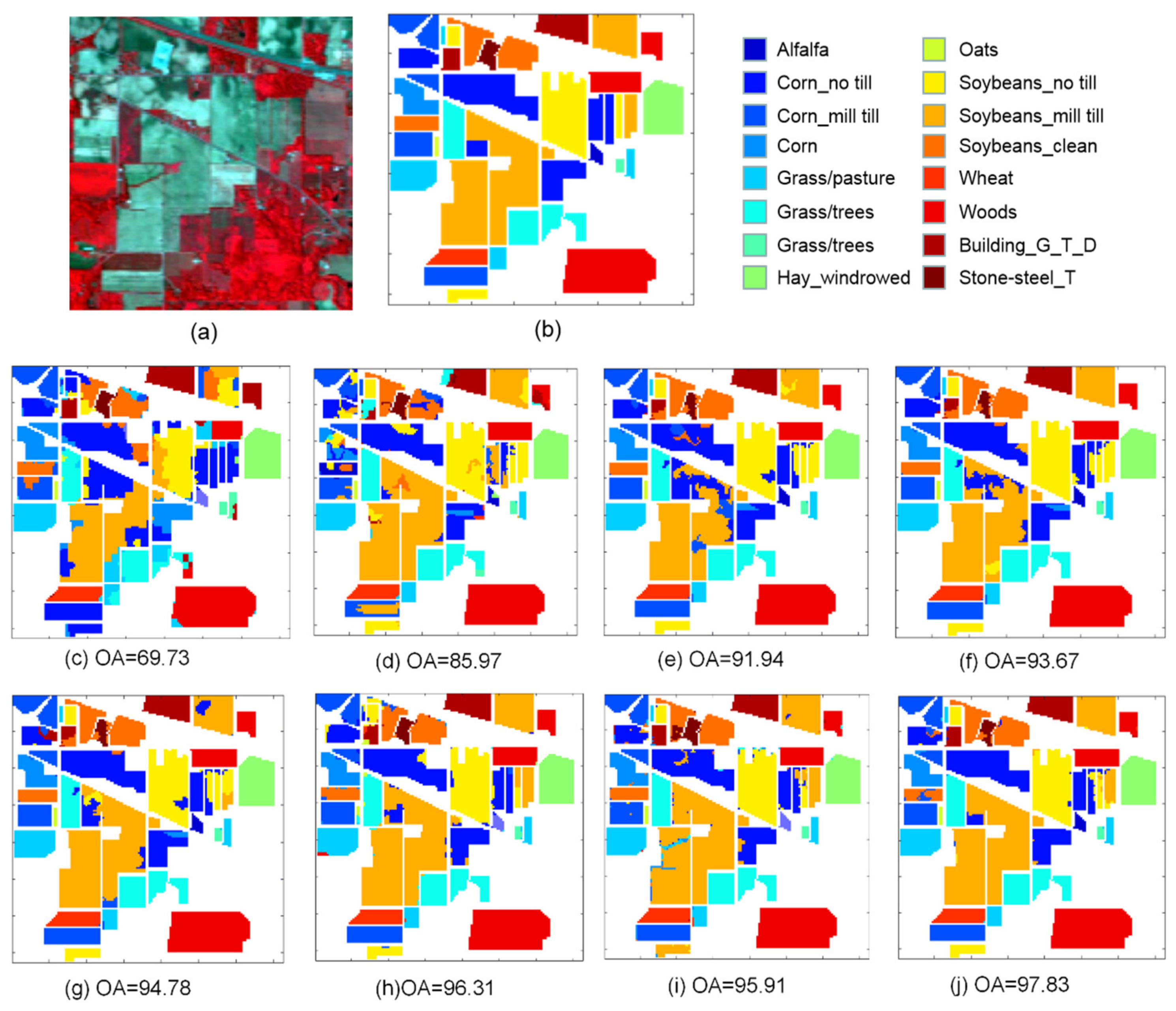
3.3. Classification Results
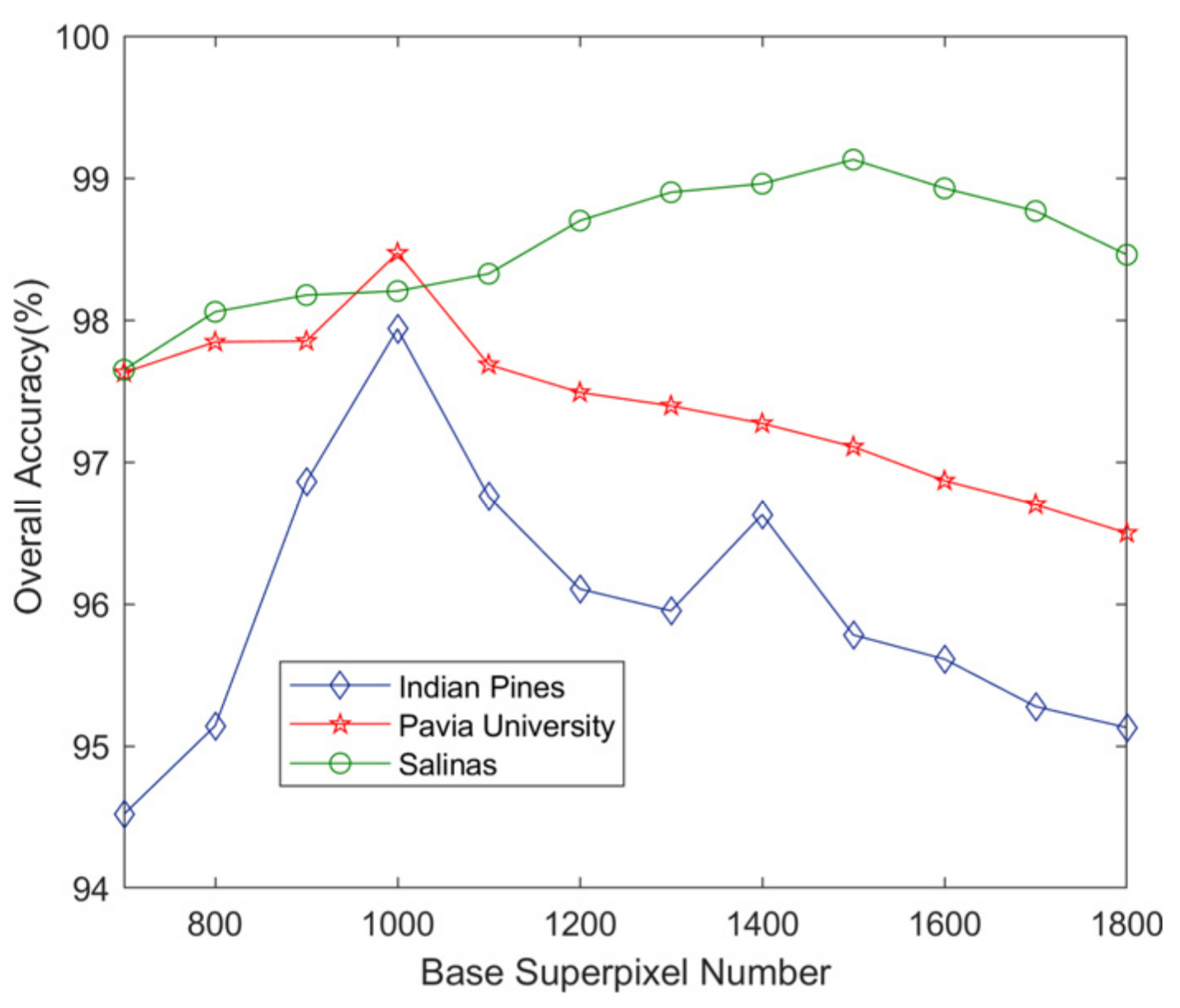
4. Effect of the Number of Superpixels and Different Number of Training Samples
5. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, X.; Chen, Y.; Ghamisi, P. Heterogeneous transfer learning for hyperspectral image classification based on convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3246–3263. [Google Scholar] [CrossRef]
- Jiao, L.; Feng, J.; Liu, F.; Sun, T.; Zhang, X. Semisupervised affinity propagation based on normalized trivariable mutual information for hyperspectral band selection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 2760–2773. [Google Scholar] [CrossRef]
- Romaszewski, M.; Glomb, P.; Cholewa, M. Semi-supervised hyperspectral classification from a small number of training samples using a co-training approach. ISPRS J. Photo. Remote Sens. 2016, 121, 60–76. [Google Scholar] [CrossRef]
- Sellami, A.; Farah, M.; Riadh, I.; Solaiman, F. Hyperspectral imagery classification based on semi-supervised 3-D deep neural network and adaptive band selection. Expert Syst. Appl. 2019, 129, 246–259. [Google Scholar] [CrossRef]
- Fang, B.; Li, Y.; Zhang, H.; Chan, J. Collaborative learning of lightweight convolutional neural network and deep clustering for hyperspectral image semi-supervised classification with limited training samples. ISPRS J. Photo. Remote Sens. 2020, 161, 164–178. [Google Scholar] [CrossRef]
- Benediktsson, J.; Palmason, J.; Sveinsson, J. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Clark, M.; Roberts, D. Species-level differences in hyperspectral metrics among tropical rainforest trees as determined by a tree-based classifier. Remote Sens. 2012, 4, 1820–1855. [Google Scholar] [CrossRef] [Green Version]
- Kanning, M.; Siegmann, B.; Jarmer, T. Regionalization of uncovered agricultural soils based on organic carbon and soil texture estimations. Remote Sens. 2016, 8, 927. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Li, B. A unified framework of multiple kernels learning for hyperspectral remote sensing big data. J. Inf. Hiding Multim. Signal Process. 2016, 7, 296–303. [Google Scholar]
- Xie, F.; Gao, Q.; Jin, C.; Zhao, F. Hyperspectral Image Classification Based on Superpixel Pooling Convolutional Neural Network with Transfer Learning. Remote Sens. 2021, 13, 930. [Google Scholar] [CrossRef]
- Barca, E.; Castrignanò, A.; Ruggieri, S.; Rinaldi, M. A new supervised classifier exploiting spectral-spatial information in the Bayesian framework. Int. J. Appl. Earth Obs. Geo. 2019, 86, 101990. [Google Scholar] [CrossRef]
- Mukherjee, S.; Prasad, S. A spatial-spectral semisupervised deep learning framework using siamese networks and angular loss. Comput. Vis. Image Underst. 2020, 194, 102943. [Google Scholar] [CrossRef]
- Kizel, F.; Benediktsson, J. Spatially Enhanced Spectral Unmixing Through Data Fusion of Spectral and Visible Images from Different Sensors. Remote Sens. 2020, 12, 1255. [Google Scholar] [CrossRef] [Green Version]
- Ghamisi, P.; Mura, M.; Benediktsson, J. A Survey on Spectral-Spatial Classification Techniques Based on Attribute Profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2335–2353. [Google Scholar] [CrossRef]
- Ghamisi, P.; Benediktsson, J.; Cavallaro, G.; Plaza, A. Automatic Framework for Spectral-Spatial Classification Based on Supervised Feature Extraction and Morphological Attribute Profiles. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2147–2160. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Shervashidze, N.; Borgwardt, K. Spatio-Spectral Remote Sensing Image Classification with Graph Kernels. IEEE Geosci. Remote Sens. Lett. 2010, 7, 741–745. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.; Plaza, A. Spectral-spatial hyperspectral image segmentation using subspace multinomial logistic regression and Markov random fields. IEEE Trans. Geosci. Remote Sens. 2012, 50, 809–823. [Google Scholar] [CrossRef]
- Dundar, T.; Ince, T. Sparse Representation-Based Hyperspectral Image Classification Using Multiscale Superpixels and Guided Filter. IEEE Geosci. Remote Sens. Lett. 2019, 16, 246–250. [Google Scholar] [CrossRef]
- Li, J.; Khodadadzadeh, M.; Plaza, A.; Jia, X.; Bioucas-Dias, J. A discontinuity preserving relaxation scheme for spectral–spatial hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. 2017, 9, 625–639. [Google Scholar] [CrossRef]
- Xie, F.; Lei, C.; Yang, J.; Jin, C. An effective classification scheme for hyperspectral image based on superpixel and discontinuity preserving relaxation. Remote Sens. 2019, 11, 1149. [Google Scholar] [CrossRef] [Green Version]
- Kang, X.; Li, S.; Benediktsson, J. Feature Extraction of Hyperspectral Images with Image Fusion and Recursive Filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3742–3752. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Duan, W.; Ren, J.; Benediktsson, J.A. Classification of Hyperspectral Images by Exploiting Spectral-Spatial Information of Superpixel via Multiple Kernels. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6663–6674. [Google Scholar] [CrossRef] [Green Version]
- Camps-Valls, G.; Gomez-Chova, L.; Muñoz-Marí, J.; Vila-Francés, J.; Calpe-Maravilla, J. Composite Kernels for Hyperspectral Image Classification. IEEE Trans. Geos. Remote Sens. Lett. 2006, 3, 93–97. [Google Scholar] [CrossRef]
- Xie, F.; Hu, D.; Li, F.; Yang, J.; Liu, D. Semi-Supervised Classification for Hyperspectral Images Based on Multiple Classifiers and Relaxation Strategy. ISPRS Int. J. Geo-Info. 2018, 7, 284. [Google Scholar] [CrossRef] [Green Version]
- Tarabalka, Y.; Benediktsson, J.; Chanussot, J.; Tilton, J. Multiple Spectral–Spatial Classification Approach for Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4122. [Google Scholar] [CrossRef]
- He, N.; Paoletti, M.E.; Haut, J.M.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Feature Extraction with Multiscale Covariance Maps for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 755–769. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, H.; He, W.; Zhang, L. Superpixel-based spatial-spectral dimension reduction for hyperspectral imagery classification. Neurocomputing 2019, 360, 138–150. [Google Scholar] [CrossRef]
- Yang, S.; Hou, J.; Jia, Y.; Mei, S.; Du, Q. Hyperspectral Image Classification via Sparse Representation with Incremental Dictionaries. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1598–1602. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral Image Classification Using Dictionary-Based Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.; Zhang, J.; Chen, Q.; Feng, J.; Jiao, L.; Zhou, H. Hyperspectral Unmixing via Low-rank Representation with Space Consistency Constraint and Spectral Library Pruning. Remote Sens. 2018, 10, 339. [Google Scholar] [CrossRef] [Green Version]
- Kwan, C.; Gribben, D.; Ayhan, B.; Li, J.; Bernabe, S.; Plaza, A. An Accurate Vegetation and Non-Vegetation Differentiation Approach Based on Land Cover Classification. Remote Sens. 2020, 12, 3880. [Google Scholar] [CrossRef]
- Cao, X.; Lu, H.; Ren, M.; Jiao, L. Non-overlapping classification of hyperspectral imagery with superpixel segmentation. Appl. Soft Comput. J. 2019, 83, 105630. [Google Scholar] [CrossRef]
- Zhan, T.; Lu, Z.; Wan, M.; Yang, G. Multiscale Superpixel Kernel-Based Low-Rank Representation for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1642–1646. [Google Scholar] [CrossRef]
- Jia, S.; Deng, X.; Xu, M.; Zhou, J.; Jia, X. Superpixel-Level Weighted Label Propagation for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5077–5091. [Google Scholar] [CrossRef]
- Fang, L.; Zhuo, H.; Li, S. Super-resolution of hyperspectral image via superpixel-based sparse representation. Neurocomputing 2018, 273, 171–177. [Google Scholar] [CrossRef]
- Li, Y.; Lu, T.; Li, S. Subpixel-Pixel-Superpixel-Based Multiview Active Learning for Hyperspectral Images Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4976–4988. [Google Scholar] [CrossRef]
- Xie, F.; Lei, C.; Jin, C.; An, N. A novel spectral-spatial classification method for hyperspectral image at superpixel Level. Appl. Sci. 2020, 10, 463. [Google Scholar] [CrossRef] [Green Version]
- Lu, T.; Li, S.; Fang, L.; Bruzzone, L.; Benediktsson, J.A. Set-to-set distance-based spectral-spatial classification of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1–13. [Google Scholar] [CrossRef]
- Tu, B.; Wang, J.; Kang, X.; Zhang, G.; Ou, X.; Guo, L. KNN-based representation of superpixels for hyperspectral image classification. IEEE J. Sel. Topics Appl. Earth Obs. Remote Sens. 2018, 11, 4032–4047. [Google Scholar] [CrossRef]
- Sellars, P.; Avilés-Rivero, A.; Chonlieb, C. Superpixel Contracted Graph-Based Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4180–4193. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.; Jiao, L.; Liu, F.; Zhao, Z.; Zhao, J. Adaptive sparse graph learning based dimensionality reduction for classification. Appl. Soft Comput. J. 2019, 82, 105459. [Google Scholar] [CrossRef]
- Xue, Z.; Du, P.; Li, J.; Su, H. Sparse Graph Regularization for Hyperspectral Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2351–2366. [Google Scholar] [CrossRef]
- Shao, Y.; Sang, N.; Gao, C.; Ma, L. Spatial and class structure regularized sparse representation graph for semi-supervised hyperspectral image classification. Pattern Recognit. 2018, 81, 81–94. [Google Scholar] [CrossRef]
- Ahmadi, S.; Mehrshad, N.; Razavi, S. Semisupervised graph-based hyperspectral images classification using low-rank representation graph with considering the local structure of data. J. Elect. Imag. 2018, 27, 063002. [Google Scholar] [CrossRef]
- Chen, M.; Wang, Q.; Li, X. Discriminant Analysis with Graph Learning for Hyperspectral Image Classification. Remote Sens. 2018, 10, 836. [Google Scholar] [CrossRef] [Green Version]
- Camps-Valls, G.; Marsheva, T.; Zhou, D. Semi-Supervised Graph-Based Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3044–3054. [Google Scholar] [CrossRef]
- Leng, Q.; Yang, H.; Jiang, J. Label Noise Cleansing with sparse Graph for Hyperspectral image Classification. Remote Sens. 2019, 11, 1116. [Google Scholar] [CrossRef] [Green Version]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Ding, Y.; Guo, Y.; Chong, Y.; Pan, S.; Feng, J. Global Consistent Graph Convolutional Network of Hyperspectral Image Classification. IEEE Trans. Instrum. Meas. 2021, 70, 1–16. [Google Scholar]
- Wan, S.; Gong, C.; Zhong, P.; Du, B.; Zhang, L.; Yang, J. Multiscale Dynamic Graph Convolutional Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3162–3177. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Zhang, Z.; Liu, X.; Cai, Z. Efficient Graph Convolutional Self-Representation for Band Selection of Hyperspectral Image. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4869–4880. [Google Scholar] [CrossRef]
- Grady, L. Random walks for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1768–1783. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Zhang, C. Semisupervised learning based on generalized point charge models. IEEE Trans. Neural Netw. 2008, 19, 1307–1311. [Google Scholar] [CrossRef]
- Liu, D.; Liu, X.; Wang, W.; Bai, H. Semi-supervised community detection based on discrete potential theory. Physica. A 2014, 416, 173–182. [Google Scholar] [CrossRef]
- Zhang, Q.; Lü, L.; Wang, W.; Zhou, T. Potential theory for directed networks. PLoS ONE 2013, 8, e55437. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, E.; Tuzel, O.; Ramalingam, S.; Chellappa, R. Entropy rate superpixel segmentation. In Proceedings of the CVPR2011, Providence, RI, USA, 20–25 June 2011; pp. 2097–2104. [Google Scholar]
- Golub, G.; Van Loan, C. Matrix Computations; JHU Press: Baltimore, MD, USA, 2012. [Google Scholar]
- Kang, X.; Li, S.; Benediktsson, J. Spectral-spatial hyperspectral image classification with edge-preserving filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2666–2677. [Google Scholar] [CrossRef]
- Tumelien, E.; Visockien, J.; Malien, V. The Influence of Seasonality on the Multi-Spectral Image Segmentation for Identification of Abandoned Land. Sustainability 2021, 13, 6941. [Google Scholar] [CrossRef]




| Indian Pines | Pavia University | Salinas | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Class | Name | Train | Test | Name | Train | Test | Name | Train | Test |
| 1 | Alfalfa | 3 | 43 | Asphalt | 342 | 6489 | Weeds_1 | 20 | 1989 |
| 2 | Corn_no till | 72 | 1356 | Meadows | 933 | 17,716 | Weeds_2 | 37 | 3689 |
| 3 | Corn_min till | 42 | 788 | Gravel | 105 | 1994 | Fallow | 20 | 1956 |
| 4 | Corn | 12 | 225 | Trees | 153 | 2911 | Fallow_P | 14 | 1380 |
| 5 | Grass/Pasture | 24 | 459 | Metal sheets | 68 | 1277 | Fallow_S | 27 | 2651 |
| 6 | Grass/Trees | 37 | 693 | Bare soil | 252 | 4847 | Stubble | 40 | 3919 |
| 7 | Grass/Pasture mowed | 2 | 26 | Bitumen | 67 | 1263 | Celery | 36 | 3543 |
| 8 | Hay_windrowed | 24 | 454 | Bricks | 184 | 3498 | Grapes | 113 | 11,158 |
| 9 | Oats | 1 | 19 | Shadows | 48 | 899 | Soil | 62 | 6141 |
| 10 | Soybean_no till | 49 | 923 | Corn | 33 | 3245 | |||
| 11 | Soybean_min till | 123 | 2332 | Lettuce_4wk | 11 | 1057 | |||
| 12 | Soybean_clean | 30 | 563 | Lettuce_5wk | 20 | 1907 | |||
| 13 | Wheat | 10 | 195 | Lettuce_6wk | 9 | 907 | |||
| 14 | Woods | 64 | 1201 | Lettuce_7wk | 11 | 1059 | |||
| 15 | Building_G_T_D | 20 | 366 | Vinyard_U | 73 | 7192 | |||
| 16 | Stone-steel_T | 5 | 88 | Vinyard_T | 18 | 1789 | |||
| 518 | 9731 | 2152 | 40,894 | 544 | 53,582 | ||||
| GCN | EPF | IFRF | SCMK | SSC-SL | MDGCN | SPCNN | SSG | |
|---|---|---|---|---|---|---|---|---|
| 1 | 93.65 ± 0.35 | 26.28 ± 6.43 | 94.41 ± 1.86 | 95.25 ± 0 | 76.51 ± 3.67 | 90.23 ± 1.47 | 96.38 ± 0.92 | 97.39 ± 1.95 |
| 2 | 51.36 ± 1.83 | 68.69 ± 5.64 | 86.14 ± 3.68 | 90.07 ± 2.54 | 94.65 ± 2.01 | 93.37 ± 1.22 | 91.96 ± 0.41 | 97.46 ± 0.55 |
| 3 | 50.30 ± 3.02 | 58.74 ± 2.62 | 84.67 ± 4.67 | 92.89 ± 3 | 92.4 ± 1.71 | 92.66 ± 4.70 | 95.80 ± 1.82 | 97.87 ± 1.49 |
| 4 | 25.41 ± 6.98 | 40.89 ± 18.71 | 73.16 ± 6.67 | 84.51 ± 3.44 | 71.25 ± 9.75 | 94.80 ± 5.68 | 89.61 ± 0.18 | 98.39 ± 2.16 |
| 5 | 0 ± 0 | 91.77 ± 2.51 | 91.18 ± 4.52 | 93.57 ± 4.20 | 92.07 ± 3.67 | 93.34 ± 3.44 | 89.32 ± 2.16 | 95.57 ± 1.87 |
| 6 | 97.52 ± 1.42 | 99.73 ± 2.77 | 98.44 ± 1.12 | 98.68 ± 1.15 | 99.34 ± 0.79 | 97.89 ± 0.70 | 99.04 ± 0.29 | 99.81 ± 0.06 |
| 7 | 98.3 ± 2.34 | 93.46 ± 8.07 | 94.62 ± 10.77 | 96.17 ± 1.35 | 97.31 ± 4.07 | 90.77 ± 7.30 | 95.1 ± 2.28 | 96.43 ± 0.24 |
| 8 | 97.46 ± 0.37 | 99.96 ± 0.13 | 100 ± 0 | 99.62 ± 0.15 | 94.58 ± 4.47 | 99.47 ± 0.56 | 99.39 ± 0.02 | 100 ± 0 |
| 9 | 100 ± 0 | 0 ± 0 | 100 ± 0 | 46.62 ± 5.21 | 82.63 ± 5.22 | 57.37 ± 30.93 | 95.06 ± 1.14 | 100 ± 0 |
| 10 | 73.58 ± 1.73 | 68.63 ± 4.93 | 87.56 ± 3.39 | 91.36 ± 2.56 | 93.65 ± 1.54 | 93.26 ± 1.46 | 92.48 ± 2.17 | 94.01 ± 0.74 |
| 11 | 78.38 ± 5.82 | 93.64 ± 2.91 | 98.03 ± 0.59 | 95.19 ± 1.9 | 96.84 ± 0.85 | 97.50 ± 0.78 | 81.02 ± 2.41 | 98.60 ± 0.81 |
| 12 | 56.37 ± 2.27 | 54.49 ± 13.27 | 74.46 ± 9.43 | 91.3 ± 2.2 | 85.81 ± 4.08 | 92.43 ± 3.17 | 97.83 ± 0.02 | 95.95 ± 1.76 |
| 13 | 99.01 ± 0.09 | 99.43 ± 0.15 | 99.07 ± 0.6 | 97.42 ± 1.23 | 98.09 ± 2.85 | 99.23 ± 1.24 | 99.43 ± 0.02 | 99.12 ± 0.43 |
| 14 | 99.6 ± 0.08 | 99.54 ± 0.25 | 98.75 ± 0.92 | 99.3 ± 0.56 | 98.96 ± 0.63 | 99.78 ± 0.13 | 96.36 ± 0.17 | 99.84 ± 0.08 |
| 15 | 76.67 ± 2.40 | 57.9 ± 12.90 | 94.97 ± 3.11 | 92.94 ± 3.76 | 95.33 ± 3.79 | 96.39 ± 5.71 | 100 ± 0 | 98.86 ± 0.28 |
| 16 | 89.24 ± 2.54 | 98.98 ± 1.07 | 98.86 ± 1.17 | 86.69 ± 6.51 | 71.14 ± 3.88 | 95.80 ± 2.98 | 98.15 ± 0.60 | 95.70 ± 1.52 |
| OA | 67.86 ± 0.59 | 82.59 ± 1.42 | 91.94 ± 1.38 | 94.21 ± 0.54 | 94.29 ± 0.61 | 95.83 ± 0.32 | 95.26 ± 0.53 | 97.85 ± 0.07 |
| AA | 70.79 ± 3.26 | 72.01 ± 3.17 | 92.15 ± 3.28 | 90.76 ± 3.05 | 90.05 ± 5.6 | 92.77 ± 2.33 | 94.89 ± 1.16 | 97.75 ± 1.80 |
| κ | 63 ± 0.02 | 80 ± 0.16 | 91 ± 0.43 | 93 ± 0.06 | 91 ± 0.01 | 95 ± 0.01 | 94 ± 0.01 | 98 ± 0.08 |
| GCN | EPF | IFRF | SCMK | SSC-SL | MDGCN | SPCNN | SSG | |
|---|---|---|---|---|---|---|---|---|
| 1 | 62.85 ± 12.37 | 99.75 ± 0.43 | 97.54 ± 1.06 | 95.94 ± 0.82 | 99.32 ± 0.12 | 99.24 ± 0.33 | 99.03 ± 0.06 | 99.76 ± 0.08 |
| 2 | 58.07 ± 2.23 | 99.94 ± 0.22 | 99.85 ± 0.14 | 95.65 ± 0.29 | 99.92 ± 0.05 | 99.73 ± 0.07 | 99.26 ± 0.03 | 99.95 ± 0.04 |
| 3 | 46.56 ± 9.28 | 72.32 ± 5.33 | 84.08 ± 5.18 | 93.60 ± 4.87 | 78.28 ± 0.25 | 97.25 ± 0.99 | 99.19 ± 0.04 | 99.37 ± 0.48 |
| 4 | 53.45 ± 8.45 | 95.77 ± 0.69 | 93.04 ± 1.24 | 95.74 ± 0.83 | 96.46 ± 0.21 | 96.22 ± 1.02 | 98.94 ± 0.16 | 88.11 ± 0.65 |
| 5 | 88.72 ± 2.51 | 99.92 ± 0.23 | 99.83 ± 0.13 | 94.33 ± 0.15 | 99.92 ± 0.29 | 98.56 ± 1.06 | 100 ± 0 | 99.73 ± 0.13 |
| 6 | 59.57 ± 6.22 | 77.25 ± 0.07 | 99.75 ± 0.03 | 96.16 ± 1.29 | 90.24 ± 0.06 | 99.99 ± 0.03 | 99.27 ± 0.02 | 99.90 ± 0.07 |
| 7 | 88.81 ± 2.27 | 90.50 ± 0.39 | 97.66 ± 1.32 | 92.23 ± 5.82 | 91.53 ± 0.26 | 97.92 ± 1.98 | 99.32 ± 0.04 | 100 ± 0 |
| 8 | 76.06 ± 2.26 | 98.91 ± 0.85 | 86.41 ± 2.12 | 95.2 ± 1.06 | 98.91 ± 0.15 | 96.14 ± 1.32 | 98.45 ± 0.04 | 98.65 ± 1.51 |
| 9 | 81.34 ± 4.52 | 96.89 ± 3.37 | 42.67 ± 2.68 | 97.59 ± 0.6 | 97.33 ± 0.28 | 93.58 ± 2.27 | 98.26 ± 0.68 | 99.62 ± 0.55 |
| OA | 75.78 ± 2.64 | 95.14 ± 0.32 | 95.73 ± 0.32 | 96.49 ± 0.15 | 96.47 ± 0.03 | 98.77 ± 0.13 | 98.53 ± 0.03 | 99.12 ± 0.12 |
| AA | 77.50 ± 3.57 | 92.36 ± 1.28 | 88.98 ± 4.30 | 95.29 ± 2.86 | 94.66 ± 0.19 | 97.63 ± 0.38 | 99.06 ± 0.28 | 98.34 ± 3.64 |
| κ | 75 ± 0.04 | 93 ± 0.43 | 94 ± 0.24 | 96 ± 0.19 | 96 ± 0.01 | 98 ± 0.01 | 98 ± 0.01 | 99 ± 0.15 |
| GCN | EPF | IFRF | SCMK | SSC-SL | MDGCN | SPCNN | SSG | |
|---|---|---|---|---|---|---|---|---|
| 1 | 100 ± 0 | 99.59 ± 1.10 | 99.80 ± 0.02 | 100 ± 0 | 100 ± 0 | 100 ± 0 | 100 ± 0 | 100 ± 0 |
| 2 | 99.78 ± 0.05 | 99.86 ± 0.16 | 99.21 ± 0.26 | 99.78 ± 0 | 97.84 ± 0.17 | 99.85 ± 0.16 | 99.16 ± 0.02 | 100 ± 0 |
| 3 | 100 ± 0 | 88.18 ± 3.03 | 100 ± 0 | 97.11 ± 0.76 | 98.38 ± 5.13 | 99.36 ± 0.93 | 100 ± 0 | 100 ± 0 |
| 4 | 92.38 ± 0.25 | 99.56 ± 0.17 | 96.27 ± 2.26 | 95.78 ± 3.33 | 96.07 ± 6.44 | 96.12 ± 4.79 | 99.67 ± 0.04 | 95.56 ± 2.73 |
| 5 | 98.91 ± 0.16 | 99.26 ± 0.34 | 97.79. ± 0.43 | 94.95 ± 0.21 | 96.9 ± 0.2 | 96.94 ± 0.88 | 99.21 ± 0.07 | 97.21 ± 1.44 |
| 6 | 99.67 ± 0.21 | 99.98 ± 0.01 | 99.28 ± 0.01 | 99.69 ± 0.18 | 95.88 ± 0.05 | 99.93 ± 0.01 | 99.02 ± 0.12 | 100 ± 0 |
| 7 | 99.40 ± 0.04 | 99.75 ± 0.03 | 99.57 ± 0.21 | 95.27 ± 0.31 | 99.85 ± 0.1 | 99.48 ± 0.70 | 99.07 ± 0.04 | 99.80 ± 0.13 |
| 8 | 68.78 ± 0.63 | 92.49 ± 0.03 | 74.34 ± 9.24 | 93.01 ± 2.7 | 95.53 ± 1.01 | 99.02 ± 0.82 | 98.45 ± 0.80 | 99.52 ± 0.33 |
| 9 | 99.90 ± 0.01 | 99.5 ± 0.62 | 99.98 ± 0 | 96.67 ± 1.85 | 96.77 ± 0.29 | 99.99 ± 0.03 | 99.81 ± 0.01 | 99.93 ± 0.05 |
| 10 | 91.91 ± 0.43 | 90.71 ± 1.65 | 98.94 ± 0.97 | 96.38 ± 1.24 | 96.84 ± 1.78 | 98.89 ± 0.82 | 98.61 ± 0.07 | 98.75 ± 0.40 |
| 11 | 99.19 ± 0.03 | 97.68 ± 1.32 | 93.87 ± 3.93 | 94.19 ± 3.39 | 98.19 ± 0.81 | 96.40 ± 1.81 | 100 ± 0 | 96.27 ± 2.11 |
| 12 | 87.66 ± 0.91 | 100 ± 0 | 98.26 ± 2.56 | 97.34 ± 3.23 | 100 ± 0 | 93.32 ± 3.91 | 93.42 ± 1.03 | 93.95 ± 1.84 |
| 13 | 98.04 ± 0.28 | 97.79 ± 0.42 | 86.24 ± 6.85 | 97.12 ± 0 | 96.83 ± 3.11 | 87.48 ± 13.82 | 98.44 ± 0.11 | 98.07 ± 0.19 |
| 14 | 95.21 ± 1.30 | 93.54 ± 6.21 | 93.45 ± 1.46 | 95.46 ± 3.68 | 92.96 ± 6.41 | 91.08 ± 3.37 | 93.22 ± 0.07 | 95.44 ± 2.38 |
| 15 | 69.01 ± 2.27 | 59.94 ± 2.47 | 89.62 ± 9.58 | 93.5 ± 3.33 | 95.04 ± 1.73 | 98.02 ± 1.76 | 93.69 ± 2.46 | 99.26 ± 0.33 |
| 16 | 97.22 ± 0.35 | 97.51 ± 2.96 | 97.51 ± 0.47 | 94.64 ± 4.66 | 94.05 ± 0.34 | 99.11 ± 2.12 | 96.71 ± 0.25 | 97.71 ± 1.97 |
| OA | 88.67 ± 0.96 | 91.55 ± 1.87 | 92.06 ± 2.07 | 96.01 ± 0.27 | 96.83 ± 0.36 | 98.41 ± 0.35 | 95.88 ± 0.14 | 98.97 ± 0.08 |
| AA | 88.63 ± 1.03 | 94.51 ± 2.7 | 92.59 ± 3.71 | 96.12 ± 1.80 | 96.01 ± 1.72 | 97.19 ± 0.81 | 98.02 ± 1.36 | 98.22 ± 1.92 |
| κ | 87 ± 0.01 | 91 ± 0.32 | 91 ± 0.58 | 96 ± 0.03 | 95 ± 0.04 | 98 ± 0.01 | 95 ± 0.12 | 99 ± 0.10 |
| GCN | EPF | IFRF | SCMK | SSC-SL | MDGCN | SPCNN | OURS | |
|---|---|---|---|---|---|---|---|---|
| IP | 58.72 ± 0.36 | 13.041 ± 0.36 | 4.732 ± 0.11 | 6.23 ± 0.09 | 15.09 ± 0.56 | 44.64 ± 0.53 | 65.83 ± 2.92 | 1.481 ± 0.01 |
| PU | 783.06 ± 2.21 | 17.564 ± 1.22 | 12.864 ± 0.56 | 12.97 ± 0.21 | 21.33 ± 1.02 | 154.16 ± 3.86 | 205.86 ± 3.51 | 4.267 ± 0.26 |
| SA | 73.59 ± 1.64 | 27.693 ± 0.21 | 14.122 ± 0.14 | 14.33 ± 0.21 | 23.77 ± 0.69 | 24.53 ± 0.91 | 51.54 ± 3.73 | 6.057 ± 0.38 |
| Indian Pines | Pavia University | Salinas | ||||
|---|---|---|---|---|---|---|
| SAM | ED | SAM | ED | SAM | ED | |
| OA | 94.8 ± 2.01 | 97.85 ± 0.07 | 97.97 ± 0.27 | 99.12 ± 0.12 | 92.12 ± 4.21 | 98.97 ± 0.08 |
| AA | 93.02 ± 9.58 | 97.75 ± 1.80 | 96.36 ± 4.82 | 98.34 ± 3.64 | 88.67 ± 8.98 | 98.22 ± 1.92 |
| κ | 94.1 ± 2.28 | 98 ± 0.08 | 97.54 ± 0.39 | 99 ± 0.15 | 91.26 ± 4.65 | 99 ± 0.10 |
| Times | 1.82 ± 0.50 | 1.481 ± 0.01 | 4.75 ± 0.07 | 4.267 ± 0.26 | 6.375 ± 0.08 | 6.057 ± 0.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Yan, F. Hyperspectral Image Classification Based on Sparse Superpixel Graph. Remote Sens. 2021, 13, 3592. https://doi.org/10.3390/rs13183592
Zhao Y, Yan F. Hyperspectral Image Classification Based on Sparse Superpixel Graph. Remote Sensing. 2021; 13(18):3592. https://doi.org/10.3390/rs13183592
Chicago/Turabian StyleZhao, Yifei, and Fengqin Yan. 2021. "Hyperspectral Image Classification Based on Sparse Superpixel Graph" Remote Sensing 13, no. 18: 3592. https://doi.org/10.3390/rs13183592
APA StyleZhao, Y., & Yan, F. (2021). Hyperspectral Image Classification Based on Sparse Superpixel Graph. Remote Sensing, 13(18), 3592. https://doi.org/10.3390/rs13183592






