Abstract
Due to the high complexity of geo-spatial entities and the limited field of view of LiDAR equipment, pairwise registration is a necessary step for integrating point clouds from neighbouring LiDAR stations. Considering that accurate extraction of point features is often difficult without the use of man-made reflectors, and the initial approximate values for the unknown transformation parameters must be estimated in advance to ensure the correct operation of those iterative methods, a closed-form solution to linear feature-based registration of point clouds is proposed in this study. Plücker coordinates are used to represent the linear features in three-dimensional space, whereas dual quaternions are employed to represent the spatial transformation. Based on the theory of least squares, an error norm (objective function) is first constructed by assuming that each pair of corresponding linear features is equivalent after registration. Then, by applying the extreme value analysis to the objective function, detailed derivations of the closed-form solution to the proposed linear feature-based registration method are given step by step. Finally, experimental tests are conducted on a real dataset. The derived experimental result demonstrates the feasibility of the proposed solution: By using eigenvalue decomposition to replace the linearization of the objective function, the proposed solution does not require any initial estimates of the unknown transformation parameters, which assures the stability of the registration method.
1. Introduction
Accurate reconstruction of geographical entities and their related environments is an important focus of three-dimensional geographic information systems, and is also a key issue for digital cities. Among all available instruments and techniques for acquiring location-based data, LiDAR has been given more attention because of its ability to directly provide reliable point clouds for the scanned objects. Considering the diversity of the available spatial entities, the acquisition of point clouds, which fully cover the entity in question, might require several observation stations. Since these acquired point clouds are defined in their own local reference frames, it is necessary to develop methods to transform them into a common reference coordinate system, which is usually known as point cloud registration.
The essence of point cloud registration is to find the most suitable similarity transformation model between the two neighbouring LiDAR stations. Currently, the most popular model for similarity transformation is the seven parameter-based Bursa model, with which a spatial transformation is explained as a rotation around the x, y and z axes; a translation along these axes; and a scaling factor based on the centroid of the coordinate system. In practice, the point cloud registration usually starts with the identification of conjugate registration primitives from neighbouring stations. Then, the unknown transformation parameters are estimated based on certain error norms, which serve as the mathematical constraints that describe the coincidence of conjugate features after registration.
According to different types of features selected as registration primitives, available point cloud registration methods can be categorized into four groups: point feature-based methods [1,2,3,4,5,6], linear feature-based methods [7,8,9,10,11], planar feature-based methods [12,13,14,15], and hybrid feature-based methods [16,17,18]. To date, point feature-based methods are the most popular option for most researchers. However, due to the irregular nature of laser point clouds, it is usually necessary to set up artificial reflectors to ensure the corresponding relationship between each pair of conjugate point features. On the other hand, when no artificial reflectors are set up, linear and planar features are usually considered more accurate than point features since they are usually extracted from LiDAR points by least squares fitting. Nevertheless, the determination of a linear feature is often based on the line direction and any one point on it. Similarly, the determination of a planar feature is often based on the normal vector and any one point on it. The diversity of their mathematical expressions makes it difficult for us to get the difference between two linear/planar features. Therefore, how to make effective use of linear and planar features in the process of point cloud registration remains challenging.
According to different solutions employed for estimating the unknown transformation parameters, available methods can be categorized into two groups: iterative methods [1,2,7,9,10,13,14,16,17,18] and closed-form methods [3,4,5,6,8,11,12,15]. The most well-known iterative methods, which follow a non-linear least-square adjustment procedure, have been adopted for various applications. However, due to the nonlinear nature of the involved mathematical model, the disadvantages of iterative methods include: (1) Before using the computer to calculate the transformation parameters, the registration model must be linearized. Therefore, the initial estimates of the transformation parameters must be provided in advance. (2) The selection of the initial estimates of the model parameters will have a serious impact on the iterative method, that is, speed and convergence of the calculation depend greatly on the accuracy of these initial estimates. In extreme cases, the iterative method may not converge at all. Different from iterative methods, closed-form methods replace the linearization of the error equation with eigenvalue decomposition, single value decomposition, and extreme value analysis of a least squares formulation of the problem. Since the closed-form methods do not require any initial estimates, the computational performance can be more efficient when compared to the iterative methods. An evaluation of accuracy, robustness and stability for the four representative point feature-based, closed-form solutions were conducted by Eggert et al. [19].
It is worth mentioning that so far, we have separately implemented the closed-form solution to a point feature-based registration algorithm [6] and to a planar feature-based registration algorithm [15]. Both of them were based on the work of Walker et al. [5]. In this paper, we once again present a closed-form solution to a linear feature-based registration algorithm. Like the two previous solutions, dual quaternions are employed to represent the spatial transformations. Moreover, Plücker coordinates, which define a line in three-dimensional space with the line direction and the line moment [20], are introduced to represent linear features in three-dimensional space. Based on the relationship between Plücker coordinates and dual quaternions, an error norm is constructed for the linear feature-based registration algorithm, detailed derivations of formulas for solving the transformation parameters are given in sequence, and two experiments are designed to verify the correctness and effectiveness of the solution.
The remainder of this paper is organized as follows. Section 2 reviews some related work. Section 3 discusses the concept and properties of the Plücker coordinates, as well as their relation to dual quaternions. The derivation of the closed-form solution to the linear feature-based registration method is also presented here. Section 4 provides the details of the experiment and the analysis of the proposed solution. Section 5 concludes the study and presents suggested future work.
2. Related Work
This study focuses on the implementation of a closed-form solution to the linear feature-based registration of LiDAR point clouds, which includes the unique representation of linear features in 3D space, as well as the dual quaternion-based representation of spatial transformation. In the remainder of this section, quaternion and its application in point cloud registration and available representative linear feature-based registration methods will be reviewed.
2.1. Quaternion’s Application in Point Cloud Registration
As a convenient and effective way to describe rotation in three-dimensional space, quaternion was first proposed by Hamilton W. R. [21], which attracted considerable attention from researchers in various fields because of its compactness and high efficiency. Sanso [22] introduced quaternion to the representation of 3D rotation and showed the calculation of the rotation matrix, translation vector, and scale factor in the absolute orientation or in the semi-analytical triangulation. Based on the introduction of unit quaternion, Horn proposed a closed-form solution to the least-squares problem of three-dimensional spatial transformation, which is applied to the absolute orientation in photogrammetry [3]. Shen et al. [23] introduced unit quaternion to represent rotation parameters and derived the formulae for computing quaternion, translation and scale parameters in the Bursa–Wolf geodetic datum transformation model from two sets of co-located 3D coordinates. Later, Zeng et al. [24] did similar work to that of Shen et al. Joseph et al. [25] proposed an empirical study to compare the performance of unscented and extended Kalman filtering for improving human head and hand tracking, in which quaternions were used to represent orientation motion signals. Based on relationships between the quaternion representing the platform orientation, the measurement of gravity from the accelerometers and the angular rate measurement from the gyros, Kim et al. [26] proposed a real-time orientation estimation algorithm based on signals from a low-cost inertial measurement unit (IMU). Mazaheri and Habib [27] compared unit quaternion in single photo space resection with existing algorithms and reported the detailed evaluation of the algorithm. Mercan et al. [28] presented an iterative algorithm formulated as a GH model of adjustment for the solution of weighted symmetric similarity transformation problems, which takes advantage of quaternion’s unique representation of 3D orthogonal rotation matrix. Later, Uygur et al. [29] showed how to evaluate the rotation angles and the full covariance matrix of the transformation parameters from the estimation results in asymmetric and symmetric 3D similarity transformations based on quaternions.
As is known, unit quaternion can only represent rotation in three-dimensional space, when applied in the seven parameter-based Helmert transformation, the rotation parameters must be calculated first, followed by the scale and translation parameters. When errors occur in the estimation of the rotation parameters, the accuracy of the scale and translation parameters will be affected. As an alternative, dual quaternion has been introduced to represent spatial transformation. With the help of a dual number, two quaternions are integrated to represent spatial rotation and translation in a unified frame. Walker et al. [5] reported the first successful application of dual quaternion in estimating rigid transformation parameters, in which rotation parameters and translation vectors can be calculated at the same time. Later, Daniilidis [30] introduced dual quaternion to relate measurements made by a sensor mounted on a mechanical link to the robot’s coordinate frame and presented a new solution with which the six unknown parameters were simultaneously calculated using the singular value decomposition. Inspired by the work that was conducted by [5], Wang et al. presented a closed-form solution to a point feature-based registration algorithm, in which the scale factor was added to the cost function, which enabled the simultaneous derivation of the rotation, translation, and scale parameters [6]. Later, Wang et al. [15] presented another closed-form solution to a planar feature-based registration algorithm. Similar work was also conducted by Prošková et al. [31,32].
2.2. Linear Feature-Based Registration Methods
As a basic kind of natural primitives, linear features widely exist in the point cloud data acquired from urban scenes and industrial sites. Compared with point features, linear features are usually extracted by the fitting and intersection of the two adjacent planes to greatly reduce the effect of random errors on feature extraction. Therefore, linear features can provide a strong tie between neighbouring LiDAR stations. In the last two decades, considerable effort has been exerted to investigate the representation of 3D lines, as well as the utilization of 3D linear features for point cloud registration. Habib et al. proposed a linear feature-constrained seven parameter-based transformation model, where each linear feature was represented by any two points lying on it to partially eliminate the adverse effect of the inconsistency in the corresponding mathematical expression [7]. Based on the above work, Wang et al. proposed a closed-form solution for the estimation of rotation using unit quaternions [8]. He and Habib conducted similar work, in which a weight modification process introduced by [33] was adopted for the estimation of the scale and translation parameters between two neighbouring stations [11]. Al-Durgham and Habib introduced a matching strategy that utilized an association matrix to store information regarding the candidate matches of the linear features, and the matrix was subsequently combined with the random sample consensus approach to derive conjugate pairs between the two scans [9].
Instead of using the modified weight matrix process, the translation and the scale parameters were estimated conventionally by minimizing the difference among conjugate linear features [8,10]. However, most of the available formulas for deriving the difference between two conjugate 3D lines are nonlinear, which requires the linearization and iterative optimization of the error equation. Furthermore, in classical vector-based representation, the non-unique representation of the 3D linear features complicates the determination of the differences between two linear features. As an alternative, Plücker coordinates, which use line direction and moment to represent a line in a 3D space, have been widely used by computer vision communities for camera pose estimation [30]. Research efforts have also been exerted to use the Plücker coordinates for point cloud registration. For example, Bartoli et al. introduced a line motion matrix to represent line transformation using the Plücker coordinate-based representation of a line [34]. The 6 × 6 matrix, which was designed to obtain the transformation parameters, was recovered by comparing the 3D Plücker coordinates. Sheng et al. used Plücker coordinates to represent the corresponding extracted linear features and estimated the registration parameters through an iterative procedure [10]. Both Bartoli et al. and Sheng et al. used iterative procedures to estimate the transformation parameters, in which the initial estimate values of unknown parameters should be determined to ensure the correct operation of the algorithm.
3. Plücker Coordinate-Based Registration Model
3.1. Plücker Coordinate-Based Representation of Spatial Lines
In essence, Plücker coordinates are equivalent to all other methods to represent linear features in three-dimensional space. However, Plücker coordinates do not depend on particular points to define linear features, which makes it convenient for us to obtain the difference between any two linear features.
Taking a line in 3D Euclidean space with the direction and a passing point as an example. With Plücker coordinates, the line can be represented by a six-tuple , where is called the line moment, that is determined by the cross product of the vector and the line direction .
Besides, given any two points and lying on a line in 3D space, the line direction and the line moment can be obtained by:
Relations among , , , and are illustrated in Figure 1, and , and represent the angle between the line and the x, y and z coordinate axes, respectively.
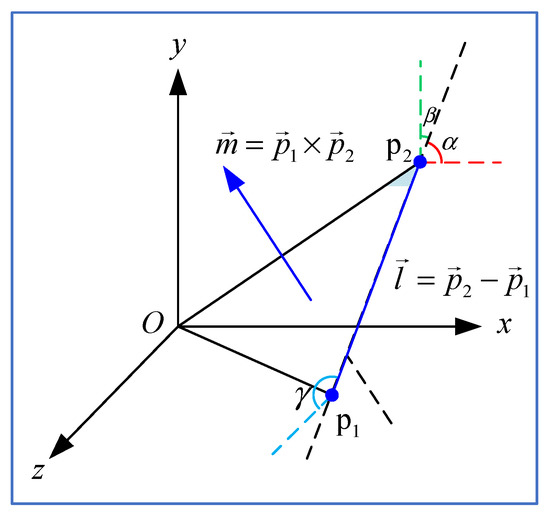
Figure 1.
Plücker coordinate-based representation of a line in a 3D space.
Supposing that and are two other points that lie on the same line as and , they can be represented as:
where and are two different coefficients.
Based on and , the line direction and the line moment can be obtained by:
Both and are scalar multiplies of and in Equation (1), which means that they represent the same line in 3D space. The combination of these six homogeneous coordinates is called the Plücker coordinates, which is expressed as:
Dividing each item of the Plücker coordinates in Equation (4) by the module of the line direction, the result is called normalized Plücker coordinates. With normalized Plücker coordinates, the magnitude of the line moment is equivalent to the distance from the origin to the line. Furthermore, the mathematical expression of a line in 3D space will be unique, thereby making the direct comparison and contrasts between two lines intuitively possible.
Noting that the line direction and the line moment in Equation (1) must be orthogonal to represent a line in 3D space, which can be represented as:
Furthermore, if quaternions are used to represent the two vectors, then Equation (4) can be re-written as:
where and .
Since the normalized Plücker coordinates fulfil all conditions of dual quaternions, thereby allowing the representation of the transformation of a line from one frame to another through the direct operation between Plücker coordinates and a dual quaternion, the development of a closed-form solution to point cloud registration method is possible. Moreover, the magnitude of the line moment is equivalent to the distance from the origin to the line after normalization.
3.2. Dual Quaternion-Based Transformation of the Plücker Coordinates
As is known, a dual quaternion refers to the aggregation of two quaternions:
When a dual quaternion is used to represent a rigid motion in 3D space, and should satisfy the following two constraints:
As is shown, Equation (6) also satisfies the two constraints, which makes it possible to represent the transformation of lines in 3D space by the operation between dual quaternions and normalized Plücker coordinates [5]. The operation between the two expressions, which is the key to constructing the error equations of the proposed solution, will be introduced in the next section.
In 3D space, the transformation of a line direction and line moment with vector algebra can be expressed as:
where and represent the direction and the moment of the line before spatial transformation, respectively, and represent the direction and the moment after spatial transformation, respectively, and , , and represent the rotation matrix, the translation vector, and the scale factor between the two coordinate systems, respectively.
According to the relation between a unit quaternion and the corresponding rotation matrix [3], the expression can be rewritten as:
where is the unit quaternion that corresponds to the spatial rotation, is the conjugate of , and .
Furthermore, the line moment in Equation (10) can be rewritten as:
Setting , Equation (10) can be further redefined as:
Using a dual quaternion, Equation (13) can be rewritten as:
When , , and , Equation (14) can be simplified as:
where is the conjugate of .
Up to now, we have proven that the operation between dual quaternions and normalized Plücker coordinates can be used to represent any spatial transformation of a line in 3D space. More importantly, the transformation from a classical vector-based representation to a dual quaternion-based representation is completely equivalent.
The subsequent section will discuss the matrix-based representation of the quaternion product, which is highly convenient for programming.
3.3. L2 Norm Minimization-Based Solution for Registration Parameters
Based on Equation (13) and according to [5], each item in Equation (13) can be further expressed as:
where and are the two quaternion matrices. The specific expressions are: and .
By substituting Equation (16) into Equation (13), we obtain the following equation:
Through transformation, Equation (17) can be rewritten as:
Considering the existence of random errors and based on the least squares theory, the essence of the linear feature-constrained registration approach is to minimize the difference between and . According to least square criteria, the following two error functions are obtained:
where and .
The registration parameters can be obtained when the expression reaches its minimum. Considering that the two items of are both positive, when each item reaches its minimum, will be minimal. The optimal value of will be obtained by minimizing Equation (19), whereas the values of and μ will be obtained by minimizing Equation (20).
3.3.1. Solution for the Unit Quaternion
By decomposition, Equation (19) can be rewritten as:
Setting and , Equation (21) can be redefined as:
The first term of Equation (22) is always positive. Thus, when reaches its maximum, will be minimal.
By using Equation (8) as a restriction, the error equation can be expressed as:
where is a Lagrange multiplication constant.
Taking the partial derivative of Equation (23) with respect to and making it equal to 0, we get:
By setting , Equation (24) can be rewritten as:
Based on Equation (25), the optimal solution corresponds to one of the four eigenvectors of matrix , and thus the optimal solution can be determined according to Equation (22).
Multiplying Equation (24) by yields:
Substituting Equation (26) into Equation (22) yields:
As can be seen, when is equal to the minimum eigenvalue of matrix , Equation (27) will be minimized.
3.3.2. Solution for the Quaternion and the Scale Factor
By decomposition, and making , , , , , , , and , Equation (20) can be rewritten as:
where is an identity matrix, and .
Similar to the method adopted previously and using Equation (9) as the restriction, the best quaternion to represent the translation can be obtained when Equation (29) is minimized.
where is a Lagrange multiplier constant.
Taking the partial derivatives of Equation (29) with respect to and separately and making them equal to 0, we get:
Using Equation (31), the scale factor can be represented as:
By substituting into Equation (30), can be defined as:
where .
Multiplying Equation (33) by yields:
with which we obtain the expression of :
The quaternion corresponding to the translation between the two neighbouring observation stations can be obtained by the following equation:
3.3.3. Algorithm Implementation
Assuming that and are the two sets of Plücker coordinates, which correspond to conjugate linear features extracted from two neighbouring stations, namely, the reference station and the unregistered station. and are their corresponding quaternions, respectively. In the implementation of the proposed Plücker coordinate-based algorithm, the following steps are suggested to obtain the seven unknown parameters:
- (1)
- Constructing matrix based on matrix . Then, calculating the minimum eigenvalue and its corresponding eigenvector of .
- (2)
- Calculating the quaternion using Equation (33).
- (3)
- Calculating the scale coefficient μ using Equation (32).
- (4)
- Calculating the quaternion using Equation (36).
With , and μ, a line in 3D space can be transformed from one coordinate system to another.
3.4. Minimum Number of Features Needed
As is known, a line in three-dimensional space has four degrees of freedom. When a pair of conjugate linear features are given, two rotation angles defined by the line direction and two translation parameters perpendicular to the line direction can be estimated.
A spatial rotation transformation has three degrees of freedom. Since a pair of conjugate linear features can only estimate two rotation angles, at least two pairs of conjugate linear features are needed to estimate the rotation transformation parameters.
A translation vector has three degrees of freedom. Since each pair of conjugate linear features can estimate two translation parameters perpendicular to the line direction, when two pairs of conjugate linear features are parallel, it is impossible to estimate the translation along the direction of the linear features. Therefore, two intersecting linear features are needed to obtain the translation parameters in point cloud registration.
As for the scaling factor, we need to estimate it with the help of the ratio of the conjugate distance from each reference frame. When only two pairs of conjugate linear features are given, we cannot obtain the distance between them, so they must be non-coplanar to ensure the estimation of the scaling factor.
To sum up in one sentence, at least two pairs of non-coplanar linear features are given to ensure the correct operation of the presented closed-form solution in this paper.
4. Results
We implement the proposed solution with C++ programming language and design two experiments, which are based on the point clouds captured from man-made buildings by two different terrestrial LiDAR instruments (Riegl LMS-Z420i and Riegl VZ-1000) to verify the effectiveness and feasibility of the proposed solution at deriving the transformation parameters.
4.1. Point Clouds Captured by Riegl LMS-Z420i
By fitting and intersecting two adjacent planes, a total of seven pairs of conjugate linear features are extracted from a man-made building by Riegl LMS-Z420i, each of which is defined by two points, namely, the start and end points (Table 1).

Table 1.
Conjugate linear features extracted from the point clouds captured by Riegl LMS-Z420i.
The configuration of the extracted linear features is displayed in Figure 2.

Figure 2.
Configuration of the extracted linear features from the two neighbouring stations. (a) Reference station; (b) Un-registered station.
The derived transformation parameters from the proposed method are presented in Table 2. To verify the correctness and the feasibility of the algorithm, results obtained by the other two linear feature-based solutions, which were proposed by Wang et al. [8] and He and Habib [11], are also shown in Table 2 for comparison.

Table 2.
Results obtained by the proposed solution and the two existing methods.
Since the scale parameter is often neglected by registration methods designed for LiDAR point clouds, the second experiment is designed to verify the validity of the calculation of the scale parameter. By scaling all coordinates of the extracted linear features from the unregistered station to half of their original, calculated transformation parameters are shown in Table 3.

Table 3.
Comparison of the registration results from the original and scaled data.
By using the same point clouds, we also compare the results of the proposed solution in this paper to another closed-form solution to a planar feature-based registration algorithm [15]. The calculated parameters of both are shown in Table 4.

Table 4.
Results obtained by the proposed solution to a linear feature-based algorithm and another closed-form solution to a planar feature-based registration algorithm.
4.2. Point Clouds Captured by Riegl VZ-1000
Similar to the previous experiment, by fitting and intersecting two adjacent planes, a total of nine pairs of conjugate linear features are extracted from another man-made building by Riegl VZ-1000, each of which is defined by two points, namely, the start and end points (Table 5).

Table 5.
Conjugate linear features extracted from the point clouds captured by Riegl VZ-1000.
The configuration of the extracted linear features is displayed in Figure 3.

Figure 3.
Configuration of the extracted linear features from the two neighbouring stations. (a) Reference station; (b) Un-registered station.
The derived transformation parameters from the proposed method are presented in Table 6. Results obtained by the other two linear feature-based solutions, which were proposed by Wang et al. [8] and He and Habib [11], are also shown in Table 2 for comparison.

Table 6.
Results obtained by the proposed method and the two existing methods.
Again, we scale all coordinates of the extracted linear features from the unregistered station to half of their original, and calculated transformation parameters are shown in Table 7.

Table 7.
Comparison of the registration results from the original and scaled data.
Once again we also compare the results of the proposed solution in this paper to another closed-form solution to a planar feature-based registration algorithm [15], and their calculated parameters are shown in Table 8.

Table 8.
Results obtained by the proposed solution to a linear feature-based algorithm and another closed-form solution to a planar feature-based registration algorithm.
5. Discussion
According to the residuals in Table 2 and Table 5, the differences between line direction vectors after registration are exactly the same for both tested algorithms. Minor deviations exist in the differences between line moments from the proposed method and the other two methods proposed by Wang et al. [8] and He and Habib [11]. The root mean square errors (RMSE) derived from the three tested algorithms are 0.0236 m, 0.0251 m and 0.0261 m for the first experiment, and are 0.0175 m, 0.0181 m and 0.0182 m for the second experiment. Therefore, we believe that the proposed method in this paper is slightly better than those used for comparison.
Based on the results shown in Table 3 and Table 6, the obtained values of the three rotation parameters and the translation vector from scaled point clouds are exactly the same as those of unscaled point clouds. In fact, when scaling all extracted linear features from the unregistered station to half of their original, the direction vector of each linear feature does not change at all. Therefore, the calculated , and are consistent with the results before scaling. As for translation vector , it is interrelated with the scaling factor . Only when the value of the scaling factor is correctly determined can the translation vector be obtained. According to the pre-set conditions, the correct value of the scaling factor should be twice the value before scaling. The results shown in Table 3 and Table 6 are completely consistent with the theoretical results.
Based on the results shown in Table 4 and Table 8, there are slight differences between the results obtained by the linear feature-based solution and the planar feature-based solution. With the point clouds captured by Riegl LMS-Z420i, the maximum difference between rotation angles is 0.0428 degrees and the maximum difference between translation parameters is 0.0496 m. With the point clouds captured by Riegl VZ-1000, the maximum difference between rotation angles is 0.0365 degrees and the maximum difference between translation parameters is 0.0468 m. It is clear that the differences between the results of the linear feature-based solution and the planar feature-based solution are similar in both experiments and both results are acceptable.
Therefore, we conclude that the proposed closed-form solution to a linear feature-based registration algorithm works well. Most important of all, the function to calculate the scaling factor makes it possible to be effectively apply to the fusion of point clouds acquired by different means (e.g., laser scanner and photogrammetry).
It is worth mentioning that each pair of corresponding linear features, which is represented by the Plücker coordinates, does not necessarily define compatible direction vectors. Eliminating the effect of incompatible linear feature directions will be one of the foci for our future work. So far, we have separately implemented all three closed-form solutions to a point feature-based, linear feature-based and planar feature-based registration of LiDAR point clouds to formulate a unified similarity transformation model in which point, linear and plane features are simultaneously included. Implementing the closed-form solution to the unified similarity transformation will be another focus of our future work.
6. Conclusions
Spatial transformation is widely used in point cloud registration, absolute orientation and navigation. According to whether the scale parameter is considered, it can be categorized into two groups, namely, rigid body transformation (six parameter-based) and similarity transformation (seven parameter-based). Comparatively, the seven parameter-based similarity transformation model is more versatile. In point cloud registration, point features are the most popular entities in implementation. However, available research on the use of linear features as a more accurate entity in three-dimensional similarity transformation is not yet mature, especially regarding the implementation of a closed-form solution.
In this paper, we propose a closed-form solution to a linear feature-based registration algorithm. Dual quaternions are employed to represent spatial transformations, and normalized Plücker coordinates are introduced to represent linear features. More importantly, the operation between dual quaternions and Plücker Coordinates are also presented, which facilitates the development of our closed-form solution. Based on the contrast between the results of the three tested linear feature-based registration algorithms, we conclude that the proposed closed-form solution is a good alternative to obtain the three-dimensional similarity transformation parameters between any two different coordinate systems. Overall, the advantages of our solution are as follows:
- (1)
- With normalized Plücker coordinates, a line in three-dimensional space has a unique mathematical expression, which makes it possible to obtain the differences between each pair of conjugate linear features, facilitating the design of our closed-form solution.
- (2)
- Unlike with iterative methods, the linearization of the objective function is omitted in the proposed closed-form solution, which makes it possible to get rid of the high dependence on the selection of those initial estimates, thus assuring the stability of the algorithm, especially in large-angle similarity transformation problems.
- (3)
- Based on the relationship between Plücker coordinates and dual quaternions, the integration of the scaling factor and dual quaternions makes it possible to realize the linear feature-based similarity transformation in three-dimensional space, which extends the application field of dual quaternions in multi-source data fusion.
Author Contributions
Conceptualization, Y.W.; methodology, Y.W.; software, Y.W.; validation, Y.W., N.Z., Z.B. and H.Z.; formal analysis, N.Z.; investigation, Y.W.; writing—original draft preparation, Y.W.; writing—review and editing, N.Z., Z.B. and H.Z.; funding acquisition, Y.W. and Z.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China, grant number 2017YFE0119600, and by the National Natural Science Foundation of China, grant number 41271444.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors would like to thank the anonymous reviewers and editors for providing valuable comments and suggestions that helped improve the manuscript greatly.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Arun, K.S.; Huang, T.S.; Bostein, S.D. Least-squares fitting of two 3-D point sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 698–700. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Besl, P.J.; Mckay, N.D. A Method for Registration of 3-D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Horn, B.K. Closed-form solution of absolute orientation using unit quaternions. J. Opt. Soc. Am. Ser. A 1987, 4, 629–642. [Google Scholar] [CrossRef]
- Horn, B.K. Closed form solution of absolute orientation using orthonormal matrices. J. Opt. Soc. Am. Ser. A 1988, 5, 1127–1135. [Google Scholar] [CrossRef] [Green Version]
- Walker, M.W.; Shao, L.; Volz, R.A. Estimating 3-D Location Parameters Using Dual Number Quaternions. CVGIP: Image Underst. 1991, 54, 358–367. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wang, Y.; Wu, K.; Yang, H.; Zhang, H. A dual quaternion-based, closed-form pairwise registration algorithm for point clouds. ISPRS J. Photogramm. Remote Sens. 2014, 94, 63–69. [Google Scholar] [CrossRef]
- Habib, A.; Ghanma, M.; Morgan, M.; Al-Ruzouq, R. Photogrammetric and LiDAR Data Registration Using Linear Features. Photogramm. Eng. Remote Sens. 2005, 71, 699–707. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, H.; Liu, Y.; Niu, X. Linear-Feature-Constrained Registration of LiDAR Point Cloud via Quaternion. Geomat. Inf. Sci. Wuhan Univ. 2013, 38, 1057–1062. [Google Scholar]
- Al-Durgham, K.; Habib, A. Association-matrix-based sample consensus approach for automated registration of terrestrial laser scans using linear features. Photogramm. Eng. Remote Sens. 2014, 80, 1029–1039. [Google Scholar] [CrossRef]
- Sheng, Q.H.; Chen, S.W.; Liu, J.F.; Wang, H. LiDAR Point Cloud Registration based on Plücker Line. Acta Geod. Cartogr. Sin. 2016, 45, 58–64. [Google Scholar]
- He, F.; Habib, A. A Closed-Form Solution for Coarse Registration of Point Clouds Using Linear Features. J. Surv. Eng. 2016, 142, 04016006. [Google Scholar] [CrossRef]
- Khoshelham, K. Closed-form solutions for estimating a rigid motion from plane correspondences extracted from point clouds. ISPRS J. Photogramm. Remote Sens. 2016, 114, 78–91. [Google Scholar] [CrossRef]
- Pavan, N.; Santos, D.; Khoshelham, K. Global Registration of Terrestrial Laser Scanner Point Clouds Using Plane-to-Plane Correspondences. Remote Sens. 2020, 12, 1127. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.B.; Zheng, N.S.; Bian, Z.F. A Quaternion-based, Planar Feature-constrained Algorithm for the Registration of LiDAR Point Clouds. Acta Opt. Sin. 2020, 40, 2310001. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, N.; Bian, Z. A Closed-Form Solution to Planar Feature-Based Registration of LiDAR Point Clouds. ISPRS Int. J. Geo-Inf. 2021, 10, 435. [Google Scholar] [CrossRef]
- Zheng, D.H.; Yue, D.J.; Yue, J.P. Geometric feature constraint based algorithm for building scanning point cloud registration. Acta Geod. Cartogr. Sin. 2008, 37, 464–468. [Google Scholar]
- Wang, Y.; Wang, Y.; Han, X.; She, W. A Unit Quaternion based, Point-Linear Feature Constrained Registration Approach for Terrestrial LiDAR Point Clouds. J. China Univ. Min. Technol. 2018, 47, 671–677. [Google Scholar]
- Chai, S.W.; Yang, X.Q. Line primitive point cloud registration method based on dual quaternion. Acta Opt. Sin. 2019, 39, 1228006. [Google Scholar] [CrossRef]
- Eggert, D.W.; Lorusso, A.; Fisher, R.B. Estimating 3D rigid body transformations: A comparison of four major algorithms. Mach. Vis. Appl. 1997, 9, 272–290. [Google Scholar] [CrossRef]
- Hartley, R.I.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Hamilton, W.R. On quaternions, or on a new system of imaginaries in algebra. Philos. Mag. 1844, 25, 489–495. [Google Scholar]
- Sanso, F. An exact solution of the roto-translation problem. Photogrammetria 1973, 29, 203–216. [Google Scholar] [CrossRef]
- Shen, Y.Z.; Chen, Y.; Zheng, D.H. A quaternions-based geodetic datum transformation algorithm. J. Geod. 2006, 80, 233–239. [Google Scholar] [CrossRef]
- Zeng, H.; Yi, Q. Quaternion-Based Iterative Solution of Three-Dimensional Coordinate Transformation Problem. J. Comput. 2011, 6, 1361–1368. [Google Scholar] [CrossRef]
- Joseph, J.; Laviola, J. A comparison of unscented and extended Kalman filtering for estimating quaternions motion. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 3, pp. 2435–2440. [Google Scholar]
- Kim, A.; Golnaraghi, M.F. A quaternion-based orientation estimation algorithm using an inertial measurement unit. In Proceedings of the IEEE Position Location and Navigation Symposium, Monterey, CA, USA, 26–29 April 2004; pp. 268–272. [Google Scholar]
- Mazaheri, M.; Habib, A. Quaternion-Based Solutions for the Single Photo Resection Problem. Photogramm. Eng. Remote Sens. 2015, 81, 209–217. [Google Scholar]
- Mercan, H.; Akyilmaz, O.; Aydin, C. Solution of the weighted symmetric similarity transformations based on quaternions. J. Geod. 2018, 92, 1113–1130. [Google Scholar] [CrossRef]
- Uygur, S.Ö.; Aydin, C.; Akyilmaz, O. Retrieval of Euler rotation angles from 3D similarity transformation based on quaternions. J. Spat. Sci. 2020. [Google Scholar] [CrossRef]
- Daniilidis, K. Hand-Eye Calibration Using Dual Quaternions. Int. J. Robot. Res. 1999, 18, 286–298. [Google Scholar] [CrossRef]
- Prošková, J. Application of dual quaternions algorithm for geodetic datum transformation. J. Appl. Math. 2011, 4, 225–236. [Google Scholar]
- Prošková, J. Discovery of Dual Quaternions for Geodesy. J. Geom. Graph. 2012, 16, 195–209. [Google Scholar]
- Renaudin, E.; Habib, A.; Kersting, A. Featured-Based Registration of Terrestrial Laser Scans with Minimum Overlap Using Photogrammetric Data. ETRI J. 2011, 33, 517–527. [Google Scholar] [CrossRef]
- Bartoli, A.; Sturm, P. The 3D Line Motion Matrix and Alignment of Line reconstructions. Int. J. Comput. Vis. 2004, 57, 159–178. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).