Fog Season Risk Assessment for Maritime Transportation Systems Exploiting Himawari-8 Data: A Case Study in Bohai Sea, China
Abstract
:1. Introduction
2. Materials
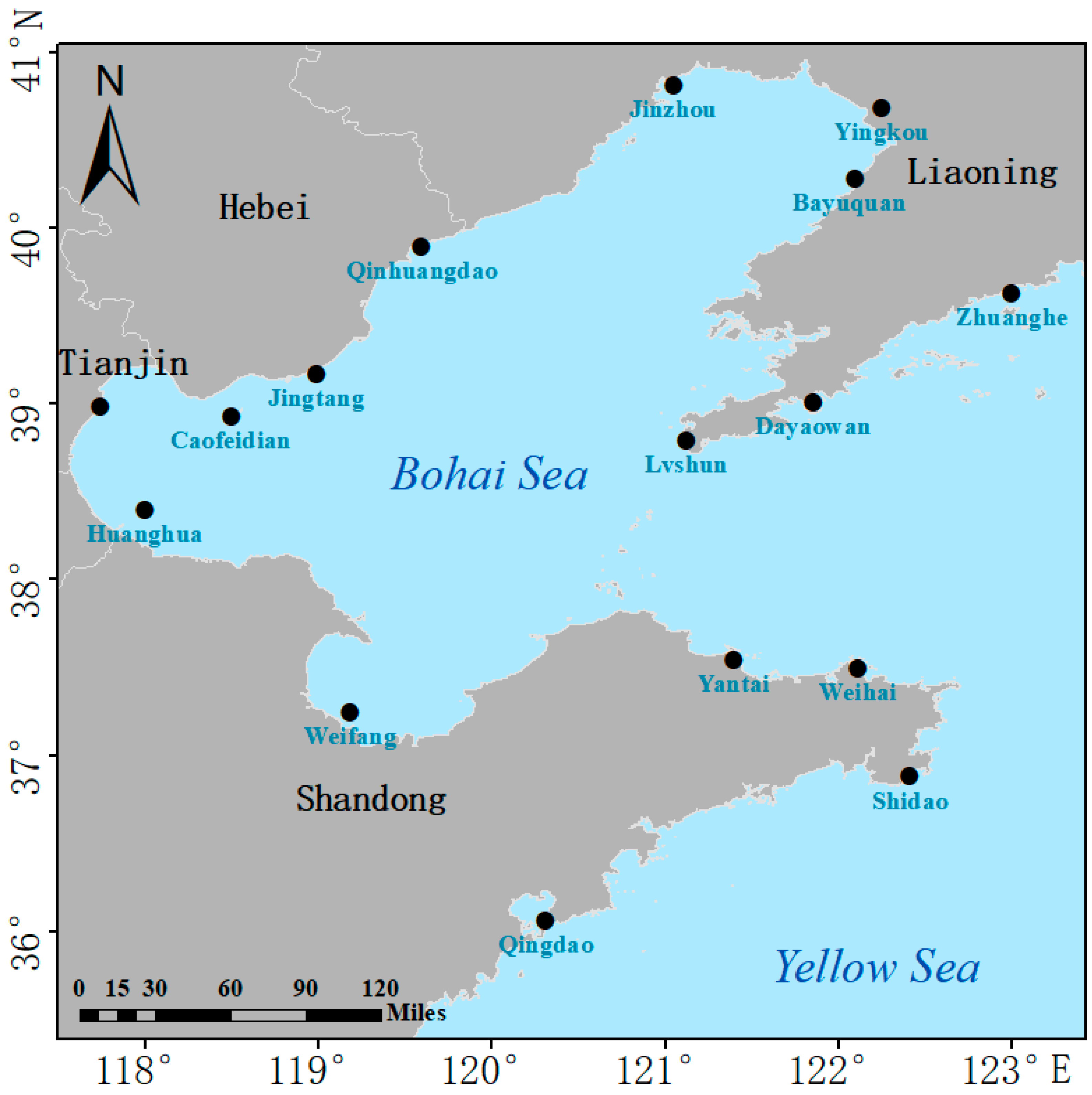
2.1. Study Area
2.2. Data
3. Methods
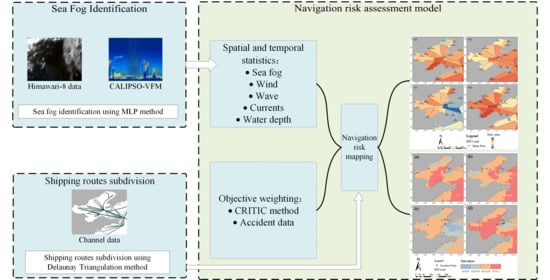
3.1. Sea Fog Identification
3.1.1. Sample Selection of Sea Fog
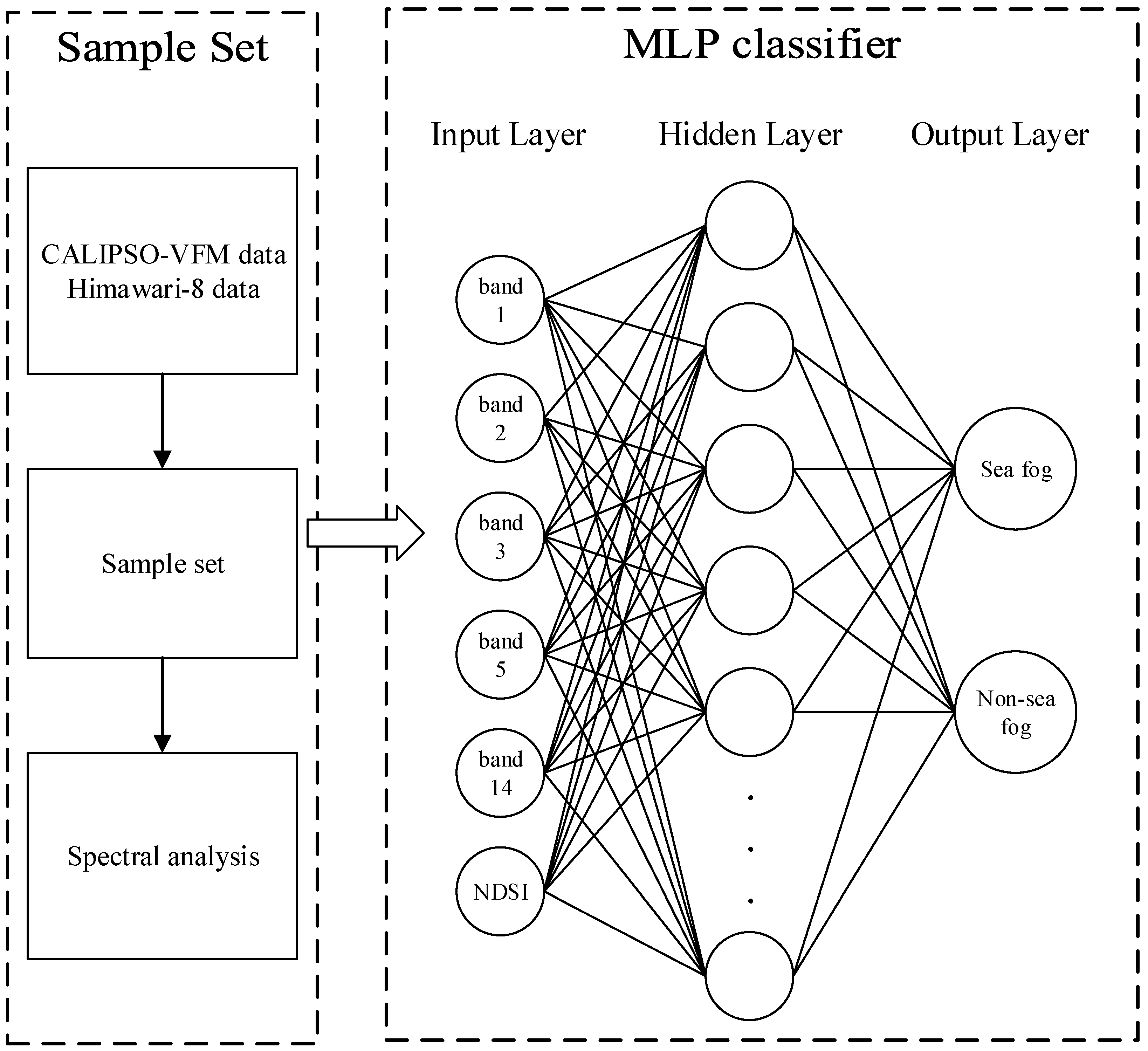
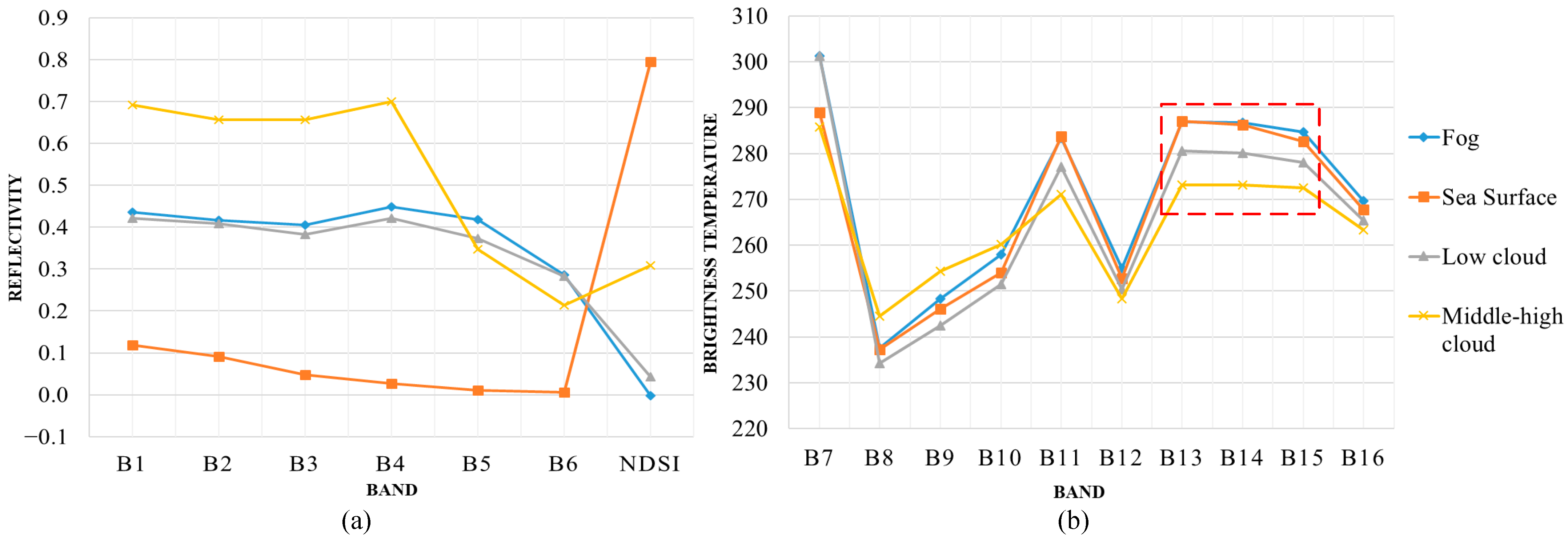
3.1.2. Feature Selection
3.1.3. Sea Fog Recognition Method Based on MLP
- Step 1: Normalize the sample values, which are scaled between [0, 1];
- Step 2: Divide the training set and testing set, and train the MLP classifier using the former;
- Step 3: Cross validation to determine the optimal parameters; and
- Step 4: Complete MLP training and verify the accuracy of the classifier.
3.2. Navigation Risk Assessment Model
3.2.1. Criteria for Navigation Risk
3.2.2. Data Processing
3.2.3. Weighting the Criteria Using CRITIC
- Step 1. The accident value of each criterion is standardized using Equation (7).
- Step 2. The standardized data are organized into an evaluation matrix. The columns represent different criteria, and the rows represent the standardized value of the same criteria, as shown in Equation (8):where represents the total number of criteria, represents the total number of accident records, and represents the standardized value.
- Step 3. Calculate the correlation coefficients, and a correlation coefficient matrix is obtained, expressed as Equation (9). Then, the conflict coefficient of each evaluation factor is calculated by Equation (10):where represents the conflict coefficient of criterion , and represents the correlation coefficients between criteria and . Note that a bigger correlation between criterion with other criteria produces a smaller .
- Step 4. Calculate the sample standard deviation of each criterion using Equation (11):where represents the sample standard deviation of criterion , and is the mean of the standardized values.
- Step 5. The amount of information for criterion is calculated with the conflict coefficient obtained in Step 3 via Equation (12):where represents the amount of information of criterion .
- Step 6. Normalize the amount of information and get the CRITIC weights for each criterion following Equation (13):where represents the CRITIC weight of criterion .
3.2.4. Shipping Routes Subdivision
- Step 1: Merge and simplify the dense shipping routes;
- Step 2: Generate equally spaced route points along the simplified shipping routes;
- Step 3: Use the Delaunay triangulation method to generate a regional Tyson polygon network with route points as the source;
- Step 4: Merge polygons from the same source to form a route subdivision;
- Step 5: Trim the boundaries manually.
3.3. Validation Methods
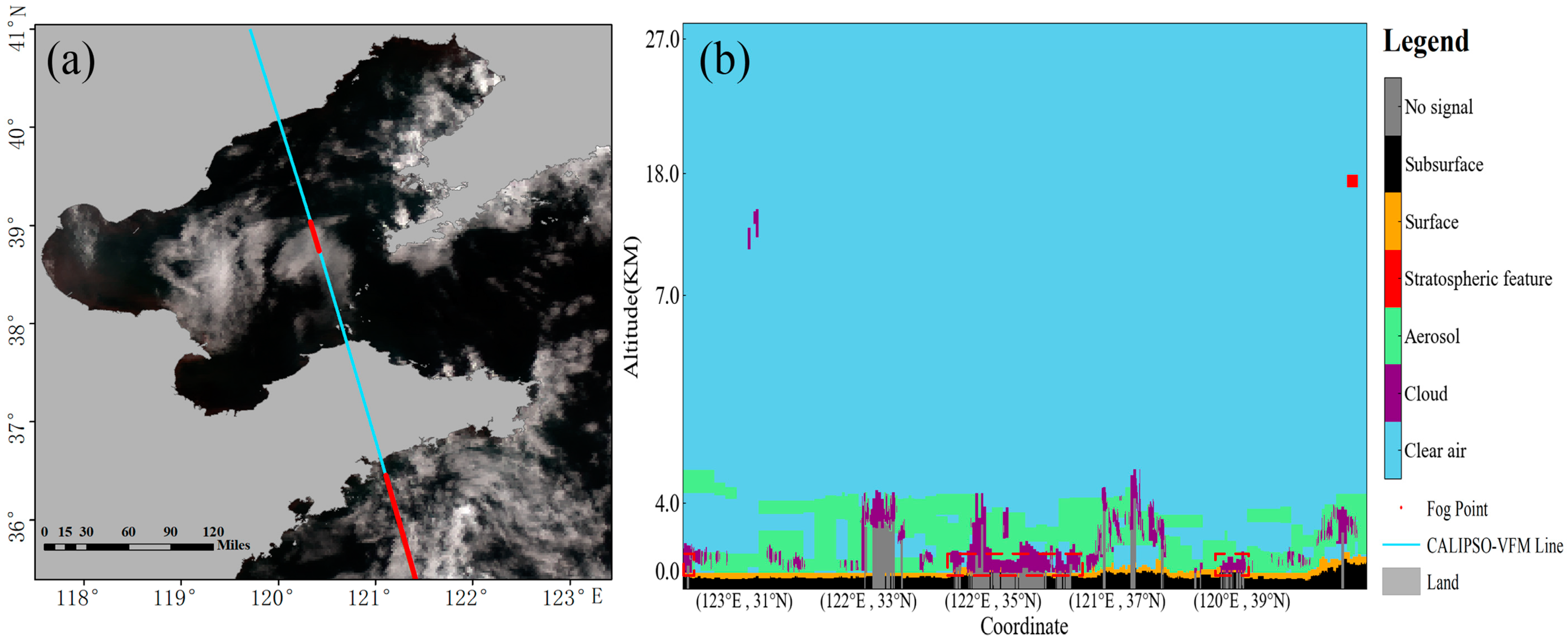
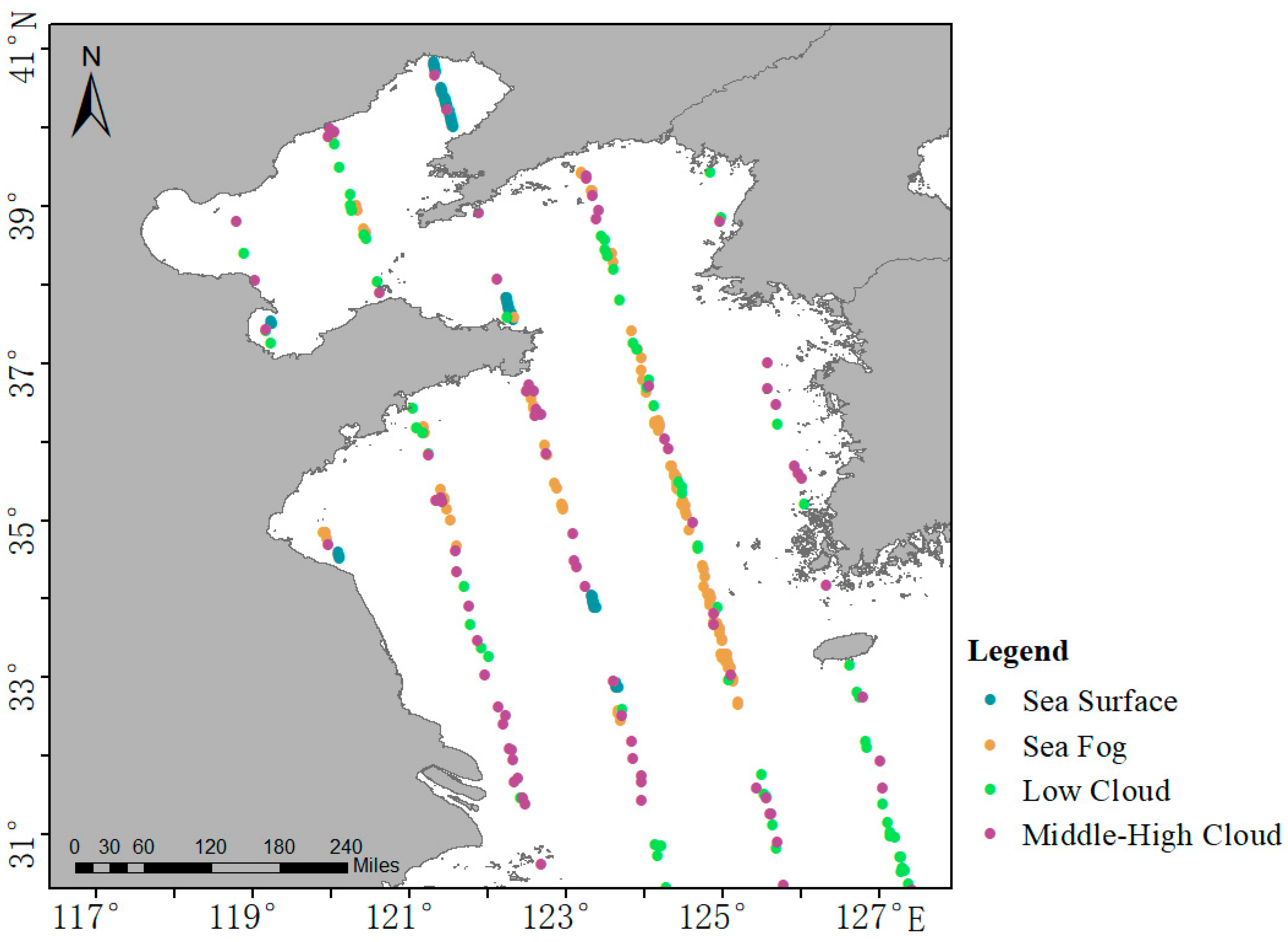
3.3.1. Sea Fog Identification Validation Using the CALIPSO-VFM Points
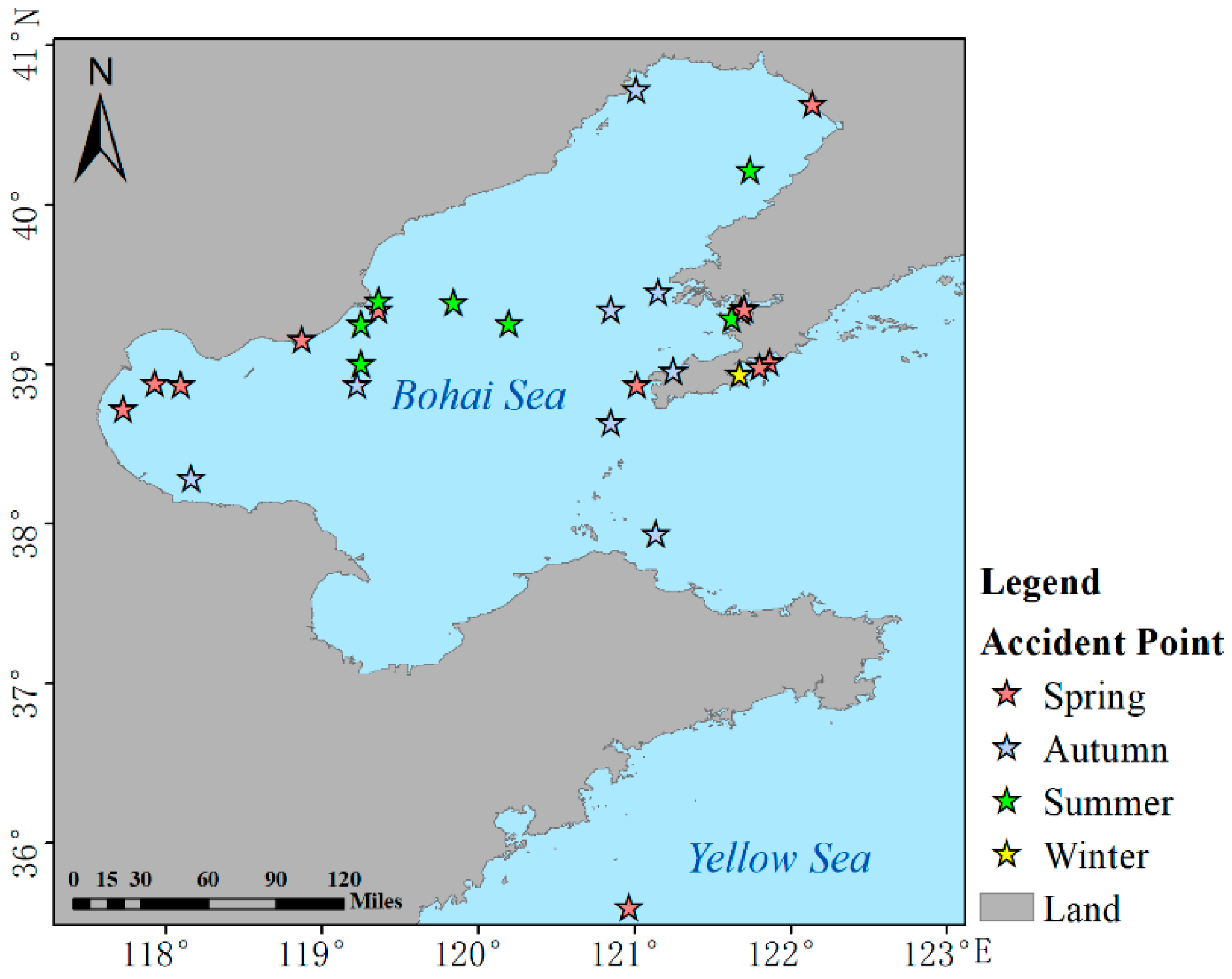
3.3.2. Navigation Risk Evaluation Validation Using the Accident Points
3.3.3. Sensitivity Analysis
4. Results
4.1. Sea Fog Identification
4.1.1. Identification Precision
4.1.2. Sea Fog Statistics
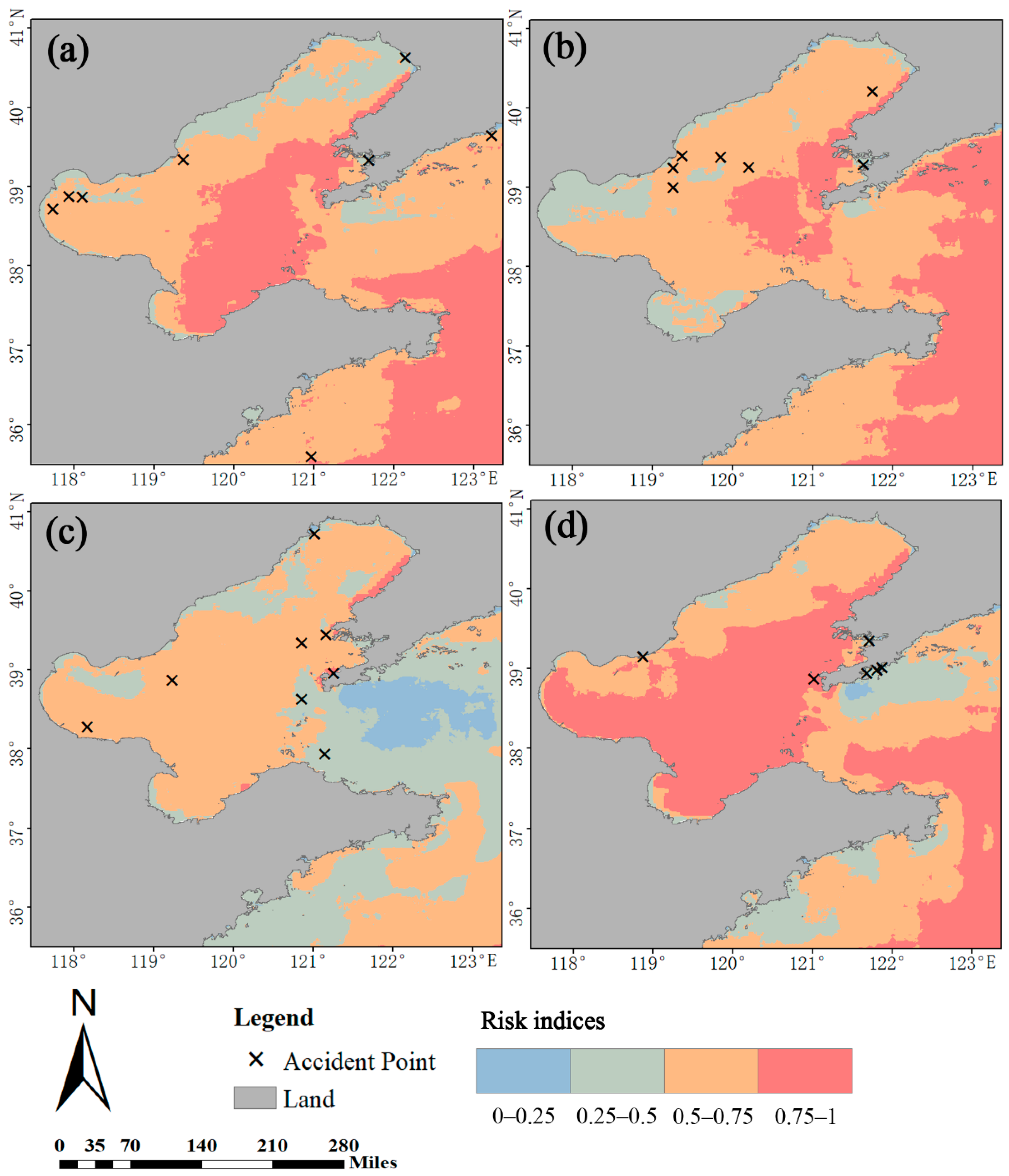
4.2. Navigation Risk Evaluation Validation
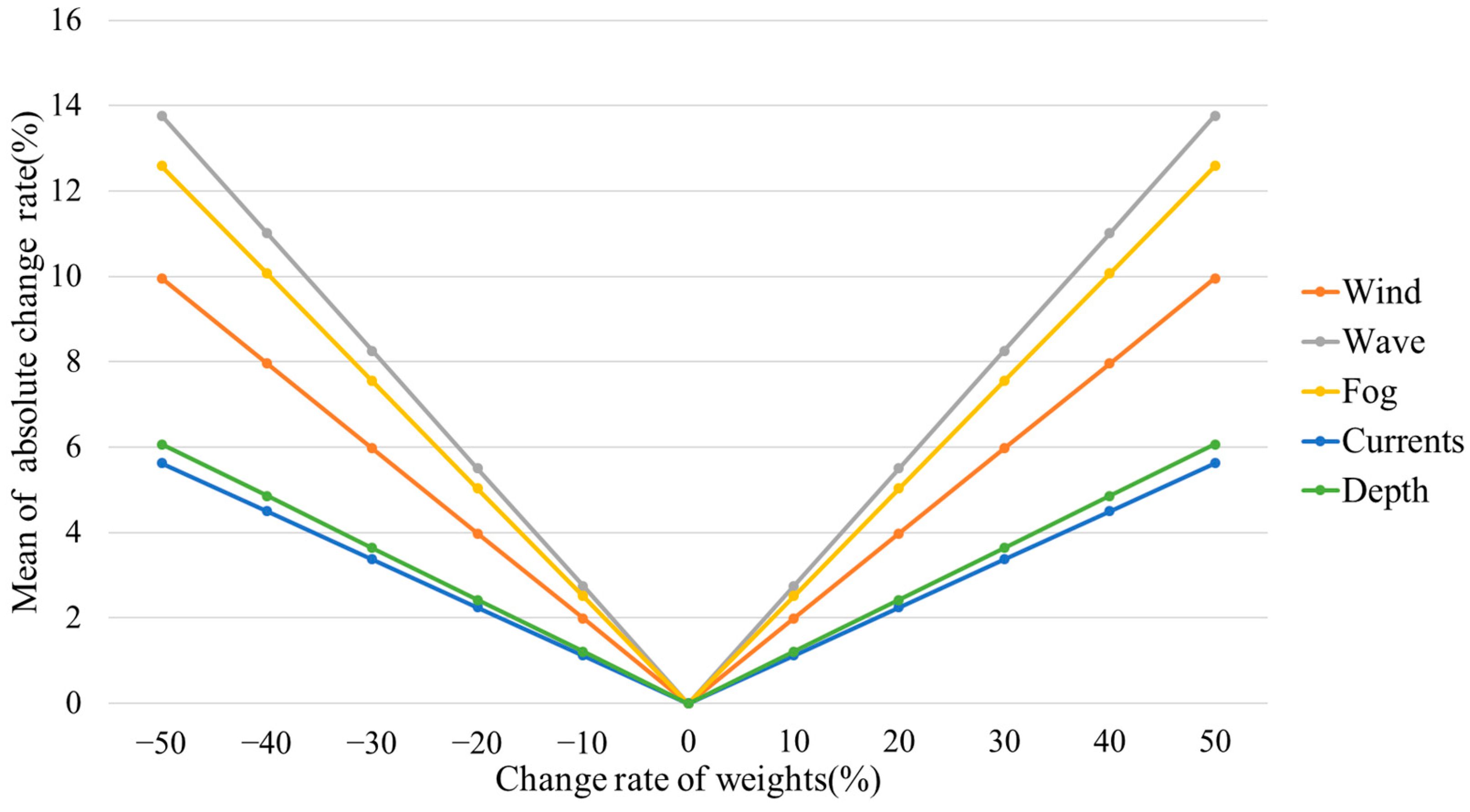
4.3. Sensitivity Analysis
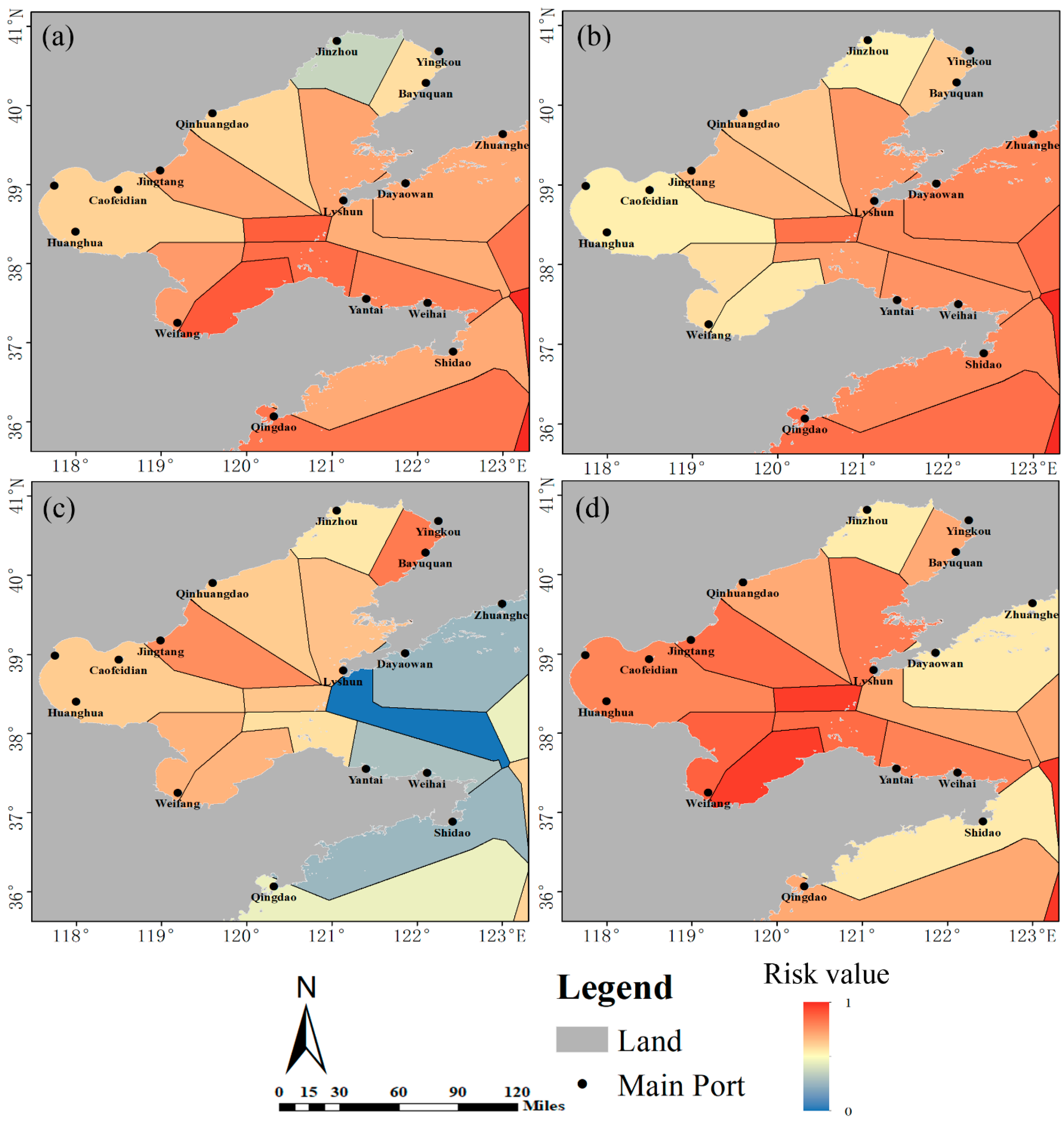
4.4. Navigation Risk Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xian, J.; Han, Y.; Huang, S.; Sun, D.; Zheng, J.; Han, F.; Zhou, A.; Yang, S.; Xu, W.; Song, Q.; et al. Novel Lidar algorithm for horizontal visibility measurement and sea fog monitoring. Opt. Express 2018, 26, 34853–34863. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Jiang, G. Research on Influencing Factors and Countermeasures of Fog Navigation in Weihai Harbour. In Proceedings of the 5th International Conference on Education, Management, Arts, Economics and Social Science, Sanya, China, 10–11 November 2018. [Google Scholar]
- Dorman, C.E.; Mejia, J.; Koračin, D.; McEvoy, D. World marine fog analysis based on 58-years of ship observations. Int. J. Clim. 2019, 40, 145–168. [Google Scholar] [CrossRef]
- Fu, G.; Guo, J.; Pendergrass, A.; Li, P. An analysis and modeling study of a sea fog event over the Yellow and Bohai Seas. J. Ocean Univ. China 2008, 7, 27–34. [Google Scholar] [CrossRef]
- Wu, D.; Lu, B.; Zhang, T.; Yan, F. A method of detecting sea fogs using CALIOP data and its application to improve MODIS-based sea fog detection. J. Quant. Spectrosc. Radiat. Transf. 2014, 153, 88–94. [Google Scholar] [CrossRef]
- Chunyang, Z.; Jianhua, W.; Shanwei, L.; Hui, S.; Yanfang, X. Sea fog detection using U-net deep learning model based on MODIS data. In Proceedings of the 2019 10th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 September 2019. [Google Scholar]
- Shin, D.; Kim, J.-H. A New Application of Unsupervised Learning to Nighttime Sea Fog Detection. Asia Pac. J. Atmos. Sci. 2018, 54, 527–544. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.-H.; Yoo, J.-M.; Choi, Y.-S. Advanced Dual-Satellite Method for Detection of Low Stratus and Fog near Japan at Dawn from FY-4A and Himawari-8. Remote Sens. 2021, 13, 1042. [Google Scholar] [CrossRef]
- Kim, D.; Park, M.-S.; Park, Y.-J.; Kim, W. Geostationary Ocean Color Imager (GOCI) Marine Fog Detection in Combination with Himawari-8 Based on the Decision Tree. Remote Sens. 2020, 12, 149. [Google Scholar] [CrossRef] [Green Version]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An Introduction to Himawari-8/9—Japan’s New-Generation Geostationary Meteorological Satellites. J. Meteorol. Soc. Jpn. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef] [Green Version]
- Ryu, H.; Hong, S. Sea Fog Detection Based on Normalized Difference Snow Index Using Advanced Himawari Imager Observations. Remote Sens. 2020, 12, 1521. [Google Scholar] [CrossRef]
- Sahin, B.; Kum, S. Risk Assessment of Arctic Navigation by using Improved Fuzzy-AHP Approach. Int. J. Marit. Eng. 2015, 157, 241–250. [Google Scholar]
- Hu, S.; Fang, Q.; Xia, H.; Xi, Y. Formal safety assessment based on relative risks model in ship navigation. Reliab. Eng. Syst. Saf. 2007, 92, 369–377. [Google Scholar] [CrossRef]
- Balmat, J.-F.; Lafont, F.; Maifret, R.; Pessel, N. A decision-making system to maritime risk assessment. Ocean Eng. 2011, 38, 171–176. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, D.; Zhang, M.; Lang, X.; Mao, W. An integrated risk assessment model for safe Arctic navigation. Transp. Res. Part A Policy Pract. 2020, 142, 101–114. [Google Scholar] [CrossRef]
- Zhang, D.; Yan, X.; Zhang, J.; Yang, Z.; Wang, J. Use of fuzzy rule-based evidential reasoning approach in the navigational risk assessment of inland waterway transportation systems. Saf. Sci. 2016, 82, 352–360. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Thai, V.V. Expert elicitation and Bayesian Network modeling for shipping accidents: A literature review. Saf. Sci. 2016, 87, 53–62. [Google Scholar] [CrossRef]
- Lim, G.J.; Cho, J.; Bora, S.; Biobaku, T.; Parsaei, H. Models and computational algorithms for maritime risk analysis: A review. Ann. Oper. Res. 2018, 271, 765–786. [Google Scholar] [CrossRef]
- Zhang, D.; Yan, X.P.; Yang, Z.L.; Wall, A.; Wang, J. Incorporation of formal safety assessment and Bayesian network in navigational risk estimation of the Yangtze River. Reliab. Eng. Syst. Saf. 2013, 118, 93–105. [Google Scholar] [CrossRef]
- Jiang, M.; Lu, J.; Yang, Z.; Li, J. Risk analysis of maritime accidents along the main route of the Maritime Silk Road: A Bayesian network approach. Marit. Policy Manag. 2020, 47, 815–832. [Google Scholar] [CrossRef]
- Wang, J.; Li, M.; Liu, Y.; Zhang, H.; Zou, W.; Cheng, L. Safety assessment of shipping routes in the South China Sea based on the fuzzy analytic hierarchy process. Saf. Sci. 2014, 62, 46–57. [Google Scholar] [CrossRef]
- Zhou, X.; Cheng, L.; Li, M. Assessing and mapping maritime transportation risk based on spatial fuzzy multi-criteria decision making: A case study in the South China sea. Ocean Eng. 2020, 208, 107403. [Google Scholar] [CrossRef]
- Zhang, S.; Jing, Z.; Li, W.; Wang, L.; Liu, D.; Wang, T. Navigation risk assessment method based on flow conditions: A case study of the river reach between the Three Gorges Dam and the Gezhouba Dam. Ocean Eng. 2019, 175, 71–79. [Google Scholar] [CrossRef]
- Yang, S.; Song, B.; Ye, S.; Xu, Q.; He, L.; Zhao, G.; Li, J.; Laws, E.A. Regional-Scale distributions of pollen and spore assemblages in alluvium around the Bohai Sea: An essential step toward understanding marine palynological sources in China. Mar. Geol. 2019, 415, 105968. [Google Scholar] [CrossRef]
- Lv, X.; Yuan, D.; Ma, X.; Tao, J. Wave characteristics analysis in Bohai Sea based on ECMWF wind field. Ocean Eng. 2014, 91, 159–171. [Google Scholar] [CrossRef]
- Tian, M.; Wu, B.; Huang, H.; Zhang, H.; Zhang, W.; Wang, Z. Impact of water vapor transfer on a Circum-Bohai-Sea heavy fog: Observation and numerical simulation. Atmos. Res. 2019, 229, 1–22. [Google Scholar] [CrossRef]
- Winker, D.M.; Vaughan, M.A.; Omar, A.; Hu, Y.; Powell, K.A.; Liu, Z.; Hunt, W.H.; Young, S. Overview of the CALIPSO Mission and CALIOP Data Processing Algorithms. J. Atmos. Ocean. Technol. 2009, 26, 2310–2323. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.; Hogan, P.J.; Wallcraft, A.J.; Baraille, R.; Bleck, R. The HYCOM (HYbrid Coordinate Ocean Model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Mayer, L.; Jakobsson, M.; Allen, G.; Dorschel, B.; Falconer, R.; Ferrini, V.; Lamarche, G.; Snaith, H.; Weatherall, P. The Nippon Foundation—GEBCO Seabed 2030 Project: The Quest to See the World’s Oceans Completely Mapped by 2030. Geosciences 2018, 8, 63. [Google Scholar] [CrossRef] [Green Version]
- Maritime Safety Administration of the People’s Republic of China. Sailing Direction On Chinese Coast: North Area; China Communications Press Limited Liability Company: Beijing, China, 2018; pp. 27–198. [Google Scholar]
- Nowak, D.; Ruffieux, D.; Agnew, J.L.; Vuilleumier, L. Detection of Fog and Low Cloud Boundaries with Ground-Based Remote Sensing Systems. J. Atmos. Ocean. Technol. 2008, 25, 1357–1368. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Y.-F.; Zhang, J.; Qin, P. An Algorithm for Daytime Sea Fog Detection over the Greenland Sea Based on MODIS and CALIOP Data. J. Coast. Res. 2019, 90, 95–103. [Google Scholar] [CrossRef]
- Hao, Z.; Pan, D.; Gong, F.; Chen, J. Sea fog characteristics based on MODIS data and streamer model. In Proceedings of the Remote Sensing of Clouds and the Atmosphere XIV, Berlin, Germany, 31 August–3 September 2009. [Google Scholar]
- Sharifzadeh, F.; Akbarizadeh, G.; Kavian, Y.S. Ship Classification in SAR Images Using a New Hybrid CNN–MLP Classifier. J. Indian Soc. Remote Sens. 2018, 47, 551–562. [Google Scholar] [CrossRef]
- Costache, R.; Pham, Q.B.; Corodescu-Roșca, E.; Cîmpianu, C.; Hong, H.; Linh, N.T.T.; Fai, C.M.; Ahmed, A.N.; Vojtek, M.; Pandhiani, S.M.; et al. Using GIS, Remote Sensing, and Machine Learning to Highlight the Correlation between the Land-Use/Land-Cover Changes and Flash-Flood Potential. Remote Sens. 2020, 12, 1422. [Google Scholar] [CrossRef]
- Zhang, C.; Pan, X.; Li, H.; Gardiner, A.; Sargent, I.; Hare, J.; Atkinson, P.M. A hybrid MLP-CNN classifier for very fine resolution remotely sensed image classification. ISPRS J. Photogramm. Remote Sens. 2017, 140, 133–144. [Google Scholar] [CrossRef] [Green Version]
- Formela, K.; Neumann, T.; Weintrit, A. Overview of Definitions of Maritime Safety, Safety at Sea, Navigational Safety and Safety in General. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2019, 13, 285–290. [Google Scholar] [CrossRef]
- Chen, C. Case study on wave-current interaction and its effects on ship navigation. J. Hydrodyn. 2018, 30, 411–419. [Google Scholar] [CrossRef]
- Heo, K.-Y.; Park, S.; Ha, K.-J.; Shim, J.-S. Algorithm for sea fog monitoring with the use of information technologies. J. Meteorol. Appl. 2014, 21, 350–359. [Google Scholar] [CrossRef]
- Pacuraru, F.; Domnisoru, L. Numerical investigation of shallow water effect on a barge ship resistance. IOP Conf. Ser. Mater. Sci. Eng. 2017, 227, 012088. [Google Scholar] [CrossRef] [Green Version]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Žižović, M.; Miljković, B.; Marinković, D. Objective methods for determining criteria weight coefficients: A modification of the CRITIC method. Decis. Mak. Appl. Manag. Eng. 2020, 3, 149–161. [Google Scholar] [CrossRef]
- Mukhametzyanov, I. Specific character of objective methods for determining weights of criteria in MCDM problems: Entropy, CRITIC and SD. Decis. Mak. Appl. Manag. Eng. 2021, 4, 76–105. [Google Scholar] [CrossRef]
- Bai, J. Estimating Multiple Breaks One at a Time. Econ. Theory 1997, 13, 315–352. [Google Scholar] [CrossRef] [Green Version]
- Xu, E.; Zhang, H. Spatially-Explicit sensitivity analysis for land suitability evaluation. Appl. Geogr. 2013, 45, 1–9. [Google Scholar] [CrossRef]
- Khan, B.; Khan, F.; Veitch, B. A Dynamic Bayesian Network model for ship-ice collision risk in the Arctic waters. Saf. Sci. 2020, 130, 104858. [Google Scholar] [CrossRef]




| Name | Source | Data Description | Time | Purpose |
|---|---|---|---|---|
| AHI data | Japan Aerospace Exploration Agency (https://www.eorc.jaxa.jp/ptree (accessed on 1 July 2021)) | Remote sensing images from the AHI sensor [10] | 2015–2020 | Sea fog identification and calculating the frequency of monthly sea fog |
| CALIPSO-VFM | National Aeronautics and Space Administration (https://search.earthdata.nasa.gov/search (accessed on 7 July 2021 )) | Classified data of clouds and aerosols from CALIPSO lidar level-2 product [27] | 2018 | Sea fog samples and verifying the accuracy |
| Wind | European Centre for Medium-Range Weather Forecasts (https://www.ecmwf.int/ (accessed on 15 June 2021)) | 10 m wind reanalysis data from ERA5 [28] | 2015–2020 | Calculating the frequency of strong wind |
| Sea wave | European Centre for Medium-Range Weather Forecasts (https://www.ecmwf.int/ (accessed on 15 June 2021)) | Significant Wave Height reanalysis data from ERA5 [28] | 2015–2020 | Calculating the frequency of big waves |
| Ocean currents | National oceanic and atmospheric administration (https://www.ncei.noaa.gov/ (accessed on 16 June 2021)) | Analyses currents data from HYCOM [29] | 2016–2020 | Calculating the frequency of big currents |
| Water depth | British Oceanographic Data Centre (https://www.bodc.ac.uk/ (accessed on 16 June 2021)) | Global terrain model from GEBCO [30] | 2019 | Obtaining water depth data |
| Accident data | Maritme Safety Admininstration of the people’s Republic of China (https://www.msa.gov.cn/ (accessed on 1 March 2021)) | Accident data collected and disclosed by the authorities | 2015–2020 | Weighting factors and validating the risk model |
| Shipping routes | Maritme Safety Admininstration of the people’s Republic of China (https://www.msa.gov.cn/ (accessed on 1 March 2021)) | Officially recommended shipping route [31] | 2019 | Subdivision shipping route |
| Fog | Wind | Wave | Currents | Water Depth | Rainfall | Total | |
|---|---|---|---|---|---|---|---|
| Number | 13 | 17 | 18 | 7 | 9 | 4 | 68 |
| Proportion | 19.2% | 25.0% | 26.5% | 10.3% | 13.2% | 5.8% | 100% |
| Ranking | 3 | 2 | 1 | 5 | 4 | 6 |
| Wind | Wave | Sea Fog | Currents | Water Depth | |
|---|---|---|---|---|---|
| Wind | 1 | 0.76 | −0.15 | 0.23 | 0.19 |
| Wave | 0.76 | 1 | −0.17 | 0.04 | 0.12 |
| Sea fog | −0.15 | −0.17 | 1 | −0.01 | −0.12 |
| Currents | 0.23 | 0.04 | −0.01 | 1 | −0.21 |
| Depth | 0.19 | 0.12 | −0.12 | −0.21 | 1 |
| Name | Wind | Wave | Sea Fog | Currents | Water Depth |
|---|---|---|---|---|---|
| 2.97 | 3.24 | 4.46 | 3.95 | 4.02 | |
| CRITIC weights | 0.14 | 0.17 | 0.36 | 0.17 | 0.14 |
| Final weights | 0.19 | 0.23 | 0.37 | 0.09 | 0.10 |
| Rank | 3 | 2 | 1 | 5 | 4 |
| Sea Fog | Non-Sea Fog | ||
|---|---|---|---|
| H | F | ||
| Sea fog | MLP | 88 | 17 |
| NDSI | 96 | 75 | |
| M | C | ||
| Non-sea-fog | MLP | 20 | 206 |
| NDSI | 12 | 148 | |
| Methods | POD | PMD | PFD | ETS |
|---|---|---|---|---|
| MLP | 81.48% | 7.62% | 18.51% | 59.22% |
| NDSI threshold | 88.89% | 33.63% | 11.11% | 31.61% |
| Spring | Summer | Autumn | Winter | Summary | |
|---|---|---|---|---|---|
| Success | 6 | 6 | 6 | 2 | 20 |
| All accident numbers | 8 | 7 | 8 | 6 | 29 |
| Matching rate | 75% | 85% | 75% | 33% | 69.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, P.; Zeng, Z.; Zhang, J.; Liu, L.; Yang, J.; Qu, C.; Jiang, L.; Liu, S. Fog Season Risk Assessment for Maritime Transportation Systems Exploiting Himawari-8 Data: A Case Study in Bohai Sea, China. Remote Sens. 2021, 13, 3530. https://doi.org/10.3390/rs13173530
Du P, Zeng Z, Zhang J, Liu L, Yang J, Qu C, Jiang L, Liu S. Fog Season Risk Assessment for Maritime Transportation Systems Exploiting Himawari-8 Data: A Case Study in Bohai Sea, China. Remote Sensing. 2021; 13(17):3530. https://doi.org/10.3390/rs13173530
Chicago/Turabian StyleDu, Pei, Zhe Zeng, Jingwei Zhang, Lu Liu, Jianchang Yang, Chuanping Qu, Li Jiang, and Shanwei Liu. 2021. "Fog Season Risk Assessment for Maritime Transportation Systems Exploiting Himawari-8 Data: A Case Study in Bohai Sea, China" Remote Sensing 13, no. 17: 3530. https://doi.org/10.3390/rs13173530
APA StyleDu, P., Zeng, Z., Zhang, J., Liu, L., Yang, J., Qu, C., Jiang, L., & Liu, S. (2021). Fog Season Risk Assessment for Maritime Transportation Systems Exploiting Himawari-8 Data: A Case Study in Bohai Sea, China. Remote Sensing, 13(17), 3530. https://doi.org/10.3390/rs13173530