CCT: Conditional Co-Training for Truly Unsupervised Remote Sensing Image Segmentation in Coastal Areas
Abstract
:1. Introduction
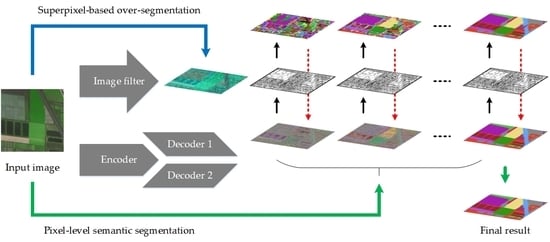
- We introduce a novel deep learning-driven approach for truly unsupervised remote sensing image segmentation in coastal areas. In this method, the advantages of both conventional and deep learning algorithms are seriously taken into consideration.
- We introduce a multi-model deep learning framework to drive our idea. To the best of our knowledge, this is the first time simultaneously applying ideas of superpixels and co-training in unsupervised image segmentation tasks.
- We adopt multiple conditional constraints, including pixel similarity, superpixel continuity, classification consistency, and decoder diversity, then specifically design a novel objective to facilitate training our framework.
- Considering the uncertainties in unsupervised learning, we perform comprehensive discussions on the settings and designs of our framework to explore the optimal determinations of the global image filter and deep learning model architectures.
2. Background
2.1. Superpixels
- The pixels with similar visual features should belong to the same superpixel.
- The contiguously distributed superpixels should be assigned as the same category.
- The scales of all superpixels should be larger than the size of the smallest object.
2.2. Co-Training
- Both classifiers can perform well and produce similar outputs on the same dataset.
- Both classifiers are simultaneously trained on strictly different images.
- Both classifiers are likely to satisfy Balcan’s condition of -expandability [42], which is a necessary and sufficient pre-condition for co-training to work.
3. Methodology
3.1. Formulation
3.2. Objective
3.2.1. Pixel Similarity
3.2.2. Superpixel Continuity
3.2.3. Category Consistency
3.2.4. Decoder Diversity
3.3. Implementation
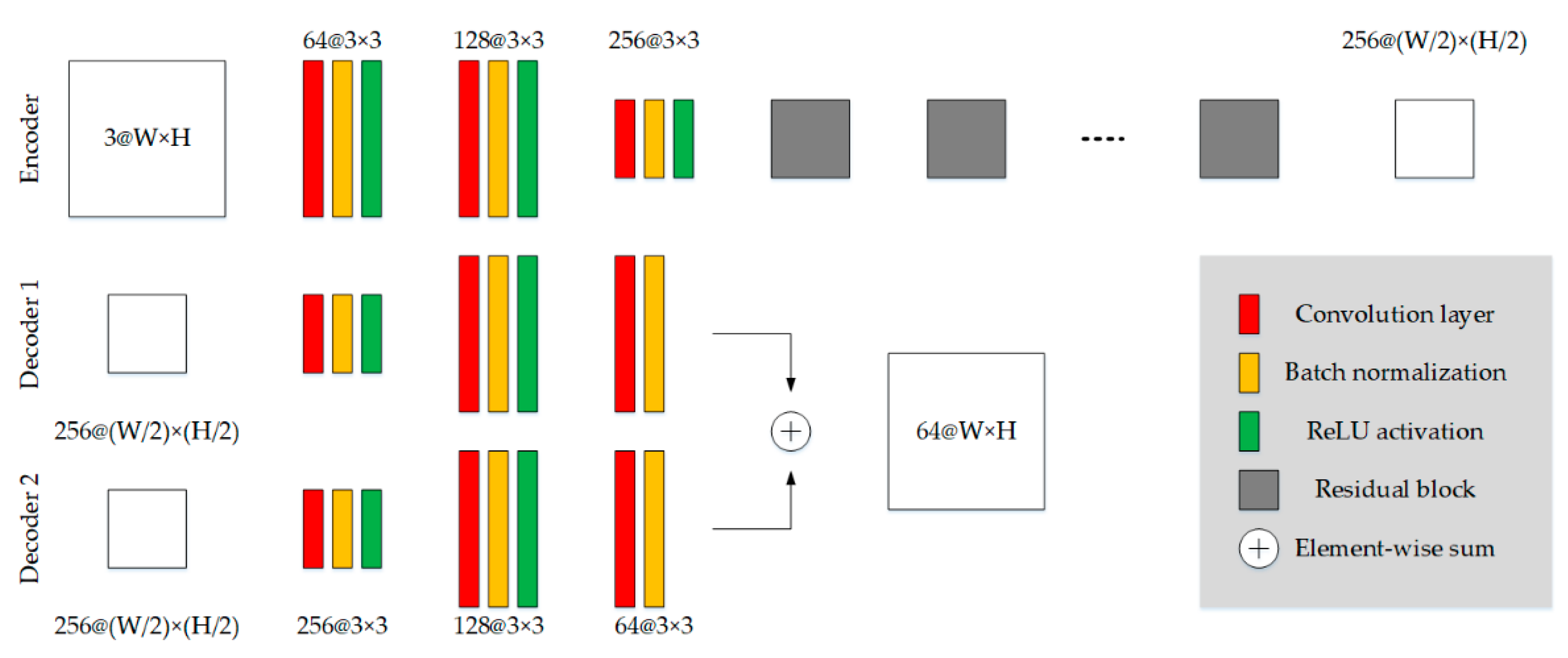
3.3.1. Network Architectures
3.3.2. Training Details
4. Experiments
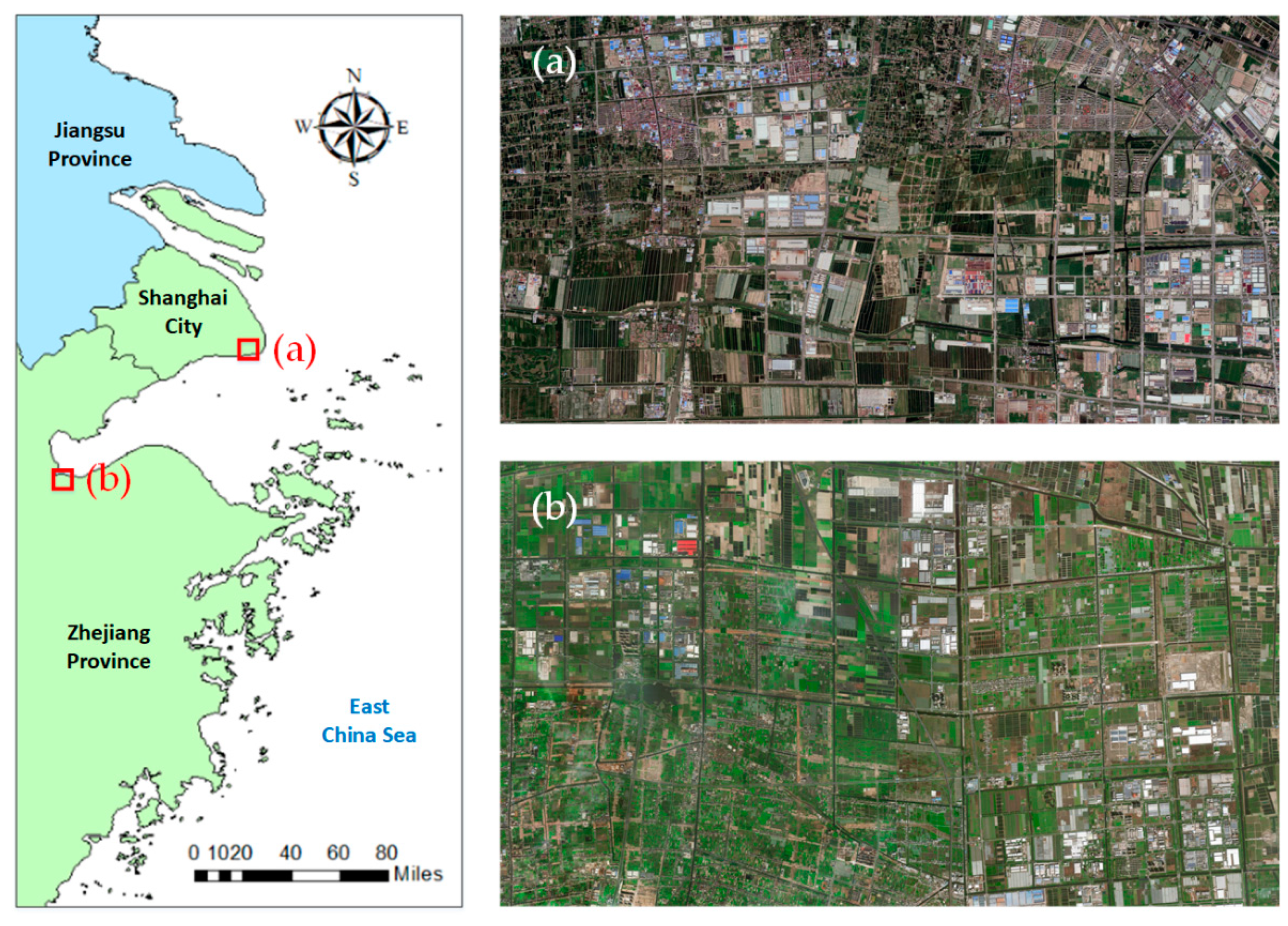
4.1. Datasets Description
4.2. Baseline Methods
4.3. Evaluation Metrics
4.4. Experimental Setup
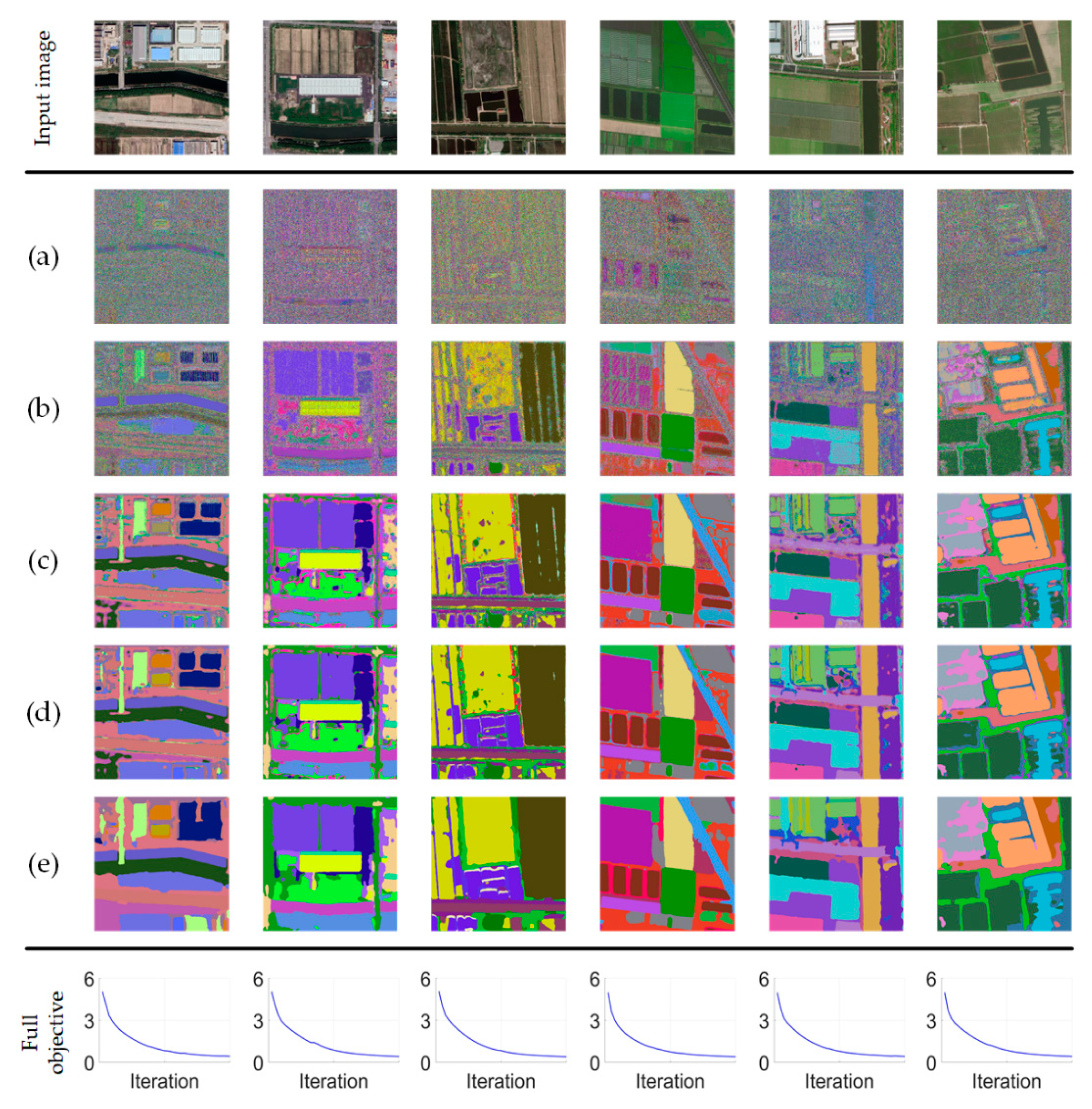
4.5. Training Visualization
4.6. Result Presentation
5. Discussion
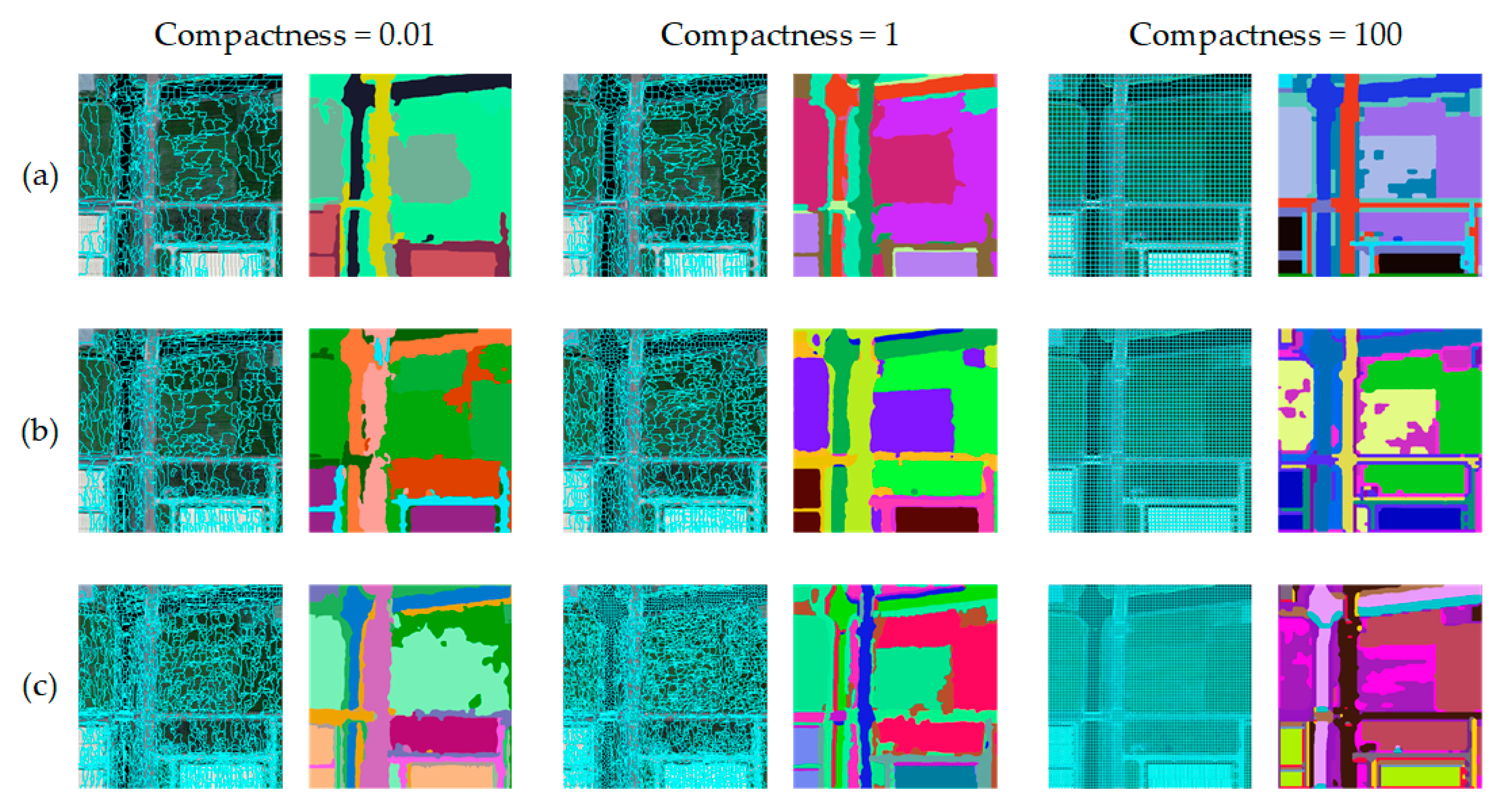
5.1. Setting of Image Filter
5.2. Design of Model Architecture
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kotaridis, I.; Lazaridou, M. Remote Sensing Image Segmentation Advances: A Meta-Analysis. ISPRS J. Photogramm. Remote Sens. 2021, 173, 309–322. [Google Scholar] [CrossRef]
- Yuan, X.; Shi, J.; Gu, L. A Review of Deep Learning Methods for Semantic Segmentation of Remote Sensing Imagery. Expert Syst. Appl. 2021, 169, 114417. [Google Scholar] [CrossRef]
- Liu, R.; Song, J.; Miao, Q.; Xu, P.; Xue, Q. Road Centerlines Extraction from High Resolution Images Based on An Improved Directional Segmentation and Road Probability. Neurocomputing 2016, 212, 88–95. [Google Scholar] [CrossRef]
- Xia, L.; Zhang, J.; Zhang, X.; Yang, H.; Xu, M. Precise Extraction of Buildings from High-Resolution Remote-Sensing Images Based on Semantic Edges and Segmentation. Remote Sens. 2021, 13, 3083. [Google Scholar] [CrossRef]
- Mongus, D.; Zalik, B. Segmentation Schema for Enhancing Land Cover Identification: A Case Study Using Sentinel 2 Data. Int. J. Appl. Earth Observ. Geoinf. 2018, 66, 56–68. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, P.; Feng, X.; Yuan, M. Separate Segmentation of Multi-Temporal High-Resolution Remote Sensing Images for Object-Based Change Detection in Urban Area. Remote Sens. Environ. 2017, 201, 243–255. [Google Scholar] [CrossRef]
- Dey, V.; Zhang, Y.; Zhong, M. A Review on Image Segmentation Techniques with Remote Sensing Perspective. In Proceedings of the ISPRS TC VII Symposium—100 Years ISPRS, Vienna, Austria, 5–7 July 2010; pp. 31–42. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. In Proceedings of the IEEE, Pasadena, CA, USA, 27–29 May 1998; pp. 2278–2324. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Network for Semantic Segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the International Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Cheng, G.; Han, J.; Lu, X. Remote Sensing Image Scene Classification: Benchmark and State of the Art. In Proceedings of the IEEE; IEEE: Piscataway, NJ, USA, 2017; Volume 105, pp. 1865–1883. [Google Scholar]
- Haut, J.M.; Fernandez-Beltran, R.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Pla, F. A New Deep Generative Network for Unsupervised Remote Sensing Single-Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6792–6810. [Google Scholar] [CrossRef]
- Witharana, C.; Bhuiyan, M.A.E.; Liljedahl, A.K.; Kanevskiy, M.; Epstein, H.E.; Jones, B.M.; Daanen, R.; Griffin, C.G.; Kent, K.; Jones, M.K.W. Understanding the Synergies of Deep Learning and Data Fusion of Multispectral and Panchromatic High Resolution Commercial Satellite Imagery for Automated Ice-Wedge Polygon Detection. ISPRS J. Photogramm. Remote Sens. 2020, 170, 174–191. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, X.; Luo, P. Transferability of Convolutional Neural Network for Identifying Damaged Buildings Due to Earthquake. Remote Sens. 2021, 13, 504. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y.; Zhang, Q.; Xiang, S.; Pan, C. Gated Convolutional Neural Network for Semantic Segmentation in High-Resolution Images. Remote Sens. 2017, 9, 446. [Google Scholar] [CrossRef] [Green Version]
- Fu, G.; Liu, C.; Zhou, R.; Sun, T.; Zhang, Q. Classification for High Resolution Remote Sensing Imagery Using a Fully Convolutional Network. Remote Sens. 2017, 9, 498. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Nguyen, D.M.; Deligiannis, N.; Ding, W.; Munteanu, A. Hourglass-ShapeNetwork Based Semantic Segmentation for High Resolution Aerial Imagery. Remote Sens. 2017, 9, 522. [Google Scholar] [CrossRef] [Green Version]
- Diakogiannis, F.I.; Waldner, F.; Caccetta, P.; Wu, C. ResUNet-a: A Deep Learning Framework for Semantic Segmentation of Remotely Sensed Data. ISPRS J. Photogramm. Remote Sens. 2020, 162, 94–114. [Google Scholar]
- Yang, X.; Li, S.; Chen, Z.; Chanussot, J.; Jia, X.; Zhang, B.; Li, B.; Chen, P. An Attention-Fused Network for Semantic Segmentation of Very-High-Resolution Remote Sensing Imagery. ISPRS J. Photogramm. Remote Sens. 2021, 177, 238–262. [Google Scholar] [CrossRef]
- Zhang, Z.; Pasolli, E.; Crawford, M.M.; Tilton, J.C. An Active Learning Framework for Hyperspectral Image Classification Using Hierarchical Segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 640–654. [Google Scholar] [CrossRef]
- Hua, Y.; Marcos, D.; Mou, L.; Zhu, X.X.; Tuia, D. Semantic Segmentation of Remote Sensing Images With Sparse Annotations. IEEE Geosci. Remote Sens. Lett. 2021. early access. [Google Scholar] [CrossRef]
- Niu, B. Semantic Segmentation of Remote Sensing Image Based on Convolutional Neural Network and Mask Generation. Math. Probl. Eng. 2021, 2021, 1–13. [Google Scholar]
- Wang, J.; Ding, C.H.Q.; Chen, S.; He, C.; Luo, B. Semi-Supervised Remote Sensing Image Semantic Segmentation via Consistency Regularization and Average Update of Pseudo-Label. Remote Sens. 2020, 12, 3603. [Google Scholar] [CrossRef]
- Protopapadakis, E.; Doulamis, A.; Doulamis, N.; Maltezos, E. Stacked Autoencoders Driven by Semi-Supervised Learning for Building Extraction from Near Infrared Remote Sensing Imagery. Remote Sens. 2021, 13, 371. [Google Scholar] [CrossRef]
- Zhang, Y.; David, P.; Gong, B. Curriculum Domain Adaptation for Semantic Segmentation of Urban Scenes. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2039–2049. [Google Scholar]
- Zou, Y.; Yu, Z.; Kumar, B.V.K.V.; Wang, J. Unsupervised Domain Adaptation for Semantic Segmentation via Class-Balanced Self-Training. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 297–313. [Google Scholar]
- Li, Y.; Yuan, L.; Vasconcelos, N. Bidirectional Learning for Domain Adaptation of Semantic Segmentation. In Proceedings of the 2019 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 6929–6938. [Google Scholar]
- Luo, Y.; Zheng, L.; Guan, T.; Yu, J.; Yang, Y. Taking a Closer Look at Domain Shift: Category-Level Adversaries for Semantic Consistent Domain Adaptation. In Proceedings of the 2019 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 2502–2511. [Google Scholar]
- Fang, B.; Kou, R.; Pan, L.; Chen, P. Category-Sensitive Domain Adaptation for Land Cover Mapping in Aerial Scenes. Remote Sens. 2019, 11, 2631. [Google Scholar] [CrossRef] [Green Version]
- Muttitanon, W.; Tripathi, N.K. Land Use/Land Cover Changes in the Coastal Zone of Ban Don Bay, Thailand Using Landsat 5 TM Data. Int. J. Remote Sens. 2005, 26, 2311–2323. [Google Scholar] [CrossRef]
- Ghosh, M.K.; Kumar, L.; Roy, C. Monitoring the Coastline Change of Hatiya Island in Bangladesh Using Remote Sensing Techniques. ISPRS J. Photogramm. Remote Sens. 2015, 101, 137–144. [Google Scholar] [CrossRef]
- Chen, J.; Chen, G.; Wang, L.; Fang, B.; Zhou, P.; Zhu, M. Coastal Land Cover Classification of High-Resolution Remote Sensing Images Using Attention-Driven Context Encoding Network. Sensors 2020, 20, 7032. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zhai, G.; Chen, G.; Fang, B.; Zhou, P.; Yu, N. Unsupervised Domain Adaptation for High-Resolution Coastal Land Cover Mapping with Category-Space Constrained Adversarial Network. Remote Sens. 2021, 13, 1493. [Google Scholar] [CrossRef]
- Wang, X.; Xiao, X.; Zou, Z.; Chen, B.; Ma, J.; Dong, J.; Doughty, R.B.; Zhong, Q.; Qin, Y.; Dai, S.; et al. Tracking Annual Changes of Coastal Tidal Flats in China During 1986-2016 Through Analyses of Landsat Images with Google Earth Engine. Remote Sens. Environ. 2020, 238, 110987. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, L.; Du, B. Deep Learning for Remote Sensing Data: A Technical Tutorial on the State of the Art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Ren, X.; Malik, J. Learning a Classification Model for Segmentation. In Proceedings of the 2003 IEEE International Conference on Computer Vision (ICCV), Nice, France, 13–16 October 2003; pp. 10–17. [Google Scholar]
- Vedaldi, A.; Soatto, S. Quick Shift and Kernel Methods for Mode Seeking. In Proceedings of the European Conference on Computer Vision (ECCV), Marseille, France, 12–18 October 2008; pp. 705–718. [Google Scholar]
- Levinshtein, A.; Stere, A.; Kutulakos, K.N.; Fleet, D.J.; Dickinson, S.J.; Siddiqi, K. TurboPixels: Fast Superpixels Using Geometric Flows. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 2290–2297. [Google Scholar] [CrossRef] [Green Version]
- Veksler, O.; Boykov, Y.; Mehrani, P. Superpixels and Supervoxels in an Energy Optimization Framework. In Proceedings of the European Conference on Computer Vision (ECCV), Heraklion, Crete, Greece, 5–11 September 2010; pp. 211–224. [Google Scholar]
- Balcan, M.-F.; Blum, A.; Yang, K. Co-Training and Expansion: Towards Bridging Theory and Practice. In Proceedings of the International Conference on Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 13–18 December 2004; pp. 89–96. [Google Scholar]
- Nigam, K.; Ghani, R. Analyzing the Effectiveness and Applicability of Co-Training. In Proceedings of the International Conference on Information and Knowledge Management (CIKM), McLean, VA, USA, 6–11 November 2000; pp. 86–93. [Google Scholar]
- Saito, K.; Ushiku, Y.; Harada, T.; Saenko, K. Adversarial Dropout Regularization. arXiv 2017, arXiv:1711.01575. [Google Scholar]
- Saito, K.; Watanabe, Y.; Ushiku, Y.; Harada, T. Maximum Classifier Discrepancy for Unsupervised Domain Adaptation. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 3723–3732. [Google Scholar]
- Zhang, J.; Liang, C.; Kuo, C.-C.J. A Fully Convolutional Tri-Branch Network (FCTN) for Domain Adaptation. arXiv 2017, arXiv:1711.03694. [Google Scholar]
- Blum, A.; Mitchell, T. Combining Labeled and Unlabeled Data with Co-Training. In Proceedings of the Annual Conference on Computational Learning Theory (COLT), Madison, WI, USA, 24–26 July 1998; pp. 92–100. [Google Scholar]
- Chen, M.; Weinberger, K.Q.; Blitzer, J. Co-Training for Domain Adaptation. In Proceedings of the International Conference on Neural Information Processing Systems (NIPS), Granada, Spain, 12–15 December 2011; pp. 2456–2464. [Google Scholar]
- Saito, K.; Ushiku, Y.; Harada, T. Asymmetric Tri-Training for Unsupervised Domain Adaptation. In Proceedings of the International Conference on Machine Learning (ICML), Sydney, NSW, Australia, 6–11 August 2017; pp. 2988–2997. [Google Scholar]
- Kanezaki, A. Unsupervised Image Segmentation by Backpropagation. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 1543–1547. [Google Scholar]
- Kim, W.; Kanezaki, A.; Tanaka, M. Unsupervised Learning of Image Segmentation Based on Differentiable Feature Clustering. IEEE Trans. Image Process. 2020, 29, 8055–8068. [Google Scholar] [CrossRef]
- Zhou, Z.-H.; Li, M. Tri-Training: Exploiting Unlabeled Data Using Three Classifiers. IEEE Trans. Knowl. Data Eng. 2005, 17, 1529–1541. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. In Proceedings of the International Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the Difficulty of Training Deep Feedforward Neural Networks. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Chia Laguna, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Susstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maire, M.; Arbelaez, P.; Fowlkes, C.; Malik, J. Using Contours to Detect and Localize Junctions in Natural Images. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. From Contours to Regions: An Empirical Evaluation. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; pp. 2294–2301. [Google Scholar]
- Lin, D.; Dai, J.; Jia, J.; He, K.; Sun, J. ScribbleSup: Scribble-Supervised Convolutional Networks for Semantic Segmentation. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 3159–3167. [Google Scholar]
- Qian, N. On the Momentum Term in Gradient Decent Learning Algorithms. Neural Netw. 1999, 12, 145–151. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in PyTorch. In Proceedings of the International Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]






| Input: | Remote sensing image: |
fordo forward: backward 1: update with backward 2: update with backward 3: update with end for | |
| Outputs: | Well-trained encoder: Well-trained decoders: and Image segmentation result: |
| Method | OA (%) | mF1 (%) | mIoU (%) | Rate (s/image) |
|---|---|---|---|---|
| gPb | 40.47 | 29.32 | 21.43 | 23.60 |
| UCM | 41.75 | 31.03 | 22.92 | 89.25 |
| BackProp | 48.94 | 39.79 | 31.15 | 0.41 |
| DFC | 50.24 | 41.46 | 32.07 | 0.55 |
| CCT | 54.87 | 47.02 | 36.96 | 0.76 |
| Method | OA (%) | mF1 (%) | mIoU (%) | Rate (s/image) |
|---|---|---|---|---|
| gPb | 41.27 | 30.68 | 22.35 | 23.60 |
| UCM | 43.22 | 33.51 | 24.67 | 89.25 |
| BackProp | 53.30 | 45.83 | 35.39 | 0.41 |
| DFC | 55.61 | 49.17 | 37.82 | 0.55 |
| CCT | 58.49 | 52.24 | 41.10 | 0.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, B.; Chen, G.; Chen, J.; Ouyang, G.; Kou, R.; Wang, L. CCT: Conditional Co-Training for Truly Unsupervised Remote Sensing Image Segmentation in Coastal Areas. Remote Sens. 2021, 13, 3521. https://doi.org/10.3390/rs13173521
Fang B, Chen G, Chen J, Ouyang G, Kou R, Wang L. CCT: Conditional Co-Training for Truly Unsupervised Remote Sensing Image Segmentation in Coastal Areas. Remote Sensing. 2021; 13(17):3521. https://doi.org/10.3390/rs13173521
Chicago/Turabian StyleFang, Bo, Gang Chen, Jifa Chen, Guichong Ouyang, Rong Kou, and Lizhe Wang. 2021. "CCT: Conditional Co-Training for Truly Unsupervised Remote Sensing Image Segmentation in Coastal Areas" Remote Sensing 13, no. 17: 3521. https://doi.org/10.3390/rs13173521
APA StyleFang, B., Chen, G., Chen, J., Ouyang, G., Kou, R., & Wang, L. (2021). CCT: Conditional Co-Training for Truly Unsupervised Remote Sensing Image Segmentation in Coastal Areas. Remote Sensing, 13(17), 3521. https://doi.org/10.3390/rs13173521