A New 1′ × 1′ Global Seafloor Topography Model Predicted from Satellite Altimetric Vertical Gravity Gradient Anomaly and Ship Soundings BAT_VGG2021
Abstract
:1. Introduction
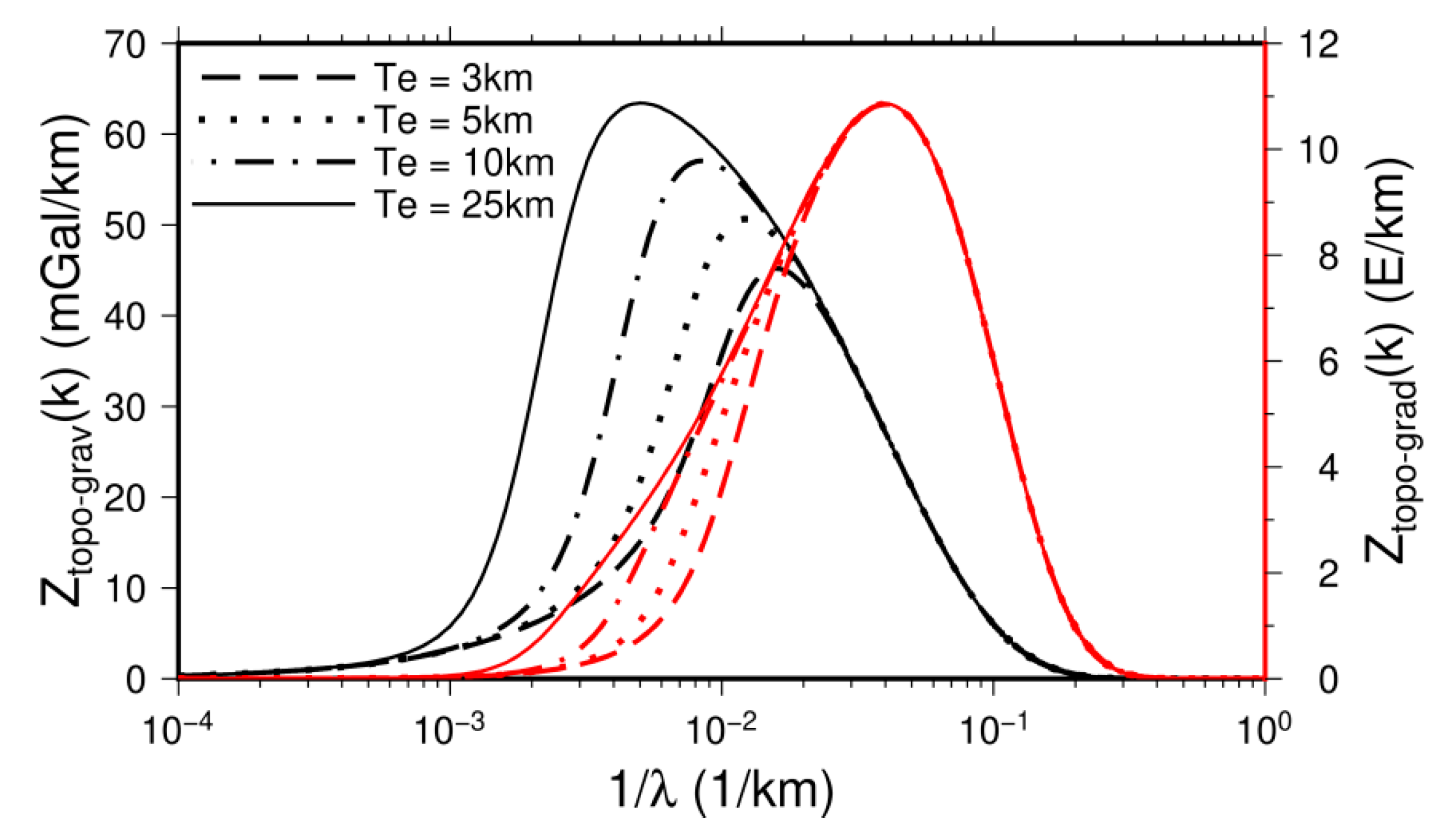
2. Theory and Methods
3. Data and Results
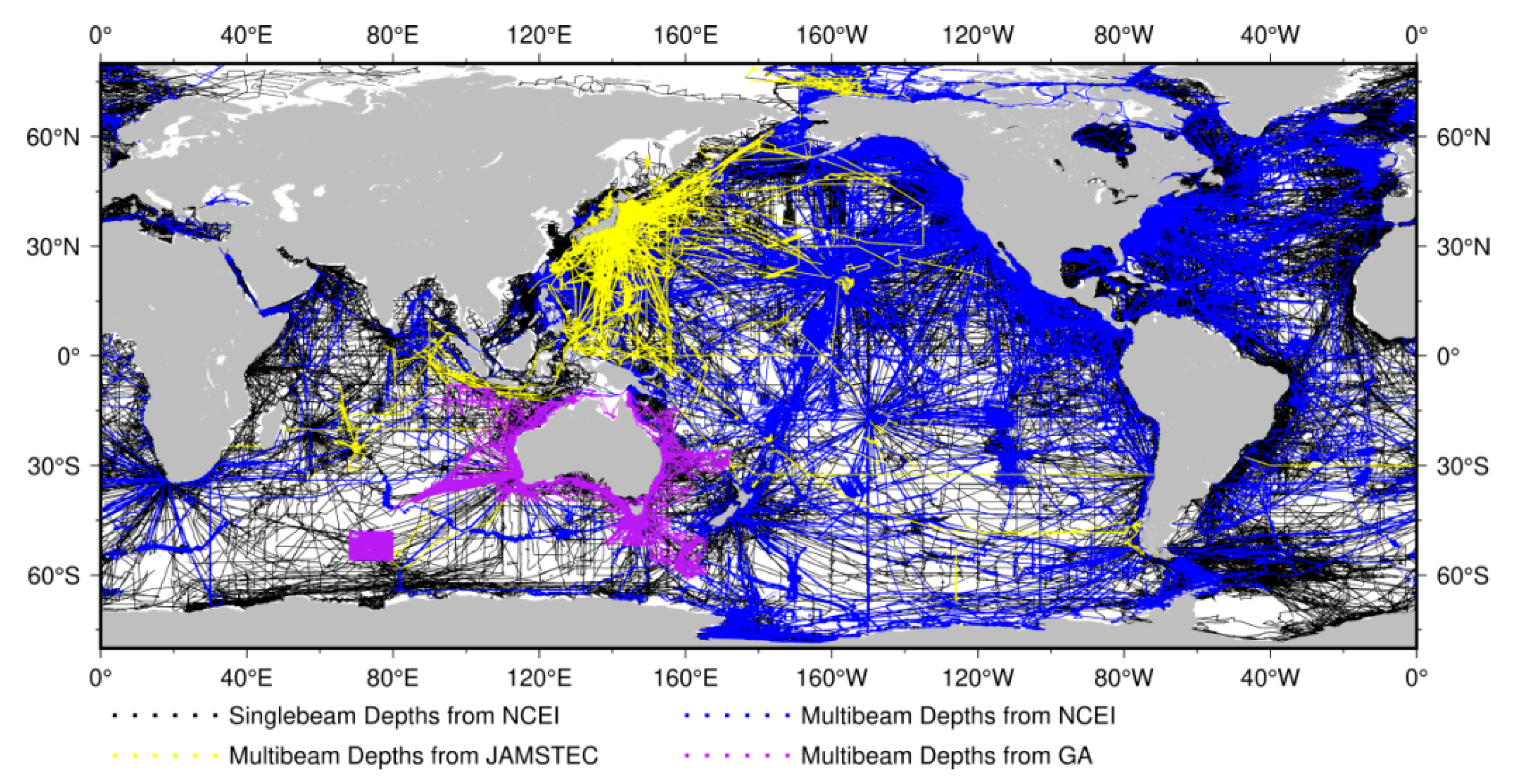
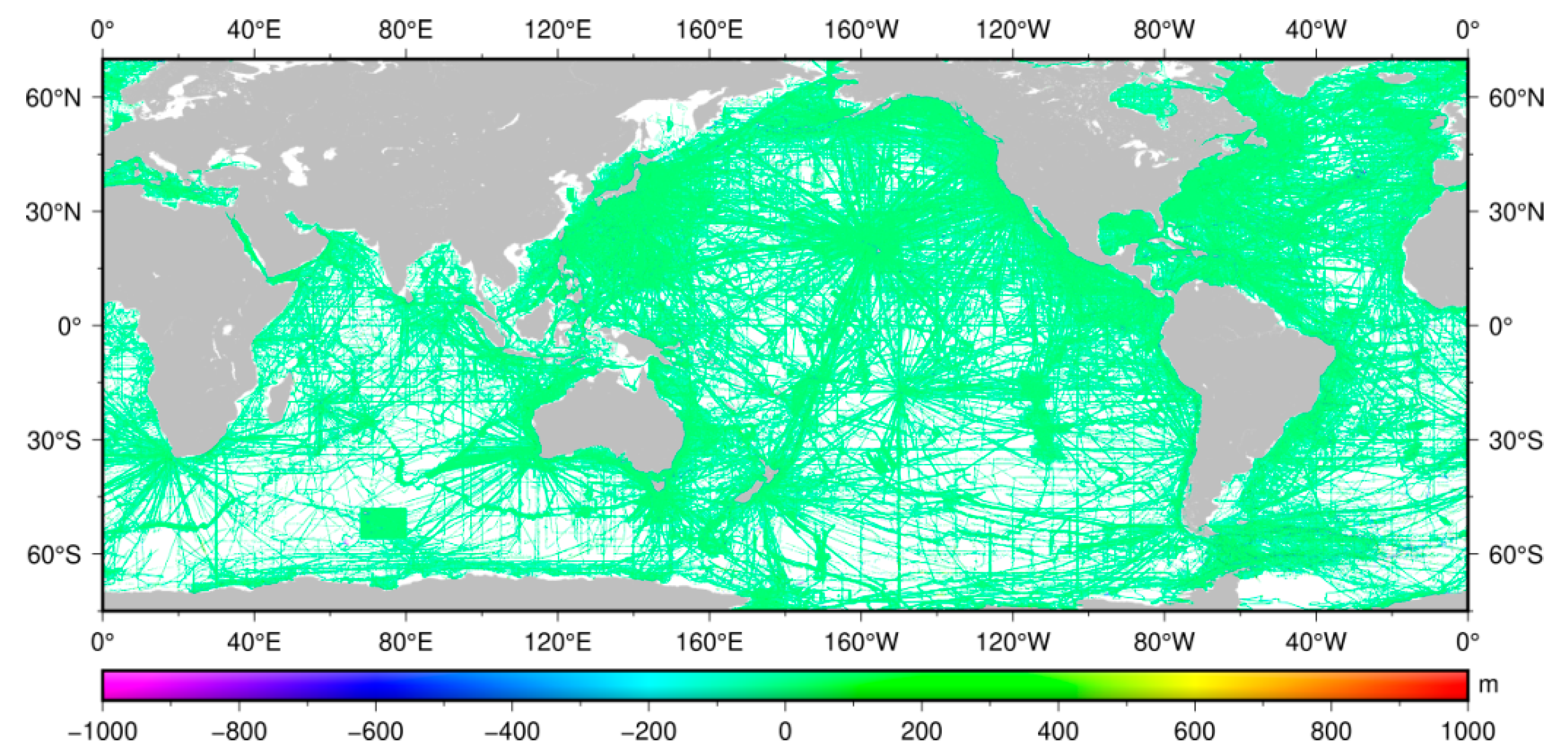
3.1. Data Sources
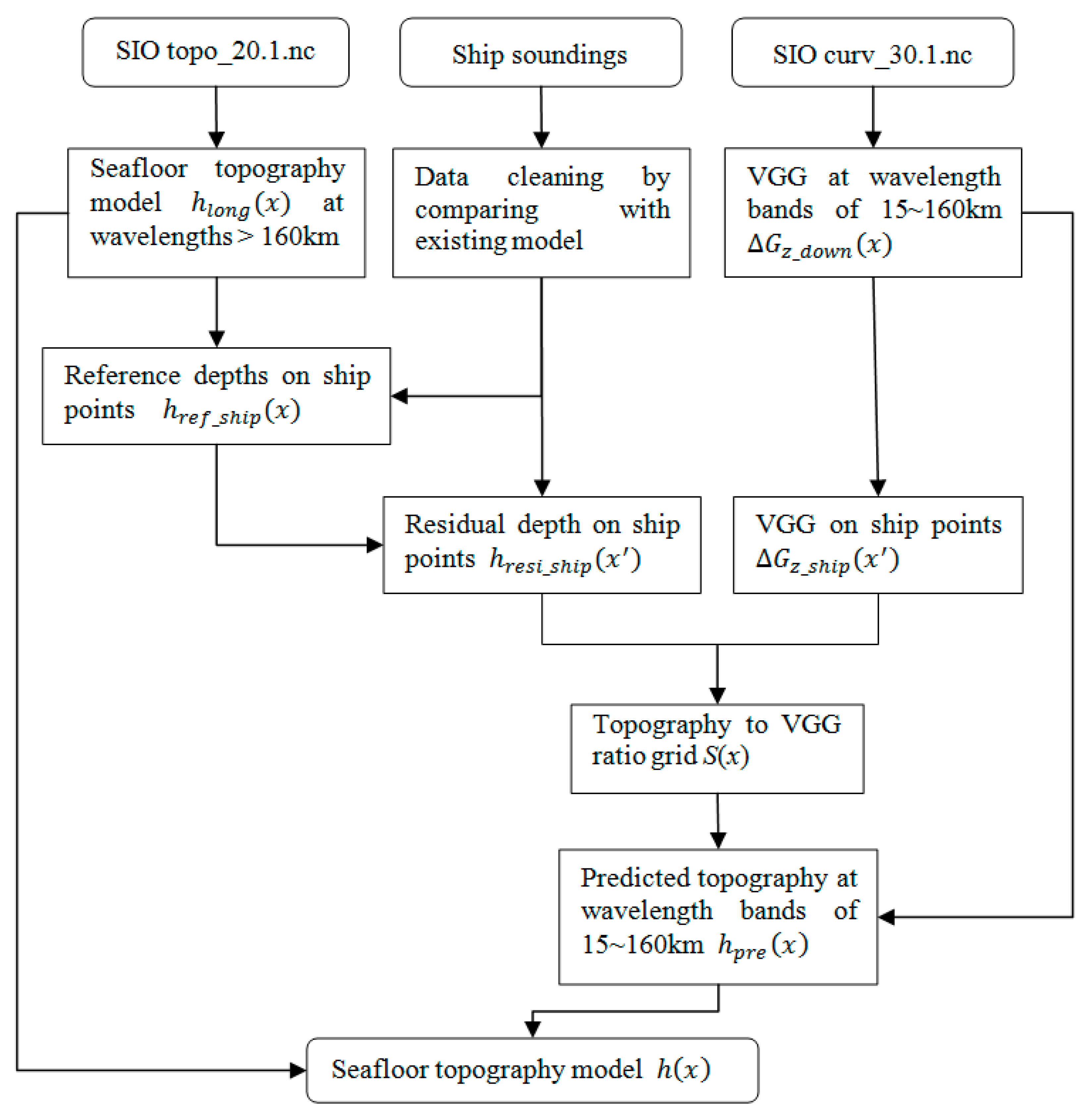
3.2. Data Processing Procedure
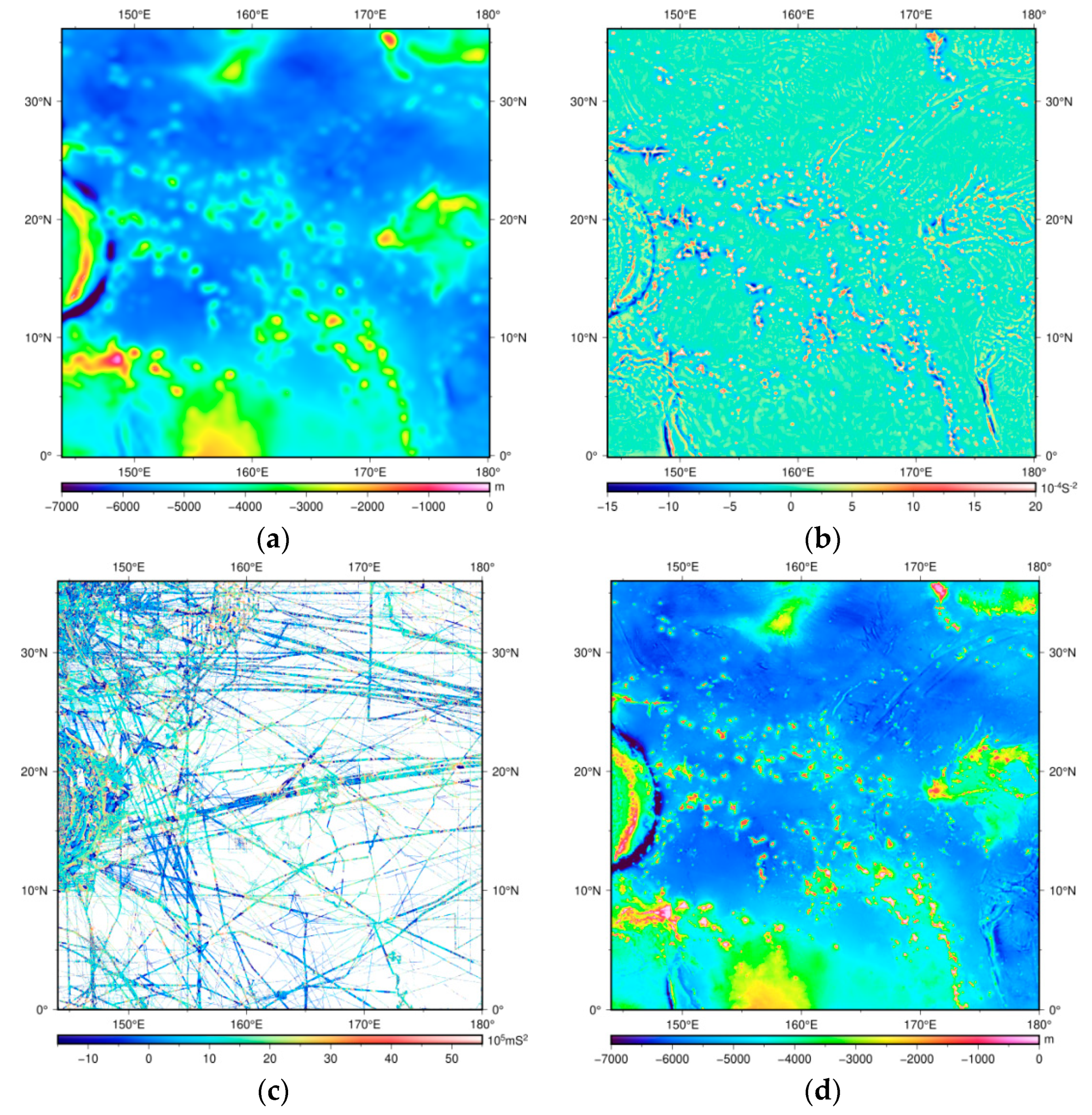
- The SIO topo_20.1.nc model was filtered to construct a reference model at wavelengths longer than 160 km, . Then, the reference depths at the ship points, , were interpolated from .
- At ship points, the residual depths, , can be calculated by subtracting from the observed depths, .
- The SIO curv_30.1.nc model was band-pass filtered, downward continued, and divided by k to construct VGG at 15~160 km wavelength bands, , and then was used to interpolate VGG at the ship points, .
- The topography-to-VGG ratios at the ship points were calculated byThe ratios were then gridded to a 1′ 1′ grid, S(x).
- The gridded ratios, S(x), and band-pass filtered VGG, , were used to constrain seafloor topography at 15~160 km wavelength bands,
- The final seafloor topography model becomes
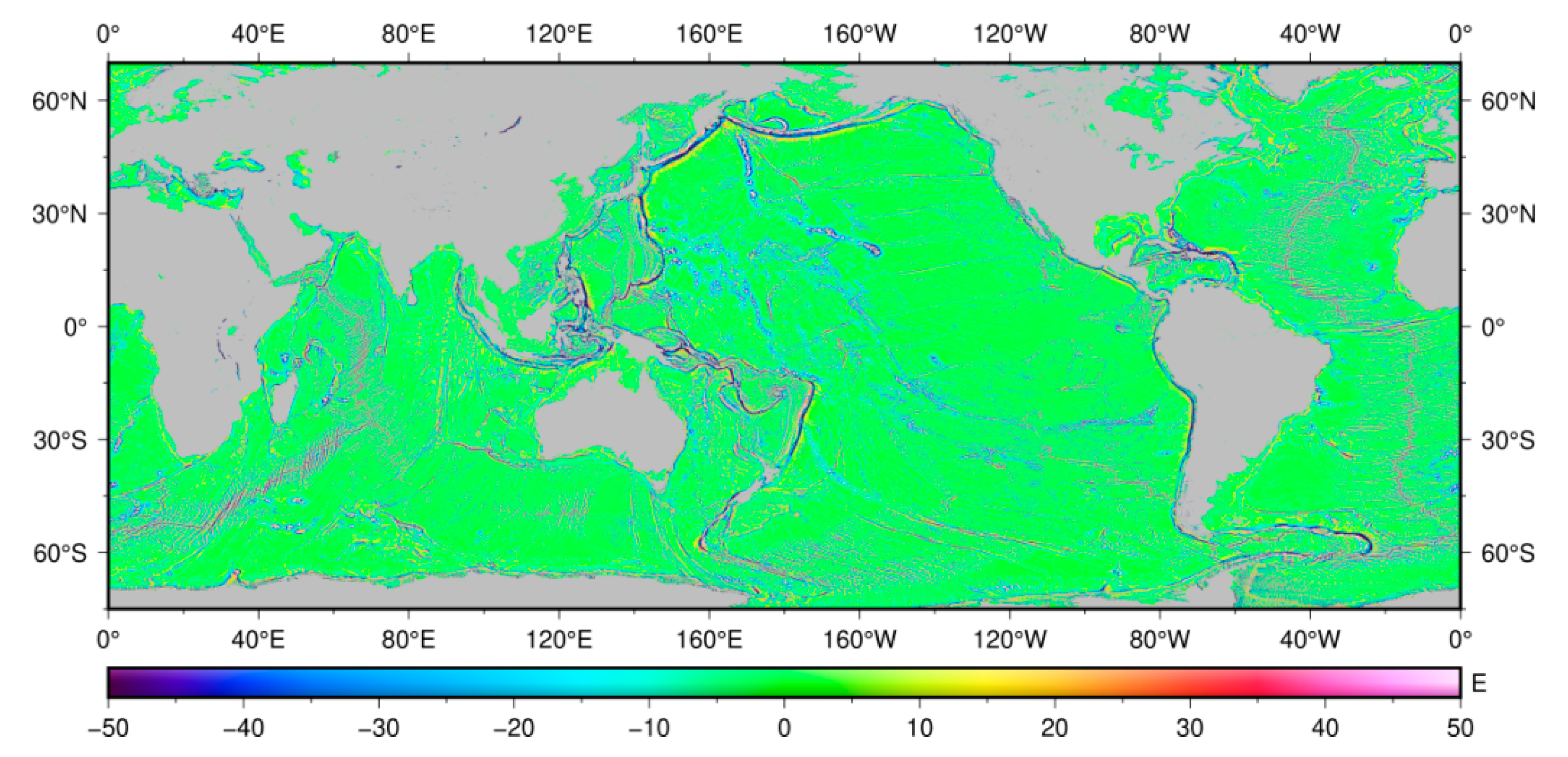
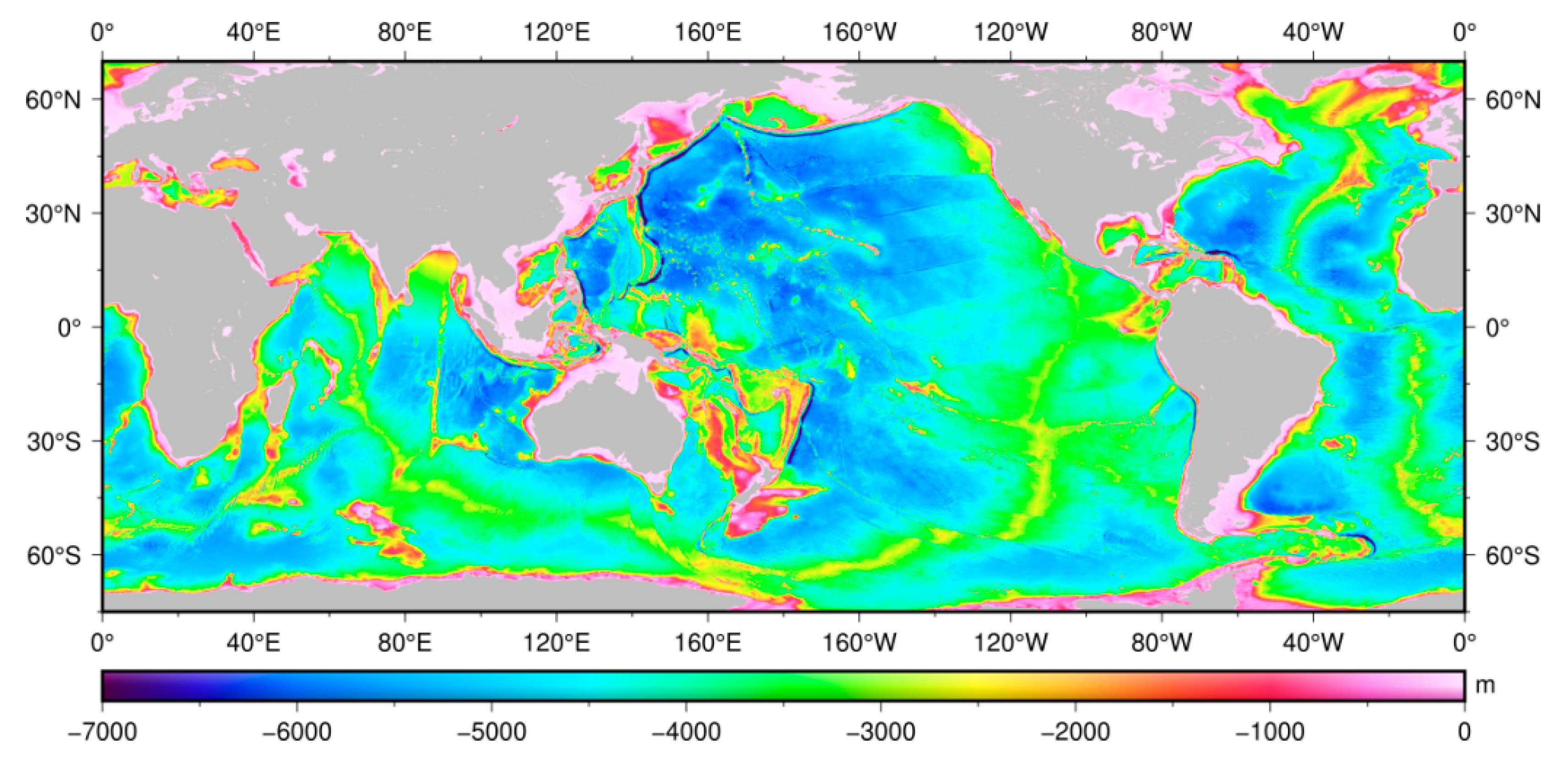
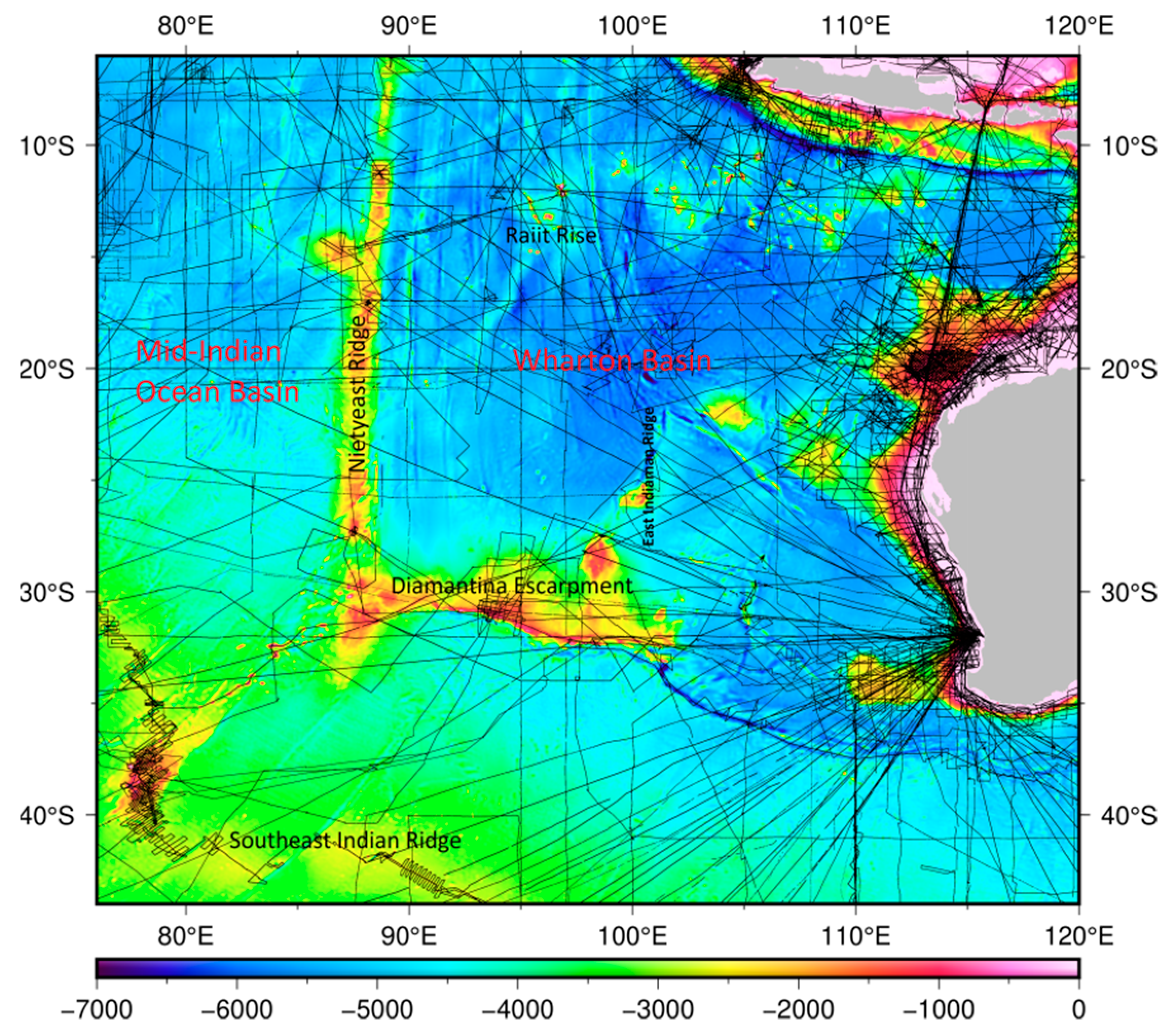
3.3. The New 1′ 1′ Global Seafloor Topography Model
4. Discussion
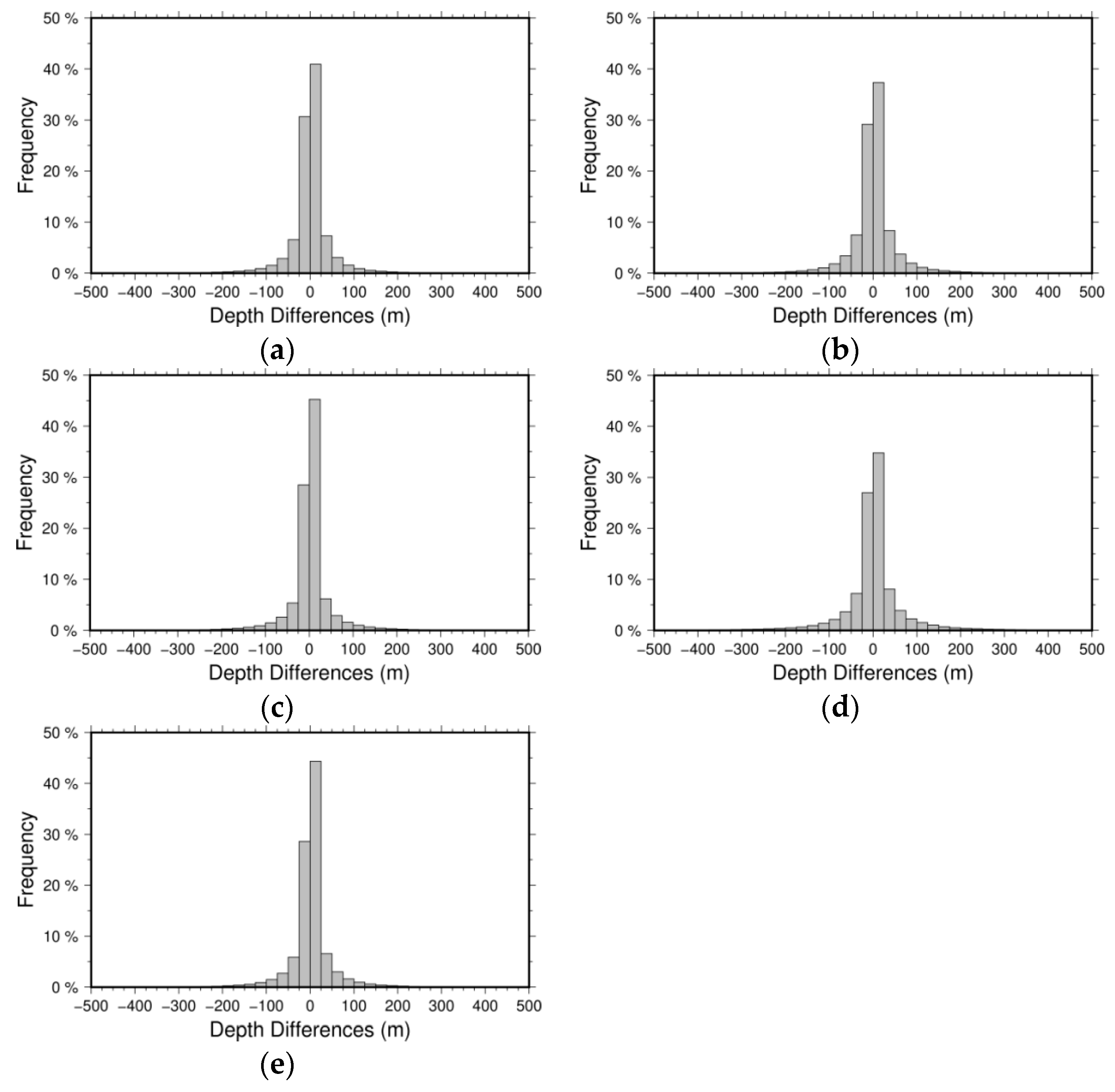
4.1. Accuracy Evaluated by Comparing with Ship Soundings and Existing Models
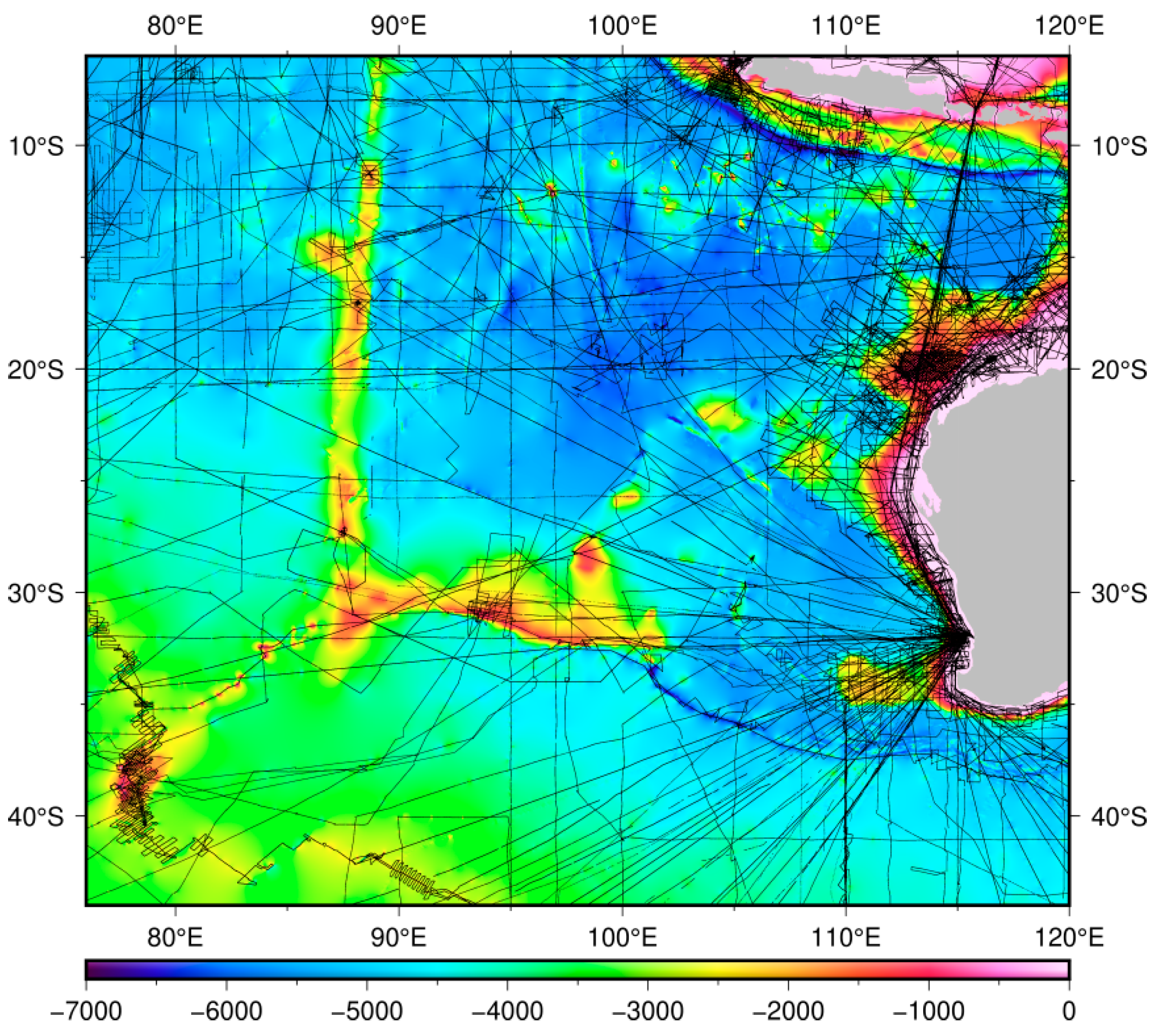
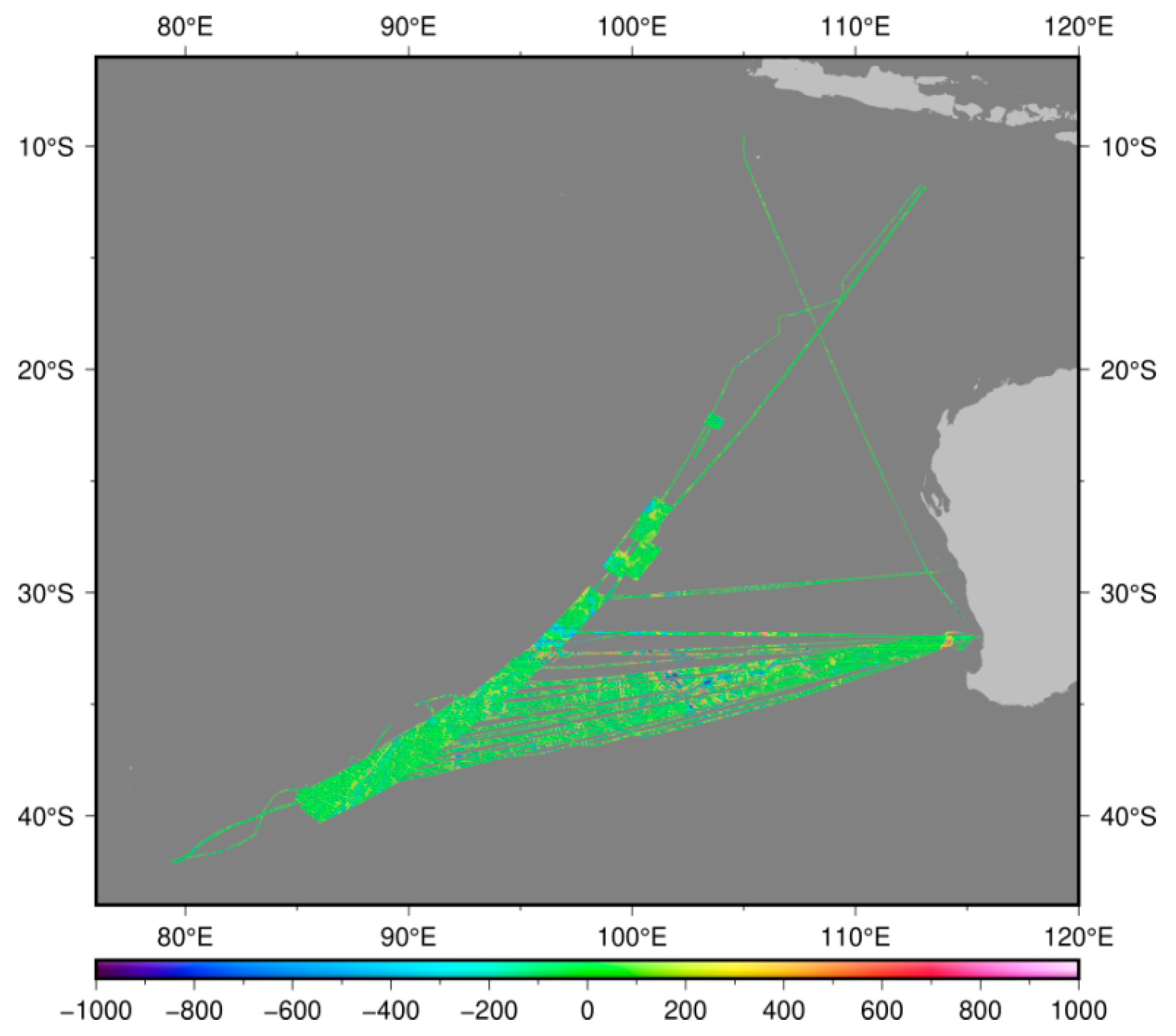
4.2. Model Evaluated by Independent Multibeam Grids of MH370 Searching Area
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mayer, L.; Jakobsson, M.; Allen, G.; Dorschel, B.; Falconer, R.; Ferrini, V.; Lamarche, G.; Snaith, H.; Weatherall, P. The Nippon Foundation-GEBCO seabed 2030 project: The quest to see the world’s oceans completely mapped by 2030. Geosciences 2018, 8, 63. [Google Scholar] [CrossRef] [Green Version]
- Tozer, B.; Sandwell, D.T.; Smith, W.H.F.; Olson, C.; Beale, J.R.; Wessel, P. Global bathymetry and topography at 15 arc sec: SRTM15+. Earth Space Sci. 2019, 6, 1847–1864. [Google Scholar] [CrossRef]
- Smith, W.H.F.; Sandwell, D.T. Conventional bathymetry, bathymetry from space, and Geodetic Altimetry. Oceanography 2004, 17, 8–23. [Google Scholar] [CrossRef]
- Smith, W.H.F.; Sandwell, D.T. Bathymetric prediction from dense satellite altimetry and sparse shipboard seafloor topography. J. Geophys. Res.-Solid Earth 1994, 99, 21803–21824. [Google Scholar] [CrossRef]
- Smith, W.H.F.; Sandwell, D.T. Global sea floor topography from satellite altimetry and ship depth soundings. Science 1997, 277, 1956–1962. [Google Scholar] [CrossRef] [Green Version]
- Ramillien, G.; Cazenave, A. Global bathymetry derived from altimeter data of the ERS-1 geodetic mission. J. Geodyn. 1997, 23, 129–149. [Google Scholar] [CrossRef]
- Anderson, O.B.; Knudsen, P. Altimetric gravity field from the full ERS-1 geodetic mission. Phys. Chem. Earth. 1996, 21, 337–341. [Google Scholar] [CrossRef]
- Anderson, O.B.; Knudsen, P. Global marine gravity field from ERS-1 and Geosat geodetic mission altimetry. J. Geophys. Res. 1998, 103, 8129–8137. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Smith, W.H.F. Marine gravity anomaly from Geosat and ERS 1 satellite altimetry. J. Geophys. Res. 1997, 102, 10039–10054. [Google Scholar] [CrossRef] [Green Version]
- Sandwell, D.T.; Smith, W.H.F. Global marine gravity from retracked Geosat and ERS-1 altimetry: Ridge segmentation versus spreading rate. J. Geophys. Res. 2009, 114, B01411. [Google Scholar] [CrossRef] [Green Version]
- Sandwell, D.T.; Garcia, E.; Wessel, P.; Chandler, M.; Smith, W.H.F. Toward 1-mGal accuracy in global marine gravity from CryoSat-2, Envisat, and Jason-1. Lead. Edge 2013, 32, 892–899. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.J.; Sandwell, D.T. Retracking of SARAL/AltiKa Radar Altimetry Waveforms for Optimal Gravity field Recovery. Mar. Geod. 2017, 40, 40–56. [Google Scholar] [CrossRef]
- Calmant, S.; Berge-Nguyen, M.; Cazenave, A. Global seafloor topography from a least-squares inversion of altimetry-based high-resolution mean sea surface and shipboard soundings. Geophys. J. Int. 2002, 151, 795–808. [Google Scholar] [CrossRef] [Green Version]
- Becker, J.J.; Sandwell, D.T.; Smith, W.H.F.; Braud, J.; Binder, B.; Depner, J.L.; Fabre, D.; Factor, J.; Ingalls, S.; Kim, S.H.; et al. Global bathymetry and elevation data at 30 Arc Seconds Resolution: SRTM30_PLUS. Mar. Geod. 2009, 32, 355–371. [Google Scholar] [CrossRef]
- Hu, M.Z.; Li, J.C.; Li, H.; Shen, C.Y.; Jin, T.Y.; Xing, L.L. Predicting Global Seafloor Topography Using Multi-source Data. Mar. Geod. 2015, 38, 176–189. [Google Scholar] [CrossRef]
- GEBCO Bathymetric Compilation Group 2020. GEBCO_2020 Grid—A Continuous Terrain Model of the Global Oceans and Land; British Oceanographic Data Centre, National Oceanography Centre, NERC: Liverpool, UK, 2020. [Google Scholar] [CrossRef]
- Wang, Y.M. Predicting bathymetry from the Earth’s gravity gradient anomalies. Mar. Geod. 2000, 23, 251–258. [Google Scholar] [CrossRef]
- Hu, M.; Li, J.; Li, H.; Xing, L. Bathymetry predicted from vertical gravity gradient anomalies and ship soundings. Geod. Geodyn. 2014, 5, 41–46. [Google Scholar]
- Hu, M.; Li, J.; Li, H.; Shen, C.; Xing, L. A program for bathymetry prediction from vertical gravity gradient anomalies and ship soundings. Arab. J. Geosci. 2015, 8, 4509–4515. [Google Scholar] [CrossRef]
- Yang, J. Seafloor Topography Estimation from Gravity Gradients. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2017. [Google Scholar]
- Fan, D.; Li, S.; Li, X.; Yang, J.; Wan, X. Seafloor topography estimation from gravity anomaly and vertical gravity gradient using nonlinear iterative least square method. Remote Sens. 2021, 13, 64. [Google Scholar] [CrossRef]
- Hu, M.; Li, J.; Xing, L. Global bathymetry model predicted from vertical gravity gradient anomalies. Acta Geod. Cartogr. Sin. 2014, 43, 558–565, 574, (In Chinese with English abstract). [Google Scholar]
- Goodwillie, A.M. User Guide to the GEBCO One Minute Grid; International Hydrographic Organization: Monaco, 2008. [Google Scholar]
- Amante, C.; Eakins, B.W. ETOPO1 1 Arc Minute Global Relief Model: Procedures, Data Sources and Analysis. In NOAA Technical Memorandum NESDIS NGDC-24; National Geophysical Data Center: Boulder, CO, USA, 2009. [Google Scholar]
- Watts, A.B. Isostasy and Flexure of the Lithosphere; Cambridge University Press: London, UK, 2001. [Google Scholar]
- Walcott, R.I. Lithospheric flexure, analysis of gravity anomalies, and the propagation of seamount chains. In The Geophysics of the Pacific Ocean Basin and its Margin, Geophysical Monograph 19; Sutton, G.H., Manghnani, M.H., Moberly, R., Eds.; American Geophysical Union: Washington, DC, USA, 1976; pp. 431–438. [Google Scholar]
- Parker, R.L. The Rapid Calculation of Potential Anomalies. Geophys. J. R. Astr. Soc. 1973, 31, 447–455. [Google Scholar] [CrossRef] [Green Version]
- McKenzie, D.P.; Bowin, C. The relationship between bathymetry and gravity in the Atlantic Ocean. J. Geophys. Res. 1976, 81, 1903–1915. [Google Scholar] [CrossRef]
- Watts, A.B. An analysis of isostasy in the world’s oceans: 1, Hawaiian-Emperor seamount chain. J. Geophys. Res. 1978, 83, 5989–6004. [Google Scholar] [CrossRef] [Green Version]
- Smith, W.H.F. On the accuracy of digital bathymetric data. J. Geophys. Res. 1993, 98, 9591–9603. [Google Scholar] [CrossRef]
- Wessel, P.; Luis, J.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The generic mapping tools version 6. Geochem. Geophys. Geosyst. 2019, 20, 5556–5564. [Google Scholar] [CrossRef] [Green Version]





| Parameters | Notation | Value |
|---|---|---|
| Density of water | 1030 kg/m³ | |
| Density of crust | 2800 kg/m³ | |
| Density of mantle | 3350 kg/m³ | |
| Mean crustal thickness | T | 7 km |
| Mean water depth | D | 4 km |
| Effective elastic thickness | Te | 3, 5, 10, 25 km |
| Young’s modulus | E | N/m² |
| Poisson’s ratio | 0.25 |
| Data Sources | Descriptions | Processes | Data Provider |
|---|---|---|---|
| Topography modelSIO topo_20.1.nc | Seafloor topography at 1 arc-minute resolution derived from altimetric gravity anomalies. | Low-pass filtered to construct model at wavelengths longer than 160 km. | SIO, UCSD |
| Altimetric VGGSIO curv_30.1.nc | Model derived from satellite altimetric missions at 1 arc-minute resolution. | Band-pass filtered and downward continued to constrain seafloor topography at 15–160 km wavelength bands | |
| Multibeam grids | Shipboard multibeam grid. | Re-sampled at each 15 arc-second grid | JAMSTEC |
| Multibeam grids | AusSeabed-2018 at 50 m resolution; MH370 searching seafloor topography at 150 m resolution; Kerguelen seafloor topography model at 100 m resolution; Macquarie seafloor topography model at 100 m resolution. | Re-sampled at each 15 arc-second grid | GA |
| Multibeam grids | Depth grids at about 100 m ~ 2 km resolution, provided by website AutoGrid service. | Re-sampled at each 15 arc-second grid | NCEI |
| Single-beam depths | ~74.66 million points | Evaluated by comparing with SIO topo_20.1.nc model | NCEI |
| Region | Model | Minimums (m) | Maximums (m) | Mean (m) | STD (m) |
|---|---|---|---|---|---|
| North Pacific (120°~280°E, 0°~70°N) | BAT_VGG2021 | −204.6 | 204.5 | 0.7 | 39.6 |
| SIO topo.20.1.nc | −207.3 | 207.3 | −0.2 | 45.0 | |
| DTU18BAT | −315.1 | 315.1 | 5.7 | 65.8 | |
| BAT_VGG2014 | −507.7 | 507.7 | 22.2 | 125.1 | |
| ETOPO1 | −497.1 | 497.1 | 11.2 | 119.7 | |
| GEBCO_08 | −757.9 | 757.9 | 29.6 | 184.7 | |
| South Pacific (120°~300°E, −75°~0°N) | BAT_VGG2021 | −246.0 | 246.0 | 1.1 | 46.7 |
| SIO topo.20.1.nc | −258.7 | 258.7 | 1.3 | 53.1 | |
| DTU18BAT | −420.6 | 420.6 | 8.0 | 91.2 | |
| BAT_VGG2014 | −595.0 | 595.1 | 30.6 | 156.2 | |
| ETOPO1 | −612.2 | 612.2 | 11.9 | 159.5 | |
| GEBCO_08 | −926.8 | 926.8 | 20.2 | 225.9 | |
| North Atlantic (280°~360°E, 0°~70°N) | BAT_VGG2021 | −201.6 | 201.7 | 1.3 | 39.8 |
| SIO topo.20.1.nc | −219.1 | 219.1 | 0.1 | 49.2 | |
| DTU18BAT | −288.0 | 288.0 | 3.1 | 63.6 | |
| BAT_VGG2014 | −451.3 | 451.3 | 14.1 | 119.0 | |
| ETOPO1 | −480.5 | 480.6 | 5.2 | 116.2 | |
| GEBCO_08 | −642.4 | 642.0 | 28.0 | 161.7 | |
| South Atlantic (−60°~20°E, −75°~0°N) | BAT_VGG2021 | −508.0 | 508.0 | 0.8 | 77.6 |
| SIO topo.20.1.nc | −319.2 | 319.3 | 1.8 | 54.5 | |
| DTU18BAT | −400.5 | 400.5 | 4.3 | 71.4 | |
| BAT_VGG2014 | −519.3 | 519.0 | 10.2 | 120.1 | |
| ETOPO1 | −546.1 | 546.1 | 6.7 | 126.1 | |
| GEBCO_08 | −753.0 | 753.0 | 24.9 | 192.9 | |
| Indian Ocean (20°~120°E, −75°~26°N) | BAT_VGG2021 | −232.6 | 232.6 | 1.3 | 41.7 |
| SIO topo.20.1.nc | −264.1 | 264.2 | −0.2 | 55.6 | |
| DTU18BAT | −420.7 | 420.7 | 6.0 | 100.1 | |
| BAT_VGG2014 | −593.9 | 593.9 | 20.9 | 160.3 | |
| ETOPO1 | −581.9 | 581.9 | 7.6 | 150.5 | |
| GEBCO_08 | −663.1 | 663.1 | 15.7 | 166.3 |
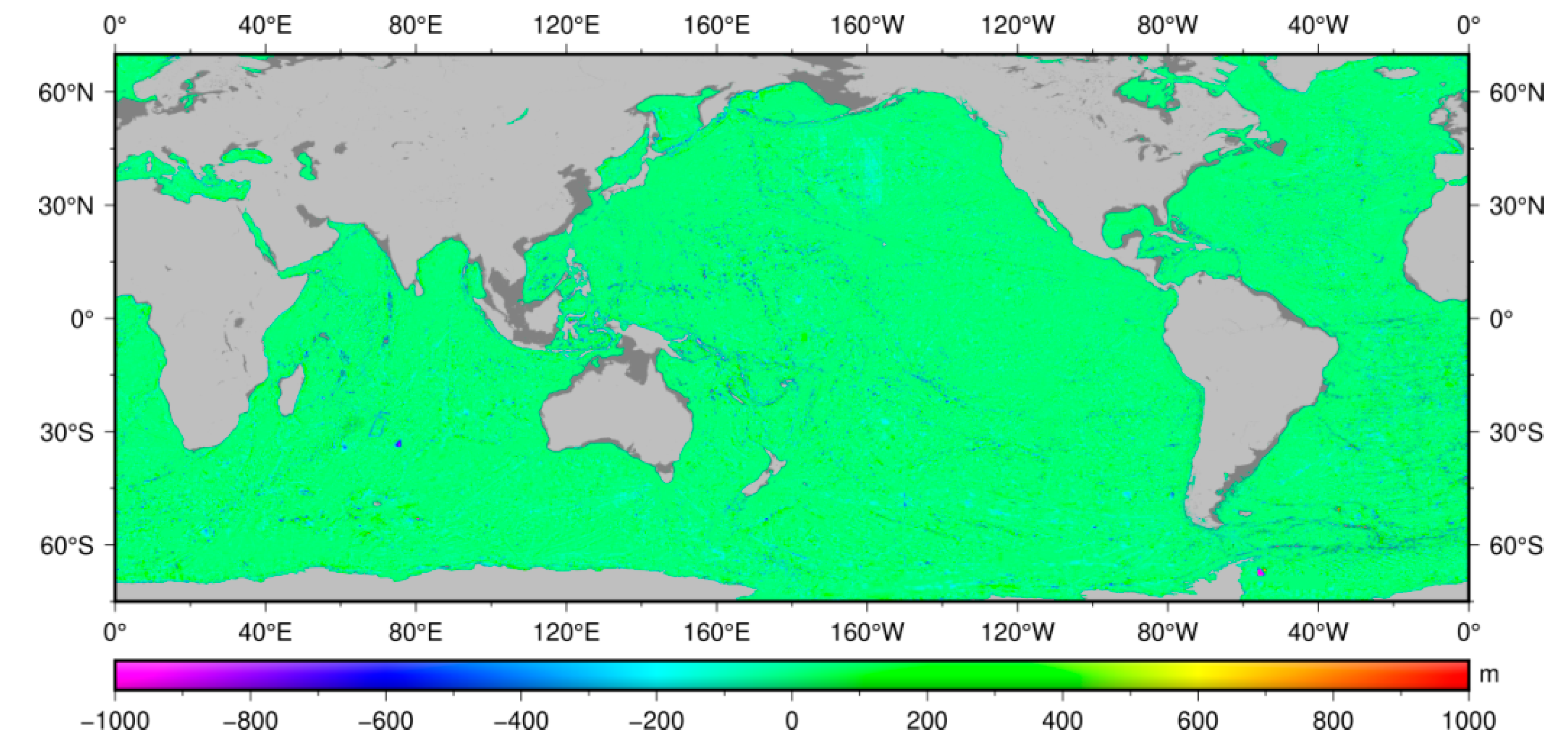
| Model | Minimums (m) | Maximums (m) | Mean (m) | STD (m) |
|---|---|---|---|---|
| BAT_Pre | −416.1 | 416.1 | 1.9 | 106.2 |
| BAT_Ship | −639.4 | 639.4 | 3.6 | 148.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, M.; Li, L.; Jin, T.; Jiang, W.; Wen, H.; Li, J. A New 1′ × 1′ Global Seafloor Topography Model Predicted from Satellite Altimetric Vertical Gravity Gradient Anomaly and Ship Soundings BAT_VGG2021. Remote Sens. 2021, 13, 3515. https://doi.org/10.3390/rs13173515
Hu M, Li L, Jin T, Jiang W, Wen H, Li J. A New 1′ × 1′ Global Seafloor Topography Model Predicted from Satellite Altimetric Vertical Gravity Gradient Anomaly and Ship Soundings BAT_VGG2021. Remote Sensing. 2021; 13(17):3515. https://doi.org/10.3390/rs13173515
Chicago/Turabian StyleHu, Minzhang, Li Li, Taoyong Jin, Weiping Jiang, Hanjiang Wen, and Jiancheng Li. 2021. "A New 1′ × 1′ Global Seafloor Topography Model Predicted from Satellite Altimetric Vertical Gravity Gradient Anomaly and Ship Soundings BAT_VGG2021" Remote Sensing 13, no. 17: 3515. https://doi.org/10.3390/rs13173515
APA StyleHu, M., Li, L., Jin, T., Jiang, W., Wen, H., & Li, J. (2021). A New 1′ × 1′ Global Seafloor Topography Model Predicted from Satellite Altimetric Vertical Gravity Gradient Anomaly and Ship Soundings BAT_VGG2021. Remote Sensing, 13(17), 3515. https://doi.org/10.3390/rs13173515





