Abstract
Non-climate-related anthropogenic processes and frequently encountered natural hazards exacerbate the risk in coastal zones and megacities and amplify local vulnerability. Coastal risk is amplified by the combination of sea level rise (SLR) resulting from climate change, associated tidal evolution, and the local sinking of land resulting from anthropogenic and natural hazards. In this framework, the authors of this investigation have actively contributed to the joint European Space Agency (ESA) and the Chinese Ministry of Science and Technology (MOST) Dragon IV initiative through a project (ID. 32294) that was explicitly designed to address the issue of monitoring coastal and delta river regions through Earth Observation (EO) technologies. The project’s primary goals were to provide a complete characterization of the changes in target scenes over time and provide estimates of future regional sea level changes to derive submerged coastal areas and wave fields. Suggestions are also provided for implementing coastal protection measures in order to adapt and mitigate the multifactor coastal vulnerability. In order to achieve these tasks, well-established remote sensing technologies based on the joint exploitation of multi-spectral information gathered at different spectral wavelengths, the exploitation of advanced Differential Interferometric Synthetic Aperture Radar (DInSAR) techniques for the retrieval of ground deformations, the realization of geophysical analyses, and the use of satellite altimeters and tide gauge data have effectively been employed. The achieved results, which mainly focus on selected sensitive regions including the city of Shanghai, the Pearl River Delta in China, and the coastal city of Saint Petersburg in Europe, provide essential assets for planning present and future scientific activities devoted to monitoring such fragile environments. These analyses are crucial for assessing the factors that will amplify the vulnerability of low-elevation coastal zones.
1. Introduction
There is increased concern relative to the growing urbanization of the world’s low-lying deltaic coastal regions and the related coastal hazards [,,] due to persistent and possibly accelerating sea level rise (SLR). Additionally, local relative SLR can be significantly modulated in coastal regions by vertical ground motions (i.e., subsidence phenomena) either due to natural processes (e.g., global isostatic adjustment, tectonics, sediment consolidation and compaction, and upstream sediment load reduction) [,,,] or induced/influenced by human activities (e.g., groundwater extraction [], land reclamation [], building construction, and consolidation []). Ground deformations can be on the same order of magnitude (or greater) than climate-induced SLR []. However, in practice, coastal ground motions are often poorly known, and little information is practically available in many cases about the spatial and temporal evolution of ground motion. Therefore, it is critical to monitor coastal delta regions by using advanced Earth Observation (EO) systems capable of detecting ongoing surface deformation phenomena, recovering their spatial extent on the ground, and following their temporal variability. This is helpful for the subsequent interpretation of natural/anthropogenic processes causing surface motion.
During the Dragon IV (D4) project (ID.32294) titled “Integrated analysis of the combined risk of ground subsidence, SLR, and natural hazards in coastal delta regions,” our primary interest was to obtain a picture of the environmental changes occurring in selected coastal areas of China and Europe. Particular case-study areas in China were the Yangtze River Delta (YRD) and the Pearl River Delta (PRD), Shanghai, and the east coast of China. In Europe, we studied the ground deformation of the coastal city of Saint Petersburg, Russia. The selected delta regions in China have historically been seriously affected by SLR and natural/anthropogenic deformation phenomena. The understanding of the physical mechanisms that induce the observed ground deformation signals is mandatory for planning proper actions to effectively manage the disaster risk in coastal areas. Indeed, in coastal cities, coastal topography and morphology changes can trigger other essential factors that affect flooding hazards. Water level changes related to SLR can induce changes in the coastal response of astronomically forced ocean tides [,] and can increase disaster and risk conditions in flood-prone regions. Coastal flooding and the associated risks to population and infrastructures have been analyzed for the selected zones, emphasizing the role and potential of existing methods relying on satellite-based remote sensing technologies. In particular, we exploited sets of EO data collected by the Sentinels (Sentinel-1 and Sentinel-2) and the COSMO-SkyMed (CSK) satellites constellations.
The principal results of the investigations performed within our Dragon IV project have been published in peer-reviewed journals over the last five years [,,,,,,,,,,,,,] and represent the starting point for future studies to be performed in the following years. We will summarize the main results of previous research related to this project in this article.
This project report is organized as follows. Section 2 describes the aforementioned ID. 32294 Dragon IV project’s overall framework, composed of three interlinked subprojects. Section 3 highlights the research themes carried out in the three subprojects. Section 4 summarizes the main research results. Overall discussion and main conclusions are addressed in Section 5.
2. Project, Subprojects, EO, and Other Data Utilization
2.1. List of SubProjects and Teams
The ID. 32294 Dragon IV project was composed of three subprojects (SPs), consisting of multiple Tasks (Ts). Table 1 summarizes the title, team composition, and project leaderships of every subproject. This article describes the achievements of the co-authors of this investigation and the project’s main achievements over the five-year lifetime of the project, as described in the following sections. The three subprojects worked independently to obtain measurements that characterize the state of some selected coastal regions in China and Europe. The results among all sub-tasks were then integrated in order to characterize the current stage and future evolution of the coastal environments analyzed.

Table 1.
Project information.
2.2. Description and Summary Table of EO and Other Data Utilized
The SAR data acquired in different periods covering the study regions were utilized for long time series interferometric analyses. Archived L0 ENVISAT ASAR (ENV) Image Mode and Alternating Polarization Mode data were used to accomplish this work. The acquisition period of the archived data was from 2002 to 2010. The image swath of image mode is I2. The polarization information of Image Mode images is VV. The archived Sentinel-1 (S1) Interferometric Wide Swath SLC data were also used. The number of archived data for the three delta regions is 374. The acquisition plan was from 2016 to 2020. In our project, COSMO-SkyMed (CSK) StripMap L0 data were also acquired. The archived Radarsat-2 (RST-2) wide data were also used. It consisted of 44 images from 2012 to 2016 (descending passes; VV polarization). In addition, Sentinel-2 MSI Level 1c data acquired from 2016 to 2020 were utilized in this work. See Table 2 and Table 3 for further details on the used EO data.

Table 2.
List of principle SAR datasets used in this study.

Table 3.
List of principle utilized EO datasets.
3. Subprojects’ Research and Approach
3.1. Detection and Interpretation of Time Evolution of Costal Environments through Integrated DInSAR, GPS and Geophysical Surveys
3.1.1. Research Aims
The principal goal of this subproject was to fully exploit satellite-based synthetic aperture radar (SAR) imageries to investigate ground displacements of coastal areas in China and Europe. The objectives of the related subproject tasks are summarized here.
(a) The generation and subsequent analysis of ground changes occurring over selected coastal zones in China (YRD and the city of Shanghai; PRD and the city of Shenzhen) and Europe (the city of Saint Petersburg). To this aim, long-term sequences of CSK (X-band), S1 (C-band), and ENV (C-band) SAR images were exploited [,,]. The displacement maps of the terrain for the selected regions were computed by using the multi-temporal Small Baseline Subset (SBAS) technique [].
(b) The retrieval of digital elevation models (DEM) of monitored coastal areas in delta regions. The availability of updated DEMs for the selected areas subjected to SLR (and/or flooding) was of fundamental importance for the achievements of the project goals. Global coverage catalogues of DEMs, imaging most of the Earth’s surface, are readily available nowadays (such as those from the Shuttle Radar Topography Mission in 2001), and new SAR missions have recently been deployed (such as the TanDEM-X mission []) for the generation of updated profiles of the terrain. However, the quality of available DEMs over highly time-varying coastal areas has not been systematically assessed yet. Within this task, the subproject aimed at primarily evaluating the accuracy of the available DEMs. Then, experiments concerning the generation of a high-resolution DEM of the investigated area were carried out using the methodical approaches developed at the KIT [,]. Specifically, an updated DEM of the Shanghai region was generated and used to realize the flood risk of this critical megacity. Further efforts are, however, required on both the methodological and experimental sides in order to generate more accurate DEMs in low-lying coastal cities, necessitating EO data with enhanced spatial and temporal resolutions.
(c) The interpretation of the mechanisms of ground movements in different geological contexts. Although the Differential Interferometric SAR (DInSAR) [,,,] results can accurately show the zones affected by ground movements and the evolution of the ground movement, they cannot determine the source of the deformation. Thus, an integrated analysis of data from multiple sources must be performed in order to interpret the mechanisms of ground movements. By understanding the mechanisms controlling ground movements, future ground changes can be predicted and assessed. For instance, in regions where ground subsidence is caused by consolidation of compressible sediments, temporal trends of subsidence have been established by using long-term time series of DInSAR observed ground deformation and geotechnical laboratory test models (e.g., []).
(d) The analysis of the correctness of forecasting models for the evolution of ground displacements in ocean-reclaimed lands. We processed SAR data of coastal areas in China subject to significant ocean-reclaimed land projects in this context. The validity of previously developed forecasting models for the city of Shanghai was extended and partially confirmed for other regions.
(e) The implementation of extended investigations on coastal flooding risk in the selected areas of China and Europe. This task aimed to interpret deformation products obtained using differential SAR interferometry approaches (i.e., deformation maps and related ground displacement time-series) and studying the sources of terrain deformation. This subproject made direct comparisons between the generated ground displacement maps and available external measurements (such as levelling and/or GPS data).
(f) The development of novel multi-temporal DInSAR processing chains. Specifically, we tested the potential of some multi-grid phase-unwrapping methods in order to retrieve ground displacement maps in moderate-to-low coherence regions. These methods require additional work to allow them to mature enough for future publications.
3.1.2. Research Approach
This sub-section summarizes the primary rationale of the conventional and advanced multi-temporal DInSAR techniques exploited within our D4 project. In particular, we focused on the popular Small Baseline Subset (SBAS) technique [], the established multi-satellite combination technique proposed in [], and a newly developed and under testing multi-grid phase-unwrapping technique [,] as well as the related DInSAR processing chains.
Multi-Temporal DInSAR Technologies and SBAS Method
We employed SAR images to generate ground displacement maps and the relevant displacement time-series in the selected coastal areas by using DInSAR. The latter relies on the computation of the phase difference between couples of SAR images (interferogram) and the measurement of the ground displacement occurring between the two satellite transits over the same scene []. Unfortunately, DInSAR can only measure the projection of the actual ground deformation along the radar Line-Of-Sight (LOS) direction but with centimetric-to-millimetric accuracy and over extended (large-scale) strips of the terrain. However, the DInSAR phase is severely corrupted by systematic noise. It contains some components that are not strictly related to the deformation signal (i.e., the residual topography, the orbital errors, and the atmospheric phase screen) that cannot be delineated using single interferograms. Several DInSAR methods have been developed over the past 20 years [,,,,,,,]. A significant role has been played by small baseline (SB) DInSAR methods [,,,] that allow the analysis of deformation signals of distributed scatterers (DS) by considering only those interferometric data pairs with small perpendicular baselines over short periods. Among the SB techniques, the SBAS approach [] has been extensively used. The rationale of the SBAS method has been detailed in several publications. Here, we only want to summarize the core procedure of the SBAS technique. It combines a set of SB interferograms arranged to form different time-overlapped subsets of data [] by imposing ground deformation time-series characterized by minimum norm velocity. With this aim, the Singular Value Decomposition (SVD) method is used for solving a rank deficient system of linear equations. It is calculated for each coherent DS target, the (unknown) displacement time-series []. A recent study [] on the theoretical accuracy of the SB methods and the SBAS technique, in particular, showed how ground deformation error bounds are in general agreement with the result of quantitative analyses that showed that the accuracy of SBAS measurements is on the order of 1 mm yr−1 and 3–5 mm, for the ground deformation velocity and each data measurement, respectively. Additional recent advancements of the methods based on distributed target deformations can be found in [,,,,].
Data Merging Techniques
Over the D4 project lifetime, DInSAR-driven data merging techniques were studied to circumvent the well-known problem that DInSAR measurements only represent projections of the actual deformation along the radar LOS direction. Most available approaches nowadays are based on the availability of a large set of SAR data acquired by complementary viewing angles from ascending and descending directions. Moreover, in our case, a general lack of a systematic acquisition plan of SAR images over the investigated zones in China, at least in the period from 2010 to 2015, resulted in the necessity of adequately connecting time-disconnected sets of multi-satellite SAR images (collected from all available SAR platforms) in order to recover long-term displacement maps []. This problem has mathematically been addressed in []. Additionally, in coastal regions, the ground displacement mechanisms are mainly responsible for vertical (e.g., subsidence) movements. Accordingly, some simplifications can be assumed; for instance, vertical ground deformation can be suitably obtained as follows []:
where and are the displacement measurements in the LOS and the vertical direction, respectively, and is the incidence angle of the electromagnetic wave on the terrain. Based on this assumption, a method for combining ground displacement computed from different heterogeneous SAR systems has been proposed in []. The combination technique relies on adapting the modified quantile-quantile adjustment (MQQA) statistical technique, which allows a straightforward combination of both time-overlapped and time-gapped cross-platform DInSAR products (i.e., vertical displacement time-series of Earth’s surface). More specifically, the time-overlapped ground deformation time-series are efficiently combined by using the MQQA method. By contrast, time-gapped data (i.e., time-series related to non-overlapped periods) are combined using the method proposed in []. At odds with existing 2D multiple-satellite DInSAR combination approaches [], which are effective when the temporal overlap among the different datasets is significant, the MQQA method benefits from statistical analysis that combines DInSAR products. It is expected to be more robust in areas with moderate-to-low coherence and with reduced time-overlapping amongst the different SAR datasets.
We also evaluated the theoretical accuracy of the east–west and vertical deformation time-series obtained using the multi-platform combination technique proposed in [], taking into account the theory of error propagation applied to the system of linear equations representing the core of the method []. The latter results were beneficial for evaluating the accuracy of the ground displacement measurements of Saint Petersburg in Russia and represent a foundation for further investigations in progress. They will be addressed within the context of ongoing global climate change, SLR, extreme water level events, and local ground subsidence effects in coastal and river delta regions through the Dragon V project titled “Global climate change, sea level Rise, Extreme Events and local ground subsidence effects in coastal and river delta regions through Novel and Integrated remote sensing approaches (GREENISH)”. Further readings on the detailed descriptions of the applied and developed methods can be found in [].
Novel DInSAR Processing Scheme Based on Multi-Grid Phase Unwrapping Approaches
The availability of measurements over a dense spatial grid is a typical aspect of DInSAR technology compared to other conventional approaches (e.g., GPS and levelling measurement campaigns). However, in regions where the density of coherent points is large, the use of a dense grid of measurement points might result in DInSAR processing inefficiency from a computational point of view, even more so when we want to investigate the temporal evolution of the detected deformation phenomena in large-swath areas or on the single-look scale []. In most cases, the limiting factor for the efficiency of the available DInSAR processing chains is represented by the phase unwrapping operation. In this project, we investigated the potential of a multi-resolution scheme for the phase unwrapping step of sequences of DInSAR interferograms that allows one to produce DInSAR deformation products at different scales of resolution. We tested the procedure by considering, for the sake of simplicity, three spatial resolution scales (2 × 10, 4 × 20, 8 × 40) with a scale factor between two neighboring resolution grids equal to ½ (i.e., one pixel at coarser grid resolution corresponds to four pixels at the following higher resolution scale). The algorithm performs its calculations starting from the coarser-resolution grid. The method allows each resolution scale to have a mask of coherent pixels denser in areas where the DInSAR fringe rate is higher, and it automatically decreases in areas characterized by a reduced fringe rate. The selection of the coherent pixels belonging to every scale is carried out using a statistical index that takes into consideration the phase deviation from one scale to another (i.e., the circular variance of the phase difference between different spatial scales):
where is the resultant vector for a given pixel of azimuth/range radar coordinates (x,y) of the phase difference vector between the two considered spatial scales, namely and . Interested readers can find a detailed description of the developed method in []. Once the mask of coherent pixels is calculated for each resolution scale, the phase unwrapping (PhU) operation is more efficiently performed on the selected set of sparse coherent pixels, with noticeable computational improvement and without losing significant information. Accordingly, the basic idea is to optimize the spatial density of coherent pixels at every scale of resolutions without violating the Nyquist sampling limitation during phase unwrapping operations.
3.2. Derivation of Storm Surge-Induced Submerged Area and Ocean Wave Field Using Satellite Images and Data in Coastal Waters
3.2.1. Research Aims
SLR is an ever-increasing global concern, as it affects every part of the planet and endangers coastal communities, infrastructure, and the environment. Additionally, ocean tides may change on short-term time scales. Tides can couple with changes in mean sea level (MSL) to amplify total water levels in sensitive regions, such as Hong Kong, which is a critical research location of this project. Recently, new methods of analyzing short-term fluctuations in ocean tides and how they are correlated with short-term fluctuations in MSL have been developed and utilized, denoted the Tidal Anomaly Correlation (TAC) method. TACs can be used to determine the fluxes of individual tidal constituents related to MSL fluctuations and the combined fluctuations in major tidal components to determine the possible changes in the highest astronomical tide (δ-HAT). Negative TACs or δ-HATs indicate that a rising sea level may partially diminish the tides, whereas a positive TAC or δ-HAT may amplify the tides. The latter case is more important since a positive tidal sensitivity increases total sea levels, often exceeding expected flood levels based on stationary tide assumptions. These results demonstrated that tidal variability associated with sea level changes occurs at a majority of worldwide locations. This method has been applied in the Pacific Ocean [,], the Atlantic Ocean [], in the Hong Kong region [], and in the Indian Ocean most recently [].
Mean sea level has shown a constant global increase over the past century [], and MSL rates show a more significant growth rate during the satellite altimetry era (since 1993), exceeding +3.0 mm/yr. Sea level rates might also be accelerating via global climate change mechanisms such as ice sheet melt and thermosteric MSL rise due to upper-ocean warming [,], which may affect different regions in different ways. However, there are significant differences observed in the regional rates of SLR, so an accurate understanding of water level dynamics requires a focused location-based approach [].
Tidal evolution has been documented at regional scales in the Eastern Pacific [], the North Atlantic [], in China [], and other regions. A complete summary of studies that have analyzed tidal changes can be found in []. The possible causes of tidal evolution are numerous and interrelated [,]. A direct driver of tidal growth is SLR and sea level variability, as tides can be directly modified by changes in water depth []. Other mechanisms related to sea level changes include friction-altering changes in water depth, resonance changes in harbor regions [], or stratification changes induced by increased upper-ocean warming [], which may modify internal tides []. On a shorter timescale, seasonal tidal variations can be due to rapid changes in water column stratification or by seasonal river flow characteristics []. The high sensitivity of tides relative to sea level changes also suggests increased impacts of storm-induced flooding since both tides and storm surge are long-wave processes [,]. Thus, there are many possible correlated mechanisms involved with SLR and tidal evolution, which can complicate the accurate determination of the exact causes of the observed variability. Yet, no matter the reason for these changes, the consequences relative to coastal zones are due to total water levels, i.e., the sum of MSL and time-variable water levels including tides and the influence of weather and other processes. Areas with large coastal population density and significant coastal infrastructure, such as Hong Kong and Shanghai, are especially susceptible to these impacts.
The impacts of long-term SLR and tidal changes are complicated by the existence of short-term correlations between sea level fluctuations and tides. Changes in tidal amplitudes can cause direct modifications to overall water levels, whereas changes in tidal phases can modulate the time of high tide occurrence. Either change may increase the impact of extreme water level events, such as storm surge or nuisance flooding, which may occur at high tide []. Locations with a strong positive correlation between short-term fluctuations of waves and MSL can amplify flood risk beyond the levels estimated by stationary tide assumptions, as MSL and tides may combine to have an amplified impact.
3.2.2. Research Approach
We investigated tidal variability associated with MSL variability by using the TAC method and utilizing tidal admittances calculated from harmonic analysis. This approach was applied in many different worldwide regions in order to understand the patterns and magnitude of tidal variability, how it can couple with MSL rise, and which areas might be most sensitive to these changes. In this report, we focus on the investigations of the Western Pacific [,], Hong Kong [], and the Indian Ocean [].
Investigations of tidal perturbations were carried out using tidal admittances [], the unitless ratio of an observed tidal constituent to its corresponding astronomical tidal potential, which helps to minimize the influence of long-period astronomical variability in tides such as the 18.61 yr nodal cycle. Monthly or yearly harmonic analyses were performed on hourly experimental tidal records and related hourly tidal potential by using the r_t_tide tidal harmonic analysis package in MATLAB [,]. The harmonic analysis process also generates MSL time-series, and a separate code is used to create tidal potentials []. Yearly harmonic analyses resolve a more significant number of tidal constituents but do not examine seasonal cycles. Therefore, both monthly and annual analyses were employed in different studies. Through this approach, time series of amplitudes A(t) and phases θ(t) are produced, from which one can construct complex amplitudes Z(t) by using the following equation.
Tidal admittances (AD) and phase differences (PD) for each constituent are then formed by using Equations (4) and (5).
The subscript “obs” or “pot” denotes either the observed data or the gravitational potential. This process uses the four largest tidal constituents: M2 (semidiurnal lunar tide), S2 (semidiurnal solar tide), and K1 and O1 (lunar-solar interactional diurnal tides). In the study of Hong Kong [], we also considered shallow-water overtides, a phenomenon deriving from the gravitational tides due to frictional effects in coastal waters.
Tidal sensitivities to sea-level fluctuations were quantified by using tidal anomaly correlations (TACs), the relationships of detrended tidal variability to detrended MSL variability, following the methods outlined in []. The sensitivity of tidal admittance and phase differences of tides and overtides to MSL perturbations is determined by calculating robust regressions between the two detrended quantities. The slope of the regression is the definition of the TAC. We also consider a proxy for the change in the highest astronomical tide (δ-HAT) by combining the largest tidal admittance amplitudes into a single time series. The detrended time series of δ-HATs can also be compared to detrended MSL variability identically as the TAC approach. All quantities are expressed in units of millimeter change in tidal amplitude for a 1 m change in sea level (mm m−1).
In our Indian Ocean study [], there was a lack of long-period tide gauge data; thus, we developed an improved novel technique designed for shorter records. Tidal admittance amplitudes and phase differences were conditioned for analysis and comparison via the Ensemble Empirical Mode Decomposition (EEMD) method [], which analyzes each time series and splits it into several modes of variability called intrinsic mode functions (IMFs). In this approach, we calculated regressions by using the IMFs generated from the EEMD process for individual tidal admittances and δ-HATs, considering single IMFs as well as combinations of IMFs. We analyzed tidal variability on three distinct frequency bands: sub-annual, annual, and inter-annual.
3.3. Projection of Sea Level Rise and Potential Submerged Area in Coastal Regions
3.3.1. Research Aims
The change of sea level in response to global warming is critical for scientific and socio-economic reasons. More frequent occurrences of land loss, flooding, storm surges, and cyclonic storm-related disasters are linked to mean sea level rise []. Thus, many sectors, including climate scientists, politicians, economists, insurance companies, public utilities, coastal property owners, and civil engineers, need an accurate and reliable projection of future sea level change and regional variation.
It has been documented that the rise in global mean sea level in the 20th century is mainly due to ocean thermal expansion and glacier melting caused by anthropogenic global warming, which is almost certain to continue in the future []. Thus, it is beneficial to investigate sea level rise over the 21st century under this scenario. Although the latest projections of global sea level change using coupled atmosphere-ocean General Circulation Models (GCMs) under global warming procedures have contributed to a general knowledge of sea level changes on a worldwide scale [], local sea level rise is still not well studied, e.g., the coast of the YRD in China. Regional sea level change could differ substantially from the global mean sea level due to regional differences in heating and circulation changes []. Therefore, the objective of our project is to combine satellite observations, in situ observations, and climate modelling in order to provide estimates of future regional sea level change and potential submerged land area during the 21st century in the YRD and adjacent coastal regions. The YRD is a highly developed region and an economic hotspot of China. It also lies at a low elevation, making the areas especially sensitive to SLR impacts in the future.
3.3.2. Research Approach
A satellite altimeter derived of monthly sea level anomaly (SLA) data from AVISO (Archiving Validation and Interpretation of Satellite Oceanography) during 1993–2016 was employed in this project, which is provided at a spatial resolution of 1/4° × 1/4°. Tide gauge data used includes long-record locations along the coast of China and short-term tide gauge data on the coast of Jiangsu Province. Shuttle Radar Topography Mission (SRTM) data with a spatial resolution of 90 m is also used for estimating the possible inundation risk of the YRD due to SLR. The three-dimensional unstructured grid Finite Volume Coast and Ocean Model (FVCOM) is used to establish a regional tidal wave and storm surge model of the East China Sea. Absolute SLR is predicted based on historical altimeter data, assuming the currently derived linear rates. The land subsidence rate (mm yr−1) along the coast of China is calculated from the long-term absolute and relative sea level changes observed by satellite altimeters and tide gauges. In this manner, we can predict the relative SLR rate. We use typhoons Fung-wong (No. 1416) and Wipha (No. 0712) as recent examples of storm surge impacts. The storm surge model of the YRD is applied to analyze the possible inundation area due to SLR and storm surges by 2050 and 2100.
4. Research Results and Conclusions
4.1. Detection and Interpretation of Time Evolution of Costal Environments through Integrated DInSAR, GPS, and Geophysical Surveys
4.1.1. Results
The 2015–2016 Ground Displacements of the Shanghai Coastal Area Inferred from a Combined CSK/Sentinel-1 DInSAR Analysis
This research analyzed the two-dimensional (2D) surface displacement components (i.e., the up-down and the east–west deformation time-series) over the ocean-reclaimed lands of Shanghai. This work, which employed SAR data collected through different satellite platforms, was fundamental to prove that the horizontal movements in the areas are an order of magnitude smaller than the long-lasting subsidence of the terrain due to the consolidation of the ocean-reclaimed lands. The research successfully utilized two sets of CSK and Sentinel-1A (S1-A) SAR data collected over the area of interest. First, the CSK and S1-A LOS displacement time-series in overlapping periods (i.e., the CSK dataset includes images acquired with descending pass from 28 February 2015 to 18 March 2016, and the S1-A dataset includes images acquired with ascending pass from 26 February 2015 to 4 March 2016) were derived by applying the SBAS technique. Then, we calculated the LOS average deformation velocity and the corresponding time series of the overlapping period from 26 February 2015 to 4 March 2016. The 2015–2016 LOS-projected mean displacement velocities for both datasets are shown in Figure 1. Subsequently, the computed LOS deformation time series were combined by using the Minimum Acceleration (MinA) combination technique [] to recover the east–west and the up-down displacement time series. Figure 2 depicts the maps of the mean displacement velocity values of the east–west and up-down components. One of the primary outcomes of this investigation was to confirm that horizontal displacements (along the east–west direction) are relatively insignificant, with rates of one-tenth of the upper and lower deformation rates in the ocean-reclaimed land. To the best of our knowledge, this is the first instance of direct evidence of the negligible east–west movement in ocean-reclaimed land obtained by DInSAR-based approaches. Details on this research study and further insights on the achieved results can be found in [].
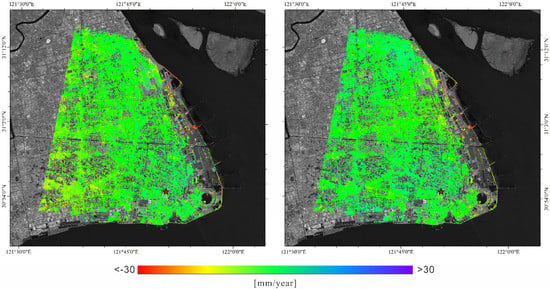
Figure 1.
LOS-projected mean displacement velocity map retrieved by processing the CSK dataset (left) and the S1-A dataset (right) in an overlapping period between 26 February 2015 and 4 March 2016. Only coherent SAR pixels common to both CSK and S1-A datasets are displayed. The red star identifies the location of the reference pixel, which is assumed to be stable (refer to []).
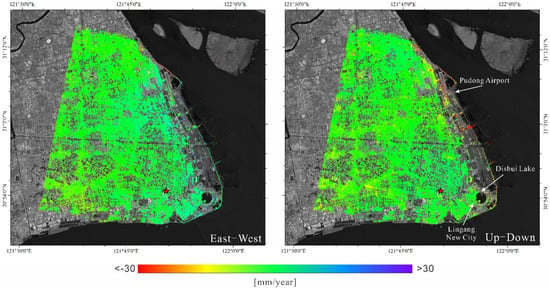
Figure 2.
The 2015–2016 two-dimensional mean displacement velocity maps: east–west map (left) and up-down map S1-A (right) (refer to []).
On the Effects of InSAR Temporal Decorrelation and Its Implications for Land Cover Classification: The Case of the Ocean-Reclaimed Lands of the Shanghai Megacity
In this work, we used 32 S1 SAR images acquired from 8 July 2015 to 26 August 2017, to determine the recent ground displacement time series in the Shanghai coastal area using the SBAS technique. As expected, the results showed that the land subsidence mainly occurs in the eastern parts of the reclamation area (Figure 3), where the maximum deformation rate reaches 35 mm/year. By using a model for the temporal decorrelation of the interferometric SAR phase measured by the coherence data, the SAR backscattering intensity data and four bands of Sentinel-2 (red, green, blue, and near-infrared band) as input data, we obtained classification results of Pudong International Airport (Figure 3). To make the results more accurate, we chose the Support Vector Machine (SVM) for supervised classification. By comparing the classification results of accurate color images and standard false-color images, we found that the overall accuracy rate increased by 22% and 11%, respectively. The KAPPA coefficient increased by 0.29 and 0.14, respectively. The results proved that in order to distinguish roads and buildings, it is convenient to use optical data (e.g., Sentinel-2 data) and coherence data. In particular, proper temporal decorrelation improves the accuracy of land cover classification, with the accuracy value ranging from 75% to 86% in the area of the Pudong international airport (see Figure 3). Details on this research study and further insights on the achieved results can be found [].
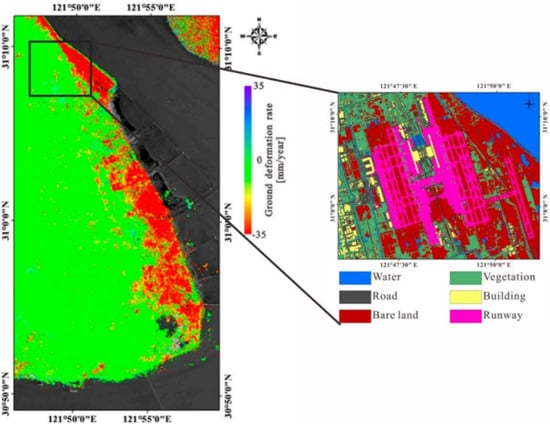
Figure 3.
The left image is the interpolated ground deformation rate in the reclamation area (around Pudong airport). The right image is the classification result of multi-source remote sensing data (refer to []).
Generation of Long-Term InSAR Ground Displacement Time-Series through a Novel Multi-Sensor Data Merging Technique
In order to continually monitor the long-term temporal evolution of the long-lasting ground subsidence processes, which may continue for decades, we developed new data merging techniques that used advanced DInSAR retrieved deformation time-series images obtained by different SAR instruments. The modified cross-mission DInSAR-driven combination technique is based on the time-overlapped and time-gapped cross-platform DInSAR time-series merging method. The MQQA method has been proposed to combine time overlapped DInSAR deformation time series derived by different SAR instruments. The performance of the MQQA method has been tested by considering the deformation measurements related to five levelling benchmarks, with results supporting the validity of the technique. An external geotechnical model can combine the time-gapped DInSAR deformation time-series of coastal ocean-reclaimed areas. Ten year deformation time series of the eastern coast of Shanghai has been produced using the developed time-overlapped and time-gapped data merging methods and three DInSAR retrieved deformation time series. The derived long-term deformation time series is beneficial for understanding the whole evolution process of slow and long-lasting ground deformation. Details on this research study and further insights on the achieved results can be found in [].
On the Characterization and Forecasting of Ground Displacements of Ocean-Reclaimed Lands
Figure 4 shows the mean deformation velocity map of Lingang New City of Shanghai from February 2007 to March 2016, using the geotechnical model and linking time-gapped data ENV and CSK deformation time-series []. The new independent RST-2 SAR data was also used to prove that the geotechnical model filling the time interval between ENV and CSK deformation products time-series is reasonable. The RMSE between the adjusted RST-2 ground deformation time series and ENV + CSK displacement time series was calculated at each common coherence point. The results show that the ENV + CSK and RST-2 ground deformations are in good agreement, except for some noisy areas disturbed by severe temporal decorrelation artefacts in coastal areas; thus, it can be proved that the used geotechnical model was correct.
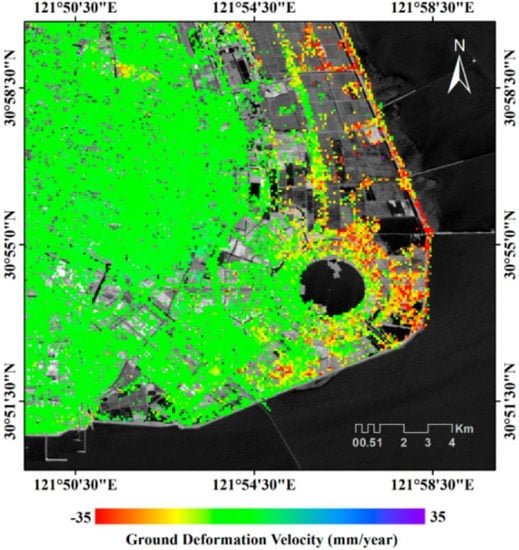
Figure 4.
Map of the mean (vertical) deformation velocity from 2007 to 2016 Lingang New City of Shanghai, as retrieved by combining the time-gapped ENV and CSK LOS displacement time-series (refer to []).
In addition to the validation of the geotechnical model, the suitability of two time-dependent models with (i) logarithmic and (ii) exponential decay [,] were studied in order to characterize the predictability of coastal ground deformations by using Shenzhen, located in the east of the PRD region of China, as the study area. The RMSE of the difference between the (vertical) deformation time-series based on InSAR and the best fit model was calculated in order to evaluate the quality of the non-linear temporal ground deformations fitting []. The results show that the performance of the geotechnical model is better than the other two models, and its RMSE is the smallest. Then, we estimated the future deformation time-series based on the three models. Details of this research and further insights on the achieved results can be found in [].
East-West and Up-Down Ground Displacement Time Series of the Saint Petersburg Coastal Region
A LOS-projected deformation time series was obtained using the SBAS algorithm for both the ascending and descending Sentinel-1A/B datasets. Results show that most parts of the city center are relatively stable, except for the western coastal area. The deformation is likely correlated to the land reclamation project conducted in recent decades. Then, the MinA technique was applied to decompose the LOS ground deformation time series into the relevant up-down and east–west ground deformation time series (Figure 5). Results demonstrate that the deformation of the city center area is mainly vertical compared with the east–west direction, which confirms that land reclamation is responsible for the observed subsidence. In addition to coastal reclamation areas, the southwest area shows ground displacement signals. This is likely due to the presence of facilities for the production of biogas. Additional analyses were also carried out to study the structural instabilities of an extensive system of dams that had been constructed to prevent the inundation of the Neva river, which can regularly affect the low-lying city of Saint Petersburg. The results evidence that some sectors of this dam’s system are more prone to structural deformations and deserve attention from local authorities. Details on this research and further insights on the achieved results can be found in [].
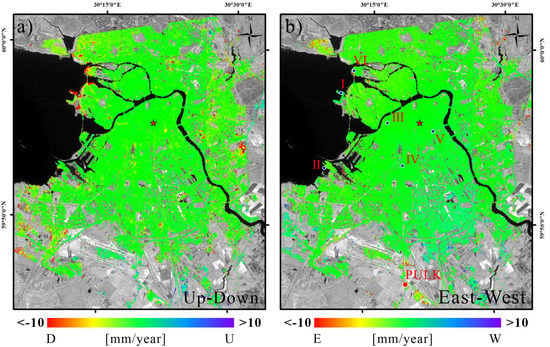
Figure 5.
Map of up-down (a) and east–west (b) mean deformation velocity in Saint Petersburg city center area for 2016–2018. The red point, labelled “PULK” in (b), is a GPS station (refer to []).
In addition, cross-validation of the InSAR results with the external GPS (location highlighted in Figure 5) measurements has been performed, and the validation result is shown in Figure 6. The root means square errors (RMSEs) between the measured displacement and the InSAR derived displacements are 3.7 mm for the up-down deformation components and 2.6 mm for the east–west components, respectively.
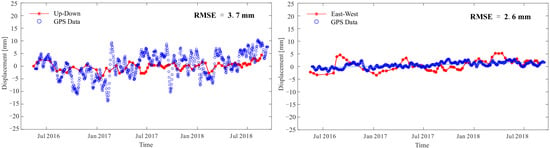
Figure 6.
Up-down and east–west deformation time series from the GPS measurement and InSAR analysis (refer to []).
Potential Inundation Areas of Shanghai
Predicted maximum inundation depths for 2012, the 2030s, and the 2050s under levee-breach and 100 year/1000 year return period flood are depicted (Figure 7) by the hydrodynamic model FloodMap [,]. Two critical discoveries can be obtained by comparing six inundation sub-maps. First, similar inundation patterns were observed in 100 year and 1000 year flood scenarios, but the inundation depths were different. This can be attributed to the topographical confinement of the ocean-reclaimed plain. In the coastal reclamation area of Shanghai, levees were repeatedly built along the shoreline with reclaimed land expanding to the sea, also in the land edges and in the inland plain. As a result, the levee-breach flow would be blocked by the inland seawall [] and confined to the recently reclaimed land. Dishui Lake, with a total area and volume storage of 5.56 km2 and 16.2 million m3, limits the further spread of coastal flood to the inland regions. Second, rapid SLR combined with extensive ground subsidence has a minor but non-linear impact on coastal inundation from 2012 to 2030 and 2050. Under a 100 year flood scenario, when the relative SLR rises by 0.44 m and 0.89 m in 2030 and 2050, respectively, the maximum inundation area is shown to increase by 6% and 15%. Similarly, compared with 2012, the average water depth is likely to increase by 0.11 m (8%) and 0.23 m (17%) by 2030 and 2050.

Figure 7.
Inundation map for Lingang New City of Shanghai in 2015, 2030, and 2050 under two simulated levee-breach inundation scenarios (100 year and 1000 year) modelled with TanDEM-X DEM and ground subsidence (refer to []).
In order to analyze the coastal flood impacts, we obtained land use of our study areas at current and future states provided by the Shanghai Institute of Surveying and Mapping. We found that wetlands and bare lands are the main types of land use at present, so the impact of floods on coastal communities is relatively small. However, the city planning of Shanghai expects accelerating urbanization in the future, and the total population is expected to increase sharply (more than 20-fold). Eventually, residential zones will rapidly expand and occupy the coastal areas around Dishui Lake. If significant subsidence combined with an intense storm event causes a levee breach, flood inundation similar to our simulation results would occur in 2030 and 2050, resulting in severe casualties and losses. Details on this research and further insights on the achieved results can be found in [].
Flood Risks in Sinking Delta Cities
Projected local sea levels and related uncertainty ranges rise gradually in the 21st century with the influence of climate change and human activities (Figure 8). The median relative SLR is projected to be at least 40 cm under RCP2.6 and at least 45 cm under RCP8.5 by 2050, with nearly equal contributions from climate change and land subsidence factors. The positions of seawall damage under a hydraulic load of the current 10 year return period are seldom distributed in the minimal weak sections of seawalls (Figure 8), mainly in the Yangtze River Estuary. During a 100 year event, both failures could synchronously occur along the coast of Baoshan and southwest of Chongming island. The failure locations extended further to Jinshan district, west of Pudong, Hengsha island, and the northeast of Chongming island during an extreme 1000 year RP event. SLR and ground subsidence act jointly to increase the risk of inundation and reliance on flood defense in delta cities. Combining reliability analysis with a hydrodynamic model, we quantified the influence of projected relative SLR on dike damages and flood hazards for Shanghai. In particular, we found that flooding tends to occur in low-lying and poorly protected rural areas of the city even under current sea levels. Without adaptive measures, the risk increases by a factor of 3–160 across the densely populated floodplain under projected SLR to 2100. Details on this research and further insights on the achieved results can be found in [].
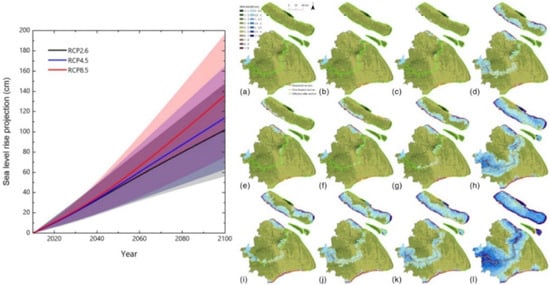
Figure 8.
Projected central estimates (50th percentile) of dike failures and flood inundation under present and future scenarios (Representative Concentration Pathways (RCP)) in Shanghai; (a–d) are ten-year flood in 2010, 2030, 2050, and 2100; (e–h) are one hundred-year flood in 2010, 2030, 2050, and 2100; (i–l) are one thousand-year flood in 2010, 2030, 2050, and 2100 (refer to []).
Multi-Grid Phase Unwrapping Methods
This research aimed to prove that, related to the highly coherent targets on the ground, deformation signals could be sufficiently detected at different scales of resolution [] using local and adaptive multilook factor (e.g., 2 × 10, 4 × 20, 8 × 40, etc.) by simultaneously optimizing the computation time and preserving as many details of the ground deformations as possible. Starting from the coarser-resolution grid (8 × 40), each pixel’s spatial high-pass phase components are calculated. Specifically, the circular variance of the high-pass phases (i.e., the phase difference between contiguous spatial scales) is exploited to identify those pixels likely related to significant deformation areas, where it is suitable to perform PhU operations, moving from one scale to another. The process is recursively applied from the coarser to the higher resolution scale (see Figure 9) until all relevant SAR coherent pixels are processed.
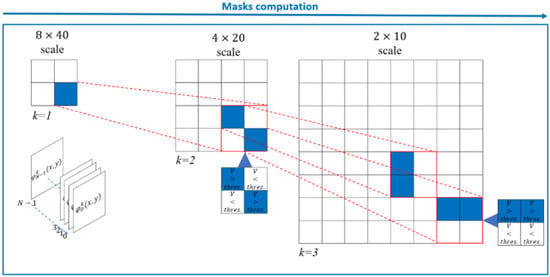
Figure 9.
Scheme of the multi-resolution (multi-scale) phase unwrapping processing procedures. An adaptive quad-tree-like decomposition strategy is adopted.
We built up a prototype of this processing tool. We applied it to the case-study area of the PRD, with a specific focus on Hong Kong Island (Figure 10), known to experience significant ground subsidence phenomena. This analysis relies on a set of 60 SAR data acquired by the Sentinel-1A/B radar sensor over the island of Hong Kong from December 2017 to January 2019. From these data, we generated a stack of 226 interferograms at three different resolution scales, 2 × 10, 4 × 20, and 8 × 40, on which we have tested the adaptive quad-tree decomposition method and subsequently computed at the 2 × 10 scale the time-series deformation and the mean deformation velocity map (see Figure 10).
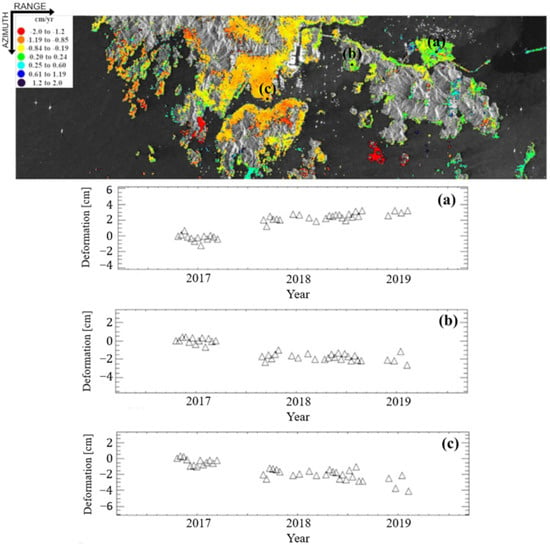
Figure 10.
Hong Kong deformation time series: (a) HK airport, (b) HK Disneyland, and (c) HK city coastal area. Note that map is shown in radar coordinates.
From the time series and the mean deformation velocity map computed at scale 2 × 10, we focused on three areas reclaimed from the sea that are characterized by significant subsidence phenomena: Hong Kong airport (Figure 10a), Hong Kong Disneyland (Figure 10b), and Hong Kong city coastal area along Victoria Harbour (Figure 10c). In terms of the required computational time, we experienced a substantial reduction of about 85% for every scale for the PhU operation. We note that these results are only preliminarily, and extended studies are still required to develop more robust and stable multi-scale phase unwrapping procedures. It is a matter for future analyses that are currently in progress. Details on this methodological research can be found in [].
4.1.2. Subproject Conclusions
Some important conclusions can be drawn from the research activities performed within this subproject:
- (I)
- The 2015–2016 ground displacements of the Shanghai coastal area inferred from a combined COSMO-SkyMed/Sentinel-1 DInSAR analysis []
By applying the SBAS technology and the MinA approach, it was found that most of the ocean-reclaimed land of Shanghai coastal areas is affected by ground deformation phenomena. However, the lateral (east–west) movement has little influence and was one-tenth of the vertical deformation rate in the ocean-reclaimed land. To the best of our knowledge, this represented the first instance of direct evidence for the negligibility of lateral movements in the observed reclaimed lands.
- (II)
- On the effects of InSAR temporal decorrelation and its implications for land cover classification: the case of the ocean-reclaimed lands of the Shanghai megacity []
This study investigated the relationships between observed InSAR coherence loss, ocean-reclaimed lands, and inherent land use changes. The results show that the joint exploitation of InSAR coherence models and Sentinel-2 observations is effective. The accuracy of land cover classification was significantly upgraded, and in some cases improvements were on the order of 8–10%.
- (III)
- Generation of long-term InSAR ground displacement time-series through a novel multi-sensor data merging technique []
We developed and exploited a modified cross-mission DInSAR-driven combination technique based MQQA method and a time-dependent geotechnical model. The data merging methods make it possible to measure slow and long-lasting ground deformation process continuously. The technique has been successfully applied to study the long-term evolution of the ground subsidence of Shanghai eastern coastal areas from 2007 to 2017. A cross-comparison analysis between the combined deformation time-series and levelling datasets has also been conducted. The result confirms the validity of the novel multi-sensor data merging approach.
- (IV)
- On the characterization and forecasting of ground displacements of ocean-reclaimed lands []
In this work, we proved the usefulness and applicability of the geotechnical model for ocean-reclaimed areas. The results demonstrate that the geotechnical model used to characterize the deformation evolution of Shanghai can also be successfully used to retrieve the deformation of other reclaimed regions in Shenzhen. Moreover, by comparing the geotechnical model with other models, our results are more reasonable for deformation prediction.
- (V)
- Investigation of ground displacement in Saint Petersburg, Russia, using multiple-track differential synthetic aperture radar interferometry []
We investigated ground displacement in the Saint Petersburg area using a multi-track InSAR technique, applied to the S-1-A/B dataset that consists of 65 images with ascending passes and 64 images with descending passes acquired from 2016 to 2018. The deformation signals are concentrated mainly in the up-down direction as compared with the east–west direction. The RMSEs of the differences between the displacements from InSAR and GPS are 3.7 mm and 2.6 mm for the up-down and the east–west directions, respectively.
- (VI)
- Long-term flood-hazard modeling for coastal areas using InSAR measurements and a hydrodynamic model: The case study of Lingang New City, Shanghai []
We generated an up-to-date, high resolution, and precise DEM of the study area with a pair of TanDEM-X images acquired on 4 November 2012. It was achieved by bistatic interferometry. We also presented an innovative method by combining two-dimensional flood models and InSAR techniques and evaluated the flood risk of Lingang New City in Shanghai under different SLR and ground subsidence scenarios. We concluded that even with rapid SLR and extensive ground subsidence, the flood inundation would occur mainly in the low-lying waterfront areas due to the protection of current seawalls. Second, due to the low exposure of population and property, the flood impacts are presently limited but may significantly increase soon with rapid urbanization and development.
- (VII)
- Flood risks in sinking delta cities []
SLR and ground subsidence are projected to augment the risk of inundation and reliance on flood defenses for delta cities. Combining reliability analysis with a hydrodynamic model, we quantified the influence of projected relative SLR on dike damages and flood hazards for Shanghai. We find that flooding tends to occur in low-lying and poorly protected rural areas of the city, even under the current sea level. Without adaptive measures, the risk increases by a factor of 3–160 across the densely populated floodplain under projected SLR to 2100.
4.2. Derivation of Storm Surge-Induced Submerged Area and Ocean Wave Fields Using Satellite Images and In Situ Coastal Data
4.2.1. Results
The TAC approach demonstrated that short-term MSL and tidal variability is correlated at many locations in the world ocean, although results are spatially variable. Around 90% of Pacific Ocean locations had significant correlations in at least one tidal constituent [], with many regions of substantial correlations, such as Japan, the South China Sea, and Australia. Analyses of the highest astronomical tide (δ-HAT) found that 35% of gauges surveyed had a sensitivity to sea level fluctuation of at least 50 mm under a 1 m sea level change (i.e., more than 5% variability) in the Pacific Ocean.
Of these results, the most significant positive TACs and δ-HAT was observed in Hong Kong. Therefore, a focused regionally study was carried out to closely investigate the tidal variability in Hong Kong []. Hong Kong has a well-developed network of 12 tide gauges, a few of which have records over 40 years long. These data were acquired from partnerships with the Hong Kong Observatory (HKO) and the Hong Kong Marine Department (HKMD). Detailed TAC analyses were carried out which considered the largest astronomical tides as well as the shallow-water overtides. At locations within highly developed harbors (e.g., Victoria Harbor and Tai Po Kau), values of the combined tidal variability expressed by the δ-HAT were highly sensitive to MSL variability and may further increase local flood levels under future MSL rise. Other locations in Hong Kong only demonstrated moderately significant TACs in individual tidal constituents but not for combined tidal amplitudes, suggesting that the dynamics in enclosed harbor areas may be frequency-dependent and related to resonance or frictional changes. Since Hong Kong has carried out extensive and rapid harbor modifications and land reclamation over the past century, this is hypothesized to be the likely cause of the observed tidal sensitivity. A map of the δ-HATs at Hong Kong locations is displayed in Figure 11 below.
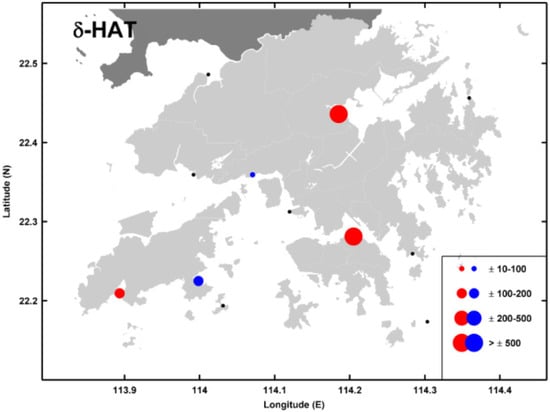
Figure 11.
The tidal anomaly correlation computed from the combination of the four largest tidal constituent amplitudes (given by the detrended sum of the M2 + S2 + K1 + O1) as a proxy for the change in the approximate highest astronomical tide (δ-HAT) relative to detrended MSL in Hong Kong, with the marker size showing the relative magnitude according to the legend, in units of mm m-1. Red/blue markers indicate positive/negative TACs, and black markers indicate TACs that are not significantly different from zero (refer to []).
An improved TAC approach was used at 73 tide gauge locations in the Indian Ocean by employing the EEMD [] method to consider multiple frequency bands of correlation (e.g., sub-annual, annual, and interannual) between MSL and tidal amplitudes. Our results showed that nearly all locations analyzed showed significant TACs in at least one frequency band, with about half of all sites being effective in all three bands in at least one of the crucial tides. Interestingly, some locations have a different trend in different frequency ranges. This suggests that tides and MSL can be influenced by multiple mechanisms active at different timescales. The annual band is often related to yearly monsoon patterns and associated causes (e.g., river discharge) in certain regions.
Conversely, the interannual band is likely related to other forms of climate variability, such as the Southern Oscillation (SO), with variations of a few years. We also revealed some regional coherence of tidal variability. The TACs of the daily tides are the dominant factors in the Arabian Sea, in most of Australia, and in Antarctica. By contrast, the TACs of the semidiurnal tides (especially M2) are more dominant in the Bay of Bengal and along most of the African coast. The δ-HAT analyses generally showed significant but small-to-moderate magnitude results, although there were some notable exceptions to this generalization. Adelaide, Wyndham, and Williamstown in Australia had exceptionally large positive δ-HATs. These locations are in semi-enclosed regions where local tidal resonances and harbor modifications may be responsible for the significant changes in tides; this further supports the results found in Hong Kong that harbors can be especially sensitive tidal variability. Other locations that showed large δ-HATs were the northeastern coast and the southern tip of Africa and the Ganges Delta. These locations may experience higher tidal ranges under future scenarios of rising mean sea levels. Figure 12 displays the results for the δ-HAT analyses in the Indian Ocean for three frequency bands of variability, with four important sub-regions shown in each sub-panel.
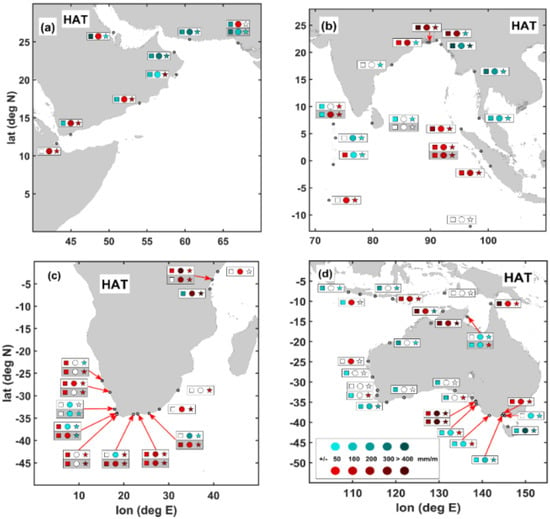
Figure 12.
δ-HAT (combined M2, S2, K1, and O1 detrended tidal variations) in four different regions of the Indian Ocean: (a) the Arabian Sea, (b) the Bay of Bengal, (c) Africa, and (d) the Australian region. Symbols inside boxes indicate three different frequency bands: squares are the sub-annual (SA) band, circles are the annual (ANN) band, and stars are the interannual (IA) band. Station names are also indicated. Color shading of the symbols indicate positive (shades of red) and negative (shades of blue) δ-HATs according to legend at the bottom right (refer to []).
4.2.2. Subproject Conclusions
The correlations of short-term tidal variability with short-term sea level fluctuations as parametrized by the TAC and δ-HAT method provide a novel and valuable metric for understanding future SLR’s possible amplification tidal-induced mechanisms. This approach is especially useful in coastal regions with large populations and significant infrastructure. The impacts of rising MSL and changing tides may impact logistics, public health, and many other factors. Throughout the Dragon 4 project, our results revealed that TACs are most impactful in a developed harbor region, often due to anthropogenic modifications. These regions are susceptible to changes in total water levels. Therefore, the effects of tidal changes should be included in the projections of future SLR scenarios in order to facilitate effective and complete coastal planning in the coming century. Furthermore, comprehensive understanding about tidal changes associated with changing background water levels may also be instructive about future storm surge related inundation. Both tides and storms are long-wave processes; thus, changes in one aspect of water level variability (i.e., a significant positive δ-HAT) may also indicate a future increase in storm surge levels at the exact location.
4.3. Projection of Sea Level Rise and Potential Submerged Area in Coastal Regions
4.3.1. Results
In this sub-project, the possible inundation risk of the YRD under the background of SLR was investigated, combining satellite data and numerical models. By the middle and end of the 21st century, SLR in the East China Sea is first predicted based on the statistical analysis of historical satellite altimeter data. Next, a regional tide model of the East China Sea is constructed by using the primitive equation Finite-Volume Community Ocean Model (FVCOM). A storm surge model of the YRD is developed (here, we take typhoons Fung-wong and Wipha as examples) in order to analyze the possible inundation area. The results show that the submergence mainly occurs in Jiangsu Province, especially Yan Cheng and Lian Yungang cities.
As shown in Figure 13, the maximum possible inundation caused by sea-level rise through tidal propagation is 2.5 × 103 km2 by 2100, 87.2% larger than that at the current sea level. During the two storm surges (Fung-wong in 2050 and Wipha in 2100), the inundation area is 8.3 × 102~2.7 × 103 km2. Submergence mainly occurs in Jiangsu Province, especially in Yancheng and Lianyungang cities. Our results suggest that the breakwater height should be at least 2 m in order to mitigate the combined impact of SLR and storm surges.
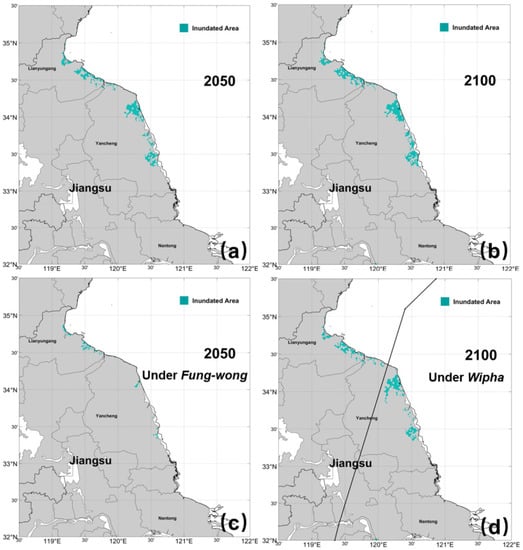
Figure 13.
Possible inundation (blue color) of the YRD due to SLR in 2050 (a) and 2100 (b) without sea walls. (c,d) are the same as (a,b), but for the cases where typhoons such as Fung-wong (2014) and Wipha (2007) approaching or passing by the study area. The solid black line shows the typhoon track.
4.3.2. Subproject Conclusions
Without any coastal protection, the maximum possible inundation caused by SLR through tidal propagation by 2100 is 2.5 × 103 km2, which is 87.2% larger than that at current sea level, and the top inundation area possible during the two storm surges considered here is 8.3 × 102~2.7 × 103 km2.
With 4 m high breakwater along the coastlines, there is no submergence observed in the case studies here under SLR by 2100, while the inundation is about 15.4 km2 during typhoons such as Wipha when the breakwater is 2 m high.
The submergence mainly occurs in Jiangsu Province, especially Yan Cheng and Lian Yungang cities. Our results suggest that the breakwater height should be at least 2 m in order to mitigate the combined impact of SLR and storm surges.
5. Main Conclusions and Projections of Project
During our Dragon 4 project lifetime (ID 32294), we have performed a series of heterogeneous experiments relying on the exploitation of differential SAR interferometry in coastal regions subject to ground subsidence and flood risk. In addition, we have an increased the understanding of the impacts of tidal evolution on coastal zones. Changes in tides are an important and often-neglected part of coastal water level changes, and recent work has demonstrated that tides may be changing as sea level rises. Thus, tides should be included in total water level projections and analyses, as shown by the work performed throughout the Dragon 4 project.
We have also taken advantage of the existing cooperation between European and Chinese parties to create a network of knowledge and collaboration beneficial for future methodological and experimental developments. Specifically, we focused on two major delta river regions in China, the YRD, and the PRD. We have used these two natural laboratories to check the performance of under-developing novel DInSAR approaches. We have used the measurements of ground deformations in the selected coastal regions to feed flooding models and to foresee the future evolution of the coastal areas of the following decades.
The achieved results represent the starting point of further analyses to be performed in the years to come, primarily aimed at the following:
- (i)
- New methods are being developed for the efficient processing of large-swath InSAR data and the combination of ground-based and satellite-based InSAR measurements, especially in disaster-prone coastal areas. In this framework, the joint utilization of SAR data acquired at different polarizations, wavelengths and illumination angles will become more and more prevailing with the advent of new global-scale SAR missions, for instance, the U.S.-India NiSAR [,] and the Argentinian SAOCOM [] sensors constellations operating at L-band, which will indeed trigger further improvements of the InSAR/SAR technology.
- (ii)
- Using SAR satellite swarms mounted on drones [,] and managed by regional authorities to help image a relatively small area on the ground, especially in coastal regions, through different viewing illumination angles. These configurations will help in better reconstructing the 3D profiles of the terrain displacement. In addition, geosynchronous SAR satellites [] offer the possibility to observe in extensive continuity regions on Earth (at the continental scale) and collected tons of data to be processed and interpreted at suitable times.
- (iii)
- Development and application of artificial intelligence (AI) methodologies [] to extract useful information from tons of processed InSAR data related to some specific regions of Earth’s surface. In particular, there is a growing interest in the SAR community in the application of AI methods for a variety of tasks, such as (1) object detection, (2) terrain surface classification, (3) surface displacement classification, (4) parameter inversion, and (5) de-speckling. All of these approaches will benefit from the availability of SAR data acquired with enhanced time repetition frequencies in the areas of interest.
- (iv)
- Enhancing the knowledge of physical mechanisms responsible for land changes utilizing coherent SAR change detection methods relying on microwave and optical EO data. The study of the effects on the small and global scale of the present-day global climate changes will likely be further enriched by the improved performance of new radar satellite. Moreover, studies on overpopulation, human mass movements, the effects of epidemics on the Earth environment, and the interrelations between the different sources of environmental changes are expected to increase in number and relevance in the following years. In this context, the SAR technology and the differential SAR interferometry methods, which have been developed over almost the last 25 years, are expected to evolve in new directions to extract new pieces of information that are still hidden both in single radar microwave image and large sequences of data (the big data paradigm) (see for instance [,]).
- (v)
- Enhancing the knowledge of tidal evolution and sea level rise patterns and mechanisms in coastal zones, especially in delta regions of interest, through the utilization of next-generation satellite altimeters such as the recently launched Sentinel-6 platform and the Chinese Haiyang (HY) instrument series.
Author Contributions
Conceptualization, Q.Z. and A.P.; methodology, Q.Z., J.P., A.D. and Q.X.; validation, Q.Z. and A.P.; formal analysis and interpretation of the results, Q.Z., J.P., A.D., Q.X., M.T., Z.L., V.Z., F.F., P.M. and A.P.; writing—original draft preparation, Q.Z., A.D., Q.X., M.T., Z.L. and A.P.; writing—review and editing, Q.Z., A.D. and A.P.; visualization, M.T., Z.L. and F.F.; supervision, Q.Z. and A.P.; project administration, Q.Z. and A.P.; funding acquisition, Q.Z. and A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of China, grant number 41801337 and 41376035, by the Research Grants of Science and Technology Commission of Shanghai Municipality, grant number 18ZR1410800, by the Fundamental Research Funds for the Central Universities of China, and by the Fund of the Director of the Key Laboratory of Geographic Information Science (Ministry of Education), East China Normal University, grant No. KLGIS2017C03.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (#41801337 and #41376035), by the Research Grants of Science and Technology Commission of Shanghai Municipality through Project 18ZR1410800, by the Fundamental Research Funds for the Central Universities of China, and by the Fund of the Director of the Key Laboratory of Geographic Information Science (Ministry of Education), East China Normal University (grant no. KLGIS2017C03). This work has been performed within the Dragon 4 ESA project ID 32294 titled “Integrated analysis of the combined risk of ground subsidence, sea-level rise, and natural hazards in coastal delta regions”, the General Research Fund of Hong Kong Research Grants Council (RGC) (CUHK 14303818), the talent startup fund of Jiangxi Normal University, and the Dragon 5 ESA project ID 58351 titled “Global Climate Change, Sea Level Rise, Extreme Events and Local Ground Subsidence Effects in Coastal and River Delta Regions through Novel and Integrated Remote Sensing Approaches (GREENISH)”. The Italian Space Agency provided us with the CSK SAR images, whereas ENV data were obtained through the CAT-ESA project n. 11461.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gornitz, V. Global coastal hazards from future sea level rise. Glob. Planet. Chang. 1991, 3, 379–398. [Google Scholar] [CrossRef]
- Wdowinski, S.; Bray, R.; Kirtman, B.P.; Wu, Z. Increasing flooding hazard in coastal communities due to rising sea level: Case study of Miami Beach, Florida. Ocean Coast. Manag. 2016, 126, 1–8. [Google Scholar] [CrossRef]
- Pethick, J.; Orford, J.D. Rapid rise in effective sea-level in southwest Bangladesh: Its causes and contemporary rates. Glob. Planet. Chang. 2013, 111, 237–245. [Google Scholar] [CrossRef]
- Rani, N.N.V.S.; Satyanarayana, A.N.V.; Bhaskaran, P.K. Coastal vulnerability assessment studies over India: A review. Nat. Hazards 2015, 77, 405–428. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Verlaan, M.; Feyen, L. Extreme sea levels on the rise along Europe’s coasts. Earth Futur. 2017, 5, 304–323. [Google Scholar] [CrossRef]
- Janekovic, I.; Mihanović, H.; Vilibić, I.; Tudor, M. Extreme cooling and dense water formation estimates in open and coastal regions of the Adriatic Sea during the winter of 2012. J. Geophys. Res. Oceans 2014, 119, 3200–3218. [Google Scholar] [CrossRef]
- Lambeck, K.; Antonioli, F.; Purcell, A.; Silenzi, S. Sea-level change along the Italian coast for the past 10,000 yr. Quat. Sci. Rev. 2004, 23, 1567–1598. [Google Scholar] [CrossRef]
- Hu, J.; Shi, B.; Inyang, H.I.; Chen, J.; Sui, Z. Patterns of subsidence in the lower Yangtze Delta of China: The case of the Suzhou-Wuxi-Changzhou Region. Environ. Monit. Assess. 2008, 153, 61–72. [Google Scholar] [CrossRef]
- Zhao, Q.; Lin, H.; Gao, W.; Zebker, H.A.; Chen, A.; Yeung, K. InSAR detection of residual settlement of an ocean reclamation engineering project: A case study of Hong Kong International Airport. J. Oceanogr. 2011, 67, 415–426. [Google Scholar] [CrossRef]
- Tang, Y.-Q.; Yang, P.; Zhao, S.-K.; Zhang, X.; Wang, J.-X. Characteristics of deformation of saturated soft clay under the load of Shanghai subway line No. 2. Environ. Earth Sci. 2007, 54, 1197–1203. [Google Scholar] [CrossRef]
- Grez, P.W.; Aguirre, C.; Farías, L.; Contreras-López, M.; Masotti, Í. Evidence of climate-driven changes on atmospheric, hydrological, and oceanographic variables along the Chilean coastal zone. Clim. Chang. 2020, 163, 633–652. [Google Scholar] [CrossRef]
- Devlin, A.T.; Jay, D.A.; Talke, S.A.; Zaron, E.D.; Pan, J.; Lin, H. Coupling of sea level and tidal range changes, with implications for future water levels. Sci. Rep. 2017, 7, 17021. [Google Scholar] [CrossRef]
- Feng, X.; Tsimplis, M.; Woodworth, P.L. Nodal variations and long-term changes in the main tides on the coasts of China. J. Geophys. Res. Oceans 2015, 120, 1215–1232. [Google Scholar] [CrossRef]
- Pan, J.; Lai, W.; Devlin, A.T. Channel-Trapped Convergence and Divergence of Lateral Velocity in the Pearl River Estuary: Influence of Along-Estuary Variations of Channel Depth and Width. J. Geophys. Res. Oceans 2020, 125, e2019JC015369. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, G.; Wang, Q.; Yang, T.; Liu, M.; Gao, W.; Falabella, F.; Mastro, P.; Pepe, A. Generation of long-term InSAR ground displacement time-series through a novel multi-sensor data merging technique: The case study of the Shanghai coastal area. ISPRS J. Photogramm. Remote Sens. 2019, 154, 10–27. [Google Scholar] [CrossRef]
- Ding, J.; Zhao, Q.; Tang, M.; Calò, F.; Zamparelli, V.; Falabella, F.; Liu, M.; Pepe, A. On the Characterization and Forecasting of Ground Displacements of Ocean-Reclaimed Lands. Remote Sens. 2020, 12, 2971. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, Q.; Ding, J.; Fedotov, A.A.; Badenko, V.; Liu, M.; Pepe, A. Investigation of the ground displacement in Saint Petersburg, Russia, using multiple-track differential synthetic aperture radar interferometry. Int. J. Appl. Earth Obs. Geoinf. 2020, 87, 102050. [Google Scholar] [CrossRef]
- Yin, J.; Zhao, Q.; Yu, D.; Lin, N.; Kubanek, J.; Ma, G.; Liu, M.; Pepe, A. Long-term flood-hazard modeling for coastal areas using InSAR measurements and a hydrodynamic model: The case study of Lingang New City, Shanghai. J. Hydrol. 2019, 571, 593–604. [Google Scholar] [CrossRef]
- Yin, J.; Jonkman, S.; Lin, N.; Yu, D.; Aerts, J.; Wilby, R.; Pan, M.; Wood, E.; Bricker, J.; Ke, Q.; et al. Flood Risks in Sinking Delta Cities: Time for a Reevaluation? Earth Futur. 2020, 8, e2020EF001614. [Google Scholar] [CrossRef]
- Mastro, P.; Falabella, F.; Pepe, A. An Adaptive Statistical Multi-grid DInSAR Technique for Studying Multi-scale Earth Surface Deformation Phenomena. In Proceedings of the 2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 32–35. [Google Scholar] [CrossRef]
- Pramudya, F.S.; Pan, J.; Devlin, A. Estimation of Significant Wave Height of Near-Range Traveling Ocean Waves Using Sentinel-1 SAR Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1067–1075. [Google Scholar] [CrossRef]
- Lei, X.; Pan, J.; Devlin, A. An ultraviolet to visible scheme to estimate chromophoric dissolved organic matter absorption in a Case-2 water from remote sensing reflectance. Front. Earth Sci. 2020, 14, 384–400. [Google Scholar] [CrossRef]
- Pepe, A. Multi-Temporal Small Baseline Interferometric SAR Algorithms: Error Budget and Theoretical Performance. Remote Sens. 2021, 13, 557. [Google Scholar] [CrossRef]
- Pepe, A.; Bonano, M.; Zhao, Q.; Yang, T.; Wang, H. The Use of C-/X-Band Time-Gapped SAR Data and Geotechnical Models for the Study of Shanghai’s Ocean-Reclaimed Lands through the SBAS-DInSAR Technique. Remote Sens. 2016, 8, 911. [Google Scholar] [CrossRef]
- Pepe, A.; Solaro, G.; Calo, F.; Dema, C. A Minimum Acceleration Approach for the Retrieval of Multiplatform InSAR Deformation Time Series. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3883–3898. [Google Scholar] [CrossRef]
- Yu, L.; Yang, T.; Zhao, Q.; Liu, M.; Pepe, A. The 2015–2016 Ground Displacements of the Shanghai Coastal Area Inferred from a Combined COSMO-SkyMed/Sentinel-1 DInSAR Analysis. Remote Sens. 2017, 9, 1194. [Google Scholar] [CrossRef]
- Ma, G.; Zhao, Q.; Wang, Q.; Liu, M. On the Effects of InSAR Temporal Decorrelation and Its Implications for Land Cover Classification: The Case of the Ocean-Reclaimed Lands of the Shanghai Megacity. Sensors 2018, 18, 2939. [Google Scholar] [CrossRef] [PubMed]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Gerhard, K.; Alberto, M.; Hauke, F.; Irena, H.; Marian, W.; Marwan, Y.; Manfred, Z. TanDEM-X: A satellite formation for high-resolution radar interferometry. Proc. Int. Radar Symp. 2007, 45, 3317–3341. [Google Scholar]
- Kubanek, J.; Westerhaus, M.; Schenk, A.; Aisyah, N.; Brotopuspito, K.S.; Heck, B. Volumetric change quantification of the 2010 Merapi eruption using TanDEM-X InSAR. Remote Sens. Environ. 2015, 164, 16–25. [Google Scholar] [CrossRef]
- Kubanek, J.; Richardson, J.; Charbonnier, S.J.; Connor, L.J. Lava flow mapping and volume calculations for the 2012–2013 Tolbachik, Kamchatka, fissure eruption using bistatic TanDEM-X InSAR. Bull. Volcanol. 2015, 77, 106. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35, L16302. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Falabella, F.; Serio, C.; Masiello, G.; Zhao, Q.; Pepe, A. A Multigrid InSAR Technique for Joint Analyses at Single-Look and Multi-Look Scales. IEEE Geosci. Remote Sens. Lett. 2021, 1–5. [Google Scholar] [CrossRef]
- Xiong, T.; Zhang, W.; Boerner, W. Phase unwrapping method based on image segmentation. Int. J. Remote Sens. 2008, 29, 4871–4877. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Mora, O.; Mallorqui, J.; Broquetas, A. Linear and nonlinear terrain deformation maps from a reduced set of interferometric sar images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2243–2253. [Google Scholar] [CrossRef]
- Tebaldini, S.; Monti-Guarnieri, A.V. On the Role of Phase Stability in SAR Multibaseline Applications. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2953–2966. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, X.; Hanssen, R.; Malhotra, R.; Chang, L. Fast Statistically Homogeneous Pixel Selection for Covariance Matrix Estimation for Multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1213–1224. [Google Scholar] [CrossRef]
- Parizzi, A.; Brcic, R. Adaptive InSAR Stack Multilooking Exploiting Amplitude Statistics: A Comparison Between Different Techniques and Practical Results. IEEE Geosci. Remote Sens. Lett. 2010, 8, 441–445. [Google Scholar] [CrossRef]
- Monti-Guarnieri, A.V.; Tebaldini, S. On the Exploitation of Target Statistics for SAR Interferometry Applications. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3436–3443. [Google Scholar] [CrossRef]
- Zhao, Q.; Pepe, A.; Gao, W.; Lu, Z.; Bonano, M.; He, M.L.; Wang, J.; Tang, X. A DInSAR Investigation of the Ground Settlement Time Evolution of Ocean-Reclaimed Lands in Shanghai. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1763–1781. [Google Scholar] [CrossRef]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorqui, J.J.; Berardino, P.; Sansosti, E. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Devlin, A.T.; Jay, D.A.; Zaron, E.D.; Talke, S.A.; Pan, J.; Lin, H. Tidal Variability Related to Sea Level Variability in the Pacific Ocean. J. Geophys. Res. Oceans 2017, 122, 8445–8463. [Google Scholar] [CrossRef]
- Devlin, A.T.; Pan, J.; Lin, H. Tidal variability in the Hong Kong region. Ocean Sci. 2019, 15, 853–864. [Google Scholar] [CrossRef]
- Devlin, A.T.; Pan, J.; Lin, H. Multi-Timescale Analysis of Tidal Variability in the Indian Ocean Using Ensemble Empirical Mode Decomposition. J. Geophys. Res. Oceans 2020, 125, e2020JC016604. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J. Sea-Level Rise from the Late 19th to the Early 21st Century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- Hamlington, B.D.; Frederikse, T.; Nerem, R.S.; Fasullo, J.T.; Adhikari, S. Investigating the Acceleration of Regional Sea Level Rise During the Satellite Altimeter Era. Geophys. Res. Lett. 2020, 47, e2019GL086528. [Google Scholar] [CrossRef]
- Domingues, C.M.; Church, J.A.; White, N.J.; Gleckler, P.J.; Wijffels, S.; Barker, P.M.; Dunn, J.R. Improved estimates of upper-ocean warming and multi-decadal sea-level rise. Nature 2008, 453, 1090–1093. [Google Scholar] [CrossRef]
- Merrifield, M.A.; Merrifield, S.T.; Mitchum, G.T. An Anomalous Recent Acceleration of Global Sea Level Rise. J. Clim. 2009, 22, 5772–5781. [Google Scholar] [CrossRef]
- Jay, D.A. Evolution of tidal amplitudes in the eastern Pacific Ocean. Geophys. Res. Lett. 2009, 36, L04603. [Google Scholar] [CrossRef]
- Ray, R.D. Secular changes in the solar semidiurnal tide of the western North Atlantic Ocean. Geophys. Res. Lett. 2009, 36, L19601. [Google Scholar] [CrossRef]
- Haigh, I.D.; Pickering, M.D.; Green, J.A.M.; Arbic, B.K.; Arns, A.; Dangendorf, S.; Hill, D.F.; Horsburgh, K.; Howard, T.; Idier, D.; et al. The Tides They Are A-Changing: A Comprehensive Review of Past and Future Nonastronomical Changes in Tides, Their Driving Mechanisms, and Future Implications. Rev. Geophys. 2020, 58, e2018RG000636. [Google Scholar] [CrossRef]
- Holleman, R.; Stacey, M.T. Coupling of Sea Level Rise, Tidal Amplification, and Inundation. J. Phys. Oceanogr. 2014, 44, 1439–1455. [Google Scholar] [CrossRef]
- Familkhalili, R.; Talke, S.A. The effect of channel deepening on tides and storm surge: A case study of Wilmington, NC. Geophys. Res. Lett. 2016, 43, 9138–9147. [Google Scholar] [CrossRef]
- Colosi, J.A.; Munk, W. Tales of the Venerable Honolulu Tide Gauge. J. Phys. Oceanogr. 2006, 36, 967–996. [Google Scholar] [CrossRef]
- Arns, A.; Dangendorf, S.; Jensen, J.; Talke, S.; Bender, J.; Pattiaratchi, C. Sea-level rise induced amplification of coastal protection design heights. Sci. Rep. 2017, 7, 40171. [Google Scholar] [CrossRef] [PubMed]
- Sweet, W.V.; Park, J. From the extreme to the mean: Acceleration and tipping points of coastal inundation from sea level rise. Earth Futur. 2014, 2, 579–600. [Google Scholar] [CrossRef]
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Leffler, K.E.; Jay, D.A. Enhancing tidal harmonic analysis: Robust (hybrid L1/L2) solutions. Cont. Shelf Res. 2009, 29, 78–88. [Google Scholar] [CrossRef]
- Cartwright, D.E.; Tayler, R.J. New Computations of the Tide-generating Potential. Geophys. J. R. Astron. Soc. 1971, 23, 45–73. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Sweet, W.; Zervas, C.; Gill, S.; Park, J. Hurricane sandy inundation probabilities today and tomorrow. Bull. Am. Meteorol. Soc. 2013, 94, S17–S20. [Google Scholar]
- Church, J.; Clark, P.; Cazenave, A.; Gregory, J.; Jevrejeva, S.; Levermann, A.; Merrifield, M.; Milne, G.; Nerem, R.S.; Nunn, P.; et al. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Church, J. Sea Level Change. Available online:http://drs.nio.org/drs/handle/2264/4605 (accessed on 23 August 2021).
- Smith, I. Smith’s Elements of Soil Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Plant, G.W. Geology, surveying, reclamation settlement. Site Prep. New Hong Kong Int. Airpt. 1998, 1, 515–517. [Google Scholar]
- Yu, D.; Lane, S.N. Urban fluvial flood modelling using a two-dimensional diffusion-wave treatment, part 1: Mesh resolution effects. Hydrol. Process. 2005, 20, 1541–1565. [Google Scholar] [CrossRef]
- Yu, D.; Lane, S.N. Urban fluvial flood modelling using a two-dimensional diffusion-wave treatment, part 2: Development of a sub-grid-scale treatment. Hydrol. Process. 2005, 20, 1567–1583. [Google Scholar] [CrossRef]
- Fan, D.; Wu, Y.; Zhang, Y.; Burr, G.; Huo, M.; Li, J. South Flank of the Yangtze Delta: Past, present, and future. Mar. Geol. 2017, 392, 78–93. [Google Scholar] [CrossRef]
- Rosen, P.; Hensley, S.; Shaffer, S.; Edelstein, W.; Kim, Y.; Centre, S.A. The NASA-ISRO SAR (NISAR) Mission dual-band Radar instrument preliminary design. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3832–3835. [Google Scholar]
- Rosen, P.A.; Kim, Y.; Kumar, R.; Misra, T.; Bhan, R.; Sagi, V.R. Global persistent SAR sampling with the NASA-ISRO SAR (NISAR) mission. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017. [Google Scholar] [CrossRef]
- Euillades, P.A.; Euillades, L.D.; Azcueta, M.; Sosa, G.J. SAOCOM 1A Interferometric Error Model and Analysis. Proceedings of Fringe 2015: Advances in the Science and Applications of SAR Interferometry and Sentinel-1 InSAR Workshop, Edinburgh, UK, 7–31 August 2015. [Google Scholar] [CrossRef][Green Version]
- Li, C.J.; Ling, H. Synthetic aperture radar imaging using a small consumer drone. In Proceedings of the 2015 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Vancouver, BC, Canada, 19–24 July 2015; pp. 685–686. [Google Scholar] [CrossRef]
- Oré, G.; Alcântara, M.S.; Góes, J.A.; Oliveira, L.P.; Yepes, J.; Teruel, B.; de Castro, V.L.B.; Bins, L.S.; Castro, F.; Luebeck, D.; et al. Crop Growth Monitoring with Drone-Borne DInSAR. Remote Sens. 2020, 12, 615. [Google Scholar] [CrossRef]
- Monti-Guarnieri, A.V.; Broquetas, A.; Recchia, A.; Rocca, F.; Ruiz-Rodon, J. Advanced Radar Geosynchronous Observation System: ARGOS. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1406–1410. [Google Scholar] [CrossRef]
- Cigna, F.; Tapete, D. Sentinel-1 Big Data Processing with P-SBAS InSAR in the Geohazards Exploitation Platform: An Experiment on Coastal Land Subsidence and Landslides in Italy. Remote Sens. 2021, 13, 885. [Google Scholar] [CrossRef]
- Papoutsis, I.; Kontoes, C.; Alatza, S.; Apostolakis, A.; Loupasakis, C. InSAR Greece with Parallelized Persistent Scatterer Interferometry: A National Ground Motion Service for Big Copernicus Sentinel-1 Data. Remote Sens. 2020, 12, 3207. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).