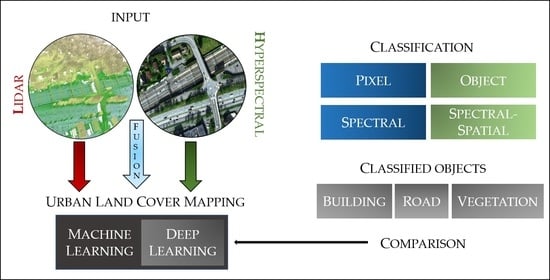
Hyperspectral and Lidar Data Applied to the Urban Land Cover Machine Learning and Neural-Network-Based Classification: A Review
Abstract
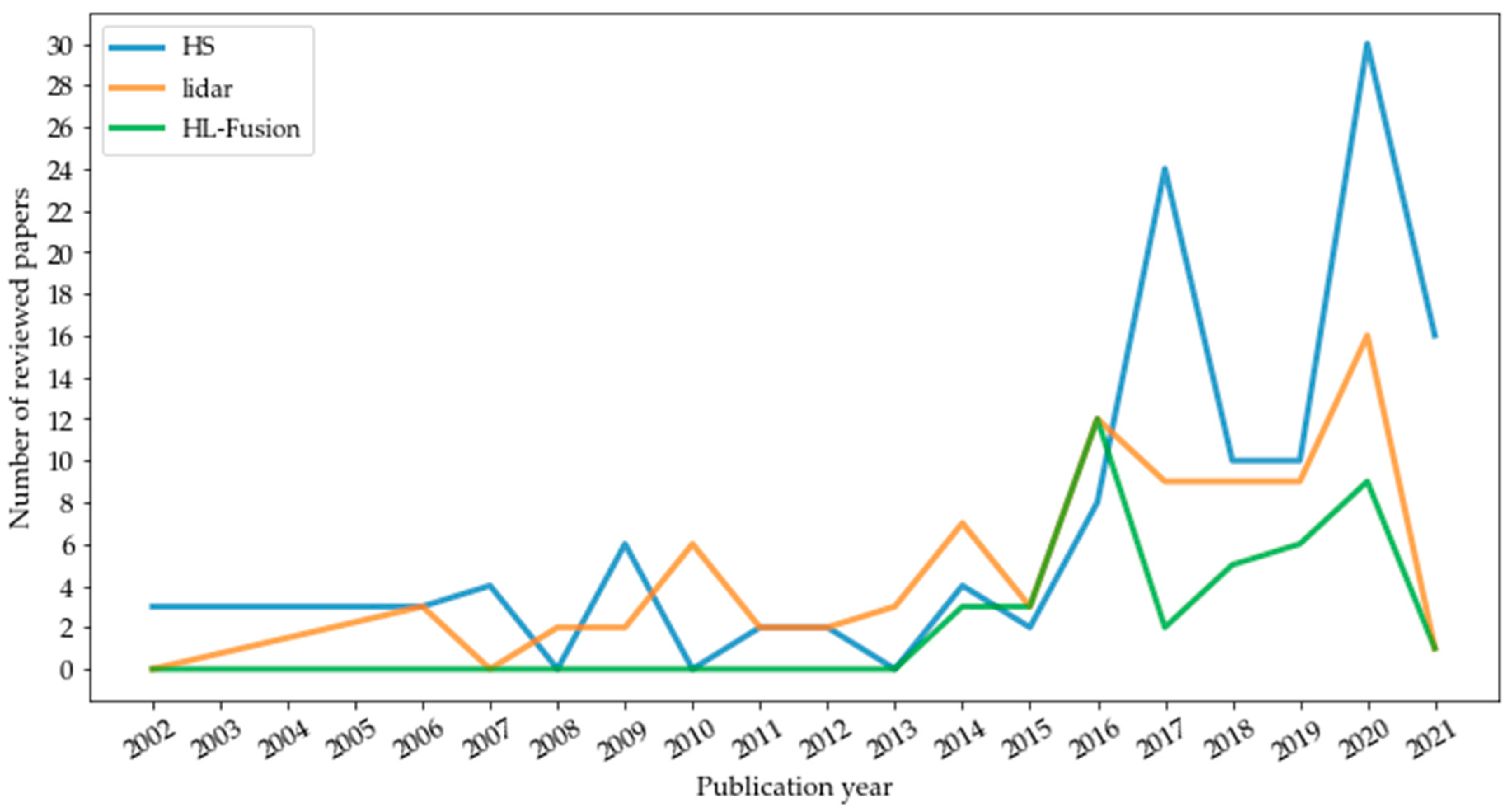
:1. Introduction
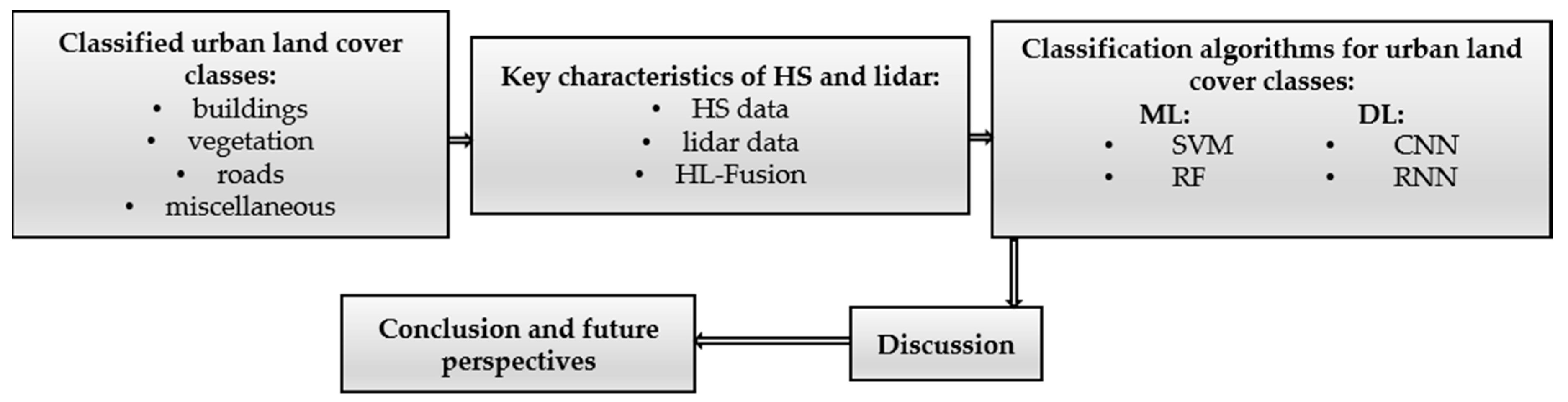
2. Classified Urban Land Cover Classes
2.1. Buildings
2.2. Vegetation
2.3. Roads
2.4. Miscellaneous
3. Key Characteristics of Hyperspectral and Lidar Data
3.1. Hyperspectral (HS) Images
3.1.1. Spectral Features
3.1.2. Spatial Information
3.2. Lidar Data
3.2.1. Height Features and Their Derivatives (HD)
3.2.2. Intensity Data
3.2.3. Multiple-Return
3.2.4. Waveform-Derived Features
3.2.5. Eigenvalue-Based Features
3.3. Common Features—HS and Lidar
3.3.1. Textural Features
3.3.2. Morphological Features
3.4. Hyperspectral-Lidar Data Fusion
4. Classification of Urban Land Cover Classes
4.1. Support Vector Machines (SVM)
4.1.1. Buildings
4.1.2. Vegetation
4.1.3. Roads
4.2. Random Forest (RF)
4.2.1. Buildings
4.2.2. Vegetation
4.2.3. Roads
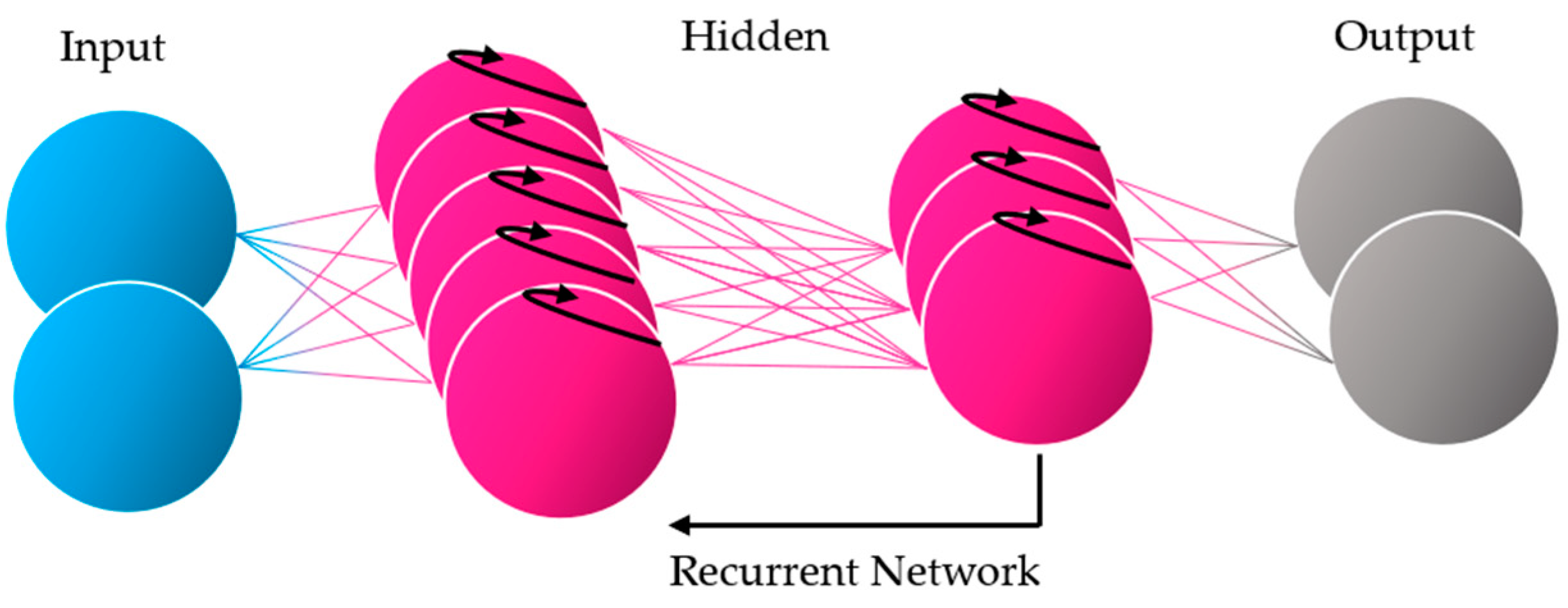
4.3. Convolutional Neural Network (CNN) and Recurrent Neural Network (RNN)
4.3.1. Buildings
4.3.2. Vegetation
4.3.3. Roads
5. Discussion
5.1. HS-Based Classification
5.2. Lidar-Based Classification
5.3. HL-Fusion Classification
6. Conclusions and Future Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Explanation |
| CHM | Canopy Height Model |
| CRF | Conditional Random Field |
| CNN | Convolutional Neural Network |
| CRNN | Convolutional Recurrent Neural Network |
| DBN | Deep Belief Networks |
| DL | Deep Learning |
| DSM | Digital Surface Model |
| DTM | Digital Terrain Model |
| GAN | Generative Adversarial Network |
| GLCM | Gray-Level Co-Occurrence Matrix |
| HD | Height features and their Derivatives |
| HS | Hyperspectral |
| HL-Fusion | Hyperspectral-Lidar fusion |
| IFOW | Instantaneous Field of View |
| Lidar | Light Detection and Ranging |
| LDA | Linear Discriminant Analysis |
| LBP | Local Binary Patterns |
| ML | Machine Learning |
| MCR | Multivariate Curve Resolution |
| NDI | Normalized Difference Index |
| NDVI | Normalized Difference Vegetation Index |
| nDSM | normalized Digital Surface Model |
| PCA | Principal Component Analysis |
| psuedoNDVI | Pseudo Normalized Difference Vegetation Index |
| RBF | Radial Basis Function |
| RF | Random Forest |
| RNN | Recurrent Neural Network |
| SAR | Synthetic Aperture Radar |
| SWIR | Shortwave-Infrared |
| SNR | Signal to Noise Ratio |
| SA | Stacked Autoencoder |
| SVM | Support Vector Machines |
| VNIR | Visible and Near-Infrared |
| VIS | Visible light |
References
- United Nations. 2018 Year in Review; United Nations: New York, NY, USA, 2018. [Google Scholar]
- Chen, F.; Kusaka, H.; Bornstein, R.; Ching, J.; Grimmond, C.S.B.; Grossman-Clarke, S.; Loridan, T.; Manning, K.W.; Martilli, A.; Miao, S. The integrated WRF/urban modelling system: Development, evaluation, and applications to urban environmental problems. Int. J. Climatol. 2011, 31, 273–288. [Google Scholar] [CrossRef]
- Lee, J.H.; Woong, K.B. Characterization of urban stormwater runoff. Water Res. 2000, 34, 1773–1780. [Google Scholar] [CrossRef]
- Forster, B.C. Coefficient of variation as a measure of urban spatial attributes, using SPOT HRV and Landsat TM data. Int. J. Remote Sens. 1993, 14, 2403–2409. [Google Scholar] [CrossRef]
- Sadler, G.J.; Barnsley, M.J.; Barr, S.L. Information extraction from remotely-sensed images for urban land analysis. In Proceedings of the 2nd European GIS Conference (EGIS’91), Brussels, Belgium, 2–5 April 1991; pp. 955–964. [Google Scholar]
- Carlson, T. Applications of remote sensing to urban problems. Remote Sens. Environ. 2003, 86, 273–274. [Google Scholar] [CrossRef]
- Coutts, A.M.; Harris, R.J.; Phan, T.; Livesley, S.J.; Williams, N.S.G.; Tapper, N.J. Thermal infrared remote sensing of urban heat: Hotspots, vegetation, and an assessment of techniques for use in urban planning. Remote Sens. Environ. 2016, 186, 637–651. [Google Scholar] [CrossRef]
- Huo, L.Z.; Silva, C.A.; Klauberg, C.; Mohan, M.; Zhao, L.J.; Tang, P.; Hudak, A.T. Supervised spatial classification of multispectral LiDAR data in urban areas. PLoS ONE 2018, 13. [Google Scholar] [CrossRef] [PubMed]
- Jürgens, C. Urban and suburban growth assessment with remote sensing. In Proceedings of the OICC 7th International Seminar on GIS Applications in Planning and Sustainable Development, Cairo, Egypt, 13–15 February 2001; pp. 13–15. [Google Scholar]
- Hepinstall, J.A.; Alberti, M.; Marzluff, J.M. Predicting land cover change and avian community responses in rapidly urbanizing environments. Landsc. Ecol. 2008, 23, 1257–1276. [Google Scholar] [CrossRef]
- Batty, M.; Longley, P. Fractal Cities: A Geometry of Form and Function; Academic Press: London, UK; San Diego, CA, USA, 1994. [Google Scholar]
- Ben-Dor, E.; Levin, N.; Saaroni, H. A spectral based recognition of the urban environment using the visible and near-infrared spectral region (0.4-1.1 µm). A case study over Tel-Aviv, Israel. Int. J. Remote Sens. 2001, 22, 2193–2218. [Google Scholar] [CrossRef]
- Herold, M.; Gardner, M.E.; Roberts, D.A. Spectral resolution requirements for mapping urban areas. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1907–1919. [Google Scholar] [CrossRef] [Green Version]
- Brenner, A.R.; Roessing, L. Radar Imaging of Urban Areas by Means of Very High-Resolution SAR and Interferometric SAR. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2971–2982. [Google Scholar] [CrossRef]
- Soergel, U. Review of Radar Remote Sensing on Urban Areas. In Radar Remote Sensing of Urban Areas; Soergel, U., Ed.; Springer: Berlin, Germany, 2010; pp. 1–47. [Google Scholar]
- Ghamisi, P.; Höfle, B.; Zhu, X.X. Hyperspectral and LiDAR data fusion using extinction profiles and deep convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10. [Google Scholar]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Debes, C.; Merentitis, A.; Heremans, R.; Hahn, J.; Frangiadakis, N.; Kasteren, T.v.; Liao, W.; Bellens, R.; Pizurica, A.; Gautama, S.; et al. Hyperspectral and LiDAR data fusion: Outcome of the 2013 GRSS data fusion contest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 550. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Fusion of hyperspectral and LiDAR remote sensing data for classification of complex forest areas. IEEE Trans. Geosci. Remote Sens. 2008. Available online: https://rslab.disi.unitn.it/papers/R59-TGARS-Dalponte.pdf (accessed on 2 May 2021).
- Sohn, H.-G.; Yun, K.-H.; Kim, G.-H.; Park, H.S. Correction of building height effect using LIDAR and GPS. In Proceedings of the International Conference on High Performance Computing and Communications, Sorrento, Italy, 21–23 September 2005; pp. 1087–1095. [Google Scholar]
- Guislain, M.; Digne, J.; Chaine, R.; Kudelski, D.; Lefebvre-Albaret, P. Detecting and correcting shadows in urban point clouds and image collections. In Proceedings of the Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 537–545. [Google Scholar]
- George, G.E. Cloud Shadow Detection and Removal from Aerial Photo Mosaics Using Light Detection and Ranging (LIDAR) Reflectance Images; The University of Southern Mississippi: Hattiesburg, MS, USA, 2011. [Google Scholar]
- Brell, M.; Segl, K.; Guanter, L.; Bookhagen, B. Hyperspectral and Lidar Intensity Data Fusion: A Framework for the Rigorous Correction of Illumination, Anisotropic Effects, and Cross Calibration. IEEE Trans. Geosci. Remote Sens. 2017. Available online: https://www.researchgate.net/publication/313687025_Hyperspectral_and_Lidar_Intensity_Data_Fusion_A_Framework_for_the_Rigorous_Correction_of_Illumination_Anisotropic_Effects_and_Cross_Calibration (accessed on 2 May 2021).
- Hui, L.; Di, L.; Xianfeng, H.; Deren, L. Laser intensity used in classification of LiDAR point cloud data. In Proceedings of the International Symposium on Geoscience and Remote Sensing, Boston, MA, USA, 8–11 July 2008. [Google Scholar]
- Liu, W.; Yamazaki, F. Object-based shadow extraction and correction of high-resolution optical satellite images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1296–1302. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, G.; Troy, A.; Cadenasso, M.L. Object-based land cover classification of shaded areas in high spatial resolution imagery of urban areas: A comparison study. Remote Sens. Environ. 2009, 113, 1769–1777. [Google Scholar] [CrossRef]
- Priem, F.; Canters, F. Synergistic use of LiDAR and APEX hyperspectral data for high-resolution urban land cover mapping. Remote Sens. 2016, 8, 787. [Google Scholar] [CrossRef] [Green Version]
- Luo, R.; Liao, W.; Zhang, H.; Zgang, L.; Scheunders, P.; Pi, Y.; Philips, W. Fusion of Hyperspectral and LiDAR Data for Classification of Cloud-Shadow Mixed Remote Sensed Scene. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017. Available online: https://telin.ugent.be/~wliao/Luo_JSTARS2017.pdf (accessed on 2 May 2021).
- Chen, Y.; Li, C.; Ghamisi, P.; Shi, C.; Gu, Y. Deep fusion of hyperspectral and LiDAR data for thematic classification. In Proceedings of the International Geoscience and Remote Sensing Symposium, Beijing, China, 10–14 July 2016. [Google Scholar]
- Li, H.; Ghamisi, P.; Soergel, U.; Zhu, X.X. Hyperspectral and LiDAR fusion using deep three-stream convolutional neural networks. Remote Sens. 2018, 10, 1649. [Google Scholar] [CrossRef] [Green Version]
- Yan, W.Y.; El-Ashmawy, N.; Shaker, A. Urban land cover classification using airborne LiDAR data: A review. Remote Sens. Environ. 2015. [Google Scholar] [CrossRef]
- Alonzo, M.; Bookhagen, B.; Roberts, D.A. Urban tree species mapping using hyperspectral and lidar data fusion. Remote Sens. Environ. 2014, 148, 70–83. [Google Scholar] [CrossRef]
- Kokkas, N.; Dowman, I. Fusion of airborne optical and LiDAR data for automated building reconstruction. In Proceedings of the ASPRS Annual Conference, Reno, Nevada, 1–5 May 2006. [Google Scholar]
- Torabzadeh, H.; Morsdorf, F.; Schaepman, M.E. Fusion of imaging spectroscopy and airborne laser scanning data for characterization of forest ecosystems. ISPRS J. Photogramm. Remote Sens. 2014, 97, 25–35. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Generative adversarial networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5046–5063. [Google Scholar] [CrossRef]
- Cao, X.; Zhou, F.; Xu, L.; Meng, D.; Xu, Z.; Paisley, J. Hyperspectral image classification with markov random fields and a convolutional neural network. IEEE Trans. Image Process. 2017, 27, 2354–2367. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017. Available online: https://www.semanticscholar.org/paper/Deep-Recurrent-Neural-Networks-for-Hyperspectral-Mou-Ghamisi/5a391667242b4a631acdd5917681b16a86523987 (accessed on 4 May 2021).
- Santara, A.; Mani, K.; Hatwar, P.; Singh, A.; Garg, A.; Padia, K.; Mitra, P. BASS Net: Band-adaptive spectral-spatial feature learning neural network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016. Available online: https://arxiv.org/pdf/1612.00144.pdf (accessed on 8 May 2021).
- Yang, X.; Li, X.; Lau, R.Y.K.; Zhang, X. Hyperspectral image classification with deep learning models. IEEE Trans. Geosci. Remote Sens. 2018, 99, 1–16. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015. [Google Scholar] [CrossRef] [Green Version]
- Yu, Q.; Gong, P.; Clinton, N.; Biging, G.; Kelly, M.; Schirokauer, D. Object-based detailed vegetation classification with airborne high spatial resolution remote sensing imagery. Photogramm. Eng. Remote Sens. 2006, 72, 799–811. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Troy, A.; Grove, J.M. Object-based land cover classification and change analysis in the Baltimore metropolian area using multi-temporal high resolution remote sensing data. Sensors 2008, 8, 1613–1636. [Google Scholar] [CrossRef] [Green Version]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Deep learning classifiers for hyperspectral imaging: A review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Jiménez, L.O.; Rivera-Medina, J.L.; Rodríguez-Díaz, E.; Arzuaga-Cruz, E.; Ramírez-Vélez, M. Integration of spatial and spectral information by means of unsupervised extraction and classification for homogenous objects applied to multispectral and hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 844–851. [Google Scholar] [CrossRef]
- Niemeyer, J.; Wegner, J.; Mallet, C.; Rottensteiner, F.; Soergel, U. Conditional random fields for urban scene classification with full waveform LiDAR data. In Photogrammetric Image Analysis; Stilla, U., Rottensteiner, F., Mayer, H., Jutzi, B., Butenuth, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6952, pp. 233–244. [Google Scholar]
- Samadzadegan, F.; Bigdeli, B.; Ramzi, P. A multiple classifier system for classification of LiDAR remote sensing data using multi-class SVM. In Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 254–263. [Google Scholar]
- Giampouras, P.; Charou, E. Artificial neural network approach for land cover classification of fused hyperspectral and LiDAR data. In Proceedings of the Artificial Intelligence Applications and Innovations, Paphos, Cyprus, 30 September–2 October 2013; pp. 255–261. [Google Scholar]
- Medina, M.A. Effects of shingle absorptivity, radiant barrier emissivity, attic ventilation flowrate, and roof slope on the performance of radiant barriers. Int. J. Energy Res. 2000, 24, 665–678. [Google Scholar] [CrossRef]
- Ridd, M.K. Exploring a V-I-S-(vegetation—impervious surface-soil) model for urban ecosystem analysis through remote sensing: Comparative anatomy for cities. Int. J. Remote Sens. 1995, 16, 2165–2185. [Google Scholar] [CrossRef]
- Haala, N.; Brenner, C. Extraction of buildings and trees in urban environments. ISPRS J. Photogramm. Remote Sens. 1999, 54, 130–137. [Google Scholar] [CrossRef]
- Shirowzhan, S.; Trinder, J. Building classification from LiDAR data for spatial-temporal assessment of 3D urban developments. Procedia Eng. 2017, 180, 1453–1461. [Google Scholar] [CrossRef]
- Zhou, Z.; Gong, J. Automated residential building detection from airborne LiDAR data with deep neural networks. Adv. Eng. Inform. 2018, 36, 229–241. [Google Scholar] [CrossRef]
- Shajahan, D.A.; Nayel, V.; Muthuganapathy, R. Roof classification from 3-D LiDAR point clouds using multiview CNN with self-attention. IEEE Geosci. Remote Sens. Lett. 2019, 99, 1–5. [Google Scholar] [CrossRef]
- Matikainen, L.; Hyyppa, J.; Hyyppa, H. Automatic detection of buildings from laser scanner data for map updating. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Dresden, Germany, 8–10 October 2003. [Google Scholar]
- Hug, C.; Wehr, A. Detecting and identifying topographic objects in imaging laser altimetry data. In Proceedings of the International Archives of the Photogrammetry and Remote Sensing, Stuttgart, Germany, 17–19 September 1997; pp. 16–29. [Google Scholar]
- Maas, H.G. The potential of height texture measures for the segmentation of airborne laserscanner data. In Proceedings of the 4th International Airborne Remote Sensing Conference and Exhibition and 21st Canadian Symposium on Remote Sensing, Ottawa, ON, Canada, 21–24 June 1999; pp. 154–161. [Google Scholar]
- Tóvári, D.; Vögtle, T. Object classifiaction in laserscanning data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2012, 36. Available online: https://www.researchgate.net/publication/228962142_Object_Classification_in_LaserScanning_Data (accessed on 8 May 2021).
- Galvanin, E.A.; Poz, A.P.D. Extraction of building roof contours from LiDAR data using a markov-random-field-based approach. IEEE Trans. Geosci. Remote Sens. 2012, 50, 981–987. [Google Scholar] [CrossRef]
- Vosselmann, G. Slope based filtering of laser altimetry data. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Amsterdam, The Netherlands, 16–22 July 2000; pp. 935–942. [Google Scholar]
- Lohmann, P.; Koch, A.; Schaeffer, M. Approaches to the filtering of laser scanner data. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Amsterdam, The Netherlands, 16–22 July 2000. [Google Scholar]
- Tarsha-Kurdi, F.; Landes, T.; Grussenmeyer, P.; Smigiel, E. New approach for automatic detection of buildings in airborne laser scanner data using first echo only. In Proceedings of the ISPRS Commission III Symposium, Photogrammetric Computer Vision, Bonn, Germany, 20–22 September 2006; pp. 25–30. [Google Scholar]
- Lodha, S.; Kreps, E.; Helmbold, D.; Fitzpatrick, D. Aerial LiDAR data classification using support vector machines (SVM). In Proceedings of the Third International Symposium on 3D Data Processing, Visualization, and Transmission, Chapel Hill, NC, USA, 14–16 June 2006; pp. 567–574. [Google Scholar]
- Rutzinger, M.; Höfle, B.; Pfeifer, N. Detection of high urban vegetation with airborne laser scanning data. In Proceedings of the Forestsat, Montpellier, France, 5–7 November 2007; pp. 1–5. [Google Scholar]
- Morsdorf, F.; Nichol, C.; Matthus, T.; Woodhouse, I.H. Assessing forest structural and physiological information content of multi-spectral LiDAR waveforms by radiative transfer modelling. Remote Sens. Environ. 2009, 113, 2152–2163. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.K.; Tseng, Y.H.; Chu, H.J. Airborne dual-wavelength LiDAR data for classifying land cover. Remote Sens. 2014, 6, 700–715. [Google Scholar] [CrossRef] [Green Version]
- Wichmann, V.; Bremer, M.; Lindenberger, J.; Rutzinger, M.; Georges, C.; Petrini-Monteferri, F. Evaluating the potential of multispectral airborne LiDAR for topographic mapping and land cover classification. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, La Grande Motte, France, 28 September–3 October 2015. [Google Scholar]
- Puttonen, E.; Hakala, T.; Nevalainen, O.; Kaasalainen, S.; Krooks, A.; Karjalainen, M.; Anttila, K. Artificial target detection with a hyperspectral LiDAR over 26-h measurement. Opt. Eng. 2015. Available online: https://www.spiedigitallibrary.org/journals/optical-engineering/volume-54/issue-01/013105/Artificial-target-detection-with-a-hyperspectral-LiDAR-over-26-h/10.1117/1.OE.54.1.013105.full?SSO=1 (accessed on 8 May 2021).
- Ghaderpour, E.; Abbes, A.B.; Rhif, M.; Pagiatakis, S.D.; Farah, I.R. Non-stationary and unequally spaced NDVI time series analyses by the LSWAVE software. Int. J. Remote Sens. 2020, 41, 2374–2390. [Google Scholar] [CrossRef]
- Martinez, B.; Gilabert, M.A. Vegetation dynamics from NDVI time series analysis using the wavelet transform. Remote Sens. Environ. 2009, 113, 1823–1842. [Google Scholar] [CrossRef]
- Okin, G.S. Relative spectral mixture analysis—A multitemporal index of total vegetation cover. Remote Sens. Environ. 2007, 106, 467–479. [Google Scholar] [CrossRef]
- Yang, H.; Chen, W.; Qian, T.; Shen, D.; Wang, J. The Extraction of Vegetation Points from LiDAR Using 3D Fractal Dimension Analyses. Remote Sens. 2015, 7, 10815–10831. [Google Scholar] [CrossRef] [Green Version]
- Widlowski, J.L.; Pinty, B.; Gobron, N.; Verstraete, M.M. Detection and characterization of boreal coniferous forests from remote sensing data. J. Geophys. Res. 2001, 106, 33405–33419. [Google Scholar] [CrossRef] [Green Version]
- Koetz, B.; Sun, G.; Morsdorf, F.; Ranson, K.J.; Kneubühler, M.; Itten, K.; Allgöwer, B. Fusion of imaging spectrometer and LIDAR data over combined radiative transfer models for forest canopy characterization. Remote Sens. Environ. 2007, 106, 449–459. [Google Scholar] [CrossRef]
- Dian, Y.; Pang, Y.; Dong, Y.; Li, Z. Urban tree species mapping using airborne LiDAR and hyperspectral data. J. Indian Soc. Remote Sens. 2016, 44, 595–603. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Wang, Y. Road extraction by deep residual u-net. IEEE Geosci. Remote Sens. Lett. 2018. Available online: https://arxiv.org/abs/1711.10684 (accessed on 8 May 2021).
- Yang, X.; Li, X.; Ye, Y.; Zhang, X.; Zhang, H.; Huang, X.; Zhang, B. Road detection via deep residual dense u-net. In Proceedings of the International Joint Conference on Neural Networks, Budapest, Hungary, 14–19 July 2019. [Google Scholar]
- Miliaresis, G.; Kokkas, N. Segmentation and object-based classification for the extraction of the building class from LiDAR DEMs. Comput. Geosci. 2007, 33, 1076–1087. [Google Scholar] [CrossRef]
- Zhao, X.; Tao, R.; Li, W.; Li, H.C.; Du, Q.; Liao, W.; Philips, W. Joint Classification of Hyperspectral and LiDAR Data Using Hierarchical Random Walk and Deep CNN Architecture. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7355–7370. [Google Scholar] [CrossRef]
- Herold, M.; Roberts, D.; Smadi, O.; Noronha, V. Road condition mapping with hyperspectral remote sensing. In Proceedings of the Airborne Earth Science Workshop, Pasadena, CA, USA, 31 March–2 April 2004. [Google Scholar]
- Kong, H.; Audibert, J.Y.; Ponce, J. General Road Detection from a Single Image. IEEE Trans. Image Process. 2010. Available online: https://www.di.ens.fr/willow/pdfs/tip10b.pdf (accessed on 7 May 2021).
- Wu, P.C.; Chang, C.Y.; Lin, C. Lane-mark extraction for automobiles under complex conditions. Pattern Recognit. 2014, 47, 2756–2767. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Lin, C.; Tsai, M.-D.; Lin, C.-L. Object-based analysis of LiDAR geometric features for vegetation detection in shaded areas. In Proceedings of the XXIII ISPRS Congress, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Poux, F.; Hallot, R.P.; Neuville, R.B. Smart point cloud: Definition and remaining challenges. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2016, 42, 119–127. [Google Scholar] [CrossRef] [Green Version]
- Arief, H.A.; Strand, G.H.; Tveite, H.; Indahl, U.G. Land cover segmentation of airborne LiDAR data using Stochastic Atrous Network. Remote Sens. 2018, 10, 973. [Google Scholar] [CrossRef] [Green Version]
- Clark, R.N. Spectroscopy of rocks and minerals, and principles of spectroscopy. In Manual of Remote Sensing, Remote Sensing for the Earth Sciences; Rencz, A.N., Ed.; John Wiley and Sons: New York, NY, USA, 1999; Volume 3. [Google Scholar]
- Signoroni, A.; Savardi, M.; Baronio, A.; Benini, S. Deep learning meets hyperspectral image analysis: A multidisciplinary review. J. Imaging 2019, 5, 52. [Google Scholar] [CrossRef] [Green Version]
- Ben-Dor, E. Imaging spectrometry for urban applications. In Imaging Spectrometry; van der Meer, F.D., de Jong, S.M., Eds.; Kluwer Academic Publishers: Amsterdam, The Netherlands, 2001; pp. 243–281. [Google Scholar]
- Ortenberg, F. Hyperspectral Sensor Characteristics. In Fundamentals, Sensor Systems, Spectral Libraries, and Data Mining for Vegetation, 2nd ed.; Huete, A., Lyon, J.G., Thenkabail, P.S., Eds.; Hyperspectral remote sensing of vegetation Volume I; CRC Press: Boca Raton, FL, USA, 2011; p. 449. [Google Scholar]
- Rossel, R.A.V.; McGlynn, R.N.; McBratney, A.B. Determining the composition of mineral-organic mixes using UV—vis—NIR diffuse reflectance spectroscopy. Geoderma 2006, 137, 70–82. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Rugege, D. Multispectral and hyperspectral remote sensing for identification and mapping of wetland vegetation:a review. Wetl. Ecol. Manag. 2010, 18, 281–296. [Google Scholar] [CrossRef]
- Heiden, U.H.W.; Roessner, S.; Segl, K.; Esch, T.; Mueller, A. Urban structure type characterization using hyperspectral remote sensing and height information. Landsc. Urban. Plan. 2012, 105, 361–375. [Google Scholar] [CrossRef]
- Roessner, S.; Segl, K.; Heiden, U.; Kaufmann, H. Automated differentiation of urban surfaces based on airborne hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1525–1532. [Google Scholar] [CrossRef]
- Townshend, J.; Justice, C.; Li, W.; Gumey, C.; McManus, J. Global land cover classification by remote sensing: Present capabilities and future possibilities. Remote Sens. Environ. 1991, 35, 243–255. [Google Scholar] [CrossRef]
- Heiden, U.; Roessner, S.; Segl, K.; Kaufmann, H. Analysis of Spectral Signatures of Urban Surfaces for their Identification Using Hyperspectral HyMap Data. In Proceedings of the IEEE/ISPRS Joint Workshop on Remote Sensing nd Data Fusion over Urban Areas, Rome, Italy, 8–9 November 2001; pp. 173–177. [Google Scholar]
- Heiden, U.; Segl, K.; Roessner, S.; Kaufmann, H. Determination of robust spectral features for identification of urban surface materials in hyperspectral remote sensing data. Remote Sens. Environ. 2007, 111, 537–552. [Google Scholar] [CrossRef] [Green Version]
- Meer, F.v.d.; Jong, S.d.; Bakker, W. Imaging Spectrometry: Basic Analytical Techniques. In Imaging Spectrometry; van der Meer, F.D., de Jong, S.M., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001; pp. 17–61. [Google Scholar]
- Franke, J.; Roberts, D.A.; Halligan, K.; Menz, G. Hierarchical Multiple Endmember Spectral Mixture Analysis (MESMA) of hyperspectral imagery for urban environments. Remote Sens. Environ. 2009, 113, 1712–1723. [Google Scholar] [CrossRef]
- Hepner, G.F.; Housmand, B.; Kulikov, I.; Bryant, N. Investigation of the integration of AVIRIS and IFSAR for urban analysis. Photogramm. Eng. Remote Sens. 1998, 64, 813–820. [Google Scholar]
- Linden, S.v.d.; Okujeni, A.; Canters, F.; Degerickx, J.; Heiden, U.; Hostert, P.; Priem, F.; Somers, B.; Thiel, F. Imaging Spectroscopy of Urban Environments. Surv. Geohpys. 2019, 40, 471–488. [Google Scholar] [CrossRef] [Green Version]
- Pillay, R.; Picollo, M.; Hardeberg, J.Y.; George, S. Evaluation of the Data Quality from a Round-Robin Test of Hyperspectral Imaging Systems. Sensors 2020, 20, 3812. [Google Scholar] [CrossRef]
- Yao, H.; Tian, L.F. Practical methods for geometric distortion correction of aerial hyperspectral imagery. Appl. Eng. Agric. 2004, 20, 367–375. [Google Scholar] [CrossRef]
- Lulla, V.; Jensen, R.R. Best Practices for Urban Hyperspectral Remote Sensing Data Acquisition and Processing. In Urban Sustainability: Policy and Praxis; Springer: Berlin/Heidelberg, Germany, 2016; pp. 43–54. [Google Scholar]
- Galbraith, A.E.; Theiler, J.; Thome, K.; Ziolkowski, R. Resolution Enhancement of Multilook Imagery for the Multispectral Thermal Imager. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1964–1977. [Google Scholar] [CrossRef]
- Pepe, M.; Fregonese, L.; Scaioni, M. Planning airborne photogrammetry and remote-sensing missions with modern platforms and sensors. Eur. J. Remote Sens. 2018, 51, 412–436. [Google Scholar] [CrossRef]
- Heiden, U.; Segl, K.; Roessner, S.; Kaufmann, H. Determination and verification of robust spectral features for an automated classification of sealed urban surfaces. In Proceedings of the EARSeL Workshop on Imaging Spectroscopy, Warsaw, Poland, 27–29 April 2005. [Google Scholar]
- Lacherade, S.; Miesch, C.; Briottet, X.; Men, H.L. Spectral variability and bidirectional reflectance behavior of urban materials at a 20 cm spatial resolution in the visible and near-infrared wavelength. A case study over Toulouse (France). Int. J. Remote Sens. 2005, 26, 3859–3866. [Google Scholar] [CrossRef]
- Herold, M.; Roberts, D.A.; Gardner, M.E.; Dennison, P.E. Spectrometry for urban area remote sensing—Development and analysis of a spectral library from 350 to 2400 nm. Remote Sens. Environ. 2004, 91, 304–319. [Google Scholar] [CrossRef]
- Ilehag, R.; Schenk, A.; Huang, Y.; Hinz, S. KLUM: An Urban VNIR and SWIR Spectral Library Consisting of Building Materials. Remote Sens. 2019, 11, 2149. [Google Scholar] [CrossRef] [Green Version]
- Manolakis, D.; Lockwood, R.; Cooley, T. Hyperspectral Imaging Remote Sensing: Physics, Sensors, and Algorithms; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Pearson, K. On lines and planes of closest fit to systems of points in space. Philos. Mag. Lett. 1901, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Pritchard, J.K.; Stephens, M.; Donnelly, P. Inference of Population Structure Using Multilocus Genotype Data. Genetics 2000, 155, 945–959. [Google Scholar] [CrossRef] [PubMed]
- Lawton, W.H.; Sylvestre, E.A. Self modeling curve resolution. Technometrics 1971, 13, 617–633. [Google Scholar] [CrossRef]
- Vidal, M.; Amigo, J.M. Pre-processing of hyperspectral images. Essential steps before image analysis. Chemom. Intell. Lab. Syst. 2012, 117, 138–148. [Google Scholar] [CrossRef]
- Pandey, D.; Tiwari, K.C. Spectral library creation and analysis of urban built-up surfaces and materials using field spectrometry. Arab. J. Geosci. 2021, 14. [Google Scholar] [CrossRef]
- Miller, D.L.; Alonzo, M.; Roberts, D.A.; Tague, C.L.; McFadden, J.P. Drought response of urban trees and turfgrass using airborne imaging spectroscopy. Remote Sens. Environ. 2020, 40. [Google Scholar] [CrossRef]
- Clark, R.N.; Swayze, G.A.; Livo, K.E.; Kokaly, R.F.; Sutley, S.H.; Dalton, J.B.; McDougal, R.R.; Gent, C.A. Imaging spectroscopy: Earth and planetary remote sensing with the USGS Tetracorder and expert systems. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Yongyang, X.; Liang, W.; Zhong, X.; Zhanlong, C. Building extraction in very high resolution remote sensing imagery using deep learning and guided filters. Remote Sens. 2018, 10. [Google Scholar]
- Teo, T.A.; Wu, H.M. Analysis of land cover classification using multi-wavelength LiDAR system. Appl. Sci. 2017, 7, 663. [Google Scholar] [CrossRef] [Green Version]
- Pandey, D.; Tiwari, K.C. New spectral indices for detection of urban built-up surfaces and its sub-classes in AVIRIS-NG hyperspectral imagery. Geocarto Int. 2020. [Google Scholar] [CrossRef]
- Zha, Y.; Gao, J.; Ni, S. Use of normalized difference built-up index in automatically mapping urban areas from TM imagery. Int. J. Remote Sens. 2003, 24, 583–594. [Google Scholar] [CrossRef]
- Estoque, R.C.; Zhang, W.; Tan, K.; Liu, Y.; Liu, S. Multiple classifier system for remote sensing image classification: A review. Sensors 2012, 12, 4764–4792. [Google Scholar]
- Shahi, K.; Shafri, H.Z.M.; Taherzadeh, E.; Mansor, S.; Muniandy, R. A novel spectral index to automatically extract road networks from WorldView-2 satellite imagery. Egypt. J. Remote Sens. Space Sci. 2015, 18, 27–33. [Google Scholar] [CrossRef] [Green Version]
- Xie, H.; Luo, X.; Xu, X.; Tong, X.; Jin, Y.; Haiyan, P.; Zhou, B. New hyperspectral difference water index for the extraction of urban water bodies by the use of airborne hyperspectral images. J. Appl. Remote Sens. 2014, 8. [Google Scholar] [CrossRef] [Green Version]
- Xue, J.; Zhao, Y.; Bu, Y.; Liao, W.; Chan, J.C.-W.; Philips, W. Spatial-Spectral Structured Sparse Low-Rank Representation for Hyperspectral Image Super-Resolution. IEEE Trans. Image Process. 2021, 30, 3084–3097. [Google Scholar] [CrossRef] [PubMed]
- Rasti, B.; Scheunders, P.; Ghamisi, P.; Licciardi, G.; Chanussot, J. Noise Reduction in Hyperspectral Imagery: Overview and Application. Remote Sens. 2018, 3, 482. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Chova, L.; Alonso, L.; Guanter, L.; Camps-Valls, G.; Calpe, J.; Moreno, J. Correction of systematic spatial noise in push-broom hyperspectral sensors: Application to CHRIS/PROBA images. Appl. Opt. 2008, 47, 46–60. [Google Scholar] [CrossRef] [Green Version]
- Bruzzone, L.; Marconcini, M.; Persello, C. Fusion of spectral and spatial information by a novel SVM classification technique. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007. [Google Scholar]
- Bovolo, F.; Bruzzone, L. A Context-Sensitive Technique Based on Support Vector Machines for Image Classification. In Proceedings of the International Conference on Pattern Recognition and Machine Intelligence, Kolkata, India, 20–22 December 2005; pp. 260–265. [Google Scholar]
- Farag, A.A.; Mohamed, R.H.; El-Baz, A. A unified framework for MAP estimation in remote sensing image segmentation. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1617–1634. [Google Scholar] [CrossRef]
- Sun, L.; Wu, Z.; Liu, J.; Xiao, L.; Wei, Z. Supervised spectral-spatial hyperspectral image classification with weighted Markov Random Fields. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1490–1503. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral-spatial hyperspectral image segmentation using subspace multinomial logistic regression and markov random fields. IEEE Trans. Geosci. Remote Sens. 2012, 50. [Google Scholar] [CrossRef]
- Wehr, A.; Lohr, U. Airborne laser scanning—An introduction and overview. ISPRS J. Photogramm. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Clode, S.; Rottensteiner, F.; Kootsookos, P.; Zelniker, E. Detection and vectorization of roads from LiDAR data. Photogramm. Eng. Remote Sens. 2007, 73, 517–535. [Google Scholar] [CrossRef] [Green Version]
- Chehata, N.; Guo, L.; Mallet, C. Airborne LiDAR feature selection for urban classification using random forests. Laserscanning 2009, 38. [Google Scholar]
- Guo, L.; Chehata, N.; Mallet, C.; Boukir, S. Relevance of airborne LiDAR and multispectral image data for urban scene classification using random forests. ISPRS J. Photogramm. Remote Sens. 2011, 66, 56–66. [Google Scholar] [CrossRef]
- Priestnall, G.; Jaafar, J.; Duncan, A. Extracting urban features from LiDAR digital surface models. Comput. Environ. Urban. Syst. 2000, 24, 65–78. [Google Scholar] [CrossRef]
- Hecht, R.; Meinel, G.; Buchroithner, M.F. Estimation of urban green volume based on single-pulse LiDAR data. IEEE Trans. Geosci. Remote Sens. 2008, 46. [Google Scholar] [CrossRef]
- Alonso, L.; Picos, J.; Bastos, G.; Armesto, J. Detection of Very Small Tree Plantations and Tree-Level Characterization Using Open-Access Remote-Sensing Databases. Remote Sens. 2020, 12, 2276. [Google Scholar] [CrossRef]
- Grohmann, C.H.; Smith, M.J.; Riccomini, C. Muli-scale Analysis of Topographic Surface Roughness in the Midland Valley, Scotland. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1200–1213. [Google Scholar] [CrossRef] [Green Version]
- Brubaker, K.M.; Myers, W.L.; Drohan, P.J.; Miller, D.A.; Boyer, E.W. The Use of LiDAR Terrain Data in Characterizing Surface Roughness and Microtopography. Appl. Environ. Soil Sci. 2013, 2013. [Google Scholar] [CrossRef]
- Brenner, C. Dreidimensionale Gebäuderekonstruktion aus digitalen Oberflächenmodellen und Grundrissen. Ph.D. Thesis, Stuttgart University, Stuttgart, Germany, 2000. [Google Scholar]
- Antonarakis, A.S.; Richards, K.S.; Brasington, J. Object-based land cover classification using airborne LiDAR. Remote Sens. Environ. 2008, 112, 2988–2998. [Google Scholar] [CrossRef]
- Charaniya, A.P.; Manduchi, R.; Lodha, S.K. Supervised parametric classification of aerial LiDAR data. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Washington, DC, USA, 27 June–2 July 2004. [Google Scholar]
- Bartels, M.; Wei, H. Maximum likelihood classification of LiDAR data incorporating multiple co-registered band. In Proceedings of the 4th International Workshop on Pattern Recognition in Remote Sensing in conjunction with the 18th International Conference on Pattern Recognition, Hong Kong, 20–24 August 2006. [Google Scholar]
- Im, J.; Jensen, J.R.; Hodgson, M.E. Object-based land cover classification using high-posting-density LiDAR data. GIsci. Remote Sens. 2008, 45, 209–228. [Google Scholar] [CrossRef] [Green Version]
- Song, J.H.; Han, S.H.; Yu, K.Y.; Kim, Y.I. Assessing the possibility of land-cover classification using LiDAR intensity data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2002, 34, 259–262. [Google Scholar]
- Yoon, J.-S.; Lee, J.-I. Land cover characteristics of airborne LiDAR intensity data: A case study. IEEE Geosci. Remote Sens. Lett. 2008, 5, 801–805. [Google Scholar] [CrossRef]
- MacFaden, S.W.; O´Neil-Dunne, J.P.M.; Royar, A.R.; Lu, J.W.T.; Rundle, A.G. High-resolution tree canopy mapping for New York City using LiDAR and object-based image analysis. J. Appl. Remote Sens. 2012, 6. [Google Scholar] [CrossRef]
- Yan, W.Y.; Shaker, A. Reduction of striping noise in overlapping LiDAR intensity data by radiometric normalization. In Proceedings of the XXIII ISPRS Congress, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Nobrega, R.A.A.; Quintanilha, J.A.; O´Hara, C.G. A noise-removal approach for LiDAR intensity images using anisotropic diffusion filtering to preserve object shape characteristics. In Proceedings of the ASPRS Annual Conference, Tampa, FL, USA, 7–11 May 2007. [Google Scholar]
- Minh, N.Q.; Hien, L.P. Land cover classification using LiDAR intensity data and neural network. J. Korean Soc. Surv. Geodesy Photogramm. Cartogr. 2011, 29.4, 429–438. [Google Scholar] [CrossRef]
- Brennan, R.; Webster, T.L. Object-oriented land cover classification of LiDAR-derived surfaces. Can. J. Remote Sens. 2006, 32, 162–172. [Google Scholar] [CrossRef]
- Wagner, W. Radiometric calibration of small-footprint full-waveform airborne laser scanner measurements: Basic physical concepts. ISPRS J. Photogramm. Remote Sens. 2010, 65, 505–513. [Google Scholar] [CrossRef]
- Mallet, C.; Bretar, F. Full-waveform topographic LiDAR: State-of-the-art. ISPRS J. Photogramm. Remote Sens. 2009, 64, 1–16. [Google Scholar] [CrossRef]
- Bretar, F.; Chauve, A.; Mallet, C.; Jutzi, B. Managing full waveform LiDAR data: A challenging task for the forthcoming years. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2008, XXXVII, 415–420. [Google Scholar]
- Kirchhof, M.; Jutzi, B.; Stilla, U. Iterative processing of laser scanning data by full waveform analysis. ISPRS J. Photogramm. Remote Sens. 2008, 63, 99–114. [Google Scholar] [CrossRef]
- Höfle, B.; Pfeifer, N. Correction of laser scanning intensity data: Data and model-driven approaches. ISPRS J. Photogramm. Remote Sens. 2007, 62, 1415–1433. [Google Scholar] [CrossRef]
- Alexander, C.; Tansey, K.; Kaduk, J.; Holland, D.; Tate, N.J. Backscatter coefficient as an attribute for the classification of full-waveform airborne laser scanning data in urban areas. ISPRS J. Photogramm. Remote Sens. 2010, 65, 423–432. [Google Scholar] [CrossRef] [Green Version]
- Neuenschwander, A.L.; Magruder, L.A.; Tyler, M. Landcover classification of small-footprint, full-waveform LiDAR data. J. Appl. Remote Sens. 2009, 3. [Google Scholar] [CrossRef]
- Jutzi, B.; Stilla, U. Waveform processing of laser pulses for reconstruction of surfacer in urban areas. Meas. Tech. 2005. Available online: https://www.researchgate.net/publication/43136634_Waveform_processing_of_laser_pulses_for_reconstruction_of_surfaces_in_urban_areas (accessed on 2 May 2021).
- Chauve, A.; Mallet, C.; Bretar, F.; Durrieu, S.; Pierrot-Deseilligny, M.; Puech, W. Processing full-waveform LiDAR data: Modelling raw signals. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2007, 36, 102–107. [Google Scholar]
- Gross, H.; Jutzi, B.; Thoennessen, U. Segmentation of tree regions using data of a full-waveform laser. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2007, 36, 57–62. [Google Scholar]
- Reitberger, J.; Krzystek, P.; Stilla, U. Analysis of full waveform LIDAR data for the classification of deciduous and coniferous trees. Int. J. Remote Sens. 2008, 29, 1407–1431. [Google Scholar] [CrossRef]
- Rutzinger, M.; Höfle, B.; Hollaus, M.; Pfeifer, N. Object-based point cloud analysis of full-waveform airborne laser scanning data for urban vegetation classification. Sensors 2008, 8, 4505–4528. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Melzer, T. Non-parametric segmentation of ALS point clouds using mean shift. J. Appl. Geod. 2007, 1, 158–170. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Mills, J.P. Factors influencing pulse width of small footprint, full waveform airborne laser scanning data. Photogramm. Eng. Remote Sens. 2010, 76, 49–59. [Google Scholar] [CrossRef]
- Doneus, M.; Briese, C.; Fera, M.; Janner, M. Archaeological prospection of forested areas using full-waveform airborne laser scanning. J. Archaeol. Sci. 2008, 35, 882–893. [Google Scholar] [CrossRef]
- Harding, D.; Lefsky, M.; Parker, G. Laser altimeter canopy height profiles. Methods and validation for closed canopy, broadleaf forests. Remote Sens. Environ. 2001, 76, 283–297. [Google Scholar] [CrossRef]
- Gross, H.; Thoennessen, U. Extraction of lines from laser point clouds. In Proceedings of the ISPRS Conference Photogrammetric Image Analysis (PIA), Bonn, Germany, 20–22 September 2006; pp. 87–91. [Google Scholar]
- West, K.F.; Webb, B.N.; Lersch, J.R.; Pothier, S.; Triscari, J.M.; Iverson, A.E. Context-driven automated target detection in 3-D data. In Proceedings of the Automatic Target Recognition XIV, Orlando, FL, USA, 13–15 April 2004; pp. 133–143. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T.T. Multi resolution gray scale and rotation invariant texture classification with local binary pattern. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Ge, C.; Du, Q.; Sun, W.; Wang, K.; Li, J.; Li, Y. Deep Residual Network-Based Fusion Framework for Hyperspectral and LiDAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2458–2472. [Google Scholar] [CrossRef]
- Peng, B.; Li, W.; Xie, X.; Du, Q.; Liu, K. Weighted-Fusion-Based Representation Classifiers for Hyperspectral Imagery. Remote Sens. 2015, 7, 14806–14826. [Google Scholar] [CrossRef] [Green Version]
- Manjunath, B.S.; Ma, W.Y. Texture features for browsing and retrieval of image data. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 837–842. [Google Scholar] [CrossRef] [Green Version]
- Rajadell, O.; García-Sevilla, P.; Pla, F. Textural Features for Hyperspectral Pixel Classification. In Proceedings of the Iberian Conference on Pattern Recognition and Image Analysis, Póvoa de Varzim, Portugal, 10–12 June 2009; pp. 208–216. [Google Scholar]
- Aksoy, S. Spatial techniques for image classification. In Signal and Image Processing for Remote Sensing; CRC Press: Boca Raton, FL, USA, 2006; pp. 491–513. [Google Scholar]
- Zhang, G.; Jia, X.; Kwok, N.M. Spectral-spatial based super pixel remote sensing image classification. In Proceedings of the 4th International Congress on Image and Signal Processing, Shanghai, China, 15–17 October 2011; pp. 1680–1684. [Google Scholar]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. Syst. 1973, 3, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Zhang, L.; Gong, W. Information fusion of aerial images and LiDAR data in urban areas: Vector-stacking, re-classification and post-processing approaches. Int. J. Remote Sens. 2011, 32, 69–84. [Google Scholar] [CrossRef]
- Puissant, A.; Hirsch, J.; Weber, C. The utility of texture analysis to improve per-pixel classification for high to very high spatial resolution imagery. Int. J. Remote Sens. 2005. [Google Scholar] [CrossRef]
- Zhang, Y. Optimisation of building detection in satellite images by combining multispectral classification and texture filtering. ISPRS J. Photogramm. Remote Sens. 1999, 54, 50–60. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L.; Li, P. An Adaptive Multiscale Information Fusion Approach for Feature Extraction and Classification of IKONOS Multispectral Imagery Over Urban Areas. IEEE Geosci. Remote Sens. Lett. 2007, 4. [Google Scholar] [CrossRef]
- Pesaresi, M.; Benediktsson, J.A. A New Approach for the Morphological Segmentation of High-Resolution Satellite Imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 309–320. [Google Scholar] [CrossRef] [Green Version]
- Soille, P.; Pesaresi, M. Advances in mathematical morphology applied to geoscience and remote sensing. IEEE Trans. Geosci. Remote Sens. 2002, 40. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Pesaresi, M.; Amason, K. Classification and feature extraction for remote sensing images from urban areas based on morphological transformations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1940–1949. [Google Scholar] [CrossRef] [Green Version]
- Jouni, M.; Mura, M.D.; Comon, P. Hyperspectral Image Classification Based on Mathematical Morphology and Tensor Decomposition. Math. Morphol. Theory Appl. 2020, 4, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Mura, M.D.; Benediktsson, J.A.; Waske, B.; Bruzzone, L. Extended profiles with morphological attribute filters for the analysis of hyperspectral data. Int. J. Remote Sens. 2010, 31, 5975–5991. [Google Scholar] [CrossRef]
- Aptoula, E.; Mura, M.D.; Lefevre, S. Vector attribute profiles for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3208–3220. [Google Scholar] [CrossRef] [Green Version]
- Sayed, W.M. Processing of LiDAR Data using Morphological Filter. Int. J. Adv. Res. 2014, 2, 361–367. [Google Scholar]
- Rottensteiner, F.; Briese, C. A new method for building extraction in urban areas from high-resolution LiDAR data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2002, 34, 295–301. [Google Scholar]
- Morsy, S.S.A.; El-Rabbany, A. Multispectral LiDAR Data for Land Cover Classification of Urban Areas. Sensors 2017, 17, 958. [Google Scholar] [CrossRef] [Green Version]
- Suomalainen, J.; Hakala, T.; Kaartinen, H.; Räikkönen, E.; Kaasalainen, S. Demonstration of a virtual active hyperspectral LiDAR in automated point cloud classification. ISPRS J. Photogramm. Remote Sens. 2011, 66, 637–641. [Google Scholar] [CrossRef]
- Hakala, T.; Suomalainen, J.; Kaasalainen, S.; Chen, Y. Full waveform hyperspectral LiDAR for terrestrial laser scanning. Opt. Express 2012, 20. [Google Scholar] [CrossRef]
- Hughes, G.F. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef] [Green Version]
- Asner, G.P.; Knapp, D.E.; Boardman, J.; Green, R.O.; Kennedy-Bowdoin, T.; Eastwood, M.; Martin, R.E.; Anderson, C.; Field, C.B. Carnegie Airborne Observatory-2: Increasing science data dimensionality via high-fidelity multi-sensor fusion. Remote Sens. Environ. 2012, 124, 454–465. [Google Scholar] [CrossRef]
- Brell, M.; Rogass, C.; Segl, K.; Bookhagen, B.; Guanter, L. Improving sensor fusion: A parametric method for the geometric coalignment of airborne hyperspectral and LiDAR data. IEEE Trans. Geosci. Remote Sens. 2016, 54. [Google Scholar] [CrossRef] [Green Version]
- Brell, M.; Segl, K.; Guanter, L.; Bookhagen, B. 3D hyperspectral point cloud generation: Fusing airborne laser scanning and hyperspectral imaging sensors for improved object-based information extraction. ISPRS J. Photogramm. Remote Sens. 2019, 149, 200–214. [Google Scholar] [CrossRef]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Feitosa, R.Q.; Meer, F.v.d.; Werff, H.v.d.; Coillie, F.v.; et al. Geographic Object-Based Image Analysis—Toward a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [Green Version]
- Campagnolo, M.L.; Cerdeira, J.O. Contextual classification of remotely sensed images with integer linear programming. In Proceedings of the Computational Modeling of Objects Represented in Images: Fundamentals, Methods, and Applications, Niagara Falls, NY, USA, 21–23 September 2016; pp. 123–128. [Google Scholar]
- Jong, S.M.D.; Hornstra, T.; Maas, H. An integrated spatial and spectral approach to the classification of Mediterranean land cover types: The SSC method. Int. J. Appl. Earth Obs. Geoinf. 2001, 3, 176–183. [Google Scholar] [CrossRef]
- Bhaskaran, S.; Paramananda, S.; Ramnarayan, M. Per-pixel and object-oriented classification methods for mapping urban features using IKONOS satellite data. Appl. Geogr. 2010, 30, 650–665. [Google Scholar] [CrossRef]
- Baker, B.A.; Warner, T.A.; Conley, J.F.; McNeil, B.E. Does spatial resolution matter? A multi-scale comparison of object-based and pixel-based methods for detection change associated with gas well drilling operations. Int. J. Remote Sens. 2013, 34, 1633–1651. [Google Scholar] [CrossRef]
- Johnson, B.; Xie, Z. Unsupervised image segmentation evaluation and refinement using a multi-scale approach. ISPRS J. Photogramm. Remote Sens. 2011, 66, 473–483. [Google Scholar] [CrossRef]
- Zhong, P.; Gong, Z.; Li, S.; Schönlieb, C.B. Learning to diversify deep belief networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, H.; Eom, K.B. Active deep learning for classification of hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhao, X.; Jia, X. Spectral-spatial classification of hyperspectral data based on deep belief network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, Y.; Zhao, X.; Wang, G. Spectral–Spatial Classification of Hyperspectral Image Using Autoencoders. In Proceedings of the 9th International Conference on Information, Communications Signal Processing, Tainan, Taiwan, 10–13 December 2013; pp. 1–5. [Google Scholar]
- Tao, C.; Pan, H.; Li, Y.; Zhou, Z. Unsupervised spectral-spatial feature learning with stacked sparse autoencoder for hyperspectral imagery classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2438–2442. [Google Scholar]
- Yue, J.; Mao, S.; Li, M. A deep learning framework for hyperspectral image classification using spatial pyramid pooling. Remote Sens. Lett. 2016, 7, 875–884. [Google Scholar] [CrossRef]
- Campbell, J.B. Introduction to Remote Sensing, 3th ed.; Guilford Press: New York, NY, USA, 2002; p. 621. [Google Scholar]
- Enderle, D.I.M.; Weih, R.C., Jr. Integrating supervised and unsupervised classification methods to develop a more accurate land cover classification. J. Ark. Acad. Sci. 2005, 59, 65–73. [Google Scholar]
- Shabbir, S.; Ahmad, M. Hyperspectral Image Classification—Traditional to Deep Models: A Survey for Future Prospects. arXiv 2021, arXiv:2101.06116. [Google Scholar]
- Liu, C.; He, L.; Li, Z.; Li, J. Feature-driven active learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 341–357. [Google Scholar] [CrossRef]
- Richards, J.A. Remote Sensing Digital Image Analysis: An. Introduction, 3rd ed.; Springer-Verlag New York, Ed.; Springer: Secaucus, NJ, USA, 1999. [Google Scholar]
- Garcia, S.; Zhang, Z.L.; Altalhi, A.; Alshomrani, S.; Herrera, F. Dynamic ensemble selection for multi-class imbalanced datasets. Inf. Sci. 2018, 445–446, 22–37. [Google Scholar] [CrossRef]
- Lv, Q.; Feng, W.; Quan, Y.; Dauphin, G.; Gao, L.; Xing, M. Enhanced-Random-Feature-Subspace-Based Ensemble CNN for the Imbalanced Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3988–3999. [Google Scholar] [CrossRef]
- Paing, M.P.; Pintavirooj, C.; Tungjitkusolmun, S.; Choomchuay, S.; Hamamoto, K. Comparison of sampling methods for imbalanced data classification in random forest. In Proceedings of the 11th Biomedical Engineering International Conference, Chaing Mai, Thailand, 21–24 November 2018; pp. 1–5. [Google Scholar]
- Momeni, R.; Aplin, P.; Boyd, D.S. Mapping Complex Urban Land Cover from Spaceborne Imagery: The Influence of Spatial Resolution, Spectral Band Set and Classification Approach. Remote Sens. 2016, 8, 88. [Google Scholar] [CrossRef] [Green Version]
- Rasti, B.; Hong, D.; Hang, R.; Ghamisi, P.; Kang, X.; Chanussot, J.; Benediktsson, J.A. Feature Extraction for Hyperspectral Imagery: The Evolution from Shallow to Deep (Overview and Toolbox). IEEE Geosci. Remote Sens. Lett. 2020, 8, 60–88. [Google Scholar] [CrossRef]
- Rauber, P.E.; Fadel, S.G.; Falcao, A.X.; Telea, A.C. Visualizing the hiden activity of artificial neural networks. IEEE Trans. Vis. Comput. Graph. 2017, 23, 101–110. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. A new deep convolutional neural network for fast hyperspectral image classification. ISPRS J. Photogramm. Remote Sens. 2018, 145, 120–147. [Google Scholar] [CrossRef]
- Yu, S.; Jia, S.; Xu, C. Convolutional neural networks for hyperspectral image classification. Neurocomputing 2017, 219, 88–98. [Google Scholar] [CrossRef]
- Zhou, W.; Kamata, S. Multi-Scanning Based Recurrent Neural Network for Hyperspectral Image Classification. In Proceedings of the 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021. [Google Scholar]
- Lee, H.; Kwon, H. Contextual deep CNN based hyperspectral classification. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3322–3325. [Google Scholar]
- Seidel, D.; Annighöfer, P.; Thielman, A.; Seifert, Q.E.; Thauer, J.H.; Glatthorn, J.; Ehbrecht, M.; Kneib, T.; Ammer, C. Predicting Tree Species From 3D Laser Scanning Point Clouds Using Deep Learning. Front. Plant. Sci. 2021, 12. [Google Scholar] [CrossRef]
- Huang, L.; Chen, Y. Dual-Path Siamese CNN for Hyperspectral Image Classification with Limited Training Samples. IEEE Geosci. Remote Sens. Lett. 2020, 18, 518–522. [Google Scholar] [CrossRef]
- Neagoe, V.E.; Diaconescu, P. CNN Hyperspectral Image Classification Using Training Sample Augmentation with Generative Adversarial Networks. In Proceedings of the 13th International Conference on Communications (COMM), Bucharest, Romania, 18–20 June 2020. [Google Scholar]
- Haut, J.M.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Li, J. Hyperspectral Image Classification Using Random Occlusion Data Augmentation. IEEE Geosci. Remote Sens. Lett. 2019. [Google Scholar] [CrossRef]
- Yu, C.; Han, R.; Song, M.; Liu, C.; Chang, C.I. A Simplified 2D-3D CNN Architecture for Hyperspectral Image Classification Based on Spatial-Spectral Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13. [Google Scholar] [CrossRef]
- Hochreiter, S. The Vanishing Gradient Problem During Learning Recurrent Neural Net and Problem Solutions. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Camps-Valls, G.; Tuia, D.; Bruzzone, L.; Benediktsson, J.A. Advances in hyperspectral image classification: Earth monitoring with statistical learning methods. IEEE Signal. Process. Mag. 2014, 31, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Linden, S.v.d.; Janz, A.; Waske, B.; Eiden, M.; Hostert, P. Classifying segmented hyperspectral data from a heterogeneous urban environment using support vector machines. J. Appl. Remote Sens. 2007, 1. [Google Scholar]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral image classification using deep pixel-pair features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Fauvel, M.; Chanussot, J.; Benediktsson, J.A. Evaluation of kernels for multiclass classification of hyperspectral remote sensing data. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Toulouse, France, 14–19 May 2006; pp. II-813–II-816. [Google Scholar]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Plaza, A.; Benediktsson, J.A.; Boardman, J.W.; Brazile, J.; Bruzzone, L.; Camps-Valls, G.; Chanussot, J.; Fauvel, M.; Gamba, P.; Gualtieri, A.; et al. Recent advances in techniques for hyperspectral image processing. Remote Sens. Environ. 2009, 13, 110–122. [Google Scholar] [CrossRef]
- Mallet, C.; Soergel, U.; Bretar, F. Analysis of full-waveform LiDAR data for classification of urban areas. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2008, 37, 85–92. [Google Scholar]
- Zhang, Y.; Cao, G.; Li, X.; Wang, B. Cascaded random forest for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018. [Google Scholar] [CrossRef]
- Matikainen, L.; Karila, K.; Hyyppä, J.; Litkey, P.; Puttonen, E.; Ahokas, E. Object-based analysis of multispectral airborne laser scanner data for land cover classification and map updating. ISPRS J. Photogramm. Remote Sens. 2017, 128, 298–313. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Mei, S.; Ji, J.; Bi, Q.; Hou, J.; Du, Q.; Li, W. Integrating spectral and spatial information into deep convolutional neural networks for hyperspectral classification. In Proceedings of the International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016; pp. 5067–5070. [Google Scholar]
- Ran, L.; Zhang, Y.; Wei, W.; Zhang, Q. A hyperspectral image classification framework with spatial pixel pair features. Sensors 2017, 17, 2421. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vaddi, R.; Manoharan, P. Hyperspectral image classification using CNN with spectral and spatial features integration. Infrared Phys. Technol. 2020, 107. [Google Scholar] [CrossRef]
- Ge, Z.; Cao, G.; Li, X.; Fu, P. Hyperspectral Image Classifiacation Method Based on 2D-3D CNN and Multibranch Feature Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5776–5788. [Google Scholar] [CrossRef]
- Vaddi, R.; Manoharan, P. CNN based hyperspectral image classification using unsupervised band selection and structure-preserving spatial features. Infrared Phys. Technol. 2020, 110. [Google Scholar] [CrossRef]
- Guo, H.; Liu, J.; Xiao, Z.; Xiao, L. Deep CNN-based hyperspectral image classification using discirmnative multiple spatial-spectral feature fusion. Remote Sens. Lett. 2020, 11. [Google Scholar] [CrossRef]
- Wang, J.; Song, X.; Sun, L.; Huang, W.; Wang, J. A Novel Cubic Convolutional Neural Network for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4133–4148. [Google Scholar] [CrossRef]
- Gong, H.; Li, Q.; Li, C.; Dai, H.; He, Z.; Wang, W.; Li, H.; Han, F.; Tuniyazi, A.; Mu, T. Multiscale Information Fusion for Hyperspectral Image Classification Based on Hybrid 2D-3D CNN. Remote Sens. 2021, 13, 2268. [Google Scholar] [CrossRef]
- Kutluk, S.; Kayabol, K.; Akan, A. A new CNN training approach with application to hyperspectral image classification. Digit. Signal. Process. 2021, 113. [Google Scholar] [CrossRef]
- Yin, J.; Qi, C.; Chen, Q.; Qu, J. Spatial-Spectral Network for Hyperspectral Image Classification: A 3-D CNN and Bi-LSTM Framework. Remote Sens. 2021, 13, 2353. [Google Scholar] [CrossRef]
- He, X.; Chen, Y.; Lin, Z. Spatial-Spectral Transformer for Hyperspectral Image Classification. Remote Sens. 2021, 13, 498. [Google Scholar] [CrossRef]
- Rao, M.; Tang, P.; Zhang, Z. A Developed Siamese CNN with 3D Adaptive Spatial-Spectral Pyramid Pooling for Hyperspectral Image Classification. Remote Sens. 2020, 12, 1964. [Google Scholar] [CrossRef]
- Pan, S.; Guan, H.; Chen, Y.; Yu, Y.; Goncalves, W.N.; Junior, J.M.; Li, J. Land-cover classification of multispectral LiDAR data using CNN with optimized hyper-parameters. ISPRS J. Photogramm. Remote Sens. 2020, 166, 241–254. [Google Scholar] [CrossRef]
- Xie, J.; Chen, Y. LiDAR Data Classification Based on Automatic Designed CNN. IEEE Geosci. Remote Sens. Lett. 2020. [Google Scholar] [CrossRef]
- Hang, R.; Li, Y.; Ghamisi, P.; Hong, D.; Xia, G.; Liu, Q. Classification of Hyperspectral and LiDAR Data Using Coupled CNNs. IEEE Trans. Geosci. Remote Sens. 2020, 68, 4939–4950. [Google Scholar] [CrossRef] [Green Version]
- Feng, Q.; Zhu, D.; Yang, J.; Li, B. Multisource Hyperspectral and LiDAR Data Fusion for Urban Land-Use Mapping based on a Modified Two-Branch Convolutional Neural Network. ISPRS Int. J. Geoinf. 2019, 8, 28. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Li, W.; Du, Q.; Gao, L.; Zhang, B. Feature Extraction for Classification of Hyperspectral and LiDAR Data Using Patch-to-Patch CNN. IEEE Trans. Cybern. 2020, 50, 100–111. [Google Scholar] [CrossRef]
- Morchhale, S.; Pauca, V.P.; Plemmons, R.J.; Torgersen, T.C. Classification of pixel-level fused hyperspectral and LiDAR data using deep convolutional neural networks. In Proceedings of the 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016; pp. 1–5. [Google Scholar]
- Chen, Y.; Li, C.; Ghamisi, P.; Jia, X.; Gu, Y. Deep fusion of remote sensing data for accurate classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1253–1257. [Google Scholar] [CrossRef]
- Wu, H.; Prasad, S. Convolutional recurrent neural networks for hyperspectral data classification. Remote Sens. 2017, 9, 298. [Google Scholar] [CrossRef] [Green Version]
- Venkatesan, R.; Prabu, S. Hyperspectral image features classification using deep learning recurrent neural networks. J. Med. Syst. 2019, 43. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Scalable recurrent neural network for hyperspectral image classification. J. Supercomput. 2020. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Y.; Jiang, K.; Li, C.; Jiao, L.; Zhou, H. Spatial sequential recurrent neural network for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1–15. [Google Scholar] [CrossRef]
- Hao, S.; Wang, W.; Salzmann, M. Geometry-Aware Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2448–2460. [Google Scholar] [CrossRef]
- Vapnik, V. The support vector method of function estimation. In Nonlinear Modeling; Suykens, J.A.K., Ed.; Springer-Science-Business Media: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Camps-Valls, G.; Bruzzone, L. Kernel-based methods for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2005, 43. [Google Scholar] [CrossRef]
- Gualtieri, J.A.; Chettri, S.R.; Cromp, R.F.; Johnson, L.F. Support vector machines applied to AVIRIS data. In Proceedings of the Summaries of the Airborne Earth Science Workshop, Pasadena, CA, USA, 8–11 February 1999. [Google Scholar]
- Gualtieri, J.A.; Cromp, R.F. Support vector machines for hyperspectral remote sensing classification. Proc. SPIE 1998, 221–232. [Google Scholar]
- Melgani, F.; Lorenzo, B. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Camps-Valls, G.; Serrano-López, A.J.; Gómez-Chova, L.; Martín-Guerrero, J.D.; Calpe-Maravilla, J.; Moreno, J. Regularized RBF networks for hyperspectral data classification. Image Anal. Recognit. 2004, 429–436. [Google Scholar]
- Mercies, G.; Lennon, M. Support vector machines for hyperspectral image classification with spectral-based kernels. In Proceedings of the International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003. [Google Scholar]
- Camps-Valls, G.; Gomez-Chova, L.; Munoz-Mari, J.; Vila-Frances, J.; Calpe-Maravilla, J. Composite kernels for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2006, 3, 93–97. [Google Scholar] [CrossRef]
- Okwuashi, O. Deep support vector machine for hyperspectral image classification. Pattern Recognit. 2020, 103. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef] [Green Version]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inform. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef]
- Amini, S.; Homayouni, S.; Safari, A. Semi-supervised classification of hyperspectral image using random forest algorithm. In Proceedings of the International Geoscience and Remote Sensing Symposium, Quebec, QC, Canada, 13–18 July 2014. [Google Scholar]
- Niemeyer, J.; Rottensteiner, F.; Soergel, U. Classification of urban LiDAR data using conditional random field and random forests. In Proceedings of the Joint Urban Remote Sensing Event, Sao Paulo, Brazil, 21–23 April 2013; pp. 139–142. [Google Scholar]
- Jackson, Q.; Landgrebe, D. Adaptive bayesian contextual classification based on markov random fields. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2454–2463. [Google Scholar] [CrossRef] [Green Version]
- Izquierdo, A.; Lopez-Guede, J.M. Active Learning for Road Lane Landmark Inventory with Random Forest in Highly Uncontrolled LiDAR Intensity Based Image. In Proceedings of the 15th International Conference on Soft Computing Models in Industrial and Environmental Applications, Burgos, Spain, 16–18 September 2020. [Google Scholar]
- Romero, A.; Gatta, C.; Camps-Valls, G. Unsupervised deep feature extraction for remote sensing image classification. IEEE 2015. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.; Salakhutdinov, R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Ekanadham, C.; Ng, A. Sparse deep belief net model for visual area v2. Adv. Neural Inf. Process. Syst. 2008, 20, 873–880. [Google Scholar]
- Masci, J.; Meier, U.; Ciresan, D.; Schmidhuber, J. Stacked convolutional auto-encoders for hierarchical feature extraction. In Proceedings of the International Conference on Artificial Neural Networks, Espoo, Finland, 14–17 June 2011; pp. 52–59. [Google Scholar]
- Kavukcuoglu, K.; Sermanet, P.; Boureau, Y.L.; Gregor, K.; Mathieu, M.; LeCun, Y. Learning convolutional feature hierarchies for visual recognition. Adv. Neural Inf. Process. Syst. 2010. [Google Scholar]
- Lecun, Y.B.Y.; Bottou, L.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Sermanet, P.; Eigen, D.; Zhang, X.; Mathieu, M.; Fergus, R.; Lecun, Y. OverFeat: Integrated recognition, localization and detection using convolutional networks. In Proceedings of the 2nd International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54. [Google Scholar] [CrossRef] [Green Version]
- Prokhorov, D.V. Object recognition in 3D LiDAR data with recurrent neural network. In Proceedings of the Computer Vision and Pattern Recognition Workshop, Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Waske, B.; Benediktsson, J.A.; Arnason, K.; Sveinsson, J.R. Mapping of hyperspectral AVIRIS data using machine-learning algorithms. Can. J. Remote Sens. 2009, 35, 106–116. [Google Scholar] [CrossRef]
- Senchuri, R.; Kuras, A.; Burud, I. Machine Learning Methods for Road Edge Detection on Fused Airborne Hyperspectral and LIDAR Data. In Proceedings of the 11th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 March 2021. [Google Scholar]





| Classifier | Input | Domain | Class | Features | Advantages | Limitations | Study |
|---|---|---|---|---|---|---|---|
| SVM | HS | spectral | building, vegetation, road | spectral | High accuracy among classes with low material variations | Low accuracy among classes with high material variations (synthetic grass, tennis court) or similar material classes (road, highway) | [40] |
| Insensitive to noisy data, high accuracy (vegetation, water) | Spectral similarities of materials (misclassification of roofs and other impervious surfaces, impervious and non-vegetated pervious surfaces) | [238] | |||||
| vegetation, road | High accuracy among classes with low material variations (metal sheets, vegetation) | Misclassified bricks as gravel and asphalt as bricks | [239] | ||||
| Accurate classifi-cation with limited training data set | [240] | ||||||
| spectral-spatial | vegetation, road | spectral, spatial | Adding spatial information im-proves overall accu-racy and genera-lization | Misclassification of bricks requires knowledge about spatial features (maybe not available in the spectral library) | [241] | ||
| Integration of spatial and spectral features (contextual SVM) | [242] | ||||||
| SVM | Lidar | building, vegetation, road | HD, intensity | Robust and accurate classification | Misclassified small isolated buildings, rounded building edges | [64] | |
| building, vegetation | full-waveform | Can handle geometric features of 3D point cloud | Not balanced classes lead to misclassification (grass and sand) | [243] | |||
| multiple-return, intensity, morphology, texture | Fusion of single SVM classifiers and textu-ral features improve the final results | Misclassification (building classified as tree class) due to limited training data | [48] | ||||
| building, vegetation, road | HD, intensity, spectral | Spectral features performed better than geometrical features in classifi-cation based on multispectral lidar | Geometrical features cannot discriminate among low height classes: grass, road | [120] | |||
| building | HD, intensity, texture, spatial | GLCM features (mean and entropy) improve building classification | The magnitude of temporal change of buildings cannot be achieved using SVM, misclassification between trees and buildings | [53] | |||
| building, vegetation, road | HD, intensity, morphology, spectral | Morphological features with nDSM improve road and building classifi-cation based on multispectral lidar | nDSM provided misclassification between grass and trees | [53] | |||
| building, vegetation, road | HD, full-waveform | Dual-wavelength lidar improves land cover classification, especially low and high vegetation, and soil and low vegetation | Very low accuracy of low and high vegetation applying SVM on single wavelength lidar | [67] | |||
| SVM | HL-Fusion | spectral-spatial vs. object-based | roof, vegetation, road | HS: spectral Lidar: HD, intensity | The hyperspectral point cloud is robust and provides better results for vegetation and tin roof than grid-based fusion | Accuracy of hyperspectral point cloud classification depends on the proportion between point density of lidar and spatial resolution of HS, very complex in processing (in comparison to grid data) | [200] |
| spectral-spatial | vegetation | HS: spectral Lidar: HD | Overall accuracy increased, adding spatial to spectral features | Spatial features introduced misclassification errors in individual tree species | [76] | ||
| RF | HS | spectral | vegetation, road | spectral | High classification accuracy of vegetation, good robustness, insensitive to noise | Cascaded RF provides more generalization per-formance than standard RF | [244] |
| RF | Lidar | building, vegetation | full-waveform, HD, eigenvalue-based, multi-return | The ability of RF to select important features | Misclassification of grass (natural ground) and roads (artificial ground) | [136] | |
| building, vegetation, road | HD, intensity, texture | Overall high accuracy, multispectral lidar especially promising for ground-level classes (roads, low vegetation) | Misclassification of gravel and asphalt | [245] | |||
| RF | HL-Fusion | building, vegetation, road | HS: spectral Lidar: HD | The ability of RF to select essential features | [18] | ||
| CNN | HS | spectral-spatial | building, road | raw | High overall accuracy with original raw data | Single-class low accuracy (highway, railway), limited training data | [40] |
| vegetation, road | Very high overall accuracy, insensitive to noise [42,239], CNN in combination with Markov Random Fields im-proves overall accu-racy taking into account complete spectral and spatial information [36], spectral and spatial features extracted simultaneously (full advantage of structu-ral properties) [246] | The model achieved worse overall accuracy on other datasets (Indian pines), computationally expensive, misclassification of bricks and gravel, requires larger data set than standard ML [42,239], time-consuming, limited training data [36] | [36,39,42,219,225,229,230,239,246,247,248,249,250,251,252,253,254,255,256,257,258] | ||||
| CNN | Lidar | object-based | building | HD | Applicable to large-scale point cloud data sets due to a low number of input features [54] overall high accuracy with applying multiview rasters of roofs [55] | Misclassified buildings as vegetation (especially buildings with complex roof configuration) due to limited and too homo-geneous training data, sparse point density [54], height derived features are not sufficient to extract various roof types, require a large training data set [55] | [54,55] |
| building, vegetation, road | multi-wavelength intensity, HD | Time-effective due to the simplicity of the model | Trajectory data, strip registration and radiometric correction not included | [259] | |||
| pixel-based | HD | Automatic design of CNN for robust features extraction and high accuracy | Time-expensive search and training | [260] | |||
| CNN | HL-Fusion | spectral-spatial | building, vegetation, road | HS: spectral Lidar: HD, spatial | Generalization capability, improved accuracy when fusing HS and LiDAR | Not efficient in handling high-dimensional data compared to standard ML classifiers | [16] |
| HS: spectral, spatial Lidar: HD | Oversmoothing problems in classification results | [29,261,262] | |||||
| HS: spectral, spatial Lidar: HD, spatial | Effective extraction of essential features, reduced noise | [30,263] | |||||
| spectral-spatial | vegetation, road | Improved accuracy of fused data, deep neural network used for feature fusion improved the classi-fication results [264] | [80,265] | ||||
| pixel-based | building, vegetation, road | HS: spectral Lidar: HD | Remarkable misclassification of objects made from similar materials (parking lots, roads, highway) | [264] | |||
| CRNN | HS | spectral-spatial | building, vegetation, road | spectral, spatial | Does not require fixed input length, effectively extracted contextual information | Big training data set required | [266] |
| vegetation, road | [39] | ||||||
| RNN | HS | spectral | building, vegetation, road | spectral | Performs better than standard ML algo-rithms and CNNs | Issues with differentiation of asphalt/concrete made objects (roads, parking lot, highway) requires a longer calculation time | [37] |
| vegetation, road | [267,268] | ||||||
| spectral-spatial | vegetation, road | texture, morphology, spatial | Adding spatial features to the classification improves the overall and class accuracy, high level features can represent complex geometry | Computational time and memory-expensive | [256,269,270] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuras, A.; Brell, M.; Rizzi, J.; Burud, I. Hyperspectral and Lidar Data Applied to the Urban Land Cover Machine Learning and Neural-Network-Based Classification: A Review. Remote Sens. 2021, 13, 3393. https://doi.org/10.3390/rs13173393
Kuras A, Brell M, Rizzi J, Burud I. Hyperspectral and Lidar Data Applied to the Urban Land Cover Machine Learning and Neural-Network-Based Classification: A Review. Remote Sensing. 2021; 13(17):3393. https://doi.org/10.3390/rs13173393
Chicago/Turabian StyleKuras, Agnieszka, Maximilian Brell, Jonathan Rizzi, and Ingunn Burud. 2021. "Hyperspectral and Lidar Data Applied to the Urban Land Cover Machine Learning and Neural-Network-Based Classification: A Review" Remote Sensing 13, no. 17: 3393. https://doi.org/10.3390/rs13173393
APA StyleKuras, A., Brell, M., Rizzi, J., & Burud, I. (2021). Hyperspectral and Lidar Data Applied to the Urban Land Cover Machine Learning and Neural-Network-Based Classification: A Review. Remote Sensing, 13(17), 3393. https://doi.org/10.3390/rs13173393