Modal Parameters Identification of Bridge Structures from GNSS Data Using the Improved Empirical Wavelet Transform
Abstract
:1. Introduction
2. Methodology
2.1. The Improved EWT
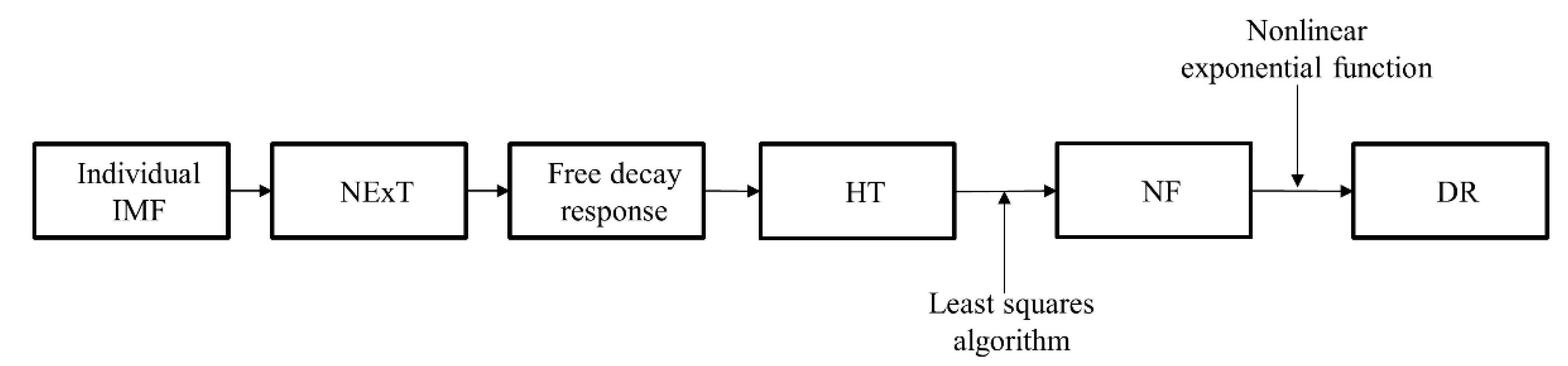
2.2. Modal Parameters Identification Based on the Improved EWT
3. Numerical Studies
3.1. Numerical Study on a 4-Storey Steel Frame Model
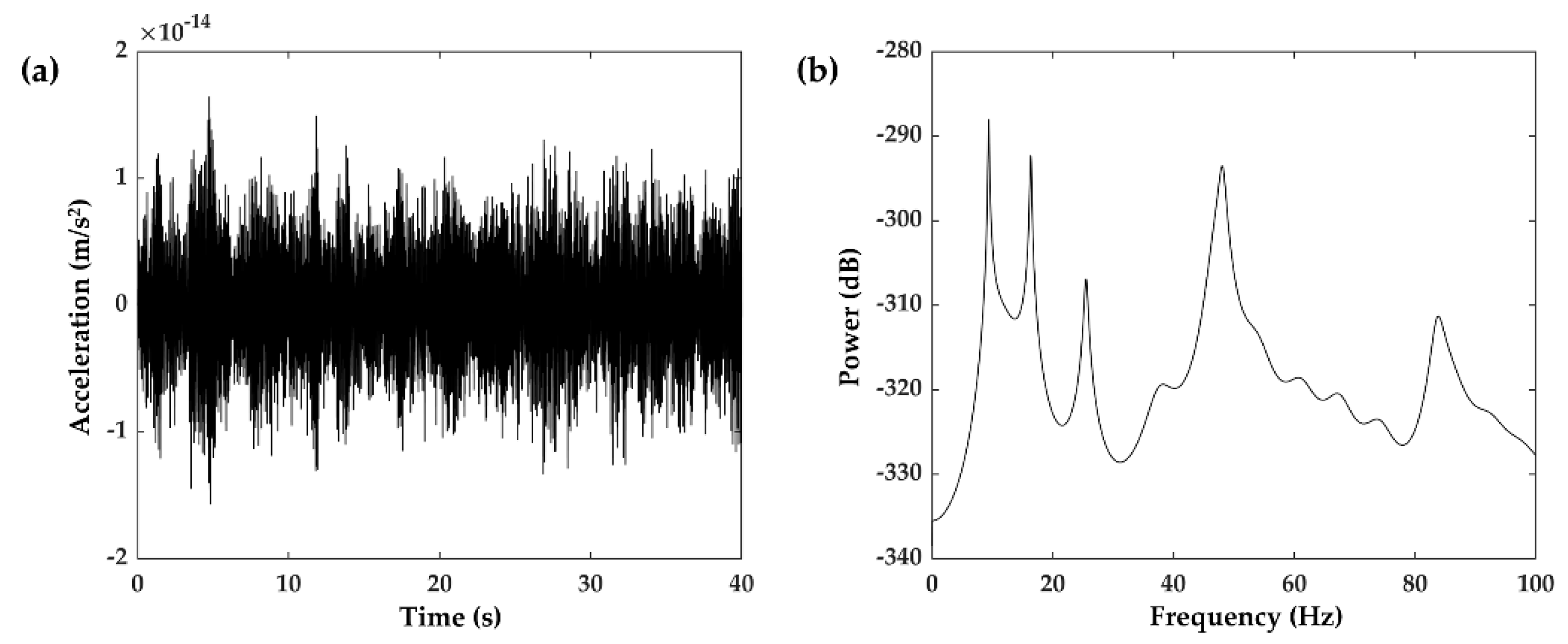
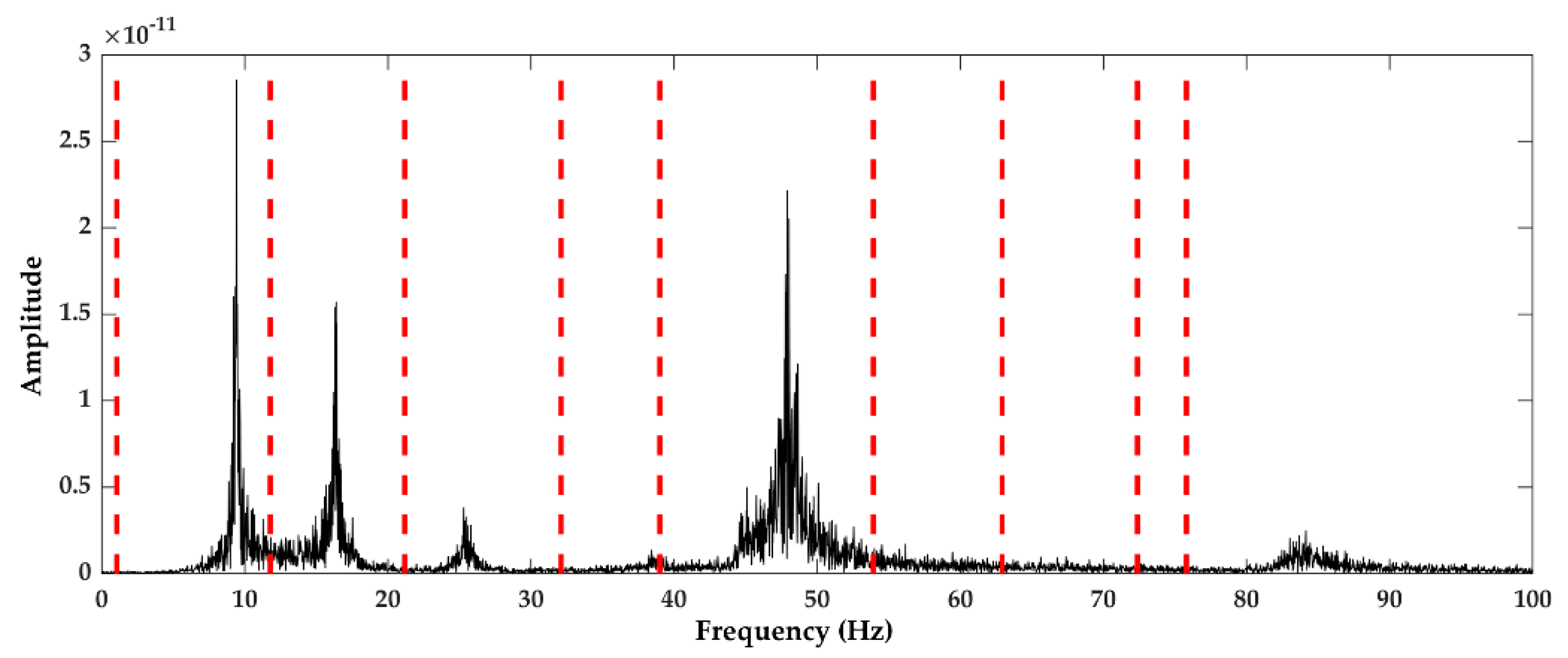
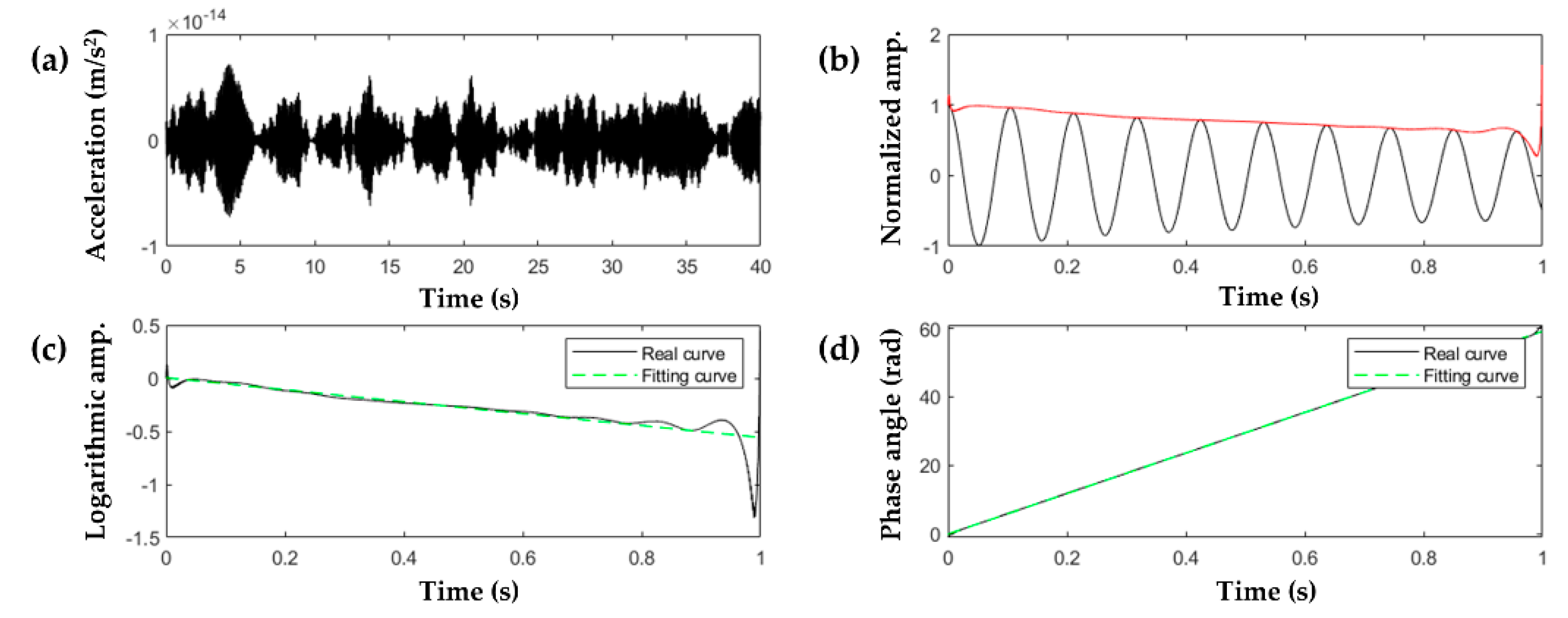
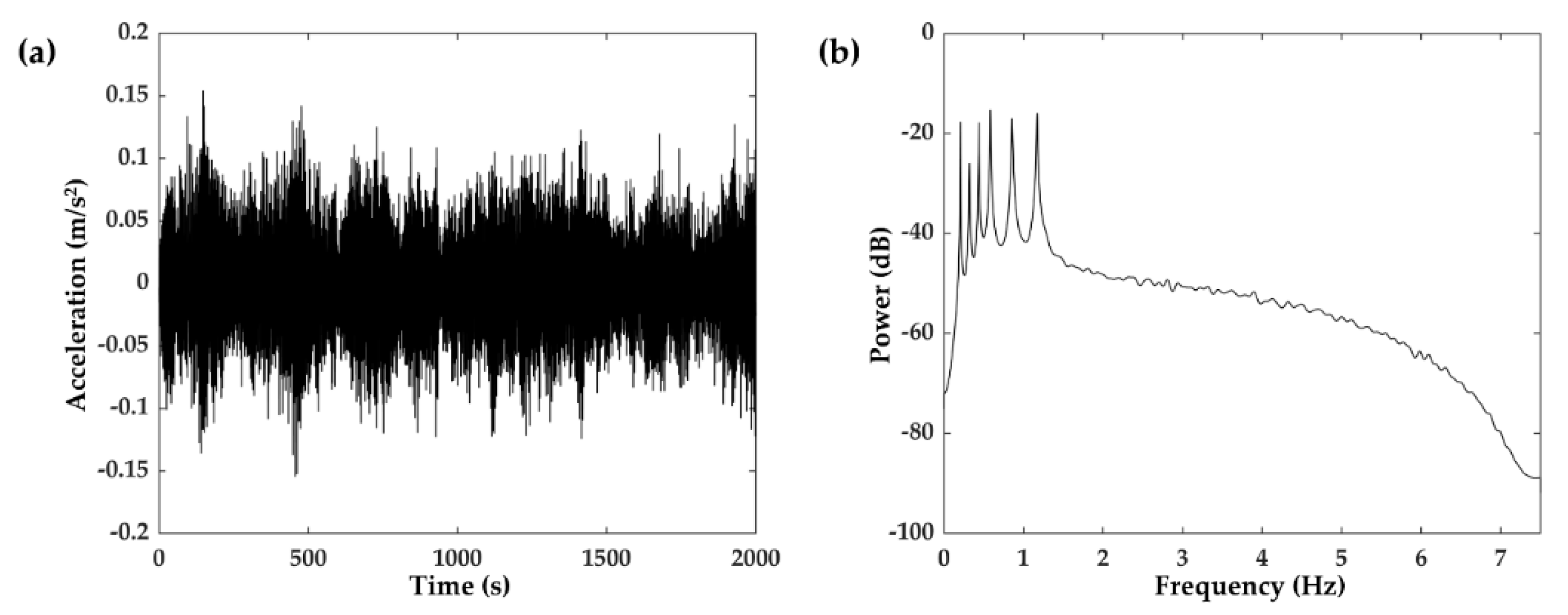
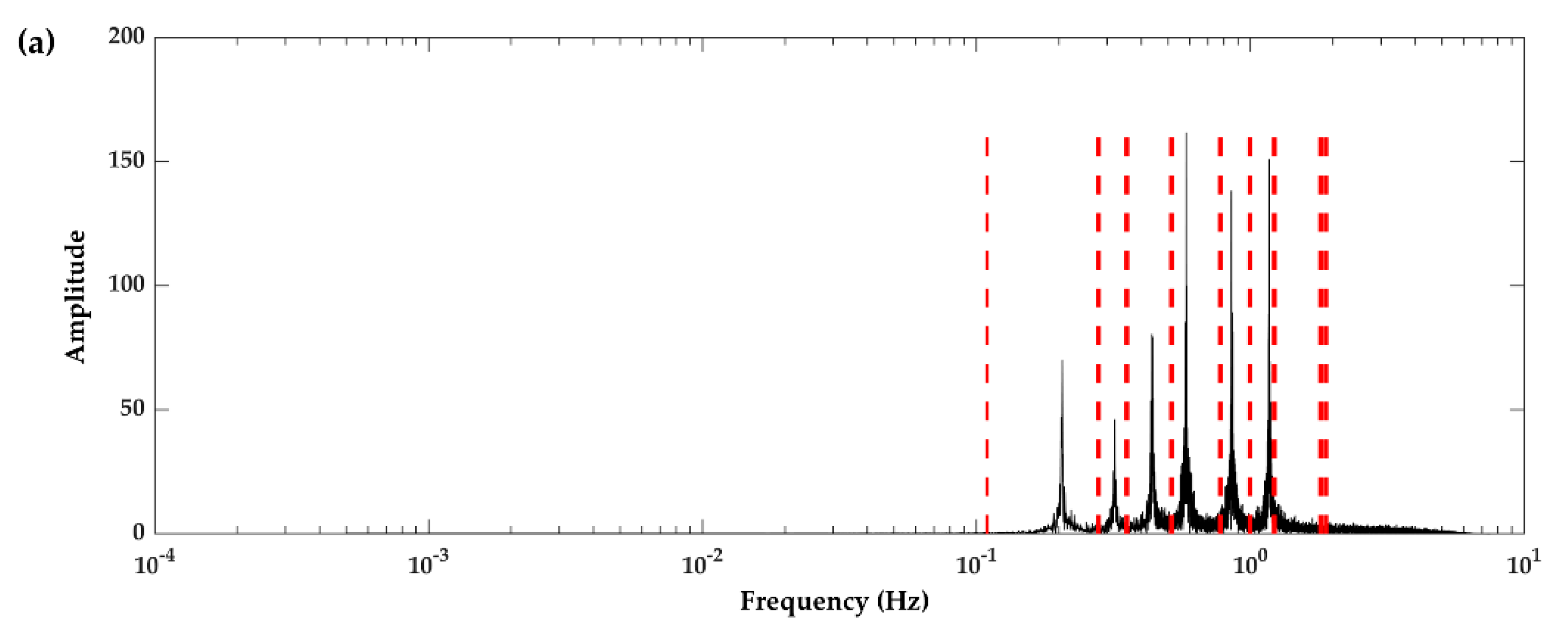
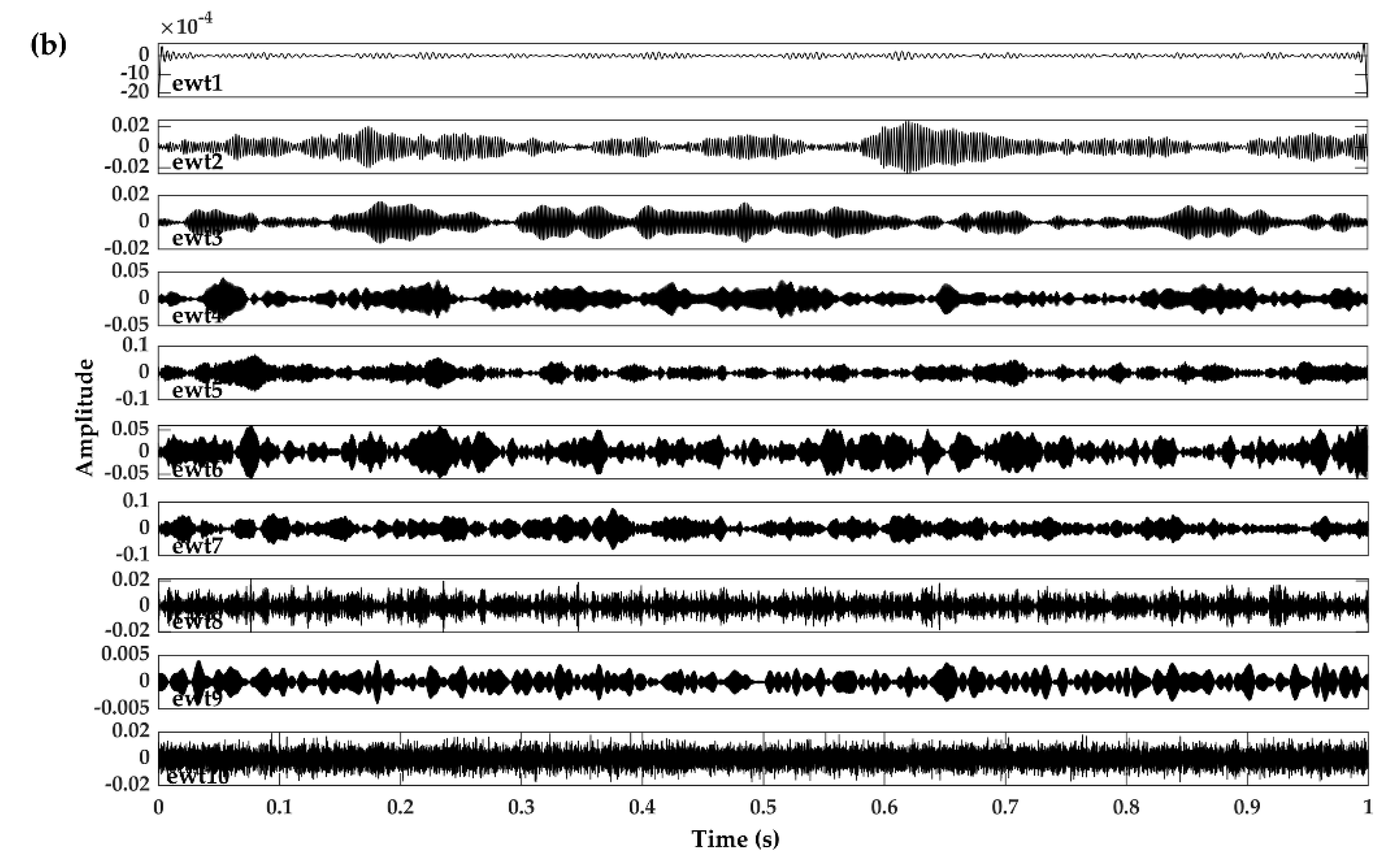
3.2. Numerical Study on Acceleration Response Data of a Suspension Bridge
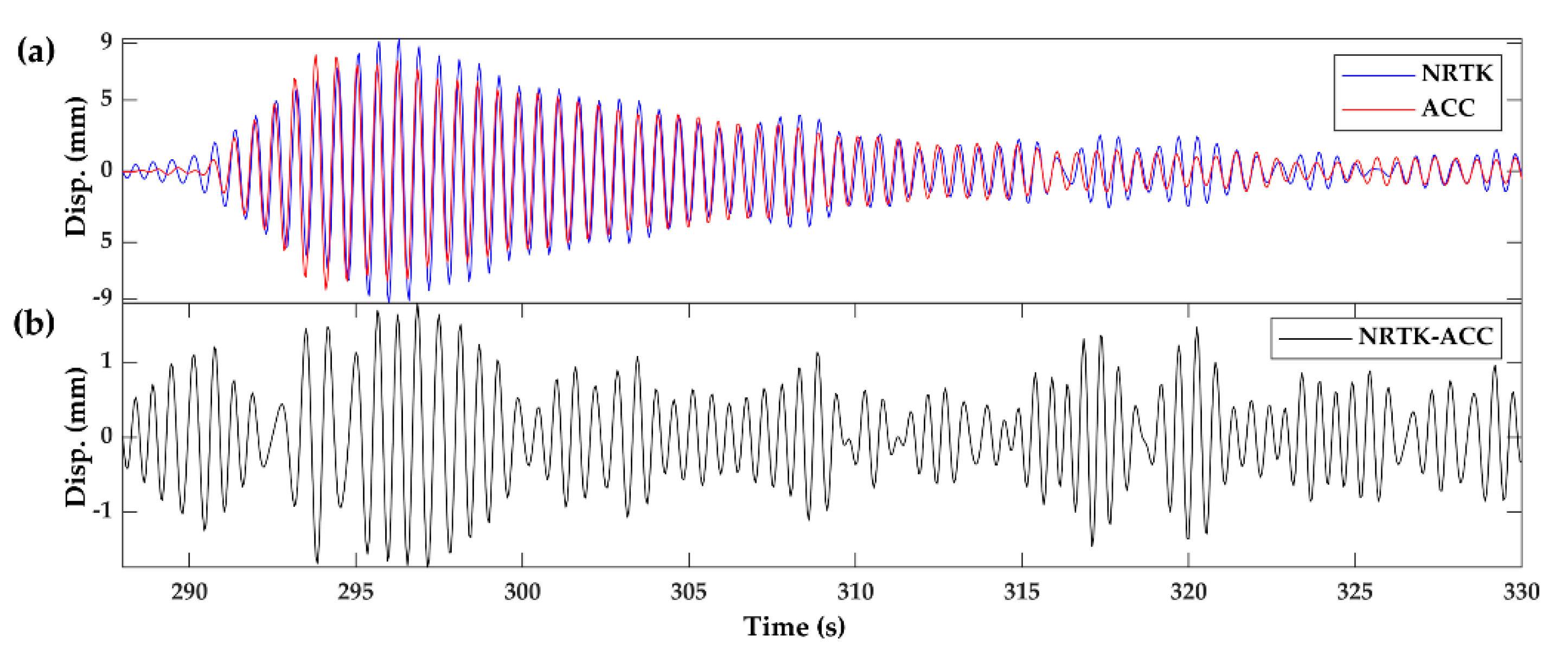
4. Field Experiments
4.1. Engineering Background
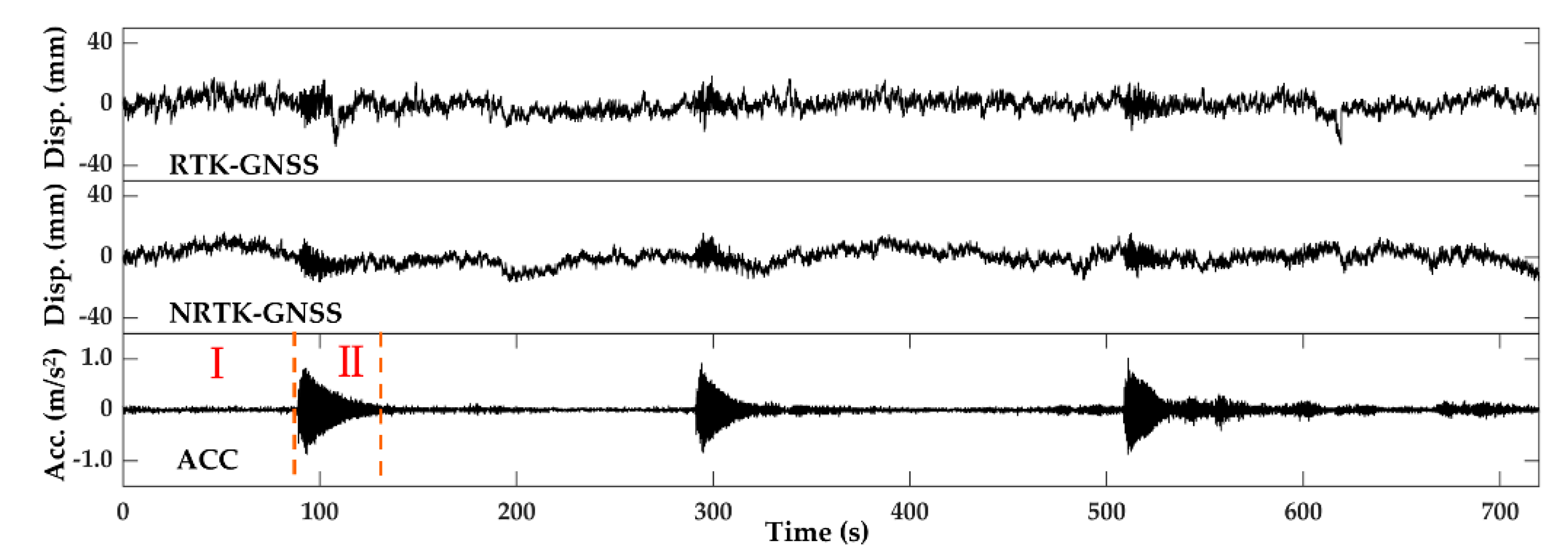
4.2. Data Processing and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | The Full Name |
| GNSS | Global Navigation Satellite System |
| EWT | Empirical Wavelet Transform |
| NExT | Natural Excitation Technique |
| HT | Hilbert Transform |
| WT | Wavelet Transform |
| CWT | Continuous Wavelet Transform |
| LSWA | Least-Squares Wavelet Analysis |
| WWA | Weighted Wavelet Analysis |
| EMD | Empirical Mode Decomposition |
| EEMD | Ensemble Empirical Mode Decomposition |
| MEMD | Multivariate Empirical Mode Decomposition |
| IMF | Intrinsic Mode Function |
| MUSIC | Multiple Signal Classification |
| NF | Natural Frequency |
| DR | Damping Ratio |
| SET | Synchro-Extracting Transform |
| LWM | Local Window Maxima |
| AM-FM | Amplitude Modulation-Frequency Modulation |
| DOF | Degrees-of-Freedom |
| FEA | Finite Element Analysis |
| RTK | Real-Time Kinematic |
| NRTK | Network Real-Time Kinematic |
| PPK | Post-Processing Kinematic |
| CORS | Continuous Operation Reference Station |
| ACC | Accelerometer |
| TF | Time–frequency |
| SNR | Signal-to-Noise Ratio |
| RMSE | Root Mean Square Error |
| R | Correlation Coefficient |
References
- Shen, N.; Chen, L.; Liu, J.B.; Wang, L.; Tao, T.Y.; Wu, D.W.; Chen, R.Z. A review of Global Navigation Satellite System (GNSS)-based dynamic monitoring technologies for structural health monitoring. Remote Sens. 2019, 11, 1001. [Google Scholar] [CrossRef] [Green Version]
- Moschas, F.; Stiros, S. Dynamic deflections of a stiff footbridge using 100-Hz GNSS and accelerometer data. J. Surv. Eng. 2015, 141, 04015003. [Google Scholar] [CrossRef]
- Yu, J.Y.; Meng, X.L.; Yan, B.F.; Xu, B.; Fan, Q.; Xie, Y.L. Global Navigation Satellite System-based positioning technology for structural health monitoring: A review. Struct. Control Health Monit. 2020, 27, e2467. [Google Scholar] [CrossRef] [Green Version]
- Gaxiola-Camacho, J.R.; Bennett, R.; Guzman-Acevedo, G.M.; Gaxiola-Camacho, I.E. Structural evaluation of dynamic and semi-static displacements of the Juarez Bridge using GPS technology. Measurement 2017, 110, 146–153. [Google Scholar] [CrossRef]
- Xi, R.J.; Chen, H.; Meng, X.L.; Jiang, W.P.; Chen, Q.S. Reliable dynamic monitoring of bridges with integrated GPS and BeiDou. J. Surv. Eng. 2018, 144, 04018008. [Google Scholar] [CrossRef]
- Yu, L.N.; Xiong, C.B.; Gao, Y.; Zhu, J.S. Combining GNSS and accelerometer measurements for evaluation of dynamic and semi-static characteristics of bridge structures. Meas. Sci. Technol. 2020, 31, 125102. [Google Scholar] [CrossRef]
- Zhou, W.; Feng, Z.R.; Liu, D.S.; Wang, X.J.; Chen, B.B. Modal parameter identification of structures based on short-time narrow-banded mode decomposition. Adv. Struct. Eng. 2020, 23, 3062–3074. [Google Scholar] [CrossRef]
- Fan, Q.; Meng, X.L.; Nguyen, D.T.; Xie, Y.L.; Yu, J.Y. Predicting displacement of bridge based on CEEMDAN-KELM model using GNSS monitoring data. J. Appl. Geod. 2020, 14, 253–261. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Hussan, M.; Kim, D. Time-series analysis of GPS measurements for long-span bridge movements using wavelet and model prediction techniques. Adv. Space Res. 2019, 63, 3505–3521. [Google Scholar] [CrossRef]
- Kaczmarek, A.; Kontny, B. Identification of the noise model in the time series of GNSS stations coordinates using wavelet analysis. Remote Sens. 2018, 10, 1611. [Google Scholar] [CrossRef] [Green Version]
- Ji, K.; Shen, Y.; Wang, F. Signal extraction from GNSS position time series using weighted wavelet analysis. Remote Sens. 2020, 12, 992. [Google Scholar] [CrossRef] [Green Version]
- Ghaderpour, E.; Ghaderpour, S. Least-squares spectral and wavelet analyses of V455 Andromedae time series: The life after the super-outburst. Publ. Astron. Soc. Pac. 2020, 132, 114504. [Google Scholar] [CrossRef]
- Barbosh, M.; Singh, P.; Sadhu, A. Empirical mode decomposition and its variants: A review with applications in structural health monitoring. Smart Mater. Struct. 2020, 29, 093001. [Google Scholar] [CrossRef]
- Civera, M.; Surace, C. A comparative analysis of signal decomposition techniques for structural health monitoring on an experimental benchmark. Sensors 2021, 21, 1825. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Hu, Y.; Li, F.; Li, H.; Liu, C. An enhanced empirical wavelet transform for noisy and non-stationary signal processing. Digit. Signal Process. 2017, 60, 220–229. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Gilles, J.; Heal, K. A parameterless scale-space approach to find meaningful modes in histograms—Application to image and spectrum segmentation. Int. J. Wavelets Multiresolut. Inf. Process. 2014, 12, 1450044. [Google Scholar] [CrossRef]
- Akbari, H.; Sadiq, M.T.; Rehman, A.U. Classification of normal and depressed EEG signals based on centered correntropy of rhythms in empirical wavelet transform domain. Health Inf. Sci. Syst. 2021, 9, 1–15. [Google Scholar] [CrossRef]
- Liao, Z.R.; Zhang, Y.F.; Li, Z.Y.; He, B.B.; Lang, X.; Liang, H.; Chen, J.H. Classification of red blood cell aggregation using empirical wavelet transform analysis of ultrasonic radiofrequency echo signals. Ultrasonics 2021, 114, 106419. [Google Scholar] [CrossRef]
- Liu, H.; Yu, C.Q.; Wu, H.P.; Duan, Z.; Yan, G.X. A new hybrid ensemble deep reinforcement learning model for wind speed short term forecasting. Energy 2020, 202, 117794. [Google Scholar] [CrossRef]
- Kalra, M.; Kumar, S.; Das, B. Seismic signal analysis using Empirical Wavelet Transform for moving ground target detection and classification. IEEE Sens. J. 2020, 20, 7886–7895. [Google Scholar] [CrossRef]
- Yu, H.; Li, H.R.; Li, Y.L. Vibration signal fusion using improved empirical wavelet transform and variance contribution rate for weak fault detection of hydraulic pumps. ISA Trans. 2020, 107, 385–401. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Park, H.S.; Adeli, H. A novel methodology for modal parameters identification of large smart structures using MUSIC, empirical wavelet transform, and Hilbert transform. Eng. Struct. 2017, 147, 148–159. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. A new music-empirical wavelet transform methodology for time-frequency analysis of noisy nonlinear and non-stationary signals. Digit. Signal Process. 2015, 45, 55–68. [Google Scholar] [CrossRef]
- Xin, Y.; Hao, H.; Li, J. Operational modal identification of structures based on improved empirical wavelet transform. Struct. Control Health Monit. 2019, 26, e2323. [Google Scholar] [CrossRef]
- Xia, Y.X.; Zhou, Y.L. Mono-component feature extraction for condition assessment in civil structures using empirical wavelet transform. Sensors 2019, 19, 4280. [Google Scholar] [CrossRef] [Green Version]
- Xin, Y.; Hao, H.; Li, J. Time-varying system identification by enhanced empirical wavelet transform based on synchroextracting transform. Eng. Struct. 2019, 196, 109313. [Google Scholar] [CrossRef]
- Dong, S.; Yuan, M.; Wang, Q.; Liang, Z. A modified empirical wavelet transform for acoustic emission signal decomposition in structural health monitoring. Sensors 2018, 18, 1645. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, L.; He, Y. The power spectrum estimation of the AR model based on motor imagery EEG. In Mechatronics and Intelligent Materials Iii, Pts 1-3; Chen, R., Sung, W.P., Kao, J.C.M., Eds.; Advanced Materials Research; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2013; Volumes 706–708, pp. 1923–1927. [Google Scholar]
- Xue, B.; Hong, H.; Zhou, S.; Chen, G.; Li, Y.; Wang, Z.; Zhu, X. Morphological filtering enhanced empirical wavelet transform for mode decomposition. IEEE Access 2019, 7, 14283–14293. [Google Scholar] [CrossRef]
- Liu, X.L.; Jiang, M.Z.; Liu, Z.Q.; Wang, H. A morphology filter-assisted extreme-point symmetric mode decomposition (MF-ESMD) denoising method for bridge dynamic deflection based on ground-based microwave interferometry. Shock Vib. 2020, 2020, 8430986. [Google Scholar] [CrossRef]
- Pei, Q.; Li, L. Structural modal parameter identification based on natural excitation technique. In Advanced Research on Civil Engineering, Materials Engineering and Applied Technology; Zhang, H., Jin, D., Zhao, X.J., Eds.; Advanced Materials Research; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2014; Volume 859, pp. 167–170. [Google Scholar]
- Dyke, S.; Agrawal, A.K.; Caicedo, J.M.; Christenson, R.; Gavin, H.; Johnson, E.; Nagarajaiah, S.; Narasimhan, S.; Spencer, B. NEES: Database for Structural Control and Monitoring Benchmark Problems. 2015. Available online: https://datacenterhub.org/resources/257 (accessed on 12 May 2021).
- Johnson, E.A.; Lam, H.F.; Katafygiotis, L.S.; Beck, J.L. Phase I IASC-ASCE structural health monitoring benchmark problem using simulated data. J. Eng. Mech. 2004, 130, 3–15. [Google Scholar] [CrossRef]
- Cheynet, E.; Daniotti, N.; Jakobsen, J.B.; Snæbjörnsson, J. Improved long-span bridge modeling using data-driven identification of vehicle-induced vibrations. Struct. Control Health Monit. 2020, 27, e2574. [Google Scholar] [CrossRef]
- Yu, J.Y.; Meng, X.L.; Shao, X.D.; Yan, B.F.; Yang, L. Identification of dynamic displacements and modal frequencies of a medium-span suspension bridge using multimode GNSS processing. Eng. Struct. 2014, 81, 432–443. [Google Scholar] [CrossRef]
- Yu, J.Y.; Yan, B.F.; Meng, X.L.; Shao, X.D.; Ye, H. Measurement of bridge dynamic responses using network-based real-time kinematic GNSS technique. J. Surv. Eng. 2016, 142, 04015013. [Google Scholar] [CrossRef]
- Meng, X.L.; Dodson, A.H.; Roberts, G.W. Detecting bridge dynamics with GPS and triaxial accelerometers. Eng. Struct. 2007, 29, 3178–3184. [Google Scholar] [CrossRef]





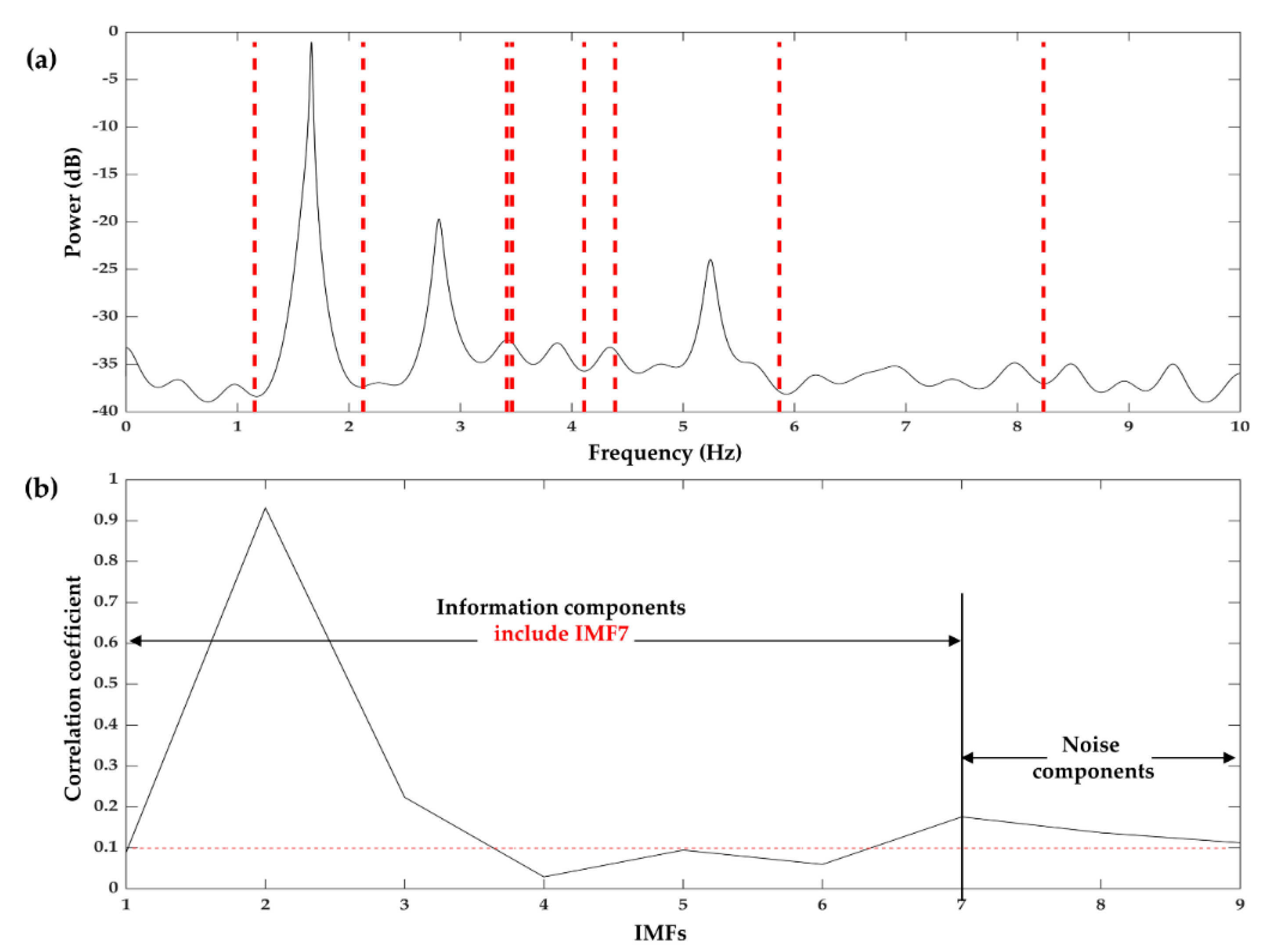


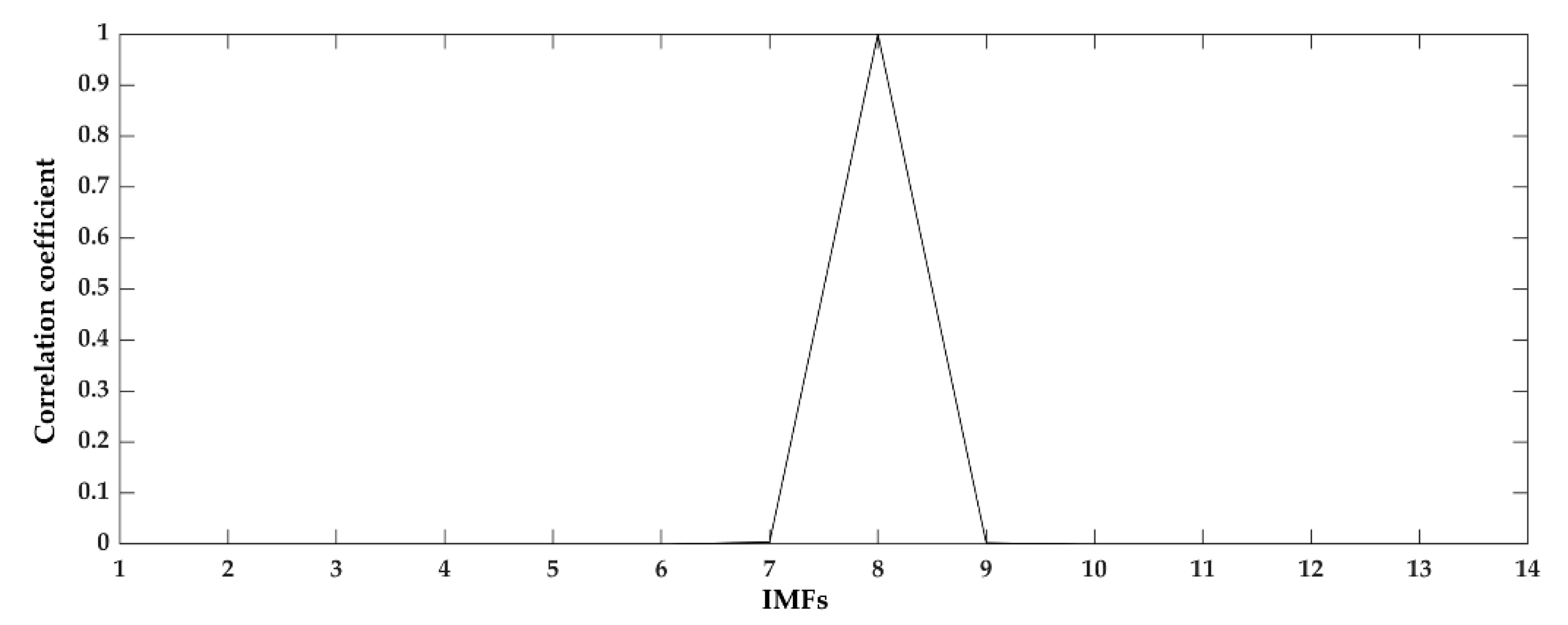
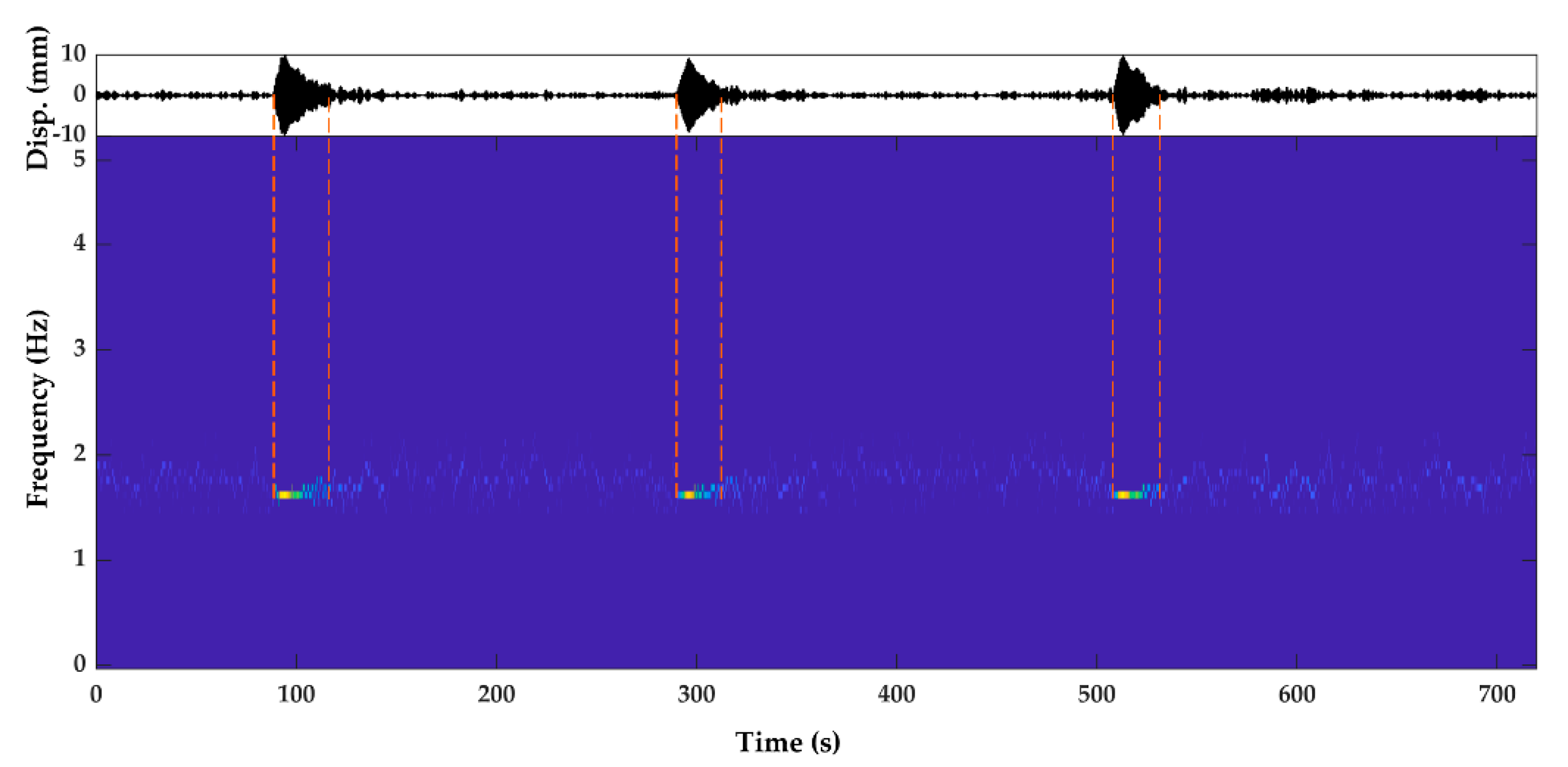
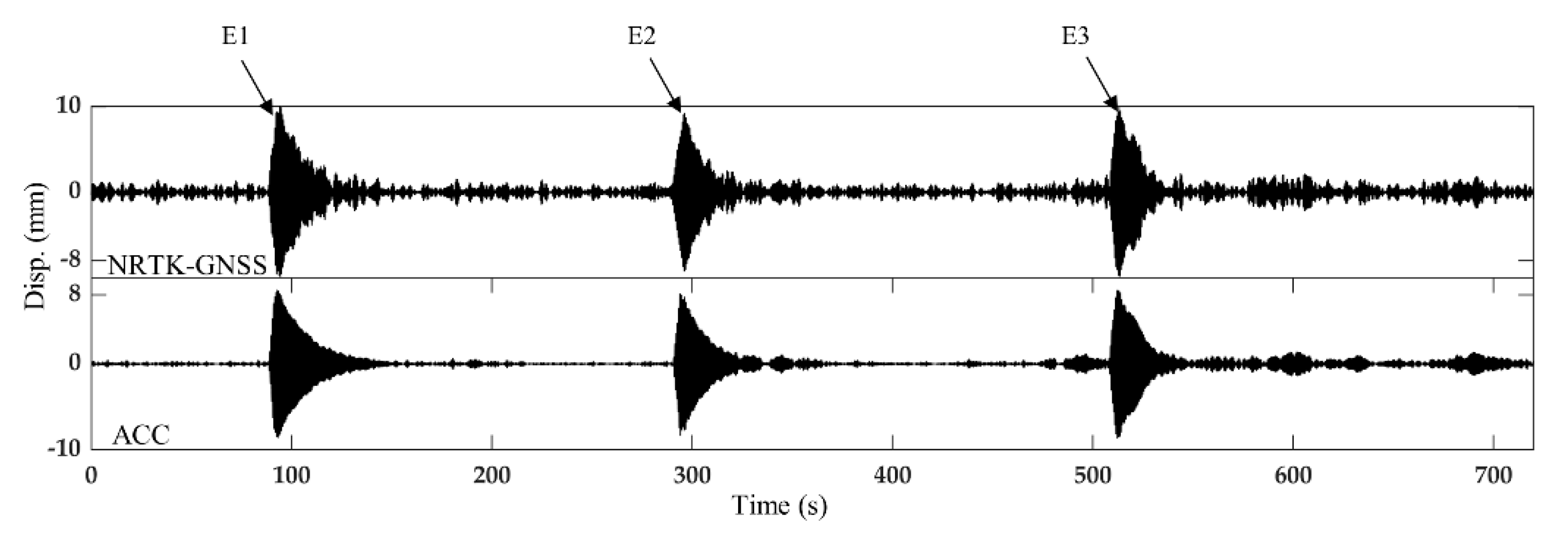
| IMF | FEA | Proposed Method | Difference | |||
|---|---|---|---|---|---|---|
| NF (Hz) | DR (%) | NF (Hz) | DR (%) | NF (%) | DR (%) | |
| 2 | 9.41 | 1.0 | 9.4051 | 0.96 | 0.05 | 4 |
| 3 | 16.38 | 1.0 | 16.3540 | 1.0 | 0.16 | 0 |
| 4 | 25.54 | 1.0 | 25.4529 | 1.02 | 0.34 | 2 |
| 6 | 48.01 | 1.0 | 47.9889 | 0.96 | 0.04 | 4 |
| IMF | Target Value | Proposed Method | Difference | |||
|---|---|---|---|---|---|---|
| NF (Hz) | DR (%) | NF (Hz) | DR (%) | NF (%) | DR (%) | |
| 2 | 0.2046 | 0.50 | 0.2046 | 0.53 | 0 | 6 |
| 3 | 0.3189 | 0.50 | 0.3192 | 0.52 | 0.09 | 4 |
| 4 | 0.4391 | 0.50 | 0.4381 | 0.54 | 0.23 | 8 |
| 5 | 0.5852 | 0.50 | 0.5852 | 0.54 | 0 | 8 |
| 6 | 0.8643 | 0.50 | 0.8574 | 0.67 | 0.80 | 34 |
| 7 | 1.1944 | 0.50 | 1.1718 | 0.39 | 1.89 | 22 |
| Mode | NF (Hz) | DR (%) |
|---|---|---|
| 1 | 1.6710 | 0.82 |
| 2 | 2.8434 | 0.48 |
| 3 | 5.2059 | 0.50 |
| Method | SNR (dB) | RMSE (mm) | R |
|---|---|---|---|
| EMD | 2.0424 | 1.7 | 0.6145 |
| WT | 2.4835 | 1.5 | 0.6628 |
| Proposed method | 8.7773 | 0.52 | 0.9343 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Z.; Yu, J.; Meng, X. Modal Parameters Identification of Bridge Structures from GNSS Data Using the Improved Empirical Wavelet Transform. Remote Sens. 2021, 13, 3375. https://doi.org/10.3390/rs13173375
Fang Z, Yu J, Meng X. Modal Parameters Identification of Bridge Structures from GNSS Data Using the Improved Empirical Wavelet Transform. Remote Sensing. 2021; 13(17):3375. https://doi.org/10.3390/rs13173375
Chicago/Turabian StyleFang, Zhen, Jiayong Yu, and Xiaolin Meng. 2021. "Modal Parameters Identification of Bridge Structures from GNSS Data Using the Improved Empirical Wavelet Transform" Remote Sensing 13, no. 17: 3375. https://doi.org/10.3390/rs13173375
APA StyleFang, Z., Yu, J., & Meng, X. (2021). Modal Parameters Identification of Bridge Structures from GNSS Data Using the Improved Empirical Wavelet Transform. Remote Sensing, 13(17), 3375. https://doi.org/10.3390/rs13173375







