Comparative Evaluation of Algorithms for Leaf Area Index Estimation from Digital Hemispherical Photography through Virtual Forests
Abstract
:1. Introduction
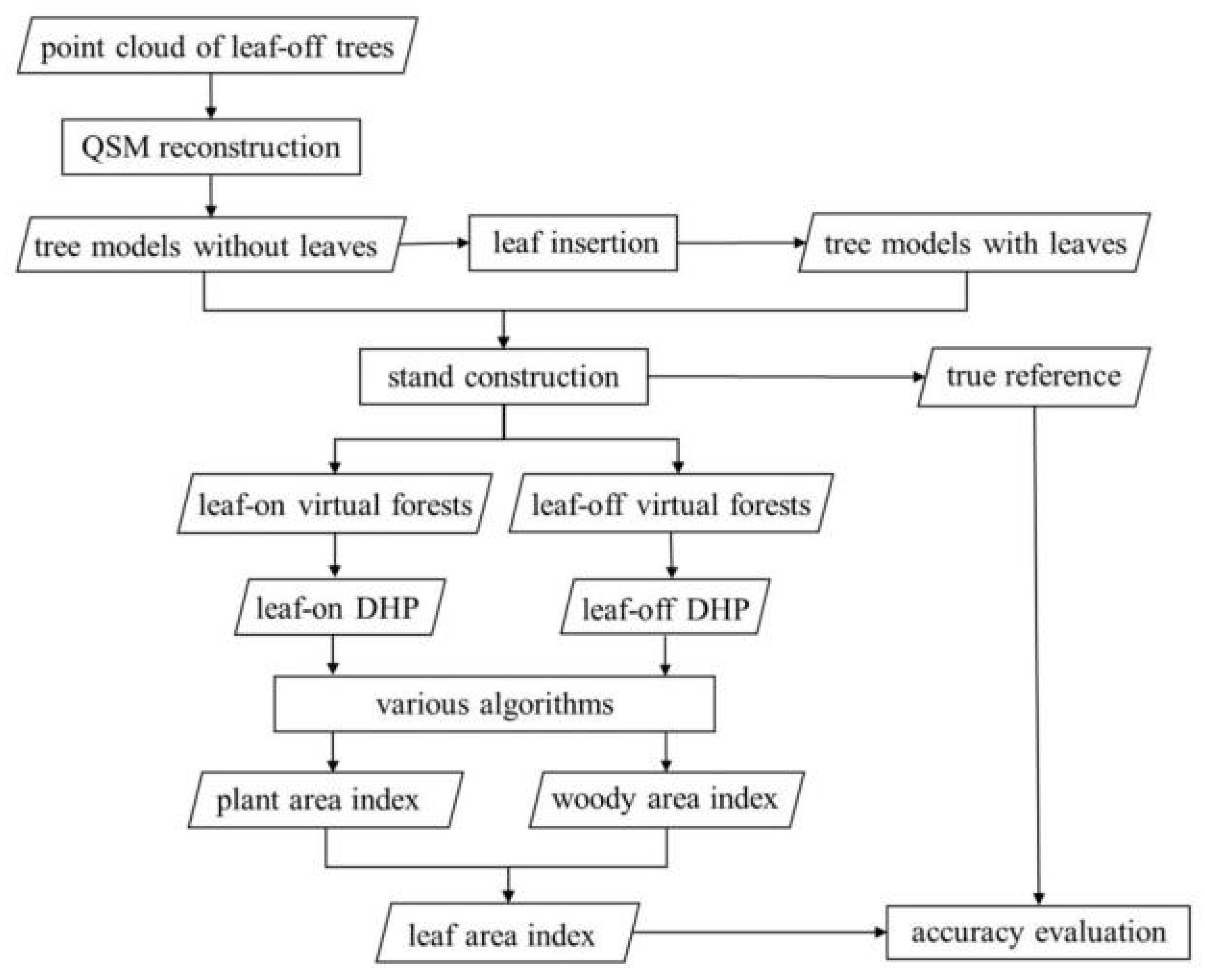
2. Materials and Methods
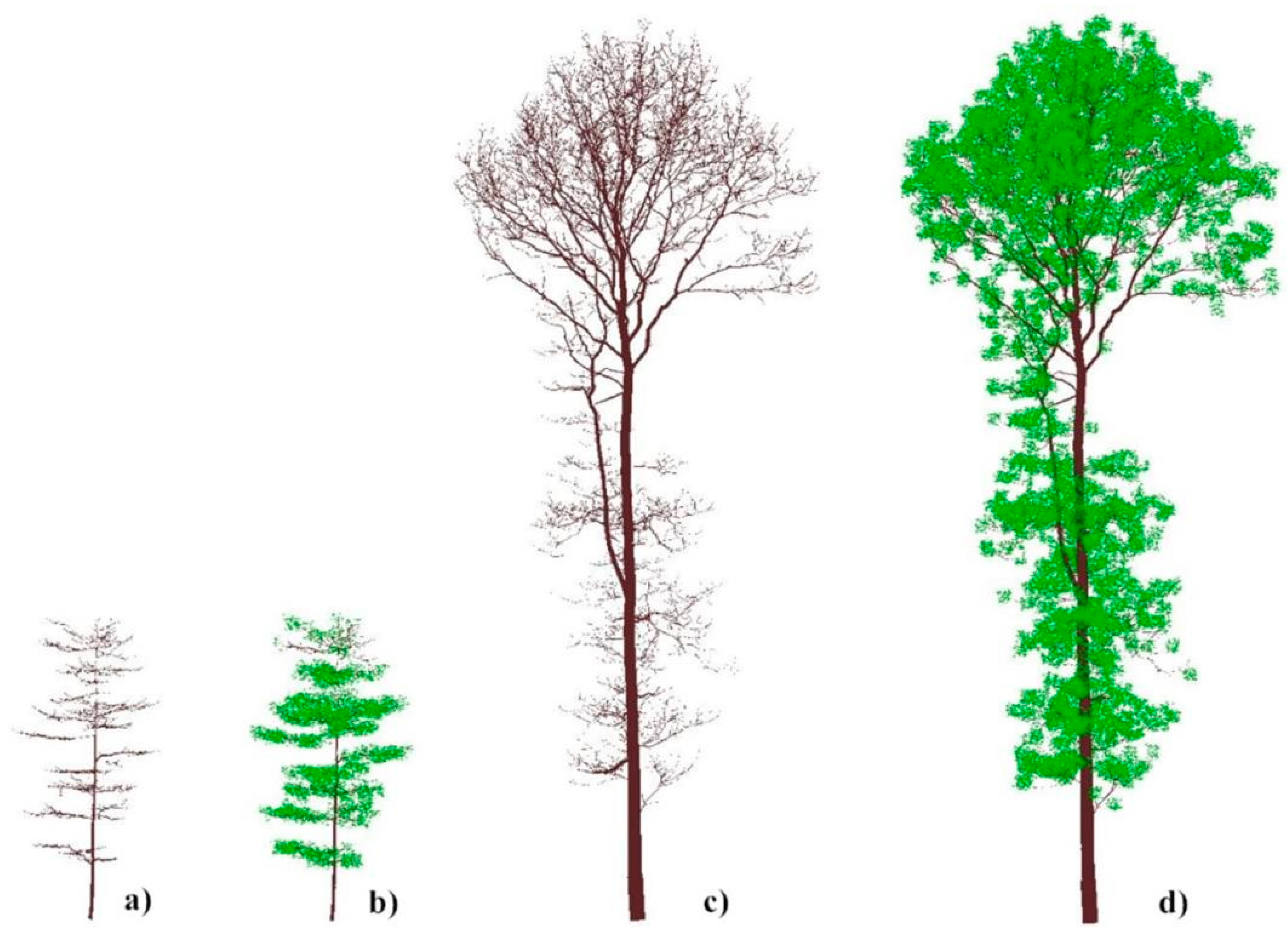
2.1. Virtual Forests Generation
2.2. Synthetic DHP Generation
2.3. LAI Estimation from DHP
2.4. Statistical Analysis
3. Results
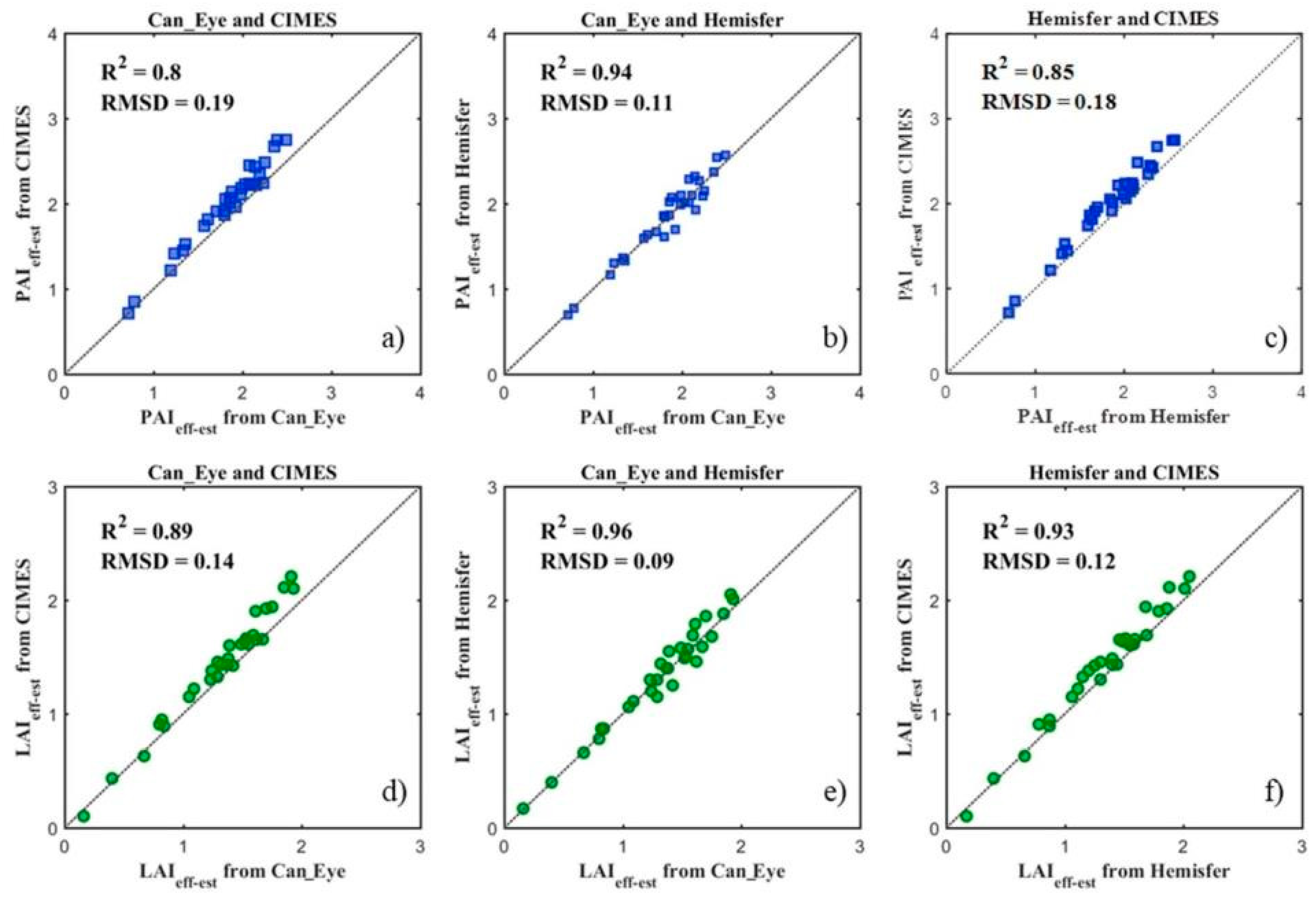
3.1. PAIeff and LAIeff Estimation Results
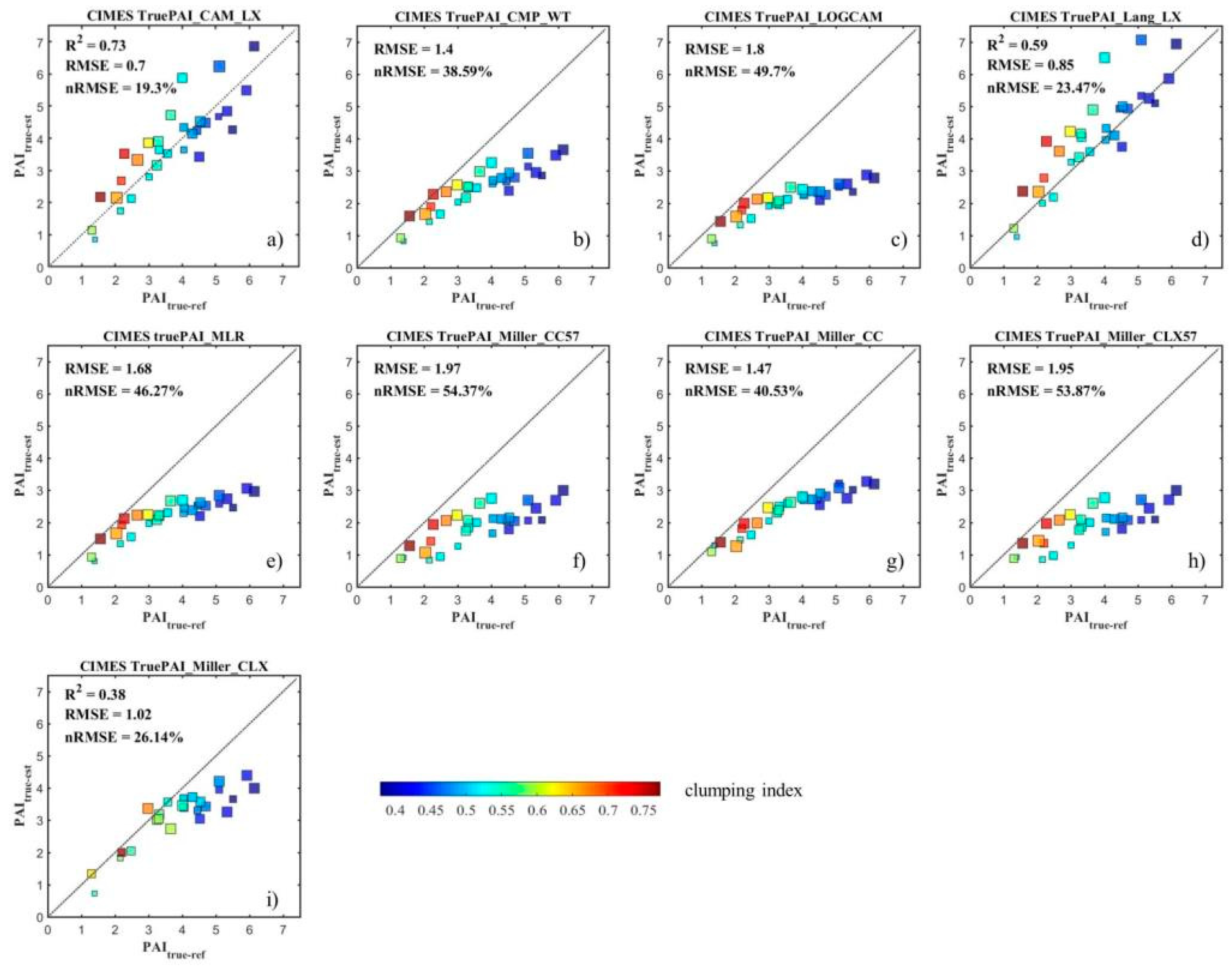
3.2. Comparison of PAItrue Estimation Accuracy
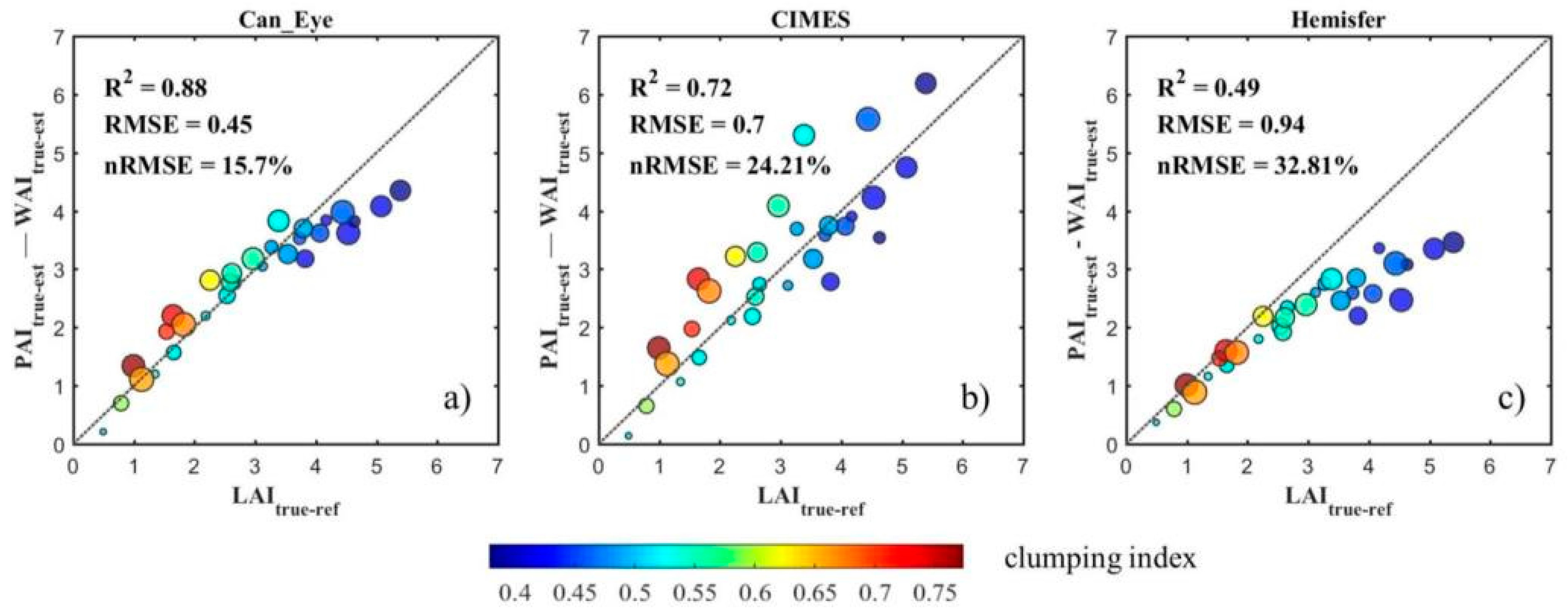
3.3. Comparison of LAItrue Estimation Accuracy
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fernandes, R.; Plummer, S.; Nightingale, J.; Baret, F.; Camacho, F.; Fang, H.; Garrigues, S.; Gobron, N.; Lang, M.; Lacaze, R.; et al. Global Leaf Area Index Product Validation Good Practices. Version 2.0. 2014; p. 76. Available online: https://lpvs.gsfc.nasa.gov/LAI/LAI_home.html (accessed on 15 June 2021).
- Skidmore, A.K.; Pettorelli, N. Agree on biodiversity metrics to track from space: Ecologists and space agencies must forge a global monitoring strategy. Nature 2015, 523, 403–406. [Google Scholar] [CrossRef] [Green Version]
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The concept of essential climate variables in support of climate research, applications, and policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- Gonsamo, A.; Walter, J.-M.N.; Pellikka, P. CIMES: A package of programs for determining canopy geometry and solar radiation regimes through hemispherical photographs. Comput. Electron. Agric. 2011, 79, 207–215. [Google Scholar] [CrossRef]
- White, K.; Pontius, J.; Schaberg, P. Remote sensing of spring phenology in northeastern forests: A comparison of methods, field metrics and sources of uncertainty. Remote Sens. Environ. 2014, 148, 97–107. [Google Scholar] [CrossRef]
- Lang, M.; Nilson, T.; Kuusk, A.; Pisek, J.; Korhonen, L.; Uri, V. Digital photography for tracking the phenology of an evergreen conifer stand. Agric. For. Meteorol. 2017, 246, 15–21. [Google Scholar] [CrossRef]
- Baret, F.; Weiss, M.; Allard, D.; Garrigue, S.; Leroy, M.; Jeanjean, H.; Fernandes, R.; Myneni, R.; Privette, J.; Morisette, J.; et al. VALERI: A network of sites and a methodology for the validation of medium spatial resolution land satellite products. Remote Sens. Environ. 2005, 76, 36–39. [Google Scholar]
- Brown, L.A.; Meier, C.; Morris, H.; Pastor-Guzman, J.; Bai, G.; Lerebourg, C.; Gobron, N.; Lanconelli, C.; Clerici, M.; Dash, J. Evaluation of global leaf area index and fraction of absorbed photosynthetically active radiation products over North America using Copernicus Ground Based Observations for Validation data. Remote Sens. Environ. 2020, 247, 111935. [Google Scholar] [CrossRef]
- Li, X.J.; Mao, F.J.; Du, H.Q.; Zhou, G.M.; Xu, X.J.; Han, N.; Sun, S.B.; Gao, G.L.; Chen, L. Assimilating leaf area index of three typical types of subtropical forest in China from MODIS time series data based on the integrated ensemble Kalman filter and PROSAIL model. ISPRS J. Photogramm. Remote Sens. 2017, 126, 68–78. [Google Scholar] [CrossRef]
- Dong, T.F.; Liu, J.G.; Qian, B.D.; He, L.M.; Liu, J.; Wang, R.; Jing, Q.; Champagne, C.; McNairn, H.; Powers, J.; et al. Estimating crop biomass using leaf area index derived from Landsat 8 and Sentinel-2 data. ISPRS J. Photogramm. Remote Sens. 2020, 168, 236–250. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, J.; Skidmore, A.K.; Premier, J.; Heurich, M. A voxel matching method for effective leaf area index estimation in temperate deciduous forests from leaf-on and leaf-off airborne LiDAR data. Remote Sens. Environ. 2020, 240, 111696. [Google Scholar] [CrossRef]
- Korhonen, L.; Korpela, I.; Heiskanen, J.; Maltamo, M. Airborne discrete-return LIDAR data in the estimation of vertical canopy cover, angular canopy closure and leaf area index. Remote Sens. Environ. 2011, 115, 1065–1080. [Google Scholar] [CrossRef]
- Liu, J.; Skidmore, A.K.; Jones, S.; Wang, T.; Heurich, M.; Zhu, X.; Shi, Y. Large off-nadir scan angle of airborne LiDAR can severely affect the estimates of forest structure metrics. ISPRS J. Photogramm. Remote Sens. 2018, 136, 13–25. [Google Scholar] [CrossRef]
- Tang, H.; Brolly, M.; Zhao, F.; Strahler, A.H.; Schaaf, C.L.; Ganguly, S.; Zhang, G.; Dubayah, R. Deriving and validating Leaf Area Index (LAI) at multiple spatial scales through lidar remote sensing: A case study in Sierra National Forest, CA. Remote Sens. Environ. 2014, 143, 131–141. [Google Scholar] [CrossRef]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An overview of global leaf area index (LAI): Methods, products, validation, and applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Piao, S.; Wang, X.; Park, T.; Chen, C.; Lian, X.; He, Y.; Bjerke, J.W.; Chen, A.; Ciais, P.; Tømmervik, H.; et al. Characteristics, drivers and feedbacks of global greening. Nat. Rev. Earth Environ. 2020, 1, 14–27. [Google Scholar] [CrossRef]
- Chianucci, F.; Cutini, A. Digital hemispherical photography for estimating forest canopy properties: Current controversies and opportunities. IForest-Biogeosci. For. 2012, 5, 290. [Google Scholar] [CrossRef] [Green Version]
- Frazer, G. Gap Light Analyzer (GLA) Imaging Software to Extract Canopy Structure and Gap Light Transmission Indices from True-Colour Fisheye Photographs, Users Manual and Program Documentation; Millbrook: New York, NY, USA, 1999; p. 36. [Google Scholar]
- Weiss, M.; Baret, F. CAN_EYE V6. 4.91 User Manual. Recuperado 2017, 12, 56. [Google Scholar]
- Schleppi, P.; Conedera, M.; Sedivy, I.; Thimonier, A. Correcting non-linearity and slope effects in the estimation of the leaf area index of forests from hemispherical photographs. Agric. For. Meteorol. 2007, 144, 236–242. [Google Scholar] [CrossRef]
- Morsdorf, F.; Kötz, B.; Meier, E.; Itten, K.; Allgöwer, B. Estimation of LAI and fractional cover from small footprint airborne laser scanning data based on gap fraction. Remote Sens. Environ. 2006, 104, 50–61. [Google Scholar] [CrossRef]
- Hymus, G.J.; Pontailler, J.Y.; Li, J.; Stiling, P.; Hinkle, C.R.; Drake, B.G. Seasonal variability in the effect of elevated CO2 on ecosystem leaf area index in a scrub-oak ecosystem. Glob. Chang. Biol. 2002, 8, 931–940. [Google Scholar] [CrossRef]
- Rudic, T.E.; McCulloch, L.A.; Cushman, K.C. Comparison of Smartphone and Drone Lidar Methods for Characterizing Spatial Variation in PAI in a Tropical Forest. Remote Sens. 2020, 12, 1765. [Google Scholar] [CrossRef]
- Canisius, F.; Fernandes, R.; Chen, J. Comparison and evaluation of Medium Resolution Imaging Spectrometer leaf area index products across a range of land use. Remote Sens. Environ. 2010, 114, 950–960. [Google Scholar] [CrossRef]
- De Kauwe, M.G.; Disney, M.I.; Quaife, T.; Lewis, P.; Williams, M. An assessment of the MODIS collection 5 leaf area index product for a region of mixed coniferous forest. Remote Sens. Environ. 2011, 115, 767–780. [Google Scholar] [CrossRef]
- Rowland, L.; da Costa, A.C.L.; Galbraith, D.R.; Oliveira, R.S.; Binks, O.J.; Oliveira, A.A.R.; Pullen, A.M.; Doughty, C.E.; Metcalfe, D.B.; Vasconcelos, S.S.; et al. Death from drought in tropical forests is triggered by hydraulics not carbon starvation. Nature 2015, 528, 119–122. [Google Scholar] [CrossRef] [Green Version]
- Demarez, V.; Duthoit, S.; Baret, F.; Weiss, M.; Dedieu, G. Estimation of leaf area and clumping indexes of crops with hemispherical photographs. Agric. For. Meteorol. 2008, 148, 644–655. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Skidmore, A.K.; Darvishzadeh, R.; Niemann, K.O.; Liu, J.; Shi, Y.; Wang, T. Foliar and woody materials discriminated using terrestrial LiDAR in a mixed natural forest. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 43–50. [Google Scholar] [CrossRef]
- Moeser, D.; Stahli, M.; Jonas, T. Improved snow interception modeling using canopy parameters derived from airborne LiDAR data. Water Resour. Res. 2015, 51, 5041–5059. [Google Scholar] [CrossRef] [Green Version]
- Thimonier, A.; Sedivy, I.; Schleppi, P. Estimating leaf area index in different types of mature forest stands in Switzerland: A comparison of methods. Eur. J. For. Res. 2010, 129, 543–562. [Google Scholar] [CrossRef]
- Ali, A.M.; Skidmore, A.K.; Darvishzadeh, R.; van Duren, I.; Holzwarth, S.; Mueller, J. Retrieval of forest leaf functional traits from HySpex imagery using radiative transfer models and continuous wavelet analysis. ISPRS J. Photogramm. Remote Sens. 2016, 122, 68–80. [Google Scholar] [CrossRef] [Green Version]
- Pisek, J.; Lang, M.; Nilson, T.; Korhonen, L.; Karu, H. Comparison of methods for measuring gap size distribution and canopy nonrandomness at Järvselja RAMI (RAdiation transfer Model Intercomparison) test sites. Agric. For. Meteorol. 2011, 151, 365–377. [Google Scholar] [CrossRef]
- Gonsamo, A.; Pellikka, P. Methodology comparison for slope correction in canopy leaf area index estimation using hemispherical photography. For. Ecol. Manag. 2008, 256, 749–759. [Google Scholar] [CrossRef]
- Glatthorn, J.; Beckschäfer, P. Standardizing the Protocol for Hemispherical Photographs: Accuracy Assessment of Binarization Algorithms. PLoS ONE 2014, 9, e111924. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jarčuška, B.; Kucbel, S.; Jaloviar, P. Comparison of output results from two programmes for hemispherical image analysis: Gap Light Analyser and WinScanopy. J. For. Sci. 2010, 56, 147–153. [Google Scholar] [CrossRef] [Green Version]
- Promis, A.; Gärtner, S.; Butler-Manning, D.; Durán-Rangel, C.; Reif, A.; Cruz, G.; Hernandez, L. Comparison of four different programs for the analysis of hemispherical photographs using parameters of canopy structure and solar radiation transmittance. Sierra 2011, 519, 36. [Google Scholar]
- Hall, R.J.; Côté, J.-F.; Mailly, D.; Fournier, R.A. Comparison of software tools for analysis of hemispherical photographs. In Hemispherical Photography in Forest Science: Theory, Methods, Applications; Springer: Berlin/Heidelberg, Germany, 2017; pp. 187–226. [Google Scholar]
- Liu, Z.L.; Jin, G.Z.; Chen, J.M.; Qi, Y.J. Evaluating optical measurements of leaf area index against litter collection in a mixed broadleaved-Korean pine forest in China. Trees-Struct. Funct. 2015, 29, 59–73. [Google Scholar] [CrossRef]
- Fang, H.L.; Ye, Y.C.; Liu, W.W.; Wei, S.S.; Ma, L. Continuous estimation of canopy leaf area index (LAI) and clumping index over broadleaf crop fields: An investigation of the PASTIS-57 instrument and smartphone applications. Agric. For. Meteorol. 2018, 253, 48–61. [Google Scholar] [CrossRef]
- Hyyppa, J. Virtual Forest. 2019. Available online: https://www.mdpi.com/journal/remotesensing/special_issues/Virtual_Forest (accessed on 15 June 2021).
- Calders, K.; Origo, N.; Burt, A.; Disney, M.; Nightingale, J.; Raumonen, P.; Akerblom, M.; Malhi, Y.; Lewis, P. Realistic Forest Stand Reconstruction from Terrestrial LiDAR for Radiative Transfer Modelling. Remote Sens. 2018, 10, 933. [Google Scholar] [CrossRef] [Green Version]
- Uusitalo, J.; Orland, B. Virtual Forest Management: Possibilities and Challenges. Int. J. For. Eng. 2001, 12, 57–66. [Google Scholar] [CrossRef]
- Leblanc, S.; Fournier, R. Hemispherical photography simulations with an architectural model to assess retrieval of leaf area index. Agric. Forest Meteorol. 2014, 194, 64–76. [Google Scholar] [CrossRef]
- Gonsamo, A.; Pellikka, P. The computation of foliage clumping index using hemispherical photography. Agric. For. Meteorol. 2009, 149, 1781–1787. [Google Scholar] [CrossRef]
- Liu, J.; Wang, T.; Skidmore, A.K.; Jones, S.; Heurich, M.; Beudert, B.; Premier, J. Comparison of terrestrial LiDAR and digital hemispherical photography for estimating leaf angle distribution in European broadleaf beech forests. ISPRS J. Photogramm. Remote Sens. 2019, 158, 76–89. [Google Scholar] [CrossRef]
- Cao, B.; Du, Y.M.; Li, J.; Li, H.; Li, L.; Zhang, Y.; Zou, J.; Liu, Q.H. Comparison of Five Slope Correction Methods for Leaf Area Index Estimation From Hemispherical Photography. IEEE Geosci. Remote. Sens. Lett. 2015, 12, 1958–1962. [Google Scholar] [CrossRef]
- Raumonen, P.; Casella, E.; Calders, K.; Murphy, S.; Åkerbloma, M.; Kaasalainen, M. Massive-scale tree modelling from TLS data. In Proceedings of the Pia15+hrigi15—Joint Isprs Conference, Munich, Germany, 5–27 March 2015; pp. 189–196. [Google Scholar]
- Woodgate, W.; Armston, J.D.; Disney, M.; Suarez, L.; Jones, S.D.; Hill, M.J.; Wilkes, P.; Soto-Berelov, M. Validating canopy clumping retrieval methods using hemispherical photography in a simulated Eucalypt forest. Agric. For. Meteorol. 2017, 247, 181–193. [Google Scholar] [CrossRef]
- Zou, J.; Zhuang, Y.; Chianucci, F.; Mai, C.; Lin, W.; Leng, P.; Luo, S.; Yan, B. Comparison of Seven Inversion Models for Estimating Plant and Woody Area Indices of Leaf-on and Leaf-off Forest Canopy Using Explicit 3D Forest Scenes. Remote Sens. 2018, 10, 1297. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.S.; Yin, T.G.; Dissegna, M.A.; Whittle, A.J.; Ow, G.L.F.; Yusof, M.L.M.; Lauret, N.; Gastellu-Etchegorry, J.P. An assessment study of three indirect methods for estimating leaf area density and leaf area index of individual trees. Agric. For. Meteorol. 2020, 292, 108101. [Google Scholar] [CrossRef]
- Grau, E.; Durrieu, S.; Fournier, R.; Gastellu-Etchegorry, J.P.; Yin, T.G. Estimation of 3D vegetation density with Terrestrial Laser Scanning data using voxels. A sensitivity analysis of influencing parameters. Remote Sens. Environ. 2017, 191, 373–388. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Akerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast Automatic Precision Tree Models from Terrestrial Laser Scanner Data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Skidmore, A.K.; Wang, T.J.; Zhu, X.; Premier, J.; Heurich, M.; Beudert, B.; Jones, S. Variation of leaf angle distribution quantified by terrestrial LiDAR in natural European beech forest. ISPRS J. Photogramm. Remote Sens. 2019, 148, 208–220. [Google Scholar] [CrossRef]
- Akerblom, M.; Raumonen, P.; Casella, E.; Disney, M.I.; Danson, F.M.; Gaulton, R.; Schofield, L.A.; Kaasalainen, M. Non-intersecting leaf insertion algorithm for tree structure models. Interface Focus 2018, 8, 20170045. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Smith, G.; Jonckheere, I.; Coppin, P. Review of methods for in situ leaf area index (LAI) determination: Part II. Estimation of LAI, errors and sampling. Agric. For. Meteorol. 2004, 121, 37–53. [Google Scholar] [CrossRef]
- Chen, J.M.; Black, T.A. Foliage area and architecture of plant canopies from sunfleck size distributions. Agric. For. Meteorol. 1992, 60, 249–266. [Google Scholar] [CrossRef]
- Ross, J. The Radiation Regime and Architecture of Plant Stands; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 3. [Google Scholar]
- Miller, J. A formula for average foliage density. Aust. J. Bot. 1967, 15, 141–144. [Google Scholar] [CrossRef]
- Walter, J.-M.N. CIMES-FISHEYE © A Package of Programs for the Assessment of Canopy Geometry and Solar Radiation Regimes through Hemispherical Photographs. Comput. Electron. Agric. 2011, 79, 207–215. [Google Scholar]
- Campbell, G.S. Derivation of an angle density function for canopies with ellipsoidal leaf angle distributions. Agric. For. Meteorol. 1990, 49, 173–176. [Google Scholar] [CrossRef]
- Wang, W.M.; Li, Z.L.; Su, H.B. Comparison of leaf angle distribution functions: Effects on extinction coefficient and fraction of sunlit foliage. Agric. For. Meteorol. 2007, 143, 106–122. [Google Scholar] [CrossRef]
- Norman, J.M.; Campbell, G.S. Canopy structure. In Plant Physiological Ecology; Springer: Berlin/Heidelberg, Germany, 1989; pp. 301–325. [Google Scholar]
- Lang, A.R.G.; Xiang, Y.Q. Estimation of leaf area index from transmission of direct sunlight in discontinuous canopies. Agric. For. Meteorol. 1986, 37, 229–243. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. Plant canopy gap-size analysis theory for improving optical measurements of leaf-area index. Appl. Optics. 1995, 34, 6211–6222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leblanc, S.G. Correction to the plant canopy gap-size analysis theory used by the Tracing Radiation and Architecture of Canopies instrument. Appl. Optics. 2002, 41, 7667–7670. [Google Scholar] [CrossRef]
- Leblanc, S.G.; Chen, J.M.; Fernandes, R.; Deering, D.W.; Conley, A. Methodology comparison for canopy structure parameters extraction from digital hemispherical photography in boreal forests. Agric. For. Meteorol. 2005, 129, 187–207. [Google Scholar] [CrossRef] [Green Version]
- Walter, J.-M.N.; Torquebiau, E.F. The computation of forest leaf area index on slope using fish-eye sensors. Comptes Rendus l’Académie Sci. Ser. III-Sci. Vie 2000, 323, 801–813. [Google Scholar] [CrossRef]
- Leblanc, S.G.; Chen, J.M. A practical scheme for correcting multiple scattering effects on optical LAI measurements. Agric. For. Meteorol. 2001, 110, 125–139. [Google Scholar] [CrossRef]
- Macfarlane, C. Classification method of mixed pixels does not affect canopy metrics from digital images of forest overstorey. Agric. For. Meteorol. 2011, 151, 833–840. [Google Scholar] [CrossRef]
- Woodgate, W.; Jones, S.D.; Suarez, L.; Hill, M.J.; Armston, J.D.; Wilkes, P.; Soto-Berelov, M.; Haywood, A.; Mellor, A. Understanding the variability in ground-based methods for retrieving canopy openness, gap fraction, and leaf area index in diverse forest systems. Agric. For. Meteorol. 2015, 205, 83–95. [Google Scholar] [CrossRef]
- Lang, A.R.G. Simplified estimate of leaf area index from transmittance of the sun’s beam. Agric. For. Meteorol. 1987, 41, 179–186. [Google Scholar] [CrossRef]
- LiCOR. LAI-2200 Plant Canopy Analyzer. Instruction Manual; Li-cor Cor.: Lincoln, NE, USA, 2009. [Google Scholar]
- Schleppi, P. Hemisfer v2.2 User Manual. 2018. Available online: https://www.schleppi.ch/hemisfer/ (accessed on 15 June 2021).
- Gonsamo, A.; Walter, J.-M.; Chen, J.M.; Pellikka, P.; Schleppi, P. A robust leaf area index algorithm accounting for the expected errors in gap fraction observations. Agric. For. Meteorol. 2018, 248, 197–204. [Google Scholar] [CrossRef]
- Richardson, A.D.; Dail, D.B.; Hollinger, D.Y. Leaf area index uncertainty estimates for model-data fusion applications. Agric. For. Meteorol. 2011, 151, 1287–1292. [Google Scholar] [CrossRef]
- Macfarlane, C.; Hoffman, M.; Eamus, D.; Kerp, N.; Higginson, S.; McMurtrie, R.; Adams, M. Estimation of leaf area index in eucalypt forest using digital photography. Agric. For. Meteorol. 2007, 143, 176–188. [Google Scholar] [CrossRef]
- Woodgate, W.; Armston, J.D.; Disney, M.; Jones, S.D.; Suarez, L.; Hill, M.J.; Wilkes, P.; Soto-Berelov, M. Quantifying the impact of woody material on leaf area index estimation from hemispherical photography using 3D canopy simulations. Agric. For. Meteorol 2016, 226, 1–12. [Google Scholar] [CrossRef]
- Zou, J.; Yan, G.J.; Zhu, L.; Zhang, W.M. Woody-to-total area ratio determination with a multispectral canopy imager. Tree Physiol. 2009, 29, 1069–1080. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Calders, K.; Origo, N.; Disney, M.; Nightingale, J.; Woodgate, W.; Armston, J.; Lewis, P. Variability and bias in active and passive ground-based measurements of effective plant, wood and leaf area index. Agric. For. Meteorol. 2018, 252, 231–240. [Google Scholar] [CrossRef]
- Toda, M.; Richardson, A.D. Estimation of plant area index and phenological transition dates from digital repeat photography and radiometric approaches in a hardwood forest in the Northeastern United States. Agric. For. Meteorol. 2018, 249, 457–466. [Google Scholar] [CrossRef]
- Jiang, C.Y.; Ryu, Y.; Fang, H.L.; Myneni, R.; Claverie, M.; Zhu, Z.C. Inconsistencies of interannual variability and trends in long-term satellite leaf area index products. Glob. Chang. Biol. 2017, 23, 4133–4146. [Google Scholar] [CrossRef] [PubMed]
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Review of methods for in situ leaf area index determination—Part I. Theories, sensors and hemispherical photography. Agric. For. Meteorol. 2004, 121, 19–35. [Google Scholar] [CrossRef]
- Asner, G.P.; Scurlock, J.M.O.; Hicke, J.A. Global synthesis of leaf area index observations: Implications for ecological and remote sensing studies. Glob. Ecol. Biogeogr. 2003, 12, 191–205. [Google Scholar] [CrossRef] [Green Version]
- He, L.M.; Chen, J.M.; Pisek, J.; Schaaf, C.B.; Strahler, A.H. Global clumping index map derived from the MODIS BRDF product. Remote Sens. Environ. 2012, 119, 118–130. [Google Scholar] [CrossRef]
- Wei, S.S.; Fang, H.L.; Schaaf, C.B.; He, L.M.; Chen, J.M. Global 500 m clumping index product derived from MODIS BRDF data (2001–2017). Remote Sens. Environ. 2019, 232, 111296. [Google Scholar] [CrossRef]
- Fischer, F.J.; Labriere, N.; Vincent, G.; Herault, B.; Alonso, A.; Memiaghe, H.; Bissiengou, P.; Kenfack, D.; Saatchi, S.; Chave, J. A simulation method to infer tree allometry and forest structure from airborne laser scanning and forest inventories. Remote Sens. Environ. 2020, 251, 112056. [Google Scholar] [CrossRef]
- Yan, G.; Hu, R.; Luo, J.; Weiss, M.; Jiang, H.; Mu, X.; Xie, D.; Zhang, W. Review of indirect optical measurements of leaf area index: Recent advances, challenges, and perspectives. Agric. For. Meteorol. 2019, 265, 390–411. [Google Scholar] [CrossRef]
- Cote, J.F.; Fournier, R.A.; Egli, R. An architectural model of trees to estimate forest structural attributes using terrestrial LiDAR. Environ. Modell. Softw. 2011, 26, 761–777. [Google Scholar] [CrossRef]
- Liu, W.W.; Atherton, J.; Mottus, M.; Gastellu-Etchegorry, J.P.; Malenovsky, Z.; Raumonen, P.; Akerblom, M.; Makipaa, R.; Porcar-Castell, A. Simulating solar-induced chlorophyll fluorescence in a boreal forest stand reconstructed from terrestrial laser scanning measurements. Remote Sens. Environ. 2019, 232, 111274. [Google Scholar] [CrossRef]




| Stand | Plot Name | Stand Size (m) | Plot Radius (m) | Stand PAItrue-ref (1) | Stand LAItrue-ref (2) | Plot PAItrue-ref (3) | Plot LAItrue-ref (4) | ALA(5) (°) |
|---|---|---|---|---|---|---|---|---|
| F1 | Plot 1 | 120 × 120 | 25 | 1.43 | 0.52 | 1.39 | 0.49 | 5 |
| F2 | Plot 2 | 120 × 120 | 25 | 1.48 | 0.89 | 1.30 | 0.79 | 30 |
| F3 | Plot 3 | 120 × 120 | 25 | 1.77 | 1.13 | 1.57 | 0.99 | 68 |
| F4 | Plot 4 | 120 × 120 | 25 | 2.13 | 1.22 | 2.03 | 1.13 | 78 |
| F5 | Plot 5 | 120 × 120 | 25 | 2.21 | 1.38 | 2.15 | 1.35 | 8 |
| F6 | Plot 6 | 120 × 120 | 25 | 2.73 | 1.90 | 2.19 | 1.54 | 32 |
| F7 | Plot 7 | 120 × 120 | 25 | 2.90 | 2.11 | 2.28 | 1.64 | 65 |
| F8 | Plot 8 | 120 × 120 | 25 | 2.34 | 1.58 | 2.48 | 1.66 | 28 |
| F9 | Plot 9 | 120 × 120 | 25 | 2.44 | 1.70 | 2.66 | 1.82 | 75 |
| F10 | Plot 10 | 120 × 120 | 25 | 3.18 | 2.33 | 3.00 | 2.18 | 10 |
| F11 | Plot 11 | 120 × 120 | 25 | 3.02 | 2.28 | 2.98 | 2.26 | 53 |
| F12 | Plot 12 | 120 × 120 | 25 | 3.67 | 2.81 | 3.32 | 2.54 | 35 |
| F13 | Plot13 | 120 × 120 | 25 | 3.96 | 3.17 | 3.24 | 2.58 | 38 |
| F14 | Plot14 | 120 × 120 | 25 | 4.06 | 3.27 | 3.29 | 2.61 | 50 |
| F15 | Plot15 | 120 × 120 | 25 | 3.39 | 2.55 | 3.56 | 2.65 | 25 |
| F16 | Plot16 | 120× 120 | 25 | 3.68 | 2.98 | 3.66 | 2.96 | 64 |
| F17 | Plot17 | 120 × 120 | 25 | 4.46 | 3.47 | 4.04 | 3.12 | 12 |
| F18 | Plot18 | 120 × 120 | 25 | 4.22 | 3.43 | 4.05 | 3.27 | 23 |
| F19 | Plot19 | 120 × 120 | 25 | 4.53 | 3.82 | 4.01 | 3.39 | 60 |
| F20 | Plot20 | 120 × 120 | 25 | 5.03 | 4.12 | 4.30 | 3.54 | 48 |
| F21 | Plot21 | 120× 120 | 25 | 4.88 | 4.09 | 4.45 | 3.73 | 20 |
| F22 | Plot22 | 120 × 120 | 25 | 5.46 | 4.58 | 4.54 | 3.79 | 45 |
| F23 | Plot23 | 120 × 120 | 25 | 5.02 | 4.23 | 4.52 | 3.82 | 40 |
| F24 | Plot24 | 120 × 120 | 25 | 6.15 | 5.29 | 4.70 | 4.07 | 42 |
| F25 | Plot25 | 120 × 120 | 25 | 5.32 | 4.36 | 5.10 | 4.17 | 15 |
| F26 | Plot26 | 120 × 120 | 25 | 6.38 | 5.53 | 5.10 | 4.44 | 72 |
| F27 | Plot27 | 120 × 120 | 25 | 5.79 | 4.98 | 5.34 | 4.53 | 70 |
| F28 | Plot28 | 120 × 120 | 25 | 5.83 | 4.92 | 5.51 | 4.63 | 18 |
| F29 | Plot29 | 120 × 120 | 25 | 6.09 | 5.18 | 5.92 | 5.07 | 58 |
| F30 | Plot30 | 120 × 120 | 25 | 6.14 | 5.42 | 6.15 | 5.39 | 55 |
| Algorithm Abbreviation | Basic Principle | References |
|---|---|---|
| P57 | 1. Use of the gap fraction at 57.5° (55°~60°) 2. The was approximated as 0.5 regardless of types 3. Clumping correction was based on the LX method 4. was set as 10 for pure segments with no gaps | [19,63] |
| v5.1 | 1. Use of the gap fraction at 0 2. The which determined was modeled by the ALA using the ellipsoidal distribution 3. PAI and ALA were inversed using a look-up table scheme, with the cost function constrained by a term of ALA (the retrieved ALA value must be close to 60° ± 30°) 4. Clumping correction was based on the LX method 5. was set as 10 for pure segments with no gaps | [19,60,63] |
| v6.1 | 1. Use of the gap fraction at 0 2. The was modeled by the ALA using the ellipsoidal distribution 3. PAI and ALA were inversed using a lookup table scheme, with the cost function constrained by a term of PAI57 (the retrieved PAI value that must be close to the one retrieved from the annulus at 57.5°) 4. Clumping correction was based on the LX method 5. was set as 10 for pure segments with no gaps | [19,60,63] |
| Miller | 1. Use of the gap fraction at 0 2. Use of Miller’s formula to estimate PAIeff 3. Clumping correction based on the LX method 4. was set as 10 for pure segments with no gaps | [19,58] |
| Algorithm Abbreviation | Basic Principle | References |
|---|---|---|
| CAM_LX | 1. Use of the gap fraction at 0 2. The was modeled by the ALA using the ellipsoidal distribution 3. Clumping correction was based on the LX method 4. Lsat was set as 10 for pure segments with no gaps | [4,59,60,63] |
| CMP_WT | 1. Use of the gap fraction at 0 2. The was modeled by the ALA using the ellipsoidal distribution 3. Clumping correction was based on the WT method 4. Lsat was set as 10 for pure segments with no gaps | [4,59,60,67] |
| LOGCAM | 1. Use of the gap fraction at 0 2. The was modeled by the ALA using the ellipsoidal distribution 3. Clumping correction was based on a modified LX method using variable azimuthal segmentations of the hemisphere | [4,59,60,63] |
| LANG_LX | 1. Use of the gap fraction at 0 2. Use of Lang’s regression method to estimate PAIeff 3. Clumping correction was based on the LX method 4. Lsat was set as 10 for pure segments with no gaps | [4,59,63,71] |
| MLR | 1. Use of the gap fraction at 0 2. Use of Lang’s regression method to estimate PAIeff 3. Clumping correction was based on a modified LX method using variable azimuthal segmentations of the hemisphere | [4,59,71] |
| Miller_CC57 | 1. Use of the gap fraction at 57.5° (55°~60°) 2. Use of Miller’s formula to estimate PAIeff 3. Clumping correction was based on the CC method | [4,58,59,64] |
| Miller_CC | 1. Use of the gap fraction at 0°~60° 2. Use of Miller’s formula to estimate PAIeff 3. Clumping correction was based on the CC method | [4,58,59,64] |
| Miller_CLX57 | 1. Use of the gap fraction at 57.5° (55°~60°) 2. Use of Miller’s formula to estimate PAIeff 3. Clumping correction was based on the CLX method | [4,58,59,66] |
| Miller_CLX | 1. Use of the gap fraction at 0°~60° 2. Use of Miller’s formula to estimate PAIeff 3. Clumping correction was based on the CLX method | [4,58,59,66] |
| AlgorithmAbbreviation | Basic Principle | References |
|---|---|---|
| CC_2000 | 1. Use of the gap fraction at 0°~60° 2. Use of the LI-COR LAI-2000 method to estimate PAIeff 3. Clumping correction was based on the CC method | [64,72,73] |
| CC_Gonsamo | 1. Use of the gap fraction at 0°~60° 2. Use of the Lang Robust regression method proposed by Gonsamo to estimate PAIeff 3. Clumping correction was based on the CC method | [64,73,74] |
| CC_Lang | 1. Use of the gap fraction at 0 2. Use of Lang’s regression method to estimate PAIeff 3. Clumping correction was based on the CC method | [64,71,73] |
| CC_Miller | 1. Use of the gap fraction at 0°~60° 2. Use of Miller’s formula to estimate PAIeff 3. Clumping correction was based on the CC method | [58,73] |
| CC_NC | 1. Use of the gap fraction at 0 2. The was modeled by the ALA using the ellipsoidal distribution 3. Clumping correction was based on the CC method | [62,64,73] |
| CC_Thimonier | 1. Use of the gap fraction at 0 2. The was modeled by the ALA using the weighted ellipsoidal distribution 3. Clumping correction was based on the CC method | [30,73] |
| LX_2000 | 1. Use of the gap fraction at 0°~60° 2. Use of the LI-COR LAI- 2000 method to estimate PAIeff 3. Clumping correction was based on the LX method | [63,72,73] |
| LX_Gonsamo | 1. Use of the gap fraction at 0 2. Use of the Lang Robust regression method proposed by Gonsamo to estimate PAIeff 3. Clumping correction was based on the LX method | [63,73,74] |
| LX_Lang | 1. Use of the gap fraction at 0 2. Use of Lang’s regression method to estimate PAIeff 3. Clumping correction was based on the LX method | [63,71,73] |
| LX_Miller | 1. Use of the gap fraction at 0°~60° 2. Use of Miller’s formula to estimate PAIeff 3. Clumping correction was based on the LX method | [58,63,73] |
| LX_NC | 1. Use of the gap fraction at 0 2. The was modeled by the ALA using the ellipsoidal distribution 3. Clumping correction was based on the LX method | [62,63,73] |
| LX_Thimonier | 1. Use of the gap fraction at 0 2. The was modeled by the ALA using the weighted ellipsoidal distribution 3. Clumping correction was based on the LX method | [30,63,73] |
| SCC_2000 | 1. Use of the gap fraction at 0°~60° 2. Use of the LI-COR LAI- 2000 method to estimate PAIeff 3. Use of Schleppi’s approach to correct for within annulus non-linearity of path lengths4.Clumping correction was based on the CC method | [20,64,72,73] |
| SCC_Gonsamo | 1. Use of the gap fraction at 0°~60° 2. Use of the Lang Robust regression method proposed by Gonsamo to estimate PAIeff 3. Use of Schleppi’s approach to correct for within annulus non-linearity of path lengths 4. Clumping correction was based on the CC method | [20,64,73,74] |
| SCC_Lang | 1. Use of the gap fraction at 0 2. Use of Lang’s regression method to estimate PAIeff 3. Use of Schleppi’s approach to correct for within annulus non-linearity of path lengths4. Clumping correction was based on the CC method | [20,71,73] |
| SCC_Miller | 1. Use of the gap fraction at 0°~60° 2. Use of Miller’s formula to estimate PAIeff 3. Use of Schleppi’s approach to correct for within annulus non-linearity of path lengths 4. Clumping correction was based on the CC method | [20,58,64,73] |
| SCC_NC | 1. Use of the gap fraction at 0 2. The was modeled by the ALA using the ellipsoidal distribution 3. Use of Schleppi’s approach to correct for within annulus non-linearity of path lengths 4. Clumping correction was based on the CC method | [20,62,64,73] |
| SCC_Thimonier | 1. Use of the gap fraction at 0 2. The was modeled by the ALA using the weighted ellipsoidal distribution 3. Use of Schleppi’s approach to correct for within annulus non-linearity of path lengths 4. Clumping correction was based on the CC method | [20,30,64,73] |
| WT_2000 | 1. Use of the gap fraction at 0°~60° 2. Use of the LI-COR LAI-2000 method to estimate PAIeff 3. Clumping correction was based on the WT method | [67,72,73] |
| WT_Gonsamo | 1. Use of the gap fraction at 0 2. Use of the Lang Robust regression method proposed by Gonsamo to estimate PAIeff 3. Clumping correction was based on the WT method | [67,73,74] |
| WT_Lang | 1. Use of the gap fraction at 0 2. Use of Lang’s regression method to estimate PAIeff 3. Clumping correction was based on the WT method | [67,71,73] |
| WT_Miller | 1. Use of the gap fraction at 0°~60° 2. Use of Miller’s formula to estimate PAIeff 3. Clumping correction was based on the WT method | [58,67,73] |
| WT_NC | 1. Use of the gap fraction at 0 2. The was modeled by the ALA using the ellipsoidal distribution 3. Clumping correction was based on the WT method | [62,67,73] |
| WT_Thimonier | 1. Use of the gap fraction at 0 2. The was modeled by the ALA using the weighted ellipsoidal distribution 3. Clumping correction was based on the WT method | [30,67,73] |
| Plot Name | Plot Name | Plot Name | |||
|---|---|---|---|---|---|
| Plot1 | 0.52 | Plot 11 | 0.63 | Plot 21 | 0.46 |
| Plot 2 | 0.60 | Plot 12 | 0.54 | Plot 22 | 0.49 |
| Plot 3 | 0.78 | Plot 13 | 0.56 | Plot 23 | 0.42 |
| Plot 4 | 0.67 | Plot 14 | 0.56 | Plot 24 | 0.46 |
| Plot 5 | 0.55 | Plot 15 | 0.52 | Plot 25 | 0.43 |
| Plot 6 | 0.72 | Plot 16 | 0.57 | Plot 26 | 0.46 |
| Plot 7 | 0.75 | Plot 17 | 0.49 | Plot 27 | 0.42 |
| Plot 8 | 0.54 | Plot 18 | 0.49 | Plot 28 | 0.38 |
| Plot 9 | 0.68 | Plot 19 | 0.53 | Plot 29 | 0.42 |
| Plot 10 | 0.54 | Plot 20 | 0.48 | Plot 30 | 0.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, L.; Akerblom, M.; Wang, T.; Skidmore, A.; Zhu, X.; Heurich, M. Comparative Evaluation of Algorithms for Leaf Area Index Estimation from Digital Hemispherical Photography through Virtual Forests. Remote Sens. 2021, 13, 3325. https://doi.org/10.3390/rs13163325
Liu J, Li L, Akerblom M, Wang T, Skidmore A, Zhu X, Heurich M. Comparative Evaluation of Algorithms for Leaf Area Index Estimation from Digital Hemispherical Photography through Virtual Forests. Remote Sensing. 2021; 13(16):3325. https://doi.org/10.3390/rs13163325
Chicago/Turabian StyleLiu, Jing, Longhui Li, Markku Akerblom, Tiejun Wang, Andrew Skidmore, Xi Zhu, and Marco Heurich. 2021. "Comparative Evaluation of Algorithms for Leaf Area Index Estimation from Digital Hemispherical Photography through Virtual Forests" Remote Sensing 13, no. 16: 3325. https://doi.org/10.3390/rs13163325
APA StyleLiu, J., Li, L., Akerblom, M., Wang, T., Skidmore, A., Zhu, X., & Heurich, M. (2021). Comparative Evaluation of Algorithms for Leaf Area Index Estimation from Digital Hemispherical Photography through Virtual Forests. Remote Sensing, 13(16), 3325. https://doi.org/10.3390/rs13163325








