An Adaptive Weighted Phase Optimization Algorithm Based on the Sigmoid Model for Distributed Scatterers
Abstract
:1. Introduction
2. Proposed Method
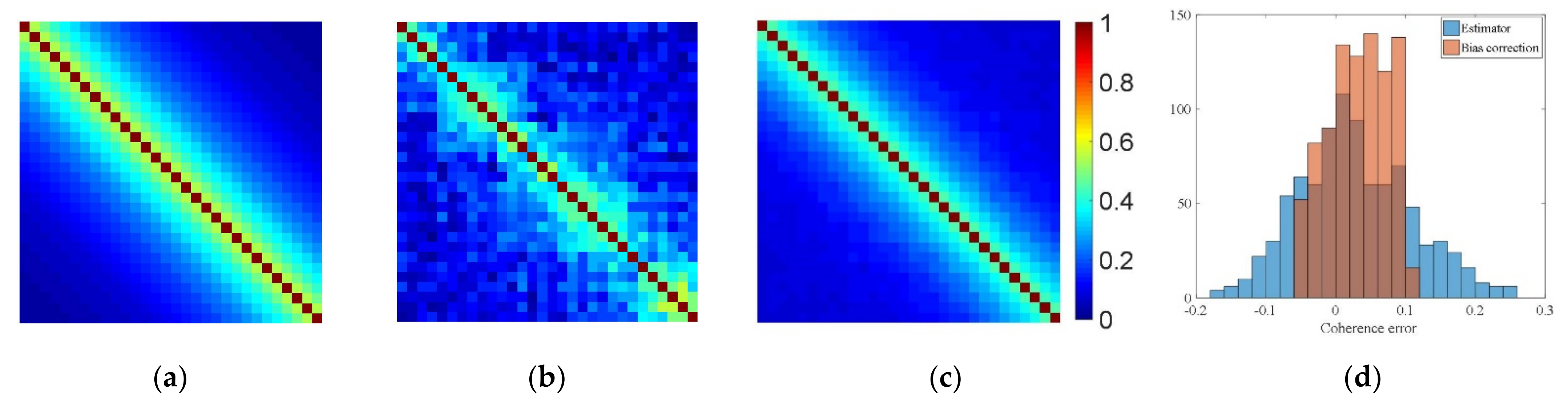
2.1. Coherence Bias Correction
2.2. The Adaptive Weight Based on the Sigmoid Model
2.3. An Efficient Solution Strategy Based on the EMI Framework
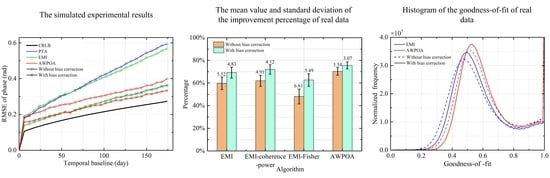
3. Experimental Results with the Simulated Data
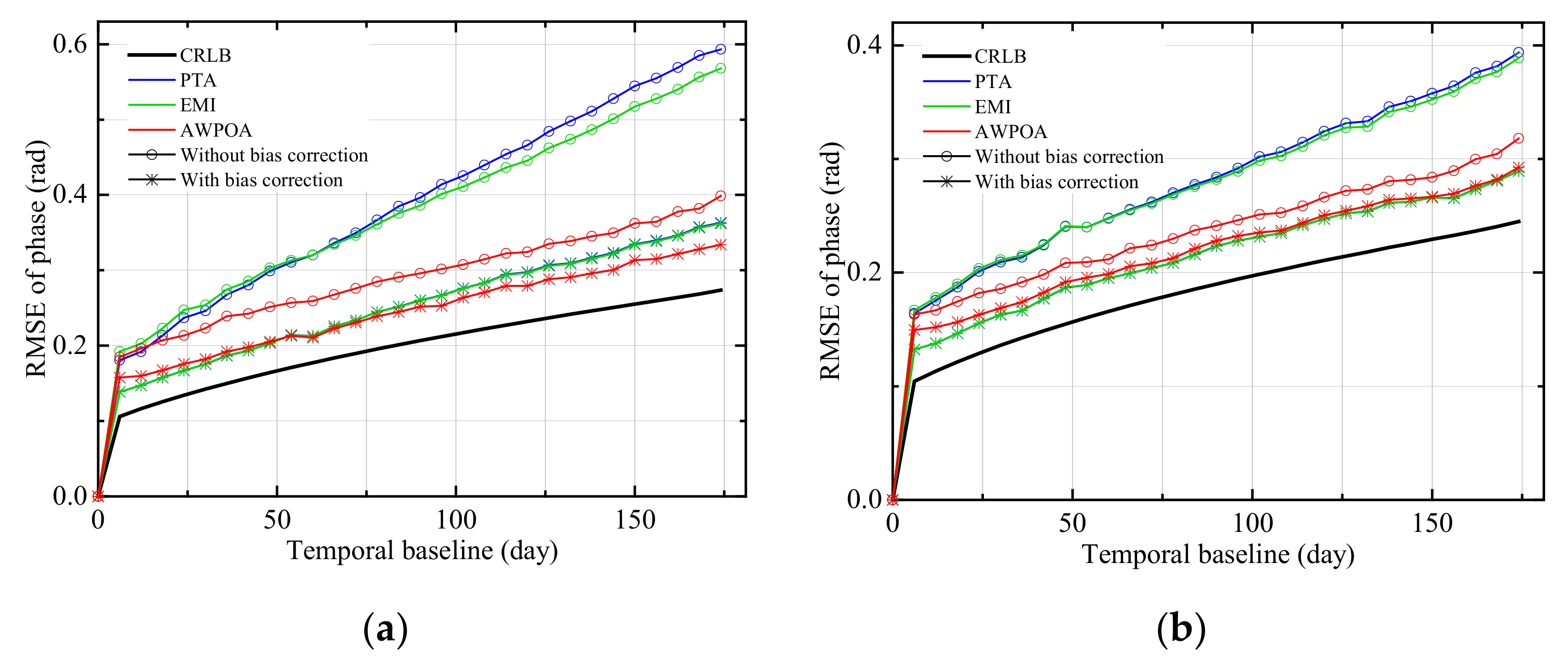
3.1. Influence of Coherence Bias Correction on Phase Optimization
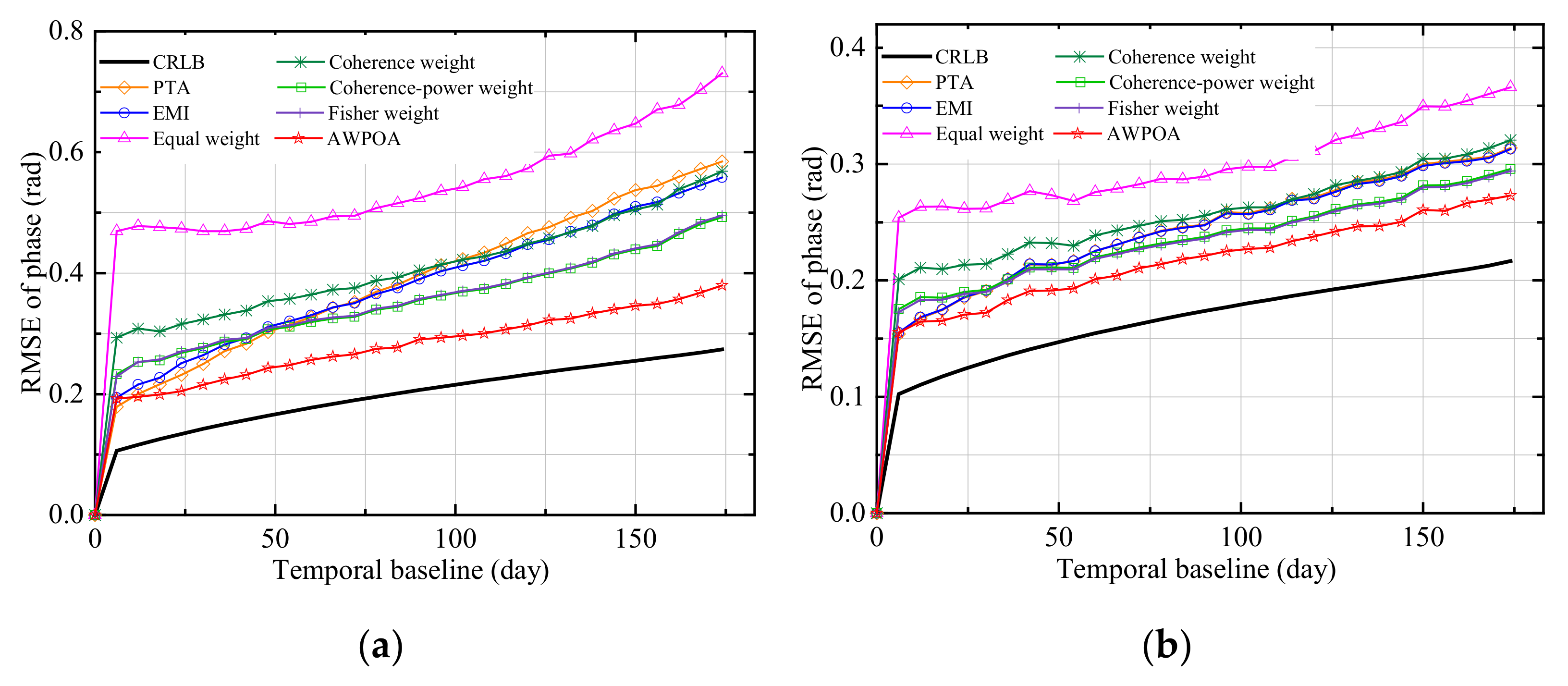
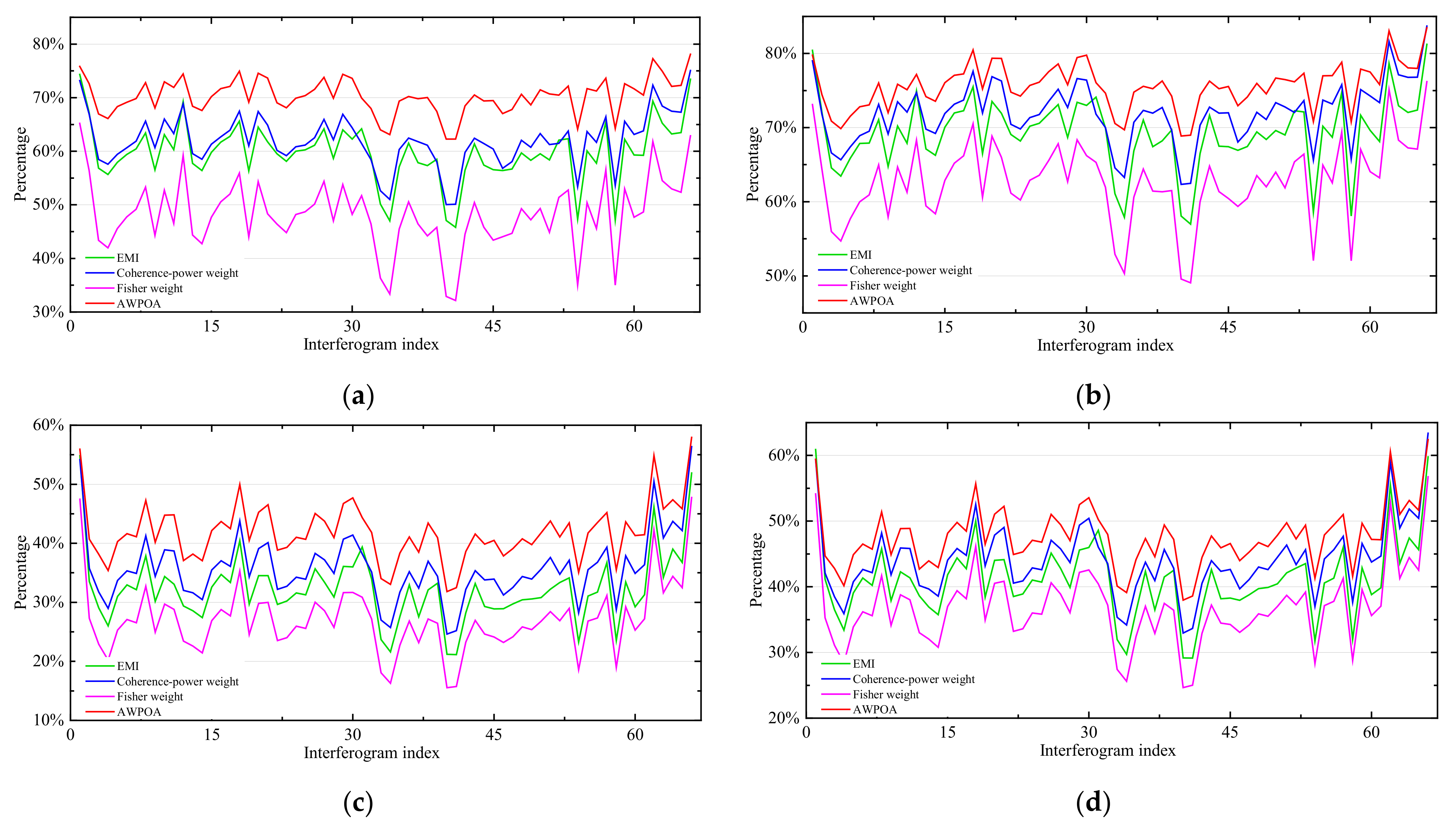
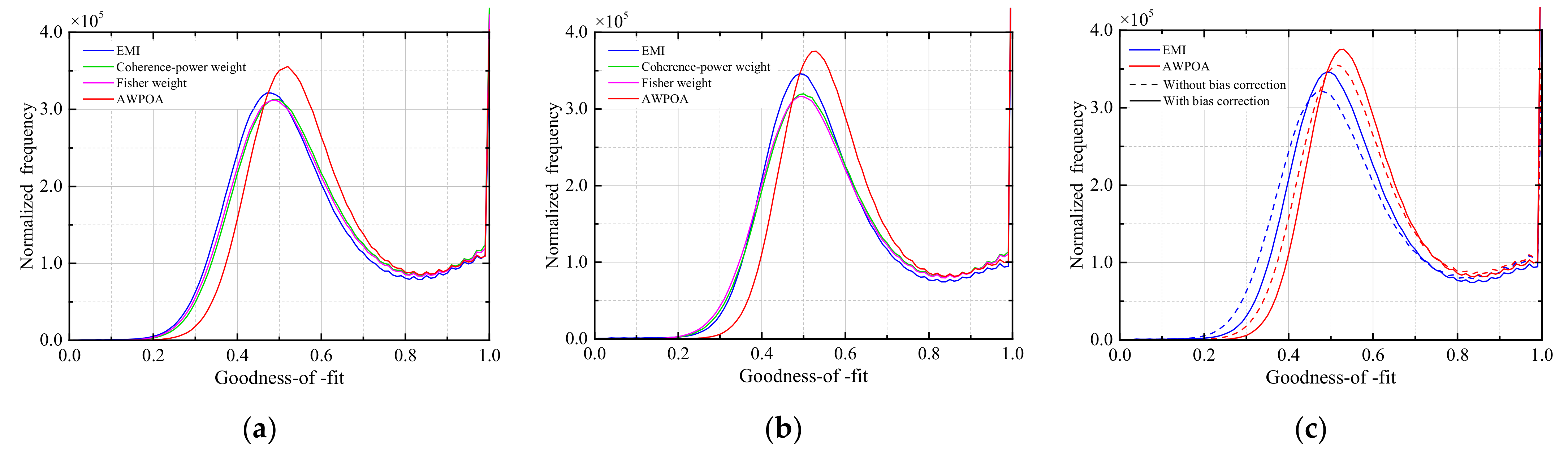
3.2. Influence of the Weight on Phase Optimization
3.3. Efficiency
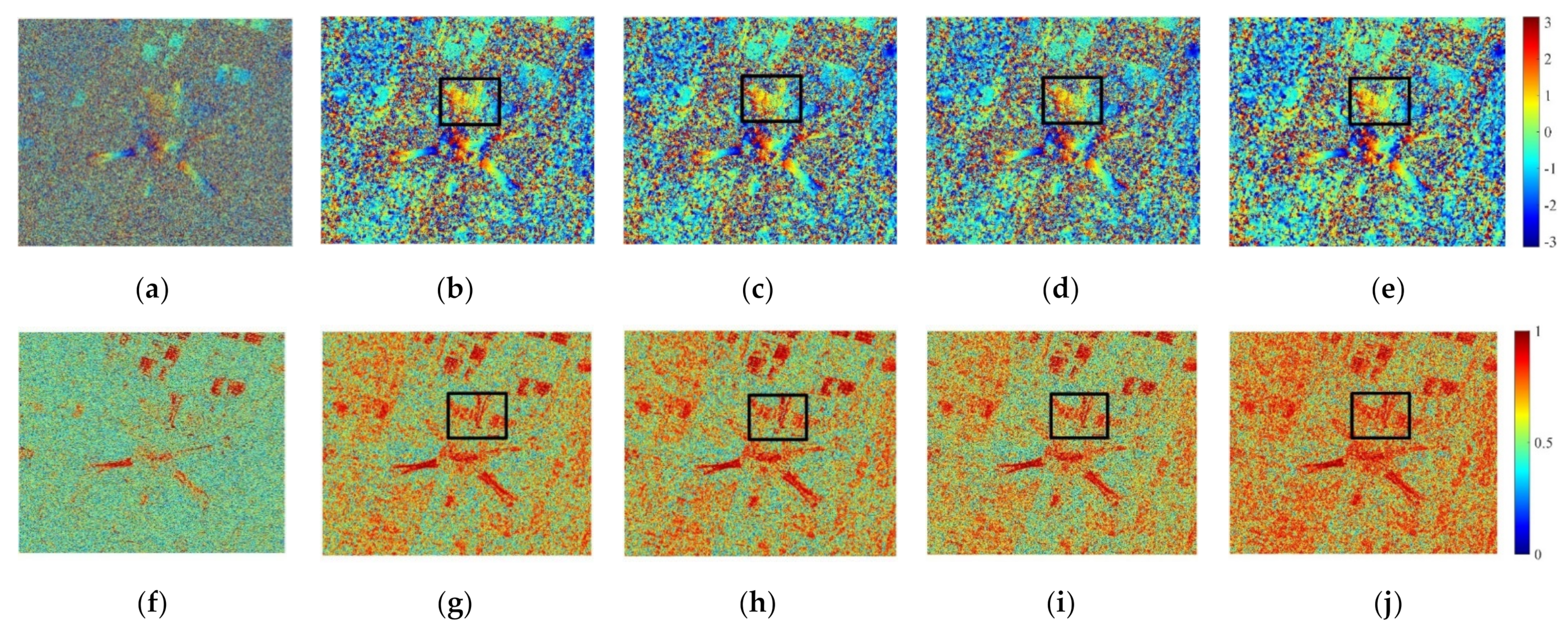
4. Experimental Results with the Real Data
4.1. Real Data 1
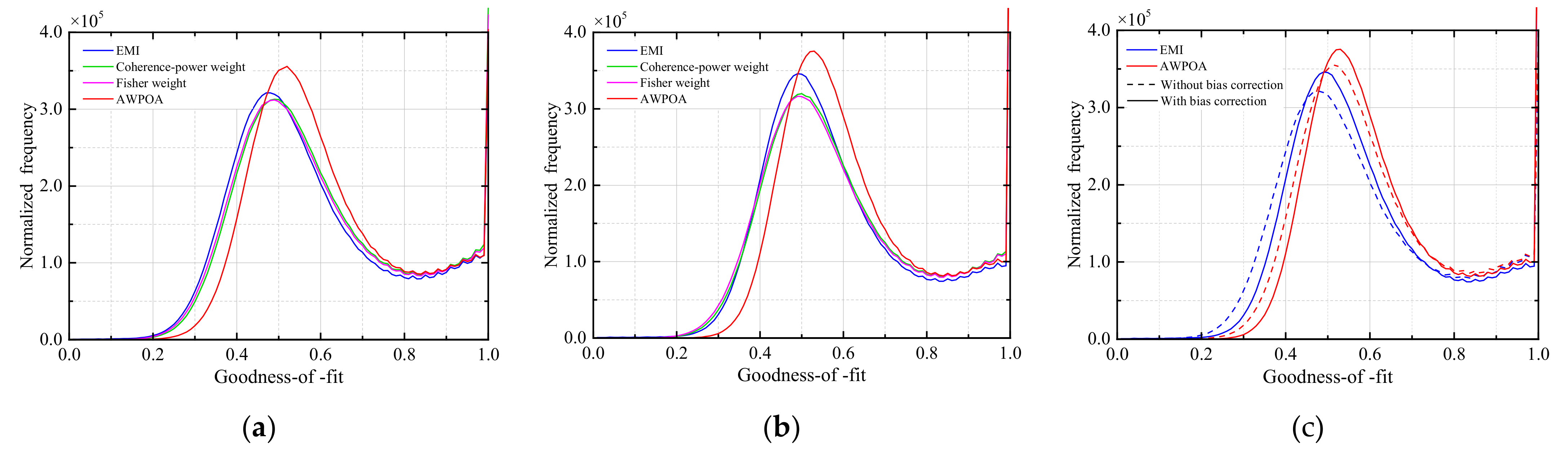
4.2. Real Data 2
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Z.; Wang, C.; Wang, M.; Wang, Z.; Zhang, H. Surface deformation monitoring in Zhengzhou city from 2014 to 2016 using time-series InSAR. Remote Sens. 2018, 10, 1731. [Google Scholar] [CrossRef] [Green Version]
- Ma, P.; Li, T.; Fang, C.; Lin, H. A tentative test for measuring the sub-millimeter settlement and uplift of a high-speed railway bridge using COSMO-SkyMed images. ISPRS J. Photogramm. Remote Sens. 2019, 155, 1–12. [Google Scholar] [CrossRef]
- Li, T.; Liu, G.X.; Lin, H.; Jia, H.G.; Zhang, R.; Yu, B.; Luo, Q.L. A hierarchical multi-temporal InSAR method for increasing the spatial density of deformation measurements. Remote Sens. 2014, 6, 3349–3368. [Google Scholar] [CrossRef] [Green Version]
- Kuang, J.; Ge, L.; Metternicht, G.I.; Ng, A.H.-M.; Wang, H.; Zare, M.; Kamranzad, F. Coseismic deformation and source model of the 12 November 2017 MW 7.3 Kermanshah Earthquake (Iran–Iraq border) investigated through DInSAR measurements. Int. J. Remote Sens. 2018, 40, 532–554. [Google Scholar] [CrossRef]
- Zhao, C.; Kang, Y.; Zhang, Q.; Lu, Z.; Li, B. Landslide identification and monitoring along the Jinsha River catchment (Wudongde Reservoir Area), China, using the InSAR method. Remote Sens. 2018, 10, 993. [Google Scholar] [CrossRef] [Green Version]
- Gaber, A.; Darwish, N.; Koch, M. Minimizing the Residual Topography Effect on Interferograms to Improve DInSAR Results: Estimating Land Subsidence in Port-Said City, Egypt. Remote Sens. 2017, 9, 752. [Google Scholar] [CrossRef] [Green Version]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef] [Green Version]
- Kampes, B.M.; Adam, N. The STUN algorithm for persistent scatterer interferometry. Proc. Fringe 2005, 2005, 1–14. [Google Scholar]
- Costantini, M.; Falco, S.; Malvarosa, F.; Minati, F. A new method for identification and analysis of persistent scatterers in series of SAR images. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Brussels, Belgium, 11–16 July 2021; pp. II-449–II-452. [Google Scholar]
- Ng, A.H.-M.; Ge, L.; Li, X.; Zhang, K. Monitoring ground deformation in Beijing, China with persistent scatterer SAR interferometry. J. Geod. 2012, 86, 375–392. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Ansari, H.; De Zan, F.; Parizzi, A. Study of Systematic Bias in Measuring Surface Deformation With SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1285–1301. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, R.; Deng, Y.; Ma, P.; Lin, H.; Wang, J. Mapping the Yellow River Delta land subsidence with multitemporal SAR interferometry by exploiting both persistent and distributed scatterers. ISPRS J. Photogramm. Remote Sens. 2019, 148, 157–173. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, L.; Tang, M.; Liao, M.; Xu, Q.; Gong, J.; Ao, M. Mapping landslide surface displacements with time series SAR interferometry by combining persistent and distributed scatterers: A case study of Jiaju landslide in Danba, China. Remote Sens. Environ. 2018, 205, 180–198. [Google Scholar] [CrossRef]
- Jiang, M.; Guarnieri, A.M. Distributed Scatterer Interferometry With the Refinement of Spatiotemporal Coherence. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3977–3987. [Google Scholar] [CrossRef]
- Mukherjee, S.; Zimmer, A.; Sun, X.; Ghuman, P.; Cheng, I. An Unsupervised Generative Neural Approach for InSAR Phase Filtering and Coherence Estimation. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Goel, K.; Adam, N. A distributed scatterer interferometry approach for precision monitoring of known surface deformation phenomena. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5454–5468. [Google Scholar] [CrossRef]
- Parizzi, A.; Brcic, R. Adaptive InSAR stack multilooking exploiting amplitude statistics: A comparison between different techniques and practical results. IEEE Geosci. Remote Sens. Lett. 2011, 8, 441–445. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhu, X.X. Robust Estimators for Multipass SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2016, 54, 968–980. [Google Scholar] [CrossRef]
- Ma, Z.-F.; Jiang, M.; Huang, T. A Sequential Approach for Sentinel-1 TOPS Time-Series Co-Registration over Low Coherence Scenarios. IEEE Trans. Geosci. Remote Sens. 2020, 1–9. [Google Scholar] [CrossRef]
- Ning, C.; Hyongki, L.; Hahn Chul, J. Mathematical framework for phase-triangulation algorithms in distributed-scatterer interferometry. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1838–1842. [Google Scholar] [CrossRef]
- Samiei Esfahany, S. Exploitation of Distributed Scatterers in Synthetic Aperture Radar Interferometry. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2017. [Google Scholar]
- Ansari, H.; De Zan, F.; Bamler, R. Efficient Phase Estimation for Interferogram Stacks. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4109–4125. [Google Scholar] [CrossRef]
- Song, H.; Zhang, B.; Wang, M.; Xiao, Y.; Zhang, L.; Zhong, H. A Fast Phase Optimization Approach of Distributed Scatterer for Multitemporal SAR Data Based on Gauss-Seidel Method. IEEE Geosci. Remote Sens. Lett. 2021, 1–5. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Li, T.; Gao, Y.; Chen, Q.; Zhang, X. An Adaptive Phase Optimization Algorithm for Distributed Scatterer Phase History Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3914–3926. [Google Scholar] [CrossRef]
- Zhao, C.; Li, Z.; Tian, B.; Zhang, P.; Chen, Q. A Ground Surface Deformation Monitoring InSAR Method Using Improved Distributed Scatterers Phase Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4543–4553. [Google Scholar] [CrossRef]
- Samiei-Esfahany, S.; Martins, J.E.; van Leijen, F.; Hanssen, R.F. Phase estimation for distributed scatterers in InSAR stacks using integer least squares estimation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5671–5687. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Tang, Y.; Zhang, H.; Wang, C. Phase estimation for distributed scatterer InSAR: A comparison between different methods. In Proceedings of the 10th European Conference on Synthetic Aperture Radar EUSAR 2014, Aachen, Germany, 2–4 June 2014; pp. 1–4. [Google Scholar]
- Fornaro, G.; Verde, S.; Reale, D.; Pauciullo, A. CAESAR: An approach based on covariance matrix decomposition to improve multibaseline–multitemporal interferometric SAR processing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2050–2065. [Google Scholar] [CrossRef]
- Cao, N.; Lee, H.; Jung, H.C. A phase-decomposition-based PSInSAR processing method. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1074–1090. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, X.L.; Hanssen, R.F.; Malhotra, R.; Chang, L. Fast statistically homogeneous pixel selection for covariance matrix estimation for multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1213–1224. [Google Scholar] [CrossRef]
- Abdelfattah, R.; Nicolas, J.M. Interferometric SAR coherence magnitude estimation using second kind statistics. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1942–1953. [Google Scholar] [CrossRef]
- Morishita, Y.; Hanssen, R.F. Temporal Decorrelation in L-, C-, and X-band Satellite Radar Interferometry for Pasture on Drained Peat Soils. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1096–1104. [Google Scholar] [CrossRef]
- Lee, J.S.; Grunes, M.R.; Kwok, R. Classification of multi-look polarimetric SAR imagery based on complex Wishart distribution. Int. J. Remote Sens. 1994, 15, 2299–2311. [Google Scholar] [CrossRef]
- Guarnieri, A.M.; Tebaldini, S. Hybrid CramÉr–Rao Bounds for Crustal Displacement Field Estimators in SAR Interferometry. IEEE Signal. Process. Lett. 2007, 14, 1012–1015. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Zan, F.D.; Rucci, A.; Tebaldini, S. Process for Filtering Interferograms Obtained from SAR Images Acquired on the Same Area. U.S. Patent No. 8,711,029, 29 April 2014. [Google Scholar]

| Methods | Without Bias Correction | With Bias Correction |
|---|---|---|
| PTA | 61.385 | 231.367 |
| EMI | 3.247 | 182.028 |
| AWPOA | 3.013 | 170.300 |
| Methods | Residues | SPD | ||||||
|---|---|---|---|---|---|---|---|---|
| Without Bias Correction | With Bias Correction | Without Bias Correction | With Bias Correction | |||||
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | |
| EMI | 59.75% | 5.52% | 69.26% | 4.83% | 32.23% | 5.86% | 41.10% | 5.89% |
| Coherence-power weight | 62.02% | 4.91% | 72.03% | 4.12% | 35.82% | 5.71% | 44.06% | 5.54% |
| Fisher weight | 48.13% | 6.61% | 62.70% | 5.49% | 27.00% | 5.90% | 36.80% | 5.95% |
| AWPOA | 70.30% | 3.31% | 75.62% | 3.07% | 41.88% | 4.91% | 47.56% | 4.70% |
| Methods | Residues | SPD | ||||||
|---|---|---|---|---|---|---|---|---|
| Without Bias Correction | With Bias Correction | Without Bias Correction | With Bias Correction | |||||
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | |
| EMI | 52.73% | 3.60% | 64.95% | 3.45% | 26.44% | 3.65% | 35.75% | 4.18% |
| Coherence-power weight | 52.11% | 3.62% | 66.69% | 3.36% | 27.33% | 3.90% | 37.37% | 4.36% |
| Fisher weight | 45.98% | 4.17% | 61.80% | 3.84% | 23.93% | 3.89% | 33.91% | 4.43% |
| AWPOA | 61.87% | 2.55% | 69.21% | 2.59% | 33.38% | 3.37% | 39.25% | 3.64% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Zhang, S.; Li, T.; Gao, Y.; Zhou, X.; Chen, Q.; Zhang, X.; Yang, C. An Adaptive Weighted Phase Optimization Algorithm Based on the Sigmoid Model for Distributed Scatterers. Remote Sens. 2021, 13, 3253. https://doi.org/10.3390/rs13163253
Li S, Zhang S, Li T, Gao Y, Zhou X, Chen Q, Zhang X, Yang C. An Adaptive Weighted Phase Optimization Algorithm Based on the Sigmoid Model for Distributed Scatterers. Remote Sensing. 2021; 13(16):3253. https://doi.org/10.3390/rs13163253
Chicago/Turabian StyleLi, Shijin, Shubi Zhang, Tao Li, Yandong Gao, Xiaoqing Zhou, Qianfu Chen, Xiang Zhang, and Chao Yang. 2021. "An Adaptive Weighted Phase Optimization Algorithm Based on the Sigmoid Model for Distributed Scatterers" Remote Sensing 13, no. 16: 3253. https://doi.org/10.3390/rs13163253
APA StyleLi, S., Zhang, S., Li, T., Gao, Y., Zhou, X., Chen, Q., Zhang, X., & Yang, C. (2021). An Adaptive Weighted Phase Optimization Algorithm Based on the Sigmoid Model for Distributed Scatterers. Remote Sensing, 13(16), 3253. https://doi.org/10.3390/rs13163253