Assessment of Global FY-3C/VIRR Sea Surface Temperature
Abstract
:1. Introduction
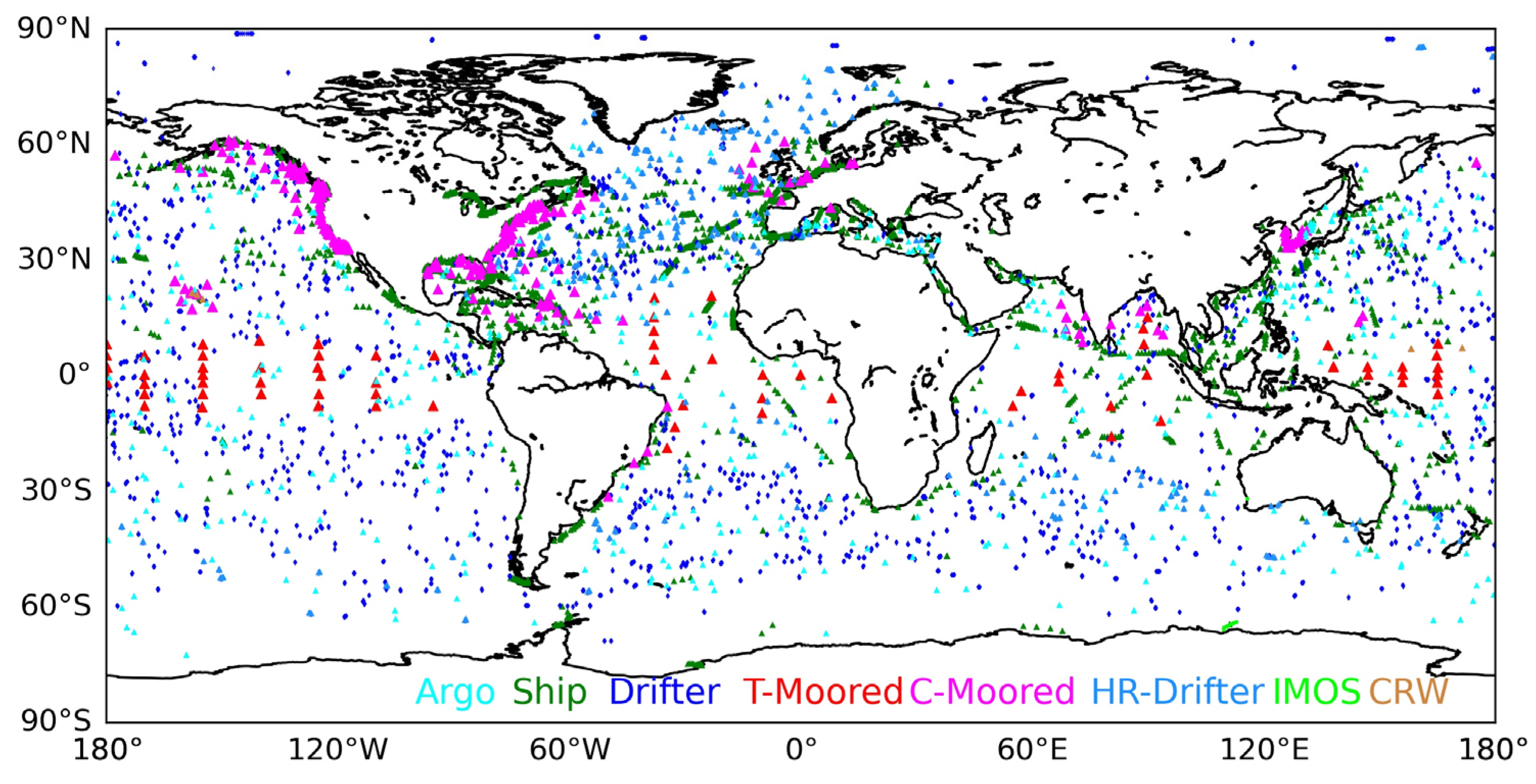
2. Dataset
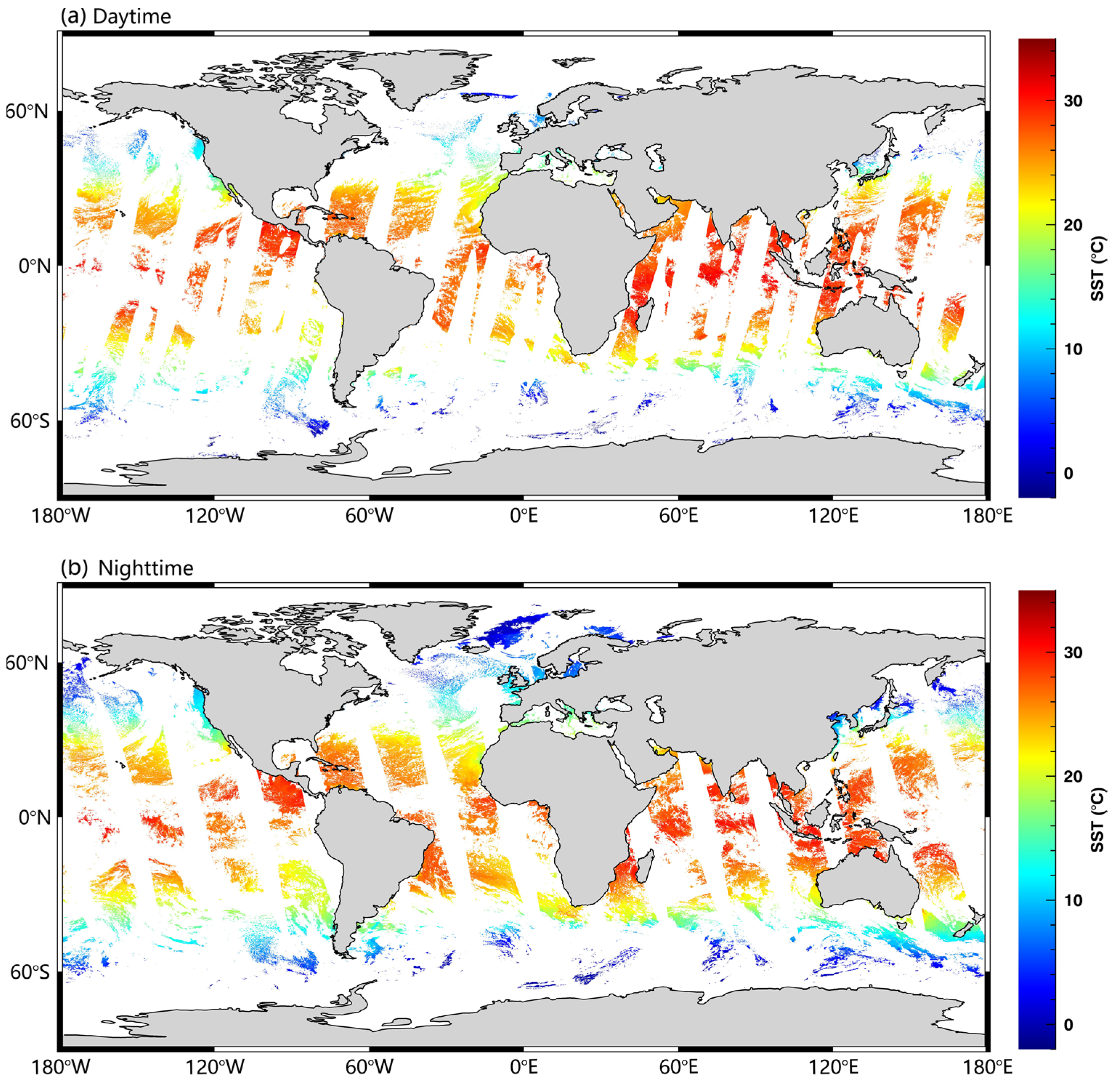
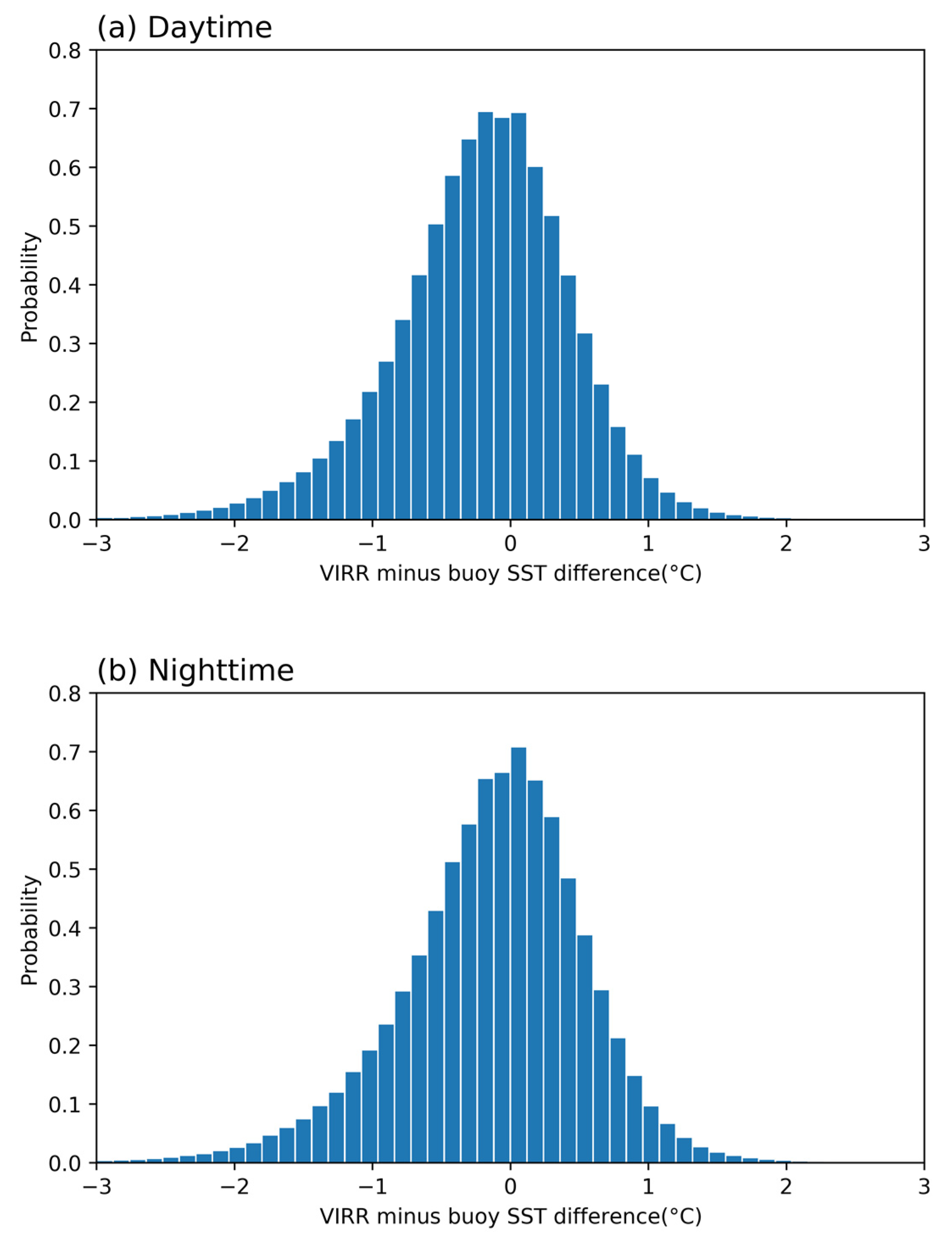
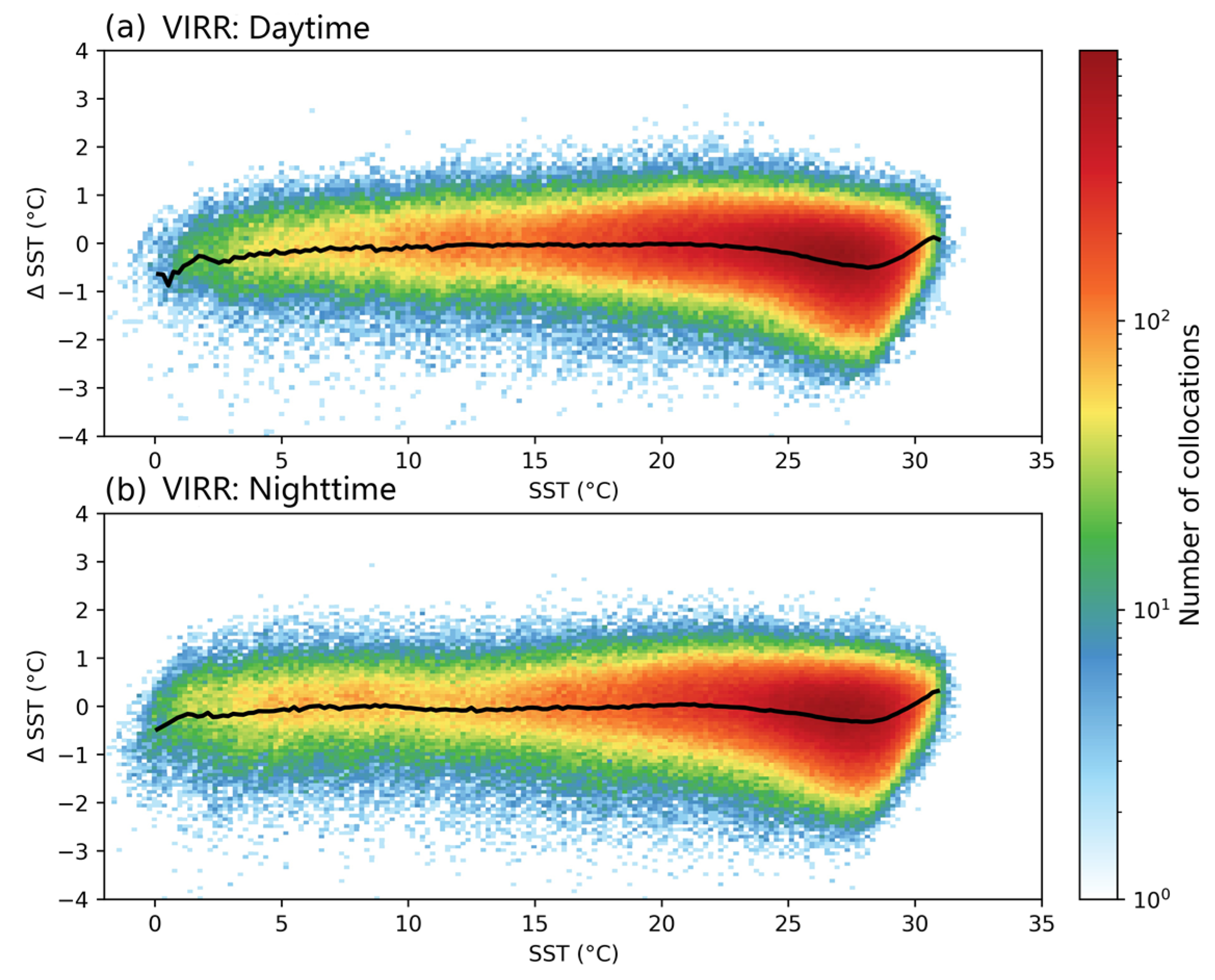
3. Comparison of VIRR SST with MODIS SST and Buoy SST
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barton, I.J.; Prata, A.J. Satellite derived sea surface temperature data sets for climate applications. Adv. Space Res. 1995, 16, 127–136. [Google Scholar] [CrossRef]
- Minnett, P.J.; Alvera-Azcárate, A.; Chin, T.M.; Corlett, G.K.; Gentemann, C.L.; Karagali, I.; Li, X.; Marsouin, A.; Marullo, S.; Maturi, E.; et al. Half a century of satellite remote sensing of sea-surface temperature. Remote Sens. Environ. 2019, 233, 111366. [Google Scholar] [CrossRef]
- Minnett, P.J.; Corlett, G.K. A pathway to generating Climate Data Records of sea-surface temperature from satellite measurements. Deep Sea Res. Part II Top. Stud. Oceanogr. 2012, 77, 44–51. [Google Scholar] [CrossRef]
- Kilpatrick, K.A.; Podestá, G.; Walsh, S.; Williams, E.; Halliwell, V.; Szczodrak, M.; Brown, O.B.; Minnett, P.J.; Evans, R. A decade of sea surface temperature from MODIS. Remote Sens. Environ. 2015, 165, 27–41. [Google Scholar] [CrossRef]
- Mcclain, E.P.; Pichel, W.G.; Walton, C.C. Comparative performance of AVHRR-based multichannel sea surface temperatures. J. Geophys. Res. Oceans. 1985, 90, 11587–11601. [Google Scholar] [CrossRef]
- Strong, A.E.; McClain, E.P. Improved Ocean Surface Temperatures From Space—Comparisons With Drifting Buoys. Bull. Am. Meteorol. Soc. 1984, 65, 138–142. [Google Scholar] [CrossRef] [Green Version]
- Walton, C.C.; Pichel, W.G.; Sapper, J.F.; May, D.A. The development and operational application of nonlinear algorithms for the measurement of sea surface temperatures with the NOAA polar-orbiting environmental satellites. J. Geophys. Res. Oceans. 1998, 103, 27999–28012. [Google Scholar] [CrossRef]
- Kilpatrick, K.A.; Podestá, G.P.; Evans, R. Overview of the NOAA/NASA advanced very high resolution radiometer Pathfinder algorithm for sea surface temperature and associated matchup database. J. Geophys. Res. Oceans. 2001, 106, 9179–9197. [Google Scholar] [CrossRef]
- Petrenko, B.; Ignatov, A.; Kihai, Y.; Stroup, J.; Dash, P. Evaluation and selection of SST regression algorithms for JPSS VIIRS. J. Geophys. Res. Atmos. 2014, 119, 4580–4599. [Google Scholar] [CrossRef]
- Embury, O.; Merchant, C.J.; Corlett, G.K. A reprocessing for climate of sea surface temperature from the along-track scanning radiometers: Initial validation, accounting for skin and diurnal variability effects. Remote Sens. Environ. 2012, 116, 62–78. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Cui, P.; Zhang, P.; Ran, M.; Lu, F.; Wang, W. FY-3C/VIRR SST Algorithm and cal/val Activities at NSMC/CMA. In Proceedings of the SPIE 9261, Ocean Remote Sensing and Monitoring from Space, Beijing, China, 10 December 2014. [Google Scholar]
- Wang, S.; Cui, P.; Zhang, P.; Yang, Z.; Hu, X.; Ran, N.; Liu, J.; Lin, M.; Qiu, H. FY-3C/VIRR Sea Surface Temperature Products and Quality Validation. J. Appl. Meteorol. Sci. 2020, 31, 729–739. [Google Scholar]
- Wang, H.; Guan, L.; Chen, G. Evaluation of Sea Surface Temperature from FY-3C VIRR Data in the Arctic. IEEE Geosci. Remote Sens. Lett. 2016, 13, 292–296. [Google Scholar] [CrossRef]
- FENGYUN Satellite Data Center. Available online: http://satellite.nsmc.org.cn/ (accessed on 12 July 2021).
- Yang, J.; Dong, C. New Generation FY LEO-Meteorological Satellite Operational Products and Applications, 1st ed.; China Science Press: Beijing, China, 2008; pp. 347–348. (In Chinese) [Google Scholar]
- Liao, Z.; Dong, Q.; Xue, C. Evaluation of sea surface temperature from FY-3C data. Int. J. Remote Sens. 2017, 38, 4954–4973. [Google Scholar] [CrossRef]
- NASA OBPG. NASA OBPG. MODIS Terra Level 3 SST Thermal IR Daily 4 km Daytime v2014.0; Ver. 2014.0; PO.DAAC: Pasadena, CA, USA, 2015; Available online: https://doi.org/10.5067/MODST-1D4D4 (accessed on 11 August 2021).
- In Situ SST Quality Monitor. Available online: https://www.star.nesdis.noaa.gov/socd/sst/iquam/ (accessed on 12 July 2021).
- Xu, F.; Ignatov, A. In situ SST Quality Monitor (iQuam). J. Atmos. Ocean. Technol. 2014, 31, 164–180. [Google Scholar] [CrossRef]
- Gentemann, C.L.; Minnett, P.J.; Ward, B. Profiles of ocean surface heating (POSH): A new model of upper ocean diurnal warming. J. Geophys. Res. Oceans 2009, 114, C07017. [Google Scholar] [CrossRef] [Green Version]
- O’Carroll, A.G.; Eyre, J.R.; Saunders, R.W. Three-Way Error Analysis between AATSR, AMSR-E, and In Situ Sea Surface Temperature Observations. J. Atmos. Ocean. Technol. 2008, 25, 1197–1207. [Google Scholar] [CrossRef] [Green Version]
- Gentemann, C.L. Three way validation of MODIS and AMSR-E sea surface temperatures. J. Geophys. Res. Oceans 2014, 119, 2583–2598. [Google Scholar] [CrossRef]
- O’Carroll, A.G.; August, T.; Le Borgne, P.; Marsouin, A. The accuracy of SST retrievals from Metop-A IASI and AVHRR using the EUMETSAT OSI-SAF matchup dataset. Remote Sens. Environ. 2012, 126, 184–194. [Google Scholar] [CrossRef]
- Stoffelen, A. Toward the true near-surface wind speed: Error modeling and calibration using triple collocation. J. Geophys. Res. Oceans 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- Saha, K.; Dash, P.; Zhao, X.; Zhang, H. Error Estimation of Pathfinder Version 5.3 Level-3C SST Using Extended Triple Collocation Analysis. Remote Sens. 2020, 12, 590. [Google Scholar] [CrossRef] [Green Version]
- Lumpkin, R.; Maximenko, N.; Pazos, M. Evaluating Where and Why Drifters Die. J. Atmos. Ocean. Technol. 2011, 29, 300–308. [Google Scholar] [CrossRef]
- Kilpatrick, K.A.; Podestá, G.; Williams, E.; Walsh, S.; Minnett, P.J. Alternating Decision Trees for Cloud Masking in MODIS and VIIRS NASA Sea Surface Temperature Products. J. Atmos. Ocean. Technol. 2019, 36, 387–407. [Google Scholar] [CrossRef]





| Year | SST Difference | Bias (°C) | SD (°C) | Median (°C) | RSD (°C) | P (±0.3 °C) | P (±0.5 °C) | P (±1 °C) |
|---|---|---|---|---|---|---|---|---|
| 2015–2019 | VIRR minus buoy (D) | −0.21 | 0.65 | −0.16 | 0.58 | 0.39 | 0.60 | 0.87 |
| MODIS minus buoy (D) | −0.10 | 0.48 | −0.09 | 0.39 | 0.54 | 0.76 | 0.95 | |
| VIRR minus MODIS (D) | −0.10 | 0.61 | −0.09 | 0.53 | 0.43 | 0.64 | 0.91 | |
| VIRR minus buoy (N) | −0.13 | 0.67 | −0.08 | 0.59 | 0.39 | 0.60 | 0.87 | |
| MODIS minus buoy (N) | −0.21 | 0.46 | −0.17 | 0.37 | 0.54 | 0.76 | 0.95 | |
| VIRR minus MODIS (N) | 0.08 | 0.67 | 0.10 | 0.58 | 0.39 | 0.59 | 0.88 |
| Year | SST Difference | Bias (°C) | SD (°C) | Median (°C) | RSD (°C) | P (±0.3 °C) | P (±0.5 °C) | P (±1 °C) | |
|---|---|---|---|---|---|---|---|---|---|
| Daytime | 2015 | VIRR minus buoy (D) | −0.40 | 0.68 | −0.36 | 0.60 | 0.33 | 0.52 | 0.82 |
| MODIS minus buoy (D) | −0.16 | 0.47 | −0.15 | 0.39 | 0.52 | 0.75 | 0.95 | ||
| VIRR minus MODIS (D) | −0.24 | 0.61 | −0.23 | 0.53 | 0.40 | 0.61 | 0.89 | ||
| 2016 | VIRR minus buoy (D) | −0.05 | 0.67 | 0.00 | 0.59 | 0.39 | 0.60 | 0.88 | |
| MODIS minus buoy (D) | −0.10 | 0.47 | −0.08 | 0.39 | 0.55 | 0.76 | 0.95 | ||
| VIRR minus MODIS (D) | 0.04 | 0.61 | 0.08 | 0.52 | 0.43 | 0.65 | 0.91 | ||
| 2017 | VIRR minus buoy (D) | −0.12 | 0.63 | −0.07 | 0.56 | 0.42 | 0.63 | 0.89 | |
| MODIS minus buoy (D) | −0.13 | 0.47 | −0.11 | 0.38 | 0.55 | 0.76 | 0.95 | ||
| VIRR minus MODIS (D) | 0.01 | 0.58 | 0.03 | 0.50 | 0.45 | 0.67 | 0.92 | ||
| 2018 | VIRR minus buoy (D) | −0.18 | 0.60 | −0.14 | 0.53 | 0.42 | 0.64 | 0.90 | |
| MODIS minus buoy (D) | −0.04 | 0.47 | −0.03 | 0.37 | 0.57 | 0.79 | 0.96 | ||
| VIRR minus MODIS (D) | −0.14 | 0.58 | −0.13 | 0.51 | 0.44 | 0.65 | 0.91 | ||
| 2019 | VIRR minus buoy (D) | −0.35 | 0.64 | −0.30 | 0.57 | 0.37 | 0.56 | 0.85 | |
| MODIS minus buoy (D) | −0.13 | 0.50 | −0.11 | 0.41 | 0.52 | 0.74 | 0.95 | ||
| VIRR minus MODIS (D) | −0.23 | 0.62 | −0.21 | 0.53 | 0.40 | 0.61 | 0.89 | ||
| Nighttime | 2015 | VIRR minus buoy (N) | −0.18 | 0.68 | −0.11 | 0.60 | 0.39 | 0.60 | 0.87 |
| MODIS minus buoy (N) | −0.27 | 0.47 | −0.23 | 0.37 | 0.51 | 0.73 | 0.94 | ||
| VIRR minus MODIS (N) | 0.10 | 0.66 | 0.11 | 0.57 | 0.39 | 0.60 | 0.88 | ||
| 2016 | VIRR minus buoy (N) | 0.08 | 0.68 | 0.15 | 0.58 | 0.37 | 0.57 | 0.87 | |
| MODIS minus buoy (N) | −0.20 | 0.46 | −0.16 | 0.37 | 0.55 | 0.76 | 0.95 | ||
| VIRR minus MODIS (N) | 0.29 | 0.67 | 0.31 | 0.56 | 0.34 | 0.54 | 0.85 | ||
| 2017 | VIRR minus buoy (N) | 0.01 | 0.64 | 0.06 | 0.54 | 0.41 | 0.63 | 0.90 | |
| MODIS minus buoy (N) | −0.20 | 0.46 | −0.15 | 0.36 | 0.56 | 0.77 | 0.95 | ||
| VIRR minus MODIS (N) | 0.20 | 0.63 | 0.22 | 0.53 | 0.39 | 0.60 | 0.89 | ||
| 2018 | VIRR minus buoy (N) | −0.18 | 0.62 | −0.14 | 0.54 | 0.42 | 0.63 | 0.89 | |
| MODIS minus buoy (N) | −0.20 | 0.46 | −0.16 | 0.36 | 0.55 | 0.77 | 0.95 | ||
| VIRR minus MODIS (N) | 0.02 | 0.63 | 0.02 | 0.54 | 0.42 | 0.63 | 0.90 | ||
| 2019 | VIRR minus buoy (N) | −0.36 | 0.66 | −0.31 | 0.61 | 0.36 | 0.54 | 0.83 | |
| MODIS minus buoy (N) | −0.20 | 0.46 | −0.16 | 0.37 | 0.54 | 0.76 | 0.95 | ||
| VIRR minus MODIS (N) | −0.16 | 0.67 | −0.15 | 0.60 | 0.38 | 0.58 | 0.87 |
| (°C) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Daytime | Nighttime | |||||||||||
| Year | 2015 | 2016 | 2017 | 2018 | 2019 | 2015–2019 | 2015 | 2016 | 2017 | 2018 | 2019 | 2015–2019 |
| VIRR | 0.55 | 0.55 | 0.50 | 0.49 | 0.52 | 0.53 | 0.58 | 0.59 | 0.54 | 0.54 | 0.55 | 0.58 |
| MODIS | 0.26 | 0.28 | 0.28 | 0.32 | 0.33 | 0.30 | 0.31 | 0.31 | 0.32 | 0.33 | 0.30 | 0.32 |
| Buoy | 0.39 | 0.38 | 0.38 | 0.34 | 0.37 | 0.37 | 0.34 | 0.34 | 0.33 | 0.31 | 0.39 | 0.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Wang, S.; Guan, L.; Liu, M. Assessment of Global FY-3C/VIRR Sea Surface Temperature. Remote Sens. 2021, 13, 3249. https://doi.org/10.3390/rs13163249
Li N, Wang S, Guan L, Liu M. Assessment of Global FY-3C/VIRR Sea Surface Temperature. Remote Sensing. 2021; 13(16):3249. https://doi.org/10.3390/rs13163249
Chicago/Turabian StyleLi, Ninghui, Sujuan Wang, Lei Guan, and Mingkun Liu. 2021. "Assessment of Global FY-3C/VIRR Sea Surface Temperature" Remote Sensing 13, no. 16: 3249. https://doi.org/10.3390/rs13163249
APA StyleLi, N., Wang, S., Guan, L., & Liu, M. (2021). Assessment of Global FY-3C/VIRR Sea Surface Temperature. Remote Sensing, 13(16), 3249. https://doi.org/10.3390/rs13163249







