Sea Surface Salinity and Wind Speed Retrievals Using GNSS-R and L-Band Microwave Radiometry Data from FMPL-2 Onboard the FSSCat Mission
Abstract
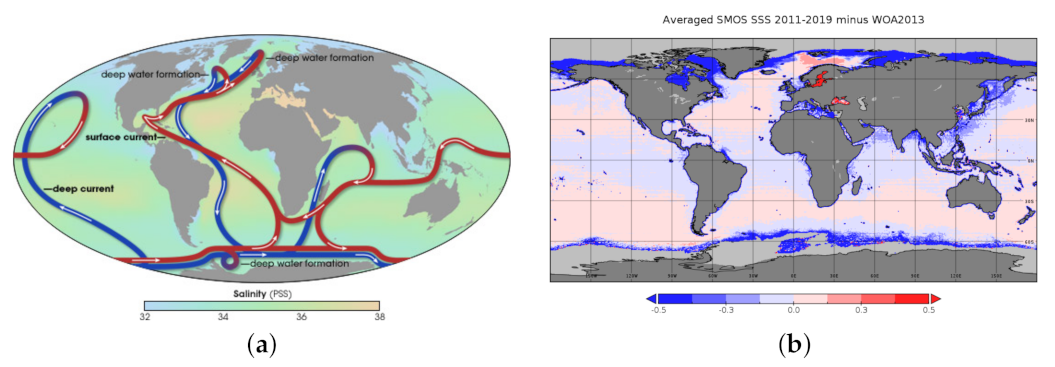
:1. Introduction
2. Review of the State of the Art
3. Methodology and Data Description
3.1. Product Description
3.2. Initial Evaluation: Correlation Matrix
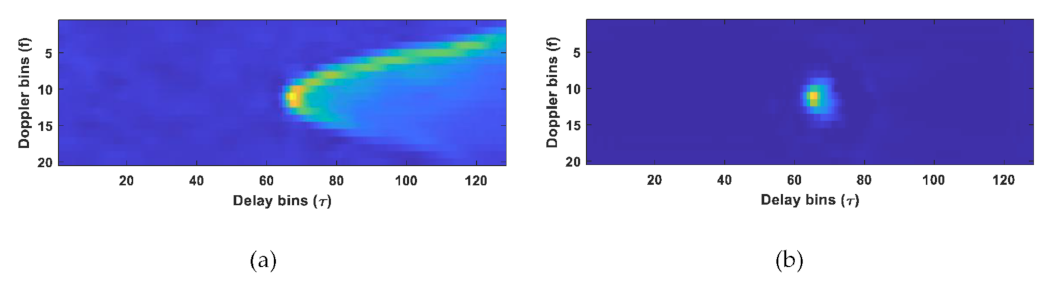
3.3. ANN Topology and Training Methodology
4. Results
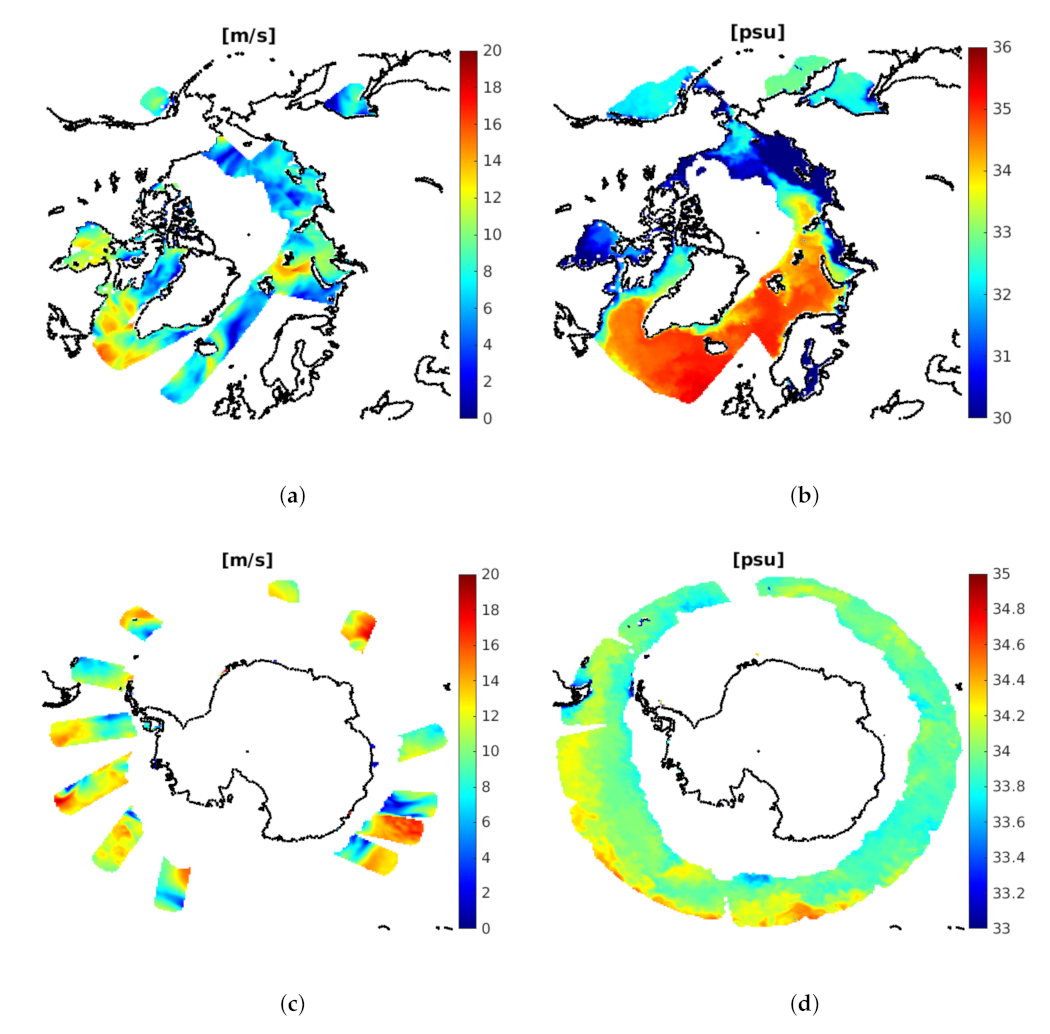
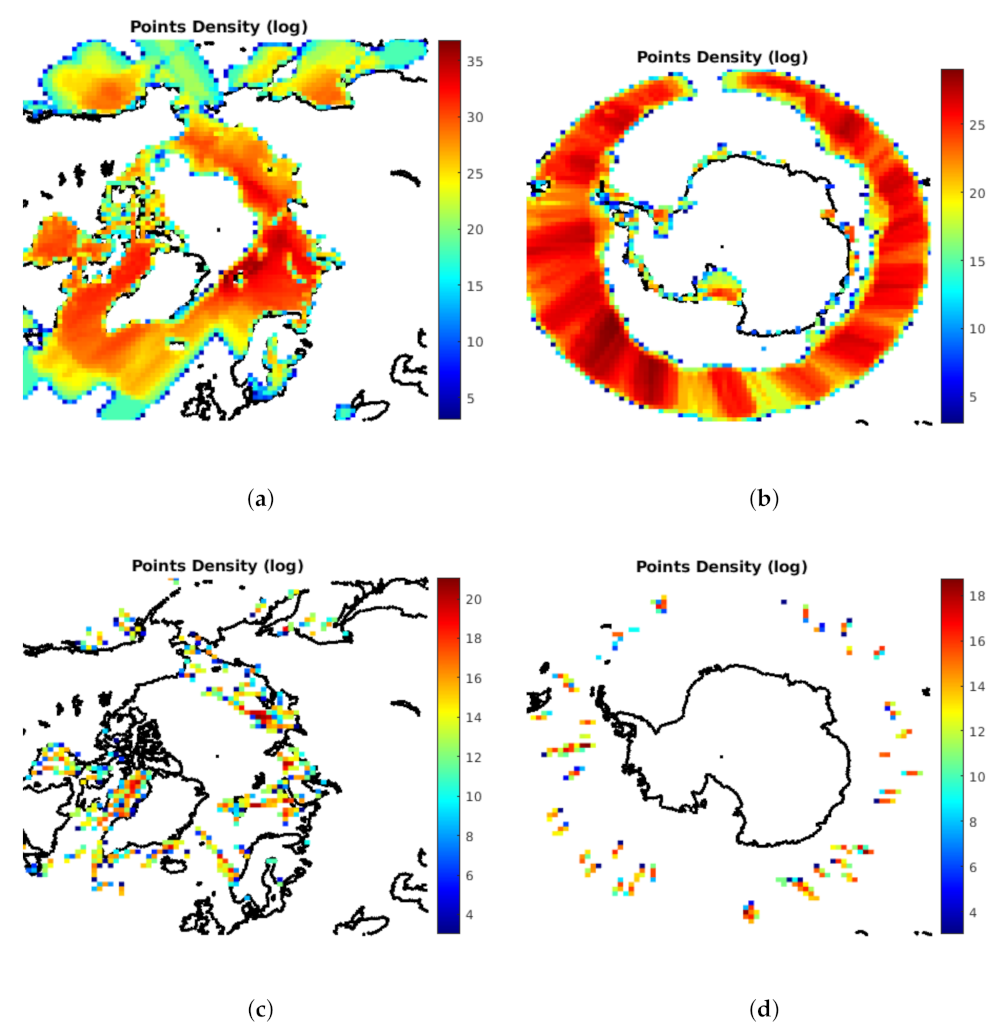
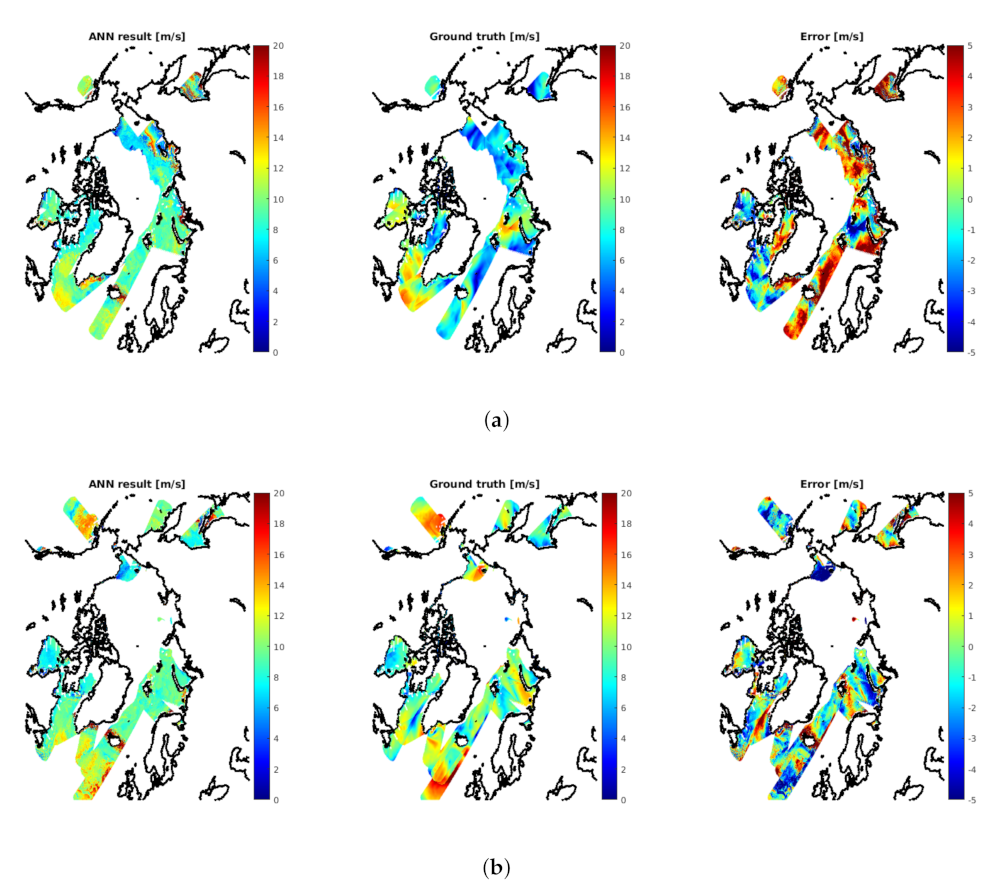
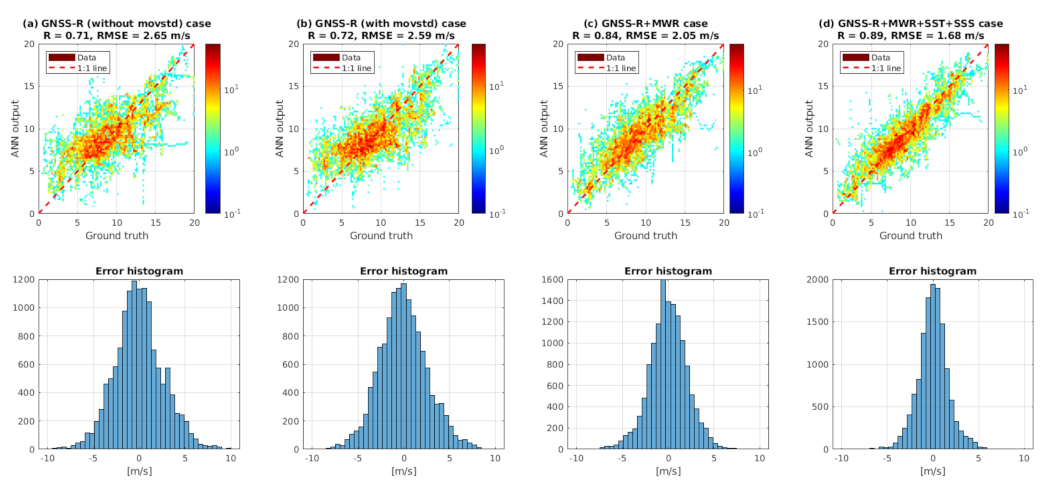
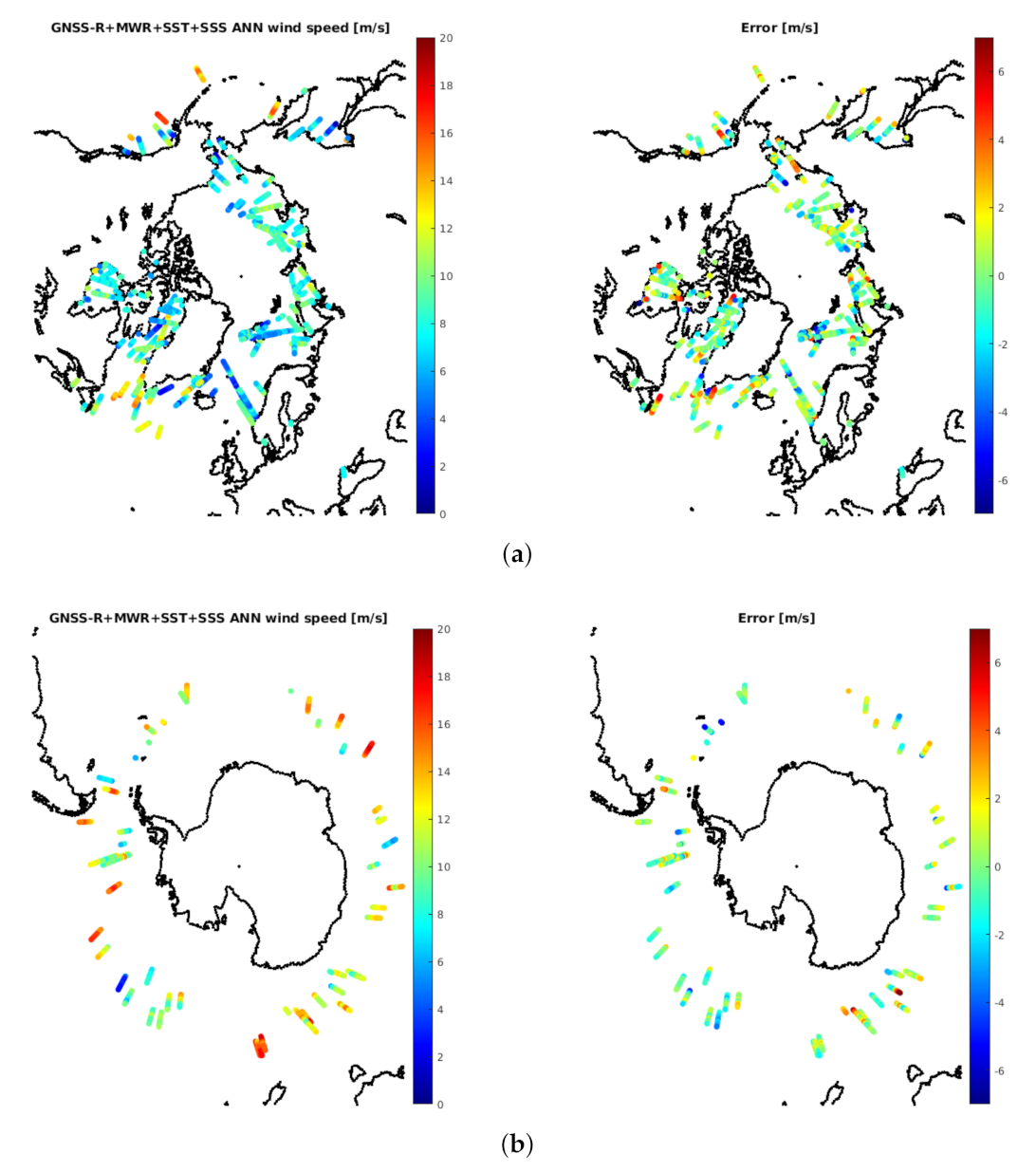
4.1. Wind Speed Results
4.1.1. Using L-Band Radiometry Data Only
4.1.2. Using GNSS-R Data Combined with the L-Band Radiometry Data
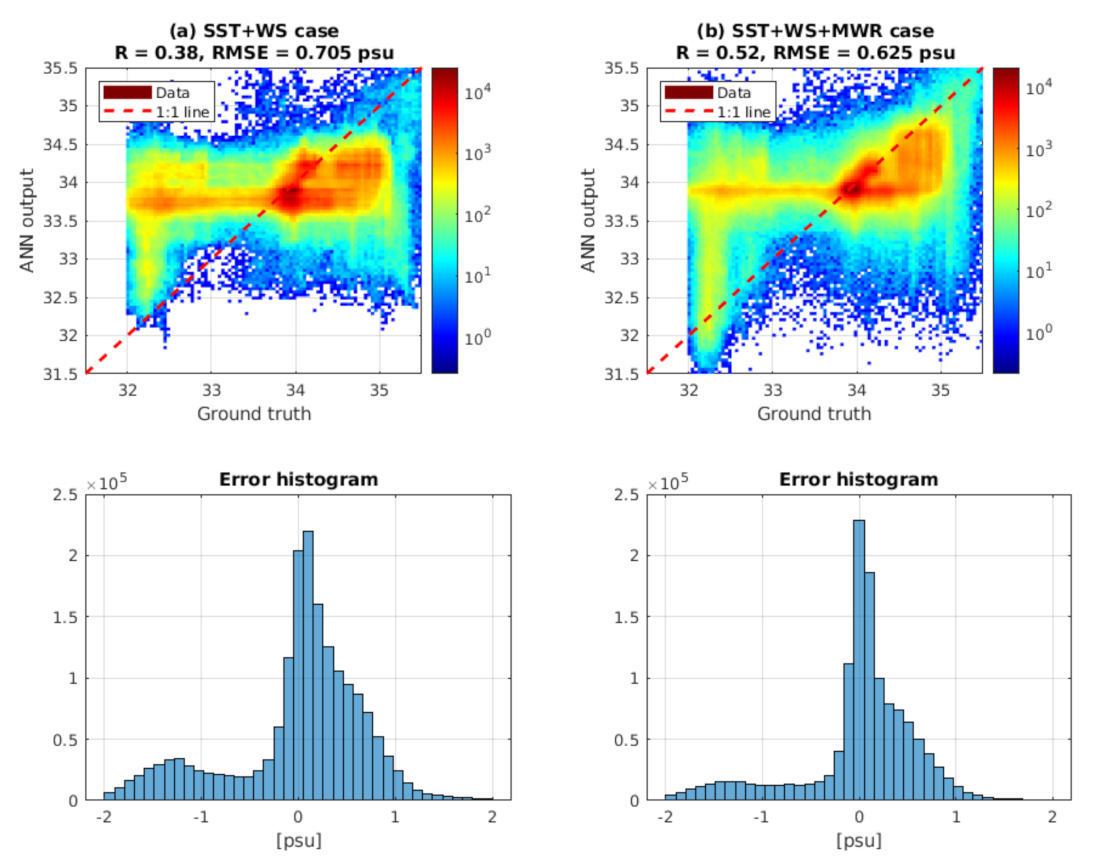
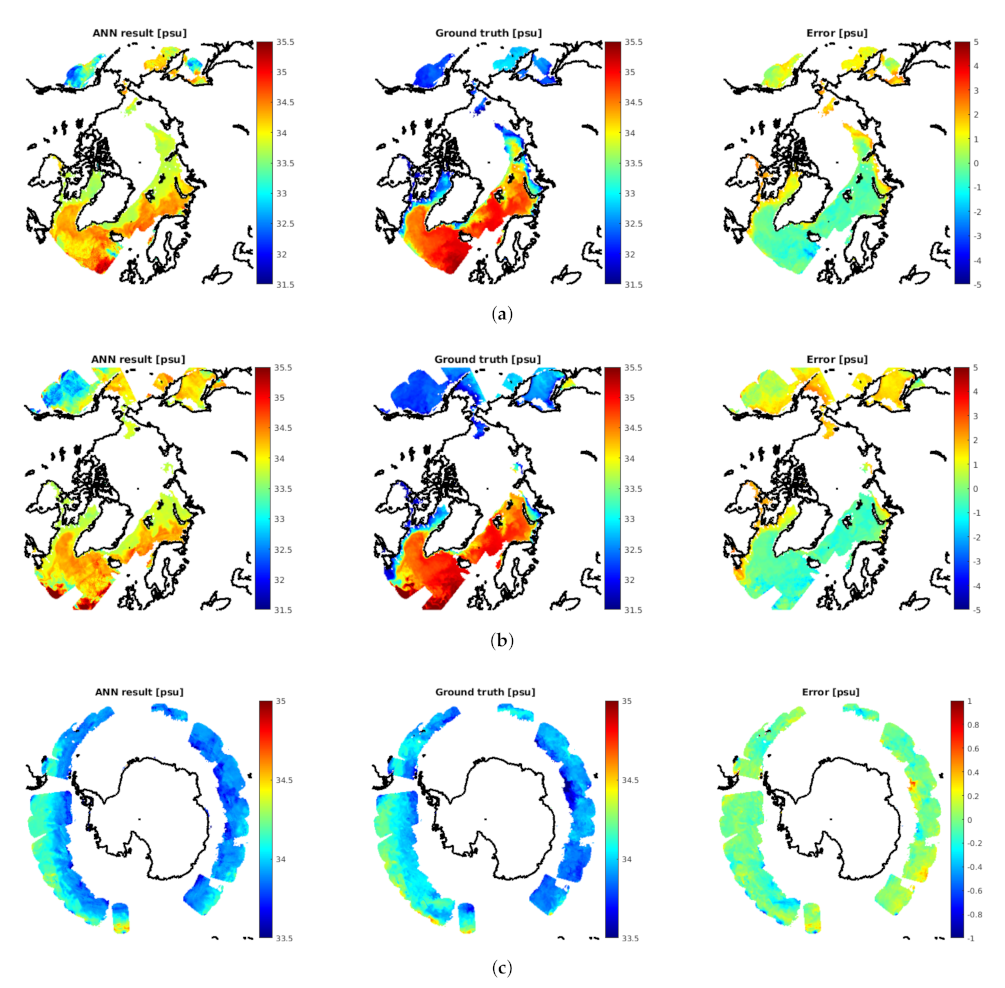
4.2. Sea Surface Salinity Results
4.2.1. Using L-Band Radiometry Data Only
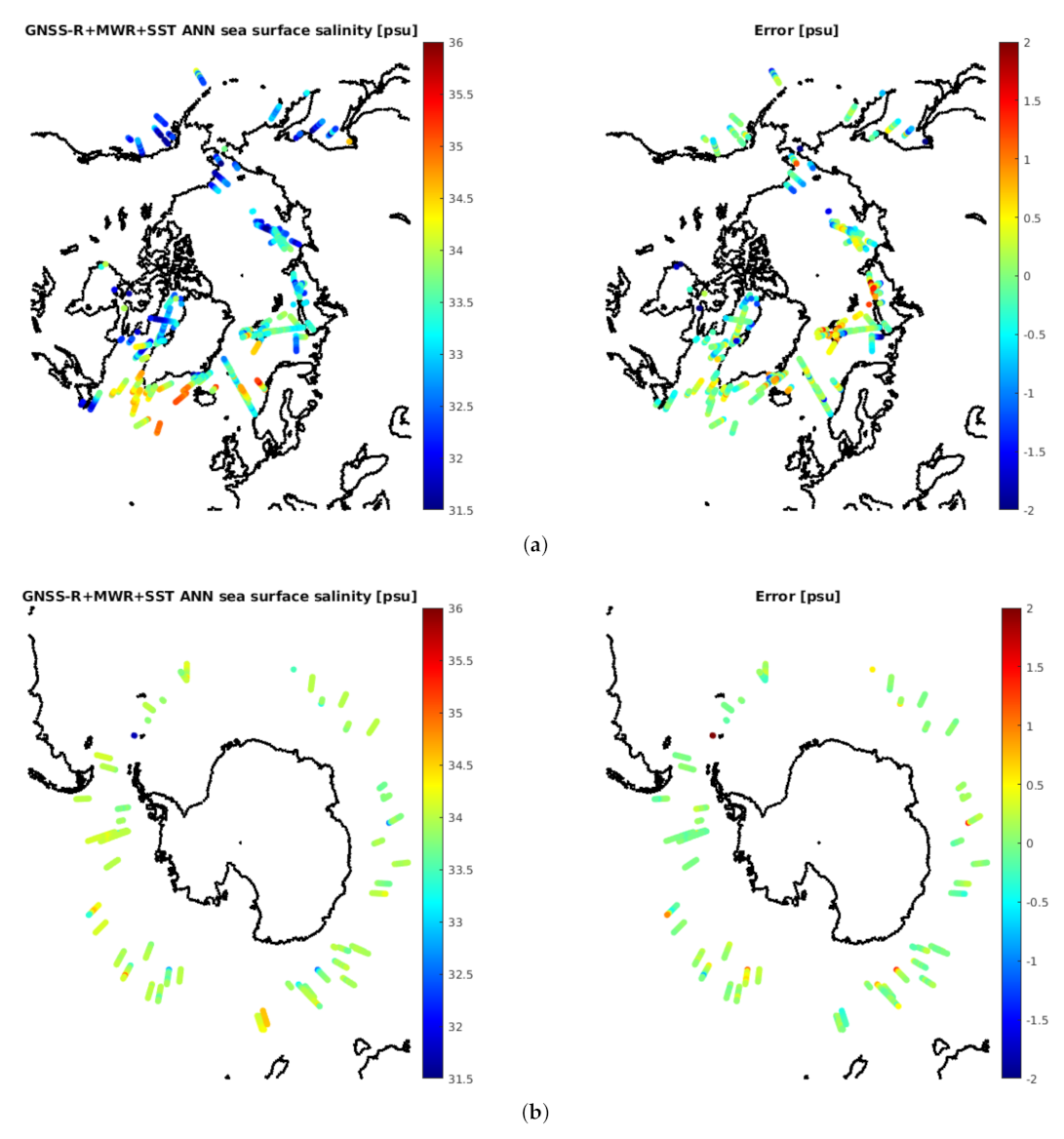
4.2.2. Using GNSS-R Data Only and in Combination with L-Band Radiometry Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GCOS. What are Essential Climate Variables? Available online: https://gcos.wmo.int/en/essential-climate-variables/abouth (accessed on 18 January 2021).
- Miralles, D.G.; Gentine, P.; Seneviratne, S.I.; Teuling, A.J. Land-atmospheric feedbacks during droughts and heatwaves: State of the science and current challenges. Ann. New York Acad. Sci. 2018, 1436, 19–35. [Google Scholar] [CrossRef] [PubMed]
- Lang, A.; Yang, S.; Kaas, E. Sea ice thickness and recent Arctic warming. Geophys. Res. Lett. 2016, 44, 409–418. [Google Scholar] [CrossRef]
- Arzel, O.; Fichefet, T.; Goosse, H. Sea ice evolution over the 20th and 21st centuries as simulated by current AOGCMs. Ocean. Model. 2006, 12, 401–415. [Google Scholar] [CrossRef]
- Latif, M.; Böning, C.; Willebrand, J.; Biastoch, A.; Dengg, J.; Keenlyside, N.; Schweckendiek, U.; Madec, G. Is the Thermohaline Circulation Changing? J. Clim. 2006, 19, 4631–4637. [Google Scholar] [CrossRef]
- UCAR Center for Science Education, The National Center for Atmospheric Research. Ocean on the Move: Thermohaline Circulation. Available online: http://scied.ucar.edu/ocean-move-thermohaline-circulation (accessed on 29 January 2021).
- Olmedo, E.; González-Haro, C.; Hoareau, N.; Umbert, M.; González-Gambau, V.; Martínez, J.; Gabarró, C.; Turiel, A. Nine years of SMOS sea surface salinity global maps at the Barcelona Expert Center. Earth Syst. Sci. Data 2021, 13, 857–888. [Google Scholar] [CrossRef]
- Ruf, C.; Unwin, M.; Dickinson, J.; Rose, R.; Rose, D.; Vincent, M.; Lyons, A. CyGNSS: Enabling the Future of Hurricane Prediction [Remote Sensing Satellites]. IEEE Geosci. Remote Sens. Mag. 2013, 1, 52–67. [Google Scholar] [CrossRef]
- Lemur-2. Gunter’s Space Page. Available online: https://space.skyrocket.de/doc_sdat/lemur-2.htm (accessed on 3 November 2020).
- Weaver, O.A.; Kerekes, J.P. The role of large constellations of small satellites in emergency response situations. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4200–4203. [Google Scholar] [CrossRef]
- Camps, A.; Golkar, A.; Gutierrez, A.; de Azua, J.A.R.; Munoz-Martin, J.F.; Fernandez, L.; Diez, C.; Aguilella, A.; Briatore, S.; Akhtyamov, R.; et al. FSSCat, the 2017 Copernicus Masters’ “ESA Sentinel Small Satellite Challenge” Winner: A Federated Polar and Soil Moisture Tandem Mission Based on 6U Cubesats. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8285–8287. [Google Scholar] [CrossRef]
- Lary, D.J.; Zewdie, G.K.; Liu, X.; Wu, D.; Levetin, E.; Allee, R.J.; Malakar, N.; Walker, A.; Mussa, H.; Mannino, A.; et al. Machine Learning Applications for Earth Observation. In Earth Observation Open Science and Innovation; Mathieu, P.P., Aubrecht, C., Eds.; Springer: Cham, Switzerland, 2018; pp. 165–218. [Google Scholar] [CrossRef] [Green Version]
- Jing, C.; Niu, X.; Duan, C.; Lu, F.; Di, G.; Yang, X. Sea Surface Wind Speed Retrieval from the First Chinese GNSS-R Mission: Technique and Preliminary Results. Remote Sens. 2019, 11, 3013. [Google Scholar] [CrossRef] [Green Version]
- Ruf, C.S.; Gleason, S.; McKague, D.S. Assessment of CyGNSS Wind Speed Retrieval Uncertainty. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 87–97. [Google Scholar] [CrossRef]
- Munoz-Martin, J.F.; Fernandez-Capon, L.; Ruiz-de-Azua, J.; Camps, A. The Flexible Microwave Payload-2: A SDR-Based GNSS-Reflectometer and L-Band Radiometer for CubeSats. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1298–1311. [Google Scholar] [CrossRef]
- Munoz-Martin, J.F.; Fernandez, L.; Perez, A.; de Azua, J.A.R.; Park, H.; Camps, A.; Domínguez, B.C.; Pastena, M. In-Orbit Validation of the FMPL-2 Instrument—The GNSS-R and L-Band Microwave Radiometer Payload of the FSSCat Mission. Remote Sens. 2020, 13, 121. [Google Scholar] [CrossRef]
- Llaveria, D.; Munoz-Martin, J.F.; Herbert, C.; Pablos, M.; Park, H.; Camps, A. Sea Ice Concentration and Sea Ice Extent Mapping with L-Band Microwave Radiometry and GNSS-R Data from the FFSCat Mission Using Neural Networks. Remote Sens. 2021, 13, 1139. [Google Scholar] [CrossRef]
- Herbert, C.; Munoz-Martin, J.F.; Llaveria, D.; Pablos, M.; Camps, A. Sea Ice Thickness Estimation Based on Regression Neural Networks Using L-Band Microwave Radiometry Data from the FSSCat Mission. Remote Sens. 2021, 13, 1366. [Google Scholar] [CrossRef]
- Munoz-Martin, J.F.; Llaveria, D.; Herbert, C.; Pablos, M.; Park, H.; Camps, A. Soil Moisture Estimation Synergy Using GNSS-R and L-Band Microwave Radiometry Data from FSSCat/FMPL-2. Remote Sens. 2021, 13, 994. [Google Scholar] [CrossRef]
- Font, J.; Camps, A.; Borges, A.; Martín-Neira, M.; Boutin, J.; Reul, N.; Kerr, Y.H.; Hahne, A.; Mecklenburg, S. SMOS: The Challenging Sea Surface Salinity Measurement From Space. Proc. IEEE 2010, 98, 649–665. [Google Scholar] [CrossRef] [Green Version]
- Reul, N.; Grodsky, S.; Arias, M.; Boutin, J.; Catany, R.; Chapron, B.; D’Amico, F.; Dinnat, E.; Donlon, C.; Fore, A.; et al. Sea surface salinity estimates from spaceborne L-band radiometers: An overview of the first decade of observation (2010–2019). Remote Sens. Environ. 2020, 242, 111769. [Google Scholar] [CrossRef]
- Emery, W.; Camps, A. Microwave Radiometry. In Introduction to Satellite Remote Sensing; Elsevier: Amsterdam, The Netherlands, 2017; pp. 131–290. [Google Scholar] [CrossRef]
- Camps, A.; Font, J.; Vall-llossera, M.; Gabarro, C.; Corbella, I.; Duffo, N.; Torres, F.; Blanch, S.; Aguasca, A.; Villarino, R.; et al. The WISE 2000 and 2001 field experiments in support of the SMOS mission: Sea surface L-band brightness temperature observations and their application to sea surface salinity retrieval. IEEE Trans. Geosci. Remote Sens. 2004, 42, 804–823. [Google Scholar] [CrossRef]
- Camps, A.; Bosch-Lluis, X.; Ramos-Perez, I.; Marchan-Hernandez, J.F.; Izquierdo, B.; Rodriguez-Alvarez, N. New Instrument Concepts for Ocean Sensing: Analysis of the PAU-Radiometer. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3180–3192. [Google Scholar] [CrossRef]
- Camps, A.; Marchán, J.F.; Valencia, E.; Ramos, I.; Bosch-Lluis, X.; Rodriguez, N.; Park, H.; Alcayde, A.; Mollfulleda, A.; Galindo, J.; et al. PAU instrument aboard INTA MicroSat-1: A GNSS-R demonstration mission for sea state correction in L-band radiometry. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, Canada, 24–29 July 2011; pp. 4126–4129. [Google Scholar] [CrossRef]
- Sabia, R.; Caparrini, M.; Ruffini, G. Potential Synergetic Use of GNSS-R Signals to Improve the Sea-State Correction in the Sea Surface Salinity Estimation: Application to the SMOS Mission. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2088–2097. [Google Scholar] [CrossRef]
- Valencia, E.; Camps, A.; Rodriguez-Alvarez, N.; Ramos-Perez, I.; Bosch-Lluis, X.; Park, H. Improving the accuracy of sea surface salinity retrieval using GNSS-R data to correct the sea state effect. Radio Sci. 2011, 46, 1–11. [Google Scholar] [CrossRef]
- Liu, B.; Wan, W.; Hong, Y. Can the Accuracy of Sea Surface Salinity Measurement be Improved by Incorporating Spaceborne GNSS-Reflectometry? IEEE Geosci. Remote Sens. Lett. 2021, 18, 3–7. [Google Scholar] [CrossRef]
- Asgarimehr, M.; Wickert, J.; Reich, S. TDS-1 GNSS Reflectometry: Development and Validation of Forward Scattering Winds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4534–4541. [Google Scholar] [CrossRef]
- Ruf, C.S.; Balasubramaniam, R. Development of the CYGNSS Geophysical Model Function for Wind Speed. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 66–77. [Google Scholar] [CrossRef]
- Asharaf, S.; Waliser, D.E.; Posselt, D.J.; Ruf, C.S.; Zhang, C.; Putra, A.W. CYGNSS Ocean Surface Wind Validation in the Tropics. J. Atmos. Ocean. Technol. 2021, 38, 711–724. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S.; Jales, P.; Gommenginger, C. Spaceborne GNSS-R Minimum Variance Wind Speed Estimator. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6829–6843. [Google Scholar] [CrossRef]
- Wang, H.Y.; Juang, J.C. Retrieval of Ocean Wind Speed Using Super-Resolution Delay-Doppler Maps. Remote Sens. 2020, 12, 916. [Google Scholar] [CrossRef] [Green Version]
- Munoz-Martin, J.F.; Onrubia, R.; Pascual, D.; Park, H.; Camps, A.; Rüdiger, C.; Walker, J.; Monerris, A. Single-Pass Soil Moisture Retrieval Using GNSS-R at L1 and L5 Bands: Results from Airborne Experiment. Remote Sens. 2021, 13, 797. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Pierdicca, N.; Costantini, F.; Floury, N. Analysis of CyGNSS Data for Soil Moisture Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2227–2235. [Google Scholar] [CrossRef]
- Chew, C.; Small, E. Description of the UCAR/CU Soil Moisture Product. Remote Sens. 2020, 12, 1558. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W.; Jin, S.; Jia, Y. Pan-tropical soil moisture mapping based on a three-layer model from CyGNSS GNSS-R data. Remote Sens. Environ. 2020, 247, 111944. [Google Scholar] [CrossRef]
- Rodriguez-Fernandez, N.J.; Aires, F.; Richaume, P.; Kerr, Y.H.; Prigent, C.; Kolassa, J.; Cabot, F.; Jimenez, C.; Mahmoodi, A.; Drusch, M. Soil Moisture Retrieval Using Neural Networks: Application to SMOS. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5991–6007. [Google Scholar] [CrossRef]
- Elecnor, D.; Cesnet; EGI; CoLAB+Atlantic. NextGEOSS Project, a European Contribution to GEOSS. Available online: https://catalogue.nextgeoss.eu/ (accessed on 13 July 2021).
- Brodzik, M.J.; Billingsley, B.; Haran, T.; Raup, B.; Savoie, M.H. EASE-Grid 2.0: Incremental but Significant Improvements for Earth-Gridded Data Sets. ISPRS Int. J. Geo-Inf. 2012, 1, 32–45. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1979 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 14 June 2018. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=overview (accessed on 20 May 2012).
- Olmedo, E.; González-Haro, C.; González, V.; Turiel, A. BEC SMOS Sea Surface Salinity Global L3 Product (V.2.0) [Dataset]; CSIC - Instituto de Ciencias del Mar (ICM): Barcelona, Spain, 2020. [Google Scholar] [CrossRef]
- OSI SAF. ASCAT L2 25 km Winds Data Record Release 1—Metop; EUMETSAT SAF on Ocean and Sea Ice: Darmstadt, Germany, 2016. [Google Scholar] [CrossRef]
- Camps, A.; Munoz-Martin, J.F. Analytical Computation of the Spatial Resolution in GNSS-R and Experimental Validation at L1 and L5. Remote Sens. 2020, 12, 3910. [Google Scholar] [CrossRef]
- Camps, A. Spatial Resolution in GNSS-R Under Coherent Scattering. IEEE Geosci. Remote Sens. Lett. 2019. [Google Scholar] [CrossRef]
- Park, H.; Pascual, D.; Camps, A.; Martin, F.; Alonso-Arroyo, A.; Carreno-Luengo, H. Analysis of Spaceborne GNSS-R Delay-Doppler Tracking. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1481–1492. [Google Scholar] [CrossRef]
- Ying, X. An Overview of Overfitting and its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Burden, F.; Winkler, D. Bayesian Regularization of Neural Networks. In Methods in Molecular Biology™; Humana Press: Totowa, NJ, USA, 2008; pp. 23–42. [Google Scholar] [CrossRef]
- Reynolds, J.; Clarizia, M.P.; Santi, E. Wind Speed Estimation From CYGNSS Using Artificial Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 708–716. [Google Scholar] [CrossRef]
- Balasubramaniam, R.; Ruf, C. Neural Network Based Quality Control of CYGNSS Wind Retrieval. Remote Sens. 2020, 12, 2859. [Google Scholar] [CrossRef]
- Karnin, E.D. A simple procedure for pruning back-propagation trained neural networks. IEEE Trans. Neural Netw. 1990, 1, 239–242. [Google Scholar] [CrossRef]
- Meissner, T.; Ricciardulli, L.; Wentz, F.J. Capability of the SMAP Mission to Measure Ocean Surface Winds in Storms. Bull. Am. Meteorol. Soc. 2017, 98, 1660–1677. [Google Scholar] [CrossRef]
- Cotton, J.; Francis, P.; Heming, J.; Forsythe, M.; Reul, N.; Donlon, C. Assimilation of SMOS L-band wind speeds: Impact on Met Office global NWP and tropical cyclone predictions. Q. J. R. Meteorol. Soc. 2018, 144, 614–629. [Google Scholar] [CrossRef]
- Rivas, M.B.; Stoffelen, A. Characterizing ERA-Interim and ERA5 surface wind biases using ASCAT. Ocean. Sci. 2019, 15, 831–852. [Google Scholar] [CrossRef] [Green Version]
- Olmedo, E.; Gabarró, C.; González-Gambau, V.; Martínez, J.; Ballabrera-Poy, J.; Turiel, A.; Portabella, M.; Fournier, S.; Lee, T. Seven Years of SMOS Sea Surface Salinity at High Latitudes: Variability in Arctic and Sub-Arctic Regions. Remote Sens. 2018, 10, 1772. [Google Scholar] [CrossRef] [Green Version]
- Bao, S.; Wang, H.; Zhang, R.; Yan, H.; Chen, J. Comparison of Satellite-Derived Sea Surface Salinity Products from SMOS, Aquarius, and SMAP. J. Geophys. Res. Ocean. 2019, 124, 1932–1944. [Google Scholar] [CrossRef]





| Model | Target Output | Description |
|---|---|---|
| SST + SSS | WS | Validation set without FMPL-2 data |
| SST + SSS + MWR | WS | WS retrieval using FMPL-2 and SST + SSS data |
| GNSS-R | WS | WS retrieval over specular reflection points using GNSS-R data (not using movstd()) from FMPL-2 |
| GNSS-R | WS | WS retrieval over specular reflection points using GNSS-R data (using movstd()) from FMPL-2 |
| GNSS-R + MWR | WS | WS retrieval over specular reflection points using combined GNSS-R and L-band radiometry data from FMPL-2 |
| GNSS-R + MWR + SST + SSS | WS | WS retrieval over specular reflection points using combined GNSS-R and L-band radiometry data from FMPL-2, and aided by the SST and SSS data sets |
| Model | Target Output | Description |
|---|---|---|
| SST + WS | SSS | Validation set without FMPL-2 data |
| SST + WS + MWR | SSS | SSS retrieval using FMPL-2 and SST + WS data |
| GNSS-R | SSS | SSS retrieval over specular reflection points using GNSS-R data (not using movstd()) from FMPL-2 |
| GNSS-R | SSS | SSS retrieval over specular reflection points using GNSS-R data (using movstd()) from FMPL-2 |
| GNSS-R + MWR | SSS | SSS retrieval over specular reflection points using combined GNSS-R and L-band radiometry data from FMPL-2 |
| GNSS-R + MWR + SST | SSS | SSS retrieval over specular reflection points using combined GNSS-R and L-band radiometry data from FMPL-2, and aided by the SST data set |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munoz-Martin, J.F.; Camps, A. Sea Surface Salinity and Wind Speed Retrievals Using GNSS-R and L-Band Microwave Radiometry Data from FMPL-2 Onboard the FSSCat Mission. Remote Sens. 2021, 13, 3224. https://doi.org/10.3390/rs13163224
Munoz-Martin JF, Camps A. Sea Surface Salinity and Wind Speed Retrievals Using GNSS-R and L-Band Microwave Radiometry Data from FMPL-2 Onboard the FSSCat Mission. Remote Sensing. 2021; 13(16):3224. https://doi.org/10.3390/rs13163224
Chicago/Turabian StyleMunoz-Martin, Joan Francesc, and Adriano Camps. 2021. "Sea Surface Salinity and Wind Speed Retrievals Using GNSS-R and L-Band Microwave Radiometry Data from FMPL-2 Onboard the FSSCat Mission" Remote Sensing 13, no. 16: 3224. https://doi.org/10.3390/rs13163224
APA StyleMunoz-Martin, J. F., & Camps, A. (2021). Sea Surface Salinity and Wind Speed Retrievals Using GNSS-R and L-Band Microwave Radiometry Data from FMPL-2 Onboard the FSSCat Mission. Remote Sensing, 13(16), 3224. https://doi.org/10.3390/rs13163224







