Abstract
Deep learning techniques have greatly improved the efficiency and accuracy of building extraction using remote sensing images. However, high-quality building outline extraction results that can be applied to the field of surveying and mapping remain a significant challenge. In practice, most building extraction tasks are manually executed. Therefore, an automated procedure of a building outline with a precise position is required. In this study, we directly used the U2-net semantic segmentation model to extract the building outline. The extraction results showed that the U2-net model can provide the building outline with better accuracy and a more precise position than other models based on comparisons with semantic segmentation models (Segnet, U-Net, and FCN) and edge detection models (RCF, HED, and DexiNed) applied for two datasets (Nanjing and Wuhan University (WHU)). We also modified the binary cross-entropy loss function in the U2-net model into a multiclass cross-entropy loss function to directly generate the binary map with the building outline and background. We achieved a further refined outline of the building, thus showing that with the modified U2-net model, it is not necessary to use non-maximum suppression as a post-processing step, as in the other edge detection models, to refine the edge map. Moreover, the modified model is less affected by the sample imbalance problem. Finally, we created an image-to-image program to further validate the modified U2-net semantic segmentation model for building outline extraction.
1. Introduction
With the rapid development of aerospace, high-resolution remote sensing images have become increasingly accessible and convenient to use [1]. As a key element of a city’s structure, buildings play an important role in human society. Extracting building information from remote sensing images is beneficial as it allows us to quantify the spatial distribution characteristics of buildings. Such information is priceless for urban planning [2,3], disaster management [4,5], land use change [6], mapping [7,8,9] and many other applications. For the actual production activities, we tend to obtain the edges of a building, as this allows us to understand the shape, position, distribution, and other geometric features of the building in a comprehensible manner. In recent years, with the continuous advancement of deep learning technology, there has been significant progress in building edge extraction [10,11,12]; however, it is still a large challenge to automatically extract clear and precise building edges from remote sensing images in practical applications.
In the past few decades, the extraction of remote sensing-based building edges by using traditional methods has been extensively studied. These efforts can be divided into three categories: (1) edge or straight-line detection technology, (2) curve propagation techniques, and (3) segmentation technology. Based on traditional edge detection technology, the edges of an image are first extracted. Then, the edges or the straight lines are combined to form closed contours. Ultimately, a complete building contour is extracted using prior knowledge of a building’s shape. Mohammad et al. [13] extracted a straight line and obtained the connection points to identify and quantify a building roof contour through these connection points. Qi et al. [14] first used a priori knowledge to constrain the extracted lines, group the segments of the lines, and ultimately extract the polygonal building boundary. Turker et al. [15] used the support vector machine (SVM) to classify the data and build image blocks in a study area. They subsequently used the Canny operator and applied the Hough transform for each image block to retrieve straight-line segments. Finally, the straight-line segments were grouped to extract the building contours. Given a variety of discontinuous edge segments in traditional edge detection methods, a post-processing step is required to improve the accuracy of the building edge detection. To solve this problem, curve propagation techniques such as active contour extraction and the level set method have been used to extract a closed contour of a target building. For instance, Karantzalos et al. [16] used various prior information sources to construct a target energy function for the level set segmentation, which can be effectively used to extract multiple targets in an image that meets the requirements of the building shape library. Ahmadi et al. [17] used the difference between the internal and external contours of the target to form an energy function for active contour tracking to extract the target contour of a typical building. Although such methods can be used for extracting closed contours, the sensitivity of the method to the initial edge detection cannot guarantee the acquisition of a globally optimal boundary. Moreover, it is difficult to detect weak building edges by using only local information. Given the fact that the former two methods cannot fully exploit the prior global and local building information, the object-oriented segmentation technique has been widely used for building target extraction purposes. As such, Attarzadeh et al. [18] obtained optimal scale parameters through the segmentation technique. They segmented a remote sensing image and extracted multiple features to quantify the buildings through classification. Sellouti et al. [19] used the watershed algorithm to segment the input images for choosing candidate regions. Then, they classified the segmented objects using the similarity index and finally extracted the target building information using the region growing method. Thus, the segmentation technique allows for the association of global and local variables to a certain extent, but its performance strongly depends on the initial segmentation, and it is difficult to extract complex buildings.
In recent years, the rapid development of deep learning techniques has resulted in the subsequent progress of convolutional neural networks [20] in the field of computer vision including image classification [21,22,23,24], object detection [25,26,27], and semantic segmentation [28,29] methods. The deep learning techniques promoted the transformation of manual design features to autonomous learning features [30,31]. From the classification perspective, a new generation of convolutional networks led by AlexNet [24] and ResNet [21] have shown great success on image classification tasks. Based on the traditional convolutional neural network, Long et al. [29] proposed a fully convolutional network (FCN) by eliminating the original full connection layer. It realizes the pixel-to-pixel model and lays a foundation for subsequent models such as U-Net [32] or Segnet [33]. Owing to this, the FCN and its variants have been widely used in the fields of remote sensing classification [23,34] and objective extraction [35,36]. The fusion of CNN and GCN proposed by Hong et al. [37] broke the performance bottleneck of a single model and was used to extract different spatial–spectral features to further improve the classification effect.
Since deep learning technology was introduced into the remote sensing field, numerous influential studies have been published [37,38,39,40,41]. Recently, FCN has yielded robust results in remote sensing image semantic segmentation. Li et al. [42] performed a comparative analysis on applying an FCN for a building extraction, and their results proved the effectiveness of the FCN. Liu et al.’s [43] proposed SRI-net model can accurately detect large buildings that are easily ignored, while maintaining the overall shape. Huang et al. [35] proposed the DeconvNet model, using different band combinations (RGB and NRG) in the Vancouver dataset to fine-tune the model and verify its effectiveness. However, a traditional FCN easily ignores the rich low-level features and intermediate semantic features, thus ultimately blurring building boundaries [44]. To this end, some scholars utilized dilated convolution [45] or added skip connections [32] to aggregate multi-scale contexts. Moreover, in order to further optimize the extraction results, some researchers tried to use post-processing. For example, Chen et al. [46] applied conditional random fields (CRFs) for the post-processing of network output to improve the quality of boundary extraction. Li et al. [47] proposed a two-step method to implement building extraction. First, the modified CRF model was used to reduce the edge misclassification effect. Then, the prominent features of buildings were exploited to increase the expression of building edge information. Shrestha et al. [48] used CRF as a post-processing tool for segmentation results to improve the quality of building boundaries. In order to obtain a clear and complete building boundary, some researchers tried to directly extract the building boundary method. For example, Lu et al. [12] introduced the richer convolutional features (RCF) [49] edge detection network into the field of remote sensing, constructed an RCF–building network, and used terrain surface geometry analysis to refine the extracted building boundaries. Li et al. [50] proposed a new instance segmentation network to detect several key points of a single building, and then used these key points to construct the building boundary. Zorzi et al. [51] used machine learning methods to construct automatic regularization and polygonization of segmentation results. First, an FCN is used to generate a prediction map, then a generative adversarial network is used to construct boundary regularization, and finally a convolutional neural network is used to predict building corners from the regularized results. Chen et al. [10] introduced the PolygonCNN model. The network first uses the FCN variant to segment the initial building area, then encodes the building polygon vertices and combines the segmentation results, and finally uses the improved pointNet network to predict the polygon vertices and generate the building vector results. These studies further promote the solution of the vector generation problem, but a lot of experiments are still needed to improve and verify their accuracy and effectiveness.
Although deep learning technology has greatly promoted the development of remote sensing-based building edge extraction methods, high-quality building edge extraction results that can be applied to the field of surveying and mapping still face huge challenges. In the present work, we tested the feasibility of using the semantic segmentation model U2-net directly for building outline extraction, and further refined the model output by modifying the loss function of the model. The rest of the paper is organized as follows. The approach is described in Section 2. Section 3 is the experiment, including dataset introduction, experimental setup, and evaluation metrices. Section 4 reports and discusses the experimental results on the Nanjing dataset and WHU dataset, and compares with the edge detection model and semantic segmentation model, respectively. Section 5 provides our conclusions and further research plan.
2. Methods
The main idea of this study is to use the existing semantic segmentation model U2-net [52] to extract the edges of buildings in high-resolution remote sensing images in an automated manner. This section provides an overview of the network architecture. The U-type residuals are described in Section 2.2. The loss function is described in Section 2.3.
2.1. Overview of Network Architecture
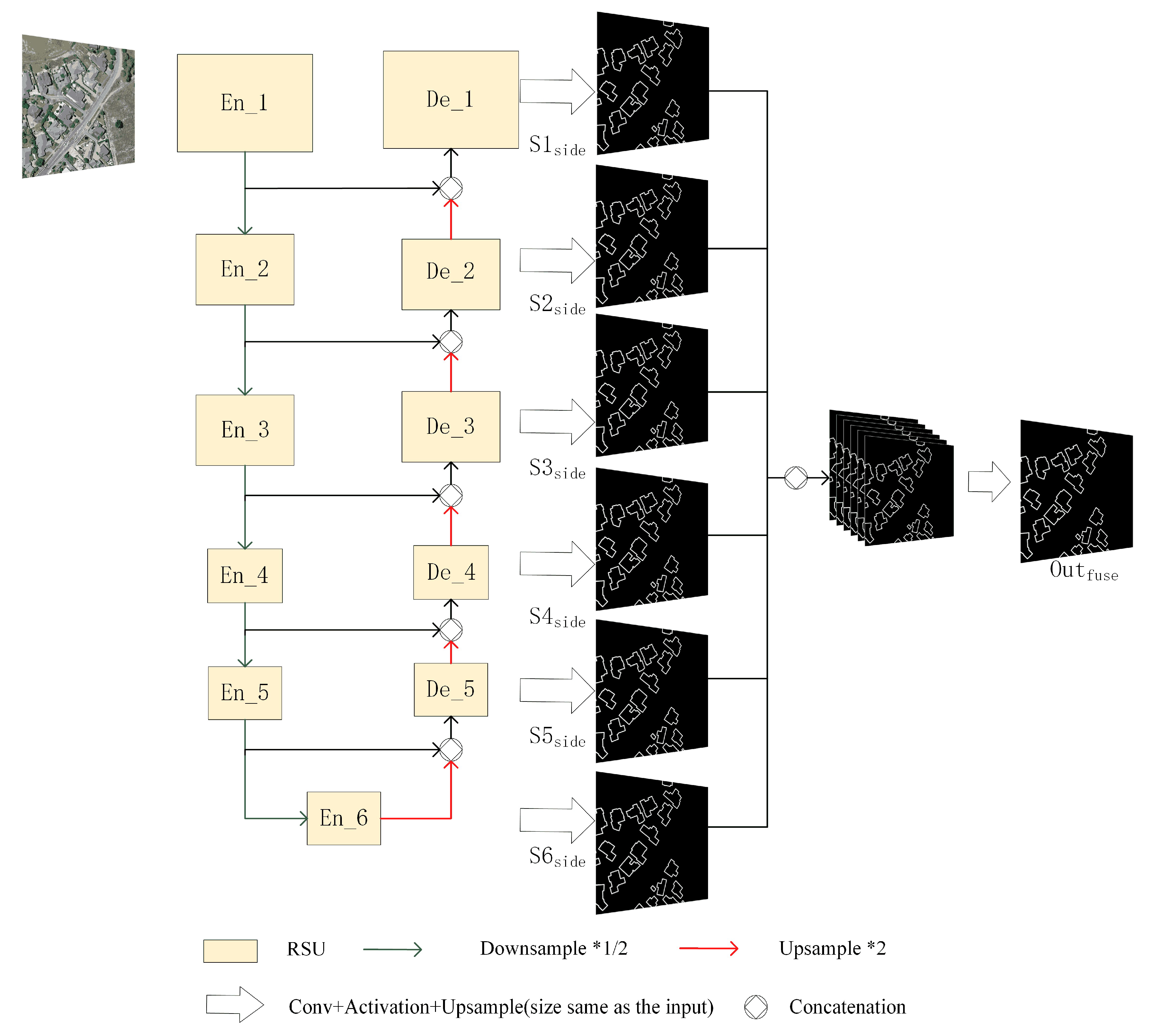
The U2-net model was proposed by Qin [52], and its structure is shown in Figure 1. Qin [52] evaluated its performance on six datasets and achieved good results. The model has also made good progress in other areas. For example, Vallejo [53] developed an application to extract the foreground of an image using this model. Tim [54] introduced an application to remove the background from a video. Finally, Scuderi [53] designed a clipping camera based on this model, which can detect relevant objects from the scene and clip them, and also developed a style transfer program based on this model.
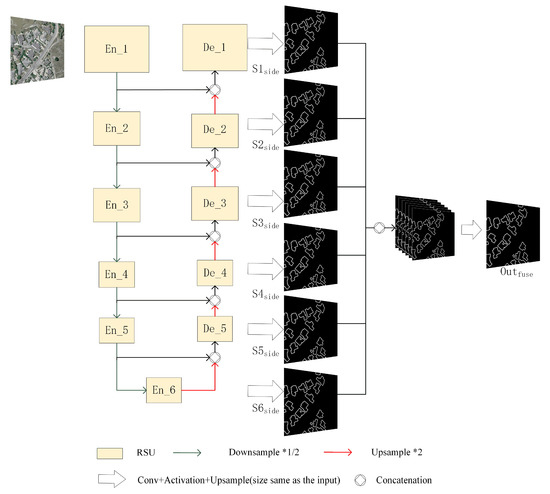
Figure 1.
U2-net architecture [52]. The network as a whole is a U-shaped structure, the basic unit is RSU, the decoder and the last encoder, respectively, produce side output, and the side output is merged in the channel direction and then passed through the convolutional layer to produce the fused output result.
The U2-net is a two-level nested U-structure. The outer layer is a large U-structure consisting of 11 stages. Each stage is populated by a residual U-block (RSU) (inner layer). Theoretically, the nested U-structure allows the extraction of multi-scale features and multi-level features more efficiently. It consists of three parts: (1) encoder, (2) decoder, and (3) map fusion module, as shown below.
(1) There are six stages in the encoder stage. Each stage is composed of an RSU. In the RSU of the first four stages, the feature map is reduced to increase the receptive field and to obtain more large-scale information. In the next two stages, dilated convolution is used to replace the pooling operation. This step is required to prevent the context information loss. Note that the receptive field is increased while the feature map is not reduced.
(2) The decoder stages have structures similar to those of the encoder stages. Each decoder stage concatenates the up-sampled feature maps from its previous stage, and those from its symmetrical encoder stage as the input.
(3) Feature map fusion using a deep supervision strategy is the last stage applied to generate a probability map. The model body produces six side outputs. These outputs are then up-sampled to the size of the input image and fused with a concatenation operation.
To summarize, the U2-net design not only has a deep architecture with rich multi-scale features, but also has low computing and memory costs. Moreover, as the U2-net architecture is only built on the RSU blocks and does not use any pre-trained backbones, it is flexible and is easy to be adapted to different working environments with little performance penalty.
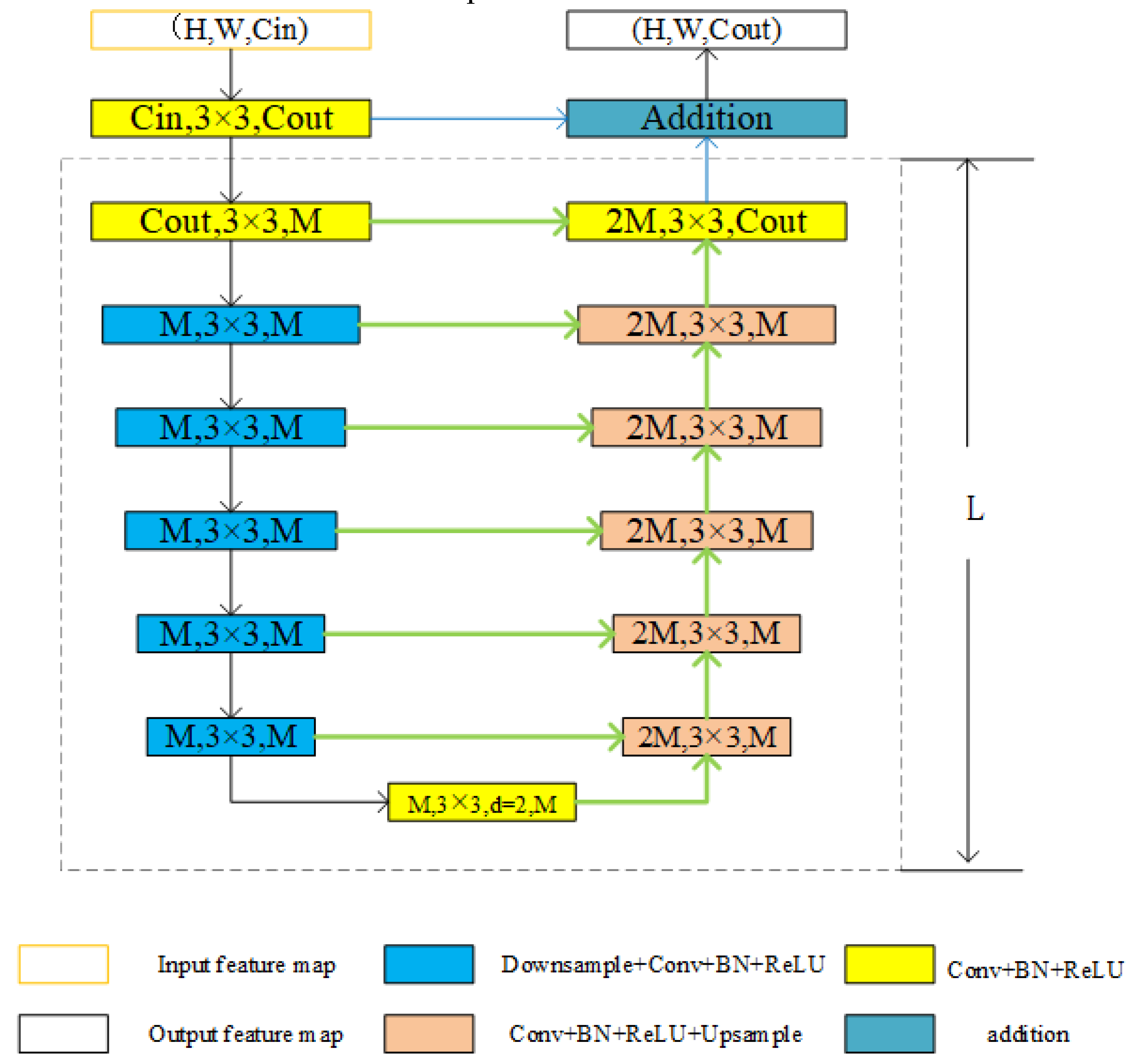
2.2. Residual U-Blocks
Unlike the previous series stacking, the RSU is a U-structure embedded residual module used to capture multi-scale features. The structure of RSU-L (Cin, M, Cout) is shown in Figure 2, where L is the number of layers in the encoder, Cin and Cout denote the input and output channels, and M denotes the number of channels in the internal layers of the RSU. The RSU consists of three main parts.
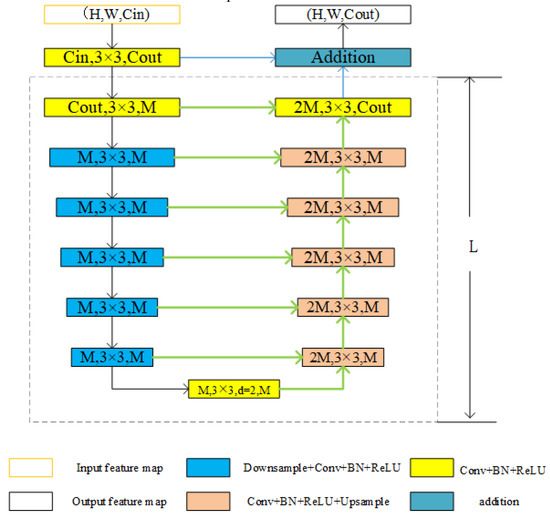
Figure 2.
Residual U-blocks [52]. A residual unit composed of a U-shaped structure. The dashed frame is a U-shaped block. The feature map obtained by the convolution operation and the output result of the U-shaped block are added to obtain the output feature map.
At the outset, the convolution layer transforms the input feature map (H, W, Cin) into an intermediate map F1(x) with a channel of Cout. This is a plain convolution layer used to extract local features. Second, a U-structure symmetric encoder–decoder with height L takes the intermediate feature map F1(x) as the input. This structure can extract multi-scale information and reduce the loss of context information caused by up-sampling. Third, the local features and the multiscale features are fused by a residual connection.
2.3. Loss
Deep supervision can restrain multiple stages in the network, and its effectiveness is verified by HED [55], RCF [49] and DexiNed [56]. This is defined in Equation (1):
where and denote the weights of each loss, and indicates the loss of the side output map. In the original version, the loss function uses binary cross entropy to calculate the loss (), as shown in Equation (2) below:
where and denote the pixel values of the ground truth and the predicted probability map obtained through the sigmoid function, respectively, and N is the total number of pixels. Our purpose was to minimize loss.
To obtain more extreme edges, we replace the binary cross entropy with multi-class cross entropy, which can help in obtaining thinner edges and directly generating binary maps. The definition is given in Equation (3) below:
where a0 represents the probability of the pixel being predicted as the background, a1 is the probability of the pixel being predicted as the building edge, represents the value of the background in the label, represents the value of the edge in the label, and , respectively, represent the length and width of the input image, and represents the total number of pixels. Different from the probability map generated by binary cross entropy, the output results of the model using multi-classification cross entropy are directly classified into background and building edge, and each pixel is limited to these two classes instead of a probability value, which is expected to make the difference between the two classes more obvious, and then the edge more refined.
3. Experiment
Our model was implemented using the machine learning library PyTorch 1.7.1 and CUDA toolkit 10.2 software. The model was trained from scratch with no pre-trained weight. To check the validity and correctness of the model, we conducted an experiment of building edge extraction on remote sensing images and compared it with the semantic segmentation and the edge detection models. This section introduces the dataset details, describes the experimental setup, and presents the evaluation criteria.
3.1. Dataset
To evaluate the effectiveness of the method, two building datasets, the Nanjing dataset and the WHU building dataset, were used. The Nanjing dataset was produced by the authors of this study, and the WHU building dataset is an international open-source dataset.
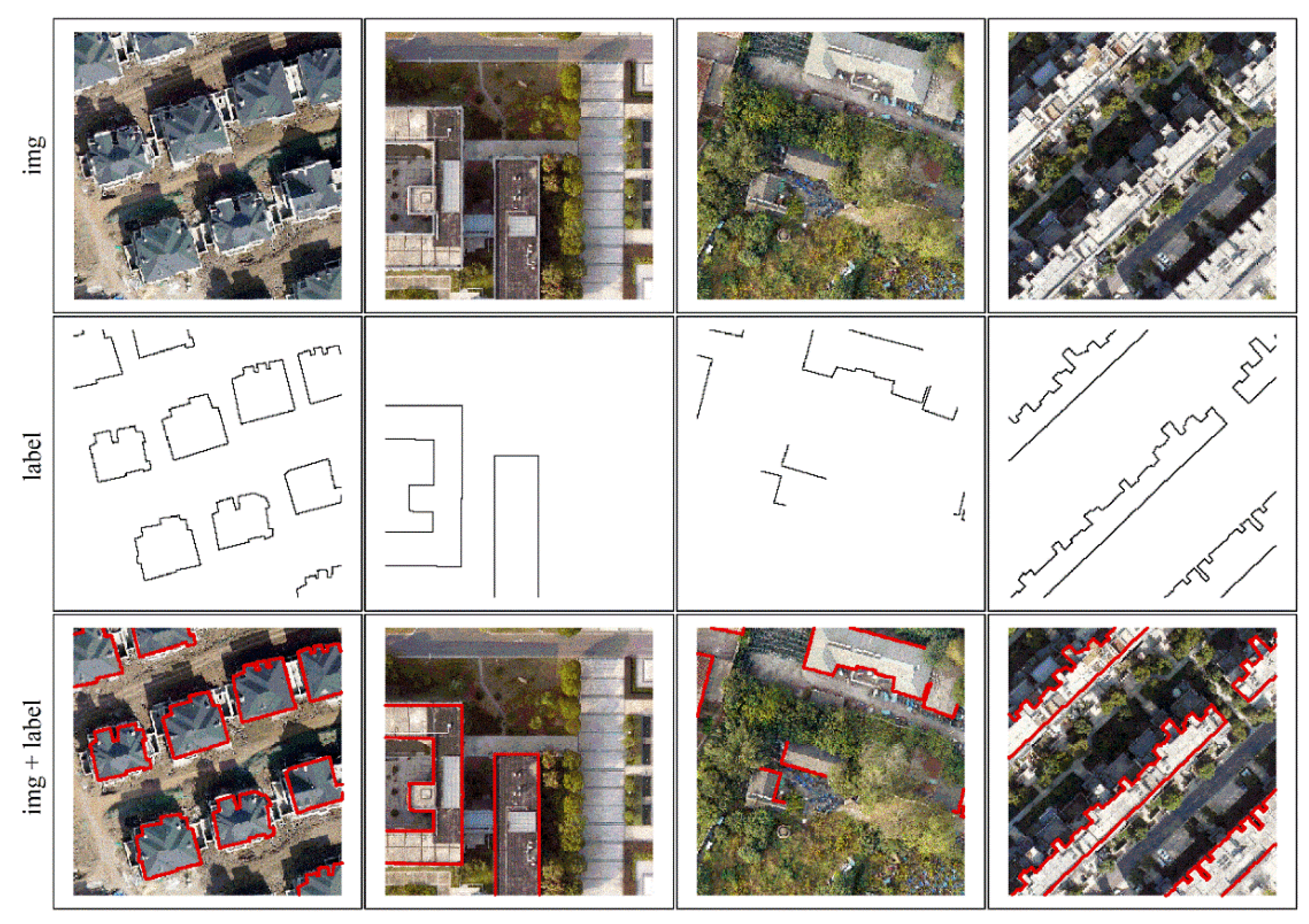
The Nanjing dataset covers a range of building types, shapes, and complex surroundings, as shown in Figure 3. It has three bands (red, green, blue) with a spatial resolution of 0.3 m. We manually annotated all labels. The whole image was cropped into 2376 pieces of 256 × 256 pixels without overlapping, and only 500 images were obtained after eliminating invalid data. We used 400 images as the training and validation sets and 100 images as the test set. Through data augmentation, including flips and rotations, 400 images were expanded to 2000 (80% were used for training and 20% for validation).
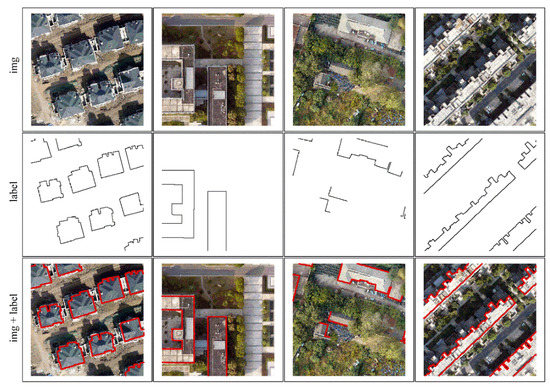
Figure 3.
The sample of Nanjing dataset.
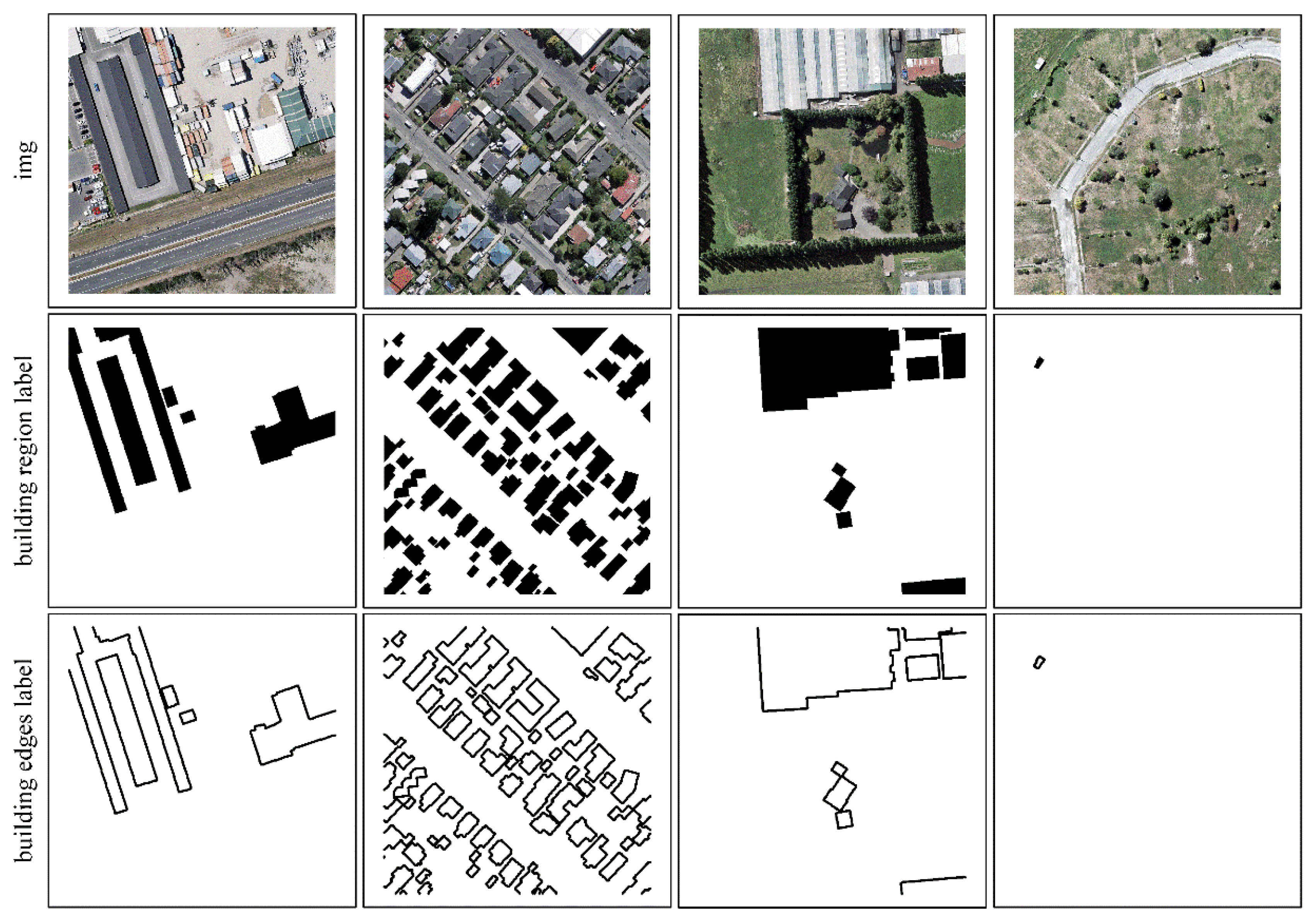
The WHU building dataset [57] contains two subsets of satellite and aerial imagery. The satellite dataset was classified into two subsets, containing 204 and 17,388 images, respectively. In this study, we used aerial imagery that covers 450 km2 of Christchurch in New Zealand, containing 8188, 512 × 512 pixel images. These images are involved in the down-sampling from 0.075 to 0.300 m. The dataset was divided into a training set (4736 images), a test set (2416 images), and a validation set (1036 images). We made several changes as the labels that did not contain buildings and the corresponding original images were eliminated (training set: 4317, test set: 1731, validation set: 1036). In addition, our label is a binary building region picture, which can be easily converted into a binary building edge picture by the Canny operator, as shown in Figure 4.
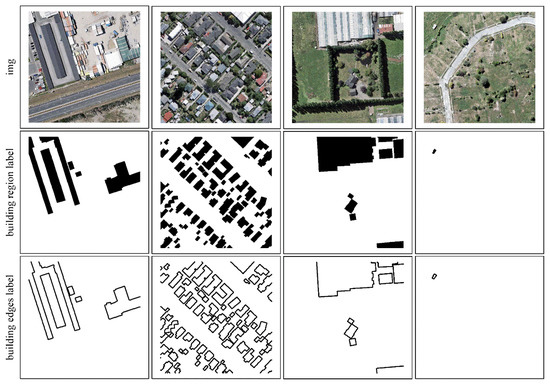
Figure 4.
The sample of WHU building dataset.
3.2. Experimental Setup
Owing to the small data volume of the Nanjing dataset, data enhancement methods were used to expand it, including up to down, left to right, and 90 rotations. To verify the effectiveness of this method, we compared it with several other models. As the essence of the semantic segmentation model and edge detection model is pixel-level prediction, we need to compare the method with the current mainstream semantic segmentation models such as FCN [29], U-Net [32], and Segnet [33]. It is compared with the edge detection models in the field of computer edges (such as HED [55], RCF [49], and DexiNed [56]) in a similar way.
We implemented and tested the model in PyTorch on a 64-bit Ubuntu 16.04 system equipped with an NVIDIA Quadro P4000 GPU. The model used the Adam optimizer, starting with a learning rate of 0.001, beta_1 of 0.9, and epsilon of 1e-8. As mentioned, the model was trained from scratch with no pre-trained weights. After each up-sampling stage, the feature map was up-sampled to the original image size through the bilinear interpolation, yielding six side outputs in total. Finally, the six side outputs were concatenated in the direction of channels to form a feature map with the same size as the input image, and the number of channels was six. Finally, a fusion result was generated through a 1 × 1 convolution. The seven output results were calculated with the label to calculate the loss, and the sum of the loss was used to complete the back propagation and parameter optimization.
3.3. Evaluation Metrics
The outputs of the model are probability maps that have the same spatial resolution as the input images. Each pixel of the predicted map had a value within the 0–1 range. The ground truth is usually a binary mask, in which each pixel is either 0 or 1 (1 indicates the background pixels; 0 indicates the edge object pixels).
To evaluate the methodological performance correctly, our approach virtually represents the deformation of semantic segmentation tasks. In particular, the four commonly used indicators in the traditional semantic segmentation were adopted, including intersection-over-union (IoU), recall, precision, and F1 score (F1). IoU is the ratio of the intersection and union of the prediction and the ground truth that is calculated (Equation (4)). Precision denotes the fraction of the identified “edge” pixels that are correct with the ground reference (Equation (5)). Recall expresses how many “edge” pixels in the ground reference are correctly predicted (Equation (6)). F1 is a commonly used index in deep learning, expressing the harmonic mean of precision and recall (Equation (7)).
where TP (true positive) is the number of pixels correctly identified with the class label “edge”, FN (false negative) indicates the number of omitted pixels with the class label of “edge”, FP (false positive) is the number of “non-edge” pixels in the ground truth that are mislabeled as “edge” by the model, and TN (true negative) is the number of correctly identified pixels with the class label of “non-edge”.
4. Results and Discussion
To assess the extraction quality results, several state-of-the-art models (Segnet [33], U-Net [32], FCN [29], RCF [49], HED [55], and DexiNed [56]) were used for the comparison with our approach using the two datasets. The edge detection model and the semantic segmentation model are essentially pixel-level predictions. Therefore, we also compared with the semantic segmentation model.
In the field of edge detection, non-maximum suppression is typically used for post-processing to refine the edge. We eliminated non-maximum suppression and implemented end-to-end model comparisons. That is closer to reality, while the contrast is more visible. Therefore, the following quantitative and qualitative analyses were based on the direct output of the model.
4.1. Nanjing Dataset Experiment
4.1.1. Comparison with Edge Detection Model
Table 1 shows the experimental results from our approach and the three comparison methods on the Nanjing dataset. As the most effective and popular models for edge detection purposes, RCF [49], HED [55], and DexiNed [56] achieved 45.33%, 55.94%, and 57.80% performance in the mIoU score, respectively. The IoU indicator is the total number of pixels that are predicted in the buildings/no-buildings edge category to the total number of pixels of all buildings/no-buildings edge categories. Given the imbalance of the samples, we used mIoU, which considers both. Two widely exploited evaluation metrics in the edge detection community were adopted. The fixed edge threshold (ODS) utilizes a fixed threshold for all prediction maps in the test set. The per-image best threshold (OIS) selects an optimal threshold for each prediction map in the test set. The F-measure of both the ODS and OIS was used in our experiments. As seen from Table 1, our approach outperforms the other models in terms of three indicators, suggesting that our approach has certain advantages for building edge extraction.

Table 1.
Experimental results on the Nanjing dataset with edge detection models.
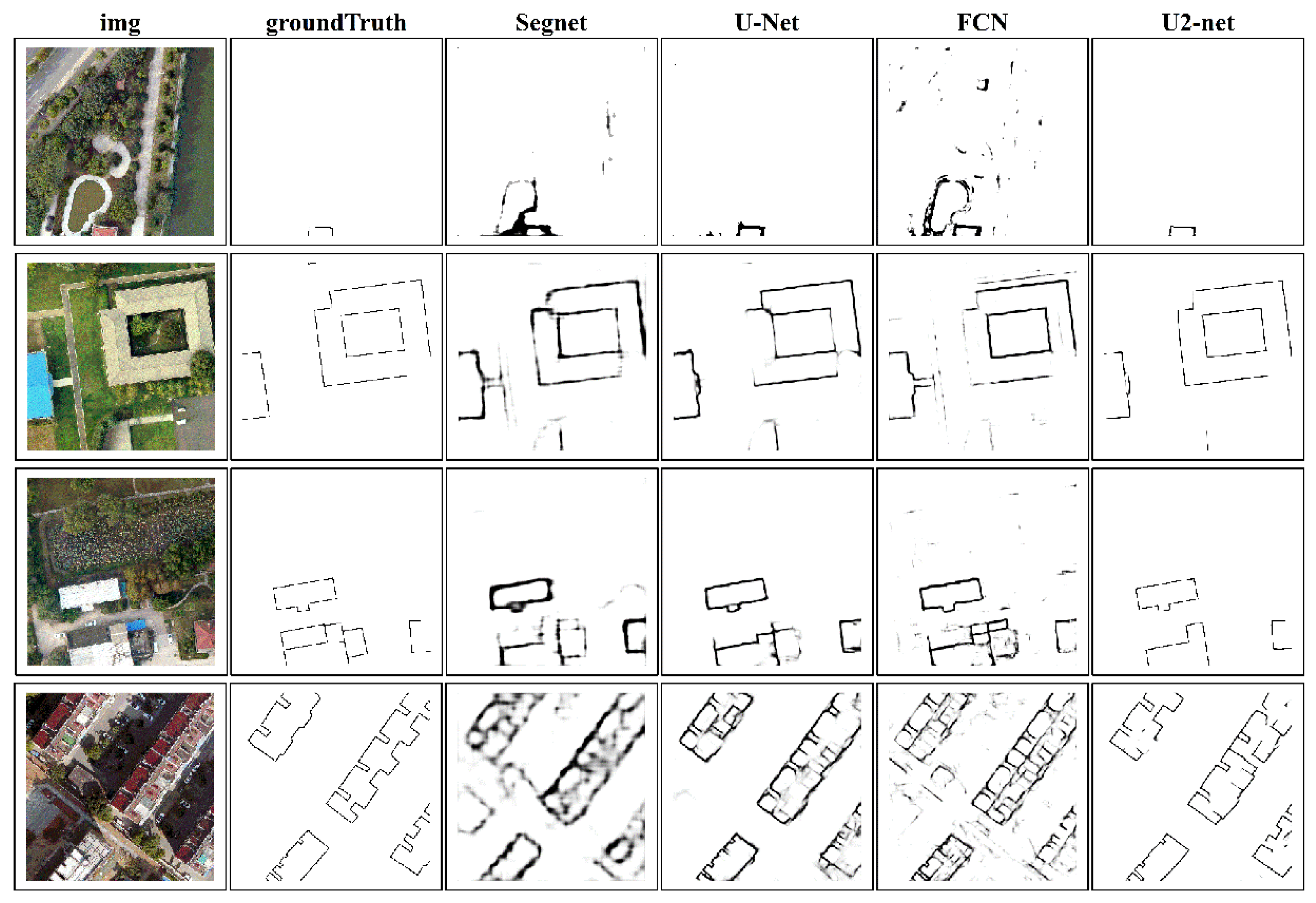
Figure 5 shows a qualitative assessment of the various models for the Nanjing dataset. We selected four representative buildings in the test set for the display. The 1st row of Figure 5 shows the results for small buildings that touch the image borders. We note that our approach has correctly extracted the building edges. Meanwhile, the other models are prone to erroneous extraction of river boundaries. The 2nd row shows the results for different types of buildings, (one type—solid blue, other type—hollow gray). As seen, our approach is suitable for the identification of the edge (both solid and hollow), while the other models only extract either solid building edges or hollow ones. The 3rd row shows buildings and a similar background and this task is challenging for all the models. We found that our approach can detect a relatively large building edge. Despite the fact that the small buildings similar to the background were ignored, our approach exhibited superior results compared with the other models. The 4th row shows that the proposed approach can work in extremely complex situations.

Figure 5.
Visual comparison of different edge detection models on Nanjing dataset.
4.1.2. Comparison with Semantic Segmentation Model
Although only few scholars have used the semantic segmentation model for edge detection, our experiment confirmed its suitability. In terms of ODS and OIS, our method has fundamental advantages over the semantic segmentation model. The results of these semantic segmentation models on the Nanjing test set are summarized in Table 2.

Table 2.
Experimental results on the Nanjing dataset with semantic segmentation models.
Similar to the above, four different building types were compared in Figure 6. The 1st row shows that both Segnet [33] and FCN [29] misinterpret the river margins for the building boundaries. Although the U-Net [32] correctly identified the building boundaries, they were insufficiently thin. The 2nd and 3rd rows show that our method can fully extract the building edges, also yielding cleaner results. The 4th row analysis indicates that the same conclusions can be made for complex buildings with irregular boundaries, thus underlining the effectiveness of our approach.
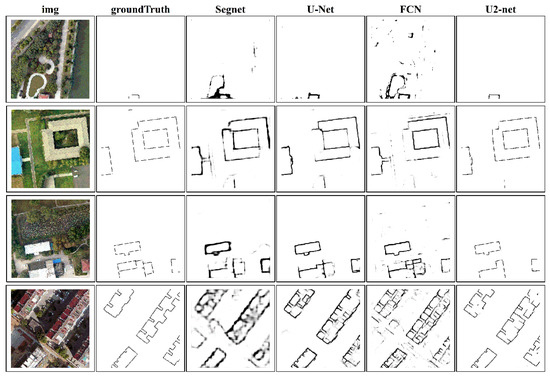
Figure 6.
Visual comparison of different semantic segmentation models on Nanjing dataset.
To summarize, we conducted comparative experiments using the semantic segmentation and edge detection models on the Nanjing dataset to verify whether our approach can yield better building recognition results. The experimental results showed that our method can provide a more complete and clean building edge. At the same time, we showed that the semantic segmentation model can obtain a clearer effect than the edge detection model with respect to the building edge. We emphasize that the semantic segmentation model does not consider the loss function for the sample imbalance problem, while the edge detection model does.
4.2. WHU Dataset Experiment
4.2.1. Comparison with Edge Detection Model
On one hand, the WHU dataset provides abundant training information. On the other hand, it contains larger data volume and different building types, thus posing additional challenges for building extraction purpose. A quantitative assessment of the various models on the WHU dataset is given in Table 3. Among the edge detection models, DexiNed [56] shows the best performance as it achieves 89.29, 89.54, and 62.22 on ODS-F1, OIS-F1, and mIoU, respectively. Our method exhibited slightly better performance compared to the other methods.

Table 3.
Experimental results on the WHU dataset with edge detection models.
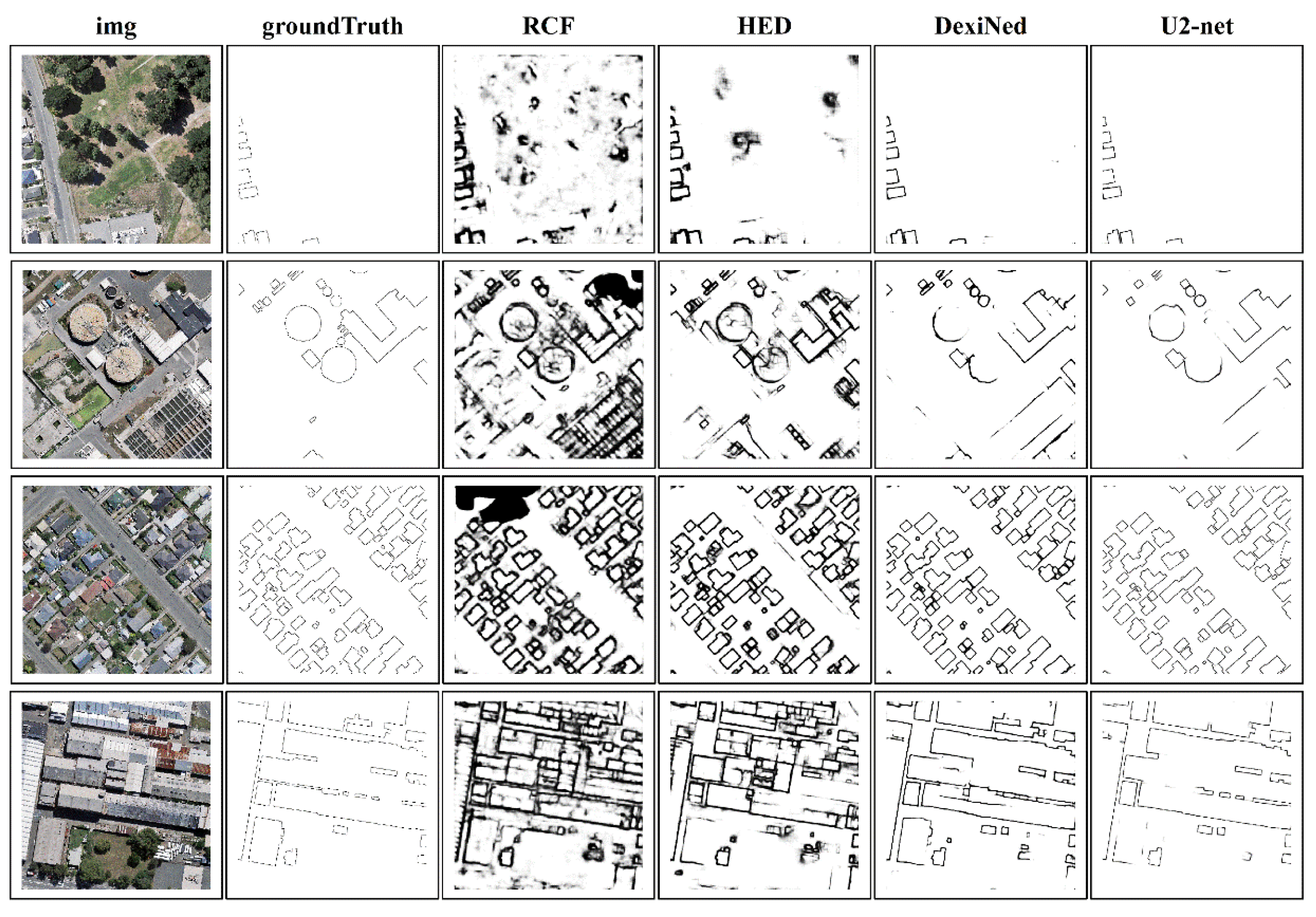
Four representative buildings were selected from the test set to qualitatively assess the experimental results on the WHU dataset (Figure 7). The 1st row shows the results of the small buildings, located close to each other and near the boundaries of the image. Although the three edge detection models can extract the building edge, there are some malignant phenomena in the extraction process that is, ultimately, not sufficiently accurate. The 2nd row illustrates the performance of the method with regard to the identification of the buildings of different sizes and shapes. As seen, the RCF [49] and HED [55] models are susceptible to interference with irrelevant information and the extraction results are not clean enough. However, the boundary extraction of circular buildings is more complete compared to DexiNed [56] and our method. The 3rd row confirms the strong ability of our method to extract dense, small building edges, while the 4th row shows the results for large and staggered buildings.
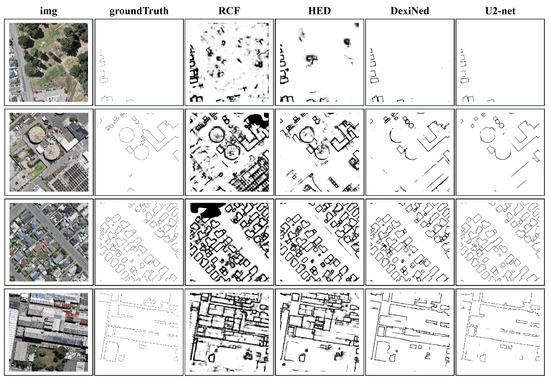
Figure 7.
Visual comparison of different edge detection models on WHU dataset.
4.2.2. Comparison with Semantic Segmentation Model
Likewise, we compared our results with the semantic segmentation model. A quantitative assessment of several methods on the WHU dataset is shown in Table 4. The experimental results indicated that Segnet [33] and U-Net [32] had similar scores on ODS-F1 and OIS-F1, and the score of mIoU of Segnet [33] was lower than that of U-Net [32], 5.04%. The indicators of the FCN [29] were low. Overall, these experiments confirmed that our method outperforms the other models with regard to these indicators.

Table 4.
Experimental results on the WHU dataset with semantic segmentation models.
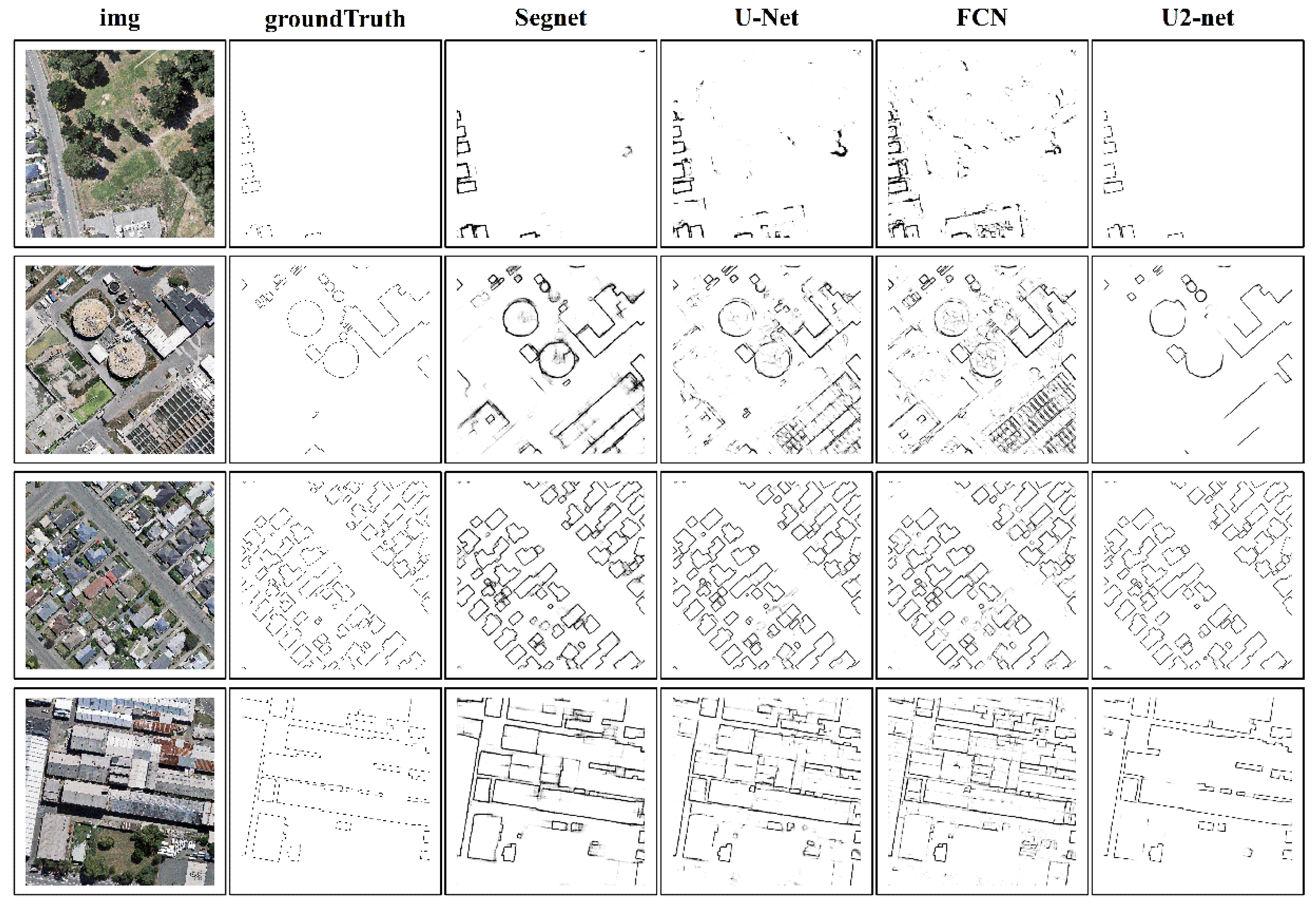
The results of the models on the WHU test set are shown in Figure 8. We selected four representative buildings in the test set as a representative example. In particular, Segnet [33] and U-Net [32], alongside our approach, yielded good results. Zhou [58] reported that Segnet [33] was based on an encoding–decoding structure, and the convolution kernel is mainly used for image feature extraction, which cannot maintain the integrity of the building. However, our experiments provide arguments that they all represent the encoding–decoding structures and provide more acceptable results than FCN [29]. The extraction results of Segnet [33] and U-Net [32] were not clean enough, and some edges were slightly thick. Meanwhile, our approach yielded more accurate results
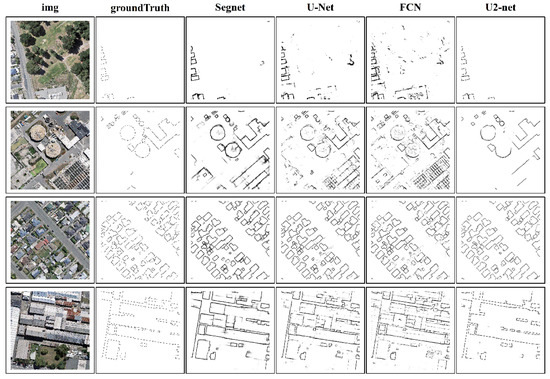
Figure 8.
Visual comparison of different semantic segmentation models on WHU dataset.
We conducted experiments on the WHU dataset in a similar way to the Nanjing dataset by applying the semantic segmentation model and edge detection, respectively. The experimental results confirm the applicability of the proposed method. We emphasize that in the domain of the computer edge detection (HED [55], RCF [49], and DexiNed [56]), sample imbalance will be considered. However, we empirically showed that the semantic segmentation model without the sample imbalance considered was better than the edge detection model with the sample balance. This finding requires further scientific investigation, whereas two cases of each model should be separately compared for explicit interpretation of this phenomenon. Moreover, in the domain of computer edge detection, non-maximum suppression (NMS) is used to optimize the results of the network output to retrieve thinner edges. Our experiment showed that NMS as a post-processing tool is not a prerequisite condition for acquiring accurate results.
Finally, we found that the indicators of the WHU dataset were much higher than those of the Nanjing dataset. We explain this finding by the presence of many buildings shaded by trees and the very irregular buildings in our data, which hampered manual annotation and model training. Furthermore, although we used data enhancement, the quantity is still only half that of the WHU dataset.
4.3. Loss Function for Clearer Edge
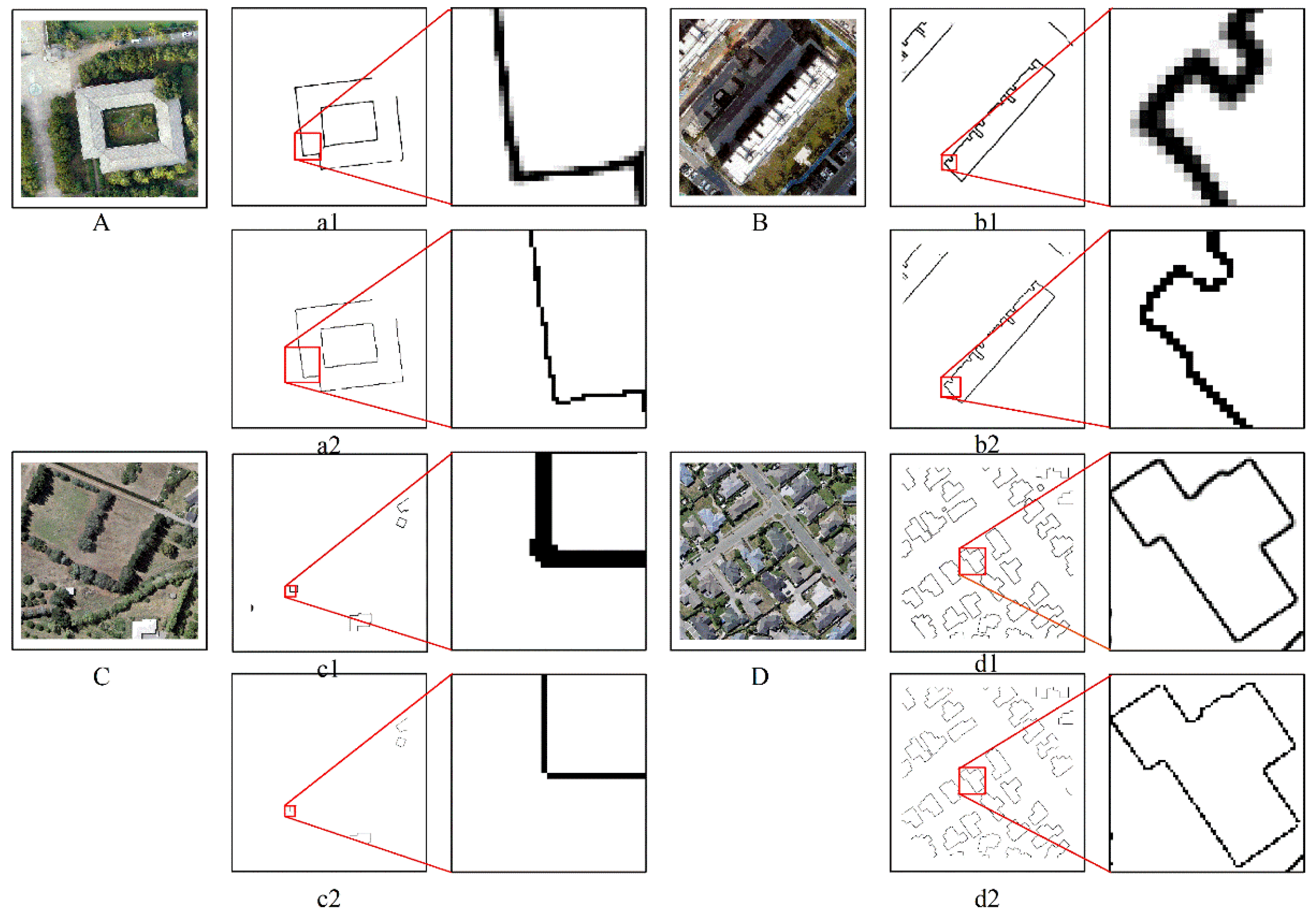
A dedicated comparison before and after the model modification is shown in Figure 9. Here, A and B are from two types of buildings in the Nanjing dataset (simple regular buildings and complex irregular buildings), while a1 and b1 are the edge detection results before model modification, and a2 and b2 are the results after the loss function modification of the corresponding models. Our modified loss function plays the role of the threshold segmentation and produces thinner building edges. C and D are two types of images from the WHU dataset. C is that buildings in the picture are sparse, and D is that the buildings in the picture are dense. Furthermore, c1 and d1 are the results before model modification, while c2 and d2 are the results after model modification. The comparison of different datasets and different types of buildings showed that after the model was modified (given the function of the threshold segmentation), the binary map is directly generated. At the same time, the edges of the buildings produced are also thinner.
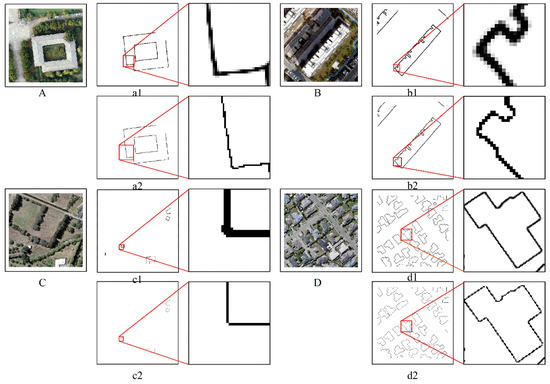
Figure 9.
Comparison of building edge details before and after model modification.
4.4. Application Prospect in Practical Work
To explore the application prospects of our findings, we implemented an image-to-image program. In simple words, we input a high-resolution remote sensing image of a non-fixed size and output its corresponding building edge map. The program completed a full workflow of image cutting, prediction, and splicing, thus realizing the automatic extraction of the building contour.
Figure 10 shows a remote sensing image of the Nanjing aerial data with a size of 13,669 × 10,931 and a resolution of 0.3 m in the same period as the training data. The final output and its corresponding edge map of the buildings are shown in the same figure. We selected five representative buildings for this analysis. For regular buildings, the edges can be predicted well, as shown in panels (a), (c) and (e) of Figure 10. For irregular buildings, most of them can predict their building edges, but there are pixel discontinuities in some building edge prediction results, as shown in panels (b) and (d) of Figure 10. As mentioned, this effect can emerge due to the lack of training data and as many buildings are shaded by trees, which hampers our training and marking.
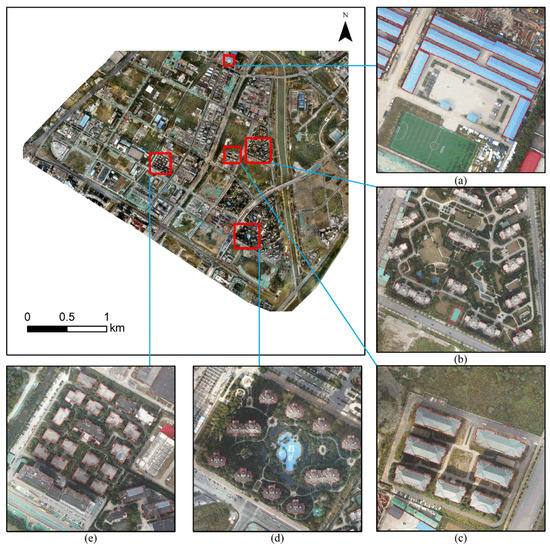
Figure 10.
Image-to-image prediction results on the Nanjing dataset (a–e).
As we did not have complete WHU image data, we mosaicked a part of the data in the test set into a large image with a size of 3072 × 2048 and a resolution of 0.3 m. We input the large image into the program to obtain the corresponding building prediction results, as shown in Figure 11. Five places were randomly selected for a more specific illustration. We found that the edges of the buildings can be extracted well, and only a few of the edges of buildings are discontinuous. The corresponding edge maps of the buildings can be obtained from the above two images of different sizes. Although there are few discontinuous edges of buildings, most of them can be predicted accurately, and the width of the predicted edges of buildings is sufficiently low. This solves the problem of processing large images in the memory that had been previously reported by Lu et al. [12,59]. Furthermore, this auspiciously provides a vital reference for the realization of the automatic edge extraction of buildings.
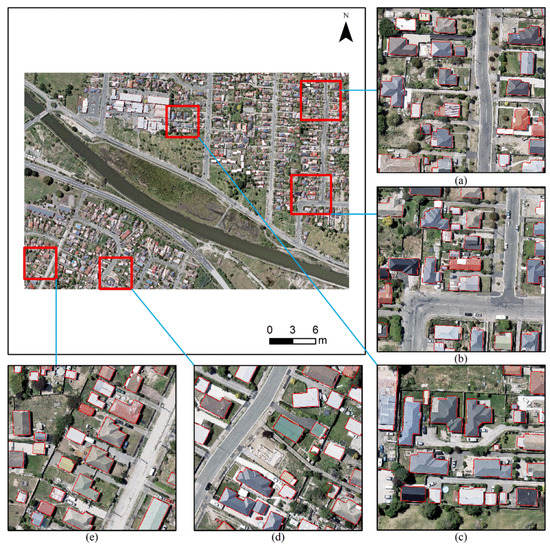
Figure 11.
Image-to-image prediction results on the WHU dataset (a–e).
5. Conclusions
This study explored a method for automated building edge extraction from remote sensing images and we used a semantic segmentation model to generate a binary map of the building outline. The U2-net model was used as the experimental model. We conducted two experiments: (a) the U2-net was directly compared with other semantic segmentation models (Segnet [33], U-Net [32], and FCN [29]) and edge detection models (RCF [49], HED [55], and DexiNed [56]) on the two datasets of WHU and Nanjing; and (b) the original binary cross-entropy loss function was replaced with a multiclass cross-entropy loss function in the U2-net. The experimental results showed that the modified U2-net stands out with three advantages for building outline extraction. First, it can provide a clearer and more precise outline without an NMS post-processing step. Second, the model exhibited better performance than the semantic segmentation models or the edge detection models. Third, the modified U2-net can directly generate a binary map of the building edge with a further refined outline. Overall, it is robust because it is somewhat immune to the sample imbalance problem. Moreover, an image-to-image method has clear prospects for practical applications in building edge extraction. In future, we plan to use more datasets to validate the modified U2-net and to further improve the model’s accuracy by incorporating the attention mechanism. This will ultimately open a window for the direct generation of vector polygons of building outlines by incorporating other nets such as the pointNet. Meanwhile, we also noted the recent achievements of graph convolutional networks (GCN) in remote sensing classification, for example, through the fusion of GCN and CNN to improve classification accuracy [37]. This provides us with a good paradigm, and the incorporation of the GCN for building edge extraction has aroused our interest, which needs further study.
Author Contributions
Conceptualization, X.L. and X.W.; methodology, X.W.; software, X.W. and D.C.; validation, X.W., W.L. and L.Z.; data curation, H.J. and W.Z.; writing—original draft preparation, X.W. and X.L.; writing—review and editing, X.L., W.L., L.Z. and D.C.; visualization, H.J. and K.Y.; supervision, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Xuzhou Science and Technology Key R&D Program (Social Development) under Project KC20172, the Postgraduate Research and Practice Innovation Program of Jiangsu Province (KYCX20_2369).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the developers in the TensorFlow community for their open-source deep learning projects. Special thanks are due to anonymous reviewers and editors for their valuable comments for the improvement of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, Y.; Gong, W.; Sun, J.; Li, W. Web-Net: A novel nest networks with ultra-hierarchical sampling for building extraction from aerial imageries. Remote Sens. 2019, 11, 1897. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.; Nevatia, R. Building detection and description from a single intensity image. Comput. Vis. Image Underst. 1998, 72, 101–121. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Hu, X.; Yang, B.; Tian, J. Editorial for Special Issue: “Remote Sensing based Building Extraction”. Rmote Sens. 2020, 12, 549. [Google Scholar] [CrossRef] [Green Version]
- Brunner, D.; Lemoine, G.; Bruzzone, L. Earthquake Damage Assessment of Buildings Using VHR Optical and SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2403–2420. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Zhang, X.; Luo, P. Transferability of Convolutional Neural Network Models for Identifying Damaged Buildings Due to Earthquake. Remote Sens. 2021, 13, 504. [Google Scholar] [CrossRef]
- Rashidian, V.; Baise, L.G.; Koch, M. Detecting Collapsed Buildings After a Natural Hazard on Vhr Optical Satellite Imagery Using U-Net Convolutional Neural Networks. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 9394–9397. [Google Scholar]
- Li, J.; Cao, J.; Feyissa, M.E.; Yang, X. Automatic building detection from very high-resolution images using multiscale morphological attribute profiles. Remote Sens. Lett. 2020, 11, 640–649. [Google Scholar] [CrossRef]
- Pham, M.-T.; Lefevre, S.; Aptoula, E. Local feature-based attribute profiles for optical remote sensing image classification. IEEE Trans. Geosc. Remote Sens. 2017, 56, 1199–1212. [Google Scholar] [CrossRef] [Green Version]
- Yao, J.; Meng, D.; Zhao, Q.; Cao, W.; Xu, Z. Nonconvex-Sparsity and Nonlocal-Smoothness-Based Blind Hyperspectral Unmixing. IEEE Trans. Image Process. 2019, 28, 2991–3006. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, L.; Waslander, S.L.; Liu, X. An end-to-end shape modeling framework for vectorized building outline generation from aerial images. ISPRS J. Photogramm. Remote Sens. 2020, 170, 114–126. [Google Scholar] [CrossRef]
- Zhao, W.; Persello, C.; Stein, A. Building outline delineation: From aerial images to polygons with an improved end-to-end learning framework. ISPRS J. Photogramm. Remote Sens. 2021, 175, 119–131. [Google Scholar] [CrossRef]
- Lu, T.; Ming, D.; Lin, X.; Hong, Z.; Bai, X.; Fang, J. Detecting building edges from high spatial resolution remote sensing imagery using richer convolution features network. Remote Sens. 2018, 10, 1496. [Google Scholar] [CrossRef] [Green Version]
- Izadi, M.; Saeedi, P. Three-Dimensional Polygonal Building Model Estimation from Single Satellite Images. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2254–2272. [Google Scholar] [CrossRef]
- Wang, J.; Yang, X.; Qin, X.; Ye, X.; Qin, Q. An Efficient Approach for Automatic Rectangular Building Extraction from Very High Resolution Optical Satellite Imagery. IEEE Geosci. Remote Sens. Lett. 2015, 12, 487–491. [Google Scholar] [CrossRef]
- Turker, M.; Koc-San, D. Building extraction from high-resolution optical spaceborne images using the integration of support vector machine (SVM) classification, Hough transformation and perceptual grouping. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 58–69. [Google Scholar] [CrossRef]
- Karantzalos, K.; Paragios, N. Recognition-Driven Two-Dimensional Competing Priors Toward Automatic and Accurate Building Detection. IEEE Trans. Geosci. Remote Sens. 2009, 47, 133–144. [Google Scholar] [CrossRef]
- Ahmadi, S.; Zoej, M.J.V.; Ebadi, H.; Moghaddam, H.A.; Mohammadzadeh, A. Automatic urban building boundary extraction from high resolution aerial images using an innovative model of active contours. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 150–157. [Google Scholar] [CrossRef]
- Attarzadeh, R.; Momeni, M. Object-Based Rule Sets and Its Transferability for Building Extraction from High Resolution Satellite Imagery. J. Indian Soc. Remote Sens. 2018, 46, 169–178. [Google Scholar] [CrossRef]
- Sellaouti, A.; Hamouda, A.; Deruyver, A.; Wemmert, C. Template-Based Hierarchical Building Extraction. IEEE Geosci. Remote Sens. Lett. 2014, 11, 706–710. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Pan, Z.; Xu, J.; Guo, Y.; Hu, Y.; Wang, G. Deep learning segmentation and classification for urban village using a worldview satellite image based on U-Net. Remote Sens. 2020, 12, 1574. [Google Scholar] [CrossRef]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Convolutional Neural Networks for Large-Scale Remote-Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 645–657. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Girshick, R. Fast r-cnn. In Proceedings of the Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. SSD: Single shot multibox detector. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016; pp. 21–37. [Google Scholar]
- Cao, F.; Liu, Y.; Wang, D. Efficient saliency detection using convolutional neural networks with feature selection. Inf. Sci. 2018, 456, 34–49. [Google Scholar] [CrossRef]
- Tan, J.H.; Fujita, H.; Sivaprasad, S.; Bhandary, S.V.; Rao, A.K.; Chua, K.C.; Acharya, U.R. Automated segmentation of exudates, haemorrhages, microaneurysms using single convolutional neural network. Inf. Sci. 2017, 420, 66–76. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Agravat, R.R.; Raval, M.S. Deep learning for automated brain tumor segmentation in mri images. In Soft Computing Based Medical Image Analysis; Elsevier: Amsterdam, The Netherlands, 2018; pp. 183–201. [Google Scholar]
- Han, J.; Zhang, D.; Cheng, G.; Guo, L.; Ren, J. Object detection in optical remote sensing images based on weakly supervised learning and high-level feature learning. IEEE Trans. Geosci. Remote Sens. 2014, 53, 3325–3337. [Google Scholar] [CrossRef] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, H.; Eom, K.B. Active Deep Learning for Classification of Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 712–724. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Cheng, G.; Wang, H.; Li, H.; Shi, L.; Pan, C. Building extraction from multi-source remote sensing images via deep deconvolution neural networks. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1835–1838. [Google Scholar]
- Bittner, K.; Adam, F.; Cui, S.; Körner, M.; Reinartz, P. Building footprint extraction from VHR remote sensing images combined with normalized DSMs using fused fully convolutional networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2615–2629. [Google Scholar] [CrossRef] [Green Version]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph Convolutional Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5966–5978. [Google Scholar] [CrossRef]
- Ji, S.; Zhang, C.; Xu, A.; Shi, Y.; Duan, Y. 3D convolutional neural networks for crop classification with multi-temporal remote sensing images. Remote Sens. 2018, 10, 75. [Google Scholar] [CrossRef] [Green Version]
- Farabet, C.; Couprie, C.; Najman, L.; LeCun, Y. Learning hierarchical features for scene labeling. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 1915–1929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vakalopoulou, M.; Karantzalos, K.; Komodakis, N.; Paragios, N. Building Detection in Very High Resolution Multispectral Data with Deep Learning Features. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1873–1876. [Google Scholar]
- Diakogiannis, F.I.; Waldner, F.; Caccetta, P.; Wu, C. Resunet-a: A deep learning framework for semantic segmentation of remotely sensed data. ISPRS J. Photogramm. Remote Sens. 2020, 162, 94–114. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; He, B.; Long, T.; Bai, X. Evaluation the performance of fully convolutional networks for building extraction compared with shallow models. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 850–853. [Google Scholar]
- Liu, P.; Liu, X.; Liu, M.; Shi, Q.; Yang, J.; Xu, X.; Zhang, Y. Building Footprint Extraction from High-Resolution Images via Spatial Residual Inception Convolutional Neural Network. Remote Sens. 2019, 11, 830. [Google Scholar] [CrossRef] [Green Version]
- Bischke, B.; Helber, P.; Folz, J.; Borth, D.; Dengel, A. Multi-task learning for segmentation of building footprints with deep neural networks. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1480–1484. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Semantic image segmentation with deep convolutional nets and fully connected crfs. arXiv 2014, arXiv:1412.7062. [Google Scholar]
- Li, E.; Xu, S.; Meng, W.; Zhang, X. Building extraction from remotely sensed images by integrating saliency cue. IEEE J.Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 906–919. [Google Scholar] [CrossRef]
- Shrestha, S.; Vanneschi, L. Improved fully convolutional network with conditional random fields for building extraction. Remote Sens. 2018, 10, 1135. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Cheng, M.-M.; Hu, X.; Wang, K.; Bai, X. Richer Convolutional Features for Edge Detection. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3000–3009. [Google Scholar]
- Li, Q.; Mou, L.; Hua, Y.; Sun, Y.; Jin, P.; Shi, Y.; Zhu, X.X. Instance Segmentation of Buildings Using Keypoints. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020. [Google Scholar]
- Zorzi, S.; Bittner, K.; Fraundorfer, F. Machine-Learned Regularization and Polygonization of Building Segmentation Masks. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 3098–3105. [Google Scholar]
- Qin, X.B.; Zhang, Z.C.; Huang, C.Y.; Dehghan, M.; Zaiane, O.R.; Jagersand, M. U-2-Net: Going deeper with nested U-structure for salient object detection. Pattern Recognit. 2020, 106, 12. [Google Scholar] [CrossRef]
- Qin, X.B. Available online: https://github.com/xuebinqin/U-2-Net (accessed on 15 July 2021).
- Tim. Available online: https://github.com/ecsplendid/rembg-greenscreen (accessed on 15 July 2021).
- Xie, S.; Tu, Z. Holistically-Nested Edge Detection. In Proceedings of the Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1395–1403. [Google Scholar]
- Poma, X.S.; Riba, E.; Sappa, A. Dense extreme inception network: Towards a robust cnn model for edge detection. In Proceedings of the Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020; pp. 1923–1932. [Google Scholar]
- Ji, S.; Wei, S.; Lu, M. Fully convolutional networks for multisource building extraction from an open aerial and satellite imagery data set. IEEE Trans. Geosci. Remote Sens. 2018, 57, 574–586. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, G.; He, G.; Long, T.; Yin, R.; Zhang, Z.; Chen, S.; Luo, B. Robust Building Extraction for High Spatial Resolution Remote Sensing Images with Self-Attention Network. Sensors 2020, 20, 7241. [Google Scholar] [CrossRef]
- Zhang, Z.; Schwing, A.G.; Fidler, S.; Urtasun, R. Monocular object instance segmentation and depth ordering with cnns. In Proceedings of the Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2614–2622. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).